摘要:非牛顿流体在微流控系统及生物医学等领域具有广泛应用. 采用分子动力学模拟方法, 以羧甲基纤维素钠分子和水分子构成的系统为研究对象, 模拟了不同剪切速度下羧甲基纤维素钠溶液的构型演变, 采用溶质分子的均方位移和近表面水分子层的相对剪切速度表征溶液黏度的变化, 着重分析了氢键作用对溶液黏度变化的影响. 结果表明: 羧甲基纤维素钠溶液中水分子与溶质分子相互吸引形成更致密的氢键网络, 使得溶液黏度增加. 当对溶液施加剪切作用时, 溶质分子上与碳相连的氢原子与水氧原子之间的径向分布函数峰值减小, 二者形成的氢键作用减弱. 在剪切作用下, 溶质分子运动加剧, 水分子对溶质分子运动的阻碍作用减小; 同时距剪切边界越近的水分子的移动速度越接近剪切速度, 随着距离增加, 水分子层的移动速度大幅度减小; 以上结果在宏观上可表现为体系的黏度降低. 剪切速度增加, 羧甲基纤维素钠溶液的剪切稀化现象愈加显著.
关键词: 非牛顿流体/
分子动力学/
剪切稀化/
氢键

English Abstract

全文HTML

--> --> -->

具有剪切稀化特性的非牛顿流体在微流控系统及生物医学等领域具有广泛应用, 其流变特性对特定功能的实现具有至关重要的影响^[1-4]. 对非牛顿流体剪切稀化特性的研究一直以来主要通过数学模型的建立加以表征. 例如, Jordi等^[5]通过突变剪切速率来确定不同分子量的聚丙烯酸酯溶液的流变特性, 从而确定其稳态黏度、启动黏度和触变行为, 结果表明, 其稳态黏度符合Ostwald-de Waele幂律流体模型; Laporte等^[6]在微通道气液两相流研究中, 采用改进后的幂律模型表征乳清蛋白分离物和黄原胶混合溶液的流变行为, 并通过改变黄原胶溶液溶质的含量对非牛顿流体在通道中的流型进行调控. Khan等^[7]在研究横向磁场和欧姆加热对一种不可压缩的非牛顿流体内能的影响时, 采用Carreau模型来表征流体的状态, 分析了非牛顿流体的径向速度和切向速度分量随幂律指数、雷诺数和韦伯数的变化情况. Roberts和Cox^[8]利用非牛顿流体Bingham模型分析了压力驱动下剪切稀化流体在弯曲通道中的速度分布, 推导出压力驱动的非牛顿流体绕二维同心环流动的速度剖面表达式.
随着数值模拟技术的发展, 对非牛顿流体流变特性的研究, 从宏观尺度向介观尺度深入. Wu等^[9]利用改进的格子玻尔兹曼方法模拟了幂律流体、Bingham流体和Herschel-Bulkley流体的非牛顿特性, 给出了它们流变特性的表达式, 并用泊肃叶流法验证了该改进方法的可行性. 结果表明, 初始屈服应力和幂指数对非牛顿流体的流变特性均有影响. Dong等^[10]建立了非牛顿流体两相流的格子玻尔兹曼模型, 在没有重力作用的情况下, 模拟了两相流在矩形粗糙通道内的流动, 证明了两相格子玻尔兹曼模型在非牛顿流体模拟中的可行性. Afrouzi等^[11]采用格子玻尔兹曼方法和边界拟合法, 研究了波纹通道中脉动非牛顿流体的流动, 分析了剪切稀化和剪切增稠非牛顿流体的流线、剪切应力等值线、回流区、表面摩擦系数和速度分布随时间和位置的变化. 结果表明, 界面摩擦系数和幂律指数成正比, 与雷诺数间接相关.
然而, 尽管已建立的模型在宏观和介观尺度上对实验现象进行了解释, 但是非牛顿流体的剪切稀化特性在微观尺度的合理解释还十分薄弱. 羧甲基纤维素钠(sodium carboxymethyl cellulose, CMC)是纤维素的羧甲基化衍生物, 是一种阴离子型高分子化合物, 易分散在水中形成透明的、具有剪切稀化特性的溶液. 由于这种离子化合物具有低挥发性、高导热性、低熔点和高溶剂容量的特点, 并可适用于多种溶剂, 在许多工业领域具有广泛应用^[12-16]. 大多数剪切稀化流体均由巨大的链状分子构成, 这种高分子溶质的分子量可达几千甚至百万. 在低流速或者静止时, 由于溶质分子互相缠结, 溶液黏度增大. 然而, 当溶液受到剪切时, 这些比较散乱缠结的链状分子受到流层之间的剪应力作用, 减少了链状分子的互相钩挂, 发生滚动旋转进而收缩成团, 呈现出剪切稀化的现象, 这种解释溶液剪切稀化现象的理论已经被大多数****所认同^[17,18]. 然而剪切稀化现象在微观尺度上的产生机理并不是十分清楚. 分子动力学(molecular dynamics, MD)模拟能够在微观尺度上揭示宏观现象, 是分析微观机理的有效手段^[19]. Graham^[20]利用MD方法空间和时间上分辨率高的特点, 研究了实验中难以精确观测到的聚合物流动诱导结晶现象, 并提出利用粗粒化模拟来解决聚合物长链无法快速计算的问题. 本文采用MD模拟的方法, 通过研究羧甲基纤维素钠的官能团与水分子之间的相互作用, 探讨羧甲基纤维素钠溶液的剪切稀化特性, 旨在揭示非牛顿流体剪切稀化现象的微观机理.

本文针对羧甲基纤维素钠分子与水分子构成的体系进行研究. CMC分子由相似的单体聚合而成的, 分子式为[C₆H₇O₂(OH)₂OCH₂COONa]_n, 实际中聚合度n大于200, 分子量由几千到百万^[4], 不同聚合度的CMC分子官能团的种类和数量占比一致. 为了能进行有效的模拟, 本文选取适当的聚合度来研究羧甲基纤维素钠溶液的剪切流变特性, 并通过密度计算验证该聚合度的合理性. 模拟采用Materials Studio 2018软件, 设定周期性边界条件.
2

-->

2.1.力场的选取与分子模型的建立

分子的能量随分子的构型变化而变化, 其能量可以看作构成分子的各个原子空间坐标的函数(分子力场函数), 分子力场参数来自于实验结果总结出的经验公式. 本文选取COMPASS力场, 其中分子力场函数广泛覆盖共价分子, 包括最常见的有机物、小的无机分子和聚合物. 该力场用一个基于库仑项和van der Waals项的离子模型来描述成键粒子, 不成键粒子间通过成对LJ 9-6势函数相互作用.
模型建立的过程为: 在Materials Studio中调取对应元素, 根据结构式设定CMC分子单体和水分子, 使用Build Polymers模块将CMC单体作为重复单元构建多个聚合度不同的CMC分子; 使用Forcite Calculation中的Geometry Optimization模块对这些分子进行优化, 基于力场COMPASS分配CMC中原子电荷, 静电力与范德瓦耳斯力都基于原子之间的LJ 9-6势函数, 最大迭代次数设为2000, 设定能量为2.0 × 10^–5 kcal/mol, 截断半径为1.0 × 10^–5 ?.
2 -->

2.2.分子聚合度的确定

CMC的分子量高达数百万, 构建如此大聚合度的分子会浪费大量的计算资源, 分析较低聚合度下纯CMC分子体系的密度稳定性可以反映聚合物的真实性质^[21]. 选取聚合度n分别为1, 2, 4, 6, 8, 10, 20, 30, 40的9种CMC分子各10个, 分子量分别为242, 484, 968, 1452, 1936, 2420, 4840, 7260, 9680. 选取的聚合度与实际情况有一定的差别, 原因是随着分子链长度的增加, 计算成本急剧上升. 对适度增加聚合度的短链进行详细的分子动力学模拟, 了解其关键的物理性质, 对后续研究长链的工作有指导意义^[20]. 使用Amorphous Cell Calculation模块构建9个仅含有CMC分子的纯CMC分子体系. 设置NPT系综, 保证分子数目不变, 系统的压强和温度保持不变, 温度设定为298 K, 对CMC溶液进行1000 ps平衡模拟, 时间步长为0.1 fs, 每2000步输出1帧模拟结果. 借助Forcite Analysis计算不同聚合度的纯CMC分子体系的密度.
2 -->

2.3.CMC分子与水分子的相互作用

溶液中分子的体系是庞大的, 在进行分子数量较多的仿真计算之前, 研究小范围内CMC分子与水分子的相互作用有助于剪切稀化机理的研究. 使用Amorphous Cell Calculation模块, 依次选取聚合度n为1, 2, 4, 6的CMC分子, 分别加入10, 20, 30, 40个水分子构建溶液体系. 与此同时, 构建仅含有相同数目水分子的体系作为对比参照. 对这些体系以NPT系综进行分子动力学模拟, 温度设定为298 K, 时间步长为0.1 fs, 模拟时间为1000 ps. 使用Lattices Parameters读取并计算平衡模拟后模型的体积, 对比含溶质分子的溶液模型和无溶质分子溶液模型体积的变化, 以分析CMC分子与水分子的相互作用.
2 -->

2.4.氢键分析和溶液的剪切模拟

CMC分子单体上包含两种氢原子, 分别为与碳链直接相连的氢原子(Hc)和与氧原子直接相连的氢原子(Ho). 其中Hc数量占总氢原子数量的79.1%, 如图1所示.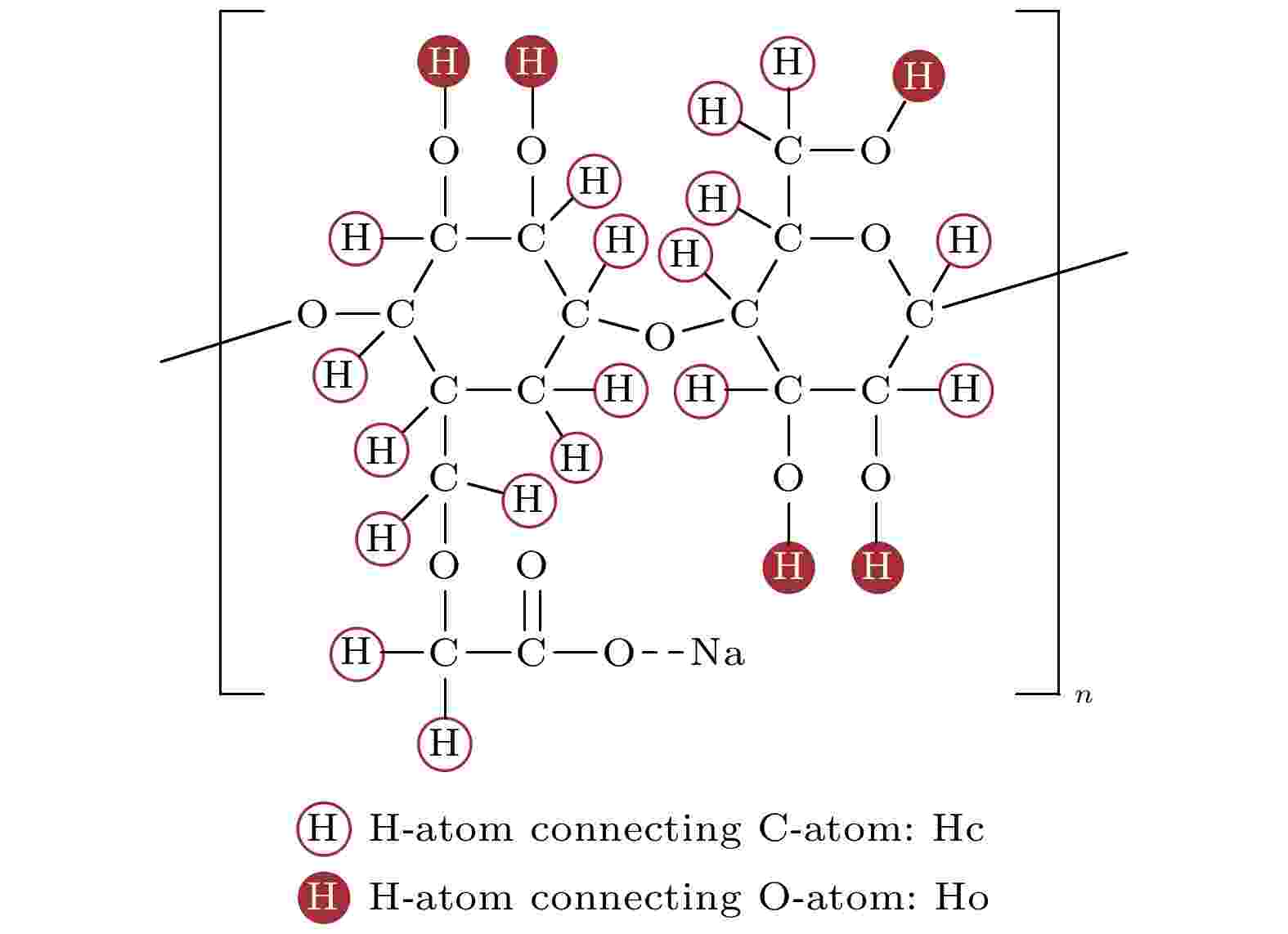
图 1 CMC分子结构示意图
Figure1. Molecular structure diagram of CMC.

由于研究的体系是CMC水溶液, 水分子之间的氢键数量占大多数, 通过氢键数量的变化难以判断CMC分子与水分子的相互作用. 因此, 选取CMC分子上Hc和水分子中氧原子Ow的相互作用, 分析CMC分子与水分子的氢键作用.
为构建CMC溶液体系, 选取18个聚合度分别为1, 2, 4, 6的CMC分子和4374个水分子建立模拟系统. 聚合度为1时的水溶液模型如图2所示, 此时体系中溶质的质量分数约为10%, 其中水分子以bond模型表示, CMC分子以CPK模型表示. 使用Amorphous Cell Calculation 模块下的Confined Shear建立剪切模拟的水溶液模型. 之后再采用Forcite Calculation 模块中的Geometry Optimization和Anneal对溶液体系进行能量最小化和退火优化, 其中退火优化初始温度设为300 K, 中间循环温度设为500 K, 每次斜坡中加热5次, 模拟1000步. 最后利用Confined Shear对体系进行剪切模拟, 模拟使用NVT系综, 保持盒子体积不变, 时间步长为0.1 fs, 总计500 ps. 受分子热运动和Materials Studio软件的限制, 剪切速度分别设置为0.1, 0.5, 1, 5, 10 ?/ps. 以铁原子作为剪切边界, 对溶液施加剪切作用, 如图3所示. 施加剪切作用后, CMC分子和水分子各自内部的强作用共价键无法破坏, 而水分子与CMC分子形成的氢键将发生改变, 本研究中采用径向分布函数对氢键作用的强度加以表征.
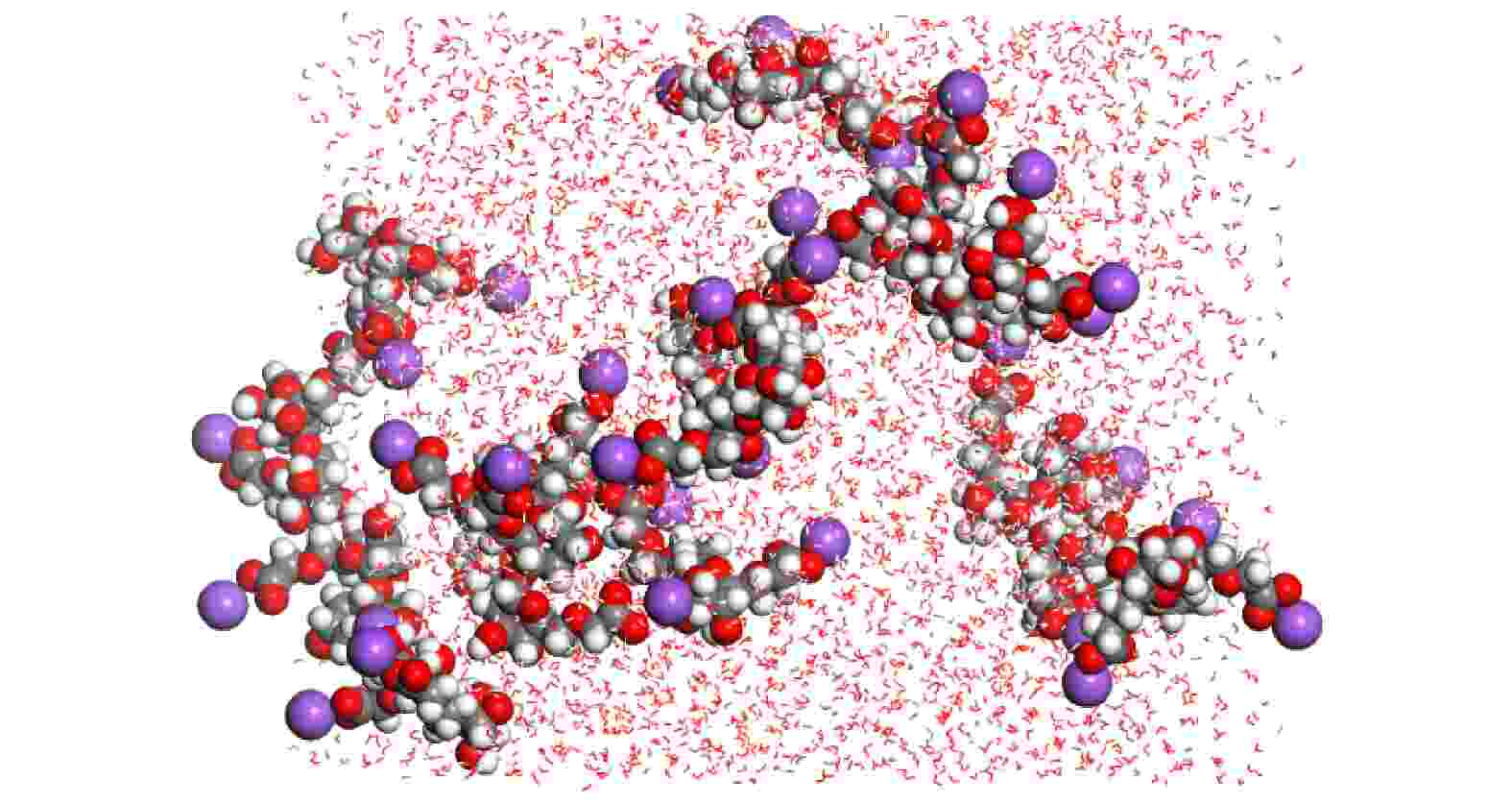图 2 CMC水溶液模型
Figure2. Model of CMC aqueous solution.

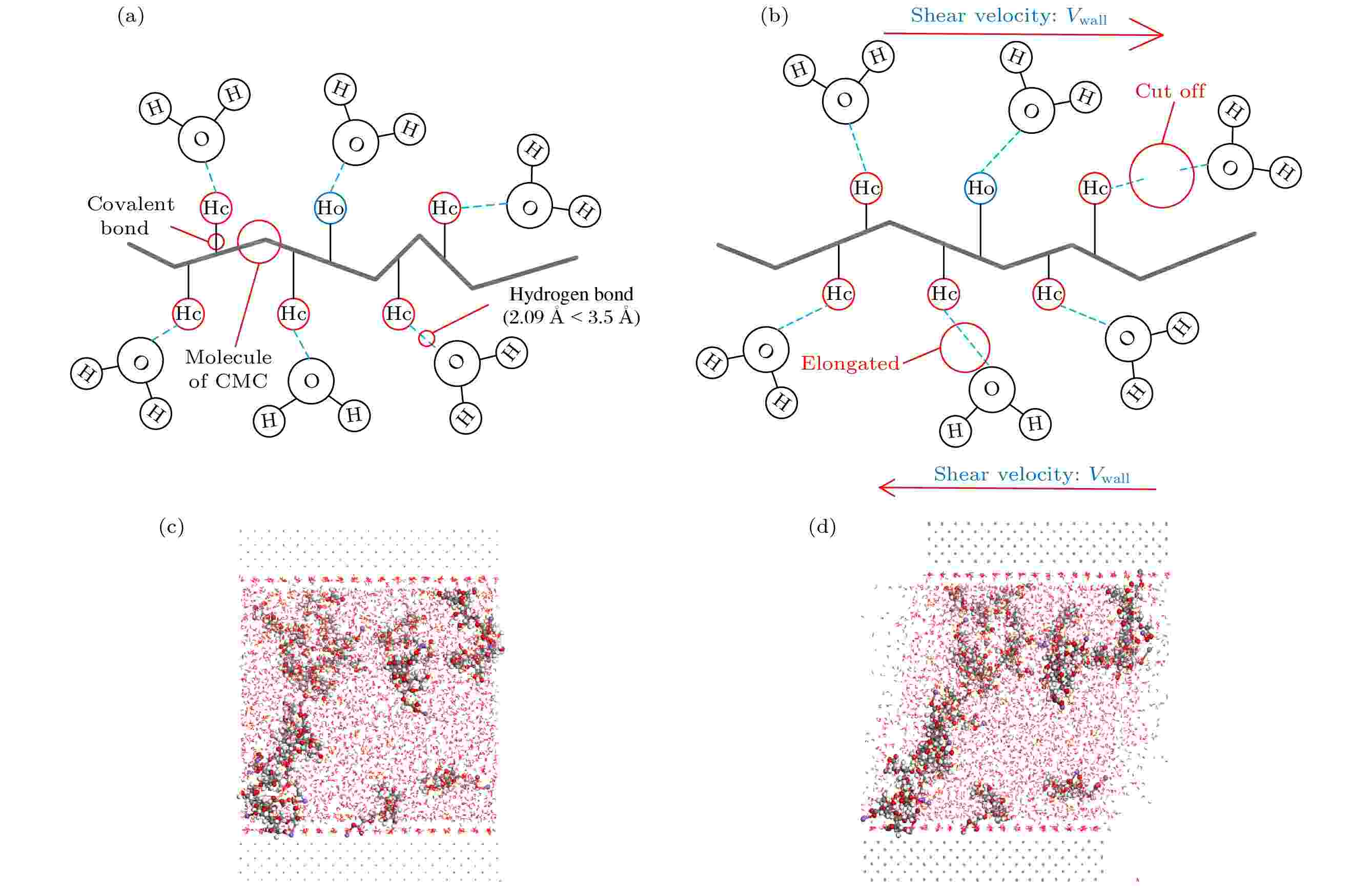图 3 剪切模拟模型　(a) 剪切运动前仿真系统示意图; (b) 剪切运动后仿真系统示意图; (c) 剪切运动前的仿真系统; (d) 剪切运动后的仿真系统
Figure3. Shear simulation model: (a) System before shearing; (b) system after shearing; (c) simulating configuration before shearing; (d) simulating configuration after shearing.

2

-->

3.1.分子模型的优化

通过COMPASS力场的约束, CMC分子和水分子单体达到能量最小化, 将构建的分子模型约束成符合力学定律的标准模型, 优化的分子模型和结构示意图如图4所示, 其中图4(a)—(d)对应1, 2, 4, 6四种聚合度.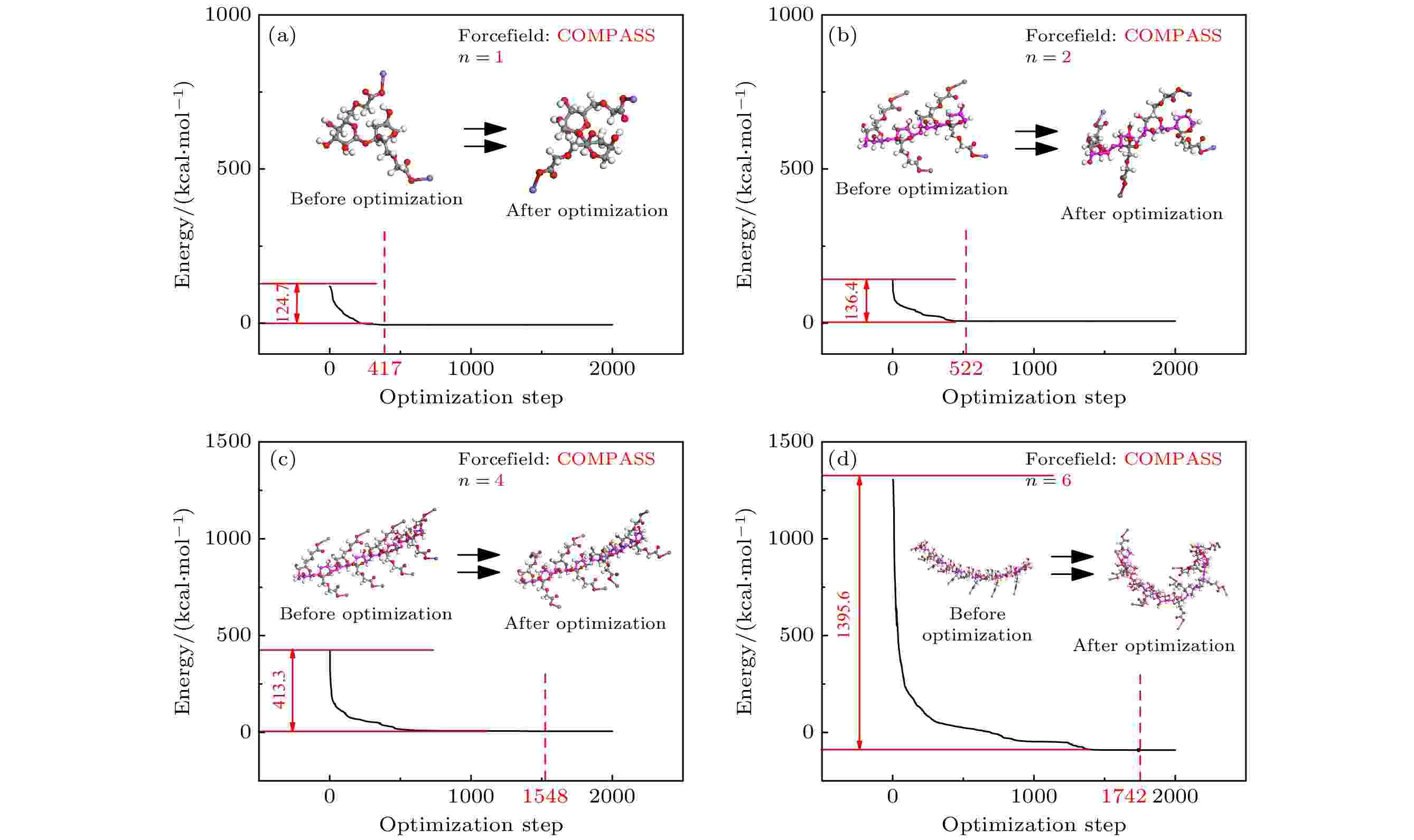
图 4 分子能量最小化和分子结构示意图　(a) n = 1; (b) n = 2; (c) n = 4; (d) n = 6
Figure4. Molecular energy minimization and molecular structure diagram: (a) n = 1; (b) n = 2; (c) n = 4; (d) n = 6.

由图4可以看出, 构建的分子在受到力场约束之前, 分子自身的能量较高, 经过力场约束, 分子的能量趋于最小化, 分子的构型由相对规则转变为不规则. 简单的分子仅需要较少的迭代次数就可以完成能量最小化, 随着分子结构复杂性的提高, CMC分子需要更多的迭代次数才能达到能量最小化; 分子能量的初始状态随机设置, 随着分子原子数和复杂程度的增加, 达到稳态所释放出来的能量越大, 即能量落差越大.
2 -->

3.2.羧甲基纤维素钠分子聚合度的确定

分子聚合度对体系密度的影响如图5所示, 随着CMC分子聚合度的增加, 纯CMC体系的密度变化不显著, 密度稳定在1.55 g/cm³左右(工业中密度约为1.6 g/cm³), 表明由聚合度小于10的CMC分子构成的溶液体系仍能反映CMC溶液的基本特征. 为了提高计算效率, 选择聚合度分别为1, 2, 4, 6的CMC分子进行剪切模拟.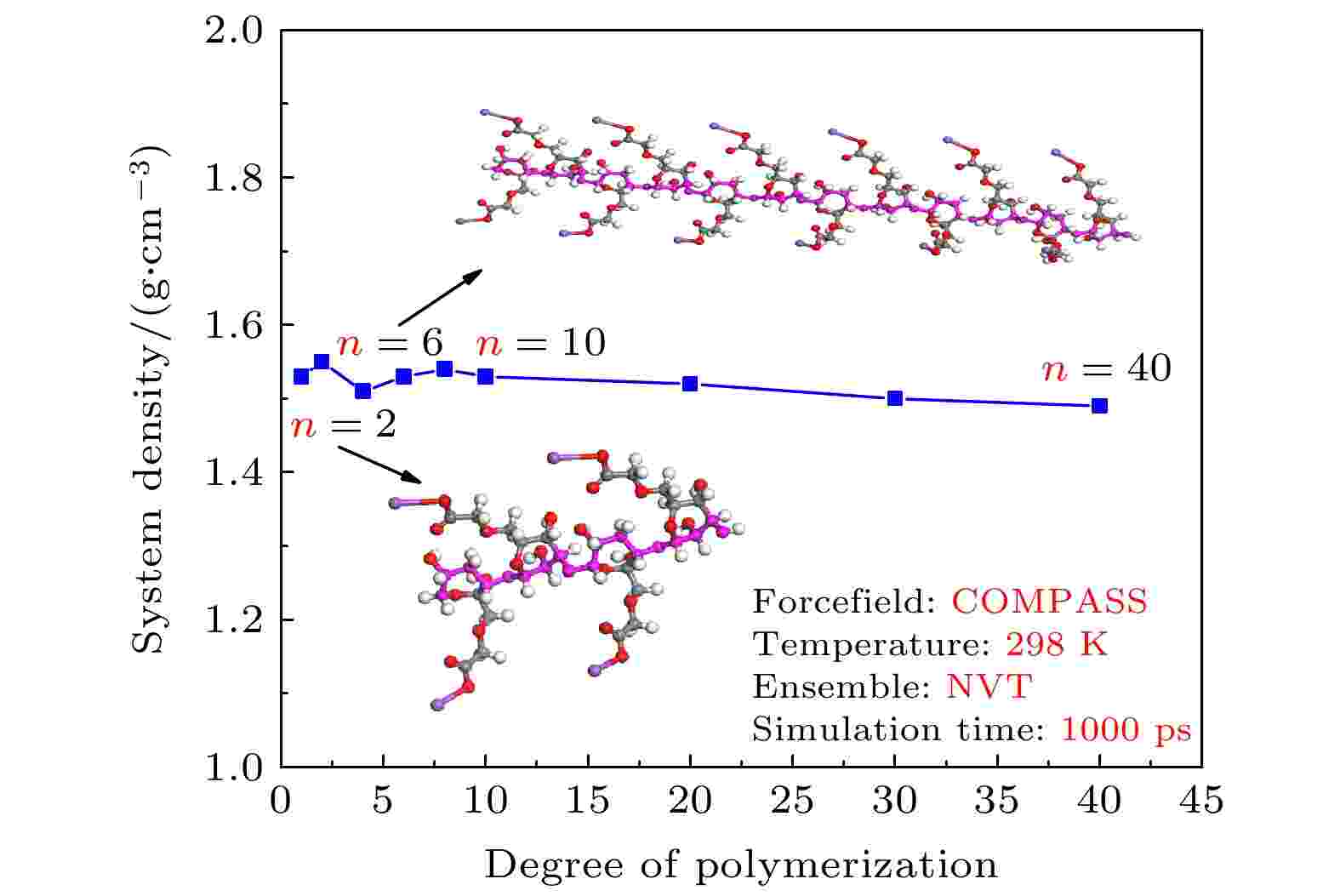
图 5 CMC分子聚合度对体系密度的影响
Figure5. Influence of CMC molecular polymerization degree on system density.

2 -->

3.3.单个CMC分子与水分子的相互作用

为了更加清晰地表征CMC分子与水分子的相互作用, 有必要研究单个CMC分子与水分子的相互作用. 图6为30个水分子和含有30个水分子和1个CMC分子(不同聚合度)体系的构型(蓝色为CMC分子上氢键的具体位置, 盒子边长为a, a的数值见 图6中).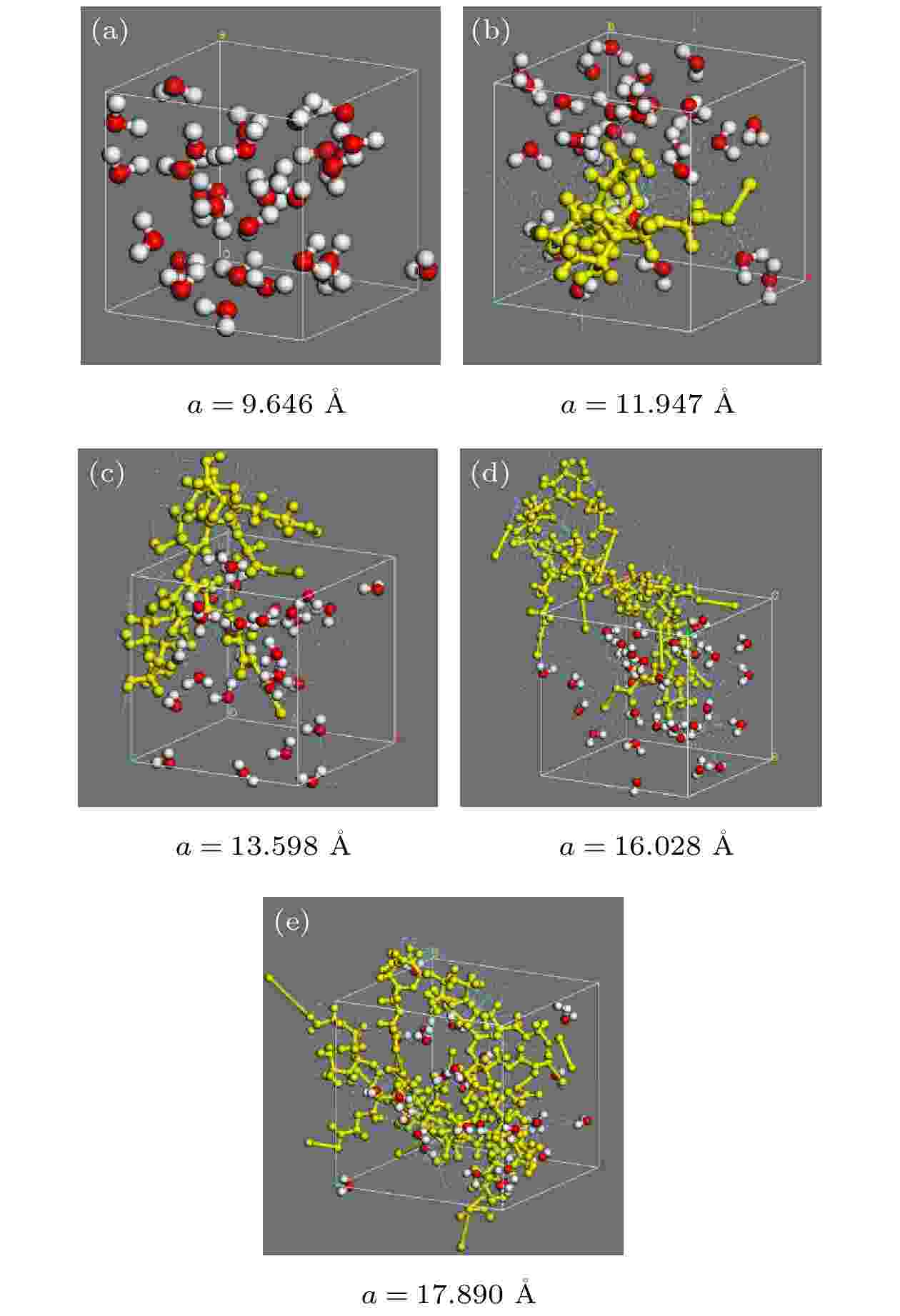
图 6 水分子和小范围CMC水溶液模型　(a) n = 0; (b) n = 1; (c) n = 2; (d) n = 4; (e) n = 6
Figure6. Models of H₂O molecule and small range CMC aqueous solution: (a) n = 0; (b) n = 1; (c) n = 2; (d) n = 4; (e) n = 6.

观察可以发现, 相对于没有溶质约束的自由水分子, 溶质与水之间的氢键的形成使水分子更加接近溶质分子, 水分子和CMC分子相互约束, 通过量化体系体积的变化可表征这种现象.
如图7所示, 仅含有水分子时(观察直线H及右侧纵坐标), 水分子的数量由10增加至40, 体系体积成倍增加. 含有1个聚合度为1的CMC分子的体系(观察直线A及左侧纵坐标), 水分子的数量同样由10增加至40, 体系体积增大, 但增大程度明显不及仅含有水分子的模型(曲线斜率越小, 增大程度越小). 含有20个水分子的体系体积相比于含有10个水分子的体系体积仅增加了27.0%; 30个水分子的体系体积相比于20个水分子的体系体积增加了21.3%, 以此类推; CMC分子聚合度为6时体系体积最大(观察直线D和左侧纵坐标), 但是随着水分子数量的增加, 体系体积增加的程度减小, 这是由于聚合度大时, CMC分子上的Hc原子增多, 官能团增多, CMC分子与水分子的氢键作用更强烈, 二者的约束作用更强. 这也体现了水分子与CMC分子相互作用是CMC分子上的官能团起主要作用.
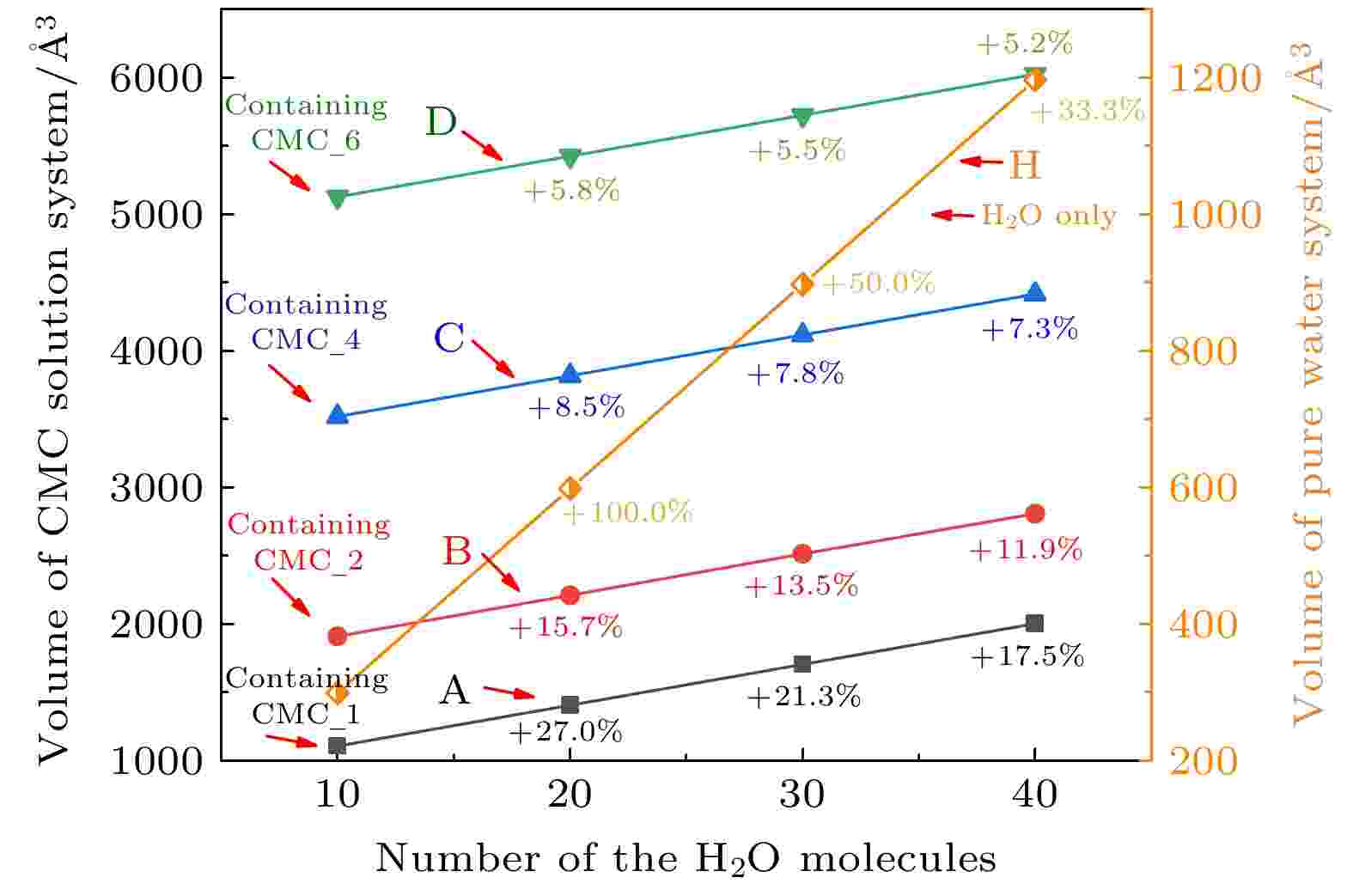图 7 水分子数量对CMC溶液和纯水体系体积的影响
Figure7. Influence of the number of water molecules on the volume of CMC solution and pure water system.

CMC分子与水分子相互作用形成氢键, 氢键作用使得水分子被拉拢聚集, 使体系更紧密, 溶液中的分子移动性变差, 使溶液黏度增加; 同时还发现, 随着CMC聚合度的增大, 体系体积的增速减小. 原因在于随着聚合度的增加, 体系内的Hc原子数量增大, Hc原子与水分子形成更多氢键使得体系更加紧密, 故水分子加入体系后, 体系体积变化的速率减小.
可以认为, CMC水溶液的黏度变化的微观原因在于水分子和CMC分子形成的氢键作用, 这种作用越强, 溶液体系越紧密, 表现出的黏度越大.
2 -->

3.4.剪切作用对氢键的影响

从以上的分析可以看出, 氢键作用决定溶液的黏度. 因此, 本节对剪切作用对分子构型和氢键的影响进行分析. 分析Hc周围水分子上的氧原子密度可得到二者的相互作用, 即分析Hc-Ow的径向分布函数.
径向分布函数g(r)的物理意义可以解释为在一个中心原子A周围距离为r处, B原子的局部密度相对于本体密度的比值. “局部密度”指A原子附近(r值小)的B原子的分布密度, “本体密度”指距A原子较远(r值大)的B原子的分布密度. 局部密度不同于系统的本体密度, 但与A原子距离远时应与本体密度相同. 简言之, 径向分布函数是对距参考粒子A距离为r处找到粒子B的相对概率的计算^[22].
径向分布函数g(r)的表达式为

$g\left( r \right) = \frac{{{\rm{d}}N}}{{4\rho {\pi ^2}}}, $

其中, dN为与原子A的距离为r到r + dr之间的分子数目, ρ为原子B的平均密度.
溶液中Hc-Ow的径向分布函数如图8所示. 可以看出, Hc-Ow的径向分布函数中2.07 ? < 3.5 ?处存在唯一峰值, 这说明在Hc原子周围氢键作用范围内存在水分子上的氧原子, 加之二者之间不可能发生化学反应, 即未发生电子交换, 故这种相互作用被认为是氢键作用^[23].
图 8 Hc-Ow径向分布函数
Figure8. Hc-Ow radial distribution function.

当剪切运动开始时, 径向分布函数的变化如图9所示. 以剪切速度1 ?/ps为例, 与相对静止状态作出的Hc-Ow径向分布函数的峰值对比. 相对于静止状态, 4种CMC分子构成的溶液体系在剪切运动后在2.07 ?处的峰值都有明显的下降, 说明Hc与Ow的氢键作用在剪切运动后有所减弱; CMC分子聚合度不同, 峰值位置不变, CMC分子的聚合度越大, 峰值的数值越大, 这说明官能团数量增加, 更多的水分子被吸引, 形成更多的氢键.
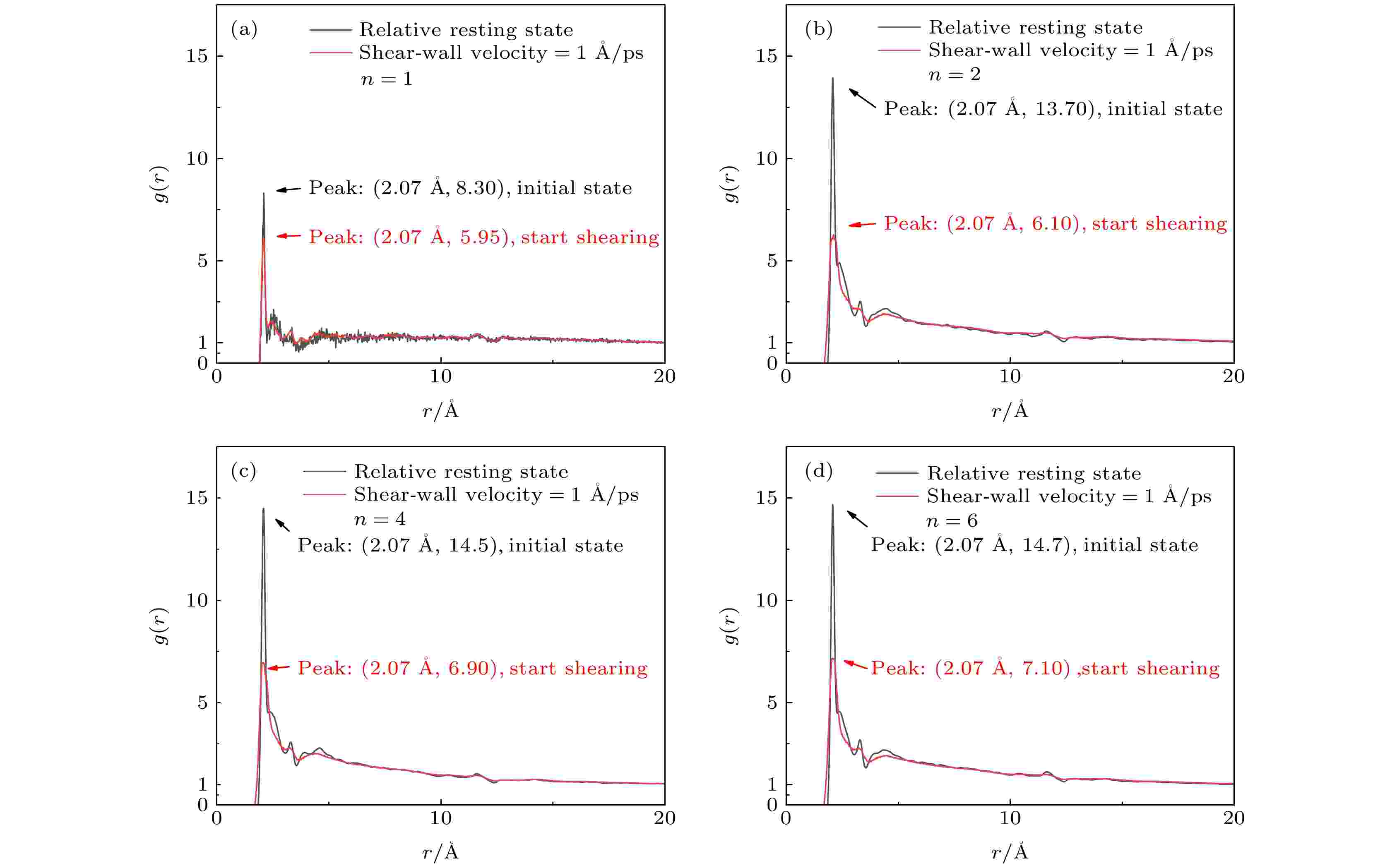图 9 开始剪切后Hc-Ow的径向分布函数与相对静止状态的对比　(a) n = 1; (b) n = 2; (c) n = 4; (d) n = 6
Figure9. Comparison between the radial distribution of Hc-Ow and the relative static state after shearing: (a) n = 1; (b) n = 2; (c) n = 4; (d) n = 6.

增加剪切速度后, 2.07 ?处峰值变化结果如图10所示. 与上文分析一致, CMC分子聚合度大时, 峰值的数值总体大于聚合度小的CMC分子. 当剪切运动开始时, 所有溶液体系在2.07 ?处的峰值都大幅度下降, 这说明剪切稀化流体在克服剪切变化阈值后, 黏度变化是最大的(模拟中剪切速度由0 ?/ps直接增大至0.1 ?/ps, 未考虑实验中黏度不变的区域), 随着剪切速度的增加, 峰值小幅度减小.
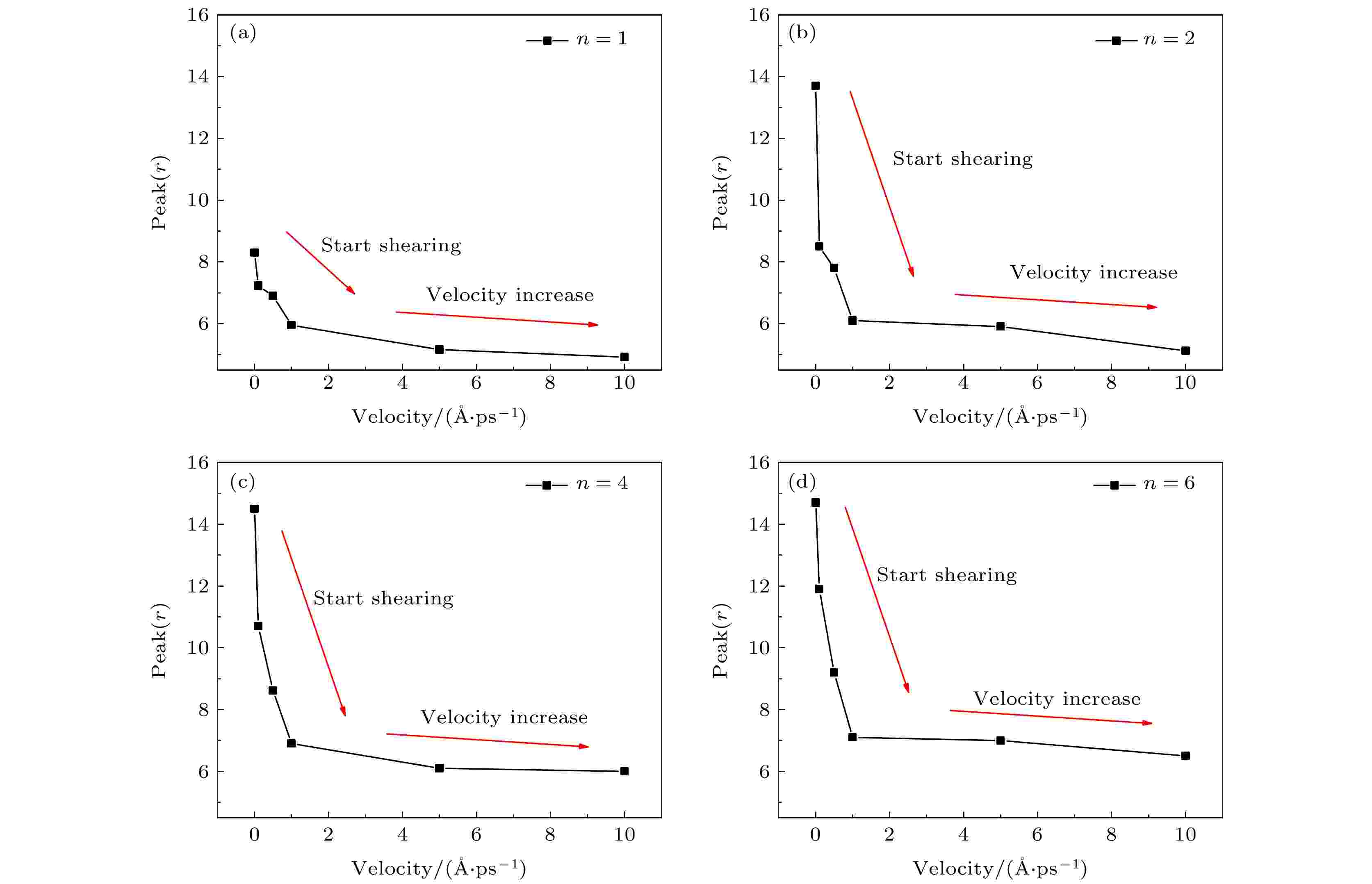图 10 Hc-Ow径向分布函数峰值随剪切速度的变化　(a) n = 1; (b) n = 2; (c) n = 4; (d) n = 6
Figure10. Variation of the peak value of Hc-Ow radial distribution function with shear rate: (a) n = 1; (b) n = 2; (c) n = 4; (d) n = 6

Hc-Ow始终存在一个位于2 ?左右的峰值, 即氢键作用. 当剪切运动开始, 峰值大幅度下降; 随着剪切速度的增加, 峰值不断减小. 这表明剪切运动和剪切速度的增加减少了氢键的数量, 但氢键的作用区域几乎不变. CMC分子与水分子的氢键作用减弱, 使得CMC分子和水分子具有更大的流动性, 因此溶液的黏度降低.
2 -->

3.5.溶液黏度的变化

通过溶质分子和水分子的相互作用可定性分析溶液的黏度变化. 本节通过分析CMC分子的位置变化, 即位移特性及近表层水分子的移动速度, 探讨溶液的黏度变化.
在剪切过程中, 观察到溶液中的各个分子状态是不同的, 如图11所示. 溶液中的水分子按受力状态可划分为四类, 第一类为与CMC分子形成氢键的水分子(例如分子1); 第二类为与剪切边界存在相互作用并吸附在剪切边界上的水分子(例如分子2); 第三类为既吸附在剪切边界上又与CMC分子形成氢键的水分子(例如分子3), 这种水分子占少数; 第四类为游离在溶液中的水分子, 只与周边水分子存在相互作用(例如分子4). 将溶质分子分为两种(不考虑CMC分子之间的相互作用), 第一种为只与水分子有相互作用的CMC分子(例如分子α); 第二种为通过自身的钠离子与剪切边界上的铁原子相互作用吸附在边界上的CMC分子(例如分子β), 还观察到β分子能通过与水分子3的相互作用来吸附在剪切边界上.
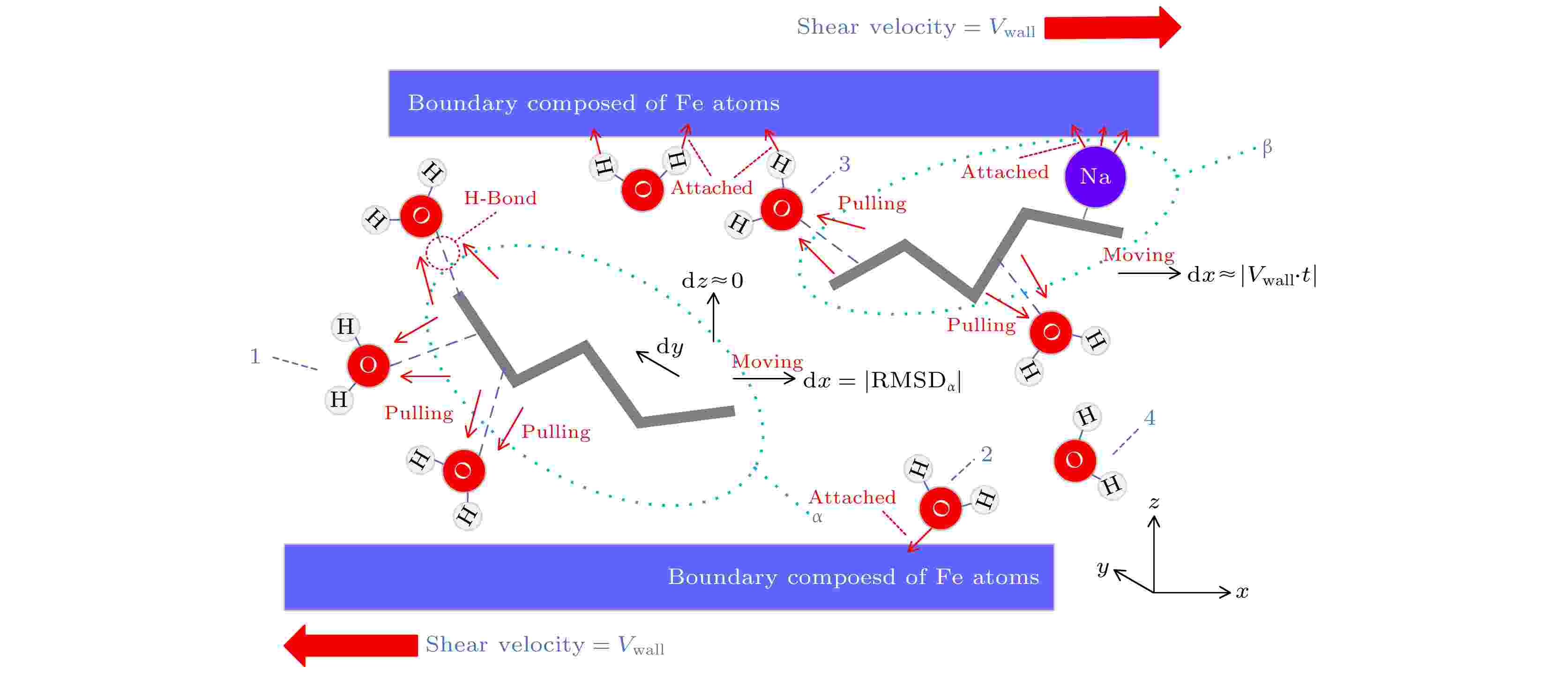图 11 剪切状态下溶液中分子的受力状态示意图
Figure11. Stress state diagram of molecules in solution under shear state.

溶液中分子的位移特性可以通过均方位移(MSD)来表示:

${\rm{MSD}} = \langle {\left| {r(t) - r\left( 0 \right)} \right|^2}\rangle ,$

其中, r(0)为分子的初始坐标, r(t)为分子位置坐标函数, 均以分子的几何中心作为分子的坐标.
由于剪切边界只在x方向移动, 溶液分子在z方向上的位移受到限制, 计算结果表明, α分子和β分子在z方向上的位移dz ≈ 0; y方向上的位移dy较少, 且不存在明显规律. 分析x方向上的位移dx, 对于β分子, 观察到其位移基本与剪切边界同步, 故认为其dx约为|V_wall·t| (t为运动时间), 氢键作用对于β分子在x方向上的位移影响不大. 对于α分子, 其在x方向上的位移变化显著, 且与水分子1的相互作用较为明显, 故重点分析此类分子在x方向上的位移.
为了得到α分子在剪切过程中水平方向的位移量, 进而分析其位移特性, 计算了两个聚合度不同的体系中每个α分子x方向的MSD_α曲线后对其数值进行开方并求和:

${\rm{RMS}}{{\rm{D}}_{\rm{\alpha }}} = \frac1{{{N_{\rm{\alpha }}}}}{{\sum\limits_{i = 1}^n {{{\sqrt {{\rm{MSD}}} }_x}} }},$

其中N_α为α分子的个数.
对于不同剪切速度下的溶液体系, 聚合度为1和6的α分子的RMSD_α曲线如图12所示.
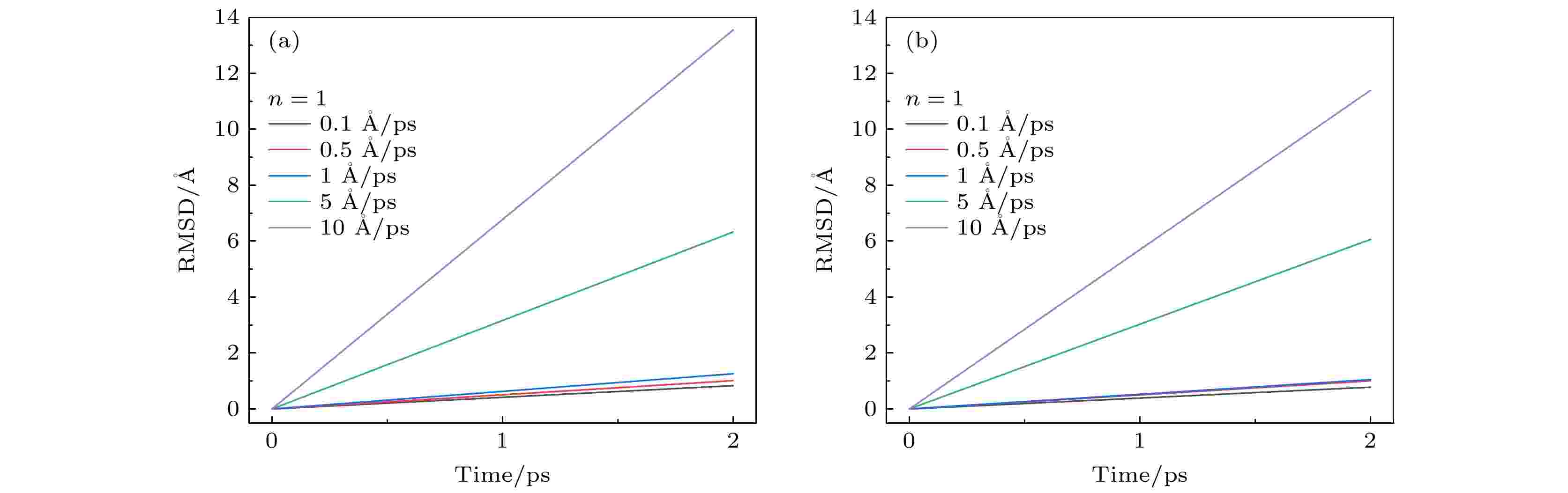图 12 不同剪切速度下CMC分子的RMSD_α曲线　(a) n = 1; (b) n = 6
Figure12. RMSD_α curves of CMC molecules at different shear rates: (a) n = 1; (b) n = 6.

图12中曲线的纵坐标为CMC分子在溶液中的水平位移dx, CMC分子在相同的时间内移动的距离越大, CMC分子运动越剧烈, 间接反映出溶液黏度越低.
对于两种聚合度的溶液体系, 剪切速度越大, CMC分子的移动速度越快, 一定时间内的位移越大, 这表明CMC分子在剪切速度增大时更容易在溶液中运动, 说明第一类和第三类水分子对其的束缚减少, 二者之间的氢键作用减弱, 溶液出现了剪切稀化现象, 这与上文对不同剪切速度下氢键作用变化的分析结果一致; 同时发现, 对于这两类不同聚合度的CMC溶液, 当剪切速度由0.1 ?/ps增加10倍至1 ?/ps时, 一定时间内的位移量分别增加了1.51倍和1.35倍. 当剪切速度由0.1 ?/ps增加100倍至10 ?/ps时, 位移量分别增加了10.76倍和10.83倍, 这表明溶质分子的位移与剪切速度呈非线性关系; 相对于聚合度为1的CMC分子, 聚合度大的CMC分子在一定时间内的水平位移更小, 这说明其受到了更多第一类和第三类水分子的阻碍, 与周边水分子形成了更多的氢键, 这与上文分析其拥有更多官能团导致其Hc-Ow径向分布函数峰值数值较大, 氢键作用较强的分析结果一致.
为进一步分析溶液中氢键作用对溶液黏度的影响, 本文还分析了水分子层和剪切边界的相互作用.
图13为CMC聚合度为1的体系在剪切速度为1 ?/ps的剪切作用下的变化情况, 简化溶液体系, 仅保留Ow和铁原子坐标信息, 通过分析表层原子Fe_L1与溶液中水氧原子Ow的径向分布函数RDF (Fe_L1-Ow)可知, 水分子在剪切边界表面分层分布, 以RDF的波谷值作为近表层水分子分层依据, 可获得OL1, OL2, OL3三层水分子层, 取体相中厚度为2.5 ?的水分子层为体相层OL4. OL1为吸附层, 移动速度与剪切边界相同. 通过计算每一层水分子x方向的均方位移得到了每一层Ow的平均水平运动速度v_OL1 = 1.00 ?/ps, v_OL2 = 0.11 ?/ps, v_OL3 = 0.09 ?/ps, v_OL4 = 0.07 ?/ps. 根据牛顿定律和体系几何尺寸推算出牛顿流体的情况下4层水分子的平均移动速度为v_NOL1 = 1.00 ?/ps, v_NOL2 = 0.92 ?/ps, v_NOL3 = 0.82 ?/ps, v_NOL4 = 0.45 ?/ps, 除吸附层外, CMC溶液的水层速度均小于牛顿流体的水层速度, 体现了CMC溶液的非牛顿特性.
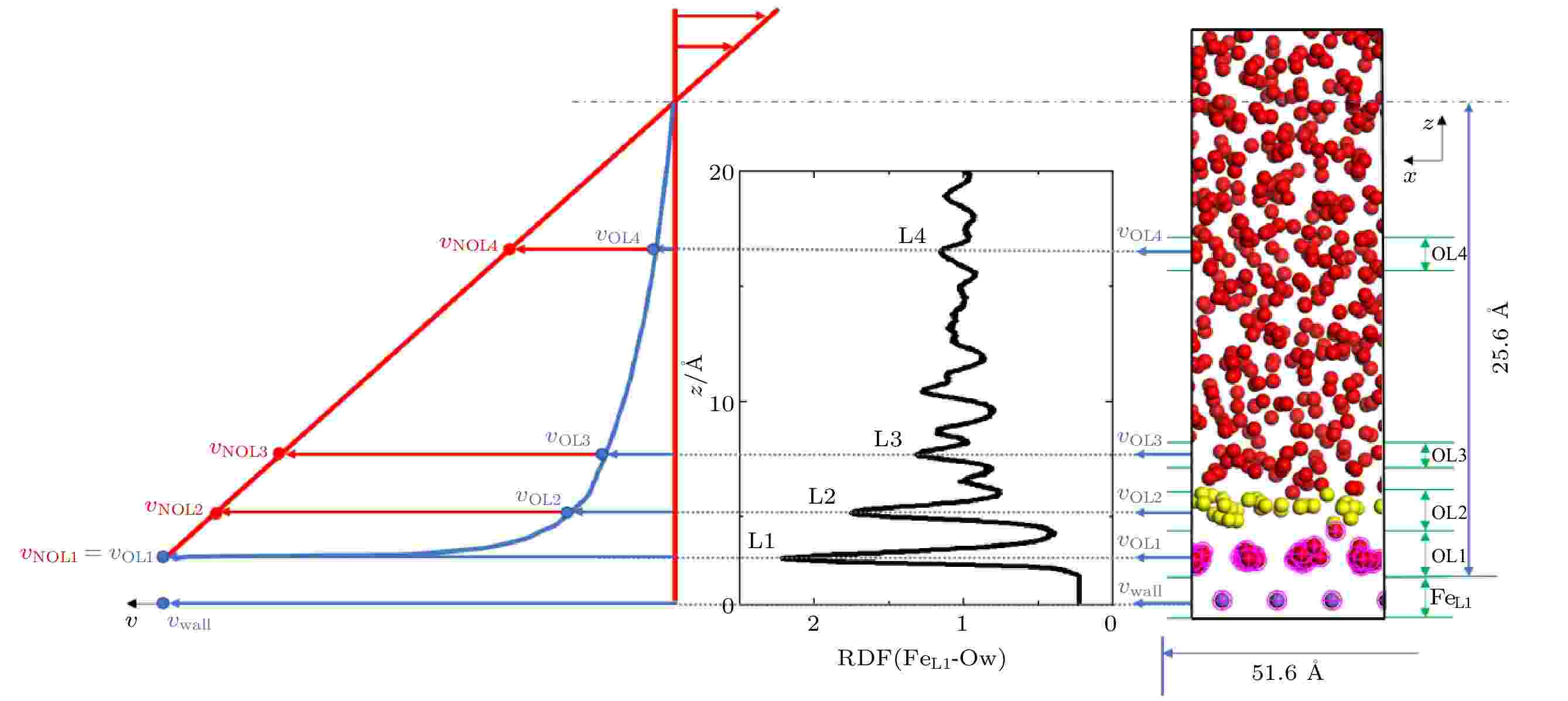图 13 水分子层的速度分布图及Fe_L1-Ow径向分布函数
Figure13. Velocity distribution diagram of water molecular layer and Fe_L1-Ow radial distribution function.

以类似的方法研究了不同剪切速度下的体系, 对于CMC聚合度为1的情况, 当剪切速度增加时, RDF (Fe_L1-Ow)不变, 即水分子层在z方向的分布不变, v_NOL的数值与剪切速度成比例增加, v_OL的数值略有增加但始终小于v_NOL. 当CMC聚合度为6时, 在每一层内的水分子个数不同于聚合度为1的情况, 但水层速度分布规律与其类似, 均体现出非牛顿特性.
由于OL1层是吸附层, 与剪切边界的相对速度基本为0, 故分析OL2层与剪切边界的相对速度. OL2层在不同剪切速度下的运动速度v_OL2, 当v_wall为0.1, 1, 10 ?/ps, CMC聚合度为1时, 对应v_OL2为0.07, 0.11, 0.61 ?/ps; 聚合度为6时, 对应v_OL2为0.08, 0.12, 0.89 ?/ps. 随着剪切速度增加, OL2的速度不断增加, OL2与剪切边界的相对速度(v_wall – v_OL2)也不断增加. 由于模拟规定了剪切边界的移动速度, 剪切边界与溶质分子相对移动速度越大, 则认为二者的相互作用越小, 剪切边界受到的阻力越小, 证明溶液呈现了剪切稀化特性.

本文通过分子动力学模拟研究了羧甲基纤维素钠溶液剪切稀化的微观机理, 得到的主要结论如下:
1) 含有CMC分子的体系, 加入更多水分子时, 体系增大的程度减小. CMC分子上的烷基与水分子形成的氢键使体系体积减小, 每一个CMC分子依靠氢键作用在自身周围形成水分子团, 使溶液黏度增加.
2) 溶液中CMC分子碳链上的氢原子与水分子的氧原子的径向分布函数的结果表明, 对溶液施加剪切作用时, 氢键作用大幅度减弱, 溶液黏度下降; 当溶液剪切速度继续增加时, 氢键作用减弱幅度降低, 导致溶液黏度下降幅度随之降低. 在剪切过程中, Hc-Ow氢键作用的减弱是羧甲基纤维素钠溶液出现剪切稀化现象的主要原因.
3) 水分子与溶质分子形成的氢键阻碍了溶质分子在溶液中的运动, 溶液内CMC分子水平位移特性的结果表明, 当剪切速度增加时, 水分子与CMC分子之间的氢键作用减弱, 导致水分子对CMC分子运动的阻碍作用减弱, CMC分子运动更剧烈; 通过分析壁面表层水分子的滑移速度分布可知, 水分子层和剪切边界的相对速度随着剪切速度的增大而增大, 剪切边界受到的阻力减小, 溶液出现剪切稀化现象, 水分子层速度的计算结果进一步验证了CMC溶液的非牛顿特性.