摘要:利用量子化学第一性原理计算, 对FeB₂₀和Fe₂B₂₀团簇的几何构型、电子结构以及由激光诱导的超快自旋动力学进行了研究. 计算结果发现, FeB₂₀团簇中Fe原子倾向吸附于B₂₀管内, 而Fe₂B₂₀团簇的两个Fe原子分居管内外时更稳定. 后者由于磁原子个数的增多, 引入了更多的d电子态而表现出结构整体能级的下移; 同时, 由于该结构两磁原子吸附环境的不同, 使得其能态具有不同自旋局域的可能性. 基于体系所得多体电子基态和激发态, 在特定激光脉冲诱导下, 在两个团簇上均实现了亚皮秒时间尺度内的超快自旋翻转和自旋交叉两种动力学过程. 其中前者均可逆, 且保真度都高达89.7%及以上, 后者保真度略低, 均在78%及以下. 另外, 在Fe₂B₂₀团簇上, 实现了两个Fe原子之间的超快自旋转移动力学, 其所需激光能量由于初末态较大的能级差和较多的中间态参与而较之其他动力学最高. 本文工作为吸附磁原子的管状硼团簇体系上所实现的超快自旋动力学功能进行了预测, 可望对其未来的实验实现以及相关自旋逻辑功能器件的设计和应用提供理论指导.
关键词: 超快自旋动力学/
磁性硼团簇/
第一性原理计算

English Abstract

全文HTML

--> --> -->

随着电子器件的广泛应用与飞速发展, 人们对信息的存储容量与读写速度等多方面的需求也日益增长, 同时高密度存储器件的尺寸也逐步微型化至原子与分子量级^[1,2], 接近了传统高密度磁性存储器件的物理极限. 为了突破传统物理极限的束缚, 革新技术, 寻找其他可能存在的新型存储器件与逻辑运算器件是目前工业发展的需求, 也是未来科学技术发展的必经之路.
电子具有两个非常重要的内禀属性: 电荷与自旋. 其中电子的电荷这一属性被众人所悉知, 并且自第二次工业革命以来也广泛应用于电气工程、通信工程、计算机科学等众多领域, 为人类与社会带来了巨大的福祉, 是现代科学技术发展不可或缺的一部分. 随着现代工业微加工技术的成熟与集成电路的普及, 电子器件的体积限度越来越小, 当其限度达到纳米量级时, 通过操纵电子的自旋自由度来实现信息的读取和传递, 较传统电子学器件表现出诸多优点, 如数据处理快、集成度高、稳定性好和能耗低等特点^[3-6]. 特别是自20世纪巨磁阻效应被发现以来, 自旋电子学作为一个新型交叉学科而受到了广泛的关注, 并得到了迅速的发展^[7], 相关自旋电子学器件也逐步成为了未来量子计算机发展的主流.
在响应速度方面, 自1996年Beaurepaire等^[8]在铁磁镍中观察到2 ps内的退磁现象以来, 激光诱导的超快自旋动力学受到了越来越多的关注^[9-17]. Scholl等^[9]通过双光子光电发射实验观察到了不同时间尺度下磁性薄膜中的退磁现象. Pfau等^[10]利用自由电子激光器产生的X射线在研究磁畴的同时探测到了在亚皮秒时间尺度内磁畴自旋结构的变化. 在理论层面上, Koopmans等^[11]提出的三温度模型, Steiauf和F?hnle^[12]提出的自旋轨道耦合和电声子耦合参与下的Elliot-Yafet机制, Battiato等^[13]的超扩散自旋输运机制等均揭示了磁性体系下的超快自旋动力学行为. 其中, 针对磁性团簇体系, Gómez-Abal和Hübner^[15]研究团队提出了Λ进程理论来描述磁光作用下的超快光学跃迁过程. 该进程通过在脉冲激光的作用下寻找自旋混合态作为桥接, 进而可以实现具有不同自旋特性的初、末态(如具有相反自旋取向或不同自旋多重度的初、末态)之间的间接跃迁^[18]. 基于该过程, 多种超快自旋动力学, 如超快自旋翻转、自旋转移、自旋交叉、退磁与磁化等^[19-21], 在分子和配合物体系得以预测, 与之相对应的可能实现的磁逻辑门^[22]、自旋的擦除效应^[23]、分子磁开关^[24]等逻辑功能也相继提出, 并在量子热力学方面也取得了一定的进展^[25,26]. 近期, 由激光诱导的亚皮秒级的自旋转移在由4.428 nm的碳链结构所桥接的两个镍原子之间也得以实现^[27]. 这些研究在揭示各体系超快自旋功能机制的同时, 也为其在分子自旋电子学相关器件的应用提供了理论指导.
硼是元素周期表中第五号元素, 因临近碳且相比于碳缺少一个电子, 这种“电子缺陷”使得硼原子只有一个价电子参与成键, 并剩下一对孤立电子对和未被占据的空轨道, 从而需通过多中心键的方式共享电子以平衡体系的电子分布^[28]. 研究发现, 硼团簇可随硼原子个数的不同呈现二维平面状结构、三维管状、多层结构及笼状等不同的构型^[29-33]. 其中, 美国布朗大学Wang研究组^[29]通过对硼团簇的光电子能谱(photoelectron spectroscopy, PES)分析和利用全局几何优化理论进行计算后发现, 当硼原子的数目低于20时, 团簇构型倾向于准平面构型, 而当增加至20及更多的时候, 团簇则倾向于三维管状或富勒烯构型, 由此提出B₂₀为硼团簇材料从二维向三维转变的临界尺寸结构, 其对硼团簇结构转变的研究与拓展低维材料的应用具有十分重要的意义与潜在的价值. 后续的实验和理论研究^[30,31,34]也均证实或利用了B₂₀团簇构型为双环形管状结构的结论. 另一方面, 硼原子独特的电子结构使得硼团簇可与其他原子结合形成具有特定功能的材料. 近年来, 对于硼团簇或硼烯结构上掺杂或吸附外来原子(如H原子, 碱金属原子, 及磁性原子等)体系, 其形成机理、几何结构、电子结构、磁性及相关应用的研究在实验和理论上均进行了大量的探索^[35-45]. 其中, Liu等^[36]在理论上证明了吸附Li原子的$ {\mathrm{B}}_{36} $和$ {\mathrm{B}}_{36}^{-} $团簇可作为一种可逆的储氢介质; Liang等^[37]发现吸附Li原子能增加管状B₂₀团簇的稳定性; Xu等^[38]运用密度泛函理论方法对MB_2n (M = Ti, Cr, Fe, Ni, Zn; n = 6, 7, 8)进行了理论研究, 发现该系列内嵌金属的硼双环配合物在切向和径向均具有双芳香性, 其中, 其非定域化的切向π轨道不与金属原子相互作用, 而其径向轨道与金属原子形成spd-π杂化; Tam等^[39]通过理论计算发现掺杂Fe原子可以使B_n (n = 14—20)团簇形成稳定的管状或富勒烯状构型. Popov等^[43]通过光电子能谱和全局几何优化理论对钴原子掺杂硼团簇$ \text{Co}{\mathrm{B}}_{16}^{-} $的稳定存在性在实验与理论上进行了证实, 并提供了可行的相关合成路径等. 然而, 目前对该类体系激发态的研究及相关自旋动力学的探索报道较少.
本文选择吸附有单原子和双原子Fe的管状B₂₀团簇(即FeB₂₀和Fe₂B₂₀)对其基态和激发态电子结构、自旋局域化以及由激光诱导的超快自旋动力学特性进行研究, 探索其实现超快自磁操控(如超快自旋翻转、超快自旋转移与超快自旋交叉)的可能性. 前期我们对内嵌单原子Co的笼状B₄₀团簇上由应变调制的超快自旋翻转动力学进行了研究^[46], 为金属硼富勒烯相关自旋器件的设计提供了新的可能性. 这里, 我们将磁原子载体从封闭笼状体系过渡到半封闭体系, 探索管状B₂₀团簇吸附单磁和双磁原子体系的自旋动力学及其新奇的特征. 选择双磁中心结构是由于其除了具有单磁结构的信息存储能力以外, 还具有信息传递功能, 在一定条件下可实现特定逻辑功能^[47]. 另外, 根据本文结构优化结果, 发现双磁中心结构的两个Fe原子分居管状B₂₀内外, 其自旋密度的转移由B₂₀曲面进行桥接, 与之前由金属或非金属原子作为桥接原子的结构有本质的区别^[48]. 因此, 鉴于该研究体系的特殊性, 其构型、能级分布特点、所实现的超快自旋动力学过程及自旋密度转移方式等都具有独特特征. 本文的研究一方面对上述特征进行第一性原理探索, 另一方面以期通过理论计算激发相关实验兴趣, 对相关结构在未来新型高密度磁性存储器件的设计和发展提供一定的理论基础, 为未来量子器件及量子计算的研究提供新颖的物理模型与思路.

基于Gaussian 16软件包^[49], 采用Hartree-Fock (HF)方法对Fe_mB₂₀ (m = 1, 2)团簇进行几何结构优化, 所采用基组为混合基组, 即Fe原子采用Lanl2dz基组, 对B原子采用STO-3G基组. 该组合基组已成功用于预测Ni₂配合物^[50]和Co@${\rm{B}}_{40}^-$富勒烯体系^[46]的电子结构、光谱性质和自旋动力学. 其中, 前者体系所计算的吸收光谱峰值与实验取得了一致, 后者体系通过与对B原子采用6-311G大基组(分子轨道范围存在一定的截断)所得的结果比较, 发现采用STO-3G小基组在降低计算成本的同时在结构构型、基态自旋密度分布尤其是动力学功能的实现上对结果影响不大. 计算中所采用的收敛标准为: 计算得到的每个原子上的力和力的均方根分别小于4.5 × 10^–4 Hartree/Bohr和3 × 10^–4 Hartree/Bohr, 其相应的位移和位移的均方根则分别小于1.8 × 10^–3 Bohr和1.2 × 10^–3 Bohr, 能量的收敛标准设置为小于10^–8 Hartree. 所得能量最低的结构稳定性均由后续无虚频的频率计算得以证实.
对于超快自旋动力学所需的多体电子基态和激发态, 采用后HF方法—对称性自适应组态相互作用方法(symmetry-adapted-cluster configuration interaction, SAC-CI方法)^[51]得出. 该方法通过考虑HF分子轨道之间的虚激发以及多组态行列式的展开形式, 将多电子体系静态相关(static correlation)和动态相关(dynamical correlation)同时较好地考虑进来^[20], 所得基态和激发态波函数较为精确, 在此基础上进行强关联体系中由激光诱导的基于Λ进程的超快自旋动力学的计算, 其结果也较为可靠.
本文中自旋动力学初态到末态的跃迁采用间接跃迁的方式, 即Λ进程^[15]. 该方式一方面对于一些受选择定则限制的直接跃迁(如电偶极近似下自旋相反的初、末态之间, 或具有不同自旋多重度的初、末态之间等), 可以突破其限制通过间接跃迁方式而得以实现; 另一方面, 其速度大多数情况下相比于直接跃迁也被证实更快. 因此, 在施加激光脉冲之前, 需要对所得多体电子态考虑自旋轨道耦合(spin-orbit coupling, SOC)效应^[52,53]和加入外部静磁场, 前者出于更真实描述强关联体系和产生Λ进程中自旋混合中间态的需要, 后者用以实现塞曼分裂, 消除自旋向上和自旋向下电子态的简并. 根据所选初、末态自旋性质的不同, 一般可实现以下若干种自旋动力学过程: 若初态与末态具有相反的自旋取向, 对应自旋翻转过程; 若初态与末态的自旋局域在两个不同的磁性中心上, 对应自旋转移过程; 若初态与末态具有不同的自旋多重度, 对应自旋交叉过程; 若初态的自旋期望值非零, 而末态的自旋期望值为零, 则可表示退磁过程, 反之则为磁化过程.
为描述激光脉冲诱导下的体系自旋动力学, 在电偶极近似下(磁偶极相互作用项通常情况下比电偶极相互作用小两个数量级, 因此本研究将其忽略不计), 所施加激光脉冲用含时哈密顿量$\widehat{H}\left(t\right)= $$ \widehat{D}\cdot {\mathit{E}}_{\mathrm{L}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}\left(t\right)$进行表示, 其中$ {\mathit{E}}_{\mathrm{L}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}\left(t\right) $是激光脉冲下的电场, $ \widehat{D} $是电偶极矩算子. 在具体计算中, 激光脉冲由6个激光参数来表示: 3个角度(θ, φ, γ)来描述方向, 激光能量, 半高全宽(FWHM)和振幅. 在脉冲激光诱导下, 体系动力学由以下相互作用绘景下的耦合方程^[21,24]描述:

$\begin{split}&{\rm{i}}\hbar \frac{\partial }{{\partial t}}{C_n}\left( t \right) \\=\;& \mathop \sum \limits_k \left\langle {{\psi _n}} \right|\hat H\left( t \right)\left| {{\psi _k}} \right\rangle {{\rm{e}}^{\tfrac{{\rm{i}}}{\hbar }\left( {{E_n} - {E_k}} \right) \cdot \left( {t - {t_0}} \right)}}{C_k}(t),\end{split}$

并通过使用具有Cash-Karp自适应性步长的五阶Runge-Kutta方法数值求解^[54]. 其中, E_n与E_k分别为未扰动$ \left| {{\psi _n}} \right\rangle $和$ \left| {\psi _{k}} \right\rangle $的本征能量, $ {C}_{n}\left(t\right) $为激光脉冲诱导下态$ \left| {\psi _{n}} \right\rangle $的系数. 为实现特定的自旋动力学过程, 具体计算中首先选择具有不同自旋特性的初、末态和合适的外部静磁场, 然后利用遗传算法程序^[55]来优化激光参数, 通过末态转移率的大小 (即保真度)来探索实现该自旋动力学过程的可能性.

2

-->

3.1.Fe_mB₂₀ (m = 1, 2)的结构

基于优化所得管状B₂₀团簇(图1(a), 直径为5.05 ?, 其初始构型直径为5.2 ?^[29,30]), 通过对具有不同单Fe原子和双Fe原子吸附位点的各构型进行结构优化, 最终得到FeB₂₀和Fe₂B₂₀团簇在自旋多重度为3下(这里三重态构型比相应闭壳层构型更稳定)的最优构型, 如图1(b)和图1(c)所示. 其稳定性均由后续进行的无虚频的频率计算得以证实. 其中对于团簇FeB₂₀ (点群对称性为C_s), 发现Fe原子吸附位置在B₂₀管中心附近时最为稳定, 其能量为E = –609.44432 Hartree, 比管外吸附结构低0.20033 Hartree (约5.451 eV, 见附录图A1(b)). 这里, 由于Fe原子参与成键的3d电子取向和轨道排布的不对称、B—B键和Fe—B键之间复杂的竞争, 以及姜泰勒效应^[39,43], 该最优构型中Fe原子并非居于B₂₀管正中心, 这与文献[39]中所得管状FeB₂₀三重态稳定C_s构型一致, 与Co原子内嵌于B₄₀富勒烯结构非几何中心现象一致^[46]. 对于Fe₂B₂₀, 其可能的吸附位置较为复杂. 通过对两个Fe原子吸附位置的所有可能的各种初始构型进行大量的尝试与优化, 发现当两个Fe原子分居B₂₀管内外时的构型(点群对称性为C_s)最稳定, 如图1(c)所示, 能量为E = –731.90894 Hartree. 其他稳定的构型(见附录中的图A1(c)、图A1(d)和图A1(e)), 如Fe二聚体垂直管轴居于管内构型(Fe—Fe键长2.06 ?), Fe二聚体居于管内外且近似平行管轴构型(Fe—Fe键长2.73 ?, 与管轴夹角37.7°)和Fe原子沿侧壁分居管外上下构型(这里, Fe二聚体垂直或平行管轴居于管外的构型均不稳定), 其能量比图1(c)所示构型分别高1.270, 0.002和4.030 eV. 图1(b)和图1(c)的俯视图分别标出了各结构的Fe—B键长参数(单位为?). 通过比较可知, 引入磁性原子使得原管状B₂₀团簇直径变长, 且均发生了一定程度的形变(与内嵌Co原子使B₄₀笼状结构变形现象类似^[46]), 其中Fe₂B₂₀中的环状结构形变更为明显. 另外, 两个磁结构形变均沿B10—B19键长呈轴对称分布^[39], 因此, 俯视图中对称轴下半部分等价的Fe1—B键长均未显示. 需要说明的是, Fe₂B₂₀团簇的两个Fe原子由于所处环境不同, 其电荷分布和自旋密度呈现不均衡性, 所计算出的多体电子基态和激发态存在具有不同自旋局域的可能性, 因此, 在合适的激光脉冲诱导下该结构具有实现自旋转移的潜力.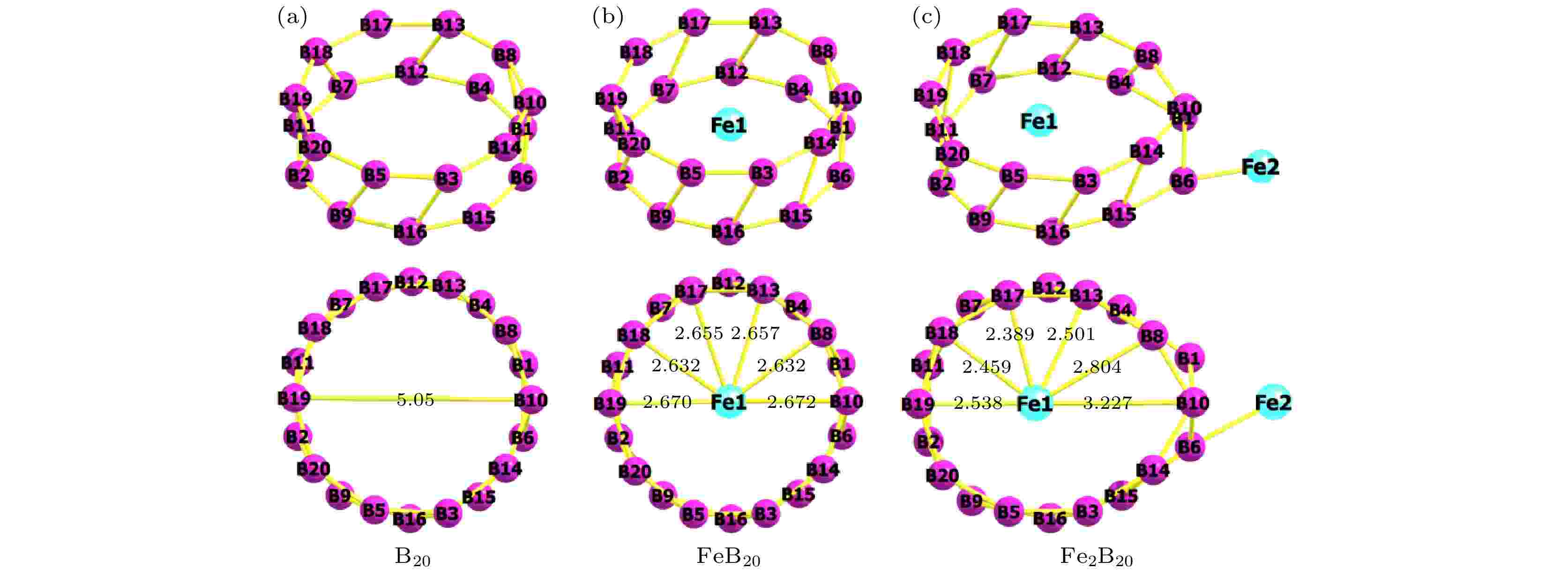
图 1 优化后的团簇结构 (侧视图和俯视图)　(a) B₂₀; (b) FeB₂₀; (c) Fe₂B₂₀; 其中, 俯视图中的键长单位为 ?
Figure1. Side- and top-viewed optimized geometries of clusters: (a) B₂₀; (b) FeB₂₀; (c) Fe₂B₂₀. The bond lengths are in ?.

2 -->

3.2.SAC-CI能级及自旋密度分布

图2给出了FeB₂₀和Fe₂B₂₀团簇在引入SOC前的最低20个三重态和最低11个单重态的SAC-CI能级图. 其中, 对后续所要讨论的各自旋动力学所涉及到的相关能态在未考虑SOC和外部静磁场时的能级位置进行了标注. 例如, 1 ¹A′和2 ³A′分别表示在不可约表示A′下体系的第一个单重态能级和第二个三重态能级, SAC表示SAC单重态能级. 需要说明的是, 点群对称性C_s有两个不可约表示A′和A′′, 其中, 隶属不可约表示A′′的各能级未涉及到文中所示动力学初、末态, 但一部分作为中间态参与了动力学过程. 另外, 一些电子态由于能量接近而在图2中无法分辨. 为便于理解, 附录A中的表A1列出了考虑SOC前后能态的能量信息及其标记情况, 其中, 考虑SOC后所加磁场沿y轴方向, 即$ \theta =90^\circ , \varphi =90^\circ $. 从两种团簇的能级分布可以看出, 其低能态(如1.5 eV以下)数目较少, 而高能态分布较为集中. 另外, 单重态所处能级位置整体偏高, 其最低的单重态能量与所得三重态基态相比分别高1.133 eV和1.490 eV, 进一步显示了三重态构型更稳定的事实. 与FeB₂₀相比, Fe₂B₂₀由于其具有较多的d电子数(或d电子态)而表现出整体能级的下移, 相应地与FeB₂₀具有相同数量的能级展宽变窄. 该能级特征有利于相关自旋动力学的初、末态的选择以及Λ进程的高效实现. 尤其是对于自旋转移, 通常情况下其具有不同单磁中心自旋局域(这里, 某个磁原子上的自旋密度值大于0.8且占自旋密度总值的75%以上即可视为单磁局域)的初、末态数目不均衡, 能级差较大, 给该动力学的中间态的搜寻带来难度, 同时极易导致Λ进程两分支跃迁强度(即跃迁概率幅值)不平衡, 降低动力学的保真度. 为说明这一点, 表1列出了Fe₂B₂₀团簇在考虑SOC和加入静磁场(大小为10^–5 atomic units, 方向为y轴, 即$ \theta =90^\circ , \varphi =90^\circ $)后具有明显单磁中心自旋局域的一些能态的信息, 包括能量、自旋期望值, 及两磁原子和B₂₀上的自旋密度. 从表1可以看出, 在所计算的71个能态(这里, 加入SOC之后每一个三重态分裂为几近简并的三个电子态)中, 仅有13个态具有较好的单磁中心自旋局域, 其中, 11个态局域在管外Fe原子上(即Fe2), 仅有两个态局域在管内Fe原子上(即Fe1), 由此可知, 管内Fe原子的自旋局域由于B₂₀管的“屏蔽”相比于管外Fe原子受到一定程度的限制, 其相应能态数目较少, 从而使自旋转移合适初、末态的选择的可能性组合大大降低. 需要说明的是, 对于单磁中心FeB₂₀团簇, 由于不存在与之竞争的其他Fe原子, 在所计算的71个能态中共有18个具有良好自旋局域的态, 且均局域在管内Fe1原子上.
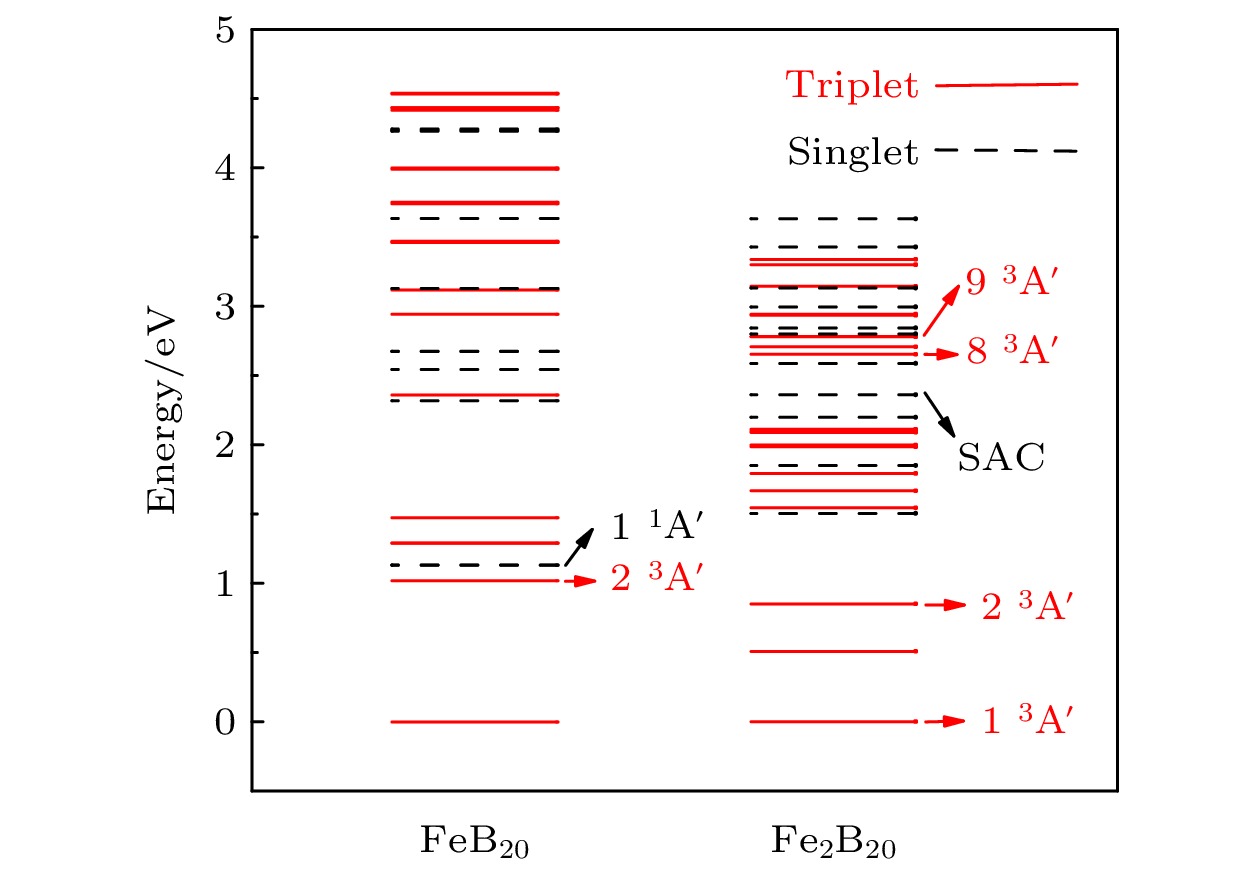图 2 FeB₂₀与Fe₂B₂₀的SAC-CI能级, 黑色虚线表示单重态, 红色实线表示三重态. 其中, 各自旋动力学所涉及的有关初、末态在未考虑自旋轨道耦合时的能级位置被明确标出
Figure2. The SAC-CI energy levels of clusters FeB₂₀ and Fe₂B₂₀. The singlet and triplet terms are denoted by the black dashed and red solid lines, respectively. The related terms from which the involved initial and final states in the spin dynamics to be discussed later originate before the inclusion of SOC are marked.

Structure	State	Energy/eV	$ \left\langle { {S}_{x} } \right\rangle $	$ \left\langle { {S}_{y} } \right\rangle $	$ \left\langle { {S}_{z} } \right\rangle $	Spin density
						Fe1	Fe2	B20
	$ \left| {1} \right\rangle $	0	0.38	–0.87	0	0.001	1.919	0.015
	$ \left| {2} \right\rangle $	0.001	–0.59	0.73	0	0.001	1.911	0.015
	$ \left| {5} \right\rangle $	0.513	0.21	–0.42	0	0.002	0.946	0.023
	$ \left| {6} \right\rangle $	0.515	–0.12	0.46	0	0.002	0.962	0.023
	$ \left| {17} \right\rangle $	1.797	0.16	–0.72	0	0.022	1.473	0.224
	$ \left| {18} \right\rangle $	1.797	–0.42	0.05	0	0.013	0.839	0.13
Fe2B20	$ \left| {19} \right\rangle $	1.797	0.26	0.67	0	0.021	1.432	0.22
(B: θ = 90°, φ = 90°)	$ \left| {25} \right\rangle $	2.002	0.41	–0.35	0	0.004	1.099	0.120
	$ \left| {26} \right\rangle $	2.003	–0.23	0.54	0	0.005	1.189	0.133
	$ \left| {39} \right\rangle $	2.658	–0.02	–0.63	0	1.114	0.084	0.261
	$ \left| {41} \right\rangle $	2.659	–0.01	0.63	0	1.114	0.084	0.261
	$ \left| {56} \right\rangle $	2.948	0.42	–0.63	0	0.026	1.412	0.305
	$ \left| {57} \right\rangle $	2.949	–0.52	0.55	0	0.026	1.411	0.303

表1Fe₂B₂₀中具有单磁中心自旋局域能态的能量、自旋期望值及自旋密度
Table1.Energies, spin expectation values, and spin density of the states with spin localized on one single magnetic atom for cluster Fe₂B₂₀.

在以上所计算的电子结构的基础上, 考虑自旋轨道耦合, 通过对所有可能的符合期望的初、末态的大量筛选及外磁场方向的不同尝试, 发现在特定激光脉冲诱导下, 超快自旋翻转和自旋交叉功能在两团簇上均得以实现, 自旋转移过程在Fe₂B₂₀团簇上也得以预测. 下面将给出这些所得不同类型的超快自旋动力学的结果, 并就其动力学细节及物理机制给出具体讨论和分析.
2 -->

3.3.超快自旋动力学

3 -->

3.3.1.超快自旋翻转动力学

根据选择定则对自旋的约束条件(?m_s = 0), 在电偶极近似下, 两个具有相反自旋取向的能态之间无法发生直接光学跃迁. 本文基于Λ进程模型, 在合适激光脉冲诱导下实现了两者之间通过中间态桥接的间接跃迁, 在FeB₂₀和Fe₂B₂₀两个团簇上分别得到了如图3(a)与图3(b)所示的自旋翻转动力学. 其中, 图3(a)初、末态分别为态$ \left| {4} \right\rangle $和态$ \left| {6} \right\rangle $, 由FeB₂₀团簇的不可约表示A′下的第二个三重态能级2 ³A′塞曼效应分裂而来, 具有相反的自旋取向; 图3(b)初、末态分别为态$ | {8}\rangle $和态$ | {9}\rangle $, 由Fe₂B₂₀团簇的不可约表示A′下的第二个三重态能级2 ³A′塞曼效应分裂而来, 具有相反的自旋取向且自旋局域在Fe2上. 具体各初、末态信息(如能量、自旋期望值、自旋局域)及所需激光参数(方向、FWHM、振幅及能量)分别详见表2和表3. 通过比较发现, Fe₂B₂₀上自旋翻转动力学所得保真度(即末态转移率)较高(93.5%), 完成时间也比FeB₂₀相应动力学缩短一半时间(约600 fs), 但是其所需激光能量较高(2.114 eV). 这是由于自旋翻转动力学所需激光的能量大多数情况下由初(或末)态与中间态的能量差所确定. 对于具有较多中间态参与的情况, 通常情况下由占据概率较大的主要中间态与初(或末)态能量差决定. 例如, 图3(a)所示动力学, 在所有参与的11个中间态中, 占据较大的中间态为态$ \left| {13} \right\rangle $和$ \left| {14} \right\rangle $(能量分别为1.313 和1.317 eV), 其与初态$ \left| {4} \right\rangle $(或末态$ \left| {6} \right\rangle $)的能量差与激光能量0.299 eV (见表3)接近. 图3(b)所示动力学中, 共有27个中间态参与, 其激光能量几乎和初(或末)态与主要中间态$ \left| {59} \right\rangle $(能量为3.002 eV)的能量差相等. 此外, 在保持相应激光参数不变的情况下, 将初、末态调换, 发现上述超快自旋翻转过程均可逆, 保真度分别达到了95.5%和83.8%. 该可逆性可归因于每个过程中参与中间态的对称性(即前半部分所参与的中间态在后半部分能找到由同一三重态分裂而来的与之相对应的态)及其占据概率振荡行为的对称性. 这里, 需要指出的是, 两个团簇上基态三重态之间也具有合适的初、末态, 但由于其基态能级较为孤立, 计算中无法找到合适的中间态促进其间接跃迁, 相应动力学所得的保真度均较低而未实现预期功能.
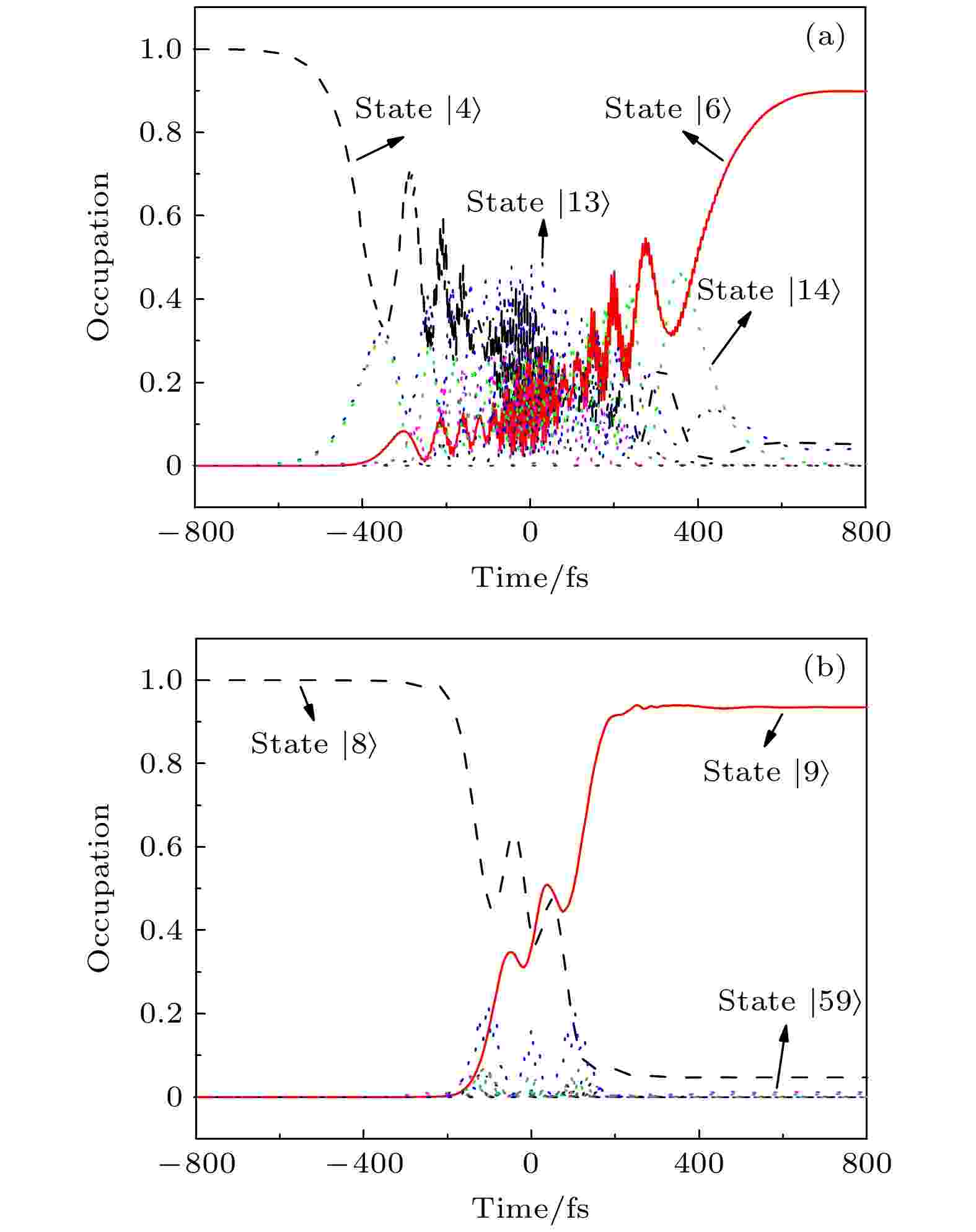图 3 超快自旋翻转动力学　(a) FeB₂₀团簇的自旋翻转过程; (b) Fe₂B₂₀团簇的自旋翻转过程. 其中各动力学中初态、末态和中间态分别由黑色虚线、红色实线和点线表示
Figure3. Ultrafast spin flip scenarios: (a) Spin-flip process in FeB₂₀; (b) spin-flip process in Fe₂B₂₀. The initial, final, and intermediate states involved in each of the spin-flip processes are represented by the black dashed, red solid, and dotted lines, respectively.

Scenario	Structure	State	Energy/eV	$ \left\langle { {S}_{x} } \right\rangle $	$ \left\langle { {S}_{y} } \right\rangle $	$ \left\langle { {S}_{z} } \right\rangle $	Spin density
							Fe1	Fe2
Flip	FeB20	$ \left| {4} \right\rangle $	1.021	–0.94	0	0	1.291	—
	(B: θ = 90°, φ = 90°)	$ \left| {6} \right\rangle $	1.022	0.94	0	0	1.291	—
	Fe2B20	$ \left| {8} \right\rangle $	0.856	0	0	0.89	0.006	1.785
	(B: θ = 0°, φ = 90°)	$ \left| {9} \right\rangle $	0.857	0	0	–0.89	0.006	1.785
Transfer	Fe2B20	$ \left| {1} \right\rangle $	0	0.38	–0.87	0	0.001	1.919
	(B: θ = 90°, φ = 90°)	$ \left| {41} \right\rangle $	2.659	0.01	0.63	0	1.114	0.084
Crossover	FeB20	$ \left| {6} \right\rangle $	1.022	0.94	0	0	1.291	—
	(B: θ = 90°, φ = 90°)	$ \left| {7} \right\rangle $	1.133	0	0	0	0	—
	Fe2B20	$ \left| {37} \right\rangle $	2.371	0	0	0	0	0
	(B: θ = 90°, φ = 90°)	$ \left| {45} \right\rangle $	2.784	0	–0.52	0	0.090	0.873

表2各自旋动力学过程中初、末态的能量、自旋期望值与自旋密度
Table2.Energies, spin expectation values, and spin densities of the initial and final states of each scenario.

Scenario	Structure	Initial/Final state	Fidelity	Laser parameters
				θ/(o)	φ(o)	γ/(o)	FWHM /fs	Amplitude /(atomic units)	Energy /eV
Flip	FeB20	$ \left| {4} \right\rangle \to \left| {6} \right\rangle $	89.7%	112.9	6.1	338.9	337.3	0.00997	0.299
	Fe2B20	$ \left| {8} \right\rangle \to \left| {9} \right\rangle $	93.5%	156.4	122.4	77.7	466.2	0.00634	2.114
Transfer	Fe2B20	$ \left| {1} \right\rangle \to \left| {41} \right\rangle $	91.9%	244.7	91.4	225.3	92.3	0.00781	2.661
Crossover	FeB20	$ \left| {6} \right\rangle \to \left| {7} \right\rangle $	77.9%	61.0	321.4	82.9	318.5	0.00783	0.212
	Fe2B20	$ \left| {37} \right\rangle \to \left| {45} \right\rangle $	74.5%	297.2	356.1	301.5	352.0	0.00306	0.416

表3超快自旋动力学过程所需的激光参数, 其中 θ和φ为入射激光在球坐标系下的方位角, γ为入射激光振动方向和光平面的夹角, FWHM为激光脉冲的半高全宽
Table3.Laser parameters for the achieved scenarios. Here, θ and φ denote the angles of the incidence in spherical coordinates, and γ is the angle between the polarization of the light and the optical plane. FWHM is the full width at half maximum of the laser pulse.

3 -->

3.3.2.超快自旋转移动力学

自旋的转移是指局域在不同磁性中心的能级之间的跃迁, 其在磁性存储与计算机逻辑运算等方面有着重要的意义. 一般来说, 与自旋翻转相比, 自旋转移较难实现. 这是由于在所计算的能级中, 无法保证分别局域在不同磁性原子上的能态同时存在. 另外, 即使存在合适的具有不同自旋局域的初、末态, 通常其能级差较大, 较难找到合适的中间态, 使其与初、末态间的跃迁强度相比拟^[48,56]. 通过对表1中所列Fe₂B₂₀团簇的候选初、末态的大量尝试, 得到了由态$ \left| {1} \right\rangle $(由不可约表示A′下的第一个三重态1 ³A′分裂而得, 在Fe1和Fe2原子上的自旋密度值分别为0.001和1.919)到态$ | {41} \rangle $(由不可约表示A′下的第八个三重态8 ³A′分裂而得, 在Fe1和Fe2原子上的自旋密度值分别为1.114和0.084)之间的动力学, 即Fe2到Fe1的自旋转移过程, 其保真度高达91.9%, 如图4所示. 需要说明的是, 由于态$ \left| {39} \right\rangle $和态$ \left| {41} \right\rangle $由同一三重态分裂而得(具有相同的自旋局域和相反的自旋方向, 见表1), 其光学跃迁性质相似, 因此, 态$ \left| {1} \right\rangle $到态$ \left| {39} \right\rangle $的超快自旋转移过程也是可实现的. 但由于其保真度只有82.7%, 且与文中所示态$ \left| {1} \right\rangle $到态$ \left| {41} \right\rangle $的自旋转移过程属于同一类跃迁(初、末态来源相同)而未被显示. 与自旋翻转动力学不同, 对于初、末态能级位置较远的自旋转移动力学, 其所需激光能量大多数情况下由初、末态之间的能量差确定(少数情况下体系可经由$ {\Xi } $过程实现跃迁^[57], 此时激光能量由其中两阶跃迁中的一阶即初态$ \to $中间态或中间态$ \to $末态的能量差确定). 这里, 该动力学由于其初、末态能量差最大(2.659 eV), 其所需激光能量(2.661 eV, 见表3)较其他动力学最高. 另外, 研究发现, 由于涉及到管外和管内磁原子之间的自旋密度转移, 该动力学共涉及到67个中间态将其进行桥接, 其中有11个单磁中心局域态(其中, 1个局域在Fe1上, 10个局域在Fe2上, 见表1), 16个同时局域在Fe2和B₂₀上(两部分自旋密度值占比范围分别为50.8%—63.7%和31.9%—38.9%), 两个同时局域在Fe1, Fe2和B₂₀上(各部分自旋密度值占比均为33%), 其余均为非局域态. 由此可知, 该自旋转移动力学过程中, Fe2到Fe1的自旋密度转移是通过B₂₀的桥接作用, 即Fe2自旋局域态(初态$ \left| {1} \right\rangle $) $\to $Fe2 + B₂₀局域中间态$\to $Fe1 + Fe2 + B₂₀局域中间态$\to $Fe1自旋局域态(末态$ \left| {41} \right\rangle $), 在非局域态的共同参与下得以实现. 这里, 虽然整个过程中所有这些中间态的占据概率并不明显, 但是他们对于整个自旋转移过程缺一不可^[50,58]. 与其他动力学相比, 虽然其参与中间态的数目最多, 但该动力学完成时间约为200 fs, 较其他动力学速度最快.
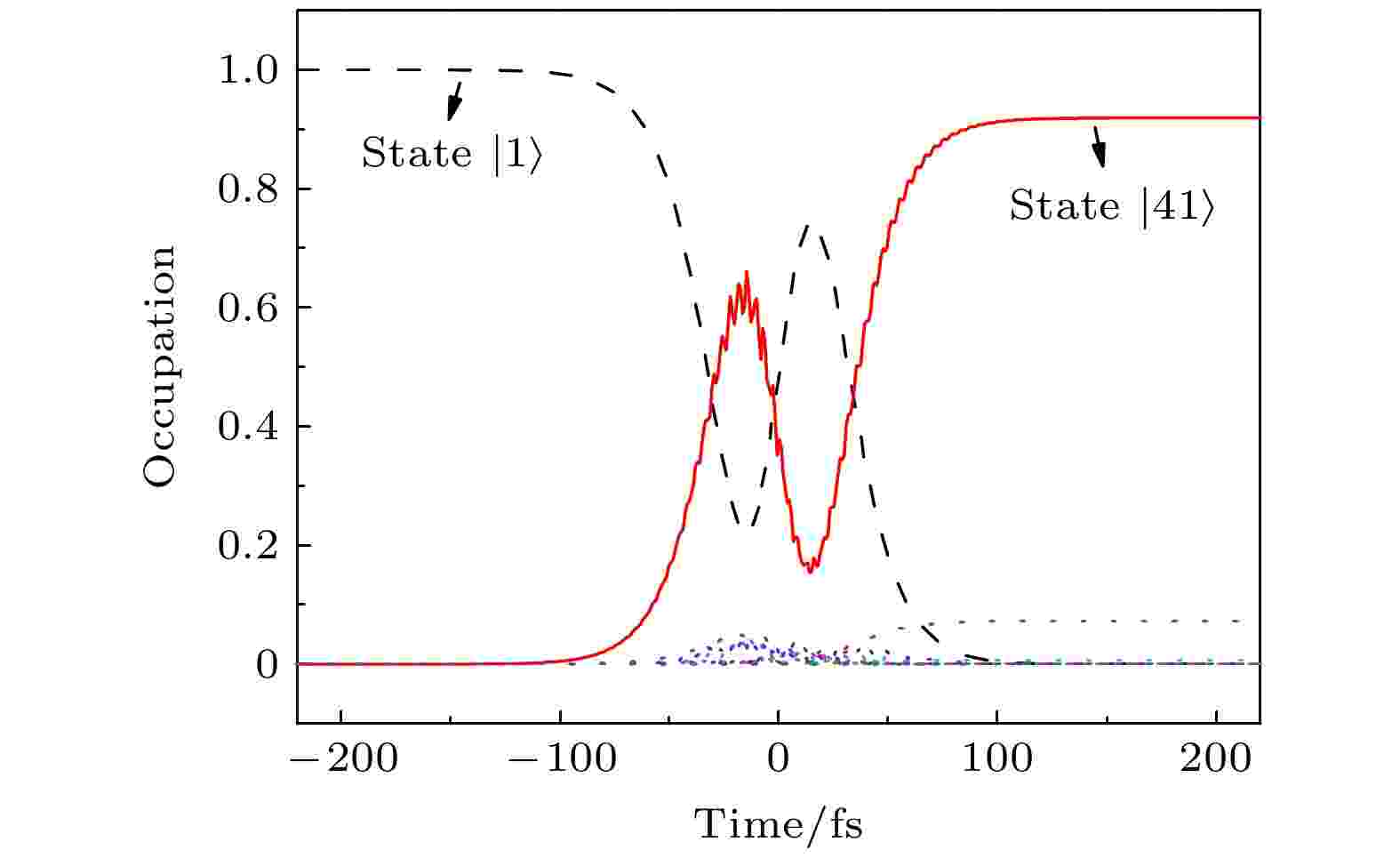图 4 Fe₂B₂₀团簇上得到的超快自旋转移动力学, 其中初态、末态和中间态分别由黑色虚线、红色实线和点线表示
Figure4. Ultrafast spin-transfer scenario in Fe₂B₂₀. The initial, final, and intermediate states involved in the spin-transfer process are represented by the black dashed, red solid, and dotted lines, respectively.

3 -->

3.3.3.超快自旋交叉动力学

自旋交叉是指不同自旋多重度(如高自旋态和低自旋态之间)的能级之间的跃迁过程, 通常发生在过渡金属分子复合物中(如Fe^[59], Co^[60], 和Mn^[61]配合物), 具有非常重要的意义与应用价值, 其在数据的存储与显示、开关效应、电致发光器件等多方面具有非常广泛的作用^[62,63]. 电偶极近似下, 不同自旋多重度之间的跃迁过程是被禁止的. 但在自旋轨道耦合作用下产生的具有自旋混合态的能级中, 该类跃迁可以在磁各向异性结构中基于Λ进程可能得以实现. 通过尝试, 本文在两个团簇上分别实现了由态$ \left| {6} \right\rangle $到态$ \left| {7} \right\rangle $和由$ \left| {37} \right\rangle $到$ \left| {45} \right\rangle $跃迁的自旋交叉动力学, 如图5所示. 其中图5(a)所示的初态$ \left| {6} \right\rangle $是由FeB₂₀团簇的不可约表示A′下的第二个SAC-CI三重态2 ³A′能级分裂而来, 末态$ \left| {7} \right\rangle $来自不可约表示A′下的第一个SAC-CI单重态1 ¹A′; 图5(b)所示的初态$ \left| {37} \right\rangle $来自Fe₂B₂₀团簇的SAC单重态能级, 末态$ \left| {45} \right\rangle $来自其不可约表示A′下的第九个三重态能级9 ³A′. 各初末态在加入SOC之前的能级位置详见图2. 与前两类所得自旋动力学相比, 自旋交叉过程所得保真度均较低, 分别为77.9%和74.5%, 进一步说明了不同自旋多重度能级之间跃迁较为困难的事实. 其中, 前者所参与的中间态中共有5个三重态和4个单重态, 后者的中间态共有10个三重态和8个单重态. 另外, 对于图5(a)初、末态能级较近的情况, 其激光能量(0.214 eV, 见表3)主要由参与的主导中间态$ \left| {10} \right\rangle $(1.271 eV)与初态(1.022 eV)的能量差来确定, 而对于图5(b)中初、末态能量相对较远的情况, 其激光能量(0.416 eV, 见表3)主要由初、末态的能量差(0.412 eV)来确定. 前者激光能量的确定具有和大多数自旋翻转情况相似的规律, 后者与如前所述的自旋转移动力学激光能量相似.
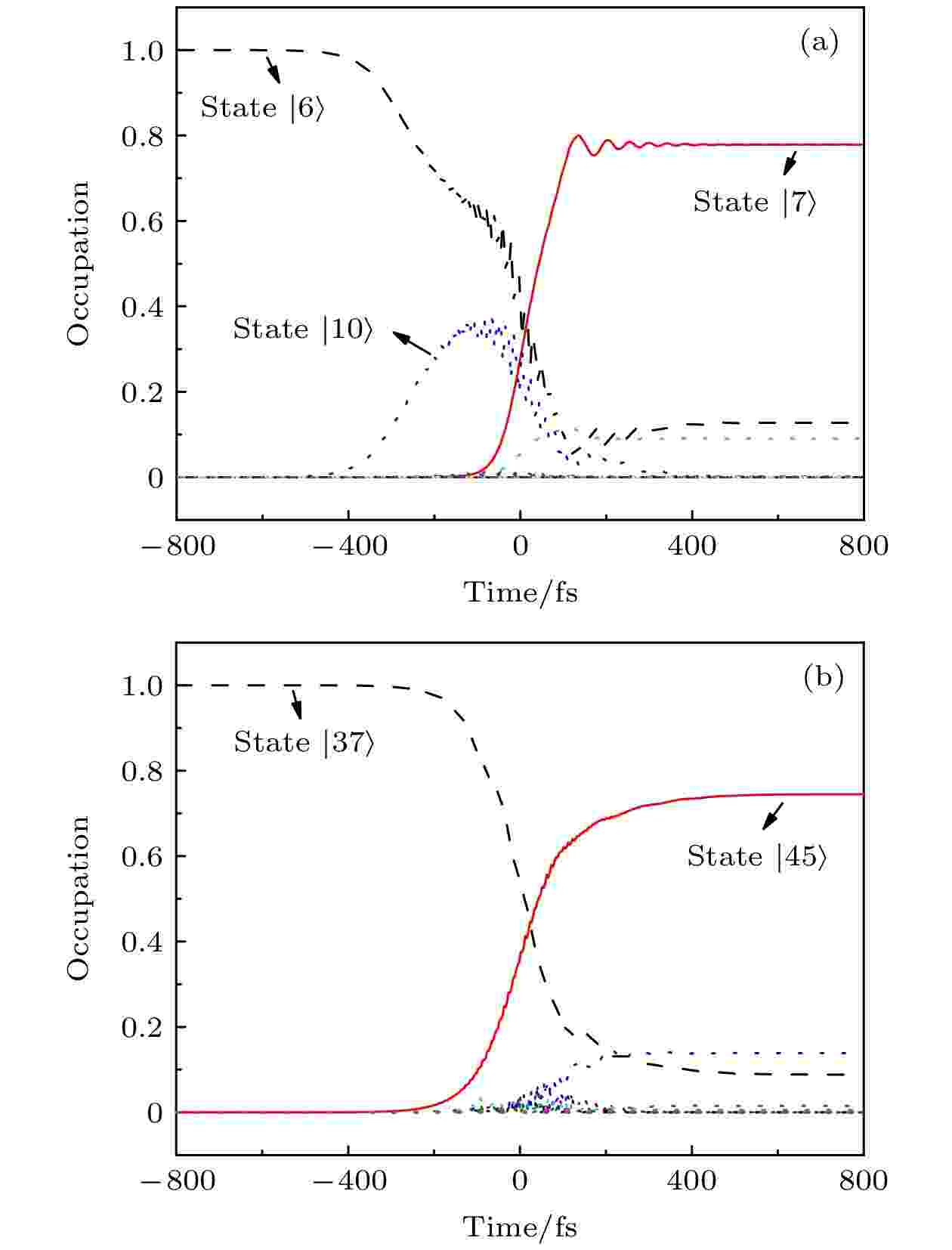图 5 超快自旋交叉动力学　(a) FeB₂₀团簇的自旋交叉过程; (b) Fe₂B₂₀团簇的自旋交叉过程; 其中各动力学中初态、末态和中间态分别由黑色虚线、红色实线和点线表示
Figure5. Ultrafast spin crossover scenarios: (a) Spin-crossover process in FeB₂₀; (b) spin-crossover process in Fe₂B₂₀. The initial, final, and intermediate states involved in each of the spin-crossover processes are represented by black dashed, red solid, and dotted lines, respectively.

本文利用量子化学第一性原理方法, 对吸附单原子和双原子Fe的硼团簇体系Fe_mB₂₀ (m = 1, 2) 的几何构型、能级分布及超快自旋动力学进行了研究. 计算结果显示, 吸附磁原子会降低管状B₂₀构型的对称性, 其中单原子Fe倾向吸附于B₂₀管内, 而双原子Fe则分居于管内外两侧. 两者能级结构中低能级分布较为稀疏, 其中, 由于Fe₂B₂₀具有更多的d电子, 其能级展开与FeB₂₀比较相对较窄. 通过选择合适的初态与末态, 在特定激光脉冲的诱导下, 两个团簇上均能实现亚皮秒时间尺度内的超快自旋翻转动力学和自旋交叉动力学, 其中前者可逆. 另外, 在Fe₂B₂₀团簇上, 实现了由Fe2到Fe1的超快自旋转移动力学, 所需的激光能量最高, 完成时间最短. 本文通过预测FeB₂₀和Fe₂B₂₀结构上由激光诱导的超快自旋动力学功能, 以期为未来相关实验的实现提供理论指导, 为实现相关逻辑功能的运算与自旋电子学器件的设计提供新的思路, 进而推动新型高密度磁性存储器件的发展.

图A1给出了优化过程中所得团簇FeB₂₀和Fe₂B₂₀的其他稳定构型(优化收敛且无虚频)的俯视和侧视图以及相应的能量和点群对称性. 其中, 图A1(a)和图A1(b)分别为FeB₂₀团簇Fe原子处于管口和管外的稳定构型, 图A1(c)—(e)分别为Fe₂B₂₀团簇Fe原子垂直管轴居于管内(Fe—Fe键长2.06 ?)、居于管内外且近似平行管轴(Fe—Fe键长2.73 ?, 与管轴夹角37.7°)和沿侧壁分居管外上下的构型. 这里, ?E表示各构型与文中相应图1(b)或图1(c)最优构型的能量差. 其他可能的构型, 因其不收敛或收敛有虚频而未被显示.
表A1列出了两个结构所计算的考虑SOC前后所有能态的能量和标记信息, 这里, 考虑SOC后所加磁场沿y轴方向, 即$ \theta =90^\circ , \varphi =90^\circ $. 其中, 前者能态标记分别就单重态和三重态能级按对称性和能量高低命名, 后者能态因塞曼分裂和自旋混合态的产生仅按能量从低到高的顺序命名(如态$ \left| {1} \right\rangle $表示能量最低态, 态$ \left| {8} \right\rangle $表示能量从低到高排序第八的能态). 同时, 文中图2所示的能态标记和各动力学相关初、末态的能量均由粗体表示(注: 对于Fe₂B₂₀团簇翻转动力学的初、末态$ \left| {8} \right\rangle $和$ \left| {9} \right\rangle $, 由于所施加磁场方向为z轴, 其考虑SOC和磁场之后的能量未在此表得以显示). 另外, 可以看出, 一些电子态由于能量值相近(如FeB₂₀的第一个和第二个单重态, 其能量值分别为1.131和1.133 eV)在图2所示的能级图中无法清晰分辨.
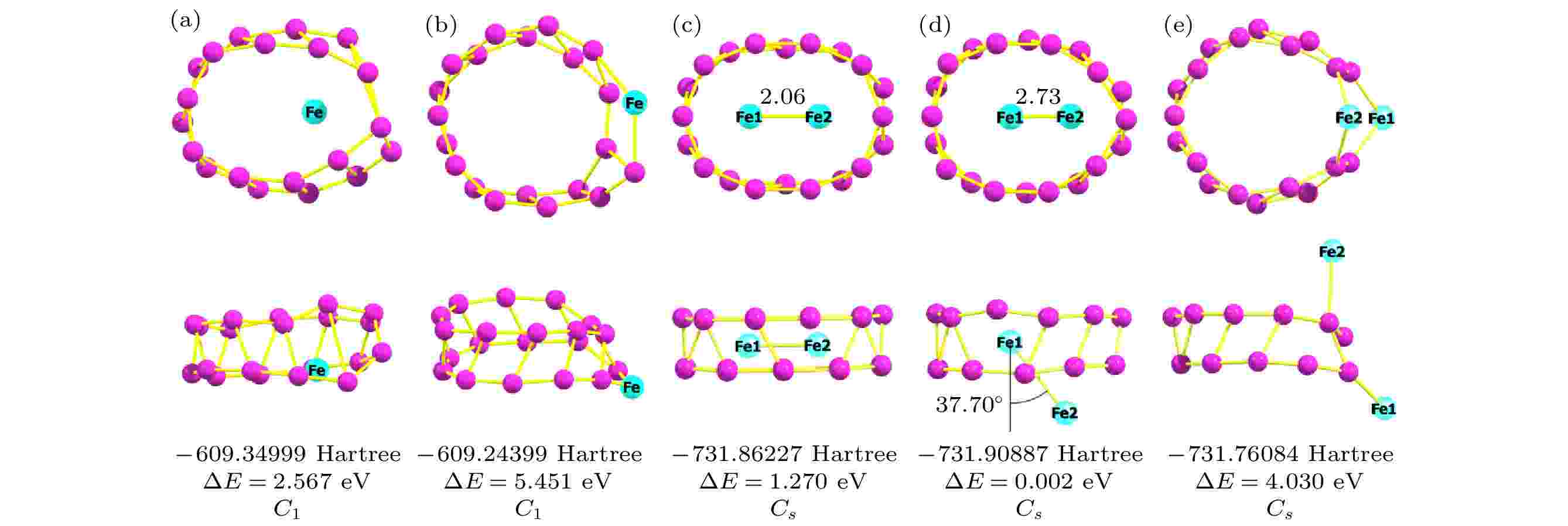图 A1 团簇FeB₂₀与Fe₂B₂₀的其他稳定构型
FigureA1. Other stable geometries of clusters FeB₂₀ and Fe₂B₂₀.

	FeB20						Fe2B20
	Before SOC		After SOC				Before SOC		After SOC
Singlet	1.131 (1 1A')		1.133				1.504 (1 1A')		1.489
	1.133 (2 1A')		1.134				1.850 (1 1A'')		1.857
	2.320 (1 1A'')		2.319				2.199 (2 1A')		2.203
	2.545 (SAC)		2.554				2.361 (SAC)		2.371
	2.676 (2 1A'')		2.677				2.587 (3 1A')		2.592
	2.676 (3 1A')		2.677				2.801 (2 1A'')		2.806
	3.130 (3 1A'')		3.132				2.843 (4 1A')		2.845
	3.636 (4 1A'')		3.638				2.996 (3 1A'')		3.002
	4.266 (5 1A'')		4.269				3.133 (5 1A')		3.136
	4.272 (4 1A')		4.272				3.429 (4 1A'')		3.434
	4.282 (5 1A')		4.285				3.632 (5 1A'')		3.637
Triplet	0.000 (1 3A')		0.000	0.0005	0.001		0.000 (1 3A')		0.000	0.0007	0.002
	1.019 (2 3A')		1.021	1.021	1.022		0.508 (1 3A'')		0.511	0.513	0.515
	1.291 (3 3A')		1.271	1.271	1.294		0.851 (2 3A')		0.854	0.857	0.857
	1.293 (1 3A'')		1.295	1.313	1.317		1.545 (2 3A'')		1.548	1.551	1.570
	1.476 (2 3A'')		1.475	1.478	1.478		1.668 (3 3A')		1.673	1.673	1.673
	2.361 (3 3A'')		2.363	2.363	2.364		1.793 (4 3A')		1.797	1.797	1.797
	2.945 (4 3A'')		2.947	2.947	2.948		1.984 (5 3A')		1.989	1.989	1.989
	3.119 (5 3A'')		3.120	3.121	3.121		1.997 (3 3A'')		2.001	2.002	2.003
	3.462 (4 3A')		3.464	3.465	3.466		2.089 (6 3A')		2.093	2.094	2.094
	3.467 (6 3A'')		3.470	3.471	3.471		2.100 (4 3A'')		2.105	2.105	2.105
	3.471 (7 3A'')		3.473	3.473	3.474		2.112 (7 3A')		2.113	2.116	2.116
	3.743 (5 3A')		3.745	3.745	3.745		2.653 (8 3A')		2.658	2.658	2.659
	3.753 (8 3A'')		3.755	3.755	3.756		2.707 (5 3A'')		2.711	2.713	2.714
	3.990 (6 3A')		3.989	3.990	3.994		2.779 (9 3A')		2.784	2.784	2.784
	4.000 (7 3A')		4.003	4.008	4.008		2.783 (6 3A'')		2.787	2.788	2.788
	4.419 (8 3A')		4.421	4.421	4.421		2.934 (10 3A')		2.939	2.939	2.940
	4.435 (9 3A'')		4.436	4.436	4.438		2.943 (7 3A'')		2.948	2.949	2.952
	4.436 (9 3A')		4.438	4.440	4.440		3.144 (8 3A'')		3.150	3.151	3.152
	4.536 (10 3A')		4.528	4.528	4.539		3.301 (9 3A'')		3.305	3.306	3.306
	4.540 (10 3A'')		4.543	4.554	4.557		3.338 (10 3A'')		3.343	3.343	3.344

表A1FeB₂₀ and Fe₂B₂₀团簇所计算能态在未考虑SOC和考虑SOC之后的能量值(单位: eV)
TableA1.Energy values of the calculated states of clusters FeB₂₀ and Fe₂B₂₀ before and after the inclusion of SOC (in eV)