摘要:采用时域有限差分方法从理论和数值上提出了一种基于临界耦合和导模共振的单层二硫化钼的四波段完美吸收器, 通过阻抗匹配和耦合模理论可以更好地分析其物理机理. 单层二硫化钼被放置在二氧化硅与具有周期性长方体空气槽结构的二维聚甲基丙烯酸甲酯层中间. 利用导向共振的临界耦合原理得到了单层二硫化钼的高效光吸收, 即在共振波长(λ₁ = 510.0 nm, λ₂ = 518.8 nm, λ₃ = 565.9 nm, λ₄ = 600.3 nm)获得了4个共振完美吸收峰, 吸收率分别为99.03%, 98.10%, 97.30%和95.41%, 同时平均吸收率在可见光光谱范围高达97.46%, 是裸单层二硫化钼的12倍以上. 从模拟结果来看, 调节结构的几何参数可以来控制单层二硫化钼的共振波长的范围, 这对提高单层二硫化钼的吸收强度和选择性具有重要的现实意义. 利用临界耦合来增强光-二氧化硅相互作用的新思想也可以应用于其他原子级薄材料. 同时, 本文也讨论了吸收器的传感性能, 发现传感器的最高品质因子、灵敏度与品质因数最高分别为1294.1, 155.1 nm/RIU和436. 这些结果表明, 所设计的结构可能为改善二维过渡金属二元化合物中的光-物质相互作用开辟有前景的技术, 并在波长选择性光致发光和光电探测中有着极好的应用前景.
关键词: 临界耦合/
二硫化钼/
完美吸收/
可见光光谱范围

English Abstract

全文HTML

--> --> -->

超材料是一种可以被用来控制电磁波并产生特殊光学特性的人造材料, 其由于具有非常规的电磁特性, 可以应用于负介质^[1-3]、完美透镜^[4]和光学隐形^[5,6], 从而得到了大家的广泛关注. 同时, 一些基于平面超材料的光学元件也具有小型化和集成化的特点. Landy等^[7]证明, 微波放大器的整体尺寸可以通过与自由空间的阻抗匹配在微波频率下提供更完美的吸收, 故到目前为止, 已经提出了许多偏振模色散, 显示出在各种领域的实际应用, 如传感^[8]、成像^[9]、隐身^[10]、光电探测器^[11]和光热转换^[12]等.
近年来, 二维(two-dimentional, 2D)材料^[13,14]因其显著的电学和光学性质而受到广泛关注, 例如石墨烯^[15]、六方氮化硼^[16]及过渡金属二硫化物^[17]. 石墨烯是一种层状二维材料, 由于它的高载流子迁移率、可调谐性和宽带响应等独特的特点, 令其已成为设计太赫兹吸收器最有前景的材料之一, 例如, Zhang等^[18]通过将石墨烯与图案化金属谐振器结合, 设计了一种极化不敏感的宽带吸收器结构; Li和Sun^[19]通过基于伞形石墨烯超表面的经典三层结构设计出了多频带可调谐的太赫兹吸收器. 然而, 虽然单层石墨烯拥有很大的可研究性, 但由于它始终具有零带隙, 因此在器件应用方面存在一定的缺陷性. 与石墨烯不同, 当过渡金属二元化合物(transition metal dichalcogenides, TMDCs) (如二硫化钼、二硒化钼、二硫化钨和二硒化钨)从宏观结构转化为2D单层结构时, 它们会成为直接带隙半导体^[20,21]. 同时TMDCs是在单层厚度下具有独特性质的新型半导体, 它所具有的光电特性引起了研究者的关注^[22]. 其中, 二硫化钼(molybdenum disulfide, MoS₂)是最典型的过渡金属硫属化合物, 它的直接带隙约为1.8 eV^[23], 在电子跃迁方面有很重要的作用. 与此同时, 因为MoS₂的直接带隙和低暗电流的特殊性质, 它被认为是更优选的2D原子级薄材料, 用于光电检测^[24]、光致发光^[25]、场效应晶体管^[26]以及光伏器件^[27]. 但是, 尽管MoS₂在光子学和光电子学应用领域的潜力很大, 但由于其固有的原子厚度使得光-物质相互作用被严重破坏, 从而导致极低的光发射和吸收^[28], 这将阻碍MoS₂应用于实际光电子器件领域. 例如, 在可见光光谱范围内, 厚度为6—7 ?的单层MoS₂的平均光吸收约为10%^[29]. 因此, 提高光-物质相互作用和光吸收的研究将在基于MoS₂的光电器件领域有着极大的发展潜力.
迄今为止, 人们在提高单层MoS₂对光的吸收方面已经有了大量的研究, 通过几种物理方法可以增强单层MoS₂和入射光之间的相互作用. 一种由于激发了高约束的塔姆等离激元模式的多层光子结构被Lu等^[30]提出, 单层MoS₂在可见光光谱范围内的绝对吸收率可达96%. Cao等^[31]设计了一种新式银光栅与分布式布拉格反射器相结合的结构, 通过银光栅的等离子共振效应作用, 可以在420至700 nm的波长范围内得到59%的平均吸收. 单层MoS₂在啁啾平面电腔中, 平均可见光吸收达到33%^[32]. 导向共振光子晶体与MoS₂相互作用, 在可见光光谱范围内吸收率为51%^[33]. 在高效光催化、光致发光和光电探测等应用方面, 具有动态波长选择特性与超高效率光吸收的多波段吸收峰的MoS₂吸收结构是不可或缺的, 但相关结构却鲜有报道.
本文利用临界耦合与导向共振提出了一种基于单层MoS₂的完美吸收器. 与现有的研究对比, 我们提出的方案可以更有效地增强单层MoS₂的光-物质相互作用, 实现了单层MoS₂的多波段可调谐超高效率的光吸收. 同时, 时域有限差分法(finite difference time domain, FDTD)模拟表明, 模拟结果与理论计算符合良好. 此外, 单层MoS₂的工作波长和吸收效率的变化与结构的周期、介质层厚度参数的大小密切相关. 因此, 本文研究方法将能在增强原子级2D材料中的光-物质相互作用方面起到更明显的效果, 同时也分析了吸收器的品质因子和普适性. 因此, 该共振结构为在可见光光谱范围内的基于TMDC可调谐多波段MoS₂完美吸收器的设计提供了不一样的研究途径, 其可用于设计制造光电探测器、化学传感器、光开关和调制器等众多光电器件.

图1(a)显示了我们所设计结构的三维(three-dimensional, 3D)示意图, 单层MoS₂被放置在二氧化硅(SiO₂)层与具有周期性长方体空气槽结构的二维聚甲基丙烯酸甲酯(PMMA)层中间. 吸收器的最底部使用银(Ag)层, 作为反射层.
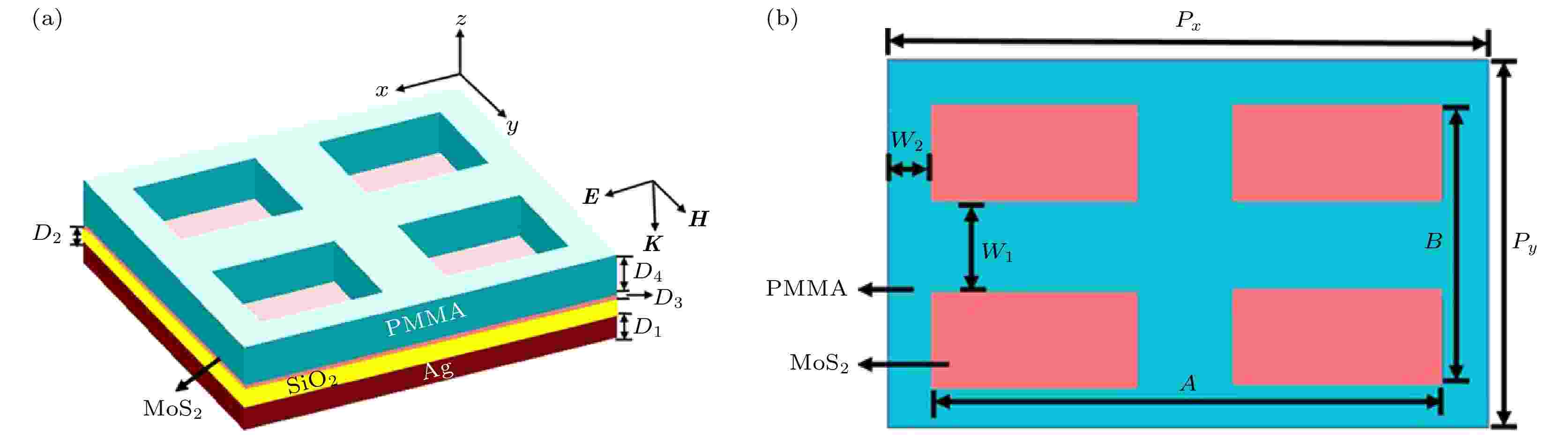图 1 (a) 单层MoS₂吸收增强系统的3D示意图; (b) 对应的俯视图; 具体的几何参数如图中所示
Figure1. (a) 3D schematic diagram of monolayer MoS₂ absorption enhancement system; (b) the corresponding top view. The specific geometric parameters are shown in the figure.

周期性长方体空气槽中的介质被设定为空气, 其折射率为1. 空气槽的深度与PMMA层的厚度一致表示为D₄, MoS₂层的厚度表示为D₃, SiO₂层和Ag反射层厚度分别表示为D₂和D₁. 空气吸收器的长方体空气槽被引入到每个单元中, 如图1(b)所示, 晶格的周期在x和y方向上表示为P_x和P_y. 空气吸收器的空气槽由四个长方体空气槽嵌入等厚的PMMA层形成. 在x和y方向每个空气槽距离边缘的宽度均为W₂, 两个空气槽之间的短间距为W₁. 同时, x方向上两个长方体之间长间距为A, y方向上两个空气槽之间长间距为B. 本文将吸收器在临界耦合状态时的结构参数当作整个性能分析部分的最优数据. 因此最优数据如下: 空气槽与PMMA层的厚度D₄ = 380 nm, SiO₂层的厚度D₂ = 175 nm, Ag层的厚度D₁ = 220 nm, 周期P_x = 1010 nm, P_y = 890 nm, 短间距W₁ = 89 nm, 宽度W₂ = 170 nm, 长间距为A = 832 nm, B = 712 nm. 在数值计算中, 我们的模拟采用了Li等^[34]实验测量得到的厚度为D₃ = 0.615 nm的单层MoS₂的波长相关复介电常数, MoS₂层的光吸收利用公式$ {A}_{\mathrm{M}\mathrm{o}{\mathrm{S}}_{2}}=\left|{P}_{\mathrm{t}}-{P}_{\mathrm{b}}\right|/{P}_{\mathrm{i}\mathrm{n}} $来计算, 其中P_t和P_b分别代表通过MoS₂层顶部和底部的功率, P_in表示入射光功率. PMMA和SiO₂的折射率分别为1.48和1.45. 本文基于Drude模型, 通过$ {\varepsilon }_{\infty } $ = 3.7, 等离激元频率w_p = 1.38 × 10¹⁶ s^–1, 阻尼常数γ = 2.73 × 10¹³ s^{–1 [35,36]}来表示Ag的复介电常数. Drude模型为^[37]

$\varepsilon \left(w\right)={\varepsilon }_{\infty }-\frac{{w}_{\mathrm{p}}^{2}}{\left({w}^{2}+\mathrm{i}\gamma w\right)}.$

在模拟过程中, 选取TM (电场E的方向和x方向平行)偏振模式下的正入射光, 垂直投射到结构上, 即θ = 0°. 本文的数值模拟通过使用基于FDTD方法的软件Lumerical Solutions进行. 关于边界条件的设置: 平行于x和y方向上选用周期边界条件, 而在垂直于z方向上添加完美匹配层, 即PML边界条件.

我们都知道使用共振可增强光吸收, 可是在可见光光谱范围中, 强共振并不会出现在单层MoS₂中. 因此, 通过将MoS₂层与谐振结构相结合产生谐振作用来弥补这个缺陷. 此外, 单层MoS₂高透光率的特性可以降低对谐振器的干扰, 令其降至最小. 首先, 通过FDTD模拟仿真了光垂直入射到MoS₂基结构上的情况, 如图2(a)所示, 计算了吸收器中的单层MoS₂ (蓝线)的吸收光谱. 为了进行比较, 也计算了无MoS₂时, 整个吸收器(红线)和单层MoS₂ (黑线)悬浮在空气中的光吸收光谱. 单层MoS₂在可见光光谱范围内的共振波长下(λ₁ = 510.0 nm, λ₂ = 518.8 nm, λ₃ = 565.9 nm, λ₄ = 600.3 nm)实现了四波段完美吸收, 而在相同的吸收波长下, 单层二硫化钼在空气中的吸收仅为8%. 由于我们所设计的吸收器中Ag衬底的厚度被设定为远厚于电磁波渗透深度的D₁ = 220 nm ^[38], 因此吸收器的透射率非常接近于0 (即T = 0), 即其为单端口耦合. 因此, 耦合模式理论(coupled-mode theory, CMT)与导向共振能够被用来解释该结构的固有性质^[39-41]. 谐振器的输入-输出特性就可以使用CMT来说明, 其中存在直接通道和间接通道, 通过两通道之间的相干干扰, 来解释吸收的增强与抑制. 我们假设在谐振器中有一个w₀的单个谐振, 其输入和输出波的振幅分别为u和y. 单层MoS₂的本征损失率为δ, 谐振腔的外漏率为γ_e. 该结构的反射系数可表示为
图 2 (a) 在D₁ = 220 nm, D₂ = 175 nm, D₃ = 0.615 nm, D₄ = 380 nm, P_x = 1010 nm, P_y = 890 nm, W₁ = 89 nm, W₂ = 170 nm, A = 832 nm, B = 712 nm时完美吸收器中的MoS₂单层(蓝线)的吸收光谱, 为了进行比较, 示出了无MoS₂整个吸收器(红线)和裸MoS₂单层(黑线)的光吸收光谱(图中Mode A对应吸收峰1, Mode B对应吸收峰2, Mode C对应吸收峰3, Mode D对应吸收峰4); (b)理想吸收峰的有效阻抗的实部(蓝线Re(Z))和虚部(绿线Im(Z))
Figure2. (a) Absorption spectrum of MoS₂ monolayer (blue line) in the perfect absorber at D₁ = 220 nm, D₂ = 175 nm, D₃ = 0.615 nm, D₄ = 380 nm, P_x = 1010 nm, P_y = 890 nm, W₁ = 89 nm, W₂ = 170 nm, A = 832 nm, B = 712 nm. For comparison, the light absorption spectra of the entire absorber without MoS₂ (red line) and bare MoS₂ monolayer (black line) are shown (Mode A corresponds to absorption peak 1, Mode B corresponds to absorption peak 2, Mode C corresponds to absorption peak 3, Mode D corresponds to absorption peak 4); (b) the real part (blue line Re(Z)) and imaginary part (green line Im(Z)) of the effective impedance showing the ideal absorption peak.

$\varGamma =\frac{y}{u}=\frac{\mathrm{j}\left(w-{w}_{0}\right)+\delta -{\gamma }_{\mathrm{e}}}{\mathrm{j}\left(w-{w}_{0}\right)+\delta +{\gamma }_{\mathrm{e}}}.$

利用A = 1–|Γ |²计算光吸收. 结合(2)式得

$A=1-{\left|\varGamma \right|}^{2}=\frac{4\delta {\gamma }_{\mathrm{e}}}{{\left(w-{w}_{0}\right)}^{2}+{\left(\delta +{\gamma }_{\mathrm{e}}\right)}^{2}}.$

从(2)式和(3)式可以发现, 当结构在w = w₀的导向共振下, 单层MoS₂的固有损失率等于导向共振(δ = γ_e)时的外部泄漏率, 也就是说外部泄漏率和固有损耗率相等是实现近单位吸收的必要条件. 在所有满足临界耦合条件的入射光中, 导向共振的泄漏率等于单层MoS₂的本征损耗率, 此时反射系数消失, 所有入射功率都被其吸收(A = 1), 则达到了临界耦合状态.
除此之外, 在宏观电磁学的层面, 当满足临界耦合条件时, 结构的阻抗将会与自由空间的阻抗(Z₀ = 1)相等. 使用下列公式来研究完美吸收器的有效阻抗:

$Z\left(w\right)=\sqrt{\frac{{\left(1+{S}_{11}(w)\right)}^{2}-{S}^{2}_{21}{(w)}}{{\left(1-S_{11}(w)\right)}^{2}-{S}^{2}_{21}{(w)} }}. $

式中, S₁₁(w)和S₂₁(w)分别代表与反射率和透射率相关的散射参数. 当系统的有效阻抗与自由空间阻抗匹配时, 由于反射被抑制, 产生了导向共振, 最终得到完美吸收^[42]. 参数反演的相对阻抗谱如图2(b)所示, 在4个共振波长处, 系统的有效阻抗的实部数值上接近于1, 同时虚部数值上接近于0, 那么系统的反射将被有效地抑制(即S₁₁(w) = 0), 这表示我们所设计的结构收获了一个好的阻抗匹配效果. 同时所有数值结果与理论分析完全相同, 吸收器被证明在四波段共振波长处达到临界耦合状态.
图3(a)和图3(b)分别为正常TM偏振光下含和不含银层结构的吸收、反射和透射光谱的数值计算. 从图3(a)可知, 所设计的结构在可见光光谱范围内的四个共振波长下(λ₁ = 510.0 nm, λ₂ = 518.8 nm, λ₃ = 565.9 nm, λ₄ = 600.3 nm)获得了完美吸收, 吸收率分别为99.03%, 98.10%, 97.30%和95.41%, 同时平均吸收率高达97.46%. 这四个完美吸收峰分别被定义为Mode A, B, C和D. 其共振吸收峰的半峰全宽(full width at half maximum, FWHM)分别为1.939, 1.515, 7.625和2.093 nm, 品质因子($Q\text{-factor} $$ = \lambda /\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}$)分别为263.03, 342.44, 74.22和286.79.
图 3 正常TM偏振光下含(a) 和不含 (b) 银反射层结构的吸收、反射和透射光谱的数值计算, 其中A代表吸收, R代表反射, T代表透射
Figure3. Numerical calculation of the absorption, reflection and transmission spectra of the structure with (a) and without (b) silver layer under normal TM polarized light, where A represents absorption, R represents reflection, and T represents transmission.

由于FWHM较窄, 这也令此吸收器在传感器检测领域拥有更大的优势. 如果吸收器不包含Ag反射层, 如图3(b)所示, 由于穿过该吸收器的电磁波显著增大, 导致结构的透射率将不再如图3(a)所示为零. 此研究结果也正面验证了超材料吸收器的理论, 在超材料吸收器中, 金属层会阻止电磁波通过吸收器, 从而导致零传输.
当入射光垂直入射到吸收器时, 周期性超单元的图案化PMMA可以支持面内引导模式, 该模式通常被图案化PMMA强烈限制而不与外部辐射耦合. 我们模拟仿真了上述最优参数下改变空气槽形状时的吸收光谱, 如图4所示. 从图4可以明显地看出, 三种情况下, 长方体空气槽((图4(a))对应的吸收器表现出最优的吸收特性. 而在相同结构参数下, 交叉椭圆盘空气槽(图4(b))和三棱柱空气槽(图4(c))对应的吸收器所产生的吸收光谱却杂乱无章, 并且吸收峰的吸收率也没有达到完美吸收. 这说明长方体周期单层MoS₂基完美吸收器在光吸收性能方面具有较大的研究价值和实际应用价值.
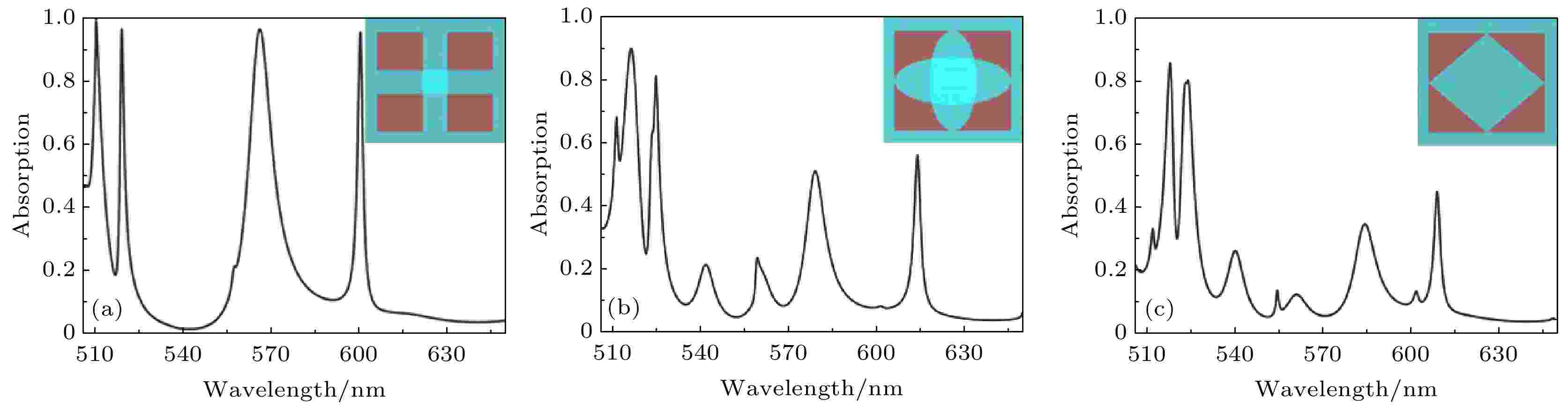图 4 在D₁ = 220 nm, D₂ = 175 nm, D₃ = 0.615 nm, D₄ = 380 nm, P_x = 1010 nm, P_y = 890 nm, A = 832 nm, B = 712 nm条件下, 空气槽为(a) 长方体、(b) 交叉椭圆盘与 (c) 三棱柱时的吸收光谱
Figure4. Absorption spectra when the air groove is (a) cuboid, (b) cross-elliptic disk, (c) triangular prism. D₁ = 220 nm, D₂ = 175 nm, D₃ = 0.615 nm, D₄ = 380 nm, P_x = 1010 nm, P_y = 890 nm, A = 832 nm, B = 712 nm,

除此之外, 绘制了518.8 nm (共振波长)和542.0 nm (非共振波长)条件下x -y, y -z和x -z三个截面的电场(|E|)分布. 通过图5(a)—(f)来对比和讨论同一谐振模式的临界耦合和非临界耦合的横向电场图. 在临界耦合状态下, 当腔被触发(共振模式)时^[43], 出现图2(a)中蓝色曲线的吸收峰Mode B (518.8 nm), 如图5(a)—(c)所示, 在此共振波长处, 单层MoS₂周围的电场强度分布显著增强, 而吸收器没有受到刺激. 与之不同的是, 当在非临界耦合状态时, 即542.0 nm的非共振波长下, MoS₂层周围的电场强度分布很弱, 此时无损系统的反射系数为1, 如图5(d)—(f)的电场分布图所示, 系统在该波长下发展到过耦合条件. 对比共振波长与非共振波长的x -y截面电场, 其位于结构的上方, 在共振波长518.8 nm处, 大部分电场分布在空气槽的单层MoS₂周围, 而空气槽位置的电磁场由于共振几乎被MoS₂完全吸收. 但在非共振波长(542.0 nm)处的x -y截面电场强度由于x方向谐振腔内的入射光场未被完全消耗掉, 所以结构在共振模式时的吸收强度明显比非共振模式大. 而y -z电场分布处于共振时, 电场主要分布在y方向的两端形成驻波模式, 而非共振情况下的电场图显示出整体强度不高. 最后x -z方向上的共振和非共振模式也有着一样的特点.
图 5 MoS₂吸收器在(a)?(c) 共振模式B (共振波长为518.8 nm)下x -y, y -z和x -z截面的电场(|E|)分布的模拟结果; 在垂直入射下, (d)?(f) 非共振模式(非共振波长542.0 nm)时其x -y, y -z和x -z截面的电场(|E|)分布的模拟结果
Figure5. Simulated electric field (|E|) distributions of (a)?(c) resonance mode B (resonant wavelength of 518.8 nm) in x -y, y -z and x -z based on the MoS₂ absorber; (d)?(f) simulated electric field (|E|) distributions of non-resonant mode (non-resonant wavelength 542.0 nm) in x -y, y -z and x -z under normal incidence.

图6给出了四个共振波长在x -y, y -z和x -z三个截面的不同剖视图, 以此阐述临界耦合所带来的光吸收增强的物理机制. 图6(a)—(d)、图6(e)—(h)与图6(i)—(l)分别代表四个共振波长达到临界耦合状态时在x -y, y -z和x -z三个截面的电场剖视图. 四个共振模式在结构中有着不同的位置, 其所对应的共振峰对应不同阶数的GMR (guided mode resonance): 510.0 nm的零阶GMR (即GMR0模), 518.8 nm的一阶GMR (即GMR1模), 565.9 nm的二阶GMR (即GMR2模), 以及600.3 nm的三阶GMR (即GMR3模). 共振吸收效应因为MoS₂周围的传导模式捕获入射光产生. MoS₂层周围的局部电磁场能量被MoS₂吸收, 进而能有效地提升器件的吸收强度. 在这里, 以GMR0模为例, 可以看见周期模式沿y方向形成典型的驻波剖面, 这说明系统中存在GMR. 所以当入射波和泄漏的侧向波导模式之间的相位匹配得到满足时, 可以成功激发GMR^[44-46].
图 6 (a)?(d) x -y截面的电场图; (e)?(h) y -z截面的电场图; (i)?(l) x -z截面的电场图 (图中Mode A对应吸收峰1, Mode B对应吸收峰2, Mode C对应吸收峰3, Mode D对应吸收峰4, λ₁ = 510.0 nm, λ₂ = 518.8 nm, λ₃ = 565.9 nm, λ₄ = 600.3 nm)
Figure6. (a)?(d) Electric field diagrams of the x -y cross section; (e)?(h) the electric field diagrams of the y -z cross section; (i)?(l) the electric field diagrams of the x -z cross section. Mode A corresponds to absorption peak 1, Mode B corresponds to absorption peak 2, Mode C corresponds to absorption peak 3, Mode D corresponds to absorption peak 4. λ₁ = 510.0 nm, λ₂ = 518.8 nm, λ₃ = 565.9 nm, λ₄ = 600.3 nm.

在通过上述的讨论后, 可以发现实现临界耦合的关键点是令外部泄漏率等于固有损失率. 同时, 也可以发现在可见光光谱范围内, 结构的固有损耗主要来自MoS₂, 其吸收几乎与作用波长无关, 固有损失率基本没有变化. 结构的几何参数可以调节外部泄漏率的大小, 且结构的泄漏率对耦合谐振峰值波长有所贡献. 因此, 为了更好地理解该器件临界耦合机制, 接下来首先讨论关于SiO₂厚度D₂与该结构的外漏率γ_e之间的关系, 以及改变两个长方体空气槽之间的短间距W₁对MoS₂吸收强度的影响, 结果如图7(a)和图7(b)所示. 如图7(a)所示, 当D₂从155 nm增至195 nm (间隔为10 nm), 四个共振吸收峰产生了红移, Mode A—C的吸收强度均是先增大后减小, Mode D吸收强度随着D₂的厚度增大而增大. 如图7(b)所示, 当长方体空气槽之间的短间距W₁的宽度从170 nm增长到210 nm (间隔为10 nm)时, Mode A—D的吸收峰值位置呈现出红移的变化, 且吸收强度均下降. 这个过程中, 谐振器的外漏率γ_e不断增大, 光吸收的变化趋势与耦合状态对应, 展示了该系统结构经历未耦合、临界耦合和过耦合的三种状态, 同时, 可以发现在D₂ = 175 nm和W₁ = 170 nm处出现了具有临界耦合的四波段完美吸收. 这些现象都说明这个结构具有良好的吸收峰可调谐性.
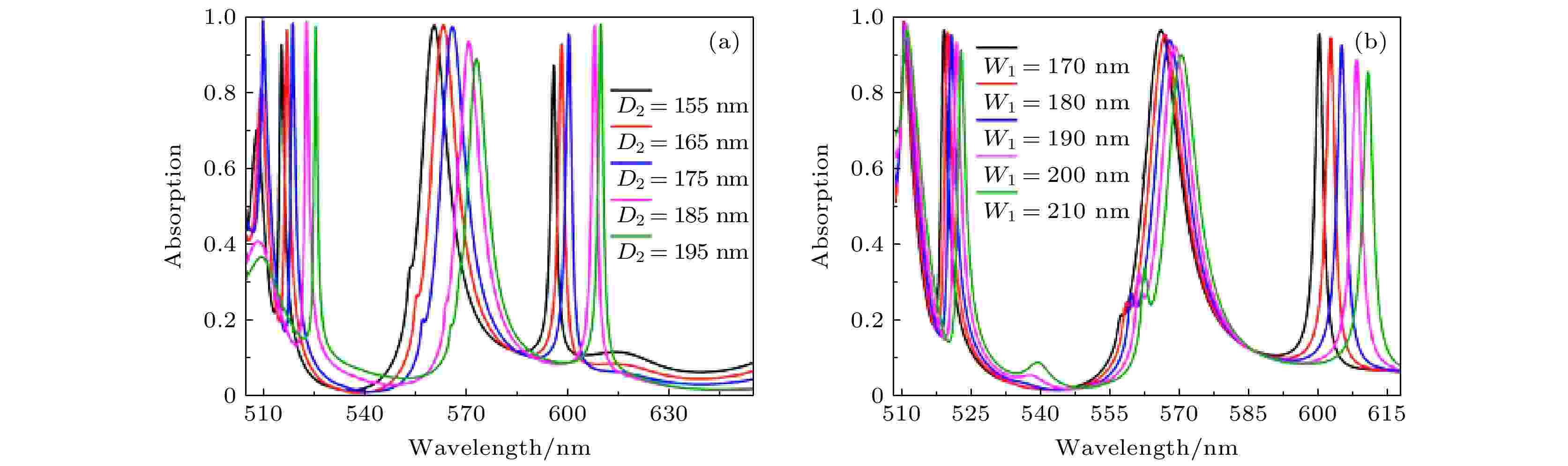图 7 (a) 当D₂从155 nm增长到195 nm时, 结构对应的光吸收情况; (b) 当W₁从170 nm增长到210 nm时, 结构对应的光吸收情况
Figure7. (a) Corresponding light absorption of the structure when D₂ increases from 155 to 195 nm; (b) the corresponding light absorption of the structure when W₁ increases from 170 to 210 nm.

此部分, 将探讨吸收器在不同PMMA厚度D₄以及W₂下的吸收特性和外漏率γ_e之间的关系. 在图8(a)中, 当D₄从330 nm增加到430 nm (间隔25 nm)时, Mode A—D的吸收率同时先增大后减小, 且在D₄ = 380 nm时同时达到完美吸收的效果. 在图8(b)中, 四个模式共振峰随着D₄的增大发生明显的红移, 且成正比变化. 同时在图8(c)可以发现当W₂从79 nm增大到129 nm时, Mode A, B和C的吸收光谱同时在W₂ = 89 nm时达到临界耦合, 而在图8(d)中其波长与W₂的关系图与图8(b)变化趋势一样(如补充材料图S1 (online)所示). 综上所述, 此吸收器具有相对较大的制造容纳度, 通过适当调整几何参数, 可以实现单层MoS₂在可见光光谱范围下的可调谐超高效光吸收.
图 8 (a) D₄与吸收率的关系图; (b) D₄与对应共振波长范围的关系图; (c) W₂与吸收率的关系图; (d) W₂与对应共振波长范围的关系图; 图中Mode A对应吸收峰1, Mode B对应吸收峰2, Mode C对应吸收峰3, Mode D对应吸收峰4
Figure8. (a) Relationship diagram between D₄ and the absorption rate; (b) the relationship diagram between D₄ and the corresponding resonance wavelength range; (c) the relationship diagram between W₂ and the absorption rate; (d) the relationship diagram between W₂ and the corresponding resonance wavelength range. Mode A corresponds to absorption peak 1, Mode B corresponds to absorption peak 2, Mode C corresponds to absorption peak 3, Mode D corresponds to absorption peak 4.

众所周知, 周期的改变对于超材料表面共振模式的频率有着极大的影响^[47-49]. 接下来将探究吸收器在不同周期P下的吸收特性和外漏率γ_e之间的关系, 如补充材料图S2和图S3 (online)所示.
当确定了吸收器的其他几何结构参数后并且达到临界耦合状态时, 讨论了周期与吸收峰波长和品质因子的函数关系, 如图9(a)—(d)所示. 当P_x增加时, 结构的品质因子有着四种不一样的变化趋势: Mode A的品质因子先减小后增加; Mode B的品质因子随着周期P_x增大而增大; 而Mode C的品质因子变化与其共振波长相类似, 均变化不明显; 最后, Mode D的品质因子与其对应的波长变化成反比, 品质因子随着周期P_x增大而增大. 除此之外, 当P_y增加时, 结构的品质因子也有着四种完全不同的变化: Mode A的品质因子先减小后增加; Mode B的品质因子与Mode A完全相反, 先增加后减小; 而Mode C的品质因子先减小后增加; Mode D的品质因子与Mode B的品质因子变化趋势相似, 都为先增加后减小. 综上所述, 在周期为P_x = 1050 nm处最大的品质因子为1294.1, 对应的FWHM与共振波长分别为0.4 nm和531.9 nm.
图 9 (a)?(d) 保持其他参数不变, 周期与吸收峰波长和品质因子的函数关系(图中Mode A对应吸收峰1, Mode B对应吸收峰2, Mode C对应吸收峰3, Mode D对应吸收峰4)
Figure9. (a)?(d) Relationship among the period, the absorption peak wavelength, and Q-factor (quality factor) when other parameters are kept constant (Mode A corresponds to absorption peak 1, Mode B corresponds to absorption peak 2, Mode C corresponds to absorption peak 3, Mode D corresponds to absorption peak 4).

表1列出了本文吸收器与其他类似结构^[30,50-54]的性能参数的对比, 其中P_x =1050 nm, 发现我们提出的吸收器具有相对较高的品质因子.

参考文献	波长/nm	半峰全宽/nm	品质因子
[30]	662	11.5	57.57
[50]	1500	20	75
[51]	679.2	8.72	77.89
[52]	663	11.35	58.32
[53]	661	9	73
[54]	408	7.34	55.59
本文	531.9	0.4	1294.1

表1所提出的吸收器与其他类似吸收器的比较
Table1.Comparisons of the proposed absorber with other similar absorbers.

吸收器的传感性能会影响其应用领域, 因此我们分析了所设计结构的传感性能, 如图10所示. 这里, n是吸收器周围介质的折射率, 调节n的大小, 从1.00增大到1.08. 从图10(a)可以看出, 四个共振吸收峰的变化清晰可见, 随着n的增加, 四个共振波长发生红移, 吸收光谱强度呈线性减小. 与此同时, 灵敏度(sensitivity, S)和品质因数(the figure of merit, FOM)都是量化传感器性能的重要依据^[55-57], 将灵敏度定义为单位折射率共振波长的位移, 表示为
图 10 (a) 四个共振峰的吸收光谱随周围介质折射率的变化而移动; (b)?(e)当周围传感介质的折射率发生变化时(折射率从1.0到1.08, 间隔为0.02), 四个峰值的FOM与FWHM和波长的关系图 (图中Mode A对应吸收峰1, Mode B对应吸收峰2, Mode C对应吸收峰3, Mode D对应吸收峰4)
Figure10. (a) Absorption spectra of the four resonance peaks move with the change in the refractive index of the surrounding medium; (b)?(e) when the refractive index of the surrounding sensing medium changes (the refractive index is from 1.0 to 1.08, the interval is 0.02), the relationships of FOM value of the four peaks and FWHM to wavelength (Mode A corresponds to absorption peak 1, Mode B corresponds to absorption peak 2, Mode C corresponds to absorption peak 3, Mode D corresponds to absorption peak 4).

$S=\frac{\Delta \lambda }{\Delta n}.$

同时评估传感器性能的另一个参数FOM可以表示为

$\mathrm{F}\mathrm{O}\mathrm{M}=\frac{S}{\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}}. $

在此, Δλ表示吸收峰的频率随折射率Δn而变化, FWHM是半峰全宽. 由(5)式计算得出, 当Mode D的FWHM为2.1 nm时, 结构的最大灵敏度为155.1 nm/RIU. 图10(b)—(e)中的蓝线与红线分别代表FOM和FWHM在不同介质折射率环境下的变化. 由图10(b)可见, Mode A的FWHM与波长随着周围介质折射率的增加而近似线性上升. 出现此现象的原因可以利用传感介质折射率的增加值可以增加偶极模式的阻尼, 从而增加光谱曲线的半峰全宽来解释. 此外, 这也将导致FOM的减小^[58]. 由图10(c)可见, Mode B的FWHM呈下降趋势, 而其FOM先增大后减小, 当折射率为1.04时, Mode B具有最优的FWHM和FOM, 分别为0.3 nm和436; Mode C的FWHM与FOM的变化趋势都与Mode A刚好相反, 如图10(d)所示, 其FOM与波长随着周围介质折射率的增加而近似线性增大; 最后, Mode D的FWHM与FOM随着折射率n的变化十分多样, 如图10(e)所示.
除此之外, 窄模式半峰全宽与宽模式相比, 相应的吸收器的品质因数会更优, 检测小频移更方便, 模式的定位也更加准确. 在这里, 也列出了一些类似传感器的FOM值, 见表2^[59-64].

参考文献	[59]	[60]	[61]	[62]	[63]	[64]	本文
FWHM/nm	50	8	3.94	97	50	100	0.3
FOM (max)	2.8	25	254	4.68	7.1	3.1	436

表2其他类似吸收器的FOM值的比较结果
Table2.Comparisons of FOM values of other similar absorbers.

上述结果表明, 折射率传感器与折射率紧密相关. 因此, 本吸收器可以用来监测或感测被测试剂的折射率变化. 同时这些高FOM传感器在生物传感器领域有着更大的发展可能性.

本文提出了一种层状结构的完美吸收器, 其由单层MoS₂覆盖在SiO₂层上, 同时在MoS₂层上方有一层具有周期性长方体空气槽的PMMA层, 底部由Ag反射层支撑. 同时也从理论计算与数值模拟两方面证实了单层MoS₂的四波段完美吸收的原因是与导向共振的临界耦合理论对电磁场的强限制以及抑制了在多孔介质中由反射和透射引起的损耗. 单层MoS₂的平均吸收率可以达到高达97.46%, 是裸单层MoS₂的12倍以上. 与此同时也研究了此结构的传感性能, 最终得到吸收器的最高品质因子、灵敏度与品质因数分别为1294.1, 155.1 nm/RIU和436. 因此, 我们的完美吸收器可能在基于TMDC的光致发光、光电探测, 甚至波长选择性超材料吸收剂中有着极大的研究潜力.