摘要:液滴撞击超亲水表面铺展之后形成的薄液膜铺展直径是喷雾冷却、降膜蒸发等传热传质过程的一项关键控制参数. 以往模型在预测超亲水表面惯性力驱动下的最大铺展直径时, 存在低韦伯数下呈反常趋势、高韦伯数下预测值偏低等问题. 针对上述问题, 本文采用高速摄像技术研究液滴撞击过程中的铺展水力学特性, 发现了以往模型未完全考虑超亲水表面的铺展特性: 球冠状液膜、高黏性阻力及重力势能做功. 本文考虑了液膜球冠形态、重力势能、辅助耗散, 修正了以往最大铺展直径的预测模型, 并建立了适用于超亲水表面最大铺展直径的预测模型. 通过对铺展过程中各能量成分分析发现, 在超亲水表面上动能、表面能、重力势能均转化为黏性耗散能, 其中: 在低韦伯数下, 表面能转化为黏性耗散能占主要作用; 在高韦伯数下, 动能转化为黏性耗散能占主要作用. 并且, 在低韦伯数下, 重力势能和辅助耗散的引入对于准确预测超亲水表面最大铺展直径具有重要作用. 将模型预测结果与实验结果比较发现, 本模型成功消除了以往模型在低韦伯数下的反常趋势, 且能较好预测宽韦伯数范围下超亲水表面最大铺展直径. 同时, 本模型可以预测亲水和疏水固体表面的液滴最大铺展直径. 超亲水表面最大铺展直径的准确预测模型的提出对喷雾冷却, 降膜蒸发中提高和控制流体铺展距离和传热效率具有重要意义.
关键词: 超亲水表面/
最大铺展直径/
重力势能/
辅助耗散

English Abstract

全文HTML

--> --> -->

液滴撞击铺展现象广泛存在于诸多工业过程, 如喷雾冷却、降液膜蒸发、喷墨打印、农药喷洒等^[1-4]. 国内外****对于液滴撞击固体壁面铺展过程的诸多影响因素: 流体物性^[5,6]、液滴大小^[7-9]、壁面结构^[10-12]、润湿性^[13,14]、粗糙度^[15]、壁面温度^[16-18]、固体壁面的倾斜角^[19,20]等展开了系统而详尽的研究. 部分****对于无初速度的静态液滴在固体壁面上的铺展特性^[21,22]也进行了深入的探讨.
液滴在惯性力驱动下在固体表面上的最大铺展直径决定着传热传质效率, 对该值进行准确的模型预测具有重要意义. 目前对最大铺展直径的研究主要方法集中于能量守恒、动量守恒和标度律分析. 动量守恒方法^[23]通过求解Navier-Stokes方程获得最大铺展直径的表达式. 标度方法^[24-26]虽然是较为经验型的研究方法, 但是可以获得较为有效的普适性预测关系式. 能量守恒方法基于初始状态和液滴达到最大铺展直径时能量相等的原理, 获得较准确的能量之间的转换关系, 从而得到最大铺展直径的准确预测关系式. 以往基于能量守恒的最大铺展直径的预测典型模型如表1所示, 其中β_m, We, Re, θ, θ_a, σ, ΔE_s分别代表最大铺展因子、韦伯数、雷诺数、平衡接触角、前进角、气液表面张力、表面能变化; C_s, C_k, P, ${\hat R_{\rm{c}}}$, κ, ${\xi _{\rm{r}}}$分别代表动能耗散系数、势能耗散系数、势能、圆环曲率半径、凹陷状修正因子、无因次液环高度. 早在1991年, Chandra和Avedisian等^[27]就开始通过能量守恒研究液滴在壁面上的最大铺展直径, 认为液滴在最大铺展直径时为液饼状, 黏性耗散发生在整个液滴内部, 推导出最大铺展直径的预测模型. 随后Pasandideh-Fard等^[28]认为绝大部分的黏性耗散应发生在黏性边界层内, 该边界层厚度可以通过求解轴对称滞止点流动条件下的层流边界层厚度获得, 并对于黏性耗散进行了修正. 上述模型认为液滴最终形态是饼状并且忽略了侧面的表面能, Mao等^[29]和Ukiwe等^[30]在Pasandideh-Fard等^[28]提出的模型基础上考虑了原先视为液饼状而忽略了的铺展液滴周边高度上的气液表面能. Lee等^[14]对铺展时间进行了修正, 认为铺展时间同样与液体表面张力有关, 从而使得黏性耗散的表达式更加准确. 为解决模型在韦伯数We较小时存在显著误差的问题, Huang等^[31]提出了辅助耗散的概念, 考虑了低We下的界面弛豫现象, 降低了模型在低We下的预测误差. Park等^[32]和Li等^[33]认为液滴的形态为球冠状, 建立了各自的最大铺展直径的预测模型. 在高We下, 液滴会出现边缘-凹陷结构, 即液滴中心部分出现凹坑, 凹坑会随着We增大而逐渐加深. 因此, Gao等^[34]采用了一个环状模型来模拟这个形态, 该模型认为液滴达到最大铺展直径时外侧存在一个截面为半圆形的环, 而内部则被看作是一个圆盘, 并且忽略了它的厚度. Wang等^[35]采用了另一个边缘-圆片模型, 探讨了中心圆片的厚度和大小与We之间的关系, 在不同We下都有着较好的预测效果.

文献	最大铺展模型预测表达式	表面润湿 性/(°)	We	液滴形态
Lee等[14]	$\begin{aligned} \rho {V_0}{D_0} + 12\sigma\qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad \\= 3\sigma (1 - \cos \theta )\beta _{\rm{m} }^2 + 8\sigma \dfrac{1}{ { {\beta _{\rm{m} } } } } + 3\sqrt { {b / c} } \rho V_{\rm{0} }^2{D_0}\beta _{\rm{m} }^{ {5 / 2} }\dfrac{1}{ {\sqrt {Re} } }\end{aligned}$	60—115	1—290	圆饼
Chandra等[27]	$\dfrac{3}{2}\dfrac{ {We} }{ {Re} }\beta _{\rm{m} }^4 + \left( {1 - \cos \theta } \right)\beta _{\rm{m} }^2 - \left( {\dfrac{1}{3}We + 4} \right) = 0$	～32	～43	圆饼
Pasandideh- Fard等[28]	${\beta _{\rm{m} } } = \sqrt {\dfrac{ {We + 12} }{ {3\left( {1 - \cos {\theta _{\rm{a} } } } \right) + 4\left( { { {We} / {\sqrt {Re} } } } \right)} } }$	27—140	27—447	圆饼
Mao等[29]	$\left( {\dfrac{ {1 - \cos \theta } }{4} + 0.35\dfrac{ {We} }{ {\sqrt {Re} } } } \right)\beta _{\rm{m} }^4 - \left( {\dfrac{ {We} }{ {12} } + 1} \right)\beta + \dfrac{2}{3} = 0$	30—120	5—1000	圆饼
Ukiwe等[30]	$\left( {We + 12} \right){\beta _{\rm{m} } } = 8 + \beta _{\rm{m} }^3\left[ {3\left( {1 - \cos \theta } \right) + 4\dfrac{ {We} }{ {\sqrt {Re} } } } \right]$	57—90	18—370	圆饼
Huang等[31]	$\begin{aligned}\frac{3}{4}\left( {\frac{ {We} }{ {\sqrt {Re} } } + \frac{ {We^*} }{ {\sqrt {Re^*} } } } \right)\beta _{\rm{m} }^4 + 3\left( {1 - \cos {\theta _{\rm{a} } } } \right)\beta _{\rm{m} }^3 \qquad\\ - \left( {We + 12} \right){\beta _{\rm{m} } } + 8 = 0, ~~{V_0} < V^* \qquad\qquad\qquad\end{aligned}$ $\begin{aligned} \frac{3}{4}\left( {\frac{ {We} }{ {\sqrt {Re} } } + \frac{ {We^*} }{ {\sqrt {Re^*} } }\frac{ {Re^*} }{ {Re} } } \right)\beta _{\rm{m} }^4 + 3\left( {1 - \cos {\theta _{\rm{a} } } } \right)\beta _{\rm{m} }^3 \\ - \left( {We + 12} \right){\beta _{\rm{m} } } + 8 = 0,~~ {V_0} > V^*\qquad\qquad\qquad \end{aligned}$	64—110	2—500	圆饼
Park等[32]	$\begin{aligned} \left( {0.33\frac{ {We} }{ {\sqrt {Re} } } - \frac{1}{4}\cos \theta + \frac{1}{2}\left( {\frac{ {1 - \cos {\theta _{\rm{a} } } } }{ { { {\sin }^2}{\theta _{\rm{a} } } } } } \right)} \right)\beta _{\rm{m} }^2 \\ - 1 - \frac{ {We} }{ {12} } + \frac{ {\Delta {E_{\rm{s} } } } }{ { {\text{π} }D_0^2\sigma } } = 0 \qquad\qquad\qquad\qquad\quad\end{aligned}$	31—113	0.2—180	球冠
Li等[33]	$\dfrac{ {We} }{ {12} }\left( {1 - {C_{\rm{k} } } - \dfrac{3}{ {2\sqrt {Re} } }\displaystyle\int_{ {H_{\rm{m} } } }^{ {H_{\rm{s} } } } { {d^2}{\rm{d} }h} } \right) = {C_{\rm{S} } }P\left( { {D_{\rm{e} } } } \right) - P\left( { {D_{ {\rm{max} } } } } \right)$	30—150	0—10	球冠
Gao等[34]	$\begin{aligned} 1 + \frac{ {We} }{ {12} } = \frac{1}{6}\left[ {\frac{1}{ { { {\hat r}_{\rm{c} } } } } + \frac{1}{ { { {\hat R}_{\rm{c} } } } } } \right] + 4{\theta _{\rm{a} } }{ {\hat r}_{\rm{c} } }{ {\hat R}_{\rm{c} } } + {\left( { { {\hat R}_{\rm{c} } } - { {\hat r}_{\rm{c} } }\sin {\theta _{\rm{a} } } } \right)^2} \\ + {\left( { { {\hat R}_{\rm{c} } } + { {\hat r}_{\rm{c} } }\sin {\theta _{\rm{a} } } } \right)^2}\left( {\frac{4}{3}\frac{ {We} }{ {\sqrt {Re} } } - \cos {\theta _{\rm{a} } } } \right) \qquad\quad\end{aligned}$	74—155	135—210	圆环
Wang等[35]	$\begin{aligned} We + 12 =\qquad \qquad\qquad \qquad\qquad \qquad\qquad\qquad\qquad\qquad\qquad \qquad\\ \frac{3}{4}\left( {\frac{ {We} }{ {\sqrt {Re} } } + \alpha \frac{ {W{e_{\rm{c} } } } }{ {\sqrt {R{e_{\rm{c} } } } } } } \right)\beta _{\rm{m} }^3 + 3\left( {1 - \cos {\theta _{\rm{a} } } } \right)\beta _{\rm{m} }^2 + 12\bigg\{ \frac{ {\xi _{\rm{r} }^2} }{ { { {\left( {1 - \cos {\theta _{\rm{m} } } } \right)}^2} } } \\ \times \bigg[ {\sin ^2}{\theta _{\rm{m} } } - \frac{ { {\beta _{\rm{m} } } } }{ { {\xi _{\rm{r} } } } }\sin {\theta _{\rm{m} } }(1 - \cos {\theta _{\rm{m} } }) + 2(1 - \cos {\theta _{\rm{m} } }) \bigg] \qquad \qquad \qquad \\ \left. + 2{\xi _{\rm{r} } }\left( {\frac{ { {\beta _{\rm{m} } } } }{2} - {\xi _{\rm{r} } }\frac{ {\sin {\theta _{\rm{m} } } } }{ {1 - \cos {\theta _{\rm{m} } } } } } \right)\left( {\left| {1 - \kappa } \right| + \frac{ { {\theta _{\rm{m} } } } }{ {1 - \cos {\theta _{\rm{m} } } } } } \right) \right\}\qquad\qquad \quad \end{aligned}$	34—100	0.1—427	环状-薄片

表1基于能量守恒的最大铺展因子的预测模型
Table1.Theoretical models for predicting the maximum spreading factor.

Panda等^[36]对超亲水表面黏性阻力进行研究, 发现黏性力与毛细力之比越大的表面亲水性越强, 当该比值大于30 × 10^–4时, 表现出超亲水性, 即超亲水表面上的黏性阻力相较其他表面更大. 对于超亲水表面黏性阻力做功的计算, 按照以往模型对于黏性耗散的处理, 显然预测结果明显偏低. 而上述通过能量守恒模型对不同固体表面上液滴最大铺展直径的研究中, 固体表面主要集中于超疏水、疏水和亲水表面; 对于超亲水表面惯性力驱动的最大铺展直径的研究相对较少. 近年来, 超亲水微纳结构表面在喷雾冷却^[37]、降液膜流动和蒸发^[38]、热管中展现出普通表面所不可比拟的高传热性能, 准确预测超亲水表面上液滴最大铺展直径显得尤为关键. 而超亲水表面相比于疏水或超疏水表面而言, 液膜铺展形态不同, 导致表面能的转化率发生明显变化, 且超亲水表面上黏性力做功比超疏水和疏水表面大很多; 在低惯性力下, 由于超亲水表面液膜的质心较低, 重力势能的变化不可忽略. 如何准确预测超亲水表面的最大铺展直径对于控制铺展面积, 调控传热速率具有重要意义. 虽然已有大量最大铺展直径模型的相关研究, 但上述模型在超亲水表面上并不完全适用; 本文采用能量守恒方法, 将铺展过程中的辅助耗散和重力势能变化纳入考量, 建立了超亲水表面液滴最大铺展直径的预测模型.

2

-->

2.1.实验装置和步骤

如图1所示, 超亲水表面液滴铺展实验系统由高速摄像系统、液滴生成系统、数据采集系统、液滴撞击系统等组成. 液滴撞击平台由恒温加热台和撞击平台组成, 撞击平台为直径为30 mm、高度为11 mm的圆柱体铜块, 且具有4个等间距的1 mm直径的热电偶孔. 铜块上表面暴露于空气中, 而下表面与恒温加热台直接相连, 且涂有导热硅油. 保温装置是由聚四氟乙烯(PTFE)的空心圆柱体构成, 实验证明该保温装置具有良好的隔热效果. 控制恒温台温度, 通过撞击铜块近壁面处插入热电偶测量获得壁面温度. 本实验中工况压力为常压, 作为实验工质的液滴选用去离子水, 液滴温度和壁面温度为20 ℃. 实验中通过直线滑动平台控制针头与表面的距离以控制撞击韦伯数We, 同时保持一台高速摄像机与液滴撞击平台水平, 从正前方拍摄, 而另一台高速摄像从斜上方向拍摄液滴撞击铺展过程. 液滴当量直径D₀ = 2.23 mm, 像素点测量误差为一个像素点尺寸0.0248 mm, 相对误差为1.11%. 直线位移平台的精度为0.03 mm, 热电偶的测量精度为 ± 0.05 ℃, 环境温度和湿度分别为20 ± 2 ℃和40 ± 5%, 本文不考虑环境温度和湿度波动对实验结果产生的误差. 雷诺数Re和韦伯数We如下:
图 1 液滴铺展实验系统(A: 高速摄像机(Photron APX RS); B: 高速摄像机(Photron Mini UX100); C: 微量注射泵(LSP01-1 BH); D: 液滴生成装置; E: 恒温台; F: 高亮光源; G: 数据采集设备; G: 精确自动控制位移的直线位移滑台)
Figure1. The droplet spreading experiment platform. (A: high speed camera (Photron APX RS); B: high speed camera (Photron Mini UX100); C: micro syringe pump (LSP01-1 BH); D: droplet generating device; E: heating platform; F: diffuse light source; G: data acquisition computer; H: linear displacement slide.

$Re = \frac{{\rho {D_0}{V_0}}}{\mu },$

$We = \frac{{\rho {D_0}V_0^2}}{\sigma },$

其中, V₀为液滴撞击速度, ρ为液体的密度, μ为液体黏度, σ为液体表面张力.
2 -->

2.2.超亲水表面的制备与表征

本实验参考Nam等^[39]的方法, 采用氧化刻蚀法制备超亲水表面. 制备过程简述如下: 铜块依次用800目、1000目、1500目、2000目、3000目水磨砂纸仔细打磨, 去离子水冲洗后, 再用丙酮、乙醇、去离子水依次超声洗, 用氮气吹干. 3000目打磨之后的光滑铜表面的电镜图如图2(a)所示, 虽然具有砂纸打磨的微米级条状痕迹, 但表面平整光滑, 无其他微观结构. 之后将铜块放入已充分预热好的Na₃PO₄·12H₂O, NaClO₂, NaOH刻蚀液中, 在96.1 ℃的水浴中氧化刻蚀15 min. 如图2(b)所示, 氧化刻蚀之后表面结构为亚微米级刀片阵列结构, 具有超亲水性, 平衡接触角约为θ = 5° ± 2°.
图 2 (a)光滑铜表面的SEM图; (b)超亲水表面SEM图
Figure2. SEM images of (a) smooth copper surface and (b) superhydrophilic surface.

2

-->

3.1.液滴在超亲水表面撞击铺展特性

液滴在光滑铜亲水表面上撞击铺展过程如图3(a)所示, 球形液滴撞击亲水表面之后, 在惯性力作用下经历5 ms左右铺展到最大铺展直径, 呈现顶部凹陷状形态, 液滴的动能转化为液膜的表面能和铺展过程的黏性耗散. 下一时刻液滴顶部会在表面张力的作用下发生震荡, 直到达到静止. 超亲水表面上撞击铺展的形态如图3(b)所示, 液滴在惯性力的作用下迅速沿径向铺展, 中心高度减小; 更多的液体向边缘铺展, 使得中心的液滴厚度减小形成凹陷. 液膜接触线水平方向上的铺展速度随着铺展半径的增大先增大后减小, 而速度的减小是表面张力和黏性力的共同作用. 液滴接触线逐渐减速的过程中, 凹陷状液膜也会逐渐回缩达到球冠状的平衡态, 在最大铺展直径时液膜形态为球冠状. 图3(b)和图3(c)对比可知, 惯性力作为铺展阶段的主要驱动力, We越高其铺展直径会越大. 液滴铺展因子β随时间的变化关系如图4所示, 超亲水表面上液滴在惯性力作用下快速铺展阶段结束后, 进入毛细力驱动的慢速铺展阶段. 惯性力作用结束后的铺展因子定义为惯性铺展阶段的最大铺展因子β_m. 相比于亲水表面的铺展过程, 超亲水表面由于其低平衡接触角具有铺展直径大, 终态液膜的重心低等特点. 另外, 由于超亲水表面微纳结构的存在, 液滴铺展过程中由于钉扎效应而引起的黏性力做功也会比疏水表面高很多.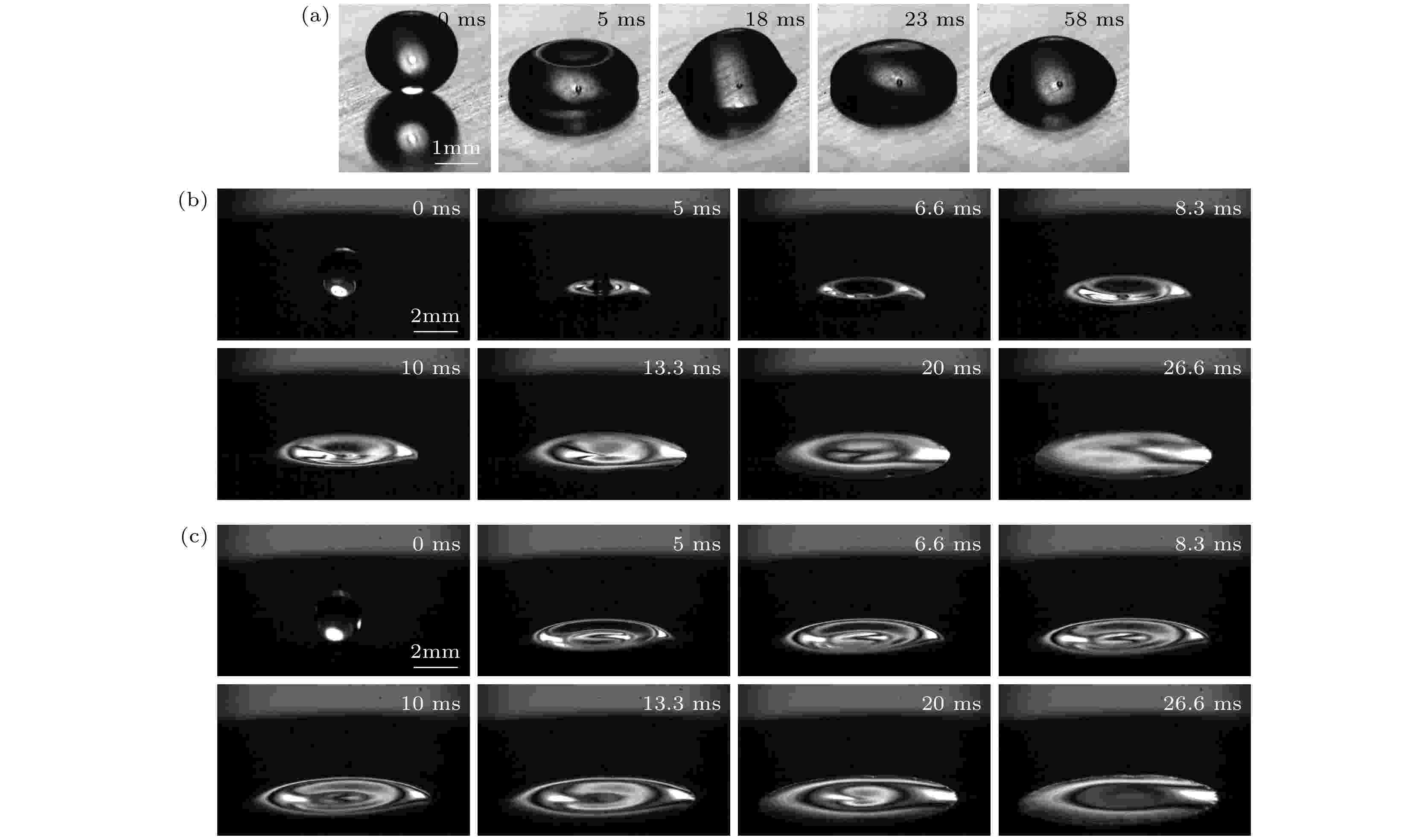
图 3 液滴铺展过程　(a)光滑铜亲水表面; (b)超亲水表面We = 1.91; (c)超亲水表面We = 25.59
Figure3. Droplet spreading process: (a) Smooth copper hydrophilic surface; (b) superhydrophilic surface at We = 1.91; (c) superhydrophilic surface at We = 25.59.

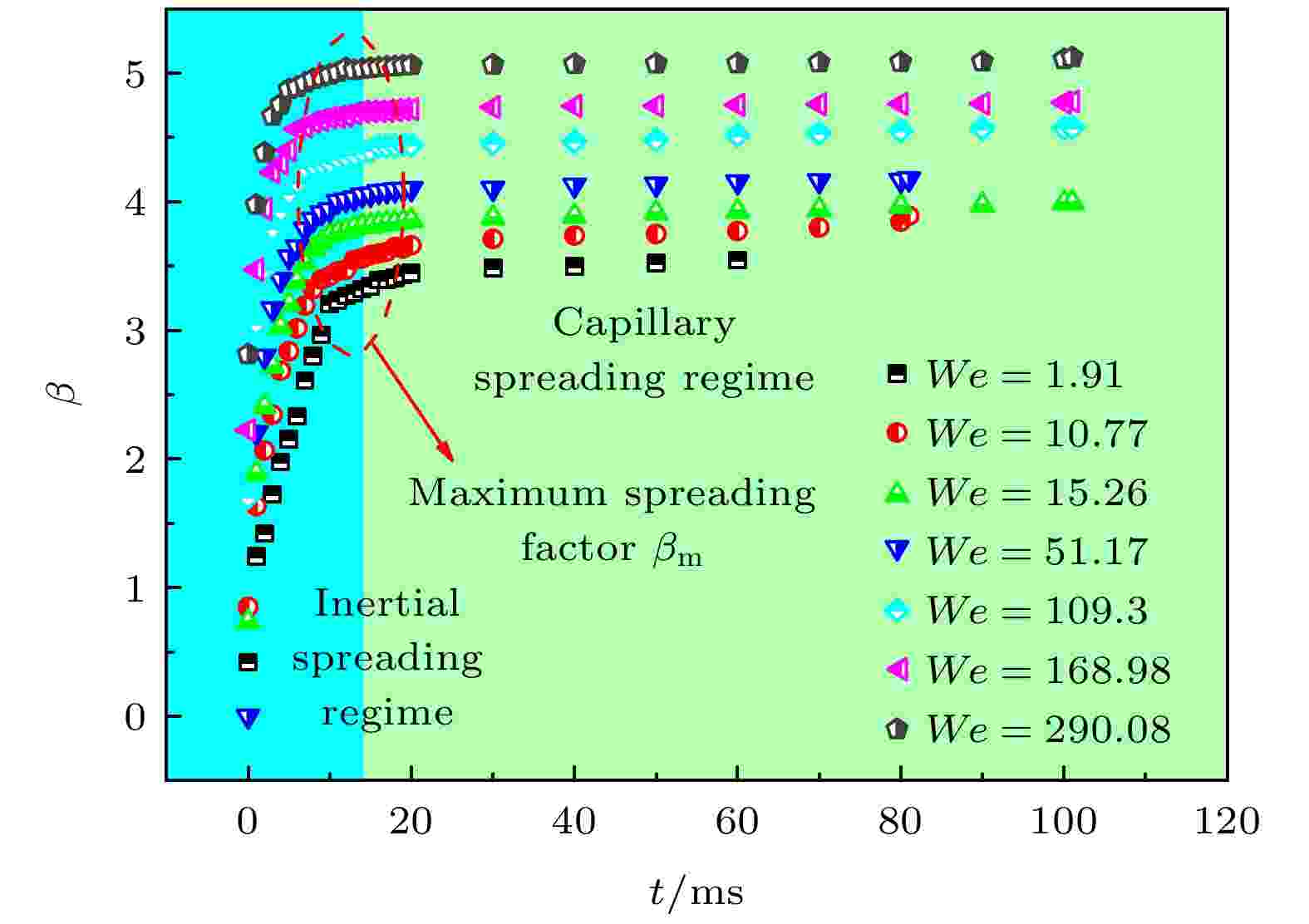图 4 液滴在不同We下撞击超亲水表面铺展因子随时间的变化过程
Figure4. The variation of spreading factor β with time

选取典型模型与实验结果对比如表2所示, 其中典型的对比模型分别是Chandra等^[27], Pasandideh-Fard等^[28], Mao等^[29], Park等^[32], Ukiwe等^[30], 以及Huang等^[31]的模型. Pasandideh-Fard等^[28]和Ukiwe等^[30]的模型在We > 50时能合理预测实验结果, 但是在We < 50时存在明显的反常现象, 上述两个模型均将液滴达到最大铺展直径时形态处理为圆饼状, 只考虑了饼状液膜的上下面积, 忽略了侧面积. 然而由于超亲水表面的表观接触角很小, 液滴形态更接近球冠状而不符合圆饼状的形态. 此外上述模型并未考虑重力势能做功和辅助耗散. 这是上述模型预测超亲水表面液滴最大铺展直径存在较大误差的原因. Chandra等^[27], Mao等^[29]及Huang等^[31]的模型同样在低We范围下存在反常现象, 而且在高We范围下预测值明显偏低; 这是由于Chandra等^[27]和Mao等^[29]未考虑重力势能和辅助耗散, 同时认为液膜形态是饼状, 并不是超亲水表面上的球冠状. Huang等^[31]虽然考虑了辅助耗散, 但是其对液膜最大铺展直径形态的修正并不适用于超亲水表面. 另外Park等^[32]和Li等^[33]采用了液膜形态为球冠状模型, 从液膜形态考虑, 该模型在亲水或超亲水的表面上显然是更加接近实际情况, 但是对于黏性耗散和重力势能的做功并未考虑, 故在低We下预测值比实际高很多, 且呈现反常趋势. 超亲水表面上液滴铺展过程中的黏性阻力显著增大, Lee等^[14]和Vadillo等^[40]认为在低We下疏水或超疏水表面上的黏性耗散很小, 显然这种处理对于黏性阻力做功更大的超亲水表面会不准确. 另外, 由于超亲水表面的铺展直径很大, 相比于超疏水或疏水表面, 重力势能的做功不可忽略. 因此, 本文在模型中引入了辅助耗散和重力势能, 考虑最大铺展时刻的球冠状液膜形态, 以期望得到超亲水表面最大铺展直径的预测模型.

V0/(m·s–1)	We	βm-exp	Chandra 等[27]	Pasandideh-Fard 等[28]	Mao等[29]	Park等[32]	Ukiwe 等[30]	Huang等[31]
0.25	1.91	3.41	2.4	6.37	3.05	11.31	5.84	0.58
0.44	5.90	3.46	2.1	4.82	2.55	7.93	4.42	0.44
0.60	10.77	3.60	1.97	4.37	2.41	6.67	4.02	0.35
0.71	15.26	3.82	1.93	4.20	2.37	6.09	3.90	0.29
0.93	25.59	3.93	1.89	4.07	2.35	5.41	3.82	0.20
130	51.17	4.08	1.90	4.08	2.38	4.9	3.93	0.12
1.50	68.59	4.26	1.91	4.13	2.41	4.78	3.93	0.10
1.89	109.3	4.43	1.93	4.26	2.47	4.67	4.07	0.06
2.35	168.98	4.70	1.97	4.42	2.54	4.66	4.24	0.04
2.8	239.89	4.90	2.00	4.57	2.60	4.72	4.39	0.03
3.08	290.08	5.00	2.02	4.67	2.64	4.76	4.48	0.02

表2超亲水表面最大铺展因子β_m实验结果与以往典型模型预测值^[27-32]之间的比较
Table2.Comparison of previous model^[27-32] prediction value of β_m with experimental data

2 -->

3.2.超亲水表面铺展模型的建立

采用能量守恒的方法, 认为撞击前的机械能和表面能等于最大铺展时刻的机械能、表面能和铺展过程中的总黏性耗散之和. 考虑液滴的动能E_k、重力势能E_p、铺展前后的表面能E_s, 以及铺展过程中的黏性耗散W_vis (viscous dissipation)和辅助耗散W_ad (auxiliary dissipation)的影响, 列能量平衡方程式:

${E_{{\rm{k0}}}} + {E_{{\rm{p0}}}} + {E_{{\rm{s0}}}} = {E_{{\rm{k1}}}} + {E_{{\rm{p1}}}} + {E_{{\rm{s1}}}} + {W_{{\rm{vis}}}} + {W_{{\rm{ad}}}}.$

如图5所示, 液滴在超亲水表面上铺展形成液膜直径较大, 最大铺展直径状态时液膜形态接近底面积较大的球冠状, 其中, H为该球冠状液滴的高度, D_max为液滴在超亲水表面上的最大铺展直径, θ为平衡接触角.
图 5 液滴在超亲水表面最大铺展直径形态
Figure5. Sketch of droplet shape at its maximum spread on superhydrophilic surface.

在本研究We范围内超亲水表面上液滴不会发生飞溅, 撞击前液滴为球状, 液滴接触到壁面的瞬间视为铺展的开始. 该模型的分析过程如下:
撞击前的初始动能为

${E_{{\rm{k0}}}} = \left( {\frac{1}{2}\rho V_0^2} \right)\left( {\frac{1}{6}{\rm{\pi }}D_0^3} \right) = \frac{1}{{12}}{\rm{\pi }}\rho V_0^2D_0^3.$

而液滴达到最大铺展直径时为静止状态, 瞬时速度为零, 动能E_k1=0.
撞击前的初始重力势能为

${E_{{\rm{p0}}}} = mg\frac{{{D_0}}}{2} = \frac{1}{{12}}{\rm{\pi }}\rho gD_{_0}^4,$

其中, m为液滴质量, g为重力加速度. 撞击前的初始表面能为

${E_{{\rm{s0}}}} = {\rm{\pi }}D_0^2\sigma .$

根据体积衡算约束式可求得球缺高度H和最大铺展直径D_max之间的关系为

$\frac{{{\rm{\pi }}H(3D_{\max }^2 + 4{H^2})}}{{24}} = \frac{1}{6}{\rm{\pi }}D_0^3.$

球缺的质心高度c为

$c = \frac{{H(D_{\max }^2 + 2{H^2})}}{{3D_{\max }^2 + 4{H^2}}}.$

即可得到终态重力势能:

${E_{{\rm{p1}}}} = mgc = \frac{1}{6}{\rm{\pi }}\rho g\frac{{D_0^3H(D_{\max }^2 + 2{H^2})}}{{3D_{\max }^2 + 4{H^2}}}.$

到达最大铺展直径时的表面能为

${E_{{\rm{s1}}}} = {E_{{\rm{s}},{\rm{lv}}}} + {E_{{\rm{s}},{\rm{sl}}}} - {E_{{\rm{s}},{\rm{sv}}}} = {\sigma _{{\rm{lv}}}}{S_{{\rm{crown}}}} + ({\sigma _{{\rm{sl}}}} - {\sigma _{{\rm{sv}}}})S.$

球冠液膜表面积为

${S_{{\rm{crown}}}} = \frac{{{\rm{\pi }}D_{\max }^2}}{{2(1 + \cos \theta )}}.$

底面积为

$S = \frac{{\rm{\pi }}}{4}D_{\max }^2.$

根据Young方程:

$\sigma \cos \theta = {\sigma _{{\rm{sv}}}} - {\sigma _{{\rm{sl}}}},$

将(11)—(13)式带入(10)式得到达到最大铺展直径时的表面能:

${E_{{\rm{s1}}}} = \sigma \frac{{\pi D_{\max }^2}}{{2(1 + \cos \theta )}} - \frac{\pi }{4}D_{\max }^2\sigma \cos \theta .$

而还有一部分能量由于液体流动过程中的黏性阻力而耗散, 对于黏性力做功:

$W = \int_0^{{t_{\rm{c}}}} {\int_{\varOmega} {\phi {\rm{d}}\varOmega \approx \phi \varOmega {t_{\rm{c}}}} } ,$

其中, φ为平均黏性耗散函数, Ω为发生耗散的液体体积, t_c为液滴到达最大铺展所用的时间. 对于自由流动铺展过程, 则边界层厚度为$\delta \!=\! 2 {{{D_0}}}/{{\sqrt {Re} }}$, 而根据Lee等^[14]的假设, 认为铺展的特征时间为

${t_{\rm{c}}} = {{{D_{\max }}}}/({{2{V_0}}}).$

取$\varOmega = {{{\text{π}}D_{\max }^2\delta }}/{4}$, 可整理得:

${W_{{\rm{vis}}}} = \frac{{{\rm{\pi }}V_0^2D_{\max }^3\rho }}{{16\sqrt {Re} }}.$

即使在无初速度的液滴自发铺展过程中, 在接触线附近的薄液层内也存在较高的黏性耗散. 以往的经典模型并未考虑这部分耗散, Huang等^[31]提出了移动接触线所带来的辅助耗散, 作为在低We下自发铺展过程中对黏性耗散的补充, 修正了以往经典模型在低We下的缺陷. 辅助耗散的表达式为

${W_{{\rm{ad}}}} = \alpha \frac{{{\rm{\pi }}V_{\rm{c}}^2D_{\max }^3\rho }}{{16\sqrt {R{e_{\rm{c}}}} }},$

其中, V_c为自发铺展的特征速度, $R{e_{\rm{c}}} = {{\rho {D_0}{V_{\rm{c}}}}}/{\mu }$为自发铺展的特征雷诺数, α表示自发铺展部分占整个铺展过程占比的参数. 当液滴初始速度V₀小于自发铺展的临界速度V_c时, 即当V₀ < V_c时, 液滴铺展的全过程都可以视作自发铺展, 则α = 1; 当V₀ > V_c时, 自发铺展只是液滴整个铺展过程中的一部分, 则α = V_c/V₀. 液滴自发铺展的临界雷诺数需要对自发铺展过程进行分析得到. 通过对无初速度纯自发条件下的液滴铺展进行分析, 从而得到自发铺展的特征速度. 认为撞击初始动能E_k = 0, 即液滴的整个铺展过程完全为自发铺展, 那么能量平衡关系和体积关系可表示为如下关系式:

${\rm{\pi }}D_0^2\sigma = {\rm{\pi }}D_{\max }^2\sigma \left( {\frac{{1 - \cos {\theta _{\rm{a}}}}}{{2{{\sin }^2}{\theta _{\rm{a}}}}} - \frac{{\cos {\theta _{\rm{a}}}}}{4}} \right) + \frac{{{\rm{\pi }}V_{\rm{c}}^2D_{\max }^3\rho }}{{16\sqrt {R{e_{\rm{c}}}} }},$

$\frac{1}{6}{\rm{\pi }}D_0^3 = \frac{{\rm{\pi }}}{{16}}\frac{{D_{\max }^3}}{{{{\sin }^3}{\theta _{\rm{a}}}}}\left( {2 - 3\cos {\theta _{\rm{a}}} + {{\cos }^3}{\theta _{\rm{a}}}} \right),$

其中, Re_c为临界速度对应的临界雷诺数, θ_a为液滴达到最大铺展直径瞬间的接触角. (19)式右侧第一项为终态表面能, 第二项为辅助耗散, 通过以上两式可得到特征速度V_c为:

$V_{\rm{c}}^3 = \dfrac{{{{\left\{ {16\sigma \left[ {\dfrac{1}{{\beta _{\rm{c}}^3}} - \dfrac{1}{{4{\beta _{\rm{c}}}}}\left( {\dfrac{2}{{1 + \cos {\theta _{\rm{a}}}}} - \cos {\theta _{\rm{a}}}} \right)} \right]} \right\}}^2}}}{{{D_0}\rho \mu }},$

${\beta _{\rm{c}}} = {\left( {\frac{{4{{\sin }^3}{\theta _{\rm{a}}}}}{{2 - 3\cos {\theta _{\rm{a}}} + {{\cos }^3}{\theta _{\rm{a}}}}}} \right)^{1/3}}.$

将(4)—(6)式、(9)式、(14)式、(17)式和(18)式带入(3)式中得到:

$\begin{split} &\frac{1}{{12}}\rho V_0^2{\rm{\pi }}D_0^3 + \frac{1}{{12}}D_0^4{\rm{\pi }}\rho g + {\rm{\pi }}D_0^2\sigma = \\ \; & \frac{1}{6}{\rm{\pi }}\rho g\frac{{D_0^3H(D_{\max }^2 + 2{H^2})}}{{3D_{\max }^2 + 4{H^2}}} + \sigma \frac{{{\rm{\pi }}D_{\max }^2}}{{2(1 + \cos \theta )}} \\ & - \frac{{\rm{\pi }}}{4}D_{\max }^2\sigma \cos \theta + \frac{{{\rm{\pi }}V_0^2D_{\max }^3\rho }}{{16\sqrt {Re} }} + \alpha \frac{{{\rm{\pi }}V_{\rm{c}}^2D_{\max }^3\rho }}{{16\sqrt {R{e_{\rm{c}}}} }}, \end{split} $

化简得到液滴最大铺展直径预测表达式:

$\begin{split} &\left( {\frac{{{D_0}}}{{12}} - \frac{1}{6}\frac{{H(D_0^2\beta _{\max }^2 + 2{H^2})}}{{3D_0^2\beta _{\max }^2 + 4{H^2}}}} \right)D_0^{}\rho g \\ =\;&\sigma \left\{ \left[ { - \frac{{\cos \theta }}{4}} \right]\beta _{\max }^2 + \frac{{\beta _{\max }^2}}{{2(1 + \cos \theta )}} - \left( {\frac{1}{{12}}We + 1} \right)\right. \\ &\left.+ \left( {\alpha \frac{{W{e_{\rm{c}}}}}{{16\sqrt {R{e_{\rm{c}}}} }}{{ + }}\frac{{W{e_{}}}}{{16\sqrt {Re} }}} \right)\beta _{\max }^{\rm{3}} \right\}.\\[-15pt] \end{split} $

液滴的最大铺展因子β_m为

${\beta _{\rm{m}}} = \frac{{{D_{\max }}}}{{{D_0}}}.$

(24)式与(21)式、(22)式、(25)式、(7)式联立可求出最大铺展因子β_m的预测值.
2 -->

3.3.超亲水表面铺展模型中的能量分析

本模型相较于以往模型, 考虑超亲水表面最大铺展时刻的球冠状液膜, 对终态表面能进行了修正, 并引入了辅助耗散W_ad和重力势能的变化ΔE_p, 而三种能量形式的修正对模型预测结果分别会造成何种影响是一个值得探究的问题. 如图6所示, 对液滴铺展过程中的能量成分分析发现, 在低We下, 液滴表面能变化占比较大, 是决定液滴铺展直径的决定性因素之一. 如图6(b)所示, 虽然重力势能的值相对较小, 在低We下大约能占到总能量变化的6%, 但也直接决定着最后预测结果的准确性. 随着We的增加, 动能和黏性耗散直线上升, 表面能和重力势能变化量相较于动能基本忽略不计. 在低We下, 表面能、动能、重力势能共同转变为黏性耗散能, 各部分能量均不可以忽略; 而在高We下, 虽然也是表面能、动能、重力势能共同转变为黏性耗散能, 但相比于动能的贡献, 表面能和重力势能的贡献可基本忽略不计.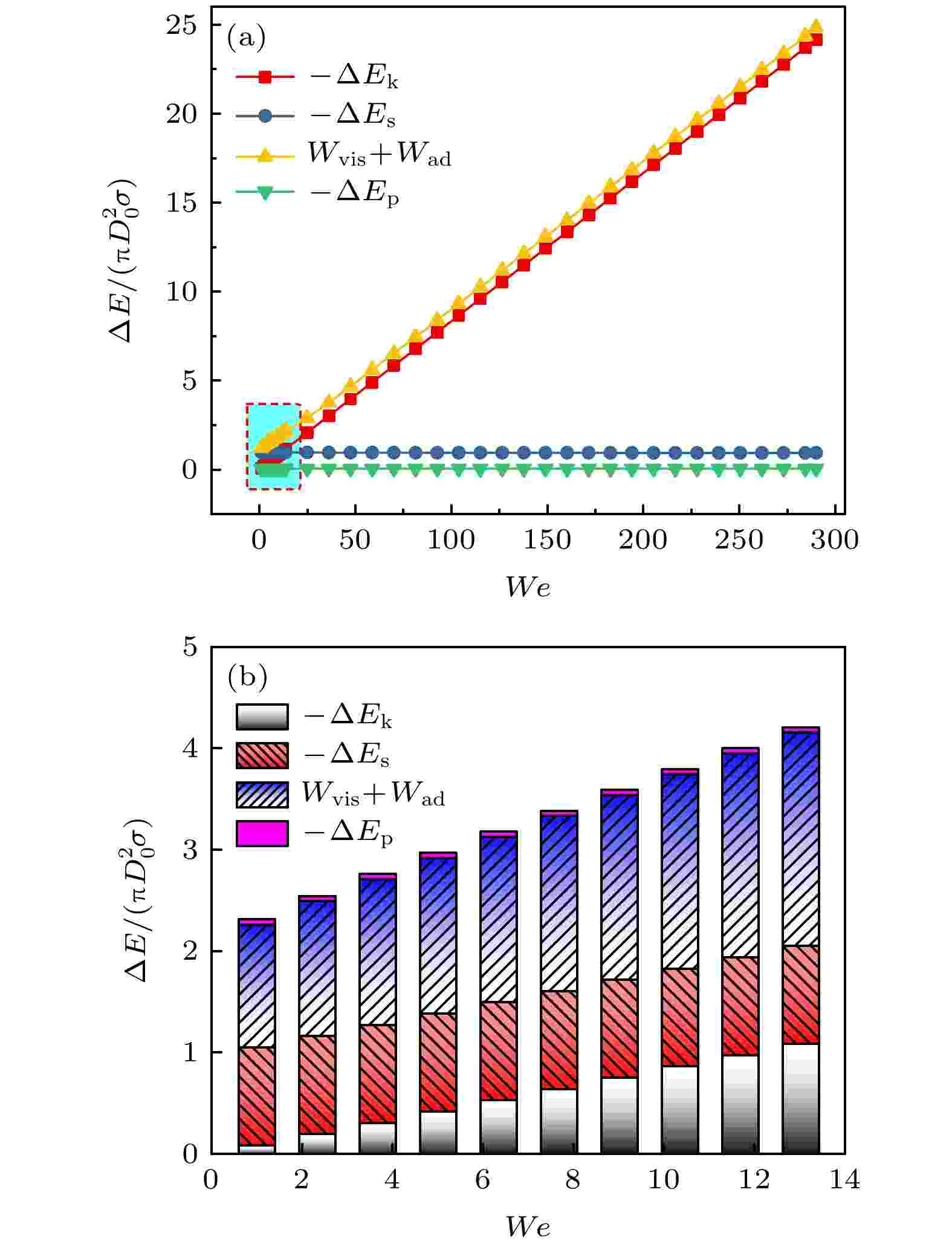
图 6 (a)模型计算的ΔE_k, ΔE_s, W, ΔE_p随We的变化; (b)低We下ΔE_k, ΔE_s, W, ΔE_p占总能量的占比(青色区域放大)
Figure6. (a) Variation of the energy component: ΔE_k, ΔE_s, W, ΔE_p with We; (b) comparison of the energy component: ΔE_k, ΔE_s, W, ΔE_p at low We

如图7(a)所示, 不计入辅助耗散的情况下, 总的黏性耗散在低We下非常小, 在无初速度的情况下(We = 0), 液滴在超亲水表面自发铺展, 此时按照(17)式计算得到的黏性耗散值为零, 而实际上只要存在黏性液体的流动过程, 黏性耗散就必然存在, 这与实际情况不符. 低We下黏性耗散的过分低估是以往模型在预测超亲水表面液滴最大铺展直径时出现反常趋势的主要原因. 辅助耗散的推导过程如3.2节所示, 通过对无初速度情况下的液滴铺展过程进行分析, 得到自发铺展过程的黏性耗散和自发铺展过程的临界速度. 当液滴初速度小于临界速度时, 整个铺展过程表现为自发铺展, 而当液滴初速度高于临界速度时, 这部分黏性耗散依然存在, 但由于自发铺展现象愈发不明显, 其影响也在不断减小. 低We下铺展过程中各项黏性耗散占比如图7(b)所示, 在低We下辅助耗散占全部黏性耗散的主要部分. 由于辅助耗散的引入, 低We下的总黏性耗散得到了正确修正, 从而提高了模型预测效果.
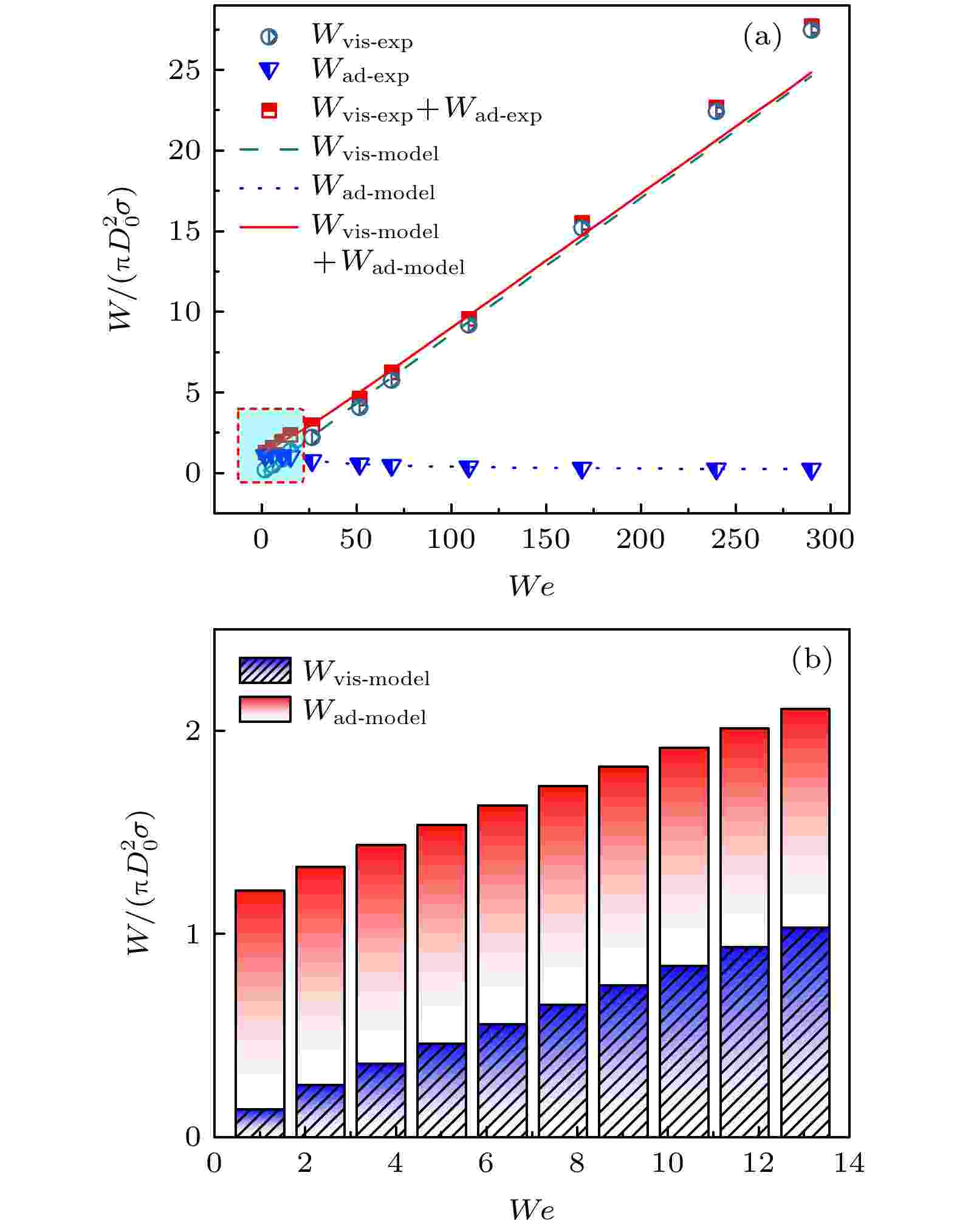图 7 (a)超亲水表面液滴铺展过程各项黏性耗散实验和模型计算值对比; b)低We下总黏性耗散中W_vis和W_ad的占比(青色区域放大)
Figure7. (a) Variation of the viscous dissipation components value with We; (b) comparison of the W_vis, W_ad at low We.

2 -->

3.4.模型预测与实验结果比较

通过联立求解(7)式、(21)式、(22)式、(24)式和(25)式可以得到在不同We下的D_max的预测值. 以往模型无法准确预测超亲水表面的最大铺展直径主要是因为未同时考虑终态球冠状表面能、辅助耗散、重力势能做功的原因. 如图8所示, 三者同时考虑的现有模型可以更加准确预测高低We下的D_max, 最大预测偏差在4%以内, 平均偏差在2%左右, 克服了以往模型与实际不符的低We反常趋势和高We下偏低的问题. 如果不考虑辅助耗散, 低We时预测结果明显偏高, 而且趋势和实际情况相反, 其原因是对黏性耗散过分低估, 消耗的动能和重力势能只能通过表面能的增大来达到守恒, 使得预测的最大铺展直径远远大于实际情况. 另外本模型考虑了液滴铺展过程中重力势能的变化, 从以往模型的预测结果来看, 在疏水或超疏水表面上完全可以忽略重力势能的变化. 不过在超亲水表面上, 由于液滴铺展面积更大, 液膜厚度更薄, 重力势能的变化会更加明显. 若不考虑这6%的重力势能, 在低We下呈现预测值明显偏大和反常的问题, 反证了重力势能的引入对于准确预测低We下超亲水表面最大铺展直径的重要性. 此外, 如表3所示, 本文模型可以预测以往经典文献^[28,29]中的接触角为37°—111°的固体表面上的液滴最大铺展直径, 除个别数据, 整体偏差在20%以内. 这充分说明了本模型对于不同润湿性固体表面具有适用性, 本模型可以预测亲水和疏水固体表面上的宽We范围内的最大铺展直径, 具有比较宽的适用条件.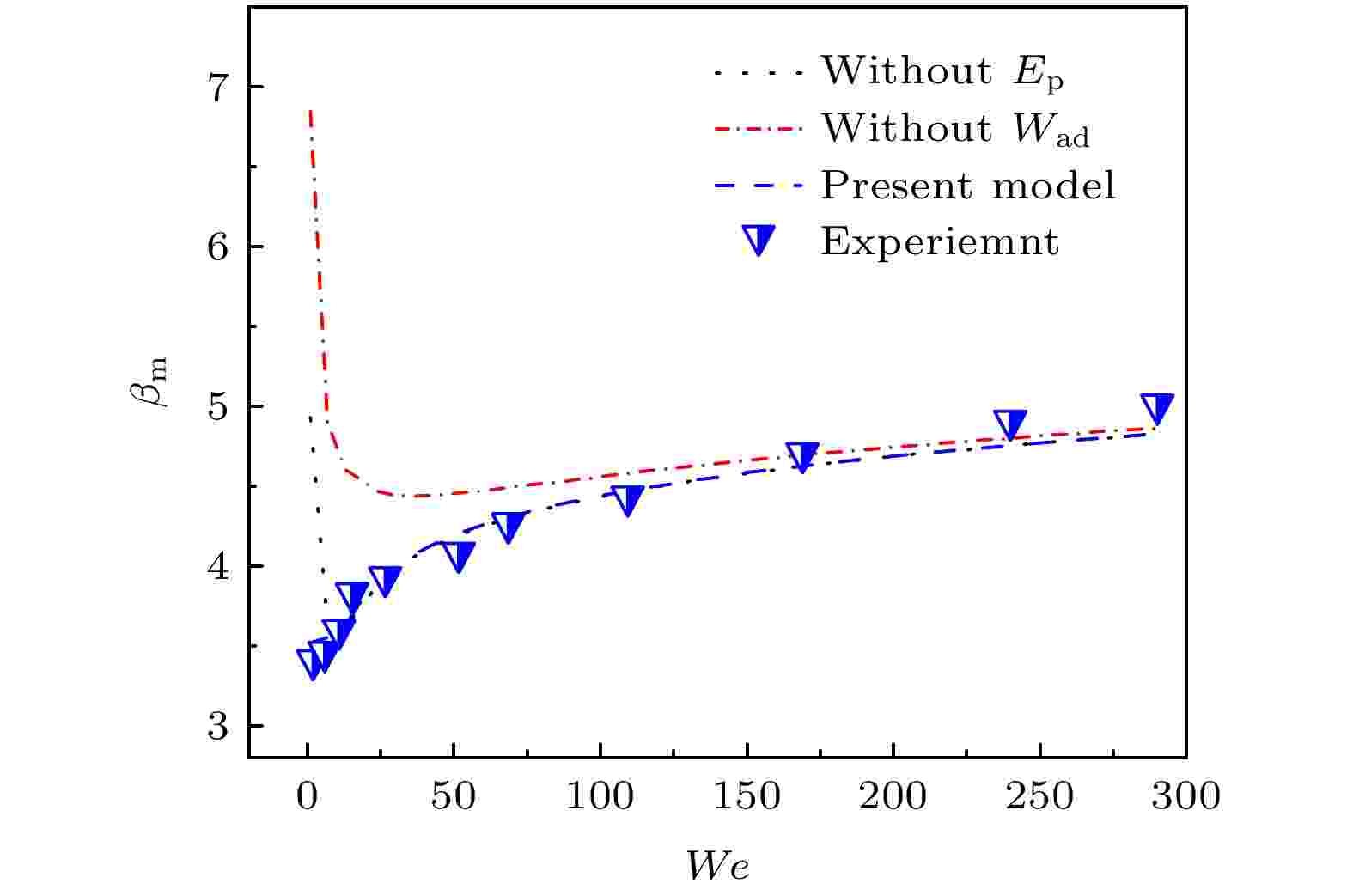
图 8 液滴在不同We下撞击超亲水表面最大铺展因子的实验和模型预测结果对比(模型包括去除重力势能或辅助耗散的模型及全部考虑的模型)
Figure8. Comparison of the current experimental measurements of β_m with the theoretical prediction from model (models includes without E_p, without W_ad and present model).

固体/液体	D0, mm	V0/(m·s–1)	We	θ/(°)	βm-exp	βm-model	(βm-exp–βm-model)/ βm-model
玻璃/水	2.7	0.55	11.21	37	1.77	2.41	0.26
玻璃/水	2.7	0.82	24.91	37	2.20	2.74	0.19
玻璃/水	2.7	1.00	37.05	37	2.53	2.94	0.14
玻璃/水	2.7	1.58	92.48	37	3.11	3.51	0.11
玻璃/水	2.7	1.86	128.17	37	3.70	3.81	0.03
玻璃/水	2.7	2.77	284.26	37	4.50	4.48	0.00
玻璃/水	2.7	3.72	512.67	37	4.94	4.89	0.01
不锈钢/水	2.7	0.55	11.21	67	1.67	1.95	0.14
不锈钢/水	2.7	0.82	24.91	67	2.16	2.28	0.05
不锈钢/水	2.7	1.00	37.05	67	2.34	2.51	0.06
不锈钢/水	2.7	1.58	92.48	67	3.09	3.13	0.01
不锈钢/水	2.7	1.86	128.17	67	3.67	3.38	0.08
不锈钢/水	2.7	2.77	284.26	67	4.42	4.15	0.06
不锈钢/水	2.7	3.72	512.67	67	4.88	4.65	0.05
石蜡/水	2.7	0.55	11.21	97	1.65	1.58	0.04
石蜡/水	2.7	0.82	24.91	97	2.10	1.91	0.10
石蜡/水	2.7	1.00	37.05	97	2.26	2.13	0.06
石蜡/水	2.7	1.58	92.48	97	3.01	2.79	0.07
石蜡/水	2.7	1.86	128.17	97	3.60	3.09	0.16
石蜡/水	2.7	2.77	284.26	97	4.32	3.89	0.11
石蜡/水	2.7	3.72	512.67	97	4.78	4.44	0.08
蜂蜡/水	0.62	2.61	59	111	2.65	2.19	0.21
蜂蜡/水	0.78	3.29	118	111	3.18	2.76	0.15
蜂蜡/水	0.89	3.71	171	111	3.45	3.09	0.11
蜂蜡/水	0.98	4.00	219	111	3.79	3.33	0.14
蜂蜡/水	1.05	4.28	271	111	3.91	3.53	0.10

表3本文模型预测值与文献^[28,29]中不同润湿性表面的最大铺展因子的实验值对比
Table3.Comparison of current theoretical model of β_m with experimental data in literature^[28,29].

本文通过高速摄像技术对超亲水表面的液滴铺展特性进行分析发现其具有铺展速度快、铺展直径大、终态液膜为球冠状且质心低等特点. 考虑终态球冠状液膜、辅助耗散、重力势能, 修正了以往最大铺展直径的预测模型, 建立了更准确的超亲水表面最大铺展直径的预测模型, 解决了以往模型在预测超亲水表面时在高We下误差偏大, 低We下趋势反常的问题. 基于对液滴在超亲水表面上球冠状形态的考虑, 修正了终态的表面能; 基于对自发铺展过程中的黏性耗散的考虑, 引入了低We下的辅助耗散, 修正了以往低We下过分低估的黏性耗散; 考虑到超亲水表面上液滴铺展面积大而造成前后液滴的重力势能变化较大, 引入了重力势能. 通过能量成分分析明确了低We下重力势能、辅助耗散等能量成分的修正对准确预测超亲水表面最大铺展直径的重要作用. 此外, 该模型可以较好地预测亲水和疏水固体表面在宽We范围下的液滴最大铺展直径.