摘要:感光细胞能接收各种强度的可见光, 并转换为生物电信号连接视神经; 这样的功能可以用光电效应来模拟. 本文利用数值计算, 分析了基于光电管耦合FitzHugh-Nagumo (FHN)神经元的动力学特性, 详细讨论了光电管的参数空间中, 混沌和簇放电模式下耦合系统的同步区间. 结果表明: 在耦合强度较小时, 耦合系统由于受迫共振表现为完全同步; 耦合强度较大时, 耦合系统倾向于相位同步. 光电管的导通状态, 即反向截止电压对系统同步具有调制作用. 这项工作有助于理解视网膜疾病, 如黄斑变性的原理.
关键词: 神经元/
光电管/
同步/
相位锁定

English Abstract

全文HTML

--> --> -->

在生物组织和系统中的每个功能单元区域都包含着成千上万的神经元, 神经元作为神经系统的基本功能单位^[1], 能感受刺激并传导兴奋, 具有联络和整合输入信息并传出信息的作用. 神经系统信号编码和传输出现故障可能导致很多的神经疾病, 比如帕金森氏症、阿尔兹海默症和癫痫等^[2]. 从实验角度直接在生物系统中开展研究是比较复杂的, 而神经元电路^[3-6]的设计和控制为研究神经元之间的信息编码和信息传递提供了有效的途径. 对比单个神经元电路模型^[4,7-10]与普通的非线性电路^[11-13]的输出序列, 调控神经元电路可以产生静息态、尖峰放电态、周期态、混沌态和簇放电态等多种复杂的放电模式.
用于搭建神经元电路的电子器件主要有电阻、电容、电感、约瑟夫森结等^[14-18], 这些电子元件也可以用来连接两个或者多个神经元电路. 实际的生物神经元在收到外界各类刺激后会产生对应的等效电流来改变神经元的输出模态, 即神经元的编码过程伴随着信号的传递. 例如, 听觉神经元可以将振动信号转化为电刺激信号; 感热神经元可以将温度热信号转化为电刺激信号; 视觉神经系统中的神经元对光信号敏感, 比如视网膜外感光是一种广泛的生物学现象, 与光的相关行为和激素的反应有关, 而一些无脊椎动物也拥有简单的感光器, 比如小龙虾的尾神经节中的感光器等^[19-22]. 因此通过神经电路的搭建构造具有感知功能的神经电路是有意义的. 电子器件例如忆阻器、热敏电阻和光电管等可以用来搭建功能性神经电路. 例如, Liu等^[23]和Li等^[24]利用光电管与神经电路嵌合产生了连续的电压源, 用以捕获外部光信号. 此外, 由于神经系统内的神经元并非孤立存在, 而是与其他神经元连接并完成特定的功能^[25-28], 因此上述电子器件也可以用来耦合神经元电路, 使耦合的神经电路系统具有感知外界信号的功能性神经系统.
从生物学角度来看, 生物需要通过进食或者其他方式补给由于生物活动而产生的能量的消耗来维持代谢过程. 而从物理学和动力学角度来看, 光电管可以吸收外界光能量转化为电信号^[29]来驱动电路, 给系统注入能量并对系统能量输运进行调节, 因此通过光电管耦合神经元电路讨论耦合系统的放电活动具有重要的意义^[30-34]. 一般耦合两个或者多个非线性电路可分为两种, 即单向耦合^[35-39]和双向耦合^[40-45]. 通常电突触是双向的. 本文通过光电管耦合两个FitzHugh-Nagumo (FHN)神经元, 在接受外界光照辐射后, 光电管向耦合系统注入能量, 从而改变耦合系统的动力学行为.

FHN神经元模型是由FitzHugh^[46]和Nagumo等^[47]提出的可激发神经元的动力学模型, 通过设置适当的参数和外部激励来描述神经元放电活动. 图1是由外部电压源驱动的神经元等效电路图, 其中N_R是非线性电阻, C表示电容, L为感应线圈, R是与感应线圈串联的电阻, i_S代表外部刺激电流, E为施加的恒定电压源, V_S为电压源, R_S为支路的电阻.
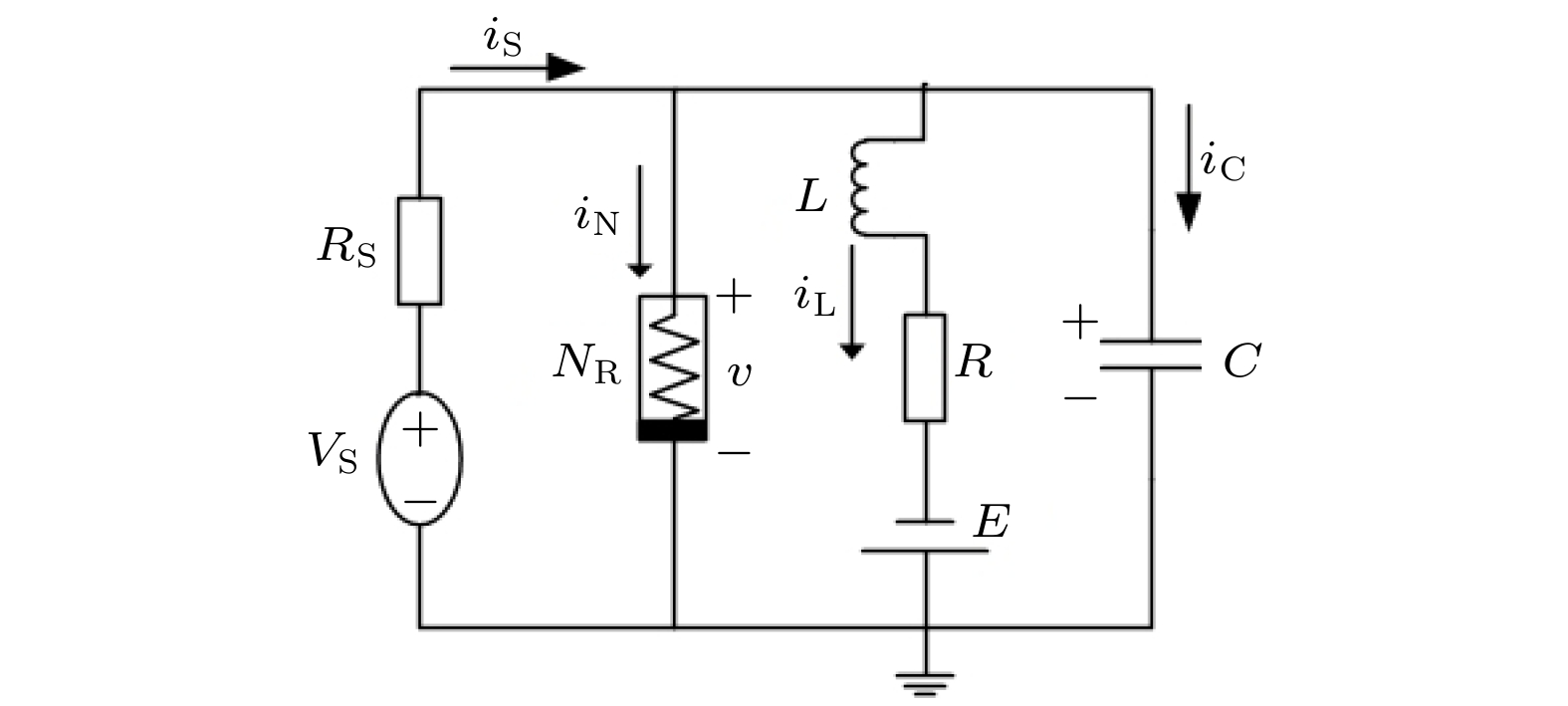图 1 FHN神经元的等效电路图
Figure1. Equivalent circuit diagram of FHN neuron.

根据基尔霍夫定律及电路中各元件电压电流关系, 图1所示的电路方程组为

$\left\{ \begin{aligned} &C\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = \frac{{{V_{\rm{S}}} - V}}{{{R_{\rm{S}}}}} - {i_{\rm{L}}} - {i_{{\rm{NR}}}}, \\& L\frac{{{\rm{d}}{i_{\rm{L}}}}}{{{\rm{d}}t}} = V - R{i_{\rm{L}}} + E, \end{aligned} \right.$

式中, V是电容C两端的电压; i_L是流经感应线圈的电流; FHN电路中非线性电阻的伏安特性为

${i_{{\rm{NR}}}} = - \frac{1}{\rho }\left( {V - \frac{1}{3}\frac{{{V^3}}}{{V_0^2}}} \right),$

其中, ρ和V₀为归一化参数; 外部激励V_S = B_S + B₀cos(2πf₀t). 为了便于数值计算和动力学分析, 将电路方程(1)的参数和变量无量纲化:

$\left\{ \begin{aligned}&x = \frac{V}{{{V_0}}},\;y = \frac{{\rho {i_{\rm{L}}}}}{{{V_0}}},\;U = \frac{{\rho {V_{\rm{S}}}}}{{{R_{\rm{S}}}{V_0}}},\;\tau = \frac{t}{{\rho C}},\\&a = \frac{E}{{{V_0}}},\;b = \frac{R}{\rho },\;c = \frac{{{\rho ^2}C}}{L},\;\xi = \frac{\rho }{{{R_{\rm{S}}}}},\\&{U_{\rm{S}}} = \frac{{\rho {B_{\rm{S}}}}}{{{R_{\rm{S}}}{V_0}}},\;{U_0} = \frac{{\rho {B_0}}}{{{R_{\rm{S}}}{V_0}}},\;f = \rho C{f_0},\;{I_0} = \frac{{2\rho {I_{\rm{H}}}}}{{{V_0}{\rm{\pi }}}},\;\\&U = {U_{\rm{S}}} + {U_0}\cos (2{\rm{\pi }}f\tau ).\,\end{aligned} \right.$

经过标度变换后, 神经元电路等效表达为无量纲的神经元振子模型:

$\left\{ \begin{aligned}&\frac{{{\rm{d}}x}}{{{\rm{d}}\tau }} = x(1 - \xi ) - \frac{1}{3}{x^3} - y + U,\\&\frac{{{\rm{d}}y}}{{{\rm{d}}\tau }} = c(x - by + a),\end{aligned} \right.$

其中, x表示跨膜电压; y表示不应期; U表示膜电流即神经元的外部激励; a, b, c分别表示膜半径、膜内流体的特征阻抗和温度系数^[48-51].
理想光电管的电压电流特性如图2所示. 图2中曲线在横坐标V轴上的截距V_a表示光电管阴极的反向截止电压, 与材料的功函数(正比于红限频率)相关, 当入射光频率大于红限频率时, 光电管产生光电流^[52]. 根据文献[23], 光电管的电流-电压关系可以描述为
图 2 光电管的电流-电压特性
Figure2. I-V characteristics of phototube.

${i_{\rm{P}}} = \frac{{2{I_{\rm{H}}}}}{{\rm{\pi }}}\arctan (V - {V_{\rm{a}}}){{ = }}\frac{{2{I_{\rm{H}}}}}{{\rm{\pi }}}\arctan ({V_1} - {V_2} - {V_{\rm{a}}}),$

其中参数i_P对应流经光电管的电流; I_H对应光电管的饱和电流; V = V₁ – V₂对应光电管的阴极和阳极侧电压差, 当光电管的阴极和阳极侧电压差增大时, 阳极对光电子的收集能力增强, 光电流增大, 耦合系统之间的信息交互能力增强; V_a对应光电管的反向截止电压, 光电管的反向截止电压越高, 则一定光强下的光电流越小. 如果用光电管耦合两个系统, 那么光电管的反向截止电压越高时, 耦合系统之间实现信息交互的电流越小, 等效的耦合调制能力较弱. (5)式通过引入表征反向截止电压的V_a项, 在一定程度上表征了单光子光电效应的这种频率选择效应.
真空光电管正常工作时不仅存在光电流, 还存在三种额外的电流, 即暗电流、本底电流和反向电流. 暗电流来源于热电子发射和噪声, 为了简单起见, 认为暗电流和工作电流相比可以忽略; 本底电流是漫反射的杂散光造成的, 通过滤波透镜可以消除它的影响; 反向电流来自阳极的光电效应, 实践中阳极材料即使逸出功较阴极大, 也会在使用过程中受到阴极污染而表现出显著的反向电流; 这也是实验过程中测到反向电压超过反向截止电压仍能测到漏电流的主要原因. (5)式给出的模型能够在一定程度上反映光电管的反向漏电.
通过光电管耦合的两个FHN神经元电路, 等效电路图如图3所示. 当两个具有外界激励的FHN电路激活时, 光电管充当电压源或者电流源为电路提供能量. 为简单起见, 先讨论两个参数相同的FHN神经元电路, 即令C₁ = C₂, L₁ = L₂, E₁ = E₂, R₁ = R₂, ${R_{{\rm{S}}{}_{\rm{1}}}} = {R_{{\rm{S}}{}_2}}$; 根据基尔霍夫定律, 图3所示耦合神经元电路的无量纲化方程可表示为
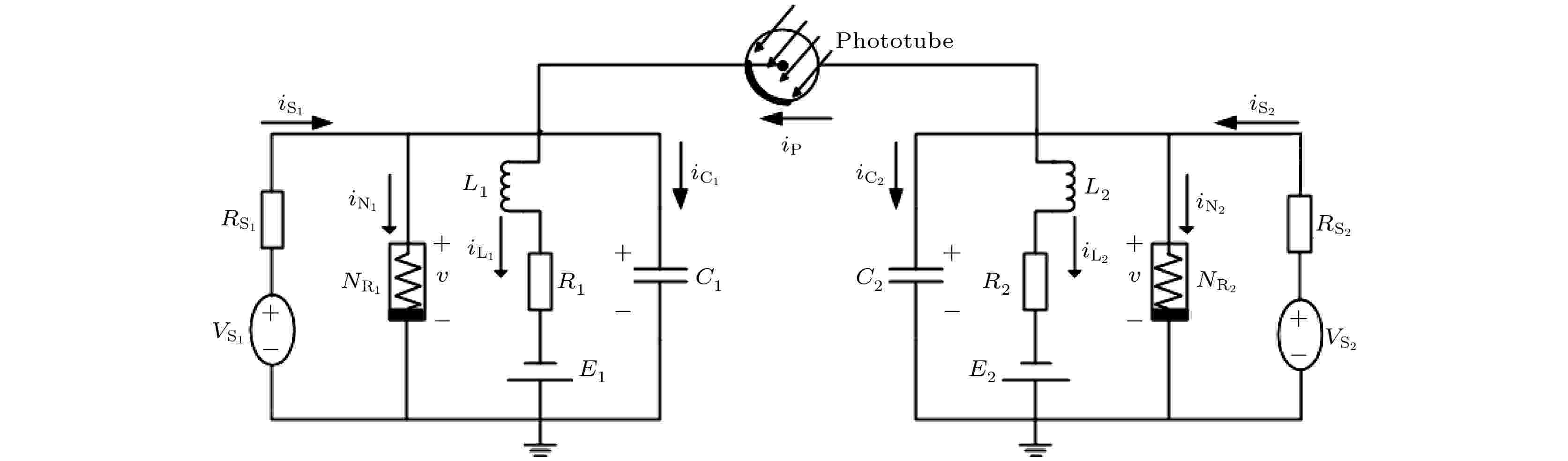图 3 光电管耦合FHN神经元系统的等效电路图
Figure3. Equivalent circuit diagram of the coupled FHN neuron system.

$\left\{ \begin{aligned}& \frac{{{\rm{d}}x}}{{{\rm{d}}\tau }} = x(1 - \xi ) - \frac{1}{3}{x^3} - y + U \\&\qquad\;+ {I_0}{\rm{arctg}}(x - x' - {u_{\rm{a}}}), \\& \frac{{{\rm{d}}y}}{{{\rm{d}}\tau }} = c(x - by + a), \\ &\frac{{{\rm{d}}x'}}{{{\rm{d}}\tau }} = x'(1 - \xi ) - \frac{1}{3}{{x'}^3} - y' + U \\ &\qquad\;- {I_0}{\rm{arctg}}(x - x' - {u_{\rm{a}}}), \\ &\frac{{{\rm{d}}y'}}{{{\rm{d}}\tau }} = c(x' - by' + a), \end{aligned} \right.$

其中耦合强度I₀与光电管饱和电流有关, u_a与光电管的反向截止电压有关. 光电管可以通过吸收外界光能量调节系统之间的能量输运, 定义光电管的瞬态功率:

${P_{\rm{g}}} = UI = {i_{\rm{P}}}({V_1} - {V_2}),$

相应的无量纲化功率为

$P = {I_0}(x - x'){\rm{arctg}}(x - x' - {u_{\rm{a}}}).$

为了判断耦合系统间的完全同步, 定义系统间误差函数为

$\theta ({e_x},{e_y}) \!=\! \sqrt {{{(x - x')}^2} + {{(y - y')}^2}} \!=\! \sqrt {e_x^2 \!+\! e_y^2} ,$

如果误差函数值随着时间演化衰减到零, 则表示系统实现完全同步. 为了计算两个系统之间的相位关系, 对时间序列x(t), x'(t)采用Hilbert变换得到相位序列:

$\left\{ \begin{aligned}&\hat x{{(}}{\mathop{{t}}\nolimits} {{)}} \!=\! - \frac{1}{{\rm{\pi }}}{\bf{p}}.{\bf{v}}.\int_{ - \infty }^{ + \infty } {\frac{{{\mathop{{x}}\nolimits} {{(}}\tau {{)}}}}{{{\mathop{{t}}\nolimits} - \tau }}{\rm{d}}\tau ,~ \hat x'{{(}}{\mathop{{t}}\nolimits} {{)}} \!=\! - \frac{1}{{\rm{\pi }}}{\bf{p}}.{\bf{v}}.,} \\&\phi (t) = \arctan\frac{{\hat x(t)}}{{x(t)}},\quad \phi '(t) = \arctan\frac{{\hat x'(t)}}{{x'(t)}},\quad \end{aligned} \right. \\[-15pt]$

其中p.v.代表柯西积分. 相应时间序列x与x' 的相位锁定关系为

$\varDelta \phi = \left| {m\phi (t) - n\phi '(t)} \right| < \varepsilon ,$

其中, m, n是整数, ε是一个极小值, 如ε ≈ 0.00001, 表示系统达到了n∶m的锁相. 本文计算m∶n = 1∶1的情况.

本节主要讨论基于光电管耦合两个FHN神经元的动力学特性, 在数值模拟中, 采用四阶Runge-Kutta算法, 积分步长h = 0.01, 计算的时间为1000个时间单位. 首先根据(4)式计算了具有外界刺激U = U_s + U₀cos(2πfτ)的单个FHN神经元模型在不同参数下的峰峰间隔(interspike interval, ISI), 系统参数选择为ξ = 0.175, U_s = 0, U₀ = 0.9, f = 0.16, 初始值为(0.2, 0.1), 计算结果如图4所示.
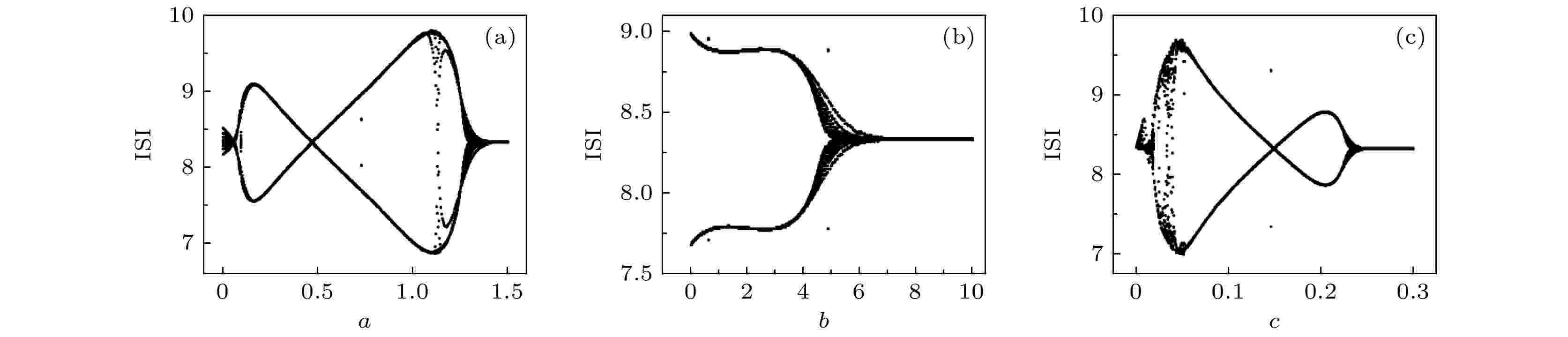图 4 单个FHN神经元在不同参数下的ISI　(a) b = 0.8, c = 0.1; (b) a = 0.7, c = 0.1; (c) a = 0.7, b = 0.8
Figure4. ISI of single FHN neuron with different parameters: (a) b = 0.8, c = 0.1; (b) a = 0.7, c = 0.1; (c) a = 0.7, b = 0.8.

从图4的结果发现, 不同的参数取值使得系统出现不同的放电模式; 当参数a, c变化时, 神经元从两周期放电模式向单周期放电转变时存在交替特征, 如图4(a)和图4(c)所示; 当参数b变化时, 神经元从两周期放电转变为单周期放电表现出较一致的特征, 如图4(b)所示; 此外, 外界激励的幅度或频率也能够影响神经元的兴奋性, 使得神经元处于不同的放电状态. 因此分类讨论了不同刺激频率下耦合两个处于不同放电状态下FHN神经元的情况, 如表1所列. 文中参数设置均为a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, U_s = 0, U₀ = 0.9, 耦合系统初始值为(0.2, 0.1; 0.2, 0.3).

频率f	0.16		0.002		0.012		0.06
放电状态	混沌放电		簇放电		尖峰放电		周期放电
反向截止电压ua	0.1	0.5	0.01	0.5	0.01	0.5	0.01	0.5
耦合分类	case 1	case 2	case 3	case 4	case 5	case 6	case 7	case 8

表1不同外界刺激频率下的耦合FHN神经元分类
Table1.Category of the coupled FHN neurons driven by external stimulation with different frequencies.

2

-->

3.1.混沌放电FHN神经元的光电管耦合(f = 0.16)

对于(6)式所示的耦合系统, 为探究耦合项中I₀和u_a的影响, 绘制出激励源频率f = 0.16情况 (case 1, 2)下, 耦合系统随I₀和u_a变化的峰峰间隔图(ISI), 如图5所示.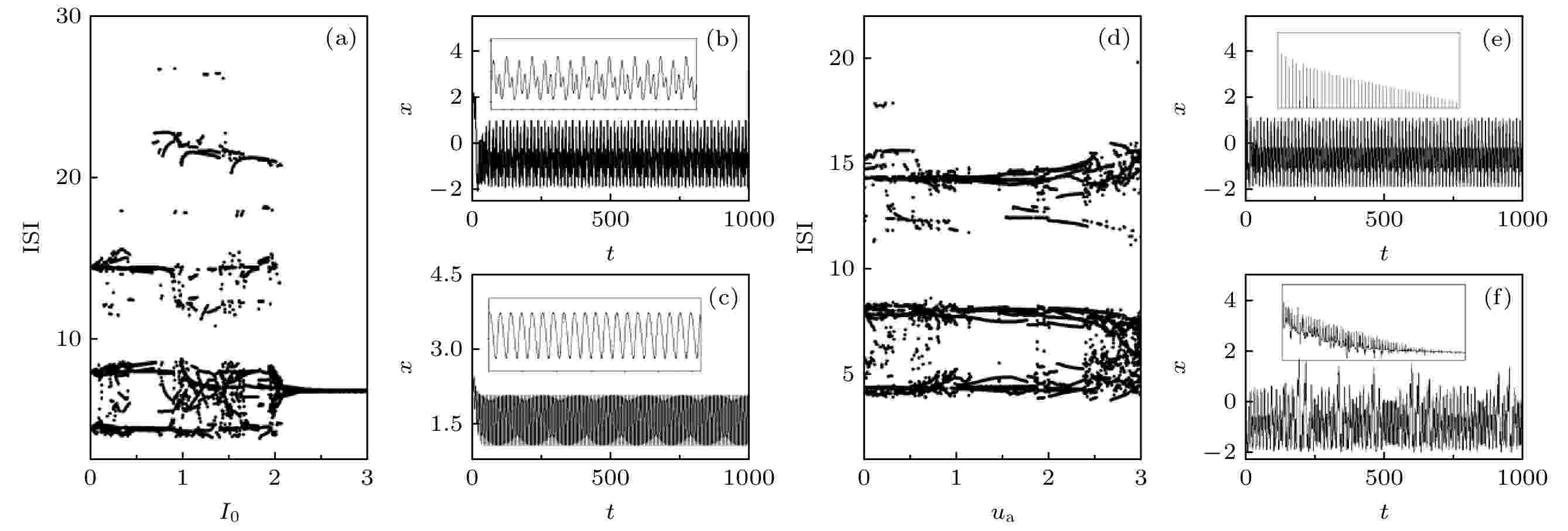
图 5 耦合系统中神经元的ISI和放电序列(f = 0.16)　(a) u_a = 0.1; (b) I₀ = 1.5, u_a = 0.1; (c) I₀ = 2.5, u_a = 0.1; (d) I₀ = 0.3; (e) u_a = 1.5, I₀ = 0.3; (f) u_a = 2.3, I₀ = 0.3
Figure5. ISI and the firing sequence of neuron in the coupled system (f = 0.16): (a) u_a = 0.1; (b) I₀ = 1.5, u_a = 0.1; (c) I₀ = 2.5, u_a = 0.1; (d) I₀ = 0.3; (e) u_a = 1.5, I₀ = 0.3; (f) u_a = 2.5, I₀ = 0.3.

从图5(a)和图5(d)可以看出, I₀和u_a会使系统的放电模式发生变化; 在外界激励U相同的情况下, 增大I₀会使系统的混沌放电转换为周期放电, 如图5(b)和图5(c)所示. 同样u_a对系统的放电模式同样具有重要的作用, 在u_a增大时系统处于混沌放电状态(图5(d)的ISI图所示), 对应的放电波形如图5(e)和图5(f)所示, 其中小图为对应参数下功率谱的计算, 图5(e)功率谱图为离散的, 可知系统是多周期的; 而图5(f)的功率谱为连续的, 可知系统处于混沌态. 对于第一种情况(case 1), 计算了参数空间中的最大误差函数θ_max与最大相位差??_max, 如图6所示.
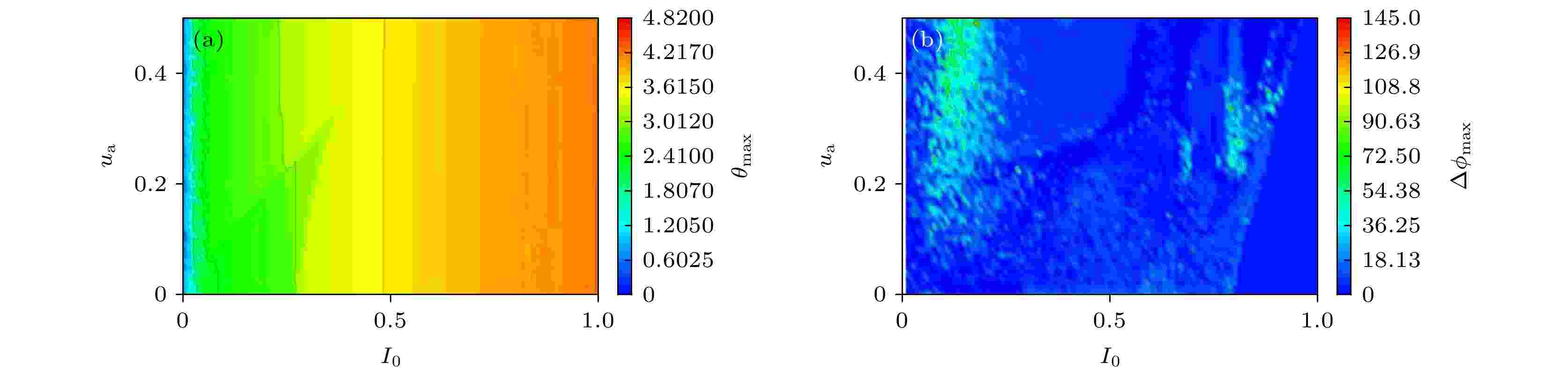图 6 u_a和I₀的参数空间中, 耦合系统(case 1)的同步区间　(a)最大误差函数θ_max; (b)最大相位差??_max
Figure6. Synchronization region of the coupled system (case 1) in the parameter space of u_a vs. I₀: (a) Maximum error function θ_max; (b) maximum phase difference ??_max.

如图6(a)所示, I₀趋于0时系统中存在完全同步流形, 但是随着I₀增大, 系统表现为去(完全)同步; 不同于完全同步, 如图6(b)所示, 随着I₀增大, 相位差减小有实现同步的倾向, 并在I₀ = 0.79时出现相位差趋于0; 但是增大u_a使得相位同步出现“舌头”, 如图6(b)右侧所示. 耦合系统的误差函数、相位差以及对应参数下的光电管功率的时间序列计算结果如图7所示.
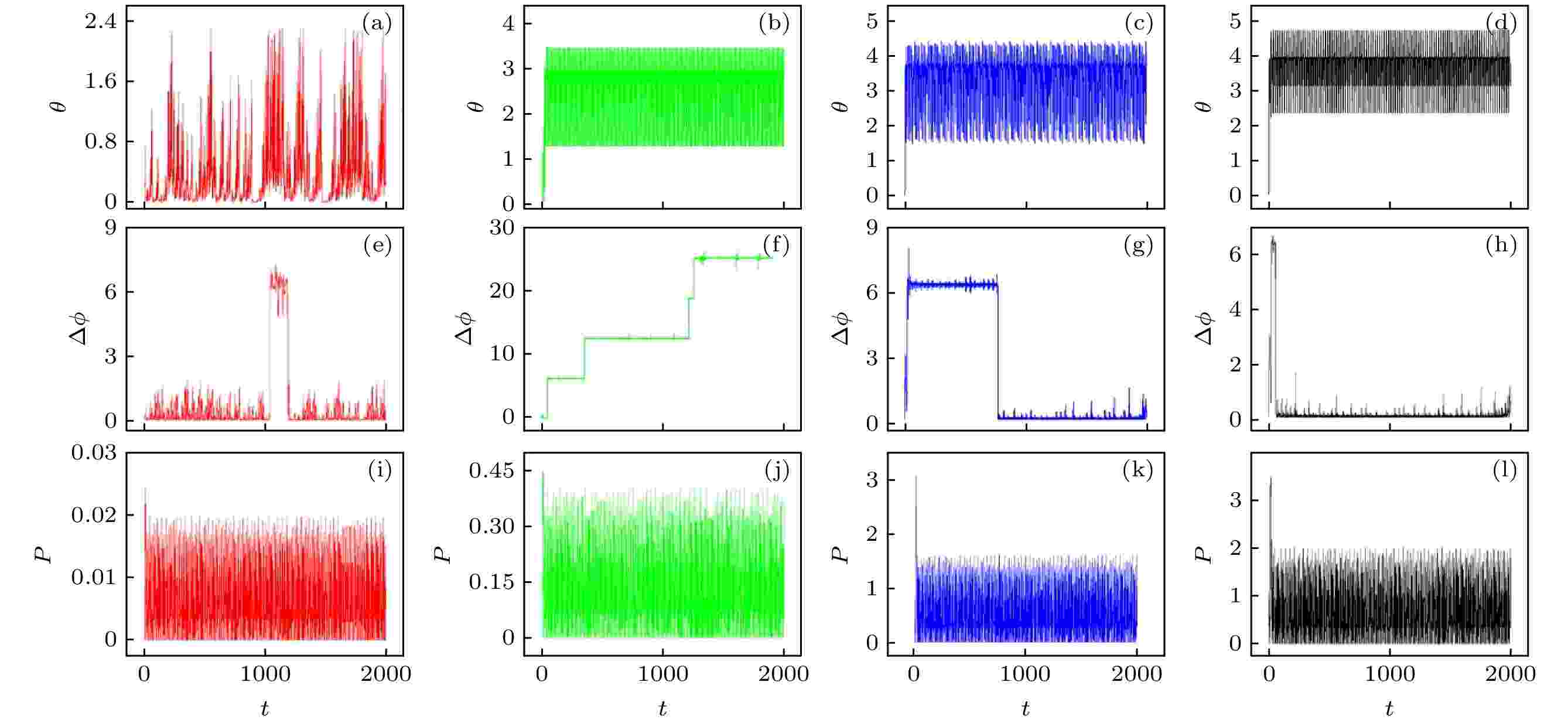图 7 误差函数、相位差和功率随时间的演化(u_a = 0.1)　(a), (e), (i) I₀ = 0.01; (b), (f), (j) I₀ = 0.2; (c), (g), (k) I₀ = 0.8; (d), (h), (l) I₀ = 1
Figure7. Evolution of error function, phase difference and power (u_a = 0.1): (a), (e), (i) I₀ = 0.01; (b), (f), (j) I₀ = 0.2; (c), (g), (k) I₀ = 0.8; (d), (h), (l) I₀ = 1.

从图7(a)—(d)可以看出, I₀的增大使得误差函数趋于增大, 系统远离完全同步; 但是如 图7(e)—(h), I₀的增大可以促进耦合系统间的相位同步. 此外, 如图7(i)—(l)所示, 随着I₀的增大, 光电管的功率不断增加, 表明光电管通过吸收光能向耦合系统注入的能量越多, 从而使耦合系统趋于相位同步; 但是通过计算光电管单位光强的功率可以发现, 在系统趋于相位同步后, 光电管单位光强的功率峰值有趋于饱和的特征. 对于第二种情况(case 2), 具有较大u_a (u_a = 0.5)时耦合系统间的误差及对应的相位差计算结果如图8所示.
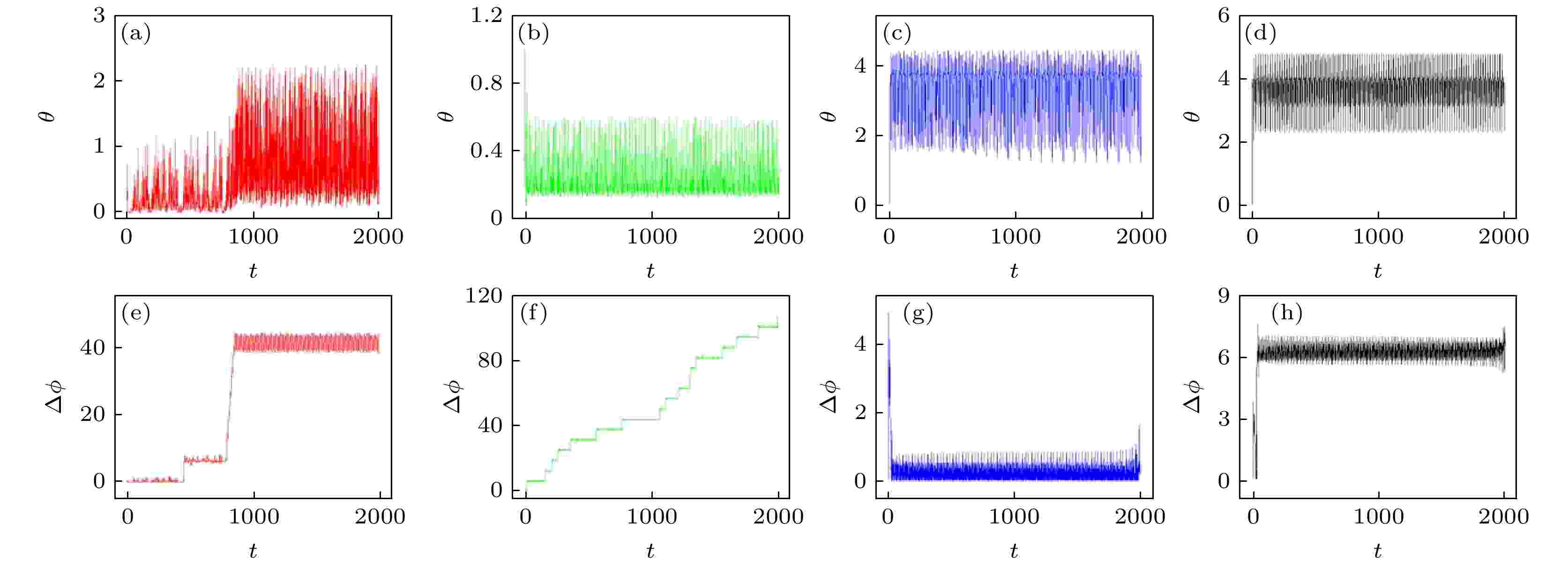图 8 系统误差与相位差随时间的演化(u_a = 0.5)　(a), (e) I₀ = 0.01; (b), (f) I₀ = 0.2; (c), (g) I₀ = 0.8; (d), (h) I₀ = 1
Figure8. Evolution of error function and phase error (u_a = 0.5): (a), (e) I₀ = 0.01; (b), (f) I₀ = 0.2; (c), (g) I₀ = 0.8; (d), (h) I₀ = 1.

从图8可以看出, 改变I₀和u_a对耦合系统的完全同步没有贡献. 以上结果与图6一致, 在讨论的参数范围内, 混沌放电的FHN神经元经由光电管耦合情况下, I₀较小时由于受迫共振可完全同步; I₀较大时趋于相位同步, 此时光电管具有较强的调节能力.
2 -->

3.2.簇放电FHN神经元的光电管耦合(f = 0.002)

根据(6)式所示的耦合系统, 考虑频率f = 0.002情况(case 3, 4)下, 耦合系统随I₀和u_a变化的峰峰间隔图(ISI), 如图9所示.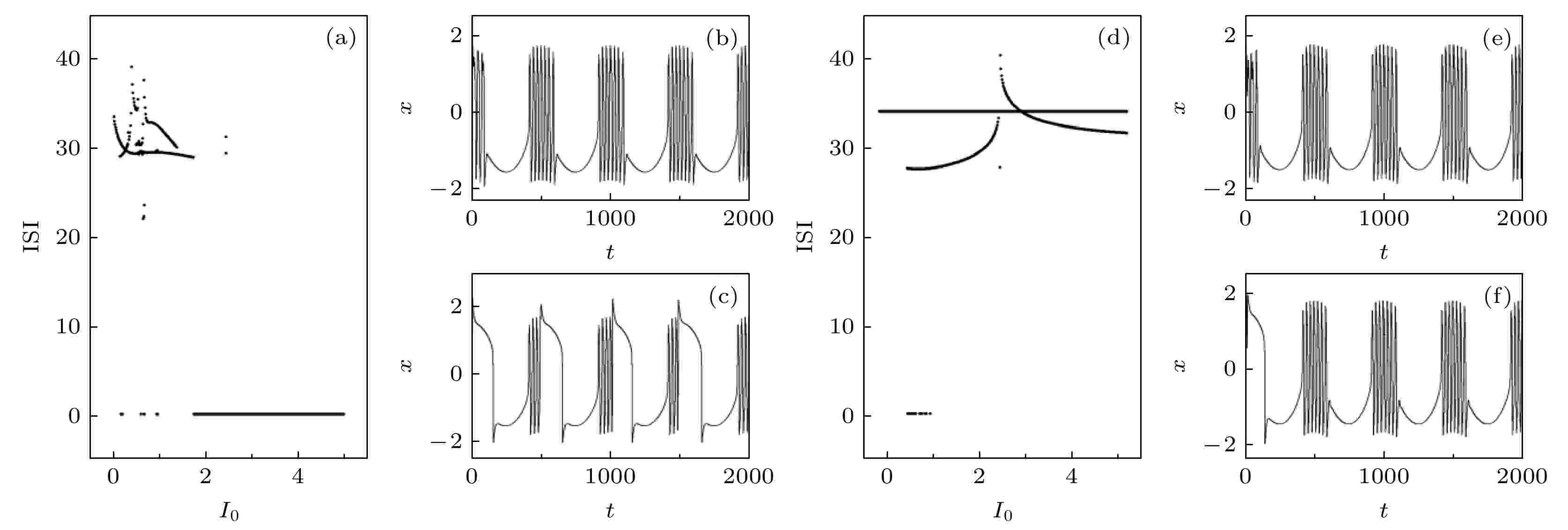
图 9 耦合系统中神经元的ISI和放电序列(f = 0.002)　(a) u_a = 0.01; (b) I₀ = 0.5, u_a = 0.01; (c) I₀ = 1.5, u_a = 0.01; (d) I₀ = 0.3; (e) u_a = 0.5, I₀ = 0.3; (f) u_a = 1.5, I₀ = 0.3
Figure9. ISI and the firing sequence of neuron in the coupled system (f = 0.002): (a) u_a = 0.01; (b) I₀ = 0.5, u_a = 0.1; (c) I₀ = 1.5, u_a = 0.1; (d) I₀ = 0.3; (e) u_a = 0.5, I₀ = 0.3; (f) u_a = 1.5, I₀ = 0.3.

图9结果表明, I₀和u_a变化不会改变系统的放电模式, 但对其谱特征会产生影响. 如图9(b)和图9(c)所示, 在外界激励U相同的情况下, I₀的变化对系统簇放电状态的影响较大; 而u_a对系统簇放电状态的影响不大, 如图9(e)和图9(f)所示. 类似3.1节, 对于第三种情况(case 3), 计算了参数空间中的最大误差函数θ_max与最大相位差??_max.
如图10所示, 类似混沌放电的情况, 在f = 0.002的情况下, 当I₀和u_a较小时系统趋于同步, 随着参数I₀的增加系统出现去同步现象; 但是参数I₀对相位同步的影响较为复杂. 以下考虑I₀较小的情况, 该区域系统的最大误差函数和最大相位差均具有下界, 如图11所示.
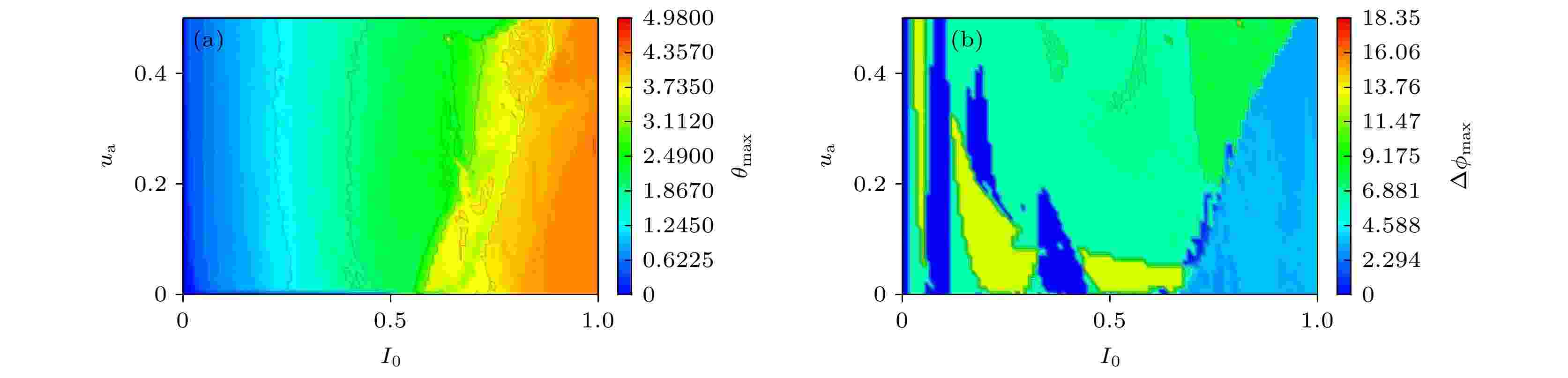图 10 u_a和I₀的参数空间中, 耦合系统(case 3)的同步区间　(a)最大误差函数θ_max; (b)最大相位差??_max
Figure10. Synchronization region of the coupled system (case 3) in the parameter space of u_a vs. I₀: (a) Maximum error function θ_max; (b) maximum phase difference ??_max.

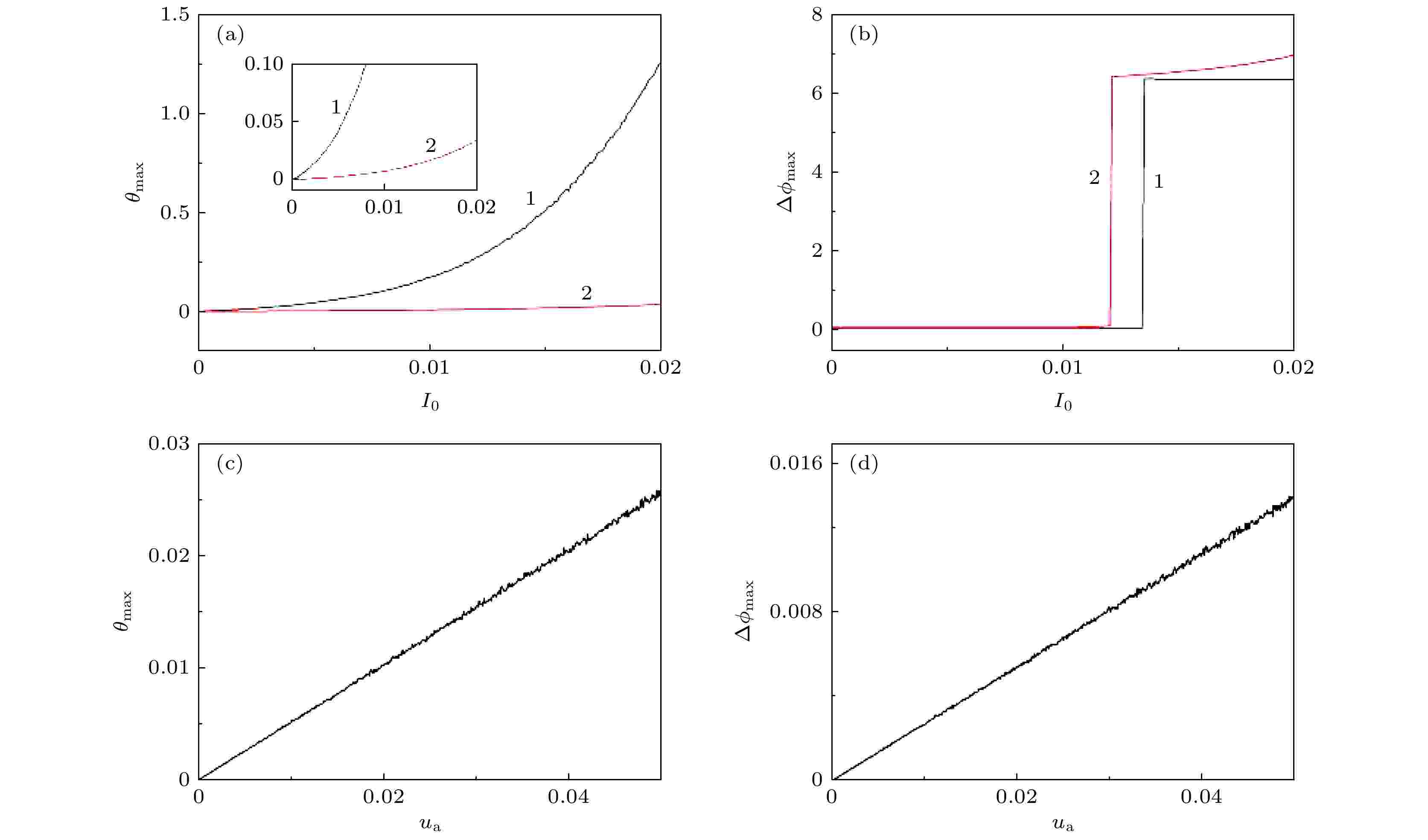图 11 最大误差函数和最大相位差随参数的变化(灰色曲线为(6)式中的非线性耦合, 红色曲线为线性耦合)　(a), (b) u_a = 0.01; (c), (d) I₀ = 0.001
Figure11. The maximum error function and the maximum phase difference change with the parameters, the grey curve represents the nonlinear coupling in Eq. (6) and the red curve is the linear one: (a), (b) u_a = 0.01; (c), (d) I₀ = 0.001.

图11(a)和图11(b)分别计算了相应参数下非线性耦合(曲线1)和线性耦合(曲线2)的情况, 结果表明, 在耦合强度较小, 即I₀ < 0.01时在有限的单位时间内系统误差峰值可以减小到零附近, 耦合系统具有可以实现完全同步的趋势; 而且不同于误差函数曲线的“软击穿”特性, 相位差函数表现为“硬”的, 但是没有观察到亚临界分岔, 且相对误差函数的阈值显著滞后. 此外, 线性耦合方式增大了可同步的参数I₀区间, 减小了相位同步的参数I₀区间. 如图11(c)和图11(d)所示, 不能区别线性和非线性耦合下最大误差函数和最大相位差随u_a变化的关系曲线; 而且相对最大误差函数, 最大相位差的增长更加缓慢. I₀和u_a的增强去同步可以理解为受迫共振效应与(线性或非线性)耦合系统的竞争关系; 当受迫共振效应强于耦合作用时, 表现为同步现象; 否则由于自突触、光电耦合等结构影响, 系统会远离同步状态. 具体参数下耦合系统间的误差、对应的相位差和光电管功率的计算结果如图12所示.
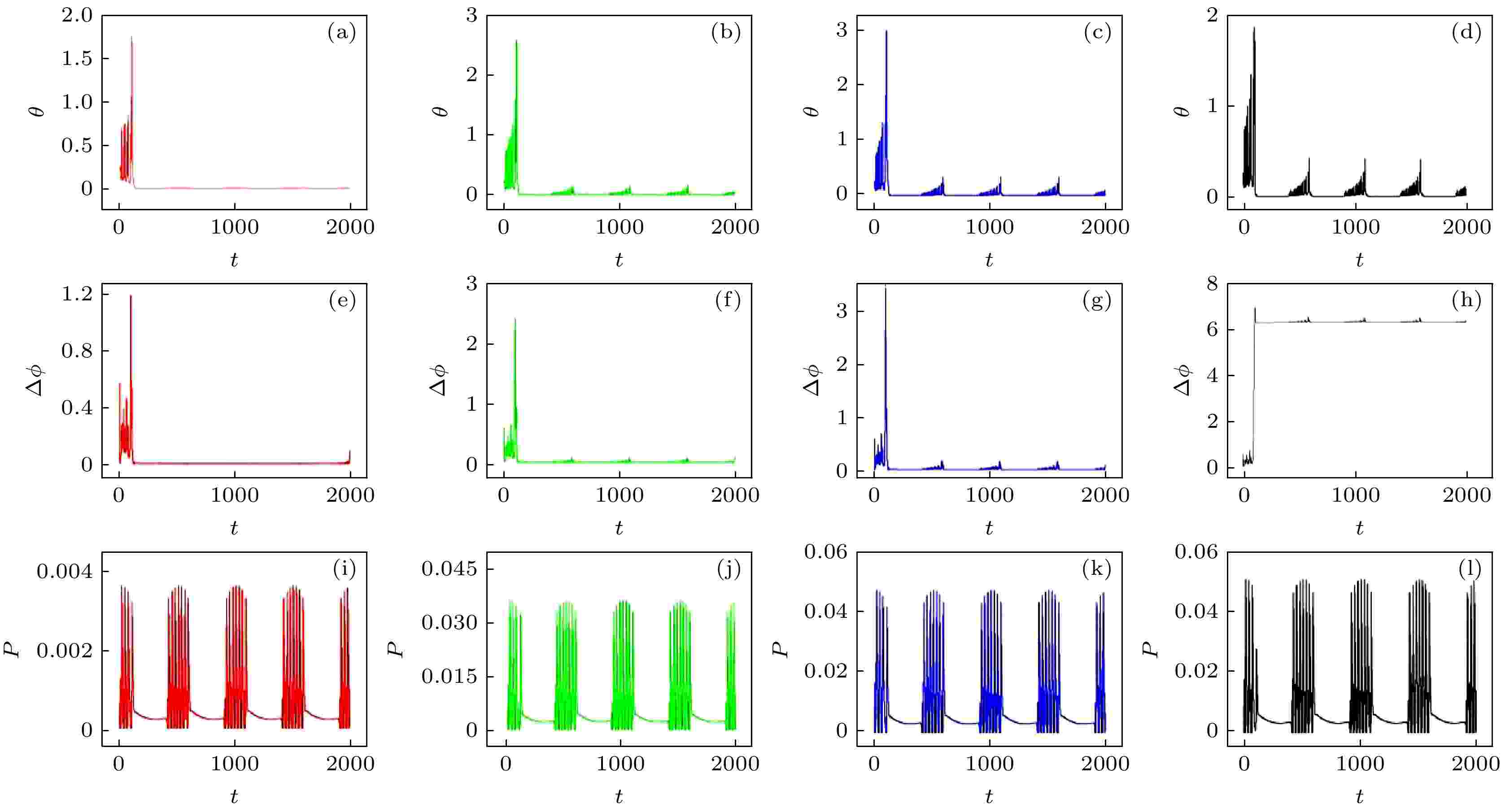图 12 系统误差、相位差和光电管功率随时间的演化(u_a = 0.01)　(a), (e), (i) I₀ = 0.001; (b), (f), (j) I₀ = 0.01; (c), (g), (k) I₀ = 0.013; (d), (h), (l) I₀ = 0.014
Figure12. Evolution of error function, phase error and phototube power (u_a = 0.01): (a), (e), (i) I₀ = 0.001; (b), (f), (j) I₀ = 0.01; (c), (g), (k) I₀ = 0.013; (d), (h), (l) I₀ = 0.014.

如图12(a)、图12(c)、图12(e)和图12(g)所示, 较小的I₀促进耦合系统间的同步; 增大I₀, 耦合系统出现间歇性完全同步, 可能是过量的能量注入引起的, 如图12(d)和图12(h)所示. 此外, 图12(i)—(l)是对应参数下光电管的功率变化, 可以看出, 当I₀继续增大时, 光电管通过光吸收调节系统能量的能力增强. 这与典型的线性反应-扩散系统的情况一致. 对于第四种情况(case 4), 具有较大的u_a (u_a = 0.5)时耦合系统间的误差及对应的相位差结果如图13所示.
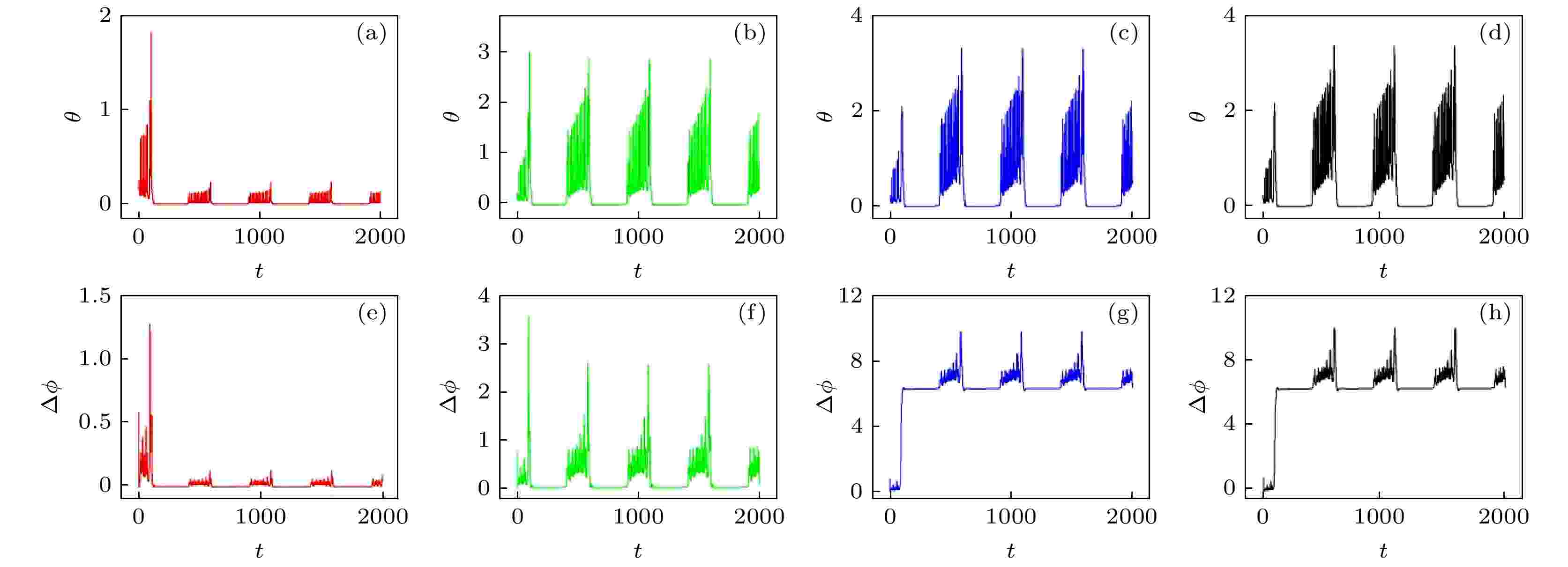图 13 系统误差与相位差随时间的演化(u_a = 0.5)　(a), (e) I₀ = 0.001; (b), (f) I₀ = 0.01; (c), (g) I₀ = 0.013; (d), (h) I₀ = 0.014
Figure13. Evolution of error function and phase error for variables (u_a = 0.5): (a), (e) I₀ = 0.001; (b), (f) I₀ = 0.01; (c), (g) I₀ = 0.013; (d), (h) I₀ = 0.014.

从图13可以看出, 具有较大的u_a时改变I₀的大小无法促进耦合系统间的完全同步和相位同步; 对比图12和图13, I₀相同的情况下, u_a大的系统较难实现完全同步和相位同步. 本文计算结果表明, 对于尖峰放电(f = 0.012)和周期放电(f = 0.06)的FHN神经元, 可能是由于与簇放电同属于周期态放电, 因此I₀和u_a对同步的影响相似.
从物理过程来看, 外界光照激励时耦合通道的光电管主要扮演非线性电阻角色, 即在两个神经元电路之间触发非线性耦合并消耗一定的能量, 从而平衡两个耦合电路的能量以及输出电压. 从动力学和实验的角度看, 对光电管的参数或耦合通道参数进行调制, 就可以实现两个神经元电路的同步. 当嵌入耦合通道的光电管被处于红限频率以上的光照激活后, 光电管则发挥调变电源的作用, 对耦合神经元电路注入能量, 进一步改变其动力学特性, 在恰当的参数范围内实现神经元电路的同步和相位锁定. 从实验角度看, 改变外界光照强度则可以调控耦合通道光电流大小, 进一步改变耦合神经元电路的输出电压特性和动力学模态, 对同步稳定性产生显著影响.

本文基于光电管耦合FHN神经元电路, 研究了影响神经元系统同步动力学的因素. 耦合FHN神经元的光电管作为电流源, 可通过调节光照强度改变光电流大小; 数值计算表明, 由于光电管能量的注入以及能量的调节和输运, 处于混沌放电模式的神经元在较强的耦合强度也能相位锁定或相位同步. 在光电管耦合的(多)周期放电的神经元(包括簇放电、尖峰放电和周期放电)中, 相位同步的区间更加复杂. 在相同耦合强度下, 具有较大反向截止电压的光电管耦合的神经元不能实现同步及锁定, 这是因为反向截止电压大的情况下, 光电管需要吸收更大的能量才能实现对系统能量的注入, 从而使耦合系统实现相位同步.