全文HTML
--> --> -->目前, ****们已对T型/Y型微通道内液滴对称/不对称分裂行为进行了实验探究、理论分析和数值模拟, 并取得了一定的成果. 王维萌等[23]对T型微通道内液滴的对称被动分裂进行可视化实验研究, 捕捉到了隧道分裂、不连续阻塞分裂、永久阻塞分裂和未分裂等4种流型, 获得了毛细数与液滴无量纲长度的经验关联式. Wang等[24]通过实验和理论研究了非对称Y型微通道中的液滴分裂行为, 指出了分裂过程中存在不分裂、隧道分裂和阻塞分裂3种流型, 讨论了母液滴长度和液滴速度对分裂特性的影响, 分析出不分裂和隧道分裂流型的临界条件l/w = 0.5414Ca–0.21(l为液滴长度, w为微通道宽度, Ca为毛细数, Ca = μu/σ, μ为黏度, u为流体速度, σ为两相界面张力), 预测了液滴分裂比, 然而流阻计算需要进一步改进. Liang等[25]采用基于相场的格子玻尔兹曼方法(lattice Boltzmann method, LBM)多相模型研究了表面润湿性、毛细数和出口流量比对Y型微通道处液滴分裂行为的影响, 结果显示, 当毛细数较大时, 液滴分裂动力行为与壁面润湿性联系密切, 对于亲水壁面, 分裂生成的子液滴会发生二次分裂, 导致液滴一部分黏附在通道壁面, 另一部分流向下游; 而对于疏水壁面, 液滴分裂后两个子液滴完全脱离通道壁面; Fu等[26]采用基于颜色模型的LBM方法数值研究了T型微通道中分叉出口压差造成的液滴不对称分裂, 对阻塞分裂过程中液滴动力学的演变进行了精确分析. 结果表明, 在阻塞分裂状态下, 两个子液滴的体积比很大程度上取决于不对称条件, 并提出通用参数As来描述液滴分裂的不对称条件. 但研究仅着眼于阻塞分裂, 还需对隧道分裂、不分裂等工况进行相应分析. 随后, Cheng等[27]采用VOF(volume of fluid)模型数值模拟了不等长分支T型微通道中液滴不对称分裂的动力学行为, 提出了液滴分裂的4种模式(primary breakup, transition breakup, bubble breakup, and non-breakup), 并根据母液滴大小和毛细数预测液滴分裂情况, 指出流体间的黏度比会显著影响临界毛细数. 但是二维(2D)模拟倾向于预测较小的临界毛细数, 因此, 需要进行三维(3D)模拟以更准确地预测液滴分裂所需的临界条件. Chen等[28]采用VOF方法3D模拟和流动可视化实验对T型微通道中微液滴的分裂机理进行了研究. 数值模拟和实验观察显示, 微液滴的流动形态共有4种, 分别是隧道分裂、不连续阻塞分裂、永久阻塞分裂和不分裂, 液滴的分裂和不分裂主要取决于毛细数和相对液滴长度所代表的界面张力的相对优势, 最后, 提出了一种用于预测液滴尺寸的经验关联式, 以说明在永久阻塞分裂工况下液滴尺寸随无量纲时间的变化. 同样基于VOF方法, 俞炜等[29]数值模拟了双重液滴在Y型微通道内的分裂过程, 详细讨论了流场演变及液滴各参数的变化, 研究表明, 外液滴颈部的收缩会因隧道的出现而减缓, 但内液滴颈部收缩基本不受影响; 隧道分裂和不分裂工况临界线符合幂律关系式, 隧道分裂和阻塞分裂工况临界线符合线性关系式. 但是该研究缺少双重液滴分裂实验的验证.
综上所述, 现有研究分析了液滴分裂模式、流型转变的临界条件和分裂动力学行为, 但对液滴不对称分裂行为理论预测还有待加强. 并且, 相对于研究更丰富的隧道分裂和阻塞分裂, 作为隧道分裂和阻塞分裂中间态的半阻塞分裂研究并不充分. 为此, 本文将结合实验以及理论研究, 详细探究T型不对称微通道中的液滴半阻塞不对称分裂机制. 通过搭建T型微通道中液滴分裂特性研究可视化实验平台, 观测半阻塞不对称分裂的流体动力学行为, 探究调控流量对分裂行为的影响, 并发展分裂比理论预测方法, 为微液滴不对称分裂提供设计优化方法和理论支撑.
2.1.芯片结构
如图1(a)所示, 本文所用微流控芯片由4部分组成: 流动聚焦微通道、辅助微通道、T型分裂微通道和调控微通道. 液滴在流动聚焦微通道内生成, 流经辅助微通道, 最后进入T型分裂微通道, 在调控微通道的控制作用下发生分裂. 流动聚焦微通道为十字形, 宽600 μm, T型分裂微通道宽w = 420 μm, 在辅助微通道处完成宽度过渡. 整块芯片的微通道深度h = 200 μm. 芯片由两块分别表面蚀刻有微槽道和表面平整的玻璃键合而成, 芯片具有良好的亲水疏油性. 辅助微通道内注入连续相流体以调整液滴流速, 进而调控主通道毛细数. T型分裂微通道的两个分支长度比为1∶2, 在较短分支下游的U型弯中部接入调控微通道以实现对液滴分裂比的调控. 流体最终从出口流出芯片.?液滴半阻塞不对称分裂示意图和实验系统图如图2和图3所示.
图 1 微流控芯片结构 (a)示意图, I-流动聚焦微通道, II-辅助微通道, III-T型分裂微通道, IV-调控微通道; (b)实物图, 其中Qc为连续相体积流量, Qd为离散相体积流量, Qf为辅助流量, Qt为调控流量Figure1. Geometric structure of the microfluidic chip: (a) Schematic diagram, I-flow focusing microchannel, II-T-shaped splitting microchannel, III-tuning microchannel; (b) actual chip, Qc is volumetric flow rate of continuous phase, Qd is volumetric flow rate of dispersed phase, Qf is volumetric flow rate of supporting continuous phase, Qt is volumetric flow rate of controlling continuous phase
2
2.2.实验设备
连续相和离散相流体均由注射泵(LSP01-1BH、LSP01-2A, 保定兰格恒流泵有限公司)注射进入芯片. 注射器和芯片流体入口由PTFE管连接. 冷光源卤素灯(XD-302)提高实验背景亮度而且避免了高温对实验流体的影响, 高速摄像机(Photron FASTCAM SA4500M-K2, 日本Photron公司)连接有显微镜(Olympus SZX7, 日本Olympus公司), 拍摄并记录液滴在T型微通道分裂的过程, 拍摄帧率为3000—8000 fps. 实验图片用ImageJ软件处理以得到液滴形貌演变参数及子液滴体积等数据.2
2.3.实验工质
实验中所用连续相为甘油水溶液, 添加有0.5 wt%的十二烷基硫酸钠(SDS), 溶液密度ρc = 1062.6 kg/m3, 动力黏度μc = 3.8 mPa·s. 实验发现, 温度较低时SDS会发生沉淀析出, 导致液体浑浊、相界面模糊, 因此实验环境温度维持在20 °C. 实验中离散相为二甲基硅油, 密度ρd = 897.9 kg/m3, 动力黏度μd = 5.0 mPa·s. 两相界面张力σ = 10.00 mN/m.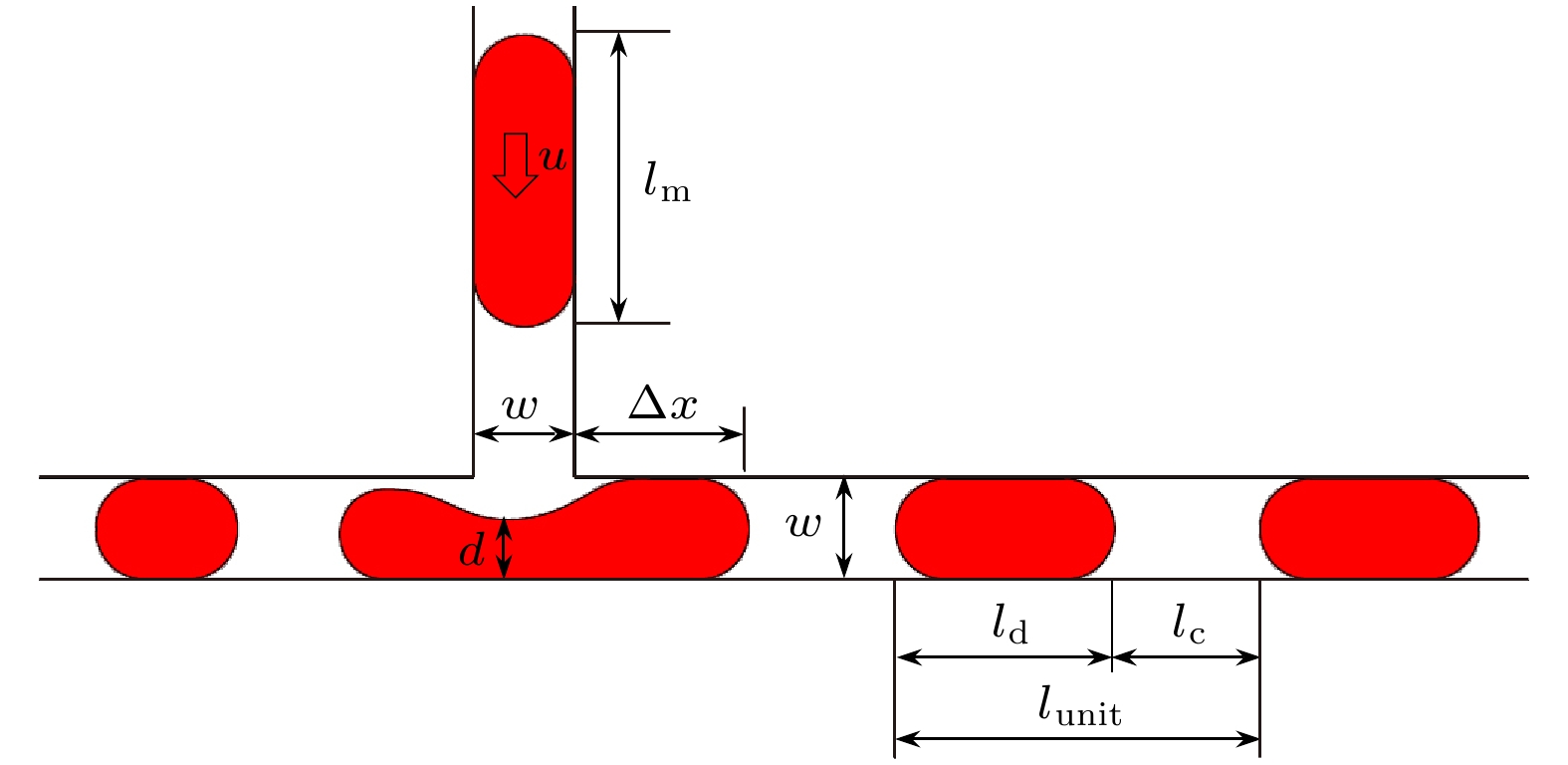
图 2 液滴半阻塞不对称分裂示意图(u为流体速度, lm为母液滴长度, w为微通道宽度, Δx为子液滴头部位移, d为液滴颈部宽度, ld为子液滴长度, lc为子液滴间距)Figure2. Schematic of droplet asymmetrical splitting with a tunnel in a T-junciton (u is velocity of the fluid, lm is length of the mother droplet, w is width of the microchannel, Δx is displacement of the head of the daughter droplets, d is width of the droplet neck, ld is length of the daughter droplet, lc is interval of daughter droplets).
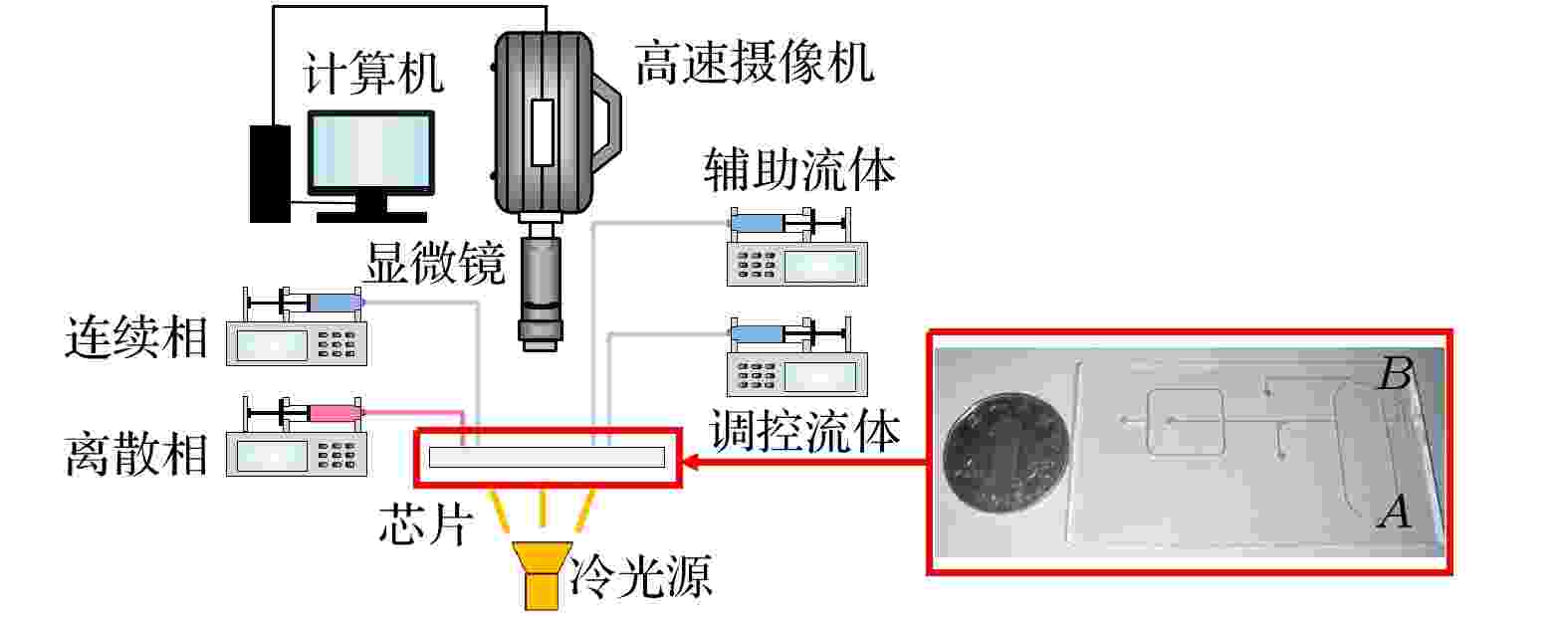图 3 实验系统图Figure3. Schematic of the experimental system.
2
3.1.典型半阻塞不对称分裂过程
图4展示了液滴在T型结构处的典型半阻塞不对称分裂过程. 整个过程分为3个阶段: 进入阶段、挤压分裂阶段和分裂后阶段. 在进入阶段(t1 —t4), 液滴在上游连续相的推动下, 头部向下游移动进入T型结直至贴住微通道壁面, 随后, 液滴向两边伸展进入两个分支通道, T型结被液滴充满, 液滴界面紧贴微通道4个壁面. 待尾部进入T型结构, 界面张力与上游连续相压力的共同作用使圆弧状的尾部由圆变直. 此后, 液滴分裂进入挤压分裂阶段(t4—t9). 在此阶段, 上游连续相的压力挤压液滴界面, 使其中部内凹成近似圆弧状颈部, 随着连续相流体的蓄积, 圆弧逐渐变大, 液滴颈部逐渐变细, 同时液滴的A头部逐渐脱离来流侧的微通道壁面, 出现明显的隧道. 隧道逐渐增大使上游的连续相压力略有下降, 仍能驱使颈部圆弧内凹面继续扩大, 颈部继续变细但速率减慢, 两子液滴头部曲率几乎相等, 均近似为半圆状. 在t6时刻, 隧道达到最大宽度, 连续相在T型结构处继续积聚, 迫使颈部愈发变细, 最终液滴颈部脱离通道上下壁面, 形成细长型, 此时颈部竖直截面为圆形, 指向内部的界面附加压力驱使液滴颈部快速收缩, 颈部迅速由圆弧状变为漏斗状最终塌陷, 液滴分裂形成两个子液滴. 此后进入分裂后阶段(t9—t11), 尾部由尖锥状迅速恢复为圆弧状, 分别进入T型微通道的两个分支, 隧道由于液滴恢复为弹状而消失.
图 4 典型半阻塞不对称分裂过程 (Qc = 400 μL/h, Qd = 40 μL/h, Ca = 5.53 × 10–4, lm/w = 4.08)Figure4. Typical droplet assymetrical splitting with a tunnel in a microfluidic T-junction (Qc = 400 μL/h, Qd = 40 μL/h, Ca = 5.53 × 10–4, lm /w = 4.08).
2
3.2.不对称分裂动力学
液滴半阻塞不对称分裂过程中, 颈部宽度是重要的演变参数. 图5给出了液滴典型半阻塞不对称分裂过程中颈部宽度的演变过程. 如图5所示, 根据颈部宽度的变化速率可将液滴挤压分裂过程分为3个阶段: 挤压前期、挤压后期和快速夹断阶段.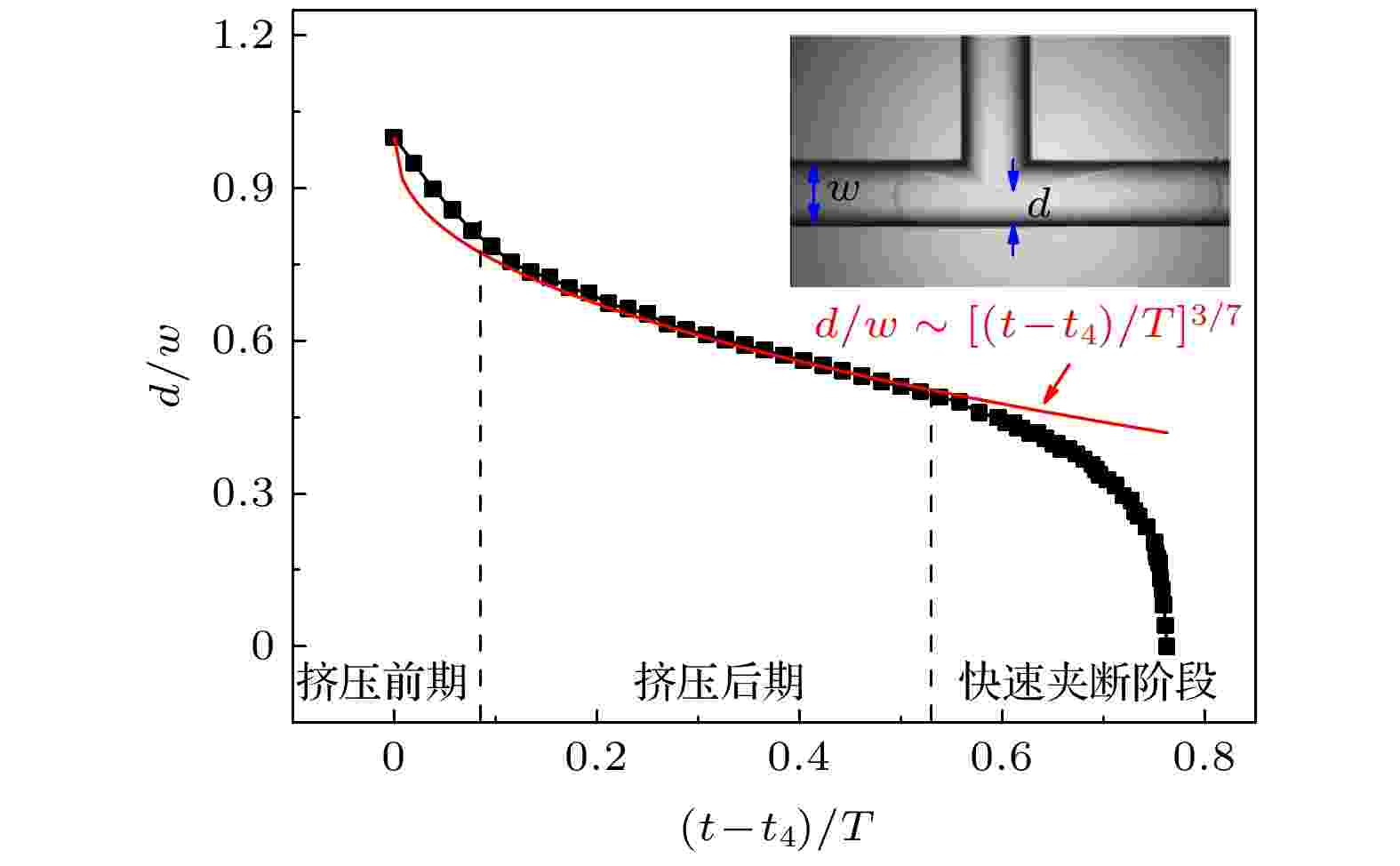
图 5 液滴颈部宽度演变过程(Qc = 400 μL/h, Qd = 40 μL/h, Qt = 0 μL/h, Ca = 5.53 × 10–4, lm /w = 4.08, T = 0.2592 s), 其中(t–t4)/T = 0时表示颈部刚开始收缩Figure5. Evolution of neck width d/w with dimensionless time (t–t4)/T (Qc = 400 μL/h, Qd = 40 μL/h, Qt = 0 μL/h, Ca = 5.53 × 10–4, lm/w = 4.08, T = 0.2592 s), where (t–t4)/T = 0 represents the neck starts contracting.
在挤压前期(0 < (t – t4)/T < 0.08, T为特征时间, T = w/[(Qc + Qd)/wh] = w2h/(Qc + Qd), 液滴颈部开始匀速收缩, 呈线性变化, 随后颈部宽度随时间变化斜率发生变化, 该过程时间持续较短, 在此阶段颈部宽度收缩速率与上游流速相当, 这是由于此阶段液滴颈部曲率半径大, 界面附加压力小, 与阻碍颈部收缩的附加压力相比, 上游连续相驱动力占主导地位.
在挤压后期(0.08 < (t – t4)/T < 0.53), 颈部宽度随时间变化呈指数关系, 持续时间较长, 这表明连续相的挤压作用与液滴界面张力作用呈一种特殊关系, 即虽然这一阶段界面附加压力逐渐增大, 但上游压力驱动作用大于附加压力的阻碍作用, 且上游压力驱动作用相对界面附加压力阻碍作用的优势逐渐降低, 这表现为液滴颈部收缩运动的加速度缓慢减小.
在快速夹断阶段(0.53 < (t – t4)/T < 0.76), 液滴颈部宽度开始加速减小直至液滴分裂. 此时液滴颈部在通道宽度平面内的曲率快速增大, 指向颈部中心的界面附加压力快速增加, 促使液滴颈部分别向A通道和B通道拉伸. 当颈部持续缩减, 直到颈部在通道高度方向上脱离微通道上下壁面, 导致只有迎着上游来流的通道壁面与之接触, 液滴颈部由2D收缩转变为3D收缩. 与颈部在通道宽度平面内的界面类似, 颈部在通道高度平面内的界面曲率越来越大, 同时促进液滴颈部中心收缩. 总的来说, 此阶段液滴颈部向心收缩界面附加压力占主导, 液滴颈部宽度剧烈收缩, 在(t – t4)/T = 0.7时呈断崖式减小, 这表明此时液滴颈部界面极度不稳定, 颈部即将夹断.
通过理论分析, Leshansky等[30]建立液滴在T型微通道中分裂几何模型, 并假定颈部为标准圆弧状, 导出颈部宽度与时间的指数关系d/w – [(t –t4)/T ]3/7. 图5很好地验证了此关系, 在挤压后期阶段, 实验数据符合此指数关系. 但在快速夹断阶段出现偏差且偏差随分裂的进行逐渐增大, 原因是上述研究假定模型为2D模型且假定液滴颈部在变形的全部过程中为标准内凹圆弧形, 忽略了实际液滴3D分裂时颈部脱离通道上下壁面所出现的液滴颈部向心收缩界面附加压力占主导, 促进液滴颈部收缩. 实验观察到, 在快速夹断阶段液滴颈部形貌快速由圆弧状变为漏斗状, 这也验证了上述分析.
图6展示了液滴半阻塞不对称分裂过程中两个子液滴前端位移情况. 图6(a)中, (t – t4)/T = 0.0—0.06这段时间内, 通道B中子液滴曲线有数值而通道A中子液滴曲线无数值, 这是因为在分裂初期, A通道内更大的流阻阻碍通道A中子液滴的移动, 通道B中子液滴的前端此时已经进入流阻较小的B通道, 而通道A中子液滴的前端尚未进入其分支通道, 造成了两个子液滴的初始位移差, 液滴分裂的不对称特点此时就已经显现. (t – t4)/T = 1.375—1.975这段时间内, 通道B中子液滴曲线近似为斜率不变的直线, 而通道A中子液滴曲线的斜率先减小, 后逐渐恢复, 与实验图像对比发现, 这段时间内, 通道A中子液滴与通道壁面之间出现了如图6(b)所示的隧道, 连续相流体流经隧道越过液滴流向下游, 由于隧道内连续相流体对液滴端部的剪切作用促使液滴内部发生涡流, 部分剪切动量转化为涡流动量, 涡流对液滴分裂的阻碍作用强于剪切对液滴的拉伸作用, 实际上阻碍了液滴分裂; 而通道B中未出现隧道, 通道B子液滴在连续相压力下持续以较大速度移动. 待两液滴彻底分裂后, 通道A中子液滴尾部在界面张力的作用下迅速恢复接近球形, 液滴界面收紧, 隧道被压缩至消失, A通道的连续相流体不能越过液滴流向下游而阻塞在液滴后部, 液滴头部和尾部压差增大, 同时涡流消失, 因此又逐渐恢复至隧道出现前的移速. 从图6(a)还可以得出, 在0.06 < (t – t4)/T < 1.375和1.975 < (t – t4)/T < 2.284这两个区间内, 通道B中子液滴曲线斜率为4.5, 通道A中子液滴曲线斜率为1.75, 斜率比为2.57∶1, 虽然与分支通道长度比2∶1有一定差距, 但与图7中Qt* = 0时液滴分裂比(2.5∶1— 2.8∶1)很接近, 这表明子液滴头部位移与子液滴分裂比有一定关系.
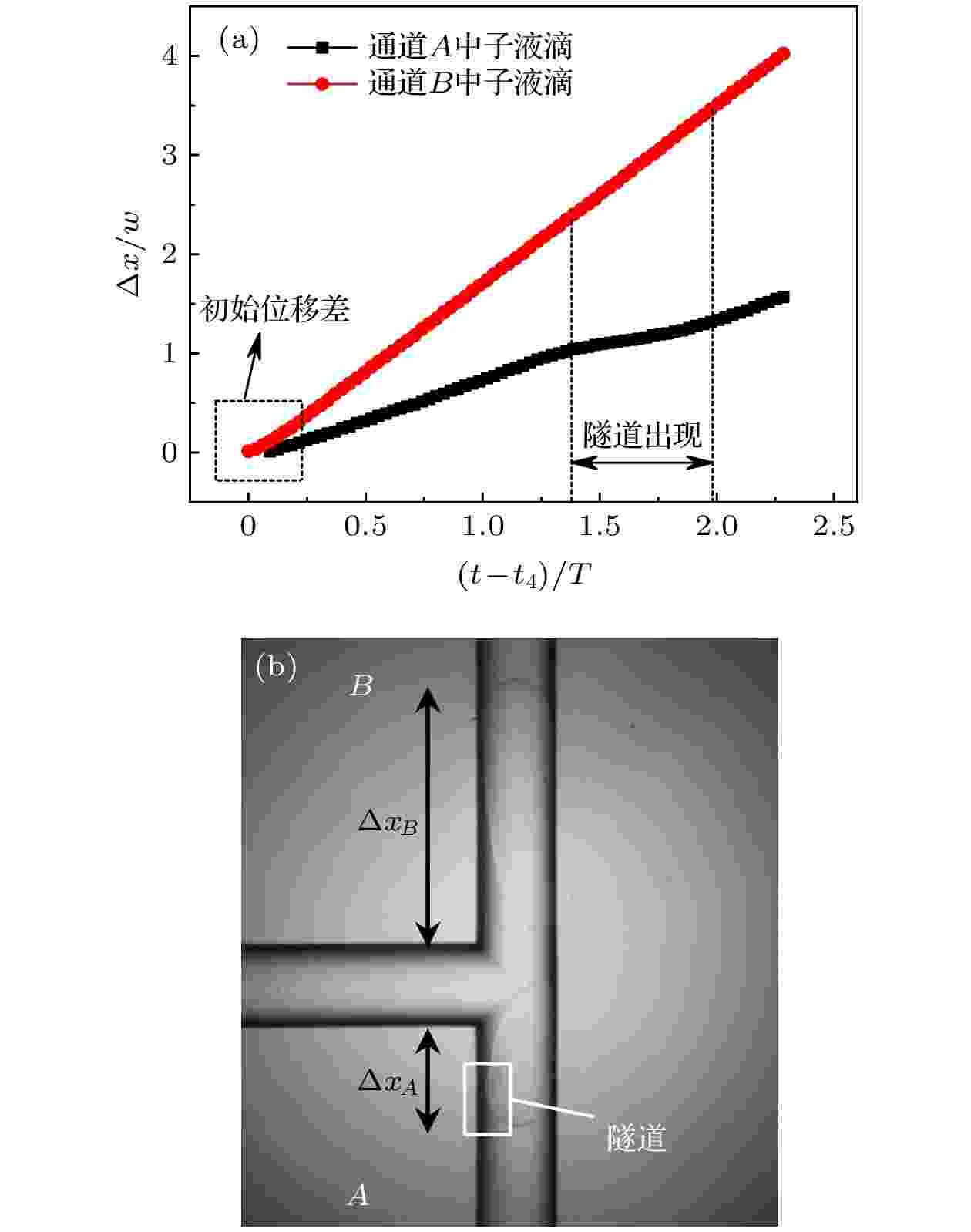图 6 分裂过程中液滴前端位移(Qc = 400 μL/h, Qd = 40 μL/h, Qt = 0 μL/h, Ca = 5.53 × 10–4, lm/w = 4.08, T = 0.2592 s), 其中(t–t4)/T = 0表示液滴头部刚开始进入分支通道Figure6. Motion of droplet front cap during splitting process (Qc = 400 μL/h, Qd = 40 μL/h, Qt = 0 μL/h, Ca = 5.53 × 10–4, lm/w = 4.08, T = 0.2592 s), where (t–t4)/T = 0 represents the head of the droplet has just entered the branch channel.
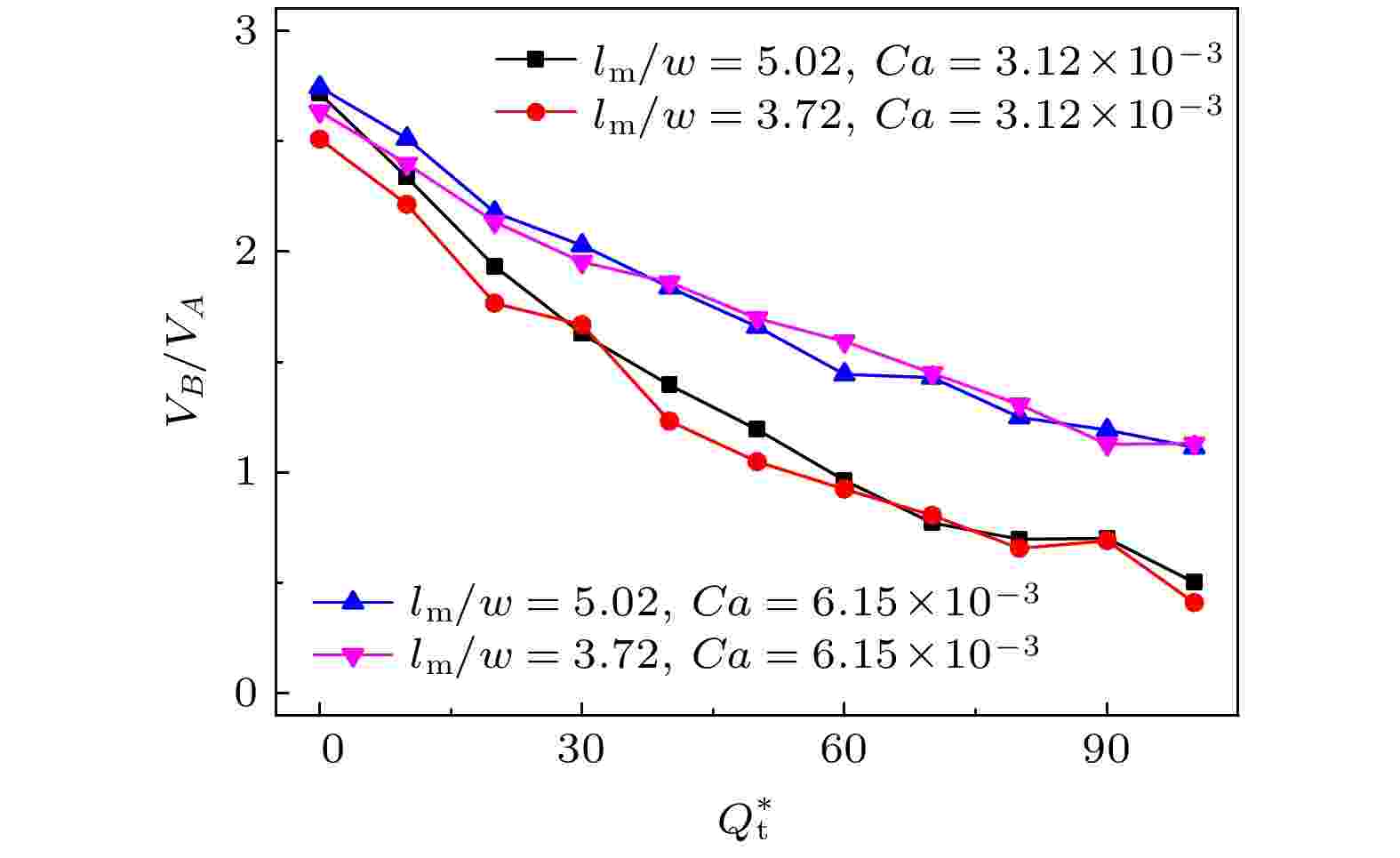图 7 调控流量Qt对液滴分裂比的影响(Qd = 50 μL/h)Figure7. Active regulation of droplet splitting ratio by tuning flow Qt (Qd = 50 μL/h).
2
3.3.分裂比预测
33.3.1.分裂比的主动调控
本研究利用调控微通道将连续相流体注入T型分裂微通道的B分支下游, 改变微通道内压力分布, 从而实现液滴分裂比的精确调控. 图7展示了调控流量Qt对液滴分裂比的主动调控作用效果. 如图所示, 随着Qt*(Qt* = Qt/Qd)的增大, 液滴分裂比VB/VA由接近3:1大幅下降. 同时, 图7还给出了主流毛细数与液滴尺寸对液滴分裂比的影响规律. 由图可知, 不同毛细数工况, 液滴分裂比随调控流量的变化明显不同. 而在当前液滴半阻塞不对称分裂情况下, 母液滴尺寸对液滴分裂比随调控流量的变化规律影响不大.3
3.3.2.分裂比预测
为了精确调控液滴不对称分裂比, 可建立液滴分裂过程压降演化模型, 理论预测不同工况下液滴不对称分裂比, 从而针对目标分裂比快速准确调节流量. 如图8所示, 将微通道流体管网类比为电路网, 液液两相流类比为电流, 压力降类比为电压差, 由并联环路压力降相等将微通道汇合点类比为两个接地零点, 实际的液滴流动即可简化如图8(b), 其中QA, QB和QC分别表示A通道、B通道和C通道内的总体积流量, ΔPA, ΔPB和ΔPC分别表示A通道、B通道和C通道内的压降.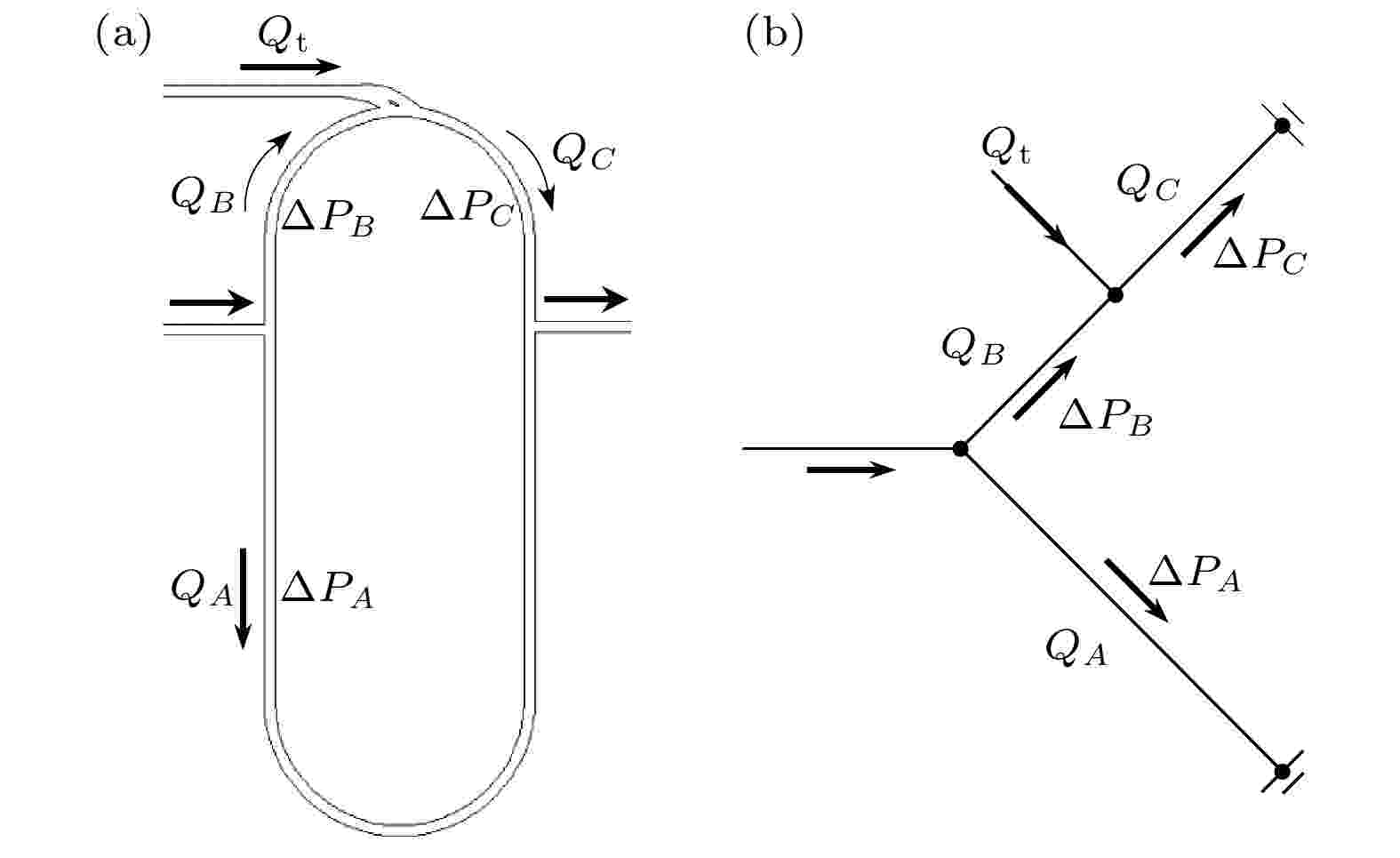
图 8 液滴不对称分裂模型 (a)实物图; (b)简化图Figure8. Asymmetrical droplet splitting model: (a) Actual microchannel; (b) simplified diagram.
由于存在液液界面, 微通道中液滴流动系统比单相流动要复杂的多[31]. 目前, 关于矩形截面微通道内弹状两相流的研究已有报道[32], 在实际流动中, 连续相流体不可避免进入液滴与通道壁面角落的间隙, 这增加了计算液滴(气泡)流动过程压降的难度. ?adosz等[33]考虑间隙影响, 推导出液液弹状流压降的计算式如下, 其中连续相压降为
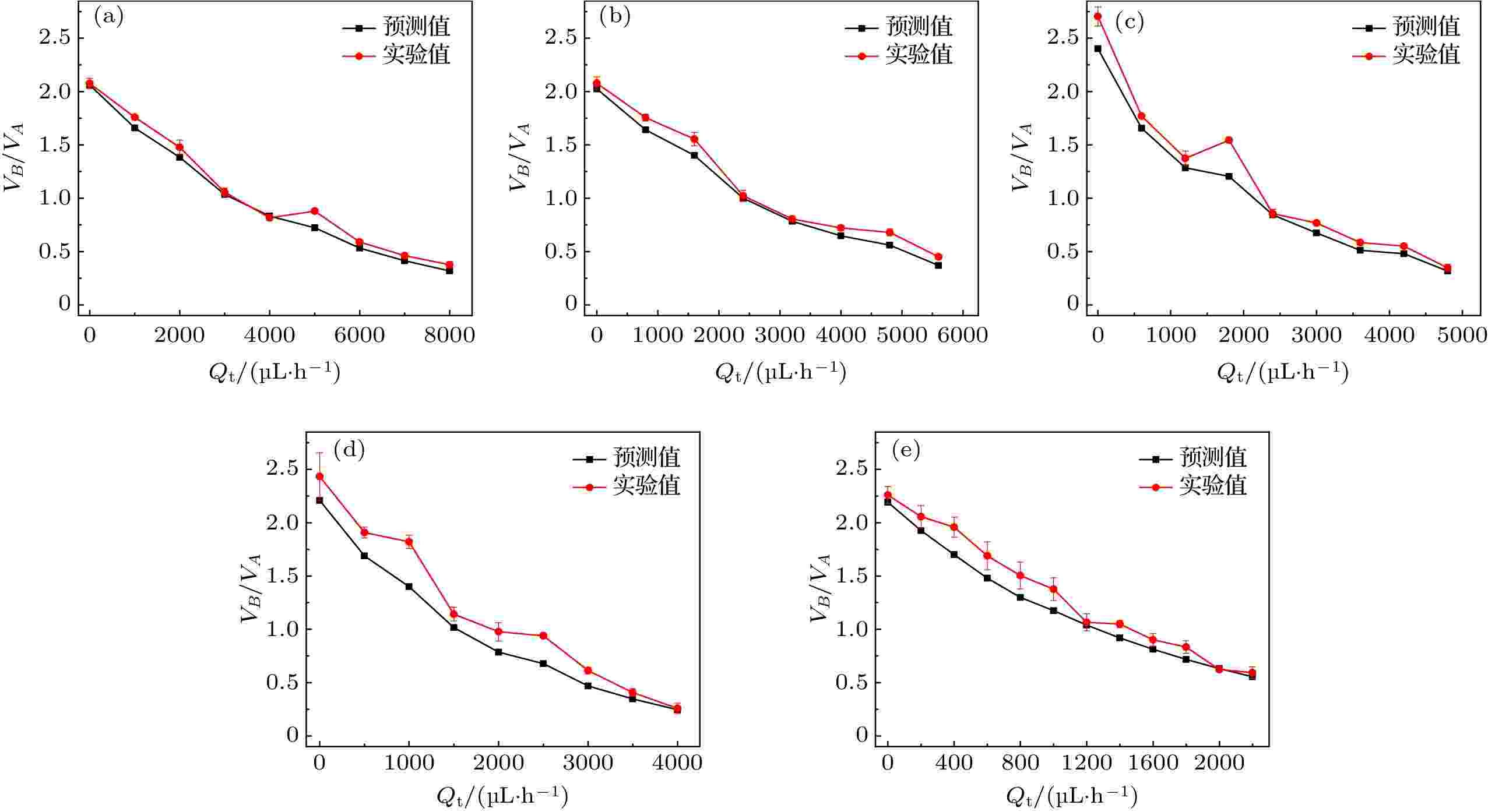图 9 调控流量Qt变化时液滴不对称分裂比预测值与实验值对比 (a) lm/w = 4.37, Ca = 5.24 × 10–3; (b) lm/w = 4.99, Ca = 3.88 × 10–3; (c) lm/w = 5.44, Ca = 3.04 × 10–3; (d) lm/w = 6.24, Ca = 2.22 × 10–3; (e) lm/w = 7.50, Ca = 1.32 × 10–3Figure9. Comparison of predicted value and experimental value of droplet asymmetric split ratio when Qt changes: (a) lm/w = 4.37, Ca = 5.24 × 10–3; (b) lm/w = 4.99, Ca = 3.88 × 10–3; (c) lm/w = 5.44, Ca = 3.04 × 10–3; (d) lm/w = 6.24, Ca = 2.22 × 10–3; (e) lm/w = 7.50, Ca = 1.32 × 10–3.
1)液滴不对称挤压分裂过程分为3个阶段: 挤压前期、挤压后期和快速夹断阶段. 在挤压前期, 液滴颈部曲率半径大, 界面张力附加压力较小, 与阻碍颈部收缩的附加压力相比, 上游连续相驱动力占主导地位, 颈部宽度随时间呈线性变化; 挤压后期, 上游压力驱动作用依然大于附加张力的阻碍作用, 颈部宽度随时间变化呈指数关系; 在快速夹断阶段, 液滴颈部向心界面附加压力占主导, 液滴颈部宽度剧烈收缩, 呈断崖式减小, 最终液滴颈部塌陷分裂成两个子液滴;
2)调节分支通道流量可对液滴不对称分裂比进行有效调控, 且在当前液滴半阻塞不对称分裂情况下, 调控作用受母液滴尺寸的影响较小, 而受毛细数的影响较大;
3)基于液滴分裂过程压降模型的液滴分裂比预测模型能够有效预测液滴分裂比.
