摘要:异质结工程是一种提高半导体材料光电性能的有效方法. 本文构建了全无机钙钛矿CsPbX₃ (X=Cl, Br, I)和二维五环石墨烯penta-graphene (PG)的新型范德瓦耳斯(vdW)异质结, 利用第一性原理研究了CsPbX₃-PG异质结不同界面接触的稳定性, 进而计算了稳定性较好的Pb-X接触界面异质结的电子结构和光电性能. 研究结果表明, CsPbX₃-PG (X=Cl, Br, I)异质结具有II型能带排列特征, 能级差距由Cl向I逐渐缩小, 具有良好的光生载流子分离能力和电荷输运性质. 此外, 研究发现CsPbX₃-PG异质结能有效拓宽材料的光吸收谱范围, 并能显著提高其光吸收能力, 尤其是CsPbI₃具有最优的光吸收性能. 经理论估算, CsPbX₃-PG的光电功率转换效率(PCE)可高达21%. 这些结果表明, 全无机金属卤化物钙钛矿CsPbX₃-PG异质结可以有效地提高半导体材料的光电性能, 预期在光电转换器件中具有重要的应用潜力.
关键词: 钙钛矿CsPbX₃/
五环石墨烯/
范德瓦耳斯异质结/
光电性能

English Abstract

全文HTML

--> --> -->

太阳能作为一种洁净的可持续能源, 对解决当前全球的能源和环境危机具有极其重要的意义. 当前, 钙钛矿型太阳能电池由于具有优异的光吸收特性(10³—10⁶ cm^–1)^[1,2]、光生载流子输运性能(约10 cm²·V^–1·s^–1)^[3]和非常高的光电功率转换效率(PCE)(3.8%—25.2%)等优点^[3-8], 预期在光伏器件方面具有十分广阔的应用前景, 从而受到人们的广泛关注^[4-10]. 虽然有机-无机杂化钙钛矿太阳能电池的PCE已超过25%^[5], 但其有机成分易挥发, 热稳定性差, 对空气中的水和氧气都比较敏感等, 严重制约了有机-无机钙钛矿太阳能电池的实际应用^[11,12]. 相比而言, 全无机钙钛矿材料因其优异的稳定性和逐渐提高的光电转换效率而成为钙钛矿太阳能电池研究领域的热点之一^[2-4]. 例如, Youngho Kang理论计算出CsPbX₃(X=Cl, Br, I) 的迁移率可达10² cm²·V^–1·s^–1[3]. Swarnkar^[13]指出用α-CsPbI₃制备的胶体钙钛矿开路电压为1.23 V, 光电转换效率约为10.77%. 赵一新教授团队^[14]制备了稳定的高结晶度的β-CsPbI₃薄膜, 其光电转换效率高达18.4%. 目前, 如何有效地改善钙钛矿材料的稳定性, 提高全无机钙钛矿的光电转换性能具有重要的研究意义.
随着太阳能光伏器件设计对材料性能需求的发展, 异质结工程作为一种改善半导体材料光电性能的有效方法, 在实验和理论上得到了广泛的研究^[15-29]. 二维层状晶体材料范德瓦耳斯(vdW)异质结^[15-19]是通过将不同的二维材料叠加, 得到的垂直异质结的组装体, 它通常可以结合各组分固有的光电特性, 综合优化材料性能. 如二维/三维钙钛矿^[1], 磷烯/石墨烯^[20], MoS₂/WS₂^[21], WS₂/石墨烯^[22], 钙钛矿/硅烯^[23], CsPbI₃/SnS^[24], CsPbI₃/BP^[25,26]和CsPbBr₃/PbSe ^[27]等诸多vdW异质结都被成功制备, 并表现出良好的光电性能. 比如, 张清林教授课题组^[27]通过可控外延生长制备了CsPbBr₃/PbSe异质结, 基于异质结的光电探测器在405 nm光照下表现出高达4.7 × 10⁴ A/W的光电流响应率. 黄楚云教授团队^[28]在理论上表明石墨烯的Dirac锥和CH₃NH₃PbI₃的直接带隙保留在石墨烯/CH₃NH₃PbI₃异质结中, 石墨烯有望成为钙钛矿太阳能电池的支撑层. 冯宏剑教授团队^[29]指出Graphene/CH₃NH₃PbI₃异质结构可形成新的p-i-n结构钙钛矿太阳能电池, 他们还研究了较多钙钛矿范德瓦耳斯异质结(CsPbI₃/SnS, CsPbI₃/BP)的界面效应和光电性质^[24,26]. 目前, 相关研究工作都表明钙钛矿和二维材料的异质结在光伏器件中具有巨大的研究和应用前景. 我们之前的理论研究发现, 2D-3D钙钛矿异质结的光吸收系数高于纯钙钛矿^[1], 不同的界面接触改变了电子和空穴的复合, 影响了钙钛矿的PCE. 这些结果表明, 异质结的构建是提高二维材料光电性能和光伏器件稳定性及PCE的有效方法.
五环石墨烯(PG)是sp²和sp³两种杂化碳原子共存的新型全碳层状结构材料. 北京大学张顺洪博士等^[30]在2015年理论预测PG能从T₁₂碳中剥离出, 并通过能量稳定性、热稳定性和机械稳定性等方面的计算表明其具有良好的结构稳定性. 自从PG被提出后, 国际上许多著名研究组先后对PG结构^[30-36]和类五环结构penta-P₂C, P₂Si^[37], PdP₂, PdAs₂^[38], PdSe₂^[39]和ZnO₂^[40]等开展了探索研究, 如刘艳平教授等^[39]通过实验和理论合作测得penta-PdSe₂表现出显著的各向异性响应吸收比: α_y/α_x在364 nm约为1.11, 532.00 nm约为1.15, 633.00 nm约为0.84, 具有很强的本征线性二色性效应. PG是一种准直接带隙半导体, 具有合适且可调的宽带隙, 独特的结构构型和优良的半导体特性, 有望在光电领域取得突破性应用. 但PG也存在很多问题, 其中亟待解决的就是本征PG的吸收光谱范围不佳. 通过PG与CsPbX₃构建vdW异质结, 可以充分利用CsPbX₃良好的光吸收性和量子转化效率; 同时, 无机层PG覆盖钙钛矿能有效提高钙钛矿材料的稳定性^[10]. 因此, CsPbX₃-PG异质结预期在光电性能应用方面具有令人期待的表现.
为了研究钙钛矿材料的稳定性, 充分利用其优越的光吸收性能和量子转化效率, 并进一步研究PG潜在的光电性能, 本文构建了全无机金属卤化物钙钛矿CsPbX₃ (X = Cl, Br, I)和PG的vdW异质结, 通过密度泛函计算研究其半导体异质结的界面特性, 并选取较稳定的Pb-X界面的CsPbX₃-PG (X = Cl, Br, I)异质结, 研究了其电子结构、界面电荷转移、动力学稳定性、光吸收率和太阳能功率转换效率等性质, 并从理论上探讨两种界面的稳定性和卤素原子X = Cl, Br, I对异质结电子结构调控的物理机制, 为基于CsPbX₃-PG光伏器件的结构设计提供理论研究参考.

本文基于密度泛函理论(DFT), 使用Vienna从头算模拟软件包(VASP)进行计算, 利用平面波超软赝势方法离子核与价电子之间的相互作用进行研究, 使用Perdew, Burke和Ernzerhof (PBE)的交换相关函数进行计算^[41-43], 考虑DFT方法很难处理vdW相互作用, 而Grimme的DFT-D2方法是应用最为广泛的一种方法, 已被证实能可靠地描述各种vdW异质结构体系, 因此本文所有计算均采用了Grimme DFT-D2修正方法^[44-46]. 经文献参考和参数测试, 布里渊区为4 × 4 × 1网格采样, 平面波基的截止能量设置为450 eV, 所有原子都经过优化, 直到原子Hellmann-Feynman力收敛至0.001 eV/ ?, 总能量变化小于1 × 10^–4 eV. 为了避免相邻单层结构之间的相互作用, 沿z轴方向创建了约15 ?的真空层. CsPbX₃-PG的能带结构和光吸收率等性质均采用PBE泛函进行计算, 在能级计算的时候加入了偶极修正, 并且考虑了杂化泛函(HSE06)和自旋轨道耦合(SOC)计算下的能级排列^[47-49].

2

-->

3.1.结构模型和稳定性

计算得到立方块体钙钛矿CsPbCl₃, CsPbBr₃, CsPbI₃的晶格常数分别为a = b = c = 5.733 ?, a = b = c = 5.993 ?, a = b = c = 6.417 ?, PG单胞的晶格常数为a = b = 3.64 ?. 异质结中CsPbX₃为四层八面体结构, 其性能与立方块体CsPbX₃相似, 且四层CsPbX₃和单层PG构成vdW异质结时旋转角度为26.57°. 在CsPbX₃-PG异质结中, 由于CsPbX₃具有两种不同的界面(Pb-X界面和Cs-X界面), CsPbX₃可以通过不同界面与PG进行界面接触, 通过计算最小化表面结合能, 可以选择更稳定、更合理的异质结. 计算界面形成能公式为

$\Delta E = ({{{E_{{\rm{TOT}}}} - {E_{{\rm{PG}}}} - {E_{{\rm{CsPb}}{X_{\rm{3}}}}}}})/{S},$

其中S是界面的面积, ${E_{{\rm{PG}}}}$是PG单层的能量, ${E_{{\rm{CsPb}}{X_3}}}$是CsPbX₃的能量, ${E_{{\rm{TOT}}}}$是异质结的总能量. 通过理论计算, CsPbX₃-PG (X = Cl, Br, I)异质结的两个不同界面接触的界面形成能如表1所列. 结果表明, Cs-X界面异质结的结合能是正值, 异质结形成过程为吸热反应, 稳定性差, 不易于实验合成; 而Pb-X界面构成的CsPbX₃-PG异质结表面结合能是负值, 为放热反应, 表明在实验上也可能更容易形成Pb-X界面的CsPbX₃-PG异质结. 因此, 本文讨论了三种Pb-X (X = Cl, Br, I)界面接触的CsPbX₃-PG异质结. CsPbCl₃-PG, CsPbBr₃-PG和CsPbI₃-PG异质结晶格失配度的结果如表1所列, 分别为0.15%, 1.33%和3.61%, 说明均可较好地匹配. 异质结形成后, 晶格失配引起的晶格应力可能会引起界面处的晶格结构畸变, 因此, 又分别从能量和动力学收敛准则对CsPbX₃-PG异质结进行优化, CsPbX₃-PG异质结如图1所示, 由于晶格失配比很小, 结构参数的变化很小, 优化的垂直层间距离d₁, d₂和d₃分别为3.18, 3.39和3.51 ?. 因此, 在构造的二维CsPbX₃-PG异质结中保持了单个组分的本征结构特征, 界面接触为vdW接触.

X	晶格失配度/%	界面形成能/(meV·?–2)
		PbX-PG	CsX-PG
Cl	0.15	–1.92	12.42
Br	1.33	–6.02	0.54
I	3.46	–5.43	1.03

表1CsPbX₃-PG异质结的晶格失配度和表面结合能
Table1.Lattice mismatch ratio and surface binding energyof PbX and CsX interface in CsPbX₃-PG heterostructures.

图 1 三种CsPbX₃-PG异质结的顶部和侧面视图　(a), (b) CsPbCl₃-PG; (c), (d) CsPbBr₃-PG; (e), (f) CsPbI₃-PG
Figure1. Top and side views of the CsPbX₃-PG heterostructure: (a), (b) CsPbCl₃-PG; (c), (d) CsPbBr₃-PG; (e) (f) CsPbI₃-PG.

为了验证CsPbX₃-PG在室温下的动力学稳定性, 在正则系综(NVT)下进行了分子动力学(AIMD)模拟. 温度和能量随着模拟时间的变化如图2所示, 在5000 fs时间内, 这三个异质结能量变化极小, 温度振荡也很小并具有周期性变化, 表明研究的CsPbX₃-PG体系满足动力学稳定性和热稳定性.
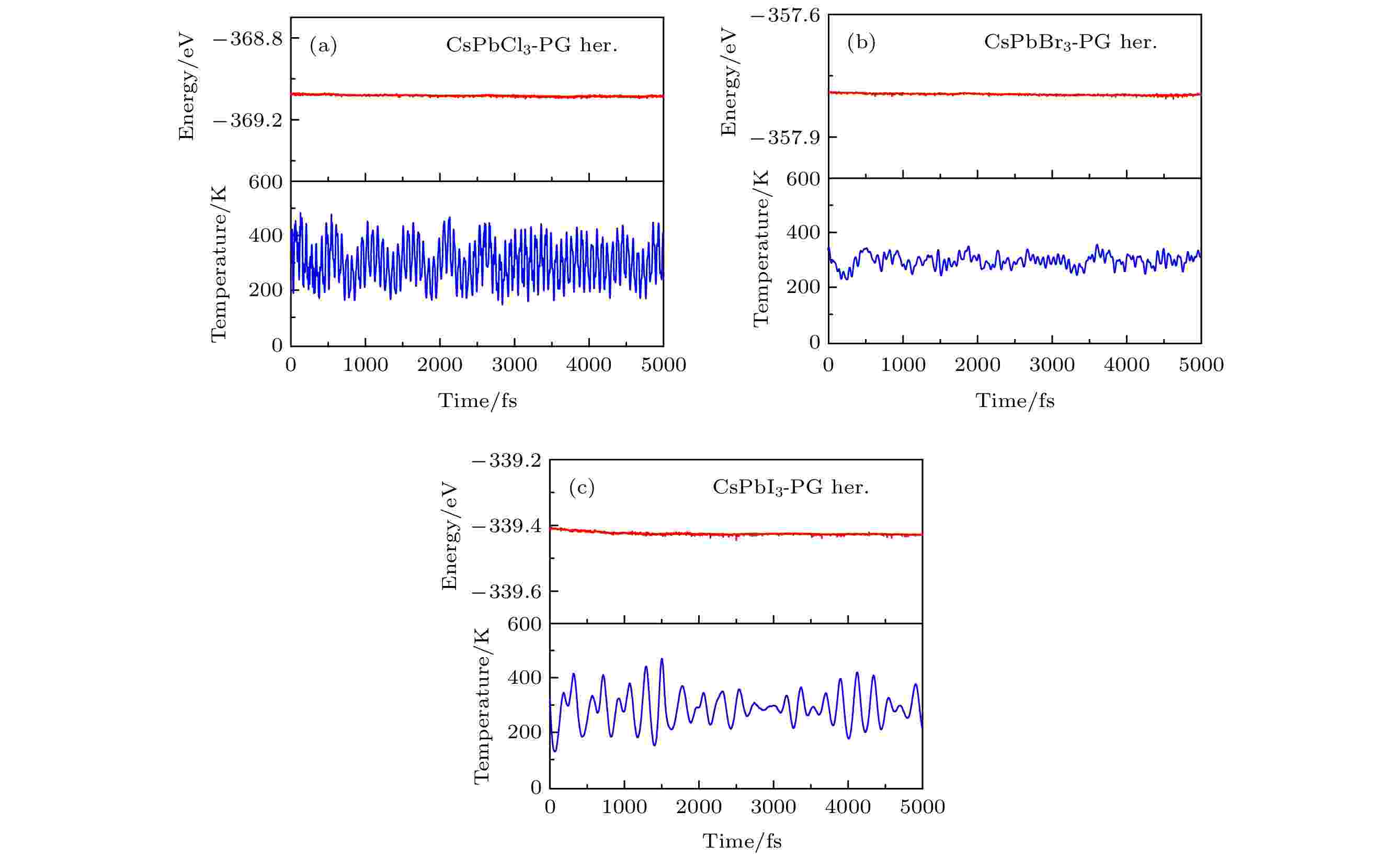图 2 分析动力学(AIMD)模拟, 能量和温度在300 K的相对于时间的波动　(a) CsPbCl₃-PG异质结; (b) CsPbBr₃-PG异质结; (c) CsPbI₃-PG异质结
Figure2. Energy and temperature fluctuation respect to time in AIMD simulation at 300 K: (a) CsPbCl₃-PG heterostructure; (b) CsPbBr₃-PG heterostructure; (c) CsPbI₃-PG heterostructure.

2 -->

3.2.电子结构

电子能带结构对研究异质结的界面性质至关重要, 接下来分析CsPbX₃-PG半导体异质结的电子结构性质. 图3(a)—图3(c)分别给出了计算的CsPbCl₃-PG, CsPbBr₃-PG, CsPbI₃-PG异质结的能带结构图, 红线和蓝线分别表示PG单层和CsPbX₃单层的能带结构图, 费米能级在图中设置为零. 结果表明, CsPbX₃-PG异质结的电子能带结构基本可以看成是两种材料能带成分的组合, CsPbX₃在接触状态下保持其直接带隙特性, PG单层保持其准直接带隙特性, 并且导带底(CBM)由PG贡献, 价带顶(VBM)由CsPbX₃贡献, CsPbCl₃-PG, CsPbBr₃-PG和CsPbI₃-PG异质结均为典型的Ⅱ型能带排列, 表明CsPbX₃-PG异质结具有较好的光生载流子分离能力. 计算的单层PG, CsPbX₃和PG-CsPbX₃异质结的带隙如表2所列, 分别处于接触前状态和接触状态. 本文主要考虑的是异质结堆叠和界面相互作用的影响, 接触前后状态取的均是异质结中经晶格应变后的超胞状态, 结果显示两种状态下PG和CsPbX₃带隙数值相差很小, 尤其是PG的带隙保持一致. 这说明层与层之间的相互作用非常弱, PG单层和CsPbX₃在异质结中保持了单层的优异性能, PG改善了CsPbX₃-PG的电子结构却不影响CsPbX₃的本征特性.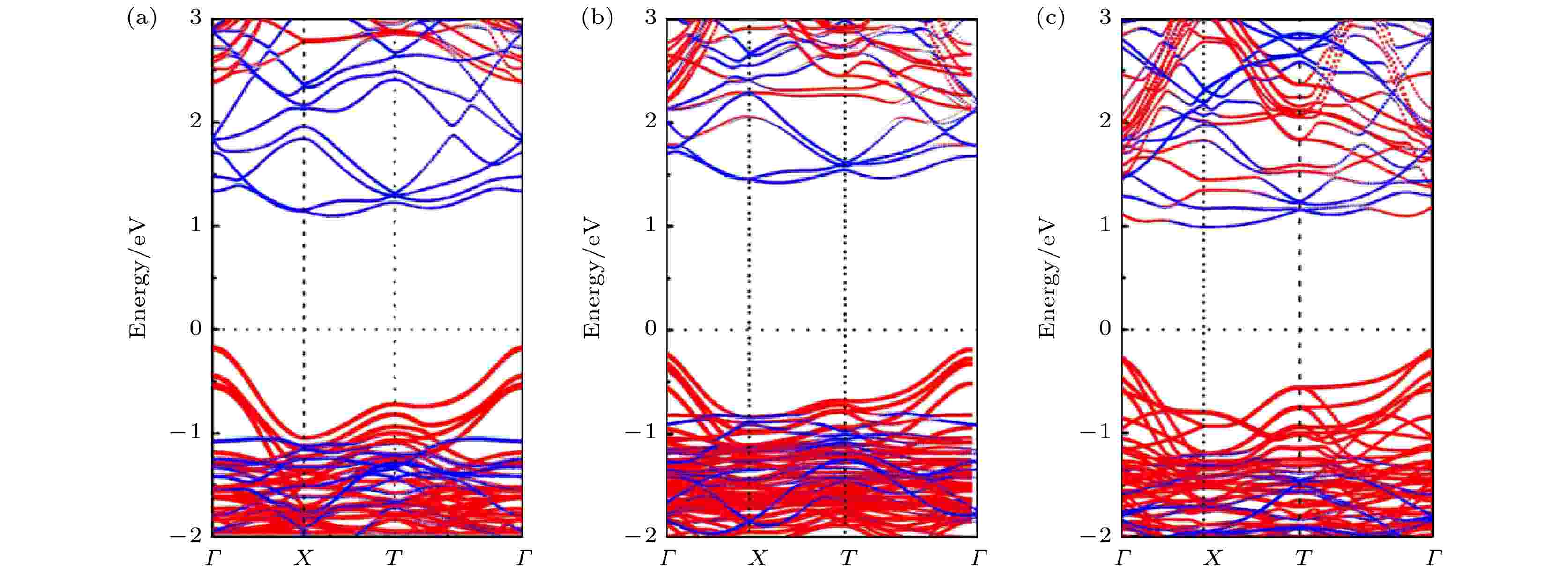
图 3 (a) CsPbCl₃-PG, (b) CsPbBr₃-PG, (c) CsPbI₃-PG异质结的能带分解图, 红, 蓝线分别代表代CsPbX₃和PG单层的能带
Figure3. Electronic band structures of heterostructures: (a) CsPbCl₃-PG; (b) CsPbBr₃-PG; (c) CsPbI₃-PG. The red and blue lines represent the energy bands of CsPbX₃ slabs and PG monolayer, respectively.

X	接触前（单结构）			接触态（异质结）
	PG	CsPbX3		PG	CsPbX3	CsPbX3-PG
Cl	2.21	2.21		2.21	2.62	1.30
Br	2.28	1.77		2.28	1.79	1.62
I	2.36	1.52		2.36	1.30	1.20

表2CsPbX₃-PG异质结接触前后带隙数据
Table2.Calculated band gaps of PG monolayer, CsPbX₃ slabs and CsPbX₃-PG heterostructures in the pre-contact state (left) and contact state (right) by PBE functional.

探索界面电荷转移对研究半导体异质结的界面性质具有重要意义. 图4中给出了CsPbX₃-PG异质结构在接触前状态和接触状态下的能级排列图, 在未接触状态下, 真空能级(E_v)设置为零; 在接触状态下, 费米能级(E_f)设置为零. 图4显示了CsPbX₃-PG异质结构能带类型均为II型排列, 表明CsPbX₃-PG异质结构将具有较好的光生载流子分离能力. 对于CsPbX₃体系, HSE06泛函预测的带隙明显高估, SOC预测的带隙则是会被低估, 而SOC对CsPbX₃体系的带边可能会有较大影响^[47-49], 因此在使用PBE计算能级排列的基础上, 再采用HSE + SOC测试了CsPbCl₃-PG, CsPbBr₃-PG, CsPbI₃-PG异质结带边的能量本征值位置, 如图4(g)—图4(i)所示. 对比PBE的结果图4(d)—图4(f)可知, 两种方法计算的带隙值相差较小(CsPbCl₃: 约0.3 eV, CsPbBr₃: 约0.2 eV, CsPbI₃: 约0.2 eV), 并且能带排列结果均为II型排列, 表明异质结具有较好的光生载流子分离能力.
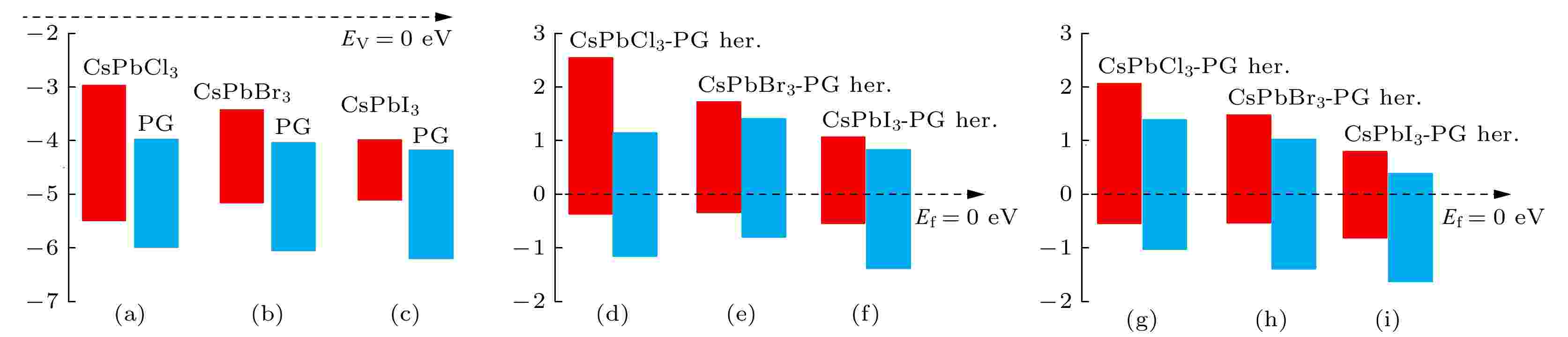图 4 CsPbX₃-PG异质结的能级排列图　(a)—(c)接触前, (d)—(f) PBE计算的接触状态, (g)—(i) HSE + SOC验证的接触状态下VBM和CBM点能量本征值. 其中, 蓝色块表示PG单层和红色块分别表示CsPbX₃（X = Cl, Br, I）的能级
Figure4. The energy level alignment diagram of the CsPbX₃-PG heterostructures: (a)–(c) the pre-contact states, (d)–(f) PBE calculated contact states and (g)–(i) HSE + SOC validated the energy eigenvalues of VBM and CBM points in the contact states. The blue blocks represent the energy level of PG monolayer and the red blocks represent the energy level of CsPbX₃ slabs [X = Cl, Br, I (from left to right)].

为了阐明CsPbX₃-PG异质结界面电荷转移的详细性质, 计算了异质结沿z方向的平面平均微分电荷密度ρ(z), 用于分析结构优化后异质结的界面耦合情况. CsPbX₃-PG异质结界面电荷转移性质如图5(a)—图5(f)所示, 沿z轴的平面平均电荷密度差和三维电荷密度差可由如下公式计算^[24]:
图 5 沿Z方向上的平面平均差分电荷密度　(a) CsPbCl₃-PG, (c) CsPbBr₃-PG, (e) CsPbI₃-PG异质结(红色区域为PG, 蓝色区域为CsPbX₃); 3D差分电荷密度 (b) CsPbCl₃-PG, (d) CsPbBr₃-PG, (f) CsPbI₃-PG异质结(黄色代表增益电子, 绿色代表损耗电子)
Figure5. The plane-averaged electron density difference along Z direction of (a) CsPbCl₃-PG, (c) CsPbBr₃-PG, (e) CsPbI₃-PG. 3D charge density difference of heterostructures: (b) CsPbCl₃-PG, (d) CsPbBr₃-PG, (f) CsPbI₃-PG. (Yellow represents gain electrons, and green represents lose electrons).

$\Delta \rho = {\rho _{{\rm{ToT}}}} - {\rho _{{\rm{PG}}}} - {\rho _{{\rm{CsPb}}{X_3}}},$

其中${\rho _{{\rm{TOT}}}}$, ${\rho _{{\rm{PG}}}}$, ${\rho _{{\rm{CsPb}}{X_3}}}$分别是CsPbX₃-PG异质结、单层PG和CsPbX₃的平面平均密度, 图中黄色意味着获得电子, 绿色意味着失去电子. 图中可看出在CsPbCl₃-PG, CsPbBr₃-PG和CsPbI₃-PG中, 由于层间耦合效应, 异质结界面上的电荷被重新分配, 由异质结界面附近的差分电荷密度得出PG层为电荷的损耗, CsPbX₃层主要为电荷的积累, 表明电子从PG层向CsPbX₃侧转移. 净电荷的积累导致界面间形成内置电场, 内置电场的方向由PG指向CsPbX₃, 而内置电场的产生将形成自发极化, 有利于电子和空穴的分离, 这意味着界面中电荷密度的重新分布将影响异质结的电位分布. 在光照情况下, 光生电子将倾向于向PG侧流移动, 光生空穴倾向于向CsPbX₃端移动, 随着光生载流子的分离积累而形成电势差.
2 -->

3.3.光电特性

研究异质结的光吸收能力对于其在光电器件中的应用具有重要意义. 吸收光谱是根据介电函数计算的:

$ \alpha \rm=\sqrt{2}\omega {\left[\sqrt{{\epsilon }_{1}{(\omega )}^{2} + {\epsilon }_{2}{(\omega )}^{2}}-{\epsilon }_{1}(\omega )\right]}^{1/2}, $

其中$\alpha $是吸收系数, ω是光学频率, ${\varepsilon _1}(\omega )$和${\varepsilon _2}(\omega )$分别是介电函数的实部和虚部, 用以下表达式计算频率相关介电函数${\varepsilon _2}(\omega )$的虚部:

$ {\epsilon }_{2}(\omega )=\frac{4}{\rm{π}{\omega }^{2}}{{\displaystyle \sum _{nn\rm{'}}{\displaystyle \int \left|{P}_{nn\rm{'}}(k)\right|^{2}}}}\frac{{\rm d}{S}_{k}}{\nabla {\omega }_{nn\rm{'}}(k)}.$

介电函数的实部${\varepsilon _1}(\omega )$可以用Kramer-Kronig关系从虚部${\varepsilon _2}(\omega )$计算,

${\varepsilon _1}(\omega ) = 1{\rm{ + }}\frac{2}{{\rm{\pi }}}P\int\nolimits_0^\infty {\frac{{\omega '{\varepsilon _2}(\omega ')}}{{\omega {'^2} - {\omega ^2}}}} {\rm{d}}\omega ',$

所有的光学性质都可从介电函数中得到^[50-52].
图6给出了CsPbX₃-PG异质结、单层PG和CsPbX₃的光吸收谱, 异质结的光吸附峰边缘均位于可见光区域. 我们发现, 与CsPbX₃和PG单层相比, CsPbCl₃-PG异质结在红外, 可见光和紫外区域的光吸收率有明显提高, 高达4 × 10⁵ cm^–1, 其中PG的光学带隙小于CsPbCl₃, 可见PG拓宽了异质结光吸收范围; CsPbBr₃-PG异质结的光吸收率扩展到红外区域, 且可见光和紫外区域明显有提高, 高达5 × 10⁵ cm^–1, CsPbBr₃的光学带隙比PG小; CsPbI₃-PG异质结在可见光和紫外区域的光吸收率稍有提高, CsPbI₃光学带隙明显小于PG, 光吸收率也高达5 × 10⁵ cm^–1. CsPbX₃-PG异质结的光吸收系数强度和吸收范围都得到明显的改善. 此外, 光吸收谱范围主要取决于带隙, CsPbX₃-PG异质结的光吸收谱范围相对于带隙较大的单层而言明显红移. 计算的光吸收谱表明, 通过构建异质结可以有效地调节PG单层的光吸收率和改善光吸收范围, CsPbX₃-PG异质结具有很好的光吸收能力和光电器件应用潜力.
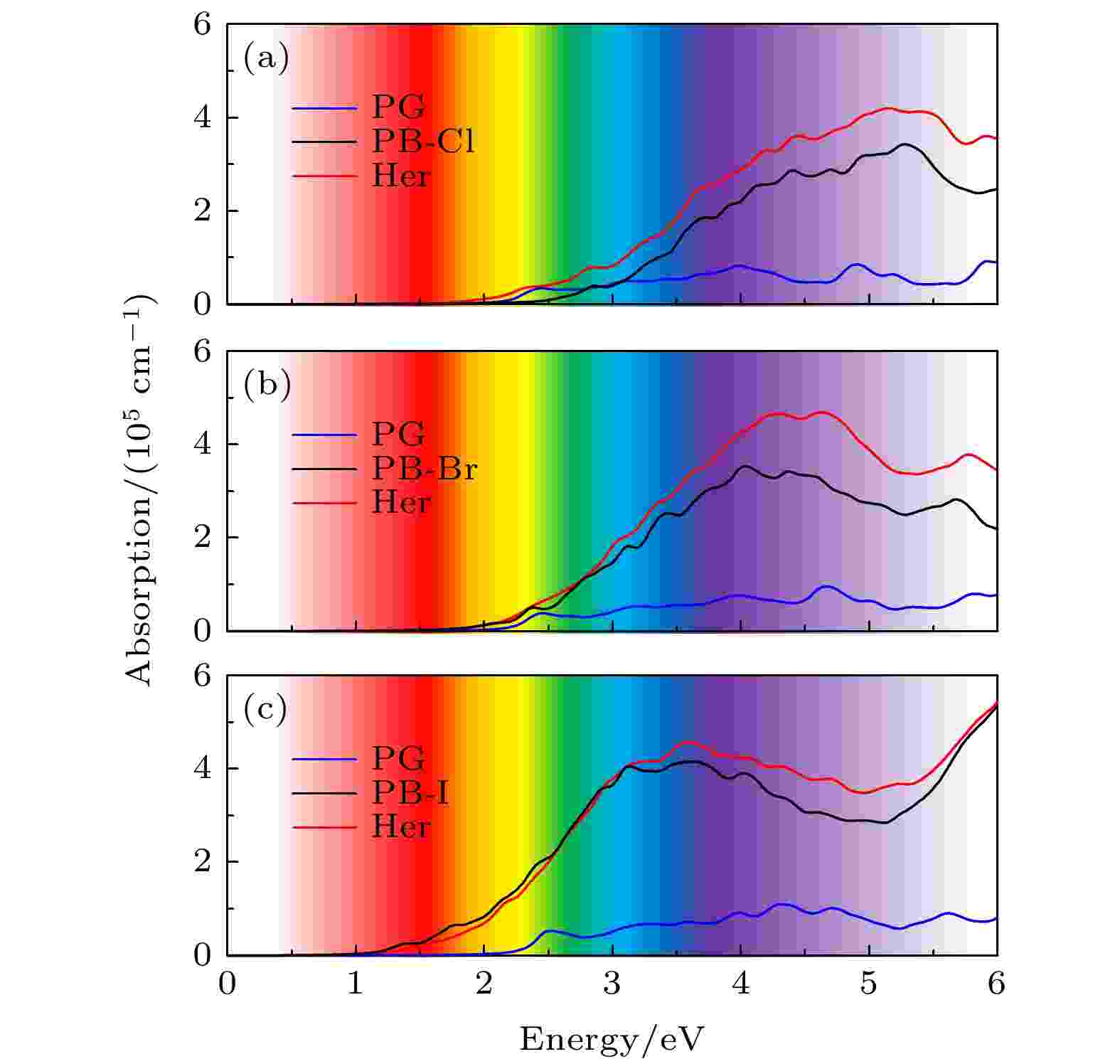图 6 光吸收谱　(a) CsPbCl₃-PG; (b) CsPbBr₃-PG; (c) CsPbI₃-PG异质结 (红线、蓝线和黑线分别代表CsPbX₃-PG (X=Cl, Br, I)异质结、CsPbX₃和PG单层的光吸收率 (X=Cl, Br, I)
Figure6. Light absorption capacity of (a) CsPbCl₃-PG, (b) CsPbBr₃-PG, (c) CsPbI₃-PG. The red, blue and black line represent the light absorption capacity of CsPbX₃-PG heterostructures, CsPbX₃ slabs and PG monolayer, respectively [X=Cl, Br, I (up-down)].

此外, 对于II型能带排列的异质结, 按照Scharber等^[52]的方法进一步估计它们的PCE, 其中PCE在100%外部量子效率极限中的上限可以表示如下:

$\begin{split} \eta & \;=\frac{{J}_{\rm{SC}}{V}_{\rm{OC}}{\beta }_{\rm{FF}}}{{P}_{\rm{polar}}}\\ & =\frac{0.65({E}_{\rm{g}}-\Delta {E}_{\rm{C}}-0.3)\displaystyle \int_0^\infty \frac{P(\hslash \varpi )}{\hslash \omega }\rm{d}(\hslash \varpi )}{{\displaystyle \int_0^\infty P(\hslash \varpi )\rm{d}(\hslash \varpi )}}, \end{split}$

其中, 带隙填充系数假定为0.65, 分子中的积分是短路电流J_sc, 使用100%的限制外部量子效率(EQE)进行计算, 而分母$P(\hbar \varpi )$是在光子能量$\hbar \varpi $的AM1.5太阳能通量, 图7所示为等高曲线范围. ${E_{\rm{g}}} - \Delta {E_{\rm{C}}} - 0.3$项是最大开路电压(V_oc)的估计值, 由有效界面间隙减去0.3 eV估算, 以解释能量转换动力学, E_g是异质结中供体的光学带隙, $\Delta {E_{\rm{C}}}$是供受体间的导带/价带偏移量conduction/valence band offset(CBO/VBO). 因此, 效率$\eta $估计为入射能量通量在100% EQE范围内标准化的产物${\rm{FF}} \cdot {V_{{\rm{OC}}}} \cdot {J_{{\rm{SC}}}}$^[52-54].
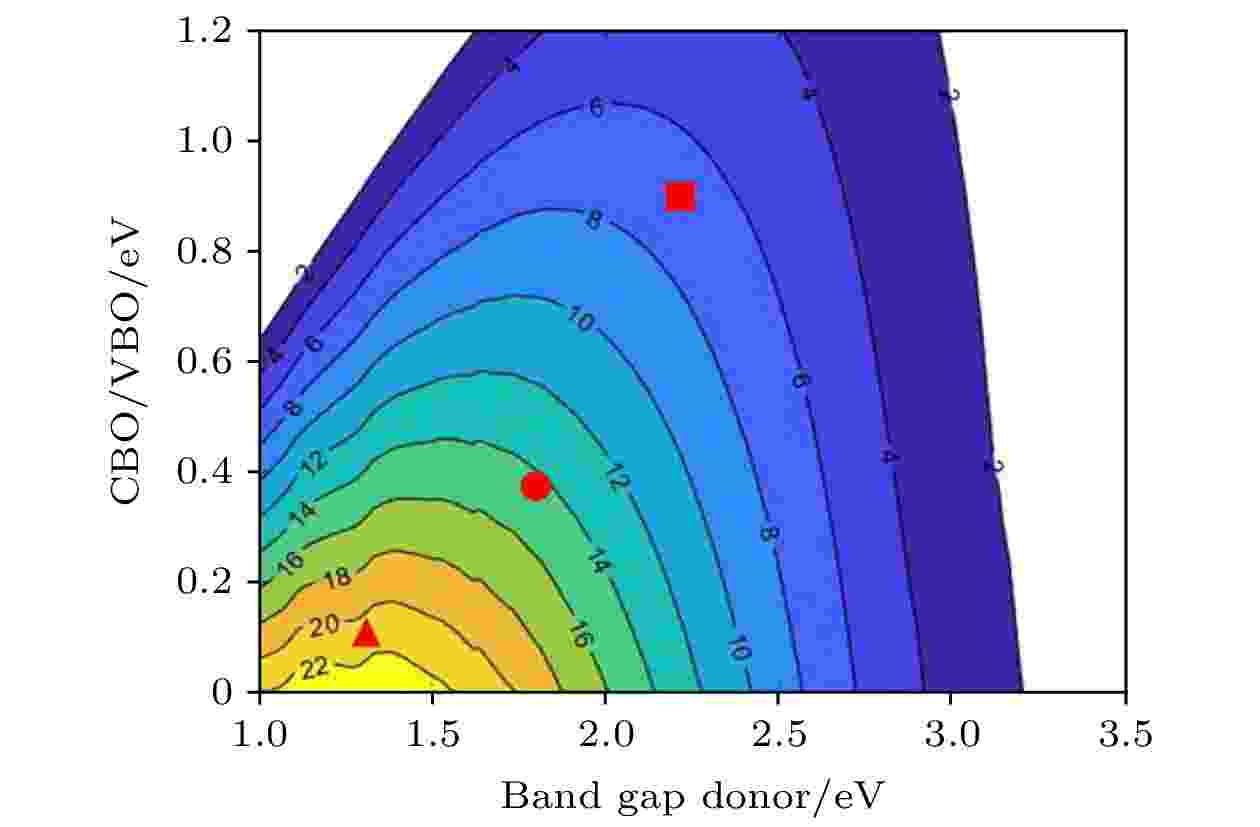图 7 CsPbX₃-PG(X=Cl, Br, I)异质结功率转换效率, 带隙和导带偏移的函数关系曲线. CsPbBr₃-PG, 红色圆形; CsPbI₃-PG: 红色三角形
Figure7. Power conversion efficiency contour plot as a function of the donor optical gap and conduction band offset ΔE_C. Red circle and triangle represent CsPbBr₃-PG and CsPbI₃-PG, respectively.

图7给出了所有II型异质结的PCE等值线图. 光伏材料要求结构具有1.0—1.8 eV的合适光学带隙, 构建异质结可以有效地将带隙缩小到一个更合适的范围, 导致更高的PCE, CsPbX₃-PG异质结的光学带隙分别取较小光学带隙值(供体)的单层, 其中CsPbCl₃-PG取PG带隙值 2.21 eV, CsPbBr₃-PG取CsPbBr₃带隙值1.79 eV, CsPbI₃-PG取CsPbI₃带隙值1.30 eV. 此外, 通过减少CBO/VBO可以改善PCE, 其中CsPbCl₃-PG取VBO值为1.28 eV, CsPbBr₃-PG和CsPbI₃-PG取CBO值分别为0.24 和0.11 eV, 并结合CBO和带隙值可在AM1.5光谱的PCE等高线上分别估算出CsPbCl₃-PG, CsPbBr₃-PG和CsPbI₃-PG的PCE约为7%, 15%和21%.

通过第一性原理计算, 提出了PG和全无机钙钛矿CsPbX₃(X=Cl, Br, I)的vdW异质结构建方案, 并计算了其电子结构和关键光伏参数. 研究结果表明, 由于PG单层与CsPbX₃之间极小的晶格失配比, 异质结在界面处保持了良好的原有性能. CsPbCl₃-PG, CsPbBr₃-PG和CsPbI₃-PG均为II型异质结, 并保持了各组分的固有电子结构. 此外, CsPbX₃还能拓宽PG-CsPbX₃异质结的吸收光谱, 增强它们的光吸收能力, 理论估算的PCE可高达21%. 能带排列, 光吸收和PCE的结果表明, PG-CsPbX₃异质结将在太阳能电池和光电探测器等光伏器件中具有巨大的应用潜力. 此外, 我们的异质结设计不局限于卤素原子的替换, 还对不同接触界面进行了稳定性测试, 适用于其他vdW异质结界面设计和原子替换的研究. 因此, 我们的研究结果不仅有助于基于PG和CsPbX₃的二维异质结的实验合成, 而且将可能为利用vdW异质结的独特优势设计高性能太阳能电池和其他电子或光电材料提供理论启示.