摘要: 飞秒光梳被广泛用于时间频率技术和精密光谱测量, 由其时频特性所衍生的绝对测距技术以可溯源、大尺寸、高精度等优点有望成为未来长度计量的最重要手段. 本文提出了一种基于飞秒光梳多路同步锁相的多波长干涉实时绝对测距方法, 使多个连续波激光器通过光学锁相环技术同步锁定到飞秒光梳梳模上, 通过多路同步相位测量和小数重合算法最终实现绝对距离测量. 所提测量方法不仅能保留传统激光干涉测距的高分辨力和精度, 而且可溯源至时间频率基准, 对高精度长度测量、尤其是对物理复现“米”的定义具有重要计量意义. 测距实验证明, 四波长干涉测距的非模糊度量程达到44.6 mm, 折射率波动导致非模糊度量程变化为纳米量级; 多波长干涉测距的非模糊度量程也受制于空气折射率的测量误差, 多波长干涉绝对测距的非模糊度量程在实验室环境下可达数米、甚至几十米, 并通过2米线性位移实验证明了多波长绝对测距的大量程和线性测量性能.
关键词: 激光绝对测距 /
飞秒光梳 /
多波长干涉 /
非模糊度量程 English Abstract Real-time absolute distance measurement by multi-wavelength interferometry synchronously multi-channel phase-locked to frequency comb and analysis for the potential non-ambiguity range Wang Guo-Chao 1,3,4 ,Li Xing-Hui 2 ,Yan Shu-Hua 3,4 ,Tan Li-Long 1 ,Guan Wen-Liang 1 1.High-tec Institute of Xi’an, Xi’an 710025, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51705523) and the Natural Science Basic Research Plan of Shaanxi Province, China (Grant No. 2018JQ5026)Received Date: 31 July 2020Accepted Date: 20 October 2020Available Online: 12 November 2020Published Online: 20 February 2021Abstract: Optical frequency combs of the femtosecond laser have been widely used in time-frequency technology and precision spectrum measurement. The absolute ranging technology derived from time-frequency characteristics of the optical frequency comb is expected to become the incomparable means of length metrology and distance measurement in the future due to its traceability to time-frequency standard and capability of large scale and high precision. This paper proposes a real-time absolute ranging method with multi-wavelength interferometry referenced to optical frequency comb, which enables multiple continuous-wave lasers to be synchronously calibrated to selected modes of the frequency comb by means of optical phase-locked loop. With synchronous phase measurement and calculation with excess fraction algorithm, absolute distance measurement by multi-wavelength interferometry is ultimately fulfilled. The proposed measurement method can not only retain high resolution and high accuracy of traditional laser interferometry, but also can be traced to a time-frequency reference, which is of metrological significance to high-precision length and distance measurement, especially to the definition of “meter” for physical reproduction. Measured results for ranging experiments have proved that the non-ambiguity range of the four-wavelength interferometer reaches 44.6 mm, and fluctuations of air refractive index cause the non-ambiguity range change with the order of nanometers. Through theoretical analysis, it is pointed out that the non-ambiguity range of the multi-wavelength interferometer in the actual measurement environment is restricted by the calculated error of air refractive index, especially the estimation accuracy and fluctuation degree of the refractive index relationship between wavelengths. And in a good laboratory conditions, the non-ambiguity range of real-time absolute ranging by frequency-comb-calibrated multi-wavelength interferometry can reach several meters or even tens of meters. At the same time, a 2-meter linear displacement comparison has been carried out, the P.V. value of the residual errors for linear fitting is 36.1 nm, and such residual errors match the magnitude of uncertainty of air refractive index calculated by empirical formula, which prove that the multi-wavelength interferometry can perform meter-level absolute ranging. The proposed research can be directly applied to precision manufacturing of large-scale semiconductors up to several meters, and is beneficial to promoting the accuracy of laser ranging for space mission.Keywords: absolute distance measurement /optical frequency comb of the femtosecond laser /multi-wavelength interferometry /non-ambiguous range 全文HTML --> --> --> 1.引 言 实现大尺寸高精度绝对距离测量对科学研究、工业生产和航空航天等众多领域具有重要意义. 激光干涉测量技术以其能实现纳米级测量精度被认为是目前精度最高的测距手段, 已广泛应用于精密工程领域[1 -3 ] ; 但由于传统激光干涉测距工作原理的本质是对干涉条纹进行整数计数和条纹细分, 对应的测距非模糊度量程(NAR)为激光波长的一半, 因此, 无法满足大尺寸装备制造和机械安装中对距离测量的要求, 迫切需要利用绝对测距(ADM)测量模式来弥补传统激光干涉测距的不足, 在实际测量中能同时兼顾非模糊度量程大、测量精度高、更新速度快、无死区光程和防光路扰断等优点[4 ,5 ] . 多波长干涉(MWI)绝对测距方法被认为是能解决上述问题的有效途径, 自提出以来就受到大量关注, 然而受限于对多波长激光光源高频率稳定度和波长跨越区间的高要求, 多波长干涉绝对测距在较长时间内一直发展缓慢[6 -8 ] . 自20世纪七八十年代开始, 诸多课题组对频率扫描干涉测距和合成波长干涉测距等绝对测距方法进行了研究报道[9 -13 ] , 但由于频率扫描法带来的非实时测量缺陷以及合成波长法所面临的量程和精度限制, 一直未能突破大尺寸、高精度和实时快速等一体化测量的瓶颈.[14 -16 ] , 其出现不仅带来了光谱计量技术的革新, 而且为大尺寸高精度激光绝对测距的实现提供了诸多新方法和新技术[17 -31 ] . 飞秒光梳在时域表现为周期性的飞秒脉冲, 在频域则表现为等频率间隔、超宽带、窄线宽、高稳定度的一系列离散谱线, 是非常理想的多波长激光光源[32 ,33 ] ; 但由于拥有几十万根准单模谱线, 平均到单根谱线的能量仅为纳焦(nJ)量级, 因此不能直接用来进行多波长干涉测量. 一种可行的解决思路是从飞秒光梳谱线中提取多个波长, 进行功率放大之后再进行干涉测量. 由此, 可将飞秒光梳作为精密光学频率标尺, 将多个连续波激光锁频至飞秒光梳上, 从而产生高频率稳定度的多波长干涉光源[34 ] . 同时, 所产生的激光频率通过锁频至飞秒光梳可溯源至原子钟时间频率基准, 相比于经典的碘饱和气体吸收氦氖激光器在频率稳定度、物理复现长度基准等方面的潜力更大, 有望在长度计量和工业精密测距等领域发挥重要作用[35 ,36 ] .2.测量原理与装置 22.1.绝对测距原理 2.1.绝对测距原理 单波长激光干涉测距公式可表示为$L = \left( m + e \right) \cdot {\lambda / 2}$ , 式中L 为待测距离, $\lambda $ 为激光波长, m 为整数条纹计数值, e 为相位测量得到的小数条纹信息, 为便于后续描述, 暂不考虑空气折射率. 由于相位测量存在2π模糊度, 单波长干涉测量必须跟踪干涉条纹的连续变化来获取整数条纹, 故只能进行相对距离测量. 当利用双波长进行测量时, 不妨设此时${\lambda _1} < {\lambda _2}$ , 则双波长干涉相位可表示为1 )式中两个式子的左右两边进行相减, 则有${\varLambda _{12}} = {{{\lambda _1}{\lambda _2}} / {\left( {{\lambda _2} - {\lambda _1}} \right)}}$ , 称为等效合成波长[37 ] . 如果${m_{\rm{1}}} - {m_{\rm{2}}} = 0$ , 那么就能直接根据${e_{\rm{1}}}$ 和${e_{\rm{2}}}$ 解算出整数条纹和距离信息, 此时L 不大于${{{\varLambda _{12}}} / 2}$ , 且${{{\varLambda _{12}}} / 2}$ 即为双波长干涉拓展后的非模糊度量程. 类似地, 当利用多个波长进行干涉测量时, 可产生一系列等效合成波长进而扩大非模糊度量程, 从而实现大量程绝对测距.图1 所示, 四个单频连续波CW激光同时锁频到对应的飞秒光梳梳模谱线上, 所选用的激光波长值大小需满足采用多波长干涉拓展NAR的波长级间融合条件(见附录B )[38 ] . 四个波长的大小关系为${\lambda _1} < {\lambda _2} < {\lambda _3} < {\lambda _4}$ , 由此可组成一条等效合成波长链, 并决定绝对测距非模糊度量程的大小, 其组成机制可描述为: 最大波长λ 4 和最小波长λ 1 组成第一级等效合成波长Λ 14 , 双波长干涉(λ 1 和λ 4 )的NAR2 为10–5 米量级; 增加波长λ 2 , λ 2 和λ 1 组成第二级等效合成波长Λ 12 , 此时三波长干涉(λ 1 , λ 2 和λ 4 )对应的NAR3 达到10–3 米量级; 四波长干涉时, 二级等效合成波长Λ 12 和Λ 34 组成第三级等效合成波长Λ 1234 , 对应的NAR4 将达到10–2 米量级. 利用飞秒光梳多路同步稳频的四波长干涉测距能实现厘米量级的NAR, 继续增加干涉波长测距NAR将进一步增大. 飞秒光梳是多波长干涉理想的频率参考源, 不仅能提供理想的多波长同步激光参考, 而且能将激光波长溯源到高稳定度的时间频率基准, 尤其适合用于多波长干涉的物理实现.图 1 基于飞秒光梳多路同步锁相的多波长干涉测距原理及非模糊度量程示意图Figure1. Schematic diagram of the synthetic wavelengths and measuring NAR of Frequency-Comb-Referenced Multi-Wavelength Interferometry.[39 ,40 ] . 假设多波长干涉测距的波长数为N , 可建立方程组:3 )式的方程组中未知数的个数始终比方程式的个数大1, 因此一般而言, 方程组的解必有无穷多个, 而且(3 )式中关于距离L 的无穷解之间将表现为一个等差数列, 公差大小表示使多波长干涉的条纹相位重合的最小长度, 该最小长度即为多波长干涉测距的非模糊度量程, 同时也等于最大等效合成波长的一半. 但如果考虑到${m_i}$ (i 为[1, N ]之间的整数)必须取整数, 在一定的距离不确定范围和允许的小数相位测量精度内, 则可得到整数条纹的唯一解. 小数重合算法的具体内容详见附录A .2.2.测距系统装置 -->2.2.测距系统装置 多波长干涉实时绝对测距系统的系统装置示意图如图2 所示. 四台分布式反馈半导体(DFB)单频激光器通过光锁相环技术(OPLL)同步锁定到由光纤光栅滤波阵列(FBGA)筛选出来的不同飞秒光梳梳模上, 然后四个不同波长的连续波激光分别通过光纤耦合器(FC)分束之后, 部分光送入光纤开关(OS)和波长计(WM)用来进行准确波长测量, 另外的主激光束又由FBGA进行光纤合束后形成多波长光源. 多波长激光再进行分束, 分别经过两个光纤耦合型声光调制器(AOM)进行频移, 移频后的光纤输出光经过扩束准直后输入到多波长干涉仪光路. 多波长干涉仪光路由两个分光棱镜(BB)、目标角锥反射镜(RR)和反射镜(M)组成, 通过光束的分合将参考光和测量光经准直器耦合到不同光纤中, 再通过FBGA进行波长解调将各波长分离开, 最后输入光电探测器阵列(PDA)后得到外差电信号, 此时所得到的多路外差电信号也与多个波长的参考和测量信号一一对应. 所探测到的参考和测量电信号经多路同步相位计进行高精度相位测量后, 将各波长的同步相位测量结果发送到计算处理单元, 再结合已知的准确波长值和监测空气参数所计算的空气折射率, 最后利用多波长干涉小数重合算法计算得到绝对距离值. 为了进行干涉信号的外差探测, 图2 中光纤AOM的移频量分别设置为40和39.96 MHz, 由此在干涉仪的参考和测量臂上都将形成大小为40 kHz的外差干涉信号, 将大大地降低探测器的带宽要求, 简化了信号处理的复杂度, 降低了系统成本. 在前面的原理分析中, 为了简化模型直接利用的是真空波长, 没有考虑空气折射率; 在实际的测量系统中, 导轨附近安装了高精度环境传感器, 通过实时测量温度、压强、湿度和CO2 浓度来监测光路中的空气折射率变化, 各传感器的测量精度分别为5 mK, 2.5 Pa, 1%和41 ppm. 此外, 为了降低空气扰动的影响, 维持环境参数的缓慢变化, 系统对测量光路及导轨还进行了密封和隔热处理.图 2 多波长干涉实时绝对测距系统. FBGA, 光纤光栅滤波阵列; OPLL, 光学锁相环; OS, 光开关; WM, 波长计; FC, 光纤耦合器; AOM, 声光调制器; C, 准直器; M, 反射镜; BS, 分光棱镜; DM, 双色镜; RR, 角锥反射镜; PDA, 光电探测器阵列Figure2. Schematic configuration diagram of real-time absolute distance measurement by Frequency-Comb-Referenced Multi-Wavelength Interferometry.3.实验结果与分析 23.1.多波长光源和相位测量结果 3.1.多波长光源和相位测量结果 图3(a) 为利用光谱仪(MS9710C, Anritsu)观察四路连续波激光经飞秒光梳同步锁相后的多波长光谱观测结果, 光谱仪上虽能清晰分辨出四个波长的不同位置, 但由于光谱仪分辨力有限, 准确的波长值则需要通过高精度波长计辅助测量来计算获取. 实验中选用High Finesse GmbH波长计WS-U10, 其探测分辨率为0.2 pm, 对应频率分辨率优于30 MHz; 而此时锁频后的激光频率${f_{{\rm{OFG}}}}$ 可表示为${f_{{\rm{OFG}}}} = {f_{{\rm{comb}}}} \pm {f_{\rm{b}}} = k{f_{\rm{r}}} + {f_{{\rm{ceo}}}} \pm {f_{\rm{b}}}$ , 式中${f_{{\rm{comb}}}}$ 为锁频对应的光梳梳模频率, k 为${f_{{\rm{comb}}}}$ 相对重复频率的整倍数, ${f_{\rm{r}}}$ , ${f_{{\rm{ceo}}}}$ 和${f_{\rm{b}}}$ 分别为飞秒光梳的重复频率、载波包络频移和锁频后的拍频, 其在本系统中的锁频大小分别为100 MHz, 30 MHz和30 MHz. 通过波长计的粗测结果和已知频率参数, 可准确计算整数k 的大小, 进而得到波长精确值, 所选用的四束激光的真空波长值大小依次为1530.279693, 1531.040888, 1554.179409和1554.937151 nm[41 ] .图 3 多波长光源和相位测量结果 (a) 多波长发生器光谱测量结果; (b) 锁频激光的频率稳定度分析结果; (c) 多路同步相位解调实时测量结果Figure3. Test results for preparation of real-time and meter-scale absolute distance measurement: (a) Parallel generated four wavelengths for MWI; (b) frequency stability evaluation; (c) simultaneously detected phases for MWI in real time.图3(b) 给出了评价锁频后激光频率稳定度的Allan方差分析结果. 通过将频率计数器(Agilent 53131A)溯源至商用原子钟(FS725-SRS), 然后记录拍频信号来实现稳定度测量和分析, 图中分别给出了锁频后${f_{\rm{r}}}$ , ${f_{{\rm{ceo}}}}$ 和${f_{\rm{b}}}$ , 对应平均时间为1—500 s的Allan方差值. 关于激光波长频率稳定度的分析, 可用锁频信号的频率稳定度进行评价, 依据上述激光频率${f_{{\rm{OFG}}}}$ 的表达式, 多波长发生器的激光频率稳定度可表示为${f_{\rm{r}}}$ , ${f_{{\rm{ceo}}}}$ 和${f_{\rm{b}}}$ 对应的Allan方差值分别为1.089 × 10–12 , 3.819 × 10–15 和2.693 × 10–14 , 由此, 以铷原子钟为频率参考, 最终用Allan方差评价的激光频率稳定度为1.090 × 10–12 (对应平均时间10 s).图3(c) 为利用四路同步的高精度数字相位计对光梳多波长干涉绝对测距装置进行实时相位解调实验的相位解调结果, 测量过程中目标反射镜固定在导轨上. 图3(c) 中给出的是测量时间为1.1 s的四路不同波长的同步相位解调结果, 采样间隔为10 ms. 多路相位计自身的相位测量线性度优于0.999, 测相同步精度优于0.0008, 1 h相位重复测量精度为0.0004, 相位计设计方案及测试结果参考文献[42 ]. 由于在多波长干涉仪光路中, 四个波长的激光所经过的干涉路径相同, 因此, 图3(c) 中所示的外差干涉测量得到的四路小数相位结果也表现出完全相同的相位波动曲线. 小数相位波动幅度P.V值达到0.14(对应约210 nm的光程), 四路相位解调结果保持高度一致的相位起伏, 时间同步且大小相当. 波长不同的两路相位解调之间的耦合相位偏差(耦合相差)的波动范围PV值优于0.009, 标准差小于0.003, 满足合成波长进行级间融合的要求. 耦合相差是衡量相位解调同步性和合成波长有效性的重要参数, 其出现的波动主要来源于激光源的多路同步锁相差异(即非完全相位同步)、相位计自身存在随机测量误差、多路相位解调的非对称误差和波长不同所带来的折射率偏差等.3.2.非模糊度量程测试实验 -->3.2.非模糊度量程测试实验 在现有相位测量精度和波长选择条件下, 四波长干涉的测距NAR为厘米量级, 而本系统由于使用双色镜引入双频激光干涉仪测量光路以及长气浮导轨的安装问题, 目标角锥反射镜可到达的测量起始位置所对应的绝对距离远大于四波长测距的NAR, 必须通过其他辅助测距手段来获取粗测距离值, 且要求粗测结果的不确定度必须小于四波长干涉NAR的一半. 依据现有激光光路及所用激光器的波长连续可调, 且扫描前后的激光波长可精确锁定至飞秒光梳上, 实验中只需对单路激光实施频率扫描干涉测量即可完成距离粗测[43 ] . 实验中扫描前后激光器都要进行锁定频率, 扫频带宽可通过与光梳的拍频锁定关系确定为3 GHz, 扫描过程中只记录整数条纹, 锁频之后才进行小数相位测量, 最终得到的测量精度为 ± 4.5 mm ($ \pm 3\sigma $ ), 远小于四波长干涉测距NAR, 具体操作步骤和技术细节可参考文献[44 ].图4 给出了两者测距的对比实验结果, 横坐标为HPI测量的参考距离值, 纵坐标为MWI系统测量的绝对距离值. 通过线性拟合, 位移量在0—40 mm范围之内的残余误差PV值为66 nm, 标准偏差为25 nm. 当所执行的位移量接近NAR时(理论计算在44.6 mm附近), 通过微小步进来精细控制导轨(基于分辨力为0.2 μm的Renishaw光栅尺的反馈控制). 如图4 中所示, 当导轨位移量超过NAR时, 在不改变粗测距离和测量条件基本不变的情况下, 测距系统得到的ADM测量值会跳变到初始测量点的距离值, 很好地验证了NAR的存在及其大小范围, 也说明了MWI测距系统必须有粗测值才能准确计算测距结果; 为了从实验数据得到准确的NAR, 可将HPI的测量结果作为参考值, 通过线性拟合结果和实测值的比较, 进而计算出此时的NAR为44.600287 mm.图 4 验证NAR的线性位移对比实验Figure4. Linear comparison between ADM by MWI and displacement by HPI for NAR demonstration.T = 24.613 ℃; 压强P = 100061.24559 Pa; CO2 浓度X = 795.220724 ppm; 相对湿度R = 26.3595%. 根据等效合成波长分析, 自由空间下的四波长干涉NAR的理论计算值为44.6002089 mm, 与四波长干涉NAR的前面实测值相差约78 nm, 主要误差来源于空气环境的不均匀、环境参数不完全精确测量、计算空气折射率的经验公式自身不确定度和拟合误差等. 考虑到环境传感器测量精度水平和Ciddor公式的不确定度水平[45 ] , 可认为NAR理论与实验值的偏差是合理的.图4 的实验准确地捕捉到某一环境条件下的具体NAR值, 因此, 在验证NAR的位移测量过程中, 通过对温度等环境参数的实时测量, 分析空气折射率随时间的变化结果, 可理论估算NAR的变化大小. 图5(a) 给出了测量过程中长达约272 s的四个波长空气折射率的变化情况, 空气折射率的大小由Ciddor公式计算, 各波长空气折射率变化可认为几乎完全一致, 仅存在一个微小的纵向偏差, 空气折射率在所测时间内的波动幅度达到3.1 × 10–8 . 图5(b) 为理论计算的四波长干涉非模糊度量程(NAR_air)随空气折射率变化的波动结果, 图中NAR_air的计算值主要集中在44.600208 mm附近, NAR_air结果的波动区间小于4 nm, 说明实验系统环境参数的短时变化对非模糊度量程大小的影响为纳米量级.图 5 空气折射率变化对NAR的影响 (a) 空气折射率的波动情况; (b) 理论NAR受空气折射率影响的计算结果Figure5. Influence of air refractive index on NAR: (a) Fluctuation of air refractive index for observation of 272 s;. (b) calculated result of theoretical NAR under the fluctuation of air refractive index.3.3.拓展NAR受空气折射率的制约关系 -->3.3.拓展NAR受空气折射率的制约关系 目前对空气折射率的获取方法主要有两种: 一种是直接利用折射率计进行现场测量的方法, 目前测量精度维持在${10^{ - 7}}$ 量级; 另一种是经验公式法, 在对环境参数进行实时监测的条件下, 通过经验公式如Ciddor公式和改进的Edlen公式等进行计算, 进而间接获取空气相折射率的估算值. 尽管经验公式的不确定度被证实可达到${10^{ - 8}}$ 水平, 但由于空气的非均匀性和大气湍流等因素, 即使使用高精度的环境传感器也很难保证其准确度[45 ,46 ] . 空气折射率对单个波长的波动虽然很大, 但是在同光路的条件下多波长的空气折射率变化是存在共模量的, 折射率之差$\left( {{n_1} - {n_i}} \right)$ 的变化量大小对利用小数重合算法找准整数相位很关键, 将直接影响多波长干涉绝对测距的量程大小. 文献[47 ]和[48 ]利用双色干涉法(波长为1550和775 nm)对测距过程中的空气折射率进行了补偿, 并通过约10 h的观测实验证实了$\Delta $ $\left( {{n_{{\rm{1550}}}} - {n_{{\rm{775}}}}} \right)$ 为${10^{ - 9}}$ 数量级. 由于本系统所选取的多波长间隔远小于双色法的波长间隔, 相比双色法, 各波长空气折射率之差的变化应该更小, 可推断本系统中$\Delta $ $\left( {{n_1} - {n_i}} \right)$ 优于${10^{ - 9}}$ 水平.${\lambda _1}$ 和${\lambda _i}$ (${\lambda _1} < {\lambda _i}$ )为例, 真空中的等效合成波长为${{{\lambda _i} \cdot {\lambda _1}} / {\left( {{\lambda _i} - {\lambda _1}} \right)}}$ , 分析可知其波长稳定性和单波长保持同一数量级, 可达到10–11 水平; 而在空气中, 其等效合成波长${\varLambda _{1 i}}_{\_{\rm{air}}}$ 可表示为${\beta _i} = {{{\lambda _i}} / {\left( {{n_1}{\lambda _i} - {n_i}{\lambda _1}} \right)}}$ 为比例放大因子, 则上式可表示为${\varLambda _{1 i}}_{\_{\rm{vac}}}\! =\! {{{\lambda _i} \cdot {\lambda _1}} / {\left( {{\lambda _i} \!-\! {\lambda _1}} \right)}}$ , $\alpha \!=\! {\beta _i} \cdot \left( {{n_1} \!-\! {n_i}} \right)$ , 则(5 )式可以写成为${\varLambda _{1 i}}_{\_{\rm{air}}}$ 的不确定度${U_{{\varLambda _{1 i}}_{\_{\rm{air}}}}}$ 可表示为8 )式中不确定度大小由等式右边三项确定, 由于${{{U_{{\varLambda _{1 i}}_{\_{\rm{vac}}}}}} / {{\varLambda _{1 i}}_{\_{\rm{vac}}}}}$ 与原子钟水平一致, 达到10–11 量级, 则只需要比较${n_1}$ 和$\alpha $ 的不确定度水平. 由于$\alpha = {\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ , 且比例放大因子${\beta _i}$ 与折射率差值${n_1} - {n_i}$ 的变化方向是背离的, 当${\lambda _1}$ 和${\lambda _2}$ 的波长间隔变大时, ${\beta _i}$ 会相应缩小, ${n_1} - {n_i}$ 则会变大; 当${\lambda _1}$ 和${\lambda _2}$ 的波长间隔变小时, ${\beta _i}$ 会变大, ${n_1} - {n_i}$ 则会变小; 但$\alpha = {\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ 基本始终保持在${10^{ - 6}}$ 数量级, 在40 nm的波长间距范围内, $\alpha $ 的波动基本维持在${10^{ - 8}}$ 量级, 在2 ℃的温度变化范围内波动变化为${10^{ - {\rm{9}}}}$ 量级, 如图6 所示.图 6 $\alpha = {\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ 随参数变化的波动大小 (a) $ {\beta _i} \cdot \left( {{n_1} - {n_i}} \right) $ 随波长间距变化的波动仿真结果; (b)${\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ 随温度变化时的波动仿真结果, 波长间隔为25 nm, 波长选定为1555 nmFigure6. Influences of the parameter variations on the value of ${\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ : (a) Fluctuation of ${\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ as variations of wavelength gap; (b) fluctuation of ${\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ as variations of ambient temperature.${\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ 随温度变化量为${10^{ - 9}}$ 量级, 因此, 根据(8 )式, 空气中的等效合成波长随环境参数的变化大小还是主要取决于单个波长空气折射率的波动情况, 由于四波长的等效合成波长为几十mm量级, 且在本实验条件下长时间的空气折射率波动可保证优于${10^{ - 7}}$ 量级, 因此${U_{{\varLambda _{1 i}}_{\_{\rm{air}}}}} \approx \left( {{{{U_{{n_1}}}} / {{n_1}}}} \right) \cdot {\varLambda _{1 i}}_{\_{\rm{air}}}$ , 这也正是前面图5 中NAR随空气折射率变化仅nm量级的原因.${\rm{Fract}}$ 表示去整函数; $\sigma $ 表示小数相位的容差, 大小一般取小数相位测量精度. 从(9 )式不能直接分析空气折射率对寻找整数相位的影响, 必须进行等式变换, 由于${\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ 的值在${10^{ - 6}}$ 数量级, (10 )式中${1 / {\left[ {1 - {\beta _i} \cdot \left( {{n_1} - {n_i}} \right)} \right]}}$ 根据泰勒级数可用多项式展开为10 )式可简化为${e_i}$ 为波长${\lambda _i}$ 的小数相位测量值, 根据(9 )式的要求, 确定整数${m_1}$ 的必要条件是$\Delta $ 运算表示取变量的波动变化范围, 由于整数${m_1}$ 已确定不变, 且${{{\lambda _i} \cdot {\lambda _1}} / {\left( {{\lambda _i} - {\lambda _1}} \right)}}$ 为真空等效合成波长, 稳定度在${10^{ - 11}}$ 水平, 则${{{\lambda _1}\! \cdot\! ({{m_1} \!+\! {e_1}})}\Big/ \!{\left( {\dfrac{{{\lambda _i} \cdot {\lambda _1}}}{{\left( {{\lambda _i} \!-\! {\lambda _1}} \right)}}} \!\right)}}$ 可近似看作固定不变, 则不等式(13 )式可简化为${\lambda _1} \cdot \left( {{m_1} + {e_1}} \right) = 2{n_1}L$ , 则(14 )式可表示为9 )式中的容差取与相位测量精度相同, 即$\sigma $ =0.01, 等效合成波长${\varLambda _{1 i}}$ 为间隔最大的两个波长${\lambda _1}$ 和${\lambda _i}$ 组成的等效合成波长, 一般不超过100 μm, 则$\sigma \cdot {\varLambda _{1 i}}/2{n_1}$ 约为0.45 μm, 在普通实验室环境下满足${10^{ - {\rm{7}}}} < \Delta \left[ {\left( {{\beta _i} \cdot \left( {{n_1} - {n_i}} \right)} \right)} \right] < {10^{ - 8}}$ , 该条件下的测距最大范围介于4.5—45 m之间; 在特殊处理的超高精环境下, $\Delta \left[ {\left( {{\beta _i} \cdot \left( {{n_1} - {n_i}} \right)} \right)} \right]$ 能达到${10^{ - 9}}$ 甚至更高, 此时多波长干涉测距的NAR上限可到达上百米量级. 以上分析是以Ciddor公式计算单个波长相折射率为基础, $\Delta \left[ {\left( {{\beta _i} \cdot \left( {{n_1} - {n_i}} \right)} \right)} \right]$ 中起主导作用的成分是$\Delta $ $\left( {{n_1} - {n_i}} \right)$ , 实际情况下的两个波长的折射率差值波动虽然与Ciddor公式的估算结果可能有微小误差, 但实际的$\Delta \left[ {\left( {{\beta _i} \cdot \left( {{n_1} - {n_i}} \right)} \right)} \right]$ 与前面仿真结果可认为是同一数量级.3.4.大量程测距实验 -->3.4.大量程测距实验 为了验证多波长干涉绝对测距系统的大距离测量能力, 开展了大量程线性位移对比实验, 测距结果与商用双频激光干涉仪(HPI)进行比较. 气浮导轨上的平移台执行位移的步进距离为100 mm, 测距是在每一个步进点位置上进行静态测量. 图7 为基于飞秒光梳多路同步锁相的MWI系统和HP5530A所进行的长度达2 m的线性位移对比测量结果. 首先, 双频激光干涉仪的位移零点与MWI系统的起始测量点坐标值相差约为850 mm; 同时, 由于两个系统的测量光路之间存在微小角度余弦误差, 测距线性误差可由两者测量值的线性拟合误差来表征. 2 m位移过程中对22个测量点进行了静态测量, 测量结果显示其残余误差的PV值为36.1 nm, 标准偏差为8.6 nm, 考虑被测距离后的相对精度达到10–8 量级, 与利用经验公式计算空气折射率的精度水平相当, 证明了多波长绝对测距系统的良好线性测量性能.图 7 MWI与商用激光干涉仪的2 m线性位移对比实验结果Figure7. Linear comparison between MWI and the commercial laser interferometer over a 2.0-meter displacement.4.结 论 本文提出的基于飞秒光梳多路同步锁相的多波长干涉实时绝对测距方法及系统, 能有效地解决传统的连续波扫频或调频干涉测量方法无法实时快速测量的难题, 并且可直接溯源至时间频率基准, 目前其测量精度和非模糊度量程主要受制于空气折射率的测不准, 但在真空环境下完全可物理复现“米”的定义. 理论和实验结果表明, 考虑空气折射率四波长干涉绝对测距非模糊度量程可达到44.6 mm, 折射率波动导致非模糊度量程变化为纳米量级; 同时, 进行了2 m线性位移对比实验, 得到了残余误差PV值为36.1 nm, 证明了多波长绝对测距系统能够进行米级绝对测距. 通过分析, 在实际测量环境下, 多波长干涉测距的非模糊度量程也受制于空气折射率的测量误差, 特别是波长之间的折射率关系式${\beta _i} \cdot \left( {{n_1} - {n_i}} \right)$ 的估算精度和波动程度; 在良好环境条件下, 基于飞秒光梳的多波长干涉实时绝对测距非模糊度量程可达到几十米, 目前, 可直接应用于米级大尺寸精密加工和大面型半导体的制造. 如果要将基于飞秒光梳的多波长干涉实时绝对测距方法应用到实验室外的环境, 需要进一步研究分析空气折射率对应波长的梯度及其随环境参数变化的精细波动模型.附录 A.多波长干涉的级间融合条件 进行多波长选择需要考虑的两个因素是小数相位测量精度和光纤光栅滤波的波长解调带宽, 相位测量精度决定了各级合成波长之间的比例因子范围以及级间融合的可行性, 波长解调带宽将决定可选择的两波长间的最小间隔. 设相位测量的$ \pm 3\sigma $ 置信区间精度为$\delta $ , 合成波长的级间比例因子表示为${\beta _k}$ , 分析第一级合成波长的级间融合, 需满足不等式:$\sqrt 2 \delta $ 为两波长的相位测量合成不确定度. 由于${\lambda _{\rm{i}}} > {\lambda _{\rm{1}}}$ , 则可由(1 )式解得1 )式推广到多级合成波长的一般表达式为M 表示合成波长Λk 所用到的波长数, 则级间融合不等式关系的一般表达式为4 )式是进行波长位置选择的重要原则.附录 B.多波长干涉小数重合算法 假设粗测距离值为${L_{\rm{0}}}$ , 测量不确定度为$\Delta L$ , 那么更精确的目标距离值L 可表示为${\lambda _{\rm{1}}}$ 所对应的干涉相位整数部分${{\rm{m}}_1}$ 满足:${\rm{INT}}$ 为取整函数, 且令$[{M_{{\rm{min}}}}, \;{M_{{\rm{max}}}}]$ 之间逐一取${m_1}$ 的参考值, 记为${m'_1}$ , 相应的参考距离$L'$ 可表示为${e'_j}$ 为根据参考距离预测的其他波长的小数相位, 其可由下式求解:${\rm{EF}} \left( \cdot \right)$ 为取小数函数. 那么, 此时波长${\lambda _j}$ 的小数相位测量值${e_j}$ 和参考值${e'_j}$ 之间存在的相位偏差?e j $\varepsilon $ ($\varepsilon {{ > 0}}$ , 且为小数相位, 由相位测量精度决定), 如果对于所有的波长, 即$j{{ = 2, 3, 4, }}\cdots, \Delta {e_j}$ , 均满足:${m'_1}$ 为正文(3 )式的解, 即${m_1} = {m'_1}$ , 相应地可以求解出其他波长的整数相位${m_i}$ . 
图 1 基于飞秒光梳多路同步锁相的多波长干涉测距原理及非模糊度量程示意图
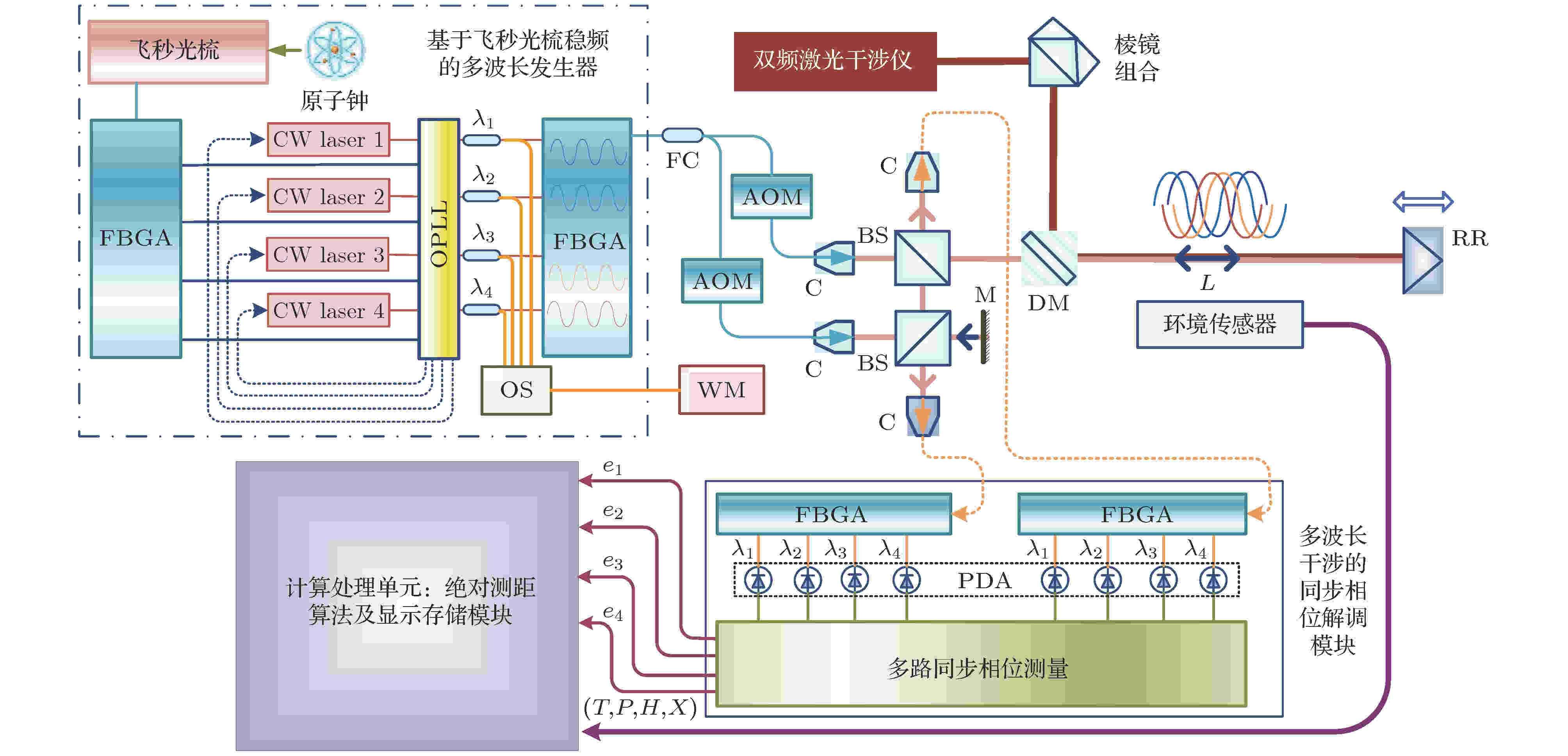图 2 多波长干涉实时绝对测距系统. FBGA, 光纤光栅滤波阵列; OPLL, 光学锁相环; OS, 光开关; WM, 波长计; FC, 光纤耦合器; AOM, 声光调制器; C, 准直器; M, 反射镜; BS, 分光棱镜; DM, 双色镜; RR, 角锥反射镜; PDA, 光电探测器阵列
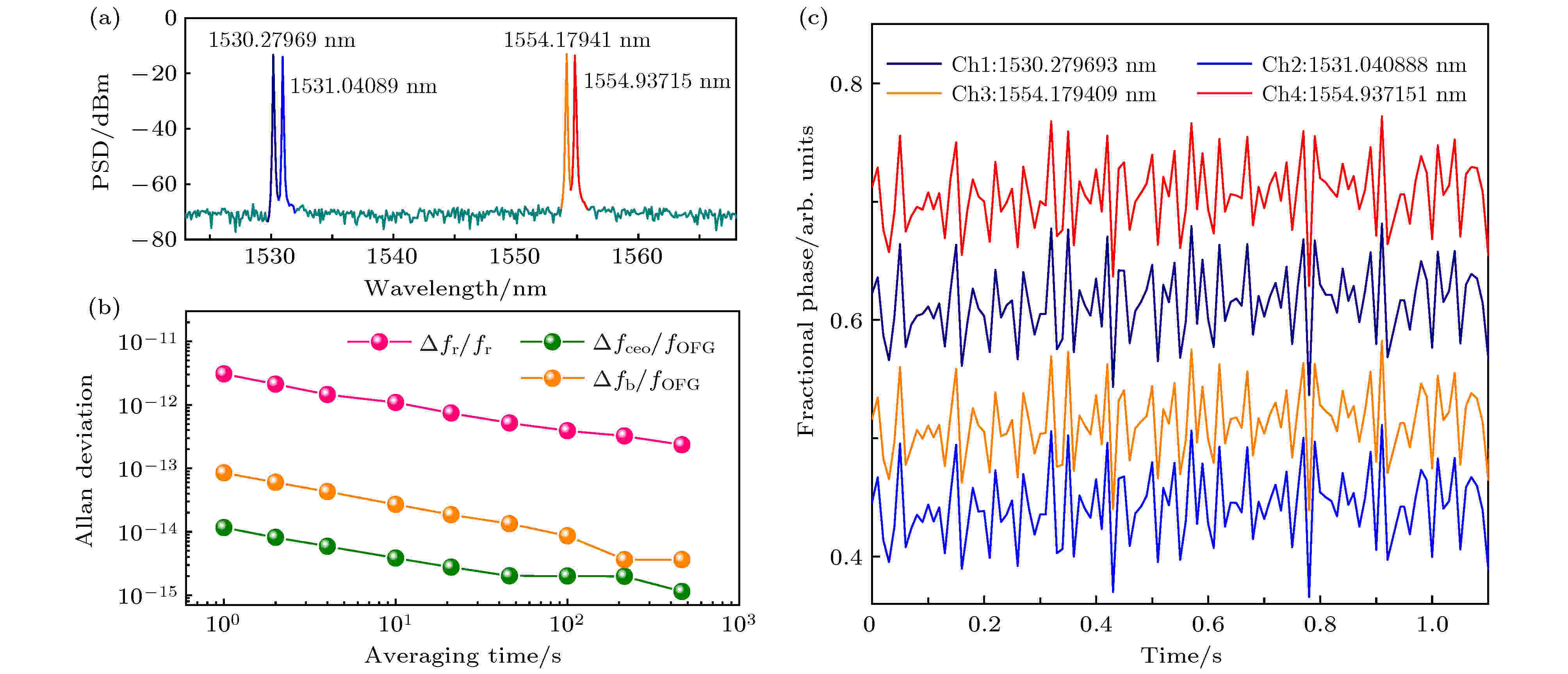图 3 多波长光源和相位测量结果 (a) 多波长发生器光谱测量结果; (b) 锁频激光的频率稳定度分析结果; (c) 多路同步相位解调实时测量结果
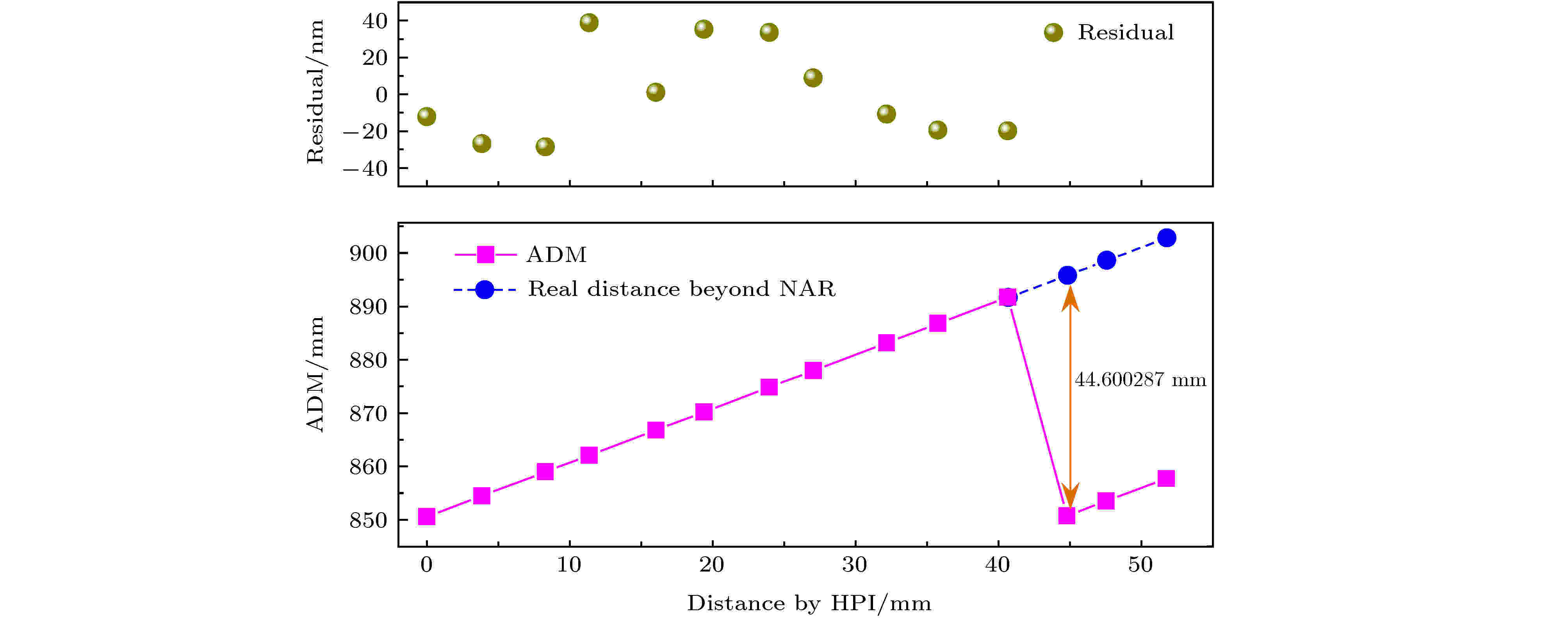图 4 验证NAR的线性位移对比实验
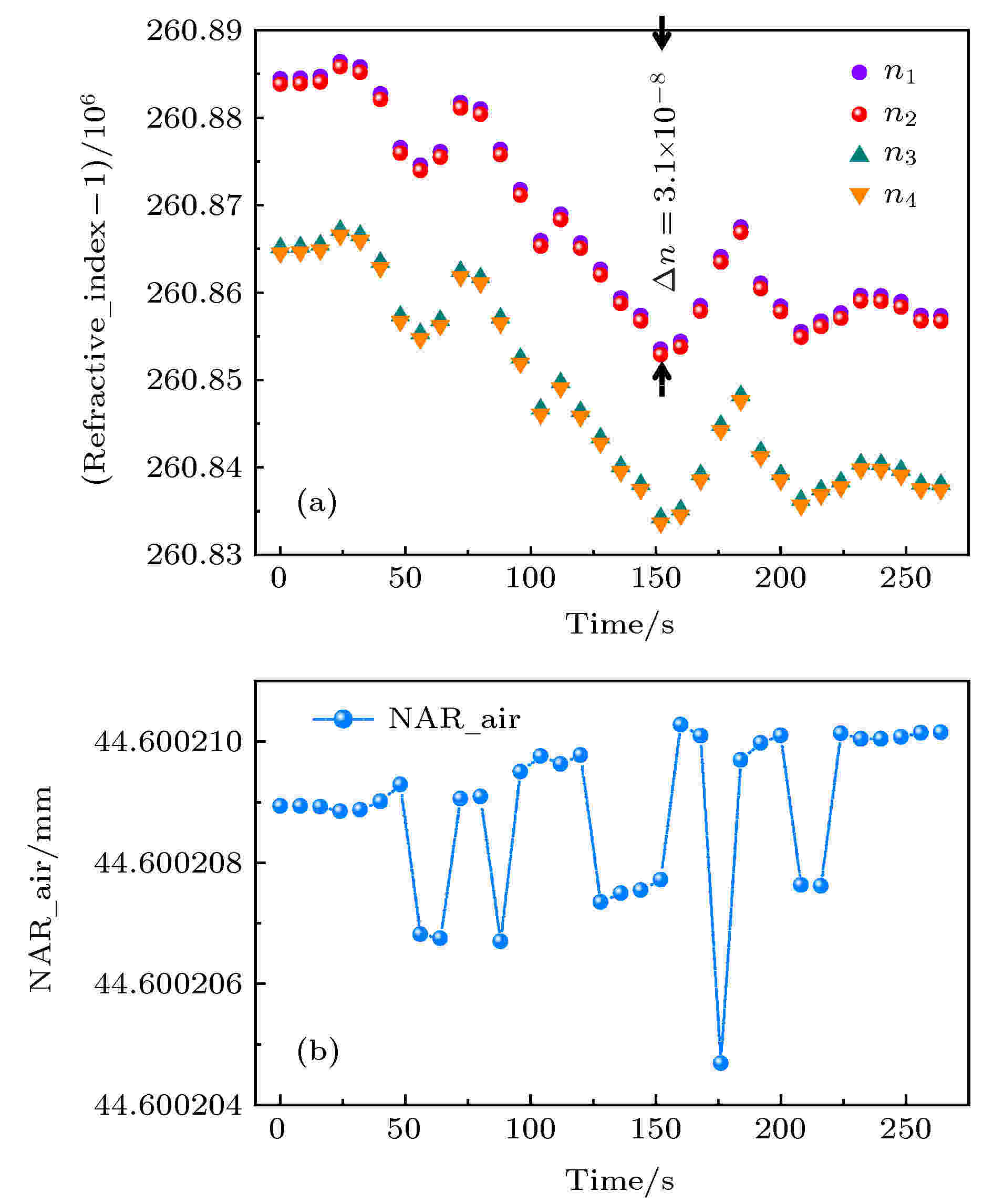图 5 空气折射率变化对NAR的影响 (a) 空气折射率的波动情况; (b) 理论NAR受空气折射率影响的计算结果
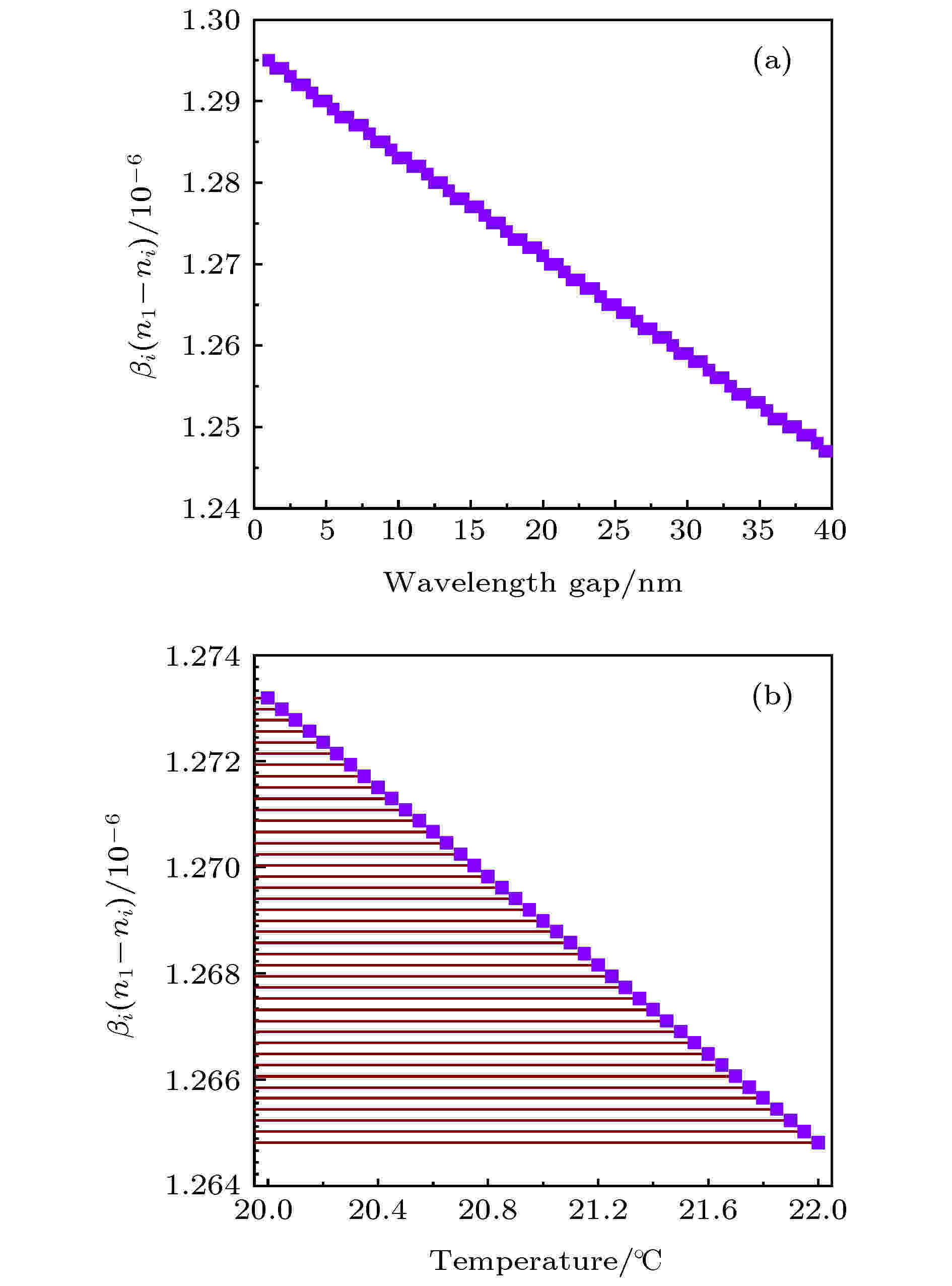图 6 
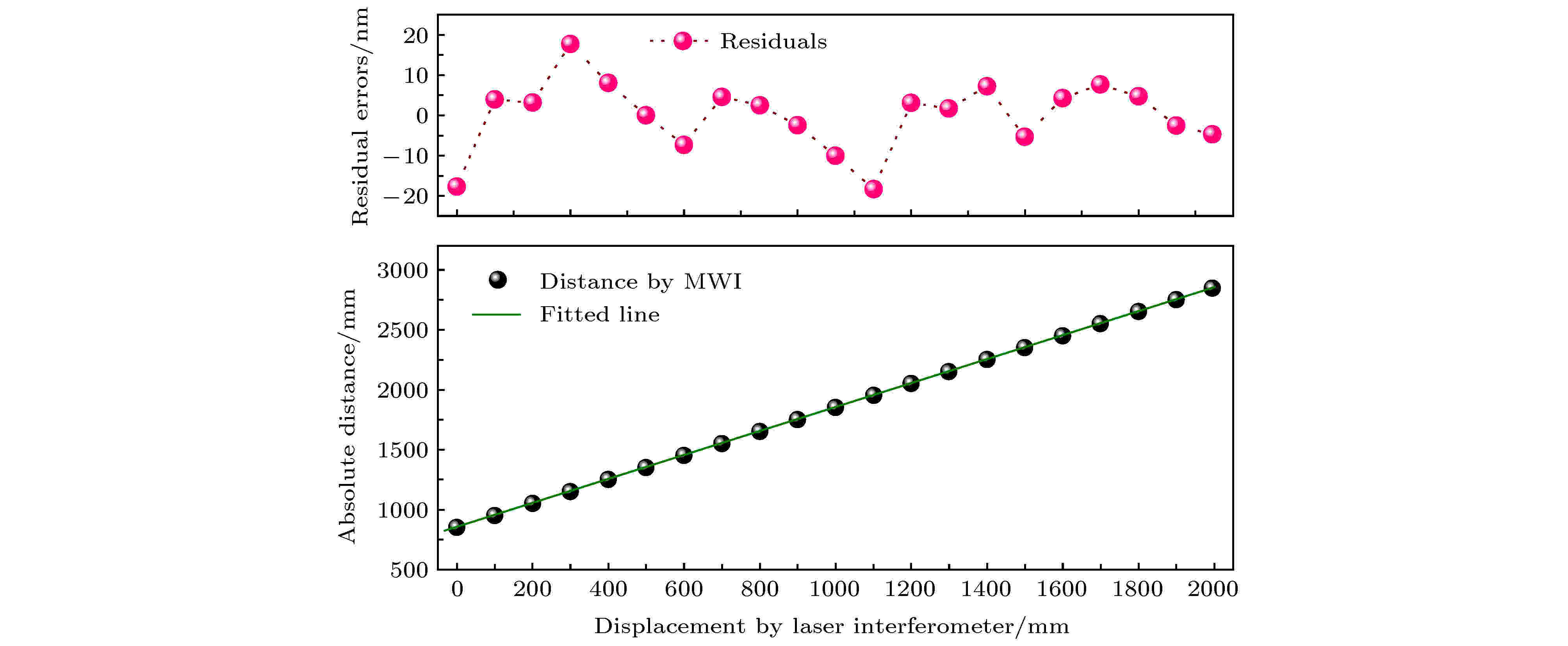图 7 MWI与商用激光干涉仪的2 m线性位移对比实验结果
