摘要:准确预测GaN半导体材料的热导率对GaN基功率电子器件的热设计具有重要意义. 本文基于第一性原理计算和经典Debye-Callaway模型,通过分析和完善Debye-Callaway模型中关于声子散射率的子模型, 建立了用于预测温度、同位素、点缺陷、位错、薄膜厚度、应力等因素影响的GaN薄膜热导率的理论模型. 具体来说, 对声子间散射项和同位素散射项基于第一性原理计算数据进行了系数拟合, 讨论了两种典型的处理点缺陷和位错散射的散射率模型, 引入了应用抑制函数描述的各向异性边界散射模型,并对应力的影响进行了建模. 热导率模型预测值和文献中典型实验数据的对比表明, 基于第一性原理计算数据拟合的热导率模型和实验测量值总体符合较好, 300 K温度附近热导率数值及其随温度变化的趋势存在20%左右的偏差. 结合实验数据和热导率模型进一步确认了第一性原理计算会高估同位素散射的影响, 给出了薄膜热导率随薄膜厚度、位错面密度、点缺陷浓度的具体变化关系, 同位素和缺陷散射会减弱薄膜热导率的尺寸效应, 主要体现在100 nm附近及更小的厚度范围.
关键词: GaN薄膜/
热导率/
Debye-Callaway模型/
第一性原理计算

English Abstract

全文HTML

--> --> -->

GaN是典型的第三代宽禁带半导体材料, 广泛应用于以高电子迁移率器件(HEMT)为代表的的高功率、高频率电子器件. 高功率和高集成度使得热管理问题成为器件设计中的瓶颈问题之一^[1,2]. 以HEMT为例, 器件总体是一个多层结构, 按生长顺序从下至上为衬底层、过渡层、GaN沟道层(1—3 μm)、AlGaN势垒层^[3]. 器件载流子工作区域在GaN和AlGaN层形成的异质界面处, 该区域也是热量产生的区域, 特征尺度在纳米量级. 热量需要从点状产热区域(纳米尺度)通过器件各功能层(微米尺度)散到基底热沉和外部环境, 以保证器件的正常工作和设定寿命. 该过程是由点及面的三维导热过程, 因此准确地预测近结区域温度场需要充分掌握和理解GaN层面向和法向的热导率及输运规律^[3].
GaN热导率的研究已开展很多, 覆盖实验测量、理论计算、建模研究. 早期实验研究报道的热导率数据具有较大的分散性, 主要是因为热导率材料生长方法和样品质量的不同^[4-12]. 此外, 受限于对GaN热物性的理解, 样品缺乏有效的表征, 包括厚度、点缺陷浓度、位错面密度、掺杂浓度、薄膜应力等. 最近较为系统的GaN热导率测量实验表明, 高纯度GaN的热导率在260 W/(m·K)左右^[13]. 本文系统整理了文献中引用较多的实验数据, 列于表1. 第一性原理计算结合晶格动力学方法和声子玻尔兹曼方程, 是研究晶体热输运性质的有效手段, 可以计算纯晶体和含同位素晶体的热导率^[14,15]. 结合格林函数法, 第一性原理计算也可以在计算量可行范围内进行点缺陷和小位错情形热导率的计算^[16,17]. 在目前已有的计算研究中, 部分研究报道了GaN纯晶体较高的热导率, 在400 W/mK左右, 含同位素晶体热导率在260 W/(m·K)左右^[18,19]. 研究中将实验热导率值相对纯晶体值较低解释为同位素或电声散射的影响^[19]. 另有部分计算研究则预测了相对接近实验值的纯晶体热导率值, 在260 W/(m·K)到330 W/(m·K)之间^[20-22]. 计算研究的差异主要源于计算中需要人为设置的部分, 采用不同泛函计算的优化结构具有不同的晶格常数, 存在2%以内的差别. 在第一性原理计算中充分保证收敛性并对晶格常数不做人为处理的情形下, GaN纯晶体的热导率在270 W/mK左右^[21,22]. 晶体材料的电学、热学性质对晶格常数较为敏感, 因此晶格常数的处理上会造成最终计算结果的较大差异. 热导率的模型研究主要依赖于经典的Debye-Callaway模型^[23], 该模型基于双弛豫时间的声子玻尔兹曼方程和德拜模型, 比较成功地应用于各种晶体材料的热导率预测中. 模型中较为关键的参数是声子散射率(或弛豫时间). 在模型研究方面, 前人的模型研究较为单一^{[7,10,12,24-26]}, 主要体现为各项散射率子模型的单一处理, 并未深入探讨所有可能的散射项来源, 以及不同散射项之间的差异性及其处理方式, 特别是边界散射的处理方式.

文献/样品		室温热导率/ (W·m–1·K–1)	厚度/μm	点缺陷浓度(缺陷元素)/cm–3	位错面密 度/cm–2	同位素
Zheng et al.[13]	KMiF	234	7—12	1.5 × 1018 (Al), 5 × 1017 cm–3 (O)	< 107	无
	KMF	195	6—8	1.5 × 1018 (Al), 5 × 1017 cm–3 (O)	< 107	有
	AM/KM	197	300—600	0.1 × 1018—20 × 1018 cm–3 (H) 0.1 × 1018—5 × 1018 cm–3 (O)	< 107	有
Shibata et al.[4]	1	252	1000	2.1 × 10–17 cm–3 (Si)	5 × 106	有
Slack et al.[5]	1	—	200	2.1 × 1016 cm–3 (O), 0.37 × 1016 cm–3 (Si)	—	有
Jezowski et al.[6]	1	218	100	1 × 1020 cm–3 (O), 1 × 1019 cm–3 (C), 1 × 1018 cm–3 (Mg), 7 × 1017 cm–3 (H), 1017 cm–3 (Si), 1 × 1018 cm–3 (Ga原子空位)	—	有
	2	188
	3	157
Je?owski et al.[7]	1	78	300	4 × 1016 cm–3 (O)	—	有
	2	162		2.6 × 1018 cm–3 (O)
	3	275		1.1 × 1020 cm–3 (O)
Simon et al.[8]	1	226	300	2.3 × 1018 cm–3 (O), 2.3 × 1018 cm–3 (Mg)	—	有
	2	211		9.7 × 1017 cm–3 (O)
	3	163		2 × 1019 cm–3 (O)
Rounds et al.[9]	1	203	300—600	4 × 1016 cm–3 (O)	—	有
	2	223		2.2 × 1017 cm–3 (Si)
	3	182		8.4 × 1018 cm–3 (H), 8.9 × 1018 cm–3 (O)
	4	200		1.5 × 1019 cm–3 (H), 1.4 × 1018 cm–3 (O), 9.8 × 1018 cm–3 (Mn)
	5	163		3.5 × 1018 cm–3 (H), 1.4 × 1018 cm–3 (O), 9.3 × 1017 cm–3 (Mg)
Li et al.[10]	S1	190	3.19	—	1.8 × 108	有
	S2	195	3.52		2.36 × 109
	S3	220	400		2 × 107
Mion et al.[11]	A	184	200	4 × 1017 (H), 1017 (C), 3 × 1016 (O), 1017 (Si)	4.06 × 107	有
	B	200	370		1.47 × 107
	C	214	1400		8.96 × 106
	D	229	2000		5.1 × 104

表1文献中的GaN薄膜室温热导率数据及样品表征
Table1.Thermal conductivity of GaN films at room temperature and characteristic from literature

在实际器件中, GaN材料以薄膜形式存在, 处在势垒层和形核层或基底中间. 在材料生长和器件运行过程中, GaN薄膜热导率会受到较多因素的影响. 即除了声子间本征散射、同位素散射对散射率的贡献外, 各种杂质原子造成的点缺陷散射、空位散射、位错散射都是实际材料中散射率的重要组成部分^{[4,5,7-9,11,12,16,17,25-27]}. 此外, GaN薄膜的厚度通常在1—3 μm, 需要考虑边界散射造成的热导率尺寸效应, 特别地, 晶体纯度越高, 越需要考虑边界散射的影响. 由于在材料生长过程中GaN和形核层或基底会存在晶格常数不匹配及在器件工作过程中存在热膨胀系数不匹配的情形, GaN薄膜会受到强度不等的面向应力, 该应力对热导率的影响也不可忽略 ^[22].
尽管目前第一性原理计算方法已经可以用来处理包括纯晶体等更多复杂情形的热输运计算, 但是受限于计算量, 计算的点缺陷和位错等结构都尺度较小. 在热导率特别是薄膜材料热导率预测方面, 系统性的模型研究仍然具有较大的优势和工程价值. 本文基于第一性原理计算的热导率和声子数据, 结合Debye-Callaway热导率模型, 对GaN薄膜室温以上热导率进行了系统的建模研究. 模型考虑了同位素、点缺陷、位错、薄膜厚度、应力对热导率的影响. 对声子间散射和声子同位素散射子模型的系数基于第一性原理计算数据进行了拟合. 相比于文献中的已有工作, 本文引入抑制函数方法, 更准确地描述边界散射造成的尺寸效应. 同时分别讨论了两种点缺陷和位错散射率模型. 最后得到本文的GaN薄膜热导率模型. 研究结果表明, 基于第一性原理计算数据拟合的热导率模型和实验测量值总体符合较好, 300 K温度附近热导率值和随温度变化趋势存在一些偏差. 根据实验数据进一步确认了第一性原理计算会高估同位素散射的影响. 最后给出了薄膜热导率随薄膜厚度、位错面密度、点缺陷浓度的具体变化关系.

2

-->

2.1.基本思路和建模基础

本文的热导率建模以Debye-Callaway模型和第一性原理计算的热导率数据为基础, 其中第一性原理计算可以提供纯晶体体材料和含同位素体材料随温度变化的热导率值. 基于Debye-Callaway模型拟合这些热导率数据, 可以得到Debye-Callaway模型中声子间散射和同位素散射的系数, 其余散射（点缺陷散射、位错散射、边界散射）则采用经典唯象模型描述^[23,28-33].
本文的第一性原理计算是在商用软件 Vienna ab initio Simulation Package (VASP)^[34]上进行的. 计算中采用了Perdew-Burke-Ernzerhof (PBE)泛函^[35]和投影缀加波(PAW)赝势^[36]. 基于收敛性测试, 截断能量选取为800 eV, 对布里渊区设置了10 × 10 × 10的Monkhorst-Pack网格^[37]. 结构优化过程中设置了严格的判别标准, 原子受力小于10^–6 eV/?, 残余应力小于 10^–2 kbar. 二阶力常数和三阶力常数均采用超胞法进行计算^[38,39], 采用的超胞参数分别为4 × 4 × 3和5 × 5 × 3, 两组参数均进行了收敛性验证, 其中三阶力常数计算中截断距离取到第5近邻原子. 采用密度泛函微扰理论计算了体系玻恩有效电荷和高频介电函数, 用于考虑极性晶体中的长距库仑相互作用. 利用得到的力常数, 基于声子动力学矩阵和费米黄金定则, 可以得到声子的简谐性质(色散关系、群速度、态密度等)和非简谐性质(弛豫时间、格留乃森常数等), 通过迭代求解声子玻尔兹曼方程, 可以得到声子热导率^[39]. 更多计算细节可以参考文献[22].
2 -->

2.2.热导率建模

3 -->

2.2.1.Debye-Callaway热导率模型

Debye-Callaway热导率模型包含两部分, 分别为倒逆散射(U散射)等阻尼散射对热导率的贡献部分和正态散射(N散射)对热导率的贡献部分. 除了在极低温情形下, GaN体系中声子N散射过程较弱, 对热导率的影响很小, 特别是在室温及更高温度情形下, N散射对热导率的贡献小于5%, 可以忽略^[22]. 因此本文只采用Debye-Callaway模型的U散射部分^[23],

$\kappa ={\left(\frac{{k}_{{\rm{B}}}}{\hslash }\right)}^{3}\frac{{k}_{B}}{2{\pi }^{2}\bar v}{T}^{3}{\int }_{0}^{{ \varTheta }_{{\rm{D}}}/T}\frac{{\tau }_{{\rm{T}}}{x}^{4}{{\rm{e}}}^{x}}{{\left({{\rm{e}}}^{x}-1\right)}^{2}}{\rm{d}}x$

其中, $\kappa $ 为热导率, $x=\dfrac{\hslash \omega }{{k}_{{\rm{B}}}T}$, $ {k}_{{\rm{B}}} $是玻尔兹曼常数, $ \hslash $是约化普朗克常数, $ \omega $是声子频率, $ T $是温度, $ \bar v $是体系平均声速, ${ \varTheta }_{{\rm{D}}}$是德拜温度, $ {\tau }_{{\rm{T}}} $是总的声子弛豫时间. 平均声速$ \bar v $采用(2)式定义

$ \bar v={\left[\frac{1}{3}\left(\frac{1}{{v}_{{\rm{T}},1}}+\frac{1}{{v}_{{\rm{T}},2}}+\frac{1}{{v}_{{\rm{L}}}}\right)\right]}^{-1}, $

其中, $ {v}_{{\rm{T}}} $为横波声速, $ {v}_{{\rm{L}}} $为纵波声速, $ {v}_{{\rm{T}}} $和$ {v}_{{\rm{L}}} $可以根据系统弹性常数和材料密度计算得到, ${v}_{\text{T/L}}= \sqrt{{C}_{\text{T/L}}/\rho }$. 沿[001]方向, 即轴向, $ {v}_{{\rm{T}}, 1/2}=\sqrt{{C}_{\text{44}}/\rho } $, $ {v}_{{\rm{L}}}=\sqrt{{C}_{\text{33}}/\rho } $;沿 [100]方向, 即垂直于轴向, ${v}_{\text{T, 1}}= \sqrt{{C}_{\text{44}}/\rho }$, $ {v}_{\text{T, 2}}=\sqrt{\left({C}_{\text{11}}-{C}_{\text{12}}\right)/\rho } $, $ {v}_{{\rm{L}}}=\sqrt{{C}_{\text{33}}/\rho } $. 模型中最重要的参数就是声子弛豫时间(散射率)、德拜温度和平均声速. 本文热导率模型研究中, 考虑的声子散射项包括声子间U散射、声子-同位素(I)散射、声子-点缺陷(P)散射、声子-位错(D)散射、边界(B)散射. 因此总的声子散射率可以根据马蒂森准则表示为

$ {\tau }_{{\rm{T}}}^{-1}={\tau }_{{\rm{U}}}^{-1}+{\tau }_{{\rm{I}}}^{-1}+{\tau }_{{\rm{P}}}^{-1}+{\tau }_{{\rm{D}}}^{-1}. $

边界散射的影响和前几种散射有所不同, 既可以简化处理表示为$ {\tau }_{{\rm{B}}}^{-1} $的形式加入到上式中, 也可以作为边界条件进行考虑. 上述散射率模型和边界散射处理将在2.2和2.3小节中讨论. 此外, 在2.3小节, 应力对热导率的影响也加入到了薄膜热导率模型中. 模型中使用的基本参数列于表2和表3, 其中晶格常数和弹性常数均来自第一性原理计算. 在引言部分已经提到, 文献中有多组不同的晶格常数计算值^{[18,19,21,22]}. 基于VASP推荐的PBE泛函, 第一性原理给出了较实验值^[40] (a = 0.319 nm, c = 5.189 nm)略大1%的晶格常数(表2). 采用人为调整的方式将计算值设为实验值会使体系存在较强应力, 声子频率和热导率计算值都会增大, 且使得后续计算结果的可解释性变差, 因此在本文建模依据的热导率计算中未对晶格常数计算值做人为调整. 因为, 晶格常数主要通过原子平均体积影响唯象散射率模型, 该影响可以忽略. 表2中的平均速度来自于基于第一性原理计算的拟合, 在3.1节中将作详细讨论.

参数	数值		参数	数值
a /?	3.219		$ \bar v $ (垂直轴向)/m·s–1	3621
c /?	5.245		$ \bar v $ (沿轴向) /m·s–1	3915
V0 /m3	1.176 × 10–29		$ \nu $(泊松比)	0.255

表2模型中使用的基本参数
Table2.Basic parameters used in the model.

C11	C33	C12	C13	C44	C66
322.7	356.6	110.4	77.7	106.2	90.0

表3GaN弹性常数分量 (单位: GPa).
Table3.Components of elastic constants of GaN (unit: GPa).

3 -->

2.2.2.声子散射率模型

声子散射率模型包括声子间散射、点缺陷散射、同位素散射、位错散射、边界散射模型. 声子间散射的模型中通常包含反映晶体基本性质的参数, 比如原胞体积、原子质量、德拜温度、格留乃森常数、声速等. 模型中包含这些参数的多少决定了模型需要拟合的程度. U过程声子散射率模型可以表示为^[28]

$ {\tau }_{{\rm{U}}}^{-1}=\frac{\hslash {\gamma }^{2}}{M{\bar v}^{2}{ \varTheta }_{{\rm{D}}}}{\omega }^{2}T{{\rm{e}}}^{-{ \varTheta }_{{\rm{D}}}/\left(3T\right)}, $

其中, $ \gamma $是格留乃森常数, $ M $为原胞内原子的平均质量. 模型的主要特征体现在频率的指数上. 根据Herring基于晶格点群对称性的分析^[41]及第一性原理计算^[42], 纤锌矿晶格中LA和TA声子的U过程散射率与声子频率的三次方成比例关系, 在(4)式中则反映到$ {\omega }^{2}T $中. 在进行拟合时可以将模型中的物性参数部分作为拟合参数, 将模型简化为

$ {\tau }_{{\rm{U}}}^{-1}=A{\omega }^{2}T{{\rm{e}}}^{-BT}, $

模型中的两个参数A和B则根据拟合第一性原理计算数据获得.
点缺陷包含杂质原子缺陷、错位原子缺陷、空位缺陷, 氮化镓生长过程中最多的还是杂质原子缺陷, 特别是人为掺杂, 包括部分空位缺陷. 在晶体中, 点缺陷对体系造成的扰动或散射强度$\varGamma$可以分解为原子质量差异造成的动能扰动${ \varGamma }_{M}$和原子间力常数与原子半径变化造成的势能扰动${ \varGamma }_{{\rm{R}}}$^[30]. 这些扰动, 一方面会增加局域性的声子态; 另一方面, 会带来局部应力, 特别是空位缺陷, 造成局部声子性质(群速度等)的改变及散射. 研究表明点缺陷造成的声子散射主要是弹性散射^[17], 因而适用于二声子图像的弛豫时间近似模型, 可以用散射率来表示. 同时, 点缺陷造成的散射是局域性的, 因此散射率的增加适用于马蒂森准则. 基于二阶微扰理论的点缺陷声子散射率^[29],

$ {\tau }_{{\rm{P}}}^{-1}=\frac{{V}_{0}{\omega }^{4}}{4{\rm{\pi }}{\bar v}^{3}} \varGamma , $

其中, $ {V}_{0} $为原子平均体积, $ {V}_{0}=\left|{a}_{1}\cdot \left({a}_{2}\times {a}_{3}\right)\right|\text{/4} = {a}^{2}c\sqrt{3}\text{/8} $, $ {a}_{i} $是原胞基矢. 根据上述分析, 散射强度包含两部分,

$ \varGamma ={ \varGamma }_{{\rm{M}}}+{ \varGamma }_{{\rm{R}}}. $

考虑缺陷位置处原子质量的差异, 可以将质量差异造成的散射强度表示为^[28]

$ { \varGamma }_{{\rm{M}}}={{\sum }_{i}{f}_{i}\left(1-\frac{{M}_{i}}{\stackrel{?}{M}}\right)}^{2}, $

其中, $ {f}_{i} $是晶体中第i种原子的相对浓度(包括宿主原子和进入的掺杂原子以及空位), $ {M}_{i} $是第i种原子的质量, $ \stackrel{?}{M} $则是体系中平均原子质量. 也可以表示为^[30,31]

$\begin{split} &\varGamma_{{\rm{M}}}=\frac{\left\langle\overline{\Delta M^{2}}\right\rangle}{\langle\bar{M}\rangle^{2}}, ~\overline{\Delta M_{n}^{2}}=\displaystyle\sum\nolimits_{i} f_{i, n}\left(M_{i, n}-\overline{M_{n}}\right)^{2}, \\&\overline{M_{n}}= \displaystyle\sum\nolimits_{i} f_{i, n} M_{i, n}, \\&\left\langle\overline{\Delta M^{2}}\right\rangle=\frac{\displaystyle\sum\nolimits_{n} c_{n} \Delta M_{n}^{2}}{\displaystyle\sum\nolimits_{n} c_{n}}, ~~\langle\bar{M}\rangle=\frac{\displaystyle\sum\nolimits_{n} c_{n} \overline{M_{n}}}{\displaystyle\sum\nolimits_{n} c_{n}},\end{split}$

其中, n表示化合物中的元素(纯晶体包含的元素, GaN晶体中则只包含Ga和N), c_n表示化合物中元素的化学计量数, $\overline {} $表示在某种元素位置处对所有种类原子求平均, $\left\langle {~} \right\rangle$代表对所有元素求平均. 对于空位散射有$ \left({M}_{i, n}-\overline{{M}_{n}}\right)=-{M}_{{\rm{v}}{\rm{a}}{\rm{c}}}-2\left\langle {\overline{M}} \right\rangle $, 其中$ {M}_{{\rm{v}}{\rm{a}}{\rm{c}}} $为空位原子质量, $ \left\langle {\overline{M}} \right\rangle $晶体平均原子质量. 若同时考虑点缺陷造成的弹性应力场, 则求和项应当包含弹性应力场的影响, 对应散射强度表示为^[28]

$ {\varGamma }_{{\rm{R}}}=\sum\limits_{i}2{f}_{i}{\left\{6.4\gamma \left(1-\frac{{R}_{i}}{\stackrel{?}{R}}\right)\right\}}^{2}, $

其中, $ {R}_{i} $是第i个原子的离子半径^[43], $ \stackrel{?}{R} $则为平均半径. 或表示为^[30]

$ { \varGamma }_{{\rm{R}}}=\varepsilon \frac{\left\langle {\overline{{{\Delta }}{R}^{2}}} \right\rangle }{{\left\langle {\overline{R}} \right\rangle }^{2}}, \;\left\langle {{{\Delta }}{R}^{2}} \right\rangle =\left\langle {\sum\limits_{i}{f}_{i}{\left({R}_{i,n}-\overline{{R}_{n}}\right)}^{2}} \right\rangle . $

其中, $ \varepsilon $是一个拟合参数, 通常取值在1—500之间, 本文取为5(主要基于模型和实验值^[13]的比较). 两种模型具有很高的相似性, 但第二种模型更为精细, 是对晶体中每个元素位置计算散射强度然后求和, 对多元化合物晶体更为合理. 本文模型计算选用第二种点缺陷散射模型, 即 (7) 式、(9) 式、(11) 式.
同位素可以作为点缺陷的一种简单特例, 因此其造成的声子散射率可以表示为^[29]

$ {\tau }_{{\rm{I}}}^{-1}=\frac{{V}_{0} \varGamma }{4{\rm{\pi }}{\bar v}^{3}}{\omega }^{4}, $

或写成包含拟合参数的形式

$ {\tau }_{{\rm{I}}}^{-1}=C{\omega }^{4}. $

其对声子散射的影响主要来自原子质量差别, 与掺杂及空位缺陷相比, 同位素原子造成的弹性应力场很小. 自然状态下⁶⁹Ga和⁷¹Ga原子的比例分别约为60.1%和39.9%, 远大于N元素两种同位素原子的比例差别, 其中¹⁴N的比例约为99.64%, ¹⁵N约为0.36%. 基于第一性原理计算中使用的同位素散射模型的分析表明, GaN中的同位素散射主要源自于Ga原子的同位素原子质量差别, N原子的同位素影响可以忽略^[13]. (13)式模型中的参数C通过拟合第一性原理计算数据获得.
GaN薄膜中, 位错主要包括刃位错、螺旋位错、混合位错. 位错散射的作用可以分为位错核心的散射和位错长程应力场的散射. 文献中描述位错散射的模型主要有两个, 第一个是Carruthers模型^[32]

$ {\tau }_{{\rm{D}}}^{-1}=\frac{1}{3}{\rho }_{{\rm{D}}}{b}^{2}{\gamma }^{2}\bar v\left|q\right|{\left[{\rm{ln}}\left(R/b\right)\right]}^{2}, $

其中:$ {\rho }_{{\rm{D}}} $为位错面密度; b为博格斯矢量, $ b=\sqrt{2}a/3 $; $ R $用来描述位错造成的应力场范围, 定义为$ 1/\sqrt{{\rho }_{{\rm{D}}}} $. 在德拜近似下, 可以退化为

$ {\tau }_{{\rm{D}}}^{-1}=\frac{1}{3}{\rho }_{{\rm{D}}}{b}^{2}{\gamma }^{2}\omega {\left[{\rm{ln}}\left(R/b\right)\right]}^{2}. $

(15)式是一个较简单的模型, 仅考虑了刃位错造成的应力场效应. 若全面考虑各种可能位错及其影响, 位错声子散射率模型可以写为^[26,28]

$\begin{split} &{\tau }_{{\rm{D}}}^{-1}={\tau }_{\text{core}}^{-1}+{\tau }_{\text{screw}}^{-1}+{\tau }_{\text{edge}}^{-1},\\ &{\tau }_{\text{core}}^{-1}=\eta {N}_{{\rm{D}}}\frac{{V}_{0}^{4/3}}{{\bar v}^{2}}{\omega }^{3},\\ &{\tau }_{\text{screw}}^{-1}=0.06{N}_{{\rm{D}}}^{{\rm{s}}}b{{}_{{\rm{S}}}{}^{2}\gamma }^{2}\omega ,\\ &{\tau }_{\text{edge}}^{-1}=0.06{N}_{{\rm{D}}}^{e}b{{}_{{\rm{E}}}{}^{2}\gamma }^{2}\omega . \end{split}$

其中, $ {N}_{{\rm{D}}} $是位错线密度, $ {b}_{{\rm{S}}}=c $, $ {b}_{{\rm{E}}}=\sqrt{2}a/3 $, $ \eta $是权重系数. 当系统温度梯度和位错线垂直时, 位错核心对声子的散射作用最强, 权重系数为1; 当温度梯度和位错线平行时, 散射作用很弱, 权重系数可以取为0, 通常认为两者兼有, 将系数取为0.55. 刃位错造成的散射率还可以表示成更复杂的形式,

$ {\tau }_{\text{edge}}^{-1}=0.06\eta {N}_{{\rm{D}}}^{e}b{{}_{{\rm{E}}}{}^{2}\gamma }^{2}\omega \left\{\frac{1}{2}+\frac{1}{24}{\left(\frac{1-2\nu }{1-\nu }\right)}^{2}{\left[1+\sqrt{2}{\left(\frac{{v}_{{\rm{L}}}}{{v}_{{\rm{T}}}}\right)}^{2}\right]}^{2}\right\}, $

其中, $ \nu $是泊松比, $ \nu ={C}_{12}/({C}_{11}+{C}_{12}) $, 横向和纵向声速根据2.1节中的公式计算. 同时还可以考虑混合位错, 其散射率模型为^[28,29]

$ {\tau }_{\text{mix}}^{-1}=0.06\eta {N}_{{\rm{D}}}^{m}{\gamma }^{2}\omega \left({b}_{{\rm{S}}}^{2}+{b}_{{\rm{E}}}^{2}\left\{\frac{1}{2}+\frac{1}{24}{\left(\frac{1-2\nu }{1-\nu }\right)}^{2}{\left[1+\sqrt{2}{\left(\frac{{v}_{{\rm{L}}}}{{v}_{{\rm{T}}}}\right)}^{2}\right]}^{2}\right\}\right). $

位错会增强声子的散射, 特别是当位错方向和声子输运方向垂直时. 但是声子-位错散射和声子间散射、声子-同位素散射、声子-点缺陷散射并不完全类似. 后三种散射的作用是均匀的、非局域化的, 因而可以较好地采用马蒂森准则进行加和. 位错散射则兼具全局性和局域性的特点, 在使用马蒂森准则时可能会出现偏差^[44]. 本文模型计算中采用第二种位错模型, 即 (16) 式—(18) 式. 考虑到实际GaN外延生长中主要产生刃位错, 模型中刃位错、螺旋位错、混合位错的分配比例分别取为80%、10%、10%.
当薄膜厚度小于体材料声子平均自由程或与之相当时, 边界散射增强, 造成热导率的尺寸效应, 此时, 边界散射成为影响薄膜热导率的另一重要因素. 边界散射对热导率的作用依具体问题的不同而不同, 受材料形状^[45-48]、导热过程是否包含内热源^[49]、热流方向与边界的关系^[33]等影响. 根据器件中GaN薄膜的导热特点, 当前处理GaN薄膜中边界散射的主要方法有两种. 第一种是把边界散射作为一种散射类型, 对其造成的声子散射率进行建模, 并通过马蒂森准则加入到上文所述的总散射率中;另外一种则是将边界散射作为声子玻尔兹曼方程的边界条件, 得到随声子努森数Kn变化的等效热导率模型, 其中Kn定义为声子平均自由程和薄膜特征长度的比值(Kn=l/L), 对应文献中温差传热薄膜结构情形^[33,45,49]. 对于第一种处理方式, 边界散射率可以表示为

$ {\tau }_{{\rm{B}}}^{-1}={ \bar v}/{L} $

其中, L为薄膜的特征长度, 通常取厚度的1/2. 在德拜近似下, 群速度不依赖于声子频率, 是一个常数, 因此边界散射率也是常数. 由于薄膜结构存在沿薄膜表面方向(面向)和垂直表面方向(法向), 相应存在面向和法向热输运及热导率. 该边界散射率模型可以描述热导率的尺寸效应, 但是不能区分法向和面向声子热输运中边界散射的不同影响, 即无法描述边界散射造成的薄膜热导率各向异性. 因此, 较为合理的处理方式是将边界散射作为声子玻尔兹曼方程的边界条件, 求解得到反映热导率尺寸效应的模型. 假设GaN边界在原子尺度上是粗糙的, 边界散射都可以视为全部漫散射, 则考虑边界散射后, 法向和面向热导率可以分别表示为^[33]

$ \frac{{\kappa }_{\text{cross}}}{{\kappa }_{0}}=\frac{1}{1+\dfrac{4}{3}\text{Kn}}, $

$ \frac{{\kappa }_{\text{in}}}{{\kappa }_{0}}\!=\!\!\left\{\!1\!-\!\frac{3}{2}\text{Kn}{\int }_{0}^{1}\!\left[\!1\!-\!{\rm{exp}}\left(\!-\!\frac{1}{\text{Kn}\sqrt{1\!-\!{\mu }^{2}}}\!\right)\!\right]\!{\mu }^{3}{\rm{d}}\mu \!\right\}, $

其中$ {\kappa }_{0} $为体材料热导率. 在模型中, (21) 式可以简化为

$ \frac{{\kappa }_{\text{cross}}}{{\kappa }_{0}}=\frac{1}{1+\dfrac{3}{8}\text{Kn}}. $

实际计算中处理法向和面向情形下边界散射的方法是将 (20)式和(22) 式的右边一项作为抑制函数加入到热导率公式中, 即

$ \kappa ={\left(\frac{{k}_{{\rm{B}}}}{\hslash }\right)}^{3}\frac{{k}_{B}}{2{{\rm{\pi }}}^{2}\bar v}{T}^{3}{\int }_{0}^{{ \varTheta }_{D}/T}\frac{S{\tau }_{T}{x}^{4}{{\rm{e}}}^{x}}{{\left({{\rm{e}}}^{x}-1\right)}^{2}}{\rm{d}}x $

其中S即为抑制函数, $\text{Kn}(\omega) \!=\! \bar v\tau (\omega)/L$. 法向情形下

$ S= 1\Big/\Big[{1+\dfrac{4}{3}\text{Kn}\left(\omega \right)}\Big], $

面向情形下

$ S={1}\Big/\Big[{1+\dfrac{3}{8}\text{Kn}\left(\omega \right)}\Big]. $

本文热导率建模采用了第二种边界散射处理模型.
2 -->

2.3.应力影响的建模分析

对于外延生长的GaN薄膜, 直接的应力测量非常困难, 较容易实现的是晶格常数的测量, 因此垂直轴向的应力可以反映在面向晶格常数(目前绝大多数器件中GaN薄膜沿极化轴生长, 因此此处应力影响研究部分默认GaN薄膜是沿极化轴生长的, 因此沿轴向为薄膜法向, 垂直轴向为面向)的变化上. 声子散射率基本的变化趋势符合压应力降低散射率、拉应力增强散射率的定性认识^[22]. 应力对声子散射的影响是均匀的、非局域性的, 应力还影响平均声速、格留乃森常数、德拜温度等, 特别是材料生长确定后受到的应力(如热膨胀系数不匹配造成的应力)同时影响声子本征散射、同位素散射、缺陷散射、位错散射. 考虑到对于拟合参数在垂直轴向的应力下的变化进行建模缺乏足够的物理意义, 且需要考虑的参数较多, 本文基于第一性原理计算得到的不同面向应力下的热导率数据对有限的垂直轴向应力下的热导率数据进行了二次多项式拟合. 图1(a)为面向应变状态下的相对热导率(热导率和自由状态热导率的比值)随温度的变化, 包含纯晶体和含同位素情形. 可以看到, 相对热导率基本不随温度和是否含同位素变化. 因此, 对沿轴向和垂直轴向两种情形分别计算了平均相对热导率(对温度和是否含同位素同时平均), 并在图1(b)中进行了拟合. 基于二次多项式拟合, 垂直轴向和沿轴向热导率随面向应变的变化分别为
图 1 (a) 面向应变下GaN相对热导率随温度和同位素的变化; (b) 相对热导率和应变的拟合关系(二次多项式拟合)
Figure1. (a) Variations of thermal conductivity ratios with respect to temperature and isotopes under in-plane strain (quadratic polynomial fitting); (b) Fitting relation between relative thermal conductivity and strain

$ {\kappa }_{{\rm{s}},{\rm{a}}/{\rm{m}}}=\left(-16{{\varepsilon }_{{\rm{s}}}}^{2}+21{\varepsilon }_{{\rm{s}}}-3.7\right){\kappa }_{0}, $

$ {\kappa }_{{\rm{s}},{\rm{c}}}=\left(-4{{\varepsilon }_{{\rm{s}}}}^{2}-2.5{\varepsilon }_{{\rm{s}}}+7.5\right){\kappa }_{0}. $

其中: $ {\varepsilon }_{{\rm{s}}} $是应力状态下面向晶格常数$ {a}_{{\rm{s}}} $和自由状态下面向晶格常数$ a $的比值, $ {\varepsilon }_{{\rm{s}}}={a}_{{\rm{s}}}/a $;$ {\kappa }_{0} $为自由状态下的热导率.

2

-->

3.1.模型的检验

第一性原理计算中可以给出考虑声子间U过程散射和同位素散射的热导率, 因此U散射率和同位素散射率模型中的参数可以根据计算数据拟合得出. 对只考虑U散射的情形, 散射率子模型中需要拟合的参数A和B实际内含了3个物性常数, 分别为格留乃森常数$ \gamma $、平均声速$\bar{v}$、德拜温度${\varTheta }_{{\rm{D}}}$. 在同时考虑同位素散射时, 拟合的参数还包括同位素散射强度$\varGamma$. 在拟合中由于参数多于拟合数据组数, 因此基于第一性原理计算数据将格留乃森常数的均方平均$ \stackrel{?}{\gamma } $取为0.86. 格留乃森常数是温度的函数, 该值为300—500 K范围内的平均值. 此外, 本文的模型研究面向GaN材料的应用背景, 重点关注300 K以上特别是300—500 K温度范围内的热导率, 因此用于参数拟合的热导率数据也选取在300—500 K温度范围. 最终, 拟合纯晶体及含同位素晶体热导率值, 可以得到拟合参数, 如表4所示. 以此得到面向和法向的格留乃森常数分别为0.84和0.88, 平均声速分别为3621 m/s和3915 m/s, 德拜温度为418 K.

拟合参数	A	B	C
垂直轴向 (a/m)	1.94 × 10–19	139	2.91 × 10–44
轴向 (c)	1.85 × 10–19	139	2.30 × 10–44

表4声子散射率模型中的拟合参数
Table4.Fitting parameters in phonon scattering sub-models.

图2 (a)和图2 (c)曲线分别为纯晶体和含同位素晶体情形下的热导率拟合结果, 其中沿轴向(c轴)热导率标注为(c), 垂直于轴向(沿a或m轴)热导率标注为(a/m). 在该参数下, 纯晶体热导率模型值和计算值的符合程度很好, 在拟合范围外200—300 K和500—600 K温度范围内, 模型值和计算值仍然吻合良好. 该结果表明了Debye-Callaway模型的热导率框架在描述GaN晶体时具有良好的适用性, 拟合参数的引入可以有效修正或弱化具体色散关系的影响.
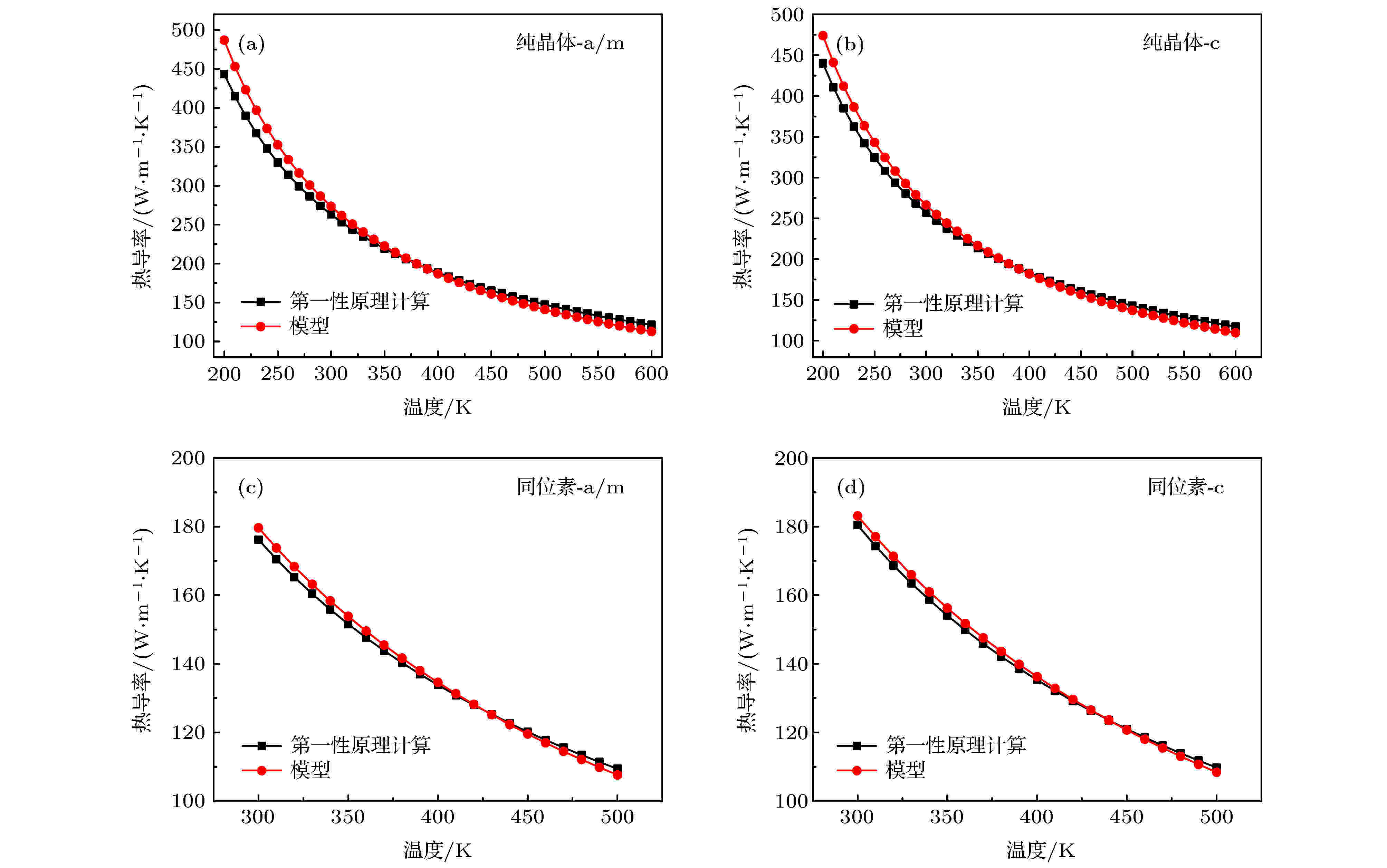图 2 基于第一性原理计算的GaN热导率数据拟合U散射率和同位素散射率模型中的参数　(a) 纯晶体垂直轴向; (b) 纯晶体沿轴向; (c) 含同位素晶体垂直轴向; (d) 含同位素晶体沿轴向
Figure2. Fitting parameters for sub-models of U scattering and isotope scattering based on thermal conductivity data from first-principles calculations: (a) Pure GaN perpendicular to polar axis; (b) pure GaN along polar axis; (c) GaN with isotopes perpendicular to polar axis; (d) GaN with isotopes along polar axis.

在图3和图4中, 将本文的薄膜热导率模型和典型实验值^[4-11,13]进行了比较. 图3 (a)中实验数据对应的GaN样品为不含同位素（或同位素增强）高纯晶体样品, 位错面密度小于10⁷ cm^–2, 无人为掺杂, 因此模型中选取了点缺陷浓度为10¹⁵ cm^–3, 厚度为7—12 μm, 模型中取厚度为9.5 μm. 该热导率数据是目前文献中仅有不含同位素(或同位素增强)GaN薄膜热导率数据的报道^[13]. 图3 (c)中实验数据对应的GaN样品为含同位素高纯晶体样品, 位错面密度小于10⁷ cm^–2, 无人为掺杂, 因此模型中选取了点缺陷浓度为10¹⁵ cm^–3, 样品厚度为6—8 μm, 模型中取厚度为7 μm. 这两组样品都是在GaN体材料上同质外延生长的, 可以认为生长过程中不存在材料和基底之间晶格常数不匹配造成的面向应力. 图3 (e)是GaN模型和体材料实验值的比较, 其中GaN样品为含同位素掺杂体材料晶体样品, 位错面密度小于10⁷ cm^–2, 有人为掺杂, 点缺陷浓度约为5 × 10¹⁸ cm^–3, 掺杂元素选为常见掺杂元素Si, 和模型预测结果符合很好. 图3结果比较显示, 模型预测的结果和实验测量结果总体符合较好, 其中不含同位素纯晶体薄膜结果中, 面向和法向热导率模型预测值略高, 热导率随温度变化的趋势也略有差异. 随温度变化趋势存在差异可能因为本文的U散射子模型中仅反映了三声子散射过程而没有考虑四声子散射的影响^[13]. 含同位素薄膜结果中, 模型预测值在实验值区间内, 热导率随温度变化的趋势也略有差异.
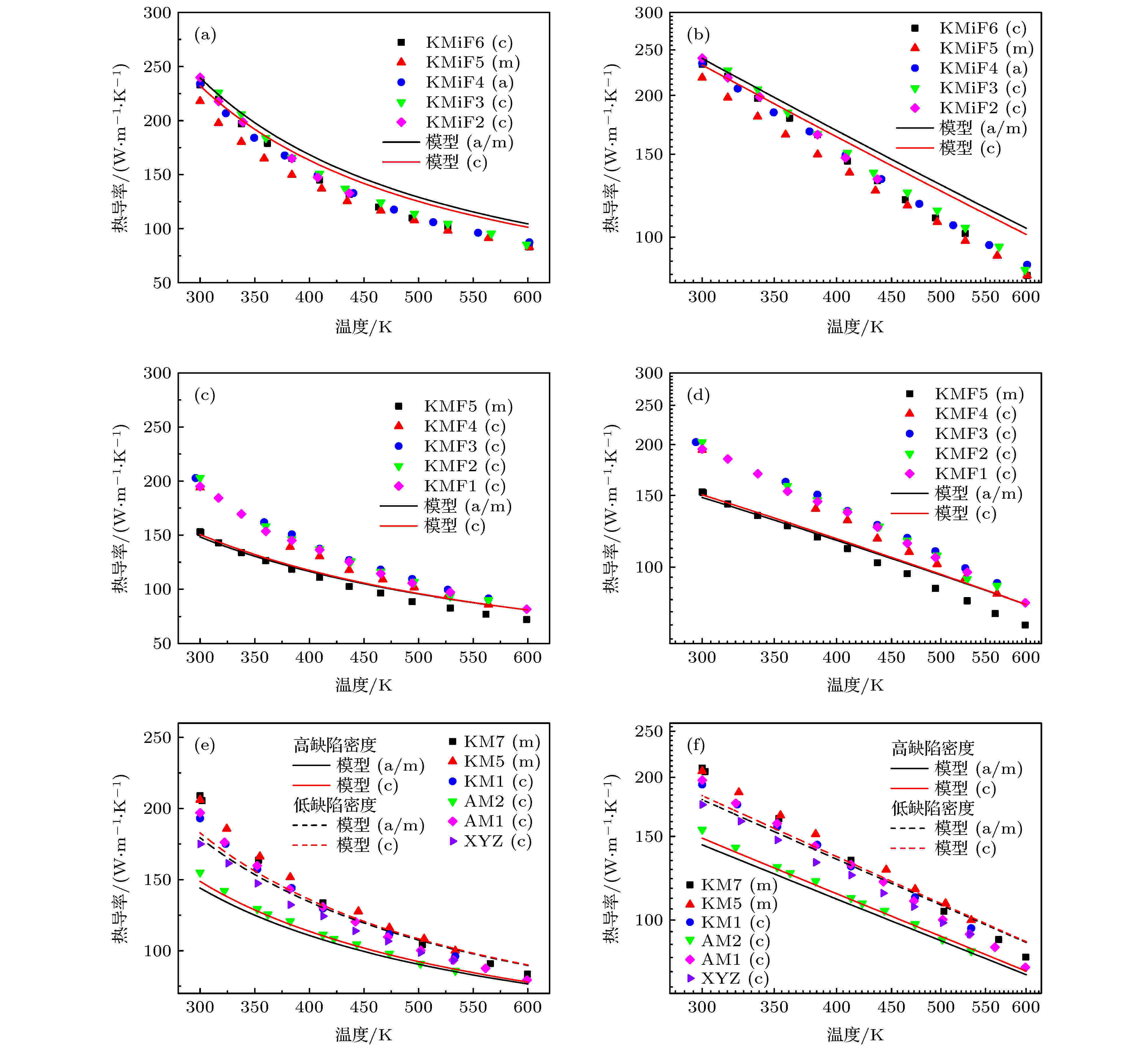图 3 热导率模型值(线)和测量值(点, 均为法向热导率)的比较.　(a), (c), (e) 分别对应三组不同的GaN薄膜样品, 实验数据来自文献 [13], 其中(a)中数据为无同位素散射的纯晶体样品. (b), (d), (f)中坐标采用了对数坐标, 图中数据分别和(a), (c), (e)相同. 样品具体表征数据可以参考表1
Figure3. Comparisons between cross-plane thermal conductivities from the model (lines) and experiments (dots) in literature^[13], in which the GaN films for (a) are pure crystal samples with enriched isotopes. Thermal conductivities of three groups GaN films are shown in (a), (c), and (e), respectively. In (b), (d), and (f), the same data are shown corresponding to (a), (c), and (e) in logarithmic coordinates. The detailed characteristics of samples can refer to Table 1.

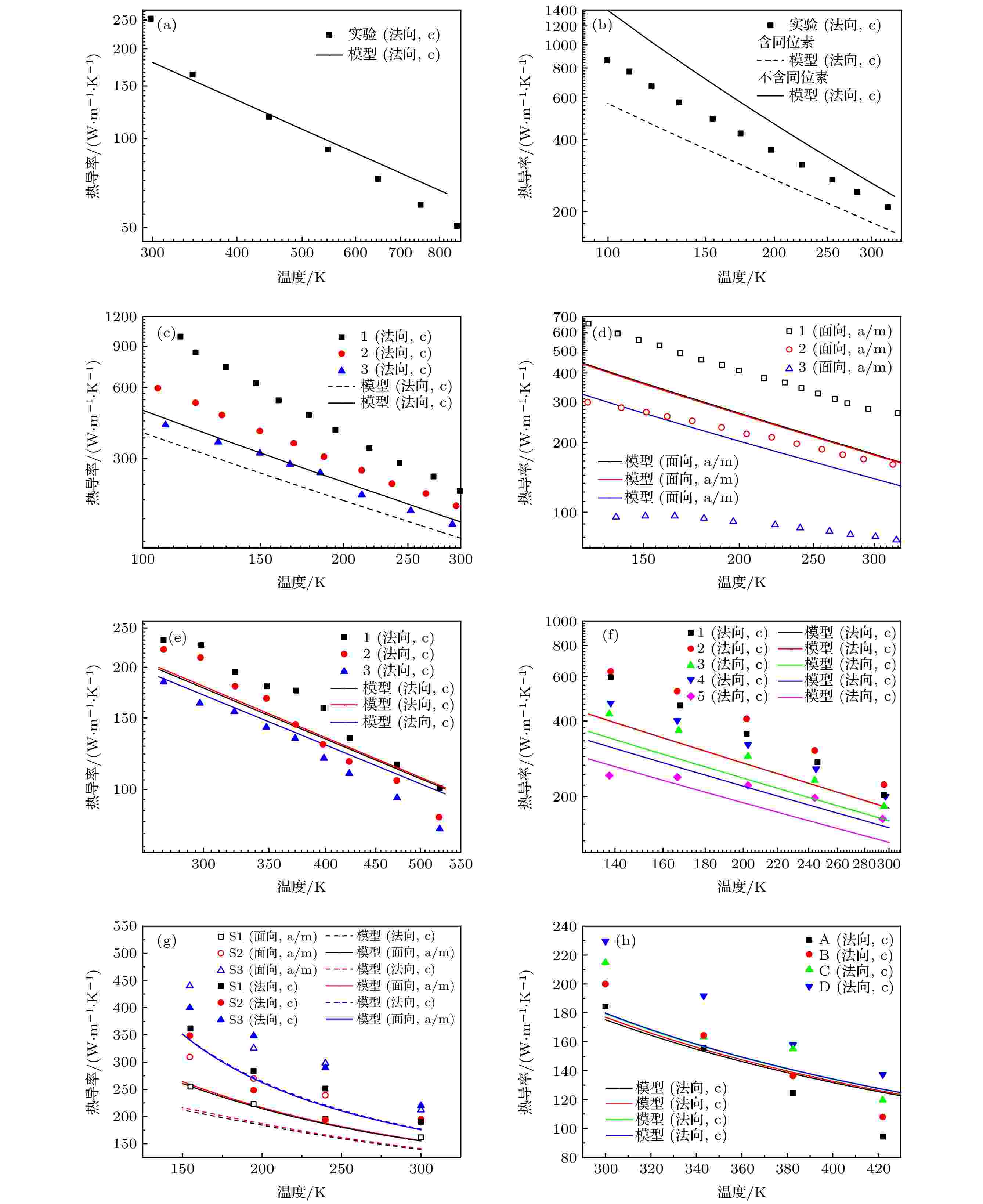图 4 热导率模型值(线)和测量值(点)的比较(线和点颜色对应), 图　(a)—(h)实验数据依次分别来自文献 [4-11]. 样品具体表征数据可以参考表1
Figure4. Comparisons between thermal conductivities from the model (lines) and experiments (dots) from literatures [4-11], the lines correspond to the dots with the same color. The detailed characteristics of samples can refer to Table 1.

图4 (a)—(h)所示是薄膜热导率模型和文献中其他实验值的比较. 文献中的GaN热导率测量值一致性较差, 表现在不同实验研究之间(文献[13]中图1 (a))和同类样品的不同测量之间(例如图4 (c)). 本文将模型和这些实验值分别进行了比较, 其中各图中的样品参数列于表1. 图4 (a)、图4 (e)、图4 (f)、图4 (h)中模型预测值和实验值符合相对较好, 特别是图4 (a)和图(e), 温度范围也在本文所侧重的300—500 K温度范围. 其他图中模型预测值较实验值普遍偏小, 实验值落在含同位素模型值和不含同位素模型值之间, 如图4 (b)所示. 还有部分实验数据与模型预测偏差过大, 比如图4 (c)中实验热导率值较模型值(不含同位素和含同位素情形)大很多, 且同一参数下的样品实验测量值也具有较大波动范围, 图4 (d)中热导率随缺陷浓度不同变化很大, 而模型预测的变化与之相比则小很多. 比较中模型预测与实验值存在较大偏差的可能原因很多. 一方面, GaN晶体生长的主流方法包括氢化物气相外延(HVPE)^[50]和氨热法^[51], 其中前者适用于在异质/同质基底上进行生长, 比如文献中生长GaN多采用的基底通常为蓝宝石或Si, 部分实验中也加入了AlN作为过渡层, 生长过程中会由于GaN和基底晶格不匹配、热膨胀系数不匹配、薄膜微小弯曲等原因受到强度未知的应力. 另一方面, 若不对生长原料进行控制, 生长的GaN薄膜都是含同位素的, 不同方法生长的薄膜中同位素比例是否和自然界中Ga的同位素比例相同, 在文献中鲜见讨论^[6]. 此外, 文献中GaN薄膜热导率测量方法有多种, 包括稳态热流法、激光闪光法、3-Omega方法、TDTR方法等, 可能进一步造成热导率测量数据的不一致性. 上述比较结果(图3和图4)表明, 本文模型和文献[13]中系统的GaN薄膜热导率测试结果总体符合较好, 和其余文献[4-11]中的部分数据符合较好, 部分数据存在较大偏差, 其可能的原因有很多, 包括实验测量的不一致性(测量方法的差异、同组实验中测量数据的波动)、材料生长方法的不同及表征的不完全(是否是同位素充足的样品和样品的应力状态等). 此外, 结合图3和图4中的热导率比较及文献中已有的讨论^[13], 基于第一性原理计算数据的热导率模型可能高估了同位素散射的影响.
2 -->

3.2.热导率受各因素的影响

本节基于GaN薄膜热导率模型讨论薄膜厚度、位错面密度、点缺陷浓度对热导率的影响. 图5为各种声子散射率的比较, 包括300 K温度下的U散射率和不同密度下的位错散射率及点缺陷散射率. 第一性原理计算中声子频率最高在20 THz附近, 但考虑到高频光学声子对热导率贡献几乎为0, 因此图中只展示了10 THz以下的低频光学声子和声学声子. 从图中可以看出, 模型中的U散射率和第一性原理计算的三声子散射率相当. 位错散射率在10¹² cm^–2时和U过程散射率处在相同的数量级. 点缺陷散射率在10¹⁸ cm^–3时已经和U过程散射率接近, 该点缺陷浓度也正是通常掺杂造成的点缺陷浓度. 此外, 比较不同位错散射和点缺陷散射模型发现, 不同模型预测的散射率比较相近, 基本在同一量级.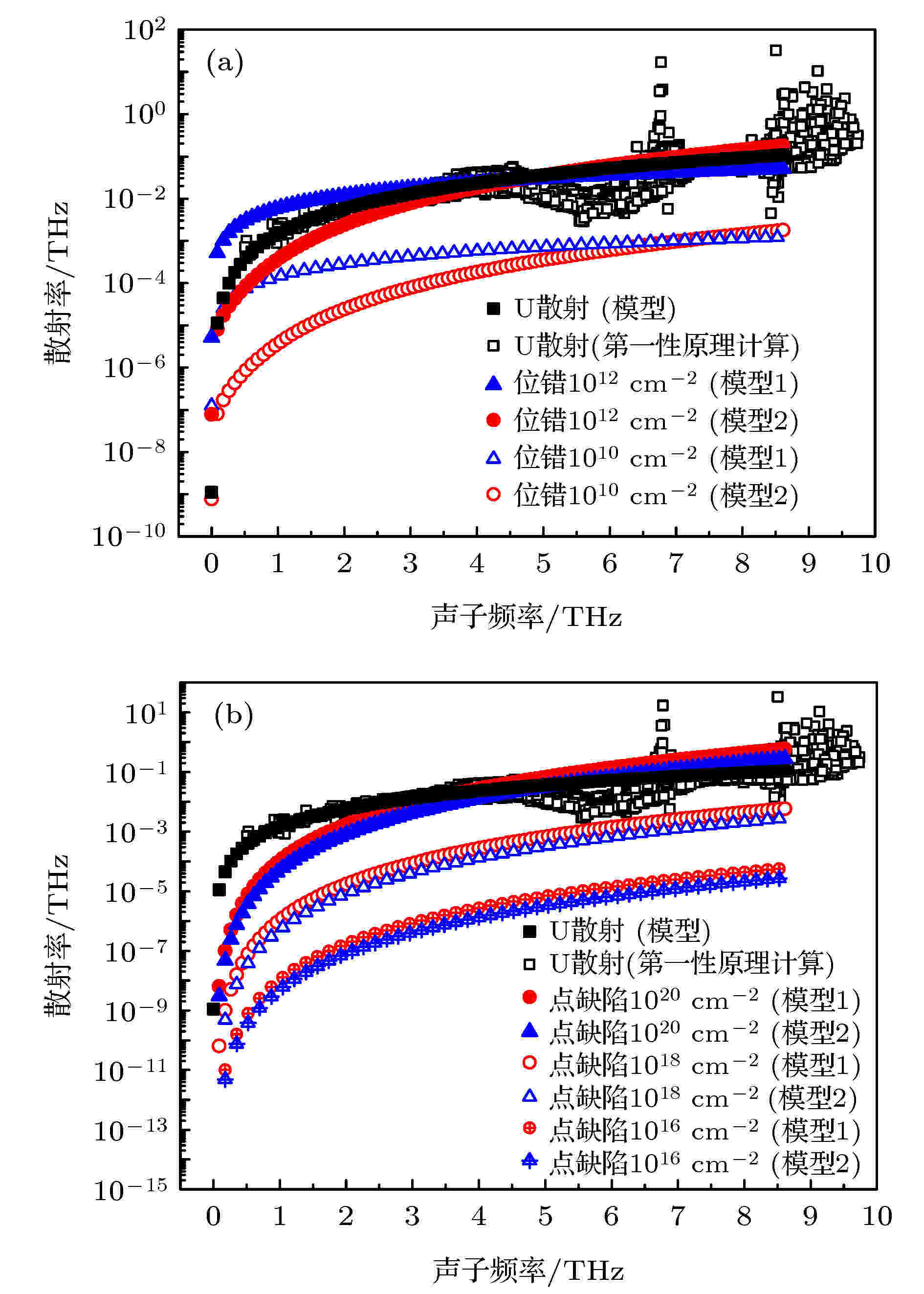
图 5 U过程声子散射率(300 K)和不同密度下参数的比较　(a)位错散射率;(b)点缺陷散射率(缺陷元素为O元素)
Figure5. Comparisons among U scattering rates at 300 K: (a) Dislocation scattering rates at two different densities; (b) point defect scattering rates at two different densities with defect atom O.

在上述基础上进一步分析了面向和法向热导率随薄膜厚度、位错面密度、点缺陷浓度的变化, 如图6所示. 图6 (a)中方形和圆形点连线表示本文模型预测的GaN薄膜归一化热导率随薄膜厚度的变化, 其中实心点连线和空心点连线分别对应无同位素纯晶体和含同位素和缺陷的情形. 两种情形下, 热导率都是在10 μm厚度左右发生明显的下降, 与第一性原理计算中随自由程变化的累积热导率结果基本一致^[22]. 同位素和缺陷会减弱尺寸效应, 但是结果显示对尺寸效应造成的影响比较小, 主要体现在100 nm附近及更小的区域. 热导率的尺寸效应体现出明显的各向异性, 对于厚度沿轴向的薄膜, 其面向热导率和法向热导率的差异一方面来自GaN热导率的本征各向异性(沿不同晶向热导率不同), 另一方面来自于边界散射的贡献, 即边界散射对法向热导率的抑制作用更强. 图6 (a)中也对比了基于文献中常用的边界散射模型((19)式)的结果, 可以看出该模型预测的面向和法向尺寸效应结果差异很小, 各向异性仅来自于平均声速的各向异性, 而无法反映边界散射造成的热导率各向异性. 图6 (b)和图6(c)是薄膜热导率分别随位错面密度和点缺陷浓度的变化, 均未考虑同位素的影响. 结果显示, 位错面密度在10¹⁰ cm^–2时已经开始造成热导率的降低, 在10¹² cm^–2时已经使热导率降低至纯晶体热导率的50%, 和散射率比较的结果一致. 点缺陷开始起作用的密度值在10¹⁸ cm^–3左右, 直至10²⁰ cm^–3使得热导率降低至纯晶体热导率的20%. 该结果表明, 通常的掺杂浓度(10¹⁸ cm^–3以上)会对GaN热导率造成显著影响.
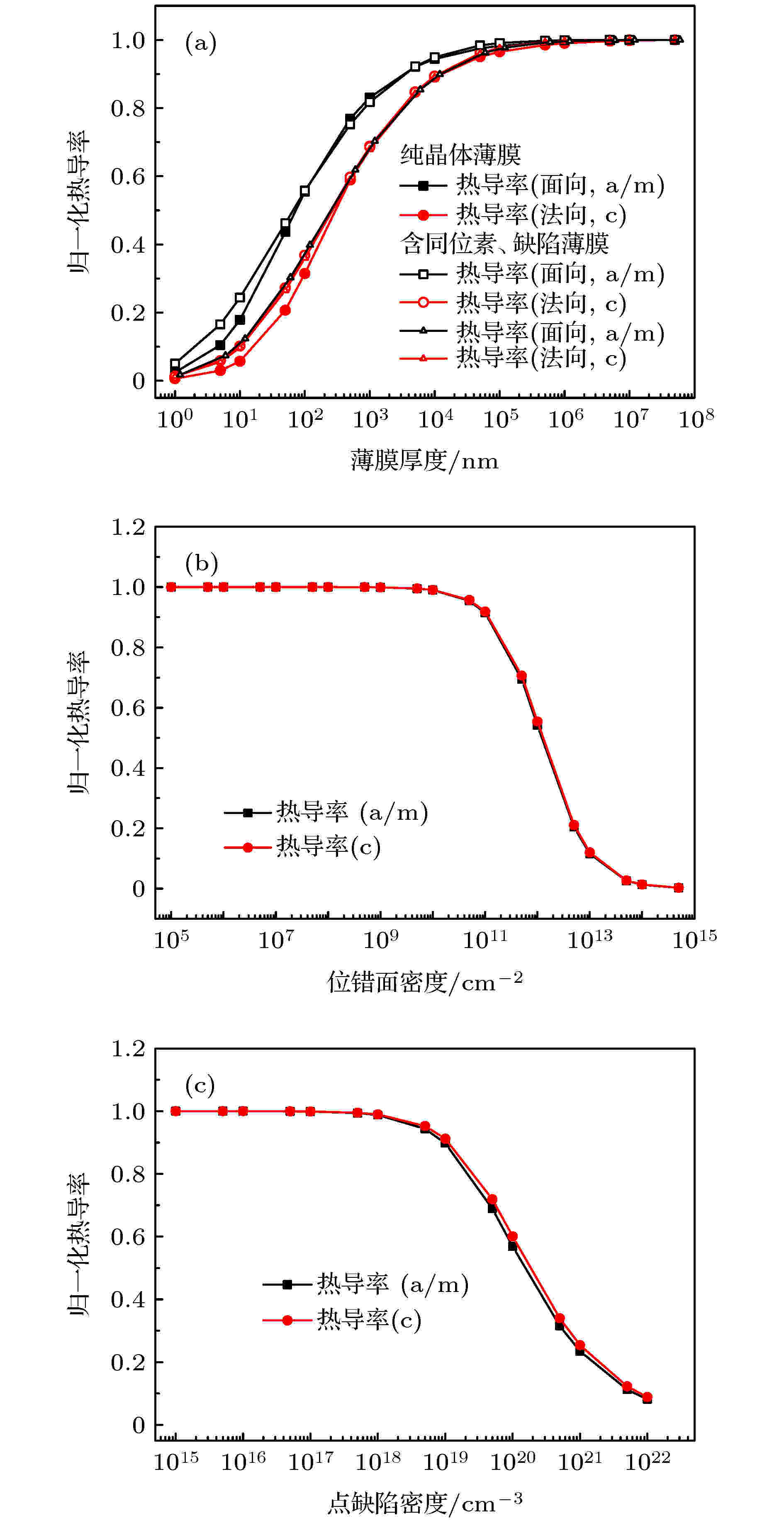图 6 室温下GaN薄膜归一化热导率随　(a) 薄膜厚度(缺陷设置为位错面密度10¹² cm^–2, 点缺陷浓度10¹⁸ cm^–3), (b) 位错面密度, (c) 点缺陷浓度的变化. (a)图中方形和圆形点线表示本文采用的抑制函数边界散射模型((23)式), 三角形点线表示文献中通常使用的边界散射模型((19)式)
Figure6. Normalized thermal conductivity of GaN films at room temperature with respect to (a) film thickness (dislocation density 10¹² cm^–2, point defect density 10¹⁸ cm^–3), (b) dislocation density, (c) point defect density. Square and circle dots represent normalized thermal conductivity with suppression function model (Eq. ((23)), and triangle dots represent normalized thermal conductivity with common used boundary scattering model (Eq. ((19)).

本文基于第一性原理计算的热导率和声子数据, 结合Debye-Callaway热导率模型, 对GaN薄膜室温以上热导率进行了系统的建模研究. 模型考虑了同位素、点缺陷、位错、薄膜厚度、应力对热导率的影响. 基于第一性原理计算数据进行拟合得到了声子间散射和声子同位素散射子模型的系数. 分别讨论了两种不同的点缺陷和位错散射率模型, 通过引入抑制函数方法, 可更为准确地描述边界散射造成的尺寸效应. 研究结果表明, 基于第一性原理计算数据拟合的热导率模型和实验测量值总体符合较好, 300 K温度附近热导率数值和随温度变化的趋势存在一些偏差. 根据实验数据进一步确认了第一性原理计算会高估同位素散射的影响. 给出了薄膜热导率随薄膜厚度、位错面密度、点缺陷浓度的具体变化关系, 热导率在10 μm厚度左右发生明显的下降, 与第一性原理计算中随自由程变化的累积热导率结果基本吻合. 同位素和缺陷会减弱尺寸效应, 但定量结果显示该影响比较小, 主要体现在100 nm附近及更小的区域. 位错和点缺陷对热导率降低起作用的面密度和密度分别为10¹⁰ cm^–2和10¹⁸ cm^–3.