删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

高温吸热管内超临界CO<sub>2</sub>传热特性的数值模拟

本站小编 Free考研考试/2021-12-29
摘要:研究超临界CO2在高温吸热管内的传热特性是将其应用于聚光太阳能热发电技术中的基础. 本文对此进行了数值模拟研究, 分析了流体温度、流动方向、系统压力、质量流率和热流密度对对流传热系数和Nu数的影响. 结果表明: 高温区 (800—1050 K) 的对流传热系数和Nu数受流动方向和系统压力的影响均很小, 但都随着质量流率的增大以及热流密度的减小而明显增大; 而随着流体温度的升高, 对流传热系数近似线性增大, Nu数则近似线性减小. 另外, 本文研究发现在高温区可忽略浮升力对传热的影响, 而由高热流密度引起的流动加速效应会明显恶化传热. 最后, 选取了八种管内超临界流体传热关联式与模拟结果进行对比, 发现使用基于热物性修正的关联式对高温区传热数据预测的结果优于使用基于无量纲数修正的关联式得到的结果, 且其中预测效果最优的关联式得到的计算结果与模拟结果之间的平均绝对相对偏差为8.1%.
关键词: 超临界CO2/
传热/
太阳能吸热管/
数值模拟

English Abstract


全文HTML

--> --> -->
1.引　言
近年来随着聚光太阳能热发电技术的不断发展, 工程上对其传热流体提出了更高的要求. CO2具有来源广泛、化学性质稳定、无毒害等优点, 并且在超临界状态 (Tc = 304 K, pc = 7.4 MPa) 下具有优越的传热特性[1]. 同时, 超临界CO2布雷顿循环在773—973 K温区的循环热效率明显高于蒸汽动力循环在此温区的循环效率[2-4]. 因此, 超临界CO2有潜力作为高温传热流体应用于聚光太阳能热发电站中[5,6]. 美国能源部在第三代聚光太阳能热发电技术路线的报告中也提出, 超临界CO2可作为新型高温传热流体应用于热发电站的吸热器中, 并指出开发新型高温传热流体的目标之一是使其在吸热器出口温度超过993 K[7].
深入认识超临界CO2在高温区的管内传热特性是将其应用于聚光太阳能热发电技术中的基础, 然而目前关于其管内传热特性的实验和数值模拟研究均大多集中在近临界点温区[8,9]. Kim等[10]对超临界CO2在垂直管内径为4.5 mm、入口温度范围为302—388 K、系统压力范围为7.5—10.3 MPa、质量流率范围为208—874 kg·m–2·s–1和热流密度范围为38—234 kW·m–2的工况下进行了对流传热实验, 研究了热流密度和质量流率对管壁面温度分布的影响. 在向上流动、热流密度适中以及质量流率较低时, 壁面温度有明显的峰值; 在向下流动时, 所有工况下壁面温度沿流动方向均单调增加; 浮升力和流动加速效应对传热有明显的影响, 并考虑了两者的作用提出了新的传热关联式. Bovard等[11]模拟研究了超临界CO2在垂直管内径为4.5和6.3 mm、入口温度为302 K、系统压力范围为6.5—8.3 MPa、质量流率范围为51—236 kg·m–2·s–1和热流密度范围为52—85 kW·m–2的管内传热特性, 得到提高质量流率和系统压力可削弱浮升力和流动加速效应对传热的影响, 也提出了考虑两种效应的新传热关联式.
然而, 将超临界CO2作为传热流体应用在塔式聚光太阳能热发电站中, 其吸热器入口温度通常要求高于773 K, 目前鲜少有关于高温区超临界CO2管内传热特性研究的公开报道[8]. Qiu等[12]对超临界CO2在槽式太阳能吸热器中的传热特性进行了数值计算, 所研究的入口温度范围为315—773.15 K、系统压力为9和20 MPa, 结果表明浮升力作用使圆管横截面出现了明显的二次涡流现象, 且近临界点温区的二次涡流速度比高温区大一个数量级. 刘占斌等[13]模拟研究了六种泡沫材料填充方式对吸热管内超临界CO2流动与换热性能以及管壁温度分布的影响. 所研究的入口温度为813 K、系统压力为20 MPa和热流密度为500 kW·m–2, 结果表明环形填充方式 (沿管内壁填充) 的流动换热综合性能最优、净吸热量最大、管壁最高温度最低且温度分布最均匀.
为了进一步研究超临界CO2在高温吸热管内的传热特性, 本文首先分析CO2在高温区与近临界点温区的热物性区别, 再基于ANSYS FLUENT软件建立吸热管内超临界CO2对流换热的三维数值模型, 分析流体温度、流动方向、系统压力、质量流率和热流密度等工况条件对对流传热系数和Nu数的影响规律, 揭示不同工况条件下的传热机理. 然后, 判别浮升力和流动加速效应在高温区对传热的影响情况, 并与八种管内超临界流体传热关联式进行对比, 找出预测效果较优的关联式. 研究结果可为超临界CO2太阳能吸热器的优化设计和安全稳定运行提供理论参考.
2.超临界CO2的热物理性质
为了了解CO2在近临界点温区 (293—350 K) 和高温区 (800—1050 K) 的热物性区别, 图1给出了CO2在压力7.5 MPa、温度范围293—1050 K下的密度、比热、热导率和黏度的变化情况[14]. 可见, CO2的热物性在近临界点温区随温度剧烈变化, 其中密度和黏度在临界点附近急剧下降, 比热和热导率则在临界点附近出现极大值. 而在高温区, CO2的热物性与近临界点温区相比变化不那么明显 (特别是比热), 且热导率和黏度在两个温区呈现相反的变化趋势. 这些因素均可能使超临界CO2在两个温区呈现不同的传热特性. 另外, 图2所示的是在高温区不同临界压力 (7.5—9 MPa) 下CO2热物性的变化情况[14]. 可见, 随着压力增大, 各热物性均有所提高, 但除密度外, 压力对热物性的影响均很小.
图 1 CO2在p = 7.5 MPa下的热物性变化　(a) T = 293—1050 K; (b) T = 293—350 K; (c) T = 800—1050 K
Figure1. Properties of CO2 at p = 7.5 MPa: (a) T = 293–1050 K; (b) T = 293–350 K; (c) T = 800–1050 K.

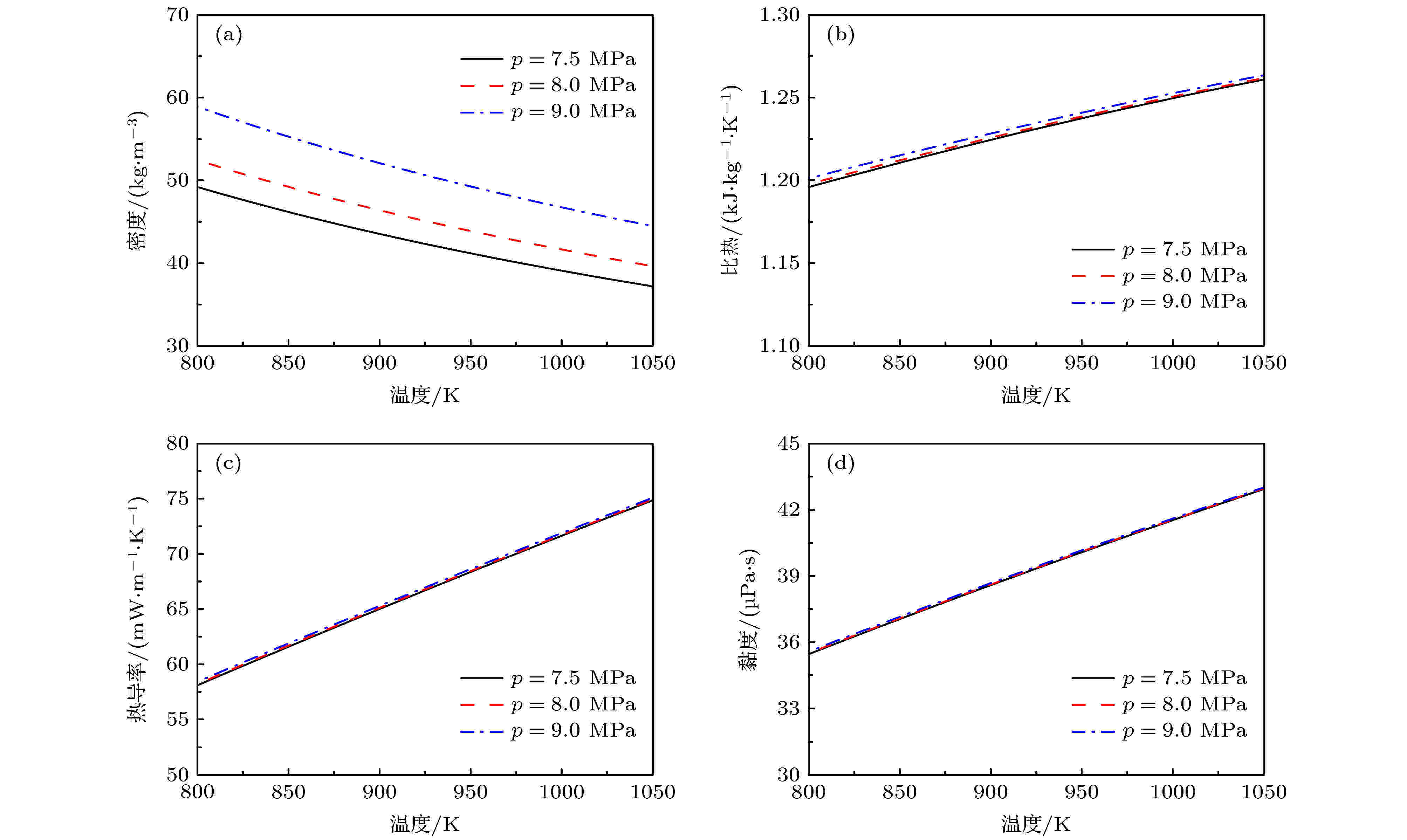图 2 CO2在高温区T = 800—1050 K, p = 7.5—9 MPa下的热物性变化　(a) 密度; (b) 比热; (c) 热导率; (d) 黏度
Figure2. Properties of CO2 at high temperature region of T = 800–1050 K with p = 7.5–9 MPa: (a) Density; (b) specific heat; (c) thermal conductivity; (d) viscosity.

3.传热模型
2
3.1.数值模型
-->

3.1.数值模型

本文所研究的吸热管, 管径为6 mm, 管长为500 mm的圆管, 计算过程中忽略圆管壁厚, 几何模型如图3所示.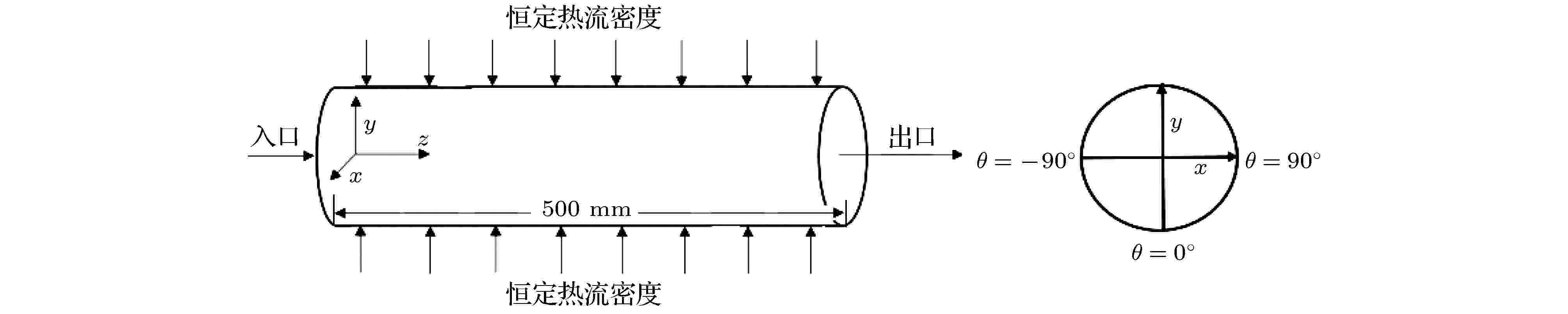
图 3 吸热管几何模型
Figure3. Geometric model of the solar receiver tube.

假设管内流动为稳态, 忽略吸热管与外界环境的换热. 对于高温区超临界CO2的流动传热数值计算, Qiu等[12]和刘占斌等[13]的计算结果显示, 采用标准k-ε湍流模型[15]可获得准确的计算结果. 因此, 本文采用标准k-ε湍流模型进行数值计算, 模型的控制方程可表示如下.
质量方程:
$\frac{\partial }{{\partial {x_i}}}\left ( {\rho {u_i}} \right) = 0. $
动量方程:
$\begin{split}&\frac{\partial }{{\partial {x_j}}}\left ( {\rho {u_i}{u_j}} \right) = \rho {g_i} - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\bigg[(\mu + {\mu _{\rm{t}}}) \\& \qquad \qquad \times \left ( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_l}}}{{\partial {x_l}}}} \right) \bigg]. \end{split}$
能量方程:
$\frac{\partial }{{\partial {x_i}}}\left ( {\rho {u_i}{c_{\rm{p}}}T} \right) = \frac{\partial }{{\partial {x_i}}}\left ( {\lambda \frac{{\partial T}}{{\partial {x_i}}}} \right) . $
湍动能k方程:
$\frac{\partial }{{\partial {x_i}}}\left ( {\rho {u_i}k} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left ( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right) \frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + {G_{\rm{b}}} - \rho \varepsilon . $
耗散速率ε方程:
$\begin{split}\frac{\partial }{{\partial {x_i}}}\left ( {\rho {u_i}\varepsilon } \right) =\;& \frac{\partial }{{\partial {x_j}}}\left[ {\left ( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right) \frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] \\&+ {c_1}\frac{\varepsilon }{k}\left ( {{G_k} + {c_3}{G_{\rm{b}}}} \right) - {c_2}\rho \frac{{{\varepsilon ^2}}}{k}. \end{split}$
这里
${G_k} = - \rho \frac{{\partial {u_j}}}{{\partial {x_i}}}\left ( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) ; $
${G_{\rm{b}}} = \beta {g_i}\frac{{{\mu _{\rm{t}}}}}{{P{r_{\rm{t}}}}}\frac{{\partial T}}{{\partial {x_i}}};$
式中, ρ为密度 (kg·m–3); g为重力系数 (m·s–2); u为速度 (m·s–1); δij为克罗内克函数, 当i = j时, δij = 1, 当i ≠ j时, δij = 0; p为压力 (Pa); μ为动力黏度 (Pa·s); μt为湍流黏度, μt = ρCμk2/ε; cp为比热 (J·kg–1·K–1); k为湍动能; ε为耗散速率; T为温度 (K); λ为热导率 (W·m–1·K–1); β为热膨胀系数 (K–1); σk和σε分别为湍动能和耗散速率对应的湍流普朗特数; c1, c2, Cμ, Prt均为模型经验常数; 湍流模型参数具体设置[12]为σk = 1.0, σε = 1.3, c1 = 1.44, c2 = 1.92, Cμ = 0.09, Prt = 0.85.
2
3.2.边界条件和求解设置
-->

3.2.边界条件和求解设置

模型的边界条件设置如下.
1) 入口: 采用质量流量入口边界条件, 速度垂直于入口截面, 流量研究范围为G = 200—500 kg·m–2·s–1.
2) 出口: 采用压力出口边界条件, 流动出口的绝对压力研究范围为p = 7.5—9 MPa.
3) 壁面: 设置为静态无滑移边界条件, 给定恒定热流密度, 研究范围为q = 100—800 kW·m–2.
使用ANSYS FLUENT软件进行吸热管内超临界CO2传热特性的数值计算, 采用SIMPEC算法求解速度与压力的耦合方程, 动量和能量方程采用QUICK格式进行离散, 湍动能和耗散速率方程采用二阶迎风格式. 模型中的CO2热物性数据来自美国国家标准与技术研究所 (NIST) 的数据库, 通过在ANSYS FLUENT中激活nist-real-gas-model功能进行直接调用. 当各控制方程的残差小于10–6, 且出口流体温度和壁面温度没有明显变化, 则认为计算收敛.
2
3.3.网格无关性验证和模型验证
-->

3.3.网格无关性验证和模型验证

采用ANSYS ICEM软件对图3吸热管三维模型进行网格划分, 网格生成效果如图4所示. 由于近壁面位置的温度梯度和速度梯度较大, 所以对近壁面处的网格进行了加密, 保证近壁面处的无量纲壁面距离 (y+) 小于1. 为了对计算网格进行无关性验证, 分别对比了网格数量为2652250, 1332250, 841000, 462250和196000时 (网格质量均大于0.7), 模拟所得的出口截面壁面温度 (Tw,o) 和对流传热系数 (ho), 如表1所列. 可见, 算例1和算例3的Tw,o和ho相对偏差分别仅为0.07%和0.14%. 因此, 在同时考虑计算精度和运算时间的情况下, 最终选择了网格数量为841000的网格进行后续的数值计算. 其中, 对流传热系数h和对应的努塞尔数Nu可由下式计算得到:
算例网格数量Tw,o/KTw,o的相对偏差/%ho/(kW·m–2·K–1)ho的相对偏差/%
126522501441.901236.70
213322501442.20.021236.40.02
38410001442.90.071235.00.14
44622501445.10.221230.10.54
51960001448.80.481223.31.09


表1网格无关性验证结果
Table1.Verification for grid independence.

图 4 吸热管三维模型网格划分 (网格数量: 841000)
Figure4. Mesh generation of the three-dimensional solar receiver tube (grid quantity: 841000).

$h = \frac{q}{{{T_{\rm{w}}} - {T_{\rm{b}}}}},$
$Nu = \frac{{hD}}{\lambda },$
式中, q为壁面热流密度 (kW·m–2); D为吸热管直径 (m); Tw为壁面温度; Tb为流体温度, 可由下式计算得到
${T_{\rm{b}}} = \frac{1}{A}\int {{T_{\rm{b}}}{\rm{d}}A} ,$
其中A为吸热管横截面流体面积 (m2).
另外, 为了验证模型的准确性, 将三种工况条件下的计算结果与文献[16]中相同工况条件下的实验数据进行了对比, 如图5所示. 可见, 三种工况条件的计算结果与实验数据均符合较好, 且壁面温度和对流传热系数的平均相对偏差分别为0.85%和3.35%, 从而验证本文的数值计算模型是可靠的.
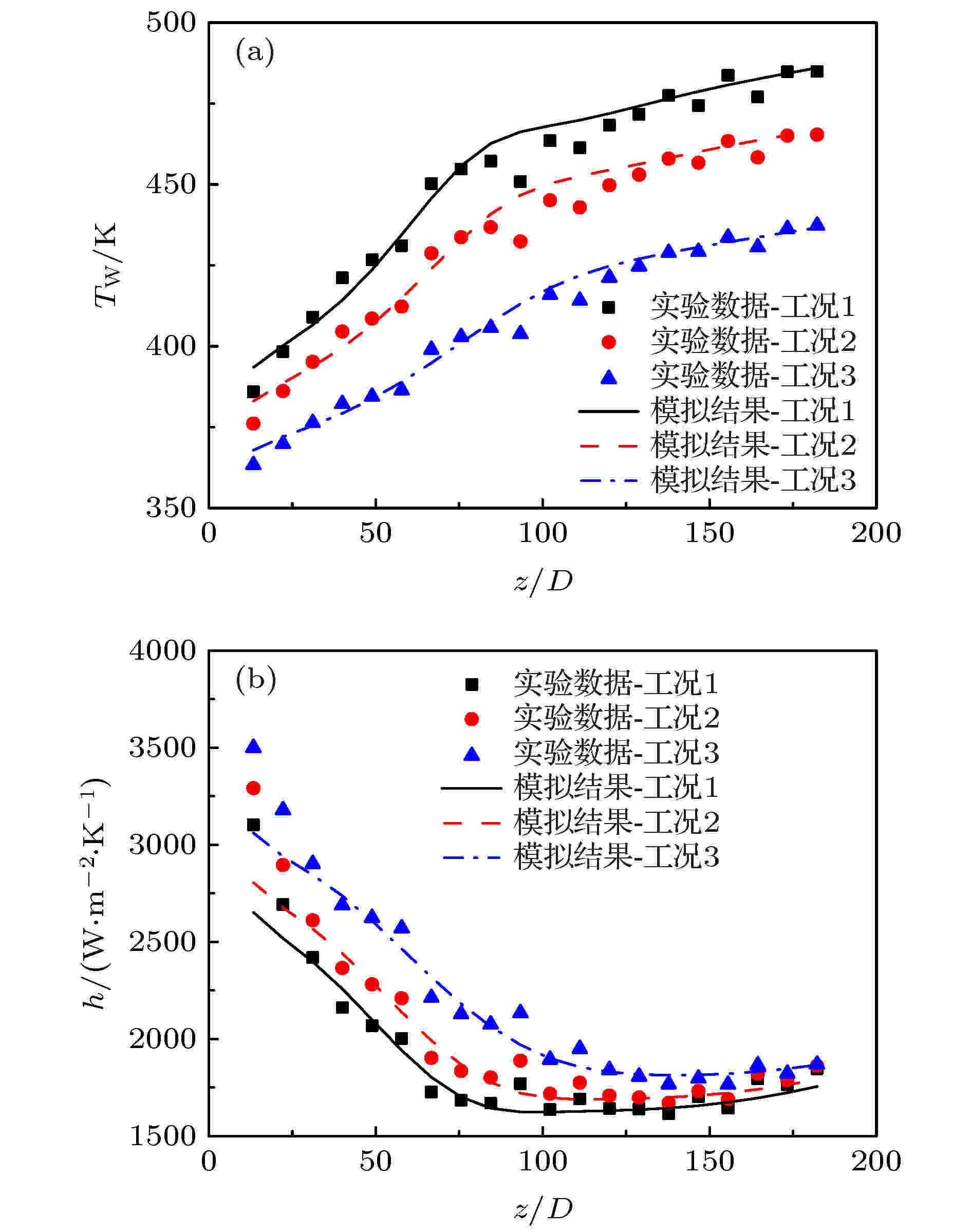图 5 模型计算结果与文献[16]实验数据的对比　(a) 壁面温度; (b) 对流传热系数; 其中, 工况1, G = 868 kg·m–2·s–1, q = 231.0 kW·m–2, p = 9.22 MPa; 工况2, G = 873 kg·m–2·s–1, q = 216.2 kW·m–2, p = 9.09 MPa; 工况3, G = 874 kg·m–2·s–1, q = 191.8 kW·m–2, p = 8.71 MPa
Figure5. Comparisons between numerical results and experimental data of Ref. [16]: (a) Wall temperature; (b) convective heat transfer coefficient. Case 1: G = 868 kg·m–2·s–1, q = 231.0 kW·m–2, p = 9.22 MPa. Case 2: G = 873 kg·m–2·s–1, q = 216.2 kW·m–2, p = 9.09 MPa. Case 3: G = 874 kg·m–2·s–1, q = 191.8 kW·m–2, p = 8.71 MPa.

4.结果与分析
2
4.1.流体温度和流动方向的影响
-->

4.1.流体温度和流动方向的影响

实际工程应用中, 超临界CO2在吸热管内的流动方向存在多种情况, 本文主要研究其在管内进行垂直向上、垂直向下和水平方向流动时的传热特性变化情况. 图6为在G = 300 kg·m–2·s–1, q = 500 kW·m–2和p = 7.5 MPa的工况下, 三种流动方向在高温区对管内超临界CO2传热特性的影响. 可见, 三种流动方向的对流传热系数均随流体温度的升高而近似线性的增大, 其中垂直向下流动的对流传热系数最高, 而垂直向上流动的对流传热系数最低, 但它们的数值偏差不大, 其绝对相对偏差小于0.68%. 这是因为CO2的密度在高温区会随着流体温度的升高而减小, 在定质量流率 (G = ρu) 下则使得流速增大, 从而增强了湍流强度, 导致对流传热系数随流体温度的升高而增大. 另外, 根据这三种极端流动方向对传热的影响结果, 可推断其他倾斜角度的流动方向对高温区超临界CO2吸热管内传热特性的影响应该也不大. 从图6还可得到Nu数随流体温度的升高是减小的, 与对流传热系数的趋势相反, 这是因为CO2的热导率在高温区是随流体温度的升高而增大的, 从而说明在高温区Nu数受CO2热导率的影响比对流传热更为明显.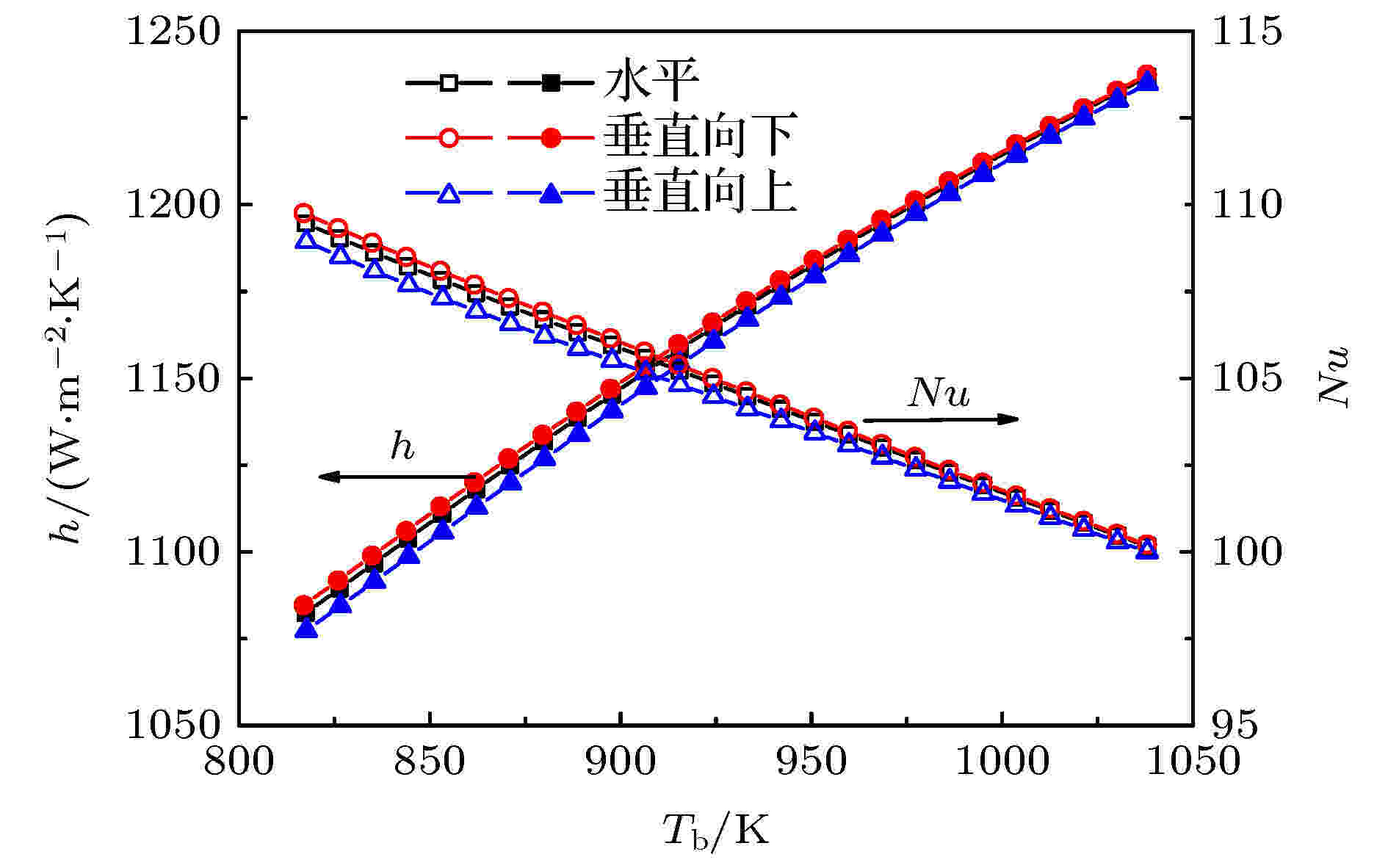
图 6 管内流体温度和流动方向在高温区对超临界CO2传热特性的影响
Figure6. Effects of fluid temperature and flow direction on heat transfer of supercritical CO2 at high temperature region.

图7给出了在z = 250 mm横截面上的管内流体温度和湍动能云图以及径向速度矢量图. 对于垂直向上和垂直向下流动, 从图7(a)可见, 流体的温度分布均呈径向对称, 最低流体温度位于管截面的中心, 且向上流动的流体径向温度梯度略高于向下流动的流体径向温度梯度. 从图7(b)可见, 垂直向上和垂直向下流动的流体径向速度分布均呈现M形. 这是由于径向温度梯度的存在使得管截面流体产生径向密度梯度, 管中心流体由于温度较低密度增大, 导致其流速降低, 而近壁面流体由于温度较高密度减小, 反而促使其流速增大, 从而形成“M”形径向速度分布. 另外, 对于吸热管内向上流动, 浮升力效应会降低边界层剪切力, 减弱湍流涡流的产生和扩散[17], 从而削弱对流换热. 而对于向下流动, 浮升力效应的影响则相反, 所以向下流动的对流传热系数高于向上流动的对流传热系数. 但从图7(c)可见, 它们的湍动能分布差别不大, 所以它们的对流传热系数也偏差不大. 而对于水平流动, 从图7(a)可见, 其流体温度分布并非呈径向对称, 最低流体温度位置是略微的向管底部偏移. 从图7(b)可见, 在水平流动的流体径向速度分布中, 管截面两边的流体是沿管壁面向上运动, 然后再沿管中心下降, 从而在管截面两边形成二次涡流. 而二次涡流的生成, 使得最低流体温度位置向管底部偏移. 另外, 水平流动的流体径向速度比垂直向上和向下流动的径向速度大一个数量级, 且水平流动的管截面两侧流体径向速度明显高于其他管截面区域. 从图7(c)可见, 虽然水平流动的流体径向速度较高, 但其湍动能反而比垂直向下流动略低. 这可能是因为水平流动中剪切力大多用于加速管截面两侧流体速度, 消耗了其湍动能. 综上所述, 三种流动方向的湍流度和传热效率均相差不大.
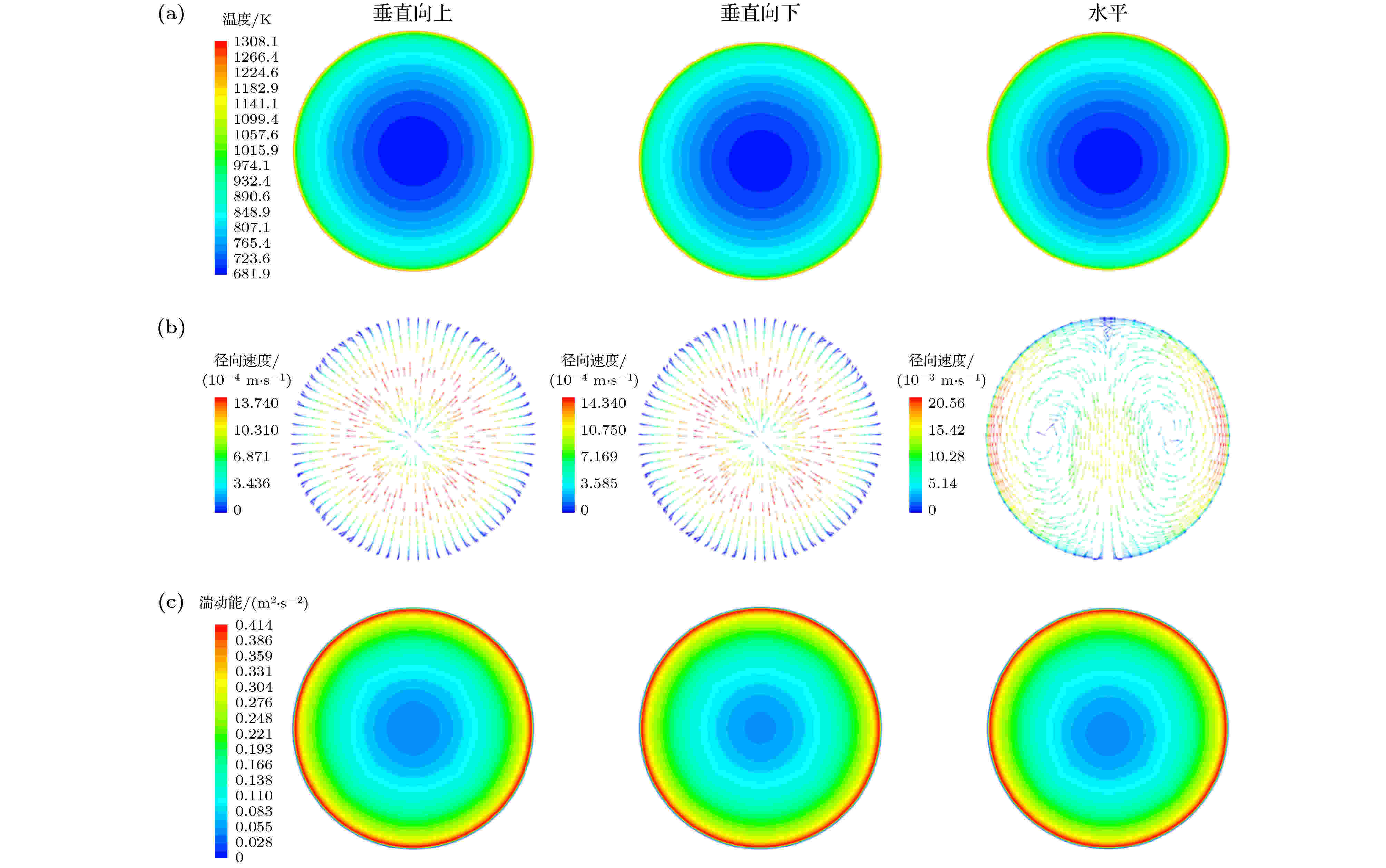图 7 z = 250 mm管截面平面上三种流动方向的流体　(a) 温度云图; (b) 径向速度矢量图; (c) 湍动能云图
Figure7. (a) Temperature contours, (b) radial velocity fields, (c) turbulence kinetic energy contours on the plane of z = 250 mm for three flow directions.

2
4.2.系统压力的影响
-->

4.2.系统压力的影响

图8为在G = 300 kg·m–2·s–1, q = 500 kW·m–2和垂直向上流动的工况下, 系统压力在高温区对管内超临界CO2传热特性的影响. 可见, 系统压力在高温区对对流传热系数的影响极小, 随着系统压力的增大, 对流传热系数最多仅减小0.17%; 而Nu数随系统压力的增大也仅有略微的减小, 最大减小量为0.51%, 且流体温度越高系统压力的影响越小. 由图2可见: 在高温区CO2的密度会随着系统压力的增大而增大, 在定质量流率下, 会使得流体流速减小, 从而削弱传热; 但另一方面CO2的热导率也会随着系统压力的增大而增大, 从而强化传热. 两者综合作用, 使得对流传热系数的变化不大. 然而, 图2也显示在高温区系统压力对CO2密度的影响明显强于热导率, 但它们对对流传热系数的影响却相当, 说明在高温区和本文所研究的系统压力范围 (7.5—9 MPa), CO2热导率对其传热特性起着重要的作用, 这也与4.1节中Nu数随流体温度增大而减小的原因一致.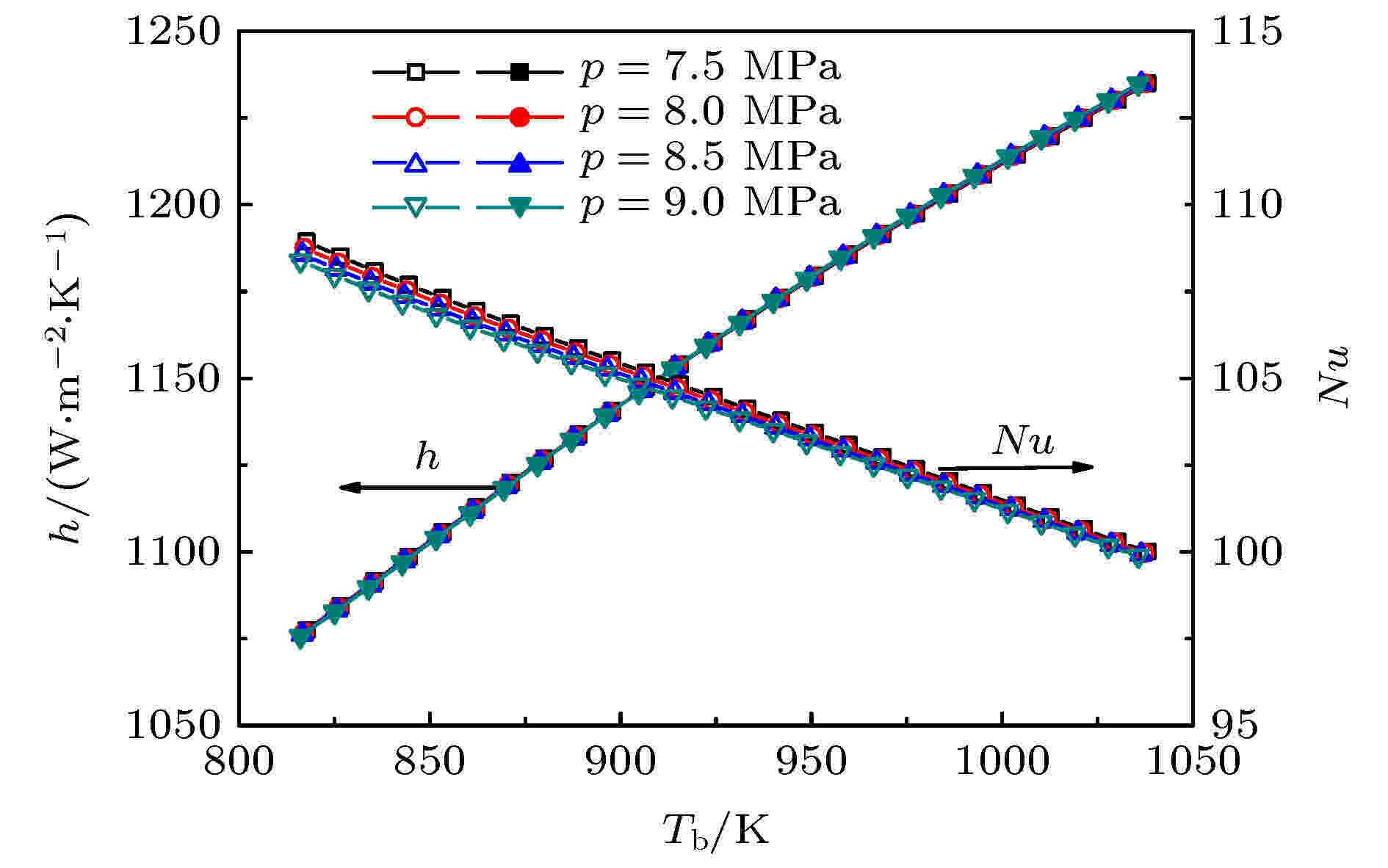
图 8 系统压力在高温区对超临界CO2传热特性的影响
Figure8. Effect of pressure on heat transfer of supercritical CO2 at high temperature region.

2
4.3.质量流率的影响
-->

4.3.质量流率的影响

图9为在p = 7.5 MPa, q = 500 kW·m–2和垂直向上流动的工况下, 流体质量流率在高温区对管内超临界CO2传热特性的影响. 可见, 高温区的对流传热系数和Nu数均随着质量流率的增大而明显增大. 这是因为质量流率越大, 流体流速也越大, 使得流体的湍流扩散速率增大, 从而增强了对流换热效应, 导致对流传热系数增大. 另外, 管壁面边界层厚度也会随着流体流速增大而减小, 导致热阻变小, 同样强化了传热.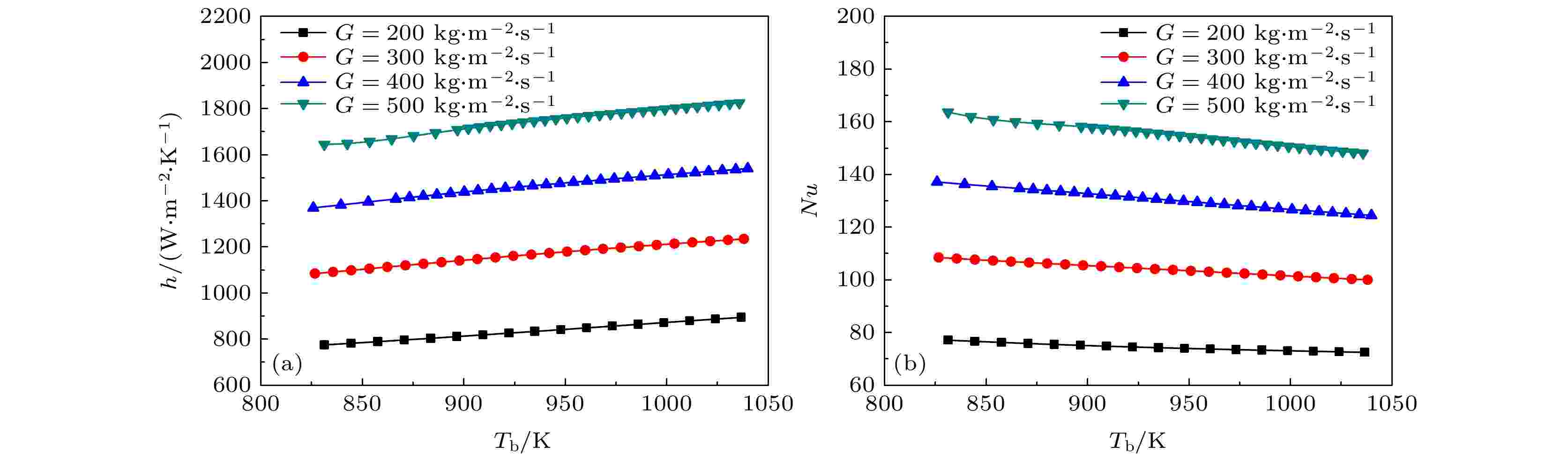
图 9 质量流率在高温区对超临界CO2传热特性的影响
Figure9. Effects of mass flux on heat transfer of supercritical CO2 at high temperature region.

2
4.4.热流密度的影响
-->

4.4.热流密度的影响

图10为在G = 300 kg·m–2·s–1, p = 7.5 MPa和垂直向上流动的工况下, 壁面热流密度在高温区对管内超临界CO2传热特性的影响. 可见, 在高温区随着热流密度的增大, 对流传热系数和Nu数均减小, 且热流密度越大其影响程度越明显. 由于随着壁面热流密度增大, 近壁面的流体温度会急剧升高, 而流体温度升高会造成其体积膨胀, 引发流动加速效应[17]. 流动加速效应所形成的速度梯度方向与流动方向是相反的[18], 这会导致近壁面处的湍流度减小. 当近壁面处的低密度流体层达到足够厚, 会使得湍流边界层转化为层流边界层, 从而导致对流传热被削弱.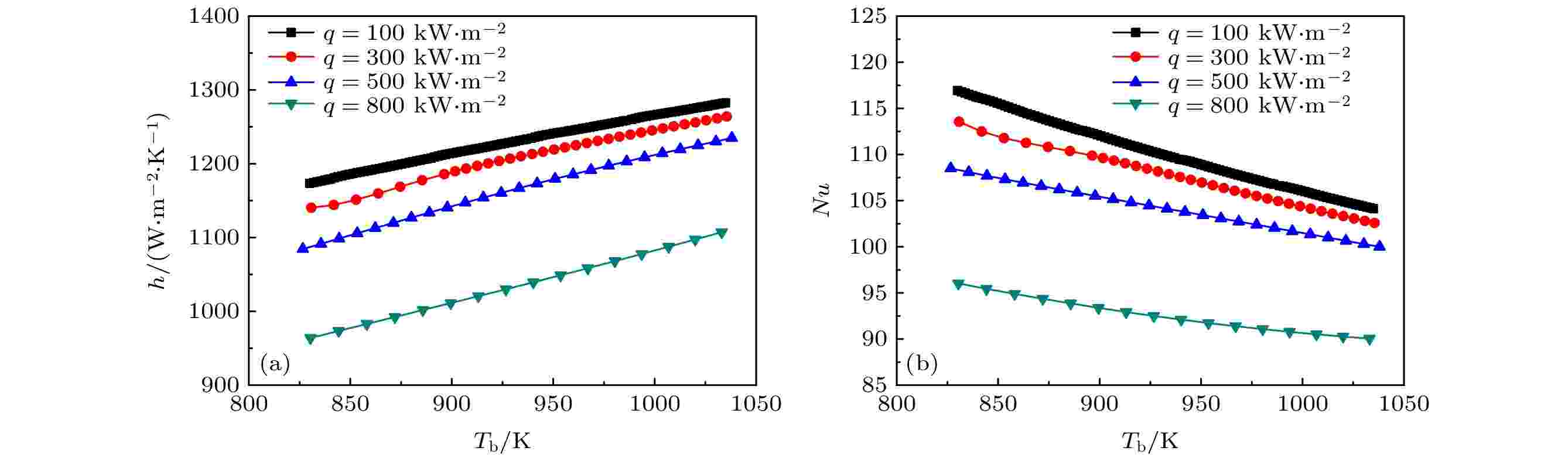
图 10 热流密度在高温区对超临界CO2传热特性的影响
Figure10. Effect of heat flux on heat transfer of supercritical CO2 at high temperature region.

2
4.5.浮升力和流动加速效应的影响
-->

4.5.浮升力和流动加速效应的影响

根据现有文献[19-22]可知, 浮升力和流动加速效应在近临界点温区对管内超临界CO2传热特性具有重要的作用. 然而, 目前不同文献对两种效应的定义各有不同, 本文采用Liu等[17]提出的判断标准, 分析在高温区浮升力和流动加速效应对管内超临界CO2传热特性的影响情况. 本文所使用的浮升力因子 (Bu) 和流动加速因子 (Ac) 定义如下: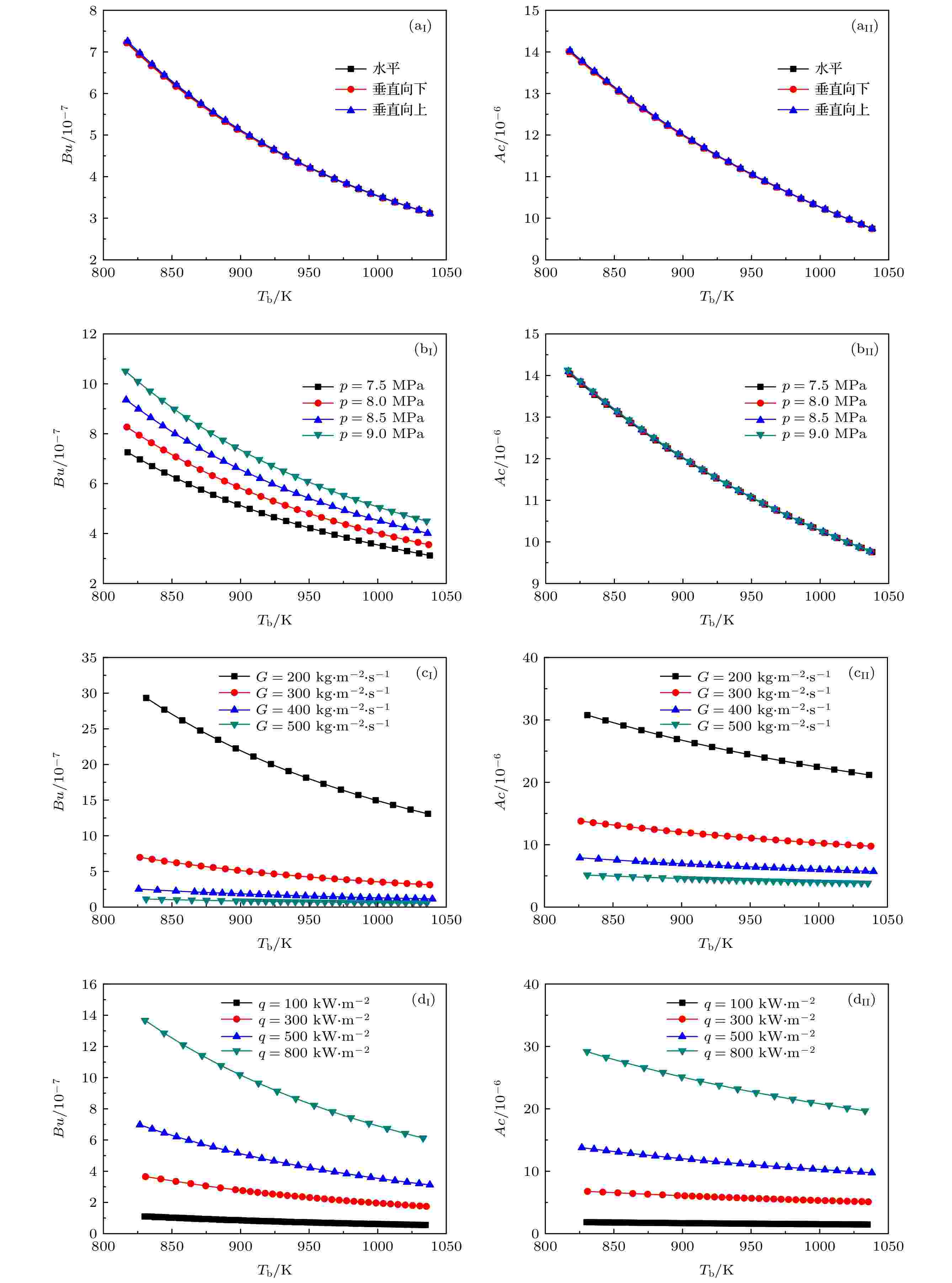
$Bu = \frac{{G{r_{\rm{m}}}}}{{Re_{\rm{b}}^{2.625}Pr_{\rm{w}}^{0.4}}}{\left ( {\frac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{w}}}}}} \right) ^{0.5}}\left ( {\frac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{b}}}}}} \right) ,$
$Ac = \frac{{4{q^ + }}}{{Re_{\rm{b}}^{0.625}}}{\left ( {\frac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{w}}}}}} \right) ^{0.5}}\left ( {\frac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{b}}}}}} \right) ,$
式中,
$G{r_{\rm{m}}} = \frac{{\left ( {{\rho _{\rm{b}}} - {\rho _{\rm{m}}}} \right) {\rho _{\rm{b}}}g{D^3}}}{{\mu _{\rm{b}}^2}},$
${\rho _{\rm{m}}} = \frac{1}{{{T_{\rm{w}}} - {T_{\rm{b}}}}}\int_{{T_{\rm{b}}}}^{{T_{\rm{w}}}} {\rho {\rm{d}}T} ,$
${q^ + } = \frac{{q{\beta _{\rm{b}}}}}{{G{c_{{\rm{p,b}}}}}},$
$R{e_{\rm{b}}} = {{GD}}/{{{\mu _{\rm{b}}}}},$
$P{r_{\rm{w}}} = {{{\mu _{\rm{w}}}{c_{{\rm{p,w}}}}}}/{{{\lambda _{\rm{w}}}}}.$
Liu等[17]指出当Bu < 1.3 × 10–5和Ac < 3.3 × 10–6时, 浮升力和流动加速效应对传热的影响小于3%, 可以忽略不计. 本文计算了不同工况条件下的Bu和Ac, 如图11所示. 如图11(aI) 和图11(aII) 所示, 在高温区随着流体温度的升高, Bu和Ac均减小, 流动方向对它们几乎没有影响, 这与流动方向对对流传热系数的影响规律一致 (图6). 如图11(bI) 和图11(bII) 所示, 随着系统压力增大, Bu会增大, 而Ac几乎不变. 但所研究系统压力范围的Bu值均远低于其阈值1.3 × 10–5, 说明此时浮升力效应对传热的影响不大, 因此即使Bu值随着系统压力的增大而增大, 对流传热系数受系统压力的影响仍很小 (图8). 如图11(cI) 和图11(cII) 所示, Bu和Ac均随着质量流率的增大而减小, 这是因为Re数会随着质量流率的增大而增大, 由 (11) 式和 (12) 式可见, Re数的增大会减小Bu和Ac. 而对于垂直向上流动, 浮升力和流动加速效应会恶化传热, Bu和Ac值的减小, 使得流体流速增大强化传热的程度高于浮升力和流动加速效应恶化传热的程度, 从而促使对流传热系数随着质量流率的增大而增大 (图9). 如图11(dI) 和图11(dII) 所示, 随着热流密度的增大, Bu和Ac均增大, 这是因为壁面和流体的温差会随着热流密度的增大而增大, 使得管内流体密度梯度增大, 从而导致浮升力和流动加速效应增强, 削弱了对流传热, 这与热流密度对对流传热系数的影响一致 (图10).
图 11 (a) 流动方向、(b) 系统压力、(c) 质量流率、(d) 热流密度在高温区对 (I) Bu和 (II) Ac的影响
Figure11. Effects of (a) flow direction, (b) pressure, (c) mass flux, (d) heat flux on (I) Bu and (II) Ac at high temperature region.

图12为在本文所研究的工况条件下, Bu和Ac的分布图. 可见, 所有工况的Bu值均远低于其阈值1.3 × 10–5, 而除了最低热流密度工况 (G = 300 kg·m–2·s–1, q = 100 kW·m–2, p = 7.5 MPa和垂直向上流动) 外, 其余工况的Ac值均高于其阈值3.3 × 10–6. 说明在本文所研究的工况条件 (高温高热流密度) 下可忽略浮升力对传热的影响, 而由高热流密度引起的流动加速效应会明显恶化传热.
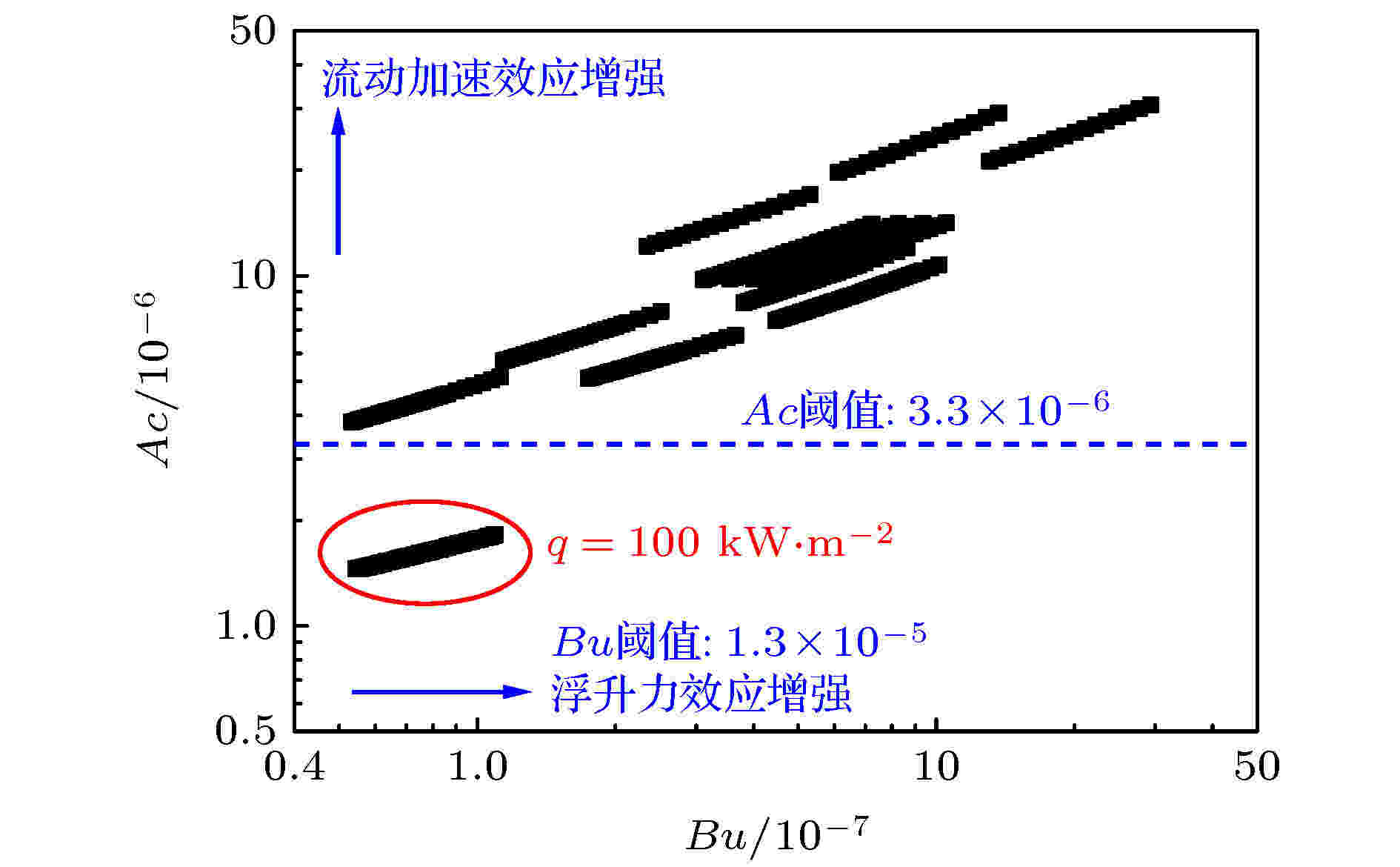图 12 Bu和Ac的分布图
Figure12. Distributions of Bu and Ac

2
4.6.与现有文献传热关联式计算结果的对比
-->

4.6.与现有文献传热关联式计算结果的对比

现有文献中关于管内超临界CO2的传热关联式大多是基于近临界点温区的传热数据提出的, 其对高温区传热数据的预测还有待评估. 表2为目前常用的八种管内超临界流体传热关联式, 其可分为基于热物性修正和基于无量纲数修正两种类型. 将关联式计算结果与模拟结果进行对比, 并采用平均绝对相对偏差 (mean absolute relative deviation, MARD) 和平均相对偏差在±20%以内的数据点占总数据量的比例 (η) 作为关联式预测能力的评估标准, MARD具体定义如下:
作者关联式和工况条件MARD/%η/%
基于热物性修正
Bishop 等[23]$Nu = 0.0069Re_{\rm{b} }^{0.9}\overline {Pr} _{\rm{b} }^{0.66}{\left( { { { {\rho _{\rm{w} } } } }/{ { {\rho _{\rm{b} } } } } } \right)^{0.43} }\left[ {1 + 2.4({D}/{L}) } \right]$22.222.3
工质: 水
p = 22.6—27.5 MPa, G = 680—3600 kg·m–2·s–1, q = 310—3500 kW·m–2
Krasnoshchekov和
Protopopov[24]		$Nu = 0.023Re_{\rm{b} }^{0.8}Pr_{\rm{b} }^{0.5}{\left( {{ { {\rho _{\rm{w} } } } }/{ { {\rho _{\rm{b} } } } } } \right)^{0.3} }{\left( {{ {\overline { {c_{\rm{p} } } } } }/{ { {c_{ {\rm{p,b} } } } } } } \right)^{0.4} }$8.1100
工质: CO2
p = 8—12 MPa, G = 2971 kg·m–2·s–1, q = 235—500 kW·m–2, Tin = 301.7—472 K
流动方向: 水平
Jackson[25]$Nu = 0.023Re_{\rm{b} }^{0.8}\overline {Pr} _{\rm{b} }^{0.5}{\left( { { { {\rho _{\rm{w} } } } }/{ { {\rho _{\rm{b} } } } } } \right)^{0.3} }$9.0100
工质: CO2
p = 7.8—9.8 MPa, Reb = 8×104—5×105, q ≤ 2600 kW·m–2
基于无量纲数修正
Liao和Zhao[26]垂直向上:18.160.7
$Nu = 0.354Re_{\rm{b} }^{0.8}Pr_{\rm{b} }^{0.4}{\left( {{ { {\rho _{\rm{w} } } } }/{ { {\rho _{\rm{b} } } } } } \right)^{1.297} }{\left( {{ {\overline { {c_{\rm{p} } } } } }/{ { {c_{ {\rm{p,b} } } } } } } \right)^{0.296} }Bo_{\rm{m} }^{ {\rm{0} }{\rm{.157} } }$
垂直向下:
$Nu = 0.643Re_{\rm{b} }^{0.8}Pr_{\rm{b} }^{0.4}{\left( { { { {\rho _{\rm{w} } } } }/{ { {\rho _{\rm{b} } } } } } \right)^{2.154} }{\left( { { {\overline { {c_{\rm{p} } } } } }/{ { {c_{ {\rm{p,b} } } } } } } \right)^{0.751} }Bo_{\rm{m} }^{ {\rm{0} }{\rm{.186} } }$
水平:
$Nu = 0.124Re_{\rm{b} }^{0.8}Pr_{\rm{b} }^{0.4}{\left( {{ { {\rho _{\rm{w} } } } }/{ { {\rho _{\rm{b} } } } } } \right)^{0.842} }{\left( {{ {\overline { {c_{\rm{p} } } } } }/{ { {c_{ {\rm{p,b} } } } } } } \right)^{0.384} }Bo_{\rm{b} }^{ {\rm{0} }{\rm{.203} } },~ Bo = { {Gr} }/{ {Re_{\rm{b} }^{2.7} } }$
工质: CO2
p = 7.4—12 MPa, G = 236—1179 kg·m–2·s–1, q = 10—200 kW·m–2, Tin = 295—385 K
Kim 等[10]$Nu = 0.226Re_{\rm{b}}^{1.174}Pr_{\rm{b}}^{1.057}{\left( {{{{\rho _{\rm{w}}}}}/{{{\rho _{\rm{b}}}}}} \right)^{0.571}}{\left( {{{\overline {{c_{\rm{p}}}} }}/{{{c_{{\rm{p,b}}}}}}} \right)^{1.032}}A{c^{0.489}}B{u^{0.0021}}$42.311.0
$Ac = \dfrac{ { {q^ + } } }{ {Re_{\rm b}^{0.625} } }{\left( {\dfrac{ { {\rho _{\rm{b} } } }}{ { {\rho _{\rm{w} } } } } } \right)^{0.5} }\left( {\dfrac{ { {\mu _{\rm{w} } } }}{ { {\mu _{\rm{b} } } } } } \right), ~Bu = \dfrac{ {G{r_{\rm{q} } } }}{ {Re_{\rm{b} }^{3.425}Pr_{}^{0.8} } }{\left( {\dfrac{ { {\rho _{\rm{b} } } }}{ { {\rho _{\rm{w} } } } } } \right)^{0.5} }\left( {\dfrac{ { {\mu _{\rm{w} } } }}{ { {\mu _{\rm{b} } } } } } \right)$
工质: CO2
p = 7.46—10.29 MPa, G = 208—874 kg·m–2·s–1, q = 38—234 kW·m–2, Tin = 302—388 K
流动方向: 垂直向上
Bovard 等[11]$Nu = 0.040063Re_{\rm{b}}^{1.40418}Pr_{\rm{b}}^{0.97767359}{\left( {\dfrac{{{\rho _{\rm{w}}}}}{{{\rho _{\rm{b}}}}}} \right)^{0.573108}}{\left( {\dfrac{{\overline {{c_{\rm{p}}}} }}{{{c_{{\rm{p,b}}}}}}} \right)^{0.11577}}A{c^{0.396203}}B{u^{0.13746}}$82.80
$Ac = \dfrac{{{q^ + }}}{{Re_b^{0.625}}}{\left( {\dfrac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{w}}}}}} \right)^{0.5}}\left( {\dfrac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{b}}}}}} \right),~ Bu = \dfrac{{G{r_{\rm{m}}}}}{{Re_{\rm{b}}^{3.425}Pr_{}^{0.8}}}{\left( {\dfrac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{w}}}}}} \right)^{0.5}}\left( {\dfrac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{b}}}}}} \right)$
工质: CO2
p = 6.5—8.335 MPa, G = 51—236 kg·m–2·s–1, q = 52—85 kW·m–2, Tin = 302 K
流动方向: 垂直向上
Liu 等[17]$Nu = 0.00075Re_{\rm{b}}^{0.93}\overline {Pr} _{\rm{b}}^{0.68}{\left( {\dfrac{{{\rho _{\rm{w}}}}}{{{\rho _{\rm{b}}}}}} \right)^{0.42}}\exp \left( {B{u^{ - 0.023}}} \right)\exp \left( {A{c^{0.079}}} \right)\left[ {1 + 2.63/\left( {L/D} \right)} \right]$28.73.5
$Bu = \dfrac{{G{r_{\rm{m}}}}}{{Re_{\rm{b}}^{2.625}Pr_{\rm{w}}^{0.4}}}{\left( {\dfrac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{w}}}}}} \right)^{0.5}}\left( {\dfrac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{b}}}}}} \right),~ Ac = \dfrac{{4{q^ + }}}{{Re_b^{0.625}}}{\left( {\dfrac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{w}}}}}} \right)^{0.5}}\left( {\dfrac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{b}}}}}} \right)$
工质: CO2
p = 7.4—10.6 MPa, G = 298.8—1506.5 kg·m–2·s–1, q = 4.7—296 kW·m–2, Tin = 257—322 K
流动方向: 垂直向上
Zhang等[19]$Nu = \left\{ \begin{gathered} 0.00672Re_{\rm{b} }^{1.414}\overline {Pr} _{\rm{b} }^{ - 0.005}{\left( {\dfrac{ { {\rho _{\rm{w} } } } }{ { {\rho _{\rm{b} } } } } } \right)^{0.448} }{\left( {\dfrac{ {\overline { {c_{\rm{p} } } } } }{ { {c_{ {\rm{p,b} } } } } } } \right)^{0.218} }Bo_{\rm{m} }^{ {\rm{0} }{\rm{.586} } },\quad {H_{\rm{b} } } < 0.9{H_{ {\rm{pc} } } } \\ 0.056Re_{\rm{b} }^{0.829}\overline {Pr} _{\rm{b} }^{0.35}{\left( {\dfrac{ { {\rho _{\rm{w} } } } }{ { {\rho _{\rm{b} } } } } } \right)^{ - 0.095} }{\left( {\dfrac{ {\overline { {c_{\rm{p} } } } } }{ { {c_{ {\rm{p,b} } } } } } } \right)^{0.214} }Bo_{\rm{m} }^{ {\rm{0} }{\rm{.142} } }, \quad {H_{\rm{b} } } \geqslant 0.9{H_{ {\rm{pc} } } } \\\end{gathered} \right.$64.90
工质: CO2
p = 7.5—10.5 MPa, G = 50—500 kg·m–2·s–1, q = 5—100 kW·m–2, Tin = 266—313 K
流动方向: 垂直向上


表2传热关联式计算结果与模拟数据的对比
Table2.Comparisons of the calculated heat transfer results by the correlations with the numerical results.

${\rm{MARD}} = \frac{1}{n}\sum\limits_1^n {\left| {\frac{{N{u_{{\rm{cal}}}} - N{u_{{\rm{num}}}}}}{{N{u_{{\rm{num}}}}}}} \right|} \times 100,$
式中Nucal, Nunum为传热关联式计算、模拟结果.
图13为其中预测效果较好的五种关联式计算结果与模拟数据对比的散点图. 从表2和图13可得, 基于热物性修正的传热关联式对本文高温区数据预测的结果优于基于无量纲数修正的关联式得到的结果, 且模拟数据均大于计算结果. 由前面的分析可得, 高温区的浮升力效应对传热的影响可忽略, 而虽然流动加速效应对传热有一定的影响, 但Nu数受导热传热的影响比对流传热的影响要大, 因此高温区的管内超临界CO2传热数据的预测使用基于热物性修正的传热关联式更合适. 其中, Krasnoshchekov和Protopopov[24]的关联式对本文传热数据预测效果最好, 其平均绝对相对偏差为8.1%, 且100%的数据点在±20%的平均相对偏差范围内.
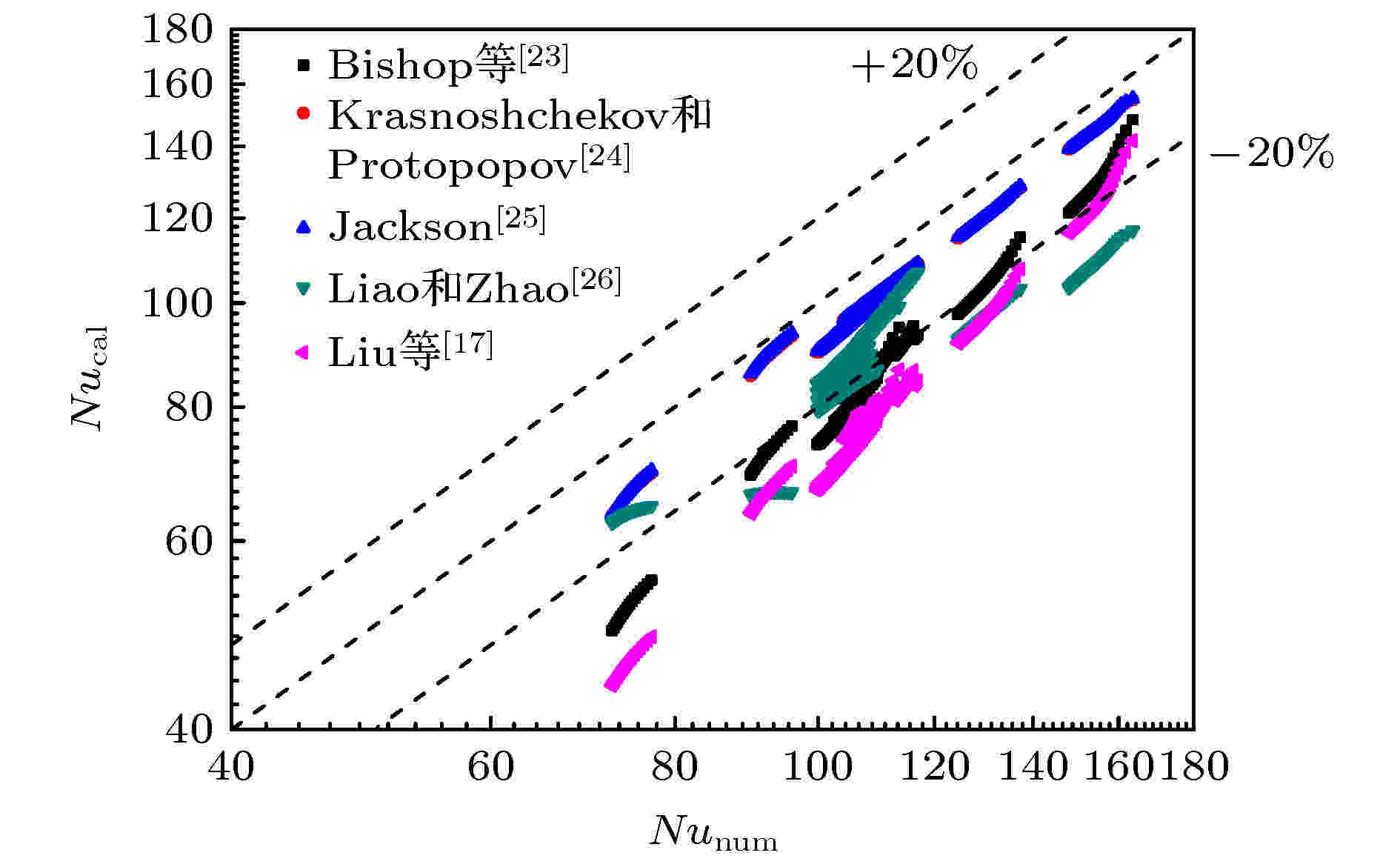图 13 传热关联式计算结果与模拟数据的对比
Figure13. Comparisons of the calculated heat transfer results by the correlations with the numerical results.

5.结　论
本文对超临界CO2在高温吸热管内的传热特性进行了数值模拟研究, 分析了流体温度、流动方向、系统压力、质量流率和热流密度对对流传热系数和Nu数的影响, 揭示了不同工况条件下的传热机理, 探究了浮升力和流动加速效应在高温区对传热的影响情况, 并选取了八种常用的管内超临界流体传热关联式与模拟结果进行了对比, 主要得到以下结论:
1) 在高温区 (800—1050 K), 随着流体温度的升高, 对流传热系数近似线性的增大, 而Nu数近似线性的减小;
2) 垂直向上、垂直向下和水平三种流动方向以及系统压力对高温区的对流传热系数和Nu数影响均很小;
3) 高温区的对流传热系数和Nu数均随着质量流率的增大和热流密度的减小而明显的增大, 且热流密度越大其影响程度越明显;
4) 在本文所研究的工况范围内, 浮升力效应对传热的影响可忽略, 而由高热流密度引起的流动加速效应会明显恶化传热;
5) 高温区的管内超临界CO2传热数据的预测使用基于热物性修正的传热关联式优于基于无量纲数修正的关联式, 且Krasnoshchekov和Protopopov[24]的关联式预测效果较优, 对模拟结果预测的平均绝对相对偏差为8.1%.
相关话题/传热 计算 系统 质量 数据
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • In掺杂<i>h</i>-LuFeO<sub>3</sub>光吸收及极化性能的第一性原理计算
    摘要:h-LuFeO3是一种窄带隙铁电半导体材料,已被证明在铁电光伏领域有较好的应用前景.然而,较低的极化强度使光生电子-空穴对复合率大,限制了h-LuFeO3基铁电光伏电池效率的提高.为改善h-LuFeO3的极化强度,提高光吸收性质,本文利用第一性原理计算方法研究了In原子在h-LuFeO3不同位 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 原子尺度构建二维材料的第一性原理计算研究
    摘要:随着信息技术的不断进步,核心元器件朝着运行速度更快、能耗更低、尺寸更小的方向快速发展.尺寸不断减小导致的量子尺寸效应使得材料和器件呈现出许多与传统三维体系不同的新奇物性.从原子结构出发,预测低维材料物性、精准合成、表征、调控并制造性能良好的电子器件,对未来电子器件的发展及相关应用具有至关重要的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 考虑磁透镜边缘场的质子成像系统优化设计
    摘要:高能质子照相系统由四极磁透镜和准直器组成,实际透镜的边缘场将影响成像系统的性能.本文将含边缘场的磁场梯度用贝尔函数近似,提出了一种含边缘场的成像系统优化方法.通过Geant4程序模拟了能量为1.6GeV的质子成像系统,并通过优化方法给出了考虑边缘场的优化后的系统参数.研究了考虑边缘场时的成像系 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 非对称自旋-轨道耦合系统的多体量子相干含时演化
    摘要:本文以具有非对称性自旋相互作用的三体自旋系统为研究对象,重点研究了三体量子相干含时演化规律.采用精确量子对角化和基于量子主方程的数值模拟方法,讨论了三体量子系统中多种量子相干组分及其退相干.研究发现,量子相干组分的含时演化与整个系统的初态量子特性紧密相关.当初态为可分离纯态时,在较短时间内,非 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于深度学习压缩感知与复合混沌系统的通用图像加密算法
    摘要:提出一种适用于灰度图像与RGB格式彩色图像的通用图像加密算法.利用双线性插值Bilinear与卷积神经网络对图像进行压缩,再使用二维云模型与Logistic组成的复合混沌系统对压缩图像加解密(滑动置乱与矢量分解),最后对解密图像进行重构.重构网络中,由卷积神经网络与双线性插值Bilinear主 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 偏振成像激光雷达与短波红外复合光学接收系统设计与分析
    摘要:基于偏振调制的三维成像激光雷达,具有测量范围远、测量精度较高、成像速度快、无运动伪像等优点,同时不受其他调制方式中增强电荷耦合器件、雪崩光电二极管阵列探测器工艺复杂、易饱和损坏等缺点限制,但存在需要双相机、成像视场角受电光晶体限制、成像质量易受到入射角度及云雾等大气条件影响等缺点.为克服上述缺 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于深度学习的联合变换相关器光学图像加密系统去噪方法
    摘要:提出了一种基于深度学习的联合变换相关器(JTC)光学图像加密系统新型去噪方法.针对JTC光学图像加密系统中解密图像噪声的问题,设计了一种基于生成对抗网络的去噪框架,并使用密集模块加强特征信息复用,提高了网络的性能.该方法通过引入通道注意力机制使网络区分不同通道的权重,学习各通道之间的关联,使网 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于Zernike模型系数优化的椭球型窗口光学系统像差校正
    摘要:传统的半球形窗口难以满足高速飞行器气动力学的需求,采用流线型外表面的非球面光学窗口技术应运而生.这种窗口会随着扫描视场角的变化产生大量动态像差,校正这类像差成为高速飞行器光电成像系统发展的关键问题.对于扫描视场为±60°的椭球形窗口光学系统,研究了静态校正和无波前探测器的自适应光学技术相结合的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 零质量射流作用下红细胞在微管道中变形的数值模拟
    摘要:因为在生物安全性和导入效率等方面的优势,基于力学方法实现基因导入日益得到学术界的重视.本文提出了一种基于零质量射流,对微管道中运动的细胞施加流体作用力,引起其发生变形,进而促使细胞膜上力敏通道开启的方法,并通过数值模拟进行了理论验证.本文采用浸没有限元法,对红细胞在微管道内运动过程中受到零质量 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 电池材料数据库的发展与应用
    摘要:基于自动化技术和计算机技术的高通量方法可快速提供数以万计的科研数据,对如何科学、高效的管理科研数据提出了新的挑战.可充放的二次电池作为一种清洁高效的能源存储器件,是电动汽车发展的关键,也是风/光电储能的首选.电池器件性能的提升与电池新材料的研发密切相关,电池材料数据库的发展可在电池材料研发中引 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.