摘要: 相比单粒子阵列, 金属纳米颗粒的二聚体阵列的共振效应受更多因素的影响, 包括阵列的组成方式、二聚体的结构和朝向、粒子的形状、大小等, 因此具有更好的可调性. 本文基于修正长波近似法, 通过引入两种粒子之间的阵列因子矩阵, 修正了两种粒子的极化率, 从而得到了二聚体阵列的消光截面的解析公式. 在此基础上, 讨论了整个阵列在不同偏振光激发下的共振的调制和偏振特性.
关键词: 散射 /
表面等离激元 /
二聚体 English Abstract Extinction cross section of dimer array of metallic nanoparticles Yin Cheng 1 ,Lu Cheng-Jie 1 ,Da Jing 1 ,Zhang Rui-Geng 1 ,Kan Xue-Fen 1 ,Han Qing-Bang 1 ,Xu Tian 2 1.College of Internet of Things Engineering, Hohai University, Changzhou 213022, China Fund Project: Project supported by the Fundamental Research Fund for the Central Universities of China (Grant No. 2017B14714), the Science and Technology Project of Changzhou, China (Grant No. CJ20180048), the Postgraduate Research & Practice Innovation Program of Jiangsu Province, China (Grant Nos. KYCX20_0433, B200203143), and the National Natural Science Foundation of China (Grant No. 61701261)Received Date: 23 June 2020Accepted Date: 06 September 2020Available Online: 03 January 2021Published Online: 20 January 2021Abstract: Surface lattice resonance (SLR) relies on both the lattice structure and its unit cell, which usually contains metallic nanoparticles. Since the full width half maximum of the lattice resonance is much narrower than that of localized surface plasmon resonance of a single particle, it is receiving attention increasingly. Based on the modified long-wavelength approximation, in this paper we derive an analytical expression for the extinction cross section of the dimer array of metallic nanoparticles. Comparing with the single particle array, good tunability can be achieved by the lattice resonance of the dimer array, which is influenced by more factors, including the arrangement of the array, the structural parameter and the rotation of the dimer, the shape and size of the particles, etc. First, the polarizabilities of the two kinds of particles in the dimer array are adjusted by introducing a matrix of the array factors, which take into account the influence of dipole fields of every particle. Then a simple expression of the resonance condition for the SLR of the dimmer array is obtained. The proposed model can be applied to a wide variety of dimer arrays of ellipsoid particles, and the applied method can be generalized to more complicated structure like polymer arrays. In this paper we further discuss the polarization dependence and ability to modulate the lattice resonance, by changing the excitation condition and the structural parameters of the dimer array. It is found that the resonances of the dimmer array can be classified as three main categories. The resonance related to the particles is independent of the variation of the dimmer arrangement or the array structure. On the other hand, the resonances corresponding to the dimmer and the array rely crucially on the structural parameters. By carefully adjusting the structural parameters, we can modulate the specific resonance effectively. This research is of theoretical importance for studying the SLR for more complicated structures and may find potential applications in the design of new photoelectric chip via nanoparticle array. Keywords: scattering /surface plasmon /dimer 全文HTML --> --> --> 1.引 言 基于金属纳米粒子的表面等离激元产生的光场局域效应一直是纳米光子学研究的核心问题. 而纳米粒子阵列结构的低维超构表面材料可以实现对电磁波的振幅、位相、偏振和空间分布等特性的有效调控, 目前已经被广泛应用于表面等离激元学、涡旋光学、非线性光学等领域[1 -5 ] . 与金属界面上的传输型表面等离子体共振和单金属粒子的局域表面等离子体共振不同, 金属纳米粒子阵列会产生一种线宽更窄的阵列共振. 这一效应所产生的共振峰在2008年首次被实验所观察[6 ] , 此后,该效应被学术界广泛关注和应用[7 ,8 ] , 如超灵敏传感、拉曼增强[9 ] 、可重塑的超棱镜[10 ] 、片上折射率传感器[11 ] 等. 由两种金属纳米粒子构成的二聚体(dimer)结构具有非常丰富的物理内涵, 其模式的分析可以基于谐振子模型[12 ] 、谐振等效电路模型[13 ] 和模式杂化模型[14 ,15 ] 等. 如果将金属纳米粒子二聚体排列成一个周期性阵列, 其共振模式必然受到二聚体的光学耦合行为的影响, 再考虑到阵列结构和入射光的偏振等影响因素, 对这种结构的阵列共振通常只采用数值仿真的方法. 相比之下, 解析方法可以更好地分析复杂现象背后的物理机理.[16 ] 将每一个金属粒子等效为一个辐射的电偶极子. 进而分析阵列中每一个粒子的辐射场对被考察粒子的极化率的影响; 基于对称性的考虑, 这种影响可以被包含在一个统一的阵列因子之中. 对于二聚体阵列而言, 即使二聚体中的两种粒子完全相同, 其所处的位置也是不同的, 因此不能像单粒子阵列做类似的处理. 在这种情况下, 本文引入阵列因子矩阵来概括同种粒子之间和异种粒子之间的相互作用, 并以此推导二聚体阵列的消光截面的解析公式. 在此基础上, 还讨论各种不同偏振激发、不同粒子、不同二聚体结构和不同阵列结构的共振效应. 本文的研究对基于金属纳米粒子二聚体阵列的超表面光电子器件的研究具有一定的指导意义.2.理论模型 研究模型如图1 所示, 含不同形状和大小的两种粒子的二聚体按照周期性的规则排列成了阵列结构. 这里需要说明的是, 本文的结论同样适用于六边形阵列等其他阵列结构, 本文分析的是如图1 所示的矩形阵列. 接下来将系统推导该二聚体阵列在不同偏振光的垂直照射下的消光系数的解析模型. 不失一般性, 假设图1 所示的矩形阵列中平行x 轴方向的周期为${\rm{d}}x$ , 平行y 轴方向的周期为${\rm{d}}y$ , 假设入射光的电场分量与x 轴之间的夹角为${\theta _{\rm{p}}}$ . 本文考虑椭球状的粒子, 其3个轴的关系为$a > b = c$ , 且长轴位于xy 平面内, 长度为a . 将二聚体中的粒子分别标记为粒子1和粒子2, 其中粒子1的中心位于原点, 其在x-y 平面内的长轴与x 轴之间的夹角为${\theta _{\rm{1}}}$ . 粒子2的中心相对于粒子1的中心(原点)偏移了矢量${{{r}}_{\rm{d}}}$ , 其在x-y 平面内的长轴与x 轴之间的夹角为${\theta _{\rm{2}}}$ . 粒子朝向与入射光偏振方向的变化会影响粒子的极化率.图 1 金属纳米颗粒二聚体的矩形阵列模型(插图显示了二聚体的排列方式)Figure1. Array of metallic nanoparticle dimers (Inset: Arrange-ment of the dimer).a 沿着x 轴, 其短轴$b, c$ 分别沿着y 轴和z 轴. 当入射光的偏振方向沿着x 轴时, 粒子的极化率为${\alpha _x}$ , 同理${\alpha _y}$ 对应着偏振方向沿着y 轴的情形,${\varepsilon _{\rm{p}}}, {\varepsilon _{\rm{m}}}$ 分别表示粒子和环境的介电系数, 且$e = \sqrt {1 - {{{b^2}} / {{a^2}}}} $ . 在本文的模型中, 入射光的偏振方向与x 轴夹角为${\theta _{\rm{p}}}$ , 因此, 粒子沿x 方向与y 方向的极化强度分量分别为${C_{{\rm{abs}}}}$ , 散射截面${C_{{\rm{sca}}}}$ 和消光截面${C_{{\rm{ext}}}}$ 与极化率之间的关系为[17 ] k 为入射光波的波数.S 来修饰粒子的极化率. 整个阵列的极化率${\alpha _{{\rm{Array}}}}$ 与单粒子的极化率$\alpha $ 之间的关系为[18 ] ${{{S}}_{\rm{m}}}$ 来描述上述机制,${S_{ij}}$ 表征阵列中所有二聚体中的第i 种粒子的极化场对被考察的二聚体中的第j 种粒子处的影响. 因此, ${S_{11}}, {S_{22}}$ 表征被考察二聚体中的粒子受到其他二聚体中所有同类粒子的影响; 而${S_{12}}, {S_{21}}$ 表征被考察二聚体中的粒子受到其他二聚体中所有异类粒子的影响. 因此, 被考察二聚体中, 两种粒子所处的实际电场${E_1}, {E_2}$ 可表示为${E_{{\rm{inc}}}}$ 为入射场, ${p_1}, {p_2}$ 分别表示两种粒子的极化强度. 代入${p_i} = {\alpha _i}{E_i}$ , 通过化简消去粒子处的实际场${E_1}, {E_2}$ , 可得9 )式给出了阵列中两种粒子的极化率的表达公式, 即10 )式是本文最重要的结论, 其正确性可以用一个简单的方法进行验证, 设${\alpha _2} = 0$ , 则(10 )式中的${\alpha _{1, {\rm{Array}}}}$ 很明显退化为(6 )式, 即当其中一种粒子不存在时, 二聚体阵列转变为单粒子阵列. 我们已经知道周期性排列的粒子会产生与阵列结构相关联的共振. (10 )式给出了二聚体阵列的阵列共振所满足的条件:11 )式的物理意义非常清楚, 根据(6 )式, 第一项乘积中的两个因子$1 - {\alpha _1}{S_{11}}$ 与$1 - {\alpha _2}{S_{22}}$ 分别与两种粒子单独形成的阵列共振有关. 而第二项显然与两种粒子相互之间的耦合有关. 因此二聚体阵列的结构共振除了与阵列的周期性有关之外, 还取决于二聚体内的两种粒子之间的位置关系. 相比单粒子阵列, 二聚体阵列在不改变阵列结构的前提下, 还可以通过对二聚体的设计来调制共振频率. 在长波近似条件下, (7 )式中的各个阵列因子S 的计算公式为[19 ] ${r_j}$ 是以被考察粒子为原点, 第j 个粒子所在位置距离原点的距离; 而${\theta _j}$ 是位矢量${{{r}}_j}$ 与该粒子的电偶极矩间的夹角. 至此, 给出了在二聚体阵列中, 根据阵列的排列规律, 对粒子的极化率进行修正. 而阵列的消光截面可以用位于阵列中心的粒子经过修正的极化率来计算, 即将描述粒子的(5 )式直接用于粒子阵列. 而整个二聚体阵列的透过率T 和消光截面之间的关系为${S_{{\rm{dimer}}}}$ 代表阵列中二聚体占有的面积.14 )式的第一个式子表明, 两种不同的粒子各自排列成的阵列结构是完全相同的; 第二个式子表明, 处在第1种粒子处观察第2种粒子的排列, 与处在第2种粒子处观察第1种粒子的排列, 所得到的结构是完全对称的. 上述条件并不难以实现, 代入(10 )式, 可以得到简化后的结果为${\alpha _{\rm{1}}}{{ = }}{\alpha _{\rm{2}}}{{ = }}{\alpha _{\rm{0}}}$ , (15 )式可更简化为3.数值模拟与讨论 球形粒子在偏振光激发下是各向同性的, 而椭球形粒子则表现出各向异性. 根据第2 节给出的理论模型, 完全可以计算出图1 所示的二聚体中含有两个具有任意位置和朝向的椭球粒子的一般情况. 但是椭球粒子的每一个轴都有对应的共振, 加上两粒子之间的相互耦合, 阵列共振和入射光的偏振方向等因素的共同影响, 会使得难以分析这些复杂现象背后的物理机理. 本文关注的重点是二聚体阵列的偏振特性, 以及阵列和二聚体的结构对共振位置的影响, 因此这一节仅仅考虑球形粒子.${\varepsilon _{{\rm{Ag}}}}$ 用经典的Drude模型表征, 则有[20 ] $\omega $ 是入射光的频率, 其他参数${\omega _{\rm{p}}} = 1.3 \times {10^{16}}\;{\rm{rad}}/{\rm{s}}$ , $\gamma = {\omega _{\rm{p}}}/200$ . 如果粒子是球形的, 其共振条件可以简单地用${\rm{Real}}\left( {{\varepsilon _{{\rm{Ag}}}}} \right) + 2 \approx 0$ 来判断. 由此可以推断银纳米球形粒子在空气中的共振频率约在250 nm附近. 进一步考虑阵列的影响, 在之前的研究中已经从理论上证明了单粒子构成的方形阵列是偏振无关的. 但显然对于二聚体阵列来说, 上述结论不再成立, 因为每一个二聚体结构本身是偏振相关的. 因此, 在下面的研究中选择方形阵列和球形粒子来避免由二聚体以外的因素带来偏振相关的特性.图2(a) 所示. 为了进行对比, 图2 还计算了单粒子阵列, 计算结果如图2(c) 所示. 方形阵列的周期为400 nm, 组成二聚体的两种粒子均为球形, 粒子1的半径为60 nm, 粒子2的半径为30 nm. 图2(c) 绘制的方形单粒子阵列由粒子1构成, 当连续改变入射光的偏振方向时, 整个阵列的透射率保持不变, 与前面的讨论一致. 不难想象, 由粒子2构成的同种阵列也是偏振无关的. 但是将两个周期相同的方形阵列按照一定规则嵌套在一起时, 透射率会变为偏振相关. 为了说明这一现象, 在图2(b) 和图2(d) 所计算的模型中, 粒子2的方形阵列相对粒子1的阵列的位移为${{{r}}_{\rm{d}}} = {200}\;{\rm{n}}{{\rm{m}}},~\angle {\rm{3}}{{\rm{0}}^ {\circ} }$ . 图2(b) 给出了一些特殊偏振角度${\theta _{\rm{p}}}$ 下的透射率曲线. 根据模型的设定, 入射光的偏振角度${\theta _{\rm{p}}}$ 是相对于x 轴定义的; 当${\theta _{\rm{p}}}{{ = 30}}^{\circ} $ 时, 偏振方向与二聚体中粒子连线方向一致, 当${\theta _{\rm{p}}} = 120^{\circ} $ 时, 偏振方向与二聚体中粒子的连线方向垂直.图 2 在不同偏振光激发下, 单粒子阵列与二聚体阵列的透过率对比 (a)两种阵列模型示意图; (b)二聚体阵列在偏振角度分别为30°, 60°和120°的情况下的透过率; (c), (d)单粒子阵列和二聚体阵列的透过率Figure2. Comparison of the transmission of two different structures under illumination with different polarization: (a) The diagrams of the two arrays; (b) the transmission spectrum of the dimer under different polarization ${\theta _{\rm{p}}} = 30^{\circ}, 60^{\circ}, 120^{\circ} $ , respectively; (c), (d) the calculated transmission of the single particle array and the dimer array, respectively.图2(c) 和图2(d) , 可以很明显发现两者的差异. 从整体上看, 波长越长, 光波无法感应到这些亚波长的粒子, 因此阵列受到的扰动比较小, 透过率偏高, 随着波长的变小, 入射场与阵列之间的相互耦合越发强烈, 因此在这一波段的透过率中, 出现了大量的共振谷. 图中在300, 230和200 nm的位置附近出现了3处共振谷, 导致了透射率的降低, 为了讨论方便, 下文将这3个共振分别称为共振1、共振2和共振3. 根据图2(b) 给出的结果, 考察偏振方向与二聚体粒子连线方向相平行(垂直)这两种特殊情况, 可以发现共振2是惟一发生变化的共振谷. 当偏振方向从30°变化为120°, 共振2位置的谷结构被峰结构取代, 因此可以判断共振2是与二聚体结构中, 两种粒子之间的相互耦合相关的, 因此表现出很强的偏振特性. 而其他共振结构仅仅出现一些扰动, 分析它们可能与方形晶格和球形粒子相关, 表现出偏振无关特性.${r_1} = {60}\;{\rm{nm}}$ 和方形阵列的周期$a = {400}\;{\rm{nm}}$ 不变, 并且令入射光的偏振方向${{{E}}_{\rm{in}}}$ 沿x 轴方向. 二聚体的其他可变的参量为: 1)两个粒子之间的距离${r_{\rm{d}}}$ ; 2)二聚体轴线方向与光偏振方向的夹角${\theta _{\rm{d}}}$ ; 3)粒子2的半径大小${r_{\rm{2}}}$ . 上述参量在图3(a) 中有详细标注, 图3(b) —(d) 分别改变了其中一种参量来考察其对阵列共振的调制作用. 当这些参数不作为变量时, 它们的取值分别为${r_{\rm{d}}} = {200}\;{\rm{nm}}$ , ${\theta _{\rm{d}}} = 30^{\circ} $ 和${r_2} = {30}\;{\rm{nm}}$ .图 3 在水平偏振光激发下, 方形二聚体阵列的透过率模拟图 (a)计算的模型和参数的定义; (b), (c), (d)二聚体结构参数对透过率的调制效果Figure3. The transmission of the square array of the nanoparticle dimers under illumination of x -axis polarized light: (a) The calculated model and the parameters definition; (b), (c), (d) the modulation on the array transmission by adjusting the dimer arrangement.图3 中的共振位置基本与图2 一致, 可以确定共振1与两个方形阵列之间的耦合有关, 这是由于改变二聚体间距${r_{\rm{d}}}$ 和粒子2半径${r_2}$ 并没有对该共振谷产生很大影响. 改变二聚体的朝向${\theta _{\rm{d}}}$ 对共振1产生比较大的影响; 当二聚体与电场偏振方向一致时, 该共振消失. 这一现象可以解释如下: 在外电场作用下, 每一个粒子都可以等效为一个电偶极子, 而电偶极子辐射场在中垂面上最强, 沿电偶极子方向最弱. 因此, 当${\theta _{\rm{d}}} = 0^{\circ} $ 时, 两种粒子阵列之间的耦合最弱, 共振消失; 反之, 当${\theta _{\rm{d}}} = {\rm{9}}0^{\circ} $ 时, 两种粒子阵列之间的耦合最强. 共振3显然与单粒子本身的共振有关, 因为只有当调节粒子粒径时, 该共振才发生明显变化.图3(b) 表明, 当二聚体中粒子间距变短时, 粒子间的模式耦合增强, 阵列共振频率发生微弱的蓝移, 随着二聚体中粒子间距变长, 粒子间耦合变弱, 阵列共振逐渐趋近于图2 中的单粒子阵列. 图3(c) 表明, 当电场偏振方向与二聚体轴线相互垂直时, 透射谱中的衰减峰被增强峰取代, 这一现象与图2 的结果相符合. 由此我们详细分析了由两种粒子排列成的同种方形阵列在嵌套成二聚体阵列时, 相关参量对整个阵列的共振的影响. 需要说明的是, 本文给出的公式可以普遍适用于各种情况, 但是这里的案例中并没有考虑椭球形粒子和其他类型的阵列, 因为太多的影响因素会使得物理现象越发错综复杂, 难以分析. 但反过来说, 这种二聚体阵列结构为调制阵列共振提供了更加充分的手段, 基于这一原理, 可制备各种基于粒子阵列超表面的光电子器件.4.结 论 本文推导了金属纳米颗粒二聚体阵列的消光截面的解析公式, 适用于各种椭球形的金属纳米粒子和各种二维的阵列结构. 理论模型考虑了激发光的偏振、二聚体的间距、朝向和阵列排列等诸多因素. 基于解析公式的数值模拟的结果表明, 相对于单粒子构成的阵列结构, 二聚体阵列存在更多的共振结构, 并且具有更好的调制特性. 针对偏振特性的分析, 可以将这些共振的成因归纳为粒子阵列结构、单颗粒子共振和二聚体之间的耦合三种. 本文提出的理论模型对深刻理解二聚体阵列共振背后的物理机理, 以及基于该结构所构建的各种光电子超表面材料具有重要的价值. 






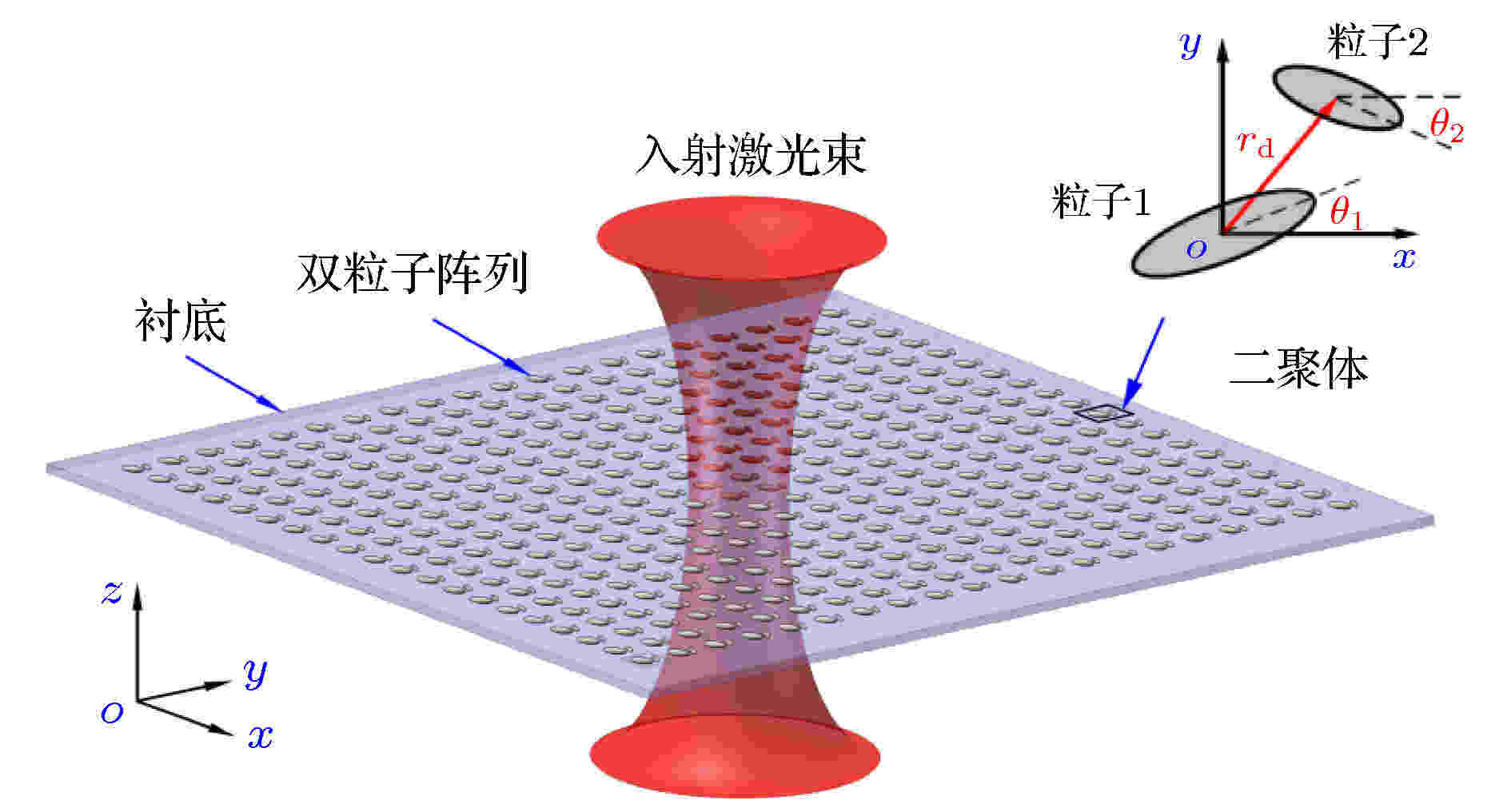 图 1 金属纳米颗粒二聚体的矩形阵列模型(插图显示了二聚体的排列方式)
图 1 金属纳米颗粒二聚体的矩形阵列模型(插图显示了二聚体的排列方式)








































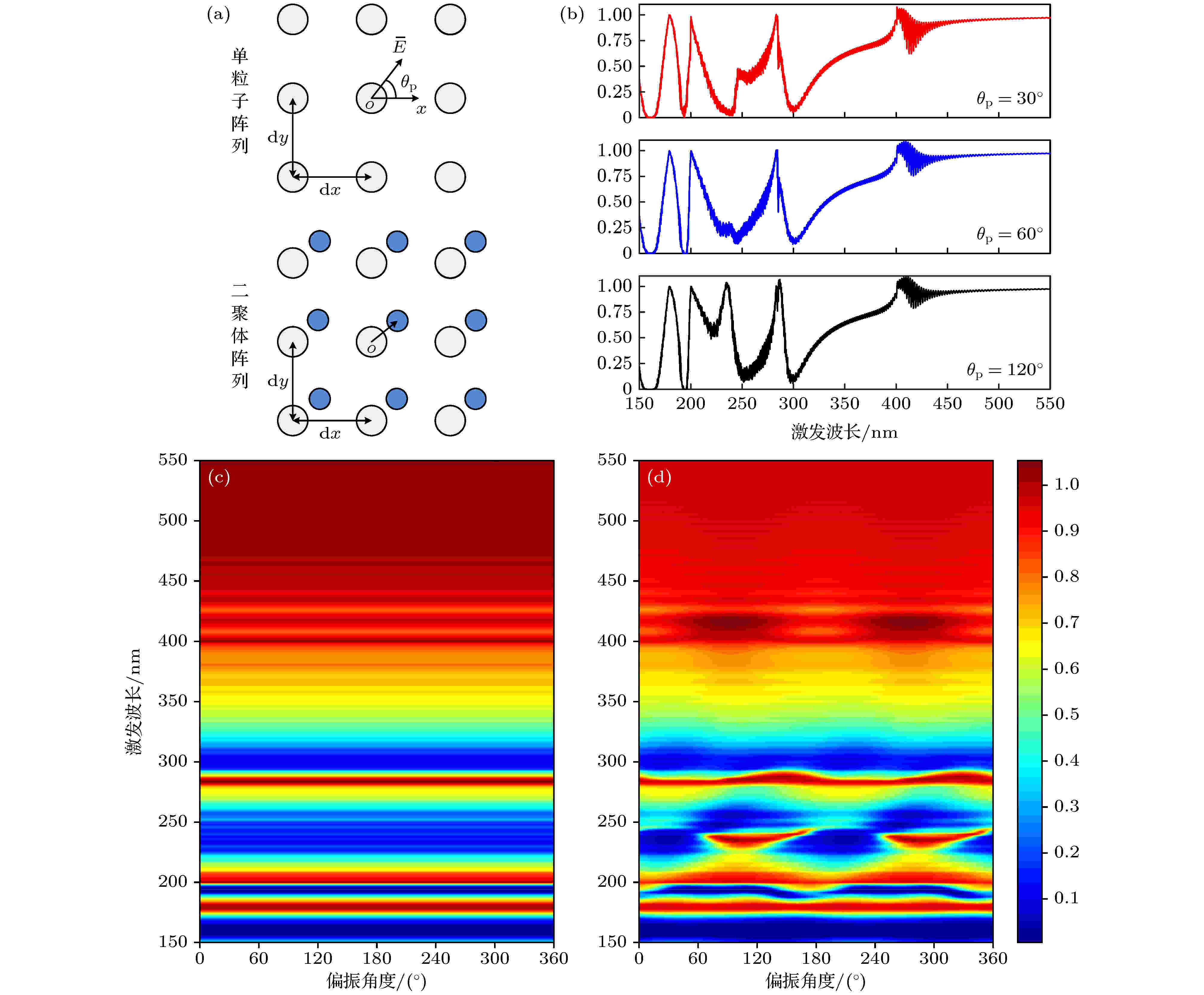 图 2 在不同偏振光激发下, 单粒子阵列与二聚体阵列的透过率对比 (a)两种阵列模型示意图; (b)二聚体阵列在偏振角度分别为30°, 60°和120°的情况下的透过率; (c), (d)单粒子阵列和二聚体阵列的透过率
图 2 在不同偏振光激发下, 单粒子阵列与二聚体阵列的透过率对比 (a)两种阵列模型示意图; (b)二聚体阵列在偏振角度分别为30°, 60°和120°的情况下的透过率; (c), (d)单粒子阵列和二聚体阵列的透过率









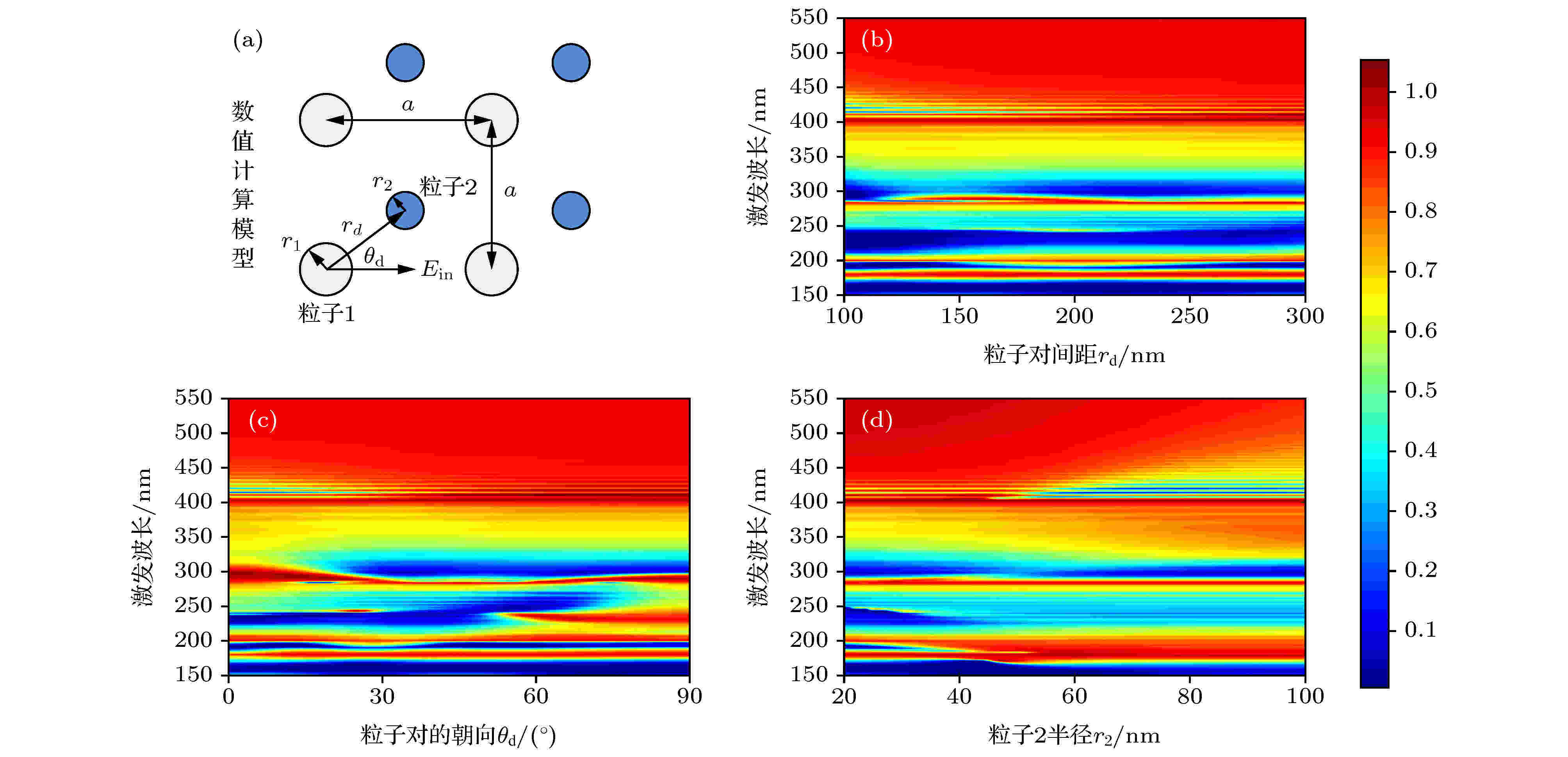 图 3 在水平偏振光激发下, 方形二聚体阵列的透过率模拟图 (a)计算的模型和参数的定义; (b), (c), (d)二聚体结构参数对透过率的调制效果
图 3 在水平偏振光激发下, 方形二聚体阵列的透过率模拟图 (a)计算的模型和参数的定义; (b), (c), (d)二聚体结构参数对透过率的调制效果




