全文HTML
--> --> -->最近, 非均匀薄膜体系中的褶皱现象也引起了人们的极大兴趣. 事实上, 不管是自然界中的地质板块和生物组织, 还是工程技术中的人工微结构, 薄膜体系都是不均匀分布的. 因而, 研究非均匀体系的褶皱现象及其对外界的响应具有更加重要的意义. 构筑非均匀薄膜体系最常用的方法是引入周期性的台阶或缺陷等结构. Bowden等[13]利用边界诱导的应力各向异性调控出有序的褶皱斑图; Wu等[14]利用预制裂纹的曲率诱导或抑制薄膜的褶皱; Um等[15]利用聚二甲基硅氧烷(PDMS)的微孔结构调控出有序褶皱阵列; Wang等[16]探索了单轴载荷下微孔型薄膜体系的褶皱形貌演化. 利用金属板或光刻胶掩模是构筑非均匀薄膜体系的另一类方法, 可制备各种类型的薄膜体系. Chan和Crosby[17]对PDMS表面进行选择性氧化处理, 调控出取向生长的褶皱斑图; Ouchi等[18]报道了PDMS基底上周期性光刻胶阵列中由单轴压缩诱导的多重褶皱模态; Ding等[19]通过铜网掩模在PDMS表面形成正交的褶皱斑图; Gurmessa和Croll[20], Nogales等[21]研究了铜网掩模构筑的薄膜体系在单轴载荷作用时的力学响应; Li等[22]则进一步探索了铜网构筑的异质薄膜体系在双轴载荷下的褶皱结构.
上述提到的非均匀薄膜体系通常在边界处具有不连续的特性, 比如薄膜厚度、基底高度、薄膜或基底的硬度等具有突变性. 最近, 人们对柔性基底上梯度薄膜的褶皱现象也进行了探索. 研究发现, 单轴压缩通常导致条纹褶皱的自发分叉[23], 而双轴压缩与厚度梯度的竞争将导致条纹型、人字型和迷宫型褶皱的共存[24]. 在此基础上, 本研究组利用编织铜网构筑了周期性的厚度梯度薄膜, 研究了厚度梯度对自发的褶皱形貌的调控效应[25]. 然而到目前为止, 周期性厚度梯度薄膜在外加载荷作用下的响应行为和力学机制, 尚不清楚. 本文采用光学显微镜和原子力显微镜研究柔性PDMS基底上周期性厚度梯度银薄膜在单轴压缩/拉伸过程中的形貌演化, 重点分析褶皱和裂纹的分布特征和演化行为, 并采用应力理论和有限元模拟对实验现象给出了合理解释.
2.1.材 料
实验用的柔性基底为聚二甲基硅氧烷(PDMS, Sylgard 184, Dow Corning), 按主剂和固化剂10∶1的重量比混合, 用玻璃棒搅拌均匀后水平静置30 min. 待气泡完全消除后, 将混合溶液倾倒在平整的器皿内, 随后在温度为70 °C的加热台上固化5 h, 使PDMS完全交联成为弹性聚合物材料. 固化后的PDMS厚度约为1.2 mm, 用刀具将其切割成宽为12 mm的矩形片. 使用自制的拉伸装置将PDMS沿长度方向固定, 夹具内的PDMS长度为25 mm, 然后将PDMS预拉伸到30 mm, 即预应变为20%(图1(a)). 在预拉伸的PDMS上覆盖编织铜网, 表面贴紧(图1(b)). 铜网由直径约为52 μm的铜线正交编织而成, 网孔的宽度(即周期)w约为125 μm(图1(c)). 应当指出, 当网孔周期与褶皱波长相当时, 它们之间会存在复杂的竞争[18,21,22]. 而本文采用的网孔周期比褶皱波长大很多, 不需要考虑这种竞争关系. 本文主要通过薄膜的厚度梯度诱导应力的重排, 从而调控褶皱和裂纹的形成与分布.
图 1 PDMS基底上周期性厚度梯度薄膜的制备流程及应变施加过程 (a) PDMS基底预拉伸至20%的预应变; (b)编织铜网覆盖到预拉伸的PDMS表面; (c)编织铜网的光学显微镜照片; (d)银薄膜沉积之后, 移除铜网, 并释放预应变至PDMS的原长; (e)进一步拉伸PDMS至任意长度LFigure1. Schematic illustration of sample preparation and loading sequence of periodic thickness-gradient films on PDMS substrates: (a) The PDMS substrate was stretched to 20% prestrain; (b) a weaved copper grid was placed on the pre-stretched PDMS surface; (c) optical micrograph of the weaved copper grid; (d) after deposition of silver film, the copper grid was removed and the prestrain was released to the original length of PDMS; (e) the PDMS substrate was further stretched to a random length, namely L.
2
2.2.薄膜沉积
采用直流磁控溅射技术在室温条件下沉积金属银薄膜, 真空腔的本底真空优于2 × 10–4 Pa, 溅射时氩气压固定在0.5 Pa, 靶基距约为80 mm, 溅射功率为76 W (电流为0.2 A, 电压为380 V). 在此功率下银薄膜的沉积速率约为30 nm/min, 溅射时间为3 min, 即平整处薄膜厚度约为90 nm. 本实验采用铜网掩模的方法, 因而薄膜厚度并不均匀分布. 由于编织铜网特定的空间三维结构, 铜线与PDMS表面并不都紧密接触, 而是大部分呈悬空状态. 在薄膜沉积过程中, 金属原子受到氩原子等粒子的频繁碰撞而改变方向, 部分金属原子能沉积到铜线覆盖处的PDMS表面, 因而在该处自然形成厚度呈连续变化的梯度薄膜[24,25]. 由于铜网为周期性排布的阵列结构, 因而最终形成的薄膜呈周期性的厚度梯度变化.2
2.3.表 征
沉积完成后, 将编织铜网小心移除, 缓慢释放预应变至PDMS的原长(图1(d)), 然后再次回到20%的预应变状态, 并进一步拉伸PDMS至任意长度(图1(e)). 实验上, 也可以先进行拉伸再逐渐释放应变, 甚至改变预应变的值. 结果表明, 应变的施加方式会改变褶皱和裂纹的形成顺序及朝向, 但不会改变褶皱和裂纹的形貌特征和演化规律. 设薄膜的原长为L0, 释放/拉伸过程中的任意长度为L, 则薄膜的机械应变可表示为
3.1.单轴压缩诱导的形貌特征
图2(a)和(b)为周期性厚度梯度薄膜在预应变释放过程中的原位形貌演化规律. 由图2可知, 编织铜网的存在使得薄膜表面形成与铜网结构一致的周期性阵列, 样品表面深色部分为铜线覆盖区域, 膜厚较小, 浅色部分为网孔中心区域, 膜厚较大. 由于薄膜的残余应力作用, 制备态的样品(
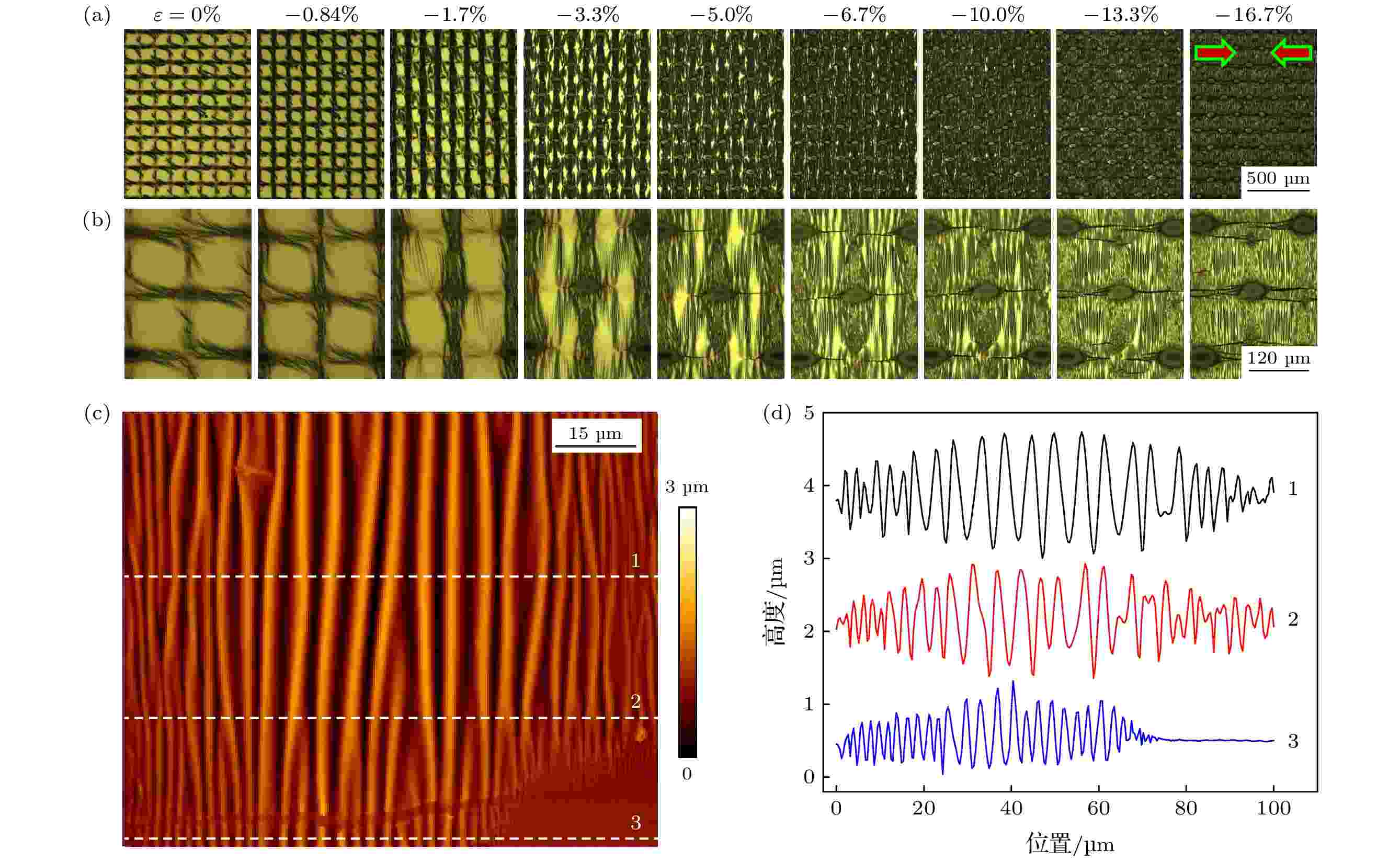图 2 PDMS基底上周期性厚度梯度Ag薄膜受单轴压缩的形貌演化及结构特征 (a)光学显微镜放大50倍的图片, 尺寸均为1042 μm × 1390 μm, 箭头指向代表压缩方向; (b)光学显微镜放大200倍的图片, 尺寸均为261 μm × 348 μm; (c)单个网孔内薄膜表面形貌的原子力显微镜图片; (d)不同位置的剖面线结构Figure2. Morphological evolutions and structural characteristics of periodic thickness-gradient Ag films on PDMS substrates under uniaxial compression: (a) Optical micrographs with 50× magnification. All the images have the size of 1042 μm × 1390 μm. The arrows represent the direction of compression. (b) Optical micrographs with 200× magnification. All the images have the size of 261 μm × 348 μm. (c) Atomic force microscopy (AFM) image of the film surface within a grid period. (d) Cross-sectional profiles of the film surface at different positions.
图2(c)显示了单个网孔内薄膜表面形貌的原子力显微镜图像, 图2(d)为不同位置的剖面线结构. 由图2可知, 褶皱均沿着垂直于机械载荷的方向排列, 呈条纹型结构, 这是由单轴机械压缩引起的[11,26]. 沿着网孔中心线的褶皱(剖面线1)具有良好的周期性变化规律, 其波长和振幅均呈现振荡行为, 在网孔中心处, 波长和振幅达到最大值, 随后逐渐衰减, 至铜网覆盖处达到最小. 偏离网孔中心线的褶皱(剖面线2)仍显示较好的振荡规律, 但波长和振幅均相应变小. 铜线覆盖处(剖面线3)褶皱的波长和振幅都显著变小, 但仍显示一定的振荡规律. 在原子力显微图的右下角(剖面线3的右侧), 褶皱结构消失, 这是因为该处正好是铜线与PDMS表面的接触点, 薄膜厚度为零. 采用编织铜网作掩模来构筑周期性厚度梯度薄膜, 简单方便, 但接触点导致的薄膜不均匀性(或缺陷)没法避免. 可以采用TEM用的平板铜网, 在沉积过程中抬起一定的高度来解决这一问题, 这也是后续要研究的课题.
为了进一步理解预应变释放过程中薄膜结构的演化规律, 系统测量了褶皱波长、裂纹长度和宽度等信息(图3). 图3(a)为预应变释放完毕后褶皱波长在一个周期范围内的分布规律, 可以发现, 中心区域的褶皱波长最大, 而铜网覆盖处的波长最小, 最大波长和最小波长之比接近于2, 与之前的实验结果一致[25]. 图3(b)为中心区域的褶皱波长(即最大波长)随机械应变的演化规律, 可以发现褶皱波长随着压缩应变的增加而持续减小.
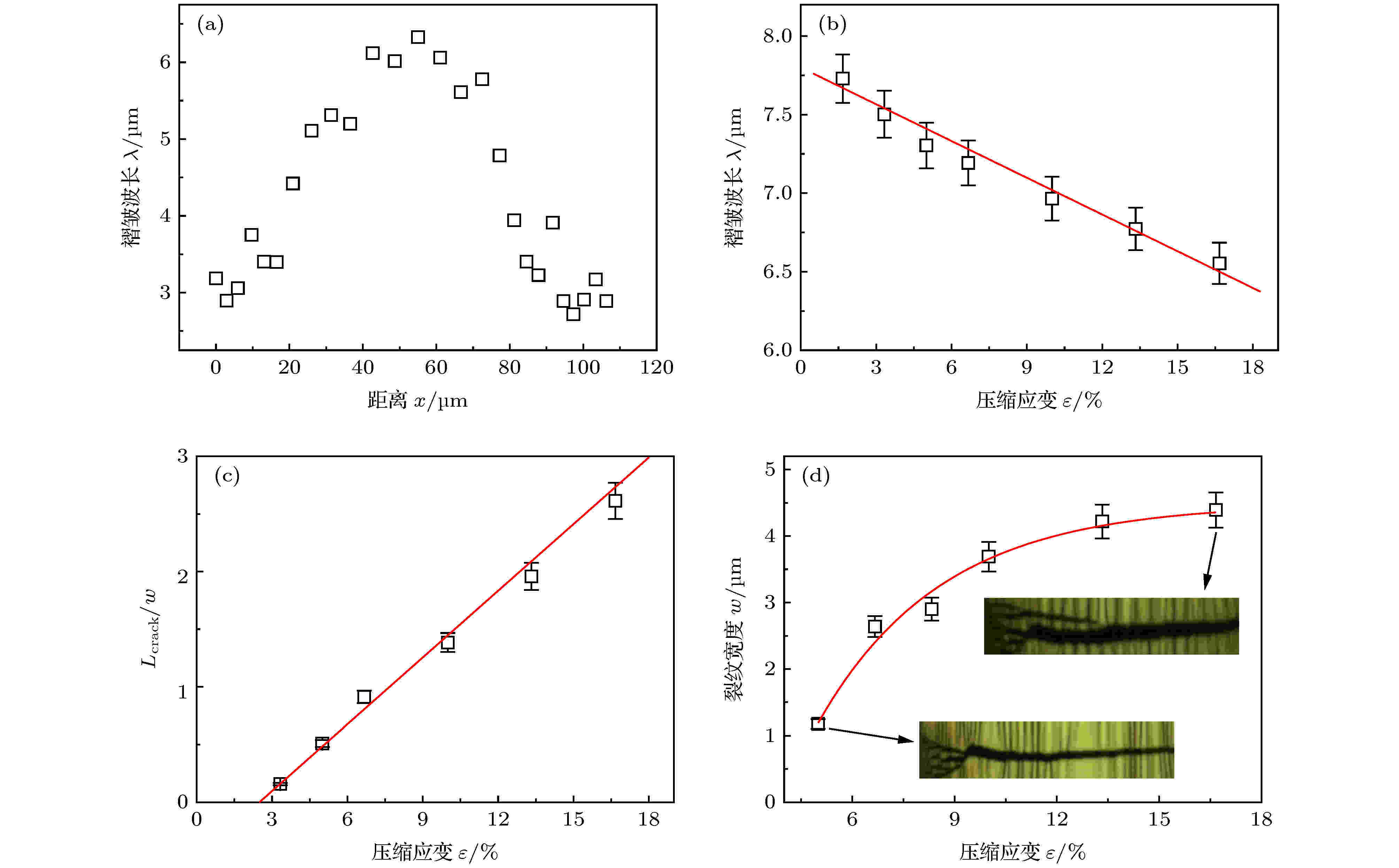图 3 (a)一个周期内褶皱波长沿着中心线的演化规律; (b)中心区域褶皱的波长与机械压缩应变的关系, 实线为手风琴模型的理论结果; (c)归一化的裂纹长度(裂纹长度与网孔宽度之比)与机械应变的关系, 实线为实验数据的线性拟合; (d)裂纹宽度与机械应变的关系, 插图为不同应变下的裂纹形貌, 尺寸均为70 μm × 16 μmFigure3. (a) Evolution of wrinkle wavelength along the center line within a grid period. (b) dependence of the wrinkle wavelength at the mesh center on the mechanical compressive strain. The solid line represents theoretical prediction of accordion model. (c) dependence of normalized crack length (the ratio of crack length to mesh width) on the mechanical strain. The solid line is a linear fit to the experimental data. (d) dependence of the crack width on the mechanical strain. The insets (both 70 μm × 16 μm) show the crack morphologies under different strains.
根据连续介质弹性理论, 当薄膜-基底体系受到的压缩应力超过某个临界值时, 薄膜将产生具有面外变形的褶皱结构. 该临界应变可表示为[13,27]
膜基体系的能量最小化(薄膜的弯曲能和基底的变形能)可导致稳定的褶皱波长, 表示为[13,27]
另一方面, 在实验中, 褶皱的临界应变、薄膜和基底的杨氏模量和泊松比均为常数, 当预应变释放完毕后, 薄膜的压缩应变也为常数(约16.7%). 因而, 根据(2)式和(3)式, 褶皱的波长只与薄膜厚度有关, 可表示为
此外, 在预应变的释放过程中, 泊松效应引起的拉伸应变会导致薄膜产生垂直于褶皱的裂纹(图2(b)). 所有裂纹都限定在膜厚较小的区域, 开始为单条裂纹的逐步扩展, 随后呈现多重裂纹的平行排布. 图3(c)显示了裂纹长度与机械应变的定量关系, 对裂纹长度进行归一化处理, 即采用裂纹长度与网孔周期的比值Lcrack/w. 由图3(c)可知, 随着机械应变的增加, Lcrack/w呈线性增加. 当Lcrack/w < 1时, 薄膜的机械应变较小, 表现为单条裂纹的逐步扩展. 当Lcrack/w = 1时, 裂纹正好贯穿整个网孔, 表现为周期性阵列内单条裂纹相互连接, 图3(c)机械应变约为6.7%. 当Lcrack/w > 1时, 膜厚较小区域不再仅限于单条裂纹, 即裂纹的数目随着机械应变的增加而增加. 图3(d)显示了裂纹的宽度随机械应变的演化规律, 随着机械应变的增加, 裂纹的宽度先快速增加, 随后逐渐达到饱和值(约为4.5 μm). 当裂纹的宽度和长度达到饱和之后, 薄膜将产生新的裂纹来释放增加的拉伸应变, 因而产生多重裂纹模态.
2
3.2.单轴拉伸诱导的形貌特征
在薄膜器件(特别是柔性电子器件)的使用过程中, 其往往受到复杂的载荷作用, 而拉伸应变对器件的力学稳定性和使用寿命影响更大. 因而, 在机械压缩的基础上, 进一步考察了Ag/PDMS体系在单轴拉伸载荷下的结构演化. 图4(a)和(b)为周期性厚度梯度薄膜在拉伸过程中的原位形貌演化规律. 可以发现, 在平行于加载方向上出现褶皱, 而在垂直方向上则出现裂纹, 该结果正好与单轴压缩时相反, 这是由应力的性质(拉伸或压缩)决定的. 与单轴压缩情况相似的是, 褶皱最先在膜厚较小区域产生, 随后逐渐扩展到膜厚较大区域. 图4(d)显示中心处褶皱的最大波长随着机械应变的增加而逐渐减小, 与图3(b)的结果一致. 同样, 褶皱的波长也符合手风琴模型的理论预测(图4(d)中红色实线).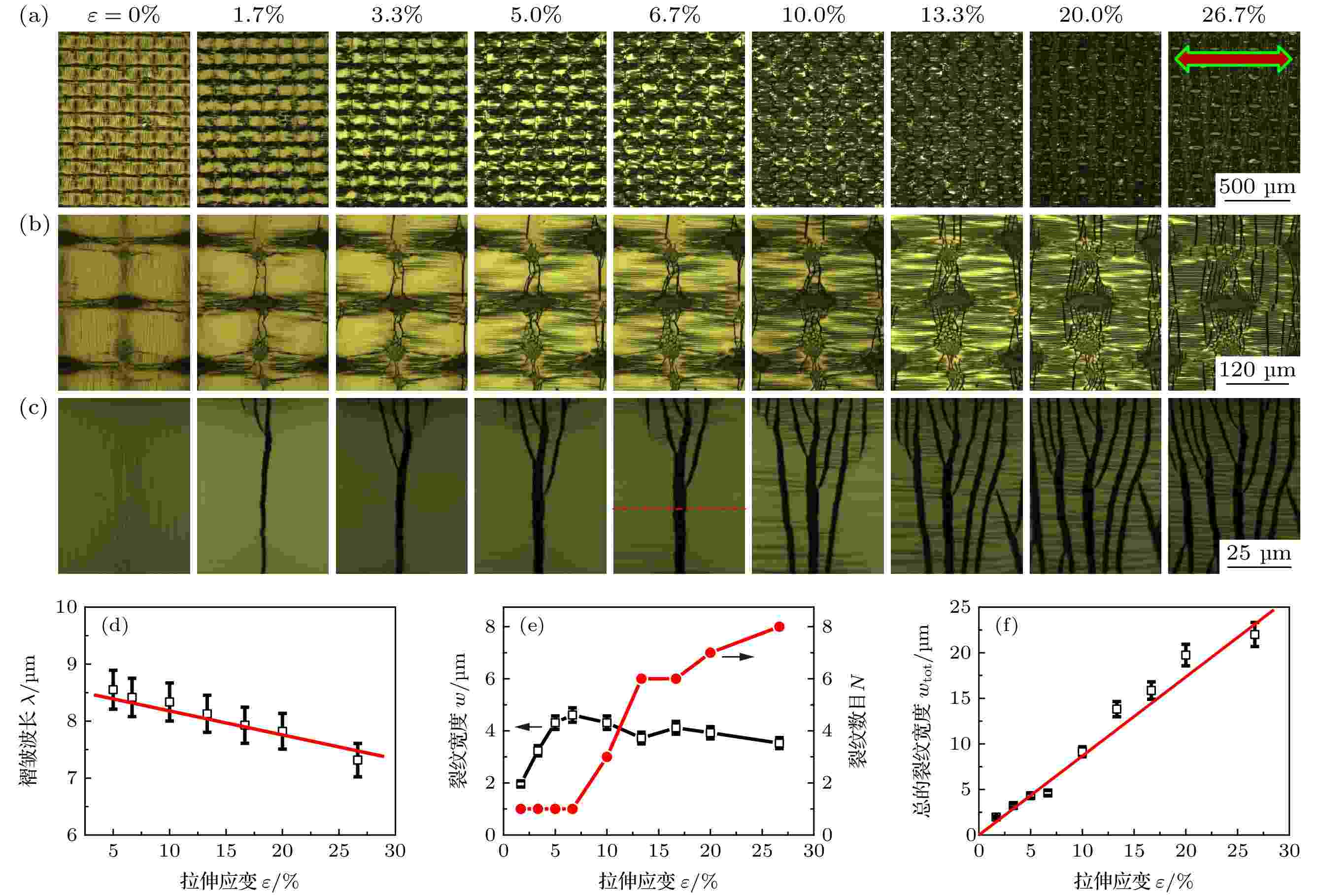
图 4 PDMS基底上周期性厚度梯度Ag薄膜受单轴拉伸的形貌演化及结构特征: (a)光学显微镜放大50倍的图片, 尺寸均为1042 μm × 1390 μm, 箭头指向代表拉伸方向; (b)光学显微镜放大200倍的图片, 尺寸均为261 μm × 348 μm; (c)光学显微镜放大500倍的图片, 尺寸均为104 μm × 139 μm; (d)中心区域的褶皱波长与机械拉伸应变的关系, 实线为手风琴模型的理论结果; (e)沿中心线的裂纹宽度和裂纹数目随应变的演化规律; (f)总的裂纹宽度与机械应变的关系, 实线为实验数据的线性拟合.Figure4. Morphological evolutions and structural characteristics of periodic thickness-gradient Ag films on PDMS substrates under uniaxial tension: (a) Optical micrographs with 50× magnification. All the images have the size of 1042 μm × 1390 μm. The arrows represent the direction of tension. (b) Optical micrographs with 200× magnification. All the images have the size of 261 μm × 348 μm. (c) Optical micrographs with 500× magnification. All the images have the size of 104 μm × 139 μm. (d) Dependence of the wrinkle wavelength at the mesh center on the mechanical tensile strain. The solid line represents theoretical prediction of accordion model. (e) Evolutions of the crack width and crack number along the center line with the tensile strain. (f) Dependence of the total crack width on the tensile strain. The solid line is a linear fit to the experimental data.
由图4(b)可知, 尽管裂纹也最先在膜厚较小区域产生, 并基本限定在这一区域, 但其结构和数目与单轴压缩时具有显著差异. 为此, 特别考察了单轴拉伸时薄膜裂纹的原位演化行为(图4(c)). 当机械应变
图4(e)显示了沿着中心线(图4(c)中的红色虚线)的裂纹宽度和裂纹数目随应变的演化规律. 当
根据材料的断裂理论[29,30], 当薄膜中储存的弹性应变能超过材料的断裂能时, 薄膜将产生开裂, 即
图 5 (a)周期性厚度梯度Ag薄膜的表面形貌, 
Figure5. (a) Surface morphology of a periodic thickness-gradient Ag film when
将
为了进一步研究拉伸应变作用下厚度梯度薄膜的形态分布, 考察
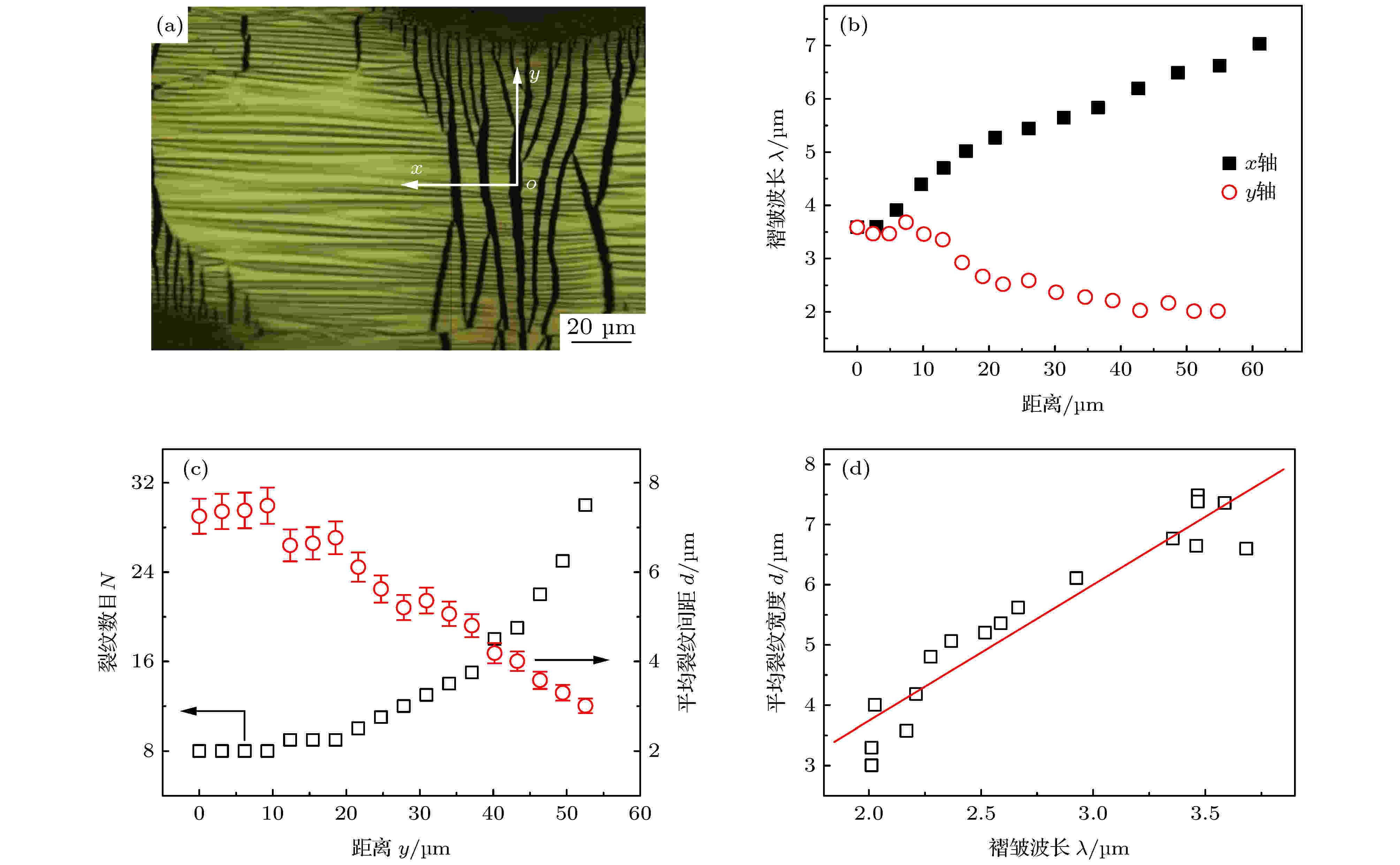图 6 (a)
Figure6. (a) Typical surface morphology of Ag film within a grid period under
对于厚度均匀的薄膜样品, 裂纹的萌生位置是随机的, 一般由薄膜缺陷诱导应力集中, 并进一步引起裂纹扩展. 裂纹形成之后, 能够有效释放周边薄膜的应力能. 在开裂后的薄膜片中, 应力在膜片中间区域具有最大值, 越靠近裂纹边界, 应力值越小. 因而, 新产生的裂纹容易在膜片中间区域萌生, 这一过程将随着应变的增加不断持续下去, 直到形成稳定的裂纹斑图. 由此形成的裂纹通常具有相仿的间距, 并且间距随应变的增加呈指数下降规律[26,31]. 而本实验研究的厚度梯度薄膜样品, 裂纹总是从膜厚较小区域逐渐扩展到膜厚较大区域(图4). 在扩展过程中, 它们的间距保持不变. 由于基底模量、拉伸应变、临界断裂应变和薄膜断裂韧性均为常数, 裂纹的平均间距与薄膜厚度成正比, 而由(4)式可知薄膜厚度与褶皱波长成正比. 因而, (7)式可以写成
2
3.3.厚度梯度薄膜褶皱的有限元模拟
为了理解薄膜体系的失稳行为及其后屈曲演化, 表面屈曲失稳的稳定性分析成为当前研究的热点. Cerda和Mahadevan[27]通过标度律法研究了薄膜拉伸产生的横向表面褶皱与材料性质的关系; Chen等[32]通过冯·卡门板理论, 得到薄膜-基底体系在均匀单向压应力下的面外正弦型褶皱波长与临界应力的理论解; Jiang等[33]将前者适用于小变形的理论进行了修正, 得到考虑有限变形影响的薄膜褶皱波长和波幅的理论解. 而对于二维和三维复杂系统, 稳定性的后屈曲分析由于涉及到失稳分岔路径的选择和非线性问题求解, 很难得到失稳理论解, 因此数值求解成为常用的分析方法. Huang等[34]通过数值频谱方法得到基底上软膜在不同的双轴加载应力下面外褶皱形貌的选择和转变; Pan等[35]通过相场法研究了薄膜-基底体系的面外褶皱和脱粘翘曲行为; Cao等[36]通过有限元法模拟了球型核壳结构在热应力作用下的表面屈曲形貌和对应的后屈曲演化; Zhang等[37]利用有限元法模拟了甜甜圈型核壳结构在热应力作用下产生的多种失稳褶皱形貌共存的现象, 并研究了曲率不均匀对褶皱形貌产生的影响.本文通过有限元方法模拟厚度梯度薄膜单轴受压时的屈曲褶皱行为, 利用有限元计算软件ABAQUS[38]来模拟厚度梯度薄膜体系在均匀单向压应力下的屈曲行为, 并追踪其褶皱的形成和演化过程. 首先对体系进行线性屈曲分析, 此步骤为特征值求解问题, 可以得到体系的屈曲模态和对应的特征值, 以此确定薄膜褶皱的临界应变以及褶皱发生的起始位置; 再将体系线性屈曲的初始模态作为结构的初始几何缺陷引入体系, 通过弧长法[39]来计算褶皱的后屈曲演化, 所引入的微小几何缺陷大小是薄膜最小厚度的3%, 来保证后屈曲模拟的稳定性和收敛性. 为简化计算, 只对薄膜的一个厚度梯度周期进行模拟, 且只考虑薄膜沿一个方向的厚度梯度, 几何截面如图7所示. 按照实验数据, 铜网的周期设定为w = 125 μm, 薄膜的最大膜厚设为h0 = 90 nm, 位于薄膜中间, 最小膜厚设为最大膜厚的一半, 位于左右两边, 将膜厚随位置的变化简化为线性. 薄膜材料为Ag, 杨氏模量
图 7 厚度梯度薄膜-基底体系的截面示意图Figure7. Schematic diagram of the thickness-gradient film-substrate system.
由于薄膜厚度梯度的存在, 当面内压应力未达到临界应力时, 面内应变的分布不均匀, 且与膜厚成反比, 薄膜两端厚度最小处的压应变最大, 而薄膜中间处的压应变最小(图8(a)). 最大应变与最小应变之比约为2∶1, 与上文通过力的传递效应推导的结果一致. 这就导致膜厚最小处率先达到临界应变, 首先发生屈曲, 通过面外褶皱释放应变, 并逐步向膜厚处扩展. 薄膜褶皱幅值与面内压应变关系曲线如图8(b)所示, 在薄膜屈曲褶皱的演化过程中, 模拟所得的临界屈曲应变为0.047%, 与通过(1)式所得理论值0.052%接近, 说明模拟结果可信.
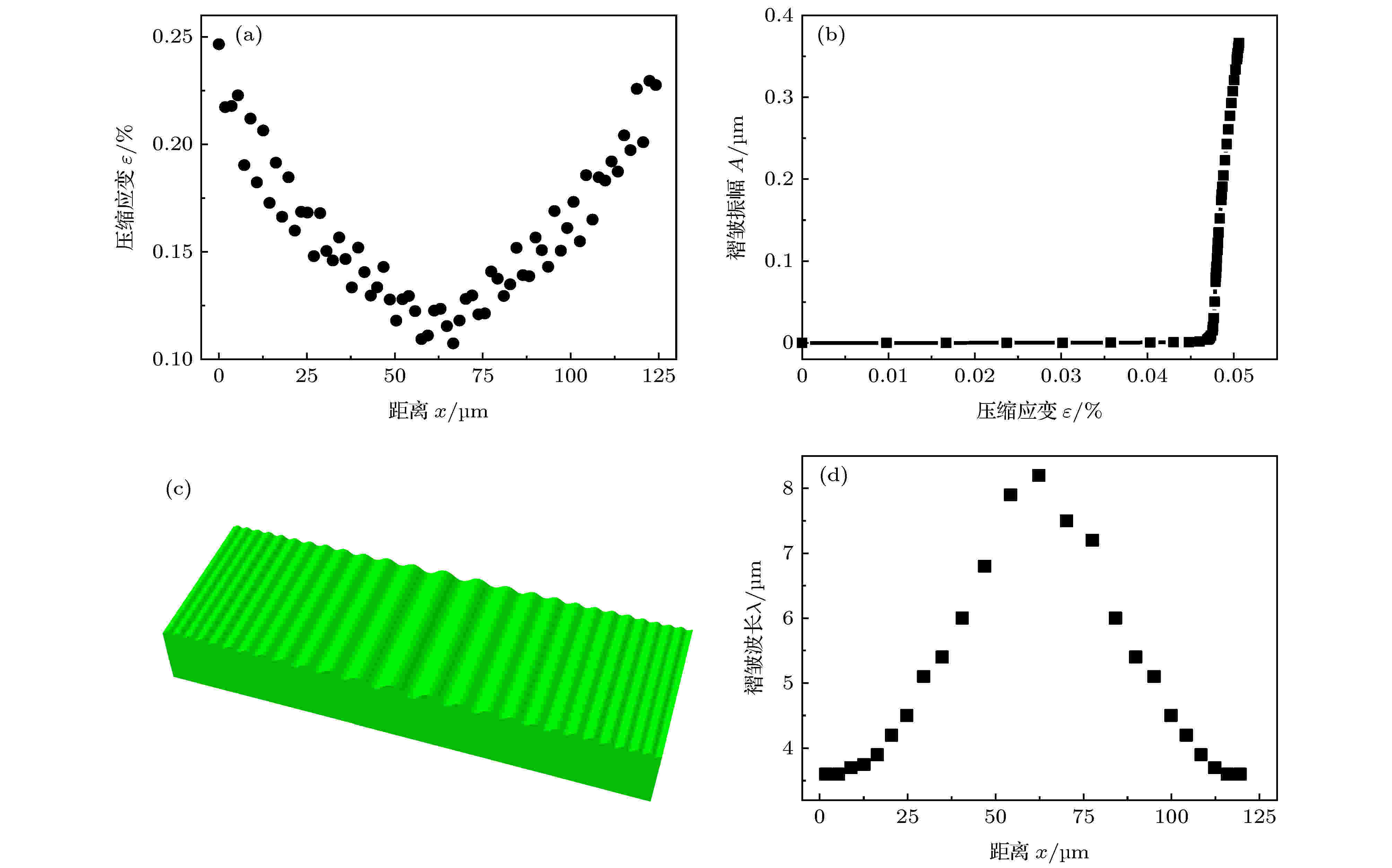图 8 有限元模拟结果 (a)一个周期内薄膜面内压应变的分布图; (b)褶皱幅值随薄膜面内压应变的演化规律; (c)一个周期内褶皱形貌的模拟图; (d)褶皱波长在一个周期的变化规律Figure8. Finite element simulation results: (a) Distribution of the in-plane compressive strain within a period; (b) evolution of the wrinkle amplitude with the in-plane compressive strain; (c) simulated wrinkle morphology within a period; (d) distribution of the wrinkle wavelength within a period.
当薄膜全部屈曲后, 其褶皱形貌如图8(c)所示,沿长度方向, 褶皱波长与膜厚成正比. 图8(d)显示了褶皱波长沿一个周期的变化规律, 波长分布情况与薄膜厚度分布一致, 可从波长分布反推得到薄膜的厚度梯度, 波长最大值和最小值之比约为2∶1, 这与(2)式的理论结果及实验中光学显微镜下的褶皱形貌一致.
1)由于编织铜网特殊的空间三维结构, 铜线覆盖处将自发形成厚度具有梯度的银薄膜, 最大膜厚与最小膜厚之比约为2∶1.
2)随着压缩应变的增加, 褶皱在膜厚较小处率先形成, 并逐渐扩展到膜厚较大区域, 褶皱波长和振幅在空间呈周期性振荡行为, 波长与膜厚成正比关系; 褶皱波长随应变的增加而减小, 服从手风琴模型的理论预言.
3)随着拉伸应变的增加, 裂纹开始在膜厚较小区域萌生扩展, 宽度增加, 最后形成多重裂纹模态; 裂纹的宽度和平均间距随薄膜厚度的增加而增加, 数目随膜厚的增加而减小.
4)采用应力理论对周期性厚度梯度薄膜的褶皱和裂纹的形貌特征和演化规律进行分析讨论, 采用有限元方法对薄膜的屈曲褶皱进行模拟计算, 完美解释了实验结果.
5)研究结果有助于深入理解周期性厚度梯度薄膜的应变效应, 并有望通过设计梯度薄膜阵列在柔性电子等领域获得应用.
