摘要:磁性斯格明子是一种具有涡旋状非共线自旋结构的准粒子, 具有独特的拓扑保护特性, 可在极低电流驱动下运动, 有望在信息技术领域获得广泛应用. 从2015年开始, 科学家已经发现了多种室温磁性斯格明子材料, 例如斯格明子多层膜、人工斯格明子材料、β-Mn型单晶材料、中心对称材料(铁氧体、六方Ni₂In型)等. 其中多层膜材料由于其制备工艺简单、可通过调节各膜层厚度优化性能、器件集成度高等优点而备受关注. 这些室温磁性斯格明子材料具有涌生电动势、拓扑霍尔效应、斯格明子霍尔效应等特性, 有望用来制备多种新型自旋电子器件, 例如赛道存储器、微波探测器、纳米振荡器等, 其中赛道存储器有望成为下一代非易失性、低能耗和高密度的存储器. 本文首先介绍了磁性斯格明子的基本特性, 然后综述了近年来室温磁性斯格明子材料的研究进展、制备技术及表征方法, 最后简单介绍了用室温磁性斯格明子材料研制赛道存储器、微波探测器等原型器件的研究进展, 展望了室温磁性斯格明子材料的未来发展趋势.
关键词: 磁性斯格明子/
室温/
赛道存储器/
微波探测器

English Abstract

全文HTML

--> --> -->

磁性材料中存在多种相互作用能, 如磁交换能、磁各向异性能、退磁场能、磁弹性能、外磁场能等^[1]. 在这些相互作用能的影响作用下, 磁性材料可存在多种稳定的自旋结构, 例如磁畴壁、涡旋、磁泡、斯格明子等^[2]. 其中斯格明子是一种具有准粒子特性的涡旋状非共线自旋结构.
在磁性材料中要形成斯格明子, 除了常见的相互作用能以外, 还需要引入手性相互作用^[1]. 常见的手性作用有长程的磁偶极相互作用、Dzyaloshinskii–Moriya(DM)相互作用、阻挫交换相互作用和四自旋交换相互作用^[1]. 由DM作用生成的斯格明子, 由于具有尺寸小(5—100 nm)且易调控、稳定性高等优点, 而受到广泛关注. 在磁性材料中, DM作用使得磁矩垂直, 而交换相互作用使得磁矩平行, 在这两种作用及其他磁性相互作用的共同影响下, 可形成斯格明子结构^[3].
斯格明子的结构如图1所示, 其中自旋单位磁矩m (x, y)是位置的函数, 斯格明子的中心自旋方向向下, 边缘处的自旋方向向上^[4]. 对于磁性材料中的自旋结构, 其拓扑特性可以用斯格明子数来表示. 斯格明子的斯格明子数是 ±1, 或其他整数. 而拥有不同斯格明子数的自旋结构之间不能通过连续变化来实现相互转化, 因此斯格明子拥有稳定的拓扑结构^[5].
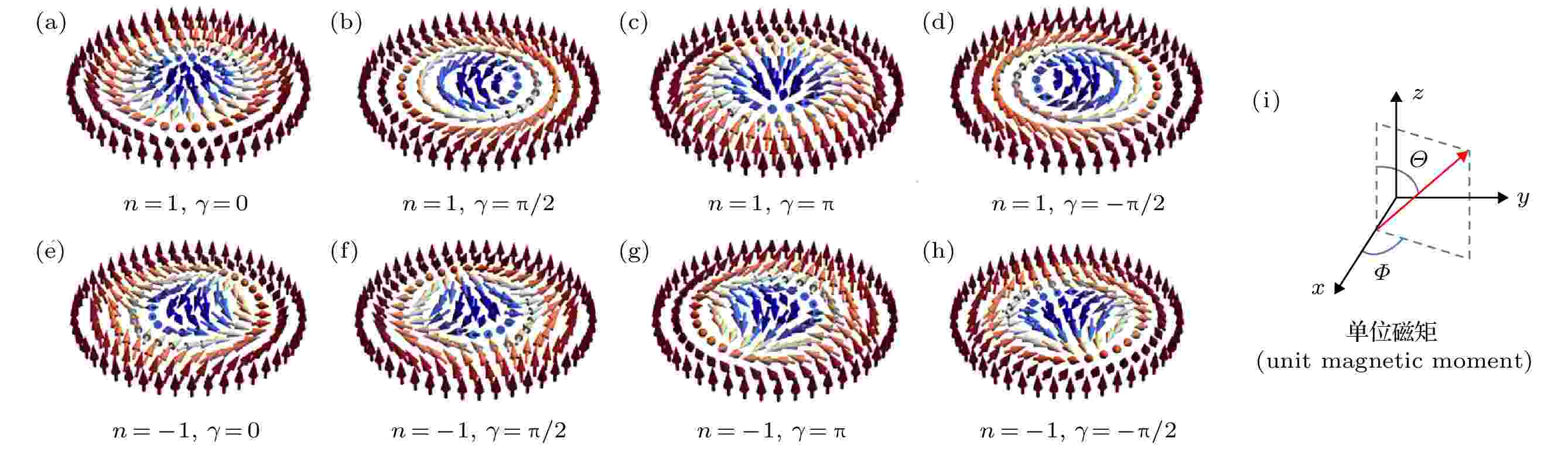图 1 不同自旋结构的斯格明子示意图　(a) 奈尔型斯格明子; (b) 布洛赫型斯格明子; (c) 奈尔型斯格明子; (d)布洛赫型斯格明子; (e)?(h) 反斯格明子; (i)单位磁矩方位示意图
Figure1. The spin structure diagram of different skyrmions: (a)Néel type skyrmion; (b) Bloch type skyrmion; (c) Néel type skyrmion; (d) Bloch type skyrmion; (e)?(h) anti-skyrmion; (i) the altitude and azimuth diagram of unit magnetic moment.

斯格明子最早是由英国物理学家Skyme^[6]于1962年得到的拓扑孤子解, 最初是用来解释原子核物理学中的强子(hadrons)的. 随后科学家发现这种准粒子存在于量子霍尔体系、玻色爱因斯坦体系、液晶及磁性材料中^[1,7,8]. 2006年, R?ssler等^[9]在理论上首次证明了可由DM作用生成基态可稳定存在的磁性斯格明子系统. 2009年, Mühlbauer等^[10]通过中子衍射首次在MnSi单晶材料中观察到磁性斯格明子的存在. 随后研究者们通过洛伦兹透射电镜、自旋极化扫描电镜等技术手段成功实现了斯格明子在实空间的成像^[11,12]. 目前磁性斯格明子可广泛存在于手性磁体(如MnSi, Cu₂OSeO₃)、磁性薄膜及多层膜系统、硬磁/软磁层材料(人工斯格明子)、中心对称材料(如铁氧体、六方Ni₂In型)等^{[10,11,13-16]}里面. 诺贝尔物理学奖获得者Fert等^[7]于2013年提出斯格明子可应用于赛道存储器, 为实现斯格明子的器件化指明了方向.
早期的研究发现, 磁性斯格明子多存在于低温环境, 且仅在极少数单晶材料中发现了室温或接近室温环境存在斯格明子. 2015年至2016年, 发现了一系列新型室温多层膜斯格明子材料, 如Ta/CoFeB/TaO_x^[17], (Ir/Co/Pt)₁₀^[18], Pt/Co/Ta, Pt/CoFeB/MgO^[19]等, 使得室温磁性斯格明子材料的研究进入了一个新阶段. 多层膜斯格明子材料具有尺寸小且可调、制备简单、温度稳定性好、器件集成度高等优点. 随着室温斯格明子材料研究的不断深入, 斯格明子材料开始在多种自旋电子器件中获得应用, 如赛道存储器、微波探测器、逻辑门、纳米振荡器等^[2].
本文首先介绍斯格明子的微磁学理论及其特有的拓扑特性和动力学特性; 其次介绍室温磁性斯格明子材料最新的研究进展, 包括多层膜材料^[14,18-21]、人工斯格明子材料^[15,22]、反铁磁/铁磁材料薄膜^[23]、β-Mn型单晶材料^[24,25]、中心对称材料(如铁氧体、六方Ni₂In型材料等)^[16,26]等; 随后介绍了斯格明子的应用, 主要介绍赛道存储器、微波探测器和纳米振荡器; 最后对室温斯格明子材料的研究现状及其在器件方面的应用进行了总结, 以期望为寻找最合适的室温斯格明子材料提供参考.

2

-->

2.1.斯格明子的微磁学结构

图1所示为典型的磁性斯格明子结构, 其中心的自旋方向向下, 边缘处的自旋方向向上. 从中心开始, 经连续改变方向, 通过面内, 逐步地过渡到边缘处. 根据过渡方式的不同, 磁性斯格明子的结构还可以进一步分为布洛赫型和奈尔型. 布洛赫型的磁矩为圆形环状分布, 如图1(a)所示; 奈尔型的磁矩为辐射状结构, 如图1(b)所示. 为了进一步了解斯格明子结构, 这里以二维材料为例介绍斯格明子的微磁学结构. 在二维平面中, 取斯格明子中心为坐标原点, 空间的位置用极坐标表示:

$x = r\cos \varphi,$

$y = r\sin \varphi, $

其中, r为单位磁矩的位置与坐标中心的距离, φ表示单位磁矩的位置与坐标中心连线与x轴正方向的夹角.
单位磁矩的分布是空间位置的函数, 在二维材料中, 可设单位磁矩分布为

${{m}}(r,\varphi) = ({m_x}(r,\varphi),{m_y}(r,\varphi),{m_z}(r,\varphi)).$

斯格明子中单位磁矩在z方向的分量为r的函数, 同时根据斯格明子的对称性, 可得

$\begin{split}\;& {{m}}(r,\varphi) = ({m_x}(r,\varphi),{m_y}(r,\varphi),{m_z}(r,\varphi)) \\ \! = & (\cos \varPhi (\varphi)\sin \varTheta (r),\sin \varPhi (\varphi)\sin \varTheta (r), \cos \varTheta (r)),\end{split} $

其中, $\varPhi $为地平经度, 表示单位磁矩与x轴方向的夹角, 是$\varphi $的函数; 而$\varTheta $为地平纬度, 表示单位磁矩与z轴方向的夹角, 是r的函数(图1(i)).
为进一步理解表达式(4)的含义, 可假设一定的边界条件, 如对于布洛赫型及奈尔型斯格明子, 可假定位于x轴正方向的单位磁矩方向与x轴夹角分别为π/2及0, 单位磁矩围绕坐标原点旋转2π; 同时可假定斯格明子满足当$r = 0$时有${m_z} = - 1$, 当$r = 1$时有${m_z} = 0$, 当$r = \infty $时有${m_z} = 1.$ Φ和φ, 及Θ和r的之间关系的具体表达式为^[4]

$\varPhi = n\phi + \gamma, $

$r = ({{1 + \cos \varTheta }})/({{1 - \cos \varTheta }}), $

其中, n取整数, 其符号正负表示斯格明子的变化方向, 符号为正时变化方向为逆时针方向, 符号为负时变化方向为顺时针方向, 大小表示单位磁矩围绕坐标原点一周旋转的周数; γ表示自旋结构的螺旋度, 常见取值为$0$, π/2, –π/2, π (图1). 当n = –1时, 所对应的自旋结构一般称为反斯格明子; 当n = 1, γ = π/2, –π/2时所对应的自旋结构为布洛赫型斯格明子; 当n = 1, γ = 0, π时所对应的自旋结构为奈尔型斯格明子.
2 -->

2.2.斯格明子的形成

在磁性材料中的各种相互作用中, 磁交换相互作用起着主要作用, 它使得磁矩的方向处于相互平行或反平行方向. 在某些材料中, 若是其他相互作用变得异常强大, 会使磁矩偏离平行或反平行方向, 进而形成丰富的磁畴结构^[2], 例如磁畴壁、磁泡、涡旋、斯格明子等^[1,2]. 除了常见的磁交换能、磁各向异性能、退磁场能、磁弹性能、外磁场能等以外, 在磁性材料中要生成磁性斯格明子, 还需引入手性相互作用. 手性相互作用是一种使得相邻磁矩相互垂直的作用, 常见的手性相互作用如表1所示. 在交换相互作用和手性相互作用的竞争下, 在一定的磁场作用和特定温度条件下, 可在磁性材料中生成磁性斯格明子结构.

作用机制	磁偶极相 互作用	DM作用	阻挫交 换作用	四自旋交换 相互作用
斯格明子 尺寸/nm	100—1000	5—100	~1	~1
典型材料	MnNiGa[16]	MnSi[10]	Fe3Sn2[26]	Fe/Ir(111)[11]

表1手性相互作用的类型^[1]
Table1.Types of chiral interactions^[1].

2 -->

2.3.DM作用

近年来, 研究多集中在由DM作用生成的斯格明子^[3]. DM作用来源于相对论效应的自旋轨道耦合的高阶作用项, 存在于空间对称破缺的材料中. 在固体材料中, 这种作用的来源是空间对称性的破缺和磁性原子间的高阶自旋轨道耦合^[10]; 而在薄膜材料中, DM作用来自磁性薄膜界面的对称破缺、磁性层和重金属层之间的强自旋轨道耦合. 对于相邻自旋, 其DM作用能的哈密顿量可表示为^[27]

${H_{{\rm{DM}}}} = - {{{D}}_{12}} \cdot ({{{S}}_1} \times {{{S}}_2}),$

其中, S₁和S₂是相邻原子间的自旋; D₁₂表示DM矢量, 由晶体的对称性所决定. 薄膜材料中D₁₂是一个平行于薄膜界面且垂直于S₁和S₂连线的矢量. 对于两个相互平行的磁矩, 当DM作用存在时, 这两个相邻磁矩的方向会向着DM矢量方向偏转.
在体材料和薄膜材料中, 假设自旋产生的磁矩是连续的, 则DM作用产生的能量密度可表示为^[2]

${\varepsilon _{{\rm{bulk}}}} = D{{m}} \cdot \nabla \times {{m}}.$

在薄膜材料中, 磁矩通常不是z的函数, 即$\dfrac{{\partial {{m}}}}{{\partial z}} = 0$, 则DM作用而产生的能量密度可表示为

${\varepsilon _{{\rm{i}} - {\rm{DM}}}} = D[{{{m}}_z}\nabla \cdot {{m}} - ({{{m}}_z} \cdot \nabla){{m}}],$

其中, ε_bulk和ε_i-DM分别表示在固体和薄膜材料中的DM作用能密度; m表示单位磁矩; m_z表示单位磁矩在z方向的分量; D为DM作用常数, 是一个与DM矢量D₁₂相关的量. D值的正负可决定斯格明子的类型. 在固体材料中, 由DM作用生成斯格明子的材料有MnSi, Mn_1–xFe_xSi, Fe_1–xCo_xSi, MnGe, Mn_1–xFe_xGe, FeGe, Cu₂OSeO₃等^[5,28], 它们多为布洛赫型斯格明子, 且多在较低的温度(16 K)下存在^[10]. 在薄膜材料中, 由于其与固体材料中DM作用特性的不同, 斯格明子为奈尔型, 例如 (Ir/Co/Pt)₁₀^[18], (Pt/Co/Ta)₁₅^[19], (Pt/CoFeB/MgO)₁₅^[19], [Pt/Gd₂₅Fe_65.6Co_9.4)/MgO]₂₀^[23], [Pt/CoFeB/MgO]₁₅^[29]等薄膜体系. 早期的研究发现, 在薄膜材料中, 斯格明子只能在极低的温度下存在, 例如Fe/Ir(111)薄膜材料等^[11]. 通过多层膜叠加的方式提高DM作用, 可以在室温下获得斯格明子. 需要指出的是, 在薄膜材料中还存在一种斯格明子磁泡, 其尺寸一般较大, 为1 μm左右, 且多为布洛赫型^[1]. 在薄膜材料中, DM作用和长程的磁偶极相互作用一般同时存在, 因此区别斯格明子磁泡和由DM作用生成的斯格明子, 主要是通过DM强弱来区分的. 后文将把由长程的磁偶极相互作用生成的斯格明子, 特别地称为斯格明子磁泡^[20,30].
2 -->

2.4.斯格明子的拓扑特性

3 -->

2.4.1.斯格明子数

斯格明子可在自旋极化电流或电场作用下运动, 同时可产生涌生电磁场作用在电子上, 从而产生拓扑霍尔效应. 而斯格明子的这些特性与斯格明子的拓扑特性密切相关. 在二维磁性材料或准二维磁性材料中, 自旋结构的拓扑特性可以用拓扑数(斯格明子数)N_sk来描述, 其定义如下^[1]:

${N_{{\rm{sk}}}} = \frac{1}{{4{\rm{\pi }}}}\iint {{{\rm{d}}^2}r{{m}}}\left(\frac{{\partial {{m}}}}{{\partial x}} \times \frac{{\partial {{m}}}}{{\partial y}}\right),$

其中, m表示单位磁矩, 是x, y的函数. 一般常见的斯格明子, 其斯格明子数N_sk通常为 ± 1. N_sk绝对值为1, 其物理意义是表示对于一个斯格明子, 其单位磁矩绕圆心旋转一周的角度为2π. N_sk的正负可表示不同类型的斯格明子, 例如当斯格明子中心的磁矩方向向下, N_sk值为负时, 表示反斯格明子, 它的磁矩围绕中心旋转时其方向的变化方向与斯格明子相反. 斯格明子是受拓扑保护的, 例如两种不同拓扑数的结构, 在绝热条件下, 不能通过连续的变化而相互转化; 同时这种拓扑结构具有非常高的稳定性, 在自旋电流的作用下, 其产生和湮灭具有滞后性^[5,15]. 对于其他自旋结构, 其拓扑数可以为零或半整数, 例如磁泡和涡旋的拓扑数为0, 半子(meron)的拓扑数为1/2^[4].
3 -->

2.4.2.拓扑霍尔效应

当电子流经斯格明子时, 电子会与磁矩产生强烈的自旋轨道耦合作用, 使得电子的自旋和斯格明子中的单位磁矩方向相互平行, 从而使得电子的运动状态发生变化, 即发生偏转而产生拓扑霍尔效应(图2 (a)). 在空间中单位磁矩的分布m (x, y, z, t)是一个随时间缓慢变化的量, 因此当电子流经具有斯格明子的材料时, 斯格明子会对电子的运动产生微扰, 于是电子运动的哈密顿量由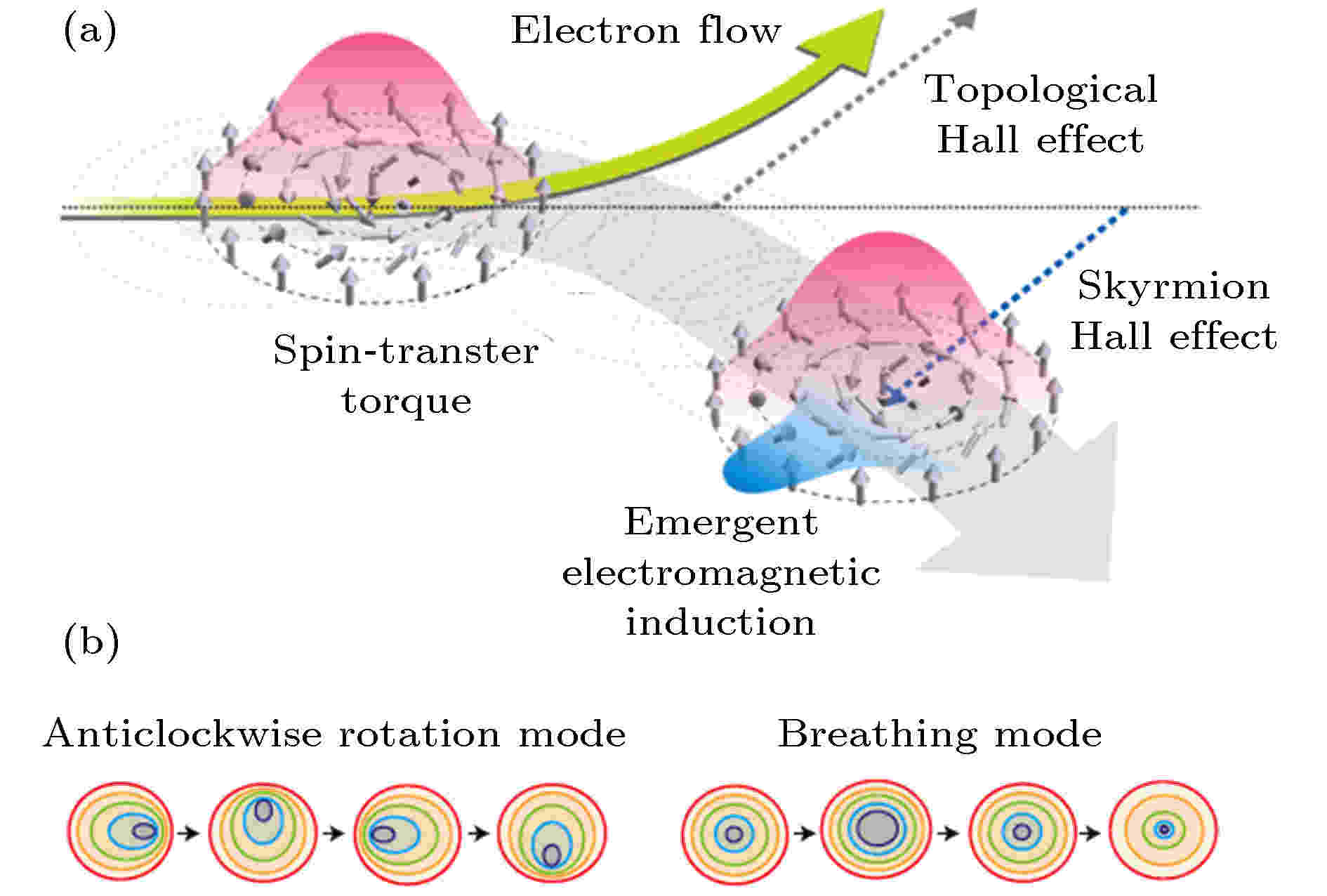
图 2 (a)斯格明子在电流作用下的运动及电子在涌生磁场作用生成的洛伦兹力作用下的偏转^[1]; (b) 斯格明子振荡示意图^[1]
Figure2. (a) Skyrmion move under the flow of electrons. Electrons are deflected by the Lorentz force due to the emergent magnetic field^[1]; (b) oscillation diagram of magnetic skyrmion^[1].

${H_0} = \frac{{{{{p}}^2}}}{{2{m_{\rm{e}}}}} - {{{J}}_{{\rm{ex}}}} \cdot {{{\sigma }}_{{z}}}$

变为^[31]

${H_0} = \frac{{{{\left({{{p}} + e{{{A}}^s}} \right)}^2}}}{{2{m_{\rm{e}}}}} - {{{J}}_{{\rm{ex}}}} \cdot {{{\sigma }}_z} - e{V^{\rm{s}}},$

其中p为电子动量, m_e为电子质量, J_ex为交换常数, ${{{\sigma }}_{{z}}}$为Pauli矩阵, 而e为电子电荷量. 微扰项A^s和V^s代表由斯格明子生成的电磁场的标矢和标势, 相应的标矢和标势可生成对电子作用的等效电磁场, 也称为涌生电磁场, 它们是坐标(x, y, z)及时间(t)的函数. 需要指出的是, 涌生电磁场和斯格明子数密切相关, 它们之间的关系为^[1,31]

${{B}}_i^{{\rm{em}}} \!=\! {\varepsilon _{ijk}}\!\left(\frac{{\partial A_k^{\rm{s}}}}{{\partial j}} \!-\! \frac{{\partial A_j^{\rm{s}}}}{{\partial k}}\right)\! = \frac{\hbar }{{2e}}{\varepsilon _{ijk}}{{m}} \cdot \!\left(\frac{{\partial {{m}}}}{{\partial j}}\! \times\! \frac{{\partial {{m}}}}{{\partial k}}\right)\!, $

${{E}}_i^{{\rm{em}}} = - \frac{{\partial {{{V}}^{\rm{s}}}}}{{\partial i}} - \frac{{\partial {{A}}_i^{\rm{s}}}}{{\partial t}} = \frac{\hbar }{e}{{m}} \cdot \left(\frac{{\partial {{m}}}}{{\partial i}} \times \frac{{\partial {{m}}}}{{\partial t}}\right), $

其中, B_i^em, E_i^em代表涌生磁场及涌生电场; A_i^s, V_i^s为标矢和标势; $\hbar $为约化普朗克常量; e为电子电荷量; ${\varepsilon _{ijk}}$是无量纲的三阶完全反对称张量.
根据麦克斯韦电磁场理论, 当斯格明子迁移时, 涌生磁场会相应地产生横向电场. 若假设斯格明子的迁移速度为v_d, 由斯格明子的迁移而产生的电场E'为

${ E'} = - {{{v}}_{\rm{d}}} \times {{B}}_{{i}}^{{\rm{em}}}.$

由于涌生电磁场及迁移电场的存在, 极化电流的电子会发生横向偏转, 从而产生电阻, 这种电阻为拓扑霍尔电阻. 通过对拓扑霍尔电阻的测量可间接表征磁性材料中的斯格明子. 在一些磁性材料中斯格明子会按照一定的规律周期性排列形成空间架构, 这些架构称为斯格明子晶格, 常见的斯格明子晶格有三方、四方相晶格(图4(a))^[24]. 在具有斯格明子晶格的单晶材料中, 如MnGe, FeGe, MnSi等单晶材料^[1]中发现了拓扑霍尔效应, 但单个斯格明子产生的涌生电场对电子偏转的相关研究则相对较少^[4].
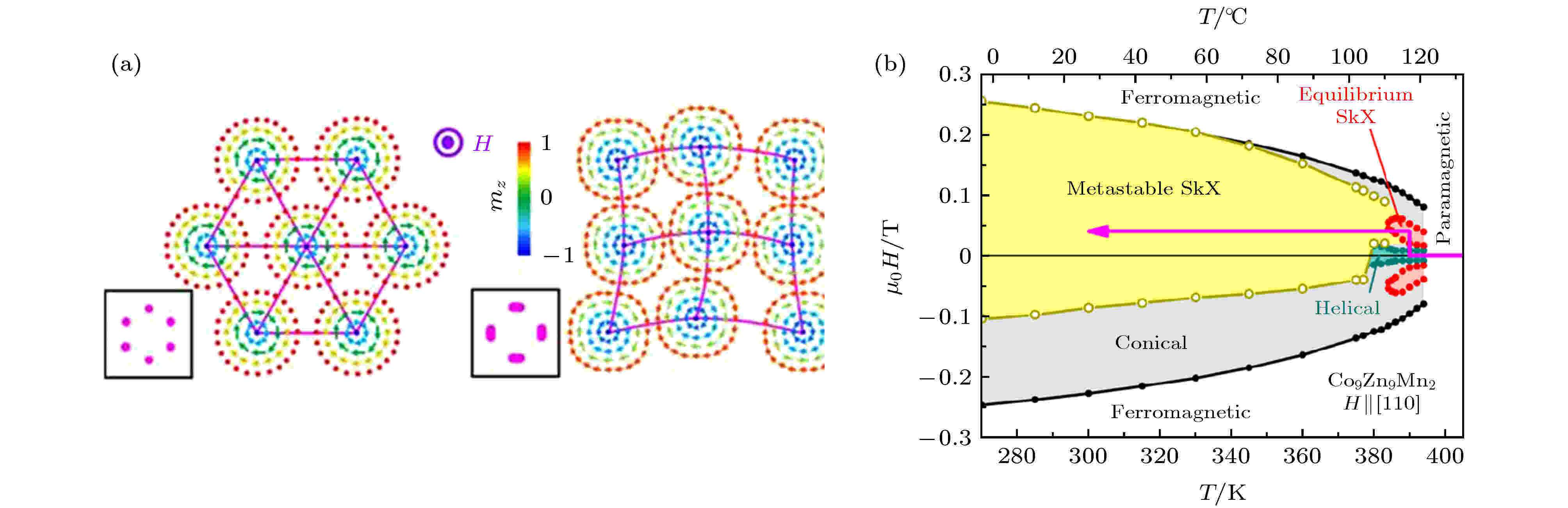图 4 (a)实空间中四方和三方斯格明子晶格示意图^[24]; (b) Co₉Zn₉Mn₂单晶的温度-磁场相图(T-H)^[24]
Figure4. (a) Schematic figures of a triangular-lattice skyrmion crystal (SkX) and a square like-lattice SkX in real space^[24]; (b) temperature(T)- magnetic field(H) state diagram of bulk Co₉Zn₉Mn₂^[24].

2 -->

2.5.斯格明子动力学

斯格明子可在外加条件作用下迁移, 其中最常见的就是在极化电流作用下的迁移. 2010年, Jonietz等^[32]在MnSi晶体中发现电流可以驱动斯格明子晶格的旋转. 2011年, Yu等^[33]在FeGe中发现, 用极低的电流密度可驱动斯格明子运动. 极化电流对斯格明子的驱动作用, 其本质是极化电流中自旋电子与磁矩的耦合作用. 单位磁矩在极化电流驱动下的运动规律可用Landau-Lifshitz-Gilbert-Slonczewski 方程来描述^[1,31]:

$\begin{split}& \frac{{\partial {{m}}}}{{\partial t}} + ({{j}} \cdot \nabla){{m}} \\={}& - {{m}} \times \frac{{\delta {{{H}}_{\rm{s}}}}}{{\delta {{m}}}} + {{m}} \left[{\alpha _{\rm{G}}}\frac{{\partial {{m}}}}{{\partial t}} + \beta ({{j}} \cdot \nabla){{m}}\right], \end{split}$

其中, m为单位磁矩, H_s是磁矩的哈密顿量, j为电流密度, ${\alpha _{\rm{G}}}$为Gilbert阻尼系数, 而$\beta $为非绝热效应系数.
若将斯格明子看作刚体, 在电流的作用下, 单个斯格明子在磁性材料中的运动规律, 可由Thiele方程获得^[1]:

${M_{\rm{s}}}\frac{{{\rm{d}}{{{v}}_{\rm{d}}}}}{{{\rm{d}}{{t}}}} + {{G}} \times ({{{j}}_{\rm{v}}} - {{{v}}_{\rm{d}}}) + k({\alpha _{\rm{G}}}{{{v}}_{\rm{d}}} - \beta {{{j}}_{\rm{v}}}) = - \nabla U,$

式中${v_{\rm{d}}} = {\rm{d}}{{R}}/{\rm{d}}t$, R表示斯格明子的质心; M_s为斯格明子的等效质量; G为陀螺矢量, G = 2πN_ske_z(e_z为z方向单位矢量); j_v为电子迁移速度; v_d为斯格明子的迁移速度; k为无量纲常数; U为由于边界、磁场、杂质等引起的势场.
Thiele方程的最重要的推论是斯格明子除了在电流方向上运动以外, 还拥有垂直于电流方向的速度: ${{{v}}_ \bot } = ({\alpha _{\rm{G}}} - \beta){{{j}}_{\rm{v}}}$, 如图2(a)所示, 这种现象称为斯格明子霍尔效应^[34]. 需要指出的是, 在电流驱动下, 斯格明子的运动速度在一定的范围内随着外加电流密度的增加而增加, 最后达到最大值. 当电流密度足够大时, 斯格明子将会消失^[14]. 同电子等不同的是, 当驱动电流消失时, 斯格明子的运动也会消失; 当再次施加电流时, 斯格明子又开始运动^[20].
斯格明子除了可在电流驱动下运动外, 还可以在外加磁场或极化电流的驱动下振荡. 目前已知的振荡方式有两种: 一种是斯格明子的中心区域作周期性的膨胀或收缩, 作呼吸式振荡(图2(b)); 另外一种是斯格明子中心围绕几何中心作周期性旋转(图2(b)). 斯格明子中心围绕几何中心旋转有两种不同旋转方式: 一种是与斯格明子手性相同的方向旋转; 另外一种是与斯格明子手性相反的方向旋转. 斯格明子自激振荡的最主要的应用是制备微波探测器^[1,2].
2 -->

2.6.低温磁性斯格明子材料

磁性斯格明子最早是在具有B20结构的材料, 如单晶MnSi^[10], Fe_0.5Co_0.5Si^[35], FeGe^[13]中发现的. 后来陆续发现磁性斯格明子存在于金属超薄层材料Fe/Ir(111)等^[11]以及Cu₂OSeO₃中^[36,37], 它们大多是在低于室温下存在(表2). 通过对低温磁性斯格明子的研究, 发现磁性斯格明子具有多种特性, 例如: 2009年, Mühlbauer等^[10]发现若干个斯格明子会以一定的规律排列在磁性材料中形成斯格明子晶格; 2010年, Jonietz等^[32]在MnSi晶体中发现电流可以驱动斯格明子晶格的旋转; 2011年, Heinze等^[11]通过分子束外延法制备出金属超薄层Fe/Ir(111), 并利用自旋极化扫描电子显微镜在Fe层上发现了斯格明子; 2013年, Romming等^[38]利用STM产生的极化电流, 首次实现了单个斯格明子的产生和湮灭; Seki等^[36,37]发现, 在多铁材料Cu₂OSeO₃中, 可通过电场调控Cu₂OSeO₃中的斯格明子; 张等^[4]发现在激光脉冲的驱动下可移动斯格明子, 等等. 但由于这些材料不能在室温下产生稳定的斯格明子结构, 对晶体的质量要求较高, 因此在应用方面受到了一定的限制^[5].

材料	材料 种类	斯格明 子种类	制备方法	斯格明子 温度/K
MnSi[10]	单晶	布洛赫	布里奇 曼法	29
Fe0.5Co0.5Si[35]	单晶	布洛赫	布里奇 曼法	25
FeGe[13]	单晶	布洛赫	布里奇 曼法	60—260
FeGe[33]	单晶	布洛赫	布里奇 曼法	250—270
Fe1–xCoxSi (x = 0.5)[39]	单晶	布洛赫	布里奇 曼法	10
Fe/Ir[11]	金属超 薄层	奈尔型	分子束 外延法	11
PdFe/Ir(1 1 1)[38]	金属超 薄层	奈尔型	分子束 外延法	4.2
Cu2OSeO3[36]	单晶	布洛赫	布里奇 曼法	60
FeGe1–xSix (x ~ 0.25)[39]	单晶	布洛赫	布里奇 曼法	95

表2低温磁性斯格明子材料
Table2.Magnetic skyrmions materials at low temperature

在2015年到2016年之间, 科学家们陆续发现了多种在室温下可稳定存在斯格明子的磁性材料. 按照材料的维度可分为薄膜材料和单晶材料. 如表3所示, 薄膜材料中包含多层膜材料^[14,18-21]、人工斯格明子材料^[15,22]、反铁磁/铁磁材料薄膜等^[23]; 单晶材料中包含β-Mn型单晶材料^[24,25]、中心对称材料(铁氧体、六方Ni₂In型)等^[16,26]. 虽然室温磁性斯格明子的某些特性与低温磁性斯格明子有很大的区别, 但室温磁性斯格明子材料的发现, 不仅丰富了材料科学的研究内容, 也必将促进磁性斯格明子材料的应用.

	材料类型		典型材料	制备方法	斯格明子温 度范围/K	斯格明子的 尺寸/nm
薄膜材料	多层膜材料		Ta/CoFeB/TaOx[17] (Ir/Co/Pt)10[18] Pt/Co/Ta, Pt/CoFeB/MgO[19]	直流溅射	室温	1000 30—90 100
	反铁磁/铁磁材料薄膜		[Pt/Gd25Fe65.6Co9.4/MgO]n[23]	直流溅射	室温	180
	人工斯格明子材料		Co/Ni/Cu(001)[15] Co/[Co/Pd]n, Co/Pd[40]	直流溅射	室温	1000
单晶材料	手性对称材料		Co8Zn8Mn4[41] Co8Zn9Mn3[25] (β-Mn结构)	布里奇曼法	284—300 311—320	> 125
	中心对 称材料	铁氧体	Ba(Fe1–xScxMg0.05)12O19[42]	布里奇曼法	室温	200
		金属间化合物	MnNiGa[16]、	布里奇曼法	100—340	90
	阻挫型		Fe3Sn2[26]	聚焦离子束技术(FIB)	100—340	300

表3室温斯格明子材料
Table3.Magnetic skyrmions materials at room temperature.

2

-->

3.1.多层薄膜材料

多层膜材料中, 斯格明子的生成主要是来自膜层间的DM作用, 它是重金属层和磁性层的界面之间自旋轨道耦合的高阶作用项. 与手性单晶不同的是, 在多层膜材料中斯格明子类型是奈尔型的. 由于多层膜可用磁控溅射来制备, 这种材料非常容易通过调节材料类型、膜层厚度、构造特殊结构等来进行优化, 因此受到广泛的关注.
2011年, Heinze等^[11]通过分子束外延法在铁磁金属Fe和重金属Ir组成的金属超薄层Fe/Ir(111)异质结构里发现了磁性斯格明子. 早期在薄膜材料中发现的斯格明子虽然尺寸小, 约1 nm, 但只能在11 K温度下存在. 室温磁性斯格明子最早由江万军等^[14] 在2015年在多层薄膜材料中发现. 他们通过溅射法制备了Ta (5 nm)/CoFeB (1.1 nm)/TaO_x (3 nm)^[14]三层膜结构, 并构造了桥式结构(图3(a)). 在电流的驱动下, 磁畴可移动, 当磁畴经过桥式结构时, 将转换成斯格明子结构. 不同于金属超薄层中的斯格明子, 江万军等^[14]获得的斯格明子为斯格明子磁泡, 尺寸约为1 μm, 还不能满足应用的要求.
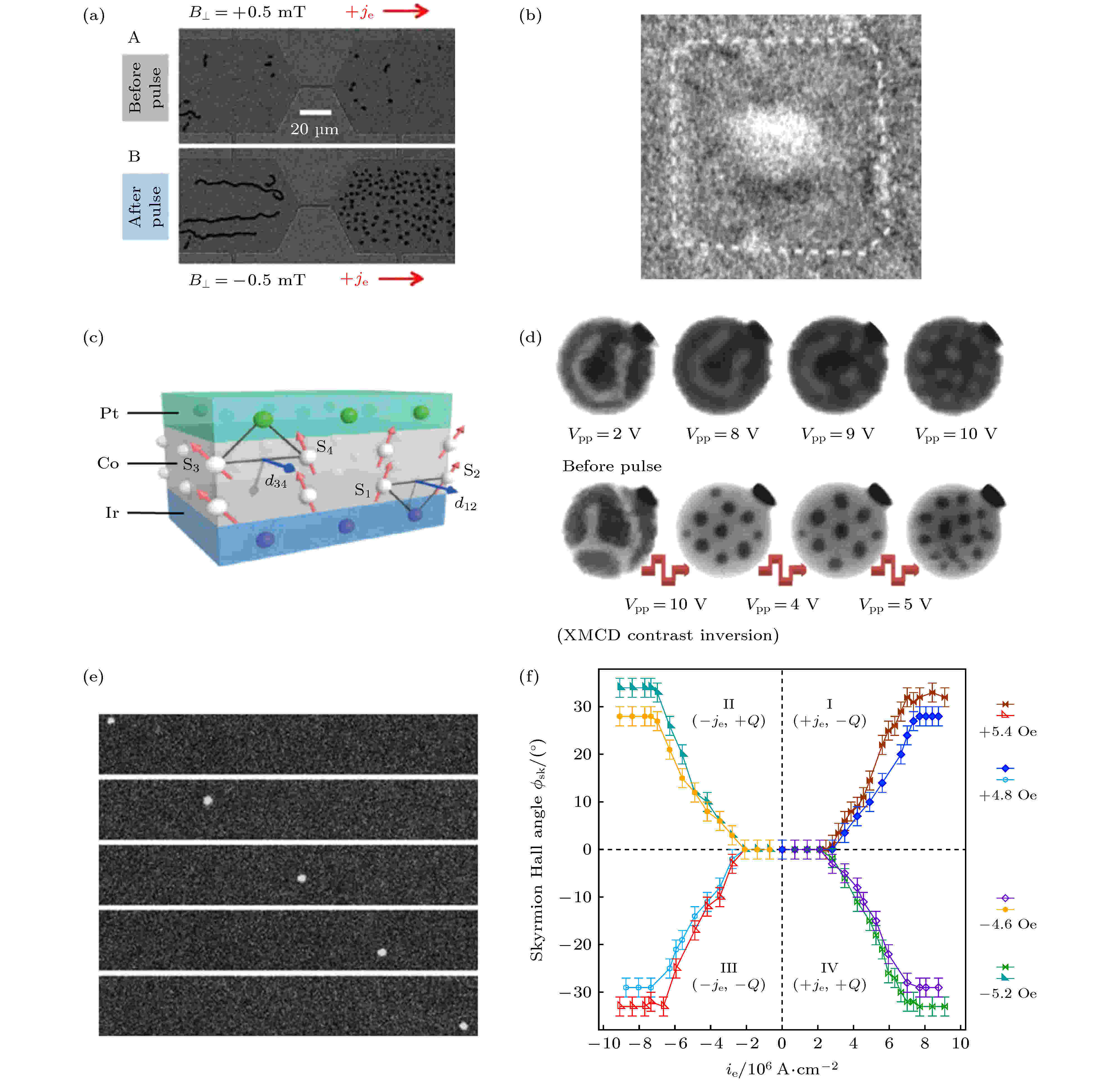图 3 (a) Ta/CoFeB/TaO_x三层膜桥式结构中斯格明子的形成^[14]; (b) 在Pt/Co/MgO三层膜正方型结构中的斯格明子^[21]; (c)在Pt和Ir层中Co层中DM作用的的叠加^[18]; (d)在脉冲10 V电场下, 迷宫磁畴转化为斯格明子^[19]; (e) 通过磁光克尔显微镜在薄膜Ta/CoFeB/TaO_x直接观察到斯格明子霍尔效应^[17]; (f)斯格明子霍尔角与电流密度的函数关系^[17]
Figure3. (a) Skyrmion bubbles realized at the exit of a constriction of Ta/CoFeB/TaO_x trilayer^[14]; (b) skyrmion realized in a square of Pt/Co/MgO trilayer^[21]; (c) additive DM for Co between Pt and Ir^[18];(d) with the electric field pulse, the labyrinth domain is transformed into the skyrmion^[19] (e) skyrmion Hall effect is clearly observed in successive Kerr microscopy images of a Ta/CoFeB/TaO_x trilayer^[17]; (f) phase diagram of the skyrmion Hall angle as a function of current density^[17].

2016年, Moreau-Luchaire等^[18]发现在室温下斯格明子可稳定存在于(Ir/Co/Pt)₁₀中. 他们利用扫描透射X射线显微镜(scanning transmission X-ray microscopy, STXM)在极低的外加磁场(B_z = 58 mT)下, 获得了小尺寸(约60 nm)的斯格明子结构. 最初的几种薄膜材料, 例如Fe/Ir^[11], PdFe/Ir(1 1 1)^[38]等, 其斯格明子只能在极低的温度11.0 K或4.2 K下存在. 最大的原因是形成斯格明子材料所需的DM作用, 会随温度升高而急剧下降, 而在(Ir/Co/Pt)₁₀多层膜中, 如图3 (c)所示, 在Ir/Co界面处和Co/Pt界面处DM作用的方向相反, 使得每一层Ir/Co/Pt具有极大的DM作用, 而通过多层膜的叠加使得DM作用进一步增强达到2 mJ/m², 从而在室温下生成磁性斯格明子结构. Moreau-Luchaire等^[18]通过实验证实, 斯格明子的尺寸大小可通过调节外加磁场的大小来调节. 2016年, Boulle等^[21]制备了Co/Pt/MgO薄膜, 利用X射线磁性圆二色性-光发射电子显微镜(X-ray magnetic circular dichroism-photoemission electron microscopy, XMCD-PEEM)发现, 通过构造尺寸为420 nm的人工正方形边界条件, 斯格明子可在无磁场的条件下存在于Co/Pt/MgO薄膜中(图3 (b)).
Woo等^[19]采用磁控溅射方法, 制备了(Pt/Co/Ta)₁₅及(Pt/CoFeB/MgO)₁₅多层膜材料, 利用磁透射X射线显微镜(magnetic transmission X-ray microscopy, MTXM)和STXM, 发现(Pt/Co/Ta)₁₅及(Pt/CoFeB/MgO)₁₅多层膜材料在室温下存在斯格明子. 与Moreau-Luchaire等^[18]的发现不同的是, (Pt/Co/Ta)₁₅及(Pt/CoFeB/MgO)₁₅两种材料的中间层Co及CoFeB与其上下两层具有相同方向的DM作用, 因此在每一周期的Pt/Co/Ta及Pt/CoFeB/MgO中有一个DM净值, 可通过多层膜的叠加来得到极高的DM值, 以此在室温下获得斯格明子结构. 而在多层膜(Pt/Co/Ta)₁₅^[19], 如图3(d)所示斯格明子的特殊Ω状结构中, 由于边界效应, 在脉冲10 V电场的作用下, 可将迷宫畴转换为斯格明子结构, 获得的斯格明子可在室温无外加磁场作用下稳定存在. Yu等^[43]利用极向克尔效应(polar magneto-optical Kerr effect, MOKE)显微镜在Ta/Co₂₀Fe₆₀B₂₀/MgO中观察到了斯格明子磁泡. Yu等^[43]发现, 即使Ta/Co₂₀Fe₆₀B₂₀/MgO中DM作用非常微弱(0.25 mJ/m²), 也会使得斯格明子的类型是奈尔型的. 在具有氧化层的多层膜材料中, 氧化层为覆盖层, 主要起着保护作用, 但有实验表明, 氧化层可以起到调节磁性层的垂直各向异性和DM作用的效果^[44].
在多层膜材料中, 除了可以获得大的DM值以外, 还可通过多层膜的周期及膜层中材料的类型来调节斯格明子的热稳定性及其手性. 2017年, Soumyanarayanan等^[45]在(Ir/Fe/Co/Pt)₁₀中, 通过调节铁磁层Fe与Co膜层厚度的比例来调节斯格明子的热稳定性及DM值. 2018年, Dovzhenko等^[46]在直径为2 μm的纳米多层膜(Pt/Co/Ta)₁₀中发现, 与一般多层膜中斯格明子的手性全部为左旋不同的是, 在(Pt/Co/Ta)₁₀的多层膜中斯格明子的手性和螺旋方式是沿着垂直膜层的方向不断演化的. 2018年, Woo等^[47]在室温下, 在Pt/GdFeCo/MgO多层膜中通过施加电流, 实现了单个斯格明子的产生或湮灭. 2018年, Woo等^[23]发现在Pt/GdFeCo/MgO多层膜中, 斯格明子可分别在Gd及FeCo亚层中产生, 在这两个膜层的斯格明子通过反铁磁耦合在一起, 称为铁磁斯格明子(ferrimagnetic skyrmions). 铁磁斯格明子在电流的驱动下运动, 可获得50 m/s的运动速度. 由于膜层间斯格明子的反铁磁耦合, 当铁磁斯格明子运动时可获得一个极小的斯格明子霍尔角θ_SkHE = 20°.
2 -->

3.2.人工斯格明子

人工斯格明子最早是2013年Sun等^[22]通过微磁学模拟预测其可能存在于CoPt/Co中. 2014年, 栗佳等^[15]等通过实验在Co/Ni/Cu(001)构造了这种结构. 实验表明在Co/[Co/Pd]_n和Co/Pd^[40]薄膜中也存在人工斯格明子结构. 人工斯格明子结构是由软磁层和硬磁层组成的微纳米结构^[22,30]. 软磁层由于形状效应, 可形成涡旋结构, 能映射到硬磁层中. 在一定的外加磁场的作用下, 可在硬磁层中形成斯格明子结构. 由于可选择高温度的磁性薄膜材料, 人工斯格明子结构中的斯格明子可在室温下稳定存在. 但由于形成软磁层涡旋所需的形状效应, 人工斯格明子无法像一般的斯格明子那样在电流的驱动作用下运动, 这必将限制它在赛道存储器等器件中的应用.
2 -->

3.3.单晶材料

3 -->

3.3.1.手性对称材料

斯格明子可存在于手性对称的磁性材料中, 例如: 具有B20结构的MnSi^[10], FeGe^[13]; 具有立方P2₁3结构的Cu₂OSeO₃^[36,48]等. 在具有B20结构的材料中, DM作用来自于晶体结构的空间对称性破缺. 这些单晶材料多在低于或接近室温才会生成斯格明子, 其中只有FeGe材料能在接近室温(278 K)下生成斯格明子^[13]. 早期在室温下可稳定存在斯格明子的单晶为β-Mn型结构的Co_10–x/2Zn_10–x/2Mn_x^[24,25], 其斯格明子仅在有限的温度范围内稳定存在. 如图4 (b)所示, 2017年, Karube等^[24]在Co₉Zn₉Mn₂合金中发现斯格明子可在390 K时稳定存在. 在外加磁场的作用下, 逐步降低温度到室温300 K, 可获得亚稳态的斯格明子晶格, 它可在较宽的温度范围内存在(300—390 K). 如图4(a)所示的三方晶格和四方晶格, 亚稳态晶格是这两种晶格的复合体, 同时它可在无外加磁场的室温下稳定存在.
3 -->

3.3.2.中心对称材料

中心对称的材料中没有DM作用, 其丰富的自旋结构主要是由磁偶极作用、单轴各向异性及交换作用生成的^[49]. 目前在具有中心对称的单晶材料中, 存在斯格明子的典型材料代表有Ba(Fe_1–xSc_xMg_0.05)₁₂O₁₉^[42], La_2–2xSr_1+2xMn₂O₇^[49], MnNiGa^[16]等. 与手性材料不同的是, 由于DM作用的缺失, 在Ba(Fe_1–xSc_xMg_0.05)₁₂O₁₉^[42]中, 斯格明子可同时随机存在于多种手性结构中. 在La_2–2xSr_1+2xMn₂O₇^[49], MnNiGa^[16]两种材料中, 存在双斯格明子结构, 每个自旋结构可看作两个手性不同的斯格明子组成, 其斯格明子数为2, 但是La_2–2xSr_1+2xMn₂O₇中的双斯格明子只能在100 K的温度下存在. 金属间化合物MnNiGa具有Ni₂In六方型结构, 斯格明子可存在于较宽温度范围(100—340 K)内. 虽然在双斯格明子材料中能观察到拓扑霍尔效应, 但是由于自身结构的特点, 双斯格明子中常难以观察到斯格明子霍尔效应. 2018年, 侯志鹏等^[26]在六方阻挫型磁体Fe₃Sn₂单晶中发现斯格明子可存在于100—400 K的温度范围, 这是目前已知的斯格明子温区范围最广的材料.
2 -->

3.4.室温磁性斯格明子在电流驱动下的运动

斯格明子具有孤子特性, 在外加电场、外加自旋极化电流及激光的作用下, 可以在磁性材料中迁移^[4]. 自旋极化电流中电子的自旋取向一致向上或向下, 可用来驱动斯格明子运动. 自旋极化电流驱动时, 斯格明子除了会沿着外加电流的方向, 还会垂直于外加电流方向运动. 因此斯格明子的运动方向会与电流方向有一夹角, 称为斯格明子霍尔角^[1]. 不同于电子等粒子, 斯格明子的运动只在电流存在时才持续运动, 而在电流消失时斯格明子则会处于静止状态.
在室温磁性斯格明子材料中, 2015年, 江万军等^[17]利用磁光克尔效应显微镜在Ta/CoFeB/TaO_x里, 首次直接观察到斯格明子霍尔效应(图3(e)). 他们发现, 在一定的范围内霍尔角随着电流密度的增大而增大, 最后趋于不变(图3(f)). 而后来在(Pt/Co/Ta)₁₅^[19], (Pt/CoFeB/MgO)₁₅^[19], [Pt/Gd₂₅Fe_65.6Co_9.4)/MgO]₂₀^[23], [Pt/CoFeB/MgO]₁₅^[29]等体系中, 人们都观测到明显的斯格明子霍尔效应, 如表4所示, 虽然斯格明子的速度最高可达到100 m/s, 但需要在外加磁场的作用下才能稳定存在. 由于焦耳效应, 电流驱动势必会产生焦耳热. 因此制备低电流密度、快速移动的室温磁性斯格明子材料具有非常诱人的前景.

材料	驱动电流/107A·cm–2	移动速度/m·s–1	霍尔角/(°)	温度	磁场/mT
Ta/CoFeB/TaOx[17]	0.62	0.75	32	室温	0.52
(Pt/Co/Ta)15[19]	3.50	50	19.4	室温	有
(Pt/CoFeB/MgO)15[19]	5.00	100	4.01	室温	有
[Pt/Gd25Fe65.6Co9.4)/MgO]20[23]	3.55	50	20	室温	145.00
[Pt/CoFeB/MgO]15[29]	4.20	100	30	室温	30.00

表4室温薄膜材料中斯格明子在电流驱动下运动
Table4.The motion of skyrmion in room temperature films driven by current.

2

-->

4.1.室温磁性斯格明子材料的制备

室温磁性斯格明子材料的常见制备方法为直流溅射法、分子束外延法及布里奇曼法等(表5). 分子束外延法是在高超真空中(10^–8 Pa), 利用各薄膜成分的分子束流, 直接喷射到衬底的真空镀膜工艺. 如早期的斯格明子材料PdFe/Ir(111)^[38]就是采用的这种方法. 采用分子束外延法制备的薄膜材料的的均匀性好、平整性高, 但是这种方法制备的成本较高, 且生长缓慢, 不适合规模化生产室温下可稳定存在的斯格明子多层膜材料.

方式	材料类型	制备时间	优点
直流溅射	薄膜材料	3 h	成本低, 适合工业量产
分子束外延	薄膜材料	> 1 d	薄膜平整度高
布里奇曼法	单晶材料	1 m	制作大尺寸器件

表5斯格明子材料常见制备方式
Table5.Common preparation method of skyrmion materials.

金属薄膜材料多采用直流溅射法制备, 它是一种常见的薄膜制备方法, 容易实现规模化生产. 室温磁性斯格明子薄膜材料多采用直流溅射法制备, 如(Pt/Co/Ir)₁₀^[18], Ta/CoFeB/TaO_x^[14], (Pt/Co/Ta)₁₅^[19], (Pt/CoFeB/MgO)₁₅^[19], (Pt/CoFeB/MgO)₁₅^[29], [Pt/(Gd₂₅Fe_65.6Co_9.4)/MgO]₂₀^[23]等. Moreau-Luchaire等^[18]采用热氧化硅基底, 用200 nm厚的Si₃N₄作为基底, 氩气的压强为0.25 Pa. 采用10 nm厚的Pt作为缓冲层, 紧接着沉积Co(0.6 nm)|Pt(1 nm)双层薄膜, 随后生长不对称结构Ir(1 nm)|Co(0.6 nm)|Pt(1 nm)₁₀. 为了使得材料符合STXM的测试要求, 可采用Si₃N₄作为基底. 多层膜制备后, 为了完成性能测试, 还需构造各种形状, 这需要与光刻、电镀等工艺相结合. 由于溅射法制备的薄膜有一定的不均匀性和缺陷, 这必将会带来一定的磁各向异性、DM作用及退磁场等不均匀性问题, 继而造成磁性斯格明子分布的不均匀及尺寸大小分布的不均匀. 在实验制备过程中需进一步考虑由于缺陷和不均匀性而导致的对斯格明子传输特性的影响.
单晶材料的生长多采用布里奇曼法(又称坩埚下降法), 该方法是将原料装进合适容器中, 在具有一个单向温度梯度内的温区内生上晶体的方法. 采用布里奇曼制备单晶时, 通常要先将粉末材料制备成多晶. 下面以Co_xZn_yMn_z (x + y + z = 20)为例^[25,41]介绍这种方法. 将总计2 g的纯Co, Zn, Mn密封在真空石英管中, 然后缓慢升温至1000 ℃ (12 h), 再缓慢降低到925 ℃ (1 ℃·h^–1), 之后对其进行水淬, 形成多晶. 随后采用布里奇曼法用超过一周的时间生长出Co₈Zn₈Mn₄单晶. 生长完毕后温度由1025 ℃降低到700 ℃, 同样进行水淬形成单晶. 对于布里奇曼法制备的单晶, 为了测试分析, 需要进行定向、切割、抛光等.
2 -->

4.2.斯格明子的表征

对于室温磁性斯格明子材料, 常见的表征手段多是基于X-射线衍射的探测手段, 例如XMCD-PEEM, STXM (表6). XMCD-PEEM主要应用于对磁性材料表面磁矩的探测, Li等^[15]首次利用XMCD-PEEM在薄膜材料中观察到斯格明子结构; Boulle等^[21]将XMCD-PEEM与光激发电子显微镜(the photoemission electron microscopy)结合起来成功观察到奈尔型斯格明子结构, 并确定了斯格明子的手性. 而STXM^[18]可应用于观察薄膜材料内部的斯格明子结构, 并可实时观察薄膜材料中斯格明子的变化, 例如STXM可被应用来监测斯格明子在电流驱动下的运动. 除了基于X-射线的探测手段外, 还可使用其他的方法探测斯格明子. 例如江万军等^[14]利用磁光克尔显微镜成功观察到了斯格明子的产生和湮灭. 但磁光克尔显微镜其分辨率有限, 难以观察到斯格明子的手性及小尺寸的斯格明子, 多用于探测尺寸大于1 μm的斯格明子. X-射线全息术(X-ray holography)^[4]提供了一种能观察小尺寸斯格明子及可实时观察斯格明子的手段. SPLEEM^[50]可被用来探测小尺寸的斯格明子, 它具有分辨率高, 探测敏感度强等优点.

方式	分辨率 /nm	优点	适用场景
XMCD- PEEM	~25	平面内高自 旋分辨率	外层磁性 斯格明子
STXM	~25	可探测磁场及电场 敏感材料实时监控	多层膜内部的斯 格明子结构
SPLEEM	~10	平面高分辨率高 的测试敏感度	原位沉积表面 的斯格明子
X射线 全息术	~10	无误差探测实时 监控(~70 ps)	纳米尺寸的多层 膜内部的斯格 明子结构
MOKEM	1000	操作简单易行	尺寸大于1 μm 的斯格明子

表6室温斯格明子的表征技术一览表^[4]
Table6.List of room temperature skyrmion characterization technologies^[4].

除了通过光学显微镜来观察外, 还可利用拓扑霍尔效应来间接观察斯格明子. 在有斯格明子存在的磁性材料中会产生涌生电磁场, 当电流流经磁性材料时, 涌生电磁场会作用在电流上而产生相应的电阻和电压, 因此可通过测量电阻的变化来间接探测斯格明子的存在. 2009年, Neubauer等^[51]在MnSi单晶中发现在某些区域霍尔效应会产生极大的偏差. 后来在单晶材料FeGe, Mn_1–xFe_xSi, SrRuO₃中也陆续发现了拓扑霍尔效应^[4]. 但在这些材料中要生成斯格明子所需的温度多低于室温. 在室温下拓扑霍尔效应报道非常少, 2019年, Shao等^[52]在室温下在Nd₃Ga₅O₁₂/Tm₃Fe₅O₁₂/Pt三层膜中成功观察到了拓扑霍尔效应.

室温磁性斯格明子的发现, 可把拓扑结构引入室温自旋电子器件. 同时基于磁性斯格明子的纳米自旋器件可有效地降低能耗. 目前磁性斯格明子有望应用于赛道存储器、微波探测器、自旋转移纳米振荡器、自旋逻辑开关及斯格明子晶格等器件^[27]. 这里仅对赛道存储器、微波探测器和自旋转移纳米振荡器作简要介绍.
2

-->

5.1.赛道存储器

赛道存储器最早是由IBM公司的Park等^[53]于2008年提出来的, 定义为以磁畴壁为信息载体的存储器, 磁畴壁可以在自旋极化电流的驱动下移动, 其结构如图5所示. 赛道存储器可以分为两种, 一种为垂直赛道存储器, 另外一种为水平赛道存储器. 其基本原理是: 赛道存储器的一端, 在电流脉冲的作用下, 被磁化形成磁畴壁; 在电流的作用下, 磁畴壁沿着赛道移动; 当移动到读取端时, 通过磁隧道结(MTJ)等元件将信息读取出来.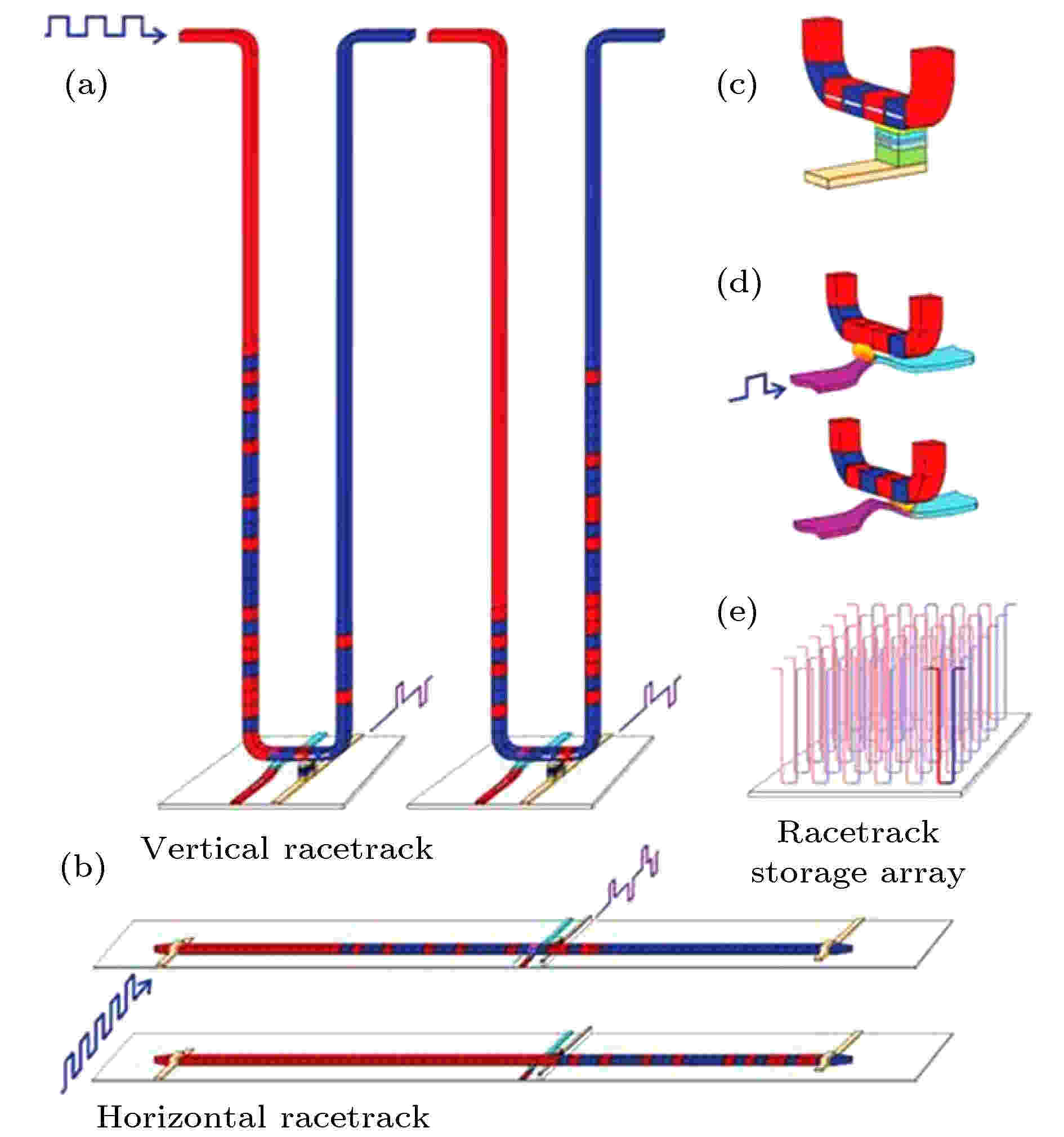
图 5 (a) 垂直赛道存储器示意图; (b) 水平赛道示意图; (c) 信息读出; (d) 信息写入; (e)赛道存储器的排列示意图^[53]
Figure5. (a) Schematic diagram of vertical racetrack; (b) schematic diagram of horizontal racetrack; (c) reading of information; (d) writing of information; (e) schematic diagram of racetrack storage array^[53].

基于斯格明子的赛道存储器, 有望制备出新一代高密度、低能耗、高稳定性的存储器. 磁畴壁的尺寸多为20—50 nm^[54], 斯格明子的尺寸可以更小, 为10—50 nm, 同时斯格明子的尺寸还可通过多种方式调控, 例如Moreau-Luchaire等^[18]实验证实, 通过磁场适当调控可使得斯格明子的尺寸进一步降低. 斯格明子在赛道存储器里的移动, 最常见的是通过极化电流驱动, Woo等^[19]在室温下利用电流密度为2.2 × 10¹¹ A/m²的极化电流驱动斯格明子运动, 在Pt/CoFeB/MgO薄膜中斯格明子在2 μm宽的赛道范围内可获得100 m/s的速度, 这一速度可实现斯格明子的快速读取. 虽然2.2 × 10¹¹ A/m²与磁畴壁的驱动电流密度相当(10¹¹—10¹² A/m²)^[54], 但磁畴壁在此电流密度下的运动速度仅为2—6 m/s ^[54], 因此获得相同读取速度的情况下, 斯格明子的能耗更低. 2016年, Zhang等^[55]预测, 采用双层的反铁磁偶合层设计, 通过上下层斯格明子的耦合作用, 可抵消斯格明子效应, 使得斯格明子对的移动速度突破1000 m/s. 若这一结果在实验上完全实现, 可使得基于斯格明子的存储速度实现飞跃. 2018年, 侯志鹏等^[26]利用聚焦离子束分析(focused ion beam, FIB)技术, 在Fe₂Sn₃单晶中基于斯格明子, 制备出了单链排列赛道存储器. 这个赛道存储器具有三层结构, 分别为600 nm厚的Fe₂Sn₃及外面两层的C和Pt. 单链排列赛道存储器具有高温度稳定性, 赛道里斯格明子可在630 K的温度下稳定存在^[26,56].
斯格明子由于自身的特点, 可实现多种形式的编码. 例如可通过斯格明子的极性、手性或螺旋度进行信息的编码. 这里介绍一种双通道赛道存储器, 与单通道最大的不同点是双通道赛道存储器是通过不同通道内斯格明子的有无进行信息编码的. Müller^[57]在薄膜表面增加纳米条, 形成两个通道. 在两个通道的中间, 在纳米条的作用下有一个非常高的势垒, 在边界效应的共同作用下, 可以将斯格明子限制在通道内运动^[58]. 这种存储器不依赖于同一赛道内斯格明子的距离, 而只依靠不同赛道内斯格明子的有无进行信息存储, 使得存储器的稳定性增加. 这种形式编码也大大增加了斯格明子间的距离, 使得信息存储密度降低^[59].
虽然目前在室温下已经在不同的材料里实现了对斯格明子的产生、操作及湮灭等各种操作, 但要制备基于斯格明子的赛道存储器, 还需要在室温下对同一材料实现斯格明子的产生、操作及湮灭, 这必将面临一定的挑战. 同时要实现高密度存储, 必将涉及到微纳米工艺问题, 例如如何在集成电路中, 对大量的斯格明子进行无差别精准的实现产生、操作及湮灭等, 也是面临的挑战之一.
2 -->

5.2.微波探测器

自旋转移力矩效应是局域磁矩同自旋极化电流相互作用, 从而使得磁矩方向发生变化的现象. 在2013年, Okamura等^[60], Seki和Mochizuki^[61]在具有斯格明子的晶体材料Cu₂OSeO₃中发现了基于斯格明子的自旋转移力矩效应(spin transfer torque, STT), 并提出利用这种效应可以制备出微波探测器. 这种微波探测器是一种新型的整流器件, 它能将微波电流信号转换成直流电压信号输出.
在薄膜材料中, 基于自旋转移力矩效应的微波探测器灵敏度比较低, 多被用来探测在MTJ中的磁矩. 而现有的微磁学模拟表明, 基于斯格明子的MTJ微波探测器在无外加磁场/无偏置电流及低功率输入的情况下(< 1.0 μW), 器件的灵敏度可以达到2000 V·W^–1[62]. Fang等^[63]基于自旋转移力矩及电压控制的磁各向异性, 在CoFeB/MgO/CoFeB/Ru/CoFe/PtMn材料体系中制备了灵敏度为900 V·W^–1的微波探测器. 图6 (a)为微波探测器及其电路原理图, 左边为MTJ多层膜, 右边为微波输入电路和电压测量电路. 在MTJ多层膜中, 从下到上依次为重金属层、自由层、隔离层和钉扎层. 其中下层重金属与自由层之间有足够强的DM作用, 使得在自由层中存在斯格明子; 两个铁磁层中具有极强的垂直各向异性, 并通过隔离层耦合, 在上层的钉扎层为一尺寸小的纳米圆形接触点.
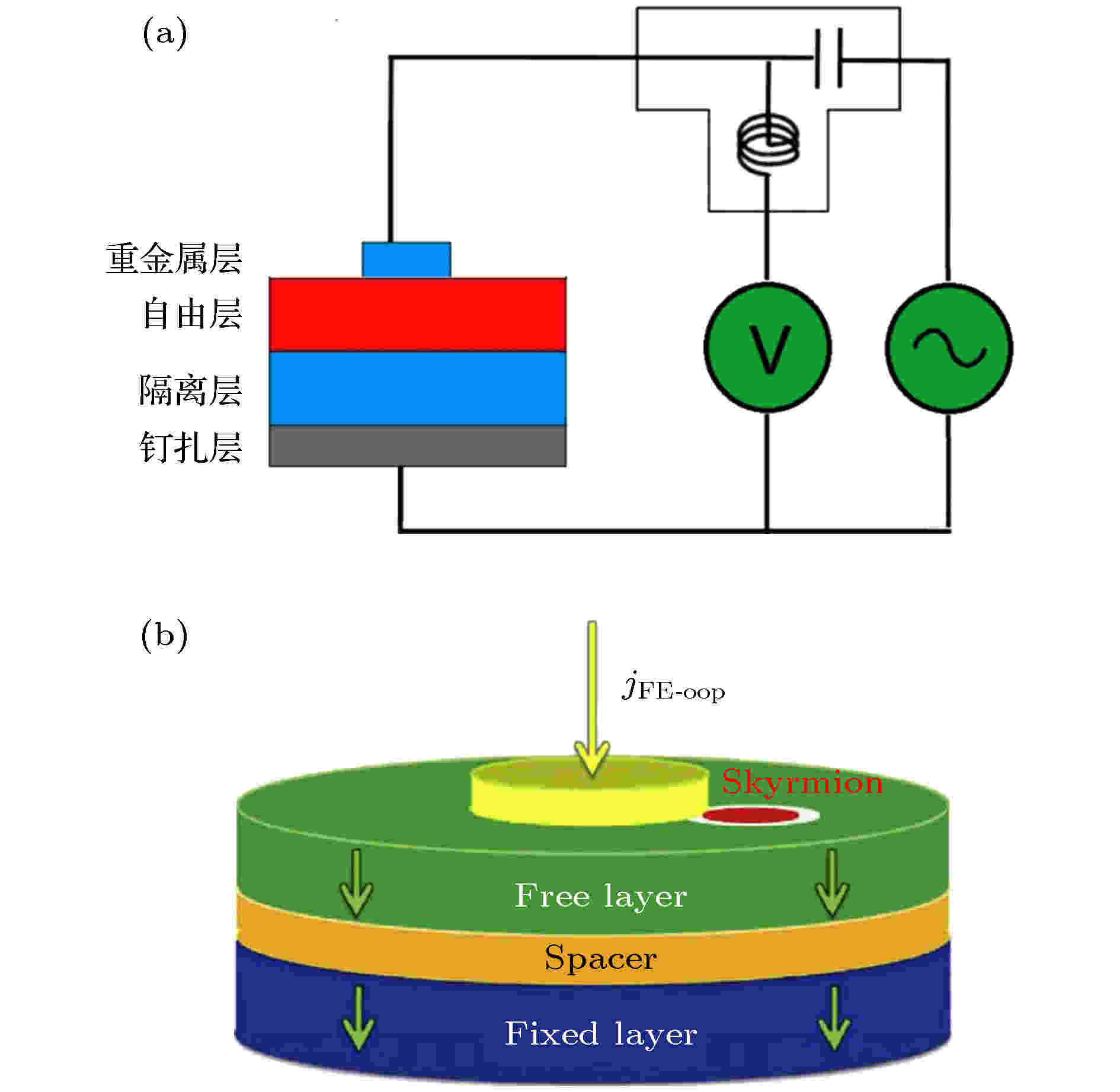图 6 (a) 微波探测器及其电路原理图; (b) 斯格明子螺旋示意图^[64]
Figure6. (a) Microwave detector devices and circuit schematics; (b) skyrmion rotates around the nano-contact^[64].

当有微波电流${i_{{\rm{MTJrf}}}} = {I_{\rm{M}}}{\rm{sin}}\left({2{\text{π}}{f_{{\rm{rf}}}}t + {\phi _{\rm{I}}}} \right)$输入MTJ多层膜时, 由于STT效应, 会引起自由层中磁化方向随着电流的变化而变化, 进而引起MTJ的电阻随电流的变化而变化, 其变化规律为: $r = {\Delta }{R_{\rm{S}}}{\rm{sin}}\left({2{\text{π}}{f_{{\rm{rf}}}}t + {\phi _R}} \right)$. 因此从MTJ输出的电压可表示为^[2]

$\begin{split}\;& {v_{{\rm{out}}}} = {i_{{\rm{MTJrf}}}} \cdot r \\={}& \frac{1}{2}{I_{\rm{M}}}{\Delta }{R_{\rm{S}}}[ {\rm{cos(}}{\phi _{\rm{I}}} - {\phi _{\rm{R}}}{\rm{)}} - {\rm{cos(}}4{\rm{\pi }}{f_{{\rm{rt}}}}t + {\phi _{\rm{I}}} + {\phi _{\rm{R}}}{\rm{)}} ].\end{split}$

所以可获得直流电压输出为

${v_{{\rm{dc}}}} = \frac{1}{2}{I_{\rm{M}}}{\Delta }{R_{\rm{S}}}\left[ {{\rm{cos(}}{\phi _{\rm{I}}} - {\phi _{\rm{R}}}{\rm{)}}} \right],$

其中, i_MTJrf代表输入的微波电流, I_M为输入电流的幅值, f_rf为微波电流的频率, t为时间, φ_I和φ_R为电流和电阻的初相位, ΔR_s为磁电阻的最大变化值, 而v_out为输出电压, v_dc为直流电压输出.
在基于斯格明子的微波探测器中, ΔR_s与斯格明子的尺寸以及接触点的直径有密切关系, 因此可通过调节斯格明子的尺寸及接触点的直径来调节探测器的灵敏度. 基于斯格明子制备的微波探测器能获得非常稳定的直流电压输出, 可以探测的微波范围在4—7 GHz.
2 -->

5.3.自旋转移纳米振荡器

自旋转移纳米振荡器也是一种基于自旋转移力矩效应的器件, 它是将直流电流输入转化为交变电流输出. 与传统的LC直流电路振荡器相比, 这种器件可通过磁场或电流对频率进行调谐, 同时具有温度稳定性高、器件尺寸比传统的LC振荡器小50倍、启动电压小(< 1 V)、易于在芯片上集成^[65]等特点. 基于斯格明子的自旋转纳米振荡器, 由于斯格明子的孤子特性, 不易受外界影响, 抗干扰能力强^[4].
在输入自旋极化电流时会有微波电流输出, 是因为斯格明子存在一种特殊的稳定态—斯格明子进动(dynamical skyrmion). 当有外加极化电流时, 斯格明子会在外加电流的作用下进动, 这种进动通常表现为斯格明子的类型在布洛赫型和奈尔型之间进行周期性的转化. 因此会输出和进动频率相同的微波电流, 斯格明子的进动所引起磁矩分布的变化是磁阻来源的原因^[66]. 基于斯格明子的纳米转移振荡器, 最早是刘荣华等^[67]在Pt(Co/Ni)多层膜中制备的. 在Pt层施加极化电流, 在极化电流的作用下Co/Ni层中会发生振荡. 当振荡频率高于铁磁频率7.5 GHz时, 振荡频率会随电流密度的增加而蓝移; 而振荡频率低于铁磁频率时, 斯格明子的振荡频率会红移. Zhang等^[64]发现了另外一种斯格明子纳米转移力矩振荡器, 其自旋转移器基于如图6(b)所示的结构, 当直流电流输入时, 斯格明子会围绕接触点周围作旋转, 磁矩分布作周期性变化, 从而产生相同周期的微波电流. 他们发现斯格明子的频率可受到磁场及接触点尺寸等的影响.

室温磁性斯格明子可存在于单晶材料或薄膜材料体系中^{[10,11,13-16]}. 在各类室温磁性斯格明子材料中, 目前最有应用价值的是多层膜材料. 磁性斯格明子有望应用于赛道存储器、微波探测器、自旋转移纳米振荡器、自旋逻辑开关及斯格明子晶格等器件中. 要实现斯格明子在器件上的应用, 这里首先必须要解决斯格明子的稳定性问题, 包括温度稳定性、电磁场稳定性等. 基于斯格明子的特性如何拓宽斯格明子在自旋电子器件里的应用范围, 将是人们关注的热点之一. 而要拓宽斯格明子的应用范围, 需要研究在高于室温下可生成斯格明子的材料, 并制备成器件. 如何降低斯格明子的尺寸及在低电流密度下驱动斯格明子运动等, 以及用其他方式驱动斯格明子的运动或进动, 也是未来研究的方向之一. 室温磁性斯格明子材料及其应用的研究必将进一步推动斯格明子理论的发展, 促进发现新型的斯格明子材料, 以研制出更多的新型自旋电子器件.
本文作者之一刘益非常感谢上海大学的敖平教授在论文写作过程中提出的宝贵建议和修改意见.