全文HTML
--> --> -->一百多年来, 研究者们相继提出了多种模型来预测地点间人类移动量, 其中两个最为经典的预测模型是引力模型[8]和介入机会模型[9]. 引力模型假设两地间的移动量与两地的人口数成正比, 与两地间距离的幂函数成反比. 但该模型是类比物理中的万有引力定律[10]提出的, 缺乏严格的理论依据. Wilson[11]以个体目的地选择问题为背景, 用最大熵原理[12]为引力模型提供了理论解释. 但是, 最大熵原理仅能给出系统最可能的宏观分布状态, 无法刻画系统中个体选择目的地的微观决策过程. 与类比物理定律得来的引力模型不同, 介入机会模型完全是从个体目的地选择行为的角度建模的. 该模型将介入机会而不是距离作为影响人类移动的一个关键因素, 这启发了后续研究者大量的工作[13]. 特别是近年来, 随着网络信息技术的迅速发展, 大量与人类移动有关的数据更容易被获取, 这为预测人类移动行为的研究提供了有力支撑. 研究者们通过对这些大数据进行人类移动行为规律的挖掘, 提出了许多新的介入机会类模型. 其中一个最有影响力的模型是Simini等[14]以美国郡间通勤为背景提出的辐射模型, 该模型实现了对地点间通勤行为的预测. 一些研究者又对辐射模型进行了推广, 提出了多种通勤预测模型, 例如基于时间成本的辐射模型[15]、辐射选择模型[16]、出行成本最优化的辐射模型[17]、流动跳跃模型[18]等. 另一个具有代表性的模型是Yan等[19]以城市内出行为背景提出的人口权重机会模型, 该模型实现了对城市内和城市间人类移动行为[20]的预测. 此外, Sim等[21]以个体选择社交对象为背景, 提出了审慎社交模型, 实现了对个体选择社交对象行为的预测. 受审慎社交模型的启发, 我们将个体选择社交对象的行为扩展到个体选择目的地行为中, 提出了机会优先选择模型[22], 实现了对城市间、城市内人类移动行为的预测. 最近, 我们又通过对多种移动类型数据的挖掘, 提出了一个统一机会模型[23], 实现了不同时空尺度下人类移动行为的预测, 为介入机会类模型提供了一个新的统一框架.
尽管上述模型假设不同, 但它们具有类似的建模思路: 都是从机会收益的角度出发, 假设个体在选择目的地时, 会比较起点收益、介入机会收益和目的地收益的大小. 不同的是, 这些模型比较各地点收益的准则不同. 本文将对这些介入机会类模型及其在空间交互和疾病传播方面的应用进行介绍, 并对这些模型未来可能的研究方向进行探讨.
1)地点机会, 指该地点能满足个体出行目的的机会数量, 一般假设这种机会数量正比于地点的人口.
2)介入机会, 指介于目的地j与起点i之间的所有地点的总机会. 这里的目的地j与起点i之间的地点指到i的距离比i到j之间的距离短的所有地点. 起点i与终点j之间的总机会, 如果不包含起终点机会记为
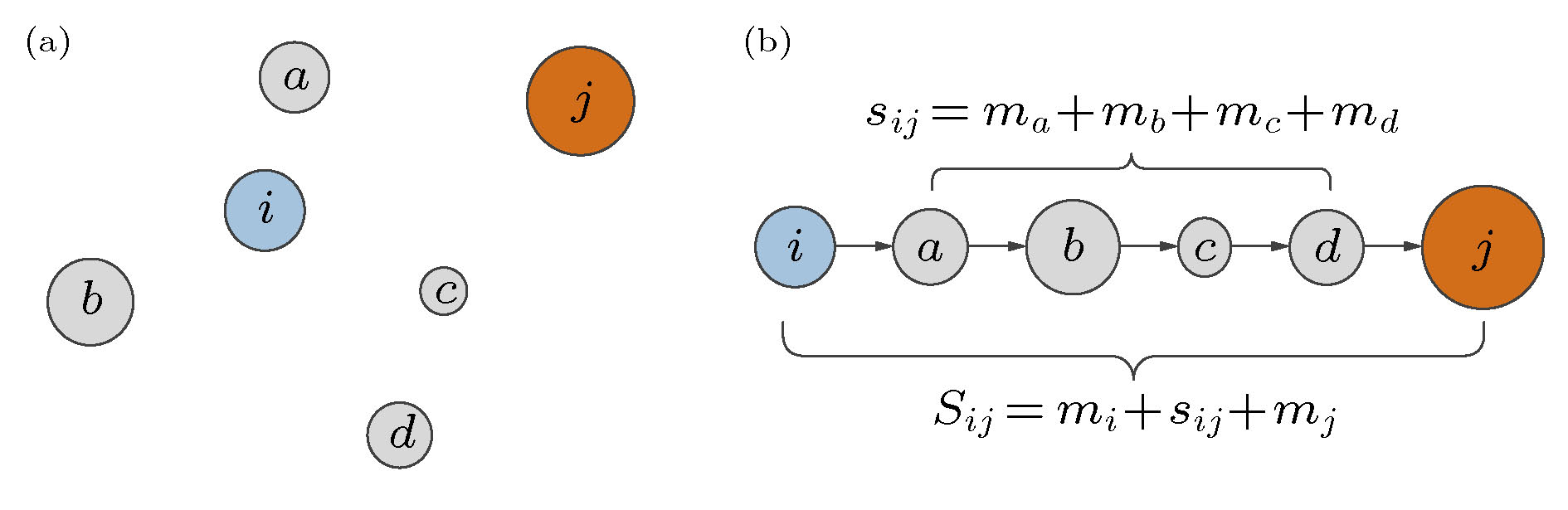图 1 介入机会说明 (a) 原始地图, 其中每个圆代表一个地点, 地点i是起点, 其他地点是潜在的目的地; 人口越多的地点, 机会越多, 圆面积越大; (b)介入机会, 按照距离起点的远近排序, 目的地j与起点i之间的所有地点的介入机会为
Figure1. Intervening opportunities illustration. (a) Sketch map. Each circle represents a location. Location i is the origin, and the other locations are potential destinations. The larger the population, the more opportunities, the larger the circle. (b) Intervening opportunities. All locations are sorted by their distance from location i. The intervening opportunities are all opportunities of the locations between i and j such that
3)机会收益值, 指地点机会带给出行者的收益值(用z来表示), 该值是一个任意连续分布为
2
2.1.介入机会模型
介入机会模型是由Stouffer[9]从个体目的地选择行为角度提出的一个微观机制类模型. 该模型的基本规则是: 对于每一个从起点出发的个体, 先将所有的潜在目的地依据与起点之间的距离由近及远进行排序, 并假设个体会以固定的概率被某个地点的机会所吸引并停留在那里. 最终得到位于起点i的个体选择地点j的概率为
从(1)式可以看出, 各个目的地被位于起点的个体选择的概率, 与目的地机会正相关, 与介入机会负相关. 也就是说, 机会越多的目的地被个体选择的概率越高, 到起点介入机会越多的目的地被个体选择的概率越低. 与引力模型相比, 尽管介入机会模型在形式上比较复杂、预测精度低, 但是该模型用排序而不是实际的空间距离来度量各目的地距离起点远近的思想, 启发了后续的大量研究工作[1].
2
2.2.辐射模型
介入机会模型是最早从个体对目的地选择的决策过程出发提出模型假设的, 并将介入机会而不是距离作为影响人类移动的核心要素. 但是该模型是一个有参数模型, 必须用历史的流量数据估计模型参数之后才能实施预测, 这在很大程度上限制了该模型的适用范围[24]. 针对这一问题, Simini等[14]以地点间通勤为研究背景建立了辐射模型. 其基本规则是: 个体在选择工作地时, 先评估工作地的机会带给他的收益值, 然后选择距离起点最近且机会收益大于起点机会收益的一个地点作为工作地, 最终得到位于起点i的个体选择地点j的概率为
从(2)式可以看出, 辐射模型是一个无参数模型. 换句话说, 该模型只需要输入各地的人口数量, 就能够预测地点间的通勤量, 显示出了巨大的应用优势. 一些研究者又将该模型推广到连续空间和交通网络上, 提出了多种通勤预测模型[15-18]. 例如, Ren等[15]用路途上花费的时间来度量各目的地距离起点远近, 提出了基于时间成本的辐射模型; Simini等[16]利用一套连续化的方法将辐射模型推广到了连续空间上, 提出了辐射选择模型; Varga等[17,18]考虑了个体在选择工作地过程中的出行费用, 提出了出行成本最优化的辐射模型. Kang等[25]通过引入尺度参数、归一化因子、出行发生量和吸引量约束, 提出了一般化辐射模型. Yang等[26]考虑了地点机会分布的异质性和空间尺度对个体目的地选择行为的影响, 建立了拓展辐射模型. 这些辐射类模型都很好地描述了个体的通勤行为, 能够准确预测地点间的通勤量. 然而, 一些研究者发现这些辐射类模型对其他类型的移动(例如城市内出行)预测精度并不高[19,20], 这说明辐射模型仍未抓准不同时空尺度下个体出行目的地选择行为的普适机制.
2
2.3.人口权重机会模型
前述辐射模型假设个体在选择目的地时只选择距离自己近的高收益地点, 不需要任何额外的参数就可以相当准确地预测地点间的通勤行为. 但在预测城市内部出行时, 闫小勇[27]发现辐射模型得到的预测结果与实际数据有较大的误差. 他们认为这是由于辐射模型的基本假设并不完全适合描述个体的出行目的地选择行为: 实际中的个体在选择目的地时, 不是仅考虑距离起点最近的高收益目的地, 而是会考虑整个区域内的所有地点. 针对这一问题, Yan等[19]提出了人口权重机会模型用来预测个体出行目的地选择行为. 该模型假设个体选择一个目的地的概率正比于目的地的机会, 反比于目的地到个体所在地点之间的人口总数. 根据以上的假设, 可以得到位于起点i的个体选择地点j的概率为
从(3)式可以看出, 人口权重机会模型也是一个无参数模型, 只需要输入各地点的人口分布, 就能够预测城市内的出行. 进一步地, Yan等[20]将人口权重机会模型与记忆性随机游走模型[28]结合得到了个体群体移动模式预测统一模型. 统一模型不仅实现了对城市间人类移动的预测, 而且能够再现个体和群体两个层面上的空间移动模式. Hu等[29]在人口权重机会模型的基础上, 提出了多因素加权收益模型. 相比人口权重机会模型, 该模型不仅考虑了地点机会, 还考虑了地点的GDP和规模因素, 能够更加准确地预测城市间出行. Forghani和Karimipour[30]通过研究人类移动网络的特性, 对人口权重机会模型进行了改进, 提出了网络社区约束模型. 该模型揭示了人类移动与城市空间结构的关系, 加深了我们对城市内部人类移动模式的理解.
2
2.4.探索类介入机会模型
受辐射模型的启发, Sim等[21]以个体选择社交对象为背景提出了审慎社交模型. 类似辐射模型, 该模型假定个体在选择社交对象时, 先将所有的潜在社交对象按照距个体的距离由近及远进行排序, 然后评估潜在社交对象的属性值(财富、能力、品德等)带给自己收益的大小, 最后会选择收益值比自己的收益值以及介入机会的收益值高的社交对象建立联系. 受人口权重模型和审慎社交模型的启发, 我们进一步将个体选择社交对象的行为扩展到个体选择目的地行为中, 建立了机会优先选择模型[22]. 该模型假设位于起点的个体在选择目的地时, 会选择收益值比起点的收益值以及介入机会收益值都高的地点. 根据以上假设, 可以得到位于地点i的个体选择地点j的概率为
从(4)式可以看出, 与辐射模型、人口权重模型类似, 审慎社交模型和机会优先选择模型仅输入各地点的人口分布就能够实施预测, 不存在可调参数. 与辐射模型相比, 审慎社交模型和机会优先选择模型都假设个体在选择选项时不只是选择距离自己最近的高收益选项. 只要选项能够给个体带来高收益, 都会被个体以一定的概率选择. 这体现了选择行为中的一种探索性倾向, 因此我们将该类模型称为探索类介入机会模型.
2
2.5.统一机会模型
前述辐射类模型能够较准确地预测通勤行为, 探索类介入机会模型能够较准确地预测城市内、城市间的出行. 这些模型建模假设不同, 尽管它们具有类似的建模思路: 假设个体在选择目的地时, 会比较起点收益、介入机会收益和目的地收益的大小, 但这两类模型比较各地点收益的准则不同. 在辐射类模型中, 个体在选择目的地时, 倾向选择目的地收益比起点收益高且介入机会的收益比起点收益低的行为, 体现了一种谨慎性倾向, 而探索类模型中的个体在选择时具有很强的探索性倾向. 我们将这两种倾向作为参数建立了一个统一机会模型, 其中探索性倾向用参数
从(5)式可以看出, 统一机会模型为介入机会类模型提供了一个统一的建模框架, 经典的辐射模型和机会优先选择模型都是该模型的特例: 当
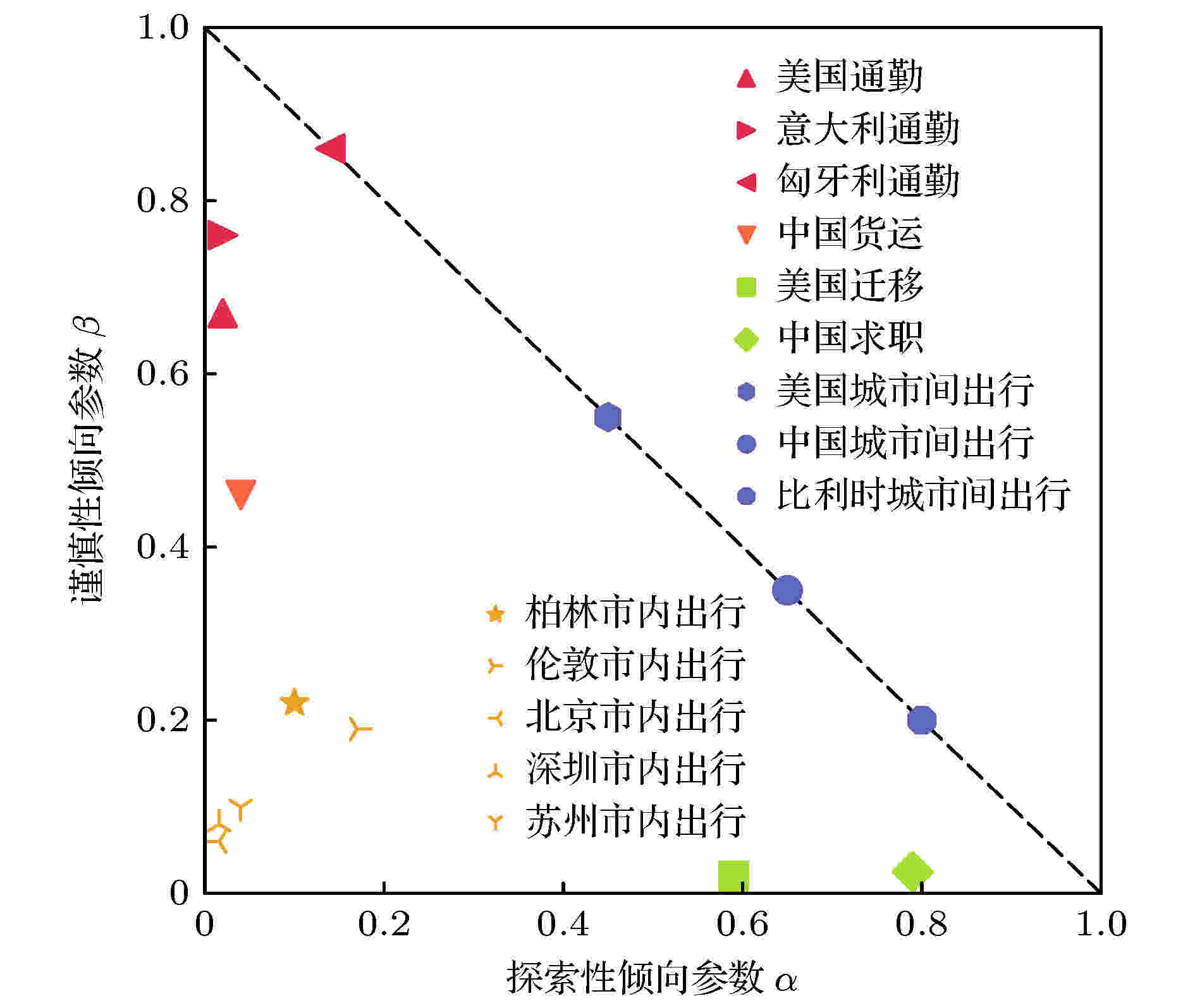图 2 统一机会模型对14个数据集的最优参数取值Figure2. The optimal values of the parameters
2
2.6.小 结
前文分别介绍了介入机会模型、辐射模型、人口权重机会模型、审慎社交模型、机会优先选择模型、统一机会模型的建模原理. 表1列出了这几种主要介入机会类模型的适用类型和有无参数的属性特征. 从表1可以看出, 介入机会模型的缺点是包含待估参数且预测精度低, 在实际中很少被采用. 它的优点是具有重要的理论价值, 启发了后续研究者对地点间人类移动行为的研究. 辐射模型弥补了介入机会模型的不足, 不包含任何待估参数, 可以较准确地预测地点间的通勤. 人口权重机会模型和机会优先选择模型也都不包含参数, 都能较准确预测城市内、城市间出行. 审慎社交模型同样也是一个无参数模型, 能较准确地预测个体间的社会交往. 这些模型的缺点是只能适用于部分类型移动的预测. 最近提出的统一机会模型则能够对求职、迁移、货运、通勤、城市内、城市间等这些不同时空尺度下的移动做出相当准确的预测. 虽然该模型包含两个参数, 但是对于相同类型的移动行为, 这两个参数的取值相似, 为同类型移动行为预测的参数设置提供了参考.| 模型名称 | 适用类型 | 有无参数 |
| 介入机会模型 | 无 | 有 |
| 辐射模型 | 通勤 | 无 |
| 人口权重机会模型 | 城市内、城市间 | 无 |
| 审慎社交模型 | 个体间社会交往 | 无 |
| 机会优先选择模型 | 城市内、城市间 | 无 |
| 统一机会模型 | 求职、迁移、货运、通勤、城市内、城市间 | 有 |
表1几种介入机会类模型的属性特征比较
Table1.Comparison of attributes of several intervening opportunity models.
2
3.1.介入机会类模型在空间交互中的应用
介入机会类模型在交通科学中被称为出行分布预测模型, 在区域学和地理经济学中被称为空间交互模型. 这类模型通过输入人口、经济产值、流出总量等反映地点规模的数据以及距离、移动成本、出行时间等反映地点间阻隔程度的相关数据就能够预测地点间的交互强度[1,24]. 其中介入机会类模型中较早提出的辐射模型在空间交互预测中获得了广泛的应用. 例如, Li等[34]运用辐射模型预测了中国337个行政区域(包括4个直辖市, 333个地级市)间的人口定向迁移量, 从人口流动的角度分析了中国城市的总体情况、区域间的交互强度以及城市群的发展状况. Wang等[35]运用辐射模型预测了中国333个地级市间从2000年到2010年的人口流动量并以此建立空间交互网络, 然后利用复杂网络科学的相关指标, 对十年间各个城市发展水平进行了评估和比较. Tian[36]首先将城市划分为若干相同规模的网格并通过建立回归模型来估计人口分布, 然后运用辐射模型对江苏省各地区间的空间交互强度进行了预测, 并且将交互强度作为判定城市、郊区和农村的指标. Zheng等[37]运用辐射模型预测了长江中游城市群内部的人口迁移量, 分析了群内城市之间的交互强度, 进一步结合交通可达性算法、城市竞争力评价指标对城市群空间交互网络构型进行了评估, 为中国其他城市群的可持续发展提供借鉴. 从这些研究中可以看出, 研究者们都是采用辐射模型来预测地点间的人口迁移量, 进而来评估地点间的交互强度. 然而, 由前述对介入机会类模型的介绍可知, 辐射模型能够很好刻画地地点间的通勤行为, 并不能完全准确地预测地点间的人口迁移量. 一些研究者也注意到了这个问题, 例如Sim等[21]采用审慎社交模型而不是辐射模型研究了英国两个城市之间有无高速铁路对空间交互强度的影响. 该模型评估了两地的旅行时间(包括从修建高速铁路前的84 min到修建高速铁路后的50 min)对空间交互强度变化的影响. 类似地, Sim等[21]又采用该模型研究了伦敦市有无横贯铁路对空间交互强度和GDP的影响. 因此, 我们认为采用包括审慎社交模型在内的探索类介入机会模型和统一机会模型等来预测地点间的交互强度, 可能会得到更切合实际的预测结果.2
3.2.介入机会类模型在疾病传播学中的应用
在疾病传播动力学中, 地点间人类移动的模式在疾病传播速度、疾病传播范围等方面扮演着重要的角色. 介入机会类模型的提出, 使研究者对疾病的传播机制有了新的认识. Kraemer等[38]通过运用辐射模型来预测地点间人类移动, 研究了埃博拉病毒在人群中传播扩散的动态过程, 揭示了人类的流动性是疾病传播的一个重要驱动因素. Dalziel等[39]运用辐射模型来描述人类的移动模式, 进而刻画了疾病在城市中传播扩散的过程, 揭示了人类移动模式的差异对疾病传播的影响. Tizzoni等[40]以地点为节点、地点间的通勤量为边, 运用辐射模型计算边的权值构建了一个通勤网络, 描述了疾病如何在通勤人群中蔓延. Wen等[41]运用辐射模型来预测社区之间的通勤行为并将其作为空间权重来捕捉人口流动的空间结构, 研究了社区结构对登革热疾病传播的影响. Kramer等[42]运用人口权重机会模型模拟了埃博拉病毒在非洲西部各区域间的传播, 突出强调了距离、人口密度、国家边界等地理因素对埃博拉病毒蔓延的重要性. Zhang等[43]以胃癌患者为研究对象, 运用人口权重机会模型预测患者选择某一个医院治疗的概率, 揭示了山西省胃癌患者在空间格局上具有的“南高北低”的变化趋势. 祖正虎等[44]以北京市的社区为节点、社区间的通勤为边建立了人群通勤接触网络, 基于人群通勤出行的接触频率和人口权重机会模型, 建立了虚拟人口间的通勤接触关系, 提出了预防新型流感大流行的策略. Zhu等[45]结合人口权重机会模型揭示的城市内人类移动行为, 研究了登革热病毒在广东省的传播模式和驱动机制, 为提高登革热疾病传播的可预测性和风险评估提供了新的见解. 特别是最近几个月, 世界各地先后爆发COVID-19疫情, 很多****又将介入机会类模型应用于COVID-19的传播建模与预测. 例如, Sj?din等[46]采用辐射模型来估计瑞典城市之间的人口迁移概率并结合年龄分层医疗需求扩展的分区模型, 展示了公共卫生干预措施如社会隔离可以有效减少COVID-19感染病例. Akhmetzhanov等[47]运用辐射模型来估计日本北海道各县之间的通勤量, 验证了各地区感染COVID-19的人数与通勤量之间存在的线性关系, 为抑制COVID-19大范围传播提供了应对策略. 总之, 这些介入机会类模型加深了我们对疾病传播行为的理解, 为预测和控制疾病的传播提供了借鉴[5].虽然本文介绍的这些介入机会类模型都是描述个体目的地选择行为的, 但是个体的空间交互对象选择行为不仅仅存在于交通系统中, 在许多其他系统中也普遍存在. 例如, 在选择社交对象时, 个体倾向选择距离自己近且认同感高的人做交流对象[21]; 在选择科研合作者时, 个体倾向选择同城或相邻城市的高水平研究者做合作伙伴[53]; 在网上购物时, 个体倾向选择虚拟空间中更接近自己喜好的商品[28]; 在虚拟游戏Pardus中, 个体倾向选择向距自己登陆城市最近的空间位置移动[54]. 这些无论真实空间还是虚拟空间中的个体选择交互对象行为, 都体现了个体在选择时对所选的人、商品、兴趣爱好、地点等排序的思想. 这些空间交互对象选择行为都能被本文介绍的介入机会类模型来刻画. 总之, 这些介入机会类模型有助于我们深入理解个体移动行为的底层机制, 在交通出行、商品贸易、社会交往、人口迁移等领域具有广阔的应用前景.
