摘要:为解决传统方法在判断离心压气机动态失稳过程中因信号强非线性导致误判错判, 针对其动态时序属非线性信号, 基于分形理论提出自适应变分模态分解(adaptive variational mode decomposition with fractal, AFVMD)方法以同时实现降噪与非线性特征提取, 采用相空间重构法还原系统动力学结构. 以某离心压气机失稳过程中叶轮动态压力数据为对象, 验证所提出算法的优越性, 分析其吸引子状态. 结果表明: 在处理具有非线性特征的含噪信号时, AFVMD比小波降噪具有更好的降噪效果与特征提取能力; 相空间将失速发展过程可视化, 最小流量状态所对应的相空间呈现“毛球状”; 随失速的发展, 相空间将逐渐发散; 经小波与AFVMD方法预处理的信号所对应相形对失速过程更加敏感; 通过经AFVMD处理的信号进行重构可更早捕获失速征兆, 其更小的最大Lyapunov指数表明该方法提升了流动混沌系统的可预测性, 为压气机失稳分析、预测提供新思路与方法.
关键词: 混沌/
Lyapunov指数/
变分模态分解/
分形

English Abstract

全文HTML

--> --> -->

由不稳定流动导致的失速与喘振对离心压气机作业性能影响显著. 若能对其流场进行准确的特征提取, 进行失稳预判, 不仅能避免灾难性事故发生, 亦可提升压气机工作效率^[1]. 压气机失稳时, 其时序压力脉动因流动不稳定导致信号具备强非线性, 增加数据复杂度, 阻碍对流动的准确分析与状态判别. 因此, 提取有效的压气机失稳非线性特征对其流动失稳机理性研究具有重要意义. 为准确分析实验所得时序信号, 时域、频域以及时频域分析法被广泛应用于流动失稳识别中. 文献[2]采用傅里叶变换分析重构失速先兆信号, 通过各流通模态幅值判别失速先兆, 结果表明流动解耦可提升失速判定准确性. 文献[3]采用谱分析与奇异值分解法通过特征值虚部判断压气机流动稳定性. Eck等^[4]和Xu等^[5]分别研究了压气机叶片信号的规则性与周期性. 研究显示: 叶片信号的不规则度与失速发展呈正相关性, 基于叶片周期性变化可做出失速预判. 文献[6]基于压升信号提出对喘振与失速的非线性控制方法, 提升喘振裕度. 文献[7]采用经验模态分解(empirical mode decomposition, EMD)与HHT (Hilbert-Huang transform)相结合, 分析了多级跨声速压气机动态特性, 结果表明, EMD-HHT方法比小波分析能更早捕捉失速预兆特征. 但EMD方法存在模态混淆与端点效应, 干扰流动模态的准确提取.
为解决EMD存在的不足, 集合经验模态分解、时空本征模态分解与局部均值分解^[8-12]等时频分解方法已被用于复杂时序解耦与特征频提取. 以上算法虽可改善模态混淆与端点效应, 但由于递归求解方式与包络线估计误差叠加仍易导致流动模态提取不准确, 对流动失速、喘振状态漏判、错判.
又因噪声环境及流动问题本身的复杂性导致被采信号具有非线性特征. 幅值、均值和标准差等传统统计值无法准确描述此非线性问题, 若特征选取不当, 亦易导致对流动状态的误判. 文献[13]基于混沌方法, 对流量脉动进行预测与不稳定分析, 结果表明最大Lyapunov指数可作为流动问题中的特征值. 相关****针对更加复杂的压气机流动, 开展最大Lyapunov指数、模糊熵与关联维数作为流动失速的判据的研究^[14-17], 结果表明流动非线性对压气机影响显著.
但以上研究未考虑压气机中流场受耦合作用与环境噪声干扰导致直接以非线性特征值作为失速判据失准. 为此, 考虑压气机中复杂的耦合效应导致压力脉动时序的非线性, 基于分形维数的无标度性, 可定量评估信号不规则度, 反映系统分形复杂度^[18]; 凭借变分模态分解方法(variational mode decomposition, VMD)^[19]在信号解耦方面的强鲁棒性, 提出了基于分形理论的改进变分模态分解(adaptive variational mode decomposition with fractal, AFVMD)方法, 实现降噪并从复杂流场中提取代表性特征. 为验证提出方法的有效性, 以某无叶扩压器的高速离心压气机上测得进喘过程的动态压力信号为研究对象, 通过流场压力重构吸引子及最大Lyapunov指数以验证所提出方法在流动失稳信息提取的有效性, 为流动预测、失速与喘振机理性研究提供理论支持与实现方法.

实验数据源自于某带无叶扩压器的高速离心压气机实验. 采用动态压力传感器、采集卡和配套机箱以60 kHz的采样频率进行高速信号采集. 监控传感器记录过程包括: 阻塞工况开始, 阀门逐渐关小, 待每个阀门开度稳定后再进行数据采集; 最小流量工况时, 阀门继续关小, 随即实验设备发出低频噪声, 表明压气机进入深喘, 并迅速进行退喘操作.
将试验数据分为最小流量工况、浅喘工况及深喘工况. 不同工况的样本划分见图1.
图 1 不同工况样本划分
Figure1. Samples divisions of the different conditions.

VMD可有效抑制包络拟合、端点效应及模态混淆等问题. 与EMD不同^[20], VMD为约束性变分问题, 在此方法中, 模态重新定义为调幅-调频信号, 表达式为

${u_k}(t) = {A_k}(t)\cos ({\varphi _k}(t)),$

式中${\varphi _k}(t)$为信号相位, ${A_k}(t)$为瞬时幅值.
通过约束变分模型, 寻求K个具有特定稀疏性的本征模态函数(intrinsic mode function, IMF)分量, 使得各分量的估计带宽和最小, 限定约束条件为各分量之和, 且等于原始信号. 为获取限定带宽的K个IMF模态分量, 先通过Hilbert变换, 得到各IMF分量${u_k}(t)$的单边际谱, 然后估计各IMF的中心频率${\omega _k}$, 与其指数信号${{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}$相乘将模态的频谱调制到相应基频带, 再计算解析信号梯度平方L²范数, 构造变分模态为

$\left\{ \begin{aligned}& \min\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} {\left( {\sum\limits_{k = 1}^K {\left\| {{\partial _t}\left[\! {\left( {\delta (t) \!+\! \frac{{\rm{j}}}{{\pi t}}} \!\right)\!*{u_k}(t)}\! \right]\!{{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|} } \right)_2},\\&{{\rm s}}{{.\rm t}}{{.}}\sum\limits_{k = 1}^K {{u_k}(t) = f(t),} \end{aligned} \right.$

式中K为模态分解个数; $\delta (t)$为单位脉冲函数; j为虚数单位; ${*}$表示卷积运算; ${\partial _t}$表示偏导运算; $\{ {{u_k}}\}=\{ {{u_1},\; {u_2},\; {u_3},\; \cdots, {u_K}} \}$表示K个IMF分量;$\{ {{\omega _k}}\}\! =\! \{ {{\omega _1},{\omega _2},{\omega _3}, \cdots\!,{\omega _K}}\}$表示各分量的中心频率.
引入惩罚因子$\alpha $及Lagrange乘子$\lambda $将约束变分问题转变为非约束变分问题, 以求解上述变分问题, 得到增广Lagrange表达式:

$\begin{split}&L(\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda ) \\&= \alpha \sum\limits_{k = 1}^K {\left\| {{\partial _t}\left[ {\left( {\delta (t) + \frac{{\rm{j}}}{{\pi t}}} \right)*{u_k}(t)} \right]{{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|} _2^2\\ &+ \left\| {f(t) - \sum\limits_{k = 1}^K {{u_k}(t)} } \right\|_2^2 + \left\langle {\lambda (t),f(t) - \sum\limits_{k = 1}^K {{u_k}(t)} } \right\rangle .\end{split}$

采用交替方向乘子算法更新迭代求解(3)式的鞍点, 获得最优解, 以将原始信号分解为K个IMF分量, 相应变量更新由(4)式—(6)式表示, 实现流程如图2所示.
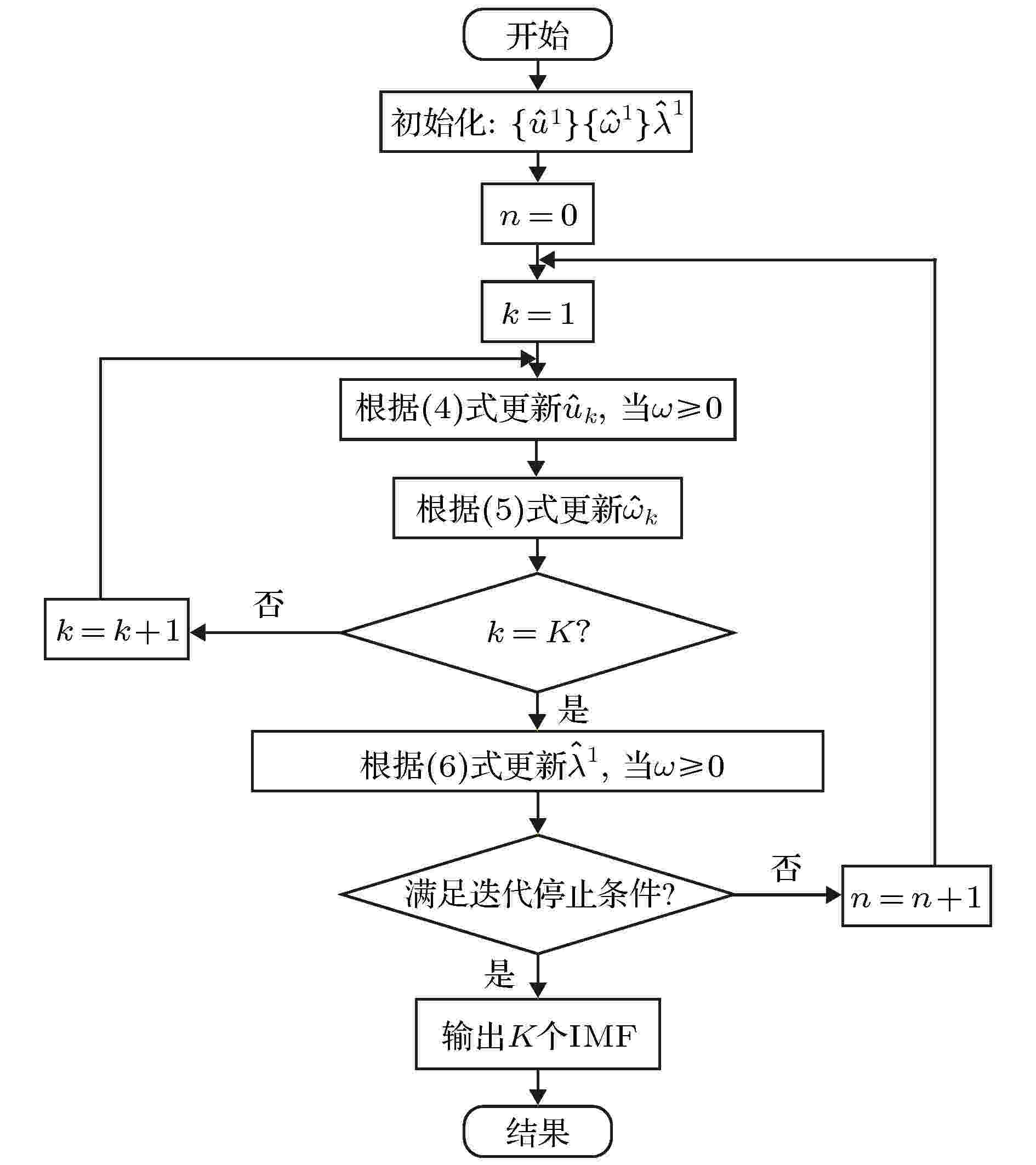图 2 VMD算法流程
Figure2. Flow diagram of the VMD algorithm.

$\hat u_k^{n + 1}(\omega ) = \frac{{\hat f(\omega ) \!-\! \displaystyle\sum\limits_{i = 1}^{k - 1} {\hat u_i^{n \!+\! 1}(\omega ) \!-\! } \displaystyle\sum\limits_{i = k + 1}^K {\hat u_i^n(\omega ) \!+\! \frac{{{{\hat \lambda }_i}(\omega )}}{2}} }}{{1 + 2\alpha {{(\omega - \omega _k^n)}^2}}},$

$\omega _k^{n + 1} = \frac{{\displaystyle\int_0^\infty {\omega {{\left| {\hat u_k^{n + 1}(\omega )} \right|}^2}{\rm{d}}\omega } }}{{\displaystyle\int_0^\infty {{{\left| {\hat u_k^{n + 1}(\omega )} \right|}^2}{\rm{d}}\omega } }},$

${\hat \lambda ^{n + 1}}(\omega ) = {\hat \lambda ^n}(\omega ) + \tau \left( {\hat f(\omega ) - \sum\limits_{k = 1}^K {\hat u_k^{n + 1}(\omega )} } \right),$

式中$\tau $为保真系数, $\wedge$表示傅里叶变换, n为迭代次数.
求解变分模型时, IMF分量的中心频率与带宽不断更新, 直至满足迭代停止条件, 表达式如下:

$\sum\limits_{k = 1}^K {\left( {\left\| {\hat u_k^{n + 1}(\omega ) - \hat u_k^n(\omega )} \right\|_2^2/\left\| {\hat u_k^n(\omega )} \right\|_2^2} \right)} < \varepsilon ,$

式中$\varepsilon $为判别精度, 本文取10^–6.
迭代停止时, 信号的频域特性已完成自适应分离, 通过逆傅里叶变换将调制信号${\hat u_k}(\omega )$转变为时域IMF分量.

分形与混沌是非线性科学及现代数学研究中十分活跃的分支, 分形可理解为局部与整体的某种相似程度, 亦可反映系统不规则度, 可用于定量描述非线性系统的分形特征^[21]; 而混沌则为时间尺度上的分形, 具有随机性、敏感性、分维性和普适性等特点, 成为量化分析非线性动力学系统的方法之一.
2

-->

4.1.计盒维数

计盒维数是用于刻画复杂系统不规则度的定量参数, 不仅可用于图形识别, 亦可进行时序分析^[22]. 盒子计数法由Sarkar和Chaudhuri^[23]基于Mandelbort的分形理论提出, 将分形维数表示为

$D = \ln ({N_r})/\ln (1/r),$

式中D为分形维数, r为网格尺度, ${N_r}$为计盒总数.
2 -->

4.2.相空间重构

Packard等^[24]提出由一维时间序列重构得到“等价”相空间以还原系统的非线性特性的方法. Auerbach等^[25]认为, 相空间可重构时间序列中隐含的动力学变化规律, 相空间重构原理与步骤如下:
由系统中可测量的一组时间序列${{\{ }}{x_i}| \, i = 1, 2,\;\cdots,\;N{\}}$重构m维相空间, 得到一组相空间矢量:

${{{X}}_i} = \{ {x_i}\,,\,{x_{i + \tau }}\,, \cdot \cdot \cdot \,,\,{x_{i + (q - 1)\tau }}\},$

式中$\tau $是延迟时间; 嵌入维数$q \geqslant 2 d + 1$, d为系统自变量个数; M小于N, 并与N有相同的数量级, $i = 1,\;2,\;\cdots,\;M;\;{{{X}}_i} \in {R^q}$.
延迟时间$\tau $和嵌入维数q选取具有重要意义. 基于Takens定理、Grassberger-Procaccia (G-P)算法和FNN(false nearest neighbors)法等方法可确定嵌入维数; 而对于延迟时间的选取, 则可通过自相关函数法、互信息函数法和经验法确定^[25,26]. 其中, 互信息函数法因可反映数据点的一般相关性在延迟时间的选取上被广泛使用. 由于FNN所需数据量较小, 故通过FNN法计算嵌入维数. 本文通过互信息函数及FNN分别确定延迟时间与嵌入维数, 并作为构建混沌相图的$[q, \tau ]$参数组合.
2 -->

4.3.最大Lyapunov指数

混沌的根源在于系统中各状态变量间非线性的相互作用, 故混沌理论以非线性动力系统为研究对象, 揭示其类似随机现象背后隐藏的真实规律.
混沌吸引子是混沌系统的基本特征之一, 根据Takens定理, 通过求取合适的延迟时间和嵌入维数, 即可通过相空间重构得到混沌系统的吸引子. 任意非线性响应信号可通过Lyapunov指数$\lambda $判断该系统是否具有混沌特性. 当$\lambda > 0$时, 表明系统具有混沌特征, 且其非线性特征随$\lambda $增大而增强, 当$\lambda < 0$时, 表明系统无混沌特征. $\lambda $可表示为

$\lambda {{ = }}\frac{1}{{{t_M} - {t_0}}}\sum\limits_{i = 0}^M {\ln \frac{{L_i'}}{{{L_i}}}},$

式中${L_i}$表示重构相空间中点i与i + 1之间的距离; $L_i'$为下一时刻两点的距离; M为相空间内所有数据点的总迭代次数^[27].

VMD虽能有效改善类EMD算法所产生的模态混淆与端点效应, 但其分解模态参数的高自由度导致参数选取直接影响了算法解耦精度.
针对压气机流动信号的非稳定及非线性特征, 考虑分形理论具有自相似性、无标度性和自仿射性等特点^[28,29], 基于分形维数可定量评估信号不规则度以反映系统分形复杂度. 分形维数越大, 说明该系统(或子系统)存在更多噪声. 噪声往往处于高频段, 而喘振与失速的特征频率多处于低频段. 同时, 凭借VMD算法中惩罚因子具有约束信号带宽的能力, 提出基于分形理论的自适应变分模态分解算法, 为流动失速、喘振机理性研究提供理论方法, 流程如图3所示.
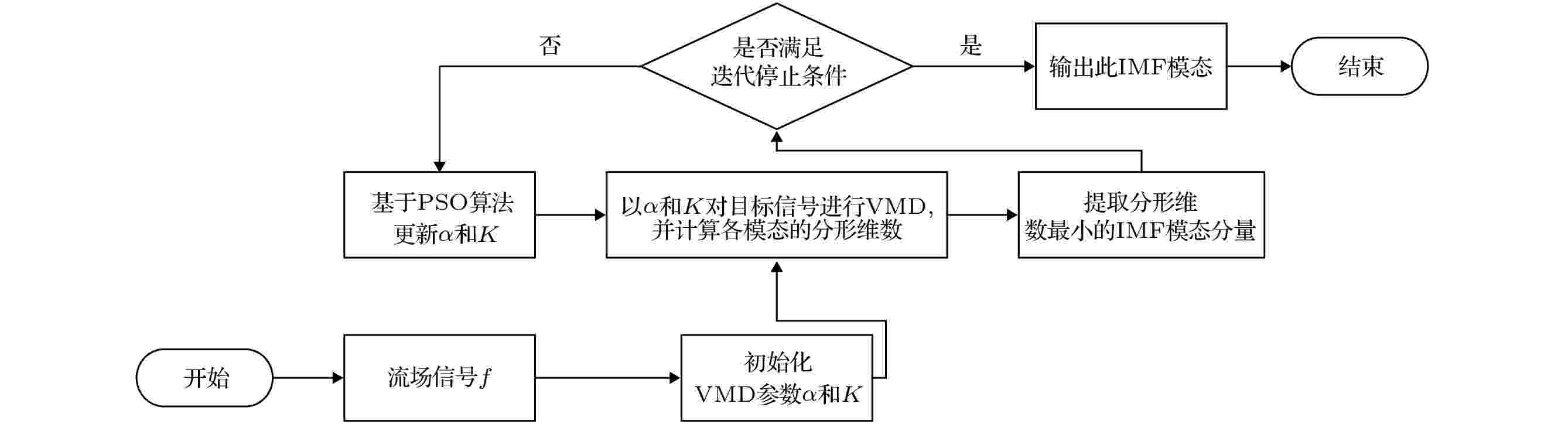图 3 AFVMD流程
Figure3. Workflow of the AFVMD.

如图4所示, 为同时实现流场信号降噪与非线性特征提取. 引入粒子群优化算法(particle swarm optimization, PSO), 交替更新由惩罚因子α及模态分解数K构成的PSO种群参数, 提取具有最小分形维数的模态分量, 以实现降噪和特征提取. 其中AFVMD的迭代停止条件与PSO进化停止条件一致, 由(11)式给出:
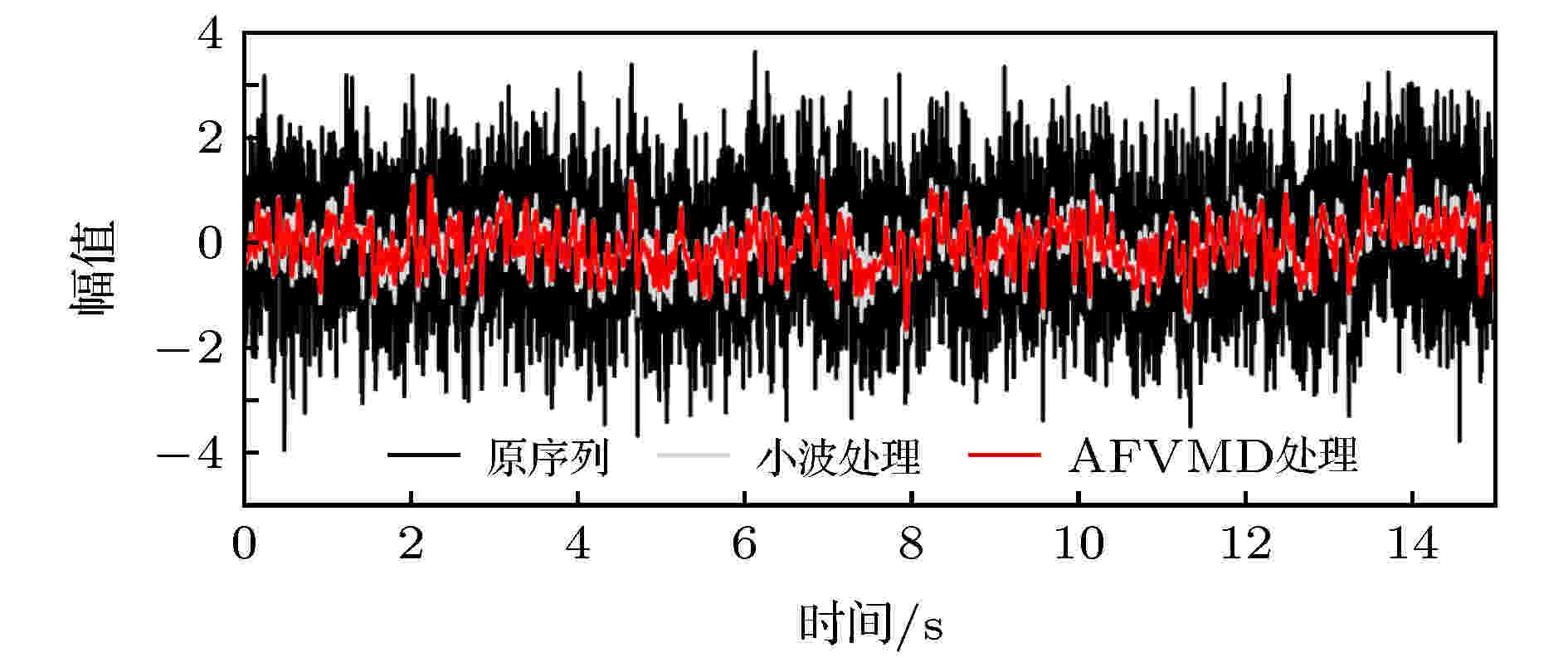图 4 FGN序列处理前后对比
Figure4. Comparison of FGN before or after the filtering.

$\varepsilon {{ = }}\min {{(}}{\mathop{\rm{Fractal}}\nolimits} ({\rm{IMF}})),$

式中Fractal(·)表示分形维数计算函数; IMF为流场经VMD分解所得各模态分量.

2

-->

6.1.AFVMD可靠性验证

为验证AFVMD算法提取自相似性信息及降噪的有效性. 以FGN(fractional Gaussian noise)序列为对象. 采用AFVMD与sym4小波方法^[30]对FGN序列进行处理, 时序信号如图4所示. 其中最佳参数组合为: 分解数K = 16, α = 600.
由图4可知, 采用AFVMD处理的FGN时序信号比小波方法降噪效果更显著. 为量化方法的有效性, 以处理后序列与原FGN序列的信噪比及其分形维数作为评判标准, 结果如表1所列.

采用方法	信噪比/dB	分形维数
未处理	—	1.74
Sym4小波	–3.87	1.49
AFVMD	–49.3	1.42

表1算法效果对比
Table1.Comparison of denoising effectiveness.

由表1可得, 与原FGN序列相比, 经小波降噪处理后的信噪比为–3.87, 经AFVMD方法处理后的信噪比为–49.3. 更低的信噪比表明经AFVMD处理的信号因所含噪声更少, 与含噪序列差异更大. 从三种时序的分形维数亦知, 原FGN序列因噪声比例较大, 序列自相似性被噪声淹没, 故分形维数较大. 经小波与AFVMD处理后的分形维数显著降低, 且AFVMD处理的时序更具有分形自相似性.
综上可证明, AFVMD在处理非线性时序时, 不仅可获取更加纯净的信息, 且所具有的分形自相似性特征更强.
2 -->

6.2.吸引子与最大Lyapunov分析

传统方法在判断失速、喘振状态时因信号的非线性导致误判、错判. 为此, 基于混沌为时间上的分形, 分形是空间上的混沌, 提出采用AFVMD方法提取压气机压力时序中纯净的非线性信息, 通过相空间重构法还原系统动力学特征.
延迟时间与嵌入维数对相空间重构的准确性影响显著, 采用互信息法与虚假邻近法^[31]分别计算原始流场、小波降噪以及采用AFVMD方法后的时间序列, 降噪前后流场压力时间序列、频谱对比见图5, 所得最佳延迟时间及嵌入维数见表2.

	延迟时间(嵌入维数)
工况	原序列	小波	AFVMD
最小流量1	11 (2)	20 (3)	24 (3)
最小流量2	4 (2)	20 (3)	23 (3)
浅喘1	4 (2)	19 (3)	33 (3)
浅喘2	4 (2)	20 (3)	30 (3)
浅喘3	13 (2)	22 (3)	36 (3)
浅喘4	4 (2)	22 (3)	36 (3)
深喘1	8 (2)	23 (3)	32 (2)
深喘2	5 (2)	26 (3)	38 (2)
深喘3	2 (2)	23 (3)	37 (2)
深喘4	17 (2)	28 (3)	32 (2)

表2最佳延迟时间及嵌入维数
Table2.Optimal parameters including delay time and embedded dimension.

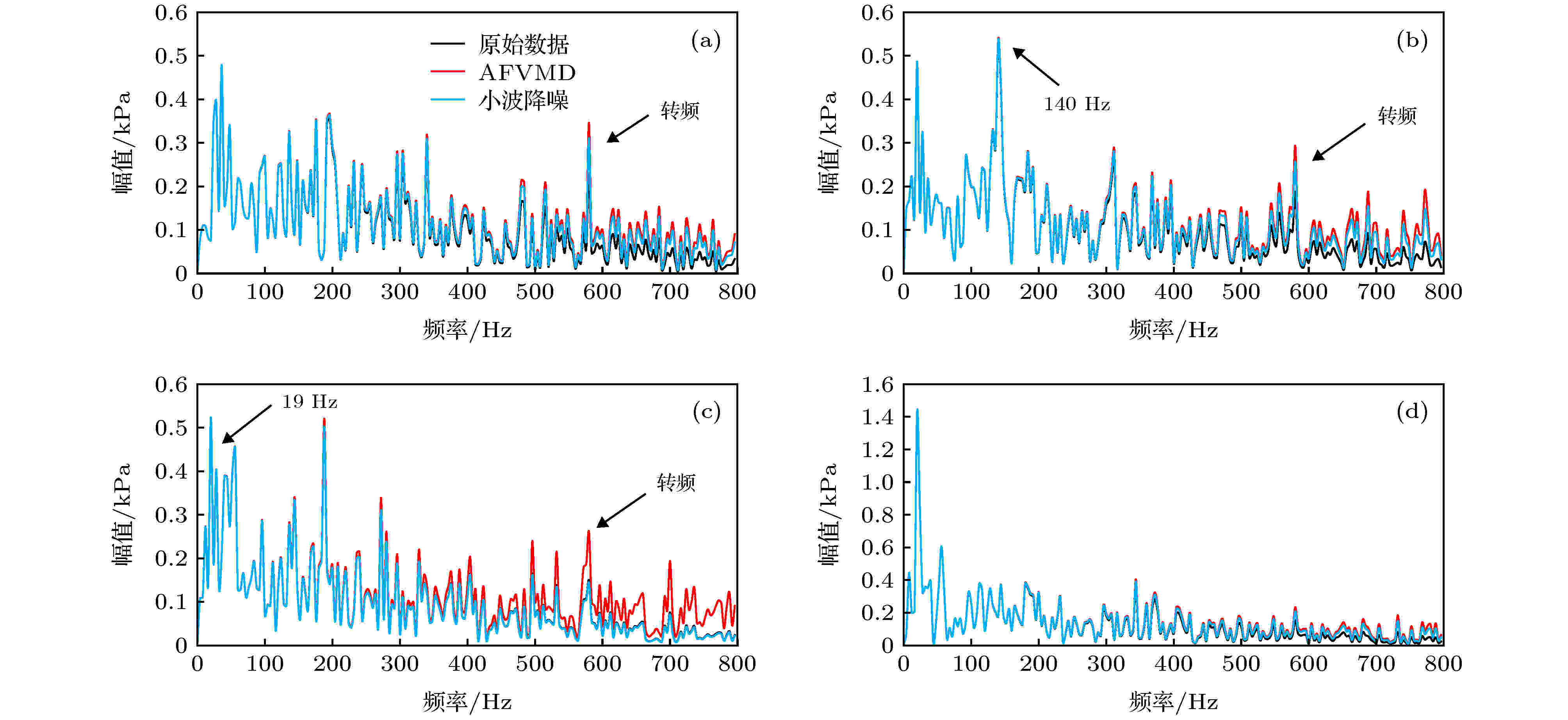图 5 流场降噪效果对比　(a) 最小流量工况1; (b) 最小流量工况2; (c) 浅喘工况1; (d) 浅喘工况2
Figure5. De-noise effectiveness comparisons of the flow field information: (a) The minimum flow condition 1; (b) the minimum flow condition 2; (c) the shallow breath condition 1; (d) the shallow breath condition 2.

由图5可知, 从“最小流量工况”与“浅喘工况”中的流场转频(约584 Hz)在AFVMD处理后比小波降噪更加明显, 体现所提出方法的优越性. 在“最小流量工况2”中, 140 Hz为最大主频, 表明此系统处于失速状态(约为主频的24%); “浅喘工况1”中, 出现主频为19 Hz的峰值, 因接近亥姆霍兹共振频率18.1 Hz^[32], 故为系统的浅喘频率, 体现所提出方法的可靠性.
基于最佳延迟时间与嵌入维数, 分别对原序列、小波处理及AFVMD处理后的信号进行相空间重构. 重构10种不同工况结果如图6所示.
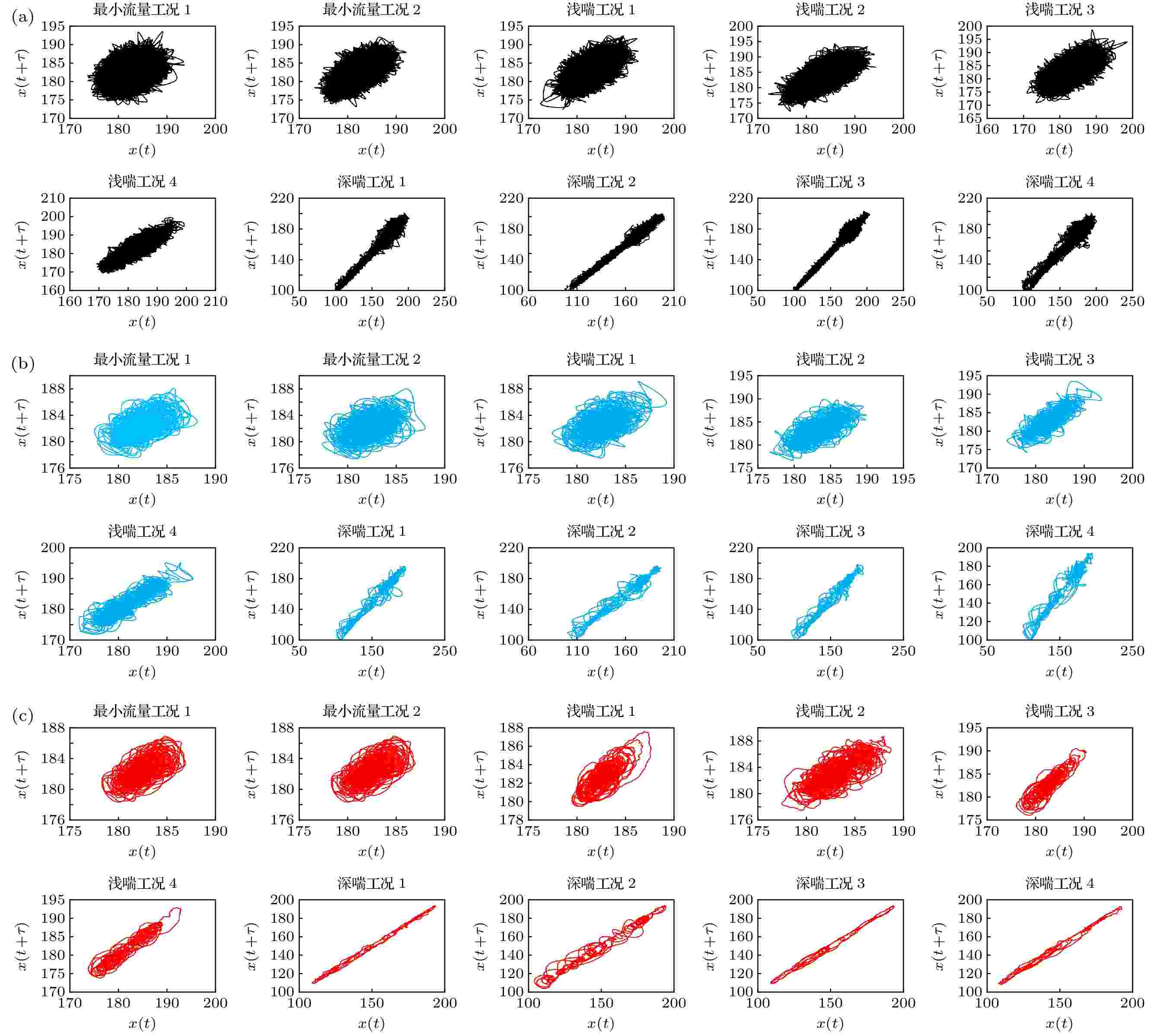图 6 不同工况相空间　(a) 原始序列; (b) 小波降噪处理序列; (c) AFVMD处理序列
Figure6. Reconstructed phase space of different conditions: (a) The original signals; (b) the signals proceed by the wavelet; (c) the signals processed by the AFVMD.

由图6可知, 压气机压力脉动信号的相空间可有效判别喘振状态, 基于混沌理论的分析法可更直观反映流场动力学可视化. 由图6(a)可知, 冗杂的混沌空间逐渐发展, 相形由“毛球状”向“细长状”演变. 但由于原始信号中存在大量噪声及其他无效信息, 导致相图在“浅喘工况4”时才表现出相空间分离趋势. 因无效信息干扰, 原始数据相空间在压气机将进入“深喘”前才展现相形差异.
如图6(b)所示, 与原流场信号混沌相图比, 经小波降噪处理后的相空间对压气机状态变化更敏感. 原本冗杂的“毛线球”相图在“浅喘工况3”时已呈分离趋势. 且当进入深喘后, 相空间隐约呈现出多环嵌套的拓扑结构.
该结果表明经过小波处理后的时序所含信息更纯净有效, 经小波降噪处理的相空间比直接采用相空间判断喘振阶段更加有效. 在此实验中, 根据相形差异, 可提前约0.25 s判断是否进入“深喘”状态.
由图6(c)可得, 采用AFVMD处理的时序在“浅喘工况1”所对应的相形已呈现分离趋势; 根据相形差异, 在此实验中可提前约1.00 s判断是否会进入“喘振”状态; 其“浅喘工况3”的相图比小波处理的“浅喘工况4”离散度更高. 进入“深喘”后, 因AFVMD不仅实现降噪, 且提取代表性分形特征, 使相空间更明显地呈现多环相扣的拓扑结构, 表明采用AFVMD方法可准确还原系统的动力学形态.
为量化预测性、突出所提出AFVMD在降噪与特征提取方面的优势, 基于最大Lyapunov大小可反映时序的可预测性^[33], 采用Wolf法, 针对不同工况, 对原数据、小波处理与AFVMD处理的信号求解最大Lyapunov指数, 结果如图7所示. 其中“标签1”—“标签10”分别表示从“最小流量工况1”发展至“深喘工况4”.
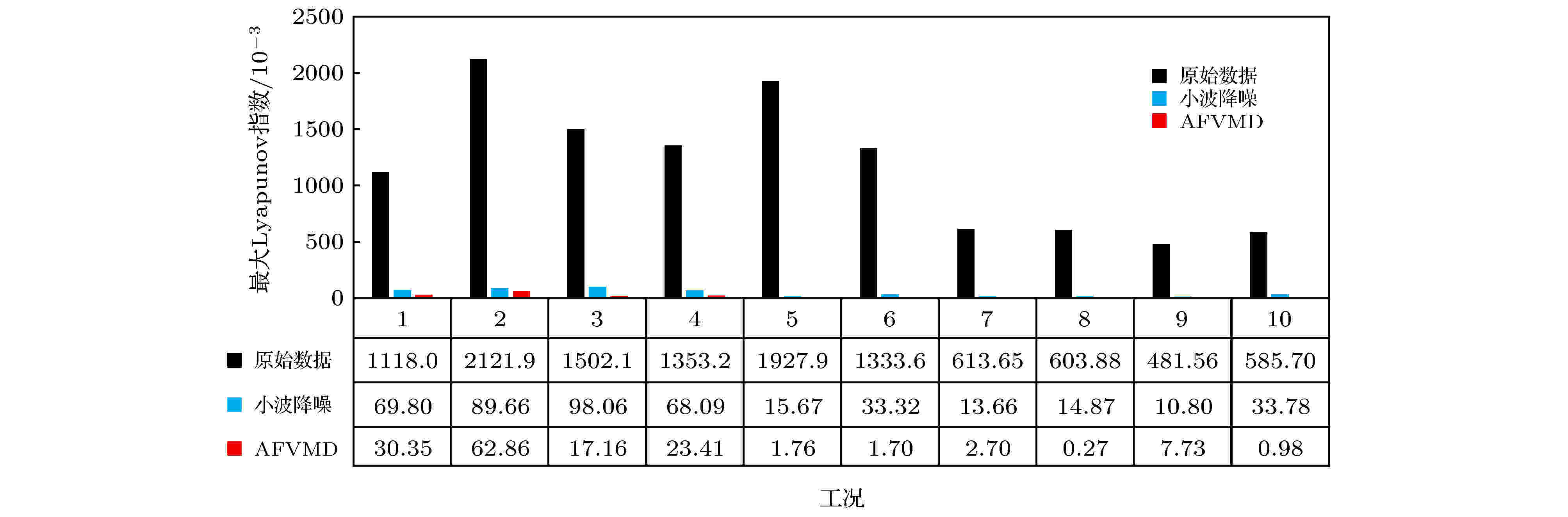图 7 不同工况最大Lyapunov指数
Figure7. The maximum Lyapunov exponents of different conditions.

如图7所示, 深喘工况下, 最大Lyapunov指数较“浅喘工况”明显降低, 全过程中最小值为0.587. 采用小波降噪处理后, 由于剔除噪声干扰, 全工况所对应的最大Lyapunov指数降低了约90%以上, 显著提升该序列的可预测性. 值得注意的是, 采用AFVMD方法在“工况5”(浅喘工况3), 其最大Lyapunov指数与原数据相比降低了约99.9%, 与小波降噪数据相比亦降低了约90%. 该结果说明, 采用AFVMD因从原数据中剔除噪声并提取非线性代表特征, 使得信号具有更小的最大Lyapunov指数, 从而提升信号的可预测性.

为解决传统方法在处理离心压气机失稳时信号处理难的问题. 基于分形维数与变分模态分解, 提出AFVMD方法, 同时实现降噪及自相似性特征提取. 以最小流量工况下叶轮出口动态压力信号为研究对象, 分别采用小波降噪及AFVMD对数据进行处理, 分析原始数据、经小波和AFVMD处理的动力学空间, 结论如下:
1) 与小波降噪方法相比, AFVMD方法在处理具有分形特征的含噪信号时, 不仅数据更纯净, 且含更多代表性分形特征. 故更适合处理含噪非线性信号;
2) 不同阶段具有不同的相空间“相形”. 基于经小波降噪后信号的相图, 可提前0.25 s判断压气机将进入“深喘”; 基于AFVMD处理的信号相图, 可至少提前1.00 s判断压气机将进入“深喘”状态, 更早捕获失速征兆. 亦体现AFVMD在处理非线性信号时的优越性;
3) 基于AFVMD与相空间重构法, 所得相图在“深喘”时具备比小波处理更清晰的多环嵌套拓扑结构, 更准确地还原系统动力学结构. 该方法为压气机失稳信号分析提供了新思路;
4) 采用AFVMD降噪并提取的信号, 与原数据与小波处理后信号相比, 其最大Lyapunov指数呈指数型减小. 更小的最大Lyapunov指数可提高对流动失速、喘振这一混沌系统的可预测性.