摘要:黑磷是一种具有直接带隙的二维材料, 其较宽的带隙填补了石墨烯和二维过渡金属硫化物之间的带隙空白, 其特殊的褶皱状晶体结构导致了其独特的面内各向异性, 使其具有了独特的力电磁响应特性. 本文基于单层黑磷设计了一种金光栅/黑磷/硅的混合等离子体结构的磁光器件. 通过金属光栅诱导异常透射显著增强透射率, 同时通过TE模式和TM混合等离子体模式匹配耦合增强了法拉第旋转效应. 在1.5 THz工作频率点, 对器件参数进行优化后, 施加5 T的外部磁场, 法拉第旋转角度可以达到2.7426°, 增益为14.434倍, 同时透射率能够保持在85%以上. 此外, 研究了黑磷的载流子密度和外部磁场对磁光器件的调谐特性. 最后, 讨论了金属光栅的类等离子模式对本征波导模式和法拉第磁光效应的影响.
关键词: 黑磷/
异常透射/
法拉第旋转

English Abstract

全文HTML

--> --> -->

磁光效应是指物质被外部磁场磁化后与光之间相互作用而引起的一些光学现象^[1]. 而法拉第效应是磁光效应的一种, 是一束偏振光经过置于磁场的物质后, 光的偏振面发生旋转的现象^[2,3]. 随着激光技术和光电子技术的发展, 法拉第效应在传感器、隔离器、调制器以及存储器件^[4–8]等领域都得到了应用. 传统的法拉第器件主要使用铁氧体和稀土掺杂石榴石等材料^[9,10], 由于旋转角度一般和光传播的距离也就是材料的厚度成正比, 所以传统的器件很难集成到微纳光学系统中去^[9,11]. 因此, 减小磁光器件到亚波长尺度是实现磁光器件集成到微纳光学系统中的关键.
近几年, 随着只有单原子厚度的二维材料的发展, 在亚波长甚至更低尺度获得法拉第效应已经成为现实. 最早是在石墨烯^[3,12,13]上实现了磁光效应、后来其他的二维材料如过渡金属硫化物^[2]和黑磷^[14–16]等也都通过理论和实验验证了磁光效应的存在. 和石墨烯、过渡金属硫化物相比, 一方面, 黑磷面内各向异性的结构, 使其在光学方面表现出了一些特殊的光学特性. 另一方面, 黑磷有较高电荷迁移率和开关比, 而且直接带隙可以从0.3 eV拓展到2.0 eV, 填补了石墨烯和过渡金属硫化物之间的带隙空白, 拓展了二维材料应用的波段; 同时, 黑磷的带隙可以通过应力、温度、化学掺杂和电压等方法进行调制, 使基于黑磷设计的器件更加灵活可调^[17–22]. 正如前面所讲, 黑磷具备磁光效应, 因此在中红外甚至太赫兹领域黑磷可以作为设计微纳尺度磁光器件的一种具有很大潜力的材料.
目前, 关于单层和多层黑磷的磁光效应的研究已经有一些报道, 2015年, Zhou 等^[23]通过理论方法研究了在外部磁场作用下的黑磷的朗道能级和磁输运特性. 同年, Zhou等^[14]和Jiang等^[15]又分别研究了多层黑磷在外部磁场作用下的光响应和电响应特性. 2019年, You等^[24]报道了单层黑磷的磁等离子体特性以及由外部磁场和各向异性晶格结构诱导的各向异性磁光响应. Li等^[21]在研究中给出了单层黑磷的法拉第旋转角度和表面电导率非对角元之间σ_xy的关系. 当前的研究表明, 单层黑磷的法拉第旋转是有非对角元σ_xy引起的. 所以和石墨烯类似, 只有在回旋频率附近, 才能产生较大的旋转角度, 这限制了单层黑磷的应用范围, 因此, 设计微纳结构来增强单层黑磷的法拉第旋转是值得研究的一个重要内容. 目前, 对于石墨烯的法拉第效应增强采用的方法主要有谐振腔^[25]、磁光子晶体^[26]和异常透射^[27]等, 而对于单层黑磷的法拉第效应增强, 除了我们课题组前面研究的通过磁光子晶体缺陷模式实现外^[11], 其他的相关报道还未看到.
在本文中, 设计了一个金光栅/黑磷/硅的混合等离子体结构(grating/BP/Si, GBPS)实现了对单层黑磷的法拉第效应的增强, 通过严格耦合波(rigorous coupled wave analysis, RCWA)的方法, 研究了光栅/硅(grating/Si, GS)结构的透射谱特性, 给出了设计磁光器件的基本方法. 由于二维材料非常薄, 厚度只有原子大小尺度, 所有一般可以采用薄膜介质模型^[28–30]或者表面电流模型^[31,32]进行表征, 本文在进行有限元仿真的过程中, 采用了表面电流的模型对黑磷进行表征. 在此基础上对结构参数进行优化, 得到了一个性能较优的磁光器件. 当设计的器件工作频率为1.5 THz时, 磁光器件的厚度远远小于半个波长, 法拉第旋转角度能够获得14.434倍的增益, 同时透射率能保持大于85%. 在此基础上, 研究了外部磁场和黑磷载流子密度对器件特性的调谐作用, 并且讨论了类等离子模式(spoof surface plasmons, SSPs)对基底波导模式和法拉第旋转角度的影响. 本文的工作对设计亚波长尺度的磁光器件具有重要的指导意义.

设计的磁光器件结构如图1所示, 周期性的金属光栅沿着y方向排布, 在x方向为无穷大延伸. 光栅的周期为L, 每个周期中, 金属条的宽度为W, 厚度为d_a. 基底为硅, 厚度为d_s. 硅的折射率为n_Si = 3.4147, 上层为金属光栅材料为金, 金的介电常数模型采用德鲁得模型进行描述, 可以有如下公式计算得到^[27]
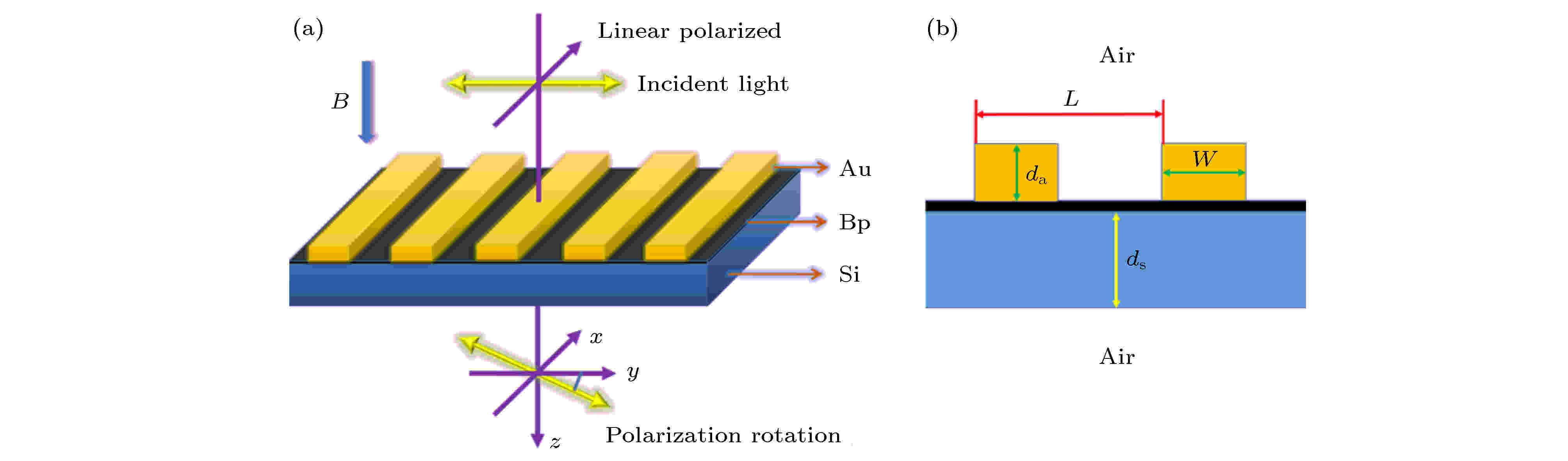图 1 磁光器件结构图　(a) 三维结构图, 底部为硅基底, 上部为金属光栅, 中间为黑磷, 磁场垂直黑磷水平面, 入射光为线偏振光; (b) 垂直面二维图, 光栅周期L, 金属条厚度d_a, 宽度W, 基底厚度d_s
Figure1. Schematic of the magneto-optical device: (a) 3D structure diagram. The Si layer is the substrate, the grating is in the top layer, and the black phosphorus (BP) is in the center laye; (b) 2D vertical plane diagram. The period of the grating is L, the thickness and the width of the metal are d_a and W, and the thickness of the substrate is d_s.

${\varepsilon _{\rm{m}}} = {\varepsilon _\infty } - \omega _{\rm{p}}^{\rm{2}}/(\omega + {\rm{i}}\omega {\omega _{\rm{\tau}} }), $

其中ε_∞ = 1, 等离子频率ω_p = 1.37 × 10¹⁶ rad/s, 阻尼频率ω_τ = 2.72 × 10¹³ rad/s, ω为角频率.
单层的黑磷放置于基底的上表面, 光栅的下表面, 施加外磁场B垂直于黑磷的表面(如图1(a)所示). 由于黑磷具有各向异性特征, 所以其表面电导率张量可以用下列矩阵表示:

${{\sigma}} = \left( {\begin{array}{*{20}{c}} {{\sigma _{xx}}}&{{\sigma _{xy}}}&0 \\ { - {\sigma _{xy}}}&{{\sigma _{yy}}}&0 \\ 0&0&{{\sigma _{zz}}} \end{array}} \right), $

其中对角元和非对角元的表面电导率都可以用半经典德鲁得模型表述, 具体公式如下^[24]:

${\sigma _{jj}} = \frac{{{\rm{i}}{n_{\rm{s}}}{e^2}}}{{{m_{jj}}}}\frac{{\omega + {\rm{i}}\zeta }}{{{{(\omega + {\rm{i}}\xi )}^2} - \omega _{\rm{c}}^{\rm{2}}}},~{\rm{ }}j = x,~y{\rm{ }}, $

${\sigma _{jk}} = - \frac{{{n_{\rm{s}}}{e^2}}}{{{m^*}}}\frac{{{\omega _{\rm{c}}}}}{{{{(\omega + {\rm{i}}\xi )}^2} - \omega _{\rm{c}}^{\rm{2}}}},~j = x,~k = y,$

其中σ_jj 是黑磷沿着x (锯齿方向)和y (扶椅方向)方向的表面电导率; σ_jk是由外部磁场激发的表面霍尔电导率; e是基本电荷1.6 × 10^–19 C; n_s 是黑磷的载流子密度, ξ是电子散射率, 可以通过η/?计算, η为10 meV, ?是普朗克常数1.05457168 × 10^–34 J·s. m*是平均质量, ω_c是磁回旋频率, 分别定义为^[24]

${m^*} = \sqrt {{m_{xx}}{m_{yy}}}, $

${\omega _c} = eB \cdot {{n}}/{m^*}, $

其中黑磷面内沿着x和y方向平均质量分别为m_xx = 0.15m₀, m_yy = 0.7m₀^[24,33], 其中m₀ = 9.10938 × 10^–31 kg 为电子静止质量. B 是外部所加在器件上的沿着z方向的磁场, n是垂直于黑磷所在平面的单位矢量.
当一束波长为λ的光以入射角γ入射到带有衬底的金属光栅, 光栅厚度 $\ll $λ 波矢满足以下条件时, 衬底中会激发形成导模:

$\frac{{2{\rm{\pi}} }}{\lambda }\sin (\gamma ) + m\frac{{2{\rm{\pi}} }}{L} = \pm \frac{{2{\rm{\pi}} }}{\lambda }{n_{{\rm{eff}}}},$

n_eff是在衬底中传播模式的有效折射率, m为光栅衍射级数. (7)式表明方程左边两个分量(入射光波矢水平分量与光栅的倒格矢)之和和衬底中导模分量满足共相位条件时, 会形成谐振透射现象, 出现类似法布里-珀罗(Fabry-Pero, FP)的谐振峰, 也即产生异常透射^[34]. 因为光栅衬底的存在, 所以不管是TE还是TM入射, 衬底中的导模都会存在. 对于TM入射, 同时还会存在SSPs, 它和衬底中导模相互耦合形成新的混合等离子体模式(waveguide-spoof surface plasmons mode, WSPM). 由于SSPs的存在及传输特性取决于光栅周期和占空比, 因此可以通过光栅参数来调节TM入射时产生的等离子混合模式的模式特性, 使它与衬底中TE导波模式达到波矢匹配, 提高TM模向TE模的转换效率, 从而增强法拉第旋光效应.
根据光栅耦合的布拉格条件(7)式和SSPs色散关系来设计同时实现异常透射和增强法拉第旋光效应的结构. 首先, 假设衬底导模为基模, 并且引入的光栅对衬底波导的传输模式没有影响^[35], 在TM偏振光垂直入射时, 可以确定期望工作频率下的法拉第旋转器衬底厚度为λ/(2n_Si), 波导的等效折射率介于空气和衬底折射率之间, 由(7)式可知光栅周期L的范围为(mλ—mλ/n_Si). 其次, 为了表征最优的器件性能, 此处定义了品质因数(figure of merit, FOM) FOM = (T)^1/2 × θ_F作为优化参数的目标. 在设定的工作频率下通过严格耦合波的方法对周期(范围为mλ—mλ/n_Si)和光栅占空比(占空比设置大于0.5, 扫描范围为0.5—1.0)进行扫描, 可以获得在考虑光栅对衬底影响下, 品质因数较优的光栅周期和金属宽度. 在此基础上, 再对光栅调制深度进行优化, 可以得到最优的品质因数. 最后, 考虑单层黑磷的影响. 由于黑磷是原子层厚度, 它对器件的透过率和波导模式的影响可看成是一个微扰, 通过有限元仿真软件对周期L再进行小范围的精确扫描, 即可得到该工作频率下品质因数最优的结构参数.
假设一束偏振光正入射到磁光器件表面, 偏振方向垂直光栅方向(TM波), 如图1所示, 则当这束偏振光透射过器件以后, 平行入射场方向的透射系数可以表示为

${t_{/\!/}}(\omega ) = {E_{/\!/}}(\omega )/E_{{/\!/}}^0(\omega ), $

其中E_//(ω)为透射场平行入射场方向的分量, $E_{/\!/}^0(\omega )$为入射场. 垂直入射场方向的透射系数可以表示为

${t_ \bot }(\omega ) = {E_ \bot }(\omega )/E_{{/\!/}}^0(\omega ), $

其中${E_ \bot }(\omega )$为透射场垂直入射场方向的分量. 因此总的透射率可以表示为:

$T = t_{/\!/}^2 + t_ \bot ^2.$

法拉第旋转角度可以表示为

$ {\theta }_{\rm{p}}={\rm{arctan}}({E}_{\perp }/{E}_{/\!/}).$

对于电场的计算, 通过有限元仿真软件Comsol实现, x和y方向上采用了周期性边界条件, 在上下空气层的两端, 把两个端口设置为完美匹配层. 一束功率为1 W的极化光波以角度γ = 0°入射到器件上. 网格的大小采用极细化的自适应网格. 当计算s极化和p极化的时候, 入射波分别设置为电场和磁场. 旋转角度可以通过(10)式计算得到. 需要注意的是, 由于黑磷非常的薄, 只有0.53 nm厚度, 在仿真的过程中采用表面电流模型来表征黑磷.

根据上述方法设计的磁光法拉第旋转器件如图1(a)所示, 其优化结构参数为: 工作频率f = 1.5 THz, 金属光栅周期L = 159.000 μm, 金属宽度W = 109.365 μm, 基底厚度d_s = 29.285 μm, 光栅调制深度d_a = 1.000 μm. 黑磷的锯齿方向沿着x方向, 扶椅方向沿着y方向. 黑磷载流子密度一般取值在(0.5—5.0) × 10¹³ cm^–2之间^[22], 而较大的载流子密度会降低透射率, 所以本文理论计算的时候载流子密度n_s = 0.5 × 10¹³ cm^–2. 为了比较, 用Comsol分别计算了单层黑磷和GBPS的透射率(T), 法拉第旋转角度(θ_F)以及品质因数(FOM). 如图2(a)所示为单层黑磷在1.45—1.55 THz 之间的透射频谱和法拉第旋转角度频谱, 其中虚线为透射频谱, 实线为法拉第旋转角度频谱. 虽然单层黑磷的透射率在85%左右, 但是法拉第旋转角度只有0.2°左右. 其品质因数频谱图如图2(b)所示, 在整个范围内品质因数都小于0.18, 磁光效应很弱. 如图2(c)所示, 虚线是GBPS的透射率, 实线是GBPS的法拉第旋转角度, 在1.45—1.55 THz范围内出现了一个明显的透射峰, 峰值大小为86.968%, 位置为1.5 THz. 这个透射峰的出现是由金属光栅引发的异常透射诱发的. 由于此时TE模式和TM等离子混合模式耦合效率较高, 极大增强了法拉第旋转角度, 使法拉第旋转角度出现了一个极大值, 如图2(c)实线所示, 法拉第旋转角度在1.5 THz到达了最大值2.7426°, 和透射峰最大值位置基本重合, 是单层黑磷直接产生法拉第旋转角度的14.434倍左右. 另外从图2(d)的品质因数频谱可以看到FOM在1.5 THz达到了最大值2.5576, 是单层黑磷的最优品质因数的15.044倍. 因此, 在所设计工作频率上, 既能通过金属光栅产生的异常透射保持透射率大于85%, 又可以通过模式耦合显著地增加法拉第旋转角度.
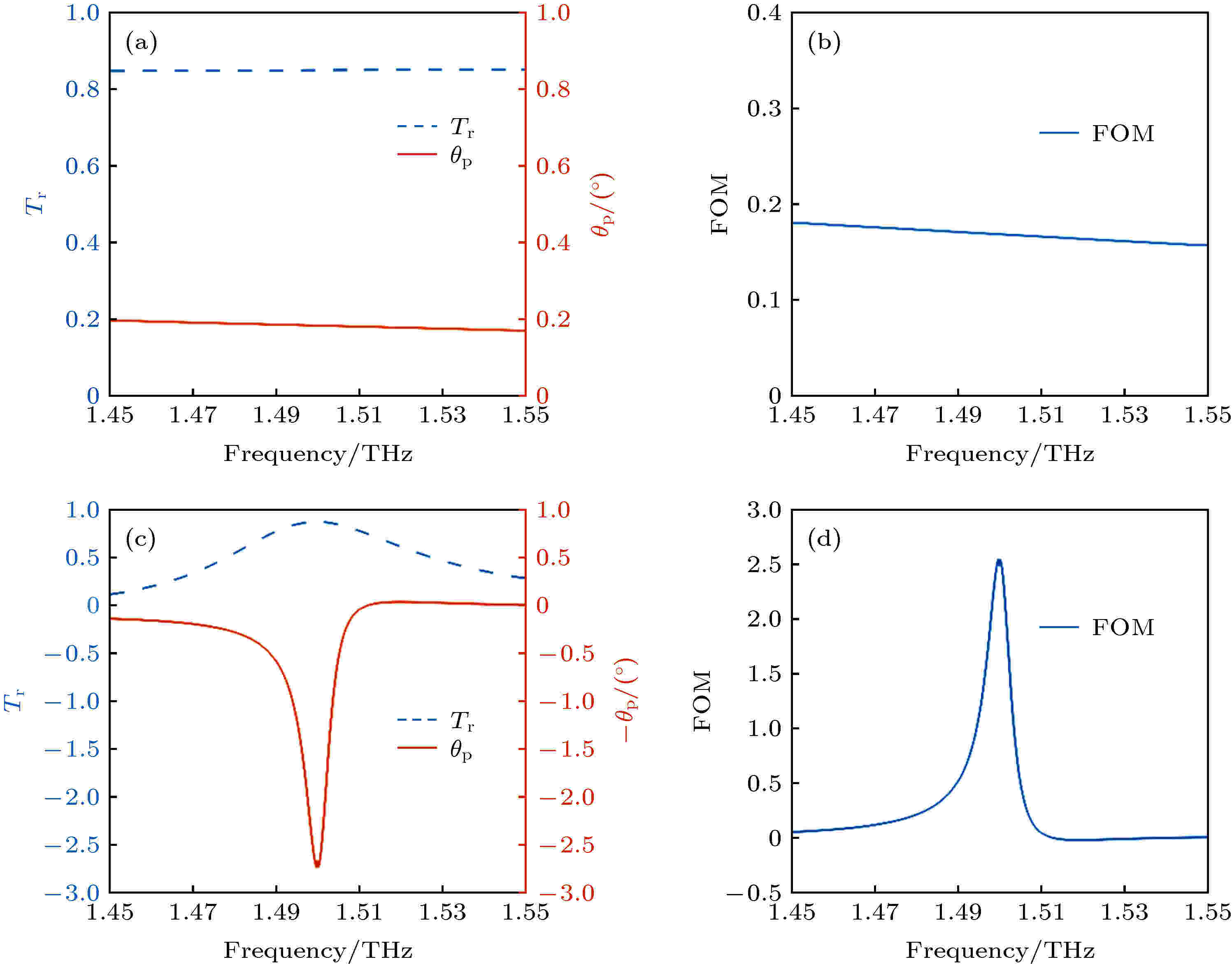图 2 单层黑磷和磁光器件透射谱、法拉第旋转角度和品质因数谱　(a) 虚线为单层黑磷的透射率频谱图, 实线为法拉第旋转角度频谱图; (b) 单层黑磷的品质因数频谱图; (c) GBPS结构的透射率频谱图和法拉第旋转角度频谱图; (d) GBPS结构的品质因数频谱图
Figure2. The transmittance, Faraday rotation angle and the figure of merit (FOM) of the monolayer BP and magneto-optical device verse the frequency: (a) The dotted line is the transmittance of the monolayer BP, and the solid line is the Faraday rotation angle of the monolayer BP; (b) the FOM of the monolayer BP; (c) the dotted line is the transmittance of the magneto-optical device with GBPS structure, and the solid line is the Faraday rotation angle of the magneto-optical device with GBPS structure; (d) the FOM of the magneto-optical device with GBPS structure.

为了解释异常透射增强黑磷法拉第旋转角度的物理机制, 首先通过Comsol仿真了在1.5 THz频率点的电场分布图, 仿真使用的结构参数和计算图2(c)使用的一致. 为了说明法拉第旋转角度产生的原因, 分别给出了TM模式下(H_x垂直yz面), GS结构和GBPS结构的电场沿x方向和y方向的分布. 如图3(a)所示, 当没有黑磷存在时, E_x分量为零, 只有E_y分量存在. 而加入黑磷后, 如图3(b)所示, GBPS下的电场不仅存在E_y分量, 同时E_x也存在, 这说明加入黑磷后, 使电磁场发生旋转, 从而产生了x分量的电场. 由此可以说明黑磷是产生法拉第旋转的关键.
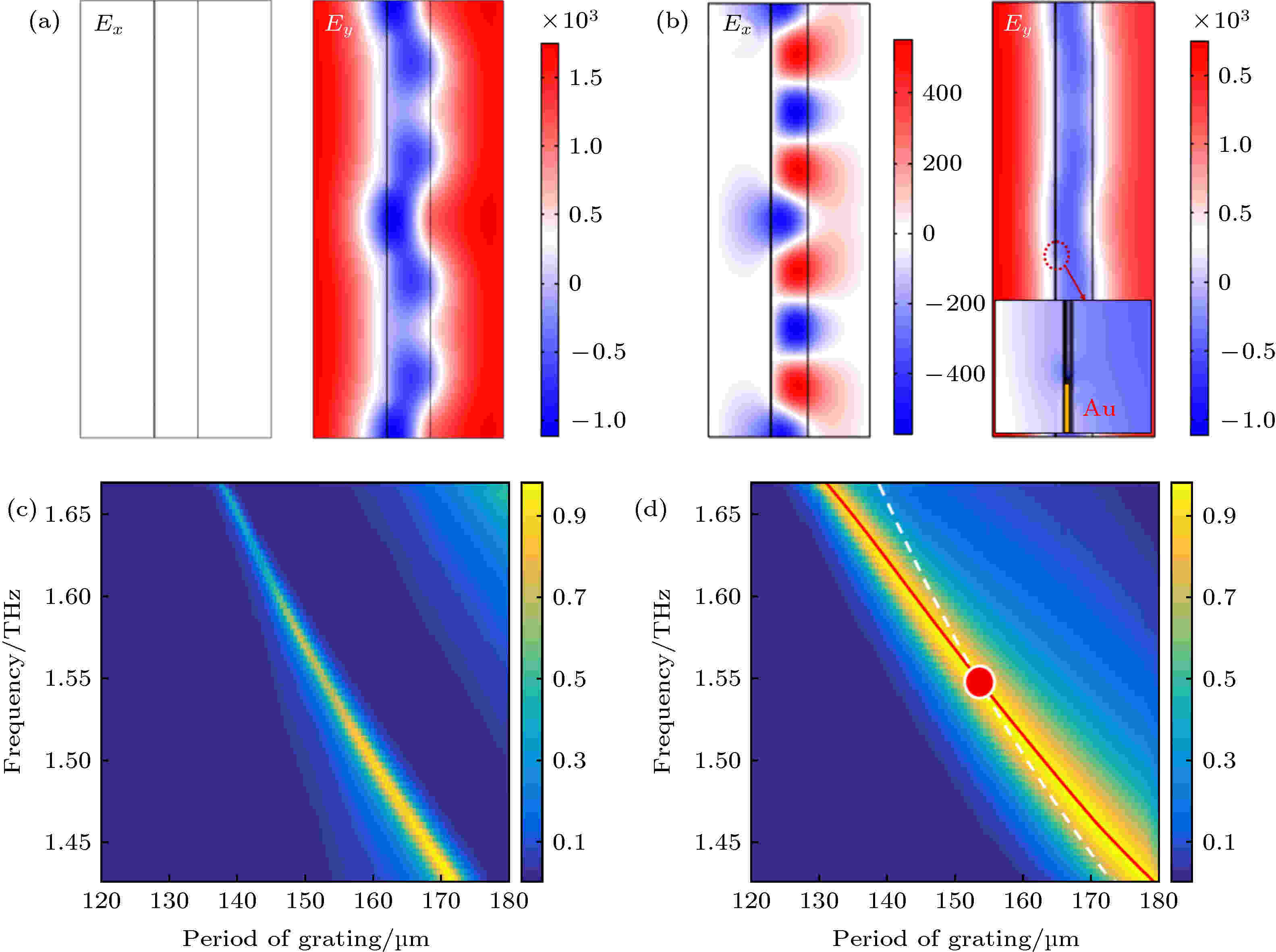图 3 磁光器件电场分布图和TE/TM透射谱　(a) GS结构, 1.5 THz时TM模式下的E_x, E_y分布图; (b) GBPS结构, 1.5 THz时TM模式下的的E_x, E_y分布图, E_y分布图中放大部分为金属光栅端子上的场分布; (c) TE模式下透射率随频率和光栅周期的变化图; (d) TM模式下透射率随频率和光栅周期的变化图
Figure3. The electric field distribution and the TE/TM transmittance spectrum of the magneto-optical device: (a) The E_x and E_y of the device without the monolayer BP in TM mode at 1.5 THz; (b) the E_x and E_y of the device with GBPS structure in TM mode at 1.5 THz, and the electric field distribution on the metal grating terminal is shown in the enlarged part of E_y; (c) variations of transmittance with frequency and grating period in TE mode; (d) variations of transmittance with frequency and grating period in TM mode.

为了进一步说明法拉第磁光效应增强的工作机制, 通过RCWA方法计算了在不同的光栅周期下, TM和TE模式下的反射谱, 以此说明其模式的变化. 除光栅周期L外, 其他的结构参数和上节内容使用的一致. 如图3(c)所示为TE模式下的透射谱, 随着光栅周期L增加, 本征模式发生了红移. 同时因为TE模式下无法激发SSPs模式, 所以此时只存基底硅层中的TE本征波导模式. 当入射波为TM时, 图3(d)为TM模式下的透射谱, 同样随着光栅周期L增加, 模式发生红移, 符合(7)式中L和λ的相对关系. 在这个模式下的电场分布如图3(b)所示, 其中电场分量E_x被局域在基底的硅波导中, 可以从场分布看到出现的为基模, 符合设计结构参数, 因此TM的本征波导模式存在. 由于TM入射激发了SSPs模式, 当SSPs模式耦合到TM的本征波导模式后会对TM的色散产生影响, 出现波导模式和SSPs模式混合的新的WSPM模式. 研究表明, 如果衬底只存在TE本征波导模式和TM本征波导模式, 那么TM和TE模式的色散曲线是不会相交的^[27,36], 所以在激发了SSPs模式而改变TM的色散后, 才出现TE和WSPM模式的色散曲线交叉的情况. 如图3(d)上的实线和虚线所示, 当不断增加光栅周期的时候, 也就是通过SSPs改变TM模式下的色散的时候, TE和WSPM模式的传播常数出现的交点, 如图3(d)中实心圆所示位置, 而且还存在一些重合的地方. 这时TE和WSPM模式满足匹配条件, 耦合效率较高. 同时如图2(b)中电场分量E_y的放大图所示, 在金属光栅的端点上, 出现了极强的电场局域, 该电场在SSPs的模式波长下与黑磷发生了强烈作用, TE和TM的转换效率达到最高值, 磁光法拉第效应达到最强. 因此, 法拉第磁光效应的增强是由于TE和WSPM模式发生耦合产生的结果, 同时高透射率是由于在模式匹配条件下异常透射引起的.
法拉第磁光效应是由于外部磁场激发霍尔表面电流而产生的. 为了揭示外部磁场对法拉第磁光效应的影响, 计算了不同外部磁场下的法拉第旋转角度和品质因数. 如图4(a)所示, 当外部磁场从3 T逐渐增加到9 T的时候, 法拉第旋转角度也随之逐渐增加, 分别为1.656°, 2.743°, 3.803°和4.829°, 对应的工作频率点保持不变. 法拉第旋转角度随外部磁场增加的幅值分别为1.087°/T, 1.06°/T 和1.026°/T, 基本呈现线性关系. 因此可以通过调制外部磁场来对旋转角度大小进行控制. 图4(b)是磁光器件品质因数随外部磁场的变化频谱图. 从图4(b)可以看到, 当外磁场逐渐增大时, 品质因数也同时和法拉第旋转角度一样成线性增加, 这反映在外部磁场变化的时候, 透射率基本保持不变. 产生透射率基本不变, 而法拉第旋转角度成线性变化的现象是因为ξ远远大于ω和ω_c, 在这个情况下可以从(4)式看到电导率的非对角元σ_xy(σ_yx)和ω_c成正比关系, 而ω_c和外部磁场B成正比关系, 法拉第旋转角度和σ_xy成正比关系, 所以法拉第旋转角度和外部磁场也成正比关系. 另外, 单层黑磷对透射率的影响主要取决于电导率的对角元张量σ_xx和σ_yy, 而从(3)式看, 在ξ远远大于ω和ω_c的情况下, 外部磁场B对σ_xx和σ_yy的影响几乎可以忽略, 所以, 在外部磁场变化的时候, 透射率基本保持变. 这个结论与我们前面的研究结论一致^[11], 通过改变磁场对法拉第旋转角度进行调节是一个有效可行的方法.
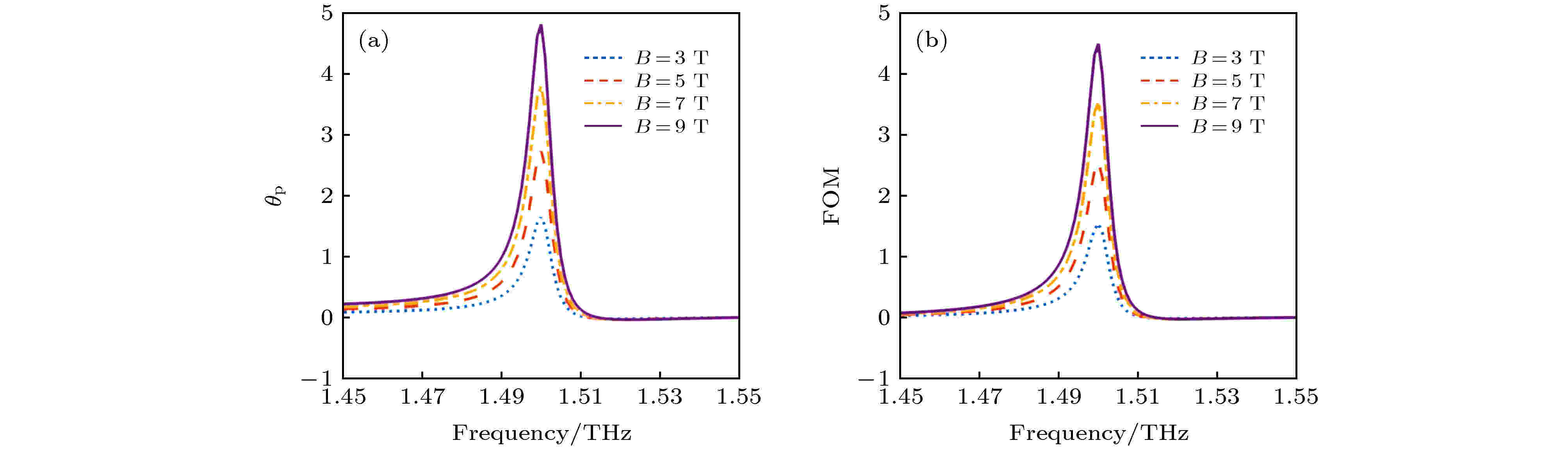图 4 外部磁场分别为3, 5, 7和9 T下的磁光器件响应图　(a) GBPS结构的透射率频谱图; (b) GBPS结构法拉第旋转角度频谱图
Figure4. The magneto-optical response diagrams of the device when the external magnetic fields are set as 3, 5, 7 and 9 T: (a) Transmission and (b) faraday rotation angle of the device with GBPS structure.

因为黑磷的载流子密度可以通过费米电压、温度和黑磷层数等手段进行调控, 所以在前面研究基础上, 进一步研究了单层黑磷载流子密度对法拉第磁光器件的影响. 在磁光器件其他参数与图2(c)保持不变的情况下, 分别计算了载流子密度为0.5n₀, 1.0n₀, 1.5n₀和2.0n₀情况下对应的法拉第旋转角度和透射率. 如图5(a)所示, 当载流子密度增加后, 工作频率点分别为1.500, 1.501, 1.503和1.504 THz, 法拉第旋转角度频谱发生了轻微蓝移, 法拉第旋转角度有所增加, 但是却没有如(4)式所示成比例增加, 原因是此处法拉第磁光器件的结构参数是在n_s = 0.5n₀情况下优化得到的, 当黑磷载流子密度发生变化后, 结构表面的表面电流特性发生了变化, 对磁光器件的共振模式产生了微扰, 破坏TE模式和TM等离子混合模式的耦合, 从而削弱了磁光效应的增强. 图5(b)的品质因数的工作频率点偏移和法拉第角度保持一致, 但是品质因数在法拉第旋转角度增大的情况下却有所下降, 这说明当载流子浓度增大后, 透射率下降较大, 造成这个原因是因为当载流子浓度增大后对角元σ_xx和σ_yy也随之增大, 造成吸收增强^[37], 所以造成品质因数下降. 结合外部磁场对法拉第磁光器件的影响, 可以通过外部磁场和载流子浓度进行一起调控, 达到工作频率点和旋转角度的动态调谐.
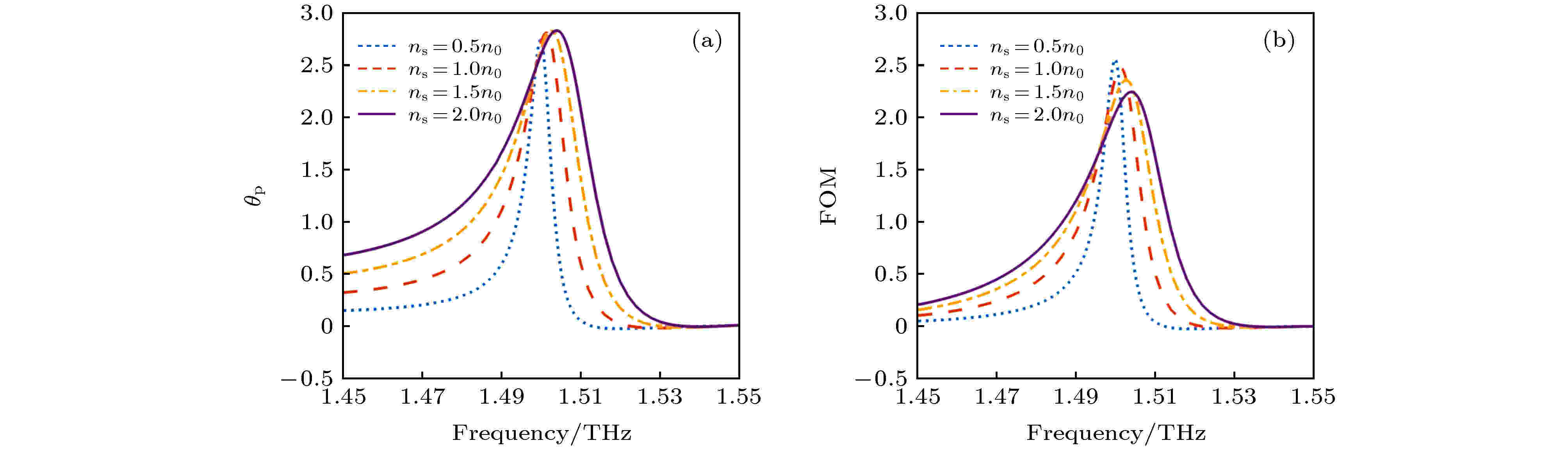图 5 不同载流子浓度下的磁光器件响应图　(a) GBPS结构的透射率频谱; (b) GBPS结构的法拉第旋转角度频谱. 黑磷载流子浓度度分别为0.5n₀, 1.0n₀, 1.5 n₀, 2.0 n₀ (n₀ = 1 × 10¹³ cm^–2)
Figure5. Magneto-optical response diagrams of the device with different carrier density of BP: (a) Transmission and (b) faraday rotation angle of the device with GBPS structure. The carrier density of BP are set as 0.5n₀, 1.0n₀, 1.5 n₀, 2.0 n₀ (n₀ = 1 × 10¹³ cm^–2).

最后, 从法拉第磁光器件的工作物理机制, 我们知道TM入射时候的SSPs对增强器件法拉第旋转起到了关键作用. 一维半无限厚的金属光栅的SSPs色散关系如下式所示^[38]:

$\sqrt {\beta {\rm{ - }}k_0^2{\varepsilon _{\rm{d}}}} = {k_0}{{(L - W)} / L} \cdot \tan ({k_0}\sqrt {{\varepsilon _{\rm{d}}}} {d_{\rm{a}}}), $

其中β是传播常数; k₀是自由空间波矢; ε_d是光栅上方的介质的介电常数; L, W, d_a为图1所示光栅的结构参数. 通过调节光栅参数来改变SSPs模式, 从而来研究SSPs模式对磁光效应的影响. 根据SSPs的色散方程可以知道通过改变光栅周期L可以来调节WSPM模式的传播常数, 达到与TE本征波导模式匹配的条件. 在这个思路指导下, 我们设计了工作频率从1.4到1.6 THz下的磁光器件, 并列出了最优品质因数下的器件结构参数和性能参数, 具体结果如表1所列.

No.	f/THz	L/μm	W/μm	ds/μm	T/%	θp/(°)
1	1.40	170.580	118.150	31.377	84.354	4.3845
2	1.45	164.650	113.160	30.750	85.256	3.4711
3	1.50	159.000	109.365	29.285	86.968	2.7426
4	1.55	153.500	105.915	28.414	87.123	2.1730
5	1.60	148.800	102.810	27.455	86.679	2.1443

表1磁光器件不同结构参数下的法拉第旋转角度和透射率
Table1.Faraday rotation and transmittance of the MO device with different structure parameters.

一方面, 从表1可以看到, 随着基底厚度不断减小, 工作频率不断增加, 也就是基底等效波长和传播常数不断变小, 符合TE本征波导模式的变化规律. 同时, 满足TE本征波导模式和WSPM模式匹配条件的光栅周期L随着工作频率增加而减少, 光栅周期L的这一变化规律符合SSPs色散方程. 另一方面, 表1中的数据可以说明, 磁光器件通过合适的结构参数设计, 在1.4—1.6 THz范围内, 可以在保持透射率大于84%的情况下, 实现单层黑磷法拉第角度大于2.1443°, 增益大于10倍以上. 因此, 通过调谐SSPs模式可以改变WSPM模式的传播常数, 使之和TE本征波导模式的传播常数匹配, 满足实现波矢匹配的条件, 从而达到在保持高透射率情况下增强法拉第磁光效应. 按照此方法, 也可以推广到其他波段的磁光器件的设计.
最后, 在设计器件的时候还需要注意一个问题, 单层黑磷在空气中的稳定性较差, 容易氧化. 为了隔离黑磷和空气的相互作用, 可以在金属光栅之间填充二氧化硅(${n_{\rm Si{O_2}}} = 1.4$). 图6中点划线所示为光栅之间填充二氧化硅后的品质因数图, 其他结构参数和计算图2(d)时保持一致. 从图6可以看到此时最大品质因数为2.544, 峰值位置为1.4995 THz, 与设计的工作频率点1.5 THz产生了偏差, 并且1.5 THz处的品质因数为2.453也有所下降. 通过进一步研究发现, 这个偏差可以通过优化光栅的宽度L进行修正. 如图6中实线所示, 光栅宽度从109.365 μm调整到110.650 μm后, 峰值位置又调整到1.5 THz, 并且品质因数为2.505, 与原设计结果基本一致. 因此, 通过填充二氧化硅实现黑磷的防氧化保护, 并且通过结构参数优化得到所需的工作频率和品质因数, 并且理论设计的器件在实际应用中是可以实现的.
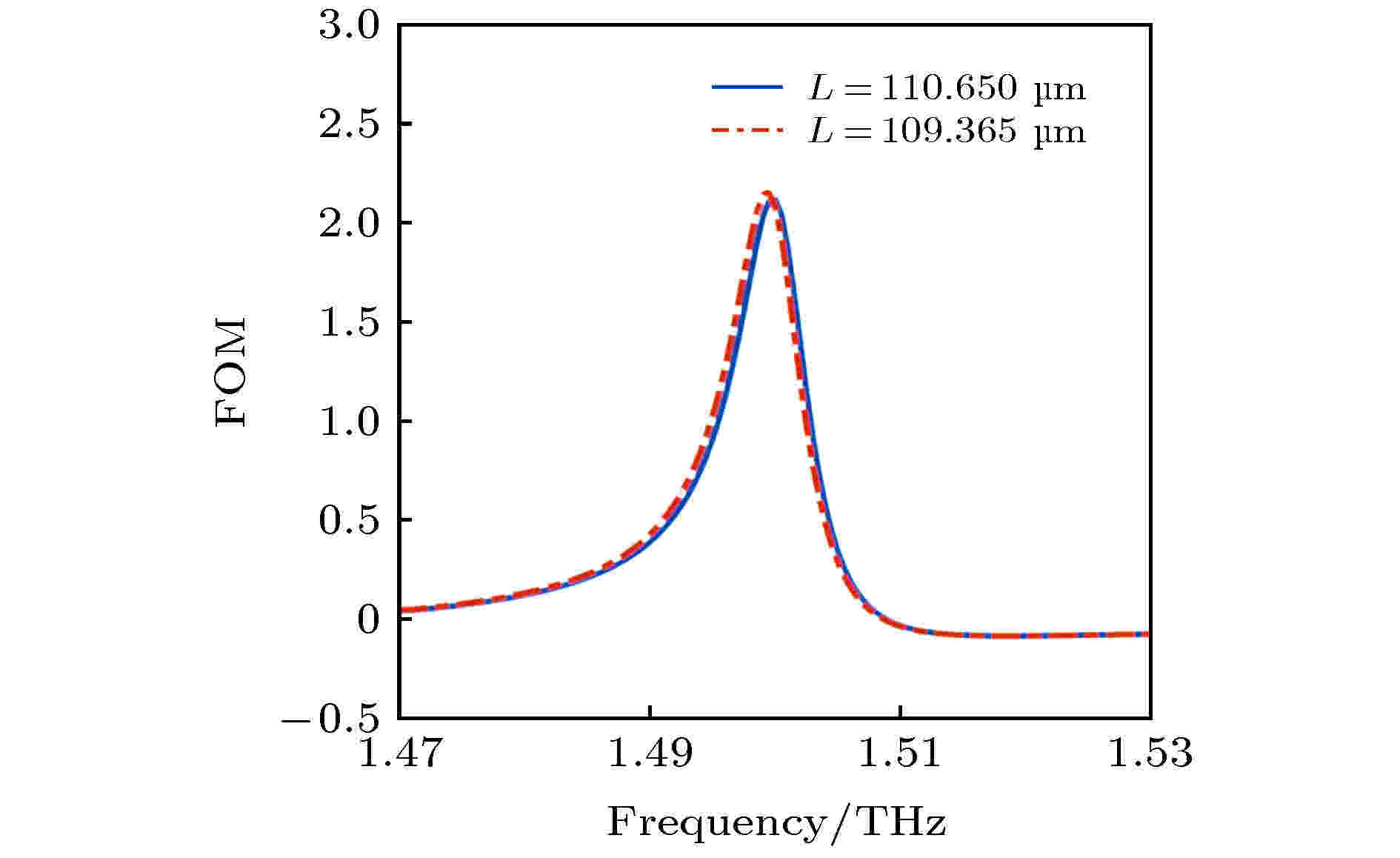图 6 光栅中间填充二氧化硅后的磁光器件品质因数, 实线表示光栅宽度为109.365 μm, 点划线表示光栅宽度为110.650 μm
Figure6. The FOM of the MO device when the grating is filled with SiO₂. The solid line indicates that the grating width is 109.365 μm, and the dashed line indicates that the grating width is 110.650 μm.

本文基于金属光栅和单层黑磷设计了一个厚度远远小于半个波长的磁光法拉第器件. 通过金属光栅引入异常透射, 在保持高透射率的情况实现了大的法拉第旋转角度. 通过仿真的方法计算了磁光法拉第器件的旋转角度和品质因数. 在1.5 THz, 能够在保持透射率大于85%的情况下实现法拉第旋转角度大于14倍的增益, 达到2.7426°. 为了解释磁光法拉第器件的物理机制, 分别从电场分布的角度和模式耦合角度进行了分析, 验证了黑磷是实现法拉第旋转的关键, 揭示了TE和WSPM模式的耦合是增强法拉第磁光效应的根本原因. 另外, 还研究了外部磁场和黑磷载流子浓度对磁光器件响应的影响, 给出了调谐磁光器件的工作特性的途径. 最后, 讨论了SSPs模式对磁光器件的作用, 并根据基本原理设计了其他工作频率下的法拉第磁光器件, 进一步验证了磁光器件的工作机制, 给出设计磁光法拉第磁光器件的基本思路. 本文的工作可以为设计易于集成到微纳光学系统的磁光器件提供帮助.