全文HTML
--> --> -->另外, 在LSM的图像重构算法方面, 目前主要有基于虚拟狭缝的图像重构方法, 但是该方法对狭缝尺寸有特定要求, 尺寸过大导致离焦信号不能完全滤除, 过小会导致在焦信号被滤除, 引起图像信息缺失. 因此, Rainer等[27]提出了基于结构光场激发的高分辨荧光显微图像重构方法, 避免了狭缝式滤除离焦信号的过程, 有效提升了图像分辨率. 但是, 其重构图像中存在伪影, 导致图像模糊. 随后, 也有研究人员利用解卷积(deconvolution, DE)算法处理LSM图像, 但分辨率的提升并不明显.
因此, 线扫描显微技术在成像速度、分辨率和光学层析能力等方面仍面临着许多亟需解决的问题, 研究和开发新型线扫描显微成像技术系统及相关图像重构算法, 进一步提升其性能, 使其更适用于活体厚样品例如活体完整细胞和组织等的高分辨快速三维成像, 对于生命科学和生物医学等领域的研究具有重要的意义. 数字微镜器件(digital micromirror device, DMD)作为高速数字光处理器件, 已广泛应用于投影、显示、无掩模光刻、光学测量、成像、全息等领域[28,29]. Vienola 等[30]以DMD作为扫描器件建立了数字线扫描检眼镜成像系统, 但该系统并不适用于生物样品荧光信号测量. 本文在实验室现有多焦点结构光照明显微镜的基础上[31], 提出了一种基于DMD的数字线扫描荧光显微成像方法(digital line-scanning fluorescence microscopy, DLSFM), 并搭建了相关显微系统, 开展了老鼠肾切片标准样品的三维光切片显微成像实验; 提出基于荧光信号标准差的DLSFM图像重构算法并编制了其图像重构程序, 结合三维Landweber DE算法[32]实现了三维高分辨光切片层析图像重构, 实验结果证明了系统的可靠性, 为LSM进一步发展及其在对完整活细胞等厚样品快速高分辨成像方面提供理论和技术基础.
2.1.系统光路设计
DLSFM光路如图1所示, 首先, 波长为488 nm固体激光器发出的光束, 经过一个4f扩束系统, 将入射光束的光斑直径扩大6倍; 随后, 扩束后的激光光束被反射镜以特定角度反射到DMD面板上, 并被开(on)状态的微镜反射进入后续的4f系统, 其中4f系统的前焦面与DMD面板重合, 并将光阑(Iris)放置在4f系统的傅里叶面, 用来滤除多余衍射级的反射光; 随后, 光线汇聚在4f系统的后焦面上形成稀疏的线条阵列, 其轴向位置与管镜前焦面重合; 最后, 被聚焦的线条阵列经管镜和物镜后缩小1/90, 成像到样品面上, 从而形成最终的多线阵激发模式. 实验中, DMD面板的像素数为1024 × 768, 像素尺寸为10.8 μm × 10.8 μm, 经过后续光学系统的缩放, 在样品面上对应的尺寸为120 nm × 120 nm. 最后, 由样品被激发后产生的荧光信号通过物镜(尼康, 60 ×, NA = 1.27水镜)、二向色镜和管镜, 聚焦到高灵敏度相机(scientific CMOS, sCMOS)(滨松, ORCA Flash 4.0 V2, 像素数2048 × 2048, 像素尺寸6.5 μm × 6.5 μm)上形成样品的像. 样品放在三维高精度电动纳米位移台上(PI, P-545.3R7Z PINano XYZ), 主要通过其进行轴向扫描, 结合DMD的横向扫描, 最终实现样品的三维成像. 另外, 由于PI纳米位移台在三个方向的重复精度优于5 nm, 远小于样品面的像素尺寸120 nm, 确保了系统的稳定性, 因此, 轴向扫描过程对系统分辨率的影响可以忽略不计.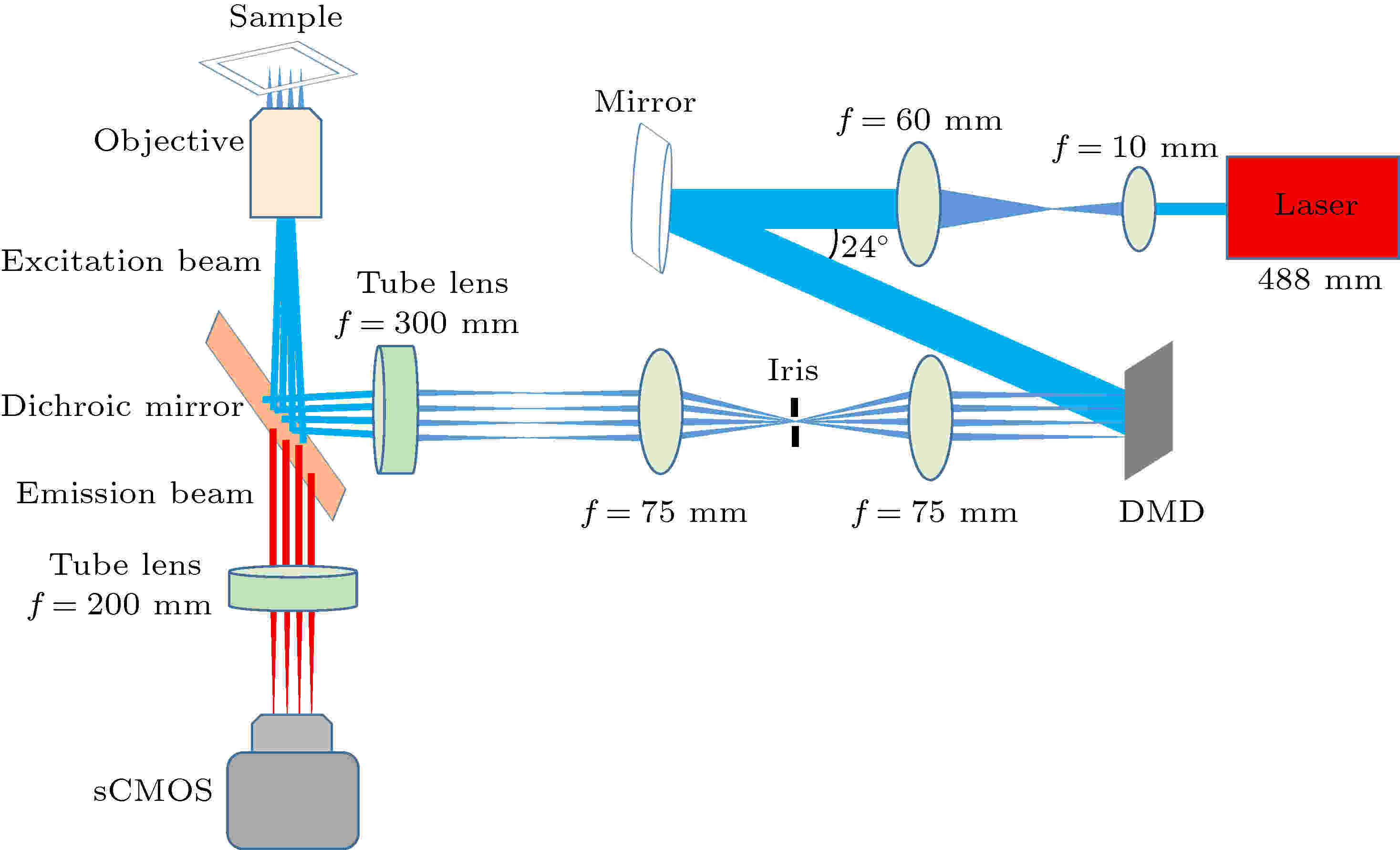
图 1 DLSFM系统光路示意图Figure1. Schematic diagram of DLSFM system.
2
2.2.系统信噪比特性分析
在DLSFM成像过程中, 通过控制DMD每列像素的“开”和“关”即偏转角度来生成多条平行线光束, 同时对样品扫描成像. 因此, 成像视场内扫描线的多少和间距决定了成像的速度和信噪比(single-to-noise ratio, SNR), 所以, 在设计系统时, 需要综合考虑这两个因素. 为了分析SNR特性, 定义DMD的填充因子F (fill factor),
首先, 通过对均匀的罗丹明荧光溶液进行线扫描成像来分析F与扫描线数的关系, 如图2所示. 通过采集单帧不同密度线条纹激发下的罗丹明荧光溶液图像, 如图2(a)所示, 并对采集的荧光溶液图像不同帧的同一平行线位置的横截面宽度进行计算, 如图2(b)所示.
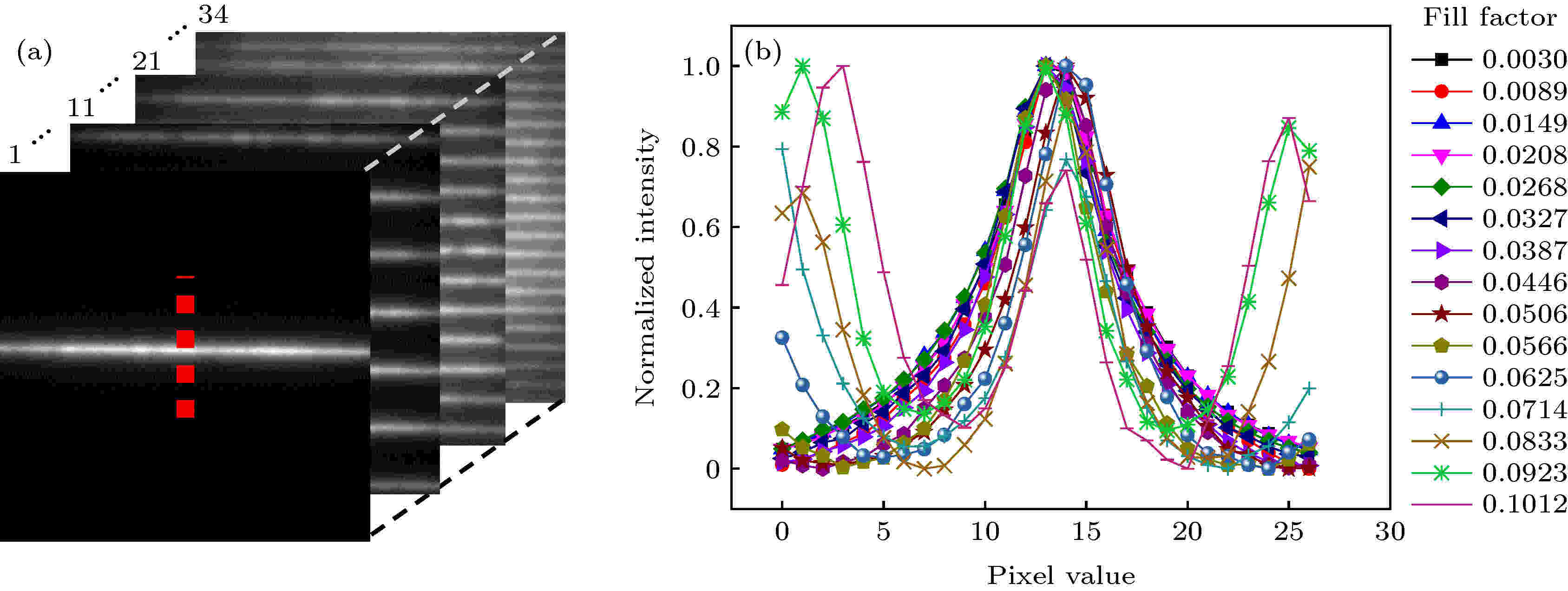图 2 DMD不同填充因子的数字线扫描成像分析 (a)不同密度线条纹激发下的罗丹明荧光溶液图像; (b) 不同帧的同扫描线位置的强度轮廓线Figure2. Digital line scan imaging analysis of DMD with different fill factor: (a) The rhodamine fluorescence solution images excited by different density scanning lines; (b) the intensity profiles through the dotted line in (a).
从图2(b)中看出, 随着F的增大, 不同线密度条件下激发样片产生荧光线条的横截面宽度几乎接近于一恒定值, 但当F增大到0.0566时, 可以看出线条的横截面强度除了中心的主峰强度外, 有一些旁瓣信号, 这主要是由于高线密度下平行线间的散射光和离焦信号导致的. 因此, 为了获取理想F情况下平行线阵列的激发数目, 需对图像SNR作进一步分析, 如图3所示. SNR定义如下:
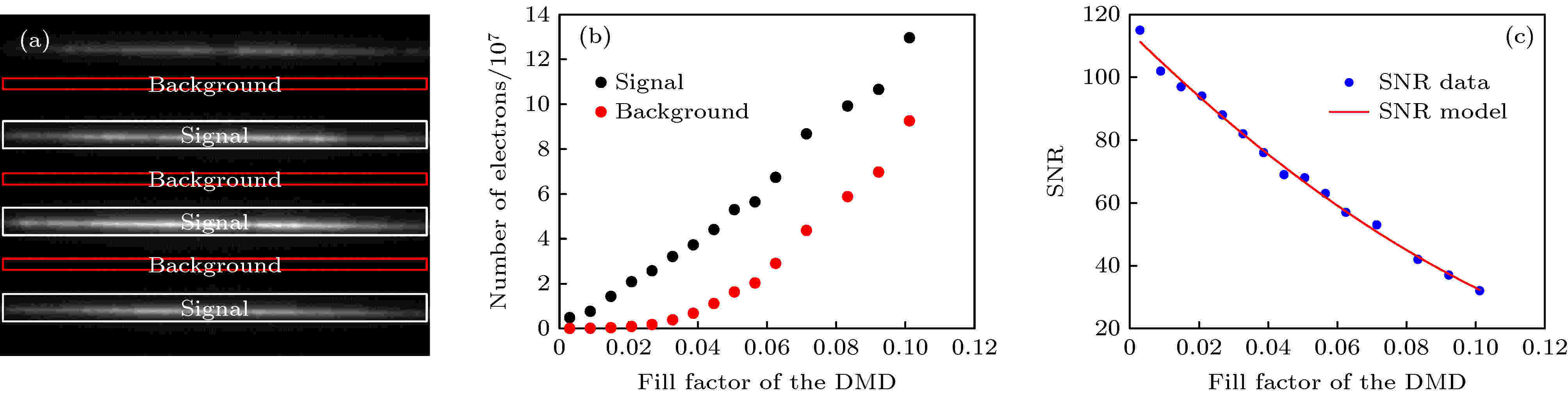图 3 DMD不同填充因子的信噪比分析 (a) 焦面信号和背景信号强度分布图; (b) 焦面信号和背景信号强度与DMD填充因子的关系曲线; (c) DMD不同填充因子的信噪比曲线Figure3. SNR analysis of DMD with different fill factor: (a) The intensity distributions of focal plane signal and background signal intensity; (b) the intensity curves of focal planne signal (black) and background signal (red); (c) the curve of the SNR versus fill factor of DMD.
由图3(b)看出, 随着F的增大, 焦面信号和背景信号强度趋于线性变化, 而图像SNR逐渐减小(图3(c)), 这主要是由于线密度增大使平行线阵列间的散射光信号导致了这一结果. 由图2(b)、图3(b),(c)看出, 当F为0.0208时, SNR比为94, 此时从物镜口发出的光功率为177 μW, 采样速率为250 Hz, 重构一幅光切片图像需要48帧扫描图像, 从成像时间和空间分辨效果进行综合分析, 此时, 成像条件最佳. 因此, 由 (1) 式, 可以计算该条件下所需的线条纹阵列数为7, 从而为后续的实验奠定了基础.
为了得到每个像元对应的标准差(standard deviation, STD)数值σ, 对每一层扫描图像的像元强度分布情况进行统计计算, 其计算式中重构图像每个像元的强度均值μ为不同扫描图像中每个像元的强度值求平均而得到. 然后, 可以计算出重构图像中每个像元的σ数值, 其表达式为
通过上述公式对线扫描图像序列进行处理, 抑制离焦背景噪声, 获得了DLSFM图像, 在此基础上可结合三维Landweber DE算法来进一步提高DLSFM图像的对比度和分辨率.
4.1.系统分辨率标定
为了验证DLSFM的成像能力, 可通过测量直径为100 nm的荧光珠对该系统的分辨率进行标定, 对视场范围内25颗荧光珠的图像进行统计平均, 得到了系统在
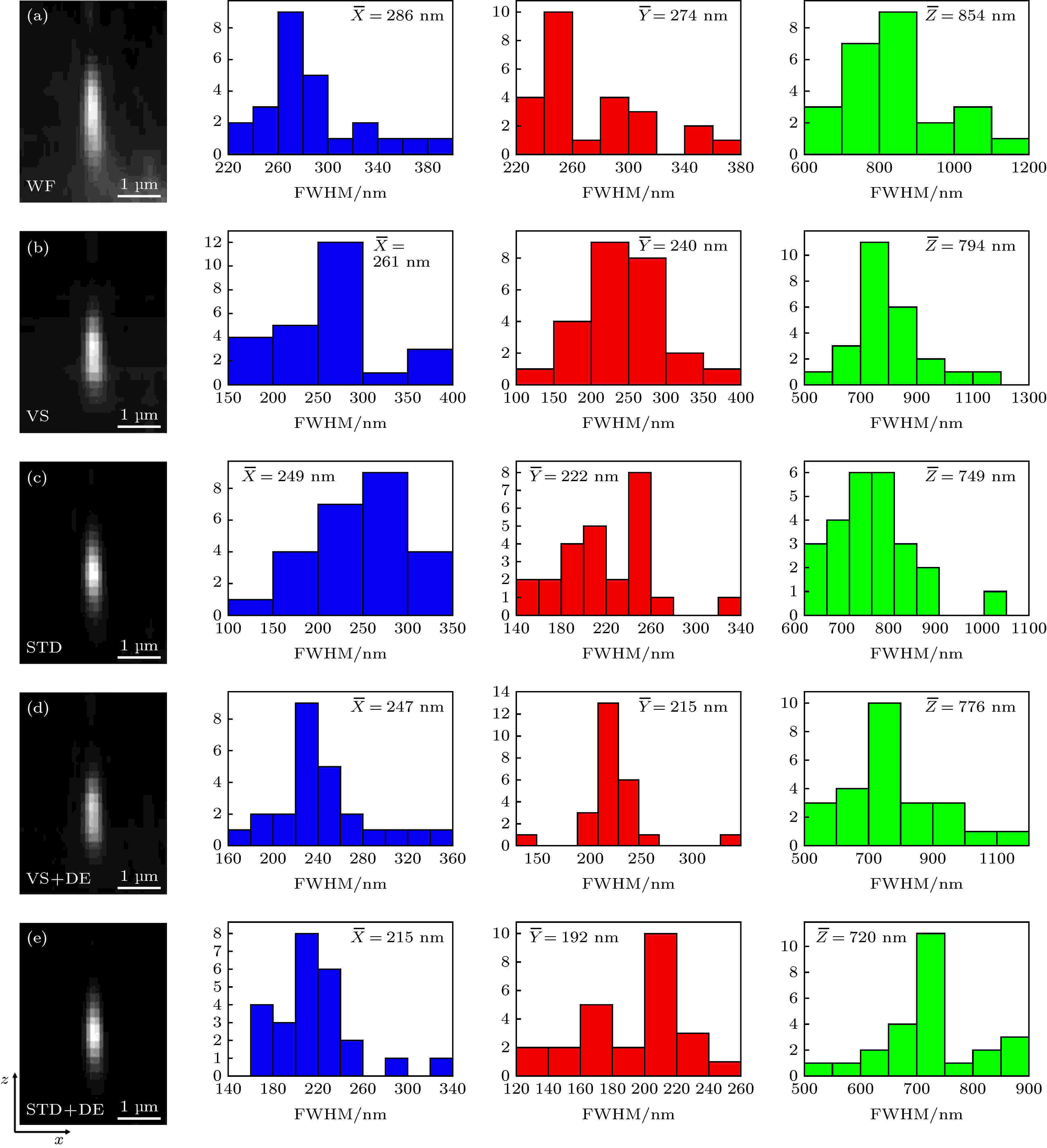图 4 100 nm荧光珠标定的系统三维空间分辨率 (a)宽场图像; (b)虚拟狭缝重构图像; (c)标准差重构图像; (d)虚拟狭缝与LW解卷积组合重构图像; (e)标准差与LW解卷积组合重构图像. 其右边对应的直方图为25颗荧光珠在沿
Figure4. 3D spatial resolution of the system calibrated by the 100 nm fluorescent bead: (a) WF image; (b) VS image; (c) STD image; (d) VS + DE image; (e) STD + DE image. The corresponding histograms on the right show the measured distribution of
首先, 利用线扫描原始图像进行直接叠加, 获得了荧光珠宽场(wide field, WF)图像. 但WF图像离焦背景噪声信号较强(图4(a)), 荧光珠在
2
4.2.老鼠肾切片三维成像实验
接下来, 利用搭建的DLSFM系统, 选用荧光标记的老鼠肾切片(FluoCellTM prepared slide#3 mouse kidney section, *AF 488 WGA, AF 568 phalloidin, Product of US)作为实验样片, 选取其中厚度为11.2 μm的肾小球作为实验对象, 进行扫描成像, 样品荧光发射光波长为568 nm, 样品面像素尺寸大小为108 nm. 在成像采集过程中, DMD上7条激发线横向并行扫描的步数为48步, 扫描速率为250 Hz, 三维电动纳米位移台轴向扫描间隔为200 nm. 因此, 共获得2688幅线扫描源图像. 这些采集的样品图像经VS、STD, 以及LandweberDE算法处理后获得样品的不同深度的光切片层析图像, 如图5所示.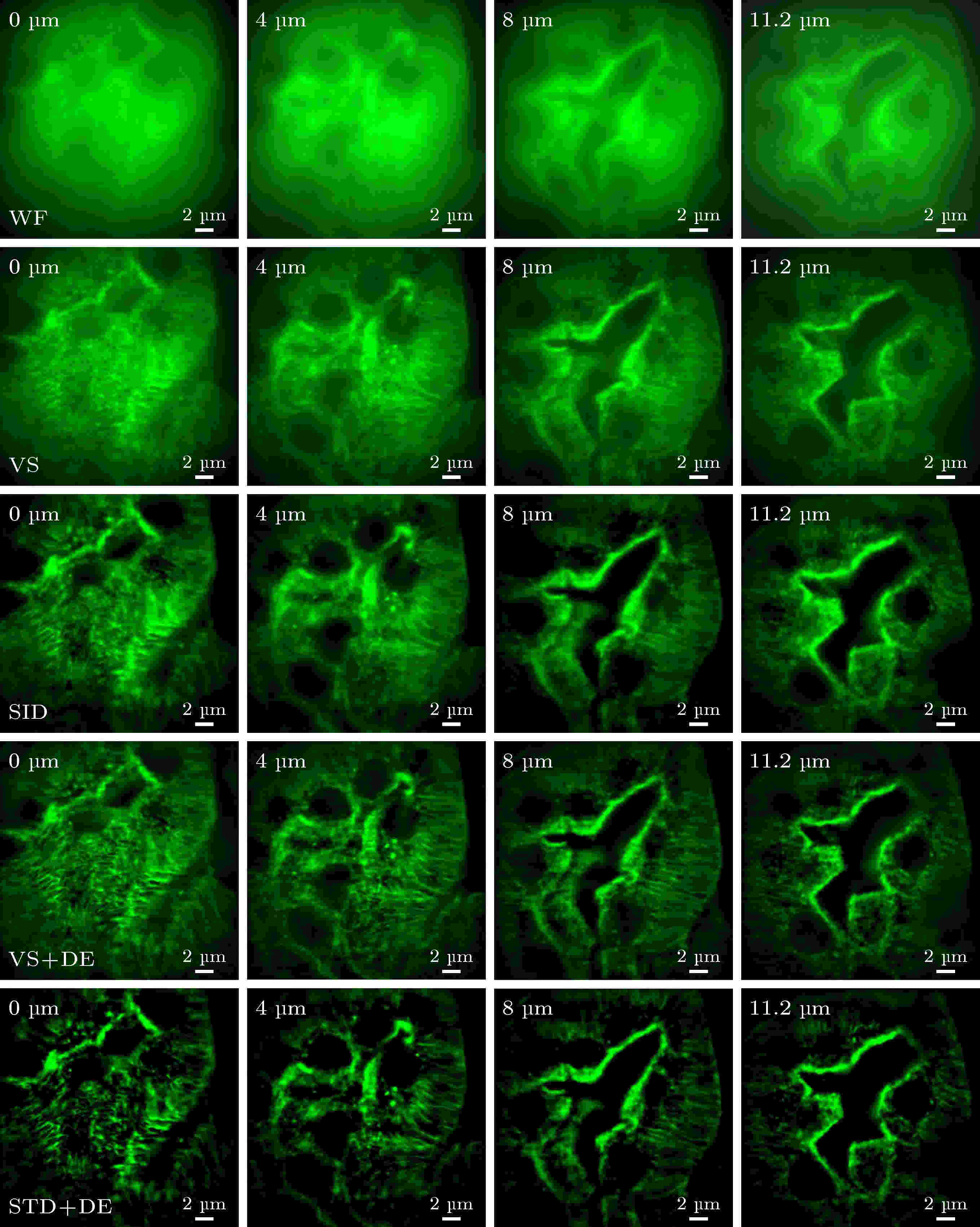
图 5 肾小球轴向光切片的重构图像Figure5. Reconstructed slice images of the same glomerulus.
从图5中可以看出, WF模糊不清, 大致能分辨外轮廓, 对于边缘细节几乎难以分辨开来, 经VS图像重构方法处理后, 离焦信号得到了一定的去除, 边缘细节得到了一定的凸显; 然而, VS图像重构方法与STD图像重构方法成像相比, 其对比度与分辨率相对较低. 利用Landweber解卷积算法在二者基础之上进行处理, 其对比度及分辨率得到了进一步改善, 尤其是对于标准差图像重构, 其经解卷积算法处理后, 样品细节结构得到了显著的凸显, 图像分辨率得到了进一步的提升.
为了细致观察其重构效果, 选取轴向深度处于8 μm处的肾小球切片的一区域进行放大, 如图6所示, 其中, 图6(a)—(f)分别为WF图像、VS图像和STD图像; 图6(a)—(c)分别经Landweber DE算法处理成像(图6(d)—(f)); 图6(i)—(n)分别为图6(a)—(f)黄色线框区域的放大.
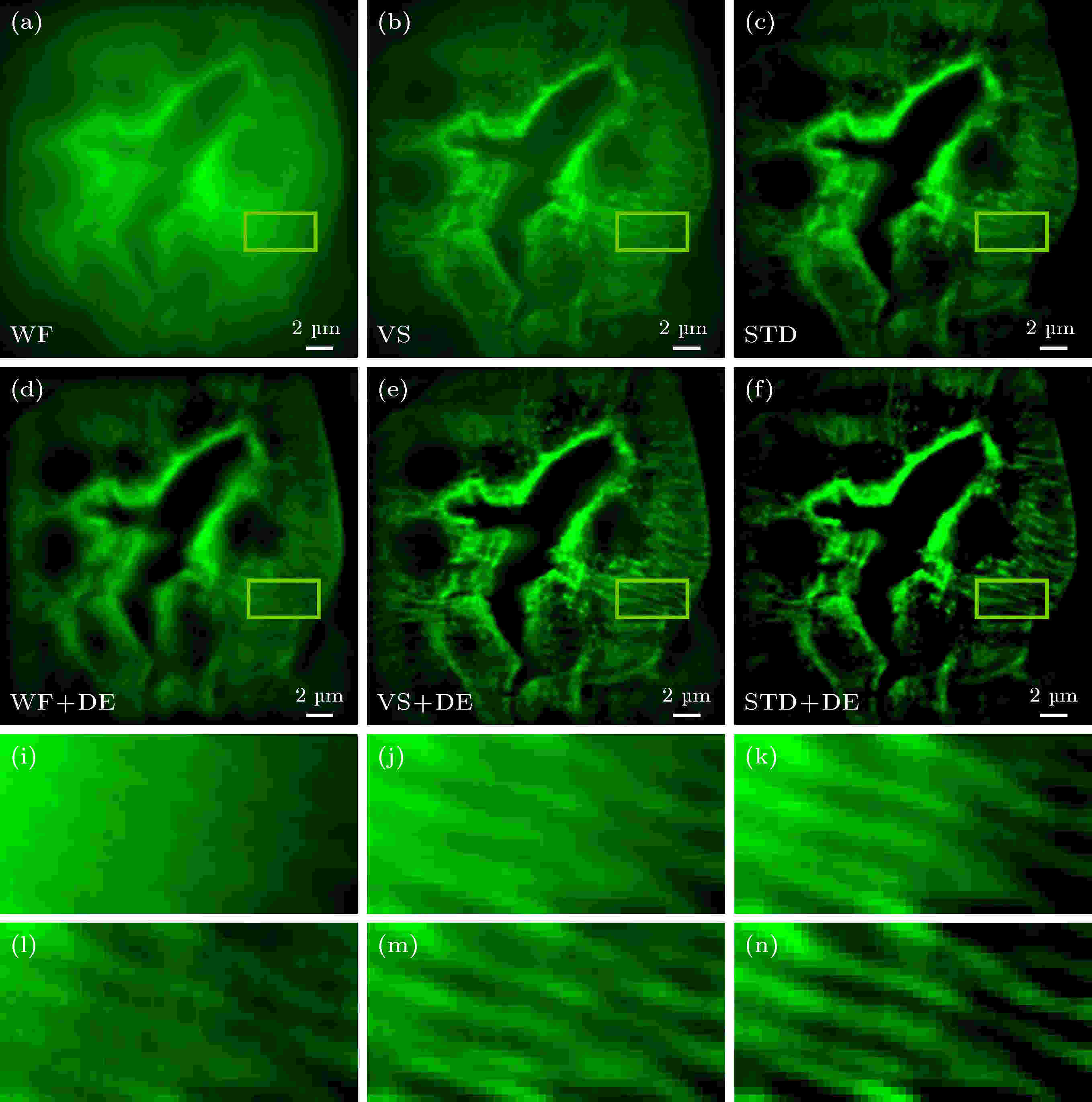图 6 不同算法的图像重构细节比较 (a)?(c) 分别为WF图像、VS图像和STD图像; (d)?(f) 分别由(a)?(c)经Landweber DE算法处理成像; (i)?(n) 分别为图(a)?(f)黄色线框区域的放大图Figure6. Comparison of image reconstruction details of different algorithms: (a)?(f) WF image, VS image, and STD image; (d)?(f) the Landweber DE images for (a)?(c); (i)?(n) magnified view of the yellow rectangular areas in (a)?(f).
从图6可以看出, 经由图6(a)—(f)黄色线框分别放大后的图6(i)—(n), 其中, 图6(l)—(n)在图6(i)—(k)的基础之上分辨率得到了进一步提升, 尤其是对于图6(n), 与图6(m)相比, 其样品结构凸显得尤为明显. 因此, 说明了数字线扫描WF、VS图像重构、STD图像重构经Landweber算法解卷积后图像分辨率得到进一步的提升, 其中STD图像对比度以及分辨率明显比VS图像重构的要高, 如图7所示, 其中, 图7(a)—(c)分别为WF图像、VS图像和STD图像; 图7(d)—(f)分别为图7(a)—(c)经Landweber解卷积算法处理成像; 图7(g)和7(h)分别为图7(a)—(f)白色虚线位置的归一化强度拟合.
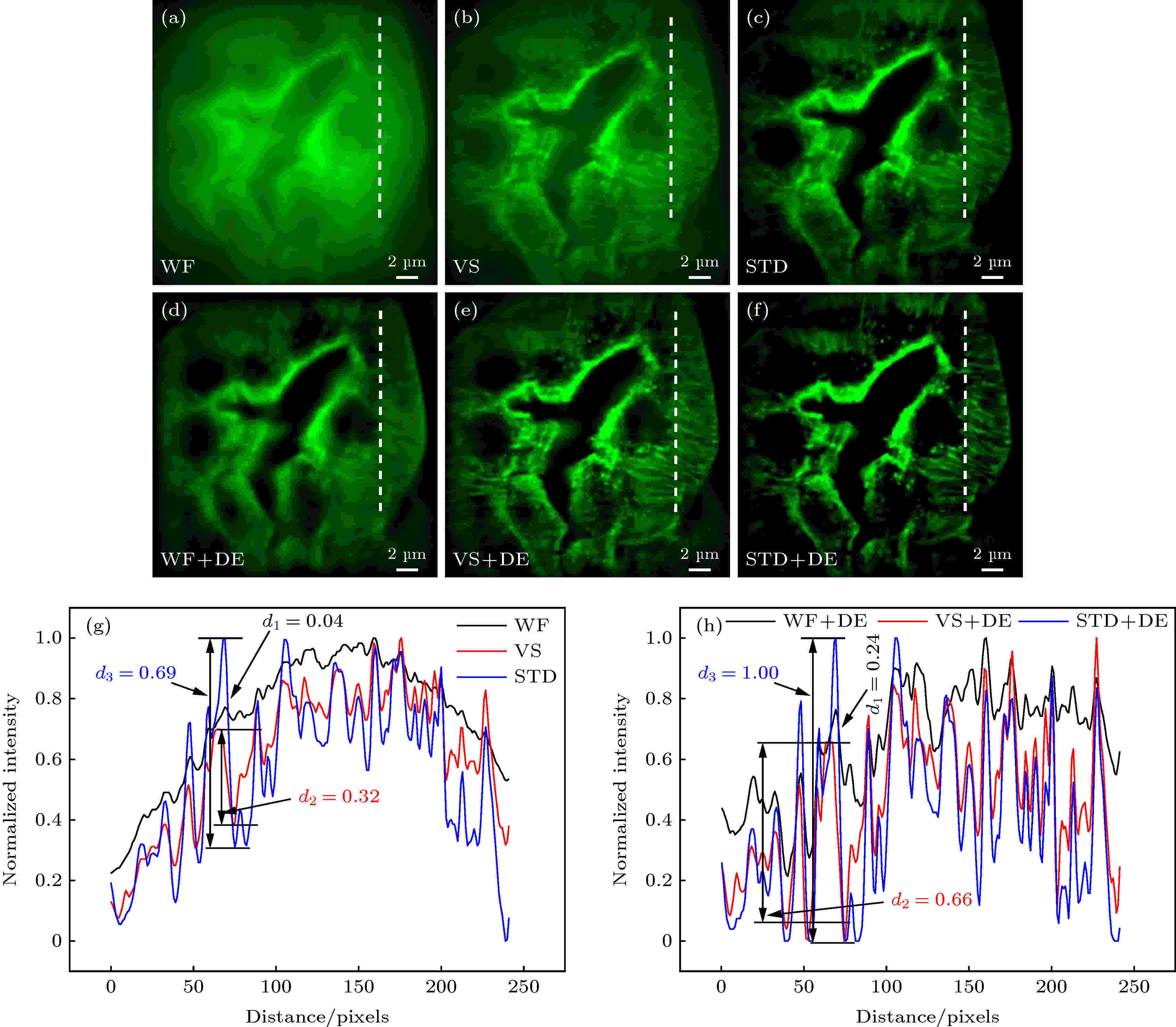图 7 不同算法重构图像的对比度比较 (a)?(c) 分别为WF图像、VS图像和STD图像; (d)?(f) 分别为图(a)?(c)经Landwebe解卷积算法处理成像; (g)?(h) 分别为图(a)?(f)白色虚线位置的归一化强度轮廓图Figure7. Contrast comparison of reconstructed images with different algorithms: (a)?(c) WF image, VS image, and STD image; (d)?(f) images obtained from (a)?(c) processed by Landwebe deconvolution algorithm; (g)?(h) the normalized intensity profiles through the white dotted line position in (a)?(f).
从图7(g),(h)可以看出, 通过Landweber DE算法处理前后, STD图像重构的强度明显比VS图像重构的要高, 与此同时, 处理后整体比处理前的要大(如图7(g), (h)所示). 处理前, STD图像、VS图像、WF图像的归一化强度变化量分别为: d3 = 0.69, d2 = 0.32, d1 = 0.04; 处理后, 其分别为: d3 = 1.00, d2 = 0.66, d1 = 0.24. 因此, 进一步验证了我们所述的结论.
根据对系统的分辨率测试和对固定生物样品成像结果可以看出, 系统的成像分辨率基本上接近系统理论的成像分辨率, 在生物样品成像过程中具有良好的信噪比.
