摘要:作为电介质大家庭的重要成员, 铁电材料以其蕴含丰富的物理性质而闻名, 并因此吸引了大量科技工作者. 压电效应是铁电材料最为重要的物理性质之一, 同时也是目前铁电材料所有物理性质中应用最为广泛的. 例如: 水声声呐系统、医疗超声探头、压电驱动器等器件的核心压电元件均为铁电材料. 本文将以时间为轴, 重点介绍钛酸铅基铁电材料压电效应的发展历史, 同时讨论铁电材料微观结构、极化状态与压电效应之间的构效关系. 本文涉及到影响铁电材料压电效应的一些重要因素, 如: “准同型相界”、“软性掺杂”、“极化旋转”、“局域结构无序”等, 希望能够在铁电功能材料的设计方面给予读者启发.
关键词: 铁电材料/
压电效应/
性能优化

English Abstract

全文HTML

--> --> -->

压电效应是指当材料受到外力(比如: 压力)作用时, 其表面会产生电荷; 或在受到电场作用下, 会发生形变的现象. 它的英文是piezoelectricity, 源于古希腊语piezein/piezo和electricity, 即: “压”而生“电”. 具有压电效应的材料统称为压电材料. 当然, 这里需要指出的是, 由于电致伸缩效应的存在, 所有电介质材料在电场作用下均可发生形变. 但是, 压电效应与电致伸缩效应的区别在于: 1)电致伸缩效应所产生的应变与电场的二次方成正比, 而压电效应所产生的应变与电场一次方成正比; 2)仅具有电致伸缩效应而不具有压电效应的电介质材料, 在应力的作用下不能产生极化强度和电荷.
压电材料是现代科学技术中不可或缺的关键材料, 它被广泛应用于医疗超声成像、水声声呐、无损检测仪、各类传感器(如加速度计)等器件中. 这些器件的性能优劣与其所使用的压电材料息息相关. 因而, 获得具有更高性能的压电材料成为了科学家们研究的重要目标.
1880年, 居里兄弟首次在石英晶体中发现了压电效应. 然而, 在这之后的30多年中, 不论从科学层面还是技术层面来看, 压电效应并没有引起太多的关注. 直到1917年, 法国科学家朗之万利用石英晶体的压电效应发明了世界上第一台主动声呐(也称朗之万声呐), 基于“回声定位”的方法成功实现了对舰船的定位. 朗之万声呐在第二次世界大战期间的大西洋战役中发挥了非常重要的作用, 也成为了压电材料发展史上最重要的一次应用展示. 正是在水声声呐系统中的成功应用, 拉开了人类探索高性能压电材料的帷幕.
相比于其他压电材料, 钙钛矿相铁电材料以压电电荷系数d_iμ和机电耦合系数k_ij值高而闻名, 是用于医疗超声换能器、水声换能器以及压电驱动器等压电器件的核心材料. 本文将重点介绍钙钛矿相压电材料的发展历史, 同时讨论材料微观结构与压电效应的构效关系.

压电效应第一次质的飞跃源于19世纪40年代钛酸钡(BaTiO₃)的发现, 其压电系数约为190 pC/N, 远高于石英的2 pC/N. 同时, BaTiO₃也是首个具有钙钛矿结构的铁电材料(铁电材料是一种具有自发极化且极化矢量可以被电场反转的一类材料, 如图1(a)所示). 此后, 用于制作超声换能器的压电材料正式进入了“铁电”时代. 在目前所有的压电材料中, 铁电材料的压电系数通常远高于非铁电材料. 在外场(应力或电场)作用下, 铁电材料的自发极化方向和强度的变化以及相应的晶胞参数变化, 是造成铁电材料具有高压电效应的关键因素. 直观上来看, 为了获得高压电效应, 铁电材料需要满足这样两个特点: 1)自发极化强度大; 2)自发极化容易被外场扰动. 基于热力学理论, 可以得到一个更准确的表达, 即: 压电系数与自发极化强度和介电常数的乘积成正比: d ～2QP_Sε, 其中, d为压电系数, P_S为自发极化强度, ε为介电常数, Q为电致伸缩系数. 在这个表达式中, 介电常数越大则表明自发极化越容易被电场扰动. 通常情况下, 铁电材料介电常数与自发极化强度是相互制约的, 因此压电效应的提升需要在这两个物理量之间进行权衡. 例如, 铁电材料居里温度越高, 它在室温条件下的极化强度越大(图1(b)); 但是, 与此同时, 极化矢量也越不容易被外场扰动, 导致介电常数下降(如图1(c)). 因此, 一味地降低居里温度, 并不能让铁电材料压电效应持续增大. 现有实验结果表明, 压电效应最大的铅基陶瓷居里温度在100 ℃附近^[1], 而压电效应最大的铌酸钾钠(KNN)基陶瓷居里温度在150 ℃附近^[2].
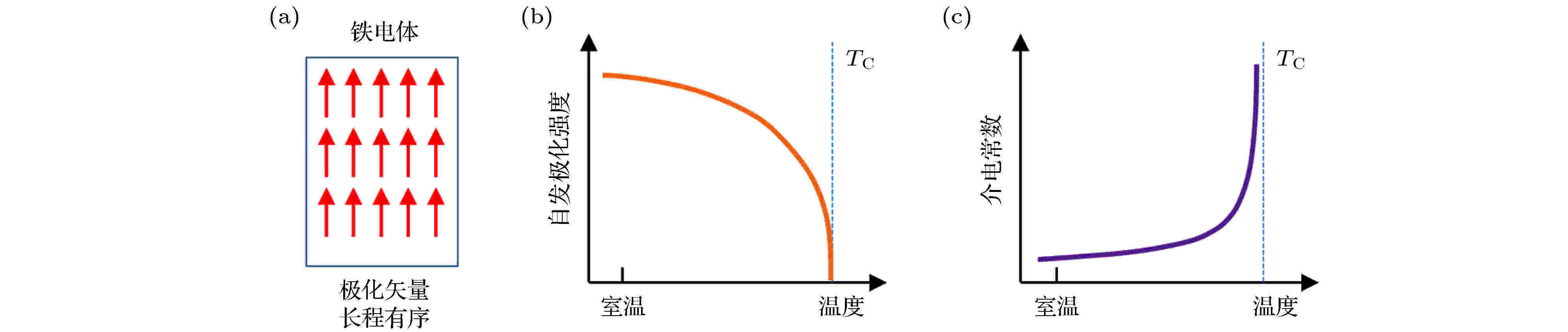图 1 (a)单畴铁电材料极化矢量长程有序示意图, 其中红色箭头代表偶极矩; (b)自发极化与温度关系示意图(以二级铁电相变为例); (c)介电常数与温度关系
Figure1. (a) Schematic drawing of long-range ordered ferroelectrics with single-domain structure, where the red arrows indicate the electric dipoles; (b) the relationship between spontaneous polarization and temperature (taking the second-order ferroelectric phase transition as an example); (c) the relationship between dielectric permittivity and temperature.

作为换能器用压电材料, 钛酸钡并没有被使用太长时间, 便被大名鼎鼎的锆钛酸铅(PbZrO₃-PbTiO₃, PZT)固熔体陶瓷所取代. 20世纪50年代, Jaffe^[3]在锆钛酸铅固熔体中发现了比钛酸钡更为优异的压电性能(d₃₃～300 pC/N)以及更好的温度稳定性. 可谓是出道即巅峰, 没有经历太长时间的基础研究, PZT陶瓷即被工业化生产, 成为了广泛应用于各行各业的压电材料. 时至今日, 世界上许多PZT陶瓷生产单位所应用的PZT组分仍是源于20世纪60或70年代.
在学术研究方面, PZT的出现为铁电压电材料领域提供了两个直到今日仍然十分热门的研究方向. 一是准同型相界(morphotropic phase boundary, MPB). 在PZT固熔体中, PbTiO₃ (PT)为四方相铁电体, 其压电系数d₃₃小于100 pC/N;PbZrO₃ (PZ)为反铁电体, 不具有压电性. 但在PT中加入PZ, 且PZ与PT的摩尔比例达到53∶47时, 晶体结构从原先PT的四方相转变为了三方相, 即自发极化方向由$ \left\langle {100} \right\rangle $方向转变为$ \left\langle {111} \right\rangle $方向. 更令人惊讶的是, 在这个组分附近, PZT的压电系数d₃₃可达约300 pC/N. 虽然三方和四方铁电相在自发极化方向上有本质的区别, 但是二者晶胞参数均十分接近立方相晶胞参数, 因此称为准同型相. 在PZT相图中, 这两个相的分界被称为“准同型相界”^[3]. 在PZT出现70年后的今天, 寻找、构建准同型相界仍然是提升铁电材料压电性能的首选方法. 从热力学角度来看, 准同型相界处的高压电性能可以从本征晶格压电畸变的角度解释. 如图2所示, 随着组分靠近准同型相界, 在极化矢量处于稳态时的自由能曲线曲率减小, 这表明: 在外场扰动下PZT自发极化矢量更容易发生旋转, 从而对压电效应产生贡献. 虽然, 这样的理解在PZT时期就已存在, 正如文献[4]所述: “polarization rotation (without being called so) is an old concept that was proposed more than 30 years ago to explain qualitatively enhanced properties of PZT in the MPB region”. 然而, 直到2000年, Fu和Cohen^[5]在Nature上发表论文, 并将这种机理称为“Polarization Rotation Mechanism”后, 才被广泛宣传. 另一方面, 在MPB附近, 畴壁运动对压电效应的贡献也被认为有显著提升, 这一点同样可基于图2进行定性的解释. 随着组分靠近MPB, 三方相与四方相之间的势垒降低. 因此, 在外场作用下, 三方相(或四方相)电畴中部分晶胞的极化矢量很容易“跳过势垒”, 从一个(亚)稳态转换到另一个(亚)稳态. 这种极化矢量的“跳转”(英文常称switch)对材料宏观介电和压电效应都会产生贡献.
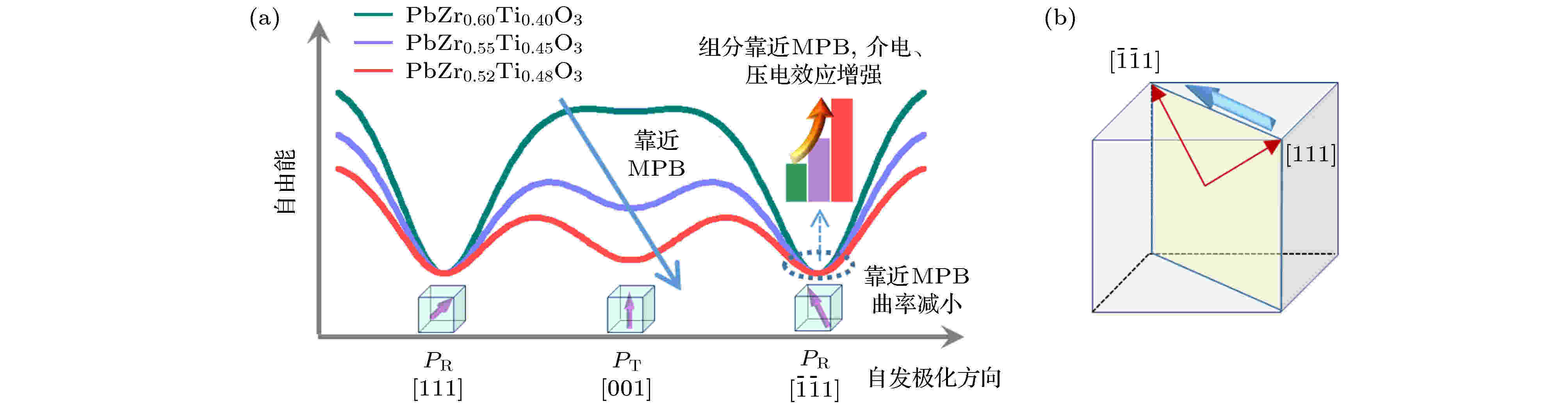图 2 (a)热力学计算得到的三种不同组分PZT自由能与自发极化方向的关系, 图中给出了自发极化在$(1\bar 10)$面内由$[111]$方向转向$[\bar 1\bar 11]$方向过程中自由能的变化情况; (b)自发极化在$(1\bar 10)$面内, 由$[111]$方向转至$[\bar 1\bar 11]$方向的示意图
Figure2. (a) Relationship between the free energy and the direction of spontaneous polarization of three PZT solid-solutions, calculated by phenomenological theory; (b) the schematic of the rotation of the spontaneous polarization from $[111]$ to $[\bar 1\bar 11]$ direction within the $(1\bar 10)$ plane.

二是掺杂改性. 在PZT中进行微量元素的掺杂, 可使其出现截然不同的性能. 从应用角度来看, 掺杂主要分为“软”和“硬”两类.“软性”掺杂可提高PZT陶瓷压电系数(d₃₃可达500—800 pC/N), 主要掺杂元素包括A位掺Ba²⁺, Sr²⁺, 镧系稀土等, B位掺Nb⁵⁺, Ta⁵⁺等; 硬性掺杂可降低PZT陶瓷中的介电损耗和机械损耗(可降低一个数量级, 例如: 介电损耗可由1%降低到1‰), 从而满足一些大功率发射型换能器的应用要求. 硬性掺杂通常是采用低价态元素来替换B位的Ti⁴⁺或Zr⁴⁺, 主要元素为Fe^2+/3+, Mn^2+/3+等.
为了设计出具有更优异性能的压电材料, 研究者们开展了大量的研究工作, 来探索PZT陶瓷的掺杂改性机理. 目前, 大多数关于掺杂机理的解释都是从畴壁运动角度出发. 简单来说, 硬性掺杂可使PZT陶瓷的电畴结构更加稳定, 在外场作用下不容易被改变, 导致压电效应以及与畴壁运动相关的损耗同时降低; 软性掺杂导致PZT陶瓷的电畴活动能力增强, 更容易被外场扰动, 因而展现出更高的压电性能. 为了辅助新材料的设计, 这种简单的认识显然是远远不够的, 我们需要知道不同的掺杂元素在PZT中扮演的角色是什么, 为什么有些掺杂能使PZT的自发极化更加稳定, 而有些却使其失稳. 遗憾的是, 经过了50余年的研究工作, ****们虽然可以相对合理地解释PZT陶瓷的硬性掺杂机理(即: B位受主杂质与氧空位形成内建电场, 此电场与电畴自发极化方向相同, 对电畴起到“钉扎”的作用, 使电畴更加稳定, 不易被外场扰动, 从而降低了压电效应以及介电、弹性损耗. 详细内容可参考文献[6, 7]), 但是对软性掺杂机理仍不清楚—引自文献[6, 7] (“Interestingly, while the origins of hardening are reasonably well understood, the reasons why PZT becomes soft with respect to the pure composition are not well understood, even after more than 50 years of intensive studies of this material.”), 显然, 揭示软性掺杂机理、获得具有更高性能的压电材料, 是当前驱动器、传感器等压电器件小型化、高精度化发展的迫切需求. 本文最后将基于近些年的研究工作, 提出一些想法. 在这之前, 先介绍另一类重要的材料体系—弛豫铁电体.

钙钛矿结构本身是一个非常有趣的晶体结构, 它对元素取代有十分高的容忍度, 这就使得人们不仅仅满足于微量掺杂. 本着没有最好只有更好的信念, 材料工作者们开展了大量的掺杂工作, 获得了许许多多的铅基钙钛矿铁电陶瓷, 这其中有一类材料自成一派, 被称为弛豫铁电体^[8-10]. 经典的弛豫铁电体主要有如下两种: 1)将PZT中的Zr完全由不等价的两种元素按照一定比例完全替换(如: Mg²⁺:Nb⁵⁺ = 1∶2, In³⁺:Nb⁵⁺ = 1∶1), 形成PMN-PT或PIN-PT固熔体; 2)在PZT中掺入7%—10%的La元素来取代A位的铅, 从而获得的PLZT. 弛豫铁电体的核心特点为: 1)在纳米尺度上存在晶体结构的不均匀(在PLZT中, 是由于La掺杂而引起的; 在PMN中, 是由于存在B位Mg²⁺和Nb⁵⁺离子的有序和无序区域, 这些区域尺寸约为几个纳米); 2)由于纳米尺度上的结构不均匀, 极性纳米微区出现在弛豫铁电体中(注: 传统意义的长程铁电畴尺寸通常在亚微米量级以上), 因而在这些材料中会观察到很强的介电弛豫现象. 由于与“纳米”结缘, 弛豫铁电相比于铁电又多了几分神秘色彩, 成为了从20世纪60年代至今铁电领域的研究热点. 弛豫铁电材料在电光调制器、电容器以及低滞后驱动器等方面均有重要应用. 例如, 作为变形镜驱动器, 20世纪90年代被用于美国哈勃望远镜, 成功提高望远镜分辨率. 但经典的弛豫铁电陶瓷, 如PMN-PT陶瓷, 在压电性能方面并没有展示出明显的优势, 因而也没有引起足够的重视. 实际上, 弛豫铁电体在压电应用方面的重要性, 一直到20世纪90年代弛豫铁电单晶生长技术的逐渐成熟后才被广泛关注.
在介绍弛豫铁电单晶之前, 先总结一下压电陶瓷在1960—1990年间的研究工作. 在这段时间, 铁电领域的前辈们合成了大量不同组分的压电陶瓷, 优化了它们的工艺, 研究了其性能. 最后, 人们总结发现, 铅基陶瓷压电效应与居里温度之间存在图3所示的制约关系^[1]. 这里需要说明一下, 压电陶瓷与半导体材料不同, 未被赋予科技革命的重任. 因此, 在使用过程中, 压电器件通常不会配备专用的控温设备, 导致在使用过程中升温明显. 另一方面, 压电材料也还承担着诸如石油探测、深海通讯等高温高压条件下的工作任务. 因此, 居里温度也就成为了考核压电陶瓷的又一个重要指标. 居里温度越高, 材料极化状态的稳定性越高, 因而温度、电场以及压力条件下稳定性都有所提高. 这样一来, 获得同时具有高压电效应和高居里温度的压电陶瓷成为一项艰巨的任务. 时至今日, 压电性能与居里温度的制约关系仍然是压电材料领域的核心瓶颈问题之一.
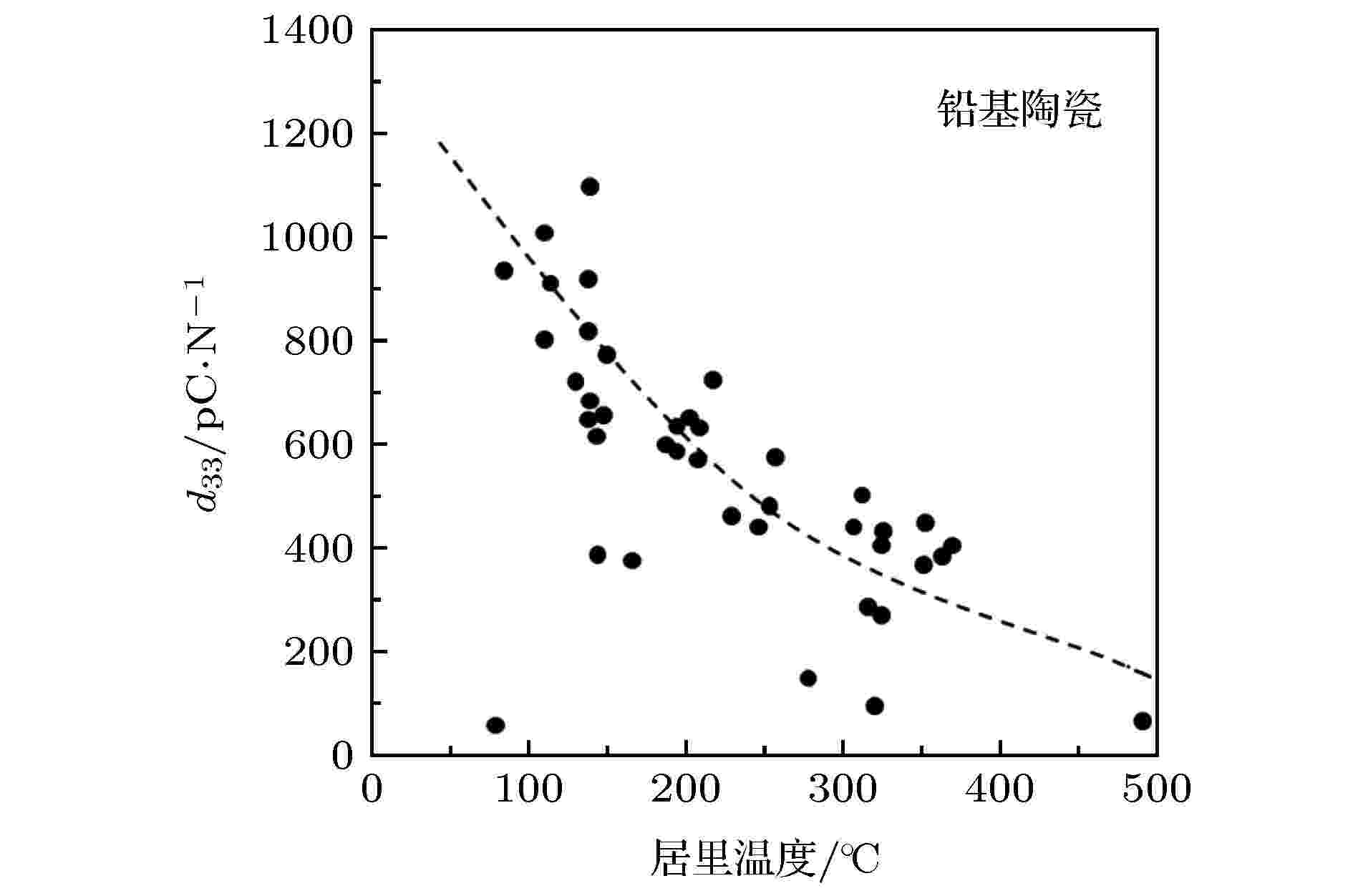图 3 铅基陶瓷压电系数d₃₃与居里温度T_C的对应关系^[1]
Figure3. Relationship between d₃₃ and T_C for lead-based ceramics^[1].

20世纪90年代中期, 弛豫铁电单晶^[11-13]的问世让人们第一次看到突破上述瓶颈问题的希望, 如图4所示^[1,13]. 在美国、日本、中国、加拿大、韩国等国家的大力推动下, 弛豫铁电单晶的生长技术迅速提升, 晶棒直径在短短的10多年时间内发展到了4 in (1 in = 2.54 cm), 并成功应用于众多医疗B超换能器中, 例如: Philips的Pure Wave系列超声探头. 这里特别需要说明的是, 文献报道弛豫铁电单晶的第一次成功生长可追溯到1973年^[11]; 同时, 早在1982年, Kuwata等^[12]就报道了PZN-0.09PT单晶的压电性能. 但是, 由于当时生长水平的限制, PZN-0.09 PT单晶的性能相比于软性压电陶瓷没有表现出明显优势, 同时由于晶体尺寸仅为几个毫米, 很多性能没有被完全表征, 导致当时并没有引起足够的重视. 包括Kuwata与Uchino本人在内, 也没有继续深入开展弛豫铁电单晶的生长研究工作, 这也使得最后因弛豫铁电单晶而闻名的人是Tom Shrout和Seung-Eek (Eagle) Park. 1995—1997年间, Shrout和Park^[13]获得了高质量的PMN-PT和PZN-PT弛豫铁电单晶, 单晶的最大压电系数达到2500 pC/N, 应变达到1.7%. 这项工作也使Shrout和Park成为了弛豫铁电单晶发展史上最为重要的两位科学家. 之后的短短数年，在包括我国中国科学院上海硅酸盐研究所罗豪甦研究员在内的一大批晶体生长学家的共同努力下，坩埚下降法被成功应用于弛豫单晶的生长，为定向生长大尺寸弛豫铁电单晶奠定了基础.
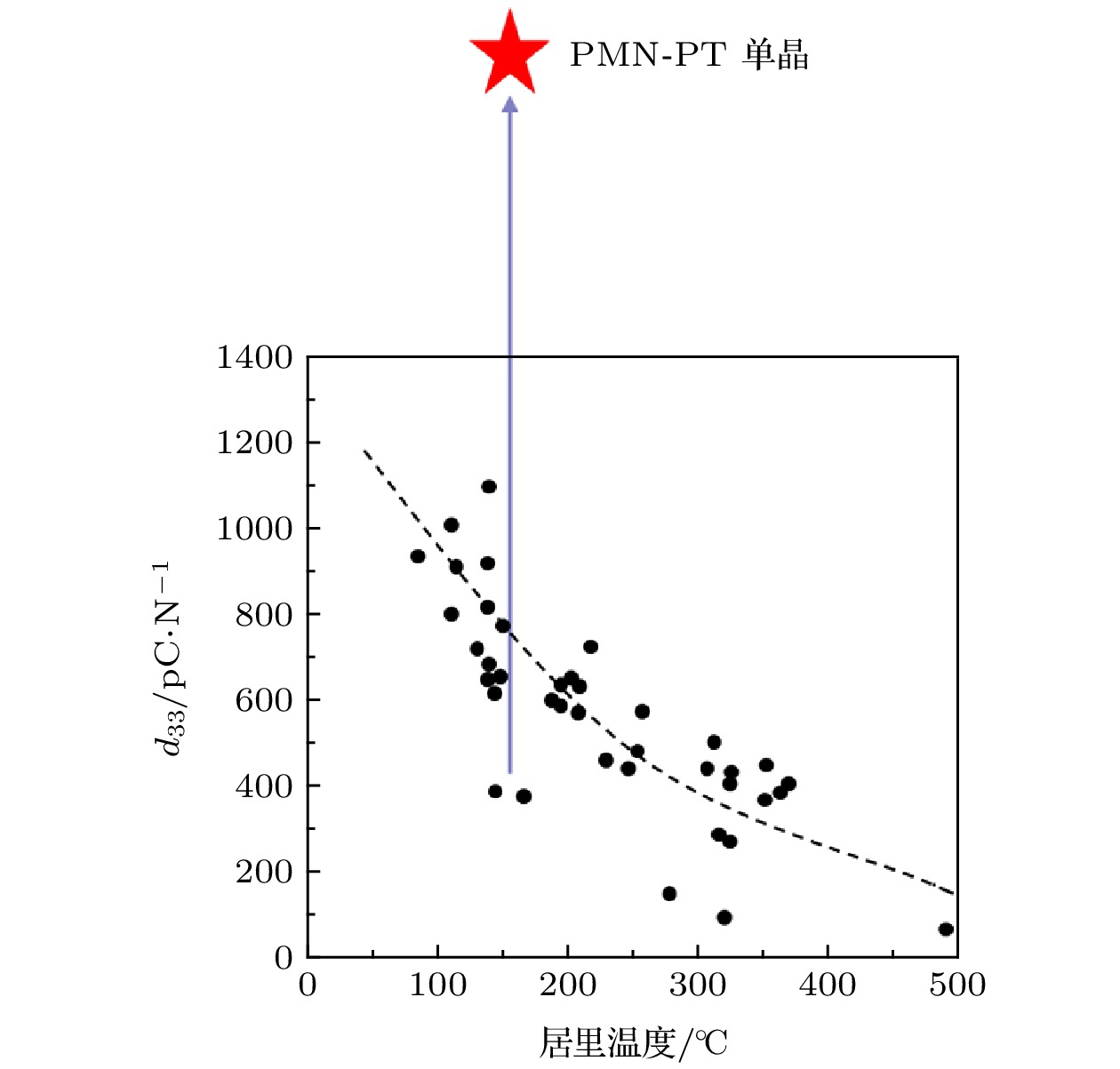图 4 弛豫铁电单晶与铅基陶瓷压电性能对比, 陶瓷数据源于文献[1], 晶体数据来源于文献[13]
Figure4. Comparison of d₃₃ between lead-based ceramics and relaxor-PT single crystals. The data of the ceramics is from Ref. [1]; the data of crystals is from Ref. [13].

除了为压电器件性能提升带来了一次机遇, 弛豫铁电单晶在基础研究方面也扮演着重要角色. 从BaTiO₃发现至今, 能制备成单晶的钙钛矿铁电材料并不多, 而尺寸能够超过10 mm的就更少. 目前, 除了PMN-PT等弛豫铁电单晶外, 只有BaTiO₃和铌酸钾钠(KNN)可以勉强达到这个尺寸. 另一方面, 许多基本测试又对晶体尺寸有一定要求, 如压电全矩阵表征、中子散射研究等. 因此, 以PMN-PT为代表的弛豫铁电单晶, 作为所有钙钛矿铁电体系中第一个能被“长大”的单晶, 为钙钛矿铁电材料结构-性能研究工作提供了材料基础.
2

-->

5.1.弛豫铁电单晶的学术价值

1)从实验角度验证了铁电材料的本征压电效应在MPB附近有显著提升
在弛豫铁电单晶出现之前, PZT陶瓷的研究工作虽然已开展了数十年, 但是人们始终无法找到合适的实验方法将本征压电效应与非本征压电效应(主要指畴壁运动)区分开. 在这种情况下, 大多数文献将PZT陶瓷在MPB附近性能的提升以及软性掺杂后压电效应的提高习惯性地归结于畴壁运动的贡献. 但这种认识的前提是: 本征压电效应的变化很小, 可以忽略. 然而实际情况是这样么? 单晶材料显然是回答这一问题的“一把利器”. 利用合适的极化条件, 沿弛豫铁电单晶的自发极化方向极化晶体, 可以获得单畴单晶, 这样便可以完全将畴壁运动的贡献排除掉. 根据电场方向与自发极化方向的关系, 单畴铁电单晶的压电效应可以简单地分为两类. 1)纵向压电效应(电场方向与自发极化方向平行), 对应于自发极化在外场作用下的“伸缩”, 即强度变化; 2)剪切压电效应(外加电场方向与自发极化方向垂直), 对应于自发极化在外场下的“旋转”, 即方向变化, 如图5所示. 从热力学角度可以很容易得到, 铁电晶体靠近顺电相时, 纵向压电效应提高; 靠近铁电-铁电相变点时(如三方-四方、三方-正交), 相应的剪切压电效应会提高. 利用弛豫铁电单晶, 可完美地实验证明了这一点. 如图6所示, 随着组分靠近准同型相界, 单畴弛豫铁电单晶的剪切压电效应大幅提高, 且远高于单畴纵向压电效应^[15]. 因此, 这里需要特别指出的是, 弛豫铁电单晶高压电效应的根源是单畴剪切压电效应. 多畴结构晶体中的高纵向压电系数均可以通过对单畴晶体性能进行坐标变换来解释. 例如: 工程上最常用到的[001]极化的三方相弛豫铁电单晶(多畴状态)压电系数d₃₃, d₃₁等^[14,15].
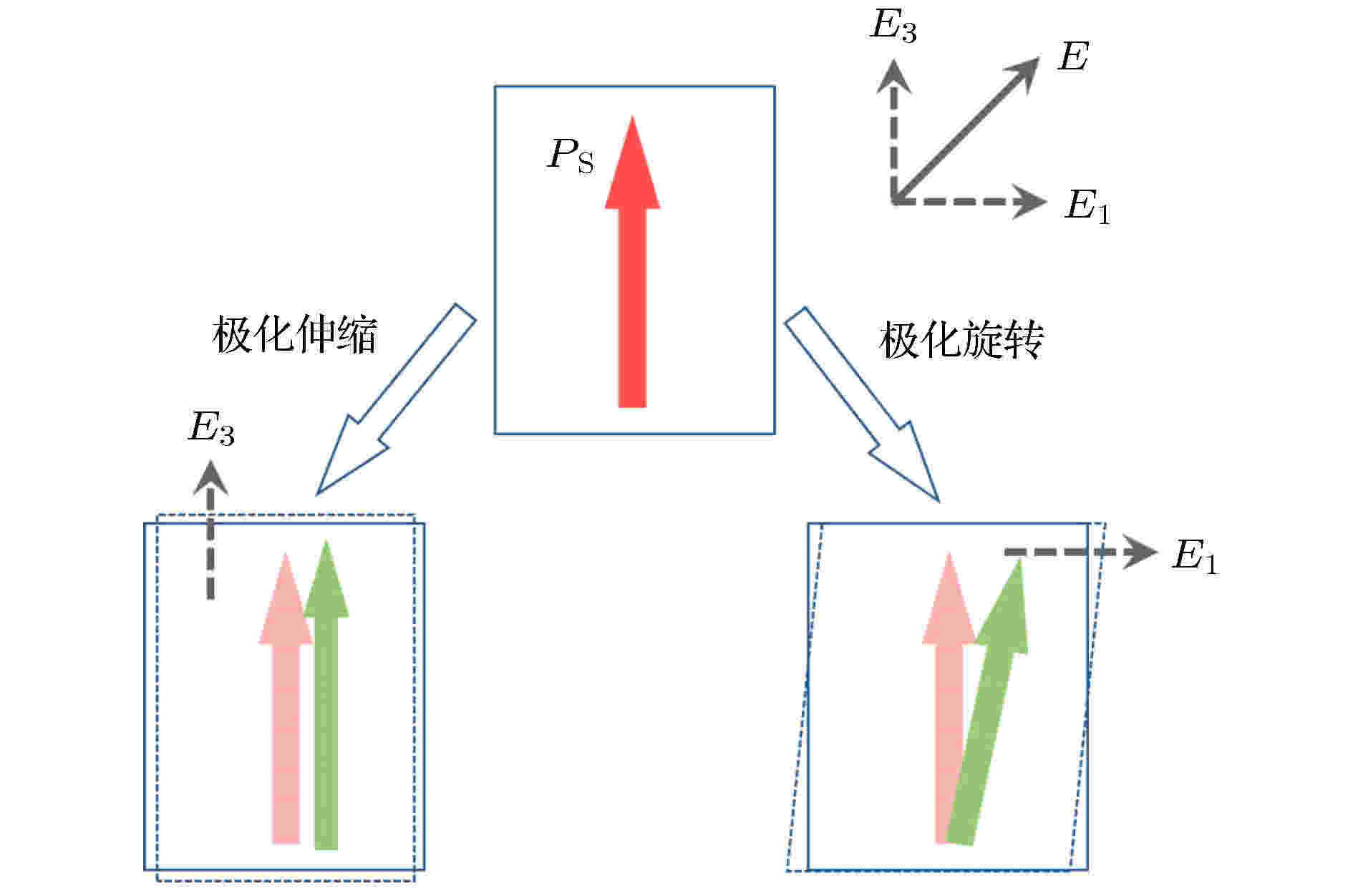图 5 剪切与纵向压电效应示意图(对于任意的铁电畴, 所受外加电场总可以按照电场与自发极化方向关系分为两类: 1)电场方向与自发极化相同的分量, E₃; 2)电场方向与自发极化垂直的分量, E₁. 图中红色箭头代表自发极化方向, 绿色箭头代表加电场后的自发极化方向)
Figure5. Schematic of shear and longitudinal piezoelectric responses. For a ferroelectric single-domain, the applied electric field can be divided into two categories: 1) The electric field (E₃) parallel to the direction of the spontaneous polarization; 2) the electric field (E₁) perpendicular to the direction of the spontaneous polarization. The red arrows represent the direction for the spontaneous polarization, and the green arrows represent the direction for the spontaneous polarization after applying an electric field.

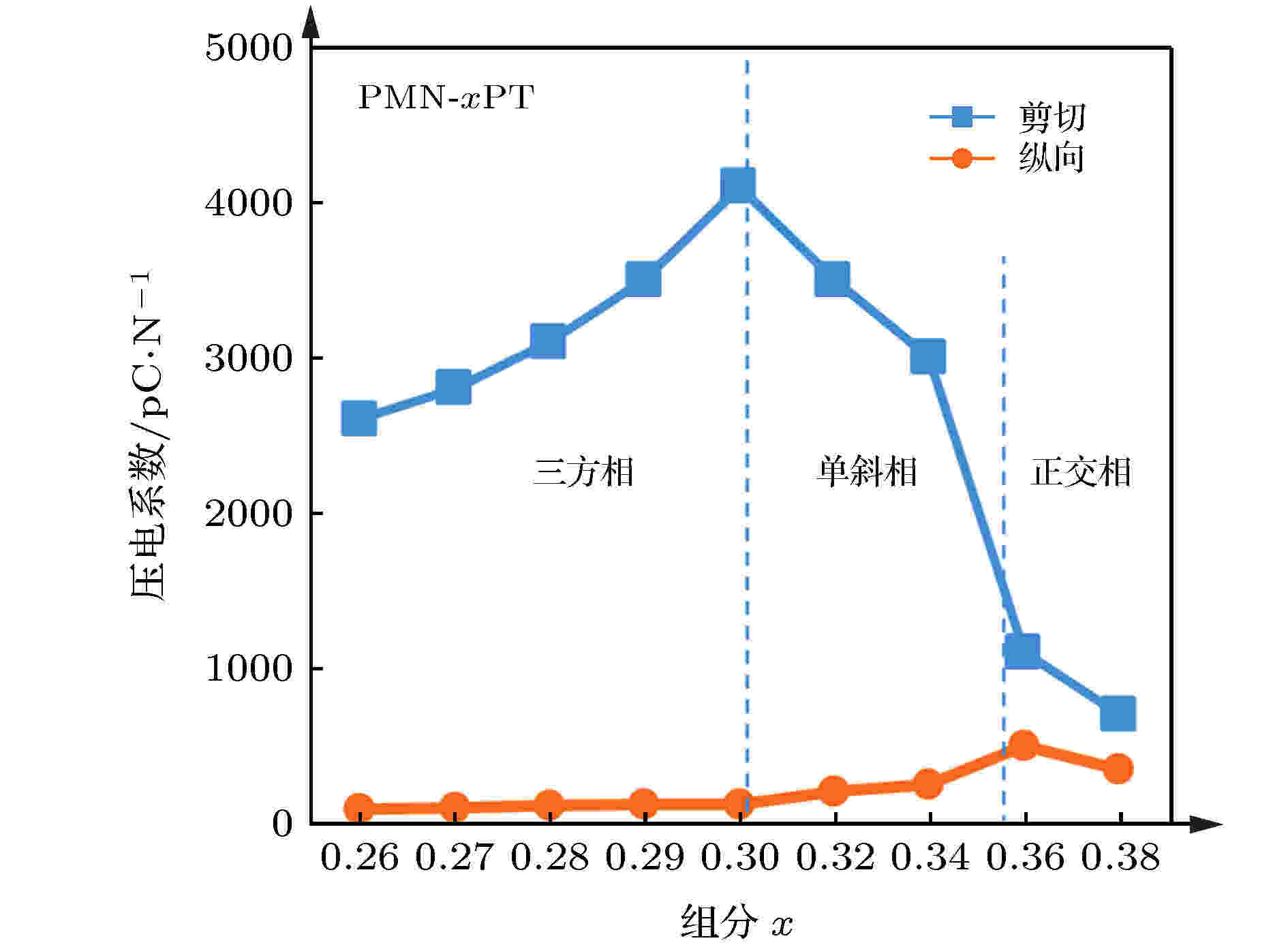图 6 单畴PMN-PT弛豫铁电单晶剪切、纵向压电效应与准同型相界的关系^[15]
Figure6. Shear and longitudinal piezoelectric properties versus MPB for single-domain PMN-PT crystals^[15].

如上所述, 弛豫铁电单晶的出现告诉我们: PT基铁电体的本征压电效应本身就可以很高(～2000 pC/N), 远高于不少****基于PZT陶瓷研究的推断, 即本征压电效应在200 pC/N量级.
2)局域结构与压电效应存在重要联系
紧接着带来的第二问题是: 高剪切压电效应是否与“弛豫铁电体”有所联系? 换句话说弛豫铁电体的结构特点, 即“局域结构在纳米尺度上的分布不均”, 是否能使其极化矢量更容易在垂直电场作用下发生旋转? 这是一个非常难以回答的问题, 也因此吸引了大量的研究人员. 然而, 到目前为止仍然存在争议. 说这个问题困难, 主要是缺乏一个“公平”的对比实验, 即: 保证所有其他条件都不变(比如: 居里温度、三方-四方相变温度), 只对晶体局域结构进行微调, 观察压电效应的变化. 对于PMN-PT单晶来说, PZT单晶是一个比较好的参照物. 因为, 同是PT基钙钛矿晶体, 相比于PMN-PT, PZT单晶在纳米尺度上的局域结构更为均匀(有中子散射实验为证, 图7^[16]). 但是, 非常可惜, 组分在准同型相界附近的PZT单晶十分难于生长, 在很长一段时间内都缺乏满足测试条件的PZT单晶. 直到2010年前后, 龙西法教授与叶作光教授才成功生长出了勉强满足测试条件的PZT单晶, 压电系数约为1000 pC/N, 大约是PMN-PT单晶的一半^[16]. 此结果在一定程度上说明了PMN-PT单晶中的局域结构不均匀很可能对压电效应有显著贡献. 但是, 这样的推断仍然不够严谨. 相比于PMN-PT而言, PZT居里温度更高, 同时在三方-四方相变温度上也有所不同, 这些都可能是造成压电效应差异的因素. 缺少关键实验证据, 那么不依赖于实验的理论计算, 如密度泛函理论计算等, 是否可以解决这个问题呢? 答案是消极的. 原因在于, 构建一个足够大的超晶胞, 涵盖PMN-PT单晶中B位离子的准确分布, 是一项在目前十分棘手的工作.
图 7 PMN与PZT单晶的中子弹性弥散散射实验结果(图中纵轴为弥散散射强度, 其强度越大, 则表示局域结构无序性越强; 插图给出了在(001)散射面附近测得的弹性散射强度等值线的形状)^[16]
Figure7. Neutron elastic diffuse scattering results for PMN and PZT single crystals. The y-axis represents the diffuse scattering intensity. The higher the intensity indicates the higher degree of the local structural heterogeneity. The inset figures give the contour maps of elastic scattering intensity measured near the (001) plane^[16].

2 -->

5.2.弛豫铁电单晶高压电效应起源的介观物理机制

2006—2016年, 笔者课题组一直从事弛豫铁电单晶压电效应起源方面的研究工作. 2010年, 我们发现了一个十分重要的实验现象: 单畴弛豫铁电单晶中与极化旋转对应的介电常数(ε₁₁/ε₂₂)在低温段出现了异常的变化, 如图8所示^[17,18]. 说它异常, 主要是因为这个现象无法用传统的热力学理论进行解释, 在出现异常的温度段并没有任何铁电相变发生. 在实验层面, 这项工作主要有以下两点贡献: 1)利用高质量单畴晶体做测试, 确定畴壁运动与介电、压电效应的低温异常衰减没有关系; 2)首次在单畴PMN-PT晶体中发现了介电弛豫现象. 这两个实验的发现使我们必须承认单畴PMN-PT单晶与理想的铁电单畴有所不同. 如图8(d)所示, 低温段, 介电、压电效应经历了一个类似于“热激活”的过程, 这是弛豫铁电单晶在室温条件下具有高压电效应的关键因素.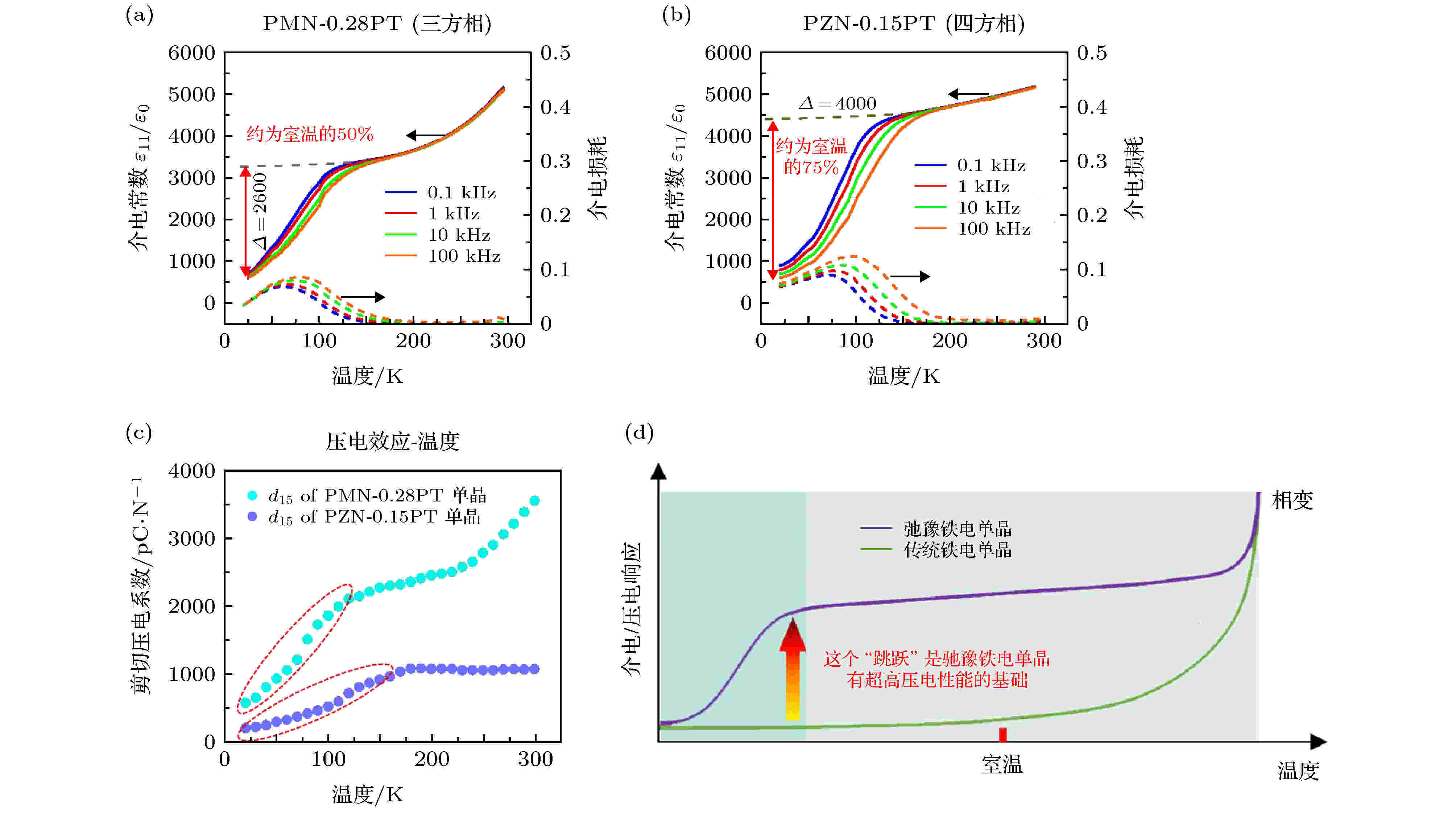
图 8 单畴弛豫铁电单晶低温介电、压电性能^[17,18]　(a)单畴三方相PMN-0.28PT单晶横向介电常数(ε₁₁); (b)单畴四方相PZN-0.15PT单晶横向介电常数(ε₁₁); (c)两种晶体的低温剪切压电系数; (d)相比于传统铁电单晶, 弛豫铁电单晶室温高性能起因的示意图
Figure8. Low-temperature dielectric and piezoelectric properties of single-domain relaxor ferroelectric single crystals^[17,18]: (a) Transverse dielectric (ε₁₁) permittivity for rhombohedral PMN-0.28PT crystal; (b) transverse dielectric (ε₁₁) permittivity for tetragonal PZN-0.15PT crystals; (c) shear piezoelectric properties for relaxor-PT crystals; (d) the origin of the ultrahigh dielectric/piezoelectric properties in relaxor-PT ferroelectric crystals when compared to the conventional ferroelectric crystals.

那么如何来解释这个实验现象呢? 单畴PMN-PT与传统意义上的单畴铁电体的主要区别在哪呢? 通过对单晶结构表征工作的调研, 我们梳理出弛豫铁电单晶在结构方面的两个重要特点: 1)弛豫铁电单晶的长程铁电畴中, 存在着一些纳米尺度的区域, 这些区域的局域结构以及极化方向与长程铁电畴有所不同; 2)在远低于居里温度的条件下, 随着温度的升高, 局域结构与长程铁电畴的区别逐渐减小, 在衍射实验中, 表现为弥散散射强度(diffuse scattering intensity)随温度升高而下降, 如图9所示^[19]. 根据弛豫铁电单晶结构特点, 在相场模拟中, 我们在一个长程铁电畴中引入了与其组分相异的极性纳米微区(如图10(a)所示), 这些区域的尺寸为3—6 nm (通过激活能推算)^[17]. 简便起见, 我们以四方相PZN-0.15PT为模拟对象. 根据实验结果, 假设铁电畴的化学组分对应的相结构为四方相, 极性纳米微区组分对应的为正交相. 当这些极性纳米微区被引入长程铁电畴后, 它们的极化方向受到两个因素影响: 一是由它们本身化学组成而决定的自由能(在相场模拟中, 用Landau-Devonshire函数表示, 简称Landau能), 它使极性纳米微区处于正交相(相的稳定性由势垒深度决定, 如图10(b)所示^[17]), 极化方向沿立方体的面对角线方向; 二是因长程铁电畴与极性纳米微区界面处极化不连续而产生的静电能和梯度能(简称为“界面能”), 这些能量驱使着极化矢量向长程铁电畴极化方向转动, 从而降低界面处极化的不连续. 一般来说, 极性纳米微区尺寸越大, 则其比表面积越小, 界面能的影响越小; 温度越高, 稳态相的势垒深度下降, 导致界面能的作用增强. 当界面能与Landau能呈现出“势均力敌”的状况时, 极性纳米微区的极化矢量处于“横向失稳”的状态, 即: 自由能曲线被“扁平化”(在稳态时, 自由能曲线曲率减小), 如图10(b)所示. “横向失稳”是指极化矢量容易发生转动, 与其对应的是“纵向失稳”, 指极化矢量容易出现“伸缩”, 即: 强度发生变化. 极化矢量的“纵向失稳”通常发生在铁电-顺电相变点.
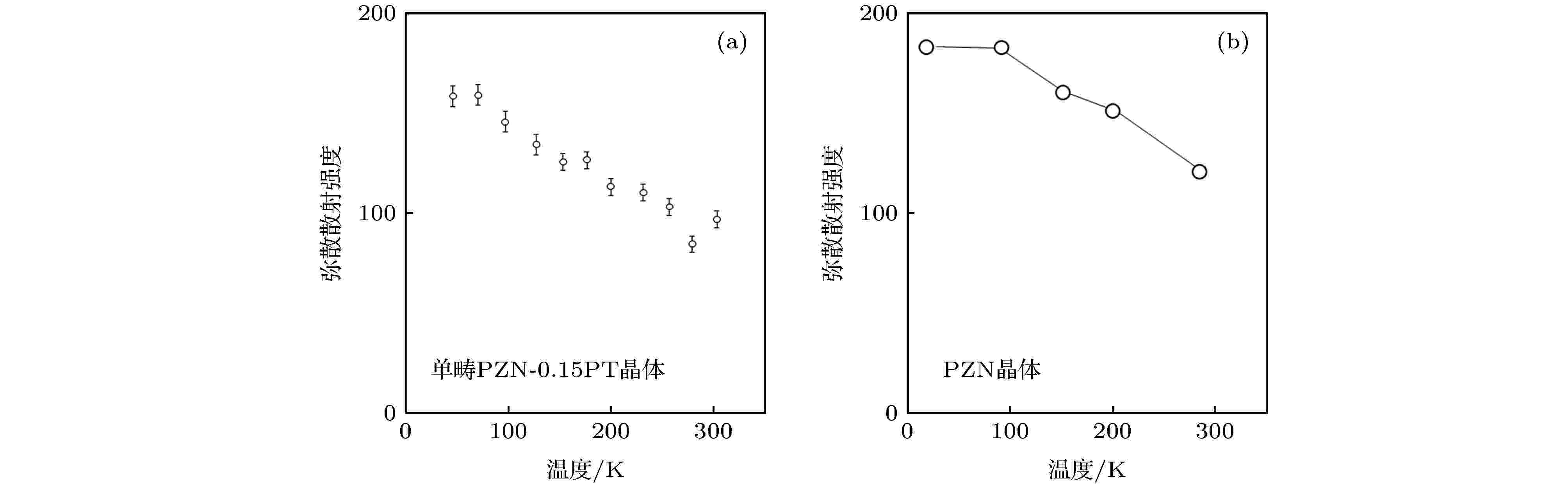图 9 (a) PZN-0.15PT单晶与(b) PZN单晶的X射线弥散散射实验结果^[19]
Figure9. X-ray diffuse scattering results of (a) PZN-0.15PT and (b) PZN crystals^[19].

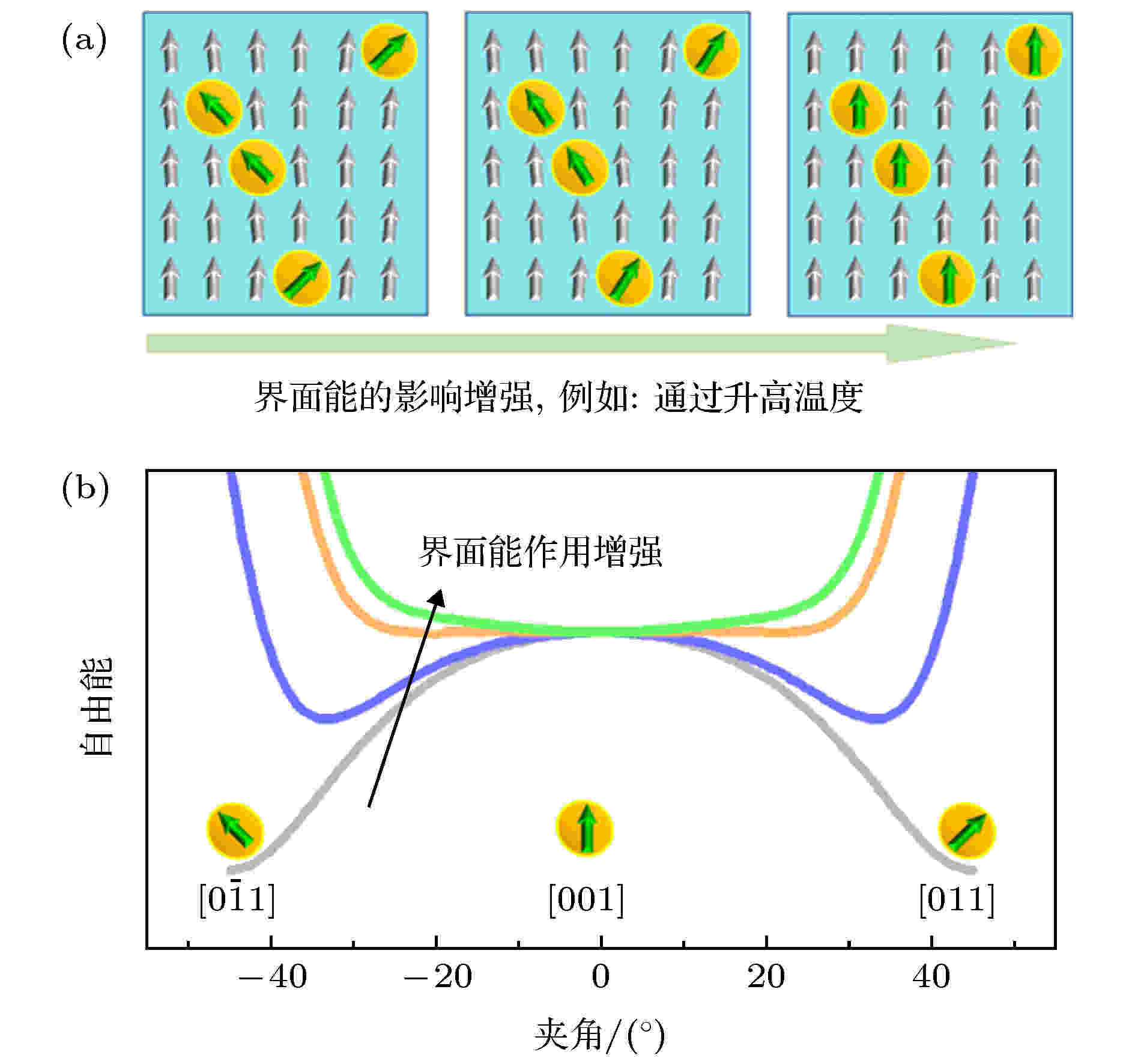图 10 (a)四方相长程铁电畴中嵌入正交相极性微区的结构示意图; (b)正交相极性微区自由能随界面能作用增强的变化(热力学计算结果), 其中横轴表示极化矢量与[001]方向的夹角^[17]
Figure10. (a) Phase-field simulated microstructural variation of a tetragonal ferroelectric with embedded orthorhombic polar nanoregions (PNRs); (b) the change of free energy profiles of the PNRs with increasing the impact of interfacial energy. The x-axis represents the angle between the polar vector and the [001] direction^[17].

图11为PZN–0.15 PT单晶的模拟结果. 温度较低时(< 50 K), 极性纳米微区Landau能的势垒深度较深, 极化状态稳定, 对宏观性能影响不大^[17]. 随着温度的升高, Landau能势垒变浅, 界面能的作用开始增大, 极性纳米微区的极化方向逐渐开始变得与长程铁电畴方向一致(图11(a)). 在这种情况下, 由于自由能曲线的“扁平化”, 极性纳米微区极化矢量非常容易受外场扰动的影响, 从而对介电、压电效应产生显著贡献(图11(b)). 图12给出了单畴PZN-0.15PT晶体在外加电场条件下极化矢量的变化情况^[17]. 可以明显地看出, 在没有外加电场时, 极性纳米微区的极化方向与长程铁电畴方向基本一致, 但是, 当电场作用时, 由于极性纳米微区的极化矢量处于“横向失稳”状态, 这些区域极化矢量的旋转角度要远大于其他区域, 从而对介电、压电效应产生贡献.
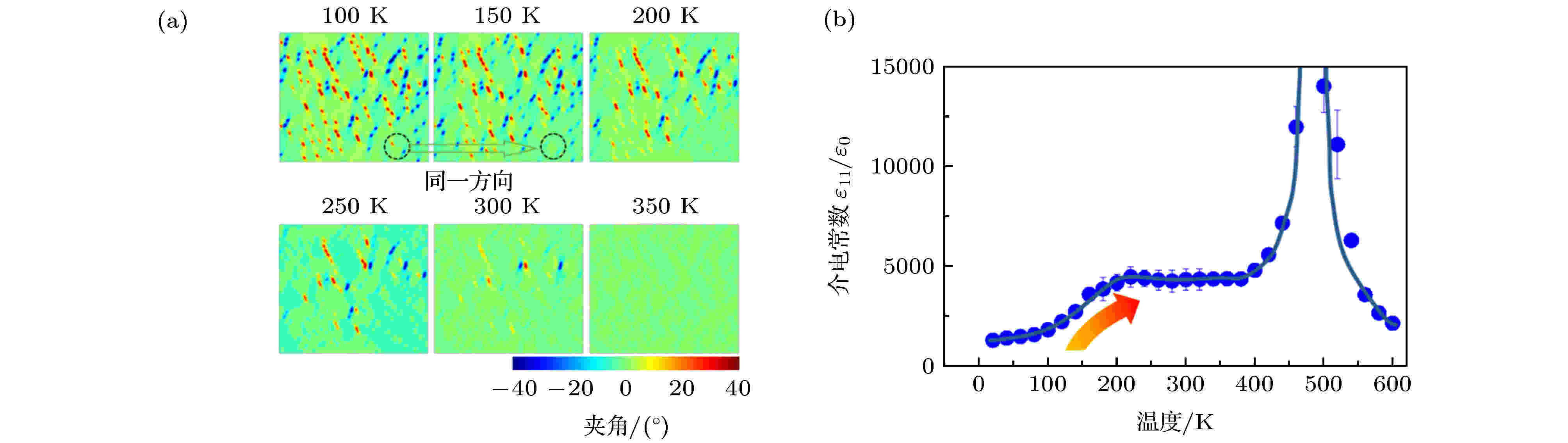图 11 单畴PZN-0.15PT的相场模拟结果　(a)极化矢量方向随温度的变化, 图中颜色代表极化矢量与水平方向的夹角; (b)横向介电常数与温度关系的模拟结果^[17]
Figure11. Phase-field simulation results of single-domain PZN-0.15PT crystal: (a) Temperature-dependent microstructural variations (the color bar denotes the angle between the polar vector and the horizontal direction); (b) the transverse dielectric permittivity versus temperature^[17].

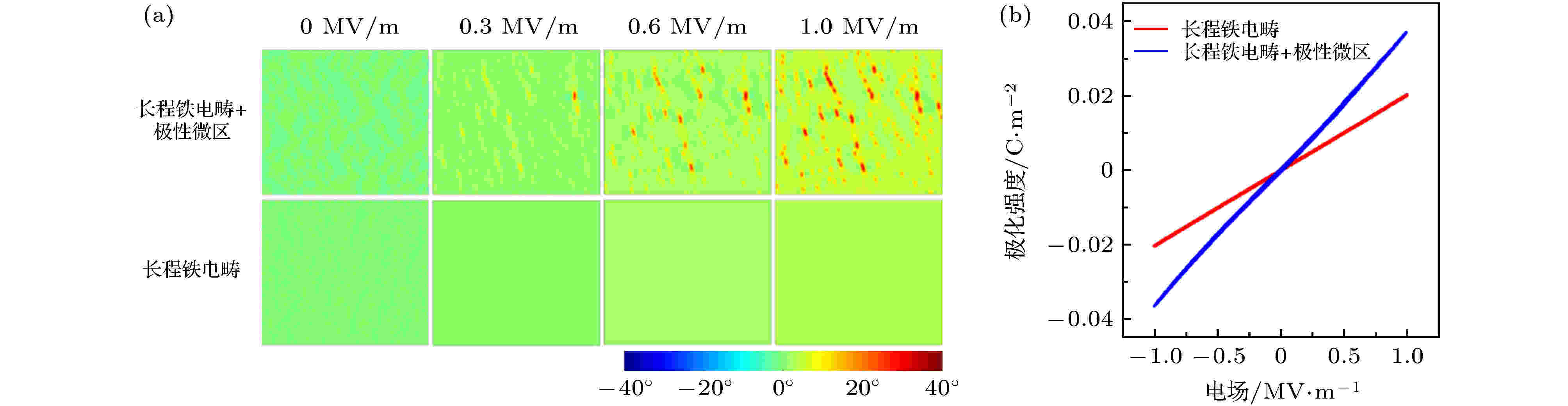图 12 温度为350 K时, 单畴PZN-0.15PT晶体在横向电场作用下介观结构变化(a)和相应的极化强度-电场(P-E)曲线(b), 图(a)中, 颜色代表极化矢量与水平方向的夹角(为了与经典铁电畴性能进行对比, 图(a)和(b)中给出了没有极性微区的长程铁电的模拟结果)^[17]
Figure12. Microstructural variation under a transverse electric field for the single-domain PZN-0.15PT crystal at 350 K and the corresponding P-E curve. In panel (a), the color represents the angle between polar vectors and the horizontal direction. Panels (a) and (b) also gave the simulated results for a classical ferroelectric single-domain (tetragonal matrix)^[17].

简单总结单畴弛豫铁电单晶相场模拟的要点: 1)在结构和性能两个方面, 模拟结果与实验结果均一致; 2)纳米尺度上的局域结构无序所造成的极化“横向失稳”, 是弛豫铁电单晶具有高性能的重要因素; 3)局域结构无序在介电温谱上有一个明显的特征: 低温介电损耗增强, 源于电场作用下纳米微区极化矢量在不同(亚)稳态之间跳转所致的能量损耗.
2 -->

5.3.Sm掺杂PMN-PT

至此, 我们给出了一个可解释弛豫铁电单晶高压电效应起源的介观机理. 然而, 机理研究的最终目标是提升材料压电性能. 因此, 我们以PMN-PT体系为例, 尝试对其局域结构进行“改进”. 对于陶瓷和单晶材料而言, 掺杂是相对简单且可能改变局域结构的方法. 然而, 面对元素周期表中众多元素, 到底应该如何来选择呢? 对于每一种掺杂陶瓷而言, 化学组分筛选(确定准同型相界), 合成、烧结工艺优化(避免杂相出现并保证结晶性), 是获得高性能的必要工作. 因此, 对掺杂元素采取地毯式的搜索显然不是明智之举, 不但耗时巨大, 而且疲劳作战可能导致关键实验数据上的遗漏. 经过文献调研, 我们发现在20世纪90年代已有工作表明: La系稀土元素掺入PMN中, 可使B位Nb:Mg有序排列区域的体积明显增大, 起到对局域结构的调控作用^[20]. 因此, 本课题组^[21]首先对镧系稀土掺杂的PMN-0.28PT进行了研究, 发现在所有La系稀土元素中, Sm对局域结构的影响最大, 表现在低温介电温谱上, 它的低温介电损耗峰最强(图13). 接下来, 课题组对Sm-PMN-PT陶瓷和单晶的制备工艺和组分进行了优化, 获得了压电系数分别为1500 pC/N和4000 pC/N的陶瓷和单晶材料^[21,22], 远高于未掺杂PMN-PT. 同时, 通过原位透射电子显微镜实验确认了Sm掺杂对PMN-PT局域结构不均匀性有增强作用. 近期, 课题组又详细对比了不同稀土元素掺杂PMN-PT陶瓷的结构与性能, 发现: 所有镧系稀土离子中, 可以完全进入PMN-PT固溶体A位、并取代Pb离子的最小离子, 就是Sm^3+[23]. 这很可能是Sm掺杂对PMN-PT局域结构造成显著影响的重要因素.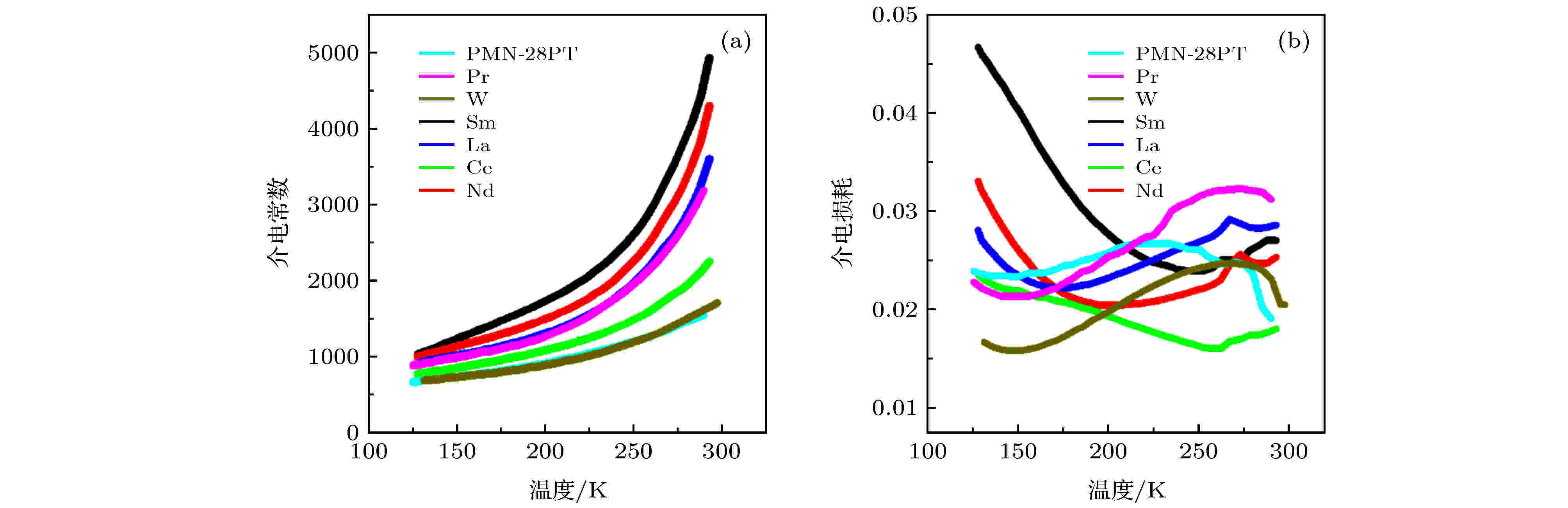
图 13 掺杂PMN-0.28PT陶瓷低温介电常数(a)和介电损耗(b)^[21]
Figure13. Low-temperature dielectric permittivities (a) and dielectric losses (b) for PMN-0.28PT ceramics^[21].

这里需要指出的是, Sm掺杂还存在另一个效果: 降低了PMN-PT的居里温度. 显然, 居里温度降低也可能是造成Sm掺杂PMN-PT性能提高的一个因素. 然而, 我们通过以下两个比较, 说明在本例中居里温度下降并不是Sm-PMN-PT压电性提高的关键因素. 1) Sm-PMN-PT与PMN-36PT的介电温谱对比. 如图14所示^[21], 只有当材料温度非常靠近居里温度时, 其介电性能才会有明显提高. 换句话说, 如果有一种方法可以只改变铁电材料的居里温度, 而不改变其他任何因素, 那么只有当居里温度降到离室温只有10—20 ℃附近时, 介电常数才会明显升高. 将PMN-36PT的居里温度向下平移70 ℃与Sm-PMN-PT相同后, 虽然PMN-36PT的室温介电常数有所提高, 但是仍远低于Sm-PMN-PT. 2) Sm-PMN-PT与Sr-PMN-PT的比较. 与Sm掺杂类似, Sr掺入PMN-PT也有降低居里温度的效果, 但是其室温介电常数远小于Sm-PMN-PT. 原因在于Sr掺入没有使PMN-PT局域结构无序性无明显增强, 这一点可由低温介电损耗无明显增大来佐证(图15)^[21].
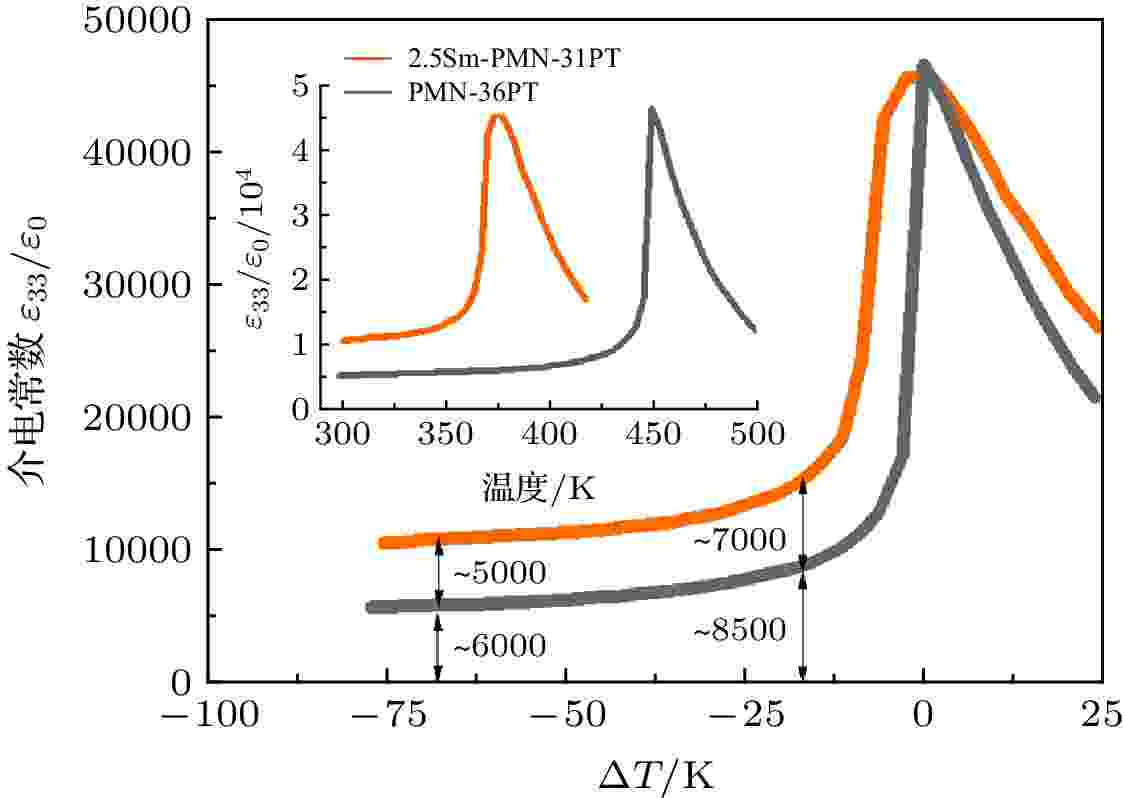图 14 Sm掺杂PMN-0.31PT陶瓷与PMN-36PT陶瓷介电性能的对比(图中横轴ΔT = T－T_C, 插图的横轴为陶瓷实际温度)^[21]
Figure14. Comparison of dielectric properties between Sm-doped PMN-0.31PT and PMN-36PT ceramics. The x-axis of the figure ΔT = T－T_C, while the x-axis of the inset figure represents the actual temperature of the ceramics^[21].

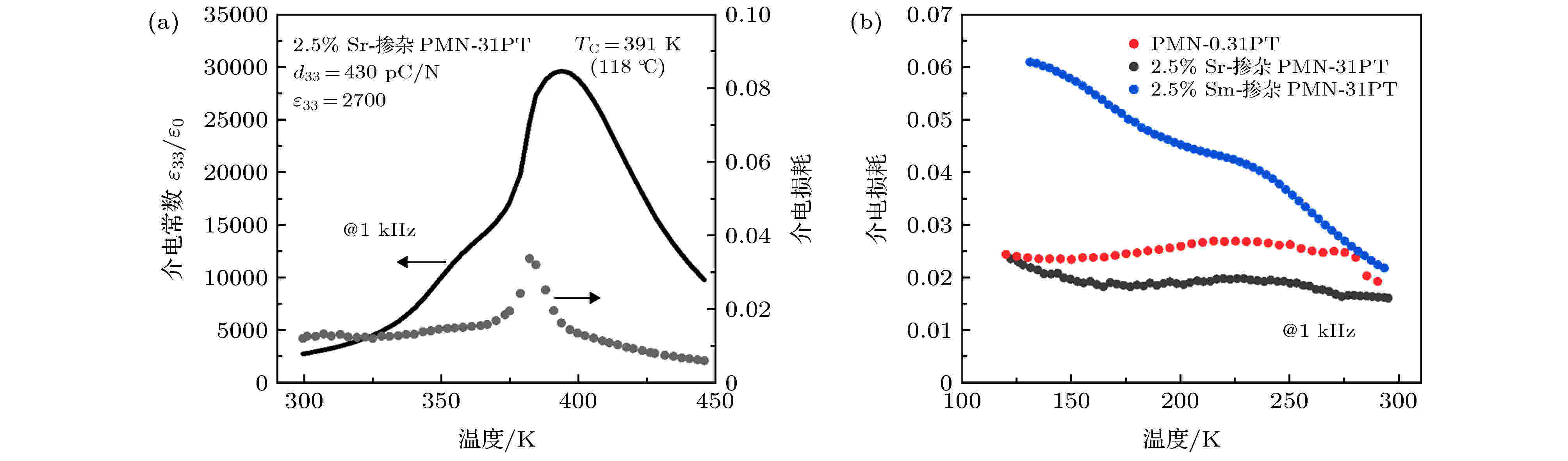图 15 (a) Sr掺杂与(b) Sm掺杂PMN-0.31PT陶瓷介电性能性能对比(图(a)中给出了Sr掺杂PMN-0.31PT的室温介电和压电系数)^[21]
Figure15. Comparison of dielectric properties between (a) Sr-doped and (b) Sm-doped PMN-0.31PT ceramics. The room temperature dielectric and piezoelectric properties of Sr-doped PMN-0.31PT are given in (a)^[21].

简单总结一下Sm掺杂PMN-PT的研究工作. 在获得室温高压电效应的同时, 这个例子更重要的意义在于: 进一步说明了调控铁电材料局域结构无序性是提升压电性能的有效方法. 当然, 由于居里温度的下降, 本例并不是最理想的例子. 若要毫无瑕疵地说明这一问题, 仍需继续努力, 在不改变居里温度的条件下实现局域结构的有效调控, 提升铁电材料压电性能.
2 -->

5.4.“软性”掺杂机理的启发

PZT中的软性掺杂作为压电陶瓷领域最重要的发现之一, 虽然已有60多年, 但是其中奥义仍然没有被揭开, 对于新型压电陶瓷材料的发展无疑是一个严重地阻碍.
虽然软性PZT种类繁多, 掺杂元素也不尽相同, 但是Nb, Mg, La是三种最经典的掺杂元素, 因而与PMN-PT以及稀土掺杂PMN-PT存在一定程度的相似度. 这就使我们得到如下推断: 除了与畴壁运动有关外, 软性PZT陶瓷高压电效应与铁电畴本身的“变软”有关, 而这是由于掺杂而引入的局域结构无序所致. 如图16所示, 软性PZT陶瓷也表现出了与Sm掺杂PMN-PT陶瓷和PMN-PT单晶类似的特征—介电损耗在低温出现明显的增强. 同时, 与硬性PZT陶瓷比较可见, 软性陶瓷的室温高性能同样是源于介电常数在室温下的一个类似于热激活的过程.
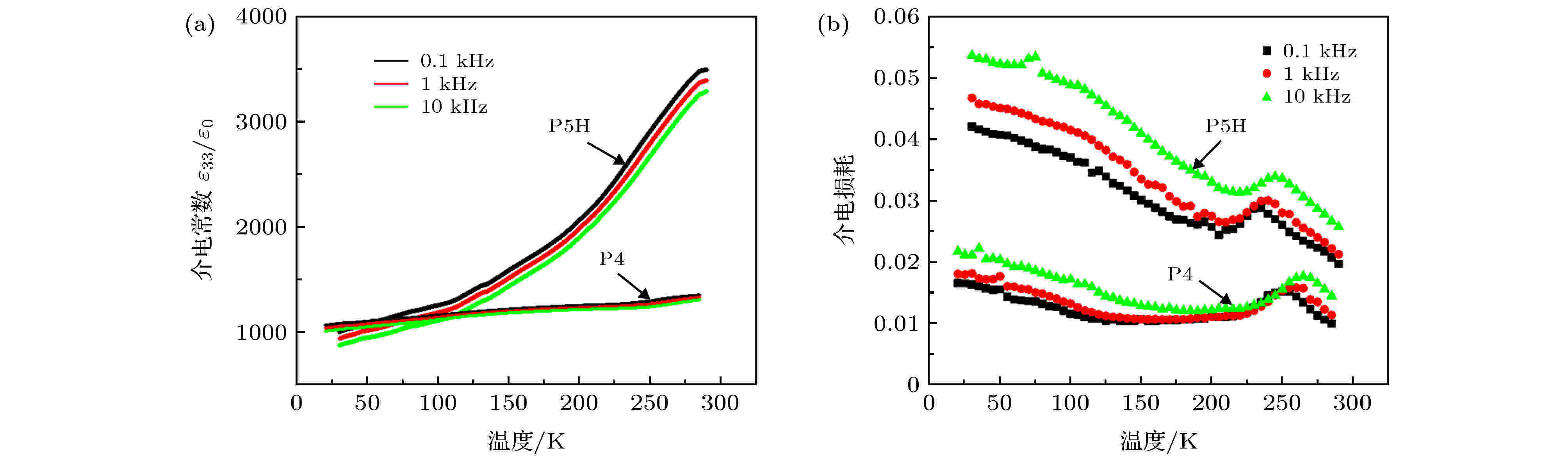图 16 软性(P5H)和硬性PZT陶瓷(P4)陶瓷低温(a)介电常数与(b)介电损耗
Figure16. Low-temperature (a) dielectric permittivities and (b) dielectric losses for soft (P5H) and hard PZT (P4) ceramics.

那么怎样的掺杂才能使铁电畴“变软”呢? 我们又该如何寻找最佳掺杂元素呢? 在总结前辈经验的基础上, 我们认为有如下几点可供参考:
1)掺杂离子要与所取代离子在半径、价态、外层电子结构等方面有明显差距
原子价态、半径以及外层电子情况比较相似时, 局域结构没有呈现显著的不均匀现象. 例如: BZT-BCT单晶, A位Ba²⁺与Ca²⁺离子、B位Zr⁴⁺与Ti⁴⁺离子, 价态一样、半径相似、外层电子结构相似, 因此在介电温谱中没有表现出局域结构不均匀的特征(图17(a)). 再比如: Ta掺杂的KNN单晶, A位K⁺与Na⁺离子、B位Nb⁵⁺与Ta⁵⁺离子, 也在价态、离子半径和外层电子结构方面相似, 因此介电温谱并未出现异常(图17(b)).
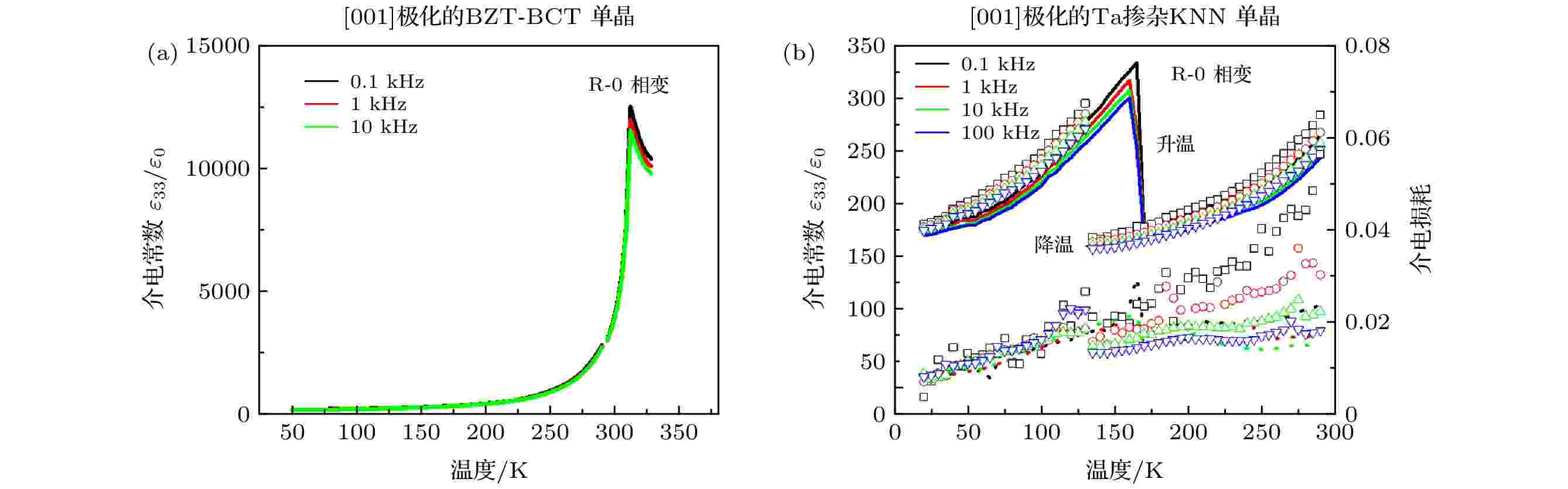图 17 两种铁电单晶的低温介电性能　(a) [001]极化的BZT-BCT单晶, 室温为三方相, 晶体为韩国H Y Lee教授提供; (b) [001]极化的Ta掺杂KNN单晶, 室温为正交相
Figure17. Low-temperature dielectric properties for (a) [001]-poled rhombohedral BZT-BCT crystal. The crystals were from Professor H Y Lee in Korea; (b) [001]-poled orthorhombic Ta-doped KNN crystal.

2)掺杂离子不宜导致氧空位出现
在钙钛矿铁电材料中, 氧空位通常可以在自发极化所产生的电场作用下发生迁移, 而迁移最终的结果通常是形成一个与自发极化方向相同的缺陷电场, 使电畴极化更加稳定, 也称“缺陷钉扎”作用, 会使陶瓷压电效应降低.
3)掺杂离子不可对偶极子的长程有序排列产生过大的破坏作用
为了获得高压电效应, 高自发极化强度是必须的. 因此, 我们并不希望掺杂元素过分地破坏偶极子的长程有序, 导致极化强度大幅降低.
最后我们需要指出的是, 畴壁密度/电畴尺寸与压电效应的关系也是铁电领域中非常重要且极具争议的科学问题. 比如: Wada等^[24]在钛酸钡晶体中发现, 电畴尺寸减小可导致晶体压电效应升高; 然而, Qiu等^[25]在三方相PMN-PT中发现, 晶体压电效应随电畴尺寸的增大而增大. 由于篇幅原因, 本文并未涉及这些问题, 有兴趣的读者可参考文献[24, 25].
今年, 恰逢铁电材料满一百周岁, 在这一百年中, 压电应用一直是支撑着铁电材料发展的核心驱动力. 本文由于篇幅所限, 仅介绍了钛酸铅基铁电材料的压电效应, 并没有介绍LiNbO₃、铌酸钾钠、铋层状结构、钨青铜结构等铁电材料. 然而, 这些铁电材料在许多压电器件中(如滤波器、高温压电传感器等)也扮演着重要角色. 长期以来, 铁电材料虽然在存储、红外成像、固态制冷等应用领域遇到很大的挑战, 但是在压电应用中, 铁电材料一直是无法取代的. 可以说, 在这一百年间, 压电效应一直为铁电材料的发展保驾护航. 于此同时, 每当在压电效应接近瓶颈时, 铁电材料总会给我们带来新的惊喜, 比如: 从BaTiO₃到PZT陶瓷, 再从PZT陶瓷发展到弛豫铁电单晶, 以及近期无铅压电材料^[26-28]和分子铁电晶体^[29,30]所取得的一系列突破等. 相信下一个惊喜离我们并不遥远.
本文是在南京大学刘俊明教授和清华大学沈洋教授的鼓励下完成的, 在此特别表示感谢. 感谢西安交通大学刘金凤博士对文字和图片的校对工作.