摘要: 以基于纳米示踪平面激光散射技术的密度场测量方法获得的
Ma = 3.0平板湍流边界层密度场实验数据为基础, 采用小波方法对湍流边界层密度脉动进行了多尺度与动态特性分析. 研究表明, 近壁区密度脉动概率密度呈偏离高斯分布, 大尺度分量对湍流边界层密度脉动起主导作用, 小尺度分量使概率密度呈“M”型分布; 采用希尔伯特变换对幅度调制效应进行分析, 结果表明超声速湍流边界层近壁处外层大尺度密度偏移会导致内层小尺度密度脉动的局部增强或减弱; 采用基于小波变换的时变谱密度估计对边界层不同高度的密度脉动进行分析, 结果表明脉动主要分布在1 MHz以内, 主导频段的密度脉动间歇性明显; 随着时间的发展, 大部分脉动存在频率从高频过渡到低频, 幅值先增加后减少的规律; 随着高度的增加, 对数区脉动主要分布在10
5 Hz以下, 尾迹区则集中在10
5 Hz以上, 边界层与主流交界处的脉动主要分布在两者相互作用形成的大尺度结构附近, 脉动能量从近壁面到主流区呈现先升高后降低的变化规律.
关键词: 超声速 /
湍流边界层 /
密度脉动 /
小波变换 English Abstract Wavelet analysis of density fluctuation in supersonic turbulent boundary layer Zhang Bo He Lin Yi Shi-He College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 91752102) and the Excellent Innovation Young Project of Changsha, China (Grant No. KQ1802031)Received Date: 18 May 2020Accepted Date: 18 June 2020Available Online: 02 November 2020Published Online: 05 November 2020Abstract: In order to obtain the time-varying information and dynamic characteristics of density fluctuation in compressible turbulence, the wavelet method is used to analyze the flow density field of zero-pressure-gradient flat plate turbulent boundary layer at Ma = 3.0, which is measured based on Nano-tracer plane laser scattering technique. Utilizing Taylor’s frozen hypothesis, the spatial signal of density field converts into the temporal signal. The one-dimensional orthogonal wavelet multi-resolution analysis is used to reveal multi-scale turbulent structures, and the results suggest that large-scale structures play a leading role in the density fluctuation of turbulent boundary layer while the small-scale structures make the probability density function (PDF) of density fluctuation manifested as an “M” distribution. The density fluctuation scalar PDF deviates from Gaussian distribution. The Hilbert transformation is used to analyze amplitude modulation effects between large- and small-scale structure, and the results suggest that positive (negative) large scale density excursion in the outer layer induces local enhancement (suppression) of the small scale density fluctuation in the inner layer near the wall. The time-varying spectral density estimation method based on the wavelet transform is used to analyze the density fluctuation at different heights of turbulent boundary layer after proving its viability in time and frequency domain. The results suggest a wide range of frequencies throughout the turbulent boundary layer, mainly distributed within 1 MHz. The density fluctuation in the dominant frequency band is intermittent, most of which transits from high frequency to low frequency while the spectral density first increases and then decreases. Near the wall, the time-frequency distributions of density fluctuation in the logarithmic layer are similar. In the middle part of the turbulent boundary layer, the frequency distribution and spectral density of the density fluctuation each reach a peak. Near the mainstream region, the spectral density decreases obviously, which is mainly distributed near the structure formed by the interaction between the boundary layer and mainstream. The wall constraint, viscous dissipation, and uniform mainstream make the fluctuation nearby the region relatively weak. As a result, the spectrum amplitude of density fluctuation first increases and then decreases from the wall to the mainstream.Keywords: supersonic /turbulent boundary layer /density fluctuation /wavelet transform 全文HTML --> --> --> 1.引 言 近年来, 随着高速飞行器的不断发展, 超声速湍流的研究受到广泛重视. 相比于低速湍流[1 ] , 超声速湍流的研究成果较少, 其中一个重要原因在于超声速流场的可压缩性, 密度变化使超声速湍流流场特性比不可压湍流更为复杂; 同时实验条件下密度场的测量比压力、速度更为困难, 因此关于密度特性的研究, 特别是密度脉动特性的研究十分缺乏. 为了更加充分地认识超声速湍流特性, 方便超声速流场雷诺应力的封闭、湍流模型的建立和数值模拟有效性的验证, 急需对超声速湍流密度脉动特性开展深入研究.[2 ,3 ] 使用数值模拟方法研究超声速湍流密度脉动的概率分布函数; 王正魁等[4 ] 提出用直接数值模拟方法获得超声速平板边界层数据, 再通过神经网络方法挖掘流场数据建立密度脉动模型; Tian等[5 ] 对湍流的数值模拟结果表明, 密度变化明显改变了湍流结构、流动拓扑结构与统计结果. 相比之下实验研究结果很少, Parziale等[6 ] 使用聚焦激光差分干涉测量激波风洞高超声速边界层的密度脉动, 观测到主导不稳定频率与第二模态相近; He等[7 ,8 ] 使用粒子图像测速(particle image velocimetry, PIV)与基于纳米示踪平面激光散射技术(nano-tracer-based planar laser scattering, NPLS)的密度场测量方法[9 ] 研究$Ma$ = 3.0平板湍流边界层, 发现密度脉动的概率密度分布与质量流量脉动较为一致, 与速度脉动相关性不大, 局部脉动超过当地平均密度20%, 表明Morkovin[10 ] 关于$Ma < 5$ 边界层密度脉动可以忽略不计的假设对$Ma \geqslant 3$ 的湍流边界层不再成立, 揭示了可压与不可压湍流边界层的显著区别.[11 ,12 ] (proper orthogonal decomposition, POD)、动力学模态分解[13 ,14 ] (dynamic mode decomposition, DMD)与小波分析等方法, 其中小波方法对实验测量信号的要求比POD, MOD方法容易满足, 可以实现一维或二维信号的尺度信息、频谱与时间变化特性的分析. Ruppert-Felsot等[15 ] 首次使用小波方法从PIV测量得到的湍流速度信号中提取相干结构, 提出小波是适合研究高度非定常非均匀流动的统计工具; 同年, 赵玉新等[16 ] 使用小波方法对混合层密度场结构进行多分辨率分析, 研究了不同尺度的密度脉动信号特征; Rinoshika和Omori[17 ] 使用正交小波变换对不同钝体湍流尾迹进行多尺度分析, 表明大尺度结构对雷诺应力贡献最大; Zheng和Jiang[18 ] 对热线风速仪获得的低速湍流边界层速度压力信号进行小波分析, 表明各尺度间歇性与湍流边界层缓冲层相干结构有关; Freund和Ferrante[19 ] 使用小波方法分析直接数值模拟获得的不可压多相流湍流能谱, 表明小波是理解多相湍流物理机理的重要工具与建立大涡模型的新途径.$Ma$ = 3.0平板湍流边界层密度场数据[8 ] , 采用正交小波变换对密度脉动进行多尺度分析, 采用希尔伯特变换分析大小尺度间的相互作用; 根据边界层流动随高度变化的特点, 采用基于小波变换的时变谱密度估计方法对不同高度的密度脉动进行分析, 研究密度脉动所含频率及其随时间的变化特性.2.实验数据与分析方法 22.1.实验数据 2.1.实验数据 本文超声速边界层湍流密度场实验数据来源于何霖[8 ] 等的研究, 实验在国防科技大学空气动力学实验室的超声速风洞中进行, 原始数据为$Ma$ = 3.0平板湍流边界层流场剖面的密度场实验测量结果. 密度场测量采用基于NPLS的超声速流动密度场测量技术, 该技术已经应用于超声速混合层[16 ,20 ] 、后台阶绕流[21 ] 、高超声速二次模态波[22 ] 等三维流场密度场测量, 相关技术细节可以参考文献[9 ].$Ma$ = 3.0平板湍流边界层实验状态如表1 所列, 该边界层速度场分布已经在文献[23 ]中进行了详细分析, 平均速度剖面与理论结果基本一致, 密度场测量样本200组, 测量位置位于风洞喷管出口下游180 mm处, 有效范围为$2\delta $ (流向)$ \times 1.5\delta $ (高度), 对应的空间分辨率为11.4 μm/pixel, 密度场的平均特性和频谱特性已经在文献[8 ]中进行了分析, 其中, 平均密度场剖面与基于速度场换算温度剖面后计算得到平均密度剖面一致. 本文基于该密度场原始测量数据, 采用多种小波方法对密度脉动开展研究.$M{a_\infty }$ ${P_0}/{\rm MPa}$ ${T_0}/{\rm K}$ ${P_\infty }/{\rm Pa}$ ${T_\infty }/{\rm K}$ ${\rho _\infty }/{\rm kg \cdot {m^{ - 3} }}$ ${U_\infty }/{\rm m \cdot {s^{ - 1} }}$ $\mu /{\rm Pa \cdot s}$ ${R_e}/{\rm m^{ - 1} }$ 3.0 0.1 300 2750 107 0.089 622.5 7.43 × 10–6 7.49 × 106
表1 风洞流场参数Table1. Flow conditions2.2.分析方法 -->2.2.分析方法 分析之前需要将拍摄得到的密度场空间信号转换为时间信号. 前期大量的实验研究发现[7 ,16 ] , 超声速流动的对流速度很高, 但拟序结构的变形却很慢, 变化速率远远小于对流速度, 边界层在拍摄瞬间的运动可看成是流场结构的整体平移, 因此可以引入泰勒假设[24 ] , 将时间信号与空间信号用流场的局部对流速度直接相关. 尽管泰勒假设对数据分析可能会产生一定影响, 但可以使时间或空间序列的实验数据得到更充分的分析, 因此在热线、PIV等数据分析中[25 -28 ] 得到广泛的应用, 在本实验中还可以克服传统的时间序列脉动测量难以同时获得多点密度数据的缺陷, 为不同高度对比分析提供帮助.[29 ] , 与傅里叶变换分解为全局函数序列相比, 小波在时频域中具有衰减性或紧支性, 可以通过伸缩平移运算对信号逐步进行多尺度细化, 最终达到高频处对时间细分, 低频处对频率细分, 满足高频对时间分辨率高、低频对频率分辨高的要求[30 ] . 湍流的非平稳特性不仅要求小波基在时域具有很良好的集中性, 同时在频域内也要有较高的分辨率. 根据海森伯不确定性原理, 一个基函数无法同时在时频域达到最高分辨率; 而对于几类正交小波(Daubechies, Meyer, Harmonic等), Mouri等[31 ] 研究表明湍流统计规律基本与这几类小波的选择无关. 本文选择了时频分辨率较高且可以进行正交变换的Meyer小波作为基函数, 其频域定义与时域波形如图1 所示, 其中ω 为频率, $\gamma $ 为四阶连续可导函数.图 1 Meyer小波频域定义与时域波形Figure1. Meyer wavelet in frequency and time domain.2.2.1.正交小波多分辨率分析 -->2.2.1.正交小波多分辨率分析 正交小波基可以消除小波空间的冗余, 使变换与重构惟一对应, 结果可以更好地反映原始信号性质. 采用Mallet算法[32 ] 对信号进行正交小波变换塔式分解与重构, 其过程概括如下.h 与尺度系数g 构造第一层分解所用的2N N –1 阶正交小波基矩阵${{{M}}_{N - 1}}$ , 依次类推直至多分辨率分析所要的分解层数, 得到正交小波基矩阵级联构成的小波分析矩阵[17 ,33 ] :f 进行分解, 得到小波系数矩阵${{WT}}$ :${{WT}}$ 分解为不同尺度空间的小波系数:M ${f_{{\rm{reconstruct}}}}$ 为重构信号, ${f_0}$ 与${f_N}$ 分别表示信号最低频段与最高频段的尺度分量, 这种分解方法称为正交小波多分辨率分析(multi-resolution analysis, MRA). 必须注意到, 多分辨率分析得到的尺度分量是信号分量, 不能直接等同于流体的尺度结构(例如破碎的湍流结构).2.2.2.幅度调制效应分析 -->2.2.2.幅度调制效应分析 Hutchins和Marusic[34 ] 对高雷诺数下壁面湍流边界层脉动速度信号进行分解, 发现大尺度结构对小尺度结构能量具有调制作用, 并在直接数值模拟数据中也发现了类似的趋势; Mathis等[35 ,36 ] 在前者基础上, 将希尔伯特变换应用在滤波得到的速度脉动小尺度分量上, 通过互相关量化尺度间幅度调制效应(amplitude modulation effects, AME); He等[37 ,38 ] 对分析过程进行了详细描述, 并对低速条件下的圆柱尾迹与湍流边界层进行了分析. 其分析过程可以概括为[38 ] , 将脉动速度信号分解成低频的大尺度分量${u_{\rm{L}}}$ 和高频的小尺度分量${u_{\rm{S}}}$ ;${u_{\rm{S}}}$ 进行希尔伯特变换得到其包络$E({u_{\rm{S}}})$ ;$E({u_{\rm{S}}})$ 进行低通滤波, 将得到的低通滤波包络${E_{\rm{L}}}\left( {{u_{\rm{S}}}} \right)$ 与大尺度分量${u_{\rm{L}}}$ 进行相关性分析, 通过相关系数量化尺度间相互作用.2.2.1 节得到的超声速湍流边界层密度脉动多尺度信息重构得到上述分析过程的大小尺度分量${u_{\rm{L}}}$ 与${u_{\rm{S}}}$ .2.2.3.时变谱密度估计 -->2.2.3.时变谱密度估计 除了正交小波变换, 还可以通过时变谱密度估计对信号进行多尺度分析. 与正交小波变换不同, 时变谱密度估计形成信号的时频图, 信号频率及其随时间变化特性更为直观; 与基于短时傅里叶变换(short-time fourier transform, STFT)时变谱相比, 基于小波变换的时变谱的时频窗自适应, 因此分辨率更高, 吉布斯效应更弱, 对短信号的分析更合适. Gurley和Kareem[39 ] , Spanos和Failla[30 ] , 曹晖等[29 ] 、白泉等[40 ] 推导了离散或连续小波变换系数与功率谱密度的关系, 并运用到地震动、脉动风、工程结构振动的分析中. 本文时变谱密度与小波系数关系式为[40 ] $S\left( {f, t} \right)$ 为频率f 、时间t 处的时变谱密度; $H\left( f \right)$ 为频率f 所对应小波函数${\psi _{a, b}}\left( t \right)$ 的频域值; $\Delta f$ 为频率f 对应的频带宽度; $WT\left( {a, b} \right)$ 为密度脉动信号$f\left( t \right)$ 经小波变换得到的小波系数, 表征不同尺度因子a (对应频率f )与平移因子b (对应时间t )的小波函数${\psi _{a, b}}\left( t \right)$ 与$f\left( t \right)$ 的相似程度,a 按幂级数进行离散, 取较小的分频基数以获得更高的频率分辨率:2.3.有效性验证 -->2.3.有效性验证 对于工程实测的湍流信号、地震动信号等, 其真实的时变谱密度函数未知, 因此需要对信号的时变谱密度估计进行有效性检验. 以本文$Ma$ = 3.0湍流边界层$y/\delta $ = 0.1高度密度脉动信号为例, 从时变谱密度的物理意义出发, 在时域和频域分别进行检验.10 )式左边对每一时刻时变谱密度$S\left( {f, t} \right)$ 的频率分布求积分, 可以得到密度脉动的能量在时间上的分布, 再对能量进行时间积分, 得到密度脉动累积能量与时间关系的Husid图; (10 )式右边${\left| {f\left( t \right)} \right|^2}$ 为实际探测到的密度脉动在t 时刻的能量分布, 对能量进行时间积分得到实际密度脉动Husid图. 通过对比左右两边得到的Husid图, 如图2(a) 所示, 检验时变谱密度估计密度脉动的时域特性的有效性.图 2 时频域有效性验证 (a) 密度脉动累积能量曲线; (b) 密度脉动功率谱估计Figure2. Verification in time and frequency domain: (a) Husid of density wave; (b) power spectral density (PSD) of density fluctuation.11 )式对时变谱密度进行时间积分并对总时间取平均, 可以将非平稳过程时变谱密度退化为平稳过程功率谱, 将其与傅里叶变换得到的功率谱结果对比, 如图2(b) 所示, 检验其频域特性的有效性.图2(a) 可以看到, 基于Meyer小波的时变谱密度估计得到的密度脉动Husid曲线与实际Husid曲线符合较好, 微小差异主要来源于基函数拟合原始信号过程中产生的吉布斯效应. 用相关系数来定量衡量曲线变化趋势的相似性, 两条曲线的变化趋势相关系数为0.998, 单点误差 < 6%, 经变换后, 脉动最终累积能量差异为4.3%; 小波变换的功率谱估计是各尺度对应频带的平均, 因此图2(b) 可以看到小波变换比傅里叶变换的功率谱估计值更平滑, 两种估计方法在频域内的分布趋势较为一致.3.实验结果与分析 23.1.瞬态密度分布 3.1.瞬态密度分布 图3(a) 为基于NPLS技术的超声速流动密度场测量技术得到的某一时刻$Ma$ = 3.0湍流边界层流向平面的密度场, 测量范围为: $x/\delta $ = 0—2, $y/\delta $ = 0—1.5, 流动方向从左往右, 坐标系原点位于喷管出口下游180 mm处. 从图3(a) 可以看到, 靠近壁面处的边界层密度较低, 延y 方向越靠近主流, 边界层密度增大的趋势越明显, 边界层内密度分布存在明显非均匀性, 这是湍流本身非定常性的一个显著特征. 对200组瞬态密度场结果进行统计平均, 得到湍流边界层平均密度场, 用瞬态密度场减去平均密度场, 得到该时刻对应的密度脉动云图如图3(b) 所示, 可以看到边界层内部存在局部高密度区域, 边界层外的主流也存在局部低密度区域, 体现了主流与湍流边界层之间的物质与能量输运. 以边界层近壁区$y/\delta $ = 0.1高度作为采样线为例, 在消除窗口背景、片光不均匀等因素影响后, 通过斜激波校准法[41 ] , 得到灰度-密度函数关系式, 通过采样线上每个像素的灰度即可以得到该点处的密度, 用瞬态密度减去平均密度场, 消除由于不同高度密度不同引起的密度脉动误差, 得到采样线高度的瞬态密度脉动空间分布曲线, 利用泰勒假设转换为时间分布曲线如图4 所示, 坐标转换方式为图 3 $Ma$ = 3.0湍流边界层流向剖面 (a) 瞬态密度场; (b) 瞬态密度脉动Figure3. Flow profile of turbulent boundary layer at $Ma$ = 3.0: (a) Instantaneous density field; (b) instantaneous density fluctuation.图 4 密度脉动时间分布曲线($y/\delta $ = 0.1)Figure4. Time distribution curve of density fluctuation ($y/\delta $ = 0.1).${u_{\rm{c}}}$ 为当地高度流动速度.${\rm{d}}x$ 为拟序结构在双腔CCD相机拍摄时间间隔${\rm{d}}t$ 内的位移, ${P_{{\rm{re}}}}$ 为图像分辨率, 该高度采样频率${f_{\rm{s}}}$ 为33 MHz.3.2.密度脉动多分辨率分析 -->3.2.密度脉动多分辨率分析 使用2.2.1 节的正交小波方法将密度脉动分解为6个尺度分量, Level 1—Level 6分别代表大尺度到小尺度6个等级, 同时对各尺度分量密度脉动进行功率谱估计, 如图5 所示. 经计算, 各尺度分量重构信号与原始信号之差不超过10–10 , 误差源于计算精度, 可认为各尺度小波分量包含原始信号的所有信息. 从图5 可以看到, 不同尺度分量对密度脉动的贡献不同, 较大尺度(Level 1, Level 2)的密度脉动幅值比最小尺度(Level 6)的密度脉动幅值大一个量级, 计算发现这两个尺度分量对原始信号密度脉动幅值贡献超过96%; 对其进行概率密度分布统计, 结果如图6 所示. 从图6 可以看到最大两个尺度Level 1与Level 2分量之和的概率密度分布已经接近原始信号的概率密度分布, 表明大尺度分量对湍流边界层密度脉动起主导作用. 此外, 原始信号与大尺度分量概率密度分布最大的区别在于密度脉动–3—0.5 g·m–3 区间, 表明该区间内Level 3—Level 6密度脉动构成的小尺度分量对原始信号概率密度分布产生显著影响, 使其呈“M型”分布, 这一结果与Zheng和Jiang[18 ] 分析低速湍流边界层的压力脉动信号得到的结果类似, 认为是脉动信号的间歇性所导致, 具体原因有待进一步研究. 对原始信号进行高斯拟合, 平坦因子为3.2, 偏斜因子为0.7, 对称中心为–1.2, 结果表明$y/\delta $ = 0.1高度密度脉动标量的统计结果呈现偏离高斯分布; 湍流统计的经典观点认为湍流标量呈高斯分布, 但近年来Eswaran和Pope[42 ] , Antonia和Mi[43 ] 的研究发现温度标量呈偏离高斯分布, 本文研究结果表明湍流边界层近壁区的密度脉动标量统计结果同样呈现偏离高斯分布.图 5 密度脉动信号多分辨率分析 (a)?(f) Level 1?Level 6代表组成原始信号6个不同尺度的分量Figure5. Multiresolution analysis of density fluctuation signal: (a)?(f) Level 1?Level 6 represent 6 different sacles’s components of original signal.图 6 原始信号和Level 1 + Level 2的概率密度函数Figure6. Probability density function (PDF) of the original signal of density fluctuation and Level 1 + Level 2.图5 的时间轴, 可以发现t = 0.5 × 10–5 s时Level 3—Level 5, t = 1.4 × 10–5 s时Level 2—Level 4等处密度脉动信号表现出明显的幅度调制效应, 本文使用He等[38 ] 的方法对大小尺度间的调制作用进行分析. 如图7(a) 所示, 大尺度分量${d_{\rm{L}}}$ 与前文相同, 由Level 1和Level 2构成, 小尺度分量${d_{\rm{S}}}$ 由Level 3—Level 6重构得到; 图7(b) 使用希尔伯特变换提取小尺度分量${d_{\rm{S}}}$ 包络, 通过滤波得到低通滤波包络${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ ; 图7(c) 对比低通滤波包络${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ 与大尺度分量${d_{\rm{L}}}$ , 可以看到${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ 与${d_{\rm{L}}}$ 显示出很高的正相关性, 这与Mathis等[35 ,36 ] 在不可压近壁湍流边界层中发现的结果相同, 表明在超声速湍流边界层$y/\delta $ = 0.1高度, 外层正(或负)的大尺度密度偏移同样会导致内层近壁处的小尺度密度脉动的局部增强(或减弱).图 7 幅度调制效应分析 (a) 大尺度分量${d_{\rm{L}}}$ 与小尺度分量${d_{\rm{S}}}$ ; (b) 小尺度分量${d_{\rm{S}}}$ 与低通滤波包络${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ ; (c) 大尺度分量${d_{\rm{L}}}$ 与低通滤波包络${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ (为方便比较, 将${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ 平均值调整到0线并放大2倍)Figure7. Analysis of amplitude modulation effects: (a) Large scale component ${d_{\rm{L}}}$ and small scale component ${d_{\rm{S}}}$ ; (b) small scale component ${d_{\rm{S}}}$ and low-pass filtered envelope ${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ ; (c) comparison between large scale component ${d_{\rm{L}}}$ and low-pass filtered envelope ${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ (for comparison, adjust the average of ${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ to the zero-line and magnify the magnitude by a factor of 2).图5(f) 所示最小尺度分量Level 6, 可以发现该尺度幅值小, 脉动明显比其他尺度分量均匀, 主要反映了实验所用纳米粒子对成像的影响. 对于正交小波多分辨率分析, 其分解本质上是一个2倍下采样的过程, 其中最小尺度Level 6反映了原始密度场与1/2分辨率密度场(22.8 μm/pixel)在细节上的差别. 赵玉新等[16 ] 采用相同的方法对超声速混合层拟序结构进行分析, 认为最小尺度分量的脉动信号实际上就是实验中单个纳米粒子成像信号在采样线上的分布. 此外从图5 右侧各尺度分量的功率谱估计可以看到, 不同尺度的脉动频率分布不同, 大尺度以低频为主, 脉动的频率范围比较集中, 比如Level 1分量脉动频段主要集中在0.004—0.25 MHz; 尺度越小, 脉动频率越高, 频率范围越广, 最小尺度脉动频段已经覆盖了7— 16 MHz. 总体来说, 边界层$y/\delta $ = 0.1高度具有较宽的频率范围, 最高可达10 MHz量级, 但功率谱密度估计显示, 从图5(c) 第3个尺度分量Level 3开始, 功率谱密度幅值已经小于最大尺度分量2个量级以上, 意味着更小尺度分量脉动功率对总体密度脉动所起的作用可能比较有限.3.3.基于小波变换的密度脉动时变谱分析 -->3.3.基于小波变换的密度脉动时变谱分析 为了更加直观体现密度脉动所含频率及其随时间的变化特性, 进一步采用基于小波变换的时变谱密度估计方法对边界层$y/\delta $ = 0.1密度脉动信号进行分析, 图8(a) 和图8(b) 为基于傅里叶变换的功率谱估计与基于小波变换的时变谱密度估计. 通过2.3 节的验证, 可以看到在数值上功率谱近似于时变谱在频率轴方向上的投影; $y/\delta $ = 0.1高度密度脉动主要分布在1 MHz以内, 与前文的分析相符, 图8(a) 功率谱密度在6.3 × 104 和1.2 × 105 Hz附近存在两个峰值, 在图8(b) 时变谱可以观察到与之对应的两条频带.图 8 密度脉动的谱分析($y/\delta $ = 0.1) (a) 基于傅里叶变换的功率谱密度估计; (b) 基于小波变换的时变谱密度估计Figure8. Spectrum analysis of density fluctuation ($y/\delta $ = 0.1): (a) Power spectrum based on Fourier transform; (b) time-varying power spectrum based on wavelet transform.图8(a) 可以看到, 基于傅里叶变换的功率谱默认信号平稳, 失去密度脉动与频率相关的时间信息, 而图8(b) 基于小波变换的时变谱可以清楚反映非平稳信号能量随频率与时间的变化过程. 结合时间轴可以看到时变谱最左侧2 × 104 Hz处有少量的低频脉动, 时间延续较长, 在20 μs处出现, 约30 μs处消失, 在40 μs处再次出现; 在时变谱右侧5 × 105 Hz附近, 有少量的瞬时高频脉动, 时间上不连续, 出现后随即消失, 体现湍流边界层非定常的特点; 在时变谱中间0.5 × 105 —3 × 105 Hz频段的密度脉动, 该频段谱密度大, 包含的脉动能量高, 持续时间基本历经全程, 而且具有明显的间歇性, 在湍流边界层$y/\delta $ = 0.1处的密度脉动中起主导作用. 此外, 主导频段的谱密度幅值等高线呈现为倾斜的椭圆, 反映边界层内密度脉动随时间变化有一个转移的过程, 以图8(b) 中A 点脉动为例, 1.7 × 105 Hz频率的脉动在时间轴19 μs处率先发生, 谱密度幅值约0.2 × 10–4 g2 ·m–6 ·Hz–1 , 随后谱密度逐渐增加, 于21 μs时在1.3 × 105 Hz处达到峰值1.5 × 10–4 g2 ·m–6 ·Hz–1 , 增长近8倍, 此时频率和谱密度幅值与图8(b) 1.2 × 105 Hz处功率谱峰值对应, 随着时间推移, 脉动的频率和谱密度逐渐减少, 直至23 μs时在0.93 × 105 Hz处消失, 体现主导频段内密度脉动从高频过渡低频, 幅值先增加后减少的特点.图8(b) 主导频段截取相近频率(60 ± 3) kHz和(113 ± 5) kHz的谱密度幅值, 结果如图9 所示, 谱密度幅值随时间变化的先后情况可以反映脉动频率随时间的变化, 其中谱密度峰值的大小与频率所处高频过渡低频的阶段有关, 此处不做讨论. 观察图9(a) 频率(60 ± 3) kHz的谱密度幅值, 可以看到其中频率较高的63 kHz谱密度幅值多次率先增大并到达峰值, 而后依次是60和57 kHz, 随后63 kHz谱密度幅值先减小, 再依次是60和57 kHz; 图9(b) 是频率较高的118 kHz谱密度幅值先增大与减小, 再依次是113和108 kHz, 相近频率的谱密度幅值变化顺序同样体现了$y/\delta $ = 0.1高度主导频段的脉动从高频过渡低频的特点.图 9 相近频率的时变谱密度 (a) (60 ± 3) kHz; (b) (113 ± 5) kHzFigure9. Time-varying power spectrum of approximate frequency: (a) (60 ± 3) kHz; (b) (113 ± 5) kHz.图10 分别为$y/\delta $ = 0.4, 0.7, 1.0高度的密度脉动时变谱. 因为不同高度的数据来源于同一张拍摄图像, 因此各高度脉动时变谱密度具有时间相关性. 从总体上看, 湍流边界层同一时间段内各高度的密度脉动频率都主要分布在1 MHz以内, 主导频段的密度脉动间歇性明显, 大部分存在与$y/\delta $ = 0.1高度类似的高频过渡低频, 谱密度先增后减的现象.图 10 不同高度的密度脉动时变谱 (a) $y/\delta $ = 0.4; (b) $y/\delta $ = 0.7; (c) $y/\delta $ = 1.0Figure10. Time-varying power spectrum of density fluctuation at different heights: (a) $y/\delta $ = 0.4; (b) $y/\delta $ = 0.7; (c) $y/\delta $ = 1.0.图10(a) —(c) 不同边界层高度的密度脉动时频分布存在较大差别. $y/\delta $ = 0.4高度脉动主要分布在105 Hz频段以内; $y/\delta $ = 0.7高度则主要集中在105 Hz以上, 同时谱密度幅值较$y/\delta $ = 0.4增长了一倍; 到$y/\delta $ = 1.0边界层与主流交界处, 谱密度幅值已经降低一个量级. 密度脉动能量从近壁面到主流区先升高后降低的变化规律, 一方面是由于黏性作用, 导致边界层近壁面速度较低, 相应的脉动能量会比较小, 另一方面是因为主流区域速度虽高, 但流场稳定, 相对脉动较小, 因此在湍流边界层中间会有一个密度脉动能量相对较高的区域.图10(c) 中$y/\delta $ = 1.0高度时变谱, 时间轴前半段几乎没有脉动分布, 对比图3(b) 中$Ma$ = 3.0湍流边界层瞬态密度脉动云图, 可以看到图像在边界层$y/\delta $ = 1.0高度前半段以主流为主, 密度脉动较为均匀, 直到后半段开始出现主流与边界层之间相互作用形成的大尺度结构, 所以图10(c) 时变谱在时间轴后半段才开始出现谱密度幅值变化, 这也从侧面说明了小波方法分析密度脉动的准确性. 因为湍流边界层外层结构速度快, 对应的脉动频率增加, 因此在$y/\delta $ = 1.0高度时变谱可以看到频率达到3 × 106 Hz的脉动存在; 至于低频部分, 考虑到主流区靠近大尺度结构区域存在密度输运, 该区域可能存在少量密度变化且相对均匀, 所以密度变化相对较小, 从频率上反映为更多低频信号的出现. 这也从另外一个方面说明, 由于超声速湍流边界层强烈的非定常性, 不同时刻瞬态密度脉动特性分析结果可能存在差别, 未来应分析更多实验样本, 归纳超声速湍流边界层密度脉动普遍规律.4.结 论 本文以$Ma$ = 3.0平板湍流边界层流向密度场实验数据为基础, 利用泰勒假设将密度脉动空间信号转化为时间信号, 针对常规统计方法难以获得湍流的时变信息与动态特性的不足, 采用正交小波变换对密度脉动进行多尺度分析, 概率密度分布与功率谱结果表明不同尺度分量对密度脉动贡献不同, 大尺度分量对湍流边界层密度脉动起主导作用, 其他的小尺度分量主要对密度脉动的概率密度分布结果产生影响, 使之呈“M”型分布, 统计结果表明密度脉动标量呈偏离高斯分布; 采用希尔伯特变换分析了大小尺度之间的幅度调制效应, 小尺度分量的低通滤波包络与大尺度分量显示出高度正相关性, 表明超声速湍流边界层近壁处外层的大尺度密度偏移会导致内层小尺度密度脉动的局部增强或减弱.$Ma$ = 3.0湍流边界层密度脉动主要分布在1 MHz以内, $y/\delta $ = 0.1高度密度脉动主要分布在0.5 × 105 —3 × 105 Hz, 在0.63 × 105 和1.2 × 105 Hz附近频段存在两个峰值, 同时含有少量的瞬时高频脉动, 出现后随即消失, 符合湍流边界层非定常的特点. 主导频段的密度脉动间歇性明显, 大部分脉动存在从高频过渡到低频, 谱密度先增加后减少的变化规律.5 Hz以下, 尾迹区则集中在105 Hz以上, 边界层与主流交界处的脉动主要分布在两者相互作用形成的大尺度结构附近; 壁面约束与黏性作用使近壁面速度较低, 密度脉动相对较小, 靠近主流区的边界层速度虽高但流场均匀, 脉动同样相对较小, 从而形成了密度脉动能量从近壁面到主流区先升高后降低的变化规律. 








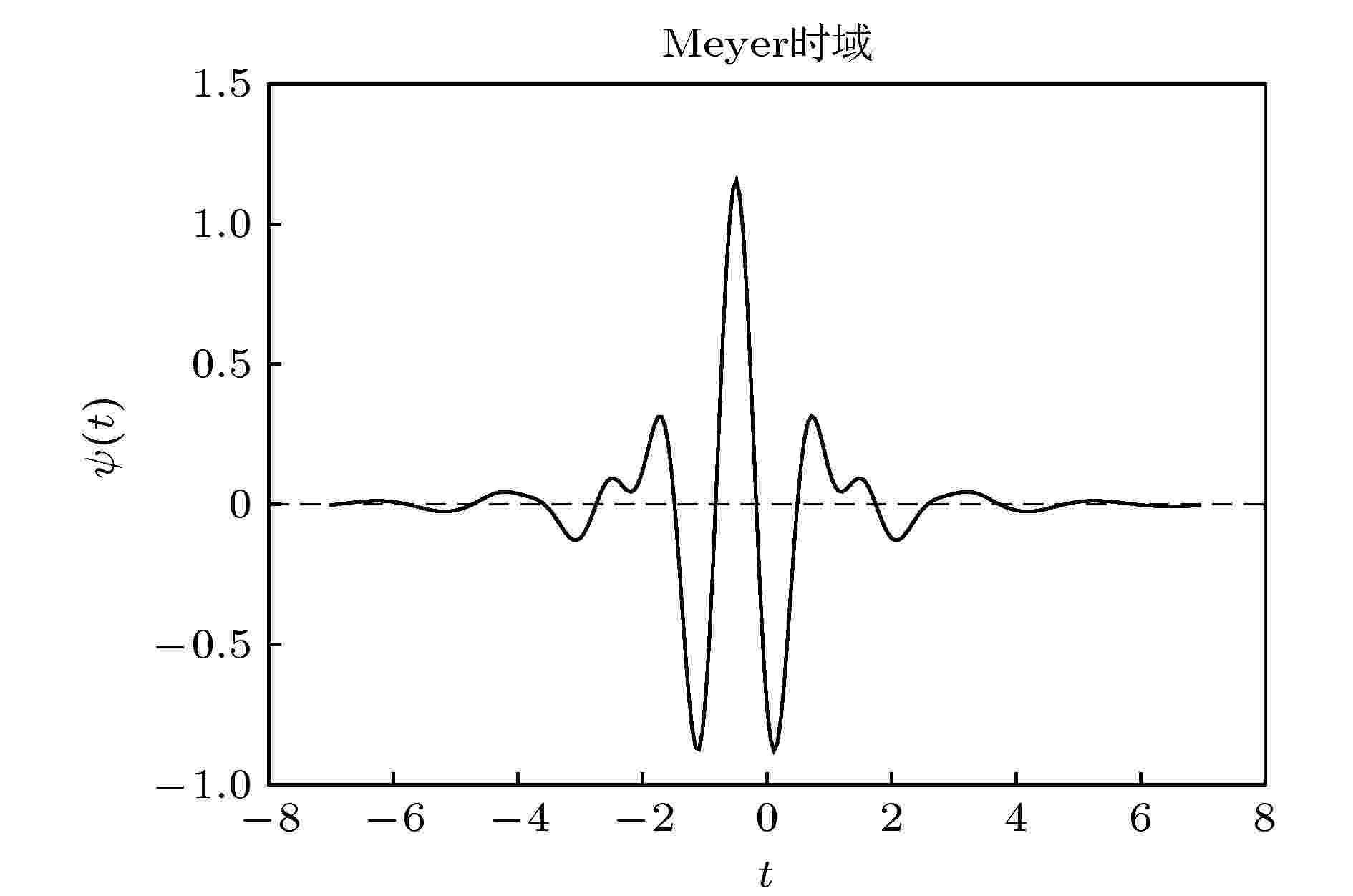 图 1 Meyer小波频域定义与时域波形
图 1 Meyer小波频域定义与时域波形






























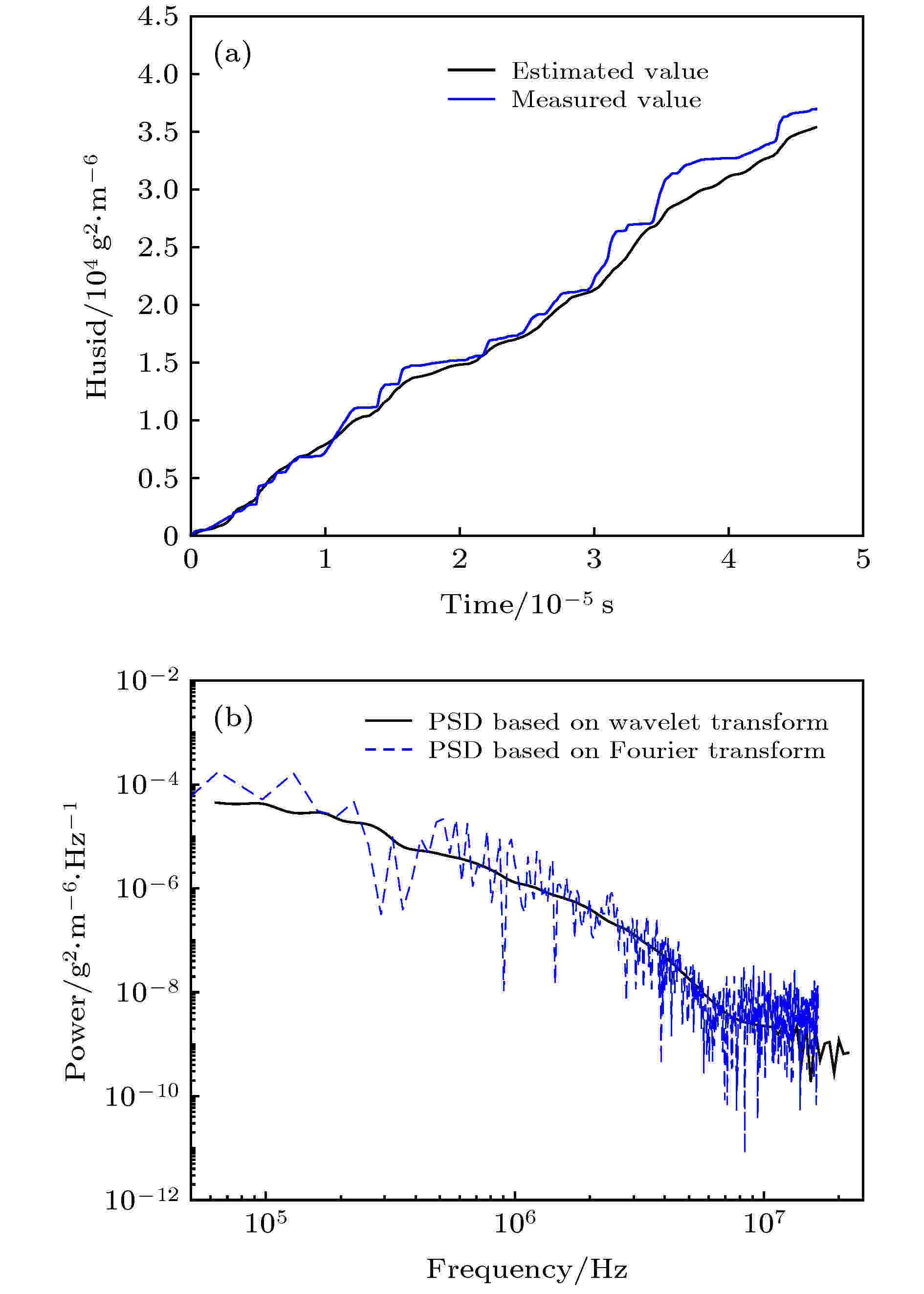 图 2 时频域有效性验证 (a) 密度脉动累积能量曲线; (b) 密度脉动功率谱估计
图 2 时频域有效性验证 (a) 密度脉动累积能量曲线; (b) 密度脉动功率谱估计





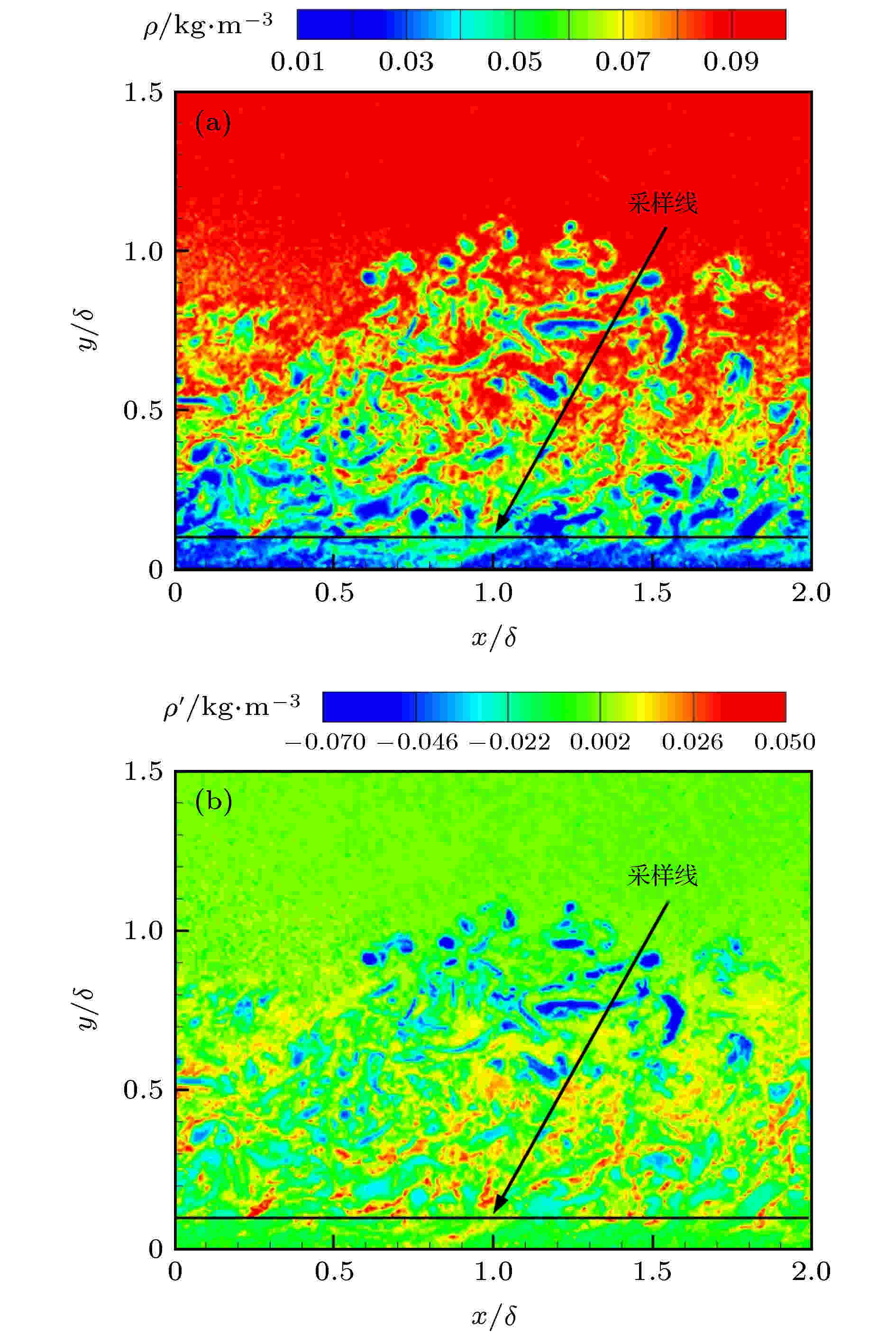 图 3
图 3 

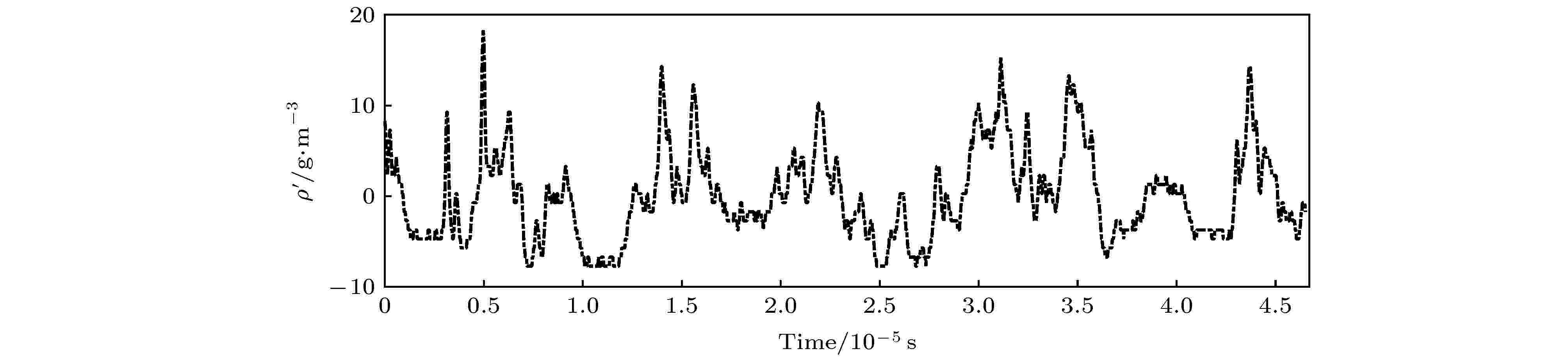 图 4 密度脉动时间分布曲线(
图 4 密度脉动时间分布曲线(







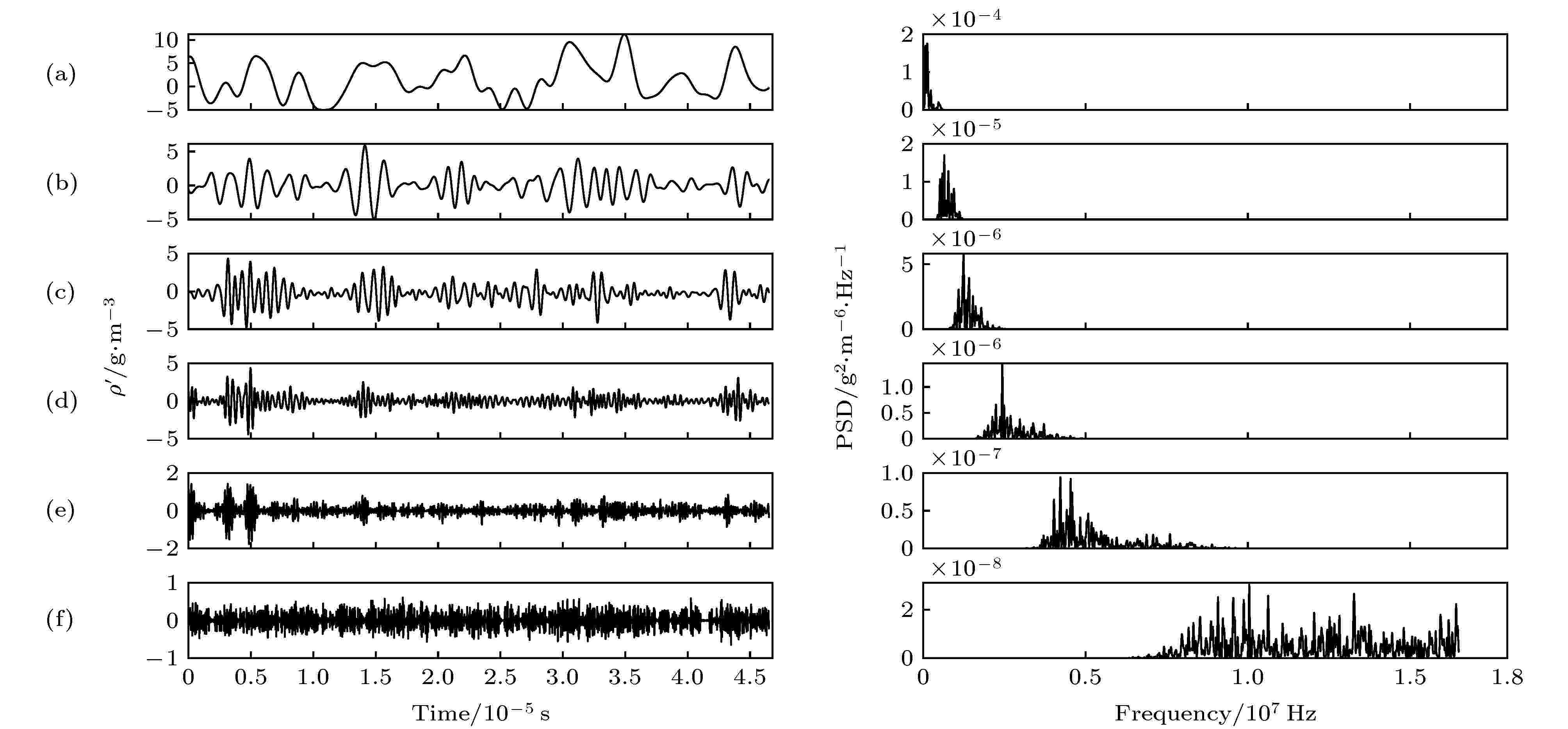 图 5 密度脉动信号多分辨率分析 (a)?(f) Level 1?Level 6代表组成原始信号6个不同尺度的分量
图 5 密度脉动信号多分辨率分析 (a)?(f) Level 1?Level 6代表组成原始信号6个不同尺度的分量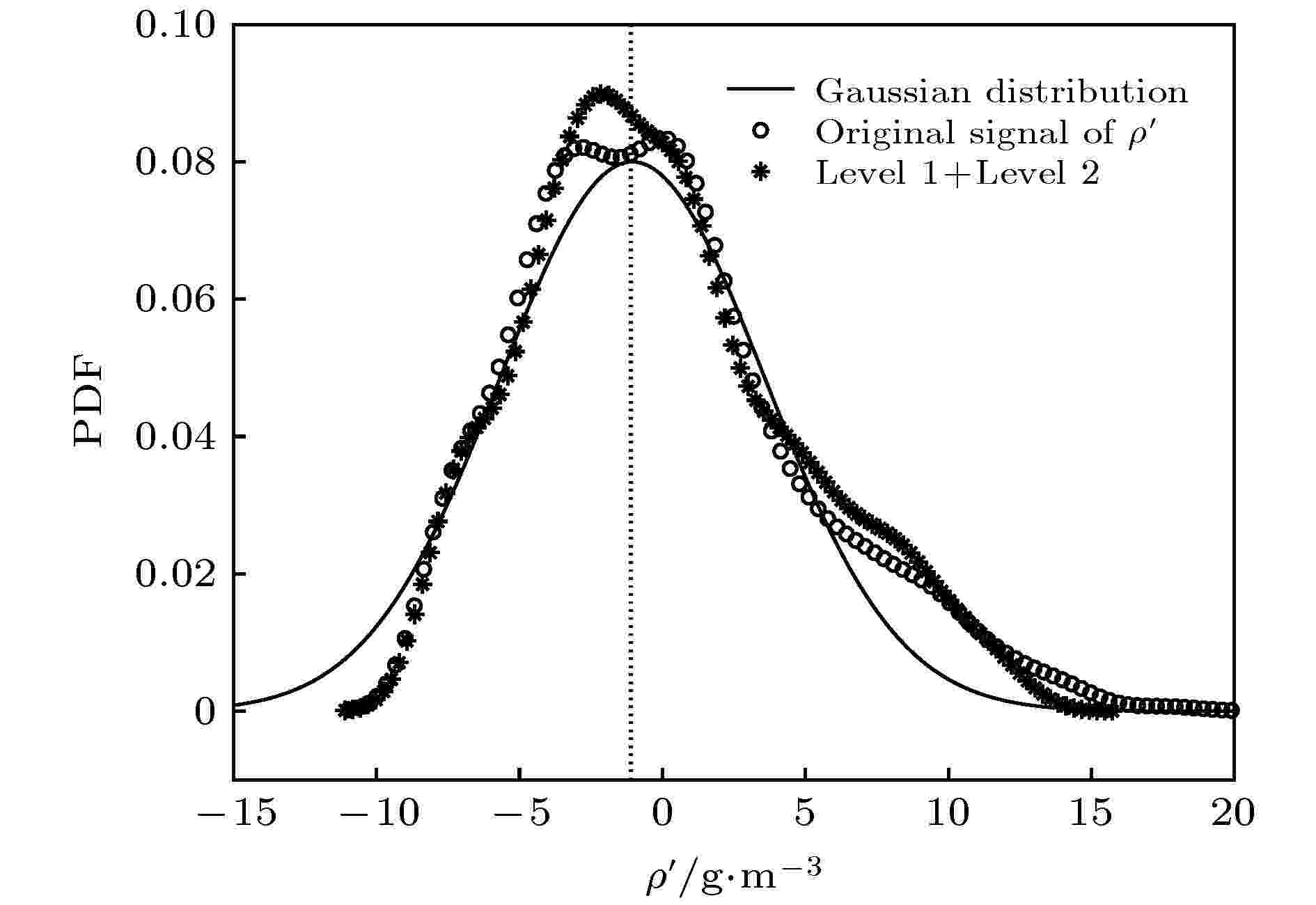 图 6 原始信号和Level 1 + Level 2的概率密度函数
图 6 原始信号和Level 1 + Level 2的概率密度函数






















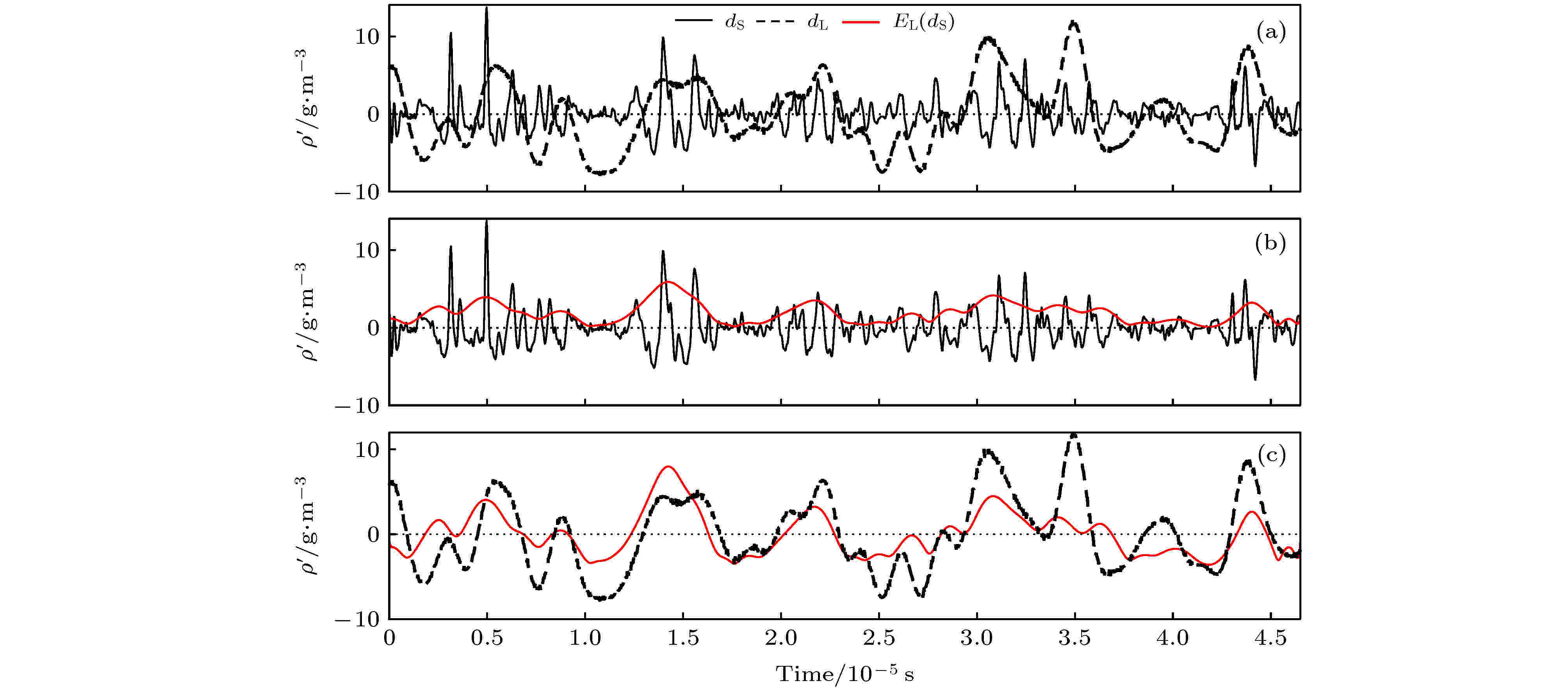 图 7 幅度调制效应分析 (a) 大尺度分量
图 7 幅度调制效应分析 (a) 大尺度分量






































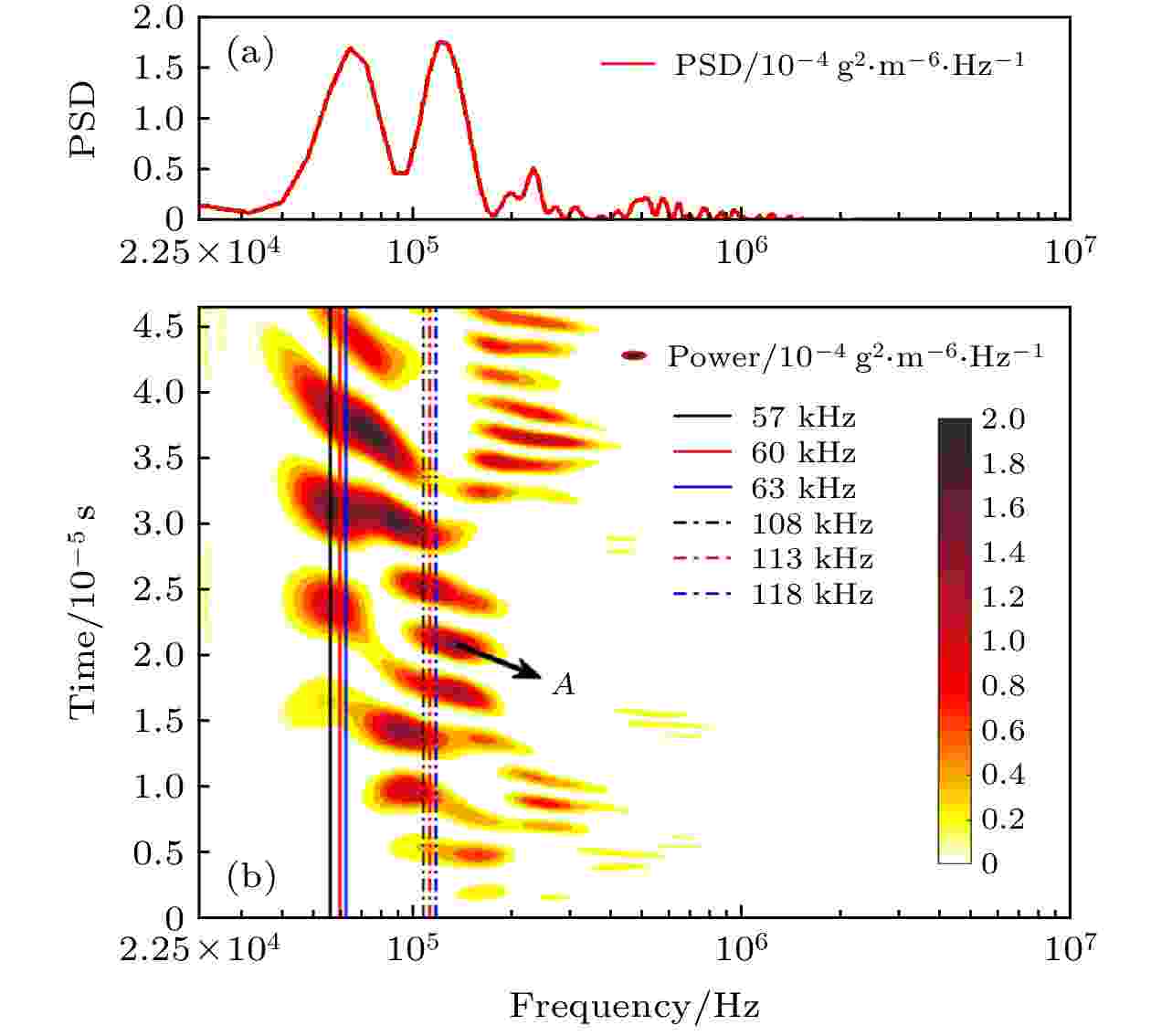 图 8 密度脉动的谱分析(
图 8 密度脉动的谱分析(



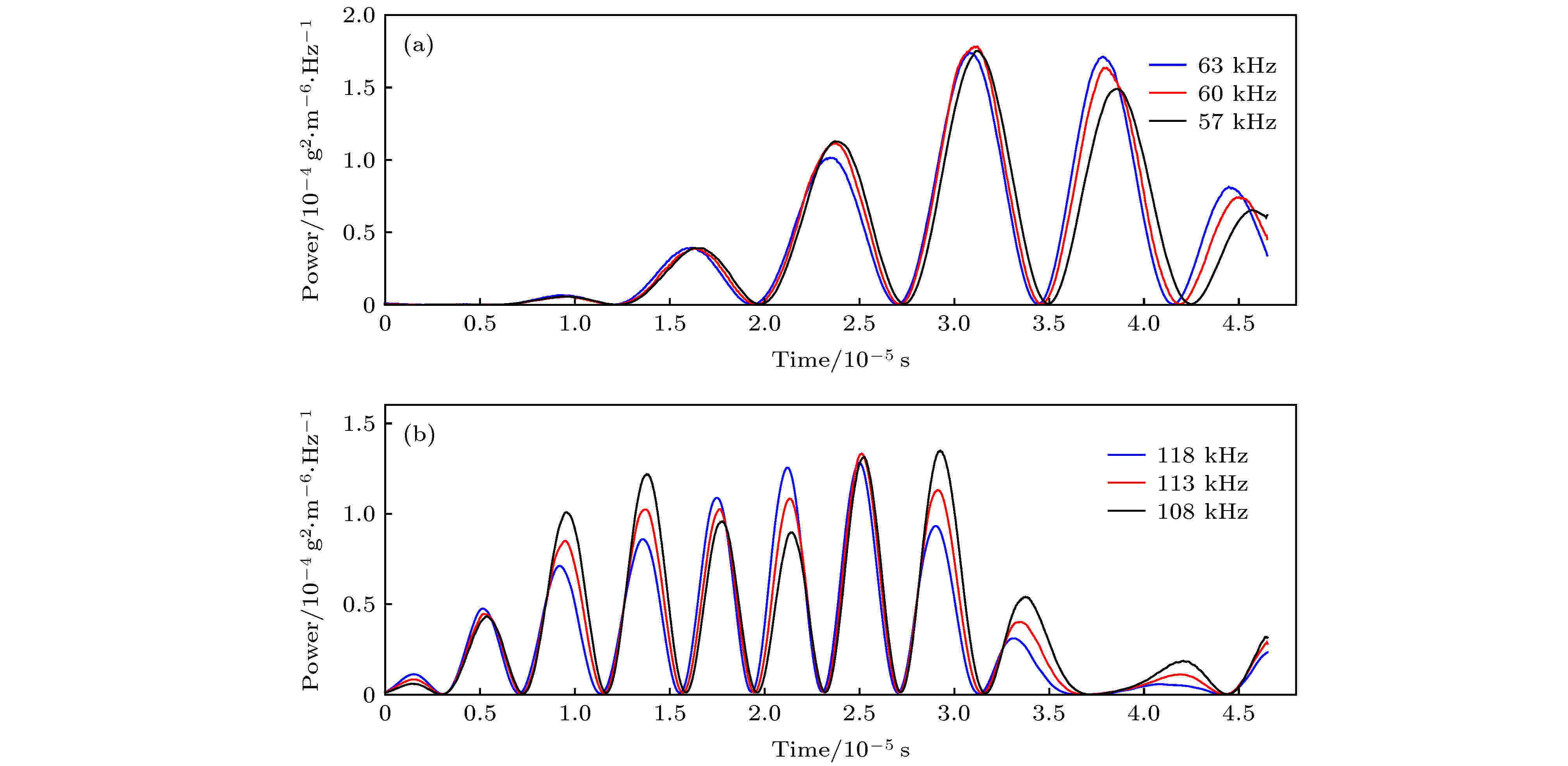 图 9 相近频率的时变谱密度 (a) (60 ± 3) kHz; (b) (113 ± 5) kHz
图 9 相近频率的时变谱密度 (a) (60 ± 3) kHz; (b) (113 ± 5) kHz



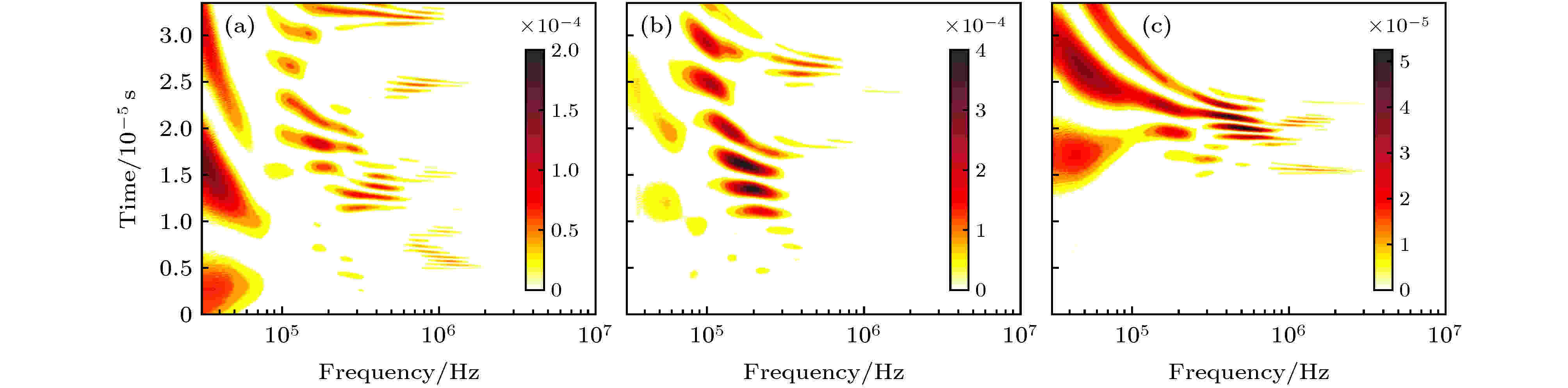 图 10 不同高度的密度脉动时变谱 (a)
图 10 不同高度的密度脉动时变谱 (a) 














































