摘要:电磁场的汇聚与增强是电磁学中一个重要的研究内容, 具备场汇聚与增强特性的电磁(光学)器件在高方向性电磁天线、激光点火、光学调控等方面有着广泛的应用前景. 目前, 电磁场增强的途径主要有两种, 一是采用构造人工电磁材料结构以实现辐射方向的控制和能量集中, 其次是采用具有高介电常数或高磁导率的材料来实现电磁场增强, 但是上述两种方式应用在光学波段具有一些局限性. 本文基于光子晶体掺杂理论, 通过介质掺杂近零媒质的方式成功实现了光场增强功能. 理论分析和数值仿真计算表明所设计的结构能够显著实现场强增强, 并适用于微波至光波波段, 应用频谱范围很宽. 作为应用探索, 本文还设计了一款工作在270 nm波长的紫外光波段点火装置. 上述工作为新型电磁(光学)器件的研制提供了新的思路.
关键词: 近零媒质/
介质掺杂/
电磁场增强

English Abstract

全文HTML

--> --> -->

场增强效应是电磁学中一个重要的研究内容. 具备场增强特性的电磁(光学)器件在激光点火、强方向性天线设计、光学调控等方面有着广泛的应用前景^[1]. 例如, 在高能物理国家激光点火项目中需要将192束激光束聚焦到一个厘米级大小的点火点上. 要将这些激光束同相聚焦于一点, 难度非常大, 所以该项目采用非常复杂的光学布局. 因此, 设计结构简单且具有高倍增强性能的光学系统成为激光点火领域的重要发展方向之一, 这也为场增强特性光学器件提供了很好的应用平台.
目前, 场增强的主流方法主要有两种: 一是采用人工电磁材料(metamaterial)构造周期结构对辐射的电磁能量进行控制和集中, 从而令通过该结构的电磁辐射具有尖锐的方向图, 该方法主要应用于高方向性天线设计, 应用频率比较低, 难以直接应用于光学频段^[2-9]; 另一种方法是采用具有高介电常数或高磁导率的材料来实现材料内部电磁场的汇聚与增强^[10-17], 此方法对于材料内部辐射点源位置和材料截面积的变化极其敏感, 并严重依赖材料的相对介电常数ε_r或相对磁导率μ_r的数值, 即当ε_r (μ_r)越大时, 材料中心场的增强才越高, 但极限增强倍数为材料相对介电常数值(ε_r)的3/4次方^[18]. 例如一个包含辐射点源的ε_r = 9的圆截面二维介质, 其圆截面中心场相比辐射源场增强了6倍, 所以材料电磁参数严重限制其场增强的效果, 显然无法满足激光点火等用途.
近年来的研究发现, 零折射率材料也具有良好的场汇聚与增强效应. 例如, 文献[19]提到近零磁导率(mu-near-zero, MNZ)材料环包围线电流的辐射场可以根据具体的几何结构得到增强或完全抑制. 但是MNZ材料难以实际制备, 且应用频率较低, 应用范围极其有限^[19-23]. 从材料实现和更宽的应用频率角度出发, 近年来研究重点转移到利用近零介电(epsilon-near-zero, ENZ)材料媒质实现内部场增强效应上^[24-30]. 上述工作对ENZ媒质实现场增强效应从理论上提供了许多启示, 但实用性方面指导仍显不足.
本文首先通过理论分析计算介质掺杂的ENZ媒质中电磁场的分布, 得出该结构中掺杂介质的中心场与ENZ媒质中场的比例关系, 并根据理论计算结果, 从实用性角度出发, 首次提出当该结构作为场强增强器件时所应满足的等效状态; 其次, 在结构满足该等效状态时, 从多方面对该结构的场强增强性能进行分析和全波数值仿真分析验证, 表明该结构能够非常显著地增强外部入射场强, 其场增强倍数完全满足激光点火等高场强应用需求, 并且在结构设计上具有很好的灵活性, 且适用于微波至光波波段的宽频谱范围; 最后, 作为实际应用探索, 设计了一款工作在270 nm紫外光波段的场增强装置. 本文工作为新型电磁(光学)点火器件的研制提供了新的思路.

为简化分析, 这里仅考虑二维(2D)的情况, 如图1所示. 图1(a)给出了一个截面积为S, 截面形状任意的2D ENZ介质, 该介质具有任意的相对磁导率μ_r0. 一个相对介电常数为ε_rd, 相对磁导率为μ_rd, 截面积为S_d的介质圆柱沿y轴嵌入该ENZ媒质中, 位置任意. 掺杂后ENZ媒质的横截面积可以表示为${S_0} = S - {S_{\rm{d}}}$. 假设该ENZ媒质中有一个交变的磁流源I_M, 受I_M的激励, ENZ媒质中分别存在磁场H₁和电场E₁, 其中磁场H₁沿着y轴方向, 且在ENZ媒质中均匀分布, 电场E₁则位于xoz面内. 同时在嵌入的介质柱内, 也会激励起电场和磁场, 分别设为H_d和E_d. 另外, 设ENZ媒质边缘的切向电场为E_t.
图 1 ENZ介质掺杂介质结构等效示意图(2D截面) (a) ENZ媒质掺杂介质结构截面图, 存在一个与截面垂直的磁流I_M; (b) 具备相同截面大小的等效ENZ介质示意图, 在该截面相同的位置存在一个与图(a)相同的的磁流I_M
Figure1. Schematics of magnetic ENZ medium filled with dielectric dopants: (a) A 2D magnetic ENZ medium with several macroscopic non-magnetic dielectric dopants and an alternating magnetic current I_M embedded in the ENZ medium whose magnetic field H₁ is polarized along y axis; (b) the equivalent homogeneous 2D ENZ medium with the same cross-sectional shape and near-zero permittivity, but a uniform equivalent relative permeability μ_eff

根据ENZ媒质的掺杂理论^[31], 图1(a)结构可等效为一个具有相同横截面的均匀ENZ介质, 其等效相对磁导率为μ_eff, 如图1(b)所示. 考虑此时该等效ENZ媒质中同样位置上有一相同的磁流激励源I_M, 则在图1(b)所示的结构中也将分别激励出磁场H₂和电场E₂. 上述等效假设能够保证图1(a)和图1(b)的结构具有相同的外辐射场, 同时各自边界上的切向电场也将相等. 而由于两个ENZ媒质中的磁场都是均匀的, 所以有H₁ = H₂.
令上述两个结构的边界曲线长度均为l, 对于图1(a)的结构有

$\begin{split}\oint\nolimits_{{l}} {{{{E}}_{\rm{t}}}} \cdot {\rm{d}}{{l}} =\; &\int\nolimits_{S} {\left( {\nabla \times {{{E}}_1}} \right) \cdot } {\rm{d}}{{S}} \\ =\;&- \int\nolimits_{{{S}_0}} {{\rm{j}}\omega {\mu _{{\rm{r}}0}}{\mu _0}{{{H}}_1} \cdot {\rm{d}}{{{S}}_0}} \\&-\int\nolimits_{{{S}_{\rm{d}}}} {{\rm{j}}\omega {\mu _{{\rm{rd}}}}{\mu _0}{{{H}}_{\rm{d}}} \cdot {\rm{d}}{{{S}}_{\rm{d}}}} - {{{I}}_{\rm{M}}},\end{split}$

对于图1(b)的结构有

$\begin{split}& \oint\nolimits_{{l}} {{{{E}}_{\rm{t}}}} \cdot {\rm{d}}{{l}} = \int\nolimits_{S} {\left( {\nabla \times {{{E}}_2}} \right) \cdot} {\rm{d}}{{S}} \\ = & - \int\nolimits_{S} {{\rm{j}}\omega {\mu _{{\rm{eff}}}}{\mu _0}{{{H}}_2} \cdot {\rm{d}}{{S}}} - {{{I}}_{\rm{M}}},\end{split}$

由于图1(a)和图1(b)的结构等效, 因此在两者各自穿过其横截面的磁通量应相等, 所以根据(1)式和(2)式, 有

${\mu _{{\rm{eff}}}}{\mu _0}{{{H}}_2} \cdot {{S}} \!=\! {\mu _{{\rm{r}}0}}{\mu _0}{{{H}}_1} \cdot {{{S}}_0} \!+\! \int\nolimits_{{S_{\rm{d}}}} {{\mu _{{\rm{rd}}}}{\mu _0}{{{H}}_{\rm{d}}} \cdot } {\rm{d}}{{{S}}_{\rm{d}}}.$

图1(a)中掺杂介质柱内的磁场H_d与ENZ媒质中的磁场H₁的关系为${{{H}}_{\rm{d}}} = {{{H}}_1}{\psi _{\rm{d}}}(r)$, 这里ψ_d(r)是标量Helmholtz方程的解^[31], 反映的是介质内部场与ENZ介质中场的比例关系, 且介质界面S_d的边界上ψ_d(r) = 1. 此处有^[31]

${\psi _{\rm{d}}}({{r}}) = \frac{{{{\rm{J}}_0}({{{k}}_{\rm{d}}}{{r}})}}{{{{\rm{J}}_0}({{{k}}_{\rm{d}}}{{{r}}_{\rm{d}}})}}, $

这里J₀表示零阶第一类圆柱Bessel函数, k_d是掺杂介质中的波数, 0 ≤ r ≤ r_d, r_d为圆柱截面半径.
(4)式说明掺杂介质内部的场是波动的, 且在中心点(r = 0)处达到最强, 即在该点体现出磁场汇聚现象, 这一点与文献[18]的结论一致. 另外, 从(1)式可得出一个重要结论, 即该结构对外辐射电场的切向分量沿着ENZ媒质边缘的环路积分应等于整个结构截面的总磁通量. 因此, 如果该结构无法对外形成有效辐射, 即ENZ媒质边缘的切向电场E_t很小或为零, 则整个结构截面的总磁通量也将很小, 从应用角度来说, 就无法形成有效的内部磁场增强效应. 所以, 为形成明显的场增强效应, 首先应保证该结构处于有效的对外辐射状态, 这样才能保证结构截面内的磁场也很强. 根据上述分析, 从实际应用角度出发, 当掺杂介质的ENZ媒质结构处于等效电磁参数近零(epsilon-mu-near-zero, EMNZ)媒质时, 其磁场增强效应是最具有实际意义的. 当该结构为等效EMNZ媒质时, ENZ区域内的场与辐射源场(或外部辐射场)一致, 因此(4)式可有效地计算该结构中嵌入介质内部对辐射源(入射场)的场增强效果, 这一点对于电磁点火装置而言最具有应用价值.

本节将根据上节的理论分析, 在介质掺杂的ENZ媒质结构等效为EMNZ媒质的前提下, 计算并分析验证其在不同条件下对辐射源的场增强效果.
2

-->

3.1.ENZ媒质内掺杂单一介质

在无耗情况下, 作为分析实例, 设ENZ媒质的横截面积为2.5$ \lambda_0^2 $ (λ₀为电磁波在自由空间中的波长, 横截面积可以任意选择). 理论分析中, ENZ媒质的磁导率可以任意取值, 考虑光学波段ENZ媒质一般为非磁性, 故设定ENZ媒质相对磁导率μ_r = 1. 在该ENZ媒质嵌入一半径为r_d的非磁性介质圆柱, 其相对介电常数ε_r1 = 6.
通过(3)式计算可得到ENZ媒质在介质掺杂后其等效磁导率μ_eff随其半径变化的曲线(图2). 可见随掺杂介质半径变化, 整个结构的等效磁导率曲线呈现明显的周期性谐振. 在每个谐振峰附近, 都存在一个μ_eff接近零的点.
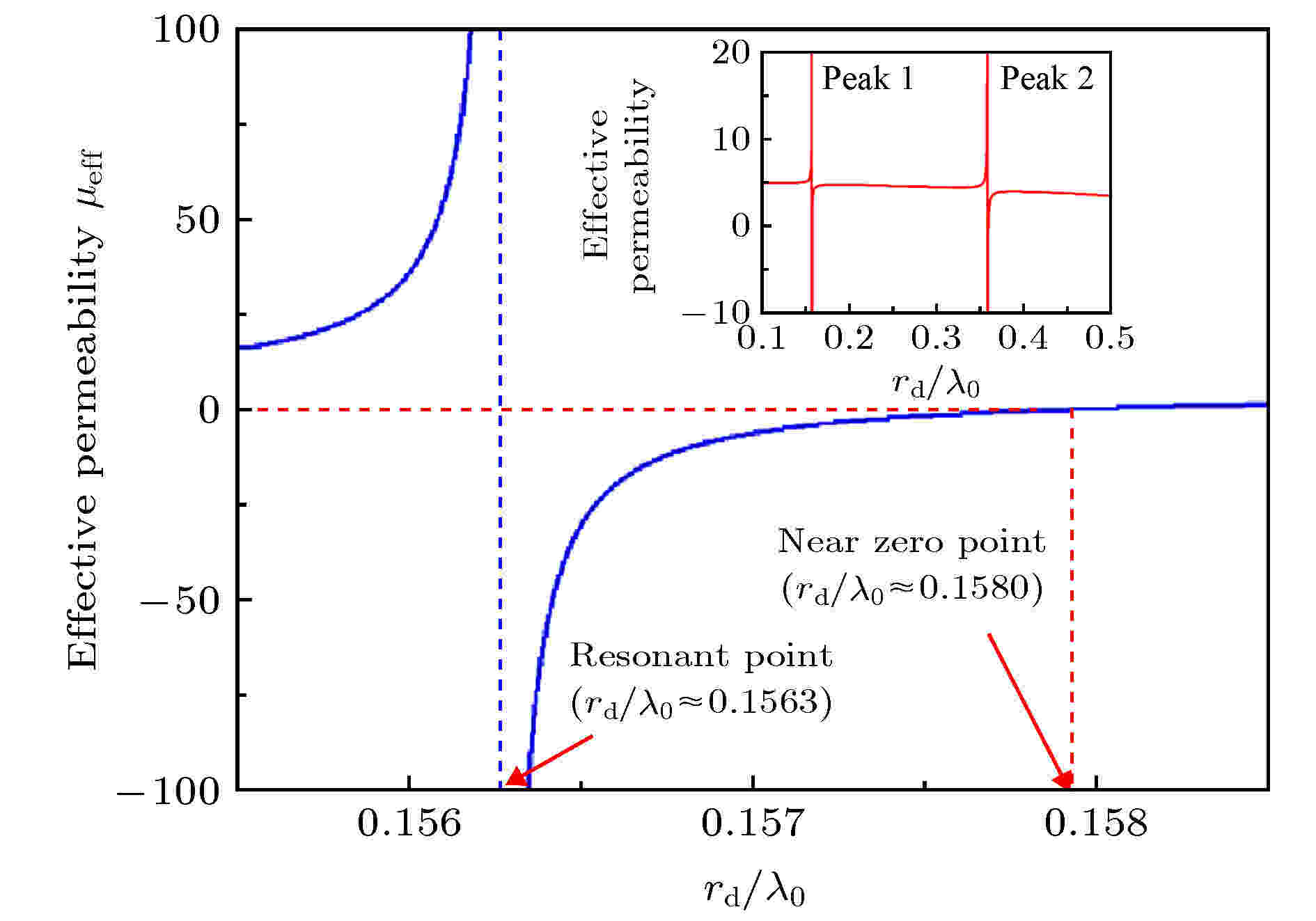图 2 ENZ媒质介质掺杂后其等效磁导率μ_eff随掺杂介质半径的变化
Figure2. Effective relative permeability (μ_eff) of the doped ENZ medium as a function of the doping rod radius.

考虑在ENZ媒质掺杂结构中的任意位置放置一个理想二维点源(磁流源, 产生y轴方向磁场), 在该结构等效为EMNZ媒质的前提下, 研究掺杂介质圆柱半径与该圆柱中心磁场增强倍数的关系. 根据图2可知, 随着掺杂介质圆柱半径的增加, 会出现一系列的谐振峰, 自然也会出现一系列的μ_eff为零的点. 根据(3)式计算出当r_d/λ₀ = 0.158, 0.363和0.572时, 该结构均可等效为EMNZ媒质(μ_eff ≈ 0), 由(4)式分别计算这三种情况下的掺杂介质内部磁场和ENZ中磁场(即激励源场)的比值ψ_d(r), 如图3(a)所示, 图3(a)中横坐标中的“0”点表示单个掺杂介质截面的圆心, 纵坐标定义为磁场强度增强系数F.
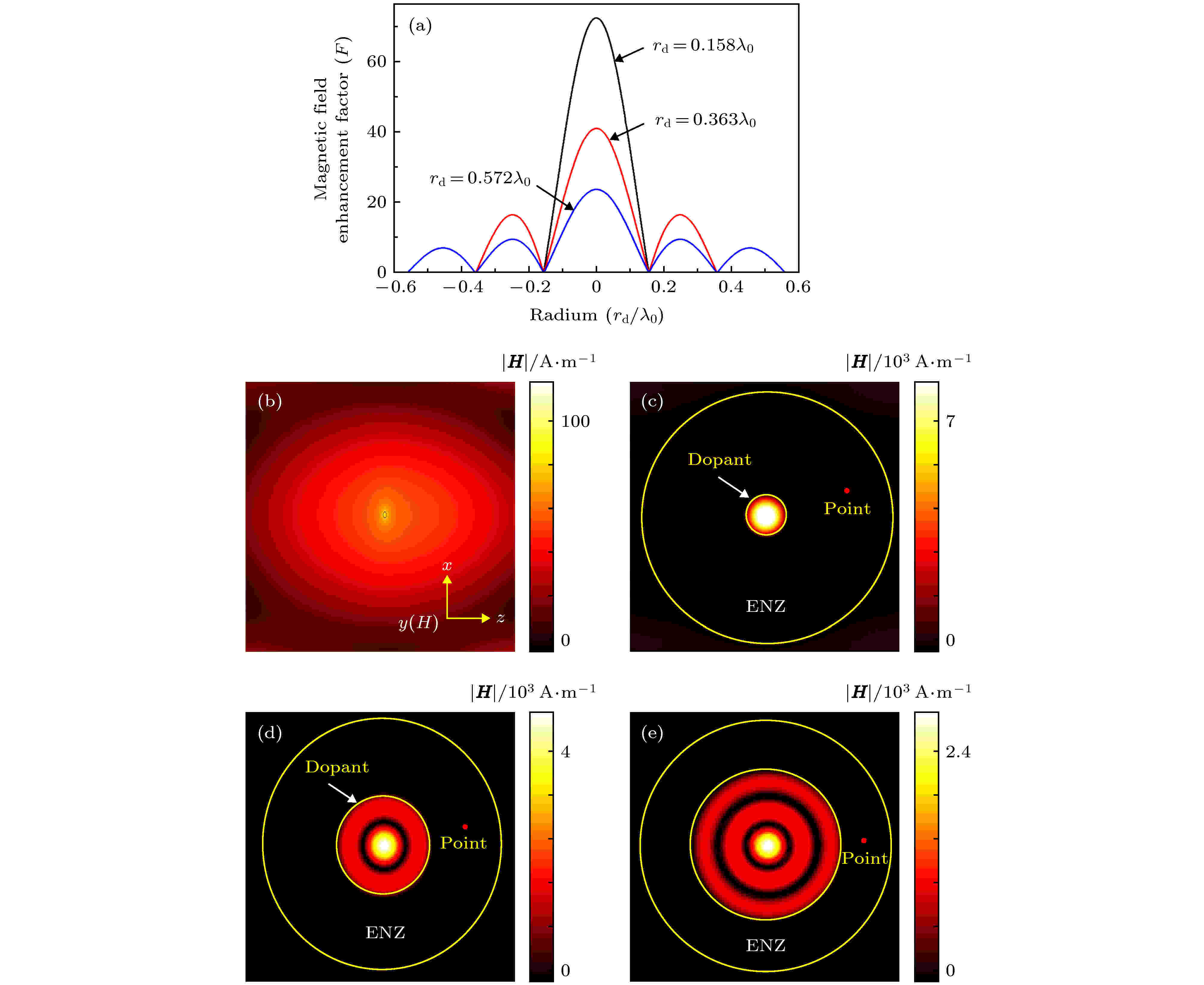图 3 掺杂介质具有不同半径时, 其内部中心磁场相对外辐射场的磁场增强倍数计算与仿真验证　(a) 掺杂介质内部中心磁场与其半径的关系曲线; (b) 理想点源的磁场仿真结果; (c), (d), (e) 掺杂介质半径分别为r_d/λ₀ = 0.158, r_d/λ₀ = 0.363和r_d/λ₀ = 0.572时掺杂介质ENZ媒质结构的磁场仿真结果
Figure3. Enhancement factors of internal magnetic field in the dopant compared with external radiation field with the different radius of dopant: (a) Enhancement factors of internal magnetic field in the dopant with different r_d; (b) the simulation result of magnetic field of point source in free space; (c), (d), (e) simulation results of magnetic field in ENZ filled with dopant with different radius of dopant (r_d/λ₀ = 0.15659, 0.35958, 0.56427), respectively.

为了验证上述结果, 采用电磁场全波数值计算软件COMSOL对其进行仿真分析验证. 如果是自由空间中的一个理想点源, 激励磁场幅度为100 A/m, 其辐射磁场分布如图3(b)所示. 其次, 如果该点源置入截面积为2.5$ \lambda_0^2 $ (xoz面)的非磁性圆柱ENZ媒质中, 并在该ENZ介质中嵌入一根介质圆柱(ε_r1 = 6, r_d/λ₀ = 0.158), 分析计算介质柱中心磁场分布, 如图3(c)所示(注: 介质柱中心磁场很大, 图中结果重点突出介质柱中心的磁场, 透射场相比太小而无法显示). 从图3(c)可以看出, 当理想点源以100 A/m的场强辐射时, 介质柱中心磁场幅值约为7100 A/m, 磁场增强约71倍, 与图3(a)的理论计算结论符合. 如果分别将介质柱的半径变换为r_d/λ₀ = 0.363和0.572, 该结构同样等效为EMNZ媒质, 其介质柱中心磁场值大约为3900和2300 A/m, 增强系数F分别为39 (图3(d))和23 (图3(e)), 均与理论计算结果符合. 分析结果不仅验证了理论分析的准确性, 也表明在整个结构等效为EMNZ媒质条件下可获得最大场增强效果.
2 -->

3.2.ENZ媒质内含多个辐射源

在实际的激光点火应用中, 若需场强要求很高, 可采用多个点火激励源, 同时提供能量叠加到同一个点火区域, 此时采用掺杂介质的ENZ媒质结构也是十分适合的. 因为ENZ媒质内部磁场均匀, 相位相同, 当几个点源置于ENZ媒质中, 其辐射场强在ENZ媒质内具有相位相同, 并能在掺杂介质中心形成完美的干涉增强效果, 使辐射能量可以完美叠加于掺杂介质的截面中心. 据此, 本节对包含多个相同辐射源的介质掺杂ENZ结构的磁场增强效应进行分析. 仍采用图3(c)的结构参数, 但在ENZ媒质中任意位置设置了两个相同的激励点源.
作为比较, 图4(a)(即图3(c))显示ENZ内为单点源时, 嵌入介质柱截面中心点的磁场幅值为7300 A/m, 场增强系数为73; 若再增加一个相同的辐射点源, 该结构介质柱截面中心点的磁场幅值增加到14000 A/m, 如图4(b)所示; 而改变两个辐射点源的嵌入位置, 结果与图4(b)相同, 如图4(c)所示; 同样保持ENZ横截面积不变, 将截面形状变为正方形, 仍得到相同的磁场分布, 如图4(d)所示. 因此, 介质掺杂ENZ媒质结构在多个源激励下, 具有良好的场强叠加增强能力, 且与源的位置及ENZ媒质截面形状无关, 这为大功率、大场强的点火装置的设计和实现提供良好的思路和途径.
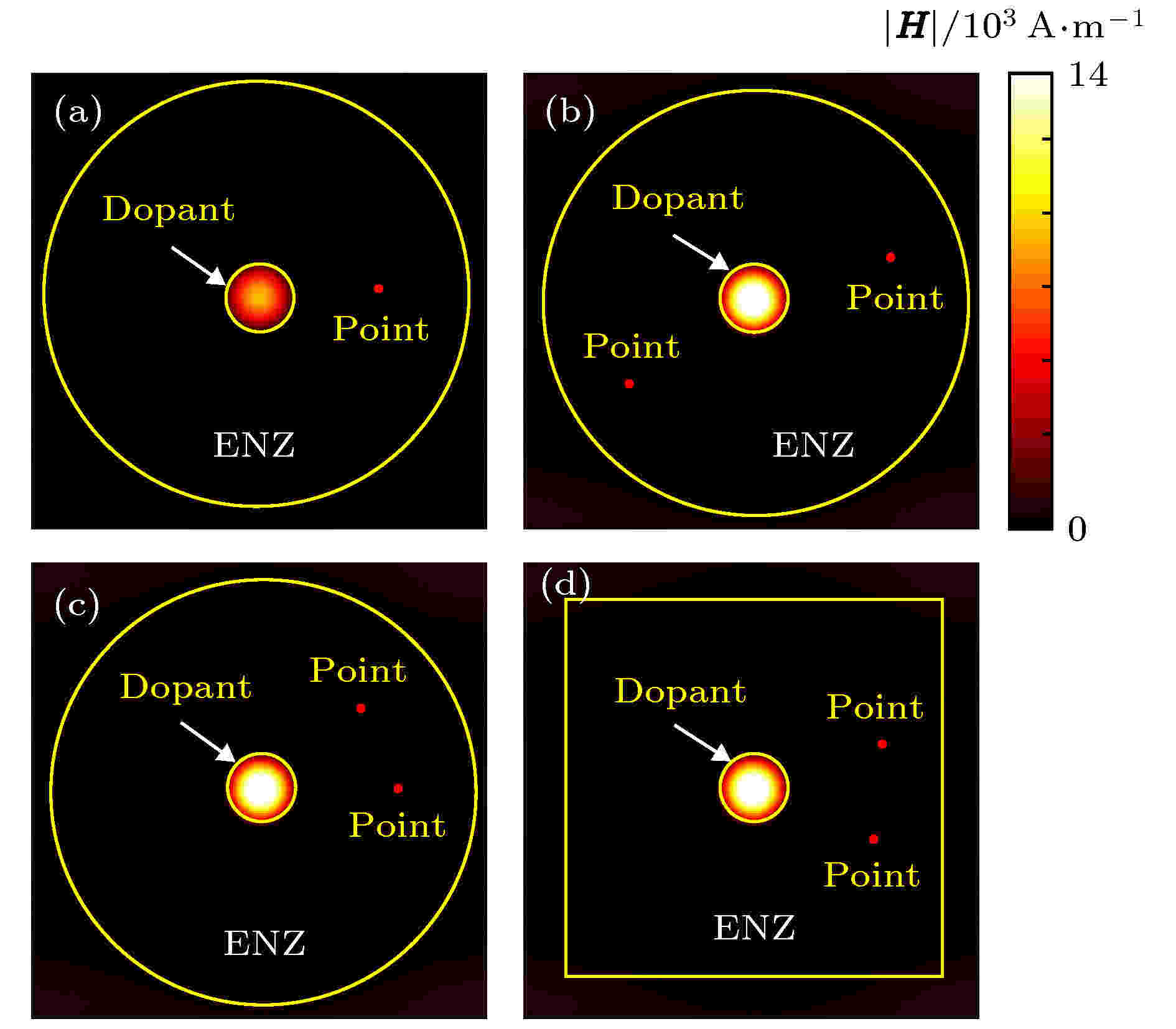图 4 掺杂介质的ENZ媒质结构分别包含单个点源和两个点源时的磁场对比仿真　(a) 掺杂介质的ENZ媒质结构包含单个点源的磁场仿真结果(ε_r1 = 6, r_d/λ₀ = 0.158); (b) 在图4(a)结构中再增加一个点源的磁场仿真结果; (c) 调整4(b)结构两个点源位置的磁场仿真结果; (d) 改变图4(c) ENZ媒质截面形状后的磁场仿真结果(点源位置任意调整, ENZ截面积不变)
Figure4. Simulation results of magnetic field in ENZ medium filled with the dopant containing different point sources, respectively: (a) One point source embedded in the ENZ medium (ε_r1 = 6, r_d/λ₀ = 0.158); (b) two point sources embedded in the ENZ medium; (c) two point sources located somewhere in ENZ medium; (d) two point sources embedded in an ENZ square (with the same cross section).

实际应用中, 在波长265—275 nm的紫外波段, 金属银的相对介电常数接近零, 变化范围为–0.75—0.75 (如图5(a)的红色曲线), 呈现ENZ媒质的特性^[32]. 本节根据前述的理论, 基于金属银薄膜, 设计了一种在265—275 nm波段的光学点火装置. 该装置中, 考虑银薄膜的截面积仍为2.5λ₀² (这里λ₀取该波段中心波长270 nm), 在银薄膜中掺杂一个横截面为圆形的非磁性介质纳米线(其相对介电常数ε_rd = 3), 根据(3)式的计算可知, 若介质纳米线半径为r_d/λ₀ = 0.226 = 61.0 nm时, 该掺杂介质银膜结构的等效磁导率μ_eff在265—275 nm波段内均接近零(见图5(a)蓝色曲线), 可等效为EMNZ媒质. 利用(4)式计算该结构中掺杂介质中心在中心频率点(波长为270 nm)的场增强倍数, 约为35.2, 场增强效果显著. 在270 nm波长的全波仿真分析结果如图5(b). 设入射光波磁场值为100 A/m. 当光波通过嵌入纳米线的银膜结构时, 掺杂介质中心的场强明显增强, 可达3500 A/m, 场增强系数达35, 与理论计算结果符合, 可见该结构可有效地应用于光学点火装置的设计和实现.
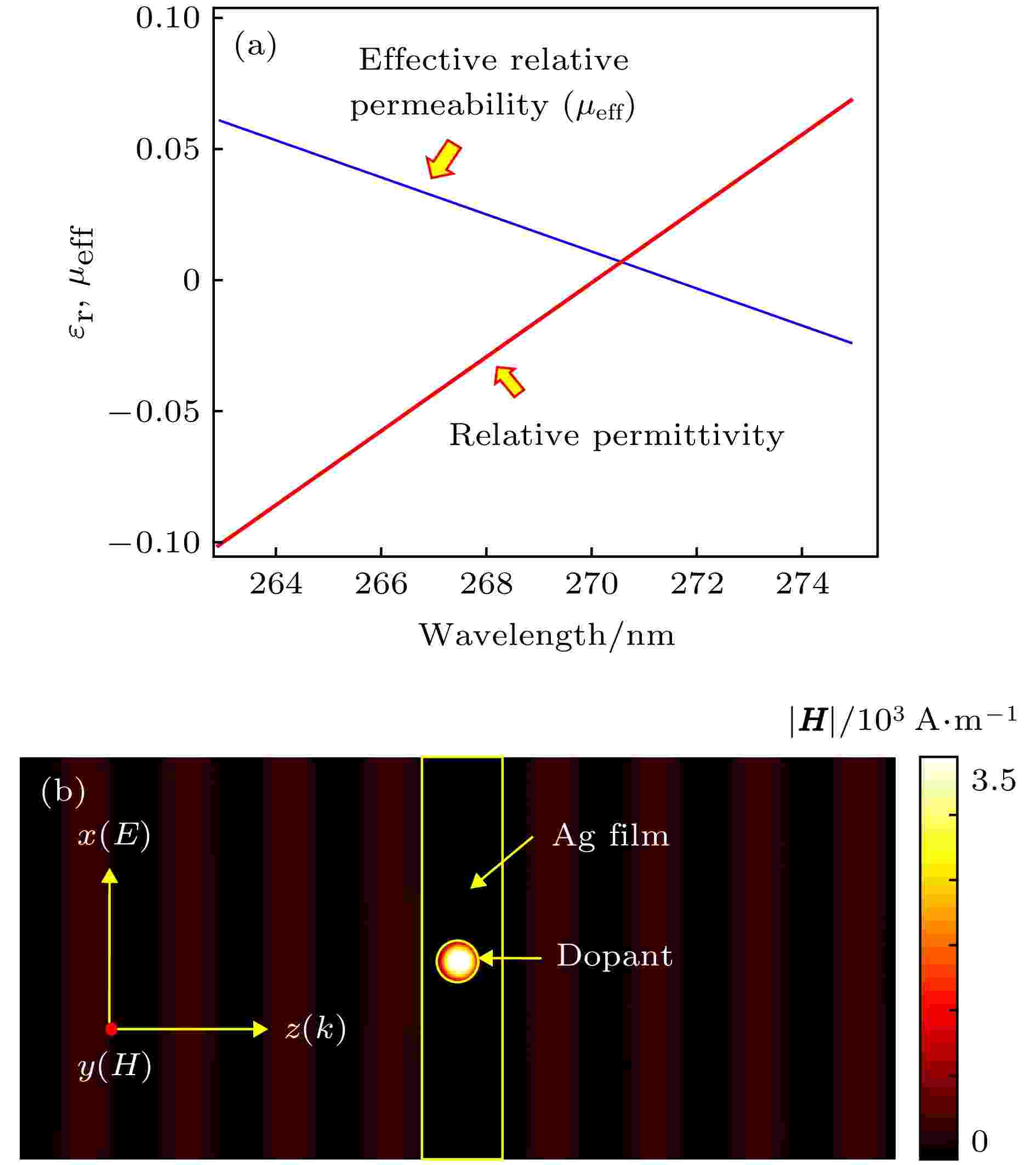图 5 265—275 nm紫外光波段点火器件的计算分析与仿真验证　(a) 265—275 nm波段银的相对介电常数以及掺杂介质的银薄膜的等效磁导率计算曲线; (b) 270 nm波长掺杂介质的银薄膜的磁场分布仿真结果
Figure5. Analysis and simulation of ignition device at wavelength of 270 nm: (a) The relative permittivity of silver film (red line) and the effective relative permeability of silver film filled with dielectric dopant at wavelength of 263 nm to 275 nm (blue line); (b) the simulation result of magnetic field in silver film filled with dielectric dopant at wavelength of 270 nm (r_d/λ₀ = 0.2261, ε_rd = 3).

本文对常规介质掺杂的ENZ媒质结构中磁场增强性能进行了全面分析, 指出该结构在等效为EMNZ媒质的前提条件下可实现最佳场增强效果. 随后在满足该前提条件下, 理论计算和全波仿真分析验证了该结构的场增强性能与各结构参数之间的关系(如ENZ和介质柱的电磁参数、介质柱的几何参数、激励源的个数等), 并在此基础上设计了一种工作在紫外波段的光学点火器件. 尽管本文在无耗条件下讨论介质掺杂ENZ材料结构的场增强特性, 但仿真分析表明, 在ENZ媒质的电磁损耗很小时, 整个结构仍可具有较好的电磁场增强性能. 分析结果显示, 在激光点火等高场强需求的实际应用中, 为了取得明显的应用效果, ENZ媒质的损耗, 即其相对介电常数的虚部应在0.01以下. 这些工作为掺杂ENZ媒质结构在场增强和光学点火器件设计等实际应用中提供了完备的理论指导, 为新型电磁(光学)场增强器件的研制提供了新的思路.