摘要:银行风险传导研究是系统性金融风险测度与防范的重点. 文献中主要研究静态银行网络拓扑结构和银行系统性风险量化, 较少考虑银行网络之间的状态转变. 针对上述问题, 提出时变状态网络模型. 根据模型, 首先用kmeans方法对各个时间段的银行网络分类, 然后通过有向最小生成树(DMST, directed minimum spanning tree)分析每一类银行网络的拓扑结构, 最后联合利用平面最大过滤图(PMFG, planar maximally filtered graph)方法构建时变银行状态网络, 该网络可用作银行风险源头的寻找和传导时变性分析. 利用时变状态网络模型研究我国15家上市商业银行2007年第四季度到2019第一季度同业拆借数据. 结果表明, 银行状态网络之间的短期连续跳跃性可有效描述金融危机的发生, 比如2008年全球金融危机发生前后出现了两个状态间的短期跳跃, 从2013年“钱荒”到2015年的股灾阶段, 先后出现了四个状态间的短期跳跃. 同时, 各个有向银行状态网络的出度和传染效应成正比, 入度和银行面临风险的稳健程度成反比. 时序的银行状态网络具有记忆性特征, 这可以为央行防范系统性风险提供决策依据.
关键词: 银行网络/
有向最小生成树/
风险传染强度/
平面最大过滤图

English Abstract

全文HTML

--> --> -->

金融网络的动态演化以及拓扑特性提取已经广泛用于金融危机的描述以及金融系统性风险的量化. 特别是银行网络, 在金融网络中占着非常重要的角色^[1]. 银行作为整个市场的资源收集者和调配者角色, 由于其经营的特殊性, 借贷、支付清算、投资等形成错综复杂的关系, 加之信息不对称, 风险更容易在银行之间传染, 从而引发金融系统性风险^[2-4].
如何准确刻画银行间复杂关联, 有效识别系统重要性银行, 动态跟踪银行风险传染路径, 对于防范金融系统性风险、金融危机预警有着至关重要的作用. 研究者通常通过构建银行网络, 研究网络结构、风险传递关系、系统性风险的传递源头以及路径等问题, 从而为科学防范系统性风险提供有效依据. 现有文献关于银行网络构和风险传递的研究方法大体涉及以下两类: 一是通过最大熵方法^[5]和最小密度法^[6]构建拆借网络; 二是通过计算银行之间的相关矩阵构建银行网络.
由于银行和银行之间的资金头寸数据不可得, 一些****采用最大熵方法构建银行之间资产负债关系网络, 并且利用拆借网络研究风险的传染. 李守伟等^[7]利用最大熵法和阈值法构建我国19家商业银行的有向网络, 并研究随机性攻击和选择性攻击对整个银行网络的影响. 结果表明, 对于随机性攻击, 银行网络具有较高的稳定性, 但是在选择性攻击时, 稳定性比较低. 范宏等^[8]根据我国上市银行2008年到2015年的年报数据构建动态演化的中国银行网络系统, 并且得出我国银行系统的系统风险在2009年达到最高值, 在2015年达到最低值. 王明亮等^[9]利用2011年50家银行年报数据, 基于矩阵法模拟分析不同网络结构不同风险冲击下单家银行发生倒闭所产生的传染效应. 结果表明, 银行挤兑造成的传染效应最大. Anand等^[6]为了构建更现实的银行同业拆借网络并保留银行间市场重要特征, 提出最小密度法, 并用最小密度法和目前最流行的最大熵方法进行对比. 结果表明, 用于压力测试时最小密度解高估了传染, 而最大熵低估了传染. 基于最小密度法, Anand等^[1]又接着利用向聚类系数作为系统性风险的测度, 并用巴西银行网络的数据进行分析. 结果表明, 有向聚类系数与国内利益呈负相关.
利用最大熵法通常会涉及到一个问题, 由于银行年报数据通常为每年一次或者每个季度一次, 而且研究多个银行之间的连续动态关系时通常会有缺失, 同时由于银行之间的拆借市场利率会影响货币供应量, 从而影响股票大盘的走势, 所以一些研究者利用资本市场的股票交易数据间接研究银行之间的风险传染. 在构建多个银行之间的关系时, 通常利用皮尔逊相关系数和随机矩阵理论、网络连接估计法、VAR模型和及格兰杰因果检验、距离矩阵法、转移熵^[10]等来研究各个银行之间的相关性, 从而构建相关矩阵. 邓向荣等^[11]用皮尔逊相关系数和随机矩阵理论构建金融风险传染模型, 然后利用格兰杰因果检验方法构建中国金融风险传染网络, 通过复杂网络指标评估金融机构的风险传染速度、范围等. 最终得出, 中国金融风险传染网络呈现多层次、多通道关联, 部分非银行机构在风险积聚中发挥关键作用. 胡利琴等^[12]利用VAR-NETWORK模型构建了我国银行间的有向网络关联图, 并进行滚动动态风险溢出效应分析, 得出在2009年中期至2010年出现一个较大的波峰, 在2011年末, 2012年末, 2013年中, 2014年中后期, 2015年中和2016年中共出现6个小波峰, 并用波峰和我国宏观经济背景以及发生的金融大事件进行比对. Constantin等^[13]将网络连接估计法引入到银行危机预警模型, 并利用该方法估算了1999 Q1–2012 Q3的171家欧洲银行的股权收益的尾部依赖性网络, 将其与银行预警模型相结合, 并证明该方法可用于提取早期预警信号和寻找金融机构之间的关系. 陈梦根和赵雨涵^[14]以国际清算银行(Bank for International Settlements, BIS)信贷数据为研究对象, 采取距离矩阵法构建银行相关矩阵, 并用最小生成树(MST, minimum spanning tree)方法构建了从1994年到2016年(一年4个网络, 每个季度一个网络)共92个网络, 分析了最小生成树树长(CTL)和标准化树长(NTL)的动态演化, 通过最小树长的动态演化对应各种危机事件. 结果表明, 中国银行业的国际地位在全球金融危机后, 稳定高于平均水平, 对金融危机冲击的敏感性在降低. 李智和牛晓健^[15]以我国16家上市银行的2012年至2016年12月交易数据为研究对象, 利用转移熵构建银行关系网络. 结果得出, 工商银行对其他银行总的风险传染效应最大, 而招商银行对其他银行总的风险传染效应最小; 交通银行面临的其他银行风险传染效应最大, 光大银行面临风险传染效应最小.
通过上述两类构建银行网络的方法, 不难发现, 最大熵法和最小密度法主要利用年报数据中的总的同业拆借数据反推银行之间的拆入和拆出, 但是构建的拆借网络是完全连接网络, 尽管利用阈值法滤除一些噪音边, 但是阈值的选取无法给定一个客观的定义, 一般是人为选取. 利用多个商业银行股票收盘价作为研究对象相对于银行年报数据的优点是可以有足够长度的数据, 便于研究动态拓扑结构的演化, 同时通过构建多个时间点的银行相关矩阵, 并且采取阈值法^[16]、最小生成树法^[17,18]等构建复杂网络^[19,20]. 然而, 利用股票数据构建银行复杂网络时会有以下缺点: 1)股票数据中包含着非常多的金融信息, 其中能反应商业银行的只是很小的一部分, 会对最后银行拆借网络的构建造成噪声影响; 2)股票数据反应的银行信息可能只是银行的业务策略或者是对市场反应的滞后表现. 最小生成树法虽然有效避免了阈值法的主观性和不唯一性, 客观滤掉了大量冗余信息, 呈现唯一的银行关系网络, 但是文献中大都利用最小生成成树法构建无向网络, 很少有涉及到有向最小生成树, 这样不利于分析银行之间的风险传导分析. 在动态分析银行网络得演化时, 研究者通常利用银行网络拓扑结构的突变对应金融危机的发生, 这样会存在一个问题: 无法将非危机拓扑突变和危机拓扑突变进行区分.
基于以上问题, 本文从银行网络构建和银行网络拓扑结构演化两方面对以往研究进行以下几点有益的补充. 首先, 对于银行网络构建中的客观唯一性以及有向性问题, 本文采取DMST法生成多个时间段的银行网络, 进行风险源头节点的寻找(识别系统重要银行)和系统性风险演化研究(风险传染方向、路径寻找). 其次, 对于银行网络拓扑序列中的危机状态和非危机状态划分问题, 本文采取kmeans^[21]方法将各个时间段的银行拆借矩阵分为若干类, 进行危机状态的特征提取. 最后, 为了进一步研究每个时间段的银行矩阵之间的关系, 本文采用距离矩阵法^[22]计算每个时间段银行拆借矩阵之间的欧式距离, 并用PMFG^[23]方法构建银行时变状态网络^[24], 用来分析各个时间状态之间的动态演化, 捕捉网络演化特征, 从而进行有效的风险预警.

2

-->

2.1.原始数据和预处理

本文从2007年—2019年《中国金融年鉴》中提取15个商业银行的每个季度的拆出、拆入资金数额. 具体的标号和相应的银行如表1所列.

编号	银行	类型	编号	银行	类型
1	浦发银行	股份制商业银行	2	民生银行	股份制商业银行
3	华夏银行	股份制商业银行	4	招商银行	股份制商业银行
5	兴业银行	股份制商业银行	6	北京银行	地方商业银行
7	上海银行	地方商业银行	8	中国农业银行	国有商业银行
9	中国交通银行	国有商业银行	10	中国工商银行	国有商业银行
11	中国建设银行	国有商业银行	12	中国银行	国有商业银行
13	中信银行	股份制商业银行	14	平安银行	股份制商业银行
15	宁波银行	地方商业银行

表1商业银行汇总
Table1.Summary of commercial banks.

其中5家国有商业银行, 3家地方商业银行, 7家股份制商业银行. 其他的城市商业银行、城市信用社、农村信用及邮政储蓄机构虽然都可以参与银行同业拆借市场, 但是他们在银行同业拆借市场中拆借数额比较少或者连续数据难以获取, 因此本文的研究数据没有包括这些金融机构. 商业银行数据的具体时间段为2007年第4季度, 2008年第1季度, ···, 2019年第1季度, 共46个时间段, 用$t = 1, \;2, \;···, \;46$表示每一个时间点, 即$t = 1$表示2007年第4季度, $t = 2$表示2008年第一季度, $ ··· , \;t = 46$表示2019年第一季度. 商业银行的拆借规模矩阵如下:

$\begin{array}{l} {{{X}}^t} = \left[ {\begin{array}{*{20}{c}} {x_{_{1,1}}^t}&{x_{_{1,2}}^t}& \cdots &{x_{_{1,N}}^t} \\ {x_{_{2,1}}^t}&{x_{_{2,1}}^t}& \cdots &{x_{_{2,N}}^t} \\ \vdots & \vdots & \ddots & \vdots \\ {x_{_{N,1}}^t}&{x_{_{N,2}}^t}& \cdots &{x_{_{N,N}}^t} \end{array}} \right]\;\begin{array}{*{20}{c}} {a_1^t} \\ {a_2^t} \\ \vdots \\ {a_N^t} \end{array} \\ \;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {\;l_1^t}&{\;\;\;l_2^t}&{\; \cdots \;\;\;\;l_N^t} \end{array}\end{array} .$

其中$x_{i, j}^t$表示在第t个时间点金融机构i对金融机构j的拆借头寸, $a_i^t = \displaystyle\sum\nolimits_{j = 1}^N {x_{i, j}^t}$表示第t个时间点金融机构i的拆出资金总额, $l_j^t = \displaystyle\sum\nolimits_{i = 1}^N {x_{i, j}^t}$表示第t个时间点金融机构j的拆入资金总额, 其中$t = 1, \;2, \;\cdots, \;46, \;N = 15$.
2 -->

2.2.方法与步骤

3 -->

2.2.1.最大熵法构建商业银行动态矩阵

对于银行同业拆借矩阵${{{X}}^t}$, 由于无法观察到$x_{i, j}^t$的数值, 而每家银行的拆出资金总额和拆入资金总额可以在年报中获取. 通过标准化, 可以把a和l视为边际分布函数$f(a)$和$f(l)$的实现值. 如果$f(a)$和$f(l)$相互独立, 则$x_{i, j}^t = a_i^t \times l_i^t$, 表明银行同业资产和负债是按边际分布函数分布于各个银行的. 然而独立假设需要拆借矩阵${X^t}$的主对角线元素为非零, 也就是银行自己给自己贷款, 这不符合现实, 所以令$i = j$时, $x_{i, j}^t = 0$, 此时拆借矩阵修正为

$\begin{array}{l} {{{X}}^{t*}} = \left[ {\begin{array}{*{20}{c}} 0&{x_{_{1,2}}^{t*}}& \cdots &{x_{_{1,N}}^{t*}} \\ {x_{_{2,1}}^{t*}}&0& \cdots &{x_{_{2,N}}^{t*}} \\ \vdots & \vdots & \ddots & \vdots \\ {x_{_{N,1}}^{t*}}&{x_{_{N,2}}^{t*}}& \cdots &0 \end{array}} \right]\;\begin{array}{*{20}{c}} {a_1^t} \\ {a_2^t} \\ \vdots \\ {a_N^t} \end{array} \\ \;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {\;l_1^t}&{\;\;\;l_2^t}&{\; \cdots \;\;\;\;l_N^t} \end{array}\end{array} .$

接着利用RAS算法(Blien和Graef^[25], 1997)估计${X^{t*}}$的元素, 具体求解形式如下:

$\begin{split}& \min \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{x}}_{i,j}^{t*}} } \ln \left(\frac{{{{x}}_{i,j}^{t*}}}{{{{x}}_{i,j}^t}}\right) \\ & s.t.\;\;\sum\limits_{i = 1}^N {{{x}}_{i,j}^t} = a_i^t\;, \\& \quad\quad\sum\limits_{j = 1}^N {{{x}}_{i,j}^t} = l_j^t, \\& \quad\quad{{x}}_{i,j}^t\; \geqslant 0.\end{split} $

其中${{x}}^*$和x为$({N^2} - N) \times 1$矢量, 包含${{{X}}^{{t * }}}$和${{{X}}^{{t}}}$的非对角线上的元素, $a_i^t$代表第i个银行t时间点的总拆出资金, $l_j^t$表示第j个银行t时间点的总拆入资金.
3 -->

2.2.2.kmeans状态划分和DMST步骤

利用最大熵方法构建多个时间段的银行拆借矩阵后, 为了探求各个时间段的银行借贷矩阵的关系, 本文通过kmeans算法分析银行拆借矩阵的动态演化研究, 分析出银行系统在各个时间段的特性, 并利用有向最小生成树方法分析银行网络的拓扑特性.
1. kmeans算法将银行拆借矩阵状态化.
kmeans算法的主要步骤是:
1) 从所有状态矩阵中随机取出k个元素, 作为k个簇的各自的中心;
2) 分别计算剩下的元素到k个簇中心的欧氏距离, 根据距离分别将它们分配给与其最相似的簇. 这里状态矩阵之间的欧氏距离定义为:

$d(m,n) = \sqrt {\sum\limits_{i = 1,j = 1}^N {{{({X_{i,j}}(m) - {X_{i,j}}(n))}^2}} } ,$

其中$ m = 1, 2, \cdots, t, \;n = 1, 2, \cdots, t$;
3) 根据聚类结果, 重新计算这k个簇各自的中心, 计算方法是取簇中所有元素各自维度的算术平均数;
4) 将全部状态矩阵按照新的中心重新聚类;
5) 重复第4)步, 直到聚类结果不再变化.
对于分成类别的k值的确定, 本文以k个簇的内部元素之间的距离和的平均值与所有元素距离和的平均值的比率为阈值, 以比率变化平缓时的k作为分类结果^[21], 将多个时间段的股票市场状态分为若干类.
2. DMST介绍和步骤.
通过kmeans算法将各个状态的银行矩阵分为若干类后, 利用有向最小生成树进一步分析每一个状态内部的网络连接. 有向最小生成树可以分析各个商业银行之间的相互作用关系, 也可以清楚得出银行之间的风险传递流向, 从而达到控制风险源头和寻找风险关键节点的作用. 有向最小生成树是基于无向最小生成树算法提出的, 无向最小生成树算法属于图论中重要的一部分, 其模型广泛存在于现实生活之中. 无向最小生成树法中经典的kruskal与prim算法^[26]可以解决对称的邻接矩阵的问题, 即两个节点之间不分相互关系时, 可以很方便地生成无向网络. 但对于利用最大熵和转移熵生成的矩阵来说, 由于不对称性, 节点和节点之间有相互关系之分, 可以用有向最小生成树来表达. 有向最小生成树(directed minimum spanning tree, DMST)^[27]又叫最小树形图, 即给有向带权图中指定一个特殊根节点, 从根节点出发的有向生成树, 要求所有距离权值的总权值最小.
DMST算法步骤如下:
1) 寻找固定根节点, 这一点可以随意选择;
2) 遍历所有的边, 从中找出除根结点外其余各点的最小入边, 累加权值, 构成新图. 接着判断该图是否存在环. 若不存在, 则该图便是所求最小树形图;
3) 如果存在环, 则把环缩放为点, 并设这个环中指向u的边权是$in[u]$, 对于每条从u出发的边$(u, i, w)$, i表示不含环的原始点, w表示原始权重. $(u, i, w)$对于不含环的原始点i的入边来说, 直接连接$(new, i, w)$, 其中$new$为新加的人工顶点. 对于每条进入u的边$(i, u, w)$, 在新图中建立边$(u, i, w - in[u])$的边, 判断由此生成的新图是否有圈, 如果有圈, 返回到第2)步重新判断;
4) 当第3)步生成的新图没有圈时, 将最后的图进行展开按照有向最小生成树的规则将闭环破去, 从而得到最终结果.
3 -->

2.2.3.PMFG方法构建时变银行状态网络

在分析状态网络内部结构后, 接着利用PMFG方法分析每一个银行状态网络之间的关系, PMFG方法的步骤如下:
1)用公式(4)计算状态矩阵之间的距离, 得到N阶的距离矩阵,

${{D}}= \left[ {\begin{aligned} {d(1,1)}&{d(1,2)}& \ldots &{d(1,n)} \\ {d(2,1)}&{d(2,2)}& \ldots &{d(2,n)} \\ \vdots & \vdots & \vdots & \vdots \\ {d(m,1)}&{d(m,2)}& \ldots &{d(m,n)} \end{aligned}} \right].$

2)将公式(5)中的距离矩阵D转化为相似度矩阵A, 其矩阵元为

${{A}}(m,n) = {{O}}(m,n) \times max({{D}}(m,n)) - {{D}}(m,n).$

公式(6)中的O表示$N \times N$维的全1矩阵, $m = 1, 2, \cdots, N, \;n = 1, 2, \cdots, N$, $\max( \cdot )$表示求最大值;
3) 将各个节点之间的相似度, 按矩阵A中的值升序排列;
4) 按顺序从排列好的权重值中选取相应的节点对, 建立连边, 如果新加的边使得网络出现非可平面, 也就是说新加的边和其余边交叉出现在一个平面上, 则放弃该连接;
5) 重复步骤4)直到所有节点加入到网络中. 最终形成的网络包含$3(N - 2)$条边.
这样就通过PMFG方法将各个时间段的银行时间状态矩阵构建为银行时变状态网络.
3 -->

2.2.4.Girvan-Newman算法分析时变状态网络的社团结构

在构建银行时变状态网络后, 为探求各个时间点之间的社团结构, 本文采取Girvan-Newman 算法^[28]进行社团分析. Girvan-Newman算法是Newnan等为了得到具有实际意义的社团结构, 定义了模块度来衡量网络划分质量, 在每个社区内部节点状态紧密地链接在一起, 而在社区之间只有少量的边把它们连接起来. 指定不同的社区个数, 计算社区划分后模块度值. 最大模块度对应的划分方式作为理想的社团结构. 社区划分模块化程度定义为

$Q = \sum\limits_{i = 1}^c {[{e_{ii}} - {b_i}^2]} = h - \left\| {{{{E}}^2}} \right\|.$

其中i表示社团编号, c表示社团数, E为一个对称邻接矩阵${{E}} = {({e_{ij}})_{c \times c}}$, $\left\| \cdot \right\|$表示取模, 其中元素${e_{ij}}$表示连接两个不同社团i和j的节点的边在所有边中的比例. h表示矩阵E中对角线上个元素之和: $h = \displaystyle\sum\nolimits_{i = 1}^c {e{}_{ii}}$, 也就是网络中社团内部节点的边占所有边的比例. ${b_i} = \displaystyle\sum\nolimits_{j = 1}^c {{e_{ij}}}$表示第i个社团中节点连边数在所有边中的比例.Q函数的值越大, 表明社团结构越明显. 在实际应用中, Q的值一般处于0.3—0.7之间. GN算法的基本流程如下:
1)计算网络中每条边的边介数;
2)找到边介数最大的边并将其移除;
3)重新计算网络中剩余各条边的边介数;
4)重复步骤2)和3), 直到每个节点是一个退化社团为止.
以上是本文的主要方法和流程步骤, 文章的主体思路和方法步骤如图1所示:
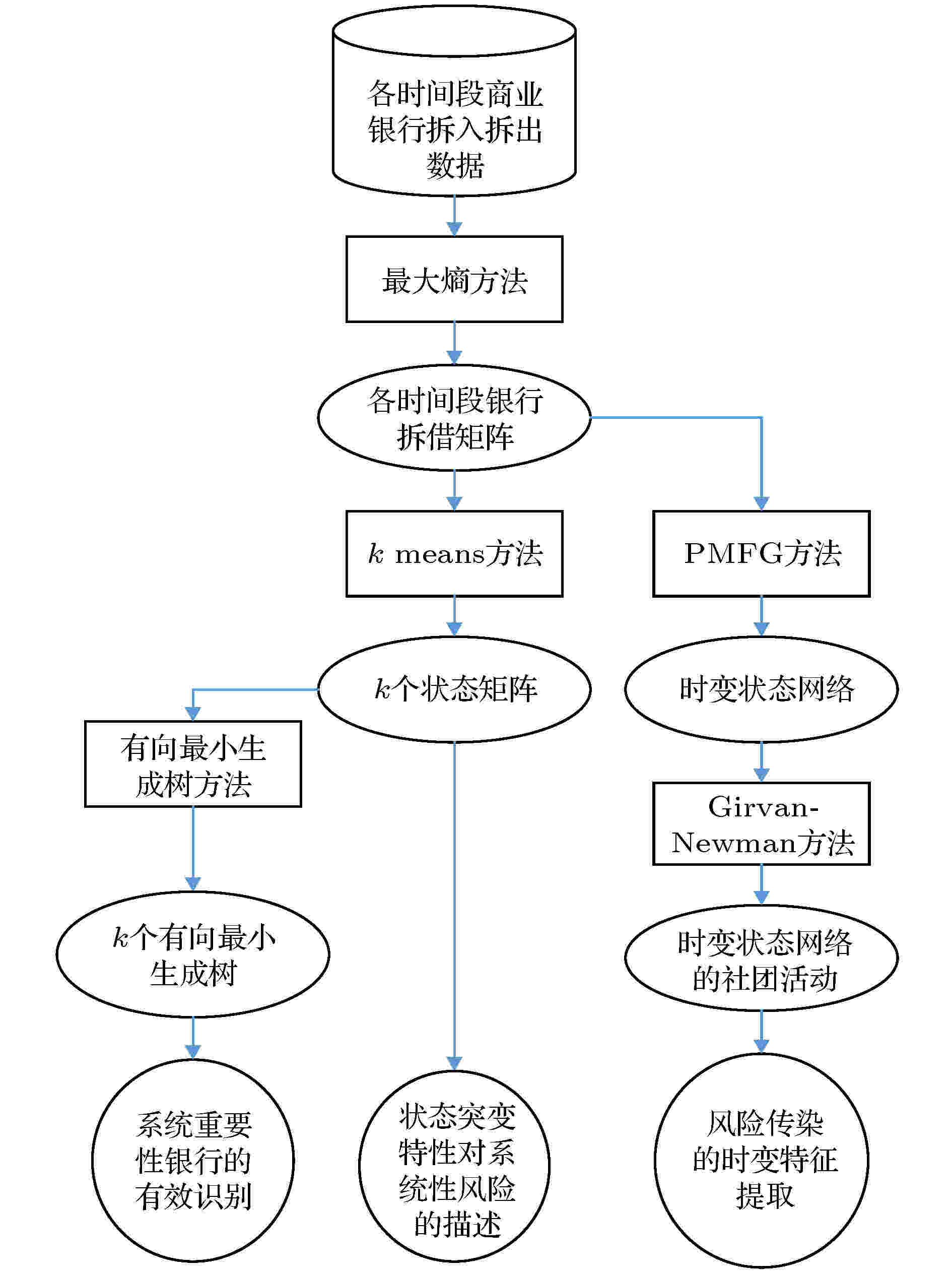图 1 主体方法和流程图
Figure1. Main method and flow chart.

2

-->

3.1.银行拆借网络的状态划分与系统性风险

3 -->

3.1.1.银行状态网络的动态突变与对应的系统性风险

通过最大熵方法, 本文构建了46个时间状态的银行拆借矩阵. 为了对这些矩阵进行状态分类, 本文采取kmeans方法对多个时间片段的银行矩阵进行归类化处理. 对于k值的确定, 本文采取文献[21]中的方法, 图2是各个k值下比率的变化, 方块表示k个簇的内部元素之间的距离和的平均值与所有元素距离和的平均值的比率, 圆圈表示这个比率的变化, 可以看出在$k = 6, 7, 8$时比率变化都比较平稳, 本文取三个数中比率变化率绝对值最小的8作为分类标准.
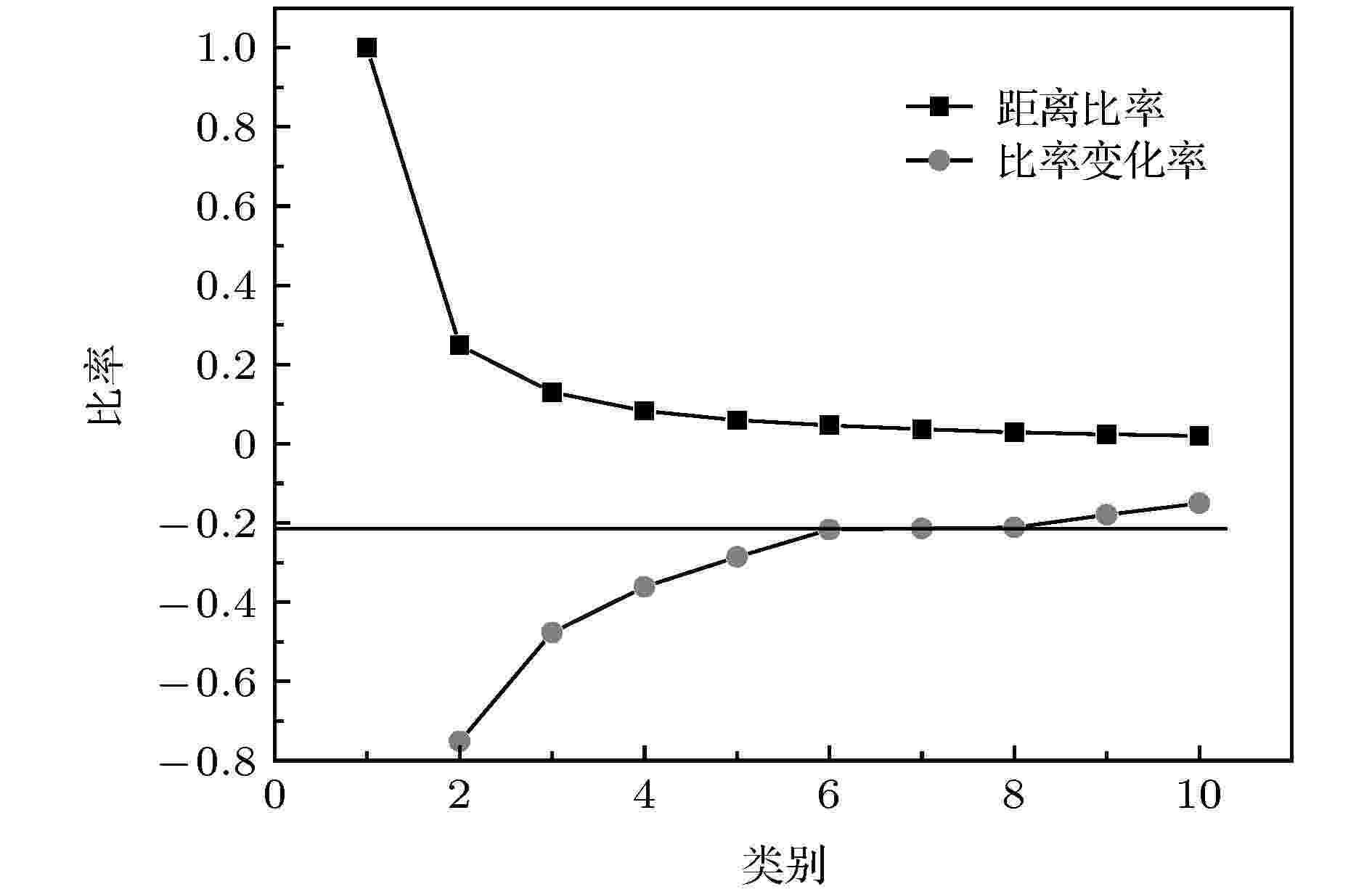图 2 距离比率与比率变化率
Figure2. Distance ratio and rate of change.

通过kmeans分类, 本文将46个时间段的银行状态矩阵分为8类, 将每个时间段所归属的类别平铺于时间轴上, 由图3可以看出, 从2007年第四季度到2019年第一季度分为了8个状态, 在状态和状态的跳跃阶段, 发生拆借矩阵的突变, 特别是在短期状态跳动阶段(定义小于等于3个片段为短期跳跃, 大于3个片段视为长期状态), 比如图3中A圆圈代表的时间阶段为2008年第二季度和2008年第三季度, 是短期的状态跳动, 从状态5跳到状态8持续了两个时间阶段, 又跳回到状态5, 其中A阶段也正好对应了2008年全球金融危机发生这个事件. 对于B圆圈, 是从状态7跳到状态2又跳到状态3时的短期状态, 这个状态正好对应了2013年年中发生的“钱荒”事件. 特别地, 注意到图3中的C圆圈和D圆圈, 是由状态3跳到状态2, 持续一个季度又跳到状态1, 又连续跳到状态6, 综合考虑从2009年中国股票一直持续跌到2014年, 直到2014年下半年迎来了疯狂地飙升. 但是, 股票市场“红热化”的繁荣现象的背后却隐藏着极大的风险隐患, 比如市场流动性过剩所导致多数行业持有共同的风险敞口, 行业间潜在的风险传染渠道迅速拓宽, 经济体系愈发脆弱. 虽然这种潜在的系统性风险积累过程可能并不会立刻对经济产生明显影响, 但当风险积累到一定程度并且出现某种负向冲击时, 系统性危机一触即发. 到2015年6月起证监会开始清查场外配资, 快速去杠杆这一冲击使得上半年积聚的风险瞬间爆发, 股市暴跌40%以上. 这种过山车式的暴涨暴跌会引发出巨大的系统性风险. 除了短期状态跳动以外, 长期和长期之间的跳动由于金融系统中产生的部分风险被系统内部控制或由于职能部门调控, 短期跳跃可以视为长期状态下产生的风险积聚突变.
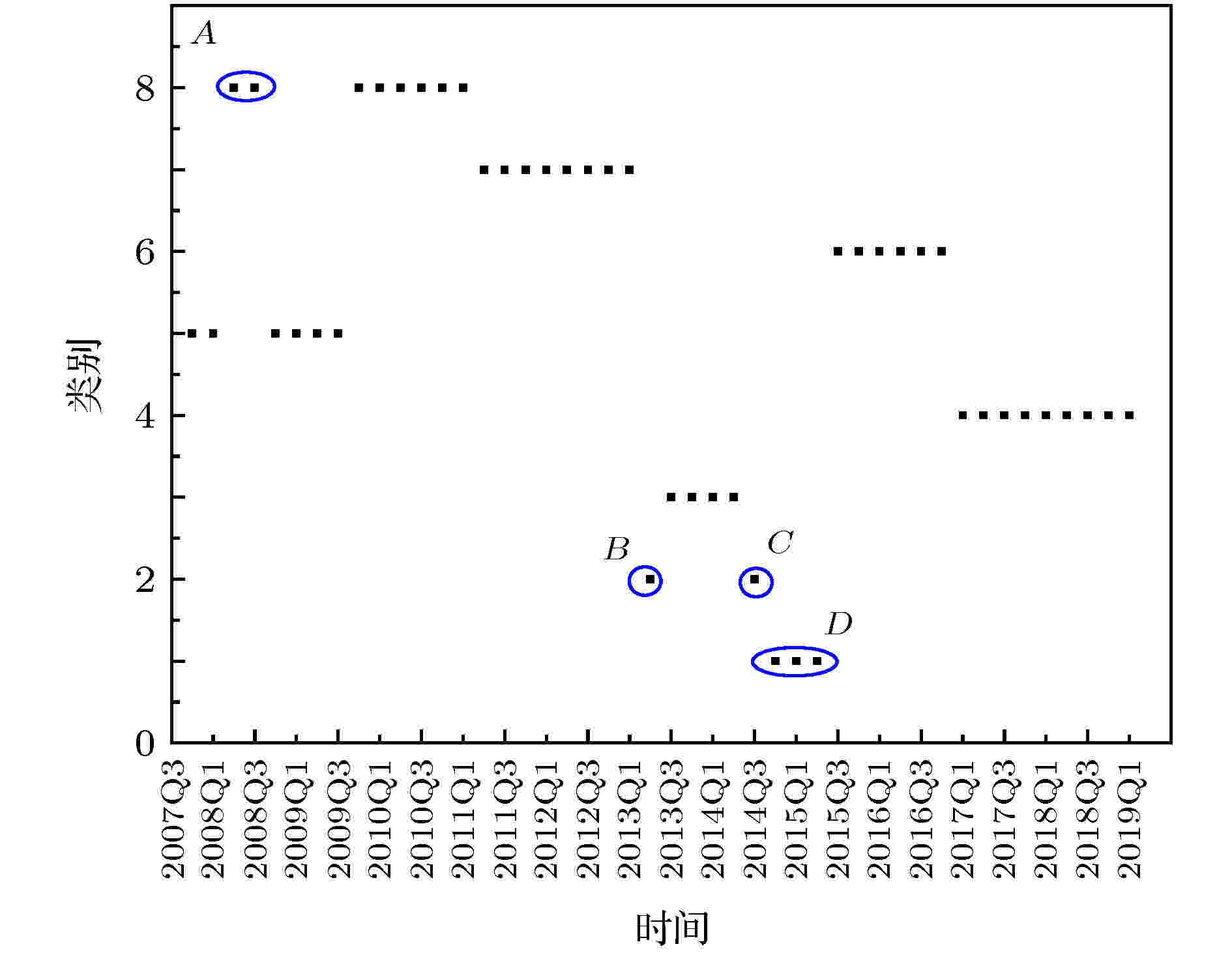图 3 银行拆借矩阵状态演化图
Figure3. State evolution of bank lending matrix.

3 -->

3.1.2.银行同业拆借矩阵相似度与时变特征

为考察拆借矩阵之间的相似度和时变特征, 本文抽取8个银行状态矩阵的矩阵色块矩阵图. 如图4所示, 8个状态矩阵也是对应图3中的8个状态. 可以看出, 除了第5个状态, 其余状态的色块表达还是比较相似的.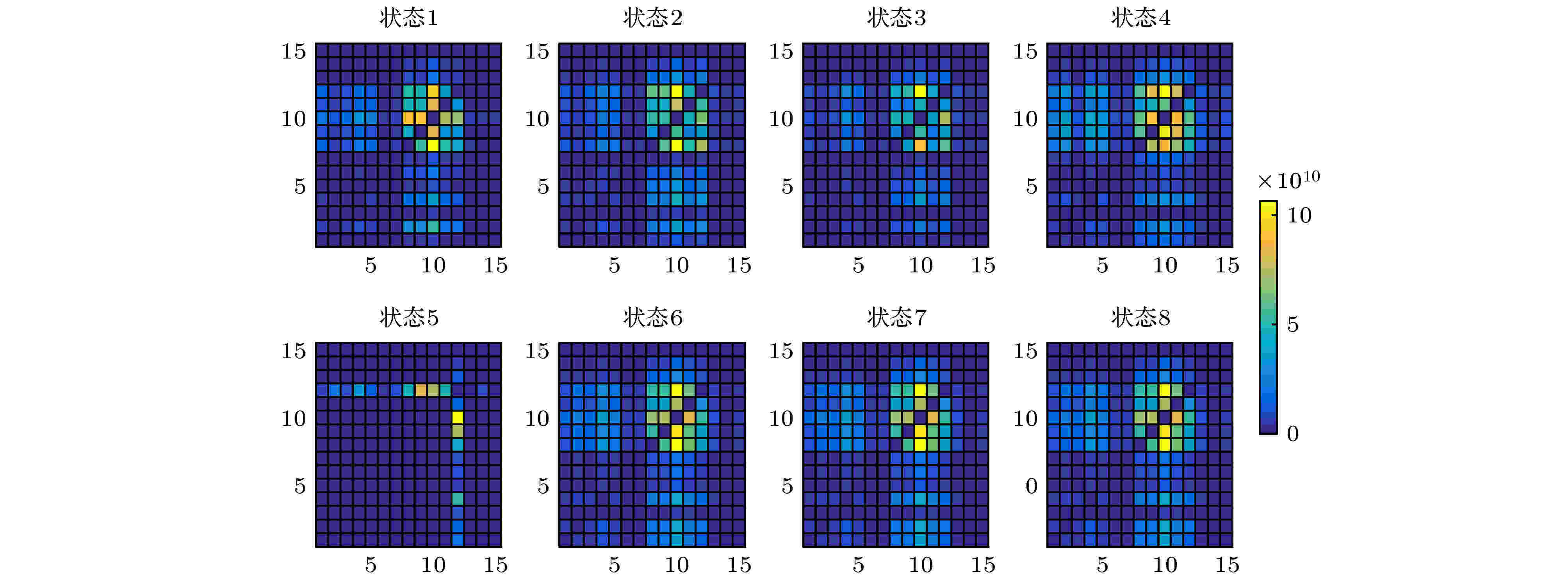
图 4 8类银行状态矩阵图
Figure4. Bank matrix diagram of 8 states.

为了研究各个状态之间的关系, 本文将8个状态矩阵向量化处理, 即将8个状态矩阵从8个15 × 15的矩阵转置为8个225 × 1的矩阵(8个225长的序列), 并计算8条序列之间的皮尔逊相关系数矩阵, 定义为

${\rho _{{s_{i,}}{s_j}}} = \frac{{\displaystyle\sum\limits_{\varepsilon = 1}^{225} {({{s}}_i^\varepsilon - \overline {{{{s}}_i}} )({{s}}_j^\varepsilon - \overline {{{{s}}_j}} )} }}{{\sqrt {\displaystyle\sum\limits_{\varepsilon = 1}^{225} {({{s}}_i^\varepsilon - \overline {{{{s}}_i}} )} } \sqrt {\displaystyle\sum\limits_{\varepsilon = 1}^{225} {({{s}}_j^\varepsilon - \overline {{{{s}}_j}} )} } }}.$

其中${{{s}}_i}, {{{s}}_j}$表示8条序列中的任意两条, ${b_i} = \displaystyle\sum\nolimits_{j = 1}^c {{e_{ij}}}$. 利用公式(8)得到的8个状态矩阵之间的相关性结果(见表2).

	状态1	状态2	状态3	状态4	状态5	状态6	状态7	状态8
状态1	1.000	0.927	0.918	0.909	0.410	0.949	0.714	0.708
状态2	0.927	1.000	0.968	0.874	0.549	0.911	0.881	0.819
状态3	0.918	0.968	1.000	0.887	0.630	0.911	0.893	0.875
状态4	0.909	0.874	0.887	1.000	0.481	0.963	0.757	0.767
状态5	0.410	0.549	0.63	0.481	1.000	0.422	0.707	0.861
状态6	0.949	0.911	0.911	0.963	0.422	1.000	0.75	0.734
状态7	0.714	0.881	0.893	0.757	0.707	0.750	1.000	0.884
状态8	0.708	0.819	0.875	0.767	0.861	0.734	0.884	1.000

表28个状态矩阵的相关矩阵
Table2.Correlation matrix of eight state matrices.

表2和图5分别为8个状态矩阵之间的相关系数矩阵和相关矩阵图. 从表2可以看出, 状态5和相邻的状态7和8的相关系数分别为0.707和0.861, 比状态5与其他相关状态的相关系数高; 状态1, 6, 4作为三个连续的状态, 1和6之间相关系数为0.949, 6和4之间相关系数为0.963, 都比状态6与其余状态之间的相关系数高. 说明各个银行状态矩阵之间存在时间延续性, 随着时间的推移, 一个状态矩阵趋向于类似的状态变化, 即相邻的状态矩阵之间的相关系数一般较高.
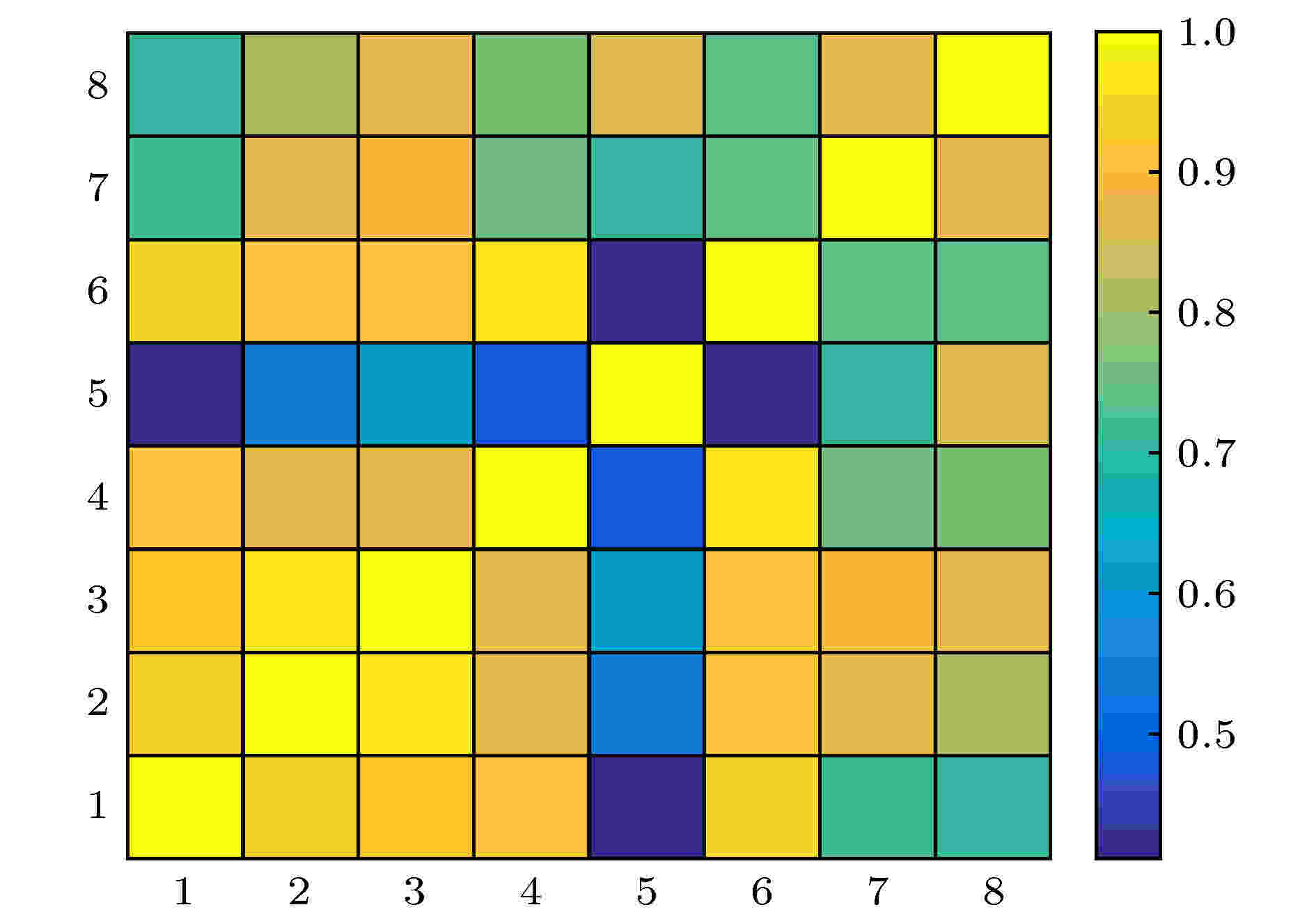图 5 各个银行状态之间的相关矩阵
Figure5. Correlation matrix between Bank states.

3 -->

3.1.3.相关矩阵与金融风险的关系

为量化研究各个状态的相关度, 本文对表2中的相关矩阵进行累加处理, 如表3所列.

状态	1	2	3	4	5	6	7	8
全局相似度	6.536	6.929	7.082	6.638	5.060	6.639	6.587	6.647

表38个状态矩阵的全局相似度
Table3.Global similarity of eight state matrices.

将每个状态和其余状态之间的相关系数的累加, 并定义为全局相似度(每个状态和其余所有状态相关性的和). 从表3可以看出, 状态5与其余状态的关系比重最小, (也可以从图5中的色块得出同样结论), 而状态3是最高的, 状态2次之. 状态5作为与其余状态区别最大的一个状态, 对应图3中的状态5的起始点: 2007第四季度, 这正是2007年10月上证综指攀升至6124点成为中国股市的历史最高的时间段. 而状态2, 3对应的正好是2013年国内发生的“钱荒”事件, 在这一阶段, 银行业开始不惜代价坚守稳健货币政化解金融风险, 同时进行去杠杆的博弈战. 因此, 金融监管机构需要高度关注潜在的系统性金融风险的积聚, 特别是银行系统状态发生转变阶段.
2 -->

3.2.有向银行网络拓扑结构与风险传染效应强度

由于银行同业拆借矩阵与金融风险高度相关, 需要研究同业拆借市场中各银行在网络中地位以及银行之间的关联, 从而分析银行风险传染与扩散的影响. 为了清晰表达银行网络中各个节点之间的相互作用, 本文利用DMST方法构建各个状态的银行网络. 图6是状态1—4的有向最小生成树图. 图7是5-8状态的有向最小生成树.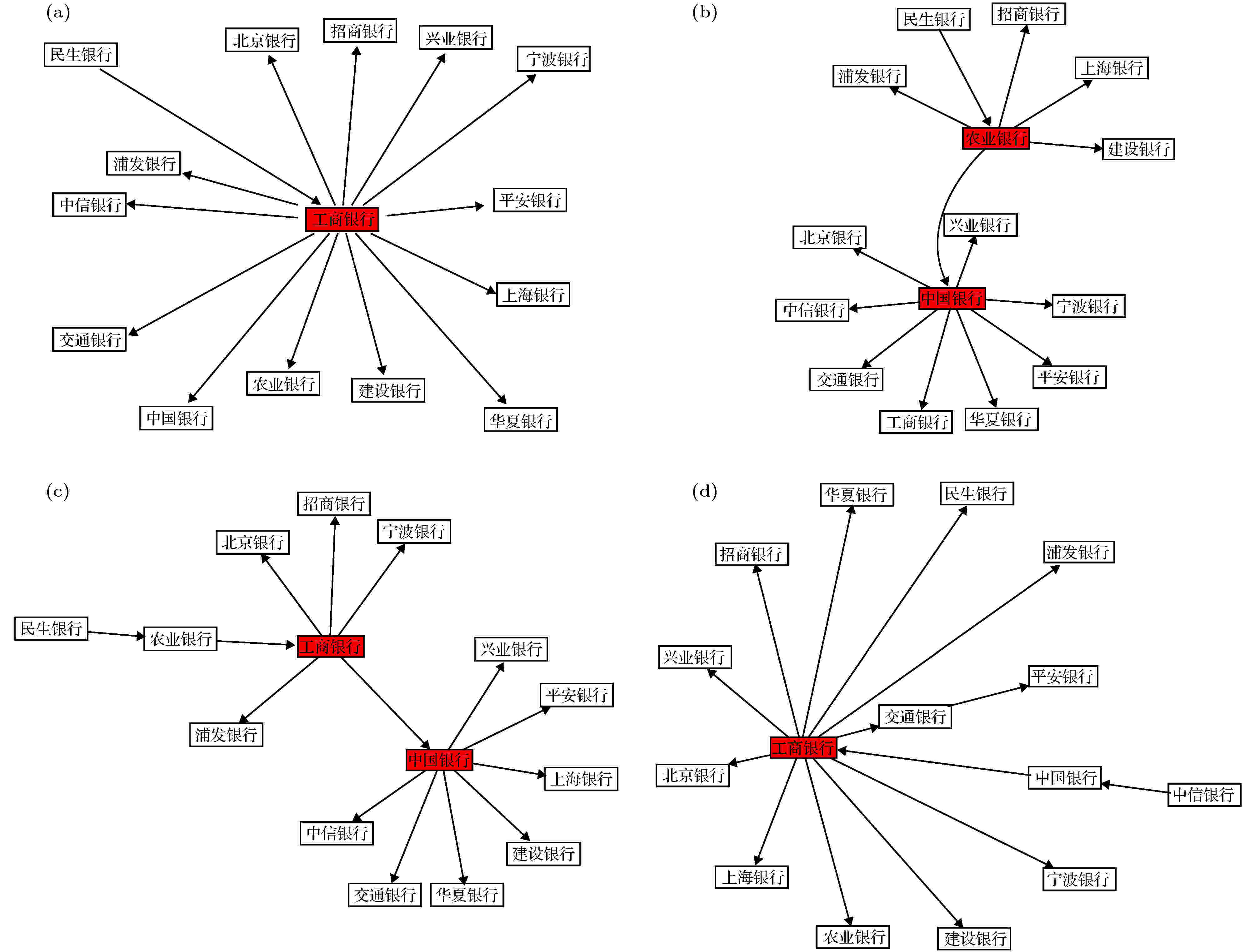
图 6 状态1—4的有向最小生成树　(a) 状态1的有向生成树; (b) 状态2的有向生成树; (c) 状态3的有向生成树; (d) 状态4的有向生成树
Figure6. . Directed network diagram of state 1 to 4: (a) Directed network diagram of state 1 (b) directed network diagram of state 2; (c) directed network diagram of state 3; (d) directed network diagram of state 4.

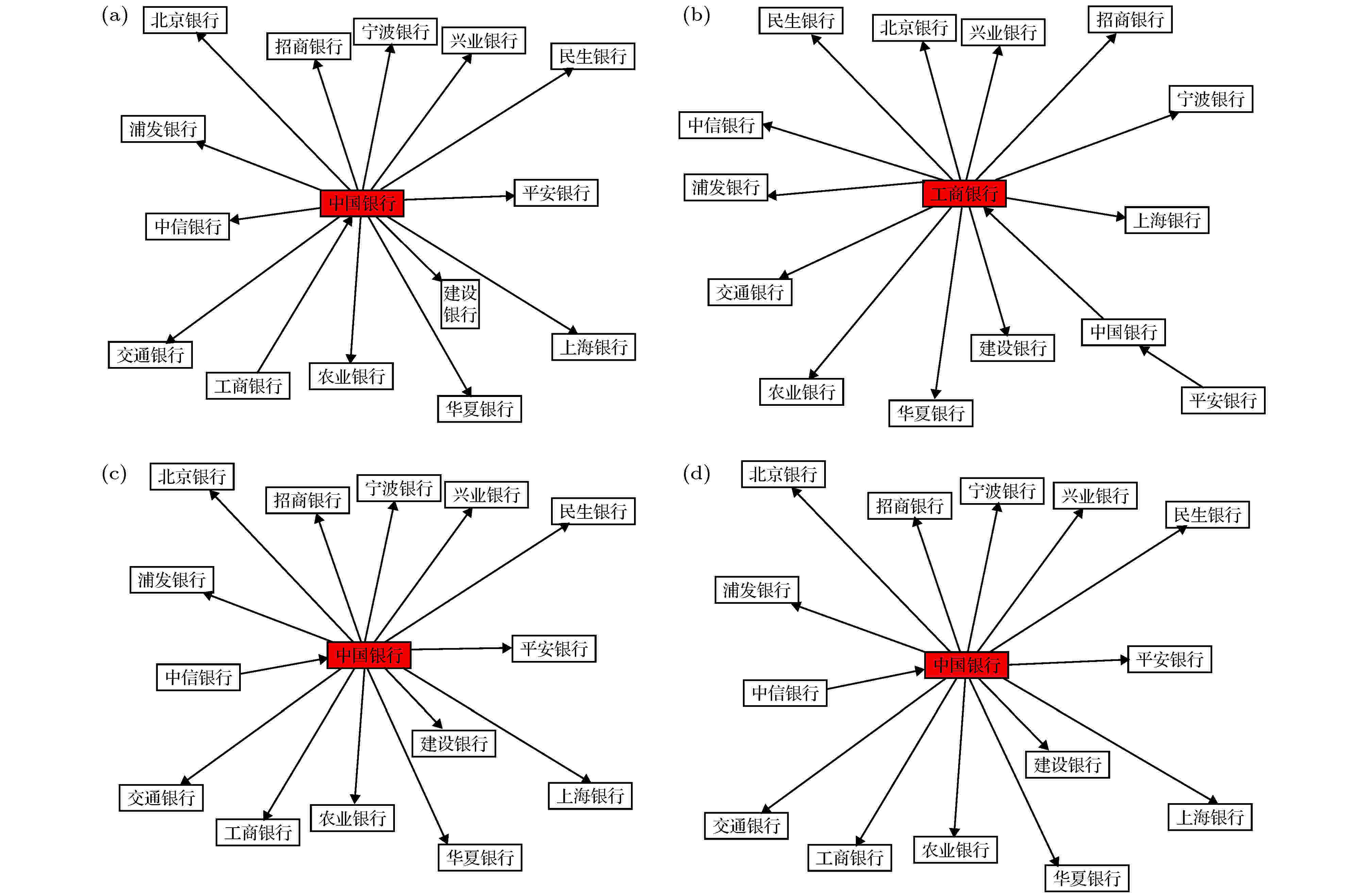图 7 状态5—8的有向最小生成树　(a) 状态5的有向生成树; (b) 状态6的有向生成树; (c) 状态7的有向生成树; (d) 状态8的有向生成树
Figure7. Directed network diagram of state 5 to 8: (a) Directed network diagram of state 5; (b) directed network diagram of state 6; (c) directed network diagram of state 7; (d) directed network diagram of state 8.

在图6的状态2中, 四大行中拆借资金传递是以农业银行为初始节点的, 农业银行传向中国银行和建设银行, 再由中国银行传向工商银行. 分析此网络的原因, 可以追溯2013年6月底“钱荒”期间多家银行紧张, 而资金充裕的中国农业银行, 同业业务收入上升, 融出资金9400亿元, 融入资金1000亿元, 差额8400亿元, 这也是农业银行作为四大行中的初始节点的原因. 对于图6中的状态3, 四大行中工商银行和中国银行都作为中心节点, 可以追溯到钱荒发生后发生了央行向工商银行注资500亿元, 中行继工行之后出现系统故障. 综合状态2和状态3与其余状态的明显区别, 可以看出, 钱荒对中国银行业的影响和其他金融危机的影响是有很大区别的. 钱荒导致商业银行的资金出现短缺, 隔夜拆借率增大, 从而改变了商业银行之间原有的较稳定的拆借结构, 所以出现状态2和状态3与其余状态的明显区别.
基于图6和图7中的8个状态的有向最小生成树, 通过统计得到每个状态的拓扑结构(见表4).

银行	状态1出度	状态2出度	状态3出度	状态4出度	状态5出度	状态6出度	状态7出度	状态8出度	头节点数	中心节点数
浦发	0	0	0	0	0	0	0	0	0	0
民生	1	1	1	0	0	0	0	0	3	0
华夏	0	0	0	0	0	0	0	0	0	0
招商	0	0	0	0	0	0	0	0	0	0
兴业	0	0	0	0	0	0	0	0	0	0
北京	0	0	0	0	0	0	0	0	0	0
上海	0	0	0	0	0	0	0	0	0	0
农业	0	5	1	0	0	0	0	0	0	1
交通	0	0	0	1	0	0	0	0	0	0
工商	13	0	5	11	1	12	0	0	1	4
建设	0	0	0	0	0	0	0	0	0	0
中国	0	8	7	1	13	1	13	13	0	5
中信	0	0	0	1	0	0	1	1	3	0
平安	0	0	0	0	0	1	0	0	1	0
宁波	0	0	0	0	0	0	0	0	0	0

表4银行状态网络拓扑特性统计
Table4.Statistics of topological characteristics of banking state network.

其中, 出度表示发出关系, 出度大表示对其它银行影响比较大, 传染效应和扩散性比较强. 入度表示接收关系, 入度大表示受其它银行的辐射影响比较大, 容易被风险传染, 系统稳健性较差. 在8个状态中, 工商银行和中国银行的出度较大, 表示对其它银行影响比较大, 容易传递风险. 比如在状态1, 4, 6下工商银行的出度分别为13, 11和12, 而在状态2, 3, 5, 7, 8下中国银行的出度分别为8, 7, 13, 13, 13, 这表示工商银行和中国银行的总风险传染效应是最大的. 这和文献 [8,15, 29]中的结果是一致的. 在中心节点数统计方面, 工商银行和中国银行也分别为4和5. 可见中国银行和中国工商银行在系统风险控制方面属于关键节点.
此外, 在8个状态中的源头节点, 主要以民生银行、中信银行、工商银行和平安银行为主, 在状态1, 2, 3中以民生银行为源头节点, 状态1, 2, 3涵盖了2013年钱荒到2015年股灾阶段, 在2013年钱荒阶段, 民生银行是第一个出来发声的银行, 在2013年6月25日休市后民生银行随即召开投资者电话会议, 声明其流动性正常. 美银美林在参加该会议后, 赞扬民生银行是一个关心少数股东权益投资者及回应投资者担忧的银行, 并称民生银行仍是中国内地少数几个“可投资的”银行之一, 建议“买入”. 此外, 巴克莱在电话会议之后, 亦给予了民生银行同步大市的投资评级. 可见, 民生银行在状态1, 2, 3期间面临风险的稳健性是最强的. 在状态4, 7, 8中, 中信银行作为头节点出现, 表示在3种状态中, 中信银行面对风险稳健性最强. 在状态5中, 中国工商银行作为头节点出现, 表示在全球金融危机发生前后, 中国工商银行面对风险的稳健性最强.
在8个状态的演化过程中, 浦发、华夏、招商、北京、上海、建设、宁波这7家商业银行的出度都是0, 说明这些银行的传染效应是最小的. 值得特别注意的是, 建设银行作为4大银行之一, 在所有状态下出度都为0, 说明国有银行中, 建设银行的向外风险传染效应最小.
2 -->

3.3.银行时变状态网络的社团结构与风险传染特征

在分析8个状态内部网络结构后, 为了探求聚成8类的46个时间段的拆借矩阵之间的时变特征以及动态演化, 本文利用PMFG方法构建时间状态网络, 并用Girvan-Newman算法^[28]进行社团划分. 如图8所示, 本文取Q值最大$Q = 0.641$时构建社团, 整个时间网络被分为5个社团. 其中, 红色社团中的圆圈A所圈住的区域为全球金融危机发生阶段, 这和图3中的A圆圈所圈内容是一致的. A圆圈中的2008Q2, 2008Q3没有和2008Q1直接相连, 这和本文3.1.1中叙述的“危机是状态和状态之间的跳跃理论”是类似的. 对于B圆圈所代表的2013年钱荒事件, 虽然和前面的时间节点2013Q1直接相连, 但是不属于一个社团, 说明2013Q1和2013Q2所代表的银行拆借网络之间的相似度比社团内部的相似度低. 对于C圆圈和D圆圈, 共属于一个社团, 并且直接相连, 表示2014年下半的股票市场“红热化”和2015年的股灾事件是一个连续的状态演化, 银行网络的拓扑结构并没有发生突变, 而是较相似. 进一步, 可以从蓝色社团中看出2019Q1所代表的节点和B圆圈所代表的钱荒事件直接连接, 并且同属于一个社团, 表示两个时间段的银行之间的拆借网络结构是相似的, 这可以为银行系统风险预警提供策略支持.
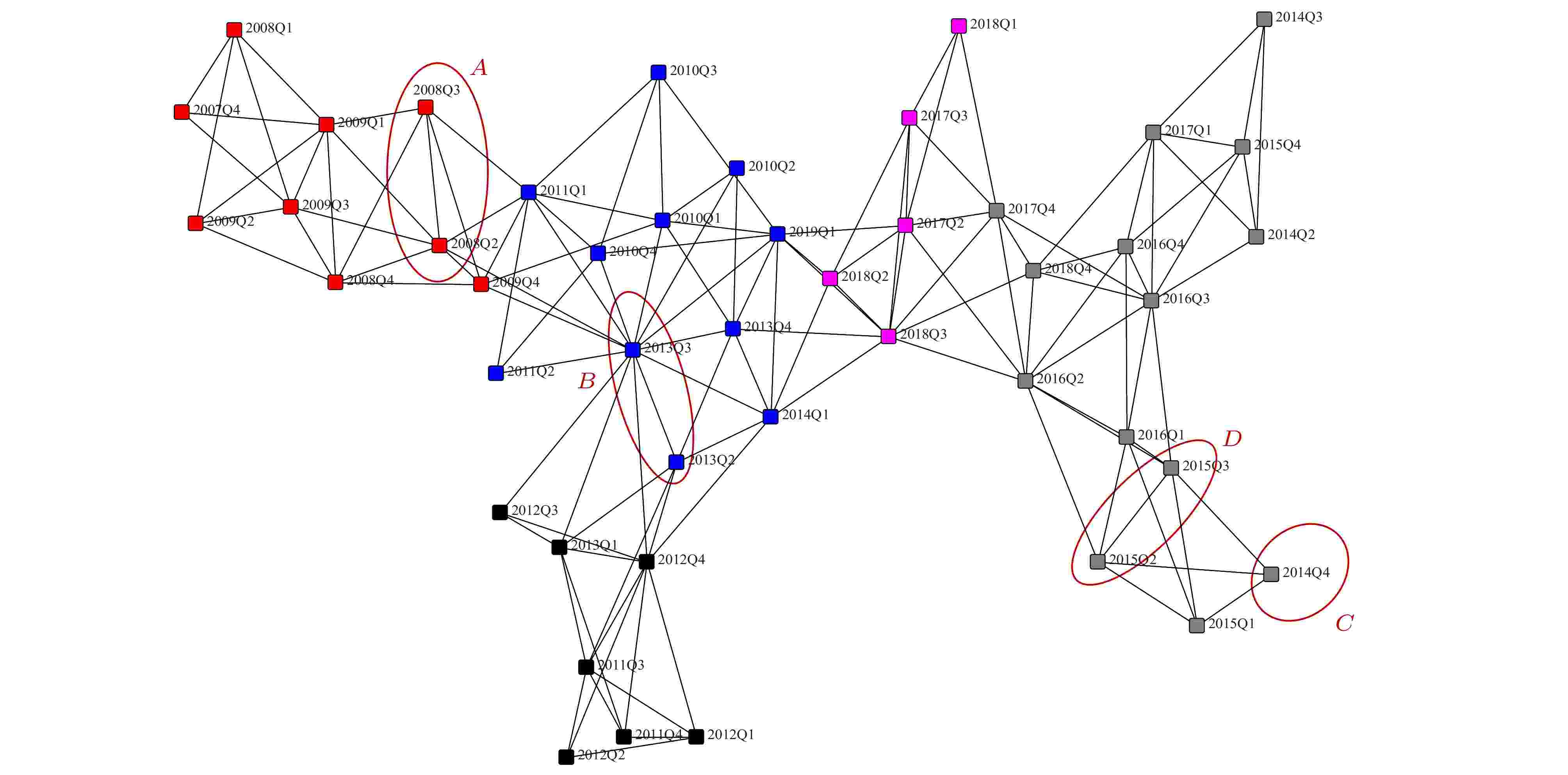图 8 各个时间状态下拆借矩阵关系
Figure8. Lending matrix relationship in different time states.

本文基于时变金融状态网络动态演化视角, 利用中国15个商业银行2007年第4季度到2019年第1季度的年报为研究数据, 采取最大熵方法构建了各个时间段的银行拆借网络. 并且通过kmeans算法将银行拆借矩阵分为8个状态, 同时利用DMST算法提高阈值法的客观性、丰富MST算法的方向性, 并对各个状态矩阵进行可视化. 最后, 本文通过PMFG算法滤除欧氏距离矩阵中阈值法难以判别的噪声信息, 并利用Girvan-Newman算法分析各个时间状态的银行网路之间的关系. 本文的主要结论和建议如下:
1) 对于连续的银行状态矩阵, 状态之间的短期连续跳跃性可以有效地刻画金融危机的发生. 2008年的全球金融危机发生前后出现了两个状态的短期跳跃, 从2013年“钱荒”一直到2015年的股灾阶段, 先后出现了四个状态的短期跳跃. 因此, 监管部门应该警惕银行状态之间的短期连续跳跃.
2) 从各个状态的有向银行网络可以看出, 不同银行的网络位置(结构)与银行风险传染效应(程度)密切相关. 其中, 国有大型商业银行在银行间市场中处于核心位置, 但四大银行的风险传染效应不同. 四大银行中, 中国银行和中国工商银行在各个状态下出度最大, 表明中国银行和中国工商银行的风险传染效用最强. 建设银行在各个状态下的出度都为零, 表明建设银行的风险传染效应最小. 从入度考虑, 民生银行和中信银行都有三个状态是头节点(入度为零), 表明民生银行和中信银行面临风险的稳健性较强. 这表明, 本文中各个状态有向生成树的动态入度研究可以为银行风险稳健性评级提供有效的量化支撑.
第3) 连续的动态银行网络之间具有记忆特征, 金融系统性风险的出现会破坏这种记忆性, 具体体现在状态网络相关性的突变. 比如, 2008年金融危机发生前后的银行状态矩阵的全局相似度是最低的, 而2013年“钱荒”后的银行状态矩阵的全局相似度是最高的, 表明两次危机的银行网络拓扑特性相差很大. 特别的, 从构建的平面最大过滤图可以看出, 2019年第一季度的银行状态网络节点和2013年“钱荒”所代表的网络节点相连, 表示两个时间状态的银行网络连接相似, 这可以为银行监管部门进行系统性风险防范提供有益的策略.
上述研究对我国防范系统性金融风险有如下政策含义: 一是有效识别在风险传染中的系统重要性银行, 实施差异化监管. 二是对风险传染扩散的形成路径(渠道)动态跟踪, 提高预警监测的效率, 阻断风险的传染扩散.