摘要:利用传统固相法制备了(1–x)K_0.5Na_0.5NbO₃-xBi(Mg_0.5Ti_0.5)O₃ (简写: (1–x)KNN-xBMT, x = 0.05, 0.10, 0.15, 0.20)无铅弛豫铁电陶瓷, 并对其相结构、微观形貌、介电特性与储能行为进行了系统的研究. 研究结果表明, 随着BMT含量的增加, (1–x)KNN-xBMT陶瓷由正常铁电体逐渐转变为弛豫铁电体, 表现出强烈的弥散相变特征, 其最大极化强度P_max随之逐渐降低. 当x = 0.15时, 陶瓷具有最大的击穿电场, 为275 kV·cm^–1. 采用间接方式对(1–x)KNN-xBMT陶瓷的储能性能进行计算, 发现当BMT的含量为x = 0.15时, 可获得最佳的储能性能: 当场强为275 kV·cm^–1时, 可释放储能密度W_rec为2.25 J·cm^–3, 储能效率η高达84%. 鉴于实际应用的需求, 对各组分陶瓷进行直接测试, 结果表明随掺杂量的增加, 储能密度W_dis呈现先增大后减小的变化趋势, 当x = 0.15时, 储能密度为1.54 J·cm^–3, 放电时间仅为88 ns. 另外, 该材料在1—50 Hz范围内具有良好的频率稳定性, 在25—125 ℃范围内具有良好的温度稳定性, 储能密度的变化量低于8%. 该研究表明KNN-BMT陶瓷在环境友好高储能密度电容器领域具有广阔的应用前景.
关键词: K_0.5Na_0.5NbO₃基/
储能性能/
无铅/
弛豫铁电/
直接测试

English Abstract

全文HTML

--> --> -->

随着电子设备的飞速发展, 大功率储能器件受到了广泛的关注. 在众多的储能器件(超级电容器、电池和介电储能电容器)中, 介电储能电容器具有充放电速度快、功率密度高、循环寿命长等优点, 在电子束、高功率微波炉、定向能武器、电磁装甲、混合动力汽车等领域显示出巨大的应用优势^[1-4]. 介电材料是大功率储能器件的核心部件, 常用的介电材料可分为两类: 聚合物和陶瓷. 聚合物材料由于具有很高的击穿电场强度(breakdown strength, BDS, 高达8000 kV·cm^–1)^[5-7], 通常具有较高的可释放储能密度W_rec. 然而, 聚合物介电材料的熔融温度较低, 其介电性能随着工作温度的升高会显著下降, 导致聚合物介电材料的工作温度范围(小于100 ℃)相对较低, 阻碍了其在混合动力汽车、航空航天、电力电子和天然气勘探等高温领域的应用. 而介电陶瓷由于其优异的温度稳定性和良好的介电性能被认为是大功率储能器件的理想候选材料^[8-11]. 但是介电陶瓷相对较低的储能密度严重制约了其实际应用进程. 因此, 探索具有高储能密度的介电陶瓷材料一直以来都是国内外****研究的热点^[12-38].
一般来说, 根据极化特性的不同, 介电陶瓷材料主要分为线性陶瓷、反铁电陶瓷、铁电陶瓷及弛豫铁电陶瓷. 其储能密度可以利用电滞回线即P-E曲线来计算^[36-38], 公式如下:
总储能密度

$ W={\int }_{0}^{P{\rm{m}}{\rm{a}}{\rm{x}}}E{\rm{d}}P; $

可释放储能密度

$ {W}_{{\rm{r}}{\rm{e}}{\rm{c}}}={\int }_{{P}_{{\rm{r}}}}^{{P}_{{\rm{m}}{\rm{a}}{\rm{x}}}}E{\rm{d}}P; $

储能效率

$ \eta = (W_{\rm rec}/W)\times 100\%. $

这里P_max, P_r, P和E分别表示最大极化强度、剩余极化强度、极化强度和外加电场. 从(2)式可知, 要获得高的W_rec, 需要大的极化差值ΔP (ΔP = P_max – P_r)和高BDS. 线性陶瓷的η和BDS较高, 而P_max较低, 故其储能密度相对较低. 反铁电陶瓷材料在充放电过程中因发生相变而容易产生裂纹, 使其充放电循环寿命较短. 铁电陶瓷的P_max较高, 但其ΔP较小, 故其储能密度和储能效率不佳. 相比而言弛豫铁电陶瓷具有较高的P_max、较低的P_r, 更适用于高储能密度电容器的开发.
近年来, 世界各国对环境保护和可持续发展提出了越来越多的要求, 因此开发无铅能源材料具有重大的意义. 为满足这些要求, 研发了一系列对环境友好的钙钛矿型铁电材料, 比如BaTiO₃ (BT)基、(Bi_0.5Na_0.5)TiO₃ (BNT)基、AgNbO₃ (AN)基、NaNbO₃ (NN)基、BiFeO₃ (BF)基和(K_0.5Na_0.5)NbO₃ (KNN)基等^[15-35]. 例如, Shen等^[22]制备了0.85BaTiO₃-0.15BiYbO₃弛豫铁电陶瓷, 其BDS仅为100 kV·cm^–1, 获得W_rec仅为0.5 J·cm^–3. Zheng等^[24]通过添加适当的化合物来调整BF陶瓷的弛豫行为以及畴结构, 在0.61BF-0.33BT-0.06Ba (Mg_1/3Nb_2/3)O₃陶瓷中, 125 kV·cm^–1时具有高的最大极化P_max和低的剩余极化P_r, 从而获得了W_rec为1.56 J·cm^–3. 文献[26-28]研究了AN基陶瓷的储能性能, 通过元素掺杂使AN基陶瓷的反铁电稳定性增强, 降低了P_r, 提高了BDS, 从而获得了较大的W_rec^[26–28]. 近几年, 对KNN基陶瓷储能性能的研究成为储能领域的热点^[29-33], 并且取得了一定的进展. Qiao等^[29]制备了0.93K_0.5Na_0.5 NbO₃-0.07Bi_0.6(Mg_1/3Nb_2/3)O₃陶瓷, 将BDS提高至160 kV·cm^–1, 其W_rec为1.3 J·cm^–3. Yang等^[32]在KNN陶瓷中添加SrTiO₃, 形成了具有弛豫特性的固溶体, 同时BDS得到大幅度提高. 在电场幅值为400 kV·cm^–1情况下, W_rec高达4.03 J·cm^–3.
通过以上工作发现, 弛豫铁电体具有高P_max、低P_r和超高的储能效率η, 因而被认为是一种很有前途的储能材料. 本文将通过在KNN基陶瓷中添加Bi(Mg_0.5Ti_0.5)O₃, 利用Bi³⁺和[Mg_0.5Ti_0.5]³⁺分别替换KNN结构的A位的Na, K离子和B位的Nb离子, 可以破坏材料原有晶体结构的原子排布, 降低晶胞对称性从而使其原有晶体结构发生畸变, 破坏KNN陶瓷的长程有序, 将KNN陶瓷由正常铁电体变为弛豫铁电体; 同时, 由于纯KNN中Na, K易挥发, 很难制备出结构致密的陶瓷, 而Bi的熔点较低, 随着BMT含量的增加可以使陶瓷在烧结的过程中产生液相降低内部缺陷, 有利于减小晶粒尺寸和孔隙率, 减小损耗, 提高材料的BDS, 从而获得较大的储能密度和储能效率. 研究思路如图1所示.
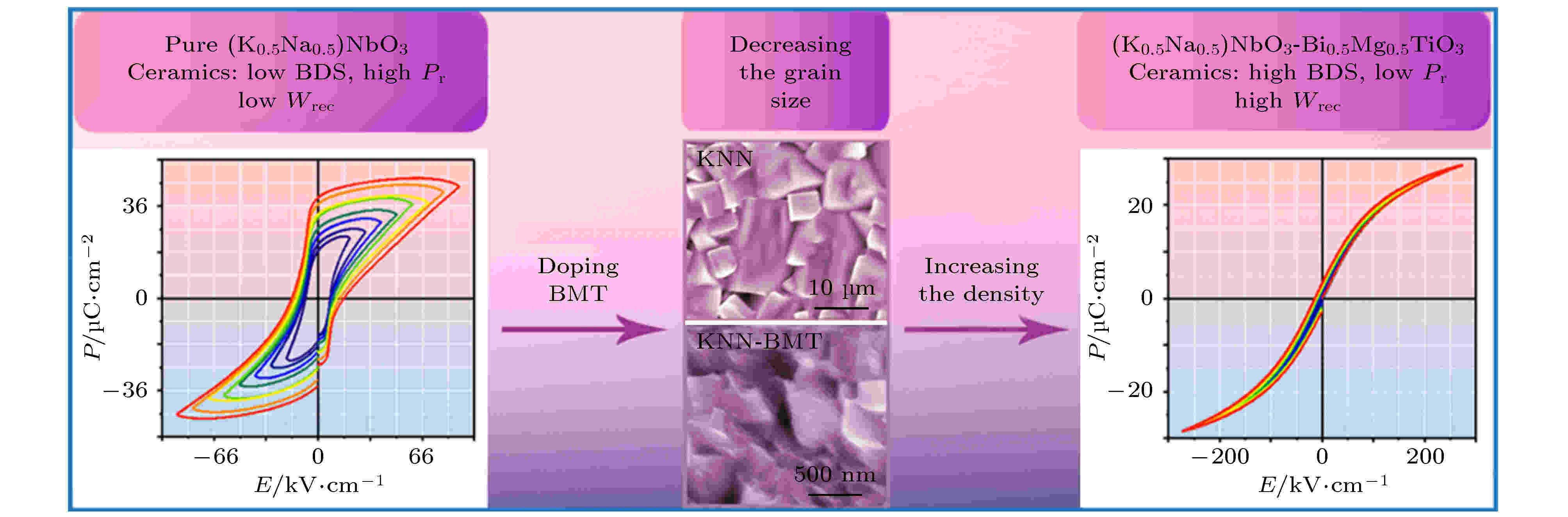图 1 通过组分掺杂减小晶粒尺寸获得铌酸钾钠陶瓷高储能密度的示意图
Figure1. Schematic diagram showing the increase of W_rec through decreasing the grain size by doping BMT in KNN ceramics.

2

-->

2.1.实验方法

采用传统的固相烧结法制备(1–x)K_0.5Na_0.5NbO₃-xBi(Mg_0.5Ti_0.5)O₃ ((1–x)KNN-xBMT)无铅弛豫铁电陶瓷. 所有原料均为国药集团化学试剂有限公司生产. 将原料碳酸钾(K₂CO₃, 99%)、碳酸钠(Na₂CO₃, 99.8%)、五氧化二铌(Nb₂O₅, 4N)、三氧化二铋(Bi₂O₃, 99%)、氧化镁(MgO, 98.5%)、二氧化钛(TiO₂, 98%)按化学计量式称量, 置于尼龙球磨罐中. 通过采用行星式球磨机(QM-3SP2, 南京大学仪器厂)将称量后的粉体进行24 h混匀. 将混匀的浆料过滤后, 在烘箱中干燥. 接下来, 将烘干后的粉体置于氧化铝坩埚中于马弗炉中预烧, 在850 ℃下保温6 h. 随后, 对预烧后的粉体再一次进行球磨24 h, 可以得到(1–x)KNN-xBMT陶瓷粉体. 然后, 用浓度为8%的聚乙烯醇溶液作为黏结剂进行造粒, 压制成直径为1 cm的陶瓷坯体. 接下来, 在200 MPa压力下对陶瓷坯体进行冷等静压, 以得到更为致密的陶瓷坯体. 随后, 将陶瓷坯体放在氧化铝坩埚中于600 ℃下进行排胶, 保温6 h. 最后, 在各组分陶瓷坯体的最佳烧结温度(分别为1080, 1090, 1100, 1110和1120 ℃)下进行烧结, 得到浅黄色的(1–x)KNN-xBMT 陶瓷样品.
2 -->

2.2.测试仪器

利用X射线衍射仪(XRD, Bruker D8 Advance, 德国)对陶瓷样品的相结构进行表征. 采用扫描电子显微镜(SEM, ZEISS Sigma 300, 德国)表征该铁电陶瓷的微观形貌. 为了进行陶瓷样品介电性能和电学性能的测试, 需将陶瓷样品打磨抛光厚度约为150 μm, 并利用离子溅射仪在陶瓷表面镀上直径为2 mm金点作为陶瓷测试样品的顶电极. 采用E4980A LCR介电性能测试仪和Linkam冷热台联用测试样品介电常数随温度的变化曲线. 陶瓷的电滞回线(P-E曲线)的测试是由综合铁电测试系统完成, 即Radiant Technologies, Inc., Albuquerque, NM系统. 采用快速充放电的脉冲系统—电阻-电感-电容(R-L-C)电路测试系统^[39,40]进行陶瓷样品储能性能和放电时间的直接测试. 如图2所示, 用一个高压电源, 连接在陶瓷样品的正负极对其充电, 然后调节电磁继电器, 使已经充电的样品作为放电源, 连接一个电阻, 同时在放电电路里连接一个示波器, 以读取陶瓷样品所释放的电流波形图^[41-45].
图 2 直接测试系统的电路示意图
Figure2. Circuit diagram of direct test system.

2

-->

3.1.相结构和微观形貌

图3为 (1–x)KNN-xBMT陶瓷的XRD图谱. 从该XRD图谱可以看出, 所有陶瓷都具有单一的钙钛矿相, 没有第二相的出现, 结晶度较高, 表明BMT进入KNN的钙钛矿晶格, 形成KNN-BMT固溶体. 从图3可以看出: 纯KNN在2θ为45°附近具有(202)和(020)两个衍射峰, 呈现为典型正交相; 随着BMT含量的增加, 这两个衍射峰逐渐转变为(200)单峰, 表现为立方相^[34]. 这表明(1–x)KNN-xBMT陶瓷的晶体结构由正交相经伪立方相逐渐转变为立方相.
图 3 (1–x)KNN-xBMT 陶瓷的XRD图
Figure3. XRD patterns of (1–x)KNN-xBMT ceramics.

图4为在最佳烧结温度下(1–x)KNN-xBMT陶瓷的表面SEM图. 从图4可以看出随着BMT含量的增加, (1–x)KNN-xBMT陶瓷晶粒逐渐减小. 为了更直观地对样品晶粒尺寸进行分析, 研究了(1–x)KNN-xBMT陶瓷的晶粒尺寸分布, 插图显示了 (1–x)KNN-xBMT陶瓷在 x = 0.05, 0.10, 0.15和0.20的平均粒径分别为850, 350, 230和195 nm. 陶瓷晶粒尺寸的减小可能是由于BMT的加入抑制了氧空位的产生, 从而减弱了高温烧结中的传质过程所致^[29,46]. 此外, 相比其他组分, BMT含量为0.15的陶瓷粒径分布更窄, 说明其晶粒尺寸均匀性较高.
图 4 (1–x)KNN-xBMT 陶瓷的表面形貌SEM图, 插图为含有平均粒径的粒径分布图　(a) x = 0.05; (b) x = 0.10; (c) x = 0.15; (d) x = 0.20
Figure4. SEM images of the (1–x)KNN-xBMT ceramics with their grain size distribution and average grain size inserted: (a) x = 0.05; (b) x = 0.10; (c) x = 0.15; (d) x = 0.20.

2 -->

3.2.介电性能

图5(a)为(1–x)KNN-xBMT陶瓷在–150 ℃至300 ℃以及KNN陶瓷在25 ℃至500 ℃温度范围内的介电常数随温度的变化曲线. 如图5(a)所示, 随温度的升高, KNN陶瓷经历了两次相变, 约在201 ℃由正交相向四方相转变, 约在402 ℃由四方相向立方相转变. 而(1–x)KNN-xBMT陶瓷在此温度范围内仅观察到一个宽泛的介电峰, 并且随BMT含量的增加, 最大介电常数所对应温度T_m分别从402 ℃降低到193, 57, 8和–6 ℃, 发生从四方相到立方相的相变. 杜红亮课题组研究表明^[30-33], 少量化合物的加入可显著降低KNN基陶瓷的相变温度, 如(1–x)KNN-xBi(Mg_2/3Nb_1/3)O₃, (1–x)KNN-xSr(Sc_0.5Nb_0.5)O₃, (1–x)KNN-xSrTiO₃, (1–x)KNN-xBiFeO₃等. 此外, 相应T_m处的最大介电常数从纯KNN陶瓷的5500减少到1000左右, 适当降低介电常数有利于提高介电击穿电场^[30,47]. 结果表明, 随着BMT掺杂量的增加, T_m附近的相变温度范围拓宽, 发生弥散相变, 说明KNN-BMT是一个弛豫铁电体. 此外, 弛豫行为也可以用修正的居里-外斯定律^[48]来分析: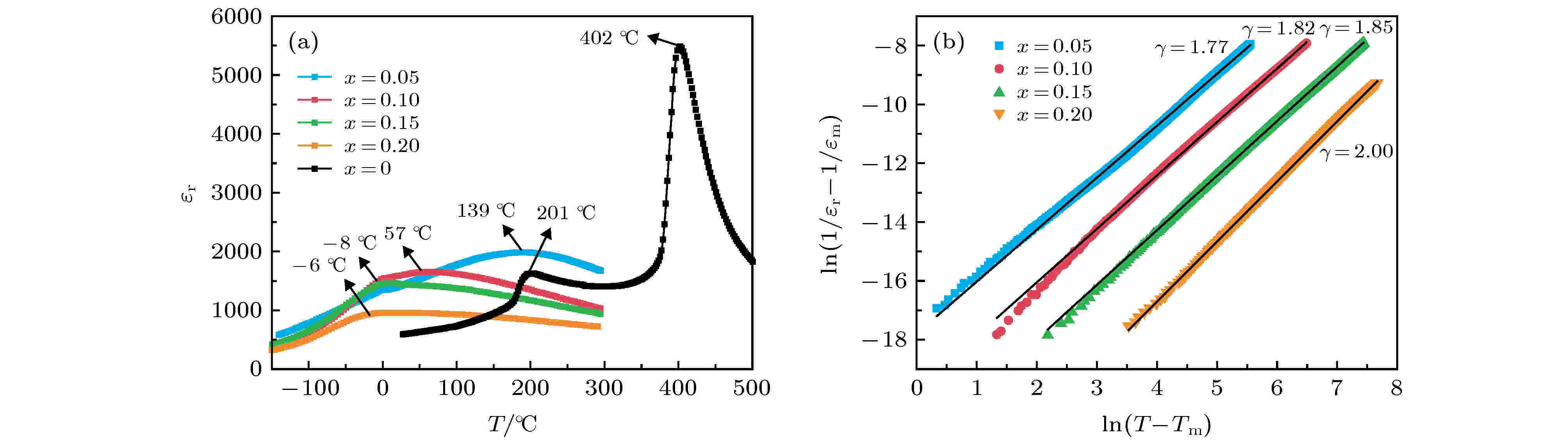
图 5 (a) (1 – x)KNN-xBMT陶瓷在–150 ℃至300 ℃以及KNN陶瓷在25 ℃至500 ℃的介电常数随温度的变化; (b) ln(1/ε_r–1/ε_m) 随ln(T–T_m)的变化
Figure5. (a) Dielectric constant as a function of temperature in a temperature range of –150 ℃ to 300 ℃ for (1 – x)KNN-xBMT ceramics and 25 ℃ to 500 ℃ for pure KNN ceramics; (b) plots of ln(1/ε_r–1/ε_m) versus ln(T–T_m) of the (1–x)KNN-xBMT ceramics.

$ \frac{1}{{\varepsilon }_{{\rm{r}}}}-\frac{1}{{\varepsilon }_{{\rm{m}}}}=\frac{{\left(T-{T}_{{\rm{m}}}\right)}^{\gamma }}{C}, $

其中γ为弥散系数, C为居里常数. 通常, 当γ = 1时, 材料为典型铁电体; 而γ = 2时, 材料为理想的弛豫铁电体. 图5(b)为(1–x)KNN-xBMT陶瓷在100 kHz时ln(1/ε_r –1/ε_m)随ln(T –T_m)的变化曲线图, 并利用拟合曲线的斜率计算得到γ值. 随BMT含量的增加, γ值明显增大. x从0.05增大到0.20时, γ从1.77增加到2.0, 表明(1–x)KNN-xBMT陶瓷具有较强的弛豫行为.
2 -->

3.3.电学性能和储能行为研究

图6为(1–x)KNN-xBMT 陶瓷在60 kV·cm^–1电场下P-E曲线和I-V电流回线. 由图6可以看出, 纯的KNN陶瓷具有典型的铁电P-E曲线, 即具有大的饱和极化P_max和剩余极化P_r以及高的矫顽场E_c. 从电流回线可以看出在一个循环电场内只有两个尖锐的电流峰出现, 再次验证纯的KNN陶瓷具有正常铁电体的特征. 在60 kV·cm^–1电场条件下, 纯KNN陶瓷的最大极化值可以达到35 μC·cm^–2, 最大剩余极化值为30 μC·cm^–2. 相比于纯KNN陶瓷, P_max, P_r和E_c随着BMT含量的增加均显著降低, 且电流回线的两个尖锐的峰随BMT含量增加也明显变得平缓, 当x = 0.1时两个电流峰几乎消失. 这是由于BMT的加入打乱了陶瓷中长程有序的铁电畴结构, 进而产生极性纳米区域, 使得陶瓷由铁电体转变为弛豫铁电体^[19,49,50]. 进一步增加BMT的含量, P-E曲线几乎变为一条直线, 由图6(e)可知在x = 0.2时P-E曲线的剩余极化值几乎为零, 相比于纯KNN陶瓷其饱和极化大幅下降. 上述现象表明, 随BMT含量的增加, 材料发生了由正常铁电体向弛豫铁电体进而向顺电体的转变.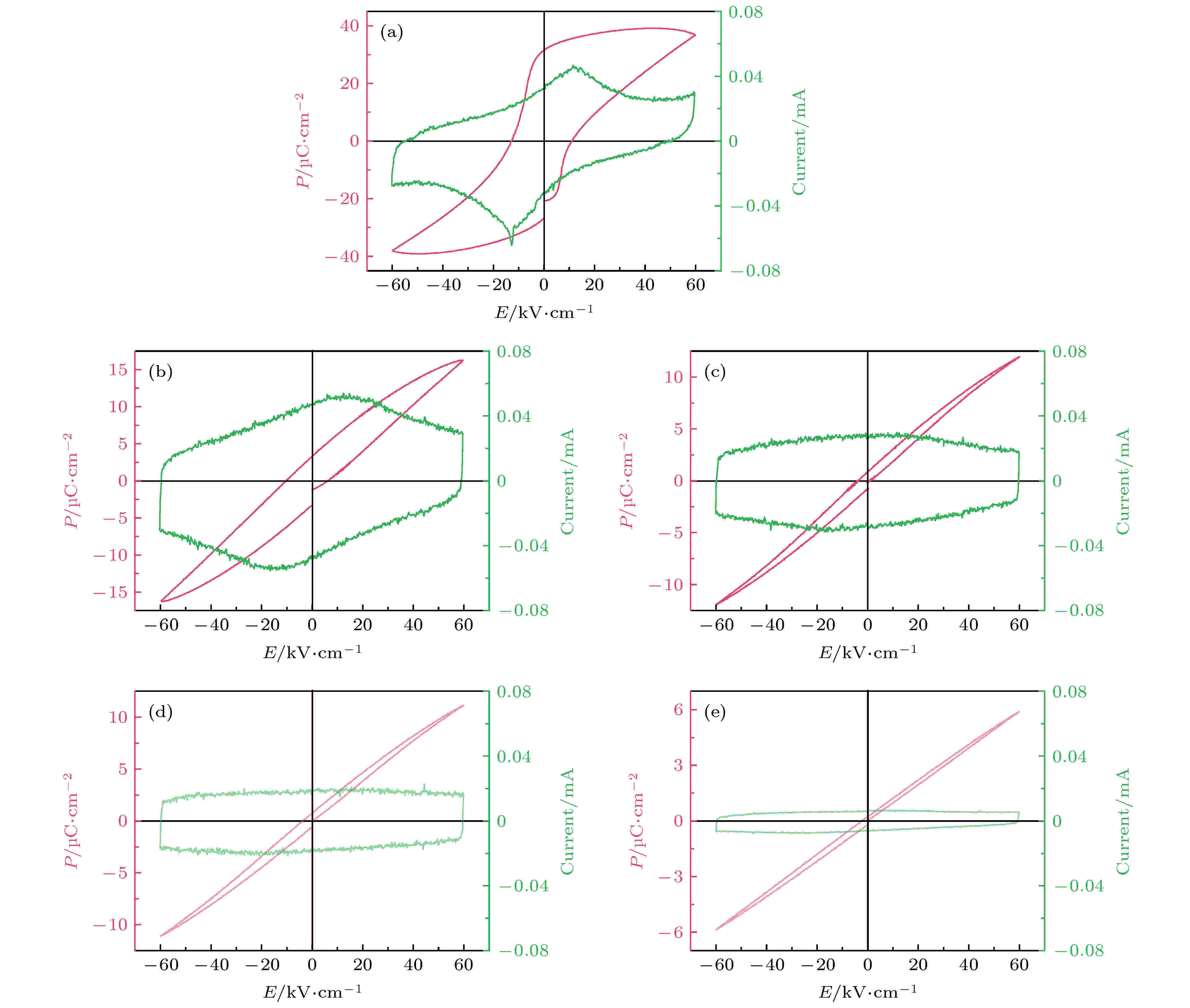
图 6 (1–x)KNN-xBMT 陶瓷在60 kV·cm^–1电场下P-E曲线和电流回线(I-E)　(a) x = 0; (b) x = 0.05; (c) x = 0.10; (d) x = 0.15; (e) x = 0.20
Figure6. P-E loop and I-E curves under 60 kV·cm^–1 electric field of the (1–x)KNN-xBMT ceramics: (a) x = 0; (b) x = 0.05; (c) x = 0.10; (d) x = 0.15; (e) x = 0.20.

图7(a)显示了(1–x)KNN-xBMT陶瓷在其击穿电场下测得的P-E曲线. 从图7(a)可以看出, 随着BMT含量的增加, P-E逐渐变纤细, 表明弛豫行为逐渐增强^[24,25]. (1–x)KNN-xBMT在x = 0.05, 0.10, 0.15和0.20时, 于各自击穿电场下P_max和P_r值分别为37.5, 25.6, 28.7, 16.2 μC·cm^–2和7.9, 2.7, 3.4, 0.8 μC·cm^–2. (1–x)KNN-xBMT陶瓷的储能密度和储能效率如图7(b)所示. 随着BMT含量x的增加, (1–x)KNN-xBMT陶瓷的W_rec先增大后减小. 在0.85KNN-0.15BMT陶瓷中获得了2.25 J·cm^–3的最大储能密度. 除了在BMT掺杂量较低(x = 0.05)时由于P_r较大而导致储能效率较低(61%)之外, 其他掺杂量的陶瓷均获得了很高的储能效率, x = 0.10, 0.15, 0.20时分别为87%, 84%和90%. 比较相同电场下(四种组分中最低的击穿电场185 kV·cm^–1)不同BMT掺杂量时的P-E曲线和储能行为, 如图7(c)和图7(d)所示. 从图7(c)和图7(d)可知, (1–x)KNN-xBMT在x = 0.05, 0.10, 0.15和0.20时, 在相同电场下它们的P_max和P_r值分别为35.6, 21.6, 24.3, 16.2 μC·cm^–2和7.0, 2.2, 2.2, 0.8 μC·cm^–2. 随着BMT含量的增加, (1–x)KNN-xBMT陶瓷的W_rec先减小后增大然后再减小, 这是因为在掺杂量较低时, (1–x)KNN-xBMT陶瓷的饱和极化值非常大, 所以掺杂量为5%时, 在相同电场下储能密度最大. 但储能效率随BMT掺杂量的增加而不断提高, 主要是因为弛豫行为逐渐增强. 相比而言, x = 0.15的陶瓷兼具较高储能密度与储能效率, 该陶瓷为最佳组分.
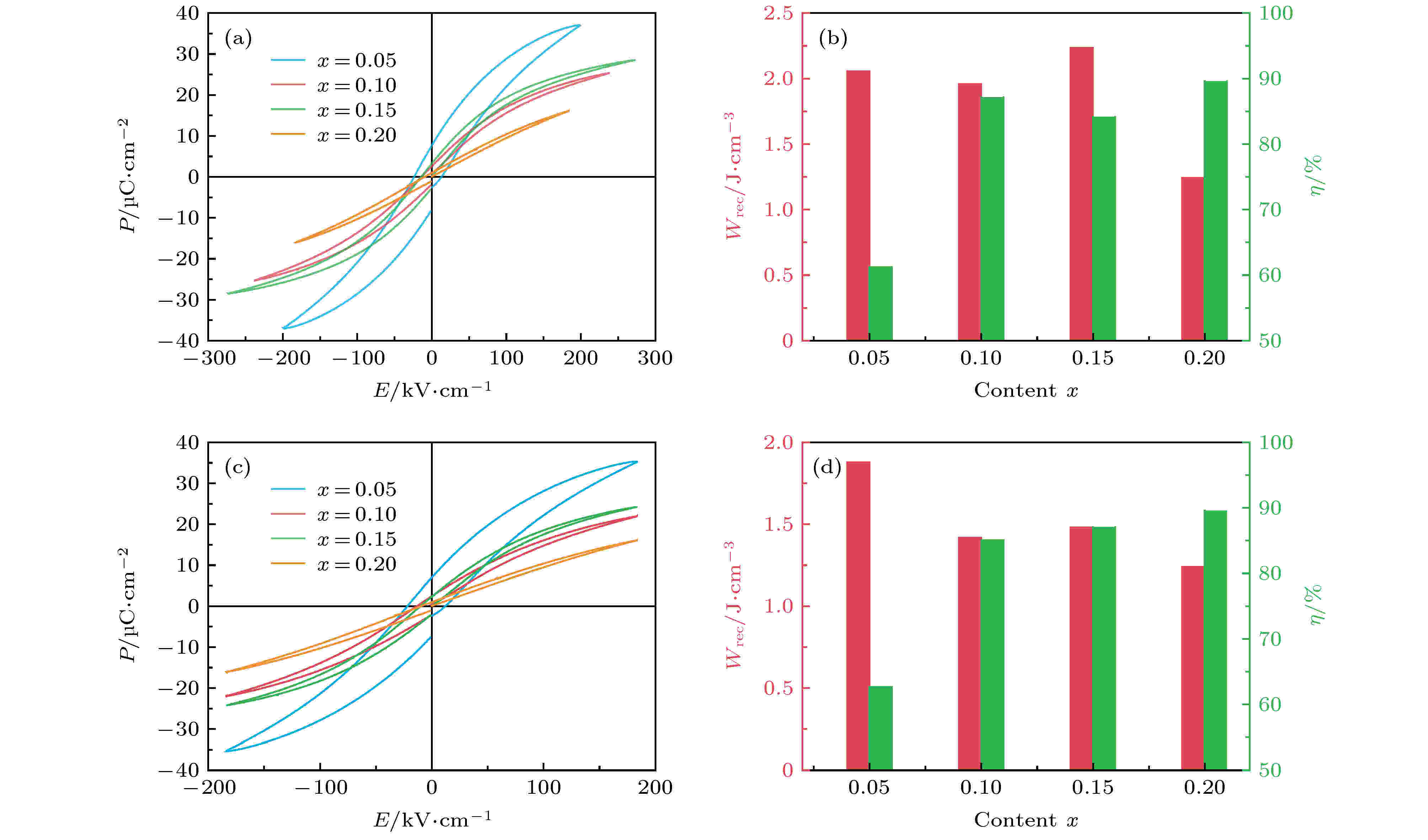图 7 (1–x)KNN-xBMT陶瓷在击穿电场下的(a) P-E图以及(b)储能密度和储能效率; (1–x)KNN-xBMT陶瓷在185 kV·cm^-1电场下的(c) P-E图以及(d)储能密度和储能效率
Figure7. (a) P-E loops, (b) W_rec and η of (1–x)KNN-xBMT ceramics at the maximum applied electric fields; (c) P-E loops, (d) W_rec and η of (1–x)KNN-xBMT ceramics under 200 kV·cm^–1 electric fields.

图8(a)为0.85KNN-0.15BMT陶瓷在不同电场下的P-E曲线. 随着电场强度从25 kV·cm^–1增加到275 kV·cm^–1, P_max值从5.2 μC·cm^–2增加到28.6 μC·cm^–2. 图8(b)显示了0.85KNN-0.15BMT陶瓷的W_rec和η随外加电场的变化, 0.85KNN-0.15BMT陶瓷的W_rec随外加电场的增大而逐渐增大, 证明了通过提高击穿电场来获得高W_rec的可行性. 正如所预期的, W_rec在最大外加电场275 kV·cm^–1时达到最大值2.25 J·cm^–3. 此外, 储能效率在整个测试电场范围内几乎都保持一个较高的85%的恒定值. 这可以归因于在整个测试电场范围内, 0.85KNN-0.15BMT陶瓷的P-E曲线保持纤细的弛豫性曲线不发生变化. 为进一步证明0.85KNN-0.15BMT陶瓷良好的储能性能, 在不同频率和不同温度下对其进行了研究. 图8(c)和图8(d)为0.85KNN-0.15BMT陶瓷在200 kV·cm^–1电场下不同频率时所得到的P-E曲线以及储能密度和储能效率随频率的变化. 从图8(c)可以看出, 随着测试频率的减小, P_s和P_r都略有增大, 但是差值基本不变, 使得储能密度基本不变. 从计算结果来看(图8(d)), 频率从1 Hz变化到50 Hz时, 储能密度分别为1.54, 1.61, 1.61, 1.60 J·cm^–3, 变化值小于5%, 具有良好的频率稳定性. 0.85KNN-0.15BMT陶瓷在150 kV·cm^–1电场下25—125 ℃范围内的测试结果如图8(e)和图8(f)所示. 图8(e)显示随着测试温度的升高, P_max和P_r都基本没有变化, 差值变化不大, 从而使得储能密度基本不变. 第三象限开口略有增大, 说明漏电有所增加, 储能效率有所降低. 从图8(f)可以看出, 当温度由25 ℃升高到125 ℃时, 储能密度由1.13 J·cm^–3先增大到1.20 J·cm^–3后又逐渐减小到1.02 J·cm^–3, 变化值小于10%, 具有较好的温度稳定性. 从多方面证明, 0.85KNN-0.15BMT陶瓷在较宽的电场范围内及较大的频率和温度范围内, 都能维持较高的储能密度及储能效率, 这使得其有着较好的应用前景.
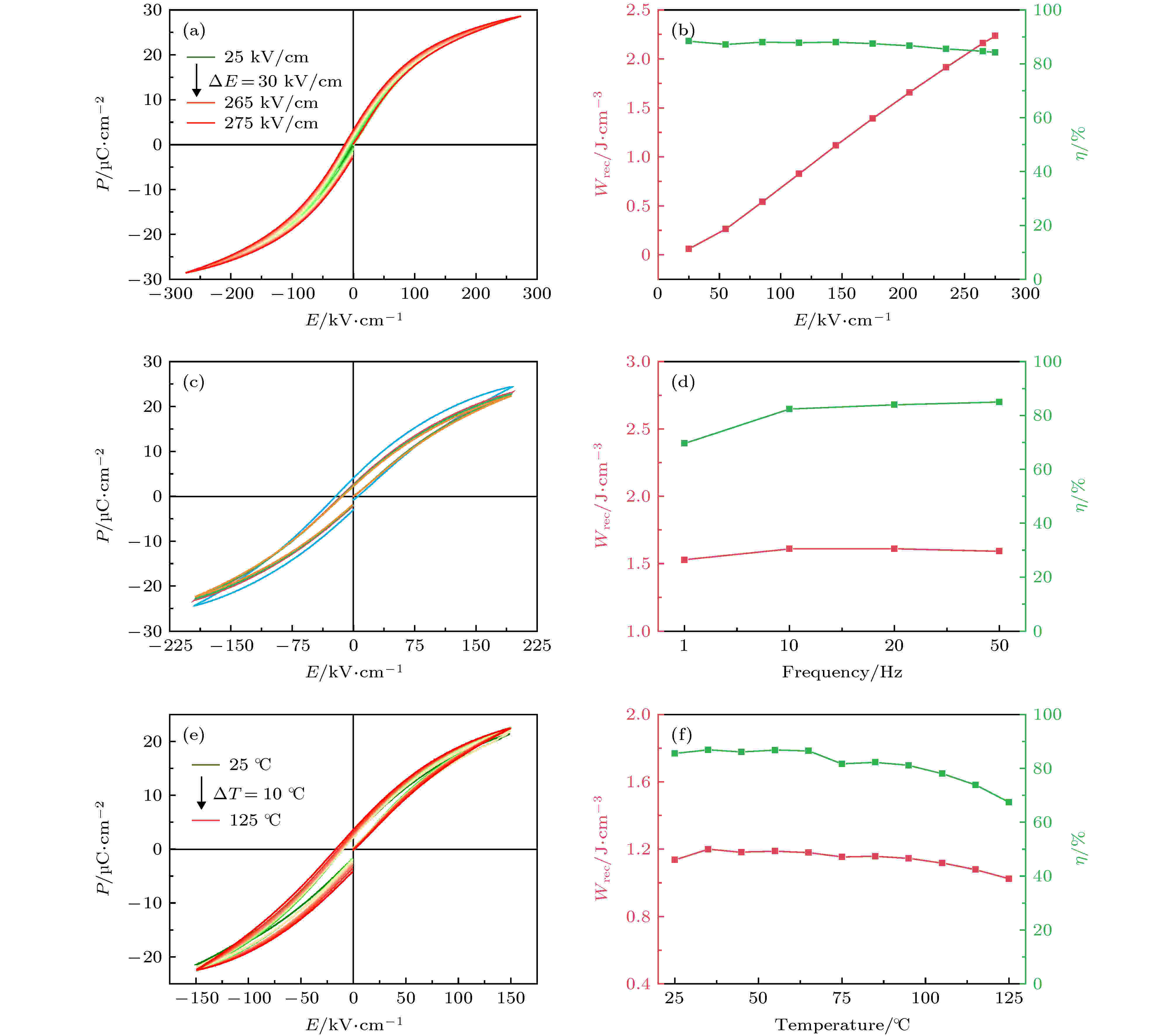图 8 0.85KNN-0.15BMT陶瓷在不同电场下的(a) P-E图以及(b)储能密度和储能效率; 在不同频率下的(c) P-E图和(d)储能密度和储能效率; 在不同温度下的(e) P-E图和(f)储能密度和储能效率
Figure8. (a) P-E loops and (b) W_rec and η under different electric fields, (c) P-E loops and (d) W_rec and η at different frequencies, (e) P-E loops and (f) W_rec and η at different temperatures of 0.85KNN-0.15BMT ceramics.

基于脉冲功率电容器的实际应用, 使用R-L-C电路测量了不同组分(1–x)KNN-xBMT陶瓷的放电电流曲线(负载电阻为200 Ω). 根据放电电流曲线, 可以利用(5)式计算样品的放电能量密度:

$ {W}_{{\rm{d}}{\rm{i}}{\rm{s}}}=\frac R{V} {\int {i}^{2}\left(t\right){\rm{d}}t}, $

其中W_dis表示快速充放电过程中释放的能量密度, 其单位为J·cm^–3; R代表负载电阻, i(t)代表示波器所检测到的放电电路中的电流波形图, V表示测试样品的体积. 图9(a)给出了(1–x)KNN-xBMT陶瓷在最大击穿电场下放电电流随时间的变化. 当掺杂量x = 0.05, 0.10, 0.15和0.20时, 对应的测试电场分别为120, 200, 200和200 kV·cm^–1, 其峰值电流分别为4.64, 8.48, 9.28和8.16 A, 测试所用的电极面积为0.0314 cm², 则与之相对应的电流密度分别为147.8, 270.1, 295.5和259.9 A·cm^–2. 从图9(b)可以看出, W_dis随着掺杂量呈现先增大后减小的趋势. 通常我们用90%的能量密度被释放所用的时间t₉₀来衡量材料放电速率的快慢. 如图9(b)所示, 所有(1–x)KNN-xBMT陶瓷样品的放电时间均小于102 ns, 表明了其放电速度较快. 在最佳掺杂量x = 0.15时, 陶瓷样品的放电时间仅为88 ns, 展现出超快的放电速度. 图9(c)是(1–x)KNN-xBMT陶瓷的直接测试和间接测试计算所得的储能密度比较图. 从图9(c)可以看出, 随着电场的增加, 由间接测试方法计算所得的储能密度值W_rec与直接测试方法所得到的储能密度W_dis呈现相同的变化趋势, 都是随掺杂量增加先增大后减小, 在掺杂量为0.15时得到最大值, 然而, W_dis略低于W_rec. 在许多文献中也观察到类似的结果^[12,19,51]. W_rec和W_dis之间的差别主要归因于P-E回线和充放电测量的不同测量机制. 通常, W_rec被定义为“准静态”结果, 因为它是从频率为10 Hz或更低的正弦波或三角波下的P-E回路导出的^[52]. 不同的是, W_dis被定义为“动态”结果, 因为它是从具有亚微秒周期的快速放电电流导出的. 结果表明, 在快速放电过程中, 畴壁运动引起的黏度增加导致W_dis下降. 一般认为, 对于实际运行中的电容器, W_dis值更接近实际结果. 当掺杂量x = 0.15时, W_rec为1.60 J·cm^–3, W_dis为1.54 J·cm^–3, 表明0.85KNN-0.15BMT 陶瓷具有良好的储能行为.
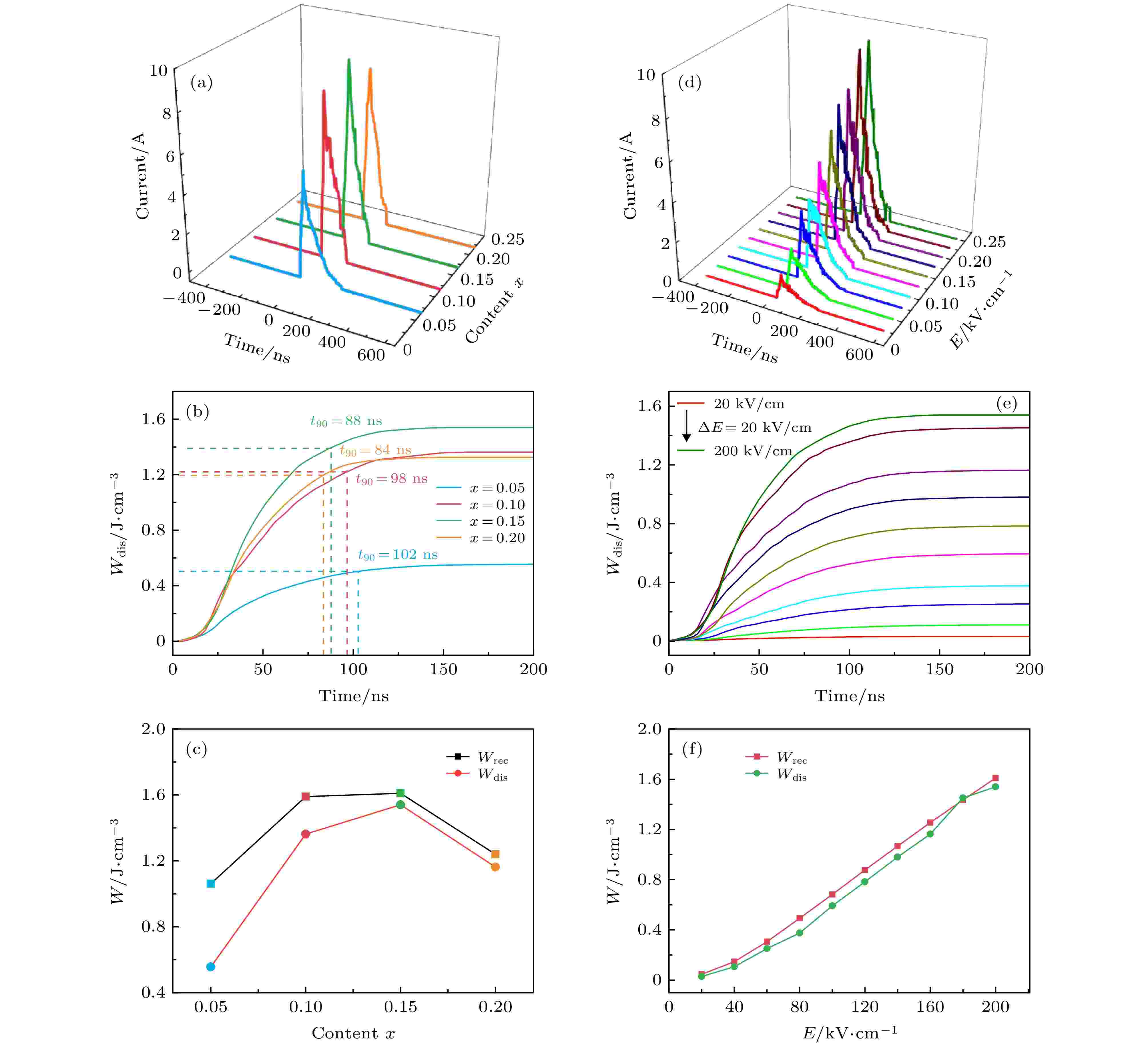图 9 (1–x)KNN-xBMT陶瓷在最大击穿电场下直接测试的(a)放电电流随时间的变化, (b)放电储能密度和放电速率t₉₀以及(c) W_dis和W_rec比较图; 0.85KNN-0.15BMT陶瓷在不同电场下直接测试的(d)放电电流随时间的变化, (e) 放电储能密度W_dis以及(f) W_dis和W_rec比较图
Figure9. (a) Pulsed discharge current curves, (b) discharge energy density W_dis and discharge time t₉₀, and (c) comparative figures of W_dis and W_rec under breakdown electric field of the (1–x)KNN-xBMT ceramics; (d) pulsed discharge current curves, (e) discharge energy density W_dis, and (f) the comparative figures of W_dis and W_rec under different electric fields of the 0.85KNN-0.15BMT ceramic

为了更直观地显示电流曲线的变化, 图9(d)描述了0.85KNN-0.15BMT 陶瓷在不同电场下的电流曲线. 放电电流和放电时间随着电场逐渐增加, 相应的放电能量密度随电场的变化如图9(e)所示. 随着电场从20 kV·cm^–1增加到200 kV·cm^–1, W_dis从0.2 J·cm^–3相应地增加到1.54 J·cm^–3, 并且在不同电场下的放电时间均非常短, t₉₀保持在80 ns左右. 图9(f)给出了采用两种测试方法计算所得的0.85KNN-0.15BMT陶瓷的储能密度图. 电场强度从20 kV·cm^–1增大到200 kV·cm^–1时, W_rec从0.05 J·cm^–3相应地增长至1.60 J·cm^–3, 而W_dis从0.03 J·cm^–3相应地增长至1.54 J·cm^–3, 在相同电场下W_rec比W_dis略大, 但相差不大. 在不同的电场强度下放电时间的持续时间非常短且稳定, 更利于其在脉冲功率电容器中的实际应用. 表1归纳了0.85KNN-0.15BMT陶瓷与其他一些无铅陶瓷材料的储能性能. 从表格数据可以看出: KNN基陶瓷比BNT基、BT基以及BF基陶瓷材料更易获得较高的BDS, 而本文工作和其他KNN基陶瓷相比在相对较低的BDS下获得了更高的η, 从而得到相对较大的W_rec.

Material systerm	Wrec/J·cm–3	η/%	BDS /kV·cm–1	Wdis/J·cm–3	t90/ns	Reference
0.88BT-0.12BMT	1.81	88	224	—	—	[20]
0.85BT-0.15BY	0.50	—	100	—	—	[22]
0.61BF-0.33BT-0.06BMN	1.56	75	125	—	—	[24]
0.7BNT-0.3ST + 0.05MnO2	0.96	74.6	95	—	—	[25]
0.8KNN-0.2SSN	2.02	81.4	295	—	—	[31]
0.85KNN-0.15ST	4.03	52	400	—	—	[32]
0.85KNN-0.15BMT	2.25	84	275	1.54	88	This work

表10.85 KNN-0.15 BMT陶瓷与其他部分无铅陶瓷储能性能的比较
Table1.Comparison of energy storage properties of 0.85 KNN-0.15 BMT ceramics and other lead-free ceramics.

本文利用传统固相法成功制备了(1–x)KNN-xBMT弛豫铁电陶瓷, 进行了相结构、微观形貌和介电行为研究, 并通过间接测试和直接测试两种方法对其储能行为进行了研究. 研究表明, 通过向KNN基陶瓷中掺杂BMT, 晶粒生长得到了抑制, 晶粒尺寸从850 nm (x = 0.05)减小到了195 nm (x = 0.20), 使陶瓷的致密度提高、孔隙率减小, 获得了较高的击穿电场. 电流回线表明: BMT的掺杂使KNN基陶瓷从正常铁电体向弛豫铁电体进而向顺电体转变. 在x = 0.15时, 获得最佳储能行为, 在击穿电场为275 kV·cm^–1时, W_rec达到2.25 J·cm^–3, η可达84%; 该材料还具有良好的频率稳定性, 在200 kV·cm^–1场强下, 1—50 Hz频率范围内, 储能密度的变化量低于5%; 同时其具有较好的温度稳定性, 在25—125 ℃温度范围内, 150 kV·cm^–1场强下, 储能密度的变化率在8%左右. 直接测试结果表明, 该组分在200 kV·cm^–1电场下, W_dis为1.54 J·cm^–3, 放电时间非常短, t₉₀仅为88 ns; 在20—200 kV·cm^–1测试范围内, 放电时间均很短, t₉₀在80 ns左右. 该研究表明KNN-BMT陶瓷在储能领域具有广泛的应用前景, 在满足可持续发展的未来能源需求方面具有潜在的应用价值.