摘要: 研究了三元过冷熔体中柱状晶体在非等温条件下受straining流作用的生长问题, 给出了柱状晶体生长形态的近似解析表达式. 发现流入的straining流加快了界面的生长速度, 而流出的straining流减缓了界面的生长速度, 即straining流使得柱状晶体的界面发生变形. 同时发现, 随着流动速度的增大, 界面变形也更为显著. 通过比较straining流对纯熔体、二元熔体、三元熔体中柱状晶体界面的影响, 发现相比于纯熔体, 柱状晶体在稀合金熔体中的界面形态受straining流的影响更大.
关键词: 柱状晶体 /
三元熔体 /
straining流 /
界面形态 English Abstract Effect of straining flow on growth of columnar crystal in ternary undercooled melt Fan Hai-Long Chen Ming-Wen School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China Received Date: 18 February 2020Accepted Date: 02 April 2020Published Online: 05 June 2020Abstract: As an important microstructure, columnar crystal growth technology, especially the growth technology of single columnar crystal plays an important role in improving the performances of semiconductor, optical devices and other related products. In many practical applications, because the alloy is composed of multi-component and there is inevitably flow in the melt, it is necessary to study the growth of columnar crystals in multi-component melt with flow separately. The growth of columnar crystal in a ternary undercooled melt subjected to straining flow under non-isothermal conditions is studied, and the approximate analytical expression for growth morphology of columnar crystal is given by using asymptotic method. It can be seen from the expression that straining flow is an important reason for irregular columnar crystal. When analyzing the effect of straining flow on the growth of columnar crystal in ternary melt, it is found that the incoming flow accelerates the growth velocity of the interface, while the outgoing straining flow reduces the growth velocity of the interface, namely, the straining flow makes the interface of columnar crystal deformed. At the same time, it is found that the interface deformation becomes more intense with the increase of flow velocity. The above conclusion can also be applied to the effect of straining flow on the interface morphology of columnar crystal in pure melt and binary melt. The comparison of the effects of straining flow on the interface of columnar crystal among pure melt, binary melt and ternary melt, shows that the interface morphology of columnar crystal in dilute alloy melt is more affected by straining flow than in the pure melt, but the more components are more easily affected by flow. However, the number of components in melt is not a decisive factor for the change of interface morphology of the columnar crystal, but the constitutional undercooling is an important factor for determining the interface morphology of multicomponent alloy. According to the conclusion of this paper, the influence of straining flow on the interface morphology of columnar crystal growth can be quantitatively predicted, which provides the necessary theoretical guidance in accurately controlling the interface morphology in the future.Keywords: columnar crystal /ternary melt /straining flow /interfacial morphology 全文HTML --> --> --> 1.引 言 在材料科学领域, 凝固过程可以看作是传热、传质的过程, 它决定着材料晶体微结构的形态及生长, 进而决定着材料的性能. 自Mullins和Sekerka[1 ] 开创性地研究了熔体中球形粒子的生长问题以来, 许多研究者开始关注这一理论, 并陆续推广到不同几何形状粒子的生长问题[2 -12 ] . 柱状晶体作为一种重要的微结构, 其生长技术特别是单个晶体的生长技术对于提升半导体、光学等相关产品的性能有着重要的作用. Coriell和Parker[13 ] 研究了溶质扩散、表面张力各向异性及界面动力学对柱状冰界面形态稳定性的影响, 得出了柱状晶体生长的临界半径. 陈亚军等[14 ] 通过实验说明了柱状晶体受晶粒淘汰机制和合并机制的共同作用. Du等[15 ] 利用相场法研究了柱状晶体的生长问题, 指出生长前沿浓度的不均匀是产生不规则柱状晶体的原因. 因为流动可以促使凝固前沿浓度的不均匀, 当然也就可以通过流动来控制柱状晶体的界面形态. 基于上述思想一些研究者开始研究各种流动对柱状晶体生长界面形态的影响. 例如, Murakami等[16 ] 通过实验研究发现柱状晶体在Cu-Al二元熔体中生长时向来流方向偏转, 且其偏转角是流动大小和熔体浓度共同作用的结果. Szajnar[17 ] 研究了Al-Cu合金的凝固过程, 指出温度的变化不足以使柱状晶向等轴晶转变, 其在实验中通过强加磁场使液态金属产生流动, 从而使凝固界面的浓度发生变化.[18 ] 研究了多组分熔体的凝固问题, 通过线性稳定性分析得出了随着组分的增加凝固前端变得更加不稳定的结论. 由此可见需要研究多组分熔体的凝固问题, 并深入研究多组分熔体中不同形状晶体微结构的生长问题. Colin[19 ] 研究了柱状晶体在三元熔体中弹性效应对界面形态影响的生长问题, 发现了一个由纯弹性效应引起的不稳定性. 由于熔体中不可避免地存在流动, 这就需要研究存在流动的多组分熔体中柱状晶体的生长问题.[20 ] 给出了柱状晶体界面形态的近似表达式. 分析了流动对柱状晶体界面形态的影响, 并比较了straining流对多组分熔体与单组分熔体柱状晶体界面形态影响的异同.2.理论模型 考虑单个初始半径为a 的无限长柱状晶体在straining流作用下的多组分过冷稀合金熔体中的生长问题. 建立以柱状晶体的中心轴为z 轴, 中心轴的中点为坐标原点O , 垂直于中心轴的横截面为$Oxy$ 平面的柱坐标系$(r, \theta, z)$ . 流场的速度U ${{U}}={c_1}x{{i}} + {c_2}y{{j}}$ 引起的, 其中${{i}}, {{j}}$ 为直角坐标系下的单位向量, $x, y$ 为直角坐标, ${c_1}, {c_2}$ 为常数且满足${c_1} + {c_2} = 0$ , 即连续性条件$\nabla \cdot {{U}} = 0$ 成立. 用${T_{\rm{L}}}$ 和${T_{\rm{S}}}$ 分别表示液相和固相的温度, ${T_{\rm{I}}}$ 表示界面温度, $C_{\rm{S}}^i$ 表示固相第个i 组分的浓度, $C_{\rm{L}}^i$ 表示液相第个i 组分的浓度, 并做如下假设: 1)扩散的相互作用、浮力效应和熔体压力忽略不计; 2)液相和固相中的密度相等; 3)由于实际中固体扩散系数比液体扩散系数小几个数量级, 故而假设溶质在液相中的扩散速率远大于固相, 即$D_{\rm{L}}^i \gg D_{\rm{S}}^i$ ; 4) 由于柱状晶体相对于整个熔体来说较小, 故而根据Mullins和Sekerka的观点, 认定远离柱状晶体几个波长的熔体为远场; 5)假设远场温度为${T_\infty }$ , 远场浓度为$C_\infty ^1$ 和$C_\infty ^2$ 且都为常数, 并视熔体为不可压缩的牛顿流体.a 为长度尺度; 特征速度$V=\dfrac{{{k_{\rm{L}}}\Delta T}}{{a\Delta H}}$ 为速度尺度, 其中${k_{\rm{L}}}$ 表示液相的热传导系数, $\Delta T = {T_{\rm{e}}} - {T_\infty }$ , ${T_{\rm e}}$ 表示平界面的液相平衡温度, ${T_\infty }$ 表示远场温度, $\Delta H$ 表示熔体单位体积的潜热; $C_{\rm{e}}^i - C_{\rm{S}}^i$ 为浓度尺度, 其中$C_{\rm{e}}^i$ 表示第i 个组分的液相平衡浓度, $C_{\rm{S}}^i$ 表示第i 个杂质的固相浓度; $\Delta H/({c_{\rm{p}}}{\rho _{\rm{L}}})$ 为温度尺度; ${{{k_{\rm{L}}}V}}/({{{c_{\rm{p}}}a}})$ 为压力尺度, 其中${\rho _{\rm{L}}}$ 为熔体的密度, ${c_{\rm{p}}}$ 为熔体的定压比热. 引入无量纲量${\kappa _{\rm{L}}}$ 表示液相的热扩散系数, ${\kappa _{\rm{S}}}$ 表示固相的热扩散系数, $D_{\rm{L}}^1$ 和$D_{\rm{L}}^2$ 分别表示液相中第一个组分和第二个组分的扩散系数, $Pr$ 是普朗特数, $\upsilon $ 表示熔体的黏度, $\nabla $ 是梯度算子, ${\nabla ^2}$ 表示拉普拉斯算子. $\varepsilon $ 是无量纲参数, 其值等于Stefan数的倒数. 无量纲参数${\lambda _{\rm{T}}}$ 表示液相和固相热扩散系数的比值.2 )—(6 )在界面$r = R(\theta, t)$ 上满足温度连续性条件、Gibbs-Thomson条件、热量守恒条件、质量守恒条件、界面无滑移条件.K 为界面的局部平均曲率, ${{{U}}_{\rm{I}}}$ 表示界面生长速度, $\gamma $ 为表面自由能, $\mu $ 为界面动力学系数, ${k_{\rm{S}}}$ 和${k_{\rm{L}}}$ 分别表示固相和液相的热传导系数, n ${{\tau }}$ 表示单位切向向量.2 )—(6 )还应满足下面的远场条件、初始条件、界面分离条件.$r \to \infty $ 时, 有$A + B = 0$ 成立.${k_i}$ 表示液相第i 个组分的分离系数.$\overline r = \varepsilon r,$ 把$\overline r,$ $r, $ $\theta, $ t 视为独立的变量, 则(2 )—(16 )式变为${{U}} = ({u_r}, {u_\theta })$ .$r \to \infty $ 时, 有3.渐近解 对于典型的金属, $\Delta H/({c_{\rm{p}}}{\rho _{\rm{L}}})$ 通常为几百K. 如 Cu的$\Delta H=1.830 \times {10^9}$ J·m–3 , ${c_{\rm{p}}}$ = 390 J·kg–1 ·K–1 , ${\rho _{\rm{L}}}$ = 8930 kg·m–3 , $\Delta H/({c_{\rm{p}}}{\rho _{\rm{L}}})$ = 525 K. Al的$\Delta H=1.{\rm{0676}} \times {10^9}$ J·m–3 , ${c_{\rm{p}}}$ = 1084 J·kg–1 ·K–1 , ${\rho _{\rm{L}}}$ = 2700 kg·m–3 , $\Delta H/({c_p}{\rho _L})$ = 365 K, 因此无量纲参数$\varepsilon $ 实际上是一个小量, 即$\varepsilon \to 0$ 时, 采用类似于Vogel和Cantor[20 ] 的方法, 求解柱状晶体生长系统(17 )式—(28 )式的渐近解. 在界面附近的区域, 做如下展开:$\bar R = \varepsilon R$ , ${\bar R_0} = \varepsilon {R_0}$ , ${\bar R_1} = \varepsilon {R_1}.$ ${\partial }/{{\partial t}} = O(1)$ , 把(29 )式—(31 )式代入(17 )式—(28 )式可得出首阶近似.$R = {R_0}$ 上, 有$r \to \infty $ 时${{U}} = ({u_r}, {u_\theta })$ 满足方程(32 ), 故有下列方程成立:38 )式可知, 当$r \to \infty $ 时有40 )式—(43 )式解得21 ], 可求得温度场和浓度场的首阶近似解为:${A_\lambda } = \ln {R_\infty } - \ln {R_0} = {N}/({{2{\lambda ^2}}}) > 0,$ $\lambda $ 是方程${\lambda ^2}\ln ({\nu ^2}{\lambda ^2}) \!+\! N \!=\! 0$ 的一个解. $N \!\ll\! 1,$ $\ln \nu^2 \!=\! 0.5772$ .${R_0}$ 的首阶近似解满足下列微分方程:48 )式可知, 当$\dfrac{{{\rm{d}}{R_0}}}{{{\rm{d}}t}} < 0$ 时, 晶体收缩; 当$\dfrac{{{\rm{d}}{R_0}}}{{{\rm{d}}t}} > 0$ 时, 晶体生长.$r \to \infty $ 时, 有21 ], 可求得一阶近似解为${C_{{\rm{L}}0}}, $ ${C_{{\rm{L}}2}}, $ $T_{{\rm{L}}10}^*, $ $T_{{\rm{L}}12}^*, $ ${C_{{\rm{S}}0}}, $ ${C_{{\rm{S2}}}}{\rm{, }}$ $T_{{\rm{S10}}}^{\rm{*}}, $ $C_{{\rm{C}}0}^1, $ $C_{{\rm{C}}2}^1, $ $C_{{\rm{C}}10}^{1*}, $ $C_{{\rm{C}}12}^{1*}, $ $C_{{\rm{C}}0}^2, $ $C_{{\rm{C}}2}^2, $ $C_{{\rm{C}}10}^{2*}, $ $C_{{\rm{C}}12}^{2*}, $ $\dfrac{{{\rm{d}}{g_0}}}{{{\rm{d}}t}}, $ $\dfrac{{{\rm{d}}{g_2}}}{{{\rm{d}}t}}, $ $\dfrac{{{\rm{d}}{b_0}}}{{{\rm{d}}t}}$ 的取值见附录 .4.讨 论 利用渐近方法研究了非等温条件下多组分稀合金熔体中柱状晶体生长的数学模型, 获得了柱状晶体生长模型界面的近似解析解. 由所得出的解析解表达式(71 )式, 可以定量分析straining流对柱状晶体界面形态的影响. 由图1 可以直观地发现在straining流的作用下, 柱状晶体的界面形态发生了明显的变化, 即柱状晶体生长的横截面不再保持圆形. 图2 给出了柱状晶体在straining流下生长的界面形态. 图3 给出了不同强度的straining流对柱状晶体界面形态的影响, 可以看出流入的straining流加强了界面的生长速度, 流出的straining流降低了界面的生长速度, 由此产生了不规则的柱状晶体. 这从物理含义方面理解实际上是由于流动改变了界面前沿的浓度, 导致晶体生长前沿浓度的不均匀, 从而产生了不规则的柱状晶体. 这一结论与文献[15 ]的结论是一致的, 但需要指出的是, 我们给出的解析解可以定量地描述这一问题, 从而为将来通过流动来精确控制柱状晶体的界面形态打下良好的基础. 图4 给出了在固定强度straining流影响下, 柱状晶体界面形态随时间变化的生长过程, 这一发现的物理意义在于可以动态地预测某一时刻柱状晶体界面的形态. 图5 比较了straining流对多组分熔体和纯熔体中柱状晶体界面形态影响, 发现多组分稀合金熔体中的柱状晶体界面形态受straining流的影响更大. 文献[18 ]在研究多组分熔体的凝固问题时指出, 随着组分的增加凝固前端变得更加不稳定, 这与我们的结论是一致的. 图6 比较了straining流对二元熔体和三元熔体中柱状晶体界面形态影响, 发现熔体中组分的多少, 并不是柱状晶体界面形态变化的决定性因素, 即不能说明三元柱状晶体的界面形态比二元柱状晶体的界面形态更容易受straining流的影响. 由图7 柱状晶体界面杂质浓度$C_{\rm{L}}^1$ 随$\theta $ 的变化情况, 可以看出柱状晶体的界面形态主要是由界面附近的溶质浓度决定的. 实际上通过(71 )式可以发现, 相比于纯熔体中柱状晶体的生长, 在多组分熔体中生长的柱状晶体的界面形态表达式更为复杂, 其中参数$M_{\rm{C}}^1 S_{\rm{p}}^1 + M_{\rm{C}}^2 S_{\rm{p}}^2$ 和$\dfrac{1}{{\lambda _{\rm{D}}^1}}M_{\rm{C}}^1 S_{\rm{p}}^1 + \dfrac{1}{{\lambda _{\rm{D}}^2}}M_{\rm{C}}^2 S_{\rm{p}}^2$ 对界面形态有着重要的影响. 为了便于分析我们假设$D_{\rm{L}}^1 = D_{\rm{L}}^2$ , 即液相中第一个组分和第二个组分的扩散系数相等, 容易得出$\lambda _{\rm{D}}^1 = \lambda _{\rm{D}}^2$ . 这时只需分析$M_{\rm{C}}^1 S_{\rm{p}}^1 + M_{\rm{C}}^2 S_{\rm{p}}^2$ 对于界面形态的影响即可. 由$M_{\rm{C}}^1 S_{\rm{p}}^1 + M_{\rm{C}}^2 S_{\rm{p}}^2$ 容易看出相比于纯熔体, 多组分熔体中柱状晶体的界面形态还主要受液相线斜率${m_1}, {m_2}$ 以及液相中第i 个杂质组分浓度$C_{\rm{L}}^i$ 的影响, 实际上这正是受到成分过冷(constitutional undercooling)影响的结果. 通过上面的分析可以得到以下结论, 稀合金熔体中柱状晶体的界面形态比纯熔体中的柱状晶体的界面形态受straining流的影响更为显著.图 1 在$Oxy$ 平面上应变流对柱状晶体形态演化的影响, 其中$t = 396, $ $\varGamma = 0.25, $ $M_{\rm{C}}^1=0.01, $ $M_{\rm{C}}^2=0.02, $ $C_{{\rm{L}}, \infty }^1 = $ 1.0, $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = $ –2.33, $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^1 = $ 0.01, $\lambda _{\rm{D}}^2 = 0.02, $ $\varepsilon = 0.05$ Figure1. The morphology evolution of columnar crystal in a straining flow on the cross-section of $Oxy$ plane at $t = 396, $ where $\varGamma = 0.25, $ $M_{\rm{C}}^1=0.01, $ $M_{\rm{C}}^2=0.02, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ E = 0.3, ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^1 = 0.01, $ $\lambda _{\rm{D}}^2 = $ 0.02, $ \varepsilon = 0.05$ 图 2 在$t = 396$ 时, 柱状晶体的界面形态. 其中$\varGamma = 0.25, $ $M_{\rm{C}}^{\rm{1}}=0.01, $ $M_{\rm{C}}^{\rm{2}}=0.02, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^1 = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05, $ $A = 0.9$ Figure2. The morphology evolution of columnar crystal in a straining flow at $t = 396, $ where $\varGamma = 0.25, $ $M_{\rm{C}}^{\rm{1}}=0.01, $ $M_{\rm{C}}^{\rm{2}}=0.02, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^1 = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05, $ $A = 0.9$ 图 3 不同强度的应变流对柱状晶体界面形态的影响, 其中$t \!=\! 256, $ $\varGamma \!=\! 0.25, $ $M_{\rm{C}}^1 \!=\! 0.01, $ $M_{\rm{C}}^2\! =\! 0.02, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^1 = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05.$ A 由左向右分别为0.9, 0.6, 0.3, 0Figure3. Interface morphology of columnar crystals affected by different sizes of straining flow, where $t = 256, $ $\varGamma = 0.25, $ $M_{\rm{C}}^1=0.01, $ $M_{\rm{C}}^2=0.02, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^1 = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05.$ A is 0.9, 0.6, 0.3, 0 from left to right, respectively.图 4 在$Oxy$ 平面上柱状晶体界面随时间的演化, 其中$\varGamma \!=\! 0.25, $ $M_{\rm{C}}^1 \!=\! 0.01, $ $M_{\rm{C}}^{\rm{2}} \!=\! 0.02, $ $C_{{\rm{L}}, \infty }^1 \!=\! 1.0, $ $C_{{\rm{L}}, \infty }^2 \!=\! 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ E = 0.3, M k = 0.01, k T = 1.23, ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05, $ $A = 0.9$ Figure4. Evolution of columnar crystal interface with time in the $Oxy$ plane, where $\varGamma = 0.25, $ $M_{\rm{C}}^1=0.01, $ $M_{\rm{C}}^{\rm{2}}=0.02, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ m 2 = –2.33, E = 0.3, M k = 0.01, k T = 1.23, ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05, $ $A = 0.9$ 图 5 应变流对不同杂质含量柱状晶体界面形态的影响, 其中$t = 256, $ $\varGamma = 0.25, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05$ Figure5. Effect of straining flow on the interface morphology of columnar crystals in different impurity content, where $t = 256, $ $\varGamma = 0.25, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05$ 图 6 应变流对不同杂质含量柱状晶体界面形态的影响, 其中$t = 256, $ $\varGamma = 0.25, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05$ Figure6. Effect of straining flow on the interface morphology of columnar crystals in different impurity content, where $t = 256, $ $\varGamma = 0.25, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}} = 0.02, $ $\varepsilon = 0.05$ 图 7 在$R, \theta $ 平面上, 柱状晶体界面杂质浓度$C_{\rm{L}}^1$ 随$\theta $ 的变化情况, 其中$t = 256, $ $\varGamma = 0.25, $ $M_{\rm{C}}^{\rm{1}}=0.01, $ $M_{\rm{C}}^{\rm{2}}=0.02, $ $C_{{\rm{L}}, \infty }^1 = 1.0, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = - 2.33, $ $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}}=0.02, $ $\varepsilon = 0.05, $ $A = 0.9$ Figure7. The change of impurity concentration at the interface of columnar crystal in the $R, \theta $ plane, where $t = 256, $ $\varGamma = 0.25, $ $M_{\rm{C}}^{\rm{1}}=0.01, $ $M_{\rm{C}}^{\rm{2}}=0.02, $ $C_{{\rm{L}}, \infty }^2 = 3.0, $ ${A_\lambda } = 3.3, $ ${m_1} = - 1.6, $ ${m_2} = $ –2.33 $E = 0.3, $ ${M_{\rm{k}}} = 0.01, $ ${k_{\rm{T}}} = 1.23, $ ${\lambda _{\rm{S}}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{1}} = 0.01, $ $\lambda _{\rm{D}}^{\rm{2}}=0.02, $ $\varepsilon = 0.05, $ $A = 0.9$ 5.结 论 本文从理论上研究了straining流对三元过冷熔体中柱状晶体生长的影响. 通过计算给出了晶体生长界面的解析表达式, 由表达式可以看出straining流是产生不规则柱状晶体的重要原因. 在分析straining流对三元熔体中柱状晶体生长的影响时, 发现流入的straining流加快了界面的生长速度, 而流出的straining流减缓了界面的生长速度. 同时发现随着流动速度的增大, 界面变形也更为显著. 我们比较了纯熔体、二元熔体和三元熔体中柱状晶体的生长, 发现合金熔体中柱状晶体的生长受straining流的影响更为显著.附录 



























































































































 图 1 在
图 1 在
































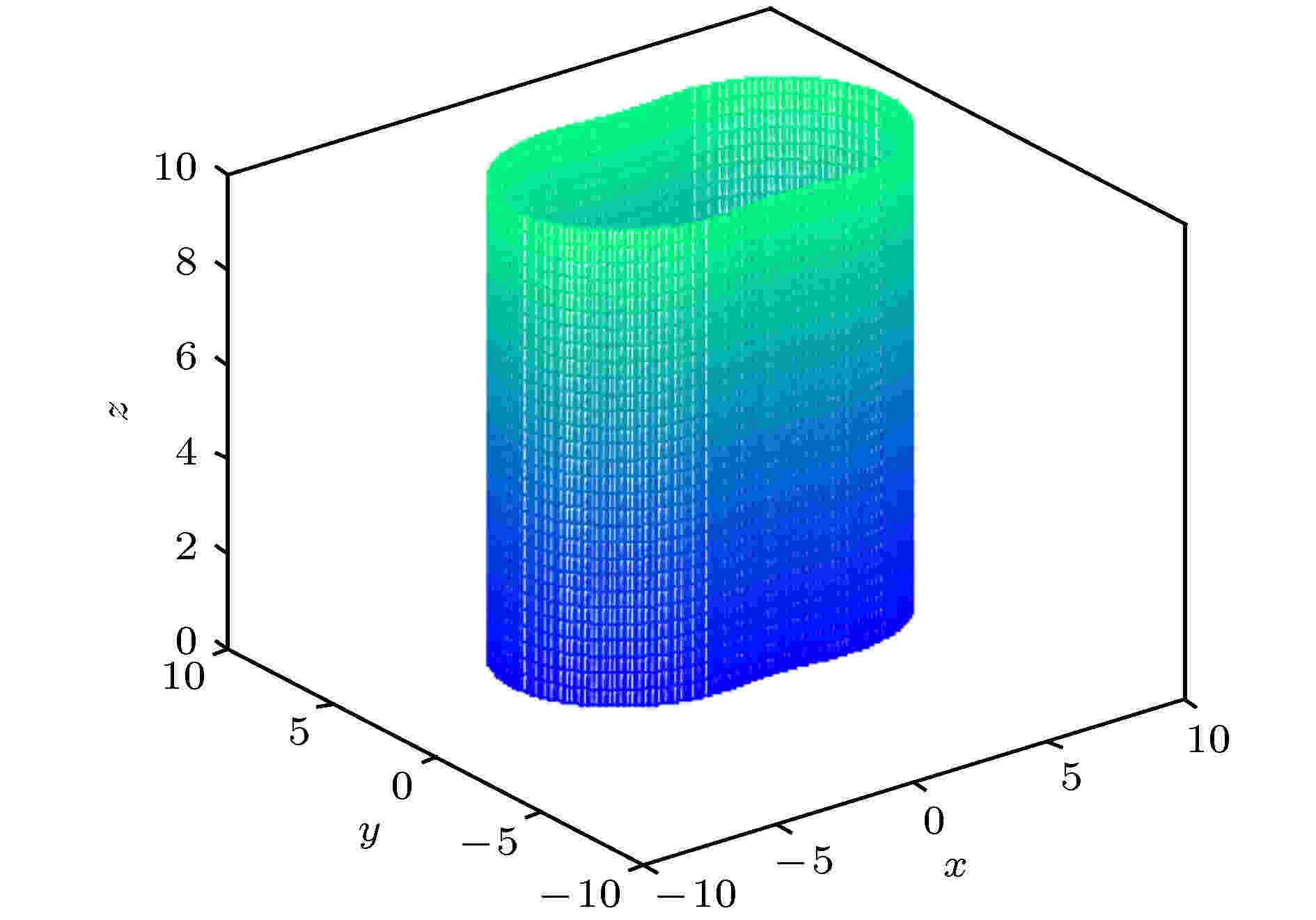 图 2 在
图 2 在

































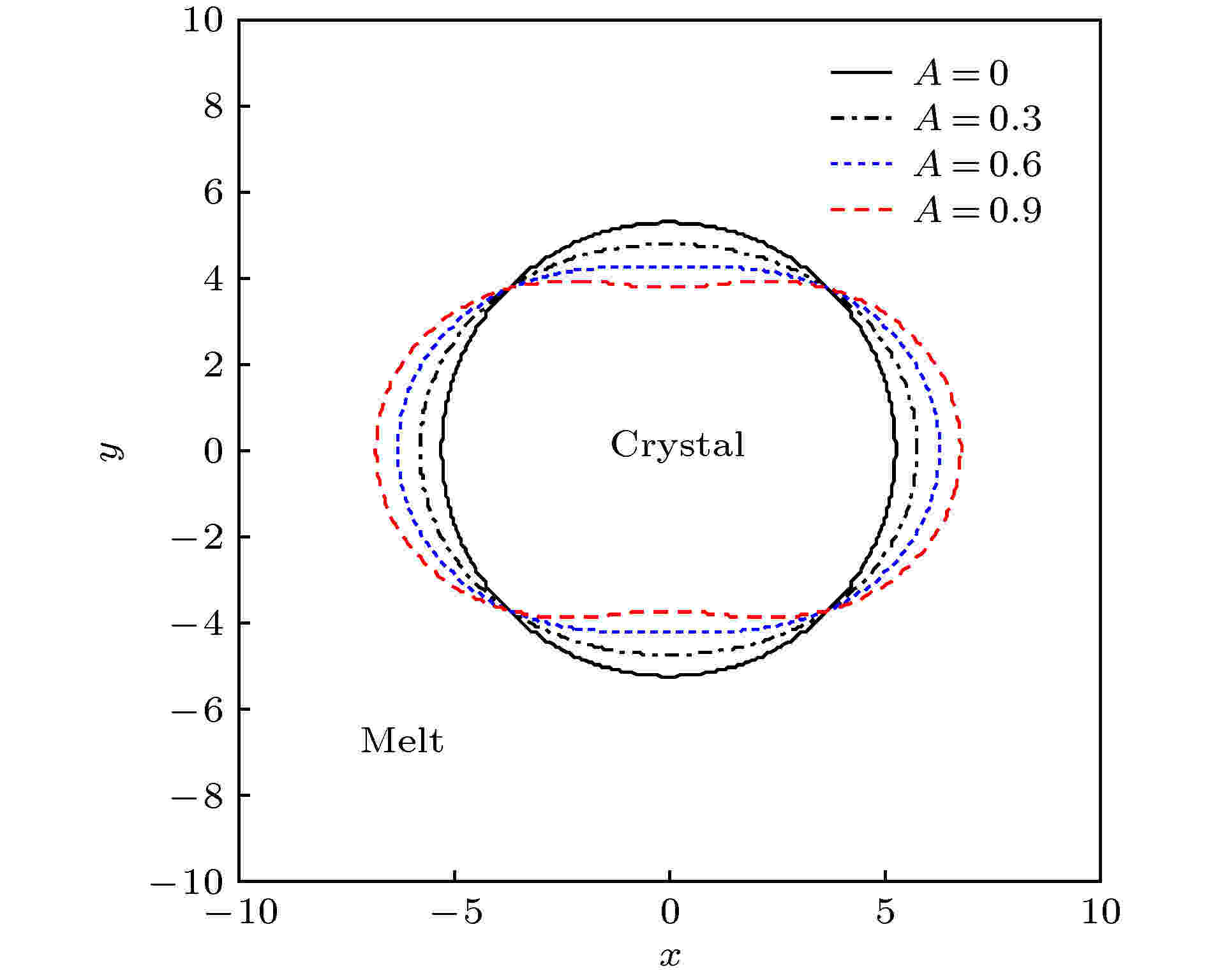 图 3 不同强度的应变流对柱状晶体界面形态的影响, 其中
图 3 不同强度的应变流对柱状晶体界面形态的影响, 其中































 图 4 在
图 4 在


























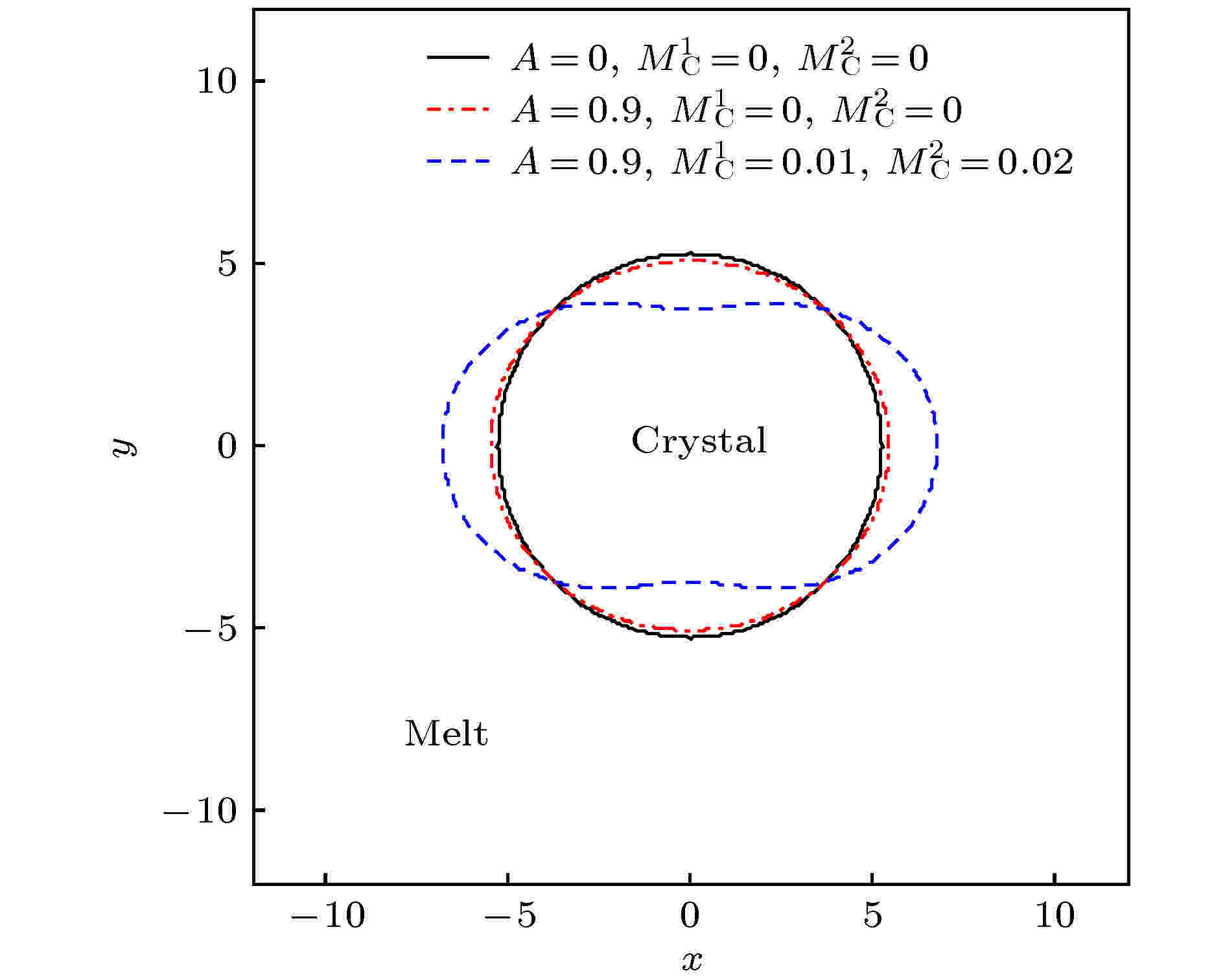 图 5 应变流对不同杂质含量柱状晶体界面形态的影响, 其中
图 5 应变流对不同杂质含量柱状晶体界面形态的影响, 其中



























 图 6 应变流对不同杂质含量柱状晶体界面形态的影响, 其中
图 6 应变流对不同杂质含量柱状晶体界面形态的影响, 其中



























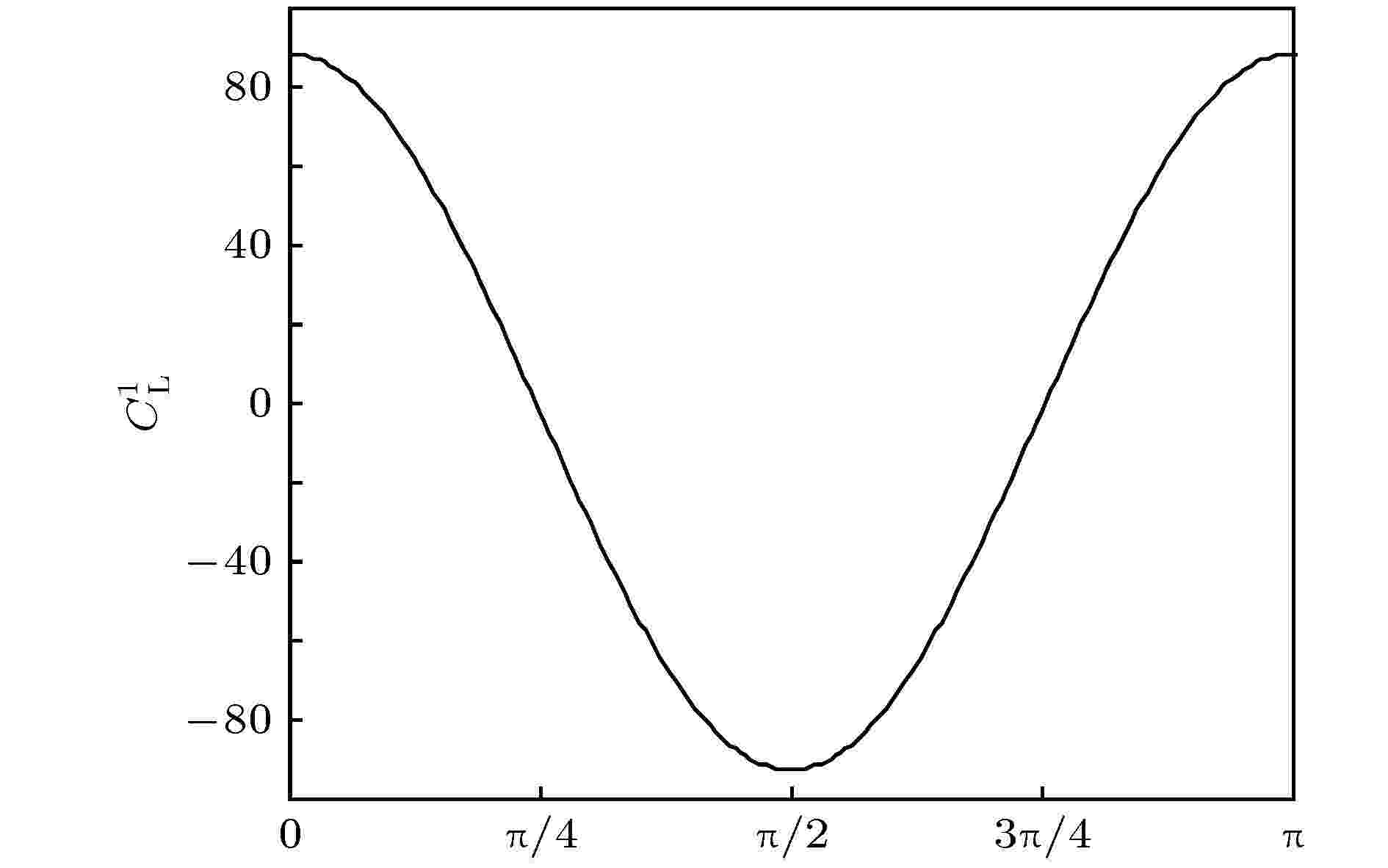 图 7 在
图 7 在




































