删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

多晶体光路配置的X射线衍射特性及在表征同步辐射光束线带宽上的应用

本站小编 Free考研考试/2021-12-29
摘要:本文报告了使用多晶体光路配置的X射线衍射实验及其用于表征上海光源BL09束线上双晶单色器出射光特性的情况. 当一个分析晶体与双晶单色器呈(+n, –n)无色散配置时, 通过退卷积得到单色器的角度带宽和相对能量带宽分别为5.40(4)'' 和1.30(1) × 10–4@10 keV; 当实验配置为(+n, +n)、(+n, –m)和(+n, +m)色散配置时, 退卷积之后测得同步辐射光束的角分布和相对能量带宽分别为26(1)''和6.3(2) × 10–4@10 keV; 处理掉双晶单色器的影响后, 可以得出与弯铁光源理论值一致的角发散度25(1)'' @10 keV. 此外, 利用多晶体的色散配置和DuMond作图的方法, 表征了一系列不同白光入射狭缝宽度下的单色器出射光的发射度和带宽的情况.
关键词: 同步辐射/
双晶单色器/
多晶体X射线衍射/
能量带宽/
DuMond作图

English Abstract


全文HTML

--> --> -->
1.引　言
X射线的能谱范围、光强、角度发散/光斑尺寸和能量分辨/能量带宽等, 是一个同步辐射光束线站的基本参数, 也是表征线站性能的基本指标. 其中X射线的能谱范围、光强、光斑尺寸等比较容易直接测得[1-4], 而光束的角发散与带宽则由于衍射现象中波长与角度的耦合, 一般不容易直接测得. 这种耦合不仅给测量单色器的能量带宽和出射光角发散带来了一些困难, 同时也带来了束线表征工作中的一些混乱[5-6]. 为此, 本文将系统地介绍多晶体X线衍射的实验配置及其在表征同步辐射光束线和束线单色器带宽/接收角上的实验.
同步辐射用户所看到的光束能量带宽/角发散等特性并不是一个一成不变的量, 它们会受到束线光源的尺寸/发散度、以及传输过程中的光学元件(狭缝、镜子等)参数和单色器分光特性等多种因素的复合影响. 由于一般出射光的能量带宽无法通过简单的测量直接获取, 因此针对同步辐射不同的工作能区、不同类型的单色器, 发展了多种表征束线、单色器能量带宽的方法[7-13]. 从一般测量的原理上论, 使用更高性能的分析器来表征束线/单色器的能量带宽是最简单明了的方法. 如在软X光束线站上, 可使用Ar、N原子中固有的能级结构作为分析器, 利用其吸收谱线来表征线站单色器的分辨率[14-16]. 但是, 在硬X光束线站上, 由于没有合适的元素吸收边可利用(带宽不够窄), 以及使用了双晶单色器(double crystal monochromator, DCM)结构的单色器, 便形成了采用第一晶(或第二晶)的摇摆曲线来表征单色器能量带宽的习惯. 随着越来越多光束线的建设, 类似束线表征的报道也越来越多, 角度与带宽的耦合模糊了单色器的本征带宽和用户所使用的束线带宽的区别, 以至于有些直接将单色器第一晶(或第二晶)的摇摆曲线半高宽换算成束线能量带宽的做法[5-6].
早在20世纪30代, DuMond提出了设计/分析单色器能量窗口的作图方法[17], 可以比较清晰地表达多晶体配置时的X线衍射的发散(接收)角度与能量带宽的函数关系. 后人称此为DuMond作图法, 是设计和解析单色器分光特性的有效工具. 因此, 测得束线单色器的DuMond图不仅能够明确得到被测束线的能量带宽和角度发散, 同时也是对同步辐射束线回归本真的表征法. 本文通过使用Si111/333分析晶体与束线的Si111双晶单色器构成的多晶体实验配置, 直接测量出该单色器的DuMond图, 测得了上海光源[18] BL09B X光学测试线上单色器的本征带宽和不同白光狭缝时束线的能量带宽.
2.晶体衍射的DuMond作图及多晶体配置时X射线衍射的分析
当一束平行白光X线入射到理想晶体上时, 若不考虑X线在晶体中的折射情况, 发生衍射的X线波长$\lambda $与入射角度$ {\theta }_{\rm{B}} $的关系之间遵从Bragg衍射公式
$2d{\rm{\sin}}{\theta }_{\rm{B}}=m \lambda,$
其中, d是晶格间距, $ {\theta }_{\rm{B}} $是衍射角度, $\lambda $是X射线波长, m是衍射的级次. 其微分形式为
$ \frac{\Delta \lambda}{\lambda}=\frac{\Delta \theta }{{\rm{tan}}{\theta }_{\rm{B}}}, $
式中的$ \Delta \theta $可以有两类解读: 一种理解是入射光束的角分布, 一种是入射中心角度的变化. 与其相对应的$ \Delta \lambda $同样也可以有两类解读: 一种是出射光束的波长带宽, 一种则是中心波长的变化. 当不特意说明时, 本文中的$ \Delta \theta$和$\Delta \lambda $都是指前一种的含义. 此外, 由于能量与波长的等价性$\left( \dfrac{\Delta \lambda }{\lambda }=-\dfrac{\Delta E}{E} \right)$, 下文中使用带宽的概念时, 不特意区分是能量的还是波长的.
2
2.1.单色器的DuMond图解
-->

2.1.单色器的DuMond图解

DuMond作图是Bragg衍射公式的图形表现形式, 其横轴是入射晶体光束的角度, 纵轴是满足衍射公式的光束的波长分布. 运动学意义上的DuMond图是一条横轴为$ {\theta }_{\rm{B}} $, 纵轴为$ {\lambda }/{2 d} $的正弦曲线. 但是, 依据动力学衍射理论[19-20], 在衍射角附近很小的一个范围$ {\omega }_{\rm{D}} $(动力学衍射达尔文宽)内, 会发生全反射现象. 因此, 即使对于完全平行的入射白光, 也会由此带来一个出射波长的带宽. 同样, 即便是单色光入射, 若入射光源有角发散的话, 晶衍射后的出射光也会有一定的角度分布$ {\omega }_{\rm{D}} $. 因此, 在动力学上, DuMond作图是有$ {\omega }_{\rm{D}} $宽度的正弦曲线带. 在晶体的动力学衍射范围内, DuMond作图可使用Bragg衍射公式的微分形式来表现.
图1为一块完美晶体对称反射时的DuMond作图. 横轴是入射光的角度分布, 纵轴是衍射光的相对波长分布. 当入射晶体的光束有一定的发散角和频谱分布时, 衍射光束的波长和角度也出现相应的展宽. 图1中的作图可表述为: 衍射方程在图中是与纵轴成衍射角$ {\theta }_{\rm{B}} $夹角的直线, 分光晶体的最小接收角是单色光的达尔文宽$ {\omega }_{\rm{D}} $(黑线), 一般情况下的接收角取决于光束的发散角$ {\theta }_{\rm{S}} $(红线). 这样一来, 衍射的最小能量窗口就是黑线表示的晶体本征的相对能量带宽$ {\Delta \lambda}_{\rm{D}}/ \lambda$. 在有了光束发散角$ {\theta }_{\rm{S}} $后, 能量带宽变成了由红线表示的系统相对能量带宽$ {\Delta \lambda}_{\rm{S}}/ \lambda$. 对于同步辐射光束线来说, 前者对应于单色器的能量带宽, 只取决于双晶单色器本身性能; 而后者则是光束线的或者说是实验用户使用的能量带宽, 与光源以及光束线上的光学元件(狭缝)都有关系. 它们的表达式可分别由(3)式和(4)式给出
图 1 完美晶体对称反射的DuMond图. 微分衍射(2)式在图中对应的是一条斜率为$ {\rm{cot}}{\theta }_{\rm{B}} $的直线带. $ {\theta }_{\rm{B}} $是运动学衍射角(晶体的折射率对X线衍射的角度位置有影响, 本文暂不考虑此方面的影响), $ {\omega }_{\rm{D}} $是动力学衍射的达尔文宽, $ {\theta }_{\rm{S}} $是光束的发散角. 当完全平行的白光入射时, 对称反射晶体的可接收和出射角度都是$ {\omega }_{\rm{D}} $, 有限的角度宽带来了相应的波长分布${{\Delta \lambda}_{\rm{D}}}/{\lambda} $. 当入射的白光带有一定的角发散时, 入射晶体的角分布变大, 影响带宽的角发散也由$ {\omega }_{\rm{D}} $变为$ {\theta }_{\rm{S}} $, 角度发散带来的波长分布也变成了${{\Delta \lambda}_{\rm{S}}}/{\lambda} $
Figure1. DuMond diagram for the symmetric Bragg geometry. The differential equation (2) of diffraction formula corresponds to the line band with a slope of $ {\rm{cot}}{\theta }_{\rm{B}} $. $ {\theta }_{\rm{B}} $ and $ {\omega }_{\rm{D}} $ represent the kinematic diffraction angle and the Darwin width of the dynamic diffraction, respectively. In this article, we ignore the change of X-ray diffraction angle position which is influenced by crystal refraction. When the incident white beam is completely parallel, both the receiving and emitting angle of the symmetric crystal are the same, which can be represented by $ {\omega }_{\rm{D}} $. The limited angle broadband introduces the corresponding wavelength distribution ${{\Delta \lambda}_{\rm{D}}}/{\lambda} $. When the incident beam with a divergence angle, the distribution of the incident angle on the crystal becomes larger which affects the angular divergence of bandwidth changing from $ {\omega }_{\rm{D}} $ to $ {\theta }_{\rm{S}} $(the divergence angle of the beam) and the wavelength distribution changing to $ {{\Delta \lambda}_{\rm{S}}}/{\lambda} $

$ \frac{{\Delta \lambda}_{\rm{D}}}{\lambda}=\frac{{\omega }_{\rm{D}}}{{\rm{tan}}{\theta }_{\rm{B}}},$
$\frac{{\Delta \lambda}_{\rm{S}}}{\lambda}=\frac{\sqrt{{\omega }_{\rm{D}}^{2}+{\theta }_{\rm{S}}^{2}}}{{\rm{tan}}{\theta }_{\rm{B}}}. $
正确区分清楚二者的含义, 无论对束线表征还是对用户实验都是有意义的.
2
2.2.多晶体实验配置的X射线衍射及其特性分析
-->

2.2.多晶体实验配置的X射线衍射及其特性分析

两块对称型晶体按照排列方式和衍射指数面的不同可组成4种配置方式实现对X射线的衍射, 分别为: (+n, –n)型、(+n, +n)型、(+n, –m)型和(+n, +m)型. 其中(n, n)表示使用同一指数面的晶体组合, (n, m)表示使用不同指数面的晶体组合; (+, –)表示两块晶体的衍射面法线位于第一晶出射光线(等同于第二晶入射光线)的两侧, (+, +)则表示两块晶体的衍射面法线位于第一晶出射光线的同侧. 图2和图3的双晶单色器的第二晶体和分析晶体分别构成(+, –)和(+, +)配置. 对于相同晶体的(+n, –n)型配置, 由于两块晶体在几何学中呈平行状态, 因此又称为是平行配置; 同时也因为通过第一晶体的光线同样可以通过第二晶体, 平行配置也称作无色散配置. (+n, –n)型配置是束线双晶单色器所采用的配置方式. 图4为分析晶体扫描单色器出射光过程的DuMond 图.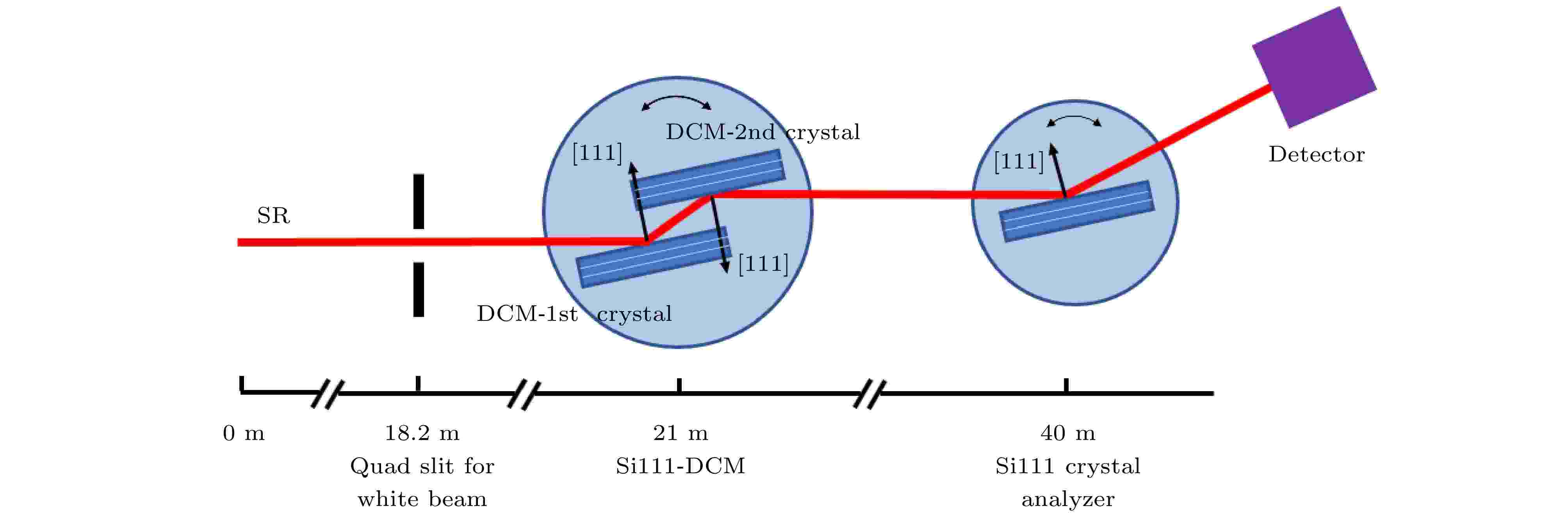
图 2 Si111双晶单色器的第二晶和Si111分析晶体构成(+1, –1)型无色散配置的实验配置图. [111]是衍射面法线的晶向
Figure2. The experimental configuration of (+1, –1) type non-dispersive consists of the second crystal of Si111-DCM and Si111 analyzer. The[111] is the crystal direction of the normal of the diffraction plane.

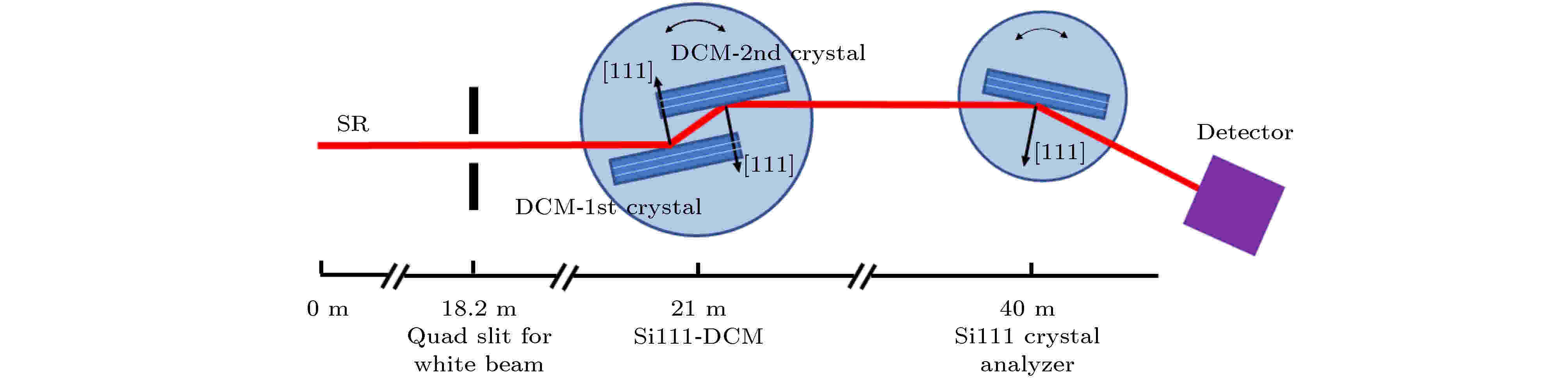图 3 Si111双晶单色器的第二晶和Si111分析晶体构成(+1, +1)型色散配置的实验配置图
Figure3. The experimental configuration of (+1, +1) type dispersive consists of the second crystal of Si111-DCM and Si111 analyzer.

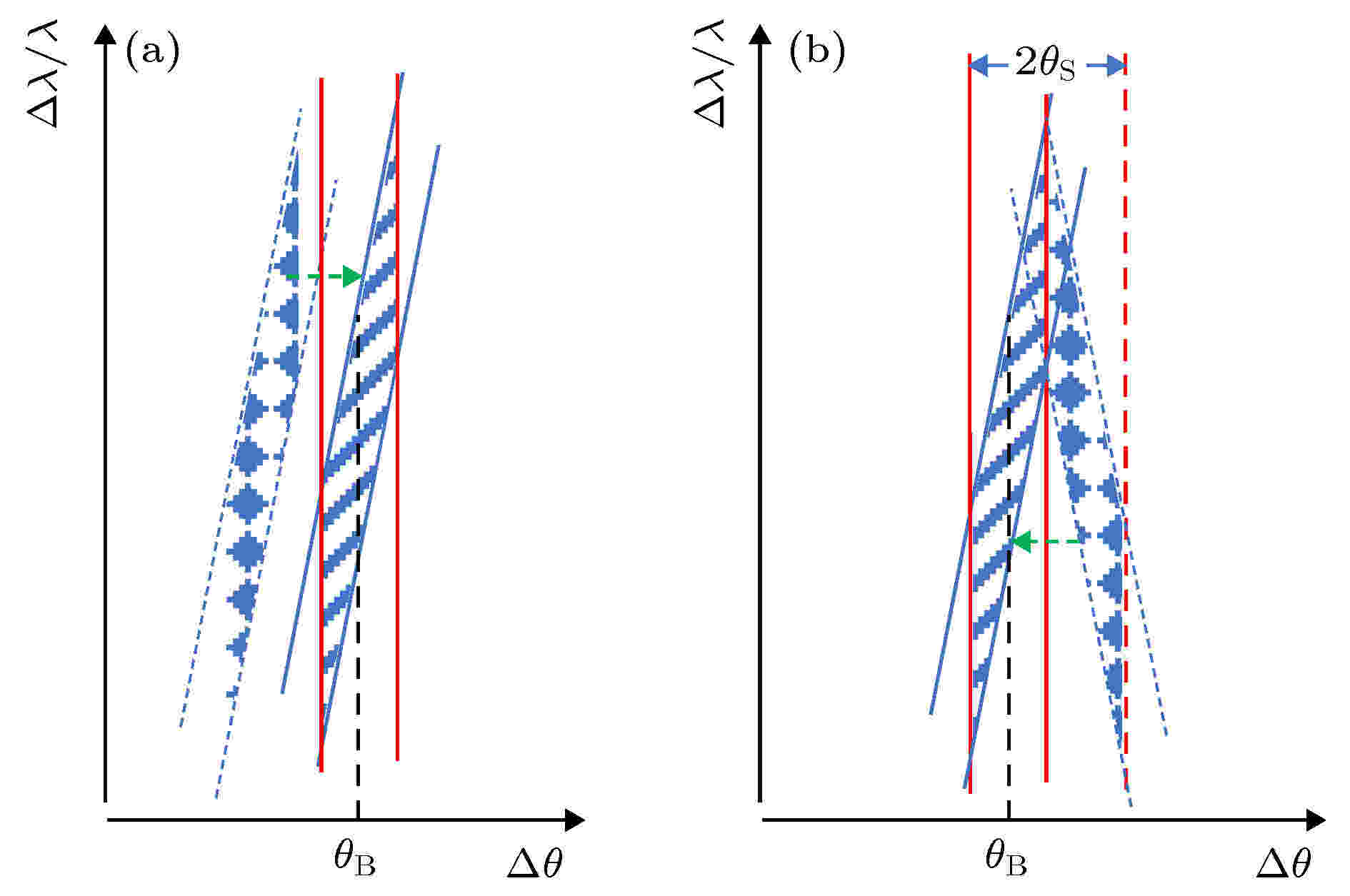图 4 (a)和(b)分别为无色散(+1, –1)配置和色散(+1, +1)配置条件下, 分析晶体扫描单色器出射光过程的DuMond图. 斜线区域是双晶单色器的DuMond窗口, 圆点的区域是分析晶体的DuMond窗口
Figure4. DuMond diagrams during scanning the output beam of DCM by analyzer. Panel (a) represents the non-dispersive (+1, –1) configuration and panel (b) represents the dispersive (+1, +1) configuration. The oblique line region is the DuMond window of the DCM. The point region is the DuMond window of the analyzer.

将上述结论用于装备了Si111双晶单色器的上海光源BL09光学测试束线和分析晶体, 则双晶单色器的第二晶和分析晶体可分别构成(+1, –1)型、(+1, +1)型、(+1, –3)型和(+1, +3)型的配置, 对应着图2、3、5和6. 在图2和图3中的分析晶体是Si111, 图5和6中的分析晶体是Si333. 图4(a)、(b)和图7(a)、(b)分别对应着图2、3和图5、6中实验配置时单色器的第二晶与分析晶体构成的DuMond图解. 在这里双晶单色器调整好之后便固定不动, 分析器晶体绕垂直于纸面的轴转动.
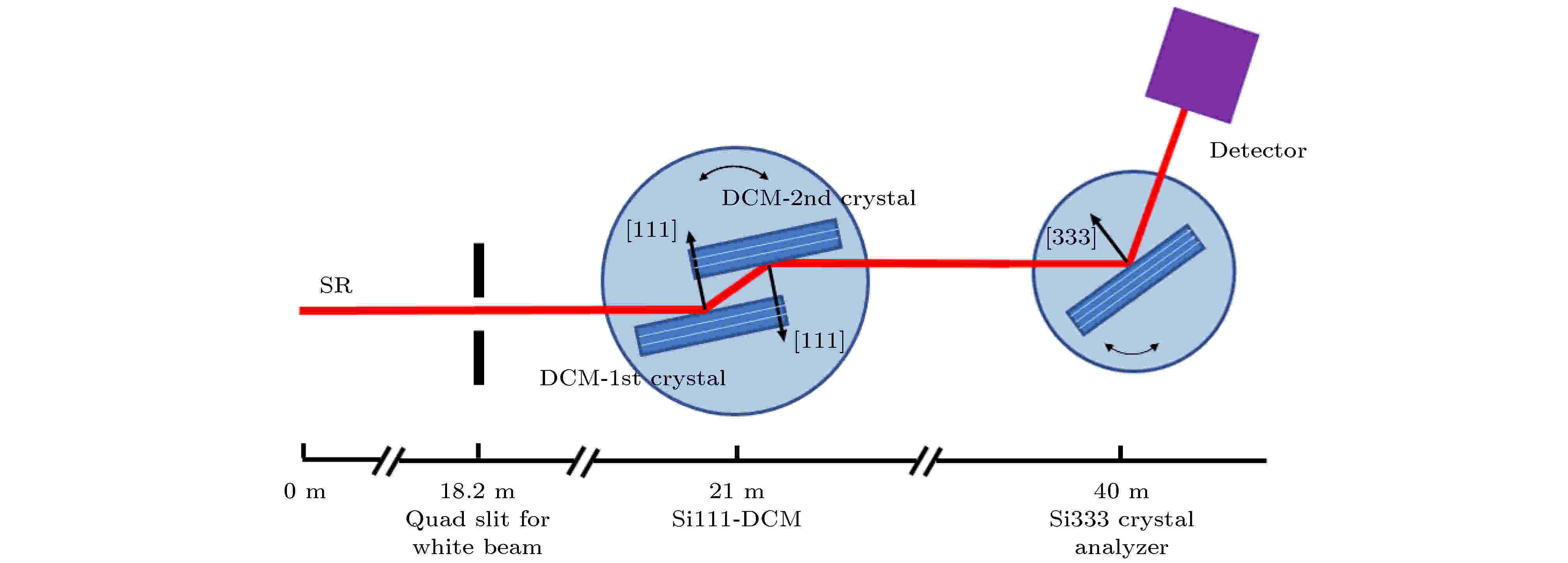图 5 Si111双晶单色器的第二晶和Si333分析晶体构成(+1, –3)型色散配置的实验配置图
Figure5. The experimental configuration of (+1, –3) type dispersive consists of the second crystal of Si111-DCM and Si333 analyzer.

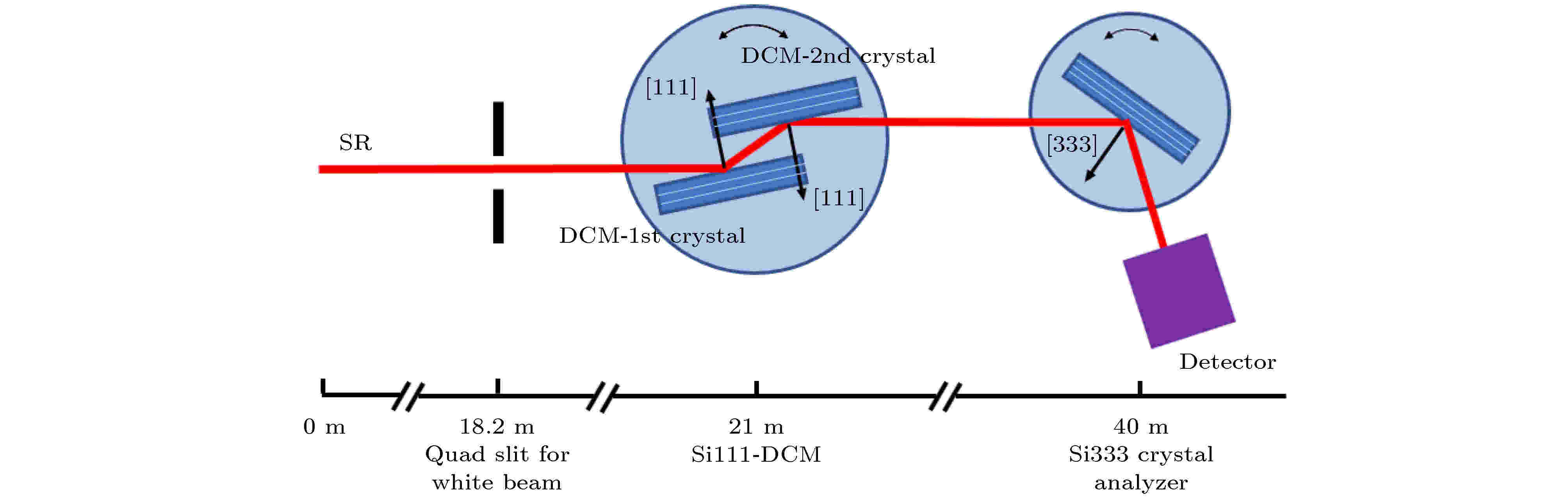图 6 Si111双晶单色器的第二晶和Si333分析晶体构成(+1, +3)型色散配置的实验配置图
Figure6. The experimental configuration of (+1, +3) type dispersive consists of the second crystal of Si111-DCM and Si333 analyzer.

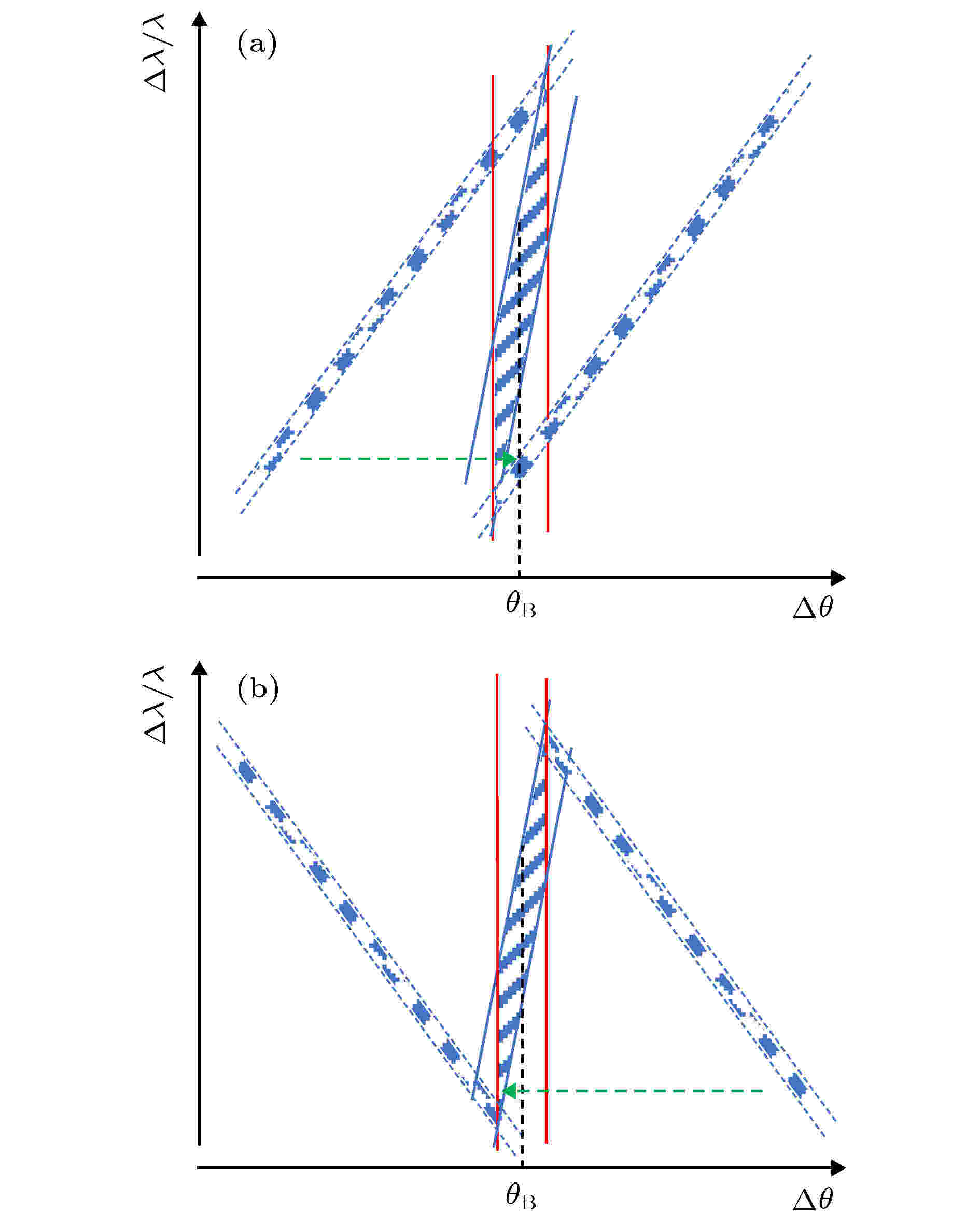图 7 (a)和(b)分别为使用Si333做分析晶体的(+1, –3)型和(+1, +3)型色散配置, 扫描单色器出射光过程的DuMond图. 绿色虚线箭头指示了扫描过程, 两个圆点的区域给出了分析晶体DuMond窗口起止位置
Figure7. DuMond diagrams during scanning the output beam of DCM by Si(333) analyzer. Panel (a) and (b) represent the (+1, –3) typeand (+1, +3) type dispersive configuration, respectively. The green dotted arrow indicates the scanning process. The two point-regions give the starting and ending position of the DuMond window of the analyzer.

对于图2所示的(+1, –1)型实验配置, 图4(a)中, 分析晶体入射光的DuMond窗口(点点区域)沿X轴的移动对应着实验中的晶体转动, Si111双晶单色器出射光的DuMond窗口是固定不动的斜线区域. 在DuMond图中, 当两个窗口有重合区域时, 在分析晶体出射光路上有光强信号出现. 这个配置在发生衍射时分析晶体输出强度的角分布只与两个窗口的角度宽度有关, 测得的摇摆曲线宽度等于双晶单色器的出射光角分布和分析晶体达尔文宽度的卷积, 不受光路上其它角度调控器件的影响. 而对于图3所示的(+1, +1)型实验配置, 由于分析晶体和双晶单色器的第二晶对称放置, 所以在图4(b)中, 分析晶体的DuMond窗口与Si111双晶单色器的DuMond窗口成镜像对称. 当分析器的窗口进入单色器的窗口时, 重合区域并不像无色散配置那样覆盖整个能量分布范围, 而是需要扫描一定的角度区域后才能覆盖整个能量带宽范围. 这使得出射光的强度变得较低(正比于窗口重合面积), 角度分布变得更宽. 由于单色器窗口中的不同波长出现在分析器不同的角度位置处, 因此这种晶体配置方式被称为色散配置. 在不考虑晶体本征达尔文宽影响时, 这个角度区域等于2倍入射到分析晶体光束发散角$ {\theta }_{\rm{S}} $. 因此晶体色散配置方式扫描得出的光强角分布(摇摆曲线)宽度会受到光束发散角的影响. 换言之, 束线上影响光束角发散的器件都会对色散配置下测得的摇摆曲线的角宽度有贡献. 但同时, 这个发散也仅与$ {\theta }_{\rm{S}} $相关, 称之为“固定”色散配置.
将分析晶体改为使用333指数重复类似图2、图3的实验配置便是(+1, –3)型和(+1, +3)型配置(图5、图6). 图7(a)和(b)分别给出了它们扫描过程的DuMond图. 图7(a)与图4(a)的区别在于所使用分析晶体的衍射面指数与上游双晶单色器的衍射面指数不一致, 即便是(+, –)型的实验配置, DuMond图中的分析晶体窗口也与双晶单色器的不平行. 在转动分析晶体时也会产生色散现象. 因此(+n, –m)型和(+n, +m)型配置都属于色散型配置. 图7(a)和(b)与图4(b)的区别在于分析晶体DuMond窗口的斜率不同, 体现在扫描结果上即是色散程度不同. 因此这两种配置都是色散型配置. 其色散程度不仅与光束的发散角$ {\theta }_{\rm{S}} $有关, 还与双晶单色器和分析晶体DuMond窗口的斜率有关. 其中, (+n, +m)型配置色散效果最大, 将其定义为“强”色散配置. 与之相应的, 将(+n, –m)型配置定义为“弱”色散配置. 值得明确的是这里的“弱”只是相对于前述的“强”而言的, 并不一定比(+n, +n)型“固定”色散配置的色散程度弱.
由图4和图7的分析可知, 无色散实验配置中的分析器对颜色(波长)分布不敏感, 其出射光的摇摆曲线仅与双晶单色器和分析晶体本身的达尔文宽相关. 而色散型实验配置中的分析器则对颜色分布敏感, 其出射光摇摆曲线的宽度不但受入射光束角发散的影响, 也受单色器出射光的波长分布和分析晶体衍射面指数的影响. 因此, 一般单色器接收角度(达尔文宽)可通过对(+n, –n)配置下测得的摇摆曲线退卷积得到, 单色器的能量带宽则可以由(3)式间接推测.
要得到入射双晶单色器光束的角发散度$ {\theta }_{\rm{S}} $或出射光的角发散度, 则需要在色散配置下的测量, 以及按照(4)式推测束线的能量带宽. 在色散配置时, 分析晶体的摇摆曲线半高宽可由(5)式给出
$\varDelta {\theta }^{2}={\omega }_{{\rm{D}}\_{\rm{M}}}^{2}+{\rm{\alpha }}^{2} {\rm{min}}\left\{\frac{{\sigma }_{\rm{SR}}^{2}+{\sigma }_{\rm{Slit}}^{2}}{{L}^{2}},{\theta }_{\rm{SR}}^{2}\right\}+{\omega }_{{\rm{D}}\_{\rm{A}}}^{2}, $
$\alpha =\left\{ {\begin{aligned}& {\left|\frac{{\rm{tan}}{\theta }_{{\rm{B}}-{\rm{A}}}}{{\rm{tan}}{\theta }_{{\rm{B}}-{\rm{M}}}}-1\right|,}&{\left(+,-\right)}, \\& {\frac{{\rm{tan}}{\theta }_{{\rm{B}}-{\rm{A}}}}{{\rm{tan}}{\theta }_{{\rm{B}}-{\rm{M}}}}+1,}&{(+,+)},\end{aligned}} \right.$
式中, $ \varDelta $是观测到的分析晶体摇摆曲线半高宽, $ {\theta }_{\rm{SR}} $是同步辐射光源本征的角发散, $ {\sigma }_{\rm{SR}} $和$ {\sigma }_{\rm{Slit}} $分别是发光点和狭缝的纵向宽度, L是狭缝位置距发光点的距离, $ {\omega }_{{\rm{D}}\_{\rm{M}}} $和$ {\omega }_{{\rm{D}}\_{\rm{A}}} $分别是双晶单色器和分析器晶体的本征带宽. 色散项系数$ \alpha $是色散配置条件下分析晶体的展宽因子, 这个因子与晶体配置方式和窗口的斜率有关, 可由(6)式给出, 其中$ {\theta }_{{\rm{B}}\_{\rm{A}}} $是分析晶体的衍射角, $ {\theta }_{{\rm{B}}\_{\rm{M}}} $是双晶单色器的衍射角. (5)式含义是色散配置时观察到的分析晶体摇摆曲线的半腰宽度与单色器带宽、束线的角度发散和分析晶体带宽关系, 第2项即是DuMond图分析中的$ {\theta }_{\rm{S}} $. 因此, 光束线的带宽可由观测值退分析器卷积并消除分析器的色散展宽得到. 对于图3、图5和图6所示的(+1, +1)型、(+1, –3)型和(+1, +3)型色散配置, 当X射线的工作能量为10 keV时, $ {\theta }_{{\rm{B}}\_{\rm{A}}} $和$ {\theta }_{{\rm{B}}\_{\rm{M}}} $分别等于36.4°和11.4°, 故其展宽因子$ \alpha $分别等于2、2.6和4.6.
由于色散配置下分析晶体摇摆曲线与光束的角发散和带宽都有关联, 通过系列地调节束线上的狭缝改变光束的发散角和测量在该发散角时的分析晶体摇摆曲线, 可以分离出来通过单色器后出射光束的角分布, 进而可以获得束线单色器的DuMond图. 获得了束线单色器的DuMond图之后, 便可以直接读出单色器的本征能量带宽、在不同狭缝宽度时的束线能量带宽、以及光源的角发散等光束线的基本信息.
3.实验配置和仪器装备
依照上述讨论的结果, 本课题组在上海光源光学测试线站(BL09B)实施了(+1, –1)、(+1, +1)、(+1, –3)和(+1, +3)的4种实验配置和调制白光狭缝测DuMond图的实验. BL09B测试线站是用于光束线设备及光学元件检测的线站. 在其光学棚屋内, 距发光点下游18.2 m处有一个四刀口白光狭缝, 距发光点21 m处有一台Si111水冷双晶单色器. 单色器的出射光进入实验棚屋, 实验光学平台距光源为40 m, 平台上装备有精密X线晶体转台(KOZHU-KTG16W, 精度0.0025''). X线探测器为PIN光电二极管(Hamamatsu S3584-08), 通过电流表(Keithley 6485)测量X线的强度. 四刀口白光狭缝既可以限制照射在单色器上的光斑尺寸和光通量, 也可以调节入射光的角分布. 实验时储存环是恒流注入模式, 电流强度为Ie = 200 mA, X线的能量选择束线验收指标的能量10 keV. 分析晶体是Si111的完美单晶, 四刀口狭缝初始值设为5000 μm × 2450 μm (H × V), 探测器处的光斑尺寸约为10 mm × 5 mm (H × V).
按照图2搭建无色散配置的实验光路, 通过使用Cu元素的吸收边校正双晶单色器的工作能量, 使其出射光能量为10 keV. 分别调整双晶单色器和分析晶体满足能量为10 keV的衍射条件以及用PIN探测器测量转动分析器角度时的衍射强度. 其具体过程为: 1)转动Si111分析晶体, 并记录这个条件下的摇摆曲线. 2)以100 μm的步长逐步减小狭缝纵向宽度, 然后重复1)的测量过程. 这样的操作可获得一系列不同狭缝宽度的分析晶体摇摆曲线. 当狭缝纵向宽度减小到950 μm时, 改变步幅为50 μm; 当狭缝纵向宽度减小到50 μm时, 改变步幅为10 μm, 直至光强为零, 不能测量到信号强度为止. 选择不等间隔的调整步幅既可以保证得到在同步辐射中心附近比较精细的角分布信息, 又可以减少整个系列测量的总次数, 节省实验时间. 在完成(+1, –1)的实验配置后, 将实验配置依次改为(+1, +1)、(+1, –3)和(+1, +3)的色散配置, 重复上述的调整狭缝的数据采集过程, 然后获得在色散配置下一系列不同狭缝宽度下摇摆曲线.
4.数据处理与分析讨论
图8(a)、(b)分别是无色散配置和色散配置的Si111分析晶体在一系列侧脸中6个不同狭缝纵向宽度时的摇摆曲线. 图8(c)是无/有色散配置时一系列摇摆曲线的半高宽随狭缝纵向宽度变化的测量结果. 图8(b)中摇摆曲线的峰值强度比图8(a)的峰值强度大约低一个量级, 角度分布变宽, 这是色散效果的缘故. 但它们的积分强度一致. 图8(a)摇摆曲线上的“小凸起”是存在高次谐波的效果. 图8(b)中宽狭缝时摇摆曲线不对称是由于狭缝的中心与电子轨道平面(光源中心)不在同一位置, 狭缝的某一个刀口失去作用造成的. 从图8(c)可以看出: 当狭缝纵向宽度由大变小时, 无色散配置测量的摇摆曲线半高宽不变, 而色散实验配置得出的摇摆曲线的半高宽随狭缝纵向尺寸的减小而降低. 这些数据与DuMond图中的定性分析的结果是一致的.
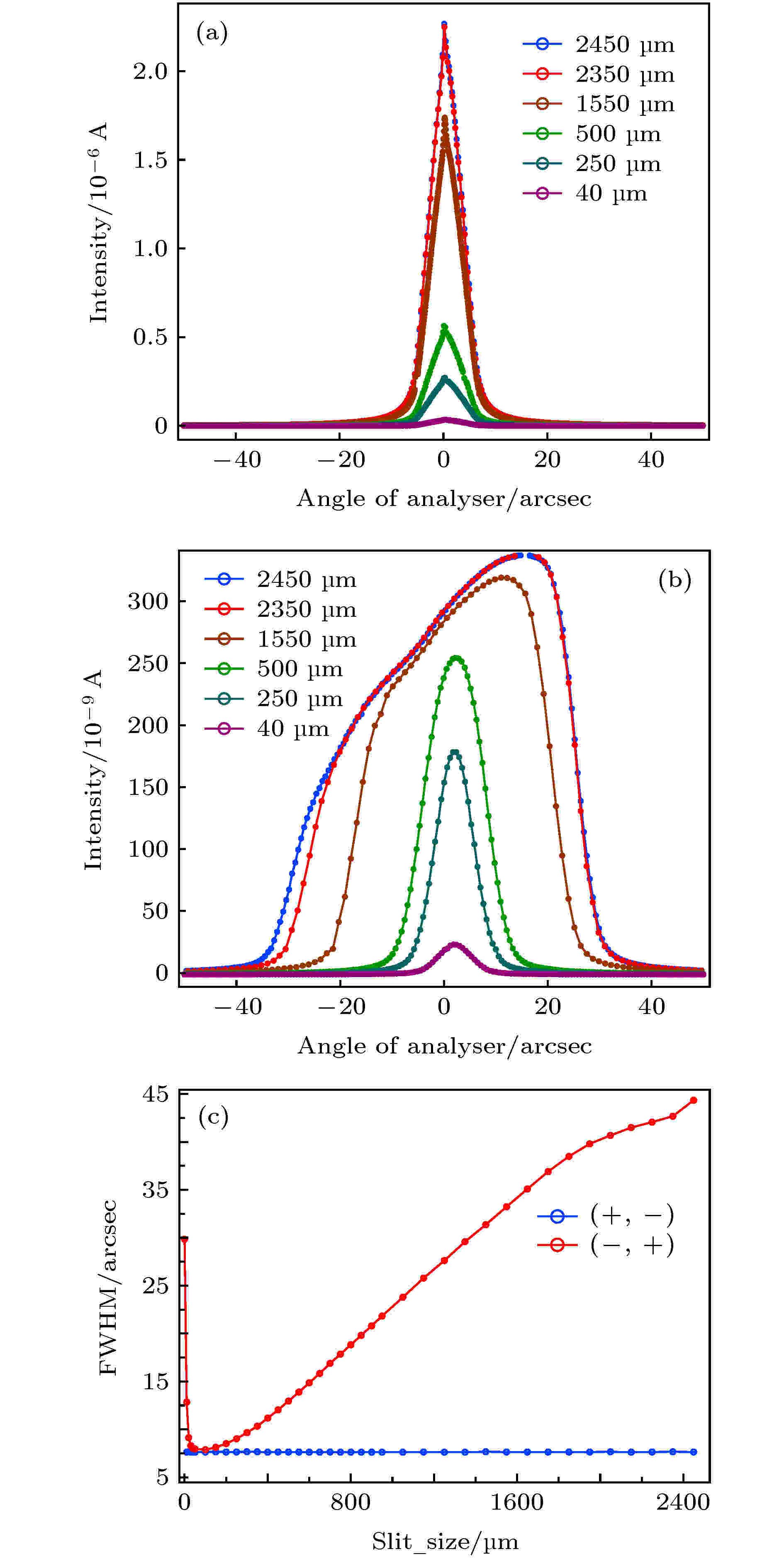图 8 (a)和(b)分别为无色散配置和“固定”色散配置条件下不同狭缝纵向宽度时Si111分析器的摇摆曲线. (c)是无色散配置和“固定”色散配置条件下随狭缝宽度调节时摇摆曲线的半高宽的曲线
Figure8. (a) and (b) give the rocking curves of the Si (111) analyzer with different slit vertical widths under the conditions of non-dispersion configuration and “fixed dispersion” configuration, respectively. (c) gives the FWHM curve of the rocking curve when the slit vertical width is adjusted under the condition of non-dispersion configuration and “fixed dispersion” configuration.

值得注意的是, 色散配置下的摇摆曲线半高宽数据(图8(c))靠右侧的半高宽值虽然随狭缝纵向宽幅的增加而变大, 但增加的速度变缓. 这是因为狭缝宽幅决定的接收角已接近光源的纵向发散角, 狭缝的角度调制作用接近失效; 而最左侧变大现象是因为在狭缝很小时, 出现狭缝的X射线衍射和小狭缝时摇摆曲线的信噪比变差, 导致了分析器的摇摆曲线半高宽变大. 在狭缝宽度较小时, 色散配置的半高宽变化变缓且趋于水平不变, 其原因是因为狭缝宽度所决定的光束接收角与单色器中晶体衍射的达尔文宽接近, 狭缝继续减小后分析晶体的达尔文宽起支配作用.
图9(a)和(b)分别给出了使用Si111分析晶体在无色散和“固定”色散配置时, 系列狭缝宽度调制条件下摇摆曲线做差分后的结果. 图中的纵轴是不同宽度的狭缝做逐差后的位置(注: 狭缝宽度等于0处与光轴中心略有差异, 但不影响结果的讨论, 为方便叙述下文把狭缝宽度等于0处描述为光轴中心), 横轴是分析器的角度位置. 对狭缝宽度做逐差的意义在于可以把图1所示束线的DuMond图从不同狭缝位置(角度)处提取出来, 即把角度从与波长的耦合关系中剥离出来. 图9(a)显示了无色散晶体配置方式的测量结果与狭缝位置无关, 这是因为无色散配置方式不能解开波长与角度的耦合关系, 摇摆曲线的峰位只出现在分析晶体的DuMond窗口与双晶单色器的DuMond窗口完全重合处. 结合图8(c)中无色散配置的摇摆曲线的半高宽不随狭缝宽度变化的结果, 我们可以得出如下结论: 无色散的实验配置因为不涉及能散的问题, 只适用于评价双晶单色器中第一晶体的应力变形, 不适合用来评价出射光的带宽. 与此相对照的是色散型的实验配置. 由于在该配置中, 衍射可以把光线中波长分布转换成角度分布, 表现在图9(b)中即是差分的结果会随狭缝逐差位置的变化而改变, 因而这种实验配置方式下可以把角度解调出来, 从而得到束线单色器的DuMond图. 不同的狭缝逐差位置意味着不同的入射晶体角度, 依据Bragg公式, 角度的分布可以转换为波长的分布. 将图9(a)和(b)纵轴的狭缝逐差位置转换为波长分布即是束线单色器的DuMond图. 但在这里为了清晰显示分析晶体差分和狭缝逐差的过程. 同时从图9(b)上已经可以获得不同狭缝宽度条件下的摇摆曲线半高宽, 应用(4)式和(5)式便可以得到束线的能量带宽. 故不再对图9做进一步处理.
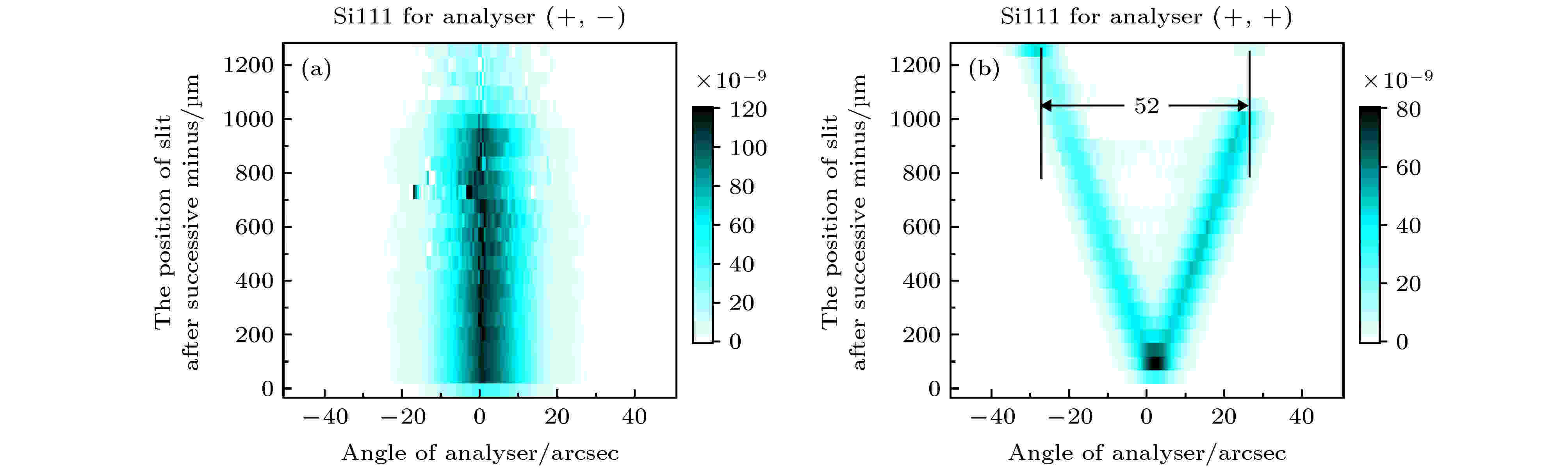图 9 (a)和(b)分别为使用Si111做分析器时, (+1, –1)和(+1, +1)实验配置条件下摇摆曲线做差分后的结果. 横轴的坐标原点对应着10 keV时分析晶体的衍射角. (b)同时还是在“固定”色散排列条件下使用Si111做分析器得到的未经狭缝(角度)——波长转换的“赝”DuMond图. 从图中可以直接读取不同狭缝宽度下得到的摇摆曲线半高宽的测量值
Figure9. (a) and (b) show the results of slit width difference of rocking curve with (+1, –1) and (+1, +1) experimental configurations with Si111 analyzer, respectively. The coordinate origin of the transverse axis corresponds to the diffraction angle of the analytic crystal at 10 keV. Also, (b) is the DuMond diagram without slit (angle) - wavelength conversion obtained using Si111 analyzer under the condition of dispersion configuration. The measured values of rocking curve FWHM with different slit widths can be read directly from the figure.

综上分析, 由图8(c)得出上海光源BL09B光学测试线的Si111双晶单色器在10 keV处的带宽为5.40(4)'', 其理论值为5.38'', 该展宽来自双晶单色器中第一晶的热变形效应. 由图9(b)“赝”DuMond图可以得出束线带宽的测量值为52(1)'', 利用(4)式和(5)式可以得出上海光源BL09B光学测试线的束线(狭缝全开)带宽为26(1)'', 其理论值为25.8''.
图10(a)和(b)分别给出了使用Si333做分析晶体的(+1, –3)型和(+1, +3)型实验配置时测得的“赝”DuMond图. 由图10(a)和(b)可以得出, 不同实验配置下分析晶体测得的束线带宽的测量值分别为67(1)''和117(1)''. 在退分析器卷积和消除色散展宽后, 得到束线的带宽为26(1)'', 与使用Si111做分析晶体得到的结果相吻合.
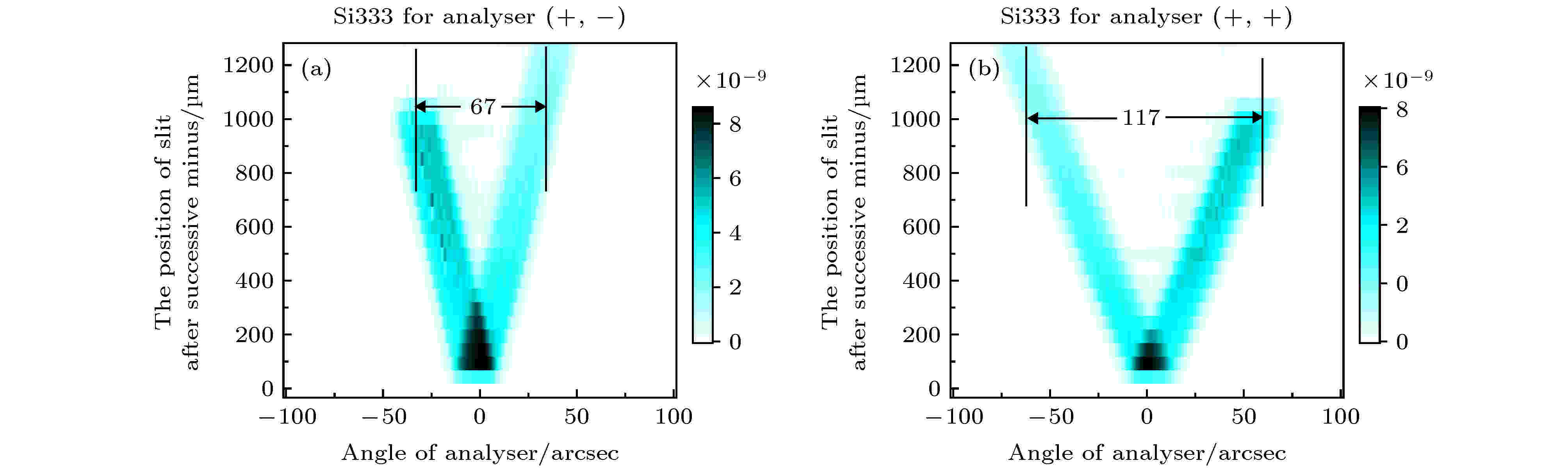图 10 (a)和(b)分别为使用Si333做分析器时, 在(+1, –3)型和(+1, +3)型实验配置条件下得到的“赝” DuMond图
Figure10. (a) and (b) give the pseudo DuMond diagram using Si333 analyzer under the condition of (+1, –3) type and (+1, +3) type dispersion configuration, respectively.

上述各种测量结果以及理论计算值一并列在表1中. 将上述测得的角宽度值代入式(2), 可以得出上海光源BL09光学测试线Si111双晶单色器在10 keV的相对能量带宽为1.30(1) × 10–4. 考虑到束线的角度发散影响后, 在狭缝全开的情况下, 得到束线在10 keV单色光时的相对能量带宽为6.3(2) × 10–4.
分析器衍射面实验配置色散类别测量值退卷积和色散展宽值理论值备注
(111)(+n, –n)无色散7.64(4)5.40(4)5.38双晶单色器带宽
(+n, +n)“固定”色散52(1)26(1)
(333)(+n, –m)“弱”色散67(1)26(1)25.8光束的带宽
(+n, +m)“强”色散117(1)26(1)


表1不同实验配置得到的实验值以及退分析器卷积和色散展宽后的值. 单位: 角秒(″)
Table1.The experimental values obtained from different experimental configurations and the values after deconvolution of the analyzer and removal of dispersion broadening. Unit: arcsec.

综上所述, 同步辐射束线的诊断需要借助于使用分析器以及一系列的诊断测量. 通过使用与双晶单色器呈无色散配置的分析器晶体, 可以测得束线单色器的带宽; 而使用色散配置的晶体分析器可以解析出束线的带宽. 在色散实验配置下, 通过对一系列入射狭缝宽度调制时的摇摆曲线进行差分, 可以获得束线的DuMond图. 此外, 虽然使用(+n, –m)型和(+n, +m)型色散实验配置也可以得到束线的能量带宽, 但是在这种条件下, 展宽因子的解析比较复杂. 故在实验条件允许的情况下, 使用与双晶单色器同衍射指数的分析晶体是方便合理的选择. 此外, 对束线角度带宽退双晶单色器角度带宽的卷积, 可以得到光源的角发散度. 由上述结果得到的上海光源BL09B光学测试线的光源角发散度为25(1)''.
5.总　结
本文分析说明了多晶体配置条件下衍射的不同特性, 并以上海光源BL09 B束线为例给出了测量实例和数据解析. 指出了(+1, –1)型无色散配置的分析晶体的摇摆曲线得到的是单色器的达尔文宽; (+1, +1)、(+1, –3)和(+1, +3)型配置的分析晶体的摇摆曲线可以得到的是用户实验中使用的光束的特性参数. 此外, 通过在色散配置下得到的一系列不同狭缝宽度的摇摆曲线, 以及对这一系列测量结果的差分处理, 可以得到一个测量光束线单色器和光源的DuMond图的方法. 利用这个方法测到了上海光源BL09B光学测试线上Si111双晶单色器的带宽为5.40(4)''@10 keV; 在狭缝纵向全打开的条件下, 光束的带宽为26(1)''@10 keV.
通过使用Si333做分析晶体的方法验证了使用色散配置的分析晶体可以获得束线DuMond图的普适性, 同时也给出了经单色器后束线的带宽. 此外, 使用由(+1, +1)、(+1, –3)和(+1, +3)型配置得到的束线带宽退除由(+1, –1)型配置得到的双晶单色器带宽的卷积得到了光源的发散角为25(1)''.
相关话题/实验 测量 光学 辐射 过程
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 确定大气边界层顶高度的新方法及数值实验
    摘要:提出了一种确定大气边界层顶高度的数值微分新方法,该方法使用了正则化技术,把对弯角廓线求导数的数值微分问题转化为求目标泛函极小值的问题,采用双参数模型函数方法来选择正则化参数,最后利用最大梯度法确定边界层顶高度.首先通过两个数值实验验证了新方法的有效性,实验结果显示,随着掩星资料噪音的增多,由差 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于四波混频过程和线性分束器产生四组份纠缠
    摘要:多组份纠缠是量子信息处理的重要资源,它的产生通常涉及到许多复杂的线性和非线性过程.本文从理论上提出了一种利用两个独立的四波混频过程和线性分束器产生真正的四组份纠缠的方案,其中,线性分束器的作用是将两个独立的四波混频过程联系起来.首先应用部分转置正定判据研究了强度增益对四组份纠缠的影响,结果表明 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 低能Cl<sup>–</sup>在Al<sub>2</sub>O<sub>3</sub>绝缘微孔膜中的输运过程
    摘要:研究了10keVCl–离子穿越Al2O3绝缘微孔膜的物理过程,发现穿越的Cl–其分布中心在初束中心即0°附近,Cl–离子穿透率下降与几何穿透一致,这是典型的直接几何穿越有一定角发散的微孔导致的结果;而出射的Cl0和Cl+以微孔轴向为中心分布,Cl+和Cl0穿透率下降慢于几何穿透.模拟计算发现沉 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于光学参量振荡器的可调谐红外激光的强度噪声特性
    摘要:红外激光光源在微量气体、高分辨率光谱分析和量子光学研究等领域具有重要的应用.本文利用锁定单共振光学参量振荡器内腔标准具的方案获得了无跳模连续调谐的红外激光输出,理论和实验研究了红外激光的强度噪声特性,分析了影响强度噪声的因素.通过控制非线性晶体的温度和标准具调制信号实现了对红外激光强度噪声的抑 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 爆轰加载下高纯铜界面Rayleigh-Taylor不稳定性实验研究
    摘要:金属界面不稳定性是内爆物理压缩过程中关注的重要问题,与传统流体界面不稳定性具有显著区别.由于相关理论和实验诊断技术的限制,目前该问题的研究还明显不足.为加深对金属界面不稳定性扰动增长行为的认识,本文建立了爆轰加载下高纯铜界面Rayleigh-Taylor不稳定性研究的实验诊断技术和数据处理方法 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 辐射对称金字塔型剪纸的力学行为
    摘要:通过在弹性薄板上引入切口,构建了多边形辐射对称金字塔型剪纸结构.利用伽辽金法求解的悬臂梁形变公式和悬臂梁组合的方法,创建了用于解释形变过程的“梁模型”,得到n个模块的正N边形金字塔结构的弹性系数与结构参数的关系公式,并求出弹性系数线性阈值的表达式,解释了该结构产生平面外扭曲的原因.利用推导的“ ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Al<sub>2</sub>O<sub>3</sub>衬底无催化剂生长GaN纳米线及其光学性能
    摘要:采用一种绿色的等离子增强化学气相沉积法,以Al2O3为衬底,Ga金属为镓源,N2为氮源,在不采用催化剂的情况下,成功制备获得了结晶质量良好的GaN纳米线.研究表明,生长温度可显著调控GaN纳米线的形貌,当反应温度为950℃时,生长出的GaN微米片为六边形;当反应温度为1000℃时,生长出了长度 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于原子重力仪的车载静态绝对重力测量
    摘要:目前大多数原子重力仪的装置复杂、体积庞大、环境适应性差,不能应用于野外进行绝对重力测量,这限制了原子重力仪的应用领域.本文利用自研的小型化原子重力仪,集成了一套车载绝对重力测量系统.该系统主要由原子重力仪、被动平台隔震系统、位姿平台调平系统、差分GPS测高系统、不间断电源供电系统及车载空调温控 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 纳米流体液滴内的光驱流动实验及其解析解
    摘要:在光透过性的流体介质中添加具有高光响应特性的纳米颗粒,可以形成光驱动纳米流体,实现对光能的高效利用.本文针对光驱纳米流体流动行为开展实验观察和理论分析研究,这是实现光驱纳米流动精确调控的理论基础.首先利用粒子图像测速技术对液滴中直径为300nm的Fe3O4颗粒在不同光源照射下受Marangon ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 涡轮导向器对旋转爆轰波传播特性影响的实验研究
    摘要:为了研究涡轮导向器对旋转爆轰波传播特性的影响,以氢气为燃料,空气为氧化剂,在不同当量比下开展了实验研究.基于高频压力传感器及静态压力传感器的信号,详细分析了带涡轮导向器的旋转爆轰燃烧室的工作模式以及涡轮导向器对非均匀不稳定爆轰产物的影响.实验结果表明:在当量比较低时,爆轰燃烧室以快速爆燃模式工 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.