摘要:通过在弹性薄板上引入切口, 构建了多边形辐射对称金字塔型剪纸结构. 利用伽辽金法求解的悬臂梁形变公式和悬臂梁组合的方法, 创建了用于解释形变过程的“梁模型”, 得到n个模块的正N边形金字塔结构的弹性系数与结构参数的关系公式, 并求出弹性系数线性阈值的表达式, 解释了该结构产生平面外扭曲的原因. 利用推导的“梁模型”公式, 并通过有限元仿真和实验的方法, 系统研究了辐射对称金字塔型剪纸结构的力学响应特征, 验证模型的准确性, 并用于已有报道的石墨烯剪纸结构的力学特征分析. 这项工作系统解释了竖直拉伸的金字塔型剪纸结构的力学响应.
关键词: 剪纸/
辐射对称/
石墨烯/
柔性器件

English Abstract

全文HTML

--> --> -->

在二维弹性薄板材料上引入切口, 形成镂空的剪纸(kirigami)结构, 可以改良材料属性^[1-4], 如传统弹性薄板不能延展的缺点. 引入剪纸结构后, 薄板受到外力作用可因内部应力的释放, 发生屈曲响应, 产生大幅度形变^[5-8]. 通过这种方式加工具有优良性能的二维薄膜材料^[9-12], 特别是对微纳米材料^[13]加工, 可以极大地改变材料的力学性能^[14,15]. 对于不能延展的电子器件, 如薄膜太阳能电池^[16], 通过剪纸结构的加工也能大幅度提高器件的延展性. Rafsanjani和Bertoldi^[7] 2017年在Phys. Rev. Lett.上发表了关于方阵穿孔薄板力学响应的研究, 在单轴拉力作用下, 剪纸结构薄板可以部分弯曲形成三维图形, 产生周期性的永久褶皱; Rafsanjani等^[8] 2019年又在Proc. Natl. Acad. Sci. U.S.A.发表了对圆柱带状剪纸结构的研究, 通过选择剪纸结构的几何参数调控剪纸单元的相变. 目前, 多数研究聚焦在水平拉伸的带状结构, 可竖直拉伸的辐射对称结构的研究, 尤其是理论研究较少.
可以竖直延展的辐射对称剪纸结构, 如金字塔结构, 有着良好的形变能力以及力学、电学特性. 2015年, Blees等^[1]在Nature上发表了关于石墨烯剪纸结构的研究, 表明金字塔型剪纸结构的石墨烯弹簧在部分条件下弹性系数为定值, 该结构有望制作具有直观视觉读数的微小力测量设备; 2016年, He等^[17]在J. Mater. Chem. A上发表了基于金字塔结构制作的超级电容器研究, 能在三维空间拉伸. 相似辐射对称结构也被用于制作可穿戴柔性传感器^[18]. 目前金字塔结构的力学行为的理论研究较少, 缺少合适模型解释其力学响应.
本文基于伽辽金法(Galerkin method)^[19]求解的悬臂梁公式对金字塔型剪纸结构的力学响应进行了理论解释. 将辐射对称的金字塔型剪纸结构分割为若干“梁单元”的组合, 建立“梁模型”, 推导得到几何参数对力学性能影响的解析解, 并对结构的受力-形变的线性阈值做了推导. 通过有限元方法(finite element method, FEM)仿真和实验测试, 对理论结果进行了验证. 利用此理论, 能定量解释辐射对称剪纸结构形变过程, 并通过对结构扭曲现象的分析, 指出不同模块切口长度L对结构不稳定性的影响.

2

-->

2.1.金字塔剪纸模型

2015年, Blees等^[1]在Nature上发表了利用石墨烯制作的微型剪纸结构的研究, 实验测得金字塔型石墨烯剪纸结构在微小力条件下, 弹性系数K = 2 × 10^–6 N·m^–1. 其剪纸结构为典型的正四边形金字塔结构, 母图案如图1(a)所示, 主要参数为: 正多边形的边数为N = 4; 模块数为n = 3; 靠近内侧的第一个模块切口长度最短, 定为L; 往外侧的相邻模块的模块切口长度为(b/2 + L + b/2), 即两侧共增加长度为b; 相邻模块的连接长度一般不变, 为x; 梁宽为w; 薄板厚度为t; 材料杨氏模量为E. 固定最外层边缘结构, 在垂直面内施加拉力F后, 在面外的拉伸形变如图1(b)所示. 图示结构(n = 3)在受力形变后, 可以分为三个形变模块, 三个模块的形变长度分别为d₁, d₂, d₃, 总形变为长度D.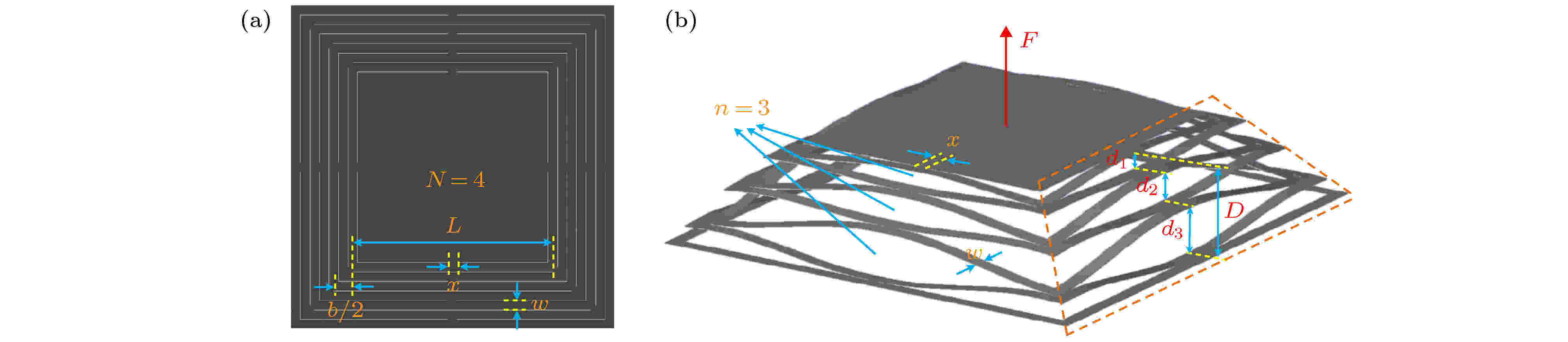
图 1 典型金字塔型剪纸结构　(a) 边数N = 4, 模块数n = 3的金字塔结构; (b) 模型在竖直拉力F作用下产生竖直形变
Figure1. Typical pyramid kirigami structure: (a) Pyramid structure with number of edges N = 4 and number of modules n = 3; (b) pyramid model produces vertical deformation under the action of vertical tension F.

为了对金字塔型剪纸结构在竖直方向形变过程进行分析, 建立了如图2的物理模型, 将此结构分为若干个悬臂梁的组合, 采用“梁模型”分析它的受力形变. 根据正四边形剪纸结构某个形变区域, 对应图1(b)拉伸模型中的一个侧面, 建立如图2(a)所示的“梁模型”. 图2(a)中共有3个“梁模块”, 分别为m₁, m₂, m₃. 每个“梁模块”可以看作由4个相同长度为(L – x + 2b)/2的“梁单元”组成. 如图2(b)的“梁单元”所示, 红色虚线区域为组成侧面结构的一个基本的“梁单元”, 近似分割为两个等效的一端受力而另一端固定的悬臂梁Beam A和Beam B. 对于Beam A来说, 可以看作左端固定的悬臂梁, 右端在受到右侧梁Beam B向下拉伸的竖直力f_A作用后向下弯曲, 产生的竖直方向挠度为d_A, 悬臂梁的长度为l_A, 宽度为w, 厚度为t. Beam B可类似定义.
图 2 由“梁单元”构成的“梁模型”　(a) 金字塔结构一个形变区域简化成的“梁模型”; (b) 悬臂梁组成的“梁单元”
Figure2. “Beam model” consisting of “beam elements”: (a) Simplified “beam model” of a deformed area of the pyramid structure; (b) “beam element” consisting of cantilever beams.

2 -->

2.2.弹性系数理论分析

在如图2(b)所示的悬臂梁Beam A模型中, 采用伽辽金法计算挠度d_A和受力f_A的关系为^[20]

$\frac{{{d_{\rm{A}}}}}{{{l_{\rm{A}}}}} = \frac{1}{3}\left( {\frac{{{f_{\rm{A}}}l_{\rm{A}}^2}}{{EI}}} \right) - \frac{1}{{28.47}}{\left( {\frac{{{f_{\rm{A}}}l_{\rm{A}}^2}}{{EI}}} \right)^3} + \cdots ,$

式中l_A是悬臂梁的长度, 对应此模型, l_A长度为图2(b)红色虚线部分“梁单元”的一半, 长度为(L – x + 2b)/4, E是材料的杨氏模量, I是梁的抗弯曲截面系数. 横截面为长方形的抗弯曲截面系数表达式为I = wt³/12, w是梁的宽度, t是梁在弯曲方向的厚度, 即弹性薄板的厚度. 对于悬臂梁在竖直方向产生的小挠度形变d_A, 可以忽略高阶项, d_A和f_A的关系近似表达为

$\frac{{{d_{\rm{A}}}}}{{{l_{\rm{A}}}}} = \frac{1}{3}\left( {\frac{{{f_{\rm{A}}}l_{\rm{A}}^2}}{{EI}}} \right),$

它的自由端弹性系数k可以表达为

${k_{\rm{A}}} = \frac{{{f_{\rm{A}}}}}{{{d_{\rm{A}}}}} = \frac{{3EI}}{{l_{\rm{A}}^3}},$

代入I后的表达式为

${k_{\rm{A}}} = \frac{{{f_{\rm{A}}}}}{{{d_{\rm{A}}}}} = \frac{{Ew{t^3}}}{{4l_{\rm{A}}^3}} = \frac{{16Ew{t^3}}}{{{{(L - x + 2b)}^3}}}.$

图2(b)红色虚线区域中的“梁单元”可以看作是两个相同悬臂梁结构Beam A和Beam B串联(类似于弹簧)的结果, 其弹性系数k为

${k_{{\rm{AB}}}} = \frac{{{f_{{\rm{AB}}}}}}{{{d_{{\rm{AB}}}}}} = \frac{{Ew{t^3}}}{{8l_{\rm{A}}^3}} = \frac{{8Ew{t^3}}}{{{{(L - x + 2b)}^3}}}.$

图2(a)的模块m₃可以看作四个红色虚线区域“梁单元”, 即四对相同悬臂梁结构Beam A和Beam B的组合. 四个“梁单元”两两并联后串联, 因此组合后的k与单一“梁单元”保持一致, 即

${k_3} = \frac{{{f_3}}}{{{d_3}}} = {k_{{\rm{AB}}}} = \frac{{8Ew{t^3}}}{{{{(L - x + 2b)}^3}}}.$

每部分的施力大小与施加在一个侧面上的拉力f₀是相等的, 即f₀ = f₁ = f₂ = f₃, 其中f₀为施加总拉力F的1/4. 因此, 各模块的形变长度d₁, d₂, d₃的关系如下:

$\frac{{{d_1}}}{{{{(L - x)}^3}}} = \frac{{{d_2}}}{{{{(L - x + b)}^3}}} = \frac{{{d_3}}}{{{{(L - x + 2b)}^3}}},$

将三个部分的d和f关系代入(7)式中, 可以得到图2(a)中一个侧面的“梁模型”的力f₀与形变D的关系为

$\begin{split} \; &\quad {k_0} = \frac{{{f_0}}}{D} = \frac{{{f_0}}}{{{d_1} + {d_2} + {d_3}}} \\ &= \frac{{8Ew{t^3}}}{{{{(L - x)}^3} + {{(L - x + b)}^3} + {{(L - x + 2b)}^3}}}.\end{split}$

在正四边形金字塔结构中存在四个相同的侧面, 即四个“梁模型”的组合, 总的拉力F和形变长度D的关系为

$K = \frac{F}{D} = \frac{{8Ew{t^3} \times 4}}{{{{(L - x)}^3} + {{(L - x + b)}^3} + {{(L - x + 2b)}^3}}},$

如此类推, 对于存在n个模块的正N边形金字塔结构的弹性系数, 推广为

$\begin{split} & K = {F}/{D} =\\ \;& \!\!\!\frac{{8Ew{t^3}N}}{{{{(L \!-\! x)}^3} \!+\! {{(L - x + b)}^3} \!+ \! \cdots \!+\! {{[L \!-\! x \!+\! (n \!- \!1)b]}^3}}}.\end{split}$

各“梁单元”的形变是导致“梁模型”整体结构形变的直接原因, 因此各模块长为x的连接处对“梁模型”的形变不起作用, 故设去掉连接长度x的梁长L_eq = L – x, 化简(10)式得到弹性系数K与辐射对称金字塔型剪纸结构的参数(边数N、模块数n、模块切口长度增加值b、梁长L_eq、梁宽w、厚度t、杨氏模量E)的关系如下:

$K = \frac{F}{D} = \frac{{32Ew{t^3}N}}{{{b^3}{n^4} + (4{L_{{\rm{eq}}}}{b^2} - 2{b^3}){n^3} + (6L_{{\rm{eq}}}^2b - 6{L_{{\rm{eq}}}}{b^2} + {b^3}){n^2} + (4L_{{\rm{eq}}}^3 - 6L_{{\rm{eq}}}^2b + 2{L_{{\rm{eq}}}}{b^2})n}}.$

2 -->

2.3.线性阈值理论分析

弹性系数K关系式(11)的适用范围受到悬臂梁理论公式的适用范围影响. 悬臂梁理论公式采用了去掉高阶项的小挠度曲线近似, 当结构形变超过保持弹性系数K为线性的最大形变, 即线性阈值D_T时, 其力学响应表现为非线性. 图3给出了基于(1)式和(2)式的悬臂梁Beam A理论曲线与小挠度近似曲线对比, 在d_A/l_A小于0.3的范围内, 两曲线近似相等, 在此范围内梁的受力与形变的关系可以采用“小挠度”近似公式计算.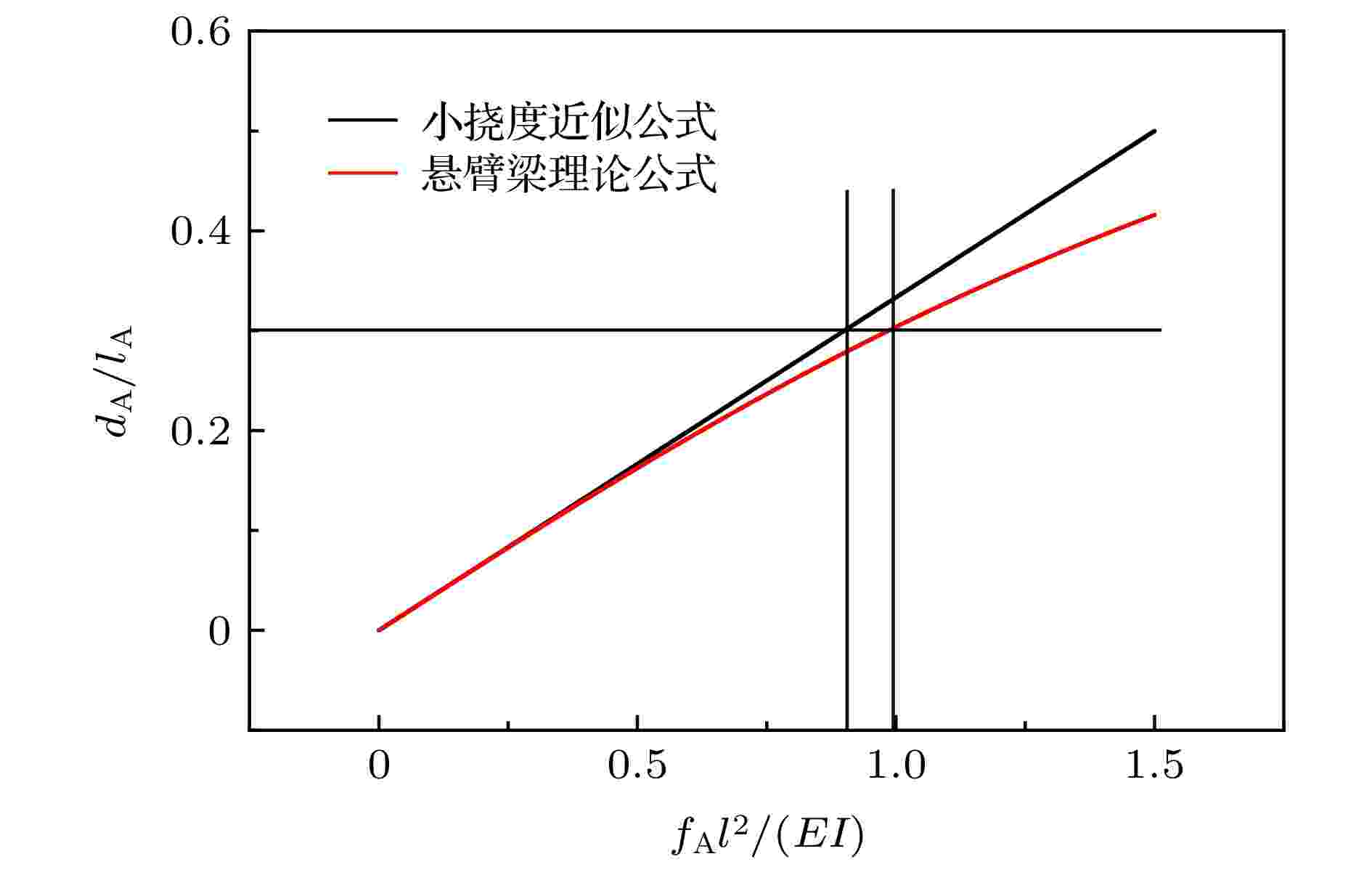
图 3 基于(1)式和(2)式的悬臂梁理论曲线与小挠度近似曲线对比
Figure3. Theoretical curve of cantilever beam compared with the approximate theoretical curve of small deflection based on Eq. (1) and (2).

对于悬臂梁Beam A来说, 纵向形变d_A与梁长l_A之比小于0.3时, 推导公式可适用. 逐步推导至“梁模块”, 线性阈值D_T为“梁模块”等效梁长的0.3倍, 如对于设置参数L = 12 mm, x = 2 mm的单一模块, 纵向形变d不超过0.3(L – x), 即不超过3 mm时, 推导公式可适用. 推导至“梁模型”, 如对于n = 3的四边形结构, 当竖直拉力F作用到3个模块上时, 由(7)式知, 在竖直拉伸过程中, 各模块的形变长度d与其对应等效梁长成比例关系. 当模块m₁形变达到线性阈值0.3(L – x)时, 代入(7)式, 可得模块m₂和m₃形变未达到线性阈值, 因此在拉伸过程中, 模块切口长度L最短的模块最先达到其线性阈值. 在此情况下, 取模块m₁的阈值为0.3(L – x), 将0.3(L – x)代入(7)式, 可得到此时模块m₂和m₃分别对应的阈值. 取三个模块的线性阈值之和, 可以得到n = 3的四边形结构保持线性拉伸时的极限长度, 即线性阈值D_T公式为

${D_{\rm{T}}} = 0.3\left[ {(L - x) + \frac{{{{(L - x + b)}^3}}}{{{{(L - x)}^2}}} + \frac{{{{(L - x + 2b)}^3}}}{{{{(L - x)}^2}}}} \right],$

对于存在n个模块的正N边形金字塔结构的线性阈值, 推广为

${D_{\rm{T}}} = 0.3\left\{ {(L - x) + \frac{{{{(L - x + b)}^3}}}{{{{(L - x)}^2}}} + \cdots + \frac{{{{[L - x + (n - 1)b]}^3}}}{{{{(L - x)}^2}}}} \right\},$

令L_eq = L – x, 化简(13)式得

${D_{\rm{T}}} = 0.3\left[ {\frac{{{b^3}{n^4} + (4{L_{{\rm{eq}}}}{b^2} - 2{b^3}){n^3} + (6L_{{\rm{eq}}}^2b - 6{L_{{\rm{eq}}}}{b^2} + {b^3}){n^2} + (4L_{{\rm{eq}}}^3 - 6L_{{\rm{eq}}}^2b + 2{L_{{\rm{eq}}}}{b^2})n}}{{4L_{{\rm{eq}}}^2}}} \right].$

需要注意的是, 在具体适用中, 由于采用“小挠度”公式进行计算, 结构弹性系数的实际值会随拉伸距离增加, 误差逐渐增大. 在形变达到线性阈值时, 会产生6%左右的理论误差. 如果为追求精确, 可以适当缩小D_T计算公式(14)的常系数0.3的值.

2

-->

3.1.FEM验证

金字塔结构剪纸的力学响应可以被切口参数调制, 如(11)式. 为验证各参数的影响, 图4展示了利用FEM软件进行多点验证, 计算正多边形弹性系数受切口参数调制的定量结果. 本文中使用ANSYS Workbench验证, 首先根据物理模型建模, 并在最上层多边形平台中心建立向上凸起表面的圆形平台作为应力施加边界, 在最下层制作和最底层结构大小相同的“回”形平台作为约束边界; 材料属性设置为: 密度300 kg/m³, 杨氏模量1.2 GPa, 泊松比0.3, 材料温度22 ℃; 网格单元大小设置为20 mm. 几何参数设置为: L = 1.26 m, x = 2 cm, 其余各参数设置在对应图中空白处给出了标注. 对模型位移进行求解后, 利用施力F和得到的结构最大形变D可以求出结构弹性系数K. 图4(a)—(c)中的点表示对三个参数验证的FEM仿真值, 弹性系数K分别与w, $ t^3 $及N呈线性变化的关系, 和K值理论公式(11)结果一致. 对于梁宽w来说, 增大w可以使弹性系数增大. 对于厚度t, 弹性系数对厚度t最为敏感, t增大为2倍, K值会增大为8倍, 若需要大幅度增强结构弹性系数, 增加t是最有效的方法. 反之亦然, 对于t为纳米级的二维材料薄膜而言, 利用此类剪纸结构, 可以获得极小的弹性系数K值, 从而测量微小力, 如光压或光镊力^[1]. 对于边数N来说, 增大N可以增大K. 但是增大N意味着需要占用更大的面积(如正六边形的金字塔结构面积是正四边形的2.6倍左右), 同时过大的N会限制b的大小, 因此之后研究均采用四边形结构.
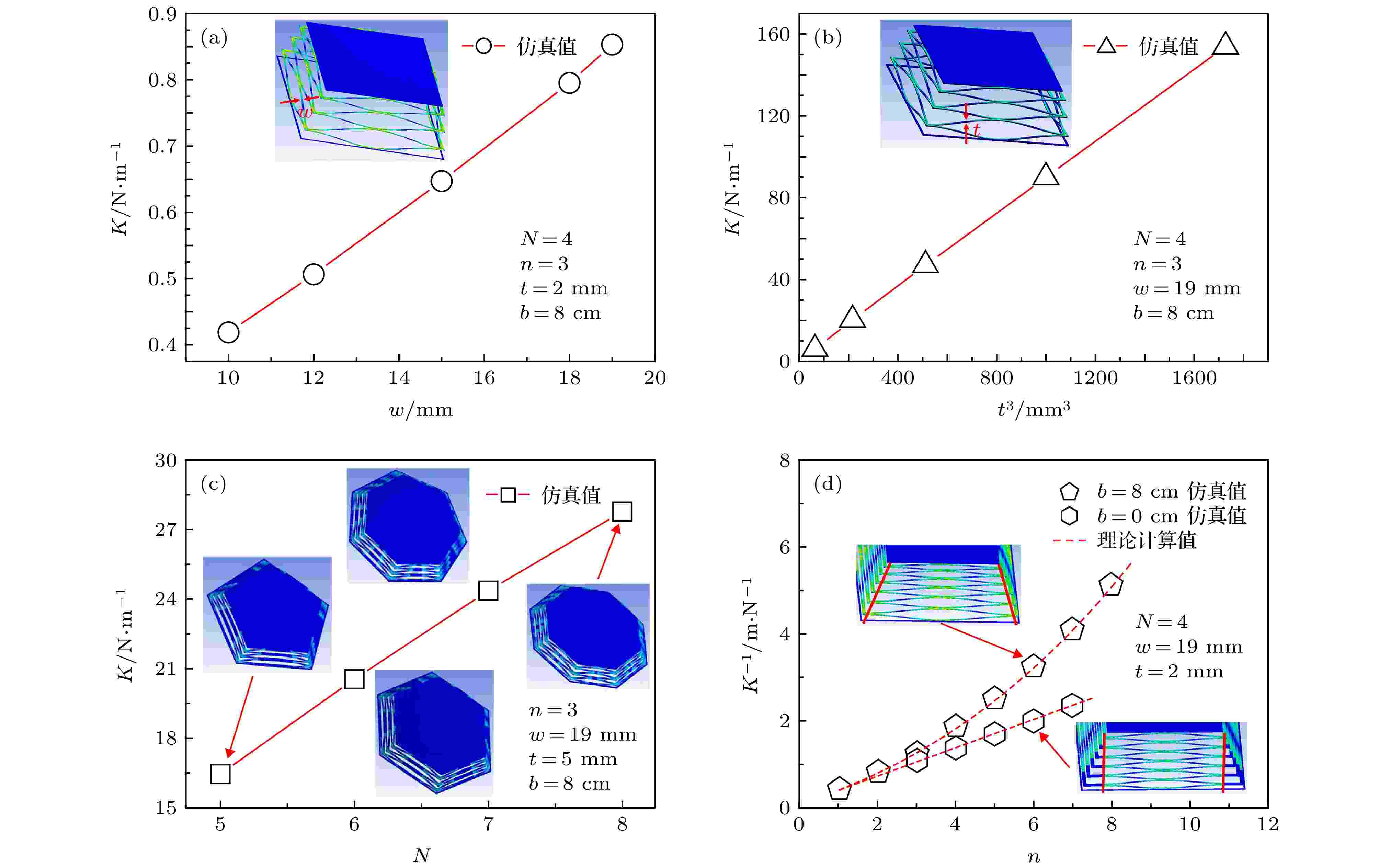图 4 FEM模拟和理论计算验证弹性系数与结构参数关系　(a)?(c) 弹性系数K分别与梁宽w、厚度t的三次方及边数N值呈线性变化关系; (d) 取不同模块切口长度L的增加值b, 验证K值与模块数n的关系, 点为模拟值, 虚线为计算值
Figure4. Verify the relationship between elastic coefficient and structural parameters through FEM simulation and theoretical calculation: (a)?(c) The elastic coefficient K varies linearly with the beam width w, the cube of thickness t, and the number of sides N; (d) take different values b to verify the relationship between the elastic coefficient K and the number of modules n. The points are simulation values, and the dotted lines are calculated values.

图4(d)中, 取不同的模块切口长度L的增加值b, 验证了K与n的关系. 图中的点为FEM仿真值, 虚线为基于弹性系数K的计算公式(11)的理论计算值, 两者保持了很好的一致性. 对于n来说, 增大n即增加“梁模块”会使K值缩小. 此外, 如图4(d)中右下角插图所示结构, 相邻模块的切口长度L均相等, 即b = 0时, 计算和模拟的对应结果为图4(d)中六边形. b = 0时该结构的力学响应可以保持很好的线性关系, 同时可以使计算更加简单; 当b > 0时, 计算和模拟的对应结果为图4(d)中五边形, K值会小于b = 0的结构, 但其线性阈值D_T会更大, 可拉伸范围更大.
2 -->

3.2.实验验证

为验证弹性系数K计算公式(11)和线性阈值D_T计算公式(14), 在弹性纸板上制作了模块数n为3的四边形金字塔结构. 纸板采用A4大小的270 g规格相片纸, 实验结构图形采用CAD (computer aided design)绘制, 用刻刀对打印好图像的纸板进行切割, 完成金字塔结构的制作. 为减小重力影响, 实验中将此结构的底端最外层结构固定在一竖直平面上, 通过水平滑动装置施加变化的水平拉力F, 用数字测力计记录其拉力F与形变D的关系. 图5(a)为实验图, 结构参数为: N = 4, n = 3, L = 7.5 cm, x = 8 mm, b = 1 cm, w = 4.5 mm, t = 280 μm.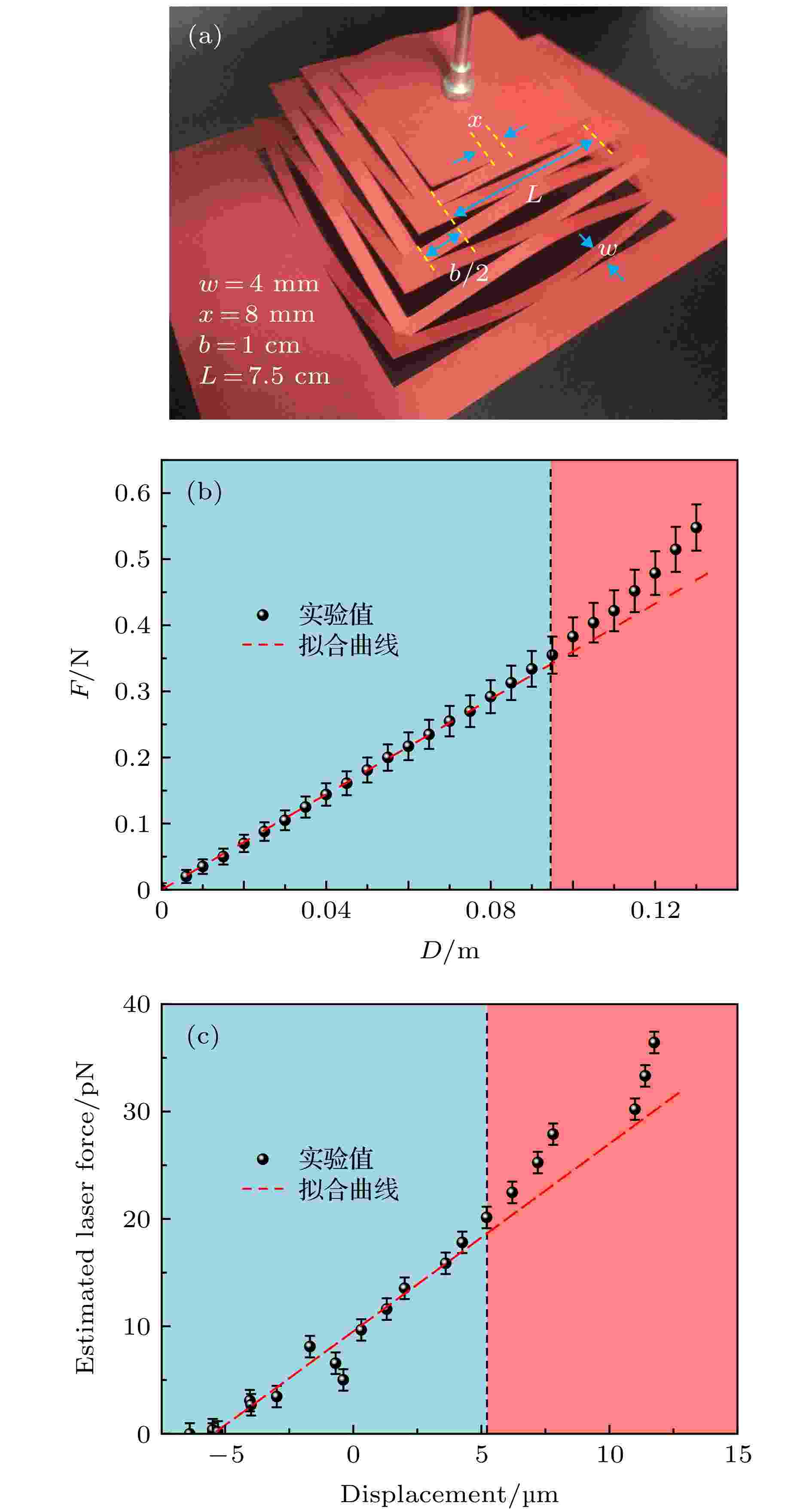
图 5 利用实验对K, D_T的计算公式(11)和(14)式进行验证　(a) 实验图; (b) 四边形实验数据, 点为测量结果, 虚线红色为线性区域拟合结果, 黑色虚线为计算出的线性阈值; (c) Nature上发表的石墨烯剪纸弹簧在激光驱动下的形变-受力结果^[1]
Figure5. The K and D_T formulas (11) and (14) are verified experimentally: (a) Experimental picture; (b) the experimental data of the quadrangular pyramid structure, the points are the measurement results, the red dotted line is the linear region fitting result, and the black dotted line is the calculated linear threshold; (c) laser-driven deformation of graphene kirigami springs published in Nature^[1].

图5(b)中黑色圆点数据为图5(a)模型对应的实验测试结果, 红色虚线为根据前10个点的线性拟合结果, 拟合弹性系数K (即直线斜率)值为3.606 N·m^–1, 将拟合K值及其他参数代入(9)式, 计算得出杨氏模量E值为1.828 GPa, 与材料测量值一致, 与相关文献报道在同一数量级^[21]. 将各参数代入线性阈值公式(12), 经过计算, 可得线性阈值D_T = 0.0946 m, 并在图5(b)中用灰色虚线将其标出. 可以直观地发现, 拉力F和形变长度D的实验数据在计算得到的线性阈值(虚线)左侧蓝色区域可以保持线性关系, 线性阈值右侧红色区域逐渐偏离线性变化. 在线性阈值处, 实际测量的拉力F与计算出的拉力值有3.5%左右的误差. 拉伸长度超过阈值后, 误差增大. 因此, 基于“梁模型”推导的弹性系数K计算公式(11)和线性阈值D_T计算公式(14)通过实验得到验证. 且对于任意弹性薄板材料, 可以利用在薄板上切割金字塔型剪纸结构, 在结构的线性阈值范围内采用 K的计算公式(11)来近似估算材料的杨氏模量E.
根据推导出的弹性系数K的计算公式(11), 弹性系数K与厚度t的三次方成正比, 因此剪纸结构如用于厚度为纳米级的二维材料, 可以获得高敏感度的微小力测量设备. 如文献[1]中采用多晶石墨烯制作金字塔型剪纸结构, 可在激光照射下产生形变, 从而直接测量激光驱动力或间接测量激光光强. 基于实验条件限制, 研究直接参考文献[1]中数据, 用于定性验证弹性系数K的计算公式(11)和线性阈值D_T的计算公式(14). 对于二维材料制作的金字塔型剪纸弹簧, 图5(c)为文献[1]中采用多晶石墨烯制作的金字塔型剪纸结构在激光驱动下产生的形变-受力估计值测量结果, 弱光强低光压下表现为线性, 并且在线性阈值处逐渐偏离拟合曲线. 文献[1]中未给出金字塔结构的具体参数, 根据实验图像, 估算出结构参数如N = 4, n = 3, w = 2 μm, t = 0.335 nm, L = 20 μm, x = 2 μm, b = 10 μm, 并根据基于“梁模型”推导的弹性系数K的计算公式, 估算材料的杨氏模量约为68 TPa. 该值相比常用石墨烯杨氏模量1.054 TPa^[22], 有一个数量级的增强, 推测是二维材料杨氏模量在弯曲状态有数量级增加^[23]所致.
针对图5(b)的实验结果, 力的测量误差会随着变形量的增加而增加, 这在变形量较大尤其是右侧的非线性区域格外明显. 在测量力的大小时, 进行了多组实验, 发现力的大小变化范围大约为力的8%, 所以将误差统一设定为受力F的8%. 在图5(b)的非线性区域, 金字塔结构受大拉力作用下, 实验值偏移理论值, 弹性系数K表现出的非线性响应是不可避免的. 影响其非线性响应的主要因素有三个, 首先, 结合 (1)式和(2)式, 可以发现舍弃掉的指数型高阶项在微小力情况下值较小, 随着受力的增大, 舍弃掉的指数型高阶项逐渐增大, 这是主要因素; 其次, 在结构拉伸过程中, 结构受力产生的应变会造成梁的扭曲, 这是另一个因素; 最后, 金字塔模型在重力影响下, 结构会产生一定的扭曲, 部分重力还可能会与拉力F抵消, 使结果偏离理论曲线.
在理论建模中, 需要考虑重力是否对模型有显著影响. “梁模型”是由若干悬臂梁的线性叠加组成的, 因此整个模型力学响应的线性特性与单个悬臂梁的线性特性保持一致. 对于图5(a)对应的实验模型, 可以将模型分为悬臂梁组成的形变区域和顶部不发生形变的多边形平台区域. 实验选择的材料面密度为270 g·m^–2. 对于悬臂梁组成的形变区域, 单个悬臂梁所受重力是微小的. 如以实验模型的底层模块计算, 组成底部模块的悬臂梁面积为2.349 × 10^–5 m², 所受重力G约为2.3 × 10^–4 N, 实验模型施力F取0.2 N时, 单个悬臂梁所受拉力约为2.5 × 10^–2 N, 相差两个数量级. 其余模块的悬臂梁所受重力更小, 可以认为重力对单个悬臂梁的线性影响可以忽略. 因此, 对于由悬臂梁组成的整个形变区域, 重力对其线性的影响可以忽略. 对于顶部不发生形变的多边形平台区域, 特别是当N取值较大时, 其平台重力G较大, 重力也可能与拉力抵消. 经过计算, 由于重力影响, 线性阈值会提前G/K左右. 因此, 对于竖直拉伸的金字塔结构中, 顶部平台的重力G会导致公式适用范围提前G/K左右, 但组成形变区域的悬臂梁重力影响可以忽略.

根据(14)式, 可以计算出金字塔型剪纸结构的拉伸线性阈值. 但当拉力较大, 金字塔结构的每一个模块会因形变发生横向的收缩, 带动相邻模块, 使梁结构产生平面外的扭曲. 此扭曲会破坏结构稳定性, 尤其是在厚度较小的二维材料中, 扭曲会导致弹性系数出现非线性变化^[23]. 因此, 在设计剪纸结构参数时, 也要考虑梁扭曲对拉伸线性阈值的影响.
图6建立了简单的几何关系用于解释辐射对称金字塔型的面外扭曲的产生原因, 此结构的偏曲过程与文献[24]中太阳能电池由二维到三维的形变过程类似. 为研究金字塔结构的偏曲影响因素, 选取其中一个模块进行了研究, 如图6(a)金字塔结构形变的实物图所示. 图6(b)为某一模块形变的简单示意图. 设单一模块的切口长度为L, 在受竖直方向拉力产生的竖直方向形变为$\Delta d$, 根据其几何关系对模块切口长度L的横向应变${\varepsilon _{\rm{T}}}$进行了推导.
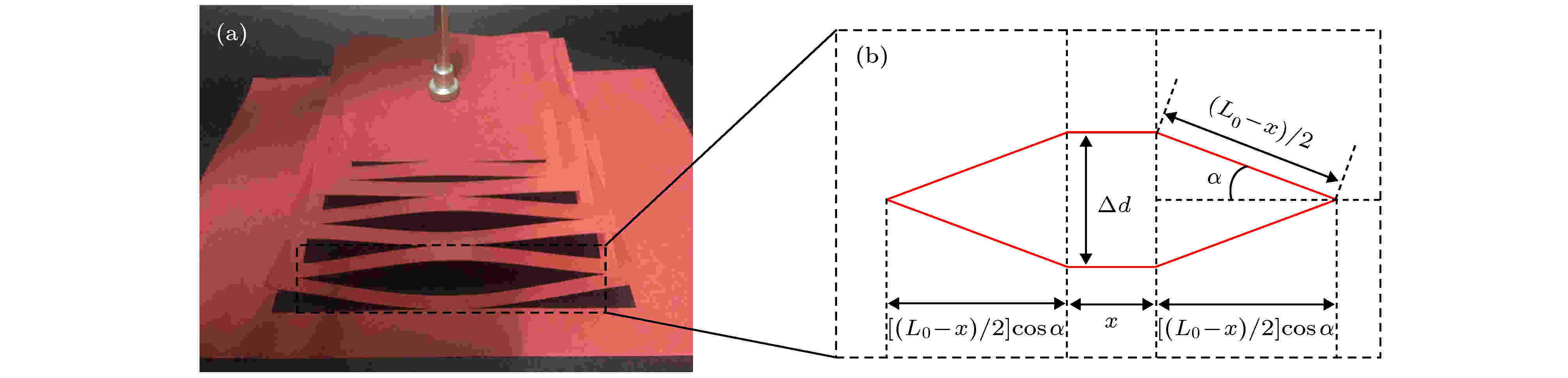图 6 模块的横向收缩　(a) 模块形变的实物图; (b) 某一模块形变的简单几何关系
Figure6. Transverse strain of a module: (a) Experimental diagram of module deformation; (b) simple geometric relationship of deformation of a single module.

该结构未经拉伸的模块切口长度为L, 在产生竖直方向形变$\Delta d$后, 其长度L₁为

${L_1} = (L - x)\cos \alpha + x,$

竖直形变引起的模块切口长度L横向应变${\varepsilon _{\rm{T}}}$为

${\varepsilon _{\rm{T}}} = \frac{{{L_1} - L}}{L} = - \frac{{(L - x)(1 - \cos \alpha )}}{L},$

其中

$\alpha = {\sin ^{ - 1}}\frac{{\Delta d}}{{L - x}},$

代入可得模块切口长度L横向应变${\varepsilon _{\rm{T}}}$为

${\varepsilon _{\rm{T}}} = - \frac1{L}{{(L - x)\left[ {1 - \sqrt {1 - {{\left(\dfrac{{\Delta d}}{{L - x}}\right)}^2}} }\, \right]}}.$

由(18)式可以看出, 不同的模块切口长度L可以调制横向应变${\varepsilon _{\rm{T}}}$, 影响梁结构扭曲. 因此合适的参数取值可以提高结构稳定性, 减小梁结构扭曲发生的可能性. 利用(18)式计算了不同模块切口长度L对横向应变${\varepsilon _{\rm{T}}}$的影响. 图7是计算结果, x取定值0.01 m, 结果表明产生同样拉伸量的情况下, 模块切口长度L越短, 引起的横向收缩就越严重, 导致梁的扭曲越严重, 为了提高结构稳定性, 应尽可能提高L长度. 图中计算了不同模块切口长度L可能导致的横向收缩${\varepsilon _{\rm{T}}}$. 在拉伸量$\Delta d$为模块切口长度L的30%时, ${\varepsilon _{\rm{T}}}$值很容易就达到5%以上, 结合线性阈值公式(14), 表明形变超过线性阈值D_T的结构, 会产生较大幅度的梁扭曲, 弹性系数会出现不可预测的非线性变化, 影响结构稳定性.
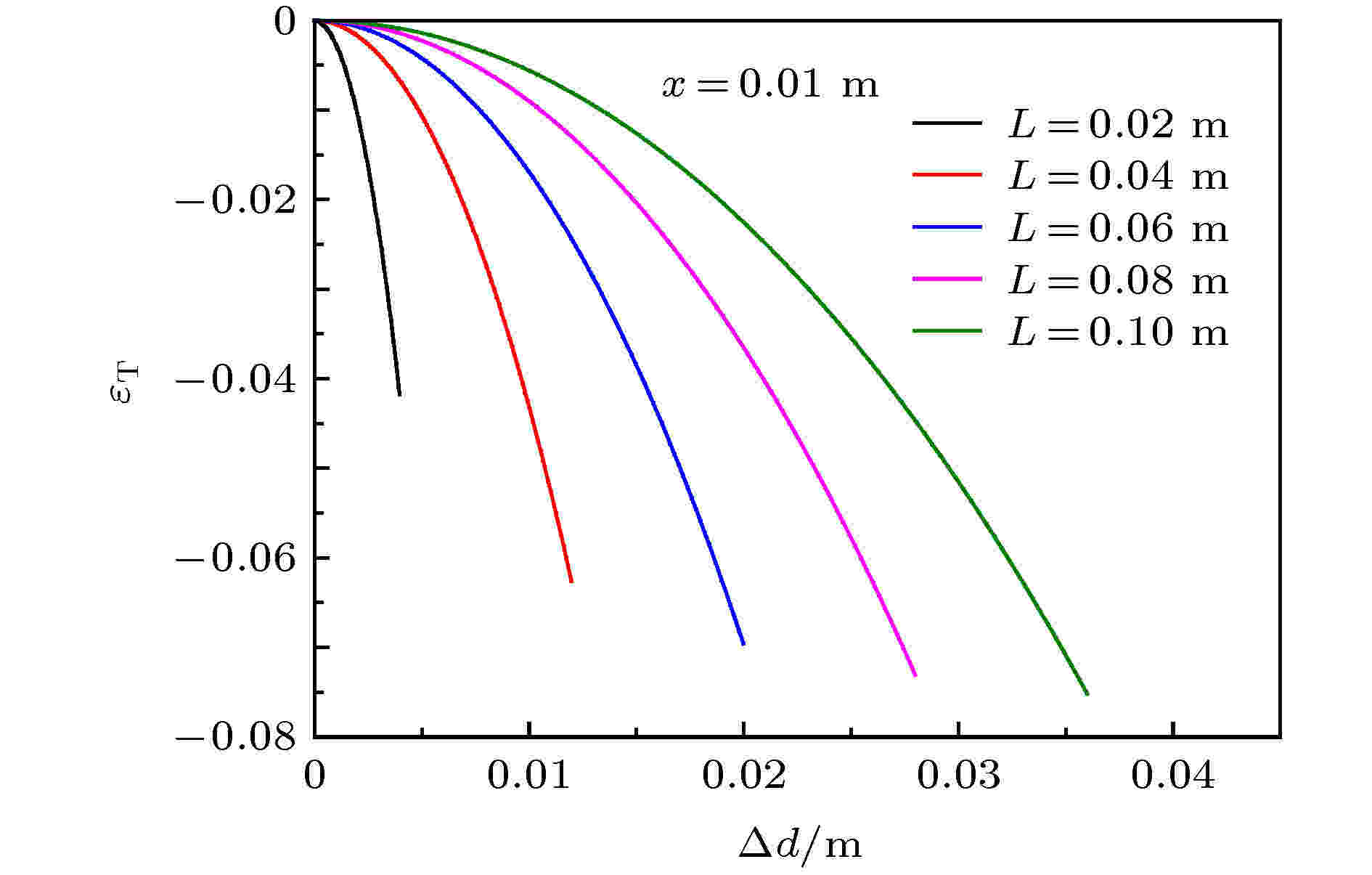图 7 不同模块切口长度L对横向应变${\varepsilon _{\rm{T}}}$的影响
Figure7. Influence of different module cut length L on transverse strain ${\varepsilon _{\rm{T}}}$.

对于结构水平拉伸时的公式适用范围, 不考虑重力, 有两个主要限制因素, 分别是线性阈值公式(14)和横向应变公式(18)的限制, 通过两公式的对比, 可以发现模块切口长度L和模块连接长度x是影响公式适用范围的主要因素. 可以通过结构的几何参数, 计算出公式的适用范围. 下面以单一模块为例进行了适用范围的分析与讨论. 对于L远大于x的单一模块, 如L = 0.1 m, x = 0.01 m的结构, 采用线性阈值公式(14)计算得到的公式适用范围为D < 0.027 m的区域; 采用(18)式计算, 令${\varepsilon _{\rm{T}}}$ = 0.3, 可以得到公式适用范围为D < 0.023 m的区域, 可以发现(18)式为主导因素, 应选择公式适用范围为D < 0.023 m的区域. 对于L略大于x的单一模块, 如L = 0.02 m, x = 0.01 m的结构, 采用线性阈值公式(14)计算得到的公式适用范围为D < 0.003 m的区域; 采用(18)式计算, 令${\varepsilon _{\rm{T}}}$ = 0.3, 可以得到公式适用范围为D < 0.00341 m的区域, 可以发现(14)式为主导因素, 应选择公式适用范围为D < 0.003 m的区域. 因此, 对于一般的结构, 为保证结果精确, 可以利用(14)式和(18)式分别计算结构拉伸长度, 取结果较小的值作为公式适用范围的约束. 对于多个模块的金字塔结构, 需要逐个计算每个模块的公式适用范围, 对所有模块求和可以得到金字塔结构的理论公式适用范围. 因此, 对于水平拉伸结构, 按照上述分析计算公式适用范围; 对于竖直拉伸结构的公式适用范围, 需要考虑重力, 公式适用范围一般相比水平拉伸结构会缩小G/K左右.

本文系统研究了辐射对称金字塔型剪纸结构的力学响应特征. 通过悬臂梁组合的方法, 构建了“梁模型”, 得到n个模块的正N边形金字塔结构的弹性系数与结构参数的关系, 并求出其线性阈值的表达式, 解释了该结构产生平面外扭曲的原因. 结合FEM仿真和实验的方法, 验证该剪纸结构弹性系数K公式以及线性阈值D_T公式的正确性, 并用于已有报道的石墨烯剪纸结构的力学特征分析. 研究结果表明, 通过剪纸结构参数, 可以有效控制辐射对称金字塔型剪纸结构的弹性系数. 在宏观领域, 金字塔型剪纸结构有望作为可控弹性系数的柔性结构应用于柔性器件领域; 在微观领域, 有望利用二维材料制作具有直观视觉读数的微小力测量设备.