删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

人脑默认模式网络的动力学行为

本站小编 Free考研考试/2021-12-29
摘要:大脑具有自适应、自组织、多稳态等重要特征, 是典型的复杂系统. 人脑在静息态下的关键功能子网络——默认模式网络(DMN)的激活处于多状态间持续跳转的非平衡过程, 揭示该过程背后的动力学机制具有重要的科学意义和临床应用前景. 本文基于功能磁共振获得的血氧水平依赖(BOLD)信号, 建立了DMN吸引子跳转非平衡过程的能量图景、吸引子非联通图、跳转关系网络等; 以高级视觉皮层和听觉等皮层活动为例, 通过对应激活DMN状态空间的分布, 以及XGBoost、深度神经网络等算法验证了DMN状态变化与外部脑区状态的密切依赖关系; 通过偏相关、收敛交叉映射等方法分析了DMN内各个脑区之间的相互作用. 本文结果有助于理解静息态下大脑内在非平衡过程的动力学机制, 以及从动力学的角度探索具有临床意义的脑功能障碍生物标志物.
关键词: 脑功能网络/
静息态/
默认模式网络/
能量图景/
状态跳转

English Abstract


全文HTML

--> --> -->
1.引　言
近年来, 非侵入式脑功能成像技术的发展促使脑科学研究进入了新的阶段[1]. 其中, fMRI (functional magnetic resonance imaging) 可通过采集大脑的低频(< 0.1 Hz)血氧水平依赖(blood oxygen level dependent, BOLD)信号, 来反映各个脑区在特定任务态或静息态下的动态激活状态. 因无创和高空间分辨率等优势, fMRI被广泛应用于脑的工作机制和脑功能障碍的研究[2-5]. 基于fMRI对大脑在任务态和静息态等状态下激活模式的研究发现了大脑的多种功能子网络, 包括默认模式网络(default mode network, DMN)、突显网络(salience network, SN)、执行控制网络(executive control network, ECN)、注意网络(attention network, AN)、视觉网络(visual network, VN)、听觉网络(auditory network, Aud)等[6].
DMN的正常运转对大脑功能的维持具有重要的意义. 2001年, Raichle等[7]提出了大脑的“默认模式”(default mode)的概念, 其对应的脑区在任务态或受到明显外部刺激时被抑制, 而在静息态时恢复并维持激活, “默认模式”被认为是大脑神经系统的基线状态. 2003年, DMN被明确提出[8], 它是维持该基线状态最核心的功能子网络, DMN网络内不同脑区的静息态神经活动具有特定的时间相干性. 此外, 静息态下脑区之间的功能连接也被发现与对应的白质纤维束物理投射关系具有一定程度上的一致性[9]. DMN的主要特征是在静息态下呈现出连续的高水平激活, 而在任务态时受到抑制[10], 已经证实它与维持觉醒和监测外部刺激等功能有关[11]. 在DMN的概念提出后, 更多与大脑基线水平, 即默认模式相关的脑区及脑区的具体功能被逐渐发现(见图1[12]). 目前认为DMN主要包括: 腹内侧前额叶皮质(Ventral Medial Prefrontal Cortex, VMPC)、背内侧前额叶皮质(Dorsal Medial Prefrontal Cortex, DMPC)、后扣带回皮质(Posterior Cingulate Cortex, PCC)、楔前叶(Precuneus)和横向顶叶皮质(Lateral Parietal Cortex, LPC).
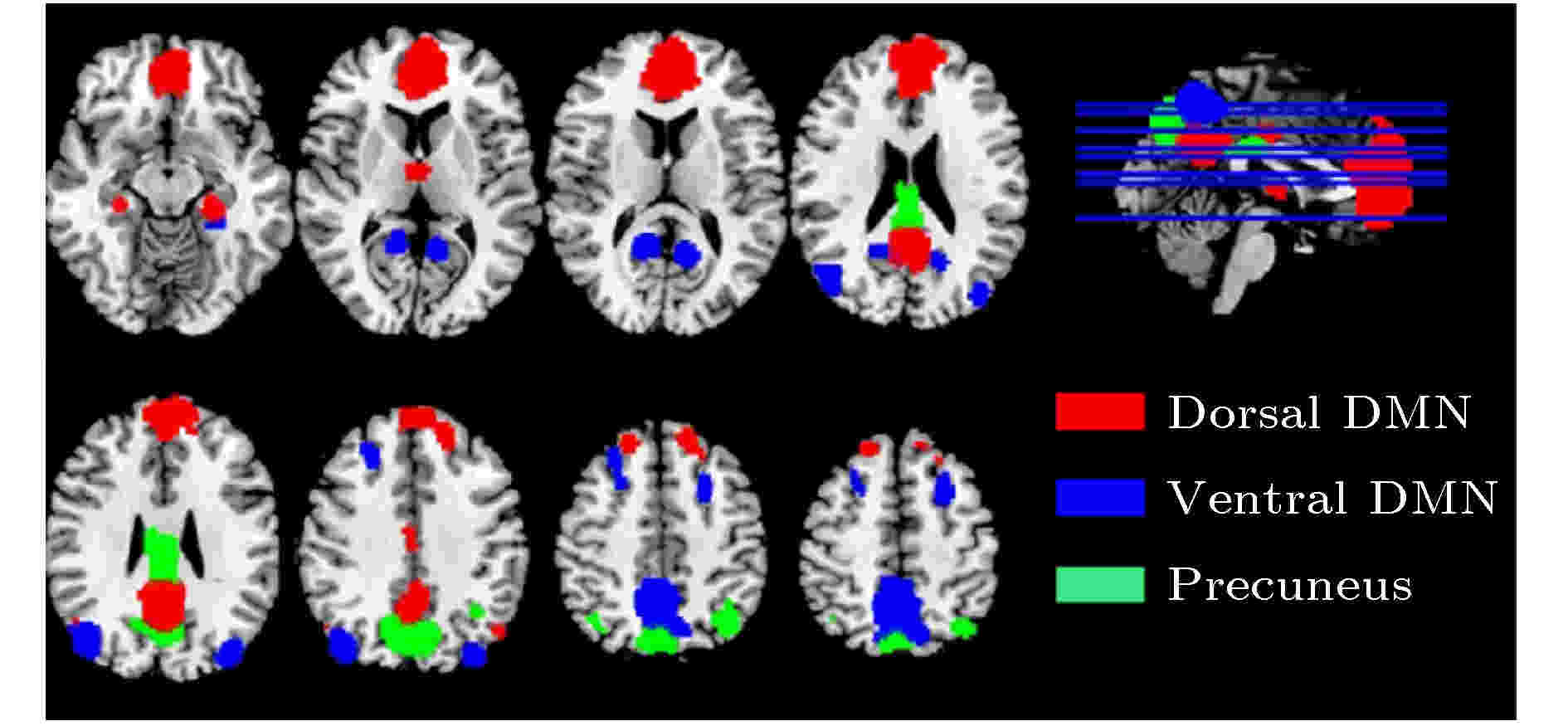图 1 大脑默认模式网络(DMN)[12]
Figure1. DMNof the brain[12].

DMN是大脑基线状态的核心功能网络, 一些常见的脑功能障碍往往同时对应DMN激活模式及功能连接的异常, 这也使得DMN活动的异常指标成为进行脑疾病的诊断和评估的潜在生物标志物[13-15], 如与正常衰老相比, 早期阿尔兹海默症(AD)患者的DMN中就存在显著的异常激活[16], 轻度认知障碍(ADHD)患者在任务态下表现出DMN去激活率明显降低[17]和DMN内网络相关性降低[18], 精神分裂症的阳性症状严重程度直接与DMN激活模式及功能连接的异常相关[19,20], 脑外伤导致的轻度脑损伤患者的DMN则无法在任务态实现去激活, 显著影响任务表现[21].
近年来, 对静息态脑活动的研究发现, DMN单个脑区的激活看似随机, 但从网络的层次却有规律可循. 静息态下DMN的状态存在更细致的子状态, 对应于不同的激活模式, 系统在多种激活模式间持续跳转, 是典型的非平衡过程, 其表现出的规律及背后的机理适合运用统计物理和非线性动力学的方法进行研究. 然而, 在这一方向上更进一步的深入研究到目前为止还尚未见到进展, 例如, 静息态DMN的子状态是否和其他脑区的功能活动有对应关系等, 需要做进一步的考察. 此外, 由于脑功能障碍对应的DMN激活模式及跳转行为与健康状态存在显著差异[13,19,20,22], 对静息态下DMN所处非平衡过程的研究具有重要的科学意义和临床应用前景, 能够帮助我们理解人脑静息态的动力学特征和工作机制, 从功能连接的角度揭示脑功能障碍的发病机理, 并为相关疾病的预防、诊断和治疗提供启发[22,23,24].
鉴于上述原因, 本文将基于静息态DMN的BOLD数据, 围绕DMN的动力学行为及其背后的机理展开研究, 所采用的方法主要包括能量图景构造[25,26]、共变行为分析、基于压缩感知的偏相关分析[27]与收敛交叉映射方法[28]等. 研究的问题包括: DMN激活行为的非平衡过程的主要特征, DMN与外部其他脑区活动的交互, DMN内部各脑区之间的相互作用, 以及对其非平衡过程动力学机理的探讨.
2.方法及结果
2
2.1.方　法
-->

2.1.方　法

3
2.1.1.数据及预处理
-->
2.1.1.数据及预处理
本文的研究采用静息态功能磁共振成像(rs-fMRI)数据来源于人类连接组计划(human connectome project, HCP)网站的公开数据集, fMRI空间分辨率为2 mm × 2 mm × 2 mm (单个体素尺寸), 时间分辨率为0.72 s (采样时间间隔), 包括55个被试, 每个被试的采样点数为T = 1200, 采样持续时间为0.72 s × 1200 = 14 min. 原始影像数据的预处理流程为: 功能与结构图像配准, 配准到标准空间, 去除白质和脑脊液信号, 头动校正, 带通滤波(0.01—0.10 Hz), 空间高斯平滑, 去漂移等. 经上述预处理后, 再根据脑区划分模板将默认模式网络相关的区域划分为23个感兴趣区 (regions of interest, ROIs), 并通过对ROI内所有体素时间序列求平均, 得到每个ROI的BOLD(血氧水平依赖)信号时间序列. 23个ROI的相关基本信息见表1.
ROILabelL/RBAXYZ
Posterior CingulatevDMN_1L31–12–6210
Middle Frontal GyrusvDMN_2L10–27–659
CulmenvDMN_3L37–30–39–20
Superior Occipital GyrusvDMN_4L19–36–8828
Posterior Cingulate GyrusvDMN_5R3115–5613
PrecuneusvDMN_67–6–6156
Middle Frontal GyrusvDMN_7R10242647
CulmenvDMN_8R3727–33–23
Angular GyrusvDMN_9R3943–7928
CerebellumvDMN_10R12–47–63
Ventral Posterior Cingulate GyruspDMN_1230–3528
PrecuneuspDMN_270–7638
Inferior Parietal LobulepDMN_3L40–39–6446
Inferior Parietal LobulepDMN_4R4039–6446
Middle Frontal GyrusdDMN_1904912
Angular GyrusdDMN_2L39–48–7332
Superior Frontal GyrusdDMN_3R6183851
Dorsal Posterior Cingulate GyrusdDMN_4310–5730
Ventral Anterior Cingulate GyrusdDMN_5240–1735
Angular GyrusdDMN_6R3948–6629
ThalamusdDMN_7–6–63
Parahippocampal GyrusdDMN_8L36–24–37–9
Parahippocampal GyrusdDMN_9R3624–21–23


表1默认模式网络ROI的名称、标签、Brodmann分区(BA)编号及位置坐标信息
Table1.Name, label, Brodmann area (BA) number, and location information of ROIs belonging to the default mode network

3
2.1.2.DMN的能量图景构造方法
-->
2.1.2.DMN的能量图景构造方法
以背侧默认模式网络(dDMN, 为DMN的核心区域)作为代表, 将其9个ROI的BOLD信号根据某阈值(一般取均值线或以均值线为中心的窄带)二值化为0或1序列, 分别对应于不活跃状态和活跃状态, 如图2所示, 编号为i的ROI的状态为σi = 0, 1($i = 1, 2, \cdots, 9$), 那么t时刻dDMN状态可表示为${{\sigma}} = \left[ {{\sigma _1}, {\sigma _2}, \cdots, {\sigma _9}} \right]$. 系统状态σ所对应的“能量”定义为
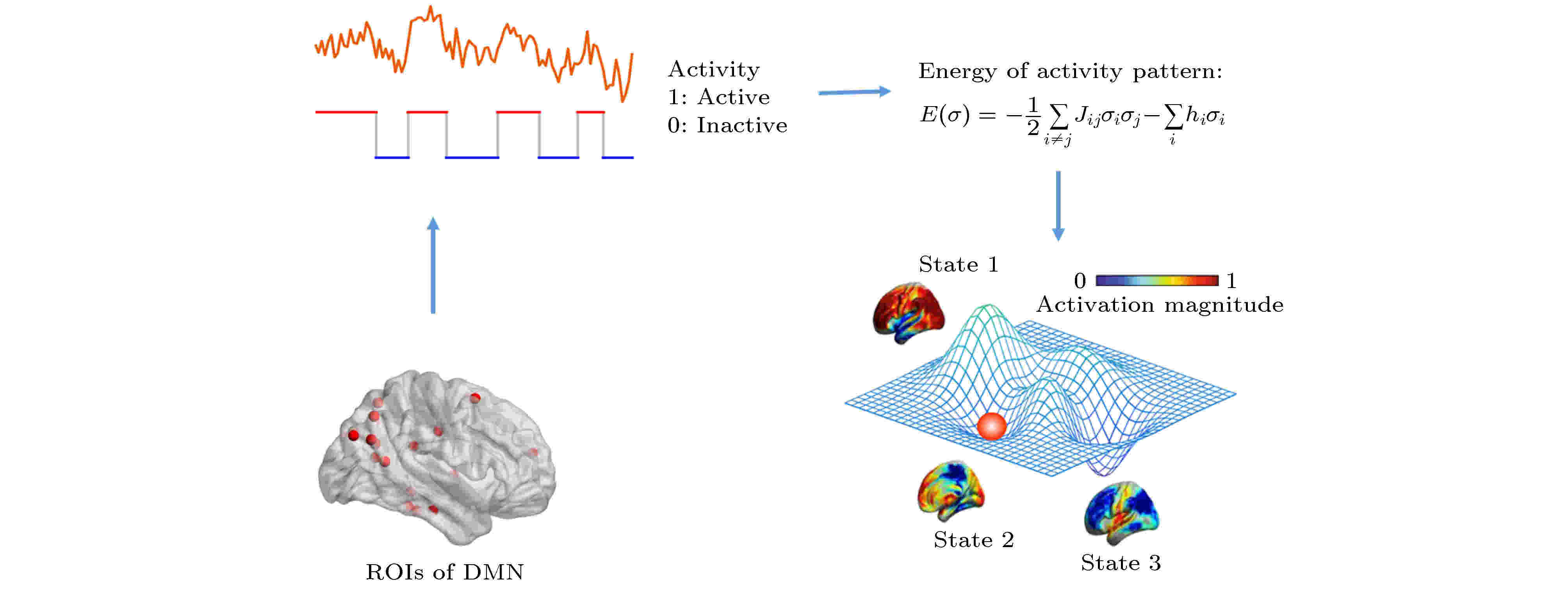图 2 DMN能量图景构造方法示意图
Figure2. Schematic diagram of the construction of DMN energy landscape.

$E\left( {{\sigma}} \right) = - \frac{1}{2}\mathop \sum \limits_{i \ne j} {J_{ij}}{\sigma _i}{\sigma _j} - \mathop \sum \limits_i {h_i}{\sigma _i},$
其中${{J}} \in {{\mathbb{R}}^{9 \times 9}}$和${{h}} \in {{\mathbb{R}}^9}$是模型的两组参数, ${J_{ii}} = 0$($i = 1, 2, \cdots, 9$). 以上能量函数给出系统状态的玻尔兹曼分布:
$P\left( {{\sigma}} \right) = \frac{1}{Z}{{\rm{e}}^{\left[ { - E\left( {{\sigma }}\right)} \right]}},$
配分函数为
$Z = \mathop \sum \nolimits_{{\sigma}} {{\rm{e}}^{\left[ { - E\left( {{\sigma}} \right)} \right]}}.$
在真实rs-fMRI数据dDMN脑区激活占比的约束条件下, 通过梯度上升算法, 不断调节(即训练)模型的两个参数J和h, 使得玻尔兹曼分布的熵
$S = - \mathop \sum \nolimits_{{\sigma}} P\left( {{\sigma}} \right)\log P\left( {{\sigma}} \right)$
最大化(训练的约束条件为${\langle {{\sigma _i}}\rangle _{{\rm{data}}}} \!=\!\displaystyle \sum \nolimits_{{\sigma}}\! ( {{{{\sigma}} _i}} )P( {{\sigma}})$, ${\left\langle {{\sigma _i}{\sigma _j}} \right\rangle _{{\rm{data}}}} = \displaystyle \sum \nolimits_{{\sigma}} {\sigma _i}{\sigma _j}P\left( {{\sigma}} \right)$, $i, j \!=\! 1, 2, \cdots, 9, ~i \ne j$), 即得到优化的模型. 根据优化的模型可得系统的能量图景.
局部极小态及能量壁垒的计算: 将dDMN状态矢量中只有一位存在差异的两个状态视为相邻状态, 因此每个dDMN状态都有9个相邻状态. 若某状态的能量小于所有9个相邻状态, 则称为局部极小态.
局部极小态的非联通图构建: 1)首先建立状态矢量构成的超晶格, 其中每个状态都与其相邻状态相连; 2)设定能量阈值, Eth, 它等于当前所有状态中最大的能量; 3)移除所有能量 ≥ Eth的状态及其连边; 4)检测超晶格中是否每个局部极小态都有至少一条路径相互联通; 5)重复步骤3)和4), 将Eth设为剩余格点中的能量最大值, 直到所有的局部极小态都互不联通. 记录下每两个局部极小态第一次不连通时所设定的Eth, 作为两者之间的势垒高度, 即可构建局部极小态的非联通图.
3
2.1.3.基于压缩感知的偏相关方法
-->
2.1.3.基于压缩感知的偏相关方法
基于脑区BOLD信号的相关性分析是构建脑功能网络的常用方法. 但相关性分析所得两变量(如DMN内部某两个ROI)间关系无法排除来自其他变量(即除这两个ROI之外的DMN内部其他ROI)的干扰, 而偏相关分析则可以在一定程度上去除其他变量的影响. 压缩感知(包括LASSO)利用系统稀疏性的先验知识辅助求解线性回归问题, 在小样本数据集的情况下优势更加突出, 甚至可解线性欠定方程组. 脑功能网络具有稀疏性这一基本特征, 而且核磁共振数据的时间序列长度一般都比较短, 利用压缩感知辅助进行偏相关分析构建脑功能网络, 不仅可以凸显网络中的重要边、自动剔除弱的伪连边, 而且还可以对基于短时间序列的相关性(或线性回归)计算的准确性起到一定的补偿. 以下将简要介绍基于压缩感知的偏相关方法[27].
假设${{{f}}_1}, {{{f}}_2}, \cdots, {{{f}}_p}$是所测p个对象的数据矢量(时间序列), 长度为n, 且已经被中心化(centered, 即${{f}}_i^{\rm{T}}{{\bf{1}}_n} = 0$, 其中${{\bf{1}}_n} \in {{\mathbb{R}}^{n \times 1}}$为所有元素均为1的n维列矢量)、标准化(normalized, 即${{f}}_i^{\rm{T}}{{{f}}_i} = 1$). 那么协方差矩阵为
${{\varSigma}} = \left[ {{\sigma _{ij}}} \right] = \left[ {\frac{{{{f}}_i^{\rm{T}}{{{f}}_j}}}{{n - 1}}} \right] \in {{\mathbb{R}}^{p \times p}},$
协方差矩阵的逆矩阵(称为精度矩阵, precision matrix)为
${{\varPi}} = {{{\varSigma}} ^{ - 1}} = \left[ {{{\text{π}} _{ij}}} \right] \in {{\mathbb{R}}^{p \times p}},$
则fi与fj之间的相关系数和偏相关系数分别为
$\begin{split}& {\rho _{ij}} = \dfrac{{{\sigma _{ij}}}}{{\sqrt {{\sigma _{ii}}{\sigma _{jj}}} }} = {{{f}}_i}^{\rm{T}}{{{f}}_j},~~ {\theta _{ij}} = - \dfrac{{{{\text{π}} _{ij}}}}{{\sqrt {{{\text{π}} _{ii}}{{\text{π}} _{jj}}} }}.\end{split}$
如果对fi作如下线性回归:
${{{f}}_i} = {\alpha _{ij}}{{{f}}_j} + {{{\epsilon}}_i},$
那么回归系数αij就等于fi与fj之间的相关系数ρij. 而如果对fi做如下线性回归:
${{{f}}_i} =\sum\limits_{j \ne i} {\beta _{ij}}{{{f}}_j} + {{{\epsilon}}_i},$
那么回归系数βij和fi与fj之间偏相关系数θij的关系为
${\theta _{ij}} = {\beta _{ij}}\sqrt {\frac{{{{\text{π}} _{ii}}}}{{{{\text{π}} _{jj}}}}} = {\beta _{ij}}\sqrt {\frac{{{\rm{var}}\left( {{{{\epsilon}}_j}} \right)}}{{{\rm{var}}\left( {{{{\epsilon}}_i}} \right)}}},$
其中${\rm{var}}\left( {{\epsilon}} \right)$表示回归残差${{\epsilon}}$的方差.
在回归系数矢量β具有比较强的先验稀疏性(在脑功能网络中这是一个合理的假设)的情况下, 可被如下LASSO回归的方法很好地估计:
${\hat \beta _{ij}} = \mathop {{\rm{argmin}}}\nolimits_{{\beta _{ij}}}\sum\limits_{i = 1}^p \bigg\| {{{{f}}_i} -\sum\limits_{j \ne i} {\beta _{ij}}{{{f}}_j}} \bigg\|_2^2 + \lambda \sum\limits_{i,j} \left| {{\beta _{ij}}} \right|.$
在通过上述方法得到β之后, 即可计算偏相关系数,
${\theta _{ij}} = {\beta _{ij}}\sqrt {\frac{{{\rm{var}}\left( {{{{\epsilon}}_j}} \right)}}{{{\rm{var}}\left( {{{{\epsilon}}_i}} \right)}}},$
其中
${{{\epsilon}}_i} = {{{f}}_i} - \mathop \sum \nolimits_{j \ne i} {\beta _{ij}}{{{f}}_j}.$

3
2.1.4.收敛交叉映射方法(CCM)
-->
2.1.4.收敛交叉映射方法(CCM)
鉴于大脑活动的典型非线性特征及fMRI所得BOLD数据采集时长有限两方面因素, 我们还将采用收敛交叉映射法(convergent cross mapping, CCM)[28]进行动力学因果性分析. CCM基于泰肯嵌入定理(Taken's embedding theorem), 通过相空间重构的方式对变量间的动力学因果性进行推断. 相较于目前广泛应用的格兰杰因果性分析(Granger causality, GC)和传递熵(transfer entropy, TE)等方法, CCM的优势在于更加适合非线性系统的处理, 并且对数据量的要求相对较低.
通过CCM方法对两个脑区BOLD时间序列X和Y进行因果性分析, 可以得到脑区间有向的动力学影响强度(directed dynamical influence), 进而构建DMN与其他脑区相互作用的脑网络. 基本步骤包括: 由X和Y时间序列分别进行相空间重构得到流形MX与MY; 根据MX的结构得到预测序列$\tilde Y$, 求得$\tilde Y$与实际序列Y的皮尔森相关系数$\rho _{_{Y|{M_X}}}$, 此系数即是变量Y对变量X影响程度的度量; 同样地, ${\rho _{_{X|{M_Y}}}}$是变量X对变量Y影响程度的度量. X与Y之间的因果方向根据$R = \rho_{_{X|{M_Y}}} - \rho_{_{Y|{M_X}}}$的符号进行判断(R > 0则表明X对Y的动力学影响更强, R < 0则反之).
2
2.2.结　果
-->

2.2.结　果

3
2.2.1.DMN静息态非平衡过程的动力学行为分析
-->
2.2.1.DMN静息态非平衡过程的动力学行为分析
3
2.2.1.1.DMN的吸引子间跳转行为特征
-->
2.2.1.1.DMN的吸引子间跳转行为特征
基于前面所述方法, 可由每个被试的数据计算得到dDMN能量图景. 这里, 高维超晶格上的能量图景的主要特征可通过非连通图(disconnectivity graph)显示, 包括吸引子能量大小及相邻最低势垒连通关系等信息, 见图3(a). 非连通图的构造是在训练得到系统能量函数表达式后, 通过搜索能量极小值, 分析各极小值对应的系统状态吸引子的位置关系, 最终保留所有吸引子及它们之间的最低翻越势垒构成的树状结构图. 图3(a)—图3(c)上下两行分别对应于被试1和被试2的结果. 以能量图景吸引域为标签对DMN活动时间序列进行着色可对其在状态空间中的分布进行观察, 见图3(b), 其中左右图为不同时刻的状态激活情况(为观察方便计, 这里使用了对同一状态轨道不同视角的展示, 即左右图观察角度不同). 三维投影空间根据23维数据主成分分析(PCA)得到的前三个主成分方向进行构造. 图3(c)给出了吸引子间状态跳转关系网络, 其中颜色与图3(a)中的吸引子一致, 节点大小等于DMN在该吸引域内出现的次数, 节点间有向边的权重表示对应方向的跳转频次, 总时长T = 1200. 比较图3(a)—图3(c)上下两行对应的两个不同被试的结果可以看到, 不同被试在静息态下其默认模式网络激活行为的动力学特征存在明显差异, 例如被试1具有较多的吸引子状态, 且存在更频繁的吸引子间切换行为, 而被试2的吸引子个数较少, 且跳转行为主要表现为局部切换(例如state 1和state 2之间, state 3和state 4之间), 这表明静息态下被试1的思维活动更加丰富、活跃, 而被试2的思维活动则相对单一且不易变化.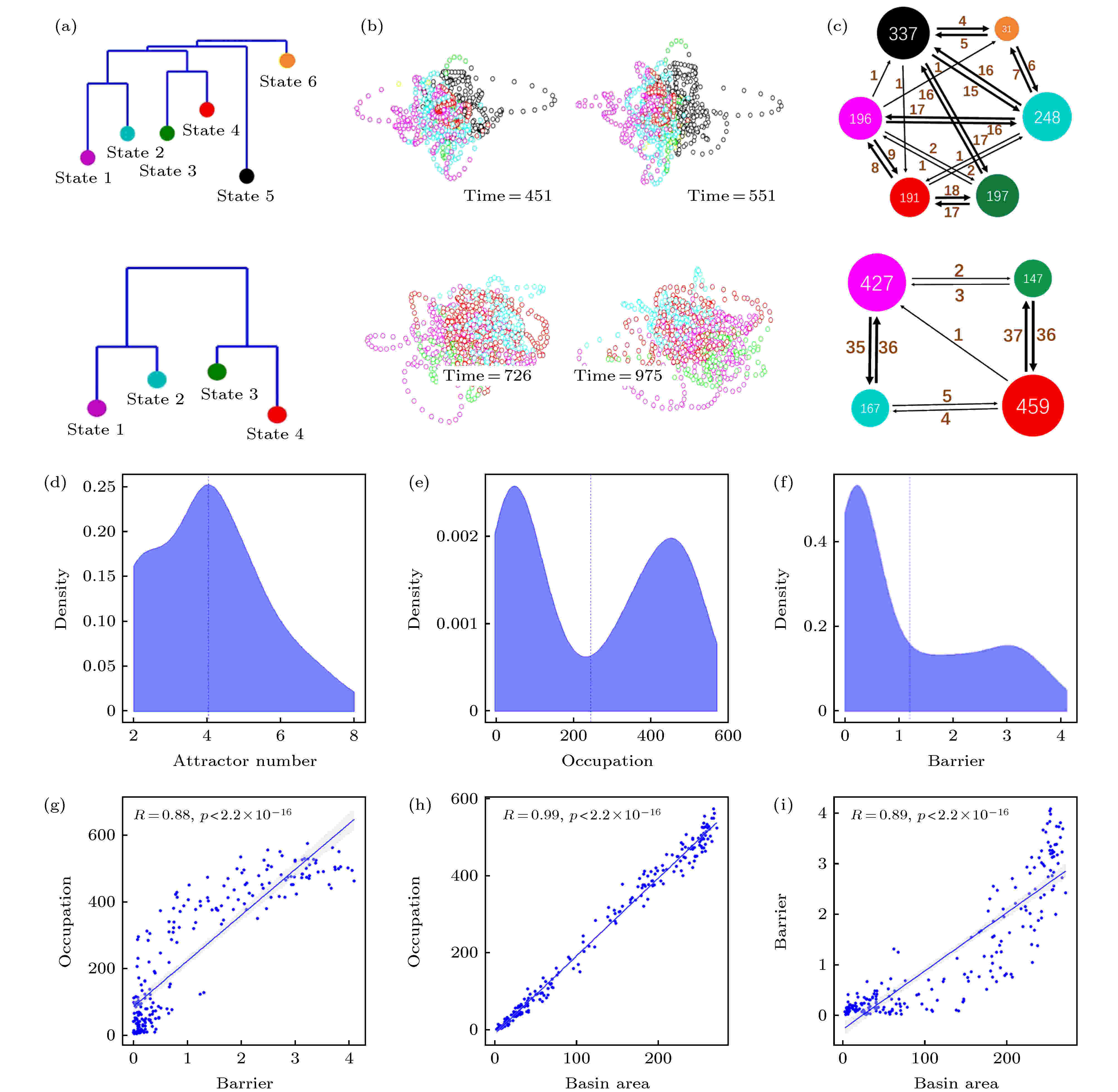
图 3 默认模式网络(DMN)激活行为的动力学特征　(a) dDMN状态能量图景中吸引子状态的非联通图(disconnectivity graph); (b)根据吸引子吸引域标签进行着色的DMN状态轨迹在3维空间的投影, 左右两图显示了同一被试轨迹不同角度的观察; (c)吸引子间跳转网络, 节点大小表示对应吸引域的访问次数, 点间有向边的权重表示对应的单向跳转频次, 总时长T = 1200. (a)?(c)中上下两行分别对应于被试1和被试2的结果; (d)?(i)为55个被试能量图景的统计分布特征: (d)吸引子数目的统计分布; (e)吸引域占据率(访问次数)的统计分布; (f)能量壁垒(势阱深度)的统计分布; (g)吸引域占据率与能量壁垒的关系; (h) 吸引域占据率与吸引域面积的关系; (i) 能量壁垒和吸引域面积的关系
Figure3. Dynamic characteristics of the resting state default mode network (DMN): (a) Disconnectivity graph of the energy landscape for the dDMN; (b) projections of the DMN state trajectories, colored according to the labels of attraction basins, in a 3-dimensional space. The left and right panels show the trajectory of the same subject from different viewing angles, respectively; (c) attractors transition networks. The nodal size indicates the visiting frequency in the corresponding attracting domain, and the weight of directed edge indicates the corresponding directed switching frequency, with the recording time T = 1200. The upper and lower rows in the panels (a)?(c) correspond to the results of test subjects 1 and 2, respectively. Panels (d)?(i) are the statistical results of energy landscapes for 55 subjects: (d) The distribution of attractor numbers; (e) the distribution of basin occupations; (f) the distribution of energy barriers; (g) dependence of basin occupation and energy barrier; (h) dependence of basin occupation and area; (i) dependence of energy barrier and area.

图3(d)—图3(i)展示了55个被试能量图景的统计分布特征. 可以看到: 吸引子数目存在明显的峰值(图3(d), 峰值位于4附近), 表明静息态下吸引子典型数目的普遍存在. 吸引域占据率(即被访问次数)呈双峰分布(图3(e)), 表明静息态下DMN的状态多处在其中某些吸引域而很少在另外的吸引域, 存在两极分化现象. 类似地, 势阱深度(即势阱最低点到最近鞍点的能量差)也呈双峰分布(图3(f)), 势阱深度和吸引域占据率的正相关关系如图3(g)所示. 图3(h)给出了吸引域被访问次数O和吸引域面积A(即吸引域内包含的状态总数)之间具有很好的线性关系$O = kA$(其中k为常数), 而具有较大面积的吸引域也往往具有较大的势阱深度, 其具体关系曲线见图3(i), 这与图3(g)中吸引域被访问次数和势阱深度之间的正相关对应. 结合DMN能量图景结构及跳转过程可以得到以下启发.
a)不同被试的能量图景吸引子数目以及吸引域间跳转行为存在差异, 分别反映了其在静息态下脑活动的丰富程度和活跃程度的差异. 这可能与不同被试的认知及思维活动特征差异有关, 也可能与被试在实验测量前的短期经历有关. 已有研究发现静息态数据采集之前被试所处环境对其静息水平存在遗留影响. 可以推测, 被试在进入静息态之前若经历了较为丰富的刺激, 所得到的DMN静息态能量图景应具有更多的吸引子状态和更频繁的跳转. 该推测还有待进一步的实验验证.
此外, 能量图景的吸引子势能、位置关系和吸引域大小等信息可提示潜在的激活模式间跳转方式. 如被试1的数据中存在跨越高势垒(见图3(a))的状态2—状态5间频繁交替的模式(状态5具有较大的吸引域), 跨越低势垒的状态3—状态4间频繁交替的相对局部的模式(其状态较为接近), 以及由上述2—5相到3—4相过渡的状态3—状态5交替的中间模式. 据此可以了解某被试在静息态下其DMN状态的特有跳转模式, 由于DMN的各个脑区激活行为与外部脑区的神经活动状态存在关联, 可以根据该跳转模式理解被试在静息态下的习惯思维活动.
b)目前基于BOLD数据对fingerprint(指纹)指标, 即稳定的个体间差异指标的探讨是一个重要的前沿科学问题[29]. 从上述分析可以看到, 不同被试的吸引子个数、状态空间轨迹构型、跳转方式等均具有特异性, 其中对特定个体相对稳定同时在不同个体之间差异较大的动力学属性可以作为潜在的动力学指纹, 并运用于对被试的个体属性及脑功能障碍的识别.
3
2.2.1.2.DMN与外部其他脑区活动的交互
-->
2.2.1.2.DMN与外部其他脑区活动的交互
以上介绍了静息态下DMN状态在不同吸引子间跳转的行为, 该非平衡过程的机理解释需要从DMN的内在动力学以及外部其他脑区的影响两方面考虑. DMN作为众多脑功能网络之一, 其状态会受到外部其他功能网络的影响. 这里我们首先以高级视觉皮层(hV)和听觉皮层(Aud)为例, 分析DMN与其他脑区激活行为的交互关系.
图4(a)给出了高级视觉皮层(hV)和听觉皮层(Aud)的BOLD时间序列, 若进行二值化, 用1和0对应激活与不激活, 则时间序列可用4种(hV, Aud)激活状态表示, 即(1, 0), (0, 1), (0, 0)和(1, 1), 图中用4种颜色示意. 为了分析DMN与hV, Aud的共变行为, 可根据同时刻的(hV, Aud)标签对DMN状态轨道进行着色, 如图4(b), 并与图3(b)中根据吸引域标签染色的轨迹进行对比. 图5(a)和图5(b)分别给出了被试1和被试2根据吸引域标签进行着色的DMN状态轨迹在2维空间(由PCA前两个主成分对应的本征矢张成)的投影, 图5(c)和图5(d)给出了被试1和被试2根据(hV, Aud)标签着色的同样的轨迹投影. 从图5可见不同的(hV, Aud)标签在DMN的状态空间中对应特定的DMN子状态区域(即吸引子及其吸引域), 说明DMN的状态与(hV, Aud)的状态有较好的对应关系. 我们通过15个被试数据的组分析对该现象进行验证, 也可见一致的现象, 见图4(c), 其中二维空间是由(通过对15个被试数据进行组PCA得到的)前两个主成分PCA1和PCA2张成, 每个点表示某被试某一时刻的DMN状态投影. 所有被试的DMN均表现出了一致地与自身(hV, Aud)存在对应关系的激活行为, 这一规律没有被DMN轨道显著的个体间差异所影响.
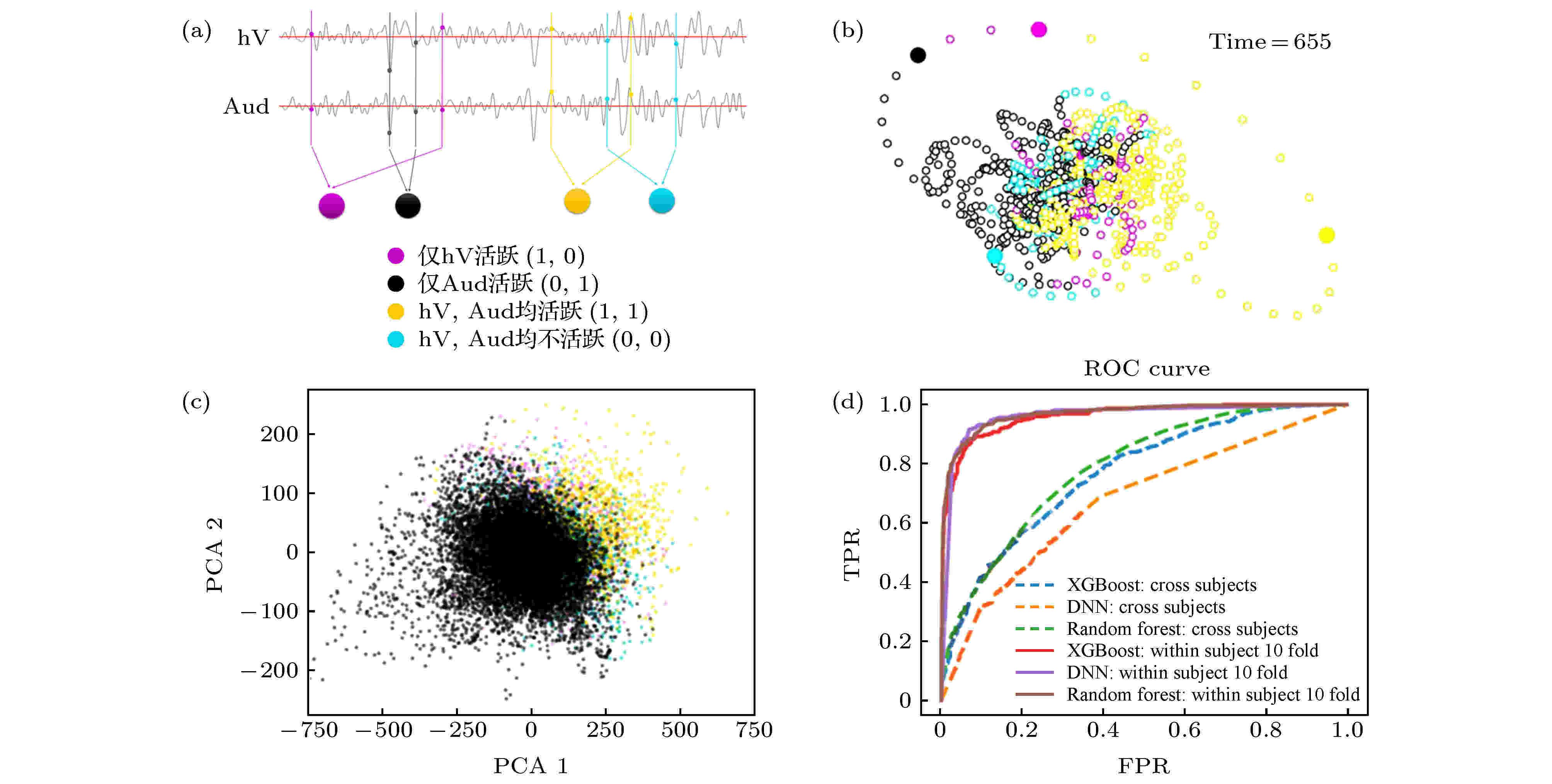图 4 默认模式网络(DMN)状态与其他脑区激活行为的共变　(a)对高级视觉皮层(hV)和听觉皮层(Aud)活动二值化, 得到4种激活状态的(hV, Aud)标签序列; (b)根据(hV, Aud)标签序列着色的DMN状态轨道; (c) DMN的23个脑区激活行为在PCA1-PAC2空间的投影; (d)对DMN的激活行为数据按照同时刻(hV, Aud)标签进行4分类训练所得ROC曲线, 其中包括XGBoost, DNN, Random Forest三种方法及两种训练方式
Figure4. Covariation of the default mode network (DMN) states with activity mode in other brain regions: (a) Binarizing the activities of high-level visual cortex (hV) and auditory cortex (Aud) to obtain (hV, Aud) label sequence; (b) DMN state orbit colored according to (hV, Aud) label sequence; (c) projection of the activity states of the 23 brain regions in the PCA1-PAC2 space; (d) the ROC curve obtained by performing 4-classes training on the (hV, Aud) labels of DMN activity data by XGBoost, DNN, Random Forest with two training schemes.

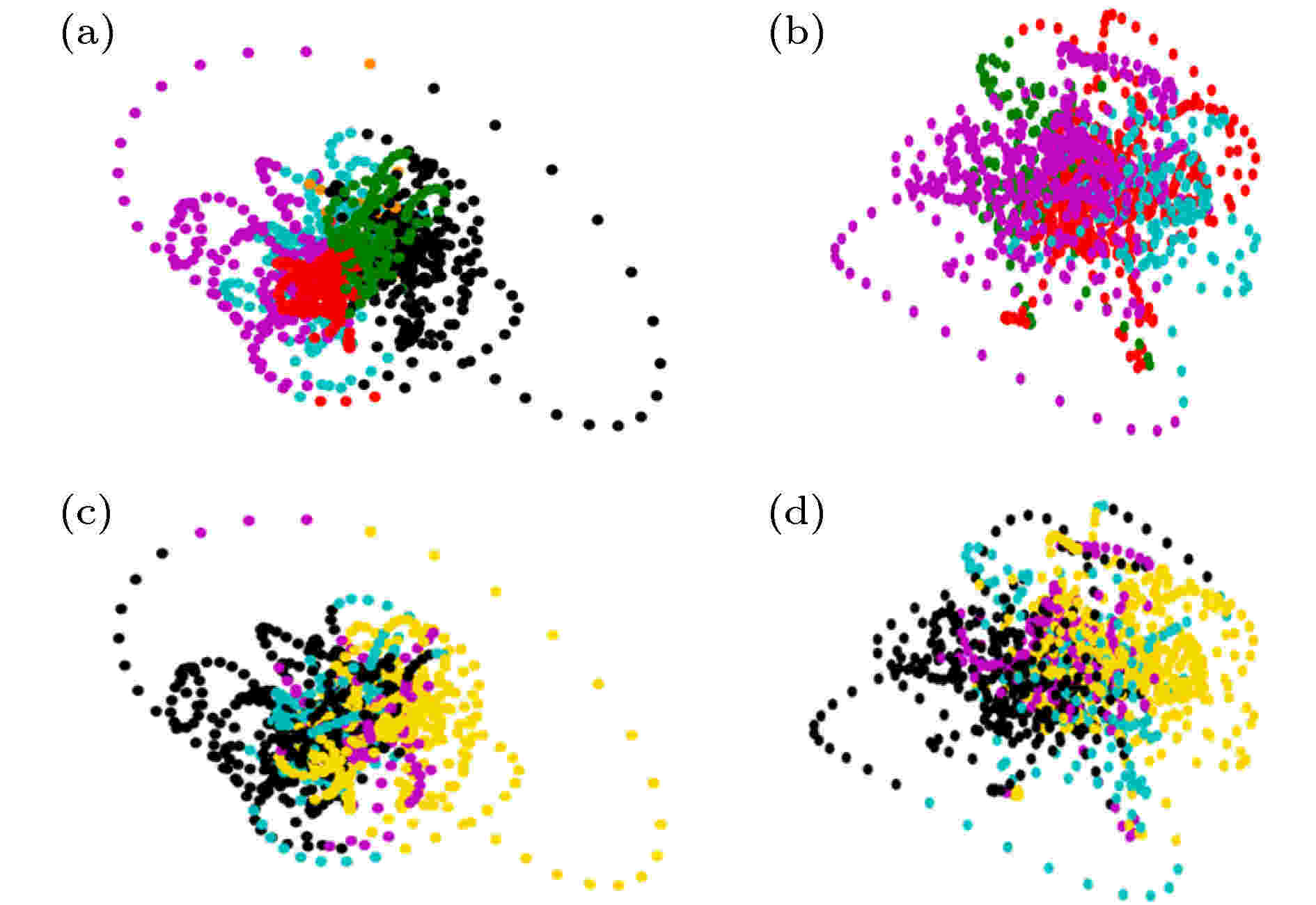图 5 DMN状态与视听觉皮层状态的对应现象　(a), (b)根据吸引子的吸引域标签着色的DMN状态轨道; (c), (d) 根据(hV, Aud)标签序列着色的DMN状态轨道; (a), (c)被试1的结果; (b)(d)被试2的结果
Figure5. Correspondence between the states of DMN and (visual, auditory) cortexes: (a), (b) DMN state orbits colored according to the labels of attraction basin; (c), (d) DMN state orbits colored according to the labels of (hV, Aud) states. (a), (c) the results of subject 1; (b)(d) the results of subject 2.

以上是从状态空间的分布特征观察DMN与(hV, Aud)的状态对应关系, 我们还可通过XGBoost, DNN(deep neural network), Random Forest等机器学习算法对上述关系进行验证. 以(hV, Aud)的4个状态作为标签, 用15个被试DMN的23个脑区激活行为的1200个采样数据对模型进行4分类训练. 图4(d)给出了对应的ROC曲线, 横坐标为假阳性率(FPR), 纵坐标为真阳性率(TPR), 图中虚线表示通过跨被试的交叉验证, 即随机选择13个被试构成训练集, 剩余的2个被试作为测试集的结果. 图中实线表示通过十折交叉验证得到的结果, 具体处理方法是对某被试的1200个数据点随机拆分为训练集和测试集, 用十折交叉验证得到结果, 再对15个被试的FPR和TPR进行平均得到ROC曲线. 从ROC曲线可以看出: 1)根据某被试DMN的状态能够得到对其自身(hV, Aud)状态的较为准确的推断, 即DMN与hV, Aud的状态存在密切的依赖关系; 2)跨被试的验证结果劣于单个被试十折交叉验证结果, 是由于DMN轨迹的个体间差异等因素所致.
从上述DMN与(hV, Aud)的对应关系可知, 静息态下DMN在多吸引子间跳转的动力学过程与DMN外部脑区活动密切相关. 需要说明的是, 静息态并非对人脑状态的严格定义, 而是BOLD数据采集的实验条件, 在静息态下, 某些事件(也可能是自发涨落)导致视觉或听觉皮层的激活, 会伴随着SN等网络参与的对DMN特定形式的抑制作用.
3
2.2.2.静息态DMN内部功能网络分析
-->
2.2.2.静息态DMN内部功能网络分析
为了分析不同被试在静息态DMN内部功能网络(这里包括关联网络和因果性网络)方面的共性特征, 我们计算了平均的结果, 得到了一些在静息态下DMN内部普遍存在的功能性结构特征.
3
2.2.2.1.静息态DMN内部的关联网络
-->
2.2.2.1.静息态DMN内部的关联网络
基于偏相关计算得到DMN的23个ROI的关系矩阵及网络(见图6(a)和图6(b)). 可以看到, 网络中强的正相关性边包括vDMN (V1-V10), pDMN (P1-P4), dDMN的主区域(D1-D6)以及左右海马旁回(parahippocampal gyrus, 图中的D8和D9)各自的内部连边. 此外, 强的正相关性连边还包括D2 (左角回, angular gyrus)-P3 (左下顶叶, inferior parietal lobule)、D4 (左背侧后扣带回, dorsal posterior cingulate gyrus)-P2 (右楔前叶, precuneus)、D4-V1 (左后扣带回, posterior cingulate)、D4-V5 (右后扣带回, posterior cingulate)、P2-V6 (左楔前叶, precuneus)、D5 (右腹侧扣带回前部, ventral anterior cingulate gyrus)-P1 (左腹后扣带回, ventral posterior cingulate gyrus)、P4 (右下顶叶, inferior parietal lobule)-V9 (右角回, angular gyrus)等, 这些强的正相关点对多为空间近邻.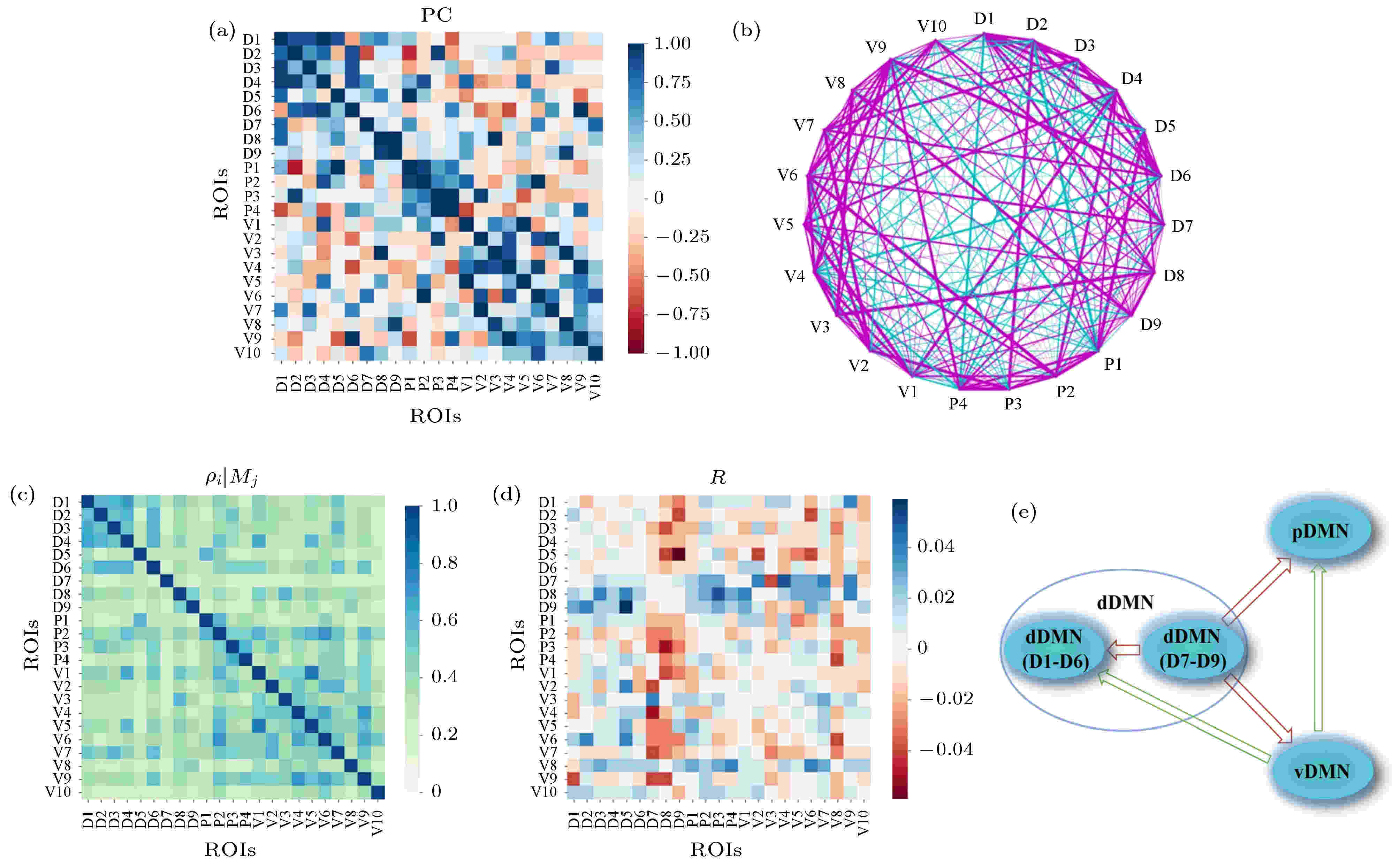
图 6 DMN内部23个ROI间关系分析　(a), (b)基于压缩感知的偏相关矩阵及网络结构, 网络中紫色线表示正相关, 青色线表示负相关, 线的粗细表示相关性强弱; (c) CCM方法中得到的ROI之间的单向影响程度${\rho _{i|{M_j}}}$, 延迟坐标嵌入维数为2, 延迟为1, 下同; (d) CCM方法得到的ROI间动力学因果性矩阵; (e)对应的ROI间动力学影响的粗粒化结果
Figure6. Relationships of the 23 ROIs within DMN: (a) Partial correlation matrix calculated based on compressive sensing; (b) the corresponding network structure, which includes the positive (magenta links) and negative (cyan links) correlations. The width of the line indicates the correlation strength; (c) the directed dynamical influence from ROI i to j, ${\rho _{i|{M_j}}}$, obtained in the CCM method. The delay coordinate embedding dimension is 2 and the delay is 1; (d) the causality matrix obtained by CCM; (e) the coarse-grained result of the corresponding influence among ROIs within DMN.

图6(a)和图6(b)中也存在强的反相关性边, 如D2-P1, P1-V9, D1-P4, D6-V4. 对于反相关性边, 一种可能的原因是信息沿着正相关性边所连成的通路传递的过程中积累的延迟相位差导致的, 并且两节点的反相关程度与该两节点之间由正相关边所组成的最短路径长度有关[30], 随着最短路径长度的增加, 反相关程度增强, 继续增加又会使其减弱(相位引起的效应). 这里我们从DMN的ROI中也观察到了类似的情况, 如D6-V9, V9-V4均为正相关, V6-D4为反相关; P1-P4, P4-V9均为正相关, P1-V9为反相关.
3
2.2.2.2.静息态DMN内部的因果网络
-->
2.2.2.2.静息态DMN内部的因果网络
图6(c)为CCM方法中得到的i脑区对j脑区的影响程度ρi|Mj, 该矩阵为近似对称的非对称矩阵. 可以看到, 其中较强的影响程度对应的脑区在偏相关分析中(图6(a))也被发现具有较强的关联性. 图6(d)给出了CCM方法得到的动力学因果性网络, 可以明显地看到DMN的子网络结构, 其中vDMN, pDMN相对分离, dDMN内部D1-D6相对一致, D7(丘脑)、D8和D9(左右海马旁回)则相对独立. CCM方法得到的结果R可对应于DMN内部区域间的信息流, 见图6(e). 在静息态下, 丘脑(D7)和左右海马旁回(D8, D9)处于DMN内部信息流的上游, dDMN中的D1—D6和pDMN是下游子网络; vDMN从丘脑和左右海马旁回接收信息, 并向pDMN和dDMN的主区域(D1—D6)发送信息. 在dDMN中, D1(内侧额叶)相对特殊, 它对pDMN和vDMN中的多个脑区都有较强的动力学影响; 在vDMN中, V3和V8(左右嘴峰, Culmen)也具有广泛的对其他脑区的影响.
3.总　结
研究表明, 大脑DMN在静息态下出现多种激活模式切换的行为, 但从复杂系统非平衡动力学的角度研究静息态DMN激活行为的工作还比较少见. 本文基于静息态fMRI数据分析了静息态DMN的动力学行为. 首先通过构造静息态DMN能量图景, 观察了不同被试在静息态的DMN状态非平衡演化过程. 为了理解该非平衡过程受到外部影响的机制, 我们以高级视觉皮层和听觉皮层为例, 通过DMN状态空间中的分布特征以及XGBoost、深度神经网络等机器学习算法, 明确了外部脑区活动与DMN状态跳转的密切关系. 这为深入理解DMN的动力学行为启发了新的思路. 文中图3与图4的结果也验证了对DMN的传统认识, 即DMN作为维持觉醒功能的网络会因外部刺激而发生状态调节. 并且, 我们的结果从能量图景与外部脑区激活模式标签对照的新视角提供了静息态下DMN的动力学状态与外部脑区(视、听觉皮层)状态之间关联的证据.
另外, 本文采用偏相关、收敛交叉映射等方法计算了DMN内部23个ROI的功能网络, 包括关联性网络和因果性网络, 识别出了部分主要功能性连接, 以及DMN内部的子网络结构和动力学影响的核心区域(见图6). 虽然DMN的动力学行为具有较大的个体间差异, 但组平均的关联网络能够反映出比较稳定的强相关边; 因果性网络给出了DMN的子网络结构, 该结构可以得到关联性网络的佐证. 这些结果印证了前人对于DMN主要内部结构的研究结论(例如DMN分为dDMN, vDMN和pDMN三大区域, 其各自具有密集的内部连接而彼此之间连接相对较少, 丘脑和海马旁回则是相对独立的功能区等). 同时, 也给出了一些新的启发, 例如根据因果性网络平均结果给出的DMN内部ROI间信息流, 我们可以得到这样的结论: 在静息态下, 1)丘脑和海马旁回是DMN其他区域的驱动者, 即信息是从丘脑和海马旁回流向DMN其他区域; 2)嘴峰(Culmen, 相应的ROIs为vDMN3和vDMN8)是DMN内很多其他区域的驱动者(甚至处于丘脑和海马旁回的上游).
上述围绕DMN内部功能连接以及与外部脑区共变特征的探讨, 增加了我们对DMN动力学行为的理解. 但由于DMN的吸引子状态激活与视听觉、突显网络等功能网络活动的相互作用具体细节机制尚不完全清楚, 目前还无法把外部脑区对DMN活动非平衡过程的影响形式化为特定的方程, 这还有待神经影像学与复杂系统等领域的联合探索. 本文基于静息态DMN状态能量图景的动力学分析方法具有潜在的应用价值, 例如: 1)已有研究发现静息态数据采集之前, 被试所处环境对其静息水平存在遗留影响(例如, 被试刚刚经历了嘈杂环境或完成任务态测试, 与充分休息后所观察到的静息态存在一定差异), 那么, 特定被试在不同“静息水平”下的DMN状态分布及切换行为就可以根据状态能量图景中各个吸引子的能量大小以及吸引域大小进行分析. 例如, “弱静息”条件下(高“温度”), DMN可能更多地在具有较大吸引域的亚稳态附近漫游, 而“强静息”条件下(低“温度”)则陷入具有较低“能量”的亚稳态附近, 即使其吸引域较小; 2)根据静息态DMN状态能量图景中各个吸引子相对位置以及吸引域构型特征, 结合DMN状态与外部脑区激活的对应关系, 预测被试在静息态下的特征“心理活动轨迹”.
感谢北京师范大学王文旭教授, 兰州大学俞连春、黄亮教授, 陕西师范大学王圣军教授的有益讨论, 以及西安交通大学黄文敏、曹玲灿、李蒙在数据处理方面的协助.
相关话题/网络 数据 过程 序列 空间
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 复杂网络上的部分同步化: 奇异态、遥同步与集团同步
    摘要:近年来,复杂网络上耦合振子的部分同步化引起了人们极大的关注,其潜在或背后的原因是部分同步化斑图在大脑网络中广泛存在,并很可能与大脑的认知或记忆等功能有密切的联系.本文对这些进展进行简单的总结与归纳,并按照****们研究的不同侧重点,将其分成三方面来进行介绍,即奇异态、遥同步与集团同步化.着重强 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 复杂网络链路可预测性: 基于特征谱视角
    摘要:近年来链路预测的理论和实证研究发展迅速,大部分工作关注于提出更精确的预测算法.事实上,链路预测的前提是网络的结构本身能够被预测,这种“可被预测的程度”可以看作是网络自身的基本属性.本文拟从特征谱的视角去解释网络的链路可预测性,并刻画网络的拓扑结构信息,通过对网络特征谱进行分析,构造了复杂网络链 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 多层网络级联失效的预防和恢复策略概述
    摘要:现实生活中,与国计民生密切相关的基础设施网络大多不是独立存在的,而是彼此之间相互联系或依赖的,于是用于研究这些系统的多层网络模型随之产生.多层网络中的节点在失效或者遭受攻击后会因“层内”和“层间”的相互作用而产生级联效应,从而使得失效能够在网络层内和层间反复传播并使得失效规模逐步放大.因此,多 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 网络直播平台数据挖掘与行为分析综述
    摘要:随着移动通信和互联网技术的不断发展,网络直播逐渐成为了新媒体环境下人们青睐的在线娱乐和信息传播方式.目前广泛应用于课堂教学、真人秀、电竞赛事、品牌营销等方面.数百万主播与数亿计观众的活跃加入和互动,产生了丰富的在线人群行为活动数据,为开展大规模人群行为动力学、平台内容推荐与检测、在线社群演化等 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种新型的液闪阵列成像屏空间分辨特性
    摘要:针对低强度射线成像,自主研制了一种像元为0.1mm高探测效率的液闪阵列屏.为此,基于倾斜刀口边缘响应的测量原理,建立了理论模拟方法和实验研究方法,对该液闪阵列屏开展了空间分辨性能研究.通过理论模拟,给出了液闪阵列屏在14MeV中子和1.25MeV伽马射线激发下的调制传递函数,并与像元为0.1, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于自归一化神经网络的脉冲星候选体选择
    摘要:脉冲星候选体选择是脉冲星搜寻任务中的重要步骤.为了提高脉冲星候选体选择的准确率,提出了一种基于自归一化神经网络的候选体选择方法.该方法采用自归一化神经网络、遗传算法、合成少数类过采样这三种技术提升对脉冲星候选体的筛选能力.利用自归一化神经网络的自归一化性质克服了深层神经网络训练中梯度消失和爆炸 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Ar原子序列双光双电离产生光电子角分布的理论计算
    摘要:基于多组态Dirc-Fock方法和密度矩阵理论,给出了原子序列双光双电离光电子角分布的计算表达式,发展了相应的计算程序.利用该程序对Ar原子3p壳层序列双光双电离过程进行了理论研究,给出了光电离的总截面、磁截面、剩余离子取向以及光电子角分布的各向异性参数与入射光子能量的函数关系.结果显示在光电 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 动态复杂网络中节点影响力的研究进展
    摘要:节点影响力的识别和预测具有重要的理论意义和应用价值,是复杂网络的热点研究领域.目前大多数研究方法都是针对静态网络或动态网络某一时刻的快照进行的,然而在实际应用场景中,社会、生物、信息、技术等复杂网络都是动态演化的.因此在动态复杂网络中评估节点影响力以及预测节点未来影响力,特别是在网络结构变化之 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光电离过程中Fe靶和V靶特征辐射的角相关研究
    摘要:在发射角120°—170°的范围内,应用硅漂移探测器以10°为间隔对中心能量为13.1keV的韧致辐射诱发Fe靶和V靶发射的典型K系X射线光谱进行了测量.得到特征X射线Kα和Kβ的特征谱线,考虑探测器对特征X射线的探测效率、靶对入射光子和出射光子吸收的校准及大气对特征X射线的吸收后,结果显示不 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一类任意<i>m</i>×<i>n</i>阶矩形网络的电特性
    摘要:任意矩形电路网络中的电位分布问题一直是科学研究的难题.本研究发展了研究电阻网络的递推-变换(RT)理论使之能够用于计算任意m×n阶电路网络模型.研究了一类含有任意边界的m×n阶矩形网络的电位分布及等效电阻,这是一个之前一直没有解决的深刻问题,因为之前的研究依赖于规则的边界条件或一个含有零电阻的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.