复杂网络链路可预测性: 基于特征谱视角

全文HTML

--> --> -->

1.引　言

近年来, 复杂网络研究迅速发展, 其学科分支在包括数学、统计物理、生物医学、化学、计算机等领域掀起研究热潮^[1-5]. 在现代信息科学领域中, 链路预测作为将复杂网络与信息科学连接起来的重要桥梁, 关心的是信息科学中最基本的问题—缺失信息的预测和还原问题^[6,7]. 即在一个网络中, 如何基于已知连边信息, 刻画网络的相似性, 进而重现因为数据缺失尚未观察到的连边, 或者预测未来网络演化过程中将要出现的连边.
目前链路预测相关理论方法研究主要围绕基于马尔科夫链、最大似然估计、概率模型、网络结构相似性等数学领域和统计物理的观点和方法展开. 早期的链路预测领域普遍关注的是马尔科夫链和机器学习, 主要存在着计算复杂度较高, 参数设置不具有普适性等问题^[8]. 也有****提出从似然分析的角度构建链路预测框架, 比较经典的有层次结构模型^[9]和随机分块模型^[10]. Pan等^[11]提出的闭路模型, 拥有比前两者更好的预测精度. 似然分析的优点在于能够从理论上帮助我们理解网络结构特征, 然而受限其自身理论的复杂性, 这类方法不是应用性很强的方法, 即使构思巧妙, 在处理大规模网络时也会显得吃力. 最早由 Taskar等^[12]提出的概率模型是数据挖掘领域的传统模型, 该模型在预测时同时运用了网络的结构信息和节点的属性信息, 概率模型拥有较高的预测精确度, 但是同时产生的高计算复杂度以及其参数设置存在非普适性, 都限制了该类方法的应用范围. 得益于David和Kleinberg^[13]在2007年有关链路预测结构相似性的论文, 基于网络结构相似性的链路预测问题在近年受到越来越多的关注. Zhou等^[14] 把链路预测问题和评价指标都进行了简化, 很多研究人员开始利用同样的数据和指标分析链路预测问题. 基于相似性的算法, 作为最简单的链路预测算法框架, 其中一系列算法复杂性低但预测精度不错的局部相似性指标的提出, 大幅度增加了链路预测在超大规模网络中的可应用性.
利用链路预测算法精准地预测网络的未知结构有着广泛的应用前景. 例如, 在军事对抗中, 通常只能侦测到敌方作战网络的部分结构信息, 如果我们可以获得更多更准确的信息, 就可以制定一定的优先级规则或重要性标准来选择性地攻击网络中的关键节点或连边^[15,16]; 在生物实验中, 研究人员需要通过大量的实验研究去推断探索细胞组分内部的交互作用, 一个具有指导作用的预测结果能有效降低实验成本并帮助人类理解生物网络连边演化机制的规律^[17,18]; 社交网络中, 读懂用户的兴趣偏好和喜怒哀乐, 对企业的发展事至关重要, 一个好的“猜你要关注”推荐能够牢牢地黏住老用户、吸引新用户^[19,20]. 此外, 一个优秀的链路预测算法往往蕴含着一种可能的网络演化机制^[21-24]. 遗憾的是, 除非站在上帝视角, 否则没有人能判断一个链路预测算法是否足够精准. 如果网络的节点对之间随机连接, 任何算法可能都会无功而返, 难以做出有效预测; 相反, 面对一个有特定的连边演化机制, 非常规则的网络, 一个足够优秀的方法能够实现精度很高的预测. 此外, 即使是同一个网络, 不同链路预测算法的准确性也不尽相同, 这种精度值只能相对地反映出网络对于某种特定预测算法的预测精度, 算法不同, 精度也随之改变, 并不能刻画网络自身的固有的链路可预测性, 很多时候, 我们都面临着是预测算法不合适还是网络本身就难以预测这样一个网络与算法的选择和匹配问题.
显然, 网络中待预测的连边集合与网络中不存在的连边集合交集为空集, 无论预测的准确性和效率如何, 理论上我们总可以通过无限加边命中所有待预测的链接. 然而这种上界是没有价值的, 不考虑成本的加边会带来巨大的成本消耗和结构噪音, 这样的情况显然偏离了链路预测的初衷. 如果能够获悉一个网络的链路信息能够多大程度被预测出来, 就能够提供一个导向, 确定当前算法是否接近或者已经达到目标网络的可预测上限. 因此, 刻画网络多大程度上能够被预测是链路预测中首先需要解决的问题, 这个问题在相关文献中被称为复杂网络的链路可预测性问题.
近年来链路预测的理论和实证研究发展迅速, 但绝大部分研究的目的都是希望提出更准确的预测算法^[25,26], 关于复杂网络链路可预测性的研究起步较晚, 相关成果少见报道. 许小可等^[27] 最早从理论上比较了各种算法的优劣, 分析多个网络演化过程中形成链接的两个节点之间的拓扑距离分布, 阐明了传统基于共同邻居相似性指标可有效进行链路预测的机理, 从理论上分析了9 种基于共同邻居相似性算法的预测上限. Lü等^[28] 提出结构一致性的概念, 认为网络“可被预测的程度”, 是网络的一种重要固有属性. 通过对已知网络进行扰动, 刻画重构的邻接矩阵和真实邻接矩阵的差异. 如果丢失的连边没有显著改变网络的结构, 那么这个网络是可预测的, 即网络的结构一致性越强, 网络可预测性越好. 熵被广泛用来测量物理系统中的无序度, Yin等^[29]设计了基于证据推理(Dempster-Shafer theory) 的链路预测算法, 从香农信息熵的视角出发, 分析了网络链路信息的可预测性.
本文拟从特征谱的视角去理解网络拓扑信息, 并刻画网络的链路可预测性. 首先基于特征谱理论给出复杂网络链路可预测性的数学描述, 提出可预测性指标. 在此基础上, 通过计算和分析不同实证网络的链路可预测性, 验证该指标的有效性.

3.基于特征谱的复杂网络链路可预测性

3.1.复杂网络的特征谱

-->

3.1.复杂网络的特征谱

复杂网络的特征谱是代数图论的基本研究课题, 经过多年的研究, 如文献[33] 所述, 已有成熟的理论体系和丰富的研究成果. 网络的特征谱提供了包含网络功能和动力学行为在内的大量信息, 可以被形容为网络的“指纹”, 即网络与其特征谱是一一对应的, 不同类别的网络有着完全不同的特征谱. 因此, 通过分析和识别特征谱, 我们就能够锁定目标网络. 进一步, 特征谱不仅是网络的“指纹”, 还是网络的“脉象”. 通过分析特征谱这一网络“脉象”, 可以得到大量的网络结构信息. 例如, 通过拉普拉斯矩阵(Laplace matrix) 的最大特征根我们可以估计网络的度序列; 分析特征谱还可以挖掘网络社区结构; 网络的中心性和二部分性也可从特征谱得出^[34-37]. 最近有研究表明, 网络的特征值谱还可以表现网络结构和动力学(例如神经与激发序列)的层次性^[38].
令$ G $

表示无向无权图, $ { A}\left( G \right) = {\left( {{a_{ij}}} \right)_{N \times N}} $

表示$ G $

的邻接矩阵, 其中若节点对$ {v_i} $

与$ {v_j} $

之间有连边, 则$ {a_{ij}} = 1 $

, 否则$ {a_{ij}} = 0 $

. 令$ {\lambda _1} \geqslant {\lambda _2} \geqslant \cdots \geqslant {\lambda _N} $

为$ { A}\left( G \right) $

的特征根, 则称集合$ \left\{ {{\lambda _i}} \right\} $

为$ G $

的特征谱(spectrum). 定义$ {d_i} $

为节点$ {v_i} $

的度. $ G $

的拉普拉斯矩阵(Laplace matrix) 可用数学公式表示为$ L\left( G \right) = D\left( G \right) - { A}\left( G \right) $

, 式中, $ D\left( G \right) = {\rm diag}\left\{ {{d_i}} \right\} $

表示节点度的对角矩阵, 显然, $ L\left( G \right) $

是对称半正定矩阵. 令$ {\mu _1} \geqslant {\mu _2} \geqslant \cdots \geqslant {\mu _N} $

表示$ L\left( G \right) $

的特征根, 则称集合$ \left\{ {{\mu _i}} \right\} $

为图$ G $

的拉普拉斯特征谱.
2

3.2.基于特征谱视角的网络链路可预测性

-->

3.2.基于特征谱视角的网络链路可预测性

近年来, 很多统计物理领域的****基于特征谱研究了图的沟通性(communicability)^[34] 和可扩张性(good expansion, GE)^[39]. 图的沟通性指网络中不同节点之间进行交流或传递信息的能力, 而可扩张性指那些既稀疏同时又高度连通的节点间的沟通能力. 实际上, 统计物理角度的沟通和扩张, 在网络信息的视角中, 可以理解为网络结构某种程度上的演化和发展. 链路预测, 作为网络信息挖掘的技术手段, 一个很重要的功能便是预测缺失连边和未来可能存在的连边. 可以说, 链路预测算法与网络连边形成机制相辅相成, 好的链路预测算法本身就给出了很多网络演化可能机制的暗示; 反之网络的链路可预测性也可以理解为网络连边演化机制的另一种表现形式. 因此, 我们可以认为, 沟通性和可扩张性这两个指标所刻画的拓扑信息从某种程度上来说和网络的链路可预测性是相似的, 即具备较好的链路可预测性的网络, 一般也具有较好的沟通性和可扩张性.
已有研究表明, 可扩张性好的网络同时也表现出良好的沟通性, 且这些网络特征谱的最大特征根$ {\lambda _1} $

远大于次大特征根$ {\lambda _2} $

, 即$ {\lambda _1} \gg {\lambda _2} $

. 我们在之前的工作中^[40] 研究了无标度网络特征谱, 同样发现不同参数的无标度网络中存在着不同程度的$ {\lambda _1} \gg {\lambda _2} $

, 即存在谱隙(spectrum gap) 现象, 如图2所示. 因此, 如果能够定量地刻画特征谱中$ {\lambda _1} $

和其他特征根之间的差距, 就能够像中医把脉一样, 定量刻画网络的链路可预测性.

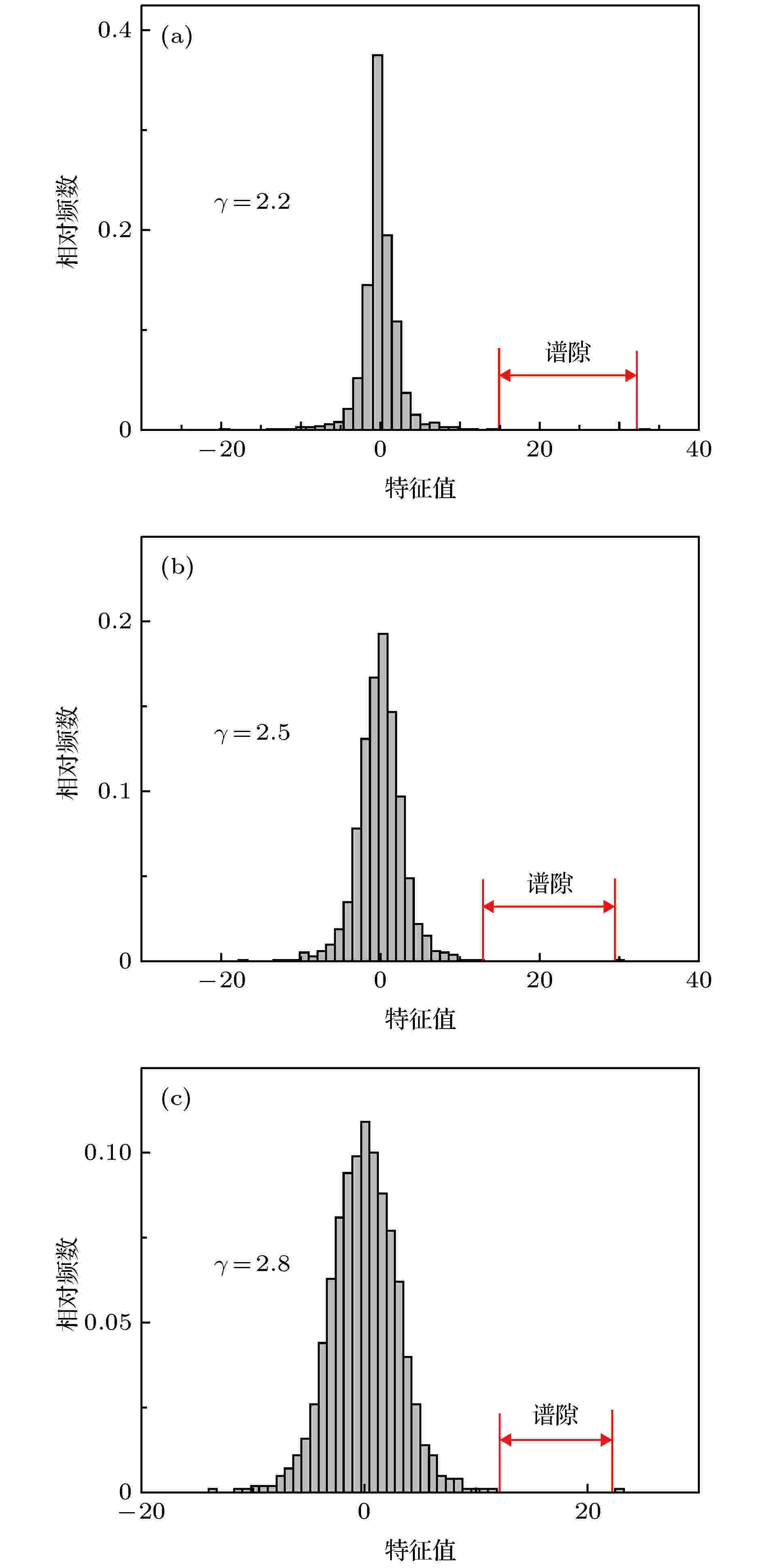图 2 无标度网络特征谱直方图
Figure2. The histograms of eigenvalues of random sacle-free networks

2

3.3.可预测性的数学表达式

-->

3.3.可预测性的数学表达式

在各种各样衡量网络结构属性的指标中, 文献[41]提出的子图中心性是基于网络特征谱的指标. 其认为闭环回路的路径长度越小, 回路信息交流越便利, 节点之间的联系越紧密, 对节点的中心性贡献越大. 节点$ i $

的子图中心性可以定义为

$ {\rm SC} (i) = {\sum\limits_{j = 1}^N {\left( \xi _j^i \right)} ^2}{{\rm e}^{{\lambda _j}}},$

其中$ {\lambda _j}\left( {j = 1, 2, \cdots, n} \right) $

是邻接矩阵A 第$ j $

个特征向量的特征值, ${ { \xi} _j }$

是$ {\lambda _j} $

所对应的特征向量, $ \xi _j^i $

是邻接矩阵第$ j $

个特征向量的第$ i $

个组分, 例如, $ {{\lambda} _1 }$

和$ {{\xi} _1} $

分别是邻接矩阵A的最大特征值及其对应的特征向量. 对于(2)式而言, 显然, SC$ ( i ) $

包含了从节点$ i $

出发, 偶数长度和奇数长度的所有的闭途径. 因此, (2)式也可以表示为

$ \begin{split} {\rm SC}(i)\;& = \sum\limits_{j = 1}^N {{{\left(\xi _j^i \right)}^2}} \cosh \left( {{\lambda _j}} \right) + \sum\limits_{j = 1}^N {{{\left(\xi _j^i \right)}^2}} \sinh \left( {{\lambda _j}} \right) \\ &= {\rm SC_{even}}(i) + {\rm SC_{odd}}(i).\\[-10pt] \end{split} $

显然, 偶数长度的闭途径更多的是一些无环的轨迹, 更多地出现在二部分图中; 而奇数长度的闭途径则不包含这部分无效的路径. 本文的研究对象是简单无权图, 因此, 奇数长度的闭途径更适合于用来描述网络中节点与其邻居间的拓扑结构关系. 我们可以将SC$ _{\rm odd}(i) $

写成如下形式^[39]:

${\rm SC_{odd}}(i) = {\left( {\xi _1^i} \right)^2}\sinh \left( {{\lambda _1}} \right) + {\sum\limits_{j = 2} {\left(\xi _j^i \right)} ^2}\sinh \left( {{\lambda _j}} \right),$

其中$ {\lambda _1} $

是网络的主特征值, $ \xi _1^i $

是主特征向量的第$ i $

个组分. 当网络存在一个巨大的谱隙(spectral gap) 时, 有$ {\lambda _1} \gg {\lambda _2} \geqslant {\lambda _3} \geqslant \cdots \geqslant {\lambda _N} $

. 因此, 在这种情况下,

$ {\left( {\xi _1^i} \right)^2}\sinh \left( {{\lambda _1}} \right) \gg {\sum\limits_{j = 2} {\left(\xi _j^i \right)} ^2}\sinh \left( {{\lambda _j}} \right), $

则

$ {\rm SC_{odd}}(i) \approx {\left( {\xi _1^i} \right)^2}\sinh \left( {{\lambda _1}} \right).$

也就是说, 要判断网络特征谱中$ {\lambda _1} $

和$ {\lambda _2} $

之间是否有足够大的谱隙. 需要检测

$\xi _1^i \propto \sqrt {{\rm SC_{odd}}(i)} - \sqrt {\sinh \left( {{\lambda _1}} \right)}.$

令$ A = {\left[{\sinh \left( {{\lambda _1}} \right)} \right]^{ - 0.5}} $

, $ \eta = 0.5 $

, (7)式可以表示为$ \xi _1^i \propto A{\left[ {\sqrt {{\rm SC_{odd}}(i)} } \right]^\eta } $

. 显然, $ \xi _1^i $

和$ {\rm SC_{odd}}(i) $

之间存在着线性关系. 因此, 我们可以在双对数形式下将(7)式改写成:

$\log \xi _1^i = 0.5\log {\rm SC_{odd}}(i) - 0.5\log \sinh \left( {{\lambda _1}} \right).$

通过测量不同情况与理想情况的偏差$ \Delta \log \xi _1^i $

, 我们可以判断网络是否具有良好的可预测性.

$\Delta \log \xi _1^i \!= \!\log \frac{{\xi _1^i}}{{{\xi _1}^{\rm ideal}(i)}} \!=\! \log {\left\{\!\! {\frac{{{{\left( {\xi _1^i} \right)}^2}\sinh \left( {{\lambda _1}} \right)}}{{{\rm SC_{odd}}(i)}}}\!\!\right\}^{0.5}}, $

当$ \Delta \log \xi _1^i \approx 0 $

时, 网络具有良好的可预测性. 由于 $ \Delta \log \xi _1^i $

是一个一维数组, 直接比较$ \Delta \log \xi _1^i $

与0 的关系并不容易, 因此, 我们构建一个可预测性的数学表达式$ p $

去测度$ \Delta \log \xi _1^i $

多大程度接近于0. 其数学表达式如下:

$ p = \exp\left[- \sum {\sqrt {{{\left( \frac{{ {{\rm SC_{odd}}(i) - {{\left( {\xi _1^i} \right)}^2}\sinh \left( {{\lambda _1}} \right)} }}{{\rm NSC_{odd}}(i)} \right)}^2}}}\;\right], $

易知, 可预测性$ p $

的值域为$ \left[ {0, 1} \right] $

, 如果偏差趋近于0, 那么$ p $

趋近于1, 表示网络的链路可预测性很好; 反之, 若网络$ p $

值较小, 表示网络的可预测性差.

4.实验结果分析

4.1.模型网络的可预测性分析

-->

4.1.模型网络的可预测性分析

相比于随机网络, BA无标度网络具有节点生长和边的偏好链接(preferential attachment)两种明确的生成机制, 即新加入的节点更倾向于与那些具有较大连接度的节点相连. 一个新节点与一个已经存在的节点$ {v_i} $

相连接的概率$ {\varPi_i} $

与节点的度$ {d_i} $

成正比:

${\varPi _i} = \frac{{{d_i}}}{{\displaystyle\sum\nolimits_j {{d_j}} }},$

这意味着, 如果我们的指标能够有效刻画网络的可预测性, 则$ p $

值会随着网络演化机制的变化而改变. 为全面比较网络演化机制对$ p $

刻画可预测性能力的影响, 我们基于(11)式, 加入参数$ \alpha $

, 调控BA模型中偏好链接机制的强度. 构造连接概率$ \varPi_i^\prime $

$ {\varPi _i}^\prime = \frac{{d_i^\alpha }}{{\displaystyle\sum\nolimits_j {d_j^\alpha } }}.$

当$ \alpha = 0 $

时, 网络生成仅由生长机制决定(在此情况下老的节点仍有更高的概率获得更多连接); 当$ \alpha = 1 $

时, 网络生成过程具有显著的偏好链接特征. 图3展示了当网络平均度为4时, 不同节点规模下可预测性$ p $

值随参数$ \alpha $

的变化, 结果表明, 随着$ \alpha $

的增加, 优先链接特性逐渐增强, 我们的指标能够捕捉到网络逐渐明显的优先链接特性, 网络的可预测性越来越好. 并且在连边机制固定的情况下, 可预测性随网络规模的变化不大, 证明$ p $

指标具有良好的稳定性.

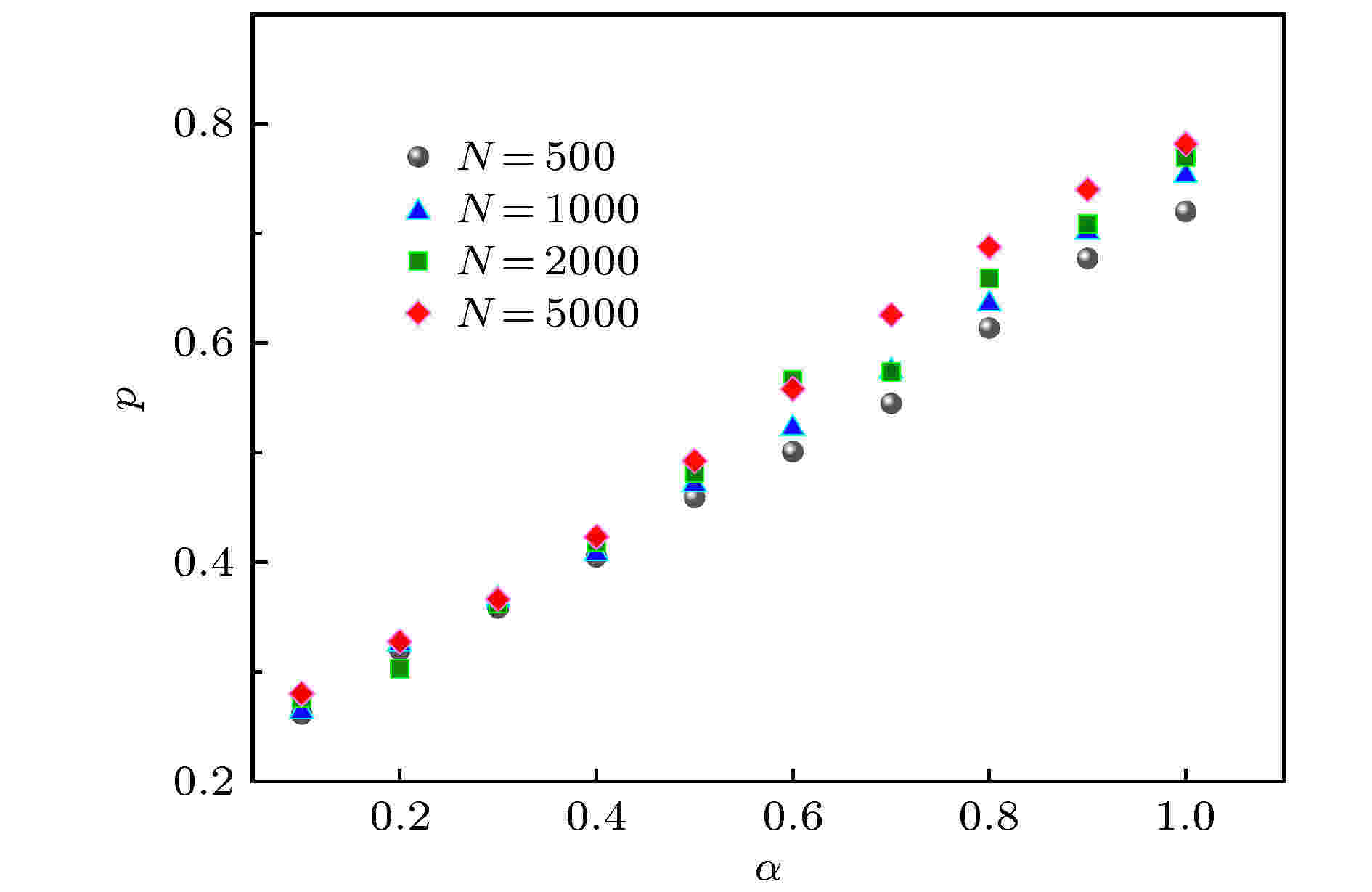图 3 不同节点规模下, 模型网络可预测性$ p $

随$ \alpha $

的变化
Figure3. The link predictability of model network versus $ \alpha $

with various $ N $

同时, 为了清晰地对比各种链路预测算法在这两类模型网络中的表现, 我们生成一个节点数为1000, 平均度为6的BA无标度网络和与之同样规模的随机网络进行对比实验, 实验结果如图4 和表1所示. 表1给出了12种基于相似性的链路预测算法在这两个模型网络中的精确度(precision). 包括 6种基于节点局部信息的相似性指标: 共同邻居(CN), Adamic-Adar(AA), 资源分配(RA), 偏好连接(PA), Individual Attraction(IA) 和CAR指标; 3 种基于路径的相似性指标: 局部路径(LP), Katz和LHN-II指标; 3种基于随机游走的相似性指标: 平均通勤时间(ACT), 重启的随机游走(RWR), 局部随机游走指标(LRW), 具体的算法原理参见文献[25]. 实验通过随机抽样的方式, 将训练集和测试集按照 9∶1 的比例进行划分, 我们固定预测连边的比例, 令L等于测试集中的连边数量.

网络	$ p $	CN	AA	RA	LP	IA	CAR	PA	Katz	RWR	ACT	LRW	LHN-II
BA网络	0.975	0.423	0.324	0.272	0.415	0.271	0.283	0.594	0.412	0.136	0.507	0.085	0.003
随机网络	0.543	0.015	0.008	0.009	0.008	0.009	0	0.030	0.008	0.002	0.020	0	0.001

表1链路预测算法在模型网络中的表现
Table1.Performance of link prediction algorithms in model networks.

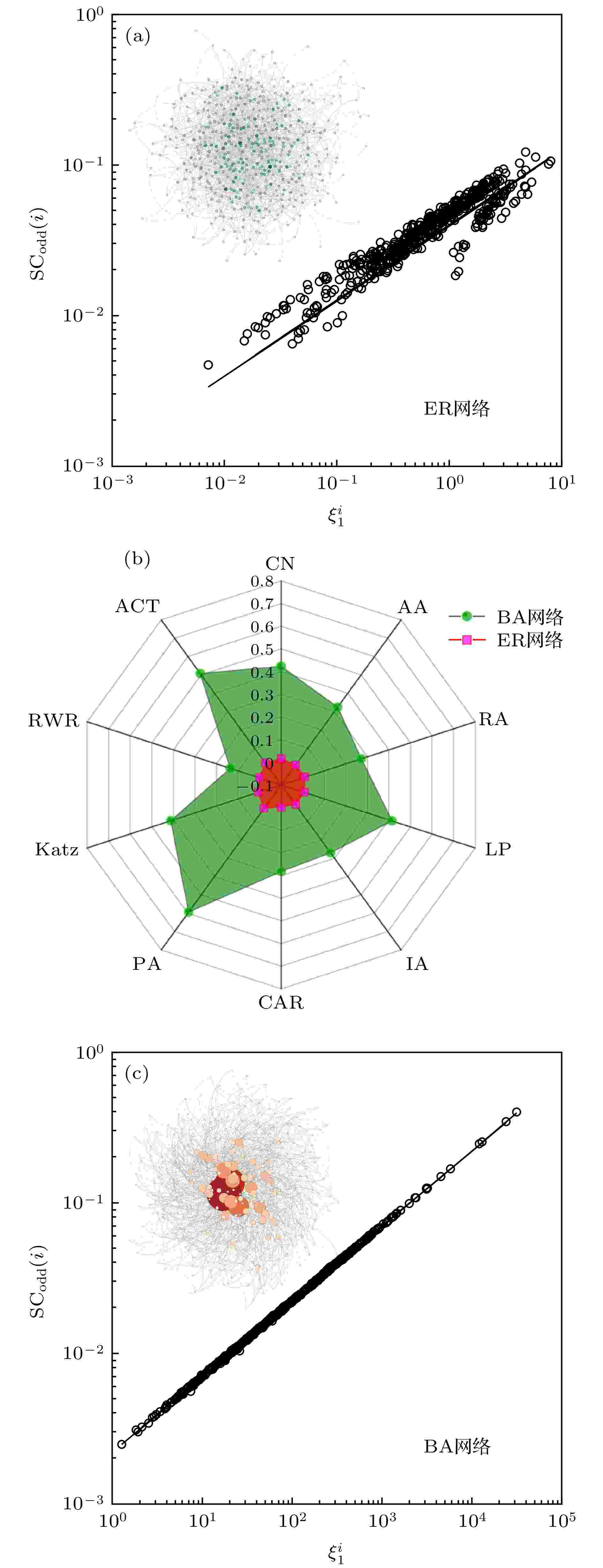图 4 无标度网络和随机网络可预测性示意图
Figure4. The link predictability of BA scale-free network and random graph

可以看到, 由于BA无标度网络中, 新的节点进入网络后会选择网络中已存在的大度节点产生链接. 网络具有固定的网络连边演化机制, 连边都是按照优先链接产生, 因此, 网络具有很好的可预测性. 在图4(c)中表现为$ \xi _1^i $

和$ {\rm SC_{odd}}(i) $

在一条直线上, 体现出(7)式表示的线性关系; 反观同样规模的随机网络, 网络中的连边以固定概率随机产生, 不根据任何演化机制和节点属性, 很难基于某一演化机制去预测连边是否存在, 网络可预测性较差. 在图4(a)中表现为$ \xi _1^i $

和$ {\rm SC_{odd}}(i) $

并不具有很强的线性关系. 图4(b)的雷达图直观地展示了链路预测算法在两类模型网络中的表现, 结果表明, 各类算法在BA无标度网络中的精确度显著优于随机网络, 这与我们对这两类网络可预测性的判断是一致的. 观察各个算法的表现, 在BA无标度网络中, PA指标表现最为出色, 这是因为PA算法的思想来源于优先链接的方法, 即连边存在的可能性大小正比于两端度值的积. 因此, PA算法对于相似性的定义更贴近于BA无标度网络的连边演化机制, 故在这类网络中有着优异的表现. 纵使BA无标度网络具有优秀的可预测性, LHN-II算法在网络中的表现却很差. 这是因为LHN-II算法是基于一般等价(regular equivalence)的思想, 其相似性的定义更多地取决于节点连接的节点之间的相似性, 即使节点对之间不存在共同邻居. 然而, 节点的属性如果不是特殊背景的网络或者有特定的标准往往是很难去量化的, 因此, 虽然无标度网络有着高的可预测性, 但LHN-II算法却不是适用于该网络的合适的链路预测算法. 上述结果初步表明, 通过计算链路可预测性$ p $

的值, 能够回答到底是不可预测的网络还是不合适的算法这个问题, 从而为决策者筛选算法提供指导意见. 上述模型网络只是真实网络一种演化机制的抽象, 真实网络在生长演化过程中往往表现出如集聚性、社团性、无标度性等多种复杂的结构特征, 为更进一步证明指标的有效性, 我们在更多真实网络中进行了实验.
2

4.2.真实网络的链路可预测性分析

-->

4.2.真实网络的链路可预测性分析

本节进一步考察可预测性指标在真实世界网络中的表现. 我们选取了各个不同领域的15个真实网络作为实验网络. 网络拓扑属性如表2所列, $ V $

和$ E $

表示网络中的节点和边, $ \left\langle k \right\rangle $

表示平均度, $ C $

表示集聚系数, $ r $

表示同配系数, $ \left\langle l \right\rangle $

表示平均最短路径长度.

网络	V	E	r	$\langle k\rangle$	$\langle l\rangle$	C
C_elegans	297	2148	–0.163	14.47	2.46	0.308
Windsurfers	43	336	–0.147	15.63	1.70	0.564
Adolescent health	2539	12969	0.251	10.22	4.52	0.142
Jazz	198	2742	0.020	27.69	2.21	0.520
USAirport	1574	28236	–0.113	35.87	3.14	0.384
Metabolic	453	4596	–0.226	20.29	2.64	0.124
Yeast	2375	11693	0.454	9.85	5.10	0.388
US powergrid	4941	6594	0.003	2.67	20.09	0.103
Physicians	241	1098	–0.056	9.11	3.02	0.552
Air Traffic Control	1226	2615	–0.015	4.27	6.10	0.063
Contiguous USA	49	107	0.233	4.37	4.26	0.406
Email	1133	5451	0.078	9.62	3.65	0.166
King James Bible	1773	9131	–0.048	10.30	3.38	0.163
Protein Stelzl	1706	6207	–0.191	7.28	5.09	0.006
Router	5022	6258	–0.138	2.49	6.45	0.033

表2不同领域真实网络拓扑属性
Table2.Basic statistics of real networks.

在实验中, 我们采用随机抽样的方法, 将训练集和测试集按照9∶1的比例进行划分, 即测试集包含10%的真实连边. 针对预测结果采取precision衡量算法的表现, 由于真实网络规模不同, 在实验时固定预测连边的比例, 令L等于测试集中的连边数量.
表3为链路预测算法在真实网络中的最大精确度 (precision)测试结果, 每个链路预测算法在每个网络运行100次取平均. 从网络间纵向比较来看, 算法在可预测性高的网络上的预测精度要明显高于可预测低的网络, 如图5大图所示, 不同颜色的圆代表不同的网络, 圆的大小与网络可预测性 $ p $

成正比. 横坐标表示网络可预测性的值, 纵坐标表示链路预测算法的最大precision值, 纵坐标越大, 算法的最大精度越高. 可以看到, 那些可预测性好的网络对应的precision值也相对较高, 如图中右侧较大的圆所示. 相比之下, 图中左下方网络的precision值较低, 其对应的网络可预测性值也较差. 值得注意的是, C_elegans网络的可预测值很高, 然而实验选取的多种基于结构相似性的链路算法在网络中的precision值普遍不高, 我们进一步计算了各类算法在该网络中的AUC值, 结果表明, 最大AUC值同样来自于LRW指标, 达到了0.907, 各类算法的平均AUC值为0.848. 因为AUC值是基于整个边列表, 而这里的L是基于前10%的边, 说明这些算法对于该网络的正确预测大部分来自于边列表的后半段, 测试的算法在该网络上的预测效率均较低, 对于该网络有待挖掘能够快速找到更多正确连边的预测算法. 图5里的箱线图则显示了对每个网络预测算法之间的比较结果. 我们发现, 除了少数网络各个预测算法的表现基本维持在同一水准外, 大多数预测算法在网络中的效果差别很大, 这也体现出网络和算法选择与匹配问题的重要性. 例如, 在Jazz网络中, CN, AA, RA等指标的precision都达到了0.5左右, 然而, 优先链接指标PA的精确度却很差, 仅为0.133. 该结果说明, 对于Jazz网络来说, 基于共同邻居的算法更能捕获爵士音乐家间的合作关系, 且这种关系不是以优先链接的形式展开的, 所以由优先链接思想演化而来, 依靠节点度乘积来刻画相似性的PA指标与Jazz网络并不匹配. 事实上, 不仅是Jazz网络, PA算法在很多真实网络中的precision值都低于其他算法, 这说明真实网络在演化生长的过程中往往表现出集聚性、社团性、无标度性、小世界性等多种结构特征, PA算法虽然能够在无标度网络中表现突出, 其相对单一的相似性刻画思想难以胜任网络结构特征比较复杂的真实网络. 类似的情况还出现在Router网络中, 该网络中大多数算法的precision值都低于0.05, 只有ACT算法的precision达到了0.164, 这说明ACT的算法思想能够更好地匹配该网络更多的结构特征. 结合表3和箱线图进行讨论分析, 能够为网络与算法间的匹配和选择问题提供帮助.

网络	p	CN	AA	RA	LP	IA	CAR	PA	Katz	RWR	ACT	LRW	SRW
C_elegans	0.999	0.100	0.107	0.105	0.101	0.108	0.094	0.058	0.101	0.105	0.055	0.110	0.108
Windsurfers	0.999	0.379	0.396	0.413	0.370	0.393	0.381	0.214	0.369	0.360	0.247	0.402	0.426
Adolescent health	0.422	0.103	0.103	0.088	0.089	0.101	0.094	0.003	0.088	0.053	0.008	0.042	0.047
Jazz	1.000	0.502	0.523	0.542	0.489	0.535	0.517	0.133	0.489	0.352	0.168	0.342	0.393
USAirport	0.998	0.333	0.336	0.364	0.332	0.332	0.330	0.280	0.332	0.087	0.294	0.076	0.080
Metabolic	0.999	0.137	0.195	0.269	0.141	0.168	0.132	0.104	0.141	0.196	0.092	0.214	0.215
Yeast	0.998	0.154	0.177	0.267	0.158	0.161	0.148	0.094	0.174	0.073	0.211	0.045	0.059
US powergrid	0.362	0.054	0.032	0.028	0.058	0.047	0.037	0.000	0.057	0.016	0.034	0.015	0.018
Physicians	0.368	0.119	0.126	0.121	0.117	0.122	0.106	0.014	0.117	0.119	0.015	0.132	0.127
Air Traffic Control	0.480	0.036	0.024	0.018	0.037	0.021	0.025	0.007	0.037	0.002	0.015	0.002	0.002
Contiguous USA	0.540	0.096	0.130	0.132	0.005	0.000	0.000	0.012	0.004	0.067	0.053	0.133	0.121
Email	0.950	0.144	0.158	0.143	0.142	0.159	0.145	0.018	0.141	0.065	0.024	0.052	0.051
King James Bible	0.960	0.167	0.270	0.446	0.163	0.256	0.176	0.078	0.163	0.186	0.069	0.197	0.224
Protein Stelzl	0.441	0.001	0.002	0.001	0.001	0.002	0.006	0.014	0.001	0.006	0.013	0.006	0.006
Router	0.511	0.051	0.029	0.020	0.056	0.031	0.055	0.022	0.055	0.006	0.164	0.005	0.005

表3链路预测算法在真实网络中的precision值
Table3.The precision of link prediction algorithms in real networks

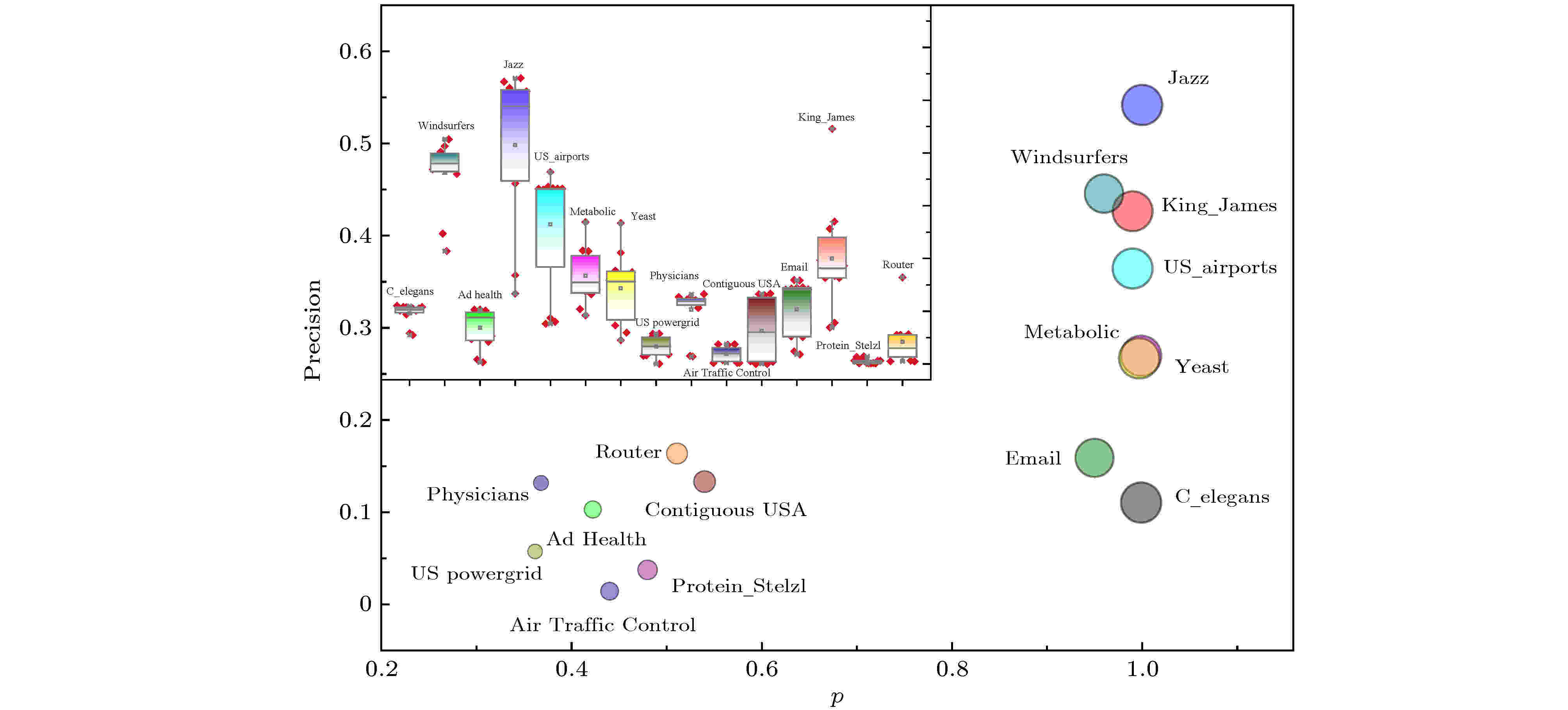图 5 预测算法在真实网络上的表现
Figure5. The performance of prediction algorithms in real networks

5.结论与展望

在网络科学和信息科学领域中, 我们常常会遇到信息缺失的情况. 链路预测作为数据挖掘领域重要的研究方向之一, 是一个长期存在的挑战和难题. 近年来有关链路预测理论和实证的研究发展迅速, 大量研究工作的重心都放在提出算法本身上, 各种各样精确度越来越高的算法层出不穷. 但是, 大量实验结果表明, 在同一网络中不同算法的精度有好有坏. 因此, 到底是不可预测的网络, 还是不合适的链路预测方法, 是一个很有挑战性问题.
本文从统计物理中图的可扩张性得到启发, 提出了一种基于特征谱的链路可预测性度量指标. 通过对网络特征谱的分析, 构造了一个指标来评价网络缺失链路的“可被预测的程度”. 模型网络和大量真实网络中的实验结果证明, 该指标能够有效地刻画网络的链路可预测性, 且能够就链路预测算法选择提供建议. 例如, 随机网络的可预测性较差, 而无标度网络的可预测性较好. 然而, 虽然各类算法在无标度网络中的精确度明显优于随机网络, LHN-II算法却不是适用于该网络的合适的链路预测算法; 在实证网络中, Jazz网络具有较好的可预测性, 一些基于共同邻居的相似性指标如CN, AA, RA表现较好, 然而优先链接指标PA的精确度却很差. 这是因为网络中音乐家之间的合作关系不是以优先链接的形式展开的, 依靠节点度乘积来刻画相似性的PA算法不是适合Jazz网络的链路预测算法. 事实上, 我们认为网络的可被预测的程度差并不绝对, 可预测性差的网络也许只是没能遇到理解它结构特征的链路预测算法. 一个好的链路预测算法背后往往有一套贴近网络生长演化的连边机制, 同样道理, 一个重要的机制往往能够提取出一种精确的链路预测算法. 链路预测的研究与网络的结构和演化密切相关, 即算法与网络连边形成机制相辅相成, 是互通的, 网络的链路可预测性即是网络连边演化机制的另一种表现形式. 我们把基于特征谱视角计算可预测性, 获取网络能够被预测的难易程度的工作视作基础, 在下一步的研究中, 拟通过对具有典型演化机制的网络进行分析, 说明预测背后的主要机制以及预测正确或者错误的原因, 去探索一些因果关系. 同时, 考虑基于特征谱挖掘和学习不同网络的拓扑结构信息, 对网络拓扑结构进行标记分类, 针对不同类型网络的连边机制, 提出与之相匹配的链路预测算法.

本站小编 Free考研考试/2021-12-29

English Abstract

Link predictability of complex network from spectrum perspective

Corresponding author:Wu Jun, wujunpla@hotmail.com;Lu Xin, xin.lu@flowminder.org

全文HTML

3.1.复杂网络的特征谱

3.2.基于特征谱视角的网络链路可预测性

3.3.可预测性的数学表达式

4.1.模型网络的可预测性分析

4.2.真实网络的链路可预测性分析

相关话题/网络 指标 结构 信息 实验

领限时大额优惠券,享本站正版考研考试资料!

复杂网络上的部分同步化: 奇异态、遥同步与集团同步

多层网络级联失效的预防和恢复策略概述

网络直播平台数据挖掘与行为分析综述

超临界Lennard-Jones流体结构特性分子动力学研究

钙钛矿电池纳米陷光结构的研究进展

相干与路径信息

a-Si:H薄膜中Si<sub><i>y</i></sub>H<sub>x</sub>结构组态的原子模拟研究

电介质/半导体结构样品电子束感生电流瞬态特性

双稳态结构中的1/2次谐波共振及其对隔振特性的影响

纳米流体液滴内的光驱流动实验及其解析解