全文HTML
--> --> -->实际上, 除了这些整体同步化外, 还存在着以非整体行为的方式体现的同步化. 比如, 在猫的视觉皮层中, 分布在不同空间位置的神经元与它们的振荡响应(40—60 Hz)是同步的[3]. 然而, 这个现象直至十年之后, 也就是2000年左右, 才引起了人们的广泛关注, 被称为部分同步化. 部分同步主要讨论两个振子以上但总振子数目不是太大的情形. 此时只有部分态变量是同步的, 而其他态变量并不与它们同步, 因此系统的轨道将收敛到一个由同步变量定义的不变线性子空间[4-7]. 比如考虑由三个振子

上述研究, 无论是同步还是部分同步, 包含的子系统数目都不大, 通常只有2—6个子系统. 另外, 这些耦合的连接方式是均匀的, 比如最近邻连接、规则连接或者全连等, 而不涉及复杂的网络结构, 因此在理解大脑的各种同步斑图方面帮助不大. 最近, 部分同步的研究有了长足的进展, 不仅仅是子系统数目扩大到成百上千的规模, 而且连接的方式也推广到多种多样[10,11], 从分组连接到复杂网络连接, 甚至到了多层网络连接[12,13]. 基于这些研究, 人们发现复杂网络上的部分同步可以展现出复杂多变、多姿多彩的斑图, 这就对大脑斑图的多样性给出了一种可能的机制. 我们知道, 大脑皮层的大尺度同步[14]与网络神经元子集的同步放电[15,16]均与认知过程密切相关, 且额叶脑区内任务相关的α波同步与顶底加工(top-down processing)的需求也高度相关[17]. 另外, 神经活动的同步斑图还与大脑无序紧密相关. 比如, 癫痫发作时, 特定脑区会变得高度同步, 其他部分则不同步[18]. 而在失去了部分脑细胞导致的帕金森氏病中, 同步活动将会在特定的脑区缺失[19]. 因此, 复杂网络上部分同步化的研究为理解大脑的高级功能, 如认知与记忆等打开了一扇新的窗口, 亟待进一步深入下去.
由于复杂网络上部分同步的复杂性, 历史上, 不同的研究小组从不同的角度得到了不同的发现, 并依据具体出现条件的不同而将其分别命名为奇异态、遥同步及集团同步等. 奇异态是最先命名的, 描述的是同步振子与无序振子的共存现象, 可对半脑睡眠与首晚效应等生物现象做出合理的解释. 遥同步是最后命名的, 描述的是不直接相连的振子之间通过中心节点发生同步但却不与中心节点上的振子同步的现象, 可用于帮助理解大脑分布式计算的内在机制. 而集团同步化居中, 描述的是复杂网络上的部分振子因具有某种对称性而形成同步集团的现象, 可帮助理解大脑同步斑图的多样性. 虽然这三种部分同步化状态发现的初始时间略有不同, 但对它们研究的进展并没有绝对的先后, 而是交替前行、相互促进的. 实际上, 这三种部分同步化状态并不是完全独立的, 甚至有时描述的是同一种现象或斑图. 本文将对这些进展进行综述, 并对它们间的相互关系进行简单的讨论.
另一方面, 奇异态的研究也拓展并丰富了非线性动力学及耦合振子理论. 长期以来, 人们一直相信同步与非同步的共存是限制在非均匀振子网络中的, 其中具有相似频率的振子可以发生同步, 而那些偏离平均频率较大的振子则保持不相关的漂移. 因此, 当发现全同振子在相同的耦合方式下也可以分离成为同步与漂移的两组, 即奇异态时, 就从根本上令人感到吃惊, 因为全同振子通常是作为整体, 表现为要么同步要么非同步的. 这样, 作为一种新的动力学状态的奇异态就实质性地拓展了我们对从同步到混乱的转变或相反的转变的认识.
事实上, 奇异态这种现象在其命名的两年前就由Kuramoto与Battogtokh[24]在Ginzburg-Landau方程中注意到了, 但当时并没有引起人们足够的重视, 这也从一个侧面说明了命名的重要性. 在这个发现中, 一个极其重要的因素是, 不同于以往的全局耦合或最近邻耦合, 甚至也不同于随机耦合, 作者采用了一种随距离衰减的指数耦合, 称为非局域耦合(nonlocal coupling). 虽然这种非局域耦合没有局域或全局耦合那么受到重视, 但它其实也有广泛的应用, 比如在约瑟夫逊结、化学振子、蜗牛壳模式的神经网络及眼优势条纹中等. Abrams与Strogatz[20]继承了这个非局域耦合的思路, 但代之以Kuramoto相振子模型. 此外, 他们还将指数衰减的耦合核改为余弦耦合核, 使得模型可以解析求解.
研究奇异态最常用到的是Kuramoto相振子模型, 这个模型因只含振荡的相位特征却没有涉及振荡的振幅而被认为是描述自然界各种振荡行为最简单的模型. Abrams与Strogatz[20]考虑的模型就是这样一个相振子环, 其方程为









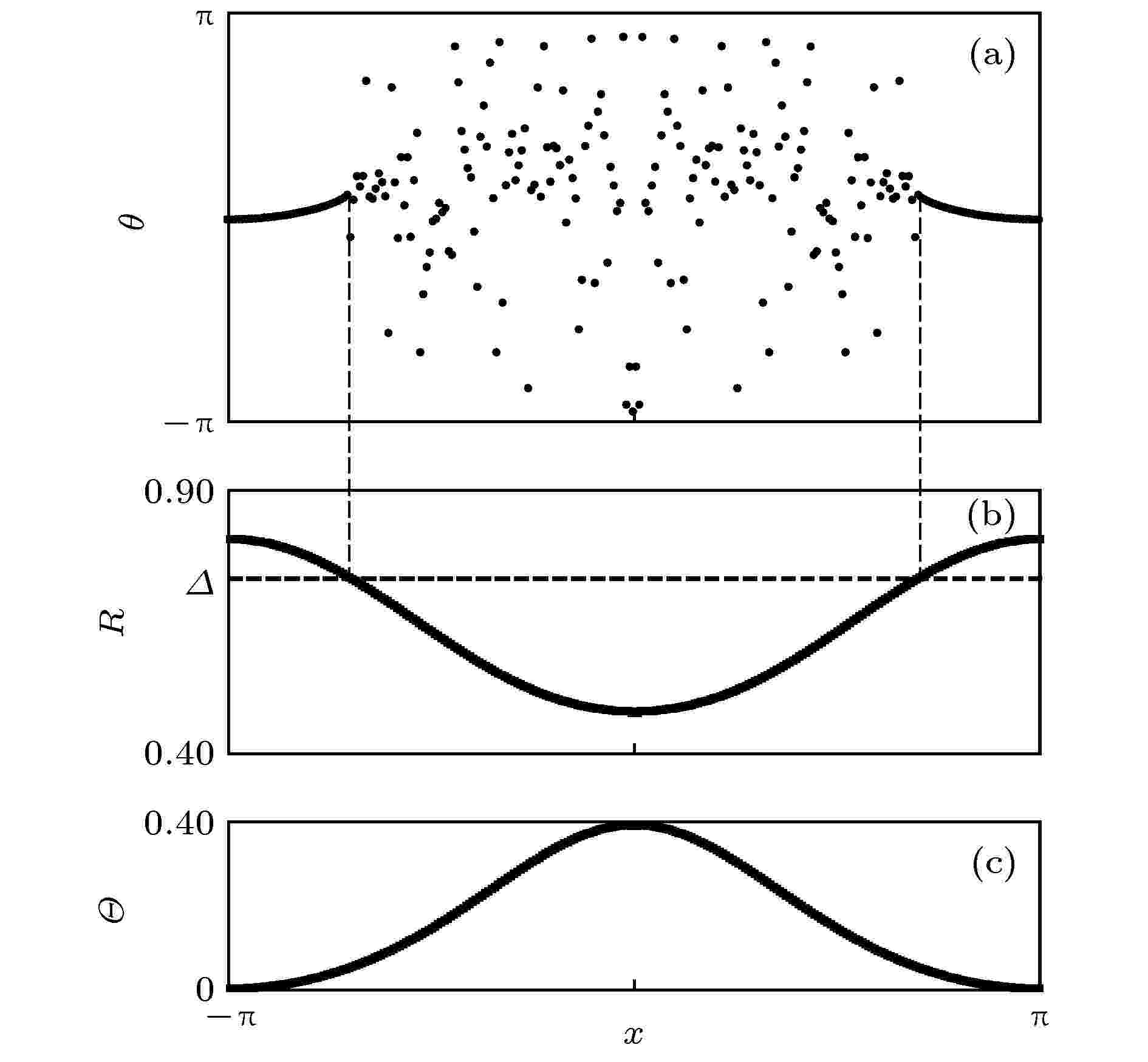 图 1 (a)奇异态的斑图, 参数:
图 1 (a)奇异态的斑图, 参数: 



Figure1. (a) Phase pattern for a chimera state, parameters:




随后, Abrams等[25]于2008年提出了一个仅包含两组相互作用的振子集团且精确可解的奇异态模型. 这个模型人为地将振子分成大小相等的两组, 各组内与组间的耦合方式完全一样, 通过初值条件选取的不同, 使得它们一个处于同步态, 而另一个处于无序态. 通过Ott与Antonsen[26]的降维方法, 他们得到了关于奇异态稳定性、动力学及分岔的精确解. 其模型如下[25]:









对于随机选择的初值, 方程(5)很容易走向同步态. 但当初值设置在奇异态附近时, 比如一组为近似同步的初值, 另一组为随机初值, 则能观察到奇异态[25]. 图2为奇异态的动力学, 只画了非同步那一组的序参量, 其满足

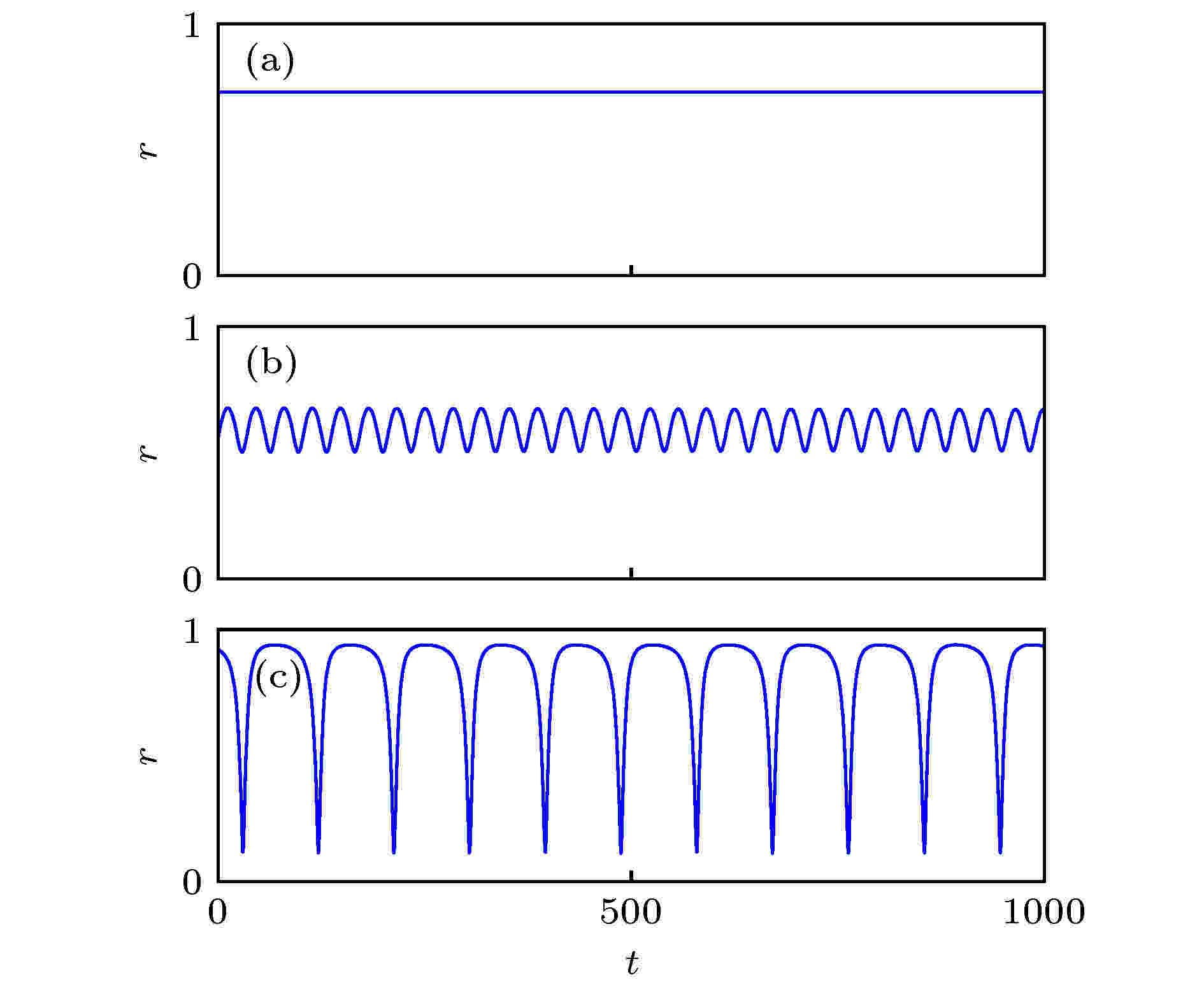 图 2 序参量r随时间的变化, 其中参数
图 2 序参量r随时间的变化, 其中参数




Figure2. Order parameter r versus time. In all three panels,





当取其他的β时, 也可能出现稳定的奇异态与呼吸奇异态, 但所需的耦合强度差A会有所不同. 借助于OA降维方法, Abrams等[25]得到了依赖于参数β与A的解析解, 并给出了各稳定区域间的边界曲线. 图3是相应的相图.
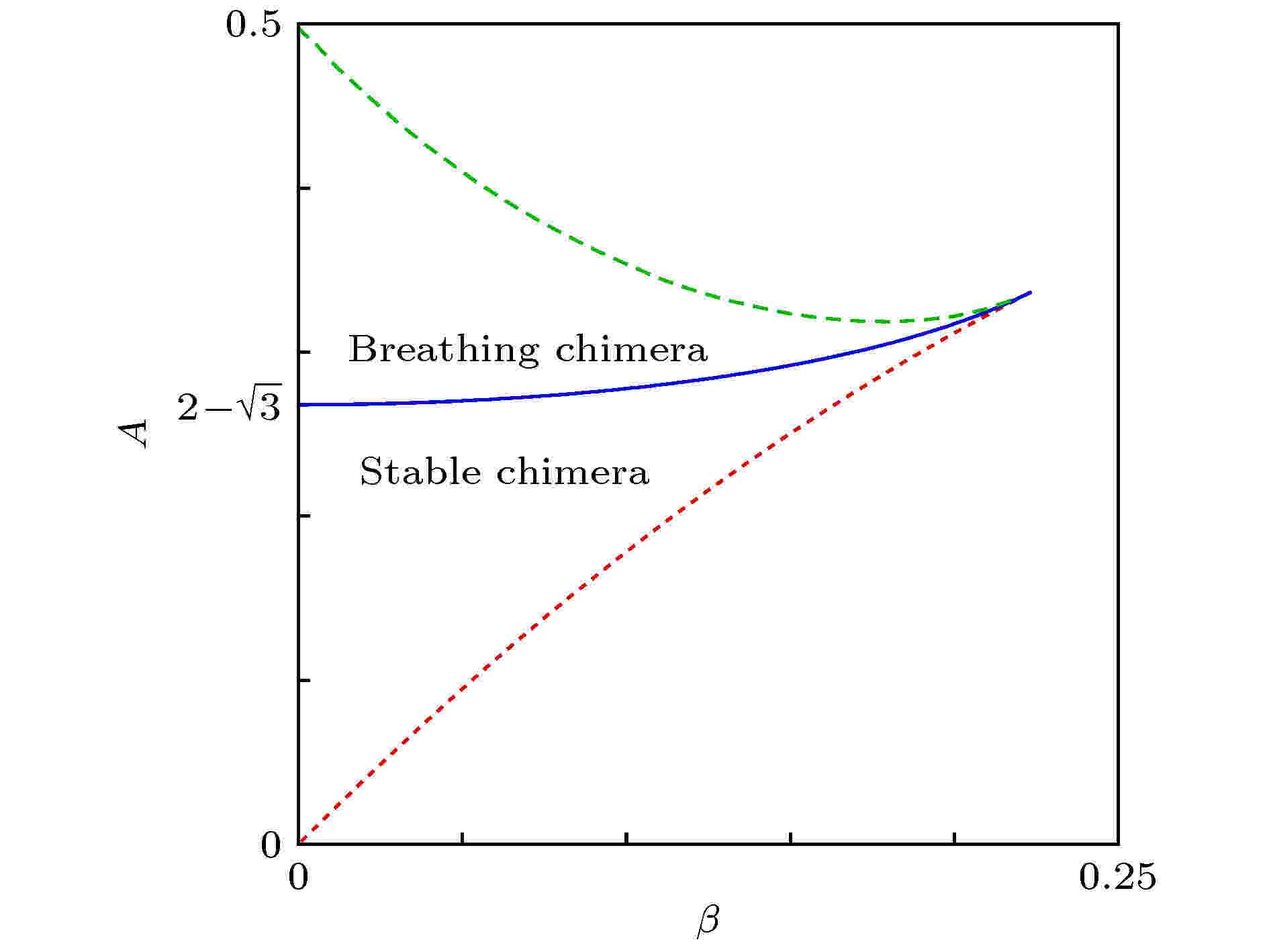 图 3 奇异态的稳定性相图 分岔曲线: 鞍-节分岔(点划线)、超临界Hopf分岔(实线), 两者都是解析发现的; 同宿分岔(虚线), 数值发现的. 改编自文献[25]
图 3 奇异态的稳定性相图 分岔曲线: 鞍-节分岔(点划线)、超临界Hopf分岔(实线), 两者都是解析发现的; 同宿分岔(虚线), 数值发现的. 改编自文献[25]Figure3. Stability diagram for chimera states. Bifurcation curves: saddle-node (dotted line) and supercritical Hopf (solid line), both found analytically; homoclinic (dashed line), found numerically. Figure adapted from Ref. [25].
上述奇异态一旦形成, 便不再改变, 因此是稳定的奇异态. 为了实现海豚与鸟类在睡眠中出现的交替奇异态, Ma等[27]引入了一个周期性的延迟信号来描述变化的外部环境. 具体做法是将方程(5)改写为





































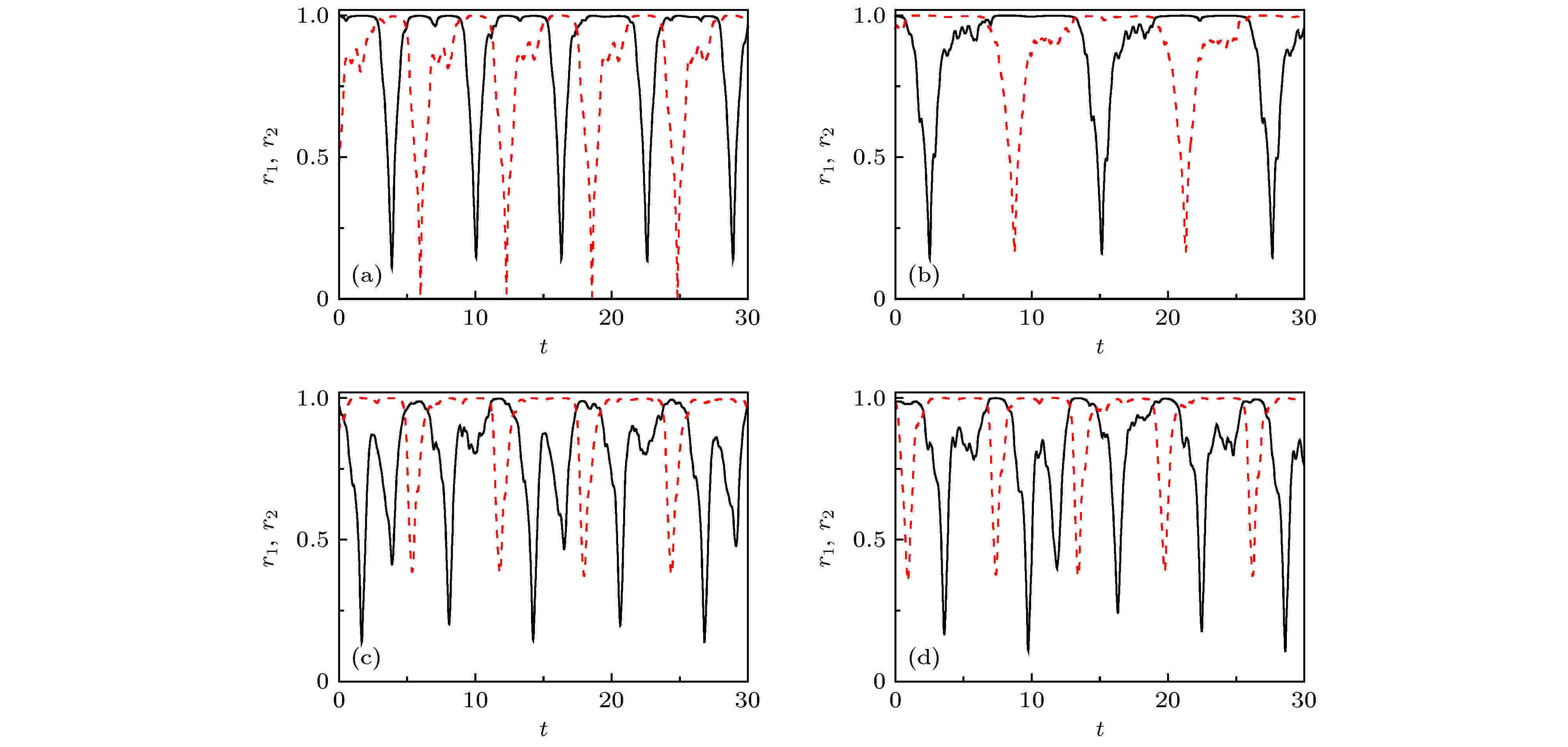 图 4 外部信号诱导的交替奇异态 (a)
图 4 外部信号诱导的交替奇异态 (a)















Figure4. Alternating chimera states induced by external signals: (a)
















当网络结构不是全连网, 而是二维或三维规则格子甚至复杂网络时, 奇异态会表现出多种多样性, 其斑图丰富多彩[29-33]. Zhu等[34]研究了复杂网络情形, 发现此时的斑图会比较混乱, 但如果按振子的有效频率进行重新排序, 则仍可见清晰的同步与无序共存. 详细的信息可见综述文献[10,11,35].
有鉴于此, 为了定量刻画奇异态, Kemeth等[36]于2016年引入了一个特征分类方法来测量奇异态. 其基本思想是测量空间关联, 即对于具有局部或非局部耦合拓扑的系统, 采用局部曲率来测量空间关联. 据此, 一维系统时局域曲率可由二阶导数测量, 一维以上的系统则由拉普拉斯算子来完成. 具体步骤如下.
i) 对于包含空间数据 f 的每一个时间步或快照, 我们用分立的拉普拉斯算子D来计算每个节点的局部曲率. 以一维情形为例, 对时间 t 时的快照, 我们计算















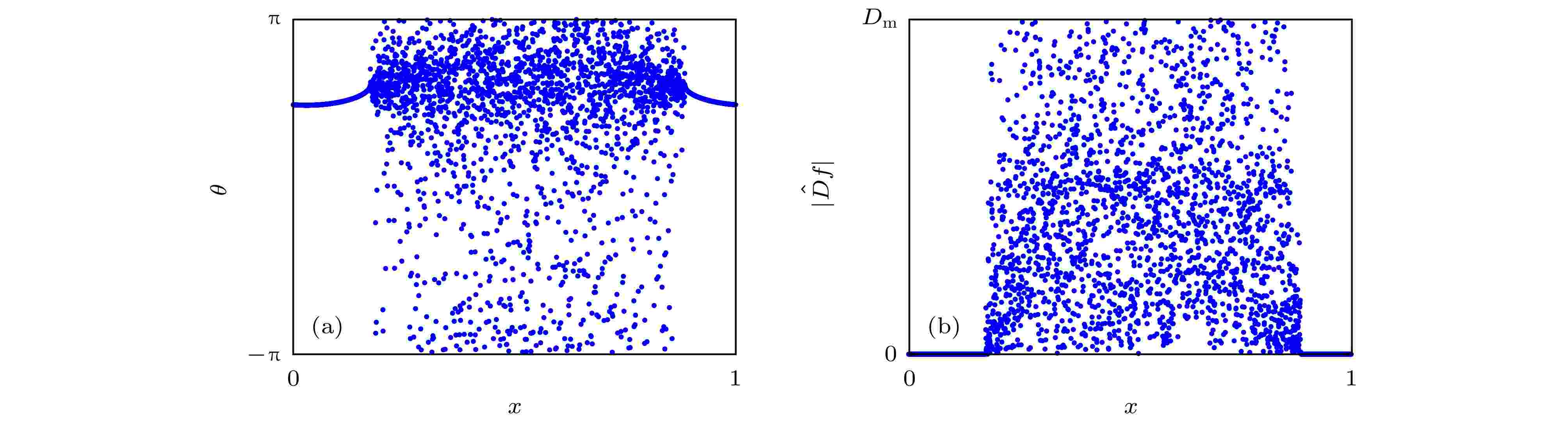 图 5 (a) 来自于Kuramoto模型的快照; (b) 将拉普拉斯算子用于(a)中的数据后得到的局部曲率的绝对值. 改编自文献[36]
图 5 (a) 来自于Kuramoto模型的快照; (b) 将拉普拉斯算子用于(a)中的数据后得到的局部曲率的绝对值. 改编自文献[36]Figure5. (a) Snapshot of the Kuramoto model; (b) absolute value of the local curvature obtained by applying the discrete Laplace operator on the data set shown in (a). Figure adapted from Ref. [36].
ii) 计算





iii) 考虑到数值模拟中的误差涨落, Kemeth等[36]建议只要局部曲率的绝对值小于最大曲率的百分之一就应该被当作相关态, 其他的为非相关态. 为此, 他们引入关联测度


奇异态概念最直接的应用就是神经系统, 特别是大脑网络, 目前这方面的研究很丰富[37-44]. 不同于一维的相振子模型, 神经元系统通常由二维或三维模型来表示, 此时的相互作用由耦合矩阵表示. 研究中比较常用到的是FitzHugh-Nagumo (FHN)神经元模型. Omelchenko等[37]为FHN模型引入了一种旋转耦合, 并发现了多奇异态. 他们将N个神经元放置在一个圆环上, 每个神经元与其最近邻的









令










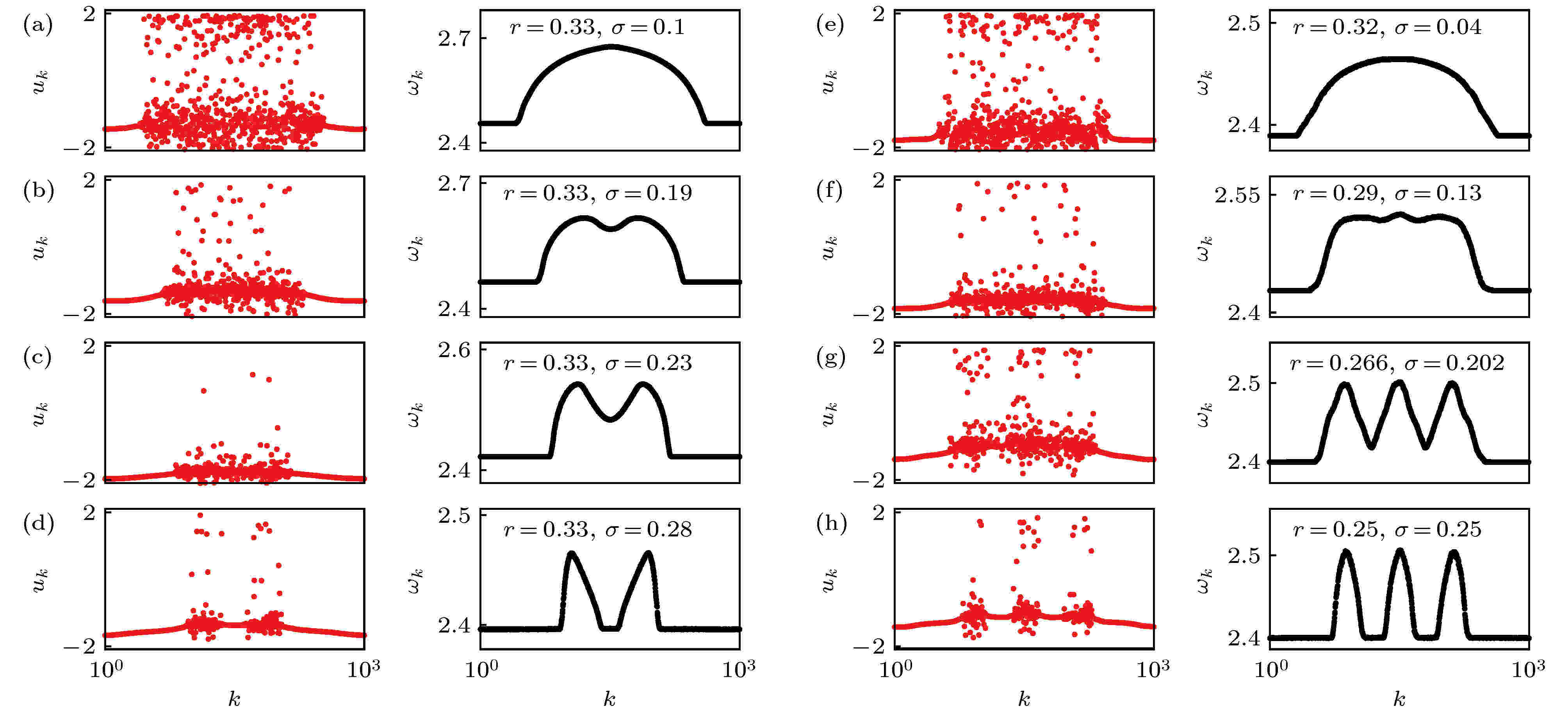 图 6 单一的非相关区域变成多个非相关区域的情形 (a)—(d)变成两个非相关区域: (e)—(h)变成三个非相关区域. 在每个子图中, 左列代表变量
图 6 单一的非相关区域变成多个非相关区域的情形 (a)—(d)变成两个非相关区域: (e)—(h)变成三个非相关区域. 在每个子图中, 左列代表变量
Figure6. Transition from a classical chimera state with one incoherent domain to multichimera states with two (a)–(d), and three (e)–(h) incoherent domains. In each panel the left column shows snapshot of variables uk, and the right column shows the corresponding mean phase velocities. Figure adapted from Ref. [37].
在大脑网络方面的应用主要是将网络结构考虑成不同大小的真实脑皮层网[13,45-47], 然后研究这些特定网络结构下的奇异态. 值得一提的是, Kang等[13]发现了对应“首晚效应”或半脑睡眠的奇异态. 他们使用的脑皮层网络数据含有998个节点、17865条边[48,49], 但其中含有9个孤立的没有边的节点. 去掉这些孤立节点后, 网络只有989个节点, 其中右半脑含有496个节点(


考虑到通过胼胝体的连边与半脑内的连边具有不同的信号传播速度, Kang等[13]提出了一个双层网模型(









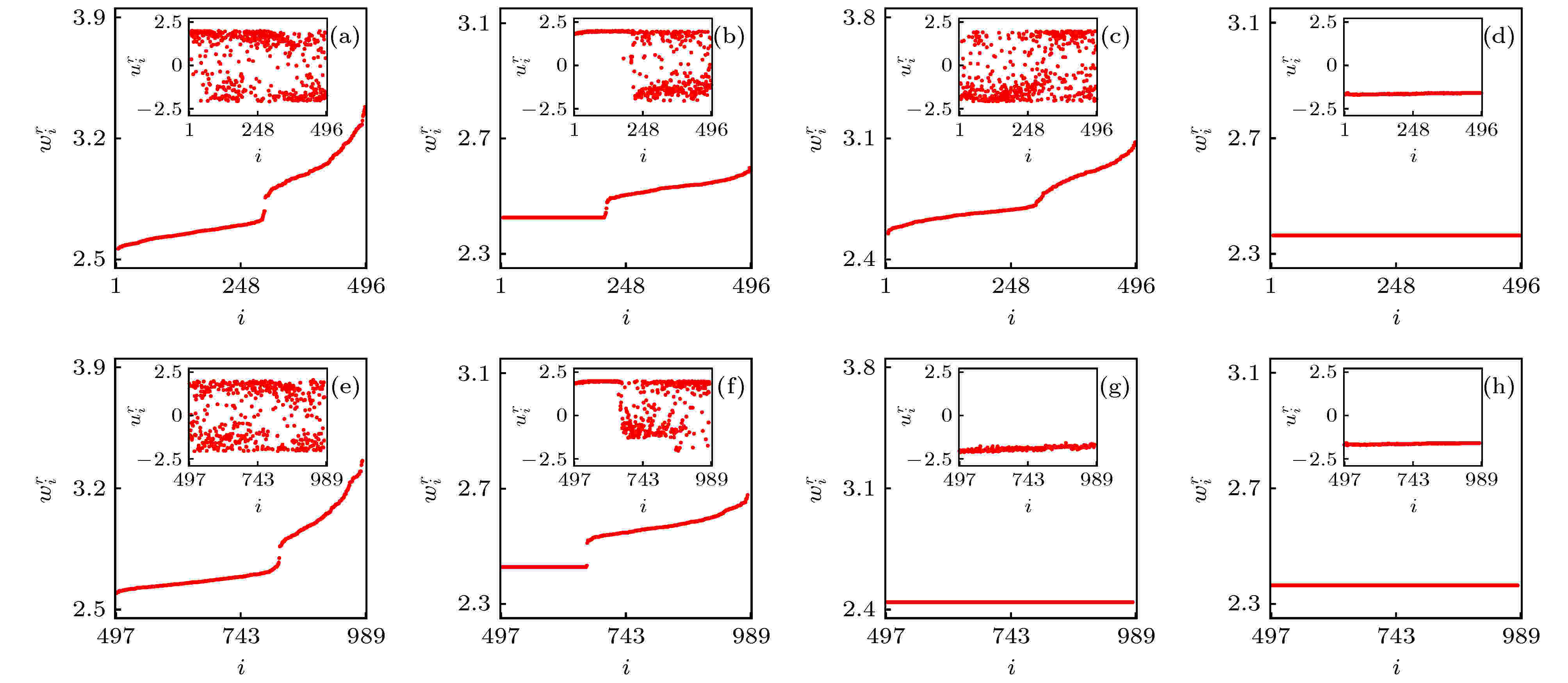 图 7 大脑皮层网中的四个典型的行为. 参数为
图 7 大脑皮层网中的四个典型的行为. 参数为













Figure7. Four typical behaviors in the cerebral cortex with














除了这些数值模拟与理论研究外, 奇异态已被数个实验证实[50-54]. 比如Martens等[52]简单地使用了两个摆座、一根弹簧和一些全同的节拍器实现了奇异态. 随着弹簧弹力系数的增大, 一个摆座上的节拍器全同步, 另一个摆座的节拍器会出现各种不同的非协同行为. 该实验无需精妙耦合计算和时间延迟, 且能容易地拓展至其他物理模型. Gambuzza等[53]则使用电路实验模拟了FHN模型的奇异态, 发现了一种静止态和同步态混合的奇异态.
遥同步是Bergner等[57]在研究星形网的相同步时引入的. 他们考虑的模型如下:




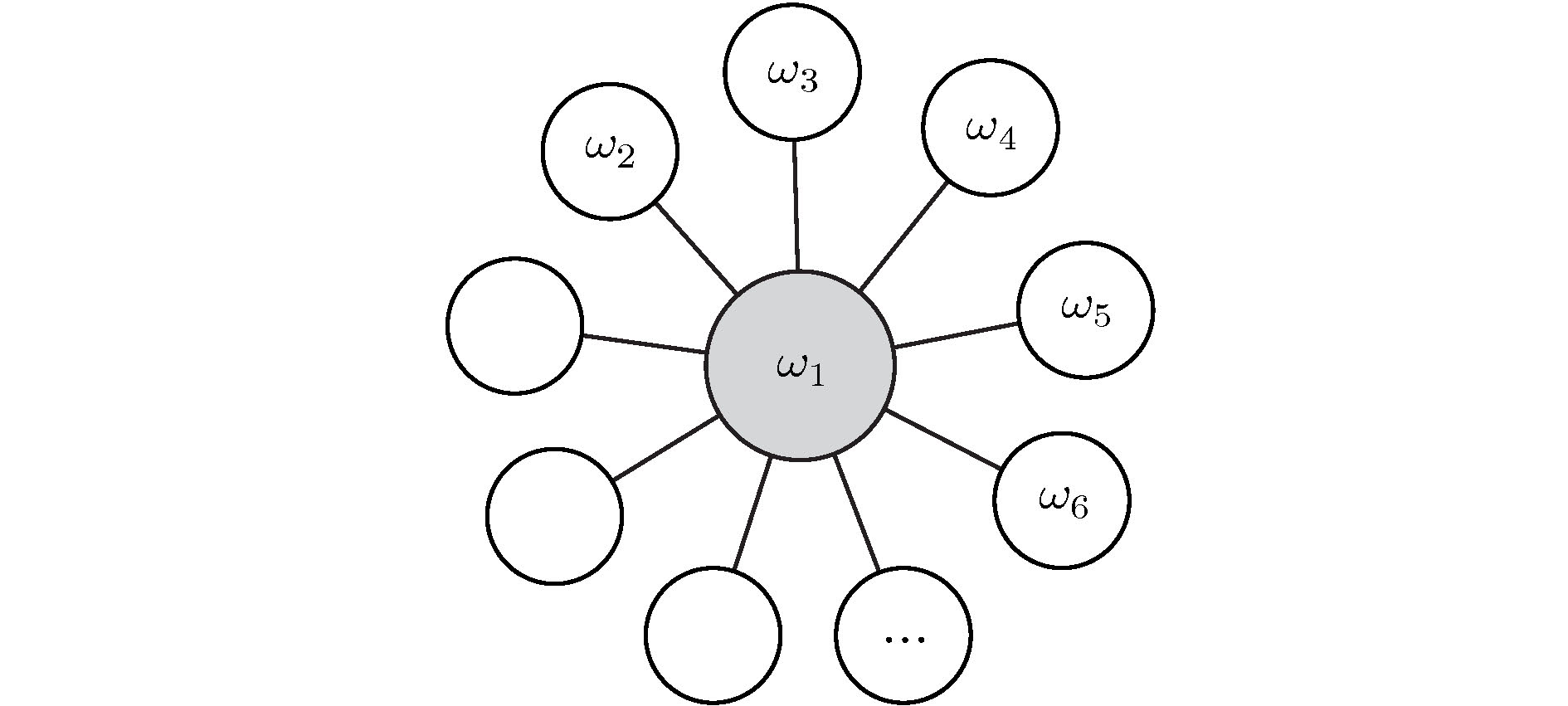 图 8 用于遥同步的星形网示意图. 改编自文献[57]
图 8 用于遥同步的星形网示意图. 改编自文献[57]Figure8. Graphic visualization of a hub network motif (star motif). Figure adapted from Ref. [57].
以








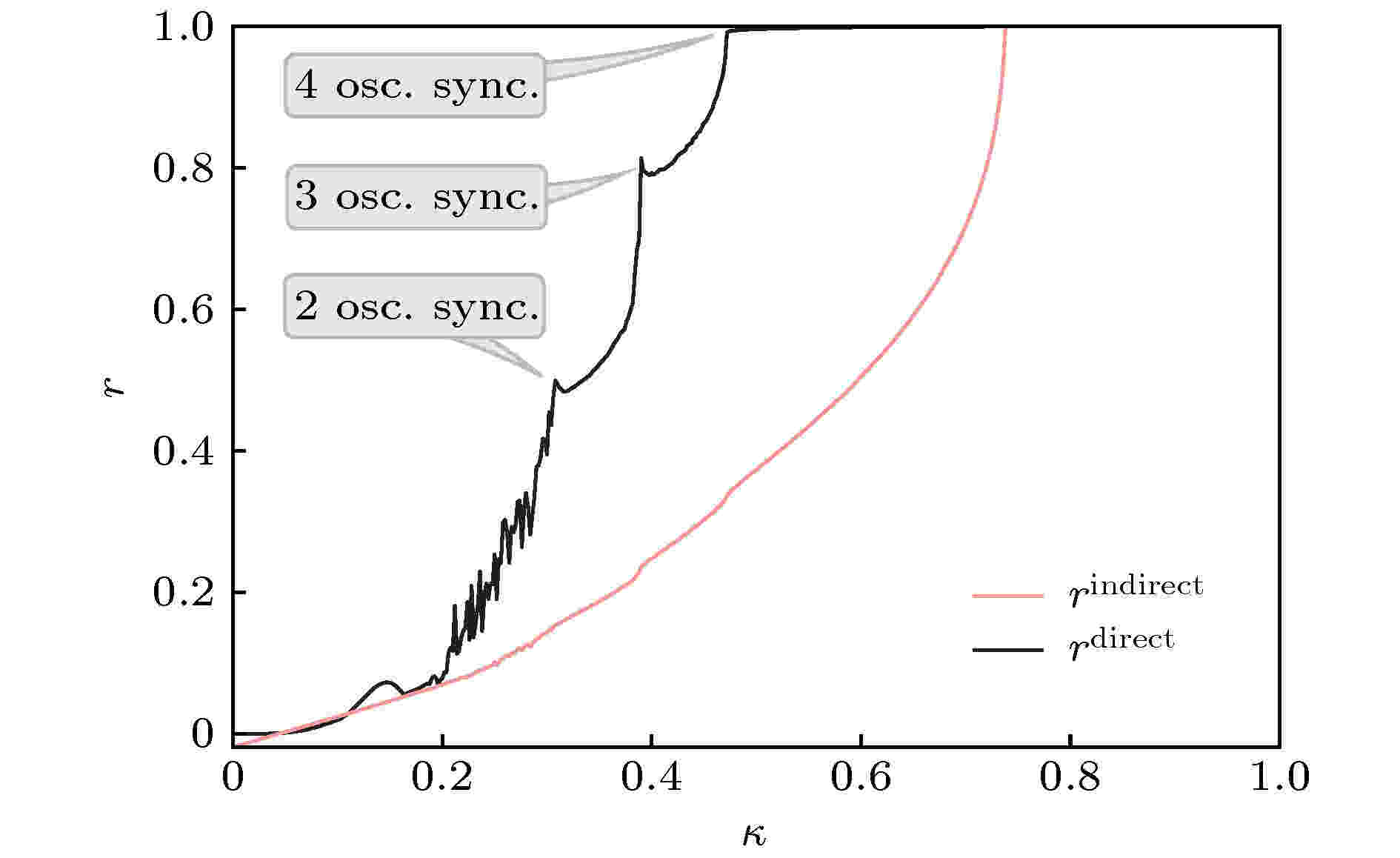 图 9 相同步的过程. 相同步的建立清晰可见, 其中的三个标注分别表明两个、三个与四个叶子节点间的同步化. 改编自文献[57]
图 9 相同步的过程. 相同步的建立清晰可见, 其中的三个标注分别表明两个、三个与四个叶子节点间的同步化. 改编自文献[57]Figure9. Transition to PS for the hub motif. From the plot the onset of RS is clearly visible. The three annotations indicate synchronization between two, three, and four peripheral oscillators, respectively. Figure adapted from Ref. [57]
为了明白遥同步的机制, Bergner等[57]将模型进一步简化为只有三个节点的情形: 两个叶子节点1与2, 由中心节点3间接连接. 为了实现节点1与2的相互同步, 节点1的活动需要传递给节点2, 反之亦然. 这就意味着节点3的动力学必须保证节点1与2的活动的传递尽可能不被改变, 为此需要满足两个条件: 首先, 为了不让中心节点与叶子节点同步, 节点3的吸引子的平均时间尺度应该与节点1与2的吸引子有很大的不同. 此外, 节点1与2的区别不应太大, 以便它们能够通过弱相互作用同步. 其次, 为了得到经过节点3的传递, 节点3的扰动必须不能衰减得太快. 将中心节点在其极限环(


叶子节点实际上是对称的, 因此Nicosia等[60]研究了网络对称性对出现遥同步的影响. 他们考虑的是带相参数的全同的Kuramoto相振子, 其相参数使得相连的振子保持特定的相差, 从而阻碍完全同步. 发现耦合网络的对称性起着重要作用, 具有相同对称性的两个节点可以同步化, 即使它们相距遥远. 这种遥同步是由网络的对称性导致的. Zhang等[61]则进一步研究了这种对称性与遥同步的关系, 将星形网的遥同步推广到了网络的情形, 称为非相干介导远程同步. 具体地, 将N个节点组织成三组

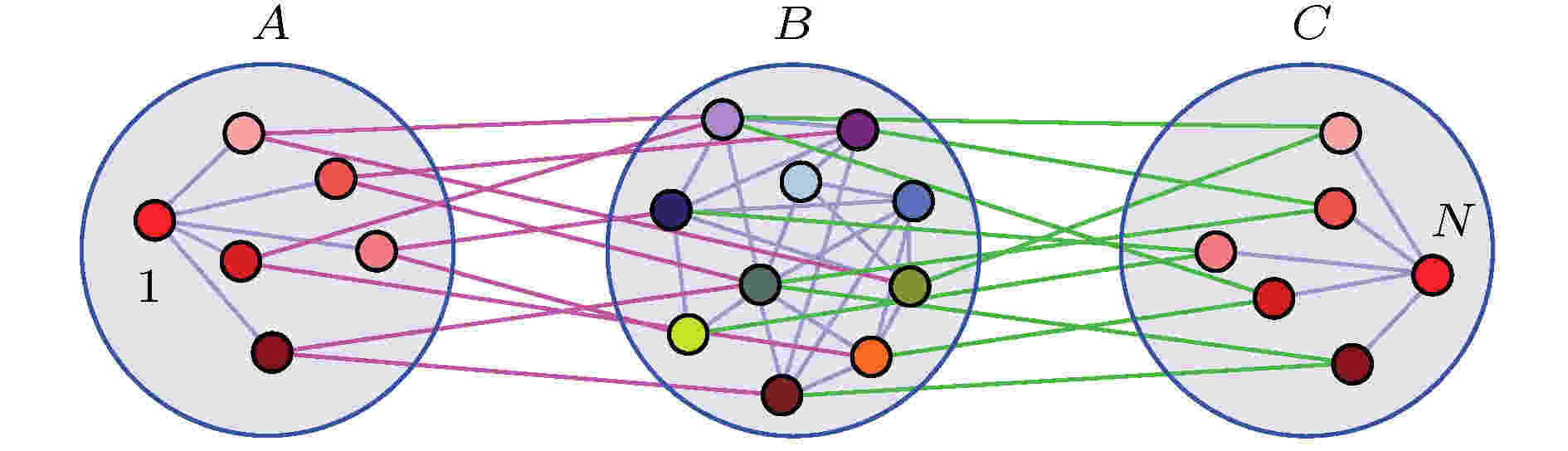 图 10 A与C组之间的遥同步同步由B组的介导来完成. 节点的颜色代表了它们的状态, 可见节点1与N是完全同步的, 而B组中节点的动力学是无关的. 改编自文献[61]
图 10 A与C组之间的遥同步同步由B组的介导来完成. 节点的颜色代表了它们的状态, 可见节点1与N是完全同步的, 而B组中节点的动力学是无关的. 改编自文献[61]Figure10. Remote synchronization between node groups A and C mediated by incoherence in group B. The colors of the nodes schematically represent their states, indicating that nodes 1 and N are identically synchronized, while the dynamics of the nodes in B are incoherent. Figure adapted from Ref. [61].
基于大脑中的遥同步现象, Kang等[62]讨论了第2节中那个真实脑皮层网络上遥同步的可能性, 发现对全同振子很难观察到遥同步. 但若考虑大脑中信号速度的有限而加进延迟时, 遥同步则成为可能. 具体地, 考虑真实脑皮层网络上每个节点为Stuart-Landau振子, 满足如下方程:










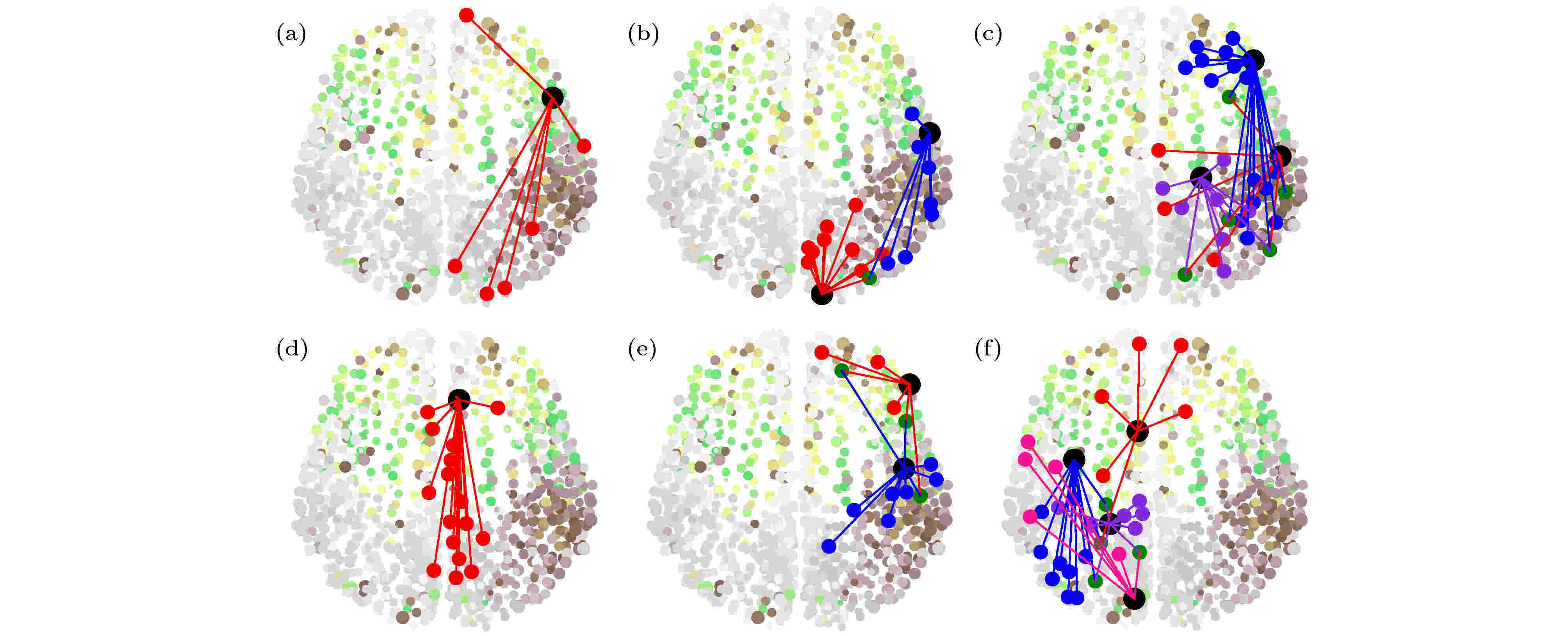 图 11 参数取
图 11 参数取

Figure11. Six typical patterns of RS for


图11的发现也不同于文献[57]中的遥同步斑图, 因此有必要进一步挖掘. 图11的第二列与第三列的一个公共特征是它们的两个中心节点是由一些公共叶子节点相连的. 由此, Kang等[62]提出了一个新的遥同步框架, 见图12, 其中红、蓝、粉红数字分别代表中心节点、叶子节点与公共叶子节点. 这个模型揭示, 当公共叶子节点的耦合强度较小时, 只能形成单个中心节点的遥同步. 但当公共叶子节点的耦合强度较大时, 两个遥同步集团可以合并成一个较大的遥同步集团, 此时那两个中心节点同步成为一个同步集团, 而所有的叶子节点成为另一个同步集团. 详情见原文, 这里不展开讨论了.
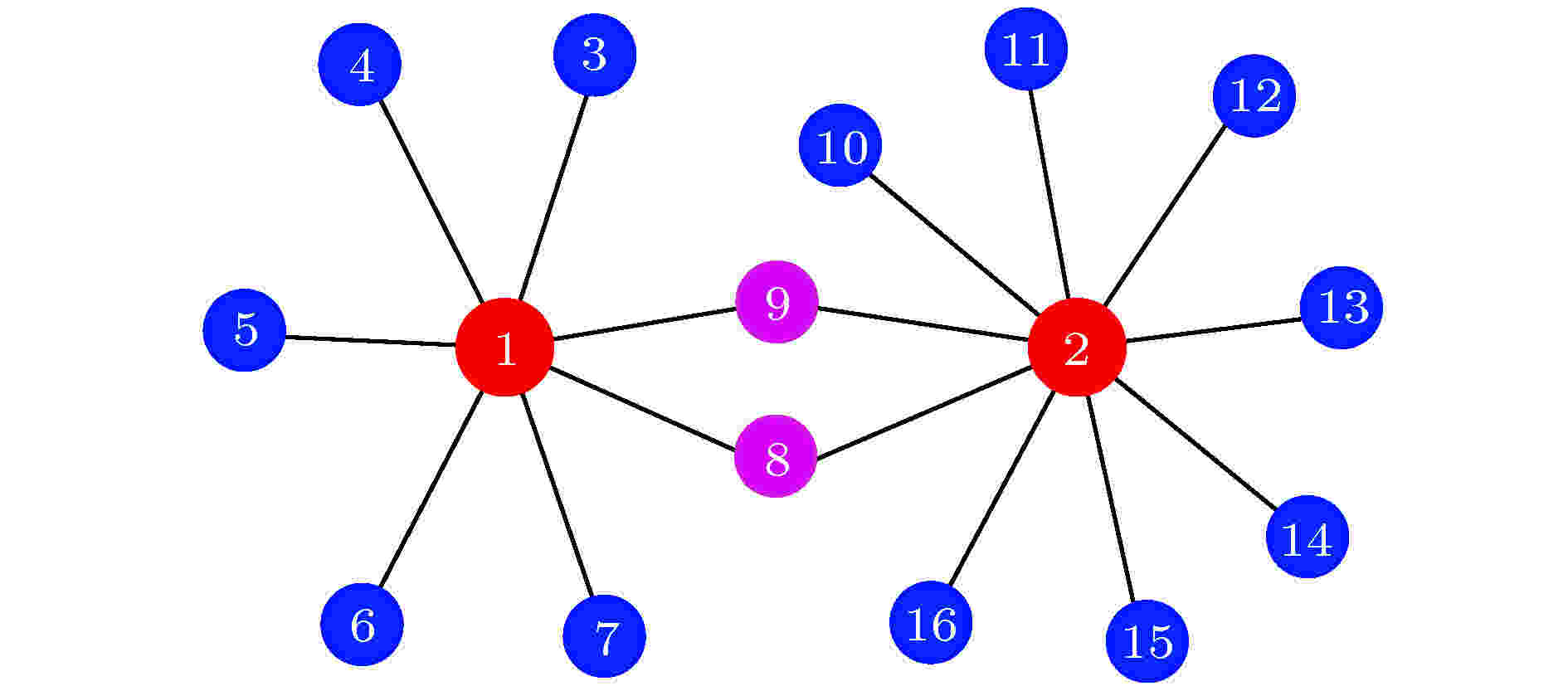 图 12 具有两个中心节点的遥同步新框架示意图, 其中红、蓝、粉红数字分别代表中心节点、叶子节点与公共叶子节点. 改编自文献[62]
图 12 具有两个中心节点的遥同步新框架示意图, 其中红、蓝、粉红数字分别代表中心节点、叶子节点与公共叶子节点. 改编自文献[62]Figure12. A schematic figure of the new framework of RS with two huns, where the nodes with red, blue and pink numbers represent the hub, leaf and common leaf nodes, respectively. Figure adapted from Ref. [62].
此外, 还有其他的一些关于遥同步的研究, 比如Gambuzza等[63]研究了多层网上的遥同步, Punetha等[64]研究了二分网上带时间延迟的遥同步, Leyva等[65]研究了多层对称网络上的遥同步等.
为了说明耦合振子网络中的对称性与集团的概念, 图13(a)展示了一个四节点网络, 其中振子是全同的、耦合是双向的[73]. 这个网络总共有六个对称. 图13(b)给出了图13(a)中交换节点1与2的一个反射, 网络结构保持不变. 图13 (c)展示了旋转



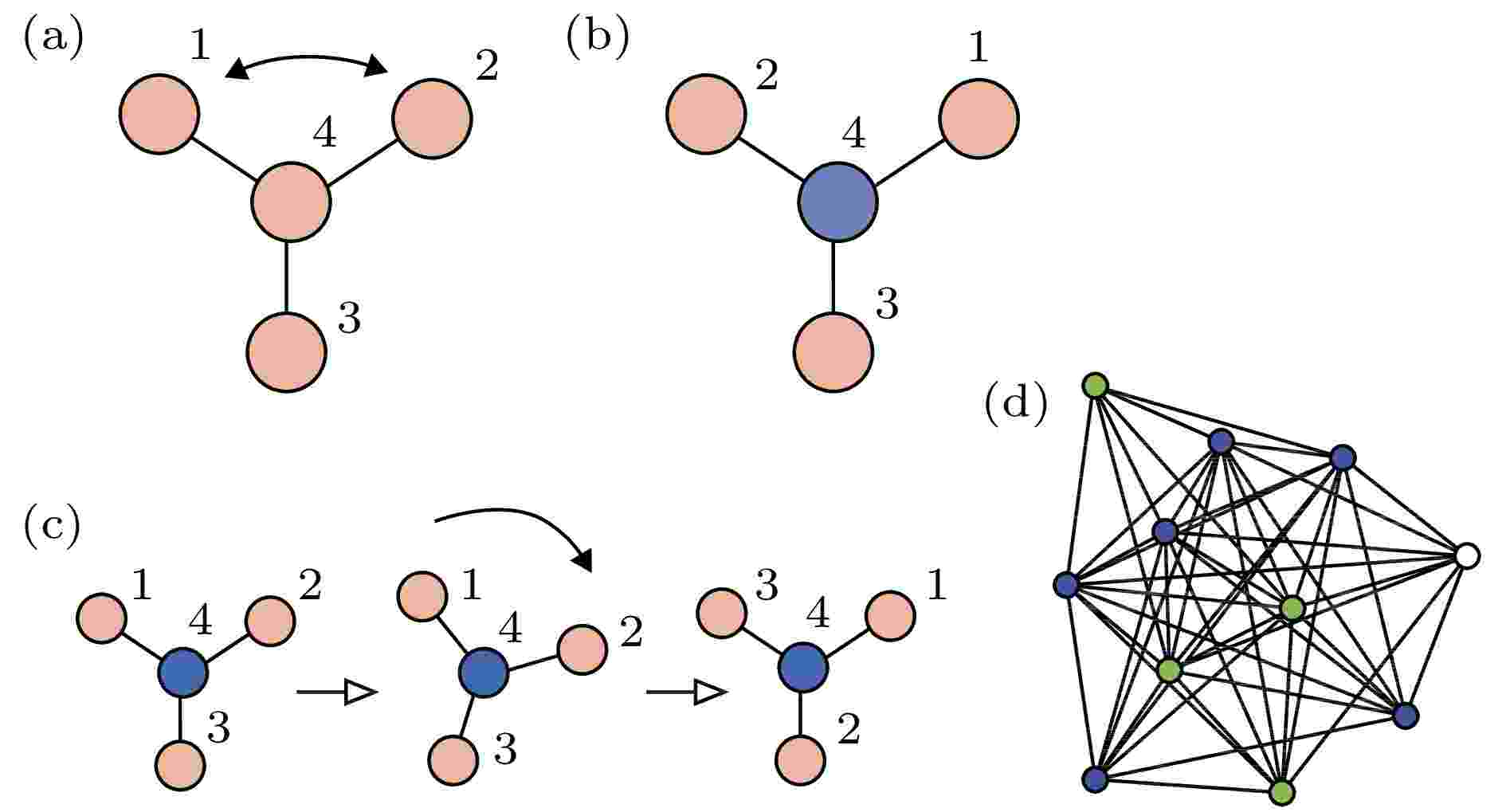 图 13 网络中对称性的例子 (a) 四个全同振子通过三根连线耦合的网络; (b) 一个反射操作后的同一网络; (c) 一个旋转操作后的同一网络; (d) 一个
图 13 网络中对称性的例子 (a) 四个全同振子通过三根连线耦合的网络; (b) 一个反射操作后的同一网络; (c) 一个旋转操作后的同一网络; (d) 一个
Figure13. Examples of symmetries in networks: (a) A network of four identical oscillators coupled through three identical links; (b) the same network after a reflection opera-tion; (c) the same network after a rotation operation; (d) an 11-node network showing three clusters (blue, green, and white). Figure adapted from Ref. [73].



在图13(a)的网络中, 节点1, 2与3有相同的运动方程, 因此如果它们从相同的初始条件出发, 就将能永久地保持同步化. 节点4不能与任何其他节点置换且也不与它们同步, 因此在图13(b)与图13(c)中将其标为不同的颜色. 这是网络中对称性与动力学间的亲密关系, 它将网络分成了两个集团1, 2, 3与4. 文献[73]讨论了对于给定的网络, 如何发现所有可能的集团同步斑图. 其主要结论是邻接矩阵的对称性对应动力学的对称性, 当它们从一个同步态出发, 可置换的节点集构成的集团就将保持同步, 即每个集团的同步态是动力学流不变的. 图14给出了所有允许的斑图, 其中属于相同集团的节点标成了同一种颜色.
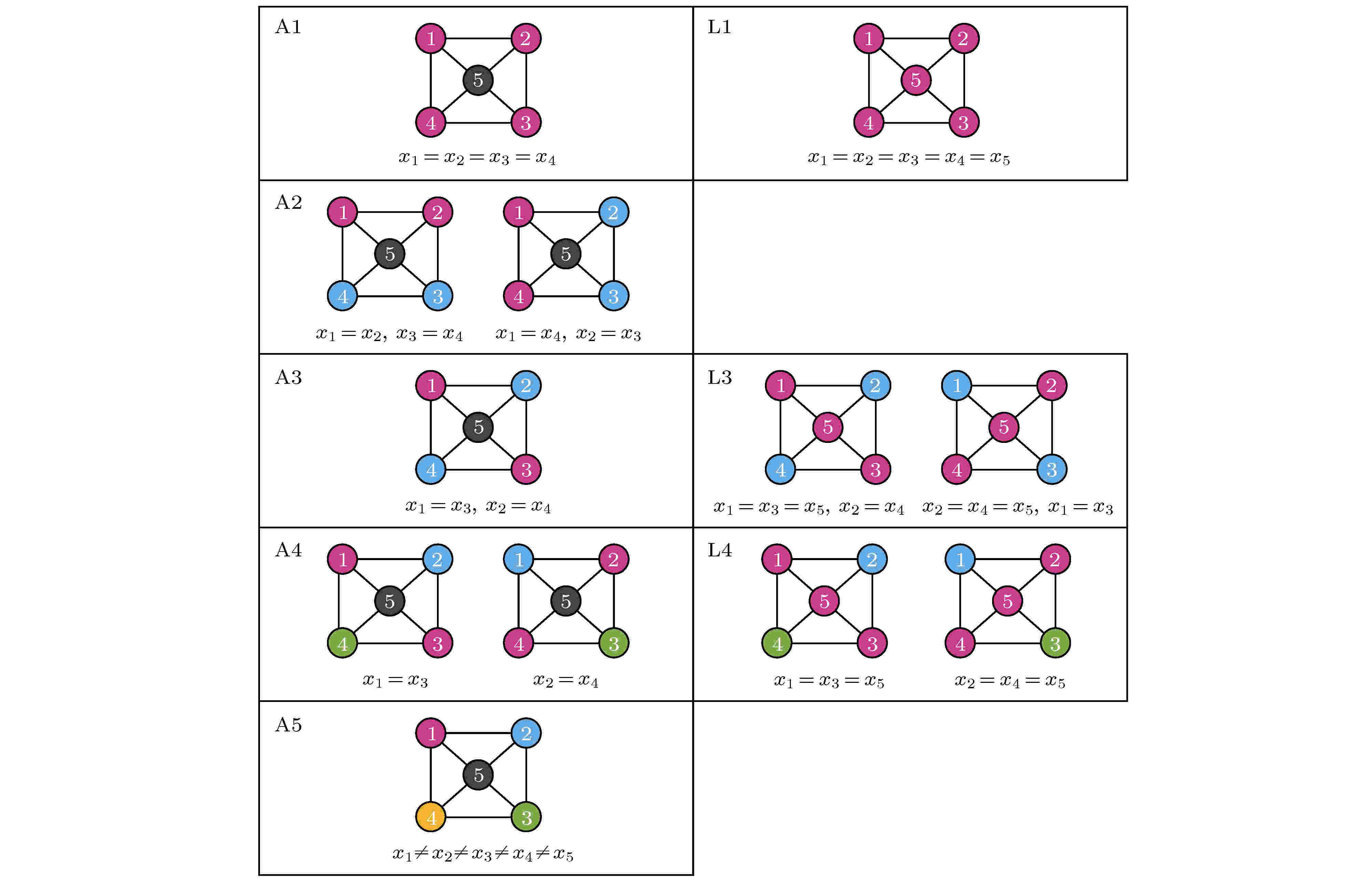 图 14 五个节点的网络中的集团斑图 左边: 当网络连接为邻接矩阵(方程(20))时所有可能的斑图; 右边: 当网络连接为拉普拉斯矩阵(方程(21))时额外的斑图. 改编自文献[73]
图 14 五个节点的网络中的集团斑图 左边: 当网络连接为邻接矩阵(方程(20))时所有可能的斑图; 右边: 当网络连接为拉普拉斯矩阵(方程(21))时额外的斑图. 改编自文献[73]Figure14. Patterns of clusters in a five-node network. Left: All possible patterns displayed when the network connectivity is given by the adjacency matrix (Eq. (20)); right: Additional patterns displayed when the network connectivity is given by the Laplacian ma-trix (Eq. (21)). Figure adapted from Ref. [73].
文献[68]指出, 基于集团的坐标变换可以更简单且更快地计算网络的对称性. 图15是关于24个节点的网络上的9个对称性集团, 其中每个集团中的节点具有相同的稳定性, 而不同的集团则稳定性不同, 且这些同步集团可唯一确定. 此外, Dahms[66]等考虑了时间延迟对全同振子网络上集体行为的影响, 发现延迟耦合确实可以诱导出不同的同步集团, 且允许集团同步的耦合矩阵在本征值谱上也显示了非常类似的对称性.
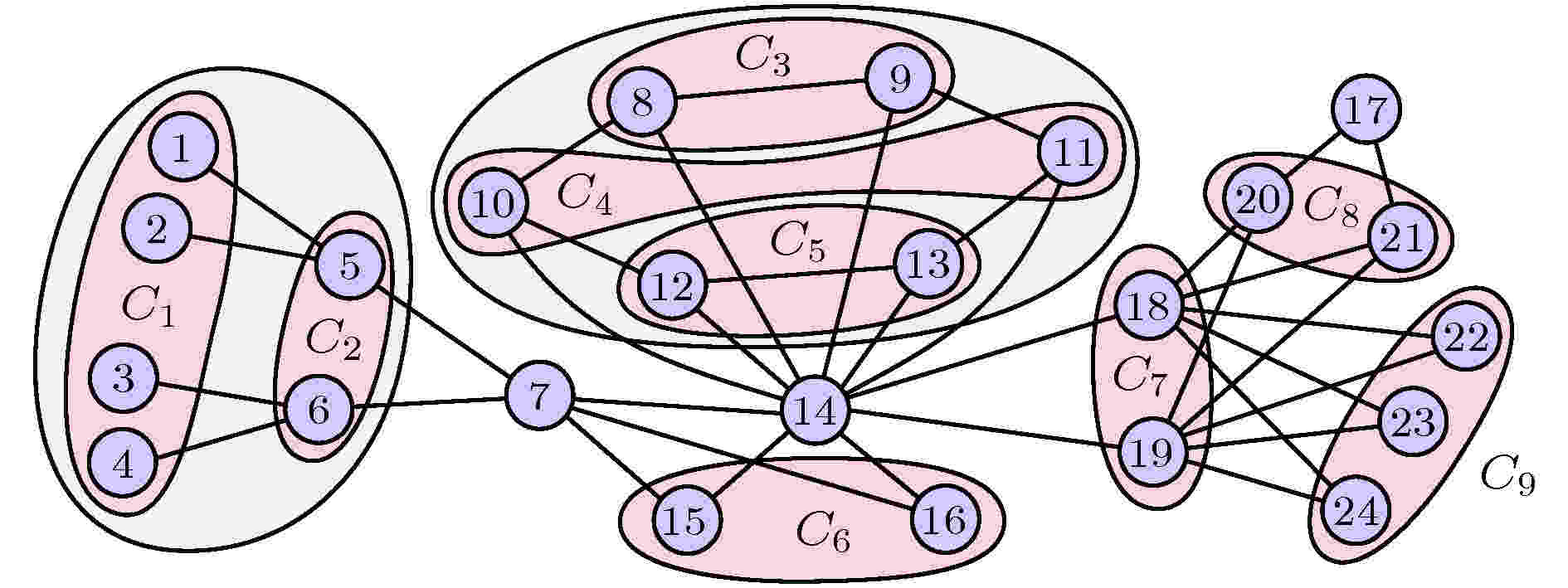 图 15 24个节点构成的网络中对称集团的分组. 改编自文献[68]
图 15 24个节点构成的网络中对称集团的分组. 改编自文献[68]Figure15. Grouping of symmetry clusters in a CS pattern for a 24-node network. Figure adapted from Ref. [68].
除了在表观形式上不相同之外, 它们三者出现的条件也不相同. 奇异态最初要求的条件是非局域耦合, 由衰减核描述. 然后这个条件推广为初始条件的不同, 但非局域耦合的要求适当放宽, 不再要求各个振子的耦合对象均有些不同, 而改为各组内个体耦合的对象完全相同, 但不同组间个体耦合的对象不相同. 再然后进一步推广为延迟系统, 此时所有个体耦合的对象可以完全相同. 遥同步主要讨论的是朗道振子系统, 本质原因是朗道振子可作为线性滤波器来传递不直接相连的节点间的耦合信息, 从而使中心节点周围的叶子节点达到同步. 遥同步最初是在星形网上进行讨论的, 现已拓展至复杂网络乃至真实的脑网络. 集团同步最初要求的是网络位置完全对称, 这就导致对称性相同的节点具有完全一样的动力学方程, 从而可达到完全同步的动力学行为. 后来这个条件推广为输入量相同即可, 因为所谓对称性保证的实际上是耦合贡献的等同.
事实上, 这三种部分同步并不是完全独立的, 而是都可看成某种局部对称性的体现. 例如奇异态中同步组内的振子实际上具有相同的对称性, 遥同步中围绕中心节点的叶子也具有完全对称的地位, 集团同步就更不用说了, 它的定义就源自对称性. 按照这个局部对称性的特点, 我们其实可以抛开直接相连或不直接相连的具体细节, 而将这三者统称为局部同步态的涌现. 在这个意义上, 就不难理解在某些系统中可以同时出现多种部分同步态. 比如图11中的遥同步振子与其他的非同步振子一起就构成了奇异态, 图12中的遥同步振子因结构对称也可当作集团同步. 同理, 对于图15中的那些同步集团中的振子, 如果它们不直接相连的话, 就是遥同步了, 比如

这三种部分同步态的研究意义就在于它们可以被很好地用来解释大脑高级功能的物理机制, 包括感知、学习与记忆等. 现在已经知道大脑神经网络具有典型的复杂网络特征, 包括度分布的异质性、小世界特征及社团结构等. 正是由于这些特征, 才保证了大脑认知活动期间广泛的斑图, 从而保障了大脑高级功能的实施. 当大脑接收到不同的信号或刺激时, 相应的动力学斑图就会被启动, 或者实现从一个斑图到另一个的转换. 具体表现就是我们观察到的对应奇异态的首晚效应、对应遥同步的分布式计算及对应集团同步的斑图多样性等.
虽然这三种部分同步的研究取得了不错的结果, 在大脑机制的阐述方面也取得了重要的进展, 但对大脑及大脑运行机制的研究依然是个长期而艰巨的任务, 还有许多开放的问题等着我们进一步研究. 下面是根据我们自己的研究经验建议的几个开放问题.
1)如何将这三种部分同步得到的现有结论充分地用于探索大脑功能的机制, 比如认知、记忆与信号传播等方面.
2)现有研究大多局限于单层网络. 由于大脑的社区结构特征, 多层复杂网络上的部分同步更值得期待. 文献[13]是这样的一个例子, 但更进一步、更深入的探讨还很缺乏.
3)如何能跳开结构层面的分析, 从更深的层面来揭示出一些更本质的东西, 比如从本征值谱分析的角度来进行分析等. 这方面的一个先期探索是关于本征模与模块化结构间的内在联系[75].
4)如何根据这三种部分同步的特征来控制各种神经疾病如帕金森氏病、癫痫、阿尔茨海默病、精神分裂症与脑肿瘤等.
5)除了这三种典型的部分同步外, 是否还存在其他的部分同步态或者根本就不能归结为部分同步但却是脑功能所必须的状态? 如果有的话, 如何去揭示它们?
我们期待部分同步化的研究在大脑神经元网络的机制与应用方面发挥越来越重要的作用. 希望本综述起到抛针引线的作用, 激励出更多、更好的工作.
