基于自归一化神经网络的脉冲星候选体选择

全文HTML

--> --> -->

1.引　言

脉冲星是一种高速自转的中子星^[1], 对其进行观测研究, 将极大推动星际介质研究^[2]、引力波探测^[3]、脉冲星导航^[4-6]等众多领域的发展. 自第一颗脉冲星被发现以来^[7], 在银河系、麦哲伦星云、球状星团中先后发现了2700多颗脉冲星^[8], 其中大部分是通过现代射电望远镜探测发现的, 例如绿岸北半球脉冲星巡天^[9](green bank north celestial cap survey, GBNCC)、Parkes多波束脉冲星巡天^[10](parkes multi-beam pulsar survey, PMPS)、高时间分辨率的宇宙脉冲星巡天^[11](high time resolution universe survey, HTRU)、低频射电(low frequency array, LOFAR)阵列巡天^[12] (LOFAR tied-array all-sky survey, LOTAAS), 这些都为脉冲星搜索奠定了基础.
脉冲星搜索首先需要检测出射电望远镜观测数据中的周期信号, 为便于分析, 一般要对这些具有周期性的观测数据进行统计描述, 以形成具有一定统计特征的脉冲星候选体^[13]. 由于受射频或噪声等因素的干扰, 这些候选体中包含着大量的非脉冲星信号, 而脉冲星信号数量却非常少^[14,15]. 为此, 需要对脉冲星候选体进行选择, 精选数据, 最后再利用射电望远镜对这些筛选后的数据进行人工分析以确定其是否为真实脉冲星^[16]. 提高候选体选择的准确率能大幅减少候选体数量, 从而极大地减轻后期的人工验证工作. 因此, 提升候选体选择性能是搜索新脉冲星的一个关键步骤.
早期的脉冲星候选体选择主要依赖人工识别, 但这是一个主观耗时且易出错的过程. 一个现代脉冲星巡天项目可以产生数百万候选体, 仅依靠人工筛选效率极低且不切实际. 因此, 近几年来, 人们的研究主要集中在机器学习方法上. Eatough等^[17]提出了第一种用于解决脉冲星候选体选择问题的机器学习方法, 该方法将每个候选体简化为一个由12个数值特征组成的集合, 然后利用一个单隐层人工神经网络(artificial neural networks, ANN)从候选体中选择脉冲星. Bates等^[18]将特征增加到22个作为ANN的输入. Zhu等^[19]提出了深度神经网络图像模式识别方法—PICS (pulsar image-based classification system). PICS 将支持向量机、人工神经网络、卷积神经网络、逻辑回归等集成结合, 采用图像模式识别的方法验证候选体的真实性. Lyon等^[20]设计了8个特征应用到高斯-黑林格快速决策树算法. Mohamed^[16]将Lyon等^[20]设计的8个特征应用到模糊k近邻分类器上. Wang等^[21]在Zhu等^[19]的基础上改进了PICS算法. 这些基于机器学习的脉冲星候选体选择方法, 有效节省了大量的人工劳动, 帮助研究人员发现了一些新的脉冲星.
如何进一步提升脉冲星候选体选择的准确率, 是机器学习方法有意义的研究点. 考虑到自归一化神经网络(self-normalizing neural networks, SNN)^[22]可以实现深层神经网络, 且通过激活函数“缩放指数线性单元(scaled exponential linear units, SELU)”引入了自归一化属性, 从而避免了深层网络在训练时出现的梯度消失和爆炸问题, 保持网络的稳定性与收敛性. 本文利用SNN构建深层网络模型以提高候选体选择的精确性. 此外, 运用遗传算法(genetic algorithm, GA)优化候选体的特征子集, 采用合成少数类过采样技术(synthetic minority over-sampling technique, SMOTE)降低不平衡率, 这些对实现高精确性的候选体选择方法具有促进作用.

2.自归一化神经网络

SNN也是由输入层、若干隐藏层及输出层组成, 每层又由多个单一神经元构成, 其中每个神经元代表一种特定的激活函数. SNN的关键就是通过激活函数SELU引进自归一化属性, 即对具有零均值与单位方差的输入变量, 通过SELU激活函数后其输出仍将收敛于零均值和单位方差. 为确保每层激活函数的输入为零均值与单位方差, 还需进行权重初始化. SELU激活函数与权重初始化是实现SNN自归一化特性的重点.
2

2.1.SELU激活函数

-->

2.1.SELU激活函数

SELU激活函数表达式为

$selu\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\lambda x,\qquad~~~~~~~~~~\, x > 0,} \\ {\lambda(\alpha {{\rm{e}}^x} - \alpha),\quad x \leqslant 0,} \end{array}} \right. $

其中$\alpha = 1.673268362 \cdots $

, $\lambda = 1.050700987 \cdots $

. 图1给出了SELU激活函数图像,可以看出该激活函数具有以下特点: 1)有用于控制平均值的负值和正值; 2)存在饱和区域(导数接近零), 以减小低层出现较大的方差; 3)部分区域斜率大于1, 如果下层方差太小则增加方差; 4)是连续的曲线, 确保存在一个不动点, 且在该点处的方差减幅会被方差增长所补偿^[22]. 这些特点使得深层神经网络在训练中都保持着方差稳定, 从而避免了梯度爆炸与梯度消失.

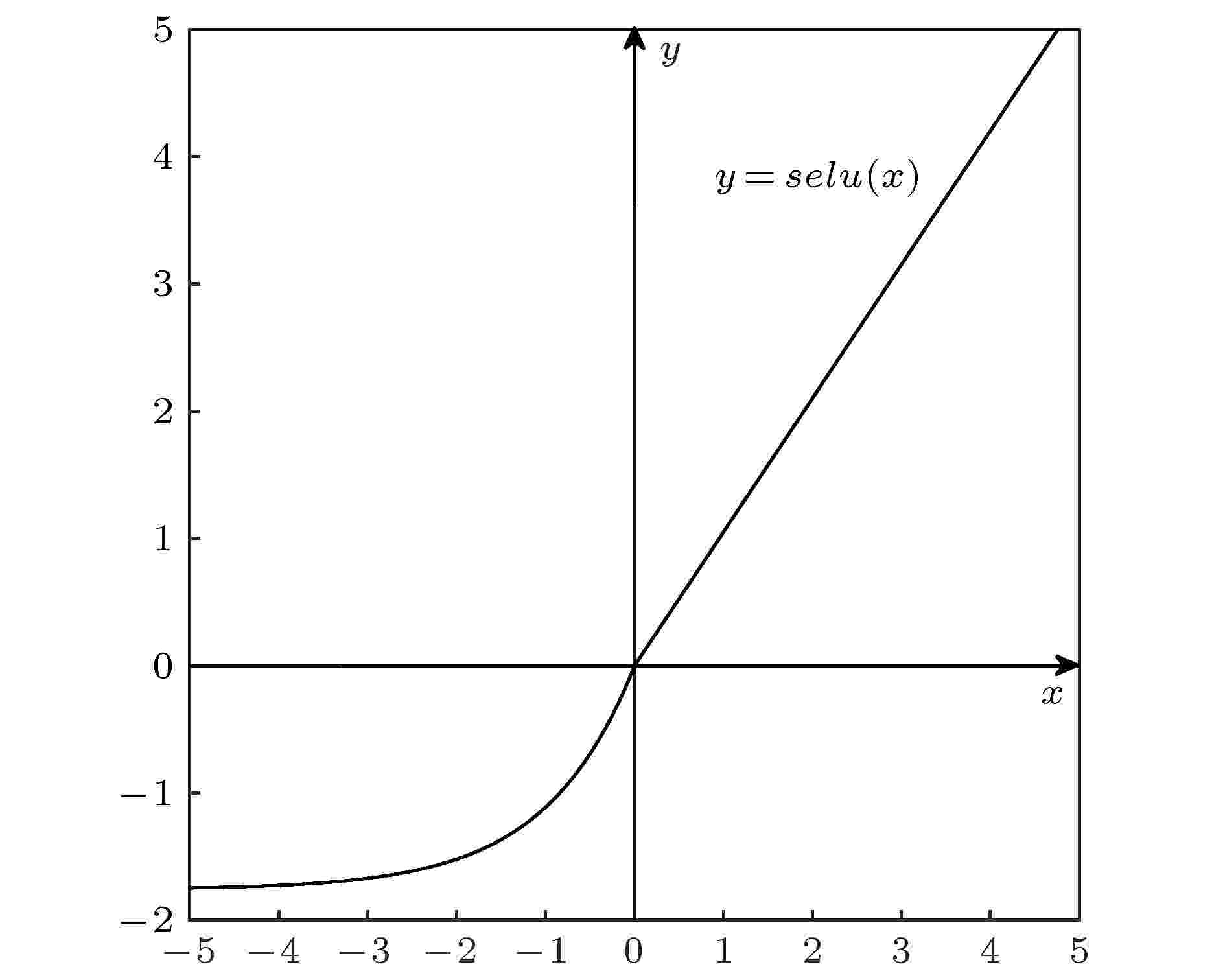图 1 SELU激活函数
Figure1. SELU activation function.

2

2.2.权重初始化

-->

2.2.权重初始化

为确保每层激活函数的输入为零均值与单位方差, 还需进行权重初始化, 对此, 可证明如下:
考虑由一个权重矩阵W连接的两个连续的网络层, 下层网络的输出是上层网络的输入. 假定下层有n个神经元且其输出变量为$\left\{ {{z_{i, {\rm{low}}}}\left| {1 \leqslant i \leqslant n} \right.} \right\}$

, 用z_low代表其向量形式, 则上层神经元的输入x_up可以表示为

${x_{{\rm{up}}}} = {{z}}_{{\rm{low}}}^{\rm{T}}w = \sum\limits_{i = 1}^n {{w_i}} {z_{i,{\rm{low}}}}, $

其中w是W的一列向量. SELU确保下层神经元输出具有零均值和单位方差, 即$\mu = E\left( {{z_{i, {\rm{low}}}}} \right) \approx 0, $

$v = {\rm Var}\left( {{z_{i, {\rm{low}}}}} \right) \approx {\rm{1}} $

. 令权重初始化为

${{\mu }_{w}}=0,~~{{\nu }_{w}}=1/n,$

用$\widetilde \mu $

和$\widetilde \nu $

分别代表x_up的均值和方差, 则有

$\tilde \mu = E\left( {{x_{{\rm{up}}}}} \right) = E\left( {{{z}}_{{\rm{low}}}^{\rm{T}}w} \right) = \sum\limits_{i = 1}^n {E[{z_{i,{\rm{low}}}}]} {w_i} \approx 0,$

$\begin{split}\; & \tilde \nu = E[{({x_{{\rm{up}}}} - \tilde \mu )^2}] = E[{x_{{\rm{up}}}}^2] \\ =& E\left[ {{\left( {z_{1,{\rm{low}}}^{\rm{T}}{w_1} + \cdots z_{i,{\rm{low}}}^{\rm{T}}{w_i} + \cdots z_{n,{\rm{low}}}^{\rm{T}}{w_n}} \right)^2}} \right],\end{split}$

其中

$\begin{split} &E[{(z_{i,{\rm{low}}}^{\rm{T}}{w_i})^2}] = {({\omega _i})^2}E[{(z_{i,{\rm{low}}}^{\rm{T}})^2}] = {({\omega _i})^2}, \\ &E[z_{i,{\rm{low}}}^{\rm{T}}z_{j,{\rm{low}}}^{\rm{T}}{\omega _i}{\omega _j}] = {\omega _i}{\omega _j}E[z_{i,{\rm{low}}}^{\rm{T}}]E[z_{j,{\rm{low}}}^{\rm{T}}] \approx {\rm{0}}.\end{split}$

所以结合(4)式可得

$\widetilde \nu = \sum\limits_{i = 1}^n {{{\left( {{w_i}} \right)}^2}} = n \cdot {\nu _w} \approx 1.$

由此可知, 权重初始化确保了激活函数输入的归一化, 是SELU实现自归一化属性的一个必要条件.

-->

3.1.GA_特征选择算法

GMO_SNN模型利用GA进行特征选择, 在原始特征空间中搜索最优特征子集. 用于特征选择的GA可以概括为三部分: 初始化种群、评估适应度、产生新种群.
初始化种群, 设定初始种群大小, 采用二进制进行基因编码, 长度为L的遗传个体编码后对应于一个L维的二进制基因串, 其中$L_i$

为1表示第i个特征包含于所选特征子集中, 否则$L_i$

为0. 例如: 有6个特征的特征集表示为$ \langle 100100\rangle $

, 则表示第1个与第4个特征被选中作为特征子集.
适应度函数的选择是GA中最关键的部分. 在特征选择问题中, 将LightGBM模型输出值作为遗传个体的适应值, 能直接反映不同特征组合对目标值的相关度, 适应值越高说明对应的特征组合越优良, 被选中的概率也越大.
产生新种群包括选择、交叉、变异, 具体采用轮盘赌算法作为选择算子, 定长基因段交叉算子, 基本位变异操作. 新的种群产生后, 通过适应度函数进行评估, 然后再选择、交叉、变异, 一直重复此步骤, 当遗传操作到达设定的最大迭代次数, 算法结束. 对末代种群中适应度值最大的个体进行解码, 就获得脉冲星候选体特征的最优子集.
2

3.2.SMOTE算法

-->

3.2.SMOTE算法

GMO_SNN模型采用SMOTE算法解决脉冲星候选体的类不平衡问题. SMOTE是一种过采样技术, 其利用K近邻与线性插值, 在距离较近的两个真实脉冲星候选体之间按照一定规则插入新的样本. 算法具体流程如下:
1)对于真实脉冲星候选体中的每一个样本r, 以欧氏距离为标准分别计算它到其他每个真实脉冲星样本的距离, 得到其K近邻, 一般K取值为5.
2)在每一个真实脉冲星样本r的5个近邻中随机选取一个样本, 假设选择近邻样本为$r_n$

.
3)对于随机选出的近邻$r_n$

, 在其与r之间按照(7)式随机线性插值, 获得合成的真实脉冲星候选体样本$\widetilde r$

$\tilde r = r + {\rm{rand}}(0,1) \times ({r_n} - r),$

其中${\rm{rand}}(0, 1)$

表示0到1之间的随机数.
2

3.3.GMO_SNN候选体选择算法

-->

3.3.GMO_SNN候选体选择算法

首先采用GA进行特征选择, 找出可以分离脉冲星与非脉冲星的最优特征子集; 然后使用SMOTE合成新的脉冲星样本加入到数据集中; 最后将数据集分为训练集与测试集, 利用训练集对SNN进行训练, 训练完成后将测试集输入到神经网络中, 得到基于GMO_SNN模型的脉冲星候选体选择结果. 具体过程如图2所示.

4.实验与结果分析

在3个独立的脉冲星候选体数据集上进行实验, 根据6个典型的机器学习评价指标评估GMO_SNN模型性能. 在搭建自归一化神经网络时, 多次实验比较不同参数下的结果, 选择最优参数以使神经网络分类效果最佳, 并在相同网络结构下与传统ANN进行对比. 另外, 还分别将GMO_SNN与SNN, GA-SNN (GA特征选择后的SNN模型), MO-SNN (SMOTE解决类不平衡问题后的SNN模型)的候选体选择结果进行对比, 进一步证明本文方法的有效性.
实验环境为Python3.6.4, 使用Numpy1.14.0, Pandas0.22.0, Sklearn0.20.1等机器学习库处理数据, 开发编译器Spyder调试算法; 利用Keras框架, 后端为Tensorflow-GPU (NVIDIA GeForce GTX 1050)搭建神经网络.
2

4.1.数据集与评价指标

-->

4.1.数据集与评价指标

3个脉冲星候选体数据集分别为HTRU 1^[25], HTRU 2^[20], LOTAAS 1^[20]. 表1列出了3个数据集的非脉冲星数、脉冲星数以及总样本数. 在数据集中, 将脉冲星视为正样本, 将非脉冲星视为负样本. 3个数据集中的候选体均采用Bates等^[18]提出的22个特征, 这些特征通过Pulsar Feature Lab^[20]提供的工具获取. 表2列出了22个特征的具体描述, 这些特征由脉冲周期P、脉冲宽度W、脉冲轮廓信噪比(signal-to-noise rate, S/N)、色散量(dispersion measure, DM)、观测频率、观测时间等处理得到^[18].

数据集	非脉冲星数	脉冲星数	总样本数
HTRU 1	89996	1196	91192
HTRU 2	16259	1639	17898
LOTAAS 1	4987	66	5053

表1脉冲星候选体数据集
Table1.Pulsar candidate datasets.

编号	特征	编号	特征
1	P	12	轮廓直方图最大值/高斯拟合的最大值
2	DM	13	对轮廓求导后的直方图与轮廓直方图的偏移量
3	S/N	14	$S/N/\sqrt {\left( {P - W} \right)/W} $
4	W	15	拟合$S/N/\sqrt {\left( {P - W} \right)/W} $
5	用sin曲线拟合脉冲轮廓的卡方值	16	DM拟合值与DM最优值取余
6	用sin²曲线拟合脉冲轮廓的卡方值	17	DM曲线拟合的卡方值
7	高斯拟合脉冲轮廓的卡方值	18	峰值处对应的所有频段值的均方根
8	高斯拟合脉冲轮廓的半高宽	19	任意两个频段线性相关度的均值
9	双高斯拟合脉冲轮廓的卡方值	20	线性相关度的和
10	双高斯拟合脉冲轮廓的平均半高宽	21	脉冲轮廓的波峰数
11	脉冲轮廓直方图对0的偏移量	22	脉冲轮廓减去均值后的面积

表2特征描述
Table2.Feature description.

在脉冲星候选体选择任务中, 使用准确率(Accuracy)、查全率(Recall)、查准率(Precision)、假阳率(false positive rate, FPR)、F1-分数(F1-score)、G-均值(G-mean)^[26]这6个评价指标对算法性能进行评估.
Accuracy表示整体正确分类的比例, 但当测试集中非脉冲星占绝大多数时, 分类器可以通过将所有样本分类为负样本来获得高准确率, 因此对于非平衡数据集仅靠准确率来评价不够科学全面, 还需要其他评价指标. Recall表示数据集中真实脉冲星候选体被正确分类的比例, 是评估脉冲星候选体选择模型一个非常重要的指标. 如果将一个真实脉冲星错误地归类为非脉冲星, 可能会漏掉脉冲星的新发现, 因此Recall越高, 分类器遗漏脉冲星的机率就越小. Precision表示被归类为正样本中实际为正样本的比例, Precision和Recall有时候会出现矛盾的情况, F1-score则同时兼顾了这两者, 定义为Precision和Recall的调和平均, 是评价分类器分类少数类的综合指标. FPR是非脉冲星被归类为真实脉冲星的比例, 当候选体选择完成之后, 会对被分类为真实脉冲星的候选体进行最终验证, 如果FPR太高, 会带来许多不必要的工作量. G-mean是正负样本准确率的比值, 衡量在非平衡数据集下模型的综合性能.
2

4.2.参数设置

-->

4.2.参数设置

GA中种群规模为20, 种群最大遗传次数为10次, 适应度函数中使用的LightGBM模型使用默认参数; 自归一化网络结构采用“conic layers”设定隐藏单元数: 即从第一层中给定的隐藏单元数开始, 根据几何级数将隐藏单元的数目减小到输出层的大小^[22]; 每个数据集使用75%的样本作为训练集, 余下作为测试集; 优化算法为“Adam”, 损失函数采用“交叉熵损失函数”. 通过实验分析, 神经网络相关参数设置如下.
1)网络层数: 选择最佳结果8层.
2)批次大小: 取32最佳.
3)学习速率: 取0.001最佳.
2

4.3.结果分析

-->

4.3.结果分析

4.3.1.网络参数的最优选择

-->

4.3.1.网络参数的最优选择

脉冲星候选体选择更加关注真实脉冲星候选体(即少数类样本)的分类准确率, 由于F1-score是评价分类器分类少数类的综合指标, 因此根据3个数据集上的平均F1-score值来确定参数, F1-score值越高, 神经网络分类效果越好.
1)网络层数的最优选择
深层次的网络结构通常会获得更好的分类效果, 但随着网络层数的增大, 网络结构也越复杂. 本文分别对隐藏层数为2, 4, 8, 9的网络进行实验, 表3列出了不同隐藏层数下的平均F1-score值. 由表3可知, 当隐藏层数为8层时效果最佳.

隐藏层数	F1-score/%
2	82.48
4	89.58
8	94.56
9	94.20

表3不同隐藏层数下的分类效果
Table3.Classification results with the different hidden layers.

2)批次大小的最优选择
为了提高神经网络的训练效率, 将训练样本分批次输入. 批次大小会对模型优化程度和训练速度产生影响. 若批训练量过小, 会增加网络训练时间; 如果批训练过大, 其分类效果会变差. 本文分别对批次大小为16, 32, 64, 128的模型进行训练, 表4列出了不同批次大小下的平均F1-score值及运行时间. 由表4可知, 随着批次减小, F1-score值在逐步上升, 但运行时间也有明显的增加. 当批次大小为16时, 其F1-score值对比批次为32时只上升了0.0031, 但其运行时间却增加了一倍. 因此综合考虑分类效果与算法运行时间, 本文神经网络的批次大小取32.

批次大小	F1-score/%	运行时间/s
16	94.87	74
32	94.56	43
64	93.90	23
128	91.05	11

表4不同批次大小下的分类效果
Table4.Classification results with the different batch size.

3) 学习速率的最优选择
学习速率是影响网络性能的一个重要参数. 过大导致损失函数振荡, 神经网络无法收敛; 过小会导致收敛速度过慢, 可能会陷入局部最优. 本文分别对学习速率为0.1, 0.01, 0.001, 0.0001时的模型进行训练, 表5列出了迭代10次后不同学习速率下的平均F1-score值. 由表5可知, 在相同的迭代次数下, 当学习速率减小时, F1-score值会降低, 模型分类效果变差. 当学习速率增大到0.1, 此时算法无法优化, 因此学习速率取值0.001最佳.

隐藏层数	F1-score/%
0.1	无法收敛
0.01	94.29
0.001	94.55
0.0001	84.10

表5不同学习速率的分类效果
Table5.Classification results with the different learning rates.

3

4.3.2.不同方法的比较

-->

4.3.2.不同方法的比较

为证明SNN的有效性, 本文对SNN与传统ANN在HTRU 2数据集上进行对比实验, 图3给出了8层神经网络训练过程中的损失函数曲线对比图, 迭代次数为100次. 损失函数是用来衡量模型预测值与真实值的不一致程度, 损失函数越小, 模型鲁棒性就越好. 由图3可知SNN模型比传统ANN具有更低的误差, 且其收敛速度明显大于ANN, 证明了SNN在深层网络中的有效性.

图 3 SNN与ANN损失函数的对比
Figure3. Comparison of the loss function between SNN and ANN.

表6分别列出了3个数据集上SNN, GA_SNN, MO_SNN, GMO_SNN的脉冲星候选体选择结果, 最优结果加粗表示.

数据集	模型	Accuracy/%	Recall/%	Precison/%	F1-score/%	FPR/%	G-mean/%
HTRU 1	SNN	99.82	92.44	93.45	92.94	0.08	96.11
	GA_SNN	99.85	92.45	95.19	93.80	0.06	96.12
	MO_SNN	99.81	94.23	97.94	96.05	0.05	97.05
	GMO_SNNNNNNNNN	99.85	95.32	98.51	96.89	0.04	97.61

HTRU 2	SNN	98.30	87.73	93.93	90.73	0.59	93.38
	GA_SNN	98.30	88.91	92.86	90.84	0.71	93.96
	MO_SNN	97.89	92.17	95.08	93.60	0.95	95.54
	GMO_SNNNNNNNNN	98.03	92.53	95.58	94.03	0.08	95.78

LOTAAS 1	SNN	99.92	93.75	100.00	96.77	0.08	96.79
	GA_SNN	99.92	100.00	93.33	96.55	0	100.00
	MO_SNN	99.69	100.00	87.10	93.10	0.31	99.84
	GMO_SNN	100.00	100.00	100.00	100.00	0	100.00

表6不同方法在3个数据集上的分类效果
Table6.Classification results with different methods on three datasets.

利用GA进行特征选择, 从候选体样本的22个特征中筛选出8个作为最优特征子集, 数据集缩减率达到63%. 以HTRU 1数据集为例, 对比表6中GA_SNN与SNN的选择结果可知, 利用最优特征子集训练分类模型, 其结果均表现出不同程度的优化, 其余两个数据集除少数几个评价指标外, 也达到了类似的效果. 表明该特征选择算法可以在压缩特征空间的同时又不丢失原有信息, 提升模型性能.
由表6中SNN与MO_SNN的评价指标可知, 利用SMOTE处理类不平衡问题后, Recall值在HTRU 1与HTRU 2数据集上分别提高了1.79和4.44个百分点, 其中LOTAAS 1数据集上Recall值达到100%, 说明该方法使分类器对非平衡学习问题具有较强的鲁棒性, 防止了分类器在训练时向丰富的非脉冲星类倾斜.
由表6可知, 在3个数据集上, 本文提出的GMO_SNN模型在Recall, Precision, F1_score, FPR以及G_mean上均优于其他模型. 例如HTRU 1数据集, 其Recall值为95.53, FPR仅有0.03, 说明该方法既能有效避免脉冲星的遗漏, 又能减少需要人工再次验证的非脉冲星候选体, 进一步证明了本文方法的有效性.
位于中国贵州省的500米口径球面射电望远镜(five-hundred-meter aperture spherical radio telescope, FAST)是目前世界上最大、最灵敏的射电天文望远镜, 其主要科学目标之一就是开展脉冲星的搜寻^[27]. FAST采用19波束接收机进行巡天, 可产生上亿量级的脉冲星候选体^[13]. 本文的候选体选择模型运用机器学习方法提高了筛选速度, 使用单个GPU每秒可以识别约2万个候选体, 同时得到高精度的选择结果. 这种速度和效率的提高能促进对FAST巡天产生的脉冲星候选体数据的实时处理, 可减小大数据量带来的筛选难度.

5.结　论

基于自归一化神经网络的脉冲星候选体选择是一种能高准确率识别真实脉冲星的有效方法. 利用GA进行特征选择, 能在压缩特征空间的同时又不丢失原有信息, 提升模型性能; 使用SMOTE处理非平衡数据集, 可降低数据集的不平衡率, 提高了分类器对少数类样本的识别能力; 采用自归一化神经网络比传统人工神经网络在深层结构中具有更高的准确率以及更快的收敛速度. 在3个脉冲星候选体数据集上的实验结果表明, 该方法既能有效避免真实脉冲星的遗漏, 又能减少非脉冲星的保留, 从而提高脉冲星搜寻的工作效率.

本站小编 Free考研考试/2021-12-29

English Abstract

Pulsar candidate selection based on self-normalizing neural networks

Corresponding author:Kang Zhi-Wei, jt_zwkang@hnu.edu.cn

全文HTML

2.1.SELU激活函数

2.2.权重初始化

3.1.GA_特征选择算法

3.2.SMOTE算法

3.3.GMO_SNN候选体选择算法

4.1.数据集与评价指标

4.2.参数设置

4.3.结果分析

4.3.1.网络参数的最优选择

4.3.2.不同方法的比较

相关话题/数据 网络 实验 优化 遗传

领限时大额优惠券,享本站正版考研考试资料!

东方超环上低杂波驱动等离子体环向旋转实验研究

热光伏能量转换器件的热力学极限与优化性能预测

肖特基钙钛矿太阳电池结构设计与优化

动态复杂网络中节点影响力的研究进展

高效外腔倍频产生426 nm激光的实验研究

快凝Pd<sub>82</sub>Si<sub>18</sub>合金原子团簇的演化特性及遗传机制

腔光子-自旋波量子耦合系统中各向异性奇异点的实验研究

粉末颗粒气力加注特性实验研究

上海光源硬X射线相干衍射成像实验方法初探

一类任意<i>m</i>×<i>n</i>阶矩形网络的电特性