摘要: 受不可逆损失的影响, 热光伏能量转换器件在高品位热能回收与利用方面受到限制. 本文揭示不可逆损失来源, 提供热光伏能量转换器件性能提升方案. 利用半导体物理和普朗克热辐射理论, 确定热光伏能量转换器件在理想条件下的最大效率. 进而考虑Auger与Shockley-Reed-Hall非辐射复合和不可逆传热损失对光伏电池的电学、光学和热学特性的影响, 预测热光伏器件优化性能. 确定功率密度、效率和光子截止能量的优化区间. 结果表明: 相比于理想热光伏器件, 非理想热光伏器件的开路电压、短路电流密度和效率有所降低; 优化热光伏电池电压、光子截止能量和热源温度, 可提升器件的功率密度和效率. 通过对比发现理论与实验结果较一致, 所得结果可为实际热光伏能量转换器件的研制提供理论指导.
关键词: 热光伏 /
细致平衡 /
热力学极限 /
非辐射复合 /
优化性能 English Abstract Thermodynamic limit and optimal performance prediction of thermophotovoltaic energy conversion devices Liao Tian-Jun Lü Yi-Xiang Department of Physics and Energy, Chongqing University of Technology, Chongqing 400054, China Received Date: 04 December 2019Accepted Date: 17 December 2019Published Online: 05 March 2020Abstract: The application of thermophotovoltaic energy conversion device to recovery and utilization of high-grade thermal energy are limited by its irreversible loss. In this work, we reveal the source of irreversible loss and provide a strategy for improving the performance of thermophotovoltaic energy conversion device. The maximum efficiency of thermophotovoltaic energy conversion device under ideal condition is determined by using the theory of semiconductor physics and Planck thermal radiation. Moreover, the effects of non-radiative recombination and irreversible heat transfer loss on the electrical, optical, and thermal characteristics of thermophotovoltaic device are considered to predict the optimal performance of thermophotovoltaic device. The optimal region of power density, efficiency, and photon cut-off energy are determined. The obtained results show that the open-circuit voltage, short-circuit current density and efficiency of non-ideal device are lower than those of ideal device. The voltage output and photon cut-off energy of thermophotovoltaic device and heat source temperature can be optimized to improve the power density and efficiency of the device. It is found that the theoretical results are in good agreement with the experimental results, which can provide some guidances fordeveloping the practical thermophotovoltaic devices.Keywords: thermophotovoltaic /detailed balance /thermodynamic limit /non-radiative recombination /optimal design 全文HTML --> --> --> 1.引 言 热光伏(TPV)是将高品位热能转化为电能的固态能源器件, 在高温燃料电池废热、工业余热、同位素衰变热、太阳能的开发与利用方面具有潜在应用[1 -6 ] . TPV主要由高温热源、热发射器、光学滤波器、光伏电池、散热系统和外部负载组成, 具有能量密度高、效率高、可移植等特点, 它的工作原理是: 高品位热源驱动热发射器辐射红外光子流, 然后被光伏电池吸收而产生电子-空穴对, 当光伏电池外接负载, 导带中的电子通过负载回到价带, 构成回路, 从而实现从热能到电能的转换[7 ,8 ] . TPV相关研究涉及半导体物理、材料科学、光学、热力学等多学科理论, 国内外****致力于通过禁带宽度的优化[7 ] 、器件的结构设计[2 ,9 ] 、辐射光谱的控制[10 ] 、热辐射的增强[11 -13 ] , 以提升TPV的性能, 从而实现热能的高效利用. 另外, TPV还可以与热辐射器件[14 ] 、热离子器件[15 -18 ] 和半导体温差热电器件[19 ] 组成耦合能量转换器件, 以提高热电转换效率.2.TPV器件的热力学极限 TPV主要由热发射器、真空间隙、光伏电池、热源和负载组成, 如图1 所示. 热发射器温度为${T_{\rm{E}}}$ , 光伏电池温度为${T_{\rm{P}}}$ , 假设光伏电池由热管理系统进行温度控制, 可认为光伏电池的温度与环境温度近似相等. 当热源持续驱动热发射器辐射红外光子流, 光伏电池将持续输出电能. 由于热发射器工作环境(与高温热源直接接触)的特殊性, 它的材质应具备耐高温的特性, 因此可以采用耐高温材料构成热发射器, 如金属钨、六方氮化硼、光子晶体材料等. 另外, 从热发射器激发的是能量为0.2—0.7 eV的光子, 而传统的半导体硅材料的带隙为1.12 eV, 硅基光伏电池无法用于TPV器件的研制, 因此, 采用Ⅲ-Ⅴ族复合半导体材料构成光伏电池. 目前比较广泛应用的有InAs (带隙为0.36 eV)、InSb (带隙为0.17 eV)、Inx 1–x Asy 1–y (带隙为0.20—0.70 eV)、GaSb (带隙为0.726 eV)等[7 ,20 ] . 本文的TPV器件模型的建立是基于半导体材料InAs, 因为该材料不仅具有较高的开路电压, 而且对红外光子具有较高的吸收效率.图 1 TPV器件的示意图Figure1. Schematic diagram of a TPV device.$\dot E$ 和光子流密度$\dot N$ 为[7 ,14 ,21 ] :$h = 6.626 \times {10^{ - 34}}\, {\rm{J}} \cdot {\rm{s}}$ 为普朗克常数, $c = 3 \times $ ${10^8}\;{\rm{m}} \cdot {{\rm{s}}^{ - 1}}$ 为真空中的光速, ${k_{\rm{B}}} = 1.38 \times {10^{ - 23}}\;{\rm{J}} \cdot {{\rm{K}}^{ - 1}}$ 为玻尔兹曼常数, ε 是光子的能量, μ 为光子的电化学势.Q 和光伏电池的电流密度J 可表示为[7 ,14 ,21 ] :$e = 1.6 \times {10^{ - 19}}\;{\rm{C}}$ 表示一个单位正电荷的电量; V 是光伏电池输出电压; $\Delta {\varepsilon _{\rm{F}}}$ 为电子和空穴的准费米能级之差, $\Delta {\varepsilon _{\rm{F}}} = \mu = eV$ . 基于以上讨论, TPV的功率密度P 和效率η 可表示为:1 )式—(6 )式, 可绘制给定3个不同热发射器温度${T_{\rm{E}}}$ 时, 效率η 随输出电压V 变化曲线, 如图2 所示, 其中, ${T_{\rm{P}}} = 300\, {\rm{K}}$ , ${\varepsilon _{\rm{g}}} = 0.36\, {\rm{eV}}$ , ${V_{{\rm{oc}}}}$ 为开路电压. 从图2 看出给定热发射器温度${T_{\rm{E}}}$ , 可优化输出电压V 获得最大效率${\eta _{{\rm{max}}}}$ . 图2 显示最大效率${\eta _{{\rm{max}}}}$ 小于卡诺效率${\eta _{{\rm{Carnot}}}}$ , 热发射器温度${T_{\rm{E}}}$ 越高, 则器件的最大效率${\eta _{{\rm{max}}}}$ 越大. 图2 还显示当电压V 处于一定区间, 增加热发射器温度${T_{\rm{E}}}$ , 效率η 反而降低, 这是由光伏器件内部热损失增加导致的. 因此, 在增加高温热源温度时, 如何降低不可逆热损失, 提高能量转换效率, 以及获得器件优化性能尤为关键, 下一部分将讨论非理想TPV器件优化性能的预测.图 2 效率η 随输出电压V 变化曲线Figure2. The curves of the efficiency η varying with the voltage V for given three values ${T_{\rm{E}}}$ .3.非理想TPV器件的优化性能 在上述讨论TPV的热力学极限时, 假设光伏电池的吸收效率为1, 并忽略了非辐射复合损失的影响. 本部分将分析非理想状态下TPV器件的优化性能. 当热光伏电池存在非辐射复合损失时, 需要修正(4 )式, 即[10 ] $R_{\rm{Rad}}$ , $R_{\rm{Srh}}$ 和$R_{\rm{Aug}}$ 分别为辐射复合率、Shockley-Reed-Hall (SRH)非辐射复合率和Auger (Aug)非辐射复合率. 光伏电池吸收的光子流$\dot N$ 为$A\left( \varepsilon \right) = 1 - \exp \left[ { - \alpha \left( \varepsilon \right)L} \right]$ 为光伏电池的吸收效率, $\alpha \left( \varepsilon \right)$ 为光伏电池的吸收系数, L 是光伏材料的厚度. 辐射复合率$R_{\rm{Rad}}$ 可表示为${R_{{\rm{Srh}}}}$ 由(10 )式决定[10 ] :${\tau _{{\rm{Srh}}}}$ 表示SRH复合寿命, ${n_{\rm{i}}}$ 是本征载流子浓度. 在300 K时SRH复合寿命${\tau _{{\rm{Srh}}}}$ 取$100 \; {\rm{ns}}$ , 本征载流子浓度${n_{\rm{i}}}$ 取${\rm{6}}.{\rm{06}} \times {\rm{1}}{{\rm{0}}^{14}}{\rm{ c}}{{\rm{m}}^{ - {\rm{3}}}}$ , Auger复合率$R_{\rm{Aug}}$ 由(11 )式决定[10 ] :${C_{\rm{n}}} + {C_{\rm{p}}} = 2.26 \times {\rm{1}}{0^{ - {\rm{27}}}}\, {\rm{c}}{{\rm{m}}^6} \cdot {{\rm{s}}^{ - 1}}$ [22 ] , ${C_{\rm{n}}}$ 与${C_{\rm{p}}}$ 分别是电子和空穴的Auger复合系数. 热发射器与光伏电池之间的辐射热流Q 为5 )式和(6 )式修正为:${T_{\rm{P}}} = 300\; {\rm{K}}$ , $L = 1\, \;{\text{μ}}{\rm{m}}$ , 令(7 )式$J = 0$ , 通过数值求解, 可获得非理想光伏电池开路电压${V_{{\rm{oc}}}}$ 与温度${T_{\rm{E}}}$ 之间的依赖关系, 如图3(a) 所示; 令(7 )式$V = 0$ , 可获得非理想光伏电池短路电流密度${J_{{\rm{sc}}}}$ 与温度${T_{\rm{E}}}$ 之间的依赖关系, 如图3(b) 所示. 令(4 )式$J = 0$ , 可绘制理想光伏电池开路电压${V_{{\rm{oc}}}}$ 随${T_{\rm{E}}}$ 变化曲线, 如图3(a) 所示. 令(4 )式$V = 0$ , 可绘制理想光伏电池短路电流密度${J_{{\rm{sc}}}}$ 随${T_{\rm{E}}}$ 变化曲线, 如图3(b) 所示. 图3 显示${V_{{\rm{oc}}}}$ 和${J_{{\rm{sc}}}}$ 两者均随${T_{\rm{E}}}$ 的升高而增加, 表明适当提高热发射器温度可提高TPV性能, 但在实际设计器件时, 需要考虑${T_{\rm{E}}}$ 过高会带来的热损耗: 从热力学角度说, 过高的${T_{\rm{E}}}$ 会不可避免地导致光伏电池的工作温度上升, 光伏电池在过高的温度下无法正常工作甚至损坏, 影响使用寿命, 因此应在合适的温度区间进行优化. 在整个曲线中, 对于相同的${T_{\rm{E}}}$ , 理想状态下的开路电压和短路电流高于非理想状态下的两个参数值, 由此可见考虑非理想状态下的非辐射复合损失对光伏电池性能的影响是非常有必要的. 从图3(a) 看出随着${T_{\rm{E}}}$ 的上升, 两个情况下${V_{{\rm{oc}}}}$ 的增加速率与差值均会下降. 从图3(b) 看出随着${T_{\rm{E}}}$ 的升高, 两个情况下${J_{{\rm{sc}}}}$ 的增加速率与差值均会上升. 从图3 的开路电压和短路电流可判断TPV是一个电流密度较大而工作电压较小的能量转换器件, 单个电池驱动负载的能力较弱, 在实际设计时, 器件尺寸尽可能小型化, 以减小输出电流和提高驱动负载能力. 若选用禁带宽度较大的III-V半导体材料, 如GaSb (0.726 eV)制造光伏电池, 可增加电池的电压输出, 然而, 从(3 )式可知禁带宽度的增加, 被电池吸收的辐射能量随之减小, 光伏电池的电能输出和效率也可能下降. 若选用禁带宽度较小的III-V半导体材料, 如InSb (0.17 eV)制造光伏电池, 可增加电池对辐射能量的吸收, 然而光伏电池的电压下降, 电流密度增加, 器件的驱动负载能力较弱. 由此可见, 半导体材料的选择对于TPV系统的设计至关重要, 在给定高温热源温度时, 可通过材料的优化选取, 获得优化性能特性.图 3 非理想和理想光伏电池特性随${T_{\rm{E}}}$ 变化的关系曲线 (a)开路电压; (b)短路电流密度Figure3. The curves of non-ideal and ideal photovoltaic cells varying with ${T_{\rm{E}}}$ : (a) open-circuit voltages; (b) short-circuit current densities.P 随热发射器温度${T_{\rm{E}}}$ 和输出电压变化的三维曲面图, 如图4(a) 所示. 给定电压V , P 随着${T_{\rm{E}}}$ 的升高而增加, 而给定热发射器温度${T_{\rm{E}}}$ 时, P 随着V 的变化呈先增加后减小趋势, 可获得局域最大功率密度, 这是由光伏电池的伏安特性所决定的. TPV的效率η 随热发射器温度和输出电压变化的三维曲面图, 如图4(b) 所示. η 均不是V 和${T_{\rm{E}}}$ 的单调函数, 可获得最大热电能量转换效率${\eta _{\max }} = 0.288$ 及相应的优化运行条件${V_{\eta} } = 0.22\, {\rm{V}}$ 和${T_{{\rm{E}}, \eta }} = 2037\, {\rm{K}}$ . 热源温度的升高使光伏电池的功率密度有一定提升, 同时也导致光伏电池内部热损耗的增加, 因此, 当${T_{\rm{E}}} > {T_{{\rm{E}}, \eta }}$ 时, 效率η 随${T_{\rm{E}}}$ 的增加而减小. 利用${V_{\eta} }$ 和${T_{{\rm{E}}, \eta }}$ 值, 可确定在最大效率时的优化电流密度${J_{\eta} } = 65.2\, \, {\rm{A}} \cdot {\rm{c}}{{\rm{m}}^{ - {\rm{2}}}}$ , 优化短路电流密度${J_{{\rm{sc}}, \eta }} = 74.9\, \, {\rm{A}} \cdot {\rm{c}}{{\rm{m}}^{ - {\rm{2}}}}$ , 优化开路电压${V_{{\rm{oc}}, \eta }} = 0.272\, \, {\rm{V}}$ . 根据${V_{\eta} }$ , ${J_{\eta} }$ , ${J_{{\rm{sc}}, \eta }}$ 和${V_{{\rm{oc}}, \eta }}$ , 可定义一个填充因子${\rm{FF }}= {{\left( {{V_{\eta} }{J_{\eta} }} \right)} / {\left( {{V_{{\rm{oc}}, \eta }}{J_{{\rm{sc}}, \eta }}} \right)}}= {\rm{ 0}}.{\rm{704}}$ 表征TPV性能的高低, FF值越靠近于1, TPV性能越高. 另外, 需要指出的是如果热发射器在高温下运行时, 其物理特性如热发射率需要具有较高的稳定性, 对材料的耐高温特性要求较高, 同时系统向环境释放的热漏也增加, 以及光伏电池使用寿命也受影响, 因此, 热发射器温度应处于${T_{\rm{E}}} \leqslant 2037\;{\rm{ K}}$ . 在上述区域, 可将TPV用于核能、聚光太阳能、工业余热的回收与利用. 考虑非辐射复合损失以后, 系统的转换效率显著下降, 与卡诺效率具有较大差异, 因此, 探索降低不可逆损失的途径, 对TPV器件性能的提升是有益的.图 4 (a)功率密度和(b)效率随${T_{\rm{E}}}$ 和V 变化三维曲面图Figure4. (a) The 3D graphs of power density and (b) efficiency as a function of ${T_{\rm{E}}}$ and V .10 ]中半导体In0.53 Ga0.47 As材料的禁带宽度${\varepsilon _{\rm{g}}}$ 为0.60 eV, 在${T_{\rm{E}}} = 1500\;{\rm{ K}}$ 和${T_{\rm{P}}} = 300\;{\rm{ K}}$ 时, 最大功率密度和最大效率分别为${\rm{2}}.{\rm{1}}\, \, {\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - {\rm{2}}}}$ 和50%. 基于该文献相关参数, 利用本文的模型进行数值模拟, 可计算出最大功率密度和最大效率分别为${\rm{2}}.{\rm{15}}\, {\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - {\rm{2}}}}$ 和59%. 另外, 文献[23 ]中半导体材料GaSb的禁带宽度${\varepsilon _{\rm{g}}}$ 为0.726 eV, 在${T_{\rm{E}}} = $ 1500 K和${T_{\rm{P}}} = 300\;{\rm{ K}}$ 时, 开路电压、短路电流和最大效率分别为${\rm{0}}.{\rm{349}}\, {\rm{V}}$ 、${\rm{3}}.{\rm{08}}\, \, {\rm{A}} \cdot {\rm{c}}{{\rm{m}}^{ - {\rm{2}}}}$ 和20.1%. 利用本文模型进行数值模拟, 可得开路电压、短路电流密度和最大效率分别为${\rm{0}}.{\rm{389}}\, {\rm{V}}$ 、${\rm{3}}.{\rm{53}}\, {\rm{A}} \cdot {\rm{c}}{{\rm{m}}^{ - {\rm{2}}}}$ 和26.4%. 由此看出, 需要进一步完善TPV器件物理模型, 使理论与实验相一致, 能为实际TPV器件的设计与研制提供理论指导.${T_{\rm{P}}}$ . 引入低温端牛顿传热方程和半导体InAs带隙${\varepsilon _{\rm{g}}}$ 、本征浓度${n_{\rm{i}}}$ 与温度${T_{\rm{P}}}$ 参数, 研究传热不可逆性对TPV性能的影响, 即[21 ] :$U = 0.2\, {\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - {\rm{2}}}} \cdot {{\rm{K}}^{ - 1}}$ 是热传导系数, ${T_{\rm{L}}} =$ 300 K是环境温度. 联立(7 )式、 (13 )式、(15 )式—(17 )式, 可确定光伏电池温度${T_{\rm{P}}}$ . 数值模拟结果发现${T_{\rm{P}}}$ 相比于${T_{\rm{L}}}$ 有明显提升. 为了降低TPV温度${T_{\rm{P}}}$ , 可在TPV器件中植入一个光学滤波器(只允许能量处于${\varepsilon _{\rm{g}}} \leqslant \varepsilon \leqslant {\varepsilon _{\rm{H}}}$ 区间的通过真空间隙被光伏电池吸收), 提高TPV的性能.${P_{{\rm{opt}}}}$ 和效率${\eta _{{\rm{opt}}}}$ 随光子截止能量${\varepsilon _{\rm{H}}}$ 变化的关系曲线图, 如图5 所示. 从图5 可看出存在一对优化值${\varepsilon _{{\rm{H}}, P}}$ 和${\varepsilon _{{\rm{H}}, \eta }}$ , 使${P_{{\rm{opt}}}}$ 和${\eta _{{\rm{opt}}}}$ 分别获得最大功率密度${P_{\max }}$ 和最大效率${\eta _{\max }}$ . 当${\varepsilon _{\rm{H}}} \geqslant {\varepsilon _{{\rm{H}}, P}}$ 时, ${P_{{\rm{opt}}}}$ 和${\eta _{{\rm{opt}}}}$ 随${\varepsilon _{\rm{H}}}$ 的增加几乎保持不变; 当${\varepsilon _{\rm{H}}} \leqslant {\varepsilon _{{\rm{H}}, \eta }}$ 时, ${P_{{\rm{opt}}}}$ 和${\eta _{{\rm{opt}}}}$ 随${\varepsilon _{\rm{H}}}$ 的减小而递减, 因此, 为了使TPV具有较高的功率密度和效率, ${\varepsilon _{\rm{H}}}$ 应处于以下区间:图 5 优化功率密度${P_{{\rm{opt}}}}$ 和效率${\eta _{{\rm{opt}}}}$ 随光子截止能量${\varepsilon _{\rm{H}}}$ 变化的关系曲线图, 其中${T_{\rm{E}}} = 1500\, {\rm{K}}$ Figure5. Optimal power density ${P_{{\rm{opt}}}}$ and efficiency ${\eta _{{\rm{opt}}}}$ as a function of photons’ cut-off energy ${\varepsilon _{\rm{H}}}$ , where ${T_{\rm{E}}} = 1500\, {\rm{K}}.$ 图5 中, 根据${\varepsilon _{{\rm{H}}, P}}$ , 可确定TPV器件在最大功率密度${P_{\max }}$ 时的效率${\eta _P}$ ; 根据${\varepsilon _{{\rm{H}}, \eta }}$ , 可确定TPV器件在最大效率${\eta _{\max }}$ 时的功率密度${P_{\eta} }$ . 从而可确定功率密度和效率的优化区间:${\varepsilon _{{\rm{H}}, P}}$ 和${\varepsilon _{{\rm{H}}, \eta }}$ 受热发射器温度的影响, 不同${T_{\rm{E}}}$ 对应不同的优化区间(18 )式—(20 )式.4.结 论 基于普朗克辐射理论, 从TPV器件的效率和功率解析表达式出发, 获得理想状态下的热力学性能极限. 考虑非辐射复合损失对TPV器件性能的影响, 对伏安特性方程进行修正, 探究非理想TPV器件的电学、热力学、光学等物理特性. 研究表明非理想TPV器件的开路电压和短路电流密度均低于理想TPV器件; 增加热发射器温度可以提高功率密度, 但受不可逆热损失影响, TPV器件的效率在一定高温区域, 随温度的升高而降低; 考虑光伏电池与环境之间的不可逆传热损失, 通过对光伏电池电压与光子截止能量等关键参数进行优化可获得最大功率密度和效率. 本文研究结果可为TPV器件的优化设计和高品位热能的回收与利用提供理论指导. 

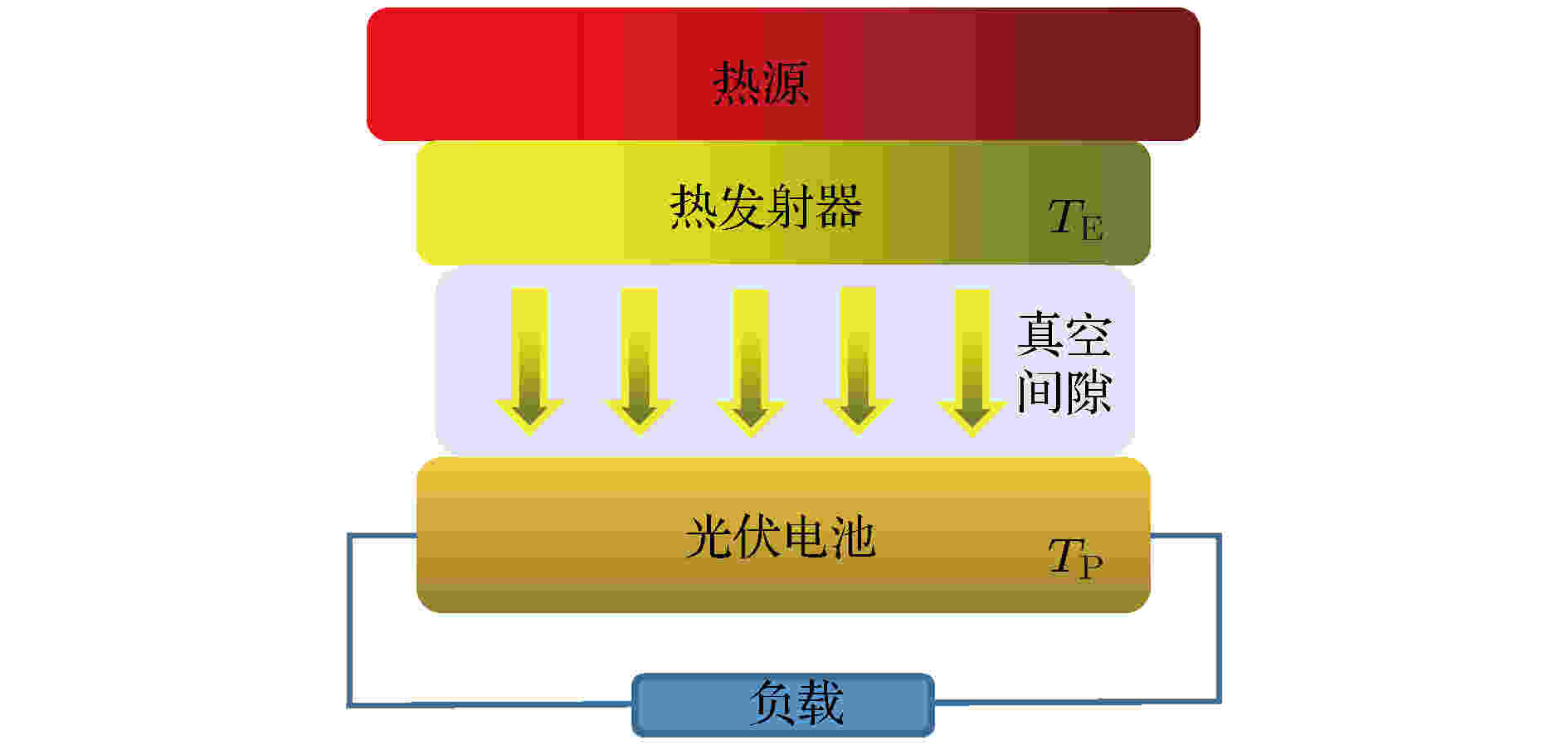 图 1 TPV器件的示意图
图 1 TPV器件的示意图





































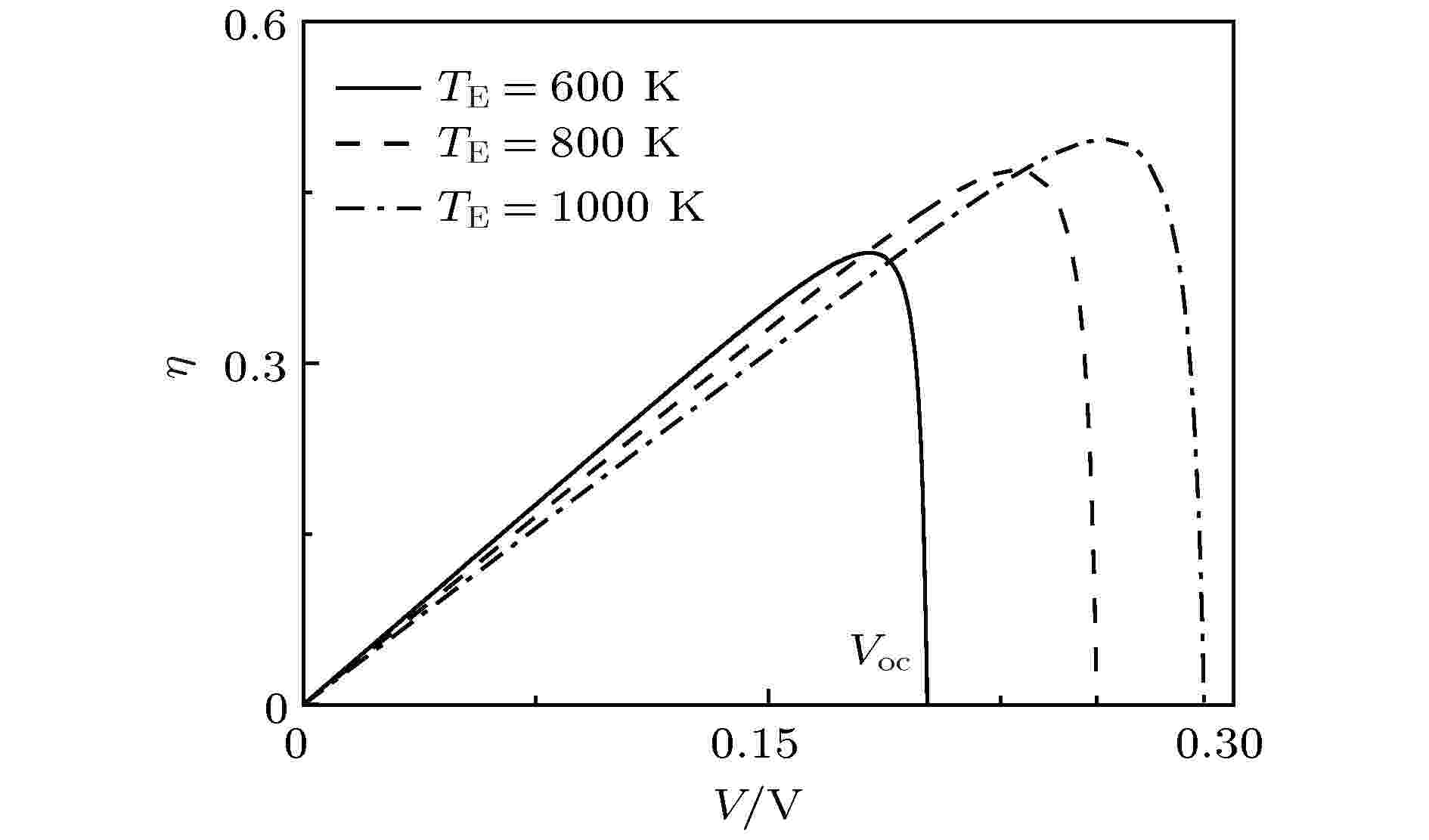 图 2 效率η随输出电压V变化曲线
图 2 效率η随输出电压V变化曲线




































































































































































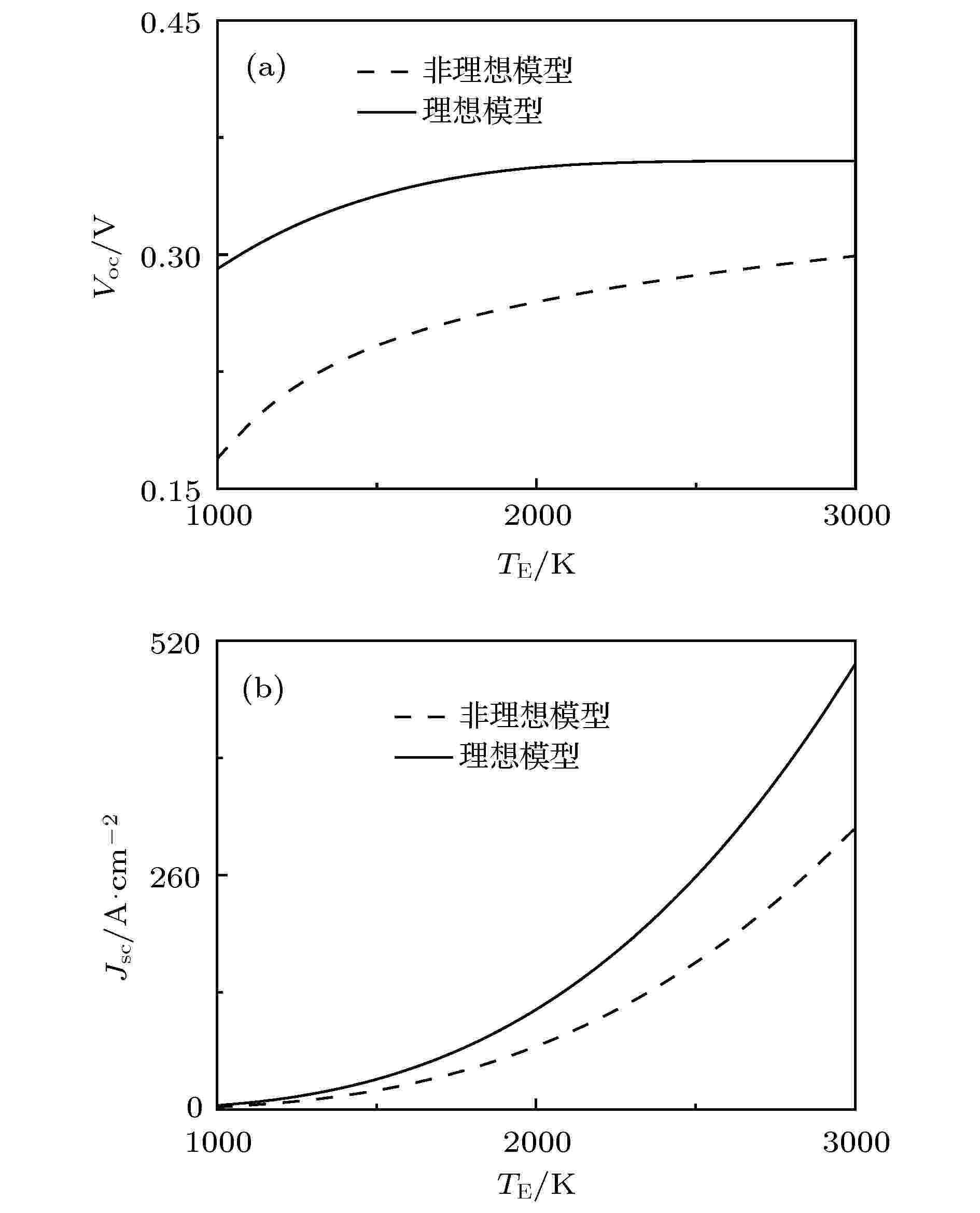 图 3 非理想和理想光伏电池特性随
图 3 非理想和理想光伏电池特性随











































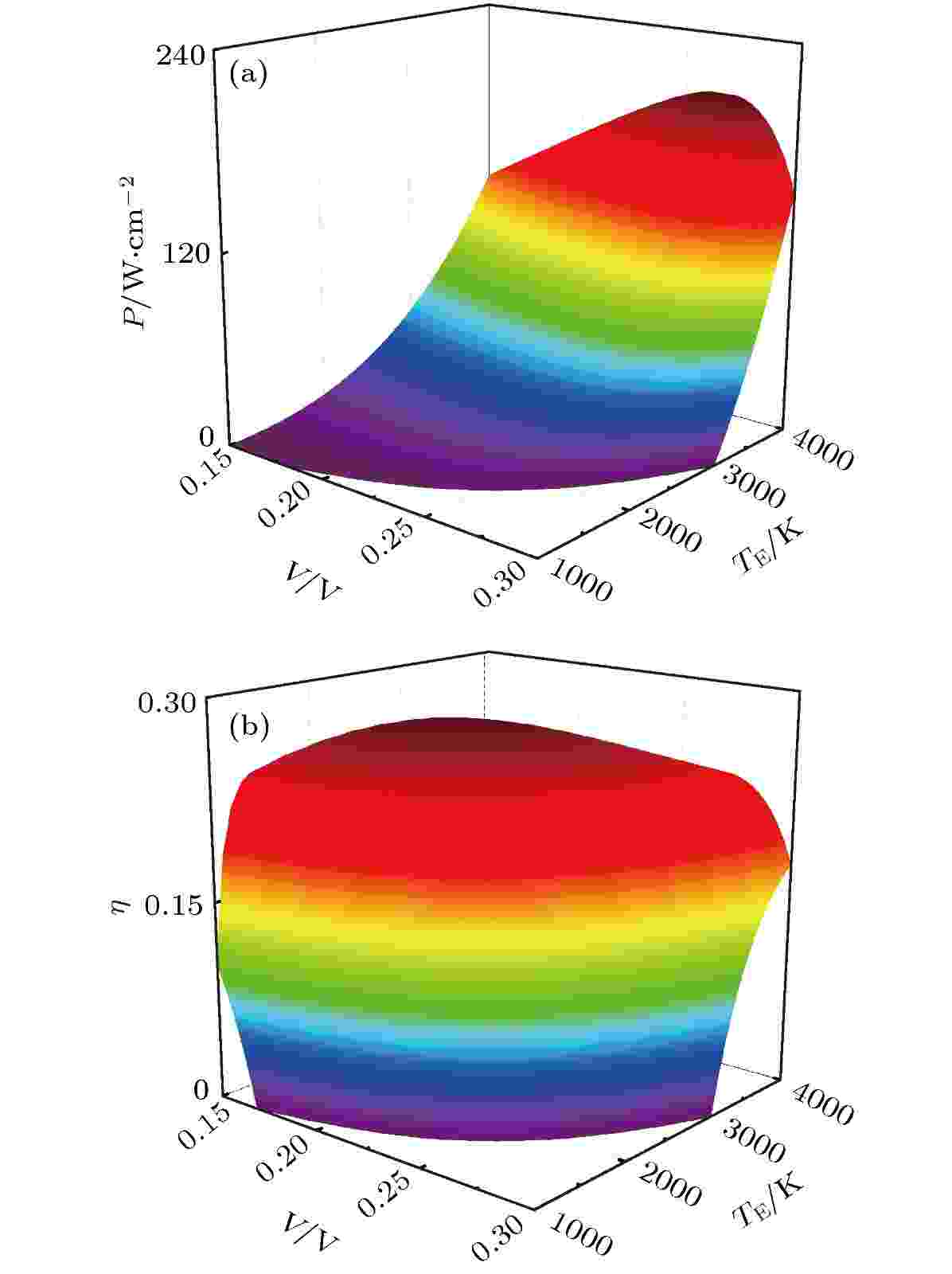 图 4 (a)功率密度和(b)效率随
图 4 (a)功率密度和(b)效率随


























































































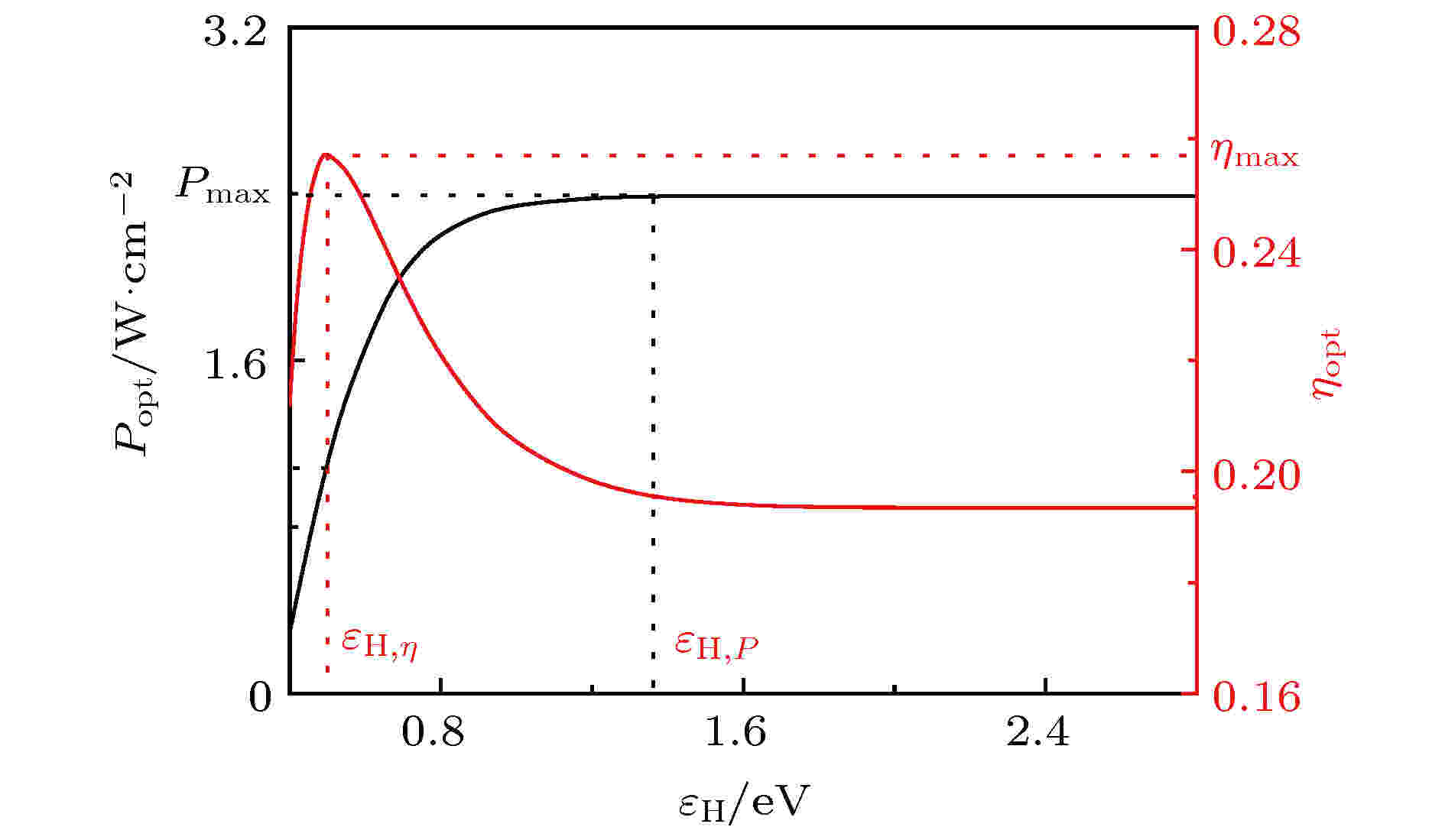 图 5 优化功率密度
图 5 优化功率密度
















