摘要:利用隐式蒙特卡罗方法模拟热辐射输运问题时, 辐射源粒子的抽样对结果的正确性很重要. 在球几何热辐射输运隐式蒙特卡罗模拟中, 通常的做法是假设单个网格(球壳)的温度不随空间变化, 即源粒子在球壳内均匀分布. 对于网格内部温度分布梯度不大的情况, 这种处理不会造成太大误差, 然而当物质的吸收系数很大或球壳较厚时, 那么单个网格内温度的空间变化也可能较大, 这种处理将导致模拟的热辐射传播速度比实际的要快. 本文分析了导致这种偏差的原因, 并基于辐射能量密度分布, 推导了球几何下辐射源粒子发射位置的概率密度函数, 提出了两种辐射源粒子空间抽样方法, 设计了抽样流程, 计算了典型的热辐射输运问题. 数值计算表明, 这两种新的源粒子空间抽样方法均能修正辐射传播速度与参考值的偏差, 解决计算结果过分依赖于网格剖分的问题. 同时, 在网格数较少、模拟粒子数较少的情况下新方法仍能得到较准确的结果, 有效提高了计算效率.
关键词: 隐式蒙特卡罗/
热辐射输运/
球几何/
空间抽样

English Abstract

全文HTML

--> --> -->

激光间接驱动的惯性约束聚变(inertial confinement fusion, ICF)中, 黑腔的温度可达上百万度, 腔壁热辐射(简称辐射)光子(X光)均匀地照射装有DT聚变材料的靶丸, 驱动飞层压缩靶丸, 实现聚变点火. 因此, 研究辐射在物质中的输运及辐射与物质的相互作用是ICF的重要研究方向. 热辐射的传播行为可用辐射输运方程来描述, 理论上可通过求解辐射输运方程及与之相耦合的物质能量方程来获得辐射场及物质温度场的时空演化规律. 由于辐射强度与物质温度的强耦合性以及辐射输运方程的非线性特性^[1], 即便数值方法求解也是非常困难的, 蒙特卡罗(Monte Carlo, MC)方法是求解辐射输运问题的重要方法之一^[2,3].
传统的直接MC方法于20世纪六十年代由Fleck^[4]提出, 但由于在很多情况下通过直接MC方法求得的结果存在过大的涨落和能量不均衡等缺点^[4,5], 因此很少被采用. 20世纪七十年代初, 加利福尼亚大学的Fleck和Cummings^[6]提出了隐式蒙特卡罗(implicit Monte Carlo, IMC)方法, 该方法的主要思想是将物质的真实吸收截面由有效吸收截面和有效散射截面代替, 并引入与隐式迭代类似的手段, 故具有天然的稳定性. IMC方法与直接MC方法相比更稳定, 计算精度、效率更高, 因此得到了广泛的应用, 国外的ICF数值模拟程序^[7]及其他辐射输运程序^[8-10]均用到了IMC方法解决其中的辐射输运问题, 部分文献^[11-15]将IMC方法的模拟结果当作其他数值方法的参考结果. 国内已有****研究并开发了IMC辐射输运模拟程序^[16], 该程序可以进行一维或三维的辐射输运数值模拟, 目前已经应用于ICF中黑腔物理的研究^[17,18].
Fleck和Cummings^[6]推导IMC辐射输运方程时, 认为“某一时间步内的某网格中温度是不随空间变化的”, 即对单一网格做了“空间等温假设”, 因此网格内的辐射粒子的发射位置可由空间均匀抽样得到, 例如在一维平板几何中, 辐射粒子的发射位置是网格左右边界之间的均匀分布函数, 本文将其称为“等温法”. 国外的三维辐射输运模拟程序Milagro^[7]、国内的半随机模拟方法^[19]以及其他基于IMC的辐射输运模拟方法^[6,11]都采用该抽样方法. 在物质的吸收系数不大或空间网格较小的情况下, 这种处理方法不会给计算结果带来明显偏差, 然而对于强吸收、大网格问题, 继续采用这种基于“等温假设”的空间均匀抽样法将导致较大误差. 为此, 文献[20]提出了基于辐射能量密度分布的新抽样法, 推导了辐射能量空间分布密度函数和辐射源粒子空间抽样公式, 解决了正交几何下, 同一网格中温差太大导致IMC模拟结果与实际结果不符的问题. 然而该方法并不适用于球几何情况, 因此本文将推导球几何情况下辐射能量的空间分布密度函数, 并提出相应的辐射源粒子抽样方法.
本文的主要内容如下, 第2节推导了球几何情况下“等温法”的辐射源粒子空间概率密度分布函数及抽样方法, 探讨了该方法的不足, 并通过数值手段获得了一个典型球对称热辐射输运问题的参考解. 第3节推导了基于能量密度分布的辐射源空间概率密度函数, 分析了IMC模拟中热辐射波传播偏快的原因, 提出了两种新的辐射源粒子抽样方法, 并设计了抽样流程. 第4节通过典型算例测试了本文提出的两种辐射源粒子抽样方法的正确性, 验证了本项研究工作对球几何情况下的IMC辐射源粒子抽样精度及计算效率有显著的改进效果.

IMC辐射输运模拟中的辐射源粒子可分成四种^[16,21]: 来自独立外源的粒子; 从网格边界进入的粒子; 从上一时间步存活下来的粒子; 从物质辐射出的粒子(以下称为“辐射源粒子”). 前三种粒子均有确定的位置参数, 而辐射源粒子在当前时间步开始时需通过随机抽样确定其初始位置.
在一维球几何情况下, IMC输运方程与物质能量方程可写为:

$\begin{split} &\frac{{\rm{1}}}{c}\frac{{\partial I}}{{\partial t}} + \mu \frac{{\partial I}}{{\partial r}} + \frac{{1 - {\mu ^2}}}{r}\frac{{\partial I}}{{\partial \mu }} + {\sigma _n}I \\ =\; & \frac{1}{{4{\text{π}}}}{f_n}{\sigma _n}{b_n}c{U_{\gamma,n}} \!+\! \frac{1}{2}{\zeta _n}\int_{ - 1}^1 {\rm{d}} \mu \int_{\rm{0}}^\infty {{\rm{d}}\nu } \cdot {f_n}{\sigma _n}I \!+\! {Q_n},\end{split}$

${C_{\rm{v}}}\frac{{\partial T}}{{\partial t}} = \int_{ - 1}^1 {{\rm{d}}\mu \int_{\rm{0}}^\infty {{\rm{d}}\nu } \cdot } {f_n}{\sigma _n}I - {f_n}{\sigma _{{\rm{P}},n}}c{U_{\gamma,n}}, $

其中, 所有带下标n的变量均表示第n个离散时间步中对应的变量值, I为辐射强度, c为真空中的光速, t为时间, r为粒子所在位置的半径, μ为方向余弦, σ为物质的吸收截面, b为归一化Planck函数, f为Fleck因子, U_γ为辐射能量密度, ζ为局域再发射系数, ν为光子频率, Q为独立外源, C_v为比热容, T为物质温度, σ_P为Planck平均吸收截面.
(1)式等号右边第一项为相空间(r, μ, ν, t)处的辐射源粒子发射密度S(r, μ, ν, t),

$S(r,\mu,\nu,t) = \frac{1}{{4{\text{π}}}}{f_n}{\sigma _n}(r,\nu ){b_n}(\nu )c{U_{\gamma,n}}(r),$

其中

${U_{\gamma,n}}(r) = aT_n^4(r), $

式中, a为辐射常数, ${T_n}(r)$是网格温度.
在$r$处dr范围内物质辐射出的能量${E_n}(r)$为

$ {E_n}(r) = {\dot E }_n(r){\rm{d}}V, $

式中, ${\dot E }_n(r)$是对方向、频率和时间积分后的单位体积发射的能量,

$ \begin{split}{\dot E }_n(r)\; & = \int_{ - 1}^1 {{\rm{d}}\mu } \int_0^\infty {{\rm{d}}\nu } \int_{{t_n}}^{{t_{n + 1}}} {S(r,\mu,\nu,t){\rm{d}}t} \\ &= {f_n}{\sigma _{{\rm{P}},n}}acT_n^4(r)\Delta t.\end{split} $

在球几何情况下, ${\rm{d}}V = 4{\text{π}}{r^2}{\rm{d}}r$.
IMC方法中, 辐射源粒子数目与其辐射的能量${E_n}(r)$呈正比, 因此, 某网格内的辐射源粒子关于半径$r$的空间分布概率密度函数可写为

$\begin{split}& f(r) = \frac{{{{\dot E }_n}(r)4{\text{π}}{r^2}}}{{\displaystyle\int_{{r_1}}^{{r_2}} {{{\dot E }_n}(r)4{\text{π}}{r^2}{\rm{d}}r} }} = \frac{{T_n^4(r){r^2}}}{{\displaystyle\int_{{r_1}}^{{r_2}} {T_n^4(r){r^2}{\rm{d}}r} }},\\ & \qquad\qquad r \in \left[ {{r_1},{r_2}} \right],\end{split}$

其中r₁, r₂分别是网格的内、外半径.
在等温假设下, ${T_n}(r) = {\overline T_n}$, ${\overline T_n}$为当前时间步的网格平均温度, 是与半径变量$r$无关的常量. 则该网格内辐射源粒子的空间分布概率密度分布为

$f(r) = {{3{r^2}}}/({{r_2^3 - r_1^3}}).$

因此在等温假设下的辐射源粒子的位置变量$r$可用反函数法直接抽样得到,

$r = \sqrt[\root{4}{3}]{{r_1^3 + \xi (r_2^3 - r_1^3)}},$

式中ξ为在[0, 1]上均匀分布的随机数. 同一网格中辐射源粒子初始位置的半径$r$均可由(9)式抽样获得, 这实际上等同于球壳内的空间均匀抽样.
在物质吸收系数小或网格较小(球壳较薄)的情况下, 网格内部的温度梯度不大, 即温度随空间(半径r)的变化不显著, ${T_n}(r) = {\overline T_n}$近似引入的偏差不大, 故这种等温法抽样对计算结果影响较小. 然而当物质的吸收系数很大或网格较大时, 网格内部温度差可能会比较大, 若用网格平均温度${\overline T_n}$取代方程(7)中的${T_n}(r)$, 则计算结果将产生较大误差. 因此, 在等温法中, 为了避免网格内部温差大所导致的问题, 就必须尽量细分网格, 使网格内温度差尽可能小, 令等温假设尽可能接近成立. 那么, 究竟要将网格剖分至多小才能使计算结果的误差不至于太大呢？如果网格太小(网格数量多)导致的问题又是什么呢？
为此, 本文设计了一个热辐射传播的球对称问题, 以分析等温法抽样对网格剖分的依赖情况, 并找到尽可能接近真解的模拟结果. 本文所有问题的计算平台为个人电脑(CPU型号Intel(R) Core(TM) i7-3770@3.4 GHz; 核数8; 内存4.00 GB; 操作系统为Windows 7旗舰版; 编译器为Intel Visual Fortran).
模型为半径0.2 cm的一维球, 其芯部(中心网格)为一温度恒为1 keV的辐射源, 一维球外表面为真空边界, 材料比热为C_v = 0.1 gJ/(cm³·keV), 吸收系数与温度的三次方呈反比, σ = σ₀/T³, σ₀ = 200, 单位为keV³/cm, 温度T的单位为keV.
系统的初始物质温度与辐射温度将分别为1和0 eV, 计算时间步长为0.01 ns, 总时长为10 ns, 网格数分别设置为20, 25, 40, 80, 100, 160, 200, 250, 320, 400, 不同网格数的计算结果如图1和图2所示.
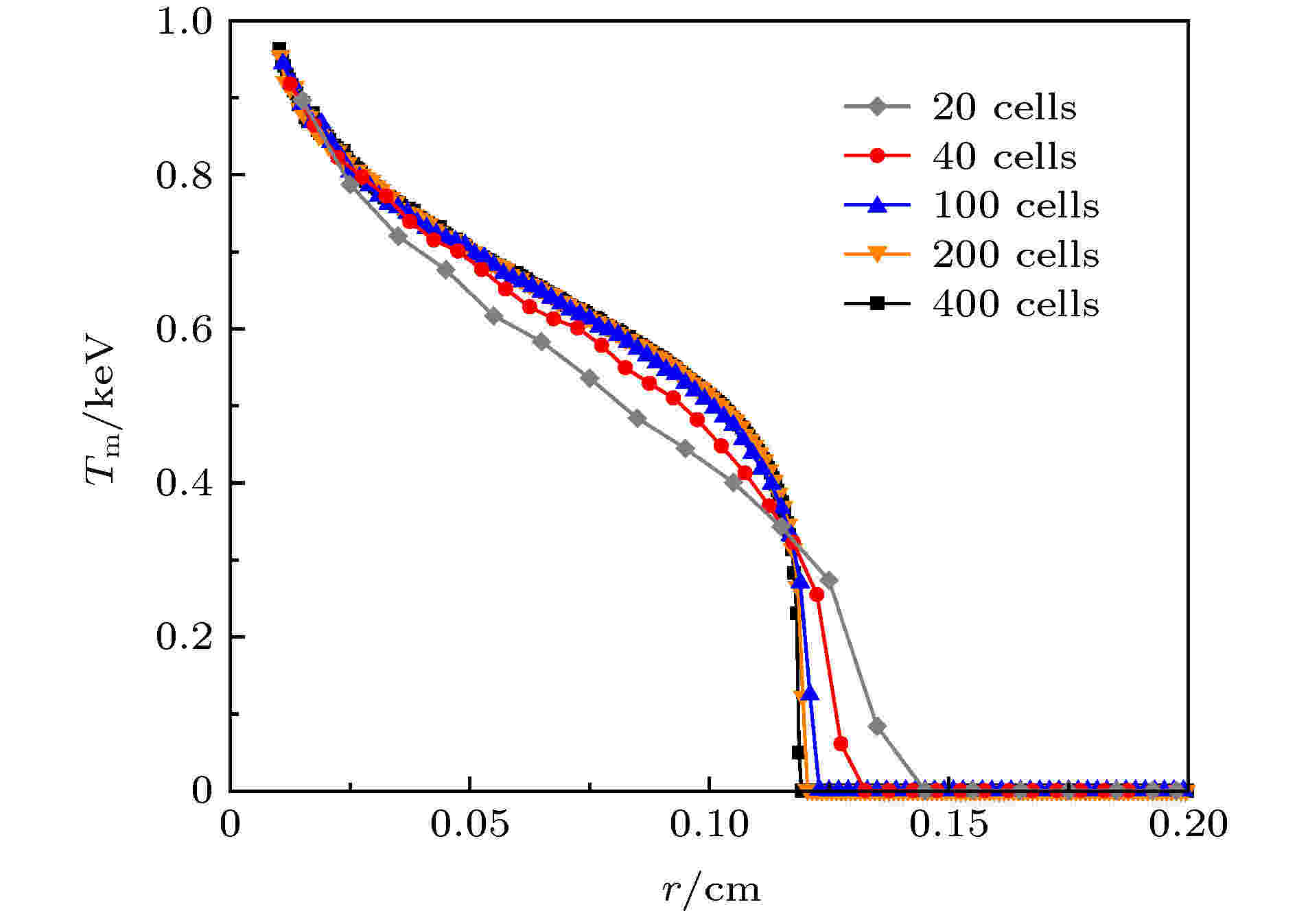图 1 不同网格数的物质温度空间分布(t = 10 ns)
Figure1. Material temperature with different cell numbers (t = 10 ns).

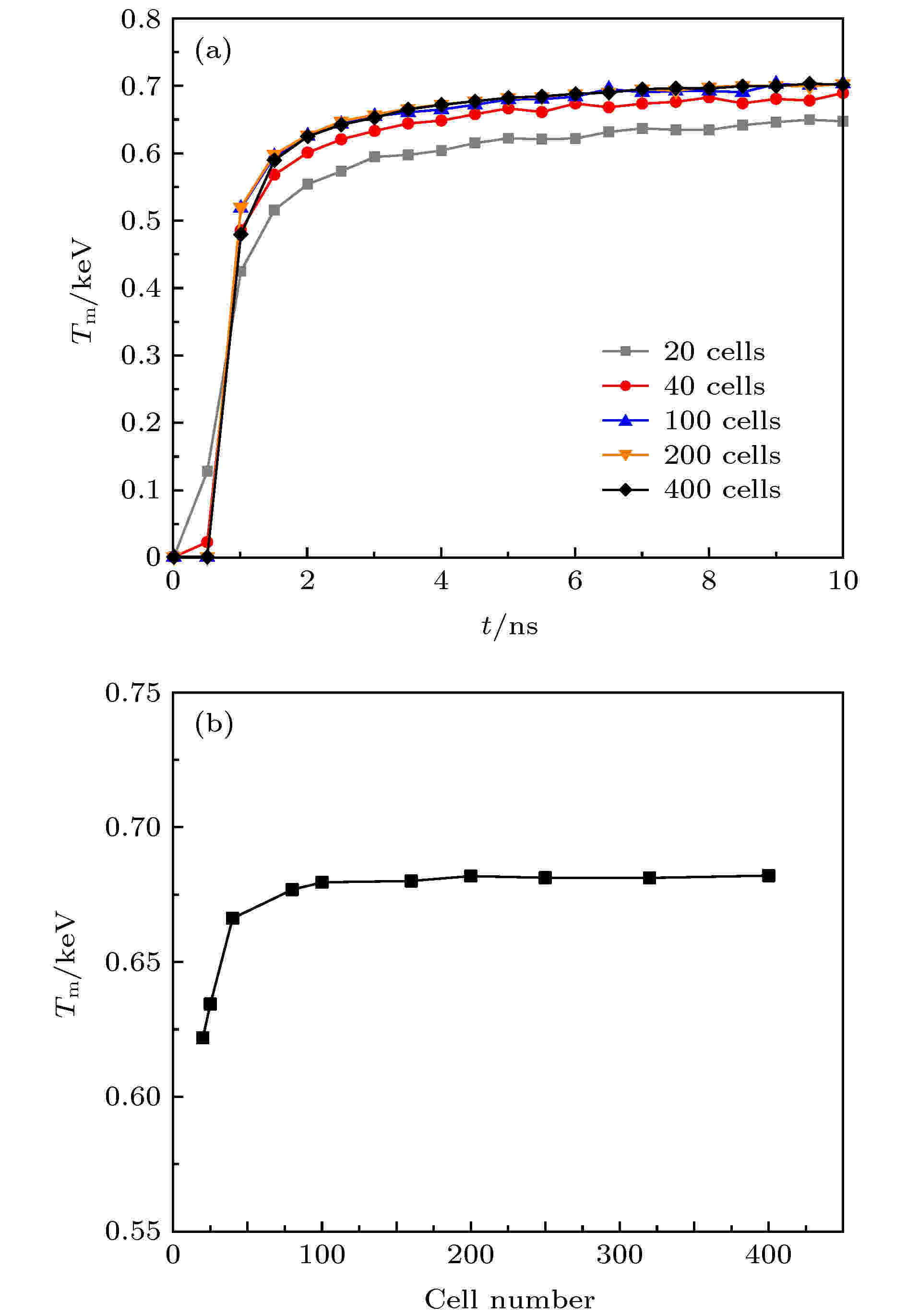图 2 物质温度的收敛情况　(a)不同网格数情况下r = 0.05 cm处的物质温度随时间的变化; (b) r = 0.05 cm处物质温度随网格数的变化(t = 5 ns)
Figure2. The convergence of material temperature: (a) Material temperature change with time in r = 0.05 cm; (b) material temperature change with cell number in r = 0.05 cm (t = 5 ns).

从图1和图2可以看出, 辐射源粒子采用等温法抽样, 不同网格剖分情况下的计算结果差异是很显著的, 这说明等温法的计算结果对空间剖分的依赖性很强, 显然这对数值模拟来说是非常不好的性质. 同时可以看出, 随着网格数的增加, 模拟结果是逐渐收敛的, 对于本问题, 当网格数达到200之后, 模拟结果就基本趋于一致了, 因此, 为了避免因网格剖分问题引入误差, 本问题的网格数至少为200.
从图1还能看出, 当网格数目较少(网格较大)时, 辐射传播的速度是偏快的, 这里稍做分析. 温度相对较高的区域辐射出的能量(粒子)更多, 其与附近温度相对较低的物质相互作用并加热低温区, 被加热的区域辐射出能量加热更远的区域, 热辐射得以向前传播. 在IMC模拟中, 系统区域被剖分为离散的网格, 在等温假设下, 对于某个网格, 抽样出的辐射源粒子均匀地分布在网格各处. 然而, 在辐射的传播过程中, 即使是某单一网格其内部也应该是有温差的, 那么辐射源粒子应该更多地分布在网格中温度较高处. 对于本问题, 更多的辐射源粒子本应分布在网格中半径更小的位置, 因此在等温假设下, 粒子的半径抽样值事实上是较理论值偏大了, 即粒子的辐射位置总体上比理论值靠前, 最终使得热辐射的传播比实际更快. 增加网格数, 即减小网格厚度可使网格内温差减小, 等温法抽样产生的误差随之减小, 理论上网格越小误差越小. 因此, 本文将网格数400的计算结果作为问题解的参考解. 为更清晰地比较各个温度曲线与参考解的偏差, 表1列出了不同网格数时温度曲线相对参考解的标准差和最大误差, 容易看出, 随着网格数的增加, 温度分布曲线相对参考解的偏差确实变小了.

Cell number	Standard deviation/eV	Maximum error/eV
20	80.8	273
40	48.7	254
100	28.9	245
200	13.0	125

表1不同网格数时的温度曲线相对参考解的标准偏差和最大误差
Table1.Relative to the reference solution, the standard deviation and the maximum error of temperature curves with different cell numbers.

既然网格尺度大了有问题, 网格小了计算结果有保证, 那么是不是应该一开始就将网格分得很小呢？这样做理论上是行得通的, 但是实践中将会带来弊端: 网格数增加后, 若保持每个时间步模拟粒子数不变, 每个网格能够分配到的粒子数就会变少, 模拟结果的统计涨落将变大. 因此为避免统计涨落过大, 单个网格分配到的粒子数必须足够多. 表2是保证单个网格分配粒子数足够多的情况下, 不同网格剖分数对应的总模拟粒子数和计算时间, 从表中可以看出, 随着网格数的增加, 模拟的总粒子数相应增加, 由此带来的后果是更多的模拟粒子花费更多的计算时间以及计算机内存, 导致模拟效率降低.

Cell number	Particle number	Computation time/s
20	1 × 104	1.80 × 103
40	2 × 104	2.72 × 103
100	5 × 104	5.74 × 103
200	2 × 105	2.28 × 104
400	4 × 105	5.06 × 104

表2不同网格数的计算时间
Table2.Computation time with different cell numbers.

从前面的模拟结果及分析得知, 网格尺度不能太大, 否则计算误差偏大. 但是如果网格尺度太小, 计算开销又太大. 那么“等温法”抽样就存在这样的问题: 究竟要剖分多少网格合适？有没有办法让计算结果不太依赖于网格剖分, 或者说在网格尺度较大的情况下计算误差仍然较小呢？下面将回答这个问题.

假设同一网格内温度与半径r的关系是线性的(以下称为“线性假设”), 这种假设在绝大多数情况下比“等温假设”的近似效果更好. 如图3所示, 某网格的内外边界半径分别为r₁, r₂, 内外边界物质温度分别为T₁, T₂, 则温度与r的关系可表示为
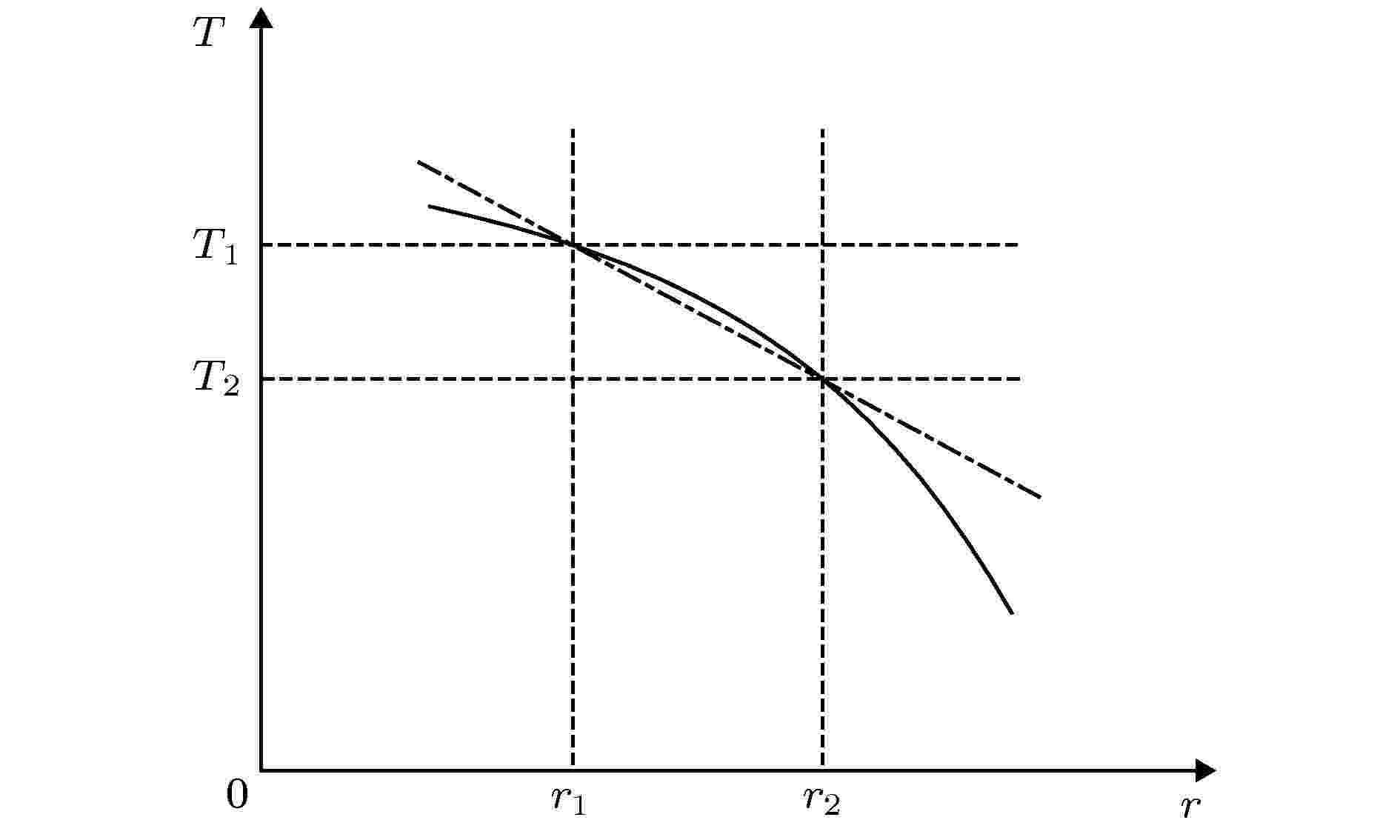图 3 网格内温度与空间的关系可近似为线性关系
Figure3. The dependence of temperature on space is approxi-mately linear.

$T(r) = kr + b, $

其中k = (T₂ – T₁)/(r₂ – r₁), b = T₁ – kr₁. 将方程(10)代入方程(7)中得

$f(r) = \frac{{{{(kr + b)}^4}{r^2}}}{{\displaystyle\int_{{r_1}}^{{r_2}} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }},\;\;\;\;r \in \left[ {{r_1},{r_2}} \right].$

为分析方程(11)与等温假设下推导出的(8)式在描述辐射源粒子空间分布时的差异, 下面以第2节热辐射输运问题中网格数为40的计算结果为例, 选取了第9, 18, 22, 26个网格(球的中心网格为第1个网格)作为辐射波的代表点. 图4为相应网格的辐射源粒子空间概率密度分布.
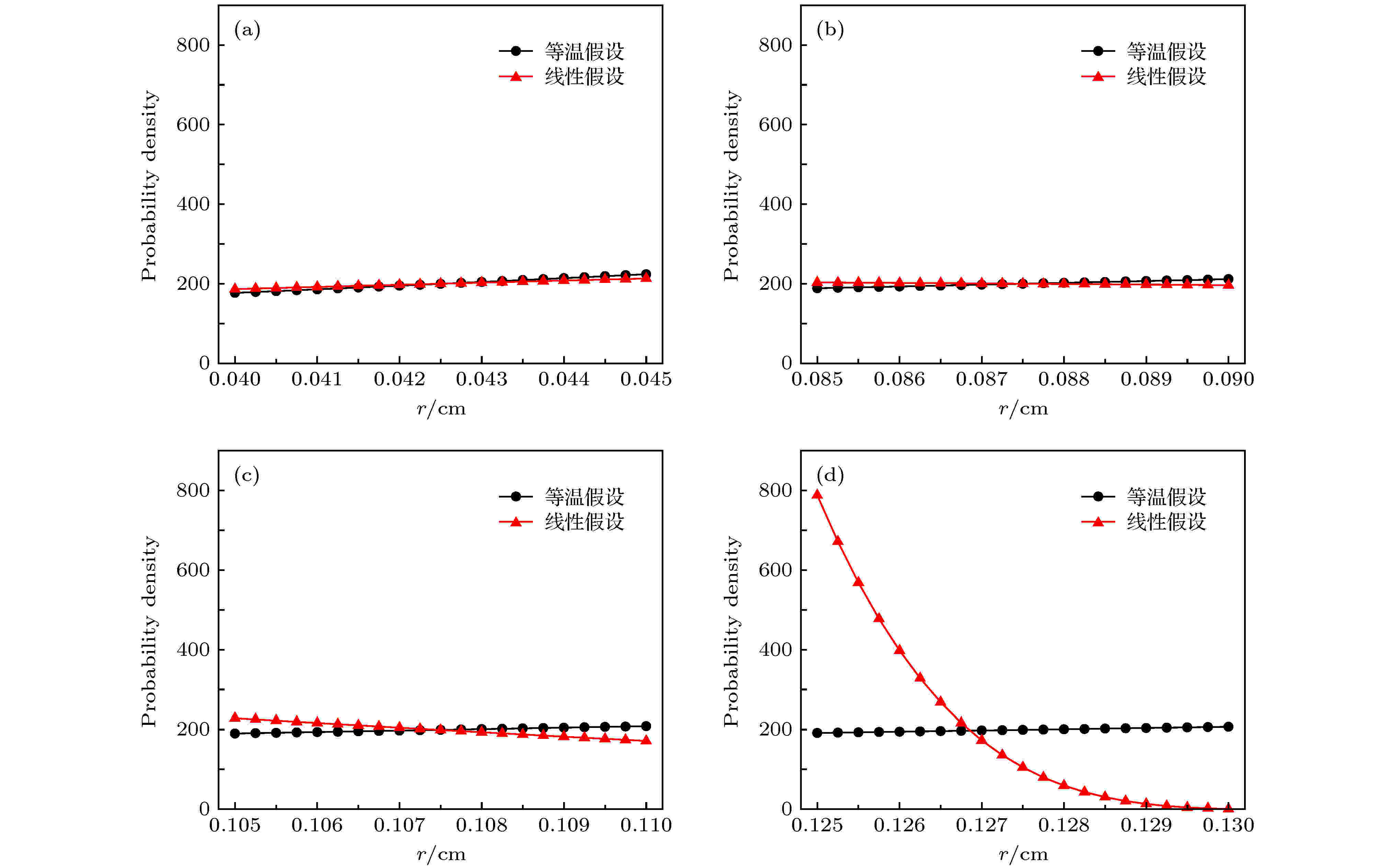图 4 辐射波不同位置的辐射源粒子空间分布概率密度　(a)网格9, 波后处; (b)网格18, 波后处; (c)网格22, 波头处; (d)网格26, 波头处
Figure4. Spatial probability density distribution of radiation source particle in different positions of radiation wave:　(a) Cell 9, in the behind of wave; (b) cell 18, in the behind of wave; (c) cell 22, in the head of wave; (d) cell 26, in the head of wave.

图4中曲线与横坐标所围成的面积代表辐射源粒子初始位置在空间分布的概率, 容易看出, 在越靠近辐射波波头、网格内温差越大的地方(图4(d)), 等温假设下辐射源粒子总体位置与线性假设偏离越远; 而在远离波头、网格内温差越小的地方(图4(a)), 两者越接近. 因此等温假设下IMC模拟中辐射波传播速度偏快主要是辐射波波头处网格辐射源粒子总体位置与实际偏差太大造成的, 印证了第2节的讨论结果.
对于方程(11)的概率密度分布函数, 如果用反函数法来抽样r值, 则需要求解一元七次方程, 比较困难. 下文给出两种新的抽样法.
1) 乘抽样法
方程(11)可写成

$f(r) = H(r){f_1}(r), $

其中

$H(r) = \frac{{{{(kr + b)}^4}(r_2^3 - r_1^3)}}{{3\displaystyle\int_{{r_1}}^{{r_2}} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }}, $

${f_{\rm{1}}}(r) = \frac{{3{r^2}}}{{r_2^3 - r_1^3}}.$

方程(14)满足概率密度函数的条件, 且H(r) ≥ 0, 令$\hat H$为H(r)的上界, 可以证明^[22]: 从f₁(r)得到的抽样值r_f若满足ξ ≤ H(r_f)/$\hat H$, 则r_f为f(r)的抽样值. 实际上f₁(r)是球壳内均匀分布函数, 容易得到其随机抽样值r_f为$\sqrt[3]{{r_1^3 + \xi (r_2^3 - r_1^3)}}$.
因此, 乘抽样法步骤为:
① 抽样得到f₁(r)的抽样值r_f ;
② 将r_f代入方程(13)中得到H(r_f) ;
③ 取出一随机数ξ, 与H(r_f)/$\hat H$比较;
④ 若ξ ≤ H(r_f)/$\hat H$, 则r_f为f(r)的抽样值, 否则返回步骤①.
2) 阶梯近似抽样法
将区间[r₁, r₂]分成m个子区间, 则每个子区间长度δr = (r₂ – r₁)/m, 第i个子区间为[r₁+(i – 1)δr, r₁ + iδr], 对方程(11)在[r₁, r₂]范围内积分,

$\begin{split}\; & F({r_2}) =\displaystyle\int_{{r_1}}^{{r_2}} {f(r'){\rm{d}}r'}\\ =\; & \frac{{\displaystyle\int_{{r_1}}^{{r_1} + {\rm{\delta }}r} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }}{{\displaystyle\int_{{r_1}}^{{r_2}} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }} + \frac{{\displaystyle\int_{{r_1} + {\rm{\delta }}r}^{{r_1}+ 2{\rm{\delta }}r} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }}{{\displaystyle\int_{{r_1}}^{{r_2}} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }}\\ & + \cdots + \frac{{\displaystyle\int_{{r_2} - {\rm{\delta }}r}^{{r_2}} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }}{{\displaystyle\int_{{r_1}}^{{r_2}} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }}\\ = \; &{P_1} + {P_2} + \cdots + {P_m}, \end{split} $

其中${P_i} = \dfrac{{\displaystyle\int_{{r_1} + (i - 1){\rm{\delta }}r}^{{r_1} + i{\rm{\delta }}r} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }}{{\displaystyle\int_{{r_1}}^{{r_2}} {{{(kr + b)}^4}{r^2}{\rm{d}}r} }} \! > \! 0$, 且${P_1} + {P_2} + \cdots + {P_m} = 1$.
因此阶梯近似抽样法的抽样步骤为:
① 取出一随机数ξ, 与$\displaystyle\sum\limits_{i = 1}^m {{P_i}}$比较;
② 若$\displaystyle\sum\limits_{k = 1}^{i - 1} {{P_k}} \leqslant \xi < \displaystyle\sum\limits_{k = 1}^i {{P_k}}$, 在第i个子区间$[r_1 + (i-1) \text{δ} r, r_1 + i\text{δ} r]$中抽取r_i, 采用等温法抽样, 则r_i为f(r)的抽样值.
需要注意的是, 对于不同问题, 乘抽样法和阶梯近似抽样法的抽样效率可能不相同, 因此在实际计算时, 选择哪种抽样法可视情况而定.

为检验乘抽样法和阶梯近似抽样法能否有效减小空间均匀抽样带来的偏差, 本节仍以第2节中的热辐射输运问题作为算例.
模型参数及计算参数与第2节中描述的相同, 进行热辐射输运模拟时, 分别采用乘抽样法和阶梯近似抽样法抽取网格辐射源粒子的初始位置, 并将计算结果与参考解比较. 图5为分别采用两种新抽样方法在不同网格数时计算得到的物质温度空间分布. 图6为两种新抽样方法在网格数为40时的计算结果与参考解的比较.
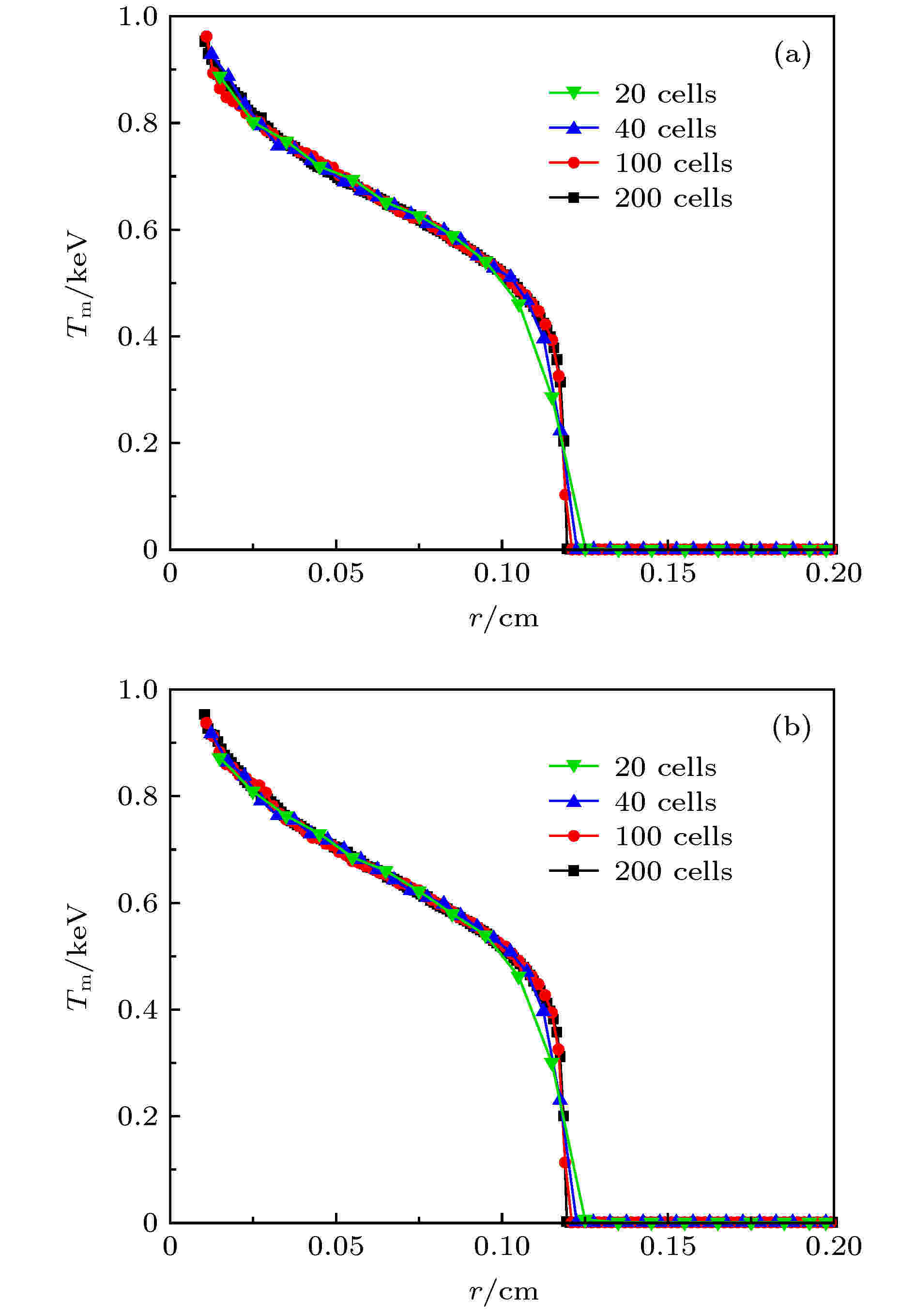图 5 不同网格数时的物质温度空间分布 (t = 10 ns)　(a)乘抽样法; (b)阶梯近似抽样法
Figure5. Material temperature with different cell numbers (t = 10 ns):　(a) Multiplying sampling method; (b) stepped approximation sampling method.

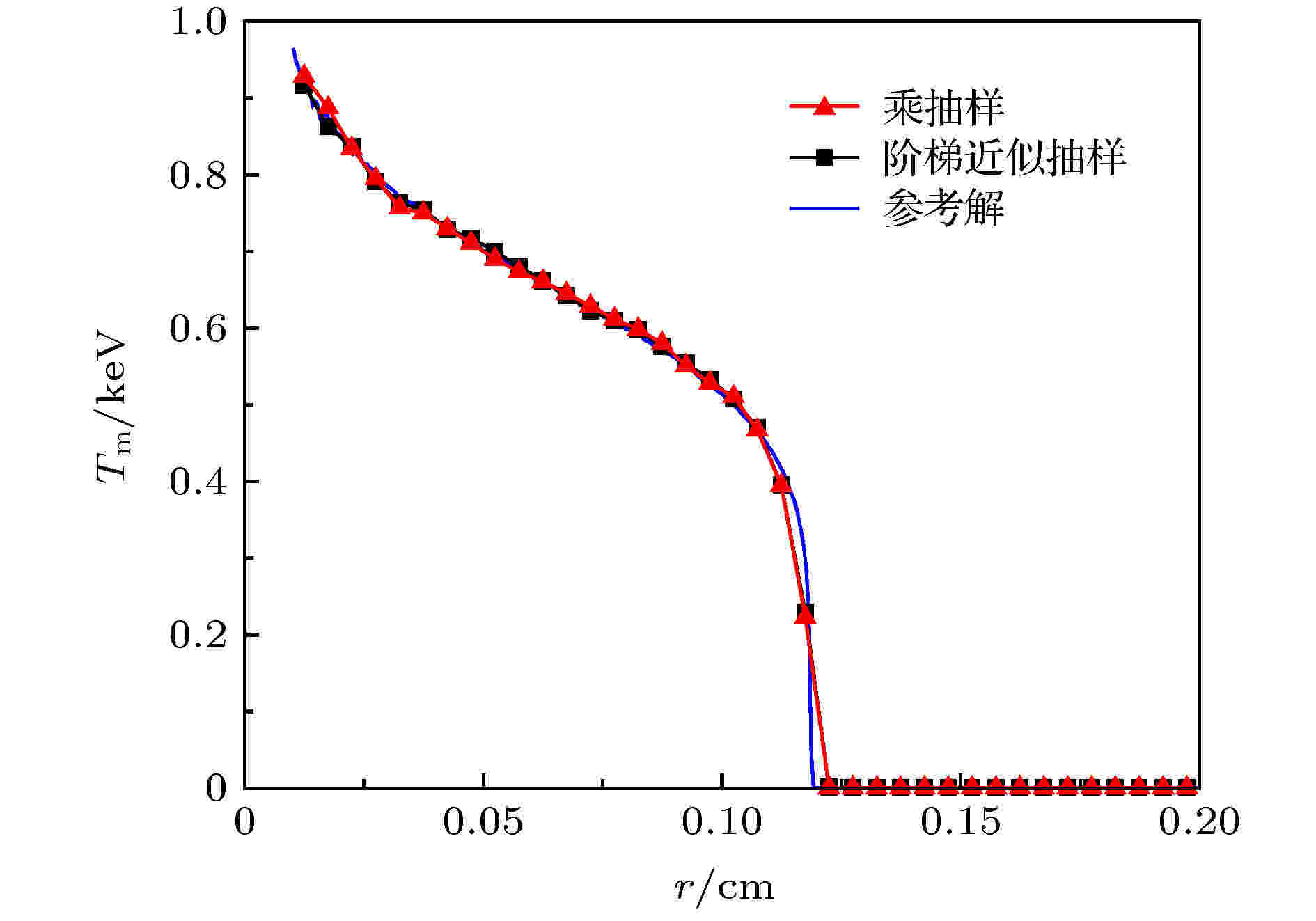图 6 网格数为40时两种新抽样法计算得到的物质温度空间分布(t = 10 ns)
Figure6. Results of two new sampling methods with 40 cells (t = 10 ns).

从图5可以看出, 除网格数为20时的计算结果外, 两种新抽样法的计算结果都没有出现明显的辐射波传播速度过快的问题. 值得注意的是, 当网格数为40时, 两种新抽样法的计算结果已经与参考解基本一致(如图6所示), 仅仅在辐射波头处与参考解有所偏差, 其原因与文献[20]中的类似, 即在波头处温度随半径r的变化规律偏离了线性, 温度线性变化假设不太适用(事实上网格数为20时的计算结果的误差也是由该原因引起的). 波头处的偏差可通过加密网格或引入更复杂的T-r关系及抽样方法解决, 该偏差对大多数热辐射输运问题的影响不大. 仅从图5和图6还不能明显地看出乘抽样法和阶梯近似抽样法对模拟结果修正的差异, 为了更加直观地比较两者的模拟结果以及两者相对等温抽样法的修正效果, 表3列出了各温度曲线相对基准解的偏差, 可以看出, 两种新抽样法得到的温度曲线同样随着网格数的增加而减小, 另外在40网格时两者的温度曲线与参考解的标准偏差已经接近甚至小于等温抽样法200网格时温度曲线的标准偏差(如表1), 而最大误差更是明显小于后者, 说明两种新抽样方法在40网格时得到的温度曲线已经和参考解相当. 至于乘抽样法和阶梯近似抽样法哪个更优, 后者的标准偏差和最大误差仅比前者略小, 因此并不能确定后者比前者更优, 具体采用哪种方法可根据实际情况确定. 总体上, 线性假设是球壳中温度空间分布规律的一种较好的近似, 由此推导出的两种新抽样方法也比等温法更符合源粒子的发射规律.

Cell number	乘抽样法			阶梯近似抽样法
	Standard deviation/eV	Maximum error/eV		Standard deviation/eV	Maximum error/eV
20	21.60	91.6		18.80	77.8
40	13.60	75.4		12.40	68.7
100	10.40	77.9		10.40	87.6
200	5.64	63.3		5.27	59.5

表3不同网格数时的温度曲线相对基准解的标准偏差和最大误差
Table3.Relative to the reference solution, the standard deviation, and the maximum error of temperature curves with difference cell numbers.

辐射源粒子抽样方法改进后, 计算结果不太依赖于网格剖分, 即只要网格尺度不是特别大(例题的20个网格), 各种网格尺度的计算结果均能基本保持一致, 因为线性假设下网格内辐射源粒子的空间分布更加符合实际, 受网格尺度的影响很小. 下面从节省计算时间角度来看新方法的改进效果, 表4是采用新旧抽样法模拟不同网格剖分模型的计算时间, 可以看出计算费用基本上均与模拟粒子数呈线性增长关系. 另一方面, 根据图6的比较可以知道, 在网格相对比较大(40个网格)的情况下, 计算结果的精度已经能够得到保证, 故利用新方法来模拟时可采用相对较少的网格和较少的粒子, 由此可以节省大量的计算机时. 对于本文例题, 如果采用旧方法, 则网格至少为200, 对应的计算机时为2.28 × 10⁴ s, 采用新方法, 则网格只需要40即可, 对应的计算机时为2.56 × 10³ s, 这大致相当于效率提升了约9倍.

Sampling method	Cell number	Particle number/104	Computation time/103 s
等温法抽样	20	1	1.80
	40	2	2.72
	100	5	5.74
	200	20	22.80
	400	40	50.60
乘抽样法	20	1	1.65
	40	2	2.56
	100	5	5.64
	200	20	22.40
阶梯近似抽样法	20	1	1.61
	40	2	2.58
	100	5	5.75
	200	20	22.40

表4计算问题所花时间
Table4.Computation time of the problem.

本文研究了球几何中辐射源粒子的空间分布, 分析了IMC方法中传统源粒子抽样方法的不足, 推导了球几何中基于能量密度分布的源粒子空间概率密度函数及相关参数的计算公式, 提出了两种新的源粒子空间抽样方法及流程, 新的空间概率密度分布函数能更准确地描述源粒子辐射的物理规律, 而且两种新抽样方法也能避免传统抽样方法在“强吸收”或“大网格”情况下计算结果偏差太大的问题. 由于在球几何中确定论方法难以得到精确的热辐射输运的解析解, 本文在传统的源粒子空间均匀抽样法下, 通过精细划分网格使计算结果收敛于真解, 并将该收敛后的结果作为两种新的源粒子抽样方法计算结果的参考解. 结果表明: 两种新抽样方法的计算结果与参考解相符, 很好地解决了“强吸收”或“大网格”情况下IMC模拟的热辐射传播速度过快的问题以及计算结果依赖于网格剖分的困扰; 同时由于新抽样法只需较少的网格、较少的粒子便可得到传统抽样法需要较多网格、较多粒子才能获得的准确结果, 故新抽样法还显著提高了计算效率, 大幅节省了计算资源. 下一步将开展复杂T-r关系下辐射源粒子精确抽样方法研究.