摘要: 淋巴系统是人体内重要的防御功能系统, 具有三大免疫功能, 首先是能够抵御细菌病毒, 使人体免于疾病的攻击; 其次是由淋巴细胞加以辅助, 清除由新陈代谢而出的产物; 最后是由淋巴细胞来修补受损的器官与组织, 使其恢复正常的生理功能。淋巴系统没有像血液循环系统中心脏一样的动力泵, 淋巴液的驱动主要靠淋巴管的自主收缩来完成(肺淋巴系统是靠肺泡的运动)。淋巴管的自主收缩循环是由淋巴肌细胞内钙离子增加产生收缩, 收缩驱动流体产生剪切力, 剪切力使淋巴内皮细胞产生一氧化氮合酶(eNOS), 一氧化氮合酶使一氧化氮增加, 一氧化氮的增加降低钙离子使淋巴管松弛, 淋巴管松弛后流体剪切率下降, eNOS下降, 一氧化氮下降, 钙离子增加, 淋巴肌细胞收缩, 开始新的周期。可见一氧化氮的浓度及其分布对淋巴管的收缩起关键作用。显然出口压力会影响淋巴管内流体的剪切率, 进而影响一氧化氮的浓度和淋巴管的收缩。为了研究淋巴管出口压力对淋巴管收缩的影响, 建立了一个晶格玻尔兹曼模型, 模拟嵌入多孔组织的初始淋巴管和有两对瓣膜的集合淋巴管, 该模型可以重现一氧化氮、钙的相互影响以及淋巴管的自主收缩, 并研究不同出口压力下一氧化氮的分布及其平均值.
关键词: 淋巴管 /
晶格玻尔兹曼方法 /
瓣膜 /
一氧化氮 English Abstract Investigation of NO content varaitaion in the lymphatic vessels under different outlet pressures by a lattice Boltzmann method He Yi-Nan 1 ,Zhang Qian-Yi 1 ,Wei Hua-Jian 1 ,Shi Juan 2 1.School of Material Science and Engineering, Guilin University of Electronic Technology, Guilin 541004, China Received Date: 22 December 2019Accepted Date: 09 March 2020Published Online: 20 May 2020Abstract: The lymphatic system is an important defense function system in the human body. It is also critical to humoral homeostasis. Local dysfunction will cause edema, immune deficiency, and a high incidence. There are intraluminal valves in the lymphatic system, which allows the lymph fluid to flow to the large veins and heart. It has three major immune functions. First, it can resist bacterial viruses and protect the human body from disease attacks. Secondly, it is supplemented by lymphocytes to remove the products produced by metabolism. In the end, The damaged organs and tissues are repaired by lymphocytes to restore normal physiological functions. The lymphatic system does not have the same pump as the heart of the blood circulatory system. The driving of lymph is mainly done by the spontaneous contraction of the lymphatics (the lung lymphatic system is compressed by the alveoli). The autonomic contraction cycle of lymphatic vessels is caused by the increase of Ca2+ in lymphocytes, and the contraction drives the fluid to produce shearing force. The shearing force produces nitric oxide synthase (eNOS) in lymphatic endothelial cells, and eNOS increases NO and increases NO. Decreasing Ca2+ relaxes lymphatic vessels, fluid shear rate decreases after lymphatic vessel relaxation, eNOS decreases, NO decreases, Ca2+ increases, lymphocytes contract, and a new cycle begins. It can be seen that the concentration of NO and its distribution play a key role in the contraction of lymphatic vessels. Obviously, export pressure affects the shear rate of fluid in the lymphatics, which in turn affects the concentration of NO and the contraction of lymphatic vessels. To investigate the effect of lymphatic outlet pressure on lymphatic vessel contraction, we established a lattice Boltzmann model to simulate the initial lymphatic vessels embedded in porous tissue and the collecting lymphatic vessels with two pairs of valves. The valve is the main source of NO. Once contraction begins, the contraction is spontaneous, self-sustaining, and the system exhibits non-linear dynamics. This model can reproduce NO and The interaction of Ca2+ and the spontaneous contraction of lymphatic vessels, and the distribution of NO under different outlet pressures and their average values were studied.Keywords: Lymphatic vessel /lattice Boltzmann method /valve /NO 全文HTML --> --> --> 1.引 言 淋巴系统由淋巴器官、淋巴液以及淋巴管道组成. 而淋巴管又分为毛细淋巴管、淋巴干及淋巴导管, 淋巴管作为淋巴液回归血液循环的闭锁管道, 与人体众多组织中的血液毛细血管平行. 淋巴液、组织液体与血浆三者之间存在着物质交换关系, 当血浆流经毛细血管时, 水和其他一些可以透过毛细血管壁的物质在毛细血管的动脉端渗出, 进入到组织细胞间隙中成为组织液, 而绝大部分的组织液在毛细血管静脉端又重新渗入到血浆中. 少量的组织液还可以渗入到毛细淋巴管, 形成淋巴, 之后淋巴经淋巴循环由左右锁骨下静脉汇入血浆中. 淋巴管允许组织液从间质间隙扩散到淋巴毛细血管, 且淋巴毛细血管可以吸收小肠中的短链脂肪酸. 弗吉尼亚大学医学院的Louveau等[1 ] 发现大脑会通过淋巴管道与免疫系统直接联结, 由于这些淋巴管独特的位置, 致使解剖学家这么多年未发现其位置, 这项新发现直接颠覆了几十年来写在教科书上的结论. 这对阿尔茨海默氏症、自闭症、帕金森症、多发性硬化症以及其他大脑疾病有着重大影响, 由此可知, 数值模拟对于研究淋巴管内协调作用有着极其重要的意义. 早期的淋巴系统网络模拟模型, 是一种简单明了的一维模型, 该种模拟基于流体力学的Navier-Stock(NS)方程, 由Margaris和Black建立[2 ] . 而后Macdonald等[3 ] 对该模型进行了改进, 只模拟了小段淋巴管. 淋巴管泵送的复杂模型可以解释振荡行为, 并且这些行为对局部的结构以及压力非常敏感.ATP , 以周期性的变化参与生理状态下淋巴管的收缩、舒张以及张力调节[4 ,5 ] . 哈佛医学院Kunert等[6 ] 和Baish等[7 ] 阐明了淋巴管泵送行为是如何通过动力学反馈在整个淋巴系统中进行协调的. NO与Ca2+ 浓度建立了自我调节的震荡反馈环路, 维持正常的淋巴功能. 然而, 这些研究在进行模拟时, 腔内瓣膜是在逆向流动期间以数学的方式插入不可渗透的壁而施加的. 虽然这种方法能够正确重现在体内观察到的行为, 但它简化了瓣膜性能, 从而忽略了瓣膜材料结构与力学性能以及产生的NO. 实际研究发现瓣膜是NO的主要来源.2.晶格玻尔兹曼方法及其基本理论 22.1.基本理论 2.1.基本理论 在计算流体动力学方面, 晶格玻尔兹曼方法(LBM)是一个非常好的工具. 迄今为止, LBM已经成功地应用到了多种复杂流体系统, 如多孔介质流[8 ] 、多相流[9 ] 、淋巴流[10 ] 等.${f_i}$ 代替布尔变量, LBM演化方程为${f_i}({{x}}, t)$ 是在x t 时刻, 具有${{{e}}_i}$ 速度的粒子分布函数. $\varOmega ({f_i})$ 是碰撞因子, 表示碰撞对于${f_i}$ 的影响.[11 ] , 碰撞项被简化为$f_i^{({\rm{eq}})}$ 是局域平衡分布函数, $\tau $ 是弛豫时间, LBM方程写为$\rho $ 是格点上流体的质量, u 图1 所示. 利用Chapman-Enskog多尺度展开[12 ] , 得到局域平衡分布函数:图 1 D2 Q9晶格玻尔兹曼模型的微观速度Figure1. Microscopic velocity of D2 Q9 lattice Boltzmann model.${\omega _i}$ 有下列形式:2.2.反向弹回边界条件 -->2.2.反向弹回边界条件 在做流体力学方面的研究时, 流体相关的规律与性质需要由边界条件来加以控制. 而LBM的基本变量是分布函数, 故LBM在构造边界条件时, 需要结合流体的宏观条件. LBM的所有边界条件都是基于反弹边界条件修改而来.图2 所示, 该模型被简单地分为两层, 白点层代表固体, 在上面的黑色点是距离边界层最近的流体点. 我们假设流体粒子从A , B , C 三个位置沿着速度方向1, 3, 5流动到边界上位置D , 当分布函数到达后, 在下一时间步流体又从位置D 沿着相反的速度方向2, 4, 6流回到流体层, 此过程满足质量守恒定律, 且边界处的平均速度是0.图 2 反向弹回示意图Figure2. Bounceback.[13 ] 可以用来改变流体流动的阻力. 调整2, 4, 6的分布函数中从1, 3, 5反向弹回和前方流体点流过来的2, 4, 6方向分布函数的比例, 即可以使边界在没有流动和自由流动之间改变.3.数值模拟结果与讨论 23.1.淋巴管模型 3.1.淋巴管模型 我们建立的淋巴管模型是由两个瓣膜限定的具有嵌入组织的单个淋巴管段, 如图3 所示. 在完全松弛状态下, 淋巴管的直径为100 μm, 即2R 0 = 100 μm. 组织液可以从左侧具有固定几何形状的多孔管道进入, 而这段管道代表了初始淋巴毛细血管[14 ] . 为了模拟淋巴毛细血管中的主要瓣膜, 该模型的实线区域是不可渗透的, 而虚线区域是半渗透的, 使用部分反弹边界条件实现[13 ] . 我们使用恒定的反弹比$\xi = 0.85$ , 这表示当压力条件有利于在此方向上的流动时, 有15%的流体可以渗透回组织. 渗透部分和不可渗透部分的面积比例为1∶1, 而淋巴毛细血管瓣膜可以使液体流入, 但禁止回流. 淋巴管的右端表示出口, 将与下游淋巴管或淋巴结连接. 在这部分, 我们引入长为234 μm的固定端, 用来提供结构支撑, 以减少右侧边界的影响.图 3 淋巴管段示意图Figure3. Lymphatic section.[11 ] . 上下淋巴管壁被分解为200段, 瓣膜分解为32段, 每段只沿 y 方向运动淋巴管内壁上的内皮细胞可以产生NO[15 ] , 且随着淋巴管内壁上剪切应力的增加而增加. 产生的NO会在流体和组织中对流和扩散:${C_{{\rm{NO}}}}$ 是 NO的浓度, ${D_{{\rm{NO}}}}$ 是NO的扩散系数, h 是化学反应速率常数. $h\Delta t$ 决定了化学反应时间, $\Delta t$ 是格子时间, 随着h 的增加, 化学反应速度增加. $K_{{\rm{NO}}}^-$ 和$K_{{\rm{NO}}}^+$ 是NO的衰减率和生成系数. 我们认为, NO的产量与切线方向的应力$\left| {\partial {\upsilon _l}/\partial {x_n}} \right|$ 成正比[16 ] . ${\upsilon _l}$ 表示淋巴管内表面的切线方向的流体速度, ${x_n}$ 表示沿着法线方向的梯度. 在淋巴管内, 瓣膜也可以产生NO.2+ 浓度决定, Ca2+ 可以进入、离开淋巴肌细胞的细胞质, 也可以通过连接点到达相邻细胞, Ca2+ 的反应扩散方程如下:${C_{{\rm{Ca}}}}$ 是Ca2+ 的浓度, ${D_{{\rm{Ca}}}}$ 是Ca2+ 从一个细胞扩散到邻近细胞的扩散系数, $K_{{\rm{Ca}}}^ - $ 是Ca2+ 的衰减率, $K_{{\rm{Ca}}}^ + $ 是Ca2+ 的产生速率, $K_{{\rm{Ca}}}^{+}{((R - {R_{\rm{l}}})/({R_{{\rm{Ca}}}} - {R_{\rm{l}}}))^{11}}$ 是淋巴管扩张产生Ca2+ 的非线性项[17 ] , R 和${R_{{\rm{Ca}}}}$ 分别是淋巴管的局域半径和非线性项的参考半径, ${R_{\rm{l}}}$ 是管子的最小半径, $\delta \uparrow $ 是一个非对称Kronecker函数, 如果${C_{{\rm{Ca}}}}$ 从低于阈值${C_{{\rm{th}}}}$ 增加到${C_{{\rm{th}}}}$ , 则该函数被设定为1, 其他情况被设置为0.3.2.淋巴管壁所受的力以及瓣膜 -->3.2.淋巴管壁所受的力以及瓣膜 有五个力施加在淋巴管壁上: 流体力F 、淋巴肌力${F_{\rm{M}}}$ 、弹性力${F_{\rm{E}}}$ 、弯曲力${F_{\rm{B}}}$ 、黏性阻力${F_{\rm{r}}}$ .F 可以通过压力张量积分求得:${\delta _{ij}}$ 是Kronecker函数且i = x , j = y , $\rho $ 是格点上流体的质量, u ${\rm{d}}{{s}}$ 最近的流体点的分布函数来代替${f_i}$ . n ${\rm{d}}{{s}}$ 上的单位矢量, ${{{u}}_s}$ 是面积${\rm{d}}{{s}}$ 的速度.${F_{\rm{M}}}$ 与上文提及的Ca2+ 浓度和NO的浓度有关:${k_{\rm{M}}}$ 是决定力的常量系数.${F_{\rm{E}}}$ 来源于淋巴管组织:$R < {R_{\rm{l}}} + \varDelta $ 时, 需将乘以一个11次幂来增加${F_{\rm{E}}}$ :${F_{\rm{B}}}$ 我们假设淋巴管的左右两侧是固定, 淋巴管的各段可以沿y 方向移动:i 表示某一离散片段.${F_{\rm{r}}}$ 在进行计算时需要考虑到淋巴管的黏弹性, 且黏性阻力作用于壁面速度$\nu $ 相反的方向上:图4 所示.图 4 静止状态下淋巴管瓣膜Figure4. The lymphatic valves at rest.y 0 是瓣膜静止或极限位置, H 是静止状态下淋巴管的位置, x 0 是瓣膜的锚点, 负正号分别代表上下瓣膜, A 起到控制瓣膜张角的作用.$F_{\rm{E}}^\nu $ , 弯曲力$F_{\rm{B}}^\nu $ , 黏性阻力$F_{\rm{r}}^\nu $ :i 表示瓣膜的某一离散片段.$F_{\rm{E}}^\nu $ :y c 代表淋巴管的中心线位置.${y_{{\rm{lp}}}}$ 时, 也同样需要增加$F_{\rm{E}}^\nu $ :[18 ] .3.3.计算参数 -->3.3.计算参数 我们采用型号为Nvidia Quadro GP100的专业级显卡, 该显卡具有较高的性价比, 拥有着16 G的显卡内存, 以及3584个CUDA核心, 一个专业级显卡所具备的CUDA核心直接反映着计算速度的快慢.$\tau = 0.75$ , υ = 0.01 cm2 /s, $D'=25$ 和D = 0.01 cm, 其中$D'$ 和D 分别代表着格子上淋巴管直径与实际上的淋巴管直径. 因此, 实际时间和空间尺度分别为T = 1.33 × 10–6 s, L = 0.0004 cm. 在本次计算中, 使用到的计算参数如表1 和表2 所列.参数 单位 数值 NO ${D_{{\rm{NO}}}}$ cm2 /s 1.2 × 10–4 $K_{{\rm{NO}}}^ - $ s–1 3.7594 $K_{{\rm{NO}}}^ + $ 无量纲 400 Ca2+ ${D_{{\rm{Ca}}}}$ cm2 /s 6.5 × 10–6 $K_{{\rm{Ca}}}^{-}$ s–1 37.6 $K_{{\rm{Ca}}}^{+}$ s–1 1.2 $K_\delta ^ + $ s–1 15038 ${C_{{\rm{th}}}}$ 无量纲 0.015 ${R_{{\rm{Ca}}}}$ cm 0.005 ${K_{{\rm{Ca}}, {\rm{NO}}}}$ 无量纲 5.3 h 无量纲 0.03
表1 Ca2+ 与NO的化学参数Table1. Chemical parameters of Ca2+ and NO.参数 单位 数值 淋巴管 ${k_{\rm{M}}}$ ${\rm{dynes}}$ 7.6 × 10–5 ${k_{\rm{E}}}$ ${\rm{dynes}}/{{\rm{cm}}^{\rm{2}}}$ 4.52 ${k_{\rm{B}}}$ ${\rm{dynes}} /{{\rm{cm}}^2}$ 9045 ${k_{\rm{r}}}$ dynes·s/cm 4.8 × 10–9 ${k_{{\rm{NO}}}}$ 无量纲 1 ${R_{\rm{l}}}$ cm 0.003 ${R_{\rm{0}}}$ cm 0.005 瓣膜 $k_{\rm{B}}^\nu $ dynes /cm2 0—0.2 $k_{\rm{E}}^\nu $ dynes /cm2 9.0 × 10–4 $k_{\rm{r}}^\nu $ dynes /cm2 0.0091 A cm–1 1500 $\varDelta $ cm 2 × 10–4
表2 淋巴管与瓣膜参数Table2. Parameters of Lymphatic and valve.${\rho _{{\rm{in}}}}$ , 出口处的密度通过施加恒定压力边界条件也保持恒定值${\rho _{{\rm{out}}}}$ [18 ] . 边界上的NO浓度保持恒定值0, 且NO可以通过流体、瓣膜结构和淋巴管壁扩散. 在我们的模拟中, 保持${\rho _{{\rm{in}}}}$ = 1. 由于淋巴液被视为水, 因此压力单位为P = (L /T )2 g·cm–3 = 9.045 × 104 g·cm?1 ·s–2 , 而入口压力保持在$3.015 \times {10^4}{\rm{g}} \cdot {\rm{c}}{{\rm{m}}^{ - 1}} \cdot {{\rm{s}}^{ - 2}}$ .3.4.淋巴管出入口压力差对NO浓度的影响 -->3.4.淋巴管出入口压力差对NO浓度的影响 我们的模拟计算表明淋巴管收缩取决于NO浓度的变化, 而NO浓度变化情况取决于流体剪切率的变化. 因此从组织到淋巴管的压差可改变流体速度和泵送状态. 为了了解淋巴管对可能遇到的组织压力变化的反应, 我们设计了压力阶跃变化的方案. 即保持入口密度不变$ {\rho _{{\rm{in}}}} = 1~{{\rm{g}}/{\rm{c}}{{\rm{m}}^{3}}} $ , 通过改变出口处密度, 进而改变压力差.表3 和表4 所列.正压力差 ${{\rho _{{\rm{out}}}}} /$g·cm–3 1.0020 1.0015 1.0010 1.0008 1.0006 1.0004 1.0002 ${\Delta \rho }/$g·cm–3 0.0020 0.0015 0.0010 0.0008 0.0006 0.0004 0.0002 ${\Delta P} /$g·cm–1 ·s–2 60.3 45.225 30.15 24.12 18.09 12.06 6.03
表3 出口压强高于入口压强时正压力差Table3. Positive pressure when outlet pressure is higher than inlet pressure.负压力差 ${\rho _{{\rm{out}}}}/$g·cm–3 1.0000 0.99998 0.99996 0.9998 0.9996 $\Delta \rho /$g·cm–3 0 –0.00002 –0.00004 –0.0002 –0.0004 $\Delta P/$g·cm–1 ·s–2 0 –0.603 –1.206 –6.03 –12.06
表4 出口压强低于入口压强时负压力差Table4. Negative pressure when outlet pressure is lower than inlet pressure.图5 是时间t = 2.296 s时管内的NO分布. 注意压差不同淋巴管的收缩周期不同[10 ] , 所以同时刻淋巴管所处的状态不同. 如图5 所示, ΔP = 30.15 g·cm–1 ·s–2 , 此时淋巴管开始收缩, 左瓣膜关闭, 右瓣膜打开, 由此产生壁面剪切率变化影响到NO的产量. 瓣膜的运动进一步增加了瓣叶表面上的剪切应力, 在瓣膜附近产生较多的NO. 由于回流的原因, 一些NO从左瓣膜流出, 高浓度的NO从打开的右侧瓣膜排出, 从右侧瓣膜周围的NO的凸型状可以看出在瓣膜附近NO浓度较高, Glenn等[19 ] 已在小白鼠的淋巴管中已经观察到此现象.图 5 t = 2.296 s时, NO浓度分布图Figure5. t = 3.003 s, NO concentration distribution map.图5 所示, ΔP = 18.09 g·cm–1 ·s–2 , 此时, 淋巴管开始松弛, 左瓣膜打开, 右瓣膜关闭. 流体从左侧流入淋巴管, 与右侧相比, 该区域产生更多NO. 即使淋巴管松弛后, NO的浓度仍然较高, 当淋巴管达到舒张期峰值时, 流体速度变小, 并且产生很少的NO. NO迅速降解或扩散, 其浓度下降. 同时, 淋巴管准备进行下一次收缩. 收缩产生较高的剪切应力, 从而产生NO, 使其充满了淋巴管.图6 所示. 且高浓度的NO会降低淋巴管中Ca2+ 的浓度, 使淋巴管停止收缩. 此时淋巴管的半径小于静止时的半径, 这意味着淋巴管内的压力低于外部. ΔP < –10 g·cm–1 ·s–2 时, NO达到饱和, 不再增加.图 6 NO平均浓度与压强差关系图Figure6. Relationship between NO average concentration and pressure difference.2+ 的浓度增加, 激发下一次收缩, 迫使淋巴液流出淋巴管. 由于出口压力增加, 淋巴管的收缩也无法提升平均流量, 因此剪切率下降造成NO的平均值下降. 且当$\Delta P$ 过高后会造成出口瓣膜无法打开, 收缩没有周期性.4.结 论 我们使用晶格玻尔兹曼方法模拟了淋巴管段的收缩, 同时采用了基于淋巴管结构力学和NO的动力学模型, 最终再现自我持续循环的淋巴收缩并输运组织液. 计算结果表明NO的平均含量随着淋巴管两端压力差的变化而变化, 在负压强差时, 随着压强差绝对值的增加趋于平稳. 而在正压强差时, 随着压强差绝对值的增加先降低而后趋于稳定. 在负压力差的情况下, 由于入口压力高于出口压力, 只要流体达到一定的流速, 这时淋巴管内可以产生足够的NO, 抑制了钙离子, 淋巴管肌细胞停止收缩, 由压差驱动流体实现收缩的最小化. 反之如果出口压力过高, 收缩也无法令瓣膜打开, 流体无法正常输运, 淋巴管内NO和钙离子就无法产生有规律的振荡, 淋巴管收缩失去规律性. 由于在淋巴管内细胞也可以产生NO, 另外瓣膜还会存在一定的渗漏, 也会产生NO, 而且癌变细胞可以产生更高的NO, 所有这些影响都是我们后续将会进一步进行研究. 







 图 1 D2 Q9晶格玻尔兹曼模型的微观速度
图 1 D2 Q9晶格玻尔兹曼模型的微观速度
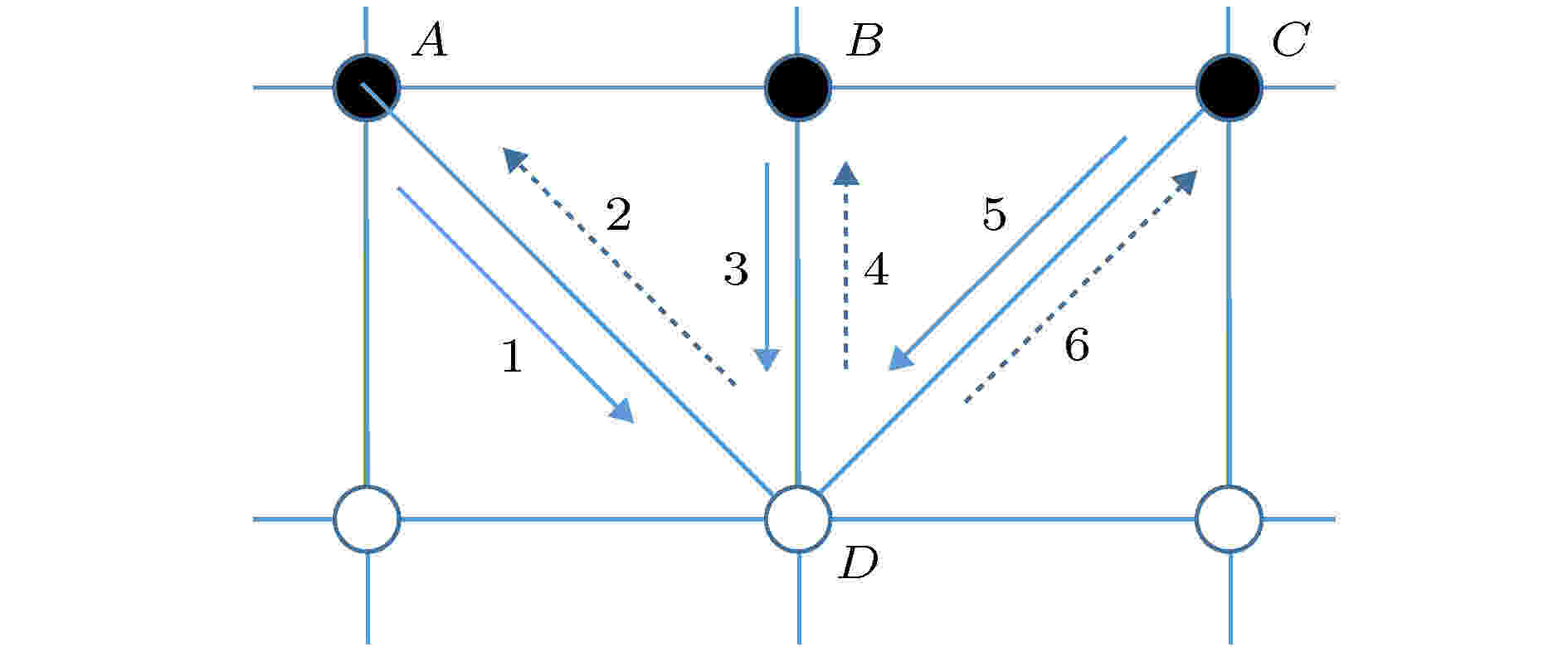 图 2 反向弹回示意图
图 2 反向弹回示意图
 图 3 淋巴管段示意图
图 3 淋巴管段示意图
















































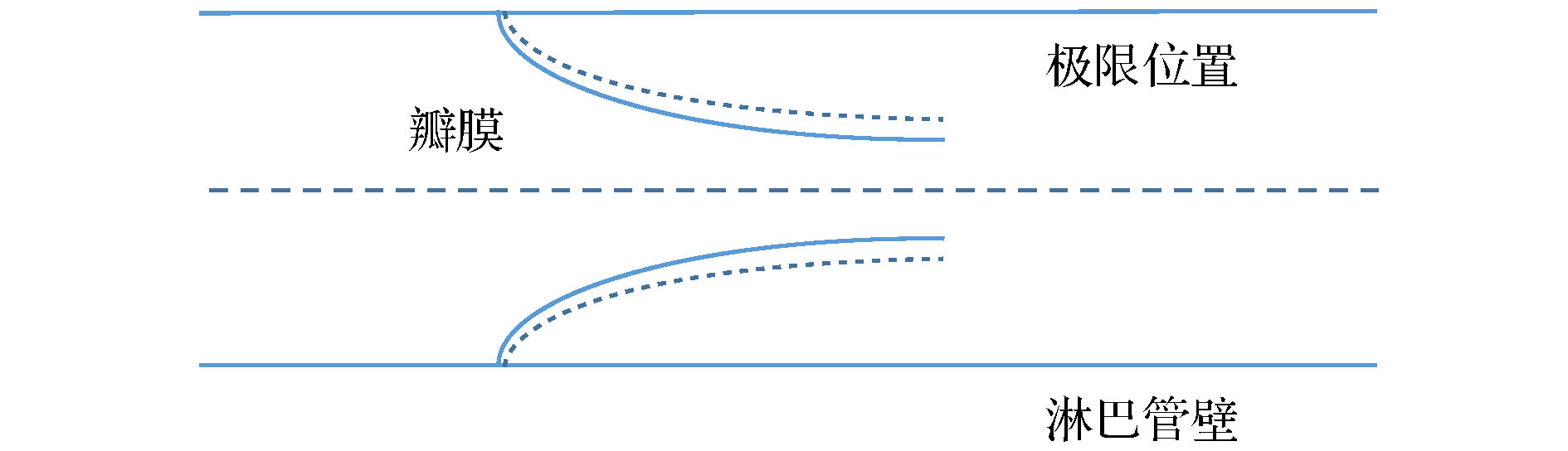 图 4 静止状态下淋巴管瓣膜
图 4 静止状态下淋巴管瓣膜















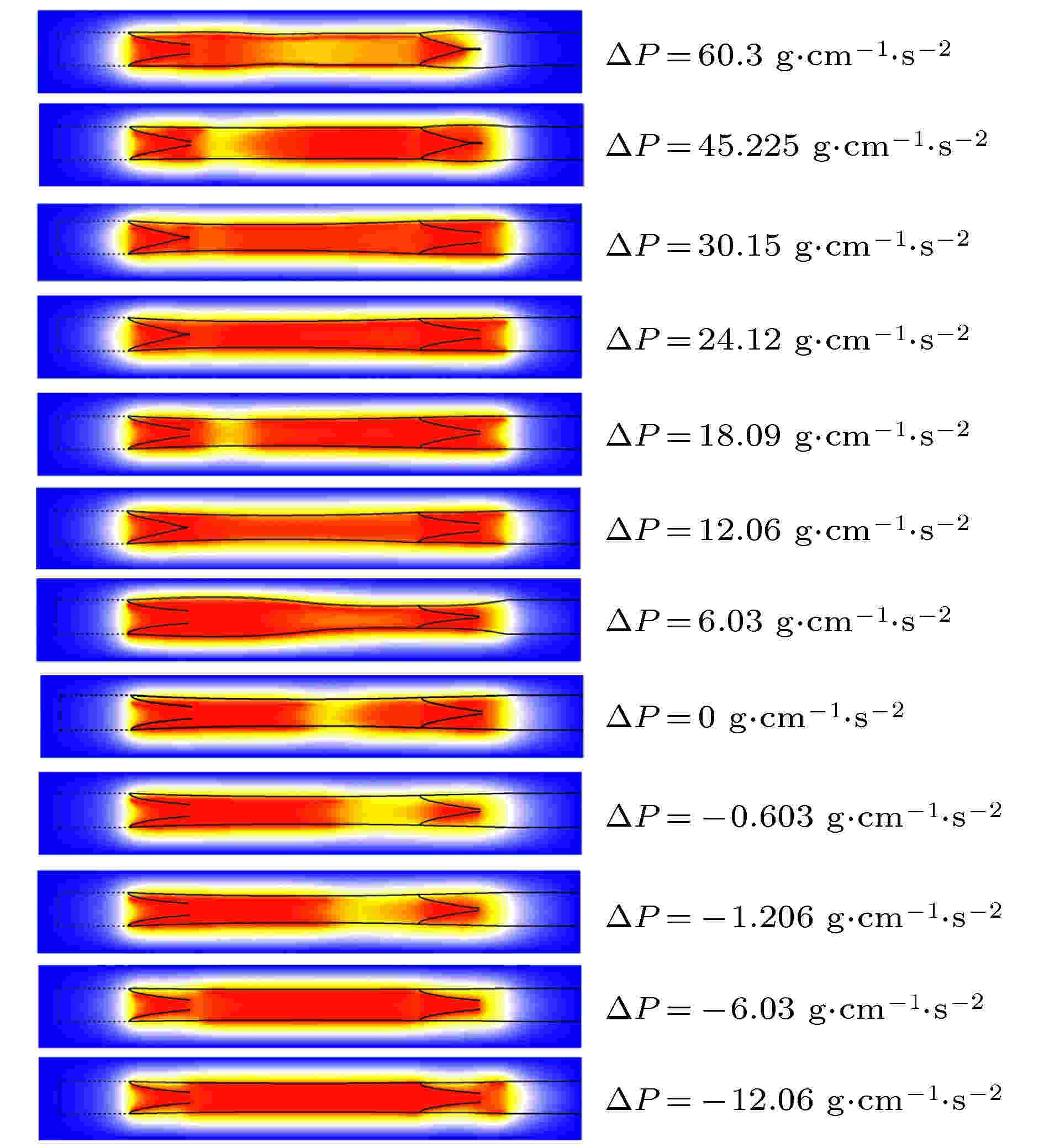 图 5 t = 2.296 s时, NO浓度分布图
图 5 t = 2.296 s时, NO浓度分布图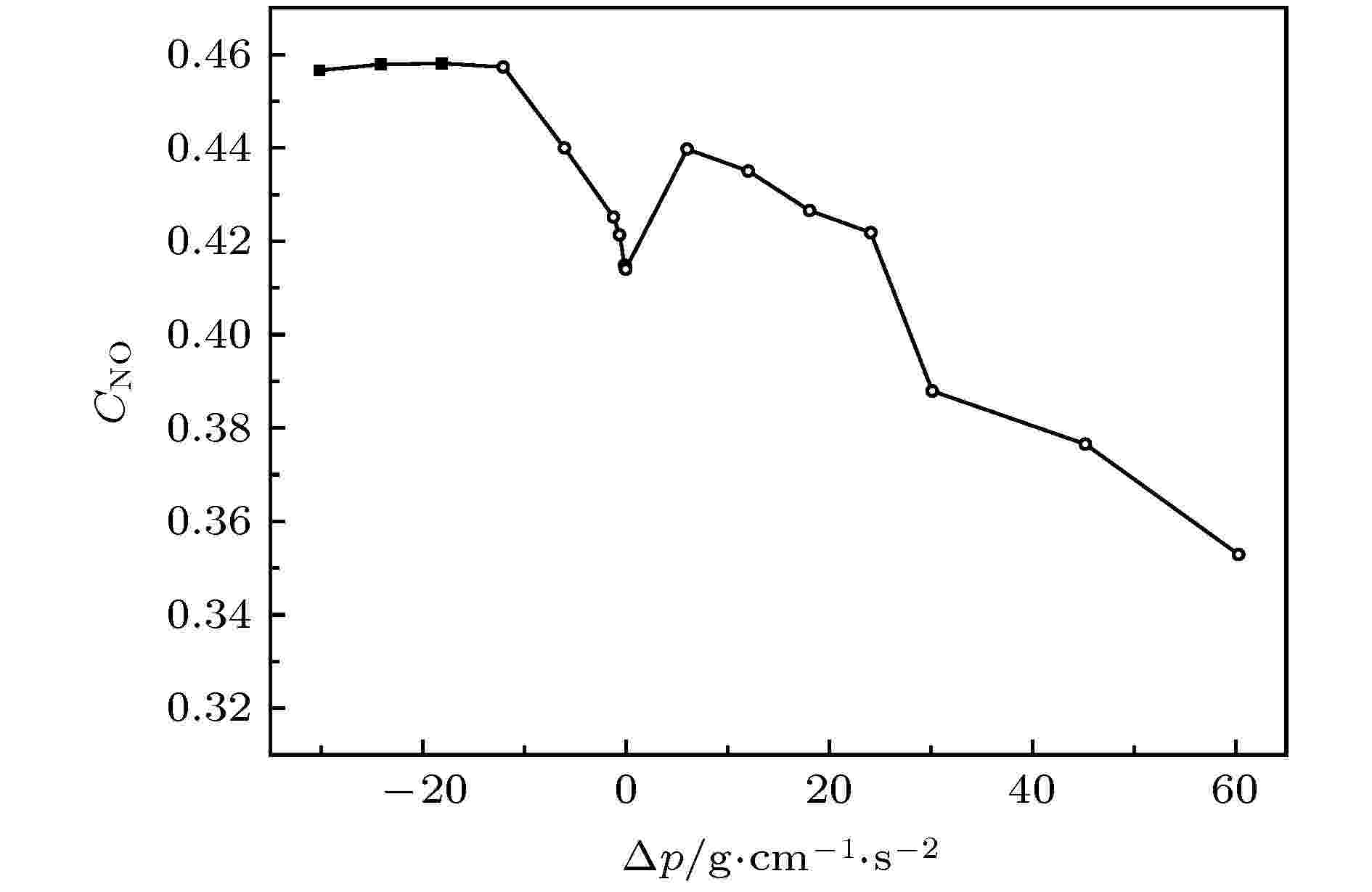 图 6 NO平均浓度与压强差关系图
图 6 NO平均浓度与压强差关系图
