全文HTML
--> --> -->目前, 国内外关于LSPR调制的研究大部分局限于单个光学波段紫外(ultraviolet, UV)/可见(visible, Vis)/近红外(near-infrared, NIR)或2个相邻波段(UV-Vis/Vis-NIR)范围内. Zhan等[16]利用纳米压印和超薄氧化铝技术结合的方法制备Ag纳米颗粒阵列, 在UV-vis-NIR波段范围内获得3个共振峰, 探究纳米粒子高度对SPR特性影响. Ji等[17]采用磁控溅射法在AAO模板上制备Ag纳米颗粒, 在UV-Vis波段范围内获得2个共振峰, 探究介电环境对LSPR吸收特性的影响. King等[18]通过电子束蒸发法制备Al纳米团簇, 在UV-vis波段范围内获得2个共振峰, 探究纳米团簇几何结构及颗粒尺寸对光学特性影响. Zhan等[19]利用AAO模板和超薄氧化铝技术结合的方法获得图案化的纳米孔, 通过电子束蒸发法制备Ag纳米颗粒阵列, 在UV-Vis波段范围内获得2个共振峰, 探究退火温度对光学特性的影响. Minamimoto等[20]通过电子束光刻法在ITO衬底上制备Au晶格结构, 在Vis波段内测得1个共振峰, 探究不同参数对光学特性的影响. Zhang等[21]提出透明导电氧化物/半导体/金属纳米线阵列结构, 在NIR波段范围内测得1个共振峰, 探究阵列周期及纳米线半径对LSPR吸收参数的影响. González-Rubio等[22]通过种子生长法制备Au纳米棒胶体, 在NIR波段范围测得1个共振峰, 探究金纳米棒长径比对峰宽的影响. 对于在UV-vis-NIR三个波段均可实现LSPR激发和调制材料的研究却鲜有报道.
本文基于阳极氧化法制备铝基纳米碗阵列模板, 利用真空蒸镀技术将Ag纳米颗粒沉积于纳米碗阵列中, 从而制得铝基银纳米阵列结构. 基于此结构, 通过改变阵列颗粒尺寸、形貌、间距等几何参数, 实现铝基银纳米阵列LSPR吸收特性的调制研究. 结合时域有限差分(finite-difference time-domain, FDTD)理论模拟, 分析讨论铝基银纳米阵列的光吸收特性的物理机制及调制规律.
2.1.Ag纳米球阵列的制备
周期性纳米球阵列结构的前期准备工作为阳极氧化铝(anodic aluminum oxide, AAO)纳米碗阵列制备, 如图1(a)—(c)所示. 将清洁的高纯铝片(纯度99.99%)在马弗炉中400—600 ℃的温度下退火4—6 h; 退火后将铝片在丙酮溶液中超声清洗5 min; 清洗后, 高纯铝片作为阳极, 铂片作为阴极, 置于冰水浴环境的抛光液(高氯酸∶乙醇体积比 = 1∶4)中, 在18 V的直流稳恒电压下进行电化学抛光2—3 min, 如图1(a)所示; 将电化学抛光后的高纯铝片作为阳极, 铂片作为阴极, 置于0.4 mol/L草酸溶液中, 在40 V直流稳恒电压下进行一次阳极氧化2—3 h (整个氧化过程需在配有磁力搅拌的冰水浴环境中进行), 得到AAO纳米管阵列, 如图1(b)所示; 在纳米管阵列生长过程中, 可通过电解液、氧化电压、氧化时间等参数来控制铝基纳米碗尺寸及有序性. 在60—70 ℃的水浴环境中对一次阳极氧化后的AAO纳米管阵列进行去氧化层处理(去氧化层腐蚀液为铬酸1.8 wt.%、磷酸6 wt.%混合溶液). 图1(c)为洗涤和干燥后孔心距为100—105 nm的AAO纳米碗阵列模板.
图 1 AAO纳米碗阵列和Ag纳米球阵列制备过程示意图 (a) 高纯铝片; (b) AAO纳米管阵列; (c) AAO纳米碗阵列; (d) Ag纳米颗粒; (e) Ag纳米球阵列Figure1. Schematic diagram of the preparation procedure for fabricating patterned aluminum templates and Ag nanosphere arrays: (a) Purity aluminum; (b) AAO nanotube arrays after the first anodization; (c) AAO nanobowl arrays after the removal of the porous alumina layer; (d) Ag nanoparticles; (e) Ag nanosphere arrays.
利用真空蒸镀技术将Ag沉积在AAO纳米碗阵列中, 进而制得Ag纳米球阵列. 实验装置如图2所示, 由LN-1004A型多源金属气相沉积系统和STM-2XM膜厚仪构成. 实验过程中, 可通过膜厚仪检测镀银厚度, 实现对银纳米球阵列尺寸和间距的有效调控(图1(d)—(e)). 利用玻璃、硅、高纯铝代替AAO纳米碗阵列, 制备普通Ag层作为对照, 与银纳米阵列制备过程实验参数严格保持一致.
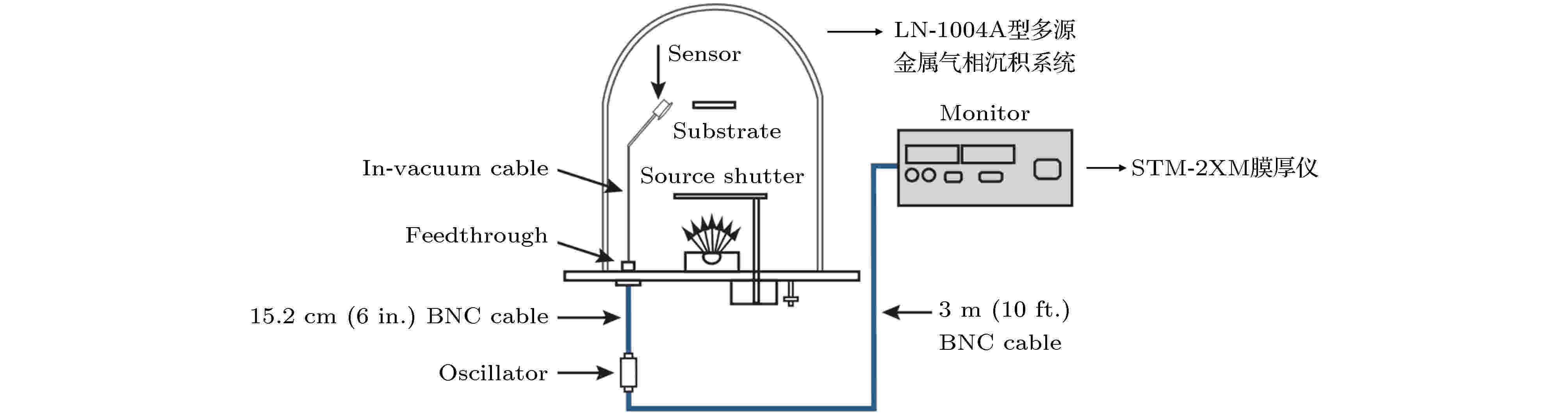图 2 真空蒸镀实验仪器示意图Figure2. Schematic diagram of vacuum evaporation apparatus.
2
2.2.表 征
通过场发射扫描电子显微镜(SEM-美国FEI公司的FEI QUANTA FEG 650)观察阵列形貌, 紫外-可见-近红外分光光度计(岛津UV-3600)测试一系列不同几何参数的纳米球阵列及对照样品的吸收光谱, 测试期间, 实验条件设置严格保持一致.2
2.3.模型建立与仿真
本文采用的仿真软件是Lumerical公司开发的FDTD Solutions, 它是一种用于数值求解Maxwell方程的模拟计算方法. 模型建立如图3所示, 从FDTD Solutions软件材料数据库中选取Al作为衬底, 衬底上放置Ag并设置为球形, Ag和Al介电常数取自Palik[23]. 定义任意相邻纳米球的球心距为100 nm, 网格区域划分为1 nm, 网格划分精度为5. 选用的光源是波长范围为300—1300 nm的平面波, 入射光从z轴反方向垂直射入, 覆盖整个模拟空间区域. 反射谱监视器放在光源上方, 透射谱监视器放在纳米碗下表面处. x轴和y轴方向选用的是周期性边界条件, 在z轴方向选用的是完全匹配层(perfectly matched layers, PML)条件. 在x-y-z轴选取一个100 nm × 173.205 nm × 100 nm的仿真区域作为最小单元, 同纳米球中心重合, 其中心坐标为(0, 0, 0). z轴的仿真区域覆盖整个监视器、光源、几何结构所构成的范围(吸收光谱被定义为A = 1－R－T, 其中R和T分别对应铝基纳米阵列的反射率和透射率). 对应实验测得数据, 在不同模型中, 分别设定纳米球直径为74, 78, 83, 86, 88, 90, 92和94 nm模拟吸收光谱.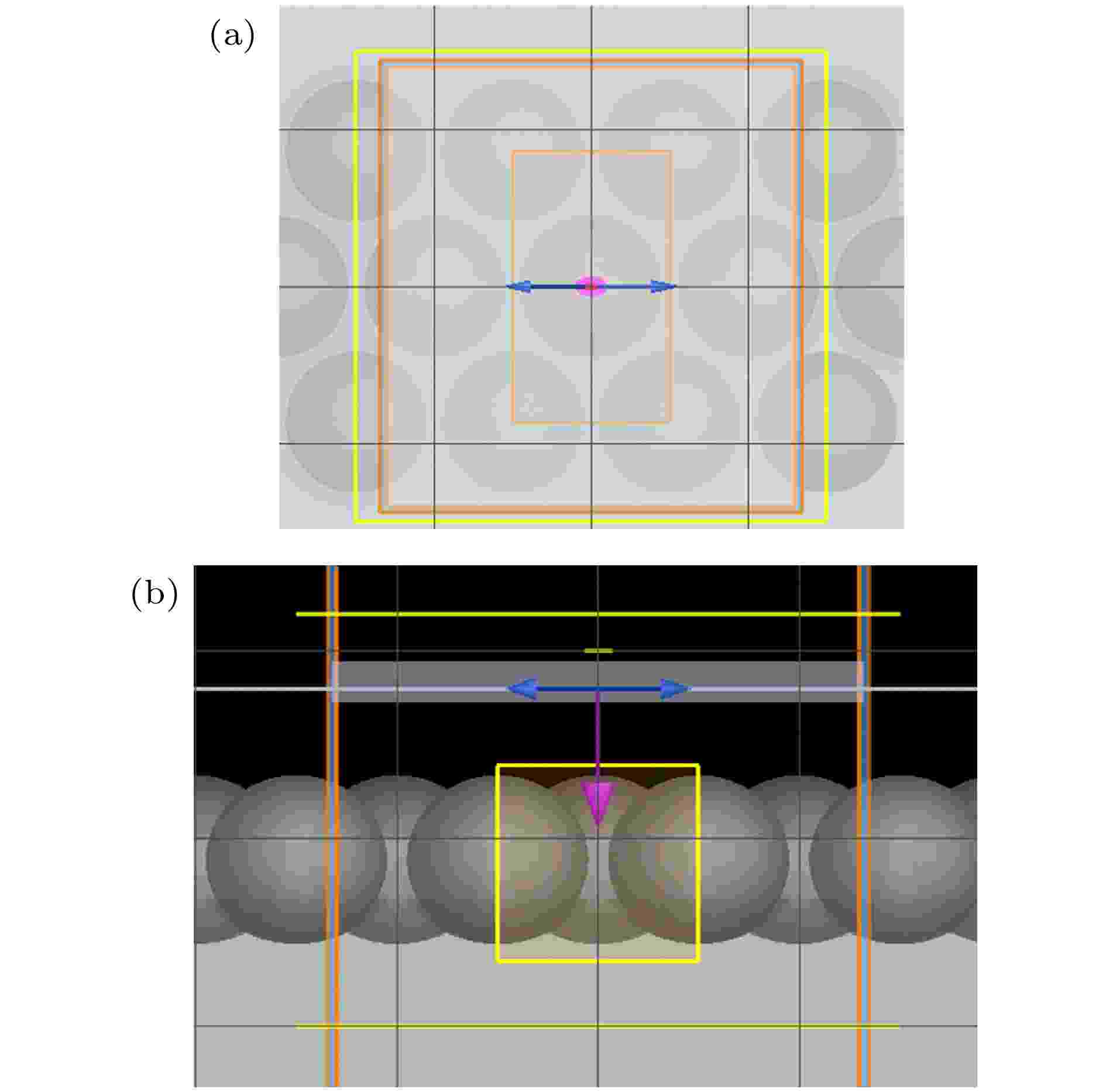
图 3 FDTD Solutions仿真模型 (a) x-y视图; (b) x-z视图Figure3. View of simulation model in FDTD Solution (a) x-y; (b) x-z.
图 4 (a) AAO纳米碗阵列SEM图; (b) Ag纳米球周期性阵列SEM图Figure4. SEM images of the (a) AAO nanobowl arrays and (b) periodic arrays of Ag nanospheres.
图4(b)中Ag纳米球的形成过程: 在真空蒸镀过程中, Ag气态粒子以基本无碰撞的直线运动到每一个纳米碗中心孔内, 一部分粒子被反射, 另一部分吸附在表面并发生扩散, 沉积原子之间产生二维碰撞, 形成团簇, 有的可能在表面发生短暂停留后又蒸发, 粒子团簇不断地与扩散粒子相碰撞, 或吸附或放出, 以此反复, 当聚集的粒子数超过某一临界值时变为稳定的核, 从而逐渐长大形成Ag纳米球[24].
贵金属纳米阵列结构的光学特性对颗粒尺寸、形貌、间距、材料及周围介电环境等因素十分敏感[16,25,26]. 本文通过控制银的蒸镀厚度有效调控纳米球阵列的颗粒直径, 图5(a)—(j)所示为一系列不同尺寸Ag纳米球阵列的SEM图. 利用Image J软件对银纳米粒子的直径进行测量, 对105个数据统计分析, 并进行高斯拟合求得平均值及误差范围, 图5(i)—(x)为粒径分布直方图, 直方图间接反映了周期性阵列中银纳米粒子尺寸的均匀程度. 图5(a)和图5(b)表明, 纳米颗粒类似AAO模板六角晶胞的形状, 据报道, 这种表面微观结构由电化学动力学导致[27], 由对应粒径直方图图5(i)和图5(ii)可知粒子平均直径分别为73.5和78.2 nm. 如图5(c)—(f)所示, 随着镀银厚度的增加, 粒子大小也逐渐增大, 并且粒径分布区间越来越相对集中, 说明周期性阵列粒子均一化程度逐渐变高, 阵列结构趋于高度有序化, 平均粒径从83.2 nm增加至90.1 nm, 如图5(iii)—(vi)所示. 图5(g)—(j)表明, 当Ag纳米粒子直径达到91.3 nm时, 阵列局部开始出现颗粒粘连, 周期性阵列结构遭到破坏, 图5(vii)—(x)可看出粒径分布区间跨度变大. 当颗粒直径大于94.2 nm (镀银厚度 > 16.7 nm)时, 如图5(k)—(n)所示, 阵列中的Ag纳米粒子大面积粘连, 周期性阵列结构完全被破坏.
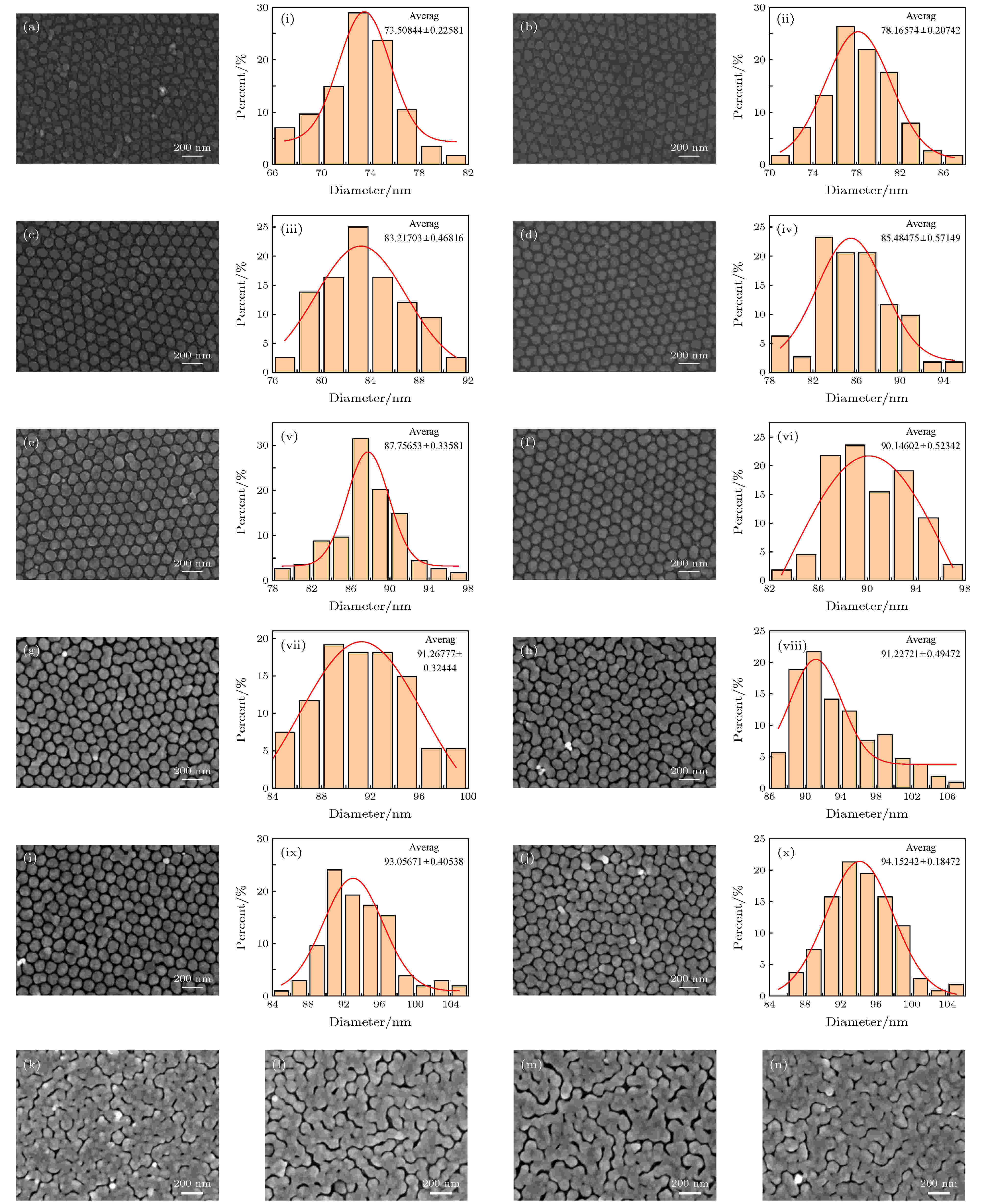图 5 不同粒径(D) Ag纳米球周期性阵列/不同厚度(T) Ag膜的SEM图 (a)?(n)及相应的粒径分布直方图(i)?(x) (a) D = 73.5 nm; (b) D = 78.2 nm; (c) D = 83.2 nm; (d) D = 85.5 nm; (e) D = 87.7 nm; (f) D = 90.1 nm; (g) D = 91.3 nm; (h) D = 91.7 nm; (i) D = 93.1 nm; (j) D = 94.2 nm; (k) T = 17.5; (l) T =18.2 nm; (m) T = 19.0 nm; (n) T = 19.7 nmFigure5. (a)?(n) SEM images of Ag nanosphere arrays/Ag film and (i)?(x) their related size distribution histograms: (a) D = 73.5 nm; (b) D = 78.2 nm; (c) D = 83.2 nm; (d) D = 85.5 nm; (e) D = 87.7 nm; (f) D = 90.1 nm; (g) D = 91.3 nm; (h) D = 91.7 nm; (i) D = 93.1 nm; (j) D = 94.2 nm; (k) T = 17.5 nm; (l) T = 18.2 nm; (m) T = 19.0 nm; (n) T = 19.7 nm.
图6(a)为不同粒径Ag纳米球阵列UV-vis-NIR吸收光谱. 从图6(a)可以看出, 不同阵列在UV-vis-NIR波段均表现出明显的电磁波吸收特性, 颗粒尺寸对于不同波段变化机制有所不同. 图6(b)为不同衬底制备Ag复合结构UV-vis-NIR吸收光谱, 对照组实验参数与银纳米阵列制备参数严格保持一致. Ag-AAO (黑色)曲线为粒径D = 90.1 nm的银纳米球阵列. 从图6(b)可以看出, 在UV波段内, 衬底为退火铝片和AAO模板的银复合结构吸收峰均为λ = 302 nm, 而硅衬底银复合结构吸收峰为λ = 255 nm, 玻璃衬底银复合结构吸收峰为λ = 313 nm, 这四种结构均出现与洛伦兹线型迥异的非对称光谱线型. 对比不同衬底, 硅和玻璃为衬底时, 共振吸收峰强度较弱, 而当铝为衬底时, 吸收峰明显增强, 这是由于银与衬底相互作用时产生感应电荷的大小与衬底的介电常数有关[28]. 吸收光谱中四种结构在约370 nm处的吸收峰为Ag的特征峰, 这归因于Ag的带间跃迁. 在Vis和NIR波段内, 相比衬底为硅和玻璃时, AAO模板制备的银纳米球阵列出现2个特有的吸收峰, 475 nm处的吸收峰相对较弱, 1002 nm处的吸收峰强而窄, 这可能与阵列结构的LSPR及周期性有关, 结合FDTD理论模拟, 下面将分段讨论阵列光学特性受尺寸调控的变化规律及不同波段共振峰的物理机制.
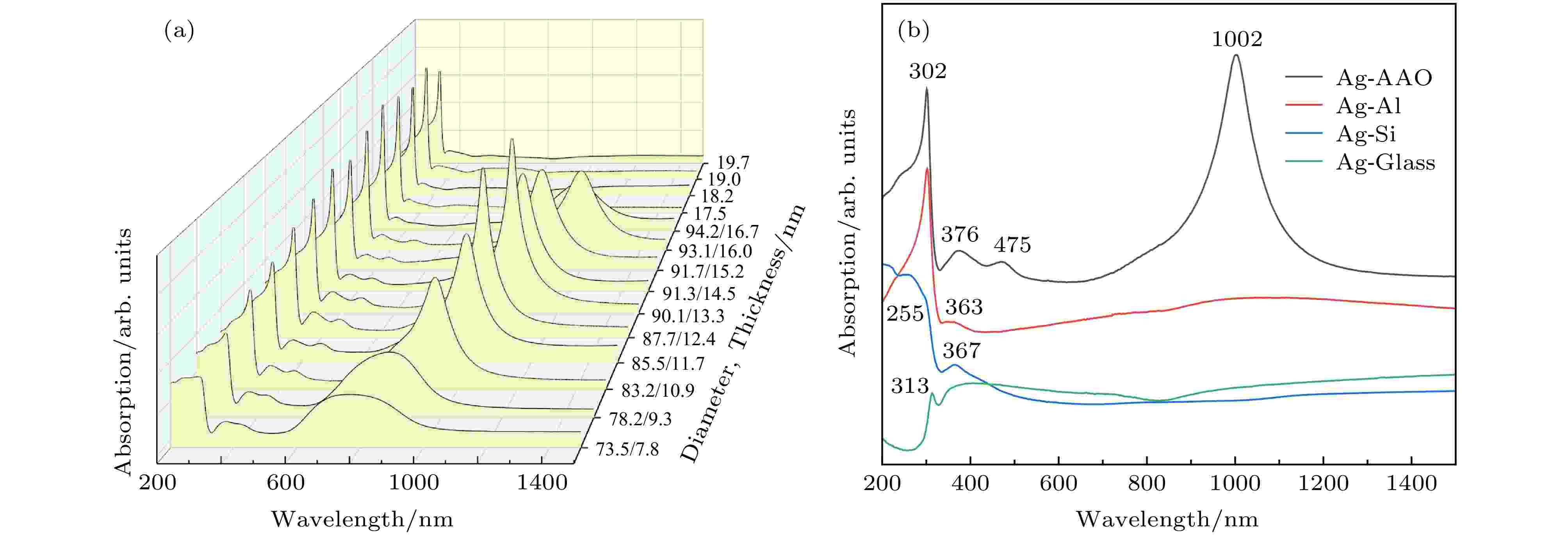图 6 (a) 沉积在AAO纳米碗上不同粒径Ag纳米球阵列UV-vis-NIR实验所得吸收光谱; (b) 不同衬底制备的银复合结构的吸收光谱Figure6. Experimental UV-vis-NIR absorption spectra of (a) Ag nanosphere arrays deposited on AAO-nanobowl with different sizes; (b) silver composite structure fabricated on different substrates.
图7(a)为UV-Vis波段不同粒径Ag纳米球阵列实验测得吸收光谱. Fano共振现象的产生源于原子系统中一个离散的激发态能级和一个连续的激发态能级相互叠加, 两个激发态之间发生量子干涉, 在特定的光频段出现零吸收现象, 从而使原子系统的光谱呈非对称线型. 在等离激元纳米结构中, Fano共振的激发需要构造出一个提供宽谱的超辐射模式(明模)和一个提供窄谱的亚辐射模式(暗模)[29,30]. 紫外波段范围内: 约300 nm处的非对称线形是由于衬底引入导致结构对称性破坏, 铝与金属银纳米球相互作用产生键合与反键合的等离激元杂化模式, 相互干涉产生Fano共振[31-33]. Fano共振中暗模式是通过与连续体的耦合而激发的.
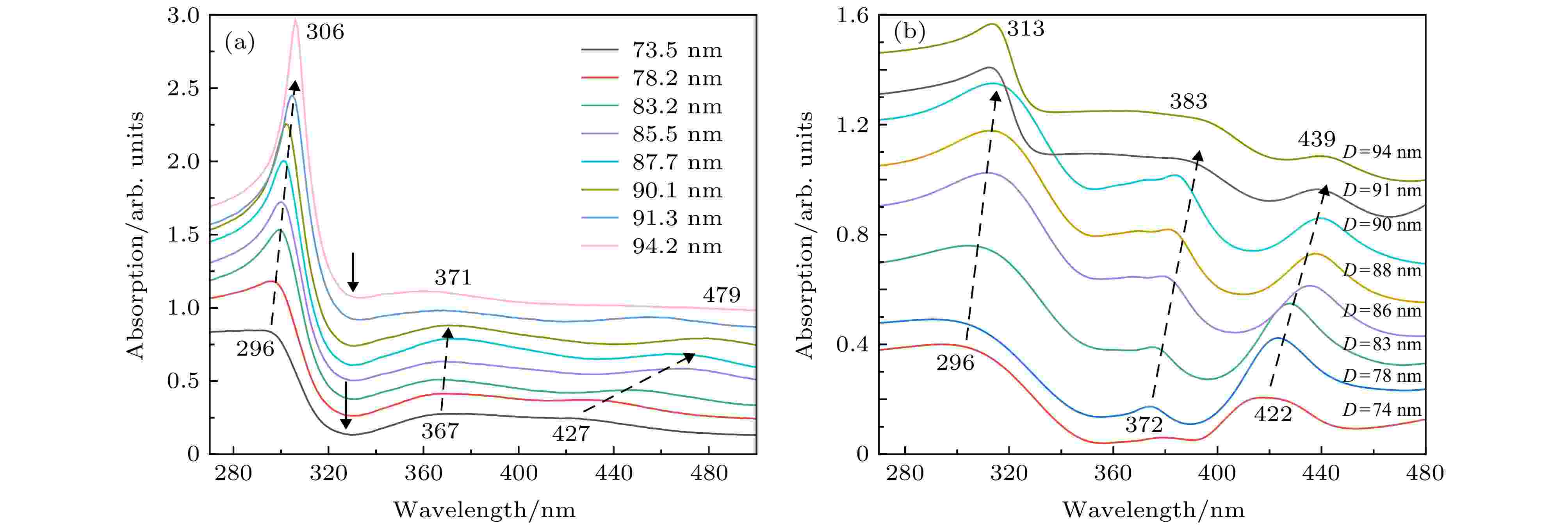图 7 (a) UV-Vis波段不同粒径Ag纳米球阵列实验所得吸收光谱和(b) FDTD模拟吸收光谱Figure7. UV-Vis absorption spectra of Ag nanosphere arrays with different sizes: (a) Experimental results; (b) FDTD simulation results
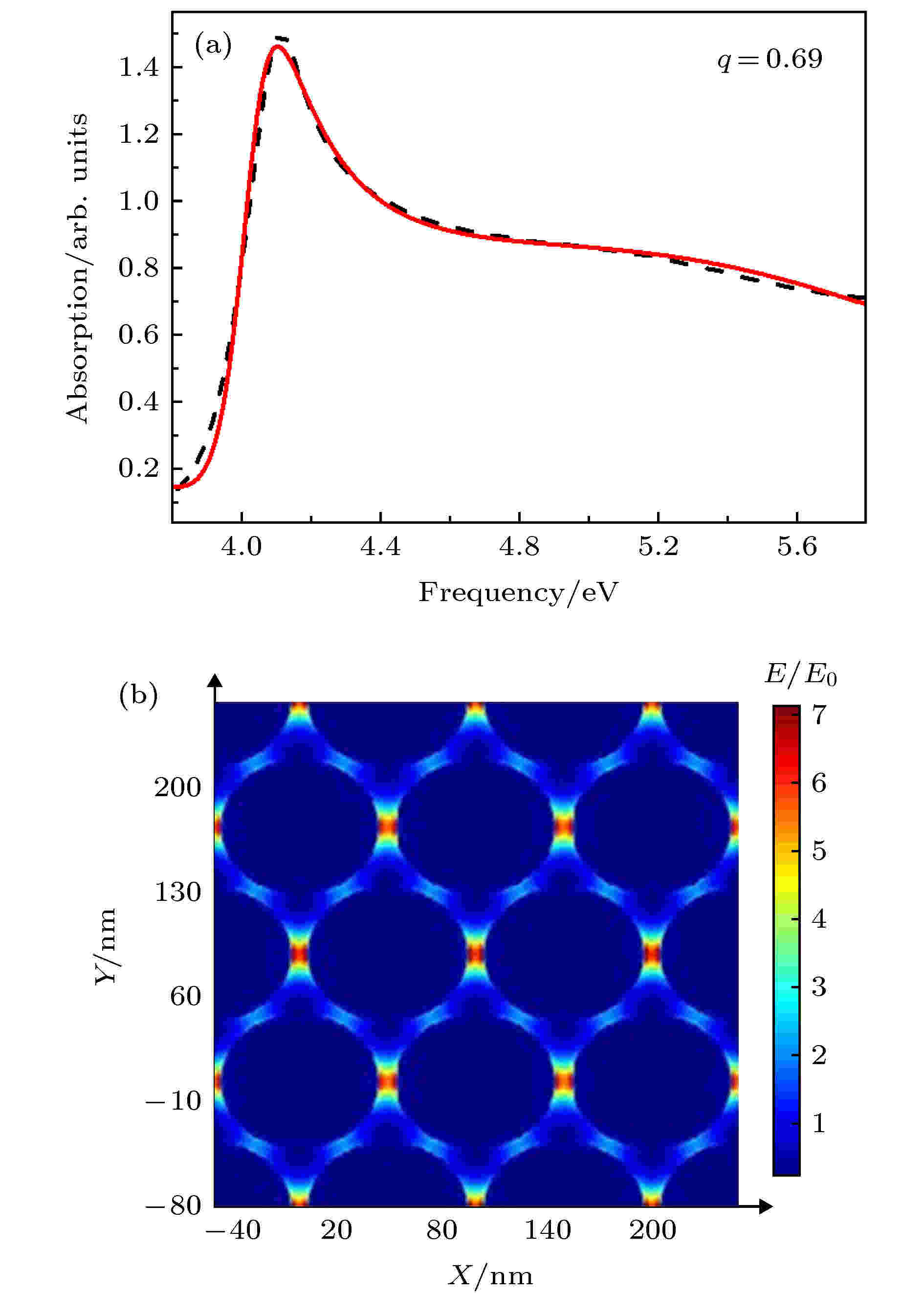图 8 (a)紫外波段Ag纳米颗粒实验测得吸收光谱(黑色虚线), 以及根据(3)式拟合得到的吸收光谱(红色); (b) Ag纳米球阵列在437 nm波长下x-y平面(z = 0)的极化电场分布Figure8. (a) UV absorption spectra of Ag nanosphere arrays (black dashed line is experimental results; red line corresponds to σt obtained by fitting the Eq. (3); (b) polarized field distributions on the x-y plane (z = 0) of the Ag nano-sphere array excited 437 nm.
Vis波段范围内: 一般来说, 随着粒子尺寸的增大, 颗粒相互靠近, 粒子内部场发生相位延迟, 由于纳米团簇中相邻纳米颗粒之间的近场耦合, 在单粒子的LSPR能量处可以激发产生更高更强的等离子体模[37]. 利用FDTD Solution软件计算了直径为90 nm, 间距为10 nm的Ag纳米球阵列在437 nm激发波长下, x-y平面(z = 0)的极化电场分布, 如图8(b)所示, 其中电场的模|E|用入射平面波电场的模|E0|作归一化. 在共振波长下, 极化电场被局域在相邻Ag纳米球缝隙之间, 说明存在强烈的耦合作用, 证实了427 nm处出现的吸收峰为银纳米球阵列的LSPR激发引起的多极模式. 随着颗粒尺寸增大时, 共振峰位红移至479 nm, 峰强开始逐渐增加. 发生红移的原因是: 纳米球表面极化电子增加, 从而使得颗粒之间吸引力增大, 加剧了表面电荷耦合作用[38,39]. 当粒子直径大于90.1 nm后开始减弱, 阵列结构无法形成时, 该共振峰消失(图6(a)). 图7(b)为UV-Vis波段FDTD理论模拟吸收光谱, 可以看出, UV-Vis波段出现的吸收峰与实验结果具有相一致的LSPR激发及调制规律. 因为多级模式对纳米结构的均匀性分布, 排序很敏感, 而计算中假设了粒子是完美的球体, 与实验制备的Ag纳米球阵列存在一定偏差, 所以计算结果与实验结果不完全重叠是合理的.
如图9(a)所示, 近红外波段范围内, 沉积颗粒直径为73.5 nm时, 约782 nm处清晰检测到共振峰. 据报道, 在金属纳米颗粒(晶格结构)光栅中, 由于光学远场的相互作用, 来自一个粒子的散射光被邻近的纳米颗粒吸收, 从而激发等离子体, 导致从辐射到消失的转变. 通过抑制辐射损耗, 晶格结构中的强耦合纳米粒子表现出窄线宽的表面晶格共振模式, 这种现象通常在瑞利异常附近观测到[20,40]. 随着颗粒直径逐渐增加至90.1 nm, 阵列有序性逐渐提高, 共振峰位发生红移, 峰值增大并达到最强, 且伴随峰宽变窄. 此后, 颗粒直径继续增加至94.2 nm时, 峰位继续红移至1107 nm处, 但峰值强度开始被抑制且峰宽逐渐展宽, 这是由于Ag纳米颗粒直径达到91.3 nm之后开始发生粘连, 阵列周期性减弱且粒子均一化程度降低所导致(如图5(g)—(j)所示). 当颗粒尺寸大于94.2 nm时, 镀银厚度为17.5—19.7 nm时, 周期性阵列结构无法形成(如图5(k)—(n)所示), 共振峰消失. 计算散射截面获得的表面等离子体共振峰随颗粒尺寸变大, 从794 nm红移至1094 nm, 与实验吸收光谱峰位及调制规律相似, 证明实验的准确性, 如图9(b)所示. 由于模拟模型趋于理想状态并不会发生颗粒粘连, 所以没有出现峰值减弱的现象.
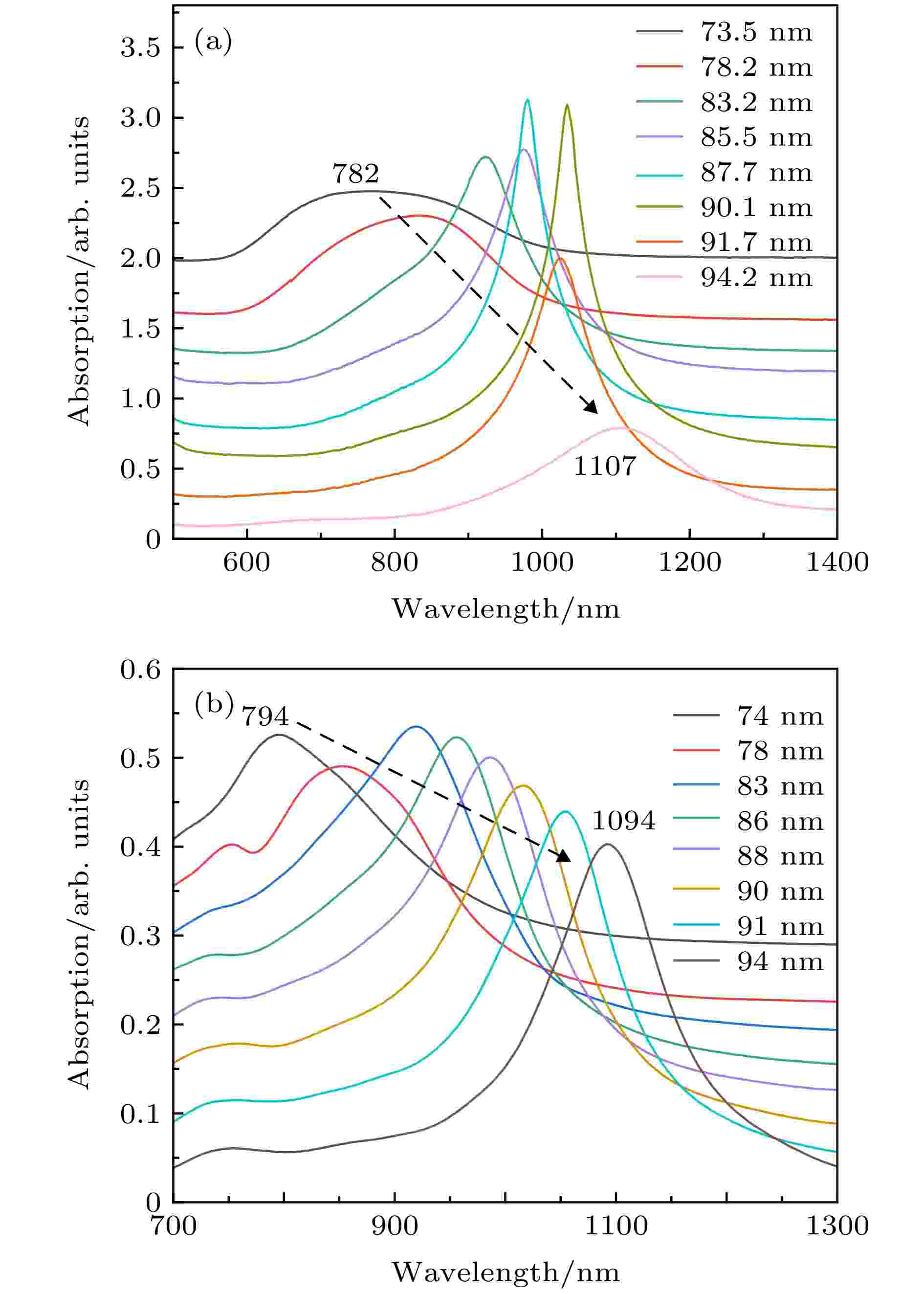图 9 (a) NIR波段不同粒径Ag纳米球阵列实验所得吸收光谱和(b) FDTD理论模拟吸收光谱Figure9. NIR absorption spectra of Ag nanosphere arrays with different sizes: (a) Experimental results; (b) FDTD simulation results.
