摘要:氢致裂纹是制约超高强度钢应用的关键问题, 掌握扩散氢的分布行为有助于弄清氢致裂纹的形成机理. 本文采用第一性原理方法计算了H原子占据α-Fe晶格间隙和空位时的情况, 得到了晶体的稳定构型及能量, 并据此分析了H原子在晶格间隙和空位中的溶解倾向; 从Mulliken布居、电子密度分布、态密度分布等角度分析了H原子与α-Fe晶体间隙和空位之间的相互作用. 结果表明: 间隙H原子倾向占据α-Fe四面体间隙位, 其1s轨道电子与Fe的4s轨道电子呈微弱共轭杂化; 空位是强氢陷阱, H原子倾向占据空位内壁附近的等电荷面. 在真空0 K条件下单空位最多稳定溶解3个H原子, 且H原子之间未表现出自发形成H₂的倾向; 间隙和空位中的H原子溶入改变了Fe晶格内电子分布导致原子结合力弱化, 并在局部区域形成反键. 基于第一性原理能量计算结果开展热力学分析, 分析结果表明大多数情况下间隙H原子都是H主要的固溶形式, H平衡溶解度计算结果与实际符合良好.
关键词: 密度泛函理论/
热力学分析/
铁素体/
扩散氢

English Abstract

全文HTML

--> --> -->

扩散氢是导致超高强度铁素体钢脆化和焊接冷裂纹产生的主要因素之一^[1], 一直以来, 人们对超高强度钢焊接氢致裂纹及氢脆进行了大量的研究, 但大都从微观组织和应力分析入手, 涉及原子尺度下的机理分析相对较少^[2]. 由于对钢铁材料研究的不断深入, 近几十年来, 基础研究人员在铁素体钢中发现了一些新现象, 比如钢中的超高浓度过饱和H区, 以及氢在应力和金属键共同影响下的加速扩散等^[3,4], H的这些行为对钢的氢脆和氢致裂纹有重要影响^[5]. 有证据表明这些现象和α-Fe晶格中的H溶解及其与点缺陷的交互作用密切相关^[5-7]. 在纳观尺度下了解含空位α-Fe和H相互作用有助于理解铁素体型高强钢的冷裂、氢脆、腐蚀等现象的物理本质. 限于实验条件所限, 目前关于α-Fe和H的相互作用研究结果主要来自于理论计算. 传统的钢球模型认为H原子优先占据α-Fe晶格四面体间隙位置, 但Fukai^[8]研究发现H原子倾向占据α-Fe晶体的八面体间隙位, 张凤春等^[9]通过密度泛函研究认为H原子倾向于占据α-Fe四面体间隙, 并通过电子结构计算讨论了α-Fe和H的相互作用, 但该研究未考虑H原子零点能对溶解倾向的影响, 并且未讨论空位对间隙H原子的影响以及H原子降低晶体结合力的原因. Du等^[10]采用PAW(projector-augmented wave) 方法中不同的广义梯度泛函计算了α-Fe晶界附近的间隙H原子溶解能并分析其逸出通道. Nazarov等^[11,12]和Hickel等^[13]讨论了γ-Fe等FCC金属的空位及空位-H缺陷复合体的形成能和空位对附近八面体间隙H原子溶解能的影响, 采用极球面投影图直观展示了空位内H原子的占位倾向, 并分析了空位附近Fe原子磁矩和自旋状态对H原子的影响, 然而对α-Fe中的H讨论较少. Ramasubramaniam等^[14]对比不同赝势下α-Fe间隙和空位H的结合能和溶解能, 但未对二者相互作用机理展开更多研究.
本文通过理论计算对含空位α-Fe中H的存在状态及分布位置进行系统分析, 基于此对不同条件下H在含α-Fe平衡溶解度进行了计算, 并开展实验验证.

本文所有计算均采用CASTEP(Cambridge sequential total energy package)进行^[15,16]. 计算选用赝势平面波方法(plane wave pseudo potential, PW-PP)和基于广义梯度近似的PBE (Perdew-Burke-Ernzerhof)形式的交换关联能泛函^[17], 考虑电子的自旋极化. 根据收敛性测试结果采用Monkhorst-Pack法^[18]确定k点数目, 本文中对不含缺陷的BCC结构的α-Fe超胞(2 × 2 × 2)几何优化和性质计算的k点取值为10 × 10 × 10; 对含缺陷的α-Fe超胞(2 × 2 × 2)几何优化和性质计算的k点取值为10 × 10 × 10, 为减少系统误差, 单个Fe原子和H₂分子的能量计算过程中的k点数目同样取为10 × 10 × 10. 态密度计算的k点取值为12 × 12 × 12, 截断能取为425 eV. 自洽场迭代收敛条件设置为 ≤ 1 × 10⁶ eV/atom; 几何优化时每个原子的能量、最大应力、最大作用力和最大位移收敛条件分别设置为5.0 × 10^–7 eV/atom, 0.05 GPa, 0.03 eV/?. 经几何优化后α-Fe晶格常数为2.8174 ?, 与实验值2.8664 ?较符合^[19].

2

-->

3.1.α-Fe晶体与间隙H原子的相互作用计算及结构预测

3 -->

3.1.1.α-Fe晶体与间隙H原子的晶体结构和能量分析

分别计算了H原子溶于α-Fe的四面体间隙位置(tetrahedral interstice site, T-site)和八面体间隙位置(octahedral interstice site, O-site)中所得的α-Fe+H晶体弛豫后稳定结构, 计算结果如图1和表1所列. 由图1和表1可见, H原子溶入α-Fe晶格间隙后, 晶格发生一定程度的畸变, 晶格常数发生变化, 晶体发生不同程度的膨胀, 其对称元素减少, 由立方晶系转变为四方晶系. H原子处于八面体间隙位置时α-Fe-H的体积膨胀量更大, 这与α-Fe中八面体间隙半径小于四面体间隙半径有关.
图 1 α-Fe+H的晶体结构　(a) T-site; (b) O-site
Figure1. Crystalline structure of α-Fe+H: (a) T-site; (b) O-site.

晶体类型	a/?	b/?	c/?	α/(°)	β/(°)	γ/(°)	V/?	空间群
α-Fe+H(T-site)	5.6843	5.6612	5.6804	89.999	89.999	90.000	5.6843	115(P-4m2)
α-Fe+H(O-site)	5.8019	5.6112	5.6112	90.000	90.000	90.000	5.8019	123(P4/mmm)

表1α-Fe+H的晶格常数和晶体结构
Table1.Lattice parameters and crystalline structure of α-Fe+H.

从能量的角度分析间隙H在α-Fe中的占位倾向, 定义晶体结合能${E_{{\rm{bind}}}}$为

$ {E_{{\rm{bind}}}} = \frac{1}{n}({E_{\rm{n}}} - {E_{{\rm{crystal}}}}), $

其中n为晶体原子数量, ${E_{\rm{n}}}$为晶体中各原子自由态能量之和, ${E_{{\rm{crystal}}}}$为该晶体的内能. 结合能${E_{{\rm{bind}}}}$可表征晶体中原子之间的结合强度.
定义含缺陷的α-Fe晶体形成能$E_{{\rm{form}}}^{\alpha\text-{\rm{ Fe}} + {\rm{def}}}$为

$E_{{\rm{form}}}^{\alpha \text-{\rm{ Fe}} + {\rm{def}}} = {E_{\alpha\text-{\rm{ Fe}} + {\rm{def}}}} - {E_{\alpha\text-{\rm{Fe}}}} - \Delta {N_i}{\mu _i},$

其中${E_{\alpha \text- {\rm{Fe}} + {\rm{def}}}}$为含缺陷的α-Fe晶体内能, ${E_{\alpha \text-{\rm{ Fe}}}}$为不含缺陷的完美α-Fe晶体内能, $\Delta {N_i}$为第i种原子的数量变化, ${\mu _i}$为第i种原子的化学势. 晶体形成能$E_{{\rm{form}}}^{\alpha \text-{\rm{ Fe}} + {\rm{def}}}$可表征完美晶体产生缺陷的难易程度.
H原子的溶解热$\Delta H_{{{\rm{sol}}}}^{\rm{H}}$为

$\Delta H_{{\rm{sol}}}^{\rm{H}} = E_{{\rm{form}}}^{{\rm{crystal}} + n{\rm{H}}} - E_{{\rm{form}}}^{{\rm{crystal}} + {\rm{(}}n -{\rm{ 1)H}}} - {\mu _{\rm{H}}},$

其中$E_{{\rm{form}}}^{{\rm{crystal}} + n{\rm{H}}}$为含有n个H原子的晶体的形成能, $E_{{\rm{form}}}^{{\rm{crystal}} + {\rm{(}}n - 1{\rm{)H}}}$为含有(n–1)个H原子的晶体的形成能, 根据(3)式可知$\Delta H_{_{{\rm{sol}}}}^{\rm{H}}$还可以表示为

$\Delta H_{{{\rm{sol}}}}^{\rm{H}} = {E_{{\rm{crystal}} + n{\rm{H}}}} - {E_{{\rm{crystal}} + {\rm{(}}n - {\rm{1)H}}}} - {\mu _{\rm{H}}},$

其中${E_{{\rm{crystal}} + (n - 1){\rm{H}}}}$和${E_{{\rm{crystal}} + n{\rm{H}}}}$分别为含有(n – 1)和n个H原子的晶体的内能, ${\mu _{\rm{H}}}$为H原子的化学势, 在真空0 K条件下可取$\dfrac{1}{2}{E_{{{\rm{H}}_{\rm{2}}}}}$, 其中${E_{{{\rm{H}}_{\rm{2}}}}}$为自由态H₂分子能量. 溶解热$\Delta H_{_{{\rm{sol}}}}^{\rm{H}}$可表征H原子在晶体中溶解的难易程度.
由于计入H原子的零点能非常重要^[20], 需要根据H原子在晶格内的声子谱计算其零点能, 零点能${E_{{\rm{ZP}}}}$按照(5)式计算^[21]:

$ {E_{{\rm{ZP}}}} = \frac{1}{2}\int {F(\omega)\hbar \omega {\rm{d}}\omega } , $

其中F(ω)为H原子在晶格内的声子态密度,$\hbar $为约化普朗克常量, ω为H原子振动的圆频率. 在计算${E_{{\rm{bind}}}}$, $E_{{\rm{form}}}^{{\rm{\alpha \text- Fe}} + {\rm{def}}}$, $\Delta H_{_{{\rm{sol}}}}^{\rm{H}}$时考虑${E_{{\rm{ZP}}}}$对晶体内能的影响.
间隙H原子晶体的能量计算结果如表2所列. 由于实际计算过程中八面体间隙中的H原子会向四面体间隙弛豫, 这从侧面说明四面体间隙是H原子的优先占位. 因此表2中仅给出四面体间隙的α-Fe+H能量计算结果.

晶体类型	${E_{{\rm{crystal}}}}$/eV	${E_{{\rm{ZP}}}}$/eV	${E_{{\rm{bind}}}}$/eV	$E_{{\rm{form}}}$/eV	$\Delta H_{{ {\rm{sol} } } }^{\rm{H} }$/eV
α-Fe+H(T-site)	–13861.050	0.246	5.182	0.390	0.390
α-Fe	–13845.344	—	5.530	—

表2α-Fe和α-Fe+H结合能、形成能和溶解热
Table2.Binding energy, formation energy, and heat of solution of α-Fe and α-Fe+H.

由表2可见, H在α-Fe的间隙溶解热$\Delta H_{{{\rm{sol}}}}^{\rm{H}}$为正值, 反应需吸热, 因此不能在0 K真空条件下形成热力学稳定的固溶体. 表2中的结合能${E_{{\rm{bind}}}}$与实验值4.29 eV出入较大^[22,23], 经分析, 误差主要与CASTEP所用的超软赝势和PBE形式的交换关联能泛函有关, 但溶解热$\Delta H_{{{\rm{sol}}}}^{\rm{H}}$与报道的计算值0.35 eV和实验值0.30 eV较符合^[14,24,25].
3 -->

3.1.2.α-Fe晶体与间隙H原子电子结构分析

弛豫后间隙H原子与最近邻Fe原子的距离提示二者可能会成键. 为研究四面体间隙中的H原子与α-Fe晶体的相互作用, 对图1(a)的构型进行了原子布居及键布居、态密度及差分电荷密度分析.
计算自由H原子, α-Fe晶体和α-Fe+H(T-site) 晶体中的原子轨道布居如表3所列. 根据H和Fe原子的核外电子表达式, H原子的价电子位于1s, Fe原子的价电子位于3d和4s, 其中3d轨道能量较高. 对比表3数据可知H在四面体间隙固溶时, H原子的1s轨道得电子, 而Fe原子的4s轨道明显失电子, 3d轨道获得了部分电子. 据此推断α-Fe-H中H近邻的Fe原子中的4s轨道受激与3d轨道杂化, 并与H原子的1s电子成键, H的电负性较强, 故得电子. 在距离间隙H原子较远处, 由于受到了间隙H原子及其近邻Fe2 (Fe4), Fe3 (Fe11)的共同作用, 晶体中的Fe1, Fe8, Fe12等原子的净电子得失只有微弱起伏, 在间隙H原子含量较多时, 这种作用可能会导致晶体内部电子浓度的不均匀, 使晶体中广泛存在相互排斥的区域, 从而降低了晶体中原子的平均结合强度^[26].

晶体类型	原子	轨道电荷占据数			总布居	净布居
		s	p	d
α-Fe-H(T-site)	H	1.34	0	0	1.34	–0.34
	Fe2, Fe4	0.62	0.66	6.65	7.93	0.07
	Fe3, Fe11	0.62	0.67	6.65	7.94	0.06
	Fe12, Fe10	0.65	0.72	6.62	7.99	0.01
	Fe1, Fe9, Fe13, Fe14, Fe16	0.65	0.72	6.62	7.99	0.01
	Fe8, Fe6	0.65	0.74	6.61	8.01	–0.01
α-Fe	Fe	0.68	0.70	6.62	8.00	0
自由态	H	1.00	0	0	1.00	0

表3α-Fe+H (T-site)晶体原子轨道布居
Table3.Atomic orbital population of α-Fe+H (T-site).

对原子间的键布居进行分析, 结果列于表4. 除间隙H原子的四个近邻Fe原子之间存在反键外, 还有部分Fe原子之间结合减弱，且晶体内原子之间的距离发生变化, 这说明间隙H原子固溶后弱化了晶体的整体结合强度, 且在局部形成薄弱区域. 比较α-Fe+H (T-site)和α-Fe+H (O-site)晶体的键布居数, 八面体间隙H原子的近邻Fe原子之间存在更强的反键, 这可能是α-Fe+H (O-site)晶体具有更高的内能和更低的结合强度的原因之一.

晶体类型	原子对	距离/?	键布居
α-Fe-H (T-site)	Fe2-H	1.6494	0.16
	Fe3-H	1.6507	0.16
	Fe2-Fe3	2.5558	–0.09
	Fe2-Fe4	2.7286	–0.14
	Fe8-Fe11	2.4783	0.17
	Fe3-Fe12	2.4471	0.18
	Fe8-Fe16	2.8401	0.05
	Fe7-Fe8	2.4601	0.15
α-Fe-H (O-site)	Fe2-Fe4	2.6287	–0.28
α-Fe	Fe-Fe	2.4400	0.14
	Fe-Fe	2.8174	0.06

表4α-Fe-H (T-site)晶体键布居
Table4.Bond population of α-Fe+H (T-site).

分析间隙H原子及其近邻Fe原子的电子态密度, 结果如图2所示. 可见间隙H原子固溶后1s电子态密度波峰向低能级迁移, 且能级发生分裂, 存在多个波峰, 其–10 — –7.5 eV的波峰与近邻Fe原子4s态电子波峰发生重叠, 说明H和Fe存在微弱的共轭效应. Fe原子的3p电子态密度在固溶前后无明显变化, 说明H与Fe的作用主要来源于H的1s电子和4s的共轭作用; 另外Fe的3d电子在该位置的波峰也有一定的增强, 说明较内层的价电子也部分参与了成键, 这和原子轨道布居分析结果较一致.
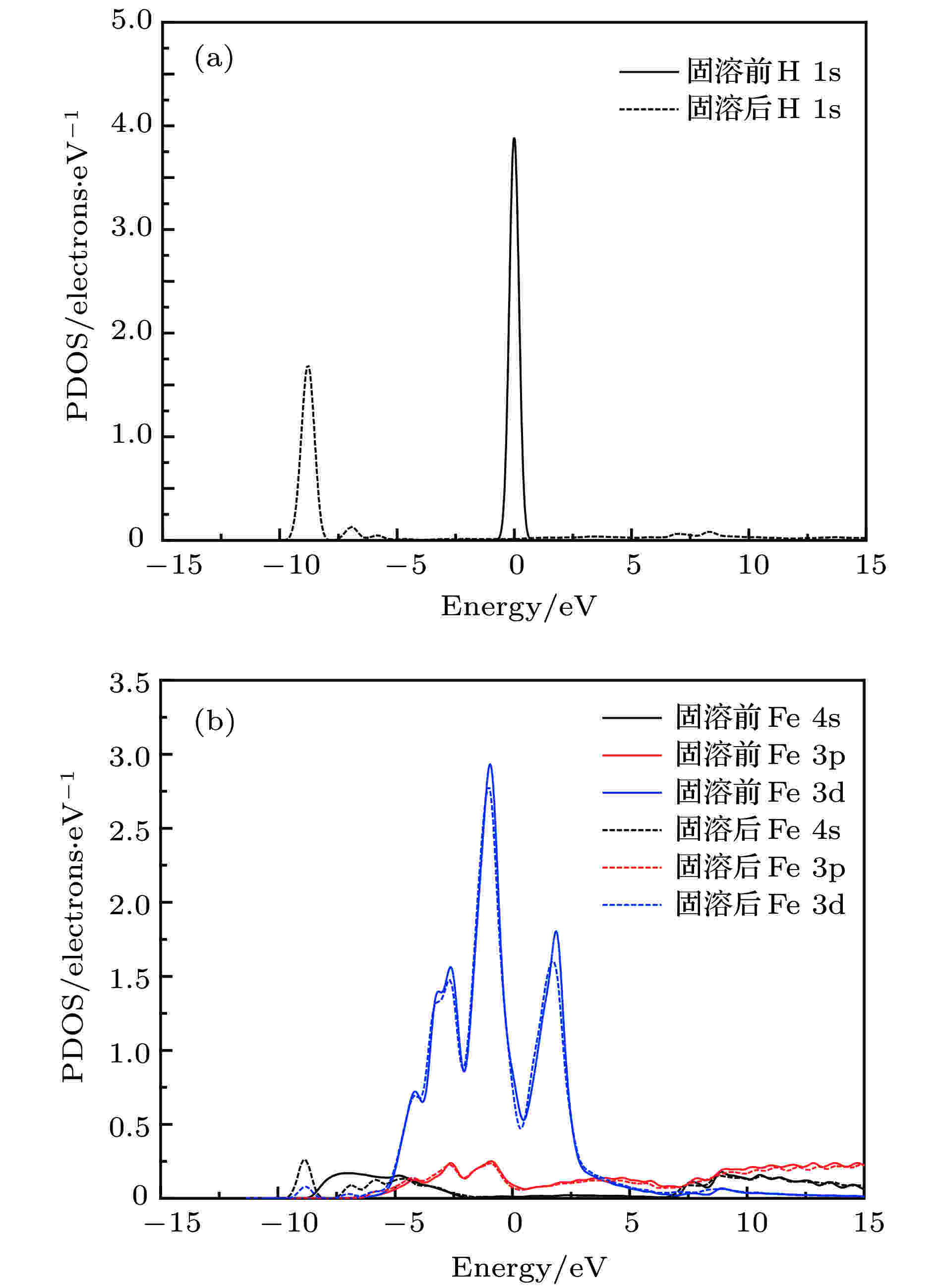图 2 α-Fe+H (T-site)的分波电子态密度　(a) 固溶前后 H 原子; (b) 固溶前后最近邻Fe原子; (c) 四面体间隙H原子; (d) 间隙H原子最近邻Fe原子
Figure2. Partial electronic density of state of α-Fe+H (T-site): (a) Free H atom and interstitial H atom; (b) Fe atom in perfect α-Fe crystal and the nearest neighbour of interstitial H atom; (c) H atom in tetrahedral interstice; (d) the nearest neighbour Fe atom of interstitial H atom.

计算图1(a)中α-Fe+H (T-site)的差分电荷密度, 结果如图3所示. 图3中蓝色为得电子, 红色为失电子. 可见H得电子, Fe2, Fe4, Fe11为H近邻原子, 与图3中出现的其他Fe相比, 其周围空间有较明显的失电子. 由于不同位置的Fe价电子受H的影响不同, 各Fe净电荷在长程范围内稍有起伏. 这说明虽然间隙H原子在α-Fe中的直接作用范围较小, 但其间接带来的晶格电荷密度变化的范围较大. 电荷密度的这种变化可以一定程度解释α-Fe+H(T-site)结合能降低的原因.
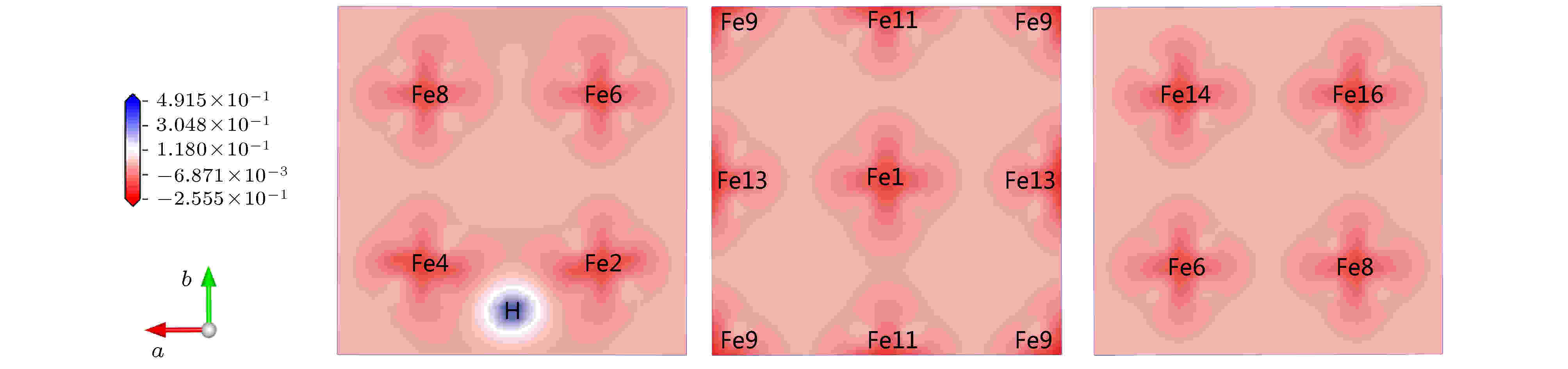图 3 α-Fe+H(T-site)的差分电荷密度
Figure3. Electron density difference of α-Fe+H(T-site).

2 -->

3.2.含空位的α-Fe+Vac晶体与H原子相互作用计算及结构预测

空位(vacancy, 以下用Vac代替)是高强钢中广泛存在的一种点缺陷, 由于空位尺寸比间隙更大, 因此可能会容纳较多的H, 在晶格中形成Vac-H复合体. 分别计算了α-Fe+Vac及含有Vac-H复合体的α-Fe+(1H-Vac)—α-Fe+(6H-Vac)晶体稳定结构, 并进行能量分析, 结果如表5, 图4和表6所列.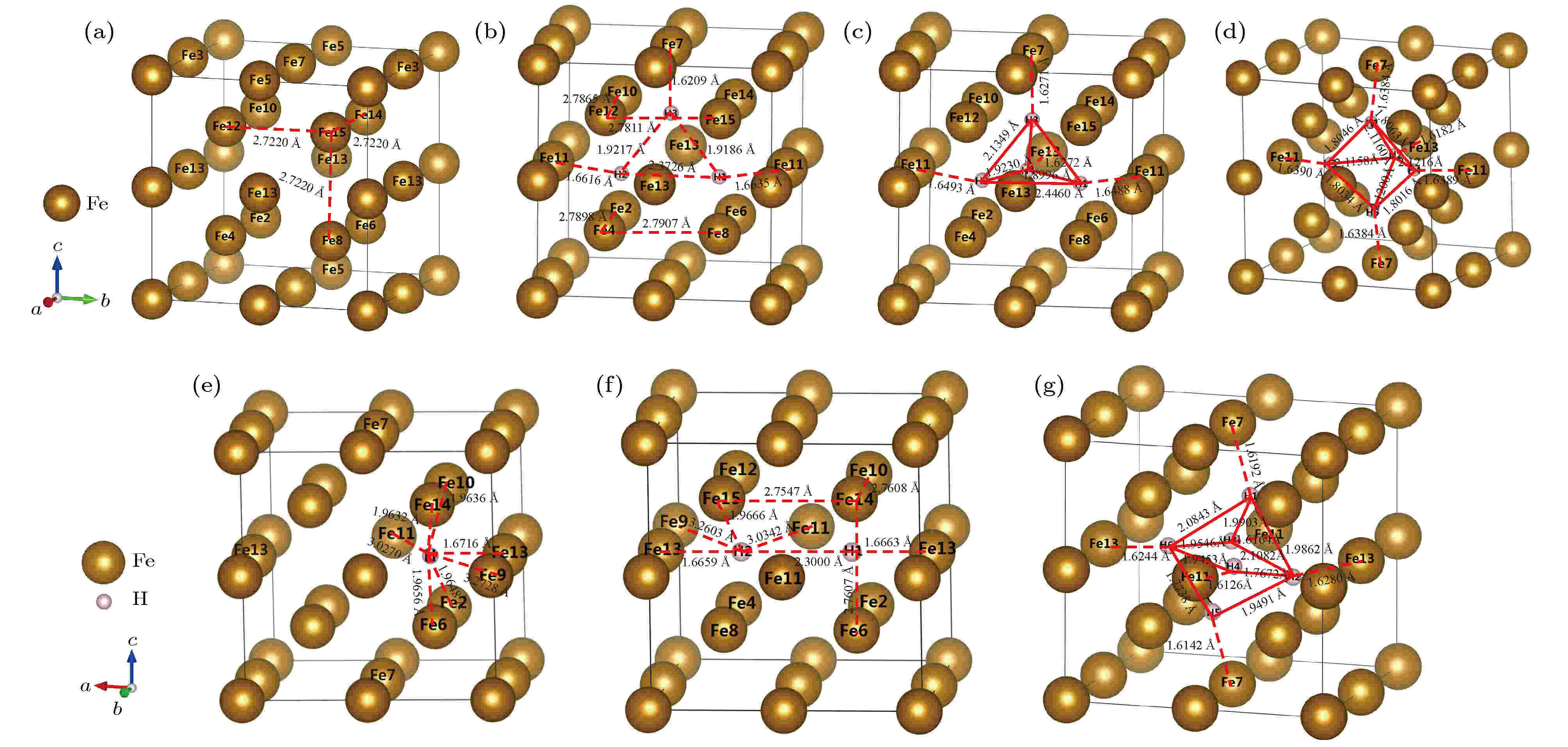
图 4 α-Fe+(nH-Vac)的晶体结构　(a) α-Fe+Vac; (b) α-Fe+(3H-Vac); (c) α-Fe+(4H-Vac); (d) α-Fe+(5H-Vac); (e) α-Fe+(1H-Vac); (f) α-Fe+(2H-Vac); (g) α-Fe+(6H-Vac)
Figure4. Crystalline structure of α-Fe+(nH-Vac): (a) α-Fe+Vac; (b)α-Fe+(3H-Vac); (c) α-Fe+(4H-Vac); (d) α-Fe+(5H-Vac); (e) α-Fe+(1H-Vac); (f) α-Fe+(2H-Vac); (g) α-Fe+(6H-Vac).

晶体类型	a/?	b/?	c/?	α/(°)	β/(°)	γ/(°)	V/?	空间群
α-Fe+Vac	5.6033	5.6033	5.6033	90.000	90.000	90.000	175.923	221${\rm{(}}Pm\overline {{\rm{3}}m} )$
α-Fe+(Vac-1H)	5.6321	5.6103	5.6103	90.000	90.001	89.999	177.270	99${\rm{(}}P{\rm{4}}MM)$
α-Fe+(Vac-2H)	5.6285	5.6285	5.6484	90.000	90.000	90.000	178.940	123(P4/MMM)
α-Fe+(Vac-3H)	5.6297	5.6598	5.6853	90.004	90.011	90.002	181.154	25(PMM2)
α-Fe+(Vac-4H)	5.6727	5.6943	5.6723	89.966	90.540	89.973	183.221	38(AMM2)
α-Fe+(Vac-5H)	5.6905	5.7086	5.7093	90.000	90.004	90.002	185.467	99${\rm{(}}P{\rm{4}}MM)$
α-Fe+(Vac-6H)	5.7407	5.7270	5.7208	89.433	89.691	89.692	188.064	5(C2)

表5α-Fe+(nH-Vac)的晶格常数和晶体结构
Table5.Lattice parameters and crystalline structure of α-Fe+(nH-Vac).

晶体类型	${E_{{\rm{crystal}}}}$/eV	${E_{{\rm{ZP}}}}$/eV	${E_{{\rm{bind}}}}$/eV	$E_{{\rm{form}}}$/eV	$\Delta H_{_{ {\rm{sol} } } }^{\rm{H} }$/eV
α–Fe+Vac	–12977.593	—	5.369	2.416	—
α–Fe+(Vac-1H)	–12993.933	0.141	5.055	1.928	–0.347
α–Fe+(Vac-2H)	–13010.262	0.295	4.777	1.450	–0.324
α–Fe+(Vac-3H)	–13026.330	0.478	4.513	1.234	–0.034
α–Fe+(Vac-4H)	–13042.359	0.670	4.275	1.056	0.014
α–Fe+(Vac-5H)	–13058.299	0.889	4.055	0.968	0.131
α–Fe+(Vac-6H)	–13073.995	1.149	3.842	1.123	0.438

表6α-Fe+(nH-Vac)的结合能、形成能和溶解热
Table6.Binding energy, formation energy, and heat of solution of α-Fe+(nH-Vac).

由表5及表6可见, 随着H原子向空位中溶入, 晶体的体积不断增大, 而α-Fe+(nH-Vac)结合能不断降低, 因此可以认为空位中H原子的溶入会降低晶体中原子的结合能力. 随着空位所结合的H原子数量增多, 总零点能加速升高, 其原因就在于空位中H原子数量增加后其自由体积减小, 振动频率增加. 通过表6中的$\Delta H_{_{{\rm{sol}}}}^{\rm{H}}$可知当考虑零点能时, 0 K真空条件下时单个空位最多只能与3个H原子稳定结合, 而不考虑零点能时, 则可以溶入5个H氢原子. 以上结果的显著差异表明H原子的量子效应在空位俘获H原子问题中不可忽略. 由表6和表2的${E_{{\rm{crystal}}}}$计算α-Fe + (nH-Vac)对H原子的陷阱能$E_{{\rm{trap}}}^{\rm{H}}$如表7所列. 由表7可见, $E_{{\rm{trap}}}^{\rm{H}}$与$\Delta H_{_{{\rm{sol}}}}^{\rm{H}}$变化趋势相符性较好. 这与以往类似研究结果较一致^[14,24].

晶体类型	$E_{{\rm{trap}}}^{\rm{H}}$/eV
	不考虑${E_{{\rm{ZP}}}}$	考虑${E_{{\rm{ZP}}}}$
α-Fe+(Vac-1H)	0.633	0.778
α-Fe+(Vac-2H)	0.623	0.627
α-Fe+(Vac-3H)	0.361	0.211
α-Fe+(Vac-4H)	0.322	–0.011
α-Fe+(Vac-5H)	0.227	–0.297
α-Fe+(Vac-6H)	–0.028	–0.772

表7α-Fe+(nH-Vac)对H原子的陷阱能
Table7.Hydrogen trapping energy of α-Fe+(nH-Vac)

结合晶体内部电子结构对图4中各α-Fe + (nH-Vac)晶体稳定构型做进一步解释和说明. 图4(a)表明含有单一空位的α-Fe+Vac晶体结构仍然属于对称性最高的立方晶系, 空位中心最近邻的8个原子Fe2, Fe4, Fe6, Fe8, Fe10, Fe12, Fe14, Fe15净电荷均为0.07, 相对失电子, 而Fe7, Fe11, Fe13相对得电子.
空位中溶入1个H原子时, 超胞中H原子并未处于弛豫后结构的空位中心, 而是占据了空位八面体间隙附近的内壁位置, 这与其他金属中的情况类似^[27,28]. 如图4(e)所示, H原子最近邻原子是Fe13, 且H-Fe13距离为1.6716 ?, 两原子连线平行于X轴, 从图4(e)可知单空位中H原子可能占据的位置共有6个.
当α-Fe+(Vac-1H)继续溶入第二个H原子, 两个H原子依然占据等电荷密度面, 且第二个H原子与第一个H原子关于空位中心对称, 二者的Y轴和Z轴坐标与Fe13一致, 此时系统能量最低, 两个H原子距离明显超过成键距离, 相比于空位中存在1个H原子的情况, 该晶体具有更高的对称性. 由表8、图5(d)和图5(e)可知, 两个H原子净电荷均为–0.20并形成反键, H原子之间区域差分电荷密度为负并接近于0, 因此空位内的H原子趋于相互排斥而不是形成H₂分子. 由图4(f)可知H在空位内的可能构型有3个. 对比图5(c)和图5(e)的等电荷密度面(电荷密度为0.24 ?^–3)和电荷密度等高线, 当空位中溶入H原子时, 空位腔中的电荷总量整体增加, 且空位远处存在电荷密度降低的区域. 可推断空位中的H能够影响较大范围的晶格电荷密度分布.
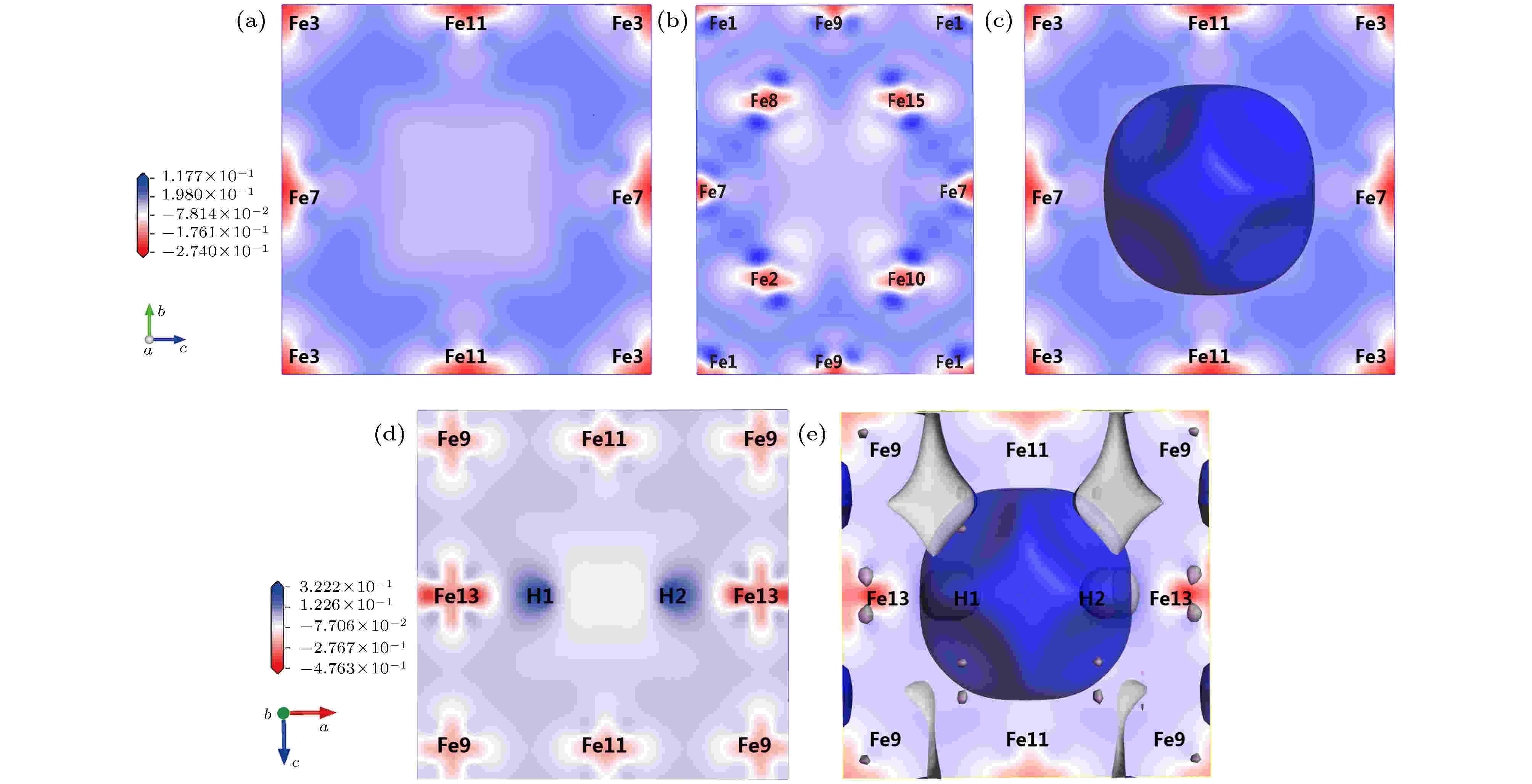图 5 α-Fe+(nH-Vac)的等电荷面和差分电荷密度　(a) α-Fe+Vac ((100)面); (b) α-Fe+Vac ((110)面); (c) α-Fe+Vac等电荷面; (d) α-Fe+(2H-Vac) ((010)面); (e) α-Fe+(2H-Vac)等电荷面
Figure5. Isoelectronic density surface and electron density difference of α-Fe+(nH-Vac): (a) Electron density difference of α-Fe+Vac in surface (100); (b) electron density difference of α-Fe+Vac in surface (110); (c) isoelectric density surface of α-Fe+Vac; (d) electron density difference of α-Fe+(2H-Vac) in surface (010); (e) isoelectric density surface of α-Fe+(2H-Vac).

晶体类型	原子	轨道电荷占据数			总布居	净布居
		s	p	d
α-Fe+Vac	Fe7, Fe11, Fe13	0.74	0.72	6.68	8.13	–0.13
	Fe3, Fe5, Fe9	0.68	0.73	6.63	8.04	–0.04
	其余Fe原子	0.66	0.67	6.60	7.93	0.07
α-Fe+(Vac-2H)	Fe13	0.71	0.71	6.73	8.15	–0.15
	Fe9	0.66	0.70	6.62	7.98	0.02
	Fe11	0.71	0.71	6.65	8.07	–0.07
α-Fe+Vac—α-Fe+(Vac-6H)	H1	1.20—1.22	0	0	1.20—1.22	–0.20— –0.22
自由态	H	1.00	0	0	1.00	0

表8α-Fe+(nH-Vac)晶体原子轨道布居
Table8.Atomic orbital population of α-Fe+(nH-Vac).

当空位溶入第3个H原子时, 第3个H原子处于靠近Fe7原子的空位内壁, 二者X和Y坐标基本一致, 三个H原子的净电荷均为负值, 因此H1和H2受H3的排斥, 沿着Z轴负方向移动, 由图4(b)可知空位内的可能构型有12个.
空位溶入第4个H原子时, 弛豫构型如图4(c), 4个H原子形成四面体结构, 由于净电荷均为负值, 因此仍然有相互排斥的倾向, H3和H4的存在使得H1和H2的X和Z坐标相比于Fe11均发生较大改变, H1和H2的存在又使H3和H4与最近邻Fe原子距离更近, H3和H4的相互作用导致其X轴和Z轴方向坐标分别发生了较大改变, 这种结构能使晶格内应力和总能达到最低, 共有12个可能构型.
空位溶入第5个H原子时, 弛豫构型如图4(d), 晶体对称性相对于α-Fe+(Vac-4H)有所提高. H原子仍形成四面体结构, 且第5个H原子位于四面体底面, 底面近似正方形, 实际上该晶体与α-Fe+(Vac-1H)具有相同的对称性, 其可能构型有6个.
空位溶入第6个H原子时, 弛豫构型如图4(g), α-Fe+(Vac-6H)晶体为三斜晶, 空位内的6个H原子形成倾斜的扁八面体, 其可能构型有6个, 根据表6可知, 该晶体的形成能和溶解热突然升高, 其稳定存在所需的氢分压远远高于本文研究对象的使用条件, 故在后续研究中不再考虑.
2 -->

3.3.空位对α-Fe四面体间隙H原子固溶的影响

由3.2节计算结果可知, α-Fe中的空位$E_{{\rm{trap}}}^{\rm{H}}$大于0.6 eV, 属于强H陷阱^[2], 间隙H原子易向空位内富集, 文献[28,29]认为Fe晶格中的空位通过产生应力应变场和改变周围Fe原子磁矩提高了对周围间隙原子的吸引作用. 本文对含空位最近邻和次近邻的间隙H原子α-Fe+Vac晶体的2 × 2 × 2大小超胞进行了构型和能量计算, 结果如表9所列. 可见不计H原子零点能的情况下, 空位周围的四面体间隙的$\Delta H_{{{\rm{sol}}}}^{\rm{H}}$最高降低了37%. 对比图6、图1和图4(a)可见, 空位最近邻的四面体间隙H有向空位方向运动的趋势.
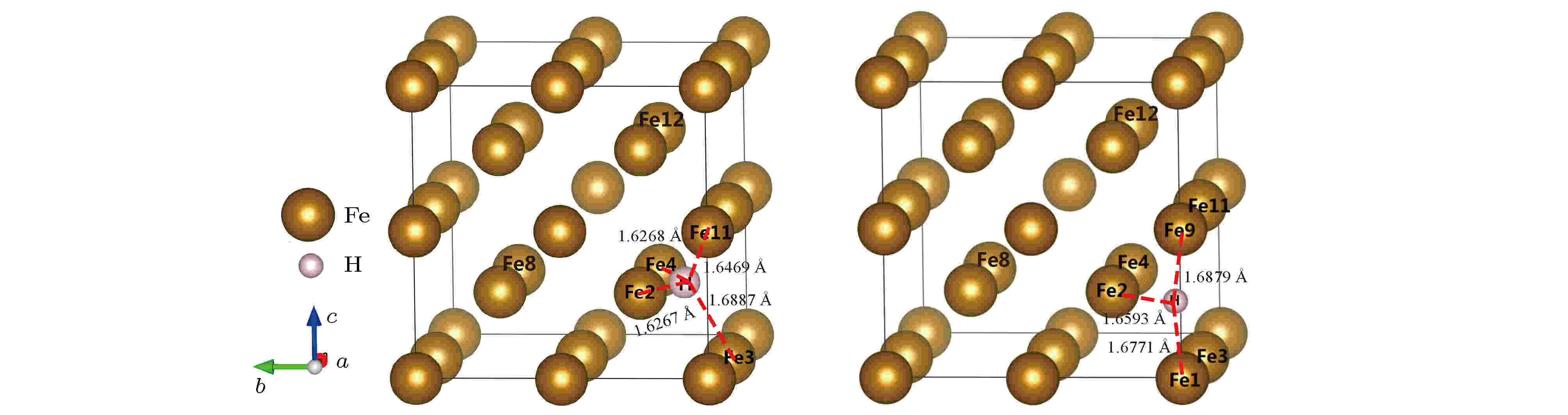图 6 α-Fe+Vac+H(T-site)的晶体结构
Figure6. Crystalline structure of α-Fe+Vac+H(T-site).

晶体类型	${E_{{\rm{crystal}}}}$/eV	${E_{{\rm{ZP}}}}$/eV	${E_{{\rm{bind}}}}$/eV	$E_{{\rm{form}}}$/eV	$\Delta H_{{ {\rm{sol} } } }^{\rm{H} }$/eV
α–Fe+Vac+H(T-site)	–12993.354 — –12993.353	0.248—0.250	5.012	2.755—2.756	0.339—0.340

表9α-Fe+Vac+H(T-site)的结合能、形成能和溶解热
Table9.Binding energy, formation energy, and heat of solution of α-Fe+Vac+H(T-site).

2

-->

4.1.α-Fe中H原子溶解问题的物理模型

假设待研究晶体内共有2 × 2 × 2超胞M个, 其中只含有单一空位的超胞数量为${N_{{\rm{vac}}}}$; 含有单一间隙H原子的超胞数量为$N_{\rm{i}}^{\rm{H}}$; 含有单一空位和四面体间隙H原子的超胞数量为$N_{{\rm{vac}} + {\rm{i}}}^{\rm{H}}$; 空位内含有1至5个H原子的超胞数量分别为$N_{{\rm{vac}}}^{{\rm{1 H}}}$—$N_{{\rm{vac}}}^{{\rm{5 H}}}$. 采用巨正则系综进行热力学分析, 巨正则系综自由能为

$J = U - TS + pV + {N_{{\rm{Fe}}}}\mu _{{\rm{Fe}}}{N_{\rm{H}}}\mu _{\rm{H}},$

其中U, S和V分别为内能、熵和晶体体积, T和p分别为系统的温度和压强. $\mu _{{\rm{Fe}}}$和$\mu _{\rm{H}}$为Fe和H的化学势, 由于$\mu _{{\rm{Fe}}}$随温度和压强的变化很小, $\mu _{{\rm{Fe}}}$近似等于$\mu _{{\rm{Fe}}}^{\rm{0}}$, $\mu _{\rm{H}}$则与环境有关. S与晶体微观构型数量有关, 结合晶体对称性和3.1与3.2节的分析结果计算构型数Ω如(7)—(9)式:

$\varOmega = {\varOmega _{\rm{1}}}\varOmega _{\rm{2}},$

${\varOmega _{\rm{1}}} = \frac{{M!}}{{{N_{{\rm{vac}}}}!N_{\rm{i}}^{\rm{H}}!N_{{\rm{vac}} + {\rm{i}}}^{\rm{H}}!N_{{\rm{vac}}}^{{\rm{1H}}}!N_{{\rm{vac}}}^{{\rm{2H}}}!N_{{\rm{vac}}}^{{\rm{3H}}}!N_{{\rm{vac}}}^{{\rm{4H}}}!N_{{\rm{vac}}}^{{\rm{5H}}}!(M - {N_{{\rm{vac}}}} - N_{\rm{i}}^{\rm{H}} - N_{{\rm{vac}} + {\rm{i}}}^{\rm{H}} - N_{{\rm{vac}}}^{{\rm{1H}}} - N_{{\rm{vac}}}^{{\rm{2H}}} - N_{{\rm{vac}}}^{{\rm{3H}}} - N_{{\rm{vac}}}^{{\rm{4H}}} - N_{{\rm{vac}}}^{{\rm{5H}}})!}},$

${\varOmega _2} = {96^{N_{\rm{i}}^{\rm{H}}}}{48^{N_{{\rm{vac}} + {\rm{i}}}^{\rm{H}}}}{6^{N_{{\rm{vac}}}^{{\rm{1H}}}}}{3^{N_{{\rm{vac}}}^{{\rm{2H}}}}}{12^{N_{{\rm{vac}}}^{{\rm{3H}}}}}{12^{N_{{\rm{vac}}}^{{\rm{4H}}}}}{6^{N_{{\rm{vac}}}^{{\rm{5H}}}}}{16^{{N_{{\rm{vac}}}} + N_{\rm{i}}^{\rm{H}} + N_{{\rm{vac}} + {\rm{i}}}^{\rm{H}} + N_{{\rm{vac}}}^{{\rm{1H}}} + N_{{\rm{vac}}}^{{\rm{2H}}} + N_{{\rm{vac}}}^{{\rm{3H}}} + N_{{\rm{vac}}}^{{\rm{4H}}} + N_{{\rm{vac}}}^{{\rm{5H}}}}},$

代入(6)式, 令$\dfrac{{\partial J}}{{\partial {N}}} = 0$并代入本文第3节中的能量计算结果, 可分别得到${N_{{\rm{vac}}}}$, $N_{\rm{i}}^{\rm{H}}$和$N_{{\rm{vac}}}^{{\rm{1 H}}}$—$N_{{\rm{vac}}}^{{\rm{5 H}}}$.
2 -->

4.2.0 K下H原子溶解倾向随化学势的变化情况

如前所述, $\mu _{\rm{H}}$与实际环境有关. 在完全无氢环境中, $\mu _{\rm{H}}$取–∞, 环境中的H活度越高, $\mu _{\rm{H}}$越大. 根据(2)式以及表2、表6和表8中各超胞在0 K时形成能. 以形成能$E_{{\rm{form}}}$为直线截距, H原子数量${N_{\rm{H}}}$为直线斜率, 即可得到各超胞的形成能随着$\mu _{\rm{H}}$变化情况如图7所示. 由图7可见, 在绝大多数情况下, Fe晶格内溶解的大部分H原子都在四面体空隙中, 只有当$\mu _{\rm{H}}$ < –2.416 eV时, α-Fe中的主要缺陷形式为α-Fe+Vac; 当0.367 eV < $\mu _{\rm{H}}$ < 0.371 eV时, 主要缺陷形式为α-Fe+(5H-Vac). 因H原子在四面体间隙中溶解形成α-Fe+H(T-site)构型的过程是吸热反应, 而少量H原子在空位中溶解是放热反应, 虽看似违反热力学定律, 但因空位缺陷需要很高的形成能, 空位数量相对于四面体间隙要少得多, 因此总体而言在四面体间隙中溶解的H原子占主导地位. 空位内H原子数量分布同样也随着$\mu _{\rm{H}}$的变化而变化, 在0.131 eV < $\mu _{\rm{H}}$ < 0.367 eV时主要为α-Fe+(5H-Vac), 在0.014 eV < $\mu _{\rm{H}}$ < 0.131 eV时主要为α-Fe+(4H-Vac), 在–0.034 eV < $\mu _{\rm{H}}$ < 0.014 eV时主要为α-Fe+(3H-Vac), 在–0.324 eV < $\mu _{\rm{H}}$ < -0.034 eV时主要为α-Fe+(2H-Vac), –0.347 eV < $\mu _{\rm{H}}$ < –0.324 eV时主要为α-Fe+(H-Vac).
图 7 0 K下缺陷形成能随μ_H变化情况
Figure7. Formation energy of defects at 0 K for different H chemical potentials.

2 -->

4.3.变温条件下空位和H原子溶解倾向随化学势的变化情况

根据4.1节建立的物理模型计算单空位、空位溶H、间隙溶H的含量如图8(a),(b),(c)所示, 可见只有富氢条件及高温条件下, 在热力学平衡条件下α-Fe才能溶有较多的H, 其中空位容纳H原子的比例较低. 基于上述结果得到含空位缺陷α-Fe中的H平衡溶解度如图9所示.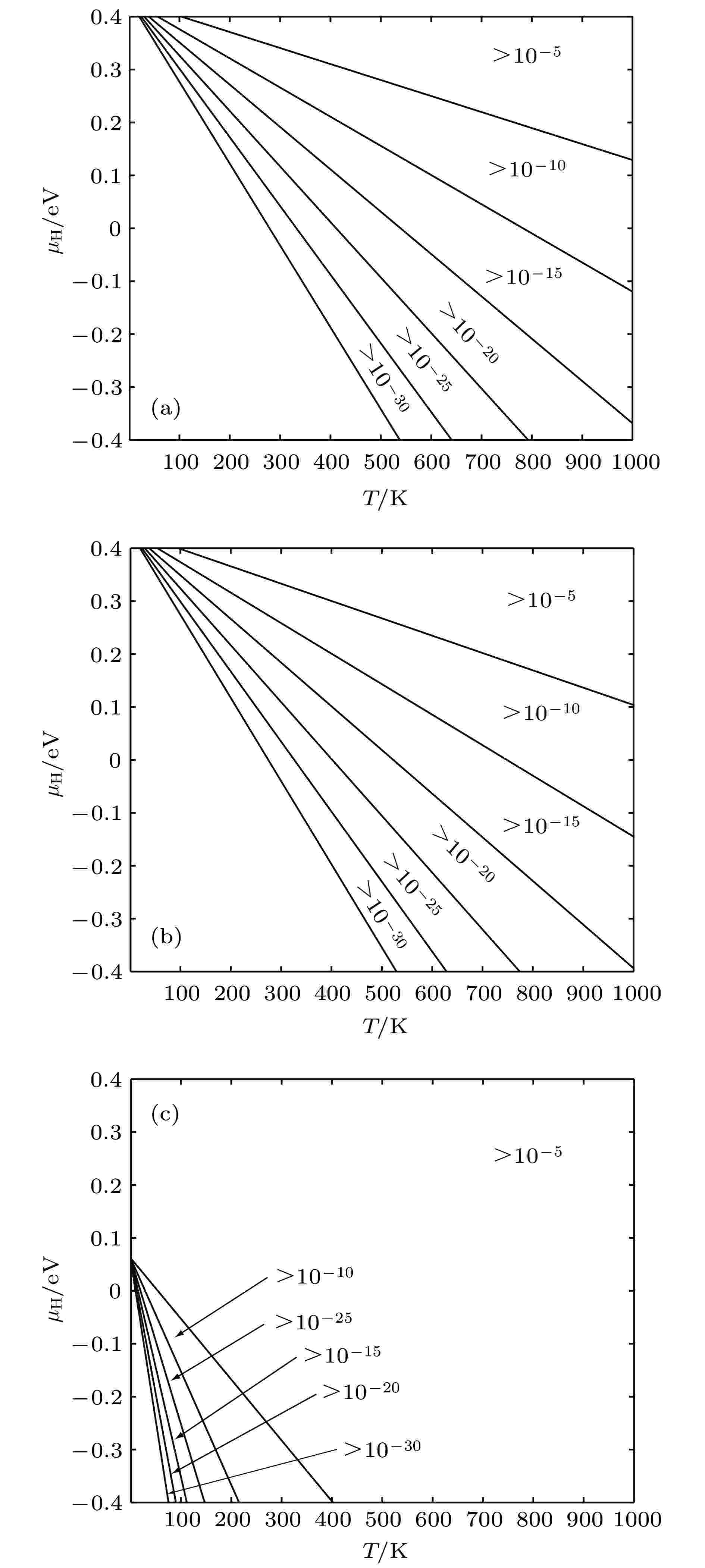
图 8 缺陷随T和μ_H变化情况　(a) 空位平衡浓度; (b) 空位内H平衡浓度; (c) 间隙H平衡浓度
Figure8. Equilibrium concentration of defects for different temperature and H chemical potentials: (a) Equilibrium concentration of vacancies; (b) equilibrium concentration of H occupying in vacancies; (c) equilibrium concentration of H occupying in interstitial positions.

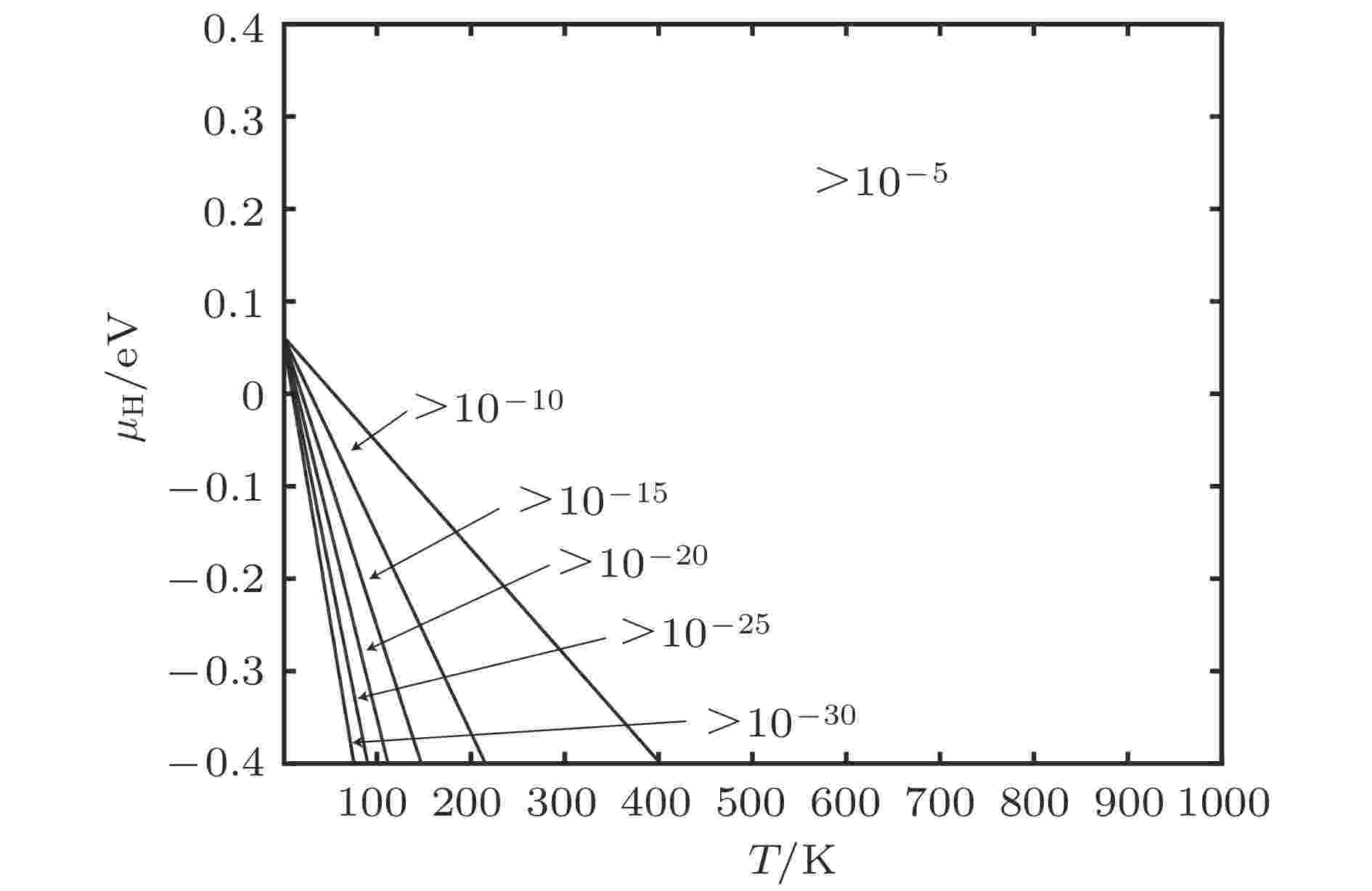图 9 含空位α-Fe晶体H总平衡浓度
Figure9. Equilibrium total concentration of H of α-Fe containing vacancies.

2 -->

4.4.实验验证

采用Devnathan-Stachurski双电解池技术对计算结果进行验证. 双电解池实验装置如图10所示, 电解池分为阴极室和阳极室, 待侧纯Fe试样夹在阴极和阳极室中间. 主单元工作电极为阳极并连接金属薄片, 辅助电极和参比电极置于NaOH溶液中. 从单元为恒电流充氢单元, 工作电极作为阴极连接于纯Fe试样上, 辅助电极和阳极置于0.1 mol/L的HCl溶液中, 阴极充氢时电解液中加入少量Na₂S. 实验开始前将试样阳极表面镀镍, 之后在阳极室施加电位, 使金属薄板相对于参比电极有一个恒正电位, 当残余电流小于1 μA时, 阴极室立即施加恒定充氢电流, 这样就在试样的阴极侧表面形成扩散H浓度为$c^{\rm{H}}$的含H层, 该含H层处于热力学平衡态, 其浓度$c^{\rm{H}}$正取决于环境温度和$\mu _{\rm{H}}$. 在标准状态下蒸馏水的$\mu _{\rm{H}}^{{\Theta }}$ = –0.41 eV^[30], pH = 7, 测得试验用阴极电解液pH值约为3.5, 阴极电解液$\mu _{\rm{H}}$通过 (10)式计算：
图 10 Devnathan-Stachurski双电解池示意图
Figure10. Schematic diagram of Devnathan-Stachurski double electrolytic cell.

${\mu _{\rm{H}}} = \mu _{\rm{H}}^{{\Theta }}{k_{\rm{B}}}T\ln a,$

其中a为溶液活度值, ${k_{\rm{B}}}$为玻尔兹曼常数, T为环境温度. 根据阴极电解液pH值及H₂S的溶度积^[31]得到阴极电解液中各离子强度, 再代入Robinson等提出的高离子强度下修正的Dyble-Hückel方程式^[31]计算离子活度系数为0.90002. 由离子活度系数计算阴极电解液活度值为2.85 × 10^–4 mol/L, 由此得到阴极电解液$\mu _{\rm{H}}$ = –0.204 eV. 根据实验温度T(298.15 K)和${\mu _{\rm{H}}}$计算H原子的平衡溶解度计算值如表10所列, 由表10可见H平衡溶解度的计算值较试验值偏低, 但仍处于一个数量级, 其原因在于本文的计算考虑的缺陷只有超胞内的间隙和空位, 且未考虑金属表面吸附, 而实际试样中晶界、位错等位置均可容纳大量H原子并提供扩散H, 因此表10中的计算值实际代表材料晶格中间隙和空位部位H的平衡溶解度, 间隙H占绝大多数, 根据H原子的平衡溶解度实验值(4.41 × 10^–2)%计算纯Fe晶格间隙H浓度占扩散H总浓度的47%. 文献[2]通过实验给出了扩散H总浓度以及晶格溶H占比, 可见计算结果与实际吻合良好, 并从侧面佐证了计算条件和分析过程的合理性.

温度/K	μH/eV	cH/%
		计算值	实验值
298.15	–0.239	2.08 × 10–2	4.41 × 10–2 2.88 × 10–2, 其中晶格溶H占总扩散H含量的43%[2]

表10H平衡溶解度计算值和实验值
Table10.Calculated and test value of equilibrium concentration of H atom.

采用密度泛函理论方法研究了含空位α-Fe中的晶体结构, 并从晶体结构、能量、电子结构角度分析了H原子在晶体内的溶解行为, 计算了H原子在含空位α-Fe晶体中的平衡溶解度, 并通过Devnathan-Stachurski双电解池进行实验验证, 得到如下结论.
1) H原子与α-Fe内最近邻Fe原子主要依靠H的1s轨道电子和Fe的4s和3p轨道杂化而微弱成键, 与以往研究结果一致.
2) 空位内的H原子优先占据八面体间隙附近的空位内壁位置, 在考虑零点能情况下, 真空0 K下单空位最多只能稳定容纳3个H原子, 且H原子之间没有自发形成H₂分子的倾向.
3) 结合能计算结果表明H原子的溶入会降低α-Fe晶体的稳定性, 并在α-Fe晶体中产生了较大范围的电荷密度起伏, 弱化晶体中原子之间的结合.
4) 通过热力学分析得出四面体间隙是α-Fe中H原子固溶的主要位置, 且随着$\mu _{\rm{H}}$和T的增加, H的平衡溶解度急剧上升, H原子更容易进入α-Fe晶体中.
5)计算结果与扩散H平衡浓度实验值吻合良好, 说明计算和分析过程合理. 但本文的研究对象限于α-Fe晶格间隙和空位缺陷, 后续将对α-Fe晶体中的晶界、位错及合金原子与H的相互作用开展研究.