删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

NO分子宏观气体热力学性质的理论研究

本站小编 Free考研考试/2021-12-29
摘要:采用量子统计系综理论, 研究了基态NO分子宏观气体摩尔熵、摩尔内能、摩尔热容等热力学性质. 首先应用课题组前期建立的变分代数法(variational algebraic method, VAM)计算获得了基态NO分子的完全振动能级, 得到的VAM振动能级作为振动部分, 结合欧拉-麦克劳林渐进展开公式的转动贡献, 应用于经典的热力学与统计物理公式中, 从而计算得到了1000—5000 K温度范围内NO宏观气体的摩尔内能、摩尔熵和摩尔热容. 将不同方法计算得到的摩尔热容结果分别与实验值进行比较, 结果表明基于VAM完全振动能级获得的结果优于其他方法获得的理论结果. 振动部分采用谐振子模型对无限能级求和计算热力学性质的方法有一定的局限性, 应当使用有限的完全振动能级进行统计求和.
关键词: NO/
变分代数法/
振动能级/
热力学性质

English Abstract


全文HTML

--> --> -->
1.引　言
在行星大气中扮演重要角色的NO气体是造成酸雨、光化学烟雾和臭氧层破坏等大气污染的主要成份之一[1-3], 且NO的分子结构与性质在生物、原子分子物理和药物学等领域一直受到人们的广泛关注[4-9]. 近年来, NO气体宏观热力学性质也成为了人们感兴趣的研究课题之一. 早在1987年, Jaffe[10]将内能划分为振动、转动和电子贡献计算了NO气体的热容, 并通过这些热容数据计算了气体混合物(含NO)的热力学温度和焓. 2005年, Capitelli等[11]获得了与火星大气相关的NO, NO2, N2O等成份的热力学性质, 为高温混合气体热力学模型的研究提供了重要的数据支撑. 2009年, Babou等[12]在多温度模型框架下, 采用双温度分区计算了NO分子在高温和非平衡介质中的热力学函数、配分函数、平均能量和旋转比热. 2012年, 邓伦华等[13]利用光外差-浓度调制吸收光谱技术测量了NO分子在12530—12850 cm–1波段的吸收光谱, 在该波段内标识出了324条跃迁谱线, 随后采用标准的$^4{\Sigma ^ - }{ - ^4}{\Pi _i}$哈密顿量模型并借助最小二乘法拟合其中的267条谱线, 获得了体系的主要分子常数和精细结构分子常数.
基于统计物理学的微观振动信息人们也能得到与双原子分子振动相关的宏观热力学量[14]. 对于NO分子微观振动信息的理论研究主要基于1950年Huber和Herzberg[15]建立的计算双原子分子振动能级表达式. 早在1975年, Billingsley[16]便采用优化价态构型多构型自洽场方法得到了基态NO分子的电子偶极矩函数和势能曲线. 2006年, Reddy等[17]依靠实验技术用改进的RKR (Rydberg-Klein-Rees)方法构建了基态NO和NO+的势能曲线, 并采用五参数(Hulburt-Hirschfelder, H-H)函数拟合获得了这些电子态的离解能. 2018年, Qin等[18]使用RKR方法获得了NO分子低阶电子态的势能曲线, 利用该势能曲线通过求解薛定谔方程确定了振动能级, 计算了NO分子平衡和非平衡状态的热力学性质.
以上研究为了解NO分子电子态的势能曲线和振动信息做出了巨大贡献. 然而, 实验上现阶段的光谱测量技术一般只能获得体系低激发振动量子态的物理信息, 对于大多数NO分子电子激发态而言, 高激发振动量子态尤其是处于离解区的数据却很难得到. 由于这一客观事实的存在, 人们通常采用简单的谐振子模型(simple harmonic oscillatormodel, SHO)来计算体系的微观振动信息, 再借助量子统计系综理论来获得系统的宏观热力学量. 如此以来, 用SHO模型计算得到的一部分实际上不存在的虚高能级也参与了统计计算, 从而导致最终的热力学计算结果往往出现较大误差. 为了获得NO分子电子态可靠的完全振动能级从而进一步研究其微观振动对宏观热力学性质的影响, 本文基于课题组前期建立的变分代数法(variational algebraic method, VAM)和能精确计算分子离解能的新解析表达式[19], 研究获得了基态NO分子的完全振动能级, 随后采用量子统计系综理论[14]计算了NO分子的热力学性质, 并将计算获得的理论结果与实验数据进行了分析和比较.
2.理论与方法
量子统计系综理论的重要基础是获取系统正确的配分函数, 再将摩尔内能、摩尔熵、摩尔振动热容表示为含有配分函数的表达形式, 从而确定系统的全部热力学性质[14]. 基态的NO分子在不考虑电子、振动和转动的相互作用时可由乘积近似模型得到其配分函数[20]:
$Q(T) = {Q_{\rm{n}}}{\rm{(}}T){Q_{\rm{e}}}(T){Q_{\rm{\upsilon }}}(T){Q_{\rm{r}}}(T),$
式中, T为系统的开氏温度, ${Q_{\rm{n}}}(T),\; {Q_{\rm{e}}}(T),\; {Q_{\rm{\upsilon }}}(T), $ Qr(T)分别表示核配分函数、电子配分函数、振动配分函数以及转动配分函数. 电子配分函数为
${Q_{\rm{e}}}(T) = \sum\limits_i^{} {{g_{\rm{e}}}(i){{\rm{e}}^{[ - {c_2} \cdot {E_{\rm{e}}}(i)/T]}}},$
式中, ${g_{\rm{e}}}(i)$表示电子能级i的简并度, ${c_2}$是第二辐射常数, ${E_{\rm{e}}}(i)$表示第i个电子能级能量, 通常取基态能量${E_{\rm{e}}} = 0$. 另外, 本文中的NO为异核双原子分子, 其核配分函数等于原子核基态的简并度${d_{\rm{s}}} = 1$. 故NO的配分函数$Q(T)$可表示为
$Q(T) = {Q_{\rm{\upsilon }}}(T){Q_{\rm{r}}}(T).$
采用正则量子系综, 体系的振动配分函数可定义为
${Q_{\rm{\upsilon }}}(T) = \sum\limits_{\upsilon = 0}^{{\upsilon _{{\rm{max}}}}} {{g_{\rm{\upsilon }}}{{\rm{e}}^{ - \beta {\kern 1pt} {E_{\rm{\upsilon }}}}}},$
式中, ${g_{\rm{\upsilon }}}$表示能级的简并度, 此处${g_{\rm{\upsilon }}} = 1$, ${E_\upsilon }$是分子内部的振动能级, $\beta = 1/(kT)$, 玻尔兹曼常数k = 1.380062 × 10–23 J/K.
由于NO具有两个电子的双重分裂影响, 其转动配分函数是${}^2{\Pi _{{1 / 2}}}$与${}^2{\Pi _{{3 / 2}}}$两个电子态的和[21], 可表示为
$ {Q_{\rm{r}}}(T){\rm{ }} = \sum\limits_{{\rm{all\ states}}\ i} {{g_i}} {{\rm{e}}^{ - hc{E_i}/(kT)}}{\rm{ }}, $
式中, ${g_i}$表示能级的简并度, h为普朗克常数, c为光速, 再根据McDowell建立的解析公式[22], NO的转动配分函数可表示为
${Q_{\rm{r}}}{\rm{(}}T) = \sum\limits_{J = 0} ( 2J + 1){{\rm{e}}^{ - \frac{{hc}}{{kT}}{E_{\rm{r}}}}},$
其中Er是转动能量, 由转动光谱常数B和转动量子数J决定:
${E_{\rm{r}}} = BJ(J + 1).$
将欧拉-麦克劳林公式应用于(6)式可以等价为如下的渐进的展开式[22]:
${Q_{\rm{r}}}(T)\sim \frac{T}{{{\varTheta _{\rm{r}}}}}\left[ {1 + \frac{1}{3}\frac{{{\varTheta _{\rm{r}}}}}{T} + \frac{1}{{15}}{{\left( {\frac{{{\varTheta _{\rm{r}}}}}{T}} \right)}^2} + \frac{4}{{315}}{{\left( {\frac{{{\varTheta _{\rm{r}}}}}{T}} \right)}^3}} \right].$
(8)式中${\varTheta _{\rm{r}}} = hcB/k$, NO的转动光谱常数B = 1.70488847 cm–1 [23].
对于常见的双原子分子组成的宏观系统, 内能是系统能量在所有微观状态上的平均值, 摩尔内能可表示为
$U = {N_{\rm{A}}}k{T^2}\frac{\partial }{{\partial T}}\ln Q(T),$
(9)式中${N_{\rm{A}}}$为阿伏伽德罗常数. 统计系统的摩尔熵表示为
$S = {N_{\rm{A}}}k\left[ {\frac{\partial }{{\partial T}}\left( {T\ln Q(T)} \right)} \right].$
统计物理中可观测的物理量是摩尔热容, 可表示为
$C_{\rm{m}}^{} = {N_{\rm{A}}}k\frac{\partial }{{\partial T}}\left[ {{T^2}\frac{\partial }{{\partial T}}\ln Q(T)} \right].$
根据上述公式通过对系统的所有能级求和可计算得到宏观热力学量. 然而, 由于实验条件的限制, 对于大多数双核体系很难获得其电子态包含高激发态在内的完全振动能级, 因此, 人们通常采用简单谐振子模型(SHO)来描述振动运动对无限个振动能级进行求和获得热力学性质, 等同于认为最大振动量子数${\upsilon _{{\rm{max}}}} \to \infty $, 得到配分函数的解析形式:
$Q_{{\rm{SHO}}}^{{\rm{cal}}}(T) \!=\! Q_{\rm{\upsilon }}^{{\rm{SHO}}}(T){Q_{\rm{r}}}(T) \!=\! \frac{{{{\rm{e}}^{ - \beta {\kern 1pt} \hbar {\omega _{\rm{e}}}/2}}}}{{1 \!-\! {{\rm{e}}^{ - \beta {\kern 1pt} \hbar {\omega _{\rm{e}}}}}}}{Q_{\rm{r}}}(T),$
其中$Q_{\rm{\upsilon }}^{{\rm{SHO}}}(T)$表示谐振子模型的振动配分函数, $\hbar = {h / {(2{\text{π}})}}$, ${\omega _{\rm{e}}}$为光谱常数, 通过(12)式可得到相关的热力学量的解析解. 实际上, 真实双原子分子各电子态的最大振动量子数${\upsilon _{{\rm{max}}}}$并非是无穷大的, 且(12)式对高于离解能实际上不存在的虚高能级进行统计求和也是不合理的, 因此不应采用简单谐振子振动模型来计算宏观系统的热力学性质.
为了获得某分子电子态的完全振动能级, 孙卫国课题组在前期的研究工作中提出了变分代数方法(VAM), 该方法的建立是根据Born-Oppenheimer近似, 利用二阶微扰理论求解薛定谔方程, 获得如下双原子分子体系振动能级的表达式[24]:
$\begin{split} {E_{\rm{\upsilon }}} =\; & {\omega _0} + ({\omega _{\rm{e}}} + {\omega _{{\rm{e0}}}})\Big( {\upsilon + \frac{1}{2}} \Big) - {\omega _{\rm{e}}}{x_{\rm{e}}}{\Big( {\upsilon + \frac{1}{2}} \Big)^2}\\& + {\omega _{\rm{e}}}{y_{\rm{e}}}{\Big( {\upsilon + \frac{1}{2}} \Big)^3} + {\omega _{\rm{e}}}{z_{\rm{e}}}{\Big( {\upsilon + \frac{1}{2}} \Big)^4} \\& + {\omega _{\rm{e}}}{t_{\rm{e}}}{\Big( {\upsilon + \frac{1}{2}} \Big)^5} + {\omega _{\rm{e}}}{s_{\rm{e}}}{\Big( {\upsilon + \frac{1}{2}} \Big)^6}\\& + {\omega _{\rm{e}}}{r_{\rm{e}}}{\Big( {\upsilon + \frac{1}{2}} \Big)^7} + \cdots, \\[-17pt]\end{split}$
其中$({\omega _0}, {\omega _{\rm{e}}}, {\omega _{{\rm{e0}}}}, {\omega _{\rm{e}}}{x_{\rm{e}}}, {\omega _{\rm{e}}}{y_{\rm{e}}}, {\omega _{\rm{e}}}{z_{\rm{e}}}, {\omega _{\rm{e}}}{t_{\rm{e}}}, \cdots )$是双原子分子的振动光谱常数, υ是振动量子数, ${E_{\rm{\upsilon }}}$是振动能级. 为了抵消实验上可能出现的测量误差, 在每个能级节点上添加了一个微小变分项$\text{δ} {E_{{\rm{\upsilon }}i}}$[19], 并将(13)式改写为
$ {{AX}} = {{E}} + \text{δ}{{E}} = {{E}}', $
其中${{A}}$为系数矩阵, ${{X}}$为双核分子光谱常数, ${{E}}$为振动能级, 分别为
$ \begin{split} &{{A}_{{\rm{\upsilon }}k}} = {\left( {\upsilon + \frac{1}{2}} \right)^k},\;\; {{X}} = {\left( {\begin{array}{*{20}{c}} {{\omega _0}} \\ {{{\omega '}_{\rm{e}}}} \\ { - {\omega _{\rm{e}}}{x_{\rm{e}}}} \\ {{\omega _{\rm{e}}}{y_{\rm{e}}}} \\ \vdots \end{array}} \right)_{m \times 1}}, \\ &{{E}} = {\left( {\begin{array}{*{20}{c}} {{E_{{\upsilon _1}}} + \text{δ} {E_{{\upsilon _1}}}} \\ {{E_{{\upsilon _2}}} + \text{δ} {E_{{\upsilon _2}}}} \\ {{E_{{\upsilon _3}}} + \text{δ} {E_{{\upsilon _3}}}} \\ \vdots \\ {{E_{{\upsilon _m}}} + \text{δ} {E_{{\upsilon _m}}}} \end{array}} \right)_{m \times 1}}, \end{split} $
其中${\omega '_{\rm{e}}} = {\omega _{\rm{e}}} + {\omega _{{\rm{e0}}}}$. 随着光谱实验装置的不断改进, 实验上产生的误差不会太大, 有约束条件
$\text{δ} {E_{{\upsilon _i}}} \to 0.$
对于某双原子分子电子态, 只需从该电子态已测量获得的n个有限实验振动能级数据中选取m个能级, 由于不同分子的不同电子态的物理性质不同, 能级的展开形式应该存在一定的差异性, 因此贡献项的个数选择也有所不同, 根据不同电子态的能级性质自由选取贡献项的个数(即$ m = 3, 4, 5,\cdots $)代入(14)式中进行数值计算, 就可获得$N = C_n^m$组振动光谱常数$({\omega _0}, {\omega '_{\rm{e}}}, {\omega _{\rm{e}}}{x_{\rm{e}}}, {\omega _{\rm{e}}}{y_{\rm{e}}}, {\omega _{\rm{e}}}{z_{\rm{e}}}, {\omega _{\rm{e}}}{t_{\rm{e}}}, \cdots )$. 再利用以下的物理判据选出一组最佳的振动光谱常数${X'}$:
$\frac{{{\rm{d}}{E_{\rm{\upsilon }}}}}{{{\rm{d}}\upsilon }}{\Big|_{\upsilon = {\upsilon _{{\rm{max}}}}}} = 0,$
$\Delta {E_{{\upsilon _{{\rm{max}}}},{\upsilon _{{\rm{max}}}} - 1}} = {E_{{{\rm{\upsilon }}_{{\rm{max}}}}}} - {E_{{\upsilon _{{\rm{max}}}} - 1}} \to \;{\rm{small}}\;{\rm{enough}},$
$D_{\rm{e}}^{{\rm{exp}}} - {E_{{\upsilon _{{\rm{max}}}}}} \to \;{\rm{small}}\;{\rm{enough}},$
$\Delta E({\rm{exp}},{\rm{cal}}) = \sqrt {\frac{1}{m}{{\sum\limits_{\upsilon = 0}^{m - 1} {\left| {{E_{\upsilon,{\rm{exp}}}} - {E_{\upsilon,{\rm{cal}}}}} \right|}^2 }}} \to 0,$
$D_{\rm{e}}^{{\rm{cal}}} \cong {E_{{\upsilon _{{\rm{max}}}}}} + \frac{{\Delta E_{{\upsilon _{{\rm{max}}}},{\upsilon _{{\rm{max}}}} - 1}^2}}{{\Delta E_{{\upsilon _{{\rm{max}}}},{\upsilon _{{\rm{max}}}} - 2}^{} - \Delta {E_{{\upsilon _{{\rm{max}}}},{\upsilon _{{\rm{max}}}} - 1}}}},$
${E_{{\upsilon _{{\rm{max}}}}}} < {\rm{D}}_e^{\rm {cal}} \leqslant D_e^{\rm {exp}},$
$0 < {\rm{Error}} = \frac{{D_{\rm{e}}^{{\rm{exp}}} - D_{\rm{e}}^{{\rm{cal}}}}}{{\Delta {E_{{\upsilon _{{\rm{max}}}},{\upsilon _{{\rm{max}}}} - 1}}}} \leqslant 1.$
(17)—(20)式是振动收敛条件, (21)式是VAM方法给出的离解能计算公式, (22)式表示计算出的振动能级正确收敛于离解能, 得到最优的一组振动光谱常数后, 将其代入振动能级的精确表达式(13)式中, 就能够对体系未知的振动能级进行预测. (17)—(23)式中, “exp”表示实验已有的数据, “cal”表示VAM计算获得的数据, $D_{\rm{e}}^{}$表示体系的离解能, $D_{\rm{e}}^{{\rm{cal}}}$表示用最高的三个振动能级代入(21)式计算得到的离解能.
综上所述, 对于基态NO分子, 加入微小的变分项抵消实验振动能级误差并利用代数方法求解其完全振动能级$\left\{ {E_{\rm{\upsilon }}^{{\rm{VAM}}}} \right\}$和离解能$D_{\rm{e}}^{{\rm{cal}}}$的方法称为变分代数法(VAM). 获得的VAM振动配分函数则为$Q_{\rm{\upsilon }}^{{\rm{VAM}}}(T)$, 因此(11)式中的摩尔热容量表示为
$ C_{{\rm{VAM}}}^{{\rm{cal}}} = {N_{\rm{A}}}k\frac{\partial }{{\partial T}}\left( {{T^2}\frac{\partial }{{\partial T}}{\rm{ln}}\left[Q_{\rm{\upsilon }}^{{\rm{VAM}}}(T){Q_{\rm{r}}}(T)\right]} \right). $
相似地, 将(24)式中的$Q_{\rm{\upsilon }}^{{\rm{VAM}}}(T)$替换成$Q_{\rm{\upsilon }}^{{\rm{RKR}}}(T)$, $Q_{\rm{\upsilon }}^{{\rm{MCSCF}}}(T)$, $Q_{\rm{\upsilon }}^{{\rm{SHO}}}(T)$则可以获得RKR热容值$C_{{\rm{RKR}}}^{{\rm{cal}}}$, 偶极子的多构型自洽场 (multi- configuration self-consistent-field calculation of the dipole moment function, MCSCF)热容值$C_{{\rm{MCSCF}}}^{{\rm{cal}}}$和谐振子热容值$C_{{\rm{SHO}}}^{{\rm{cal}}}$.
如此一来, 用VAM方法求得的热力学量的具体表现形式就不同于谐振子模型无穷项求和的形式, 减小了对实际上不存在的虚高能级进行统计求和带来的误差.
3.应用与讨论
首先应用VAM方法计算了基态NO分子的完全振动能级. 表1列出了基态NO分子VAM完全振动能级$\left\{ {E_{\rm{\upsilon }}^{{\rm{VAM}}}} \right\}$并计算了相对于实验上获得的有限精确振动能级$\left\{ {E_{\rm{\upsilon }}^{{\rm{exp}}}} \right\}$[17]的绝对误差. 如表1所列, VAM方法选出了6条($\upsilon = 0, {\rm{1}}, {\rm{3}}, {\rm{5}}, {\rm{6}}, {\rm{7}}$)最能反映基态NO分子振动行为的实验振动能级(黑体标出). 利用这6条数据计算得到了收敛于离解能的完全振动能级, 并且在低激发振动能级区域与实验振动能级符合得很好. 表1还列出了MCSCF方法得到的振动能级[16]及其与实验振动能级的绝对误差.
$\upsilon $$E_{\rm{\upsilon }}^{{\rm{exp}}}$[17]$E_{\rm{\upsilon }}^{{\rm{MCSCF}}}$[16]$E_{\rm{\upsilon }}^{{\rm{VAM}}}$$E_{\rm{\upsilon }}^{{\rm{exp}}} - E_{\rm{\upsilon }}^{{\rm{MCSCF}}}$$E_{\rm{\upsilon }}^{{\rm{exp}}} - E_{\rm{\upsilon }}^{{\rm{VAM}}}$υ$E_{\rm{\upsilon }}^{{\rm{VAM}}}$
0 948.50 948.60948.50–0.1002640240.70
1 2824.50 2824.602824.50–0.1002741310.84
24627.304672.404672.27–45.10–44.972842340.94
3 6491.90 6492.106491.90–0.2002943329.70
48283.508283.908283.43–0.400.073044275.74
5 10046.90 10047.8010046.90–0.9003145177.59
6 11782.30 11783.7011782.30–1.4003246033.69
7 13489.40 13491.7013489.60–2.30–0.203346842.41
815171.8015168.733447602.00
916823.9016819.603548310.62
1018448.0018442.063648966.35
1120044.0020035.933749567.15
1221611.8021600.993850110.90
1323151.3023136.973950595.35
1424662.4024643.564051018.15
1526144.8026120.384151376.86
1627598.5027567.044251668.92
1729023.2028983.044351891.64
1830367.884452042.23
1931720.95
2033041.62
2134329.18
2235582.84
2336801.78
2437985.07
2539131.73
$D_{\rm{e}}^{{\rm{exp}}}$52155.68$D_{\rm{e}}^{{\rm{cal}}}$52155.68
注: $E_{\rm{\upsilon }}^{{\rm{VAM}}}$中表示VAM计算所需的已知实验振动能级用黑体标出.


表1基态NO分子不同振动能级间的比较 (单位: cm–1)
Table1.Comparison of different vibrational levels of NO in the ground state (in cm–1).

将VAM方法和MCSCF方法计算的振动能级与实验能级进行比较, VAM的误差明显小于MCSCF的误差. 在实验上获得的有限精确振动能级区域, 除振动量子数为2的能级外, VAM振动能级与实验值的误差均在[－0.2, 0.067] cm－1范围内. 振动量子数为2的能级误差很大, 实验上获得的数据为4627.300 cm–1, VAM计算值为4672.274 cm–1, MCSCF的计算值为4672.000 cm–1, 两种方法误差均达到45 cm–1左右. 王建坤等[25]用多组态相互作用理论(multireference configuration interaction, MRCI)以cc-pVDZ为基组得到的理论计算结果也在4672 cm–1附近. 更直观地, 从图1可以看出, 使用(18)式和(19)式来判断VAM振动能级的数值结果在其离解区的收敛性是可靠的.
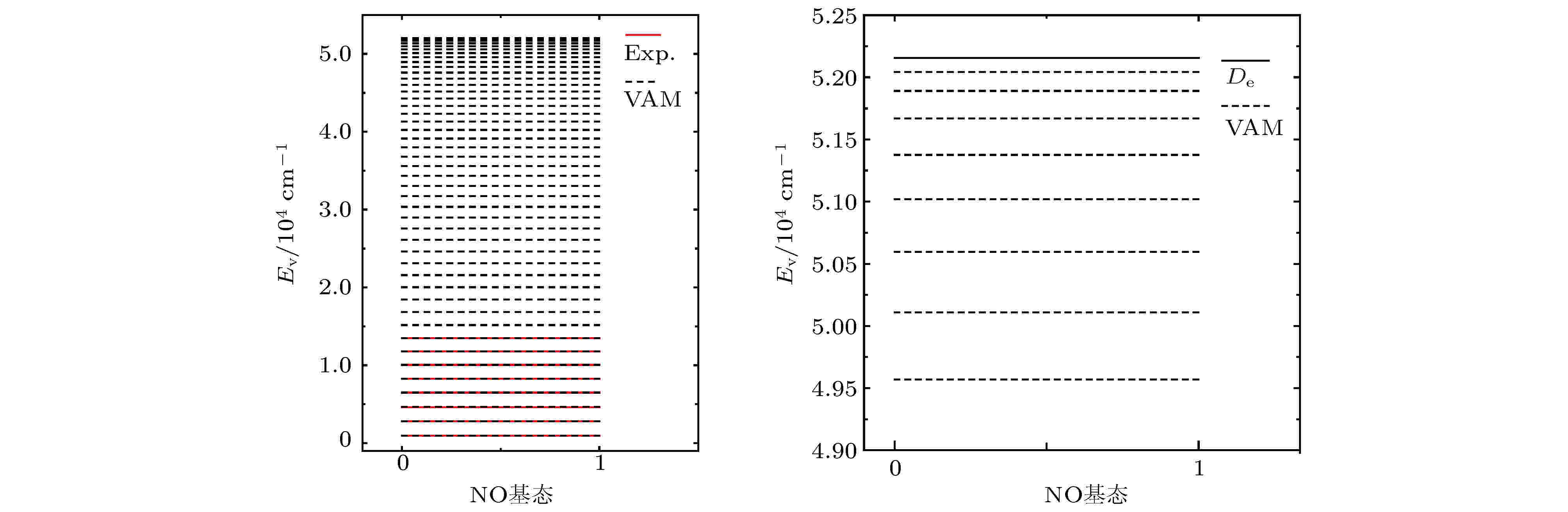图 1 VAM完全振动能级和实验能级的对比图
Figure1. Comparison between the VAM full vibrational energies and experimental ones

获得基态NO分子精确的完全振动能级后, 根据量子统计系综理论计算了1000—5000 K温度范围内NO分子气体系统摩尔内能、摩尔熵和摩尔热容. 在高温低压气体条件下, 系统处于理想气体状态, 去掉分子热运动的热容量, 剩余分子振动和转动对应热容量$C_{{\rm{exp}}}^{} = C_{\rm{p}}^{{\rm{exp}}} - R - 3 R/2 = C_{\rm{p}}^{{\rm{exp}}} -$ 5R/2, 其中普适气体常数R = 8.31441 J·K–1·mol–1. 采用Chase[26]得到的NO分子气体定压摩尔热容量的实验数据与理论计算结果进行比较. 表2和表3列出了量子统计系综理论在考虑不同振动配分函数贡献($Q_{\rm{\upsilon }}^{{\rm{RKR}}}(T)$, $Q_{\rm{\upsilon }}^{{\rm{MCSCF}}}(T)$, $Q_{\rm{\upsilon }}^{{\rm{SHO}}}(T)$, $Q_{\rm{\upsilon }}^{{\rm{VAM}}}(T)$)条件下计算得到的内能和熵.
T/K$U_{{\rm{RKR}}}^{{\rm{cal}}}$$U_{{\rm{MCSCF}}}^{{\rm{cal}}}$$U_{{\rm{SHO}}}^{{\rm{cal}}}$$U_{{\rm{VAM}}}^{{\rm{cal}}}$
100021.2821.2821.2721.28
110022.6122.6122.5922.61
120023.9823.9923.9523.98
130025.3925.4025.3425.39
140026.8426.8426.7726.84
150028.3128.3128.2328.31
160029.8029.8029.7029.80
170031.3131.3131.2031.31
180032.8432.8432.7132.84
190034.3834.3934.2434.38
200035.9435.9435.7735.94
210037.5137.5137.3237.51
220039.0939.0938.8839.09
230040.6840.6840.4540.68
240042.2842.2842.0342.28
250043.8943.8943.6143.89
260045.5045.5045.1945.50
270047.1247.1246.7947.12
280048.7548.7548.3848.75
290050.3850.3849.9950.38
300052.0152.0151.5952.01
310053.6653.6553.2053.66
320055.3055.3054.8155.30
330056.9556.9556.4356.95
340058.6058.6058.0558.60
350060.2660.2659.6760.26
360061.9261.9261.2961.92
370063.5863.5862.9163.59
380065.2565.2464.5465.25
390066.9166.9166.1766.92
400068.5868.5867.8068.60
410070.2670.2569.4370.27
420071.9371.9371.0771.95
430073.6173.6172.7073.63
440075.2975.2874.3475.32
450076.9776.9675.9777.01
460078.6578.6477.6178.69
470080.3380.3279.2580.39
480082.0182.0180.8982.08
490083.6983.6982.5383.78
500085.3885.3784.1785.48


表2使用RKR, MCSCF, SHO和VAM振动能级计算的摩尔内能 (单位: J·K–1·mol–1)
Table2.Calculated molar internal energy using RKR, MCSCF, SHO, and VAM vibrational energies as the vibrational contributions, respectively (in J·K–1·mol–1).

T/K$S_{{\rm{RKR}}}^{{\rm{cal}}}$$S_{{\rm{MCSCF}}}^{{\rm{cal}}}$$S_{{\rm{SHO}}}^{{\rm{cal}}}$$S_{{\rm{VAM}}}^{{\rm{cal}}}$
100060.5060.5060.4260.50
110061.7661.7661.6761.76
120062.9662.9662.8662.96
130064.0964.0963.9764.09
140065.1665.1665.0365.16
150066.1766.1766.0366.17
160067.1367.1366.9967.13
170068.0568.0567.8968.05
180068.9268.9268.7668.92
190069.7669.7669.5869.76
200070.5670.5670.3770.56
210071.3271.3271.1371.32
220072.0672.0671.8572.06
230072.7772.7772.5572.77
240073.4573.4573.2273.45
250074.1074.1073.8774.10
260074.7374.7374.4974.73
270075.3575.3575.0975.35
280075.9475.9475.6775.94
290076.5176.5176.2376.51
300077.0677.0676.7877.06
310077.6077.6077.3077.60
320078.1278.1277.8278.12
330078.6378.6378.3178.63
340079.1279.1278.8079.13
350079.6079.6079.2779.61
360080.0780.0779.7280.07
370080.5380.5380.1780.53
380080.9780.9780.6080.97
390081.4181.4081.0381.41
400081.8381.8381.4481.83
410082.2482.2481.8482.25
420082.6582.6482.2482.65
430083.0483.0482.6283.05
440083.4383.4283.0083.43
450083.8083.8083.3683.81
460084.1784.1783.7284.18
470084.5384.5384.0884.55
480084.8984.8984.4284.90
490085.2485.2384.7685.25
500085.5885.5785.0985.60


表3使用RKR, MCSCF、SHO和VAM振动能级计算的摩尔熵(单位: J·K–1·mol–1)
Table3.Calculated molar entropy using RKR, MCSCF, SHO, and VAM vibrational energies as the vibrational contributions, respectively (in J·K–1·mol–1).

内能、熵、热容均是重要的热力学参数, 但在实验中常常测定的是热容的值${C_{{\rm{exp}}}}$. 在表4中将得到的热容$C_{{\rm{VAM}}}^{{\rm{cal}}}$与实验测量的热容${C_{{\rm{exp}}}}$进行比较, 在1200 K时与实验值的相对误差仅为1.16%. 在整个温度区间范围内, 虽然相对误差随着温度的升高而增大, 但是最大值仅为2.36%, 小于采用其他方法计算的误差.
T/K${C_{{\rm{exp}}}}$$C_{{\rm{RKR}}}^{{\rm{cal}}}$$C_{{\rm{MCSCF}}}^{{\rm{cal}}}$$C_{{\rm{SHO}}}^{{\rm{cal}}}$$C_{{\rm{VAM}}}^{{\rm{cal}}}$${\delta _{{\rm{RKR}}}}$a${\delta _{{\rm{MCSCF}}}}$b${\delta _{{\rm{SHO}}}}$c${\delta _{{\rm{VAM}}}}$d
100013.2013.0413.0410.7213.041.22%1.22%18.82%1.22%
110013.6813.5213.5211.2413.521.18%1.18%17.85%1.18%
120014.0913.9313.9311.7313.931.16%1.16%16.77%1.16%
130014.4414.2714.2712.1714.271.17%1.17%15.69%1.17%
140014.7414.5614.5612.5814.561.19%1.19%14.66%1.19%
150014.9914.8114.8112.9414.811.21%1.21%13.70%1.21%
160015.2215.0315.0313.2615.031.23%1.23%12.83%1.23%
170015.4115.2215.2113.5515.221.26%1.26%12.04%1.26%
180015.5815.3815.3813.8115.381.29%1.29%11.35%1.29%
190015.7315.5215.5214.0415.521.33%1.33%10.73%1.33%
200015.8615.6515.6414.2515.651.36%1.37%10.18%1.36%
210015.9815.7615.7614.4315.761.41%1.41%9.71%1.41%
220016.0915.8615.8614.5915.861.45%1.45%9.29%1.45%
230016.1815.9515.9414.7415.951.48%1.49%8.92%1.48%
240016.2716.0316.0314.8816.031.52%1.53%8.59%1.52%
250016.3516.1016.1015.0016.101.56%1.57%8.31%1.56%
260016.4316.1716.1715.1016.171.61%1.61%8.07%1.61%
270016.5016.2316.2315.2016.231.65%1.65%7.85%1.65%
280016.5616.2816.2815.2916.281.69%1.70%7.67%1.69%
290016.6216.3416.3315.3816.341.74%1.74%7.51%1.73%
300016.6816.3816.3815.4516.391.77%1.78%7.37%1.77%
310016.7316.4316.4315.5216.431.82%1.83%7.25%1.80%
320016.7816.4716.4715.5816.471.87%1.88%7.16%1.85%
330016.8316.5116.5115.6416.511.91%1.92%7.08%1.88%
340016.8816.5516.5415.6916.551.96%1.97%7.01%1.92%
350016.9216.5816.5815.7416.592.01%2.02%6.96%1.95%
360016.9616.6116.6115.7916.622.06%2.07%6.91%1.99%
370017.0016.6416.6415.8316.662.12%2.13%6.89%2.03%
380017.0416.6716.6715.8716.692.18%2.19%6.86%2.06%
390017.0816.6916.6915.9116.722.24%2.25%6.85%2.09%
400017.1116.7216.7115.9416.752.31%2.32%6.85%2.13%
410017.1516.7416.7415.9716.782.38%2.40%6.86%2.16%
420017.1816.7616.7516.0016.812.46%2.48%6.86%2.18%
430017.2116.7716.7716.0316.832.55%2.57%6.88%2.21%
440017.2416.7916.7916.0516.862.64%2.66%6.90%2.24%
450017.2816.8016.8016.0816.892.74%2.76%6.93%2.26%
460017.3116.8116.8116.1016.912.85%2.86%6.96%2.29%
470017.3416.8216.8216.1216.942.96%2.99%7.00%2.31%
480017.3616.8316.8316.1416.963.09%3.11%7.04%2.32%
490017.3916.8316.8316.1616.993.22%3.25%7.08%2.35%
500017.4216.8416.8316.1817.013.37%3.38%7.13%2.36%
注: a, ${\delta _{{\rm{RKR}}}} = \left| {C_{{\rm{exp}}}^{} - C_{{\rm{RKR}}}^{{\rm{cal}}}} \right|/C_{{\rm{exp}}}^{} \times 100\% $; b, ${\delta _{{\rm{MCSCF}}}} = \left| {C_{{\rm{exp}}}^{} - C_{{\rm{MCSCF}}}^{{\rm{cal}}}} \right|/C_{{\rm{exp}}}^{} \times 100\% $; c, $ {\delta _{{\rm{SHO}}}} = \left| {C_{{\rm{exp}}} - C_{{\rm{SHO}}}^{{\rm{cal}}}} \right|/C_{{\rm{exp}}} \times 100\% $; d,$ {\delta _{{\rm{VAM}}}} = \left| {C_{{\rm{exp}}} - C_{{\rm{VAM}}}^{{\rm{cal}}}} \right|/C_{{\rm{exp}}} \times 100\% .$


表4不同摩尔热容及其与实验值的相对误差 (单位: J·K–1·mol–1)
Table4.Comparisons of different molar capacities with observed experimental ${C_{{\rm{exp}}}}$(in J·K–1·mol–1).

表4还列出了$C_{{\rm{RKR}}}^{{\rm{cal}}}$, $C_{{\rm{MCSCF}}}^{{\rm{cal}}}$和$C_{{\rm{SHO}}}^{{\rm{cal}}}$以及这些结果与实验测量的热容$C_{{\rm{exp}}}$的相对误差. 由表4知, 仅将实验获得的8个振动能级进行统计求和计算热容$C_{{\rm{RKR}}}^{{\rm{cal}}}$时, 由于大量缺乏高阶振动能级对系统的统计贡献, 热容结果总是小于实验测得的结果, 且与实验值的误差随着温度的升高而增大, 在5000 K时与实验值的相对误差达到了3.37%. 将MCSCF振动能级用于统计公式计算热容$C_{{\rm{MCSCF}}}^{{\rm{cal}}}$时, 其参与计算的最高振动能级能量为29023.2 cm–1, 仅达到离解能的55.65%, 仍然缺乏高阶振动能级对热容的贡献. 因此其结果与实验值的误差还是很大, 相对误差达到了3.38%. 而简单谐振子模型对实际上不存在的虚高能级进行统计求和, 偏离了物理事实, 计算得到的热容误差与实验值相比误差最大. 其相对误差最小时也有6.85%, 远大于使用VAM完全振动能级计算的热容与实验测得的热容值的误差. 说明简单谐振子模型对无限能级求和方法对求解宏观气体系统的热力学性质有一定的局限性. 本文未考虑激发态对配分函数的影响, 所以计算得到的热容值均小于实验值. 综上所述, 使用VAM完全振动能级作为振动贡献计算获得的热容量$C_{{\rm{VAM}}}^{{\rm{cal}}}$与实验测得热容$C_{{\rm{exp}}}$相比误差最小.
图2可以更直观地体现不同方法获得的热容计算值与热容实验值的相对误差. 由图2可知VAM热容$C_{{\rm{VAM}}}^{{\rm{cal}}}$与实验上测得的热容${C_{{\rm{exp}}}}$误差最小, 谐振子热容$C_{{\rm{SHO}}}^{{\rm{cal}}}$与实验上测得的热容${C_{{\rm{exp}}}}$误差最大. 在1000—2800 K温度范围内, $C_{{\rm{RKR}}}^{{\rm{cal}}}$, $C_{\rm VAM}^{\rm cal}$和$C_{{\rm{MCSCF}}}^{{\rm{cal}}}$三者的值较为吻合, 在2900—5000 K较高温度范围内, 较$C_{{\rm{VAM}}}^{{\rm{cal}}}$而言, $C_{{\rm{RKR}}}^{{\rm{cal}}}$和$C_{{\rm{MCSCF}}}^{{\rm{cal}}}$热容值明显偏离了实验热容${C_{{\rm{exp}}}}$. 这一结果表明, 计算热容时振动部分采用VAM方法获得完全振动能级的计算结果精度优于其他方法获得的计算结果.
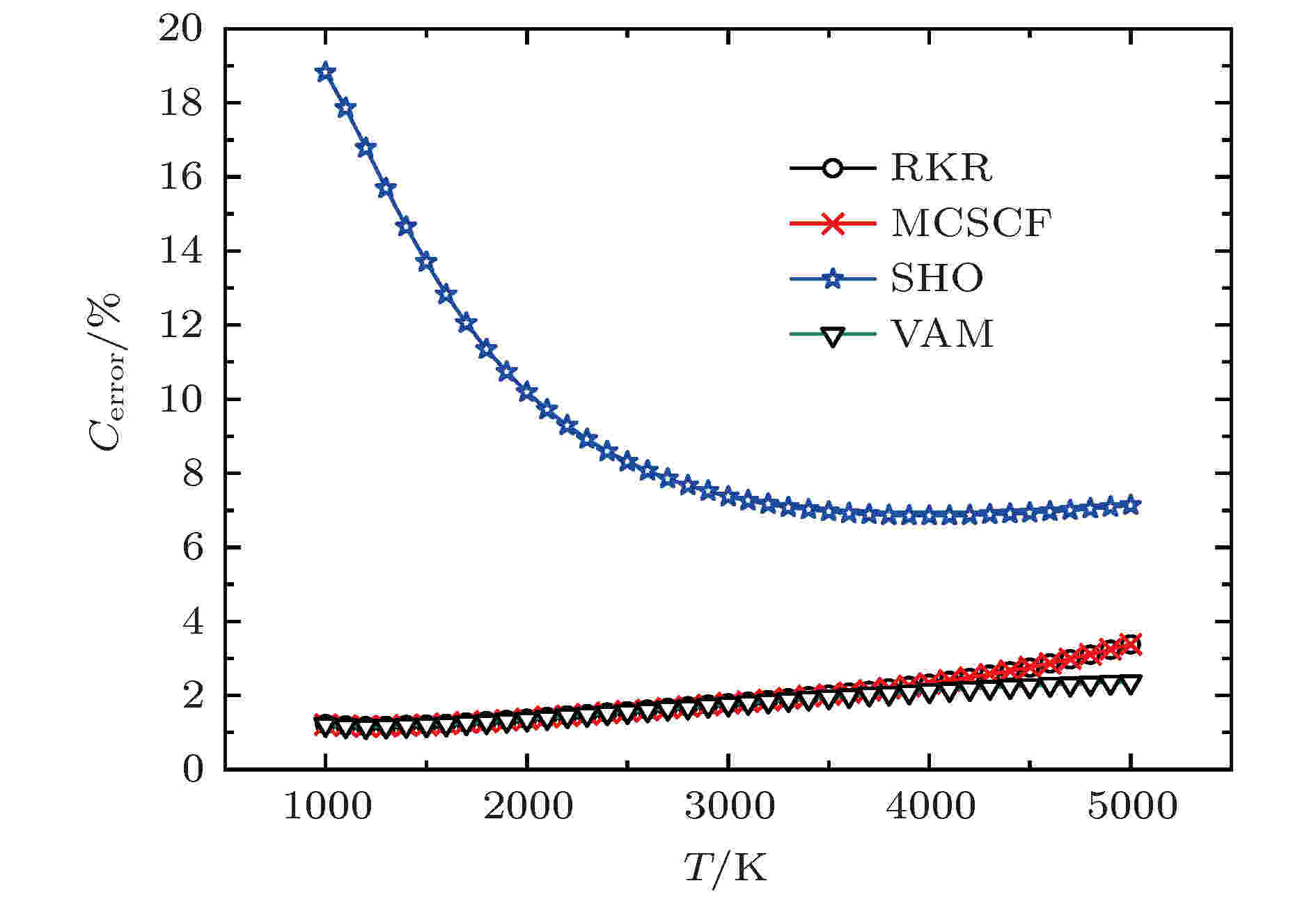图 2 不同热容相对误差的比较
Figure2. Comparison of the relative errors of different heat capacities

4.结　论
使用前期建立的VAM方法, 基于实验上获得的基态NO分子8个振动能级得到了正确收敛于实验离解能的45个完全振动能级. 发现振动量子数为2的振动能级与实验值有较大的差异, 但其他理论研究者的结果也在本文的研究结果附近. 分别将VAM完全振动能级、实验上得到的有限的振动能级、MCSCF方法得到的振动能级和简谐振子模型得到的振动能级作为振动贡献, 将欧拉-麦克劳林渐进展开公式的计算结果作为转动贡献, 用量子系综理论计算了NO气体系统的摩尔内能、摩尔熵和摩尔热容. 将不同方法计算获得的摩尔热容与实验值进行比较发现: 缺乏高阶振动能级会给求解系统的热力学性质带来较大误差; 对实际上不存在的虚高能级进行统计求和也会给计算结果带来很大误差; 振动部分采用VAM完全振动能级所计算的热容与实验上测得的热容最为吻合. 这说明使用谐振子模型和不完全振动能级对计算热力学性质均有一定的局限性, 应当使用有限的完全振动能级进行统计求和.
相关话题/计算 实验 电子 统计 系统
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 东方超环上低杂波驱动等离子体环向旋转实验研究
    摘要:旋转和旋转剪切能抑制磁流体不稳定性和增强等离子体约束.低杂波电流驱动作为未来聚变堆上可能的旋转驱动手段,探索低杂波在现有托卡马克装置上驱动等离子体旋转的驱动机制,可以为未来的聚变堆上旋转预测提供重要参考.在东方超环托卡马克装置上,早期发现了2.45GHz的低杂波能有效驱动等离子体旋转的现象,认 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • H, F修饰单层GeTe的电子结构与光催化性质
    摘要:采用基于密度泛函理论的第一性原理平面波赝势方法,计算了单层GeTe、表面氢化及氟化单层GeTe的晶体结构、稳定性、电子结构和光学性质.计算结果表明,经过修饰后,GeTe的晶格常数、键角、键长增大,且均具有较好的稳定性.电子结构分析表明,单层GeTe为间接带隙半导体,全氢化修饰、全氟化修饰以及氢 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 脉冲强磁场下的电极化测量系统
    摘要:多铁性材料是当前物质科学研究的热点,具有重要的科学研究意义和应用前景.低温和强磁场实验环境为研究多铁性材料提供了一种有效途径.脉冲强磁场下的电极化测量系统能实现最高磁场强度60T、最低温度0.5K的铁电特性测量.该系统采用热释电方法,具有磁场强度高、控温范围广、转角测量等特点,可用于强磁场下的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于新的五维多环多翼超混沌系统的图像加密算法
    摘要:本文提出了一种基于新的五维多环多翼超混沌系统的数字图像加密方法.首先,将明文图像矩阵和五条混沌序列分别通过QR分解法分解成一个正交矩阵和一个上三角矩阵,将混沌系统产生的五条混沌序列分别通过LU分解法分解成一个上三角矩阵和一个下三角矩阵,分别将两个上三角矩阵和一个下三角矩阵相加,得到五个离散后的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于量子点接触的开放双量子点系统电子转移特性
    摘要:基于量子点接触探测器(QPC)理论上研究了双量子点(DQD)系统在耗散环境和纯退相环境影响下的电子转移特性.结果表明,耗散环境中探测器导致的退相干会增大平均电流和Fanofactor随时间演化的值,并观察到量子芝诺效应的存在.在对称的DQD情况下,弛豫减小了平均电流随时间演化的震荡振幅.在非对 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 频率色散表面阻抗对真空电子太赫兹源的影响
    摘要:为了研究欧姆损耗对高频真空电子器件工作特性的影响,首先推导频率色散表面阻抗边界在三维共形粒子模拟软件UNIPIC-3D中的实现原理,并通过对有耗边界矩形谐振腔和圆波导进行模拟验证了该阻抗边界算法的正确性.采用有耗共形UNIPIC-3D模拟相对论太赫兹表面波振荡器和低电压平板格栅返波振荡器.模拟 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高效外腔倍频产生426 nm激光的实验研究
    摘要:利用与铯原子吸收线对应的852nm半导体激光作为基频光,泵浦基于周期极化磷酸钛氧钾(PPKTP)晶体的环形腔,进行高效外腔谐振倍频并产生426nm激光.在理论分析小角度环形腔内的热透镜效应基础上,发现晶体中等效热透镜中心位置并非在晶体的几何中心.在理论分析的基础上,实验上通过精密平移台精细调节 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高熵合金短程有序现象的预测及其对结构的电子、磁性、力学性质的影响
    摘要:如何有效预测高熵合金的稳态结构,是开展研究其物理及化学等性能的基础.以FeCuCrMnMo合金为例,在有限晶胞尺寸内,采用蒙特卡洛结合密度泛函理论杂化计算方法(MonteCarlo/densityfunctionaltheory,MC/DFT)预测高熵合金的平衡态结构.与准随机近似方法(spe ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 石墨烯纳米网电导特性的能带机理：第一原理计算
    摘要:通过第一原理电子结构计算来研究有序多孔纳米网的电导特性变化的能带机理.能带结构分析结果表明:石墨烯纳米网超晶格(3m,3n)(m和n为整数)的电子本征态在布里渊区中心点发生四重简并;碳空位孔洞规则排列形成的石墨烯纳米网具有由简并态分裂形成的宽度可调带隙,无论石墨烯的两个子晶格是否对等.在具有磁 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Tl<sub>0.33</sub>WO<sub>3</sub>电子结构和太阳辐射屏蔽性能第一性原理研究
    摘要:节能减排已成为当今社会发展的主题,对节约能源、提高太阳能的高效综合利用的新型窗用透明隔热材料的理论设计和研究尤其重要.本文采用基于密度泛函理论的计算方法,研究了六方相三氧化钨Tl掺杂前、后的晶格参数、电子能带结构、形成能和光学性质.研究结果表明,Tl掺杂后晶格体积增大,系统能量降为负值,体系具 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.