摘要: 传统量子系统的哈密顿是自伴算子, 哈密顿的自伴性不仅保证系统遵循酉演化和保持概率守恒, 而且也保证了它自身具有实的能量本征值, 这类系统称为自伴量子系统. 然而, 确实存在一些物理系统(如
$ {\mathcal{P}}{\mathcal{T}} $ -对称量子系统), 其哈密顿不是自伴的, 这类系统称为非自伴量子系统. 为了深入研究
$ {\mathcal{P}}{\mathcal{T}} $ -对称量子系统, 并考虑到算子
$ {\mathcal{P}}{\mathcal{T}} $ 的共轭线性性, 首先讨论了共轭线性算子的一些性质, 包括它们的矩阵表示和谱结构等; 其次, 分别研究了具有共轭线性对称性和完整共轭线性对称性的线性算子, 通过它们的矩阵表示, 给出了共轭线性对称性和完整共轭线性对称性的等价刻画; 作为应用, 得到了关于
$ {\mathcal{P}}{\mathcal{T}} $ -对称及完整
$ {\mathcal{P}}{\mathcal{T}} $ -对称算子的一些有趣性质, 并通过一些具体例子, 说明了完整
$ {\mathcal{P}}{\mathcal{T}} $ -对称性对张量积运算不具有封闭性, 同时说明了完整
$ {\mathcal{P}}{\mathcal{T}} $ -对称性既不是哈密顿算子在某个正定内积下自伴的充分条件, 也不是必要条件.
关键词: 共轭线性算子 /
共轭线性对称性 /
完整共轭线性对称性 /
$ {\mathcal{P}}{\mathcal{T}} $-对称性 /
完整$ {\mathcal{P}}{\mathcal{T}} $-对称性 English Abstract Conjugate linear symmetry and its application to $ {\mathcal{P}}{\mathcal{T}} $ -symmetry quantum theory Huang Yong-Feng 1,2 ,Cao Huai-Xin 1 ,Wang Wen-Hua 3 1.School of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710119, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11371012, 11771009, 11601300, 11571213) and the Fundamental Research Funds for the Central Universities of Ministry of Education of China (Grant Nos. GK201703093, GK201801011)Received Date: 31 July 2019Accepted Date: 18 November 2019Published Online: 05 February 2020Abstract: The Hamiltonians of classical quantum systems are Hermitian (self-adjoint) operators. The self-adjointness of a Hamiltonian not only ensures that the system follows unitary evolution and preserves probability conservation, but also guarantee that the Hamiltonian has real energy eigenvalues. We call such systems Hermitian quantum systems. However, there exist indeed some physical systems whose Hamiltonians are not Hermitian, for instance, $ {\mathcal{P}}{\mathcal{T}} $ -symmetry quantum systems. We refer to such systems as non-Hermitian quantum systems. To discuss in depth $ {\mathcal{P}}{\mathcal{T}} $ -symmetry quantum systems, some properties of conjugate linear operators are discussed first in this paper due to the conjugate linearity of the operator $ {\mathcal{P}}{\mathcal{T}}, $ including their matrix represenations, spectral structures, etc. Second, the conjugate linear symmetry and unbroken conjugate linear symmetry are introduced for linear operators, and some equivalent characterizations of unbroken conjugate linear symmetry are obtained in terms of the matrix representations of the operators. As applications, $ {\mathcal{P}}{\mathcal{T}} $ -symmetry and unbroken $ {\mathcal{P}}{\mathcal{T}} $ -symmetry of Hamiltonians are discussed, showing that unbroken $ {\mathcal{P}}{\mathcal{T}} $ -symmetry is not closed under taking tensor-product operation by some specific examples. Moreover, it is also illustrated that the unbroken $ {\mathcal{P}}{\mathcal{T}} $ -symmetry is neither a sufficient condition nor a necessary condition for Hamiltonian to be Hermitian under a new positive definite inner product.Keywords: conjugate linear operator /conjugate linear symmetry /unbroken conjugate linear symmetry /$ {\mathcal{P}}{\mathcal{T}} $-symmetry /unbroken $ {\mathcal{P}}{\mathcal{T}} $-symmetry 全文HTML --> --> --> 1.引 言 传统的量子力学中, 量子系统的状态随时间的演化由一个自伴哈密顿量$ {\mathcal{H}} $ 决定的薛定谔方程来描述. 哈密顿量的自伴性保证了系统遵守酉演化, 同时也保证了其特征值为实数. 但是, 确实存在一些物理系统, 其哈密顿不是自伴的, 但也具有实的能量本征值. Bender等[1 -3 ] 讨论了哈密顿量$ {\mathcal{H}} = $ ${ p}^2+{ x}^2({\rm i}\hat{ x})^{\epsilon} $ 谱的性质, 其中$ \epsilon $ 为实数, 说明了当$ \epsilon\geqslant 0 $ 时其特征值都是实数, 当$ \epsilon<0 $ 时会出现复特征值, 从而提出了一类非自伴哈密顿, 称为$ {\mathcal{P}}{\mathcal{T}} $ -对称哈密顿. 其中$ {\mathcal{P}} $ 是一个线性算子, 表示宇称变换, $ {\mathcal{T}} $ 是共轭线性算子, 表示时间反演变换. 由于$ {\mathcal{P}}{\mathcal{T}} $ -对称哈密顿的特征值为实数或者共轭成对出现的复数, 为了保证其特征值为实数, 又引入了完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的概念. 在此基础上, 通过引入一个$ \mathcal{C} $ 算子, 构造了一个新的正定$ \mathcal{C}{\mathcal{P}}{\mathcal{T}} $ -内积, 使得哈密顿$ {\mathcal{H}} $ 在该内积下是自伴的, 从而也遵守酉演化, 同时还说明了$ \mathcal{C} $ 算子是不唯一的[4 -7 ] . 后来, Mostafazadeh[8 -12 ] 提出了伪自伴算子的概念, 研究了伪自伴哈密顿的相关性质, 指出$ {\mathcal{P}}{\mathcal{T}} $ -对称哈密顿可以看成一类特殊的伪自伴哈密顿, 同时给出了针对Freedman-Robertson-Walker模型中哈密顿是伪自伴的例子. Bender等[13 ] 发现在$ {\mathcal{P}}{\mathcal{T}} $ -对称量子理论下, 量子系统的最优演化时间能够迅速减小甚至达到零. Zheng等[14 ] 通过设计核磁共振量子系统中具有$ {\mathcal{P}}{\mathcal{T}} $ -对称哈密顿量的时间演化实验, 证实了相应的结果. 目前, 关于$ {\mathcal{P}}{\mathcal{T}} $ -对称量子理论的研究已经涉及到了物理学及信息学的各个方面, 包括$ {\mathcal{P}}{\mathcal{T}} $ -对称性在光学领域的应用[15 ] , $ {\mathcal{P}}{\mathcal{T}} $ -对称量子场论的相关问题[16 ,17 ] , $ {\mathcal{P}}{\mathcal{T}} $ -对称量子系统中的纠缠问题[18 ] , $ {\mathcal{P}}{\mathcal{T}} $ -对称量子系统中无信号原理及其实验观测[19 ,20 ] , $ {\mathcal{P}}{\mathcal{T}} $ -对称性与图论及量子随机游走的关系[21 -23 ] 等. 此外, 还有一些其他的相关研究[24 -37 ] . 最近, Huang等[38 ] 通过弱测量模拟了缺破(broken)$ {\mathcal{P}}{\mathcal{T}} $ -对称哈密顿系统.$ {\mathcal{P}}{\mathcal{T}} $ -对称性及完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性的一些性质, 通过完整$ {\mathcal{P}}{\mathcal{T}} $ -对称哈密顿的一些具体例子, 说明完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性对张量积不具有封闭性, 同时说明完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性既不是哈密顿算子在某个正定内积下自伴的充分条件, 也不是必要条件.2.共轭线性算子的性质 本文用$ \mathbb{K} $ 表示n 维复Hilbert空间, 用$ \|{x}\| $ 表示向量$ {x}\in\mathbb{K} $ 的范数, 即$\left\| {x} \right\| = \sqrt {\left\langle {{x}|{x}} \right\rangle } $ . 用$ {\mathcal{I}} $ 表示$ {\mathbb{K}} $ 上的恒等算子. 对于$ {\mathbb{K}} $ 上的线性算子$ {\mathcal{A}} $ , 用$ {\mathcal{A}}^\dagger $ 表示线性算子$ {\mathcal{A}} $ 的Hermitian伴随算子. 若$ {\mathcal{A}} = {\mathcal{A}}^\dagger $ , 则称$ {\mathcal{A}} $ 是自伴的; 否则, 称$ {\mathcal{A}} $ 是非自伴的. 若存在可逆线性算子$ {\mathcal{B}} $ 使得$ {\mathcal{A}} = {\mathcal{B}}^\dagger {\mathcal{B}} $ , 则称$ {\mathcal{A}} $ 为正定算子; 若$ [{\mathcal{A}}, {\mathcal{B}}]: = {\mathcal{A}}{\mathcal{B}}-{\mathcal{B}}{\mathcal{A}} = 0 $ , 则称算子$ {\mathcal{A}} $ 与$ {\mathcal{B}} $ 可交换.$ M_n({\mathbb{C}}) $ 表示全体n 阶复矩阵构成的$ C^* $ -代数, ${{{I}}_n}$ 表示n 阶单位矩阵. 用$ \overline{a} $ 表示$ a\in{\mathbb{C}} $ 的复共轭, 对$ {{A}} = [a_{ij}]_{n\times n} $ , 记$ \overline{{A}} = [\overline{a_{ij}}]_{n\times n} $ , $ {{A}}^{\mathrm T} = [a_{ji}]_{n\times n} $ . 对$ {{A}}, {{B}}\in M_n({\mathbb{C}}) $ , 若存在可逆矩阵$ {{S}}\in M_n({\mathbb{C}}) $ 使得${{S}^{ - 1}}{AS} = {B}$ , 则称A B $ {{A}}\sim {{B}} $ . 如果矩阵A A $ \mathcal{E} = \{e_{i}\}_{i = 1}^n $ 为空间$ \mathbb{K} $ 的一个线性无关基(Hamel基). 因此, 空间$ \mathbb{K} $ 中的任意向量x $ {{x}} = \sum\limits_{i = 1}^nc_ie_i ,$ 其中 $ c_i\in{\mathbb{C}}\;(i = 1, $ $ 2, \cdots, n). $ 定义1 对于算子$ {\mathcal{A}}:\mathbb{K}\rightarrow\mathbb{K} $ , 若$ {\mathcal{A}} $ 为共轭线性算子.$ \mathbb{K} $ 上的任一共轭线性算子$ {\mathcal{A}} $ , 任取$ {\mathbb{K}} $ 的一个正规正交基$ \{\varepsilon_k\}_{k = 1}^n $ , 令$ { x} = \sum\limits_{k = 1}^nc_k\varepsilon_k $ , $ { y} = $ $\sum\limits_{k = 1}^nd_k\varepsilon_k $ , 则$ M = \sqrt{\sum\limits_{k = 1}^n\|{\mathcal{A}} \varepsilon_k\|^2} $ . 因此,$ \mathbb{K} $ 上的任一共轭线性算子$ {\mathcal{A}} $ 都是一致连续的.$ n\times n $ 阶矩阵$ {{A}} = [a_{ij}]_{n\times n} $ 都对应空间$ {\mathbb{K}} $ 上的一个线性算子:$ \mathbb{K} $ 上的共轭线性算子$ {\mathcal{A}} $ , 且满足$ {\mathcal{A}} e_j = $ $\sum\limits_{i = 1}^na_{ij}e_i(j = 1, 2, \cdots, n) $ . 将此关系记为$ \mathbb{K} $ 上任一共轭线性算子$ {\mathcal{A}} $ , 记$ n\times n $ 矩阵$ {{A}} = [a_{ij}] $ , 称其为共轭线性算子$ {\mathcal{A}} $ 在基$ \mathcal{E} $ 下的表示矩阵. 显然, 算子$ {\mathcal{A}} $ 与其表示矩阵A 3 )式的关系, 从而表示矩阵A 2 )式定义的算子正好为$ {\mathcal{A}} $ .$ {\mathcal{A}} $ 与矩阵A 3 )下是一一对应的, 且 对任意$ {{x}} = \displaystyle\sum\nolimits_{i = 1}^nc_ie_i\in\mathbb{K} $ , 有A $ {\mathcal{A}} $ 在基$ \mathcal{E} $ 下的表示矩阵当且仅当它们满足关系式 (4 ).$ \mathbb{K} $ 上的算子$ {\mathcal{T}}_0 $ 为$ {\mathcal{T}}_0{{x}} = \bar{{{x}}} $ . 易见, $ {\mathcal{T}}_0 $ 是共轭线性算子, 且它在基$ \mathcal{E} $ 下的表示矩阵为n 阶单位阵$ {{I}}_n $ . 于是, 对任意$ {{x}} = \sum\limits_{i = 1}^nc_ie_i\in\mathbb{K} $ , 有$ {\mathcal{A}} $ 与$ {\mathcal{T}}_0 $ 的复合算子$ {\mathcal{T}}_0{\mathcal{A}} $ 或$ {\mathcal{A}}{\mathcal{T}}_0 $ 都为线性算子, 且满足关系 $ {\mathcal{A}} = ({\mathcal{A}}{\mathcal{T}}_0){\mathcal{T}}_0 = {\mathcal{T}}_0({\mathcal{T}}_0{\mathcal{A}}) $ . 由此可见, 任意一个共轭线性算子都可以看成是一个线性算子与$ {\mathcal{T}}_0 $ 的复合, 也可以表示为$ {\mathcal{T}}_0 $ 与一个线性算子的复合. 参见图1 .图 1 共轭线性算子$ {\mathcal{A}} $ 与$ {\mathcal{T}}_0 $ 的复合算子$ {\mathcal{A}}{\mathcal{T}}_0 $ (左)与$ {\mathcal{T}}_0{\mathcal{A}} $ (右)都是线性算子, 且满足关系 $ {\mathcal{A}}=({\mathcal{A}}{\mathcal{T}}_0){\mathcal{T}}_0= $ ${\mathcal{T}}_0({\mathcal{T}}_0{\mathcal{A}}) $ Figure1. Composition operators $ {\mathcal{A}}{\mathcal{T}}_0 $ (left) and $ {\mathcal{T}}_0{\mathcal{A}} $ (right), composed of conjugate linear operators $ {\mathcal{A}} $ and $ {\mathcal{T}}_0 $ , which are linear operators and satisfy $ {\mathcal{A}}=({\mathcal{A}}{\mathcal{T}}_0){\mathcal{T}}_0={\mathcal{T}}_0({\mathcal{T}}_0{\mathcal{A}}) $ $ {\mathcal{A}}, {\mathcal{B}} $ 均为共轭线性算子, ${A}, {B}$ 为它们的表示矩阵, 则由(4 )式知: 对任意$ {{x}} =\sum\limits_{i = 1}^nc_ie_i\in\mathbb{K} $ , 有$ {\mathcal{A}}{\mathcal{B}} $ 的表示矩阵为$ {{A}}\overline{{{B}}} $ . 从而, $ {\mathcal{A}}{\mathcal{B}} = {\mathcal{I}} $ 当且仅当$ {{A}}\overline{{{B}}} = I_n $ . 于是, 共轭线性算子$ {\mathcal{A}} $ 可逆当且仅当其对应的表示矩阵A 5 )式, 可证, 当$ {\mathcal{A}} $ 为共轭线性算子, $ {\mathcal{B}} $ 为线性算子, $ {\mathcal{A}}{\mathcal{B}} $ 的矩阵表示仍为$ {{A}}\overline{{{B}}} $ .$ {\mathcal{A}}_i\;(i = 1, $ $2, \cdots, m) $ 均为共轭线性算子, $ {{A}}_i\;(i = 1, 2, \cdots, m) $ 为对应的矩阵表示, 则当$ m = 2 k $ 为偶数时, $ {\mathcal{A}}_1 $ ${\mathcal{A}}_2\cdots{\mathcal{A}}_m $ 为线性算子, 其矩阵表示为$ {{A}}_1\overline{{{A}}_2}\cdots $ ${{A}}_{2 k-1}\overline{{{A}}_{2 k}} $ ; 当$ m = 2 k+1 $ 为奇数时, $ {\mathcal{A}}_1{\mathcal{A}}_2\cdots {\mathcal{A}}_m $ 为共轭线性算子, 其矩阵表示为$ {{A}}_1\overline{{{A}}_2}\cdots {{A}}_{2 k-1}$ $ \overline{{{A}}_{2 k}}{{A}}_{2 k+1} $ .$ \sigma({\mathcal{A}}) $ 表示算子$ {\mathcal{A}} $ 的所有特征值之集, 称为$ {\mathcal{A}} $ 的谱, 即$ N_{\lambda}({\mathcal{A}}) = \ker(\lambda{\mathcal{I}}-{\mathcal{A}}) $ , 称为算子$ {\mathcal{A}} $ 对应特征值$ \lambda $ 的特征子空间.$ \sigma({\mathcal{I}}) = \{1\} $ . 由于$ \sigma({\mathcal{T}}_0)\supset\{-1, 1, -\mathrm{i}, \mathrm{i}\} $ .$ {\mathcal{A}} $ 的谱$ \sigma({\mathcal{A}}) $ 的一些性质.6 )知, $ \lambda\in\sigma({\mathcal{A}}) $ 当且仅当算子方程$ {\mathcal{A}} {{x}} = \lambda {{x}} $ 有非零解$ {{x}} =\sum\limits_{i = 1}^nc_ie_i $ 当且仅当矩阵方程$ \lambda c = A\bar{c} $ 有非零解$ c = (c_1, c_2, \cdots, c_n)^{\mathrm{T}} $ ; 此时, $ \lambda $ 称为算子$ {\mathcal{A}} $ 的特征值, 相应的非零解x $ \lambda $ 的特征向量.$ {{x}} = \sum\limits_{i = 1}^nc_ie_i\in\mathbb{K} $ 为实的, 是指其系数向量$ { c} = (c_1,\; c_2,\; \cdots,\; c_n)^{\mathrm{T}} $ 为实的, 即$ c\in{\mathbb{R}}^n $ .$ {\mathcal{A}} $ 为共轭线性算子, 且存在$ \lambda\in{\mathbb{C}}, \varphi\neq0 $ 使得$ {\mathcal{A}}\varphi = \lambda\varphi $ , 则$ {\mathcal{A}}^2\varphi = {\mathcal{A}}(\lambda\varphi) = |\lambda|^2\varphi $ . 这说明 $ |\lambda|^2 $ 为线性算子$ {\mathcal{A}}^2 $ 的特征值. 从而 $ {\mathcal{A}} $ 的谱半径满足$ {\mathcal{A}} $ 的谱$ \sigma({\mathcal{A}}) $ 为复平面上的一个有界集, 但可能为无限集(见定理1), 也可能为空集(见例1).$ 0\neq\lambda_0\in\sigma({\mathcal{A}}) $ , 则存在$ \varphi_0\neq0 $ 满足$ {\mathcal{A}}\varphi_0 = $ $\lambda_0\varphi_0 $ . 记$ \lambda_0 = r_0 {\rm e}^{\mathrm{i}\theta_0}(\theta_0\in{\mathbb{R}}, r_0>0). $ 设$ |z| = |\lambda_0 | $ , 记$ z = r_0{\mathrm{e}}^{\mathrm{i}\theta}(\theta\in{\mathbb{R}}) $ , 则$ \varphi = {\mathrm{e}}^{-\frac{\theta+\theta_0}{2}i}\lambda_0\varphi_0 $ , 则$ \varphi\neq0 $ 且满足$ {\mathcal{A}}\varphi = z\varphi $ . 从而可见, $ z\in\sigma({\mathcal{A}}) $ . 这就说明$ \{z\in{\mathbb{C}}:\ |z| = |\lambda_0 |\}\subset$ $\sigma({\mathcal{A}}) $ .$ \sigma({\mathcal{A}}) $ 的闭性. 设$ \{\lambda_k\}_{k = 1}^\infty \subset\sigma({\mathcal{A}}) $ 且$ \lim_{k\rightarrow\infty}\lambda_k = \lambda $ , 则存在非零向量列$ \{x_k\}_{k = 1}^\infty\subset{\mathbb{K}} $ 使得$ {\mathcal{A}} x_k = \lambda_kx_k\;(k = 1, 2, \cdots) $ . 由于$ {\mathcal{A}} $ 是实线性的, 所以可假设$ \|{ x}_k\| =$ 1 (k = 1, 2, ···). 于是, $ \{x_k\}_{k = 1}^\infty $ 必有收敛子列. 不妨设$ \lim_{k\rightarrow\infty} x_k = $ $ {{x}} $ , 则$ \|{{x}}\| = 1 $ . 根据$ {\mathcal{A}} $ 连续性知: $ {\mathcal{A}} {{x}} = $ $ \lambda {{x}} $ . 由此可见, $ \lambda\in\sigma({\mathcal{A}}) $ . 所以, $ \sigma({\mathcal{A}}) $ 为复平面上的闭集.定理1 设$ {\mathcal{A}} $ 为$ {\mathbb{K}} $ 上的共轭线性算子, 其表示矩阵为A $ \lambda $ 为$ {\mathcal{A}} $ 的特征值且有实的特征向量x $ \lambda $ 为A c ;$ \lambda\in\sigma({\mathcal{A}}) $ 时, 有$ |\lambda|^2\in\sigma({\mathcal{A}}^2) $ ;$ {\mathcal{A}} $ 的谱半径满足$ 0\neq\lambda_0\in\sigma({\mathcal{A}}) $ 时, 有$ \{z\in{\mathbb{C}}:\ |z| = |\lambda_0 |\} $ $\subset\sigma({\mathcal{A}}) $ ;$ \sigma({\mathcal{A}}) $ 为复平面上的有界闭集.$ \sigma({\mathcal{A}}^2)\cap(0, +\infty) = \emptyset $ 时, 必有$ \sigma({\mathcal{A}}) = \emptyset $ (例1). 于是, 如果线性算子$ {\mathcal{A}}^2 $ 没有正的特征值, 那么共轭线性算子$ {\mathcal{A}} $ 就没有特征值. 进一步, 由于$ \sigma({\mathcal{T}}_0)\supset\{-1, 1, -\mathrm{i}, \mathrm{i}\} $ 且$ {\mathcal{T}}_0^2 = {\mathcal{I}} $ , 所以由定理1(c)与定理1(d)知例1 设$ \mathbb{K} $ 为2维复线性空间, $ \{e_1, e_2\} $ 为$ \mathbb{K} $ 的一组线性无关基, $ \forall z\in{\mathbb{C}} $ , 定义算子$ {\mathcal{A}}_z $ 为$ {\mathcal{A}}_z $ 为$ \mathbb{K} $ 上的共轭线性算子, 且其表示矩阵为$ {\mathcal{A}}_z^2 $ 的表示矩阵为$ z = \mathrm{i} $ 时($ \mathrm{i} $ 为虚数单位), 有$ {{A}}_{\mathrm{i}}\overline{{{A}}_\mathrm{i}} = -I_2 $ , 从而$ {\mathcal{A}}_{\mathrm{i}}^2 = -\mathcal{I} $ . 可见, $ \sigma({\mathcal{A}}_{\mathrm{i}}^2) = \{-1\} $ . 故$ \sigma({\mathcal{A}}_{\mathrm{i}}) = \emptyset $ .$ {\mathcal{A}}_{\mathrm{i}} $ 正好为物理上的自旋$ 1/2 $ -粒子的翻转算子, 它没有特征值.3.线性算子的共轭线性对称性 下面讨论共轭线性对称算子的性质, 给出其表示矩阵具有的相似Jordan标准型. 在此基础上, 讨论完整共轭线性对称哈密顿的性质, 给出完整共轭线性对称性的等价刻画.定义2 设$ {\mathcal{H}} $ 为$ {\mathbb{K}} $ 上的线性算子, 若存在可逆的共轭线性算子$ {\mathcal{A}} $ , 使得$ [{\mathcal{A}}, {\mathcal{H}}] = 0 $ , 则称$ {\mathcal{H}} $ 为共轭线性对称的; 此时, 也称$ {\mathcal{H}} $ 为$ {\mathcal{A}} $ -对称的.引理1 [39 ] 设$ {{H}}\in M_n({\mathbb{C}}) $ , 则H $ \overline{{{H}}} $ 当且仅当H 引理2 [39 ] 设$ {{H}}\in M_n({\mathbb{C}}) $ , 则H H $ k = 1, 2, \cdots, p;\; { J}_{n_{k}}(\lambda_{k}) $ 为标准Jordan块, $ \lambda_1, \cdots, $ $\lambda_p $ 为非实数的复数, $ \lambda_{n_{p+1}}, \cdots, \lambda_{n_{r}} $ 是实数.引理3 [39 ] 设$ {{A}}\in M_n({\mathbb{C}}) $ , 则A $ {{A}}\overline{{{A}}} = {{I}} $ 当且仅当存在可逆矩阵$ {{S}}\in M_n({\mathbb{C}}) $ , 使得$ {{A}} = $ $ {{S}}\overline{{{S}}}^{-1}. $ 定理2 设$ {\mathcal{H}}$ 为$ {\mathbb{K}} $ 上的线性算子, 则以下叙述等价:$ {\mathcal{H}} $ 是共轭线性对称的;$ {\mathcal{H}} $ 的表示矩阵H $ \overline{{{H}}} $ ;$ {\mathcal{H}} $ 的表示矩阵H $ {\mathcal{H}} $ 的表示矩阵H 7 )式;$ \!{\mathcal{A}}\! $ 满足$ {\mathcal{A}}^2 \!=\! {\mathcal{I}} $ , $ [{\mathcal{A}},\!{\mathcal{H}}] \!= \!0 $ ;$ {\mathbb{K}} $ 上的可逆线性算子$ \eta $ , 使得$ {\mathcal{H}}^\dagger = \eta{\mathcal{H}}\eta^{-1} $ ;$ {\mathbb{K}} $ 上的可逆自伴线性算子$ \eta_1 $ , 使得$ {\mathcal{H}}^\dagger = \eta_1{\mathcal{H}}\eta_1^{-1} $ (即$ {\mathcal{H}} $ 为$ \eta_1 $ -伪自伴[37 ] ).证明 (i)$ \Rightarrow $ (ii). 设$ {\mathcal{H}} $ 是共轭线性对称的, 则由定义2知, 存在共轭线性算子$ {\mathcal{A}} $ 使得$ {\mathcal{H}} $ 为$ {\mathcal{A}} $ -对称. 记H A $ {\mathcal{H}} $ 和$ {\mathcal{A}} $ 的矩阵表示, 则有$ {{A}}\overline{{{H}}} = {{H}}{{A}} $ , 即$ \overline{{{H}}} = {{A}}^{-1}{{H}}{{A}} $ . 由$ {\mathcal{A}} $ 可逆知A H $ \overline{{{H}}} $ .$ \Rightarrow $ (i). 设H $ {\mathcal{H}} $ 的表示矩阵, 且$ \overline{{{H}}} $ 相似于H A $ \overline{{{H}}} = {{A}}^{-1}{{H}}{{A}} $ , 即$ {{A}}\overline{{{H}}} = {{H}}{{A}} $ . 记$ {\mathcal{A}} $ 为矩阵A $ {\mathcal{A}}{\mathcal{H}} = {\mathcal{H}}{\mathcal{A}} $ , 即$ {\mathcal{H}} $ 为$ {\mathcal{A}} $ -对称. 从而$ {\mathcal{H}} $ 为共轭线性对称的.$ \Rightarrow $ (i)成立. 下面证明(i)$ \Rightarrow $ (v).$ \Rightarrow $ (v). 设$ {\mathcal{H}} $ 为共轭线性对称的, 则由引理1知, $ {\mathcal{H}} $ 的表示矩阵H S $ {{S}}^{-1}{{H}}{{S}} = \overline{{{S}}^{-1}{{H}}{{S}}} $ . 从而$ {{H}}{{S}}\overline{{{S}}}^{-1} = $ $ {{S}}\overline{{{S}}}^{-1}\overline{{{H}}} $ . 令$ {{A}} = {{S}}\overline{{{S}}}^{-1} $ , 则$ {{H}}{{A}} = {{A}}\overline{{{H}}} $ , 同时由引理3知$ {{A}}\overline{{{A}}} = {{I}} $ . 设$ {\mathcal{A}} $ 为A $ {\mathcal{A}}^2 = {\mathcal{I}} $ , 且$ [{\mathcal{A}}, {\mathcal{H}}] = 0 $ .$ \Rightarrow $ (vi). 设H $ {\mathcal{H}} $ 的表示矩阵, 且$ \overline{{{H}}} $ 相似于H A $ \overline{{{H}}} = {{A}}{{H}}{{A}}^{-1} $ . 又因为任意复矩阵的转置矩阵与其本身相似, 从而存在可逆矩阵S $ (\overline{{{H}}})^{\mathrm{T}} = {{S}}\overline{{{H}}}{{S}}^{-1} $ , 即$ {{H}}^{\dagger} = $ $ {{S}}\overline{{{H}}}{{S}}^{-1} = {{S}}{{A}}{{H}}{{A}}^{-1}{{S}}^{-1} = {{S}}{{A}}{{H}}({{S}}{{A}})^{-1}. $ 设$ {\mathcal{H}}, \eta $ 为分别对应$ {{H}}, SA $ 的线性算子, 则有$ {\mathcal{H}}^\dagger = \eta{\mathcal{H}}\eta^{-1} $ .$ \Rightarrow $ (ii). 设存在$ {\mathbb{K}} $ 上的可逆线性算子$ \eta $ , 使得$ {\mathcal{H}}^\dagger = \eta{\mathcal{H}}\eta^{-1} $ . 记$ {\mathcal{H}}, {{A}} $ 为分别对应$ {\mathcal{H}}, \eta $ 的表示矩阵, 则A $ {{H}}^\dagger = {{A}}{{H}}{{A}}^{-1} $ . 又因为$ {{H}}^\dagger $ 和$ \overline{{{H}}} $ 相似, 从而存在可逆矩阵S $ {{H}}^\dagger = $ $ {{S}}^{-1}\overline{{{H}}}{{S}} $ . 因此$ {{A}}{{H}}{{A}}^{-1} = {{S}}^{-1}\overline{{{H}}}{{S}} $ , 从而$ \overline{{{H}}}= {{S}}{{A}}\times $ ${{H}}({{S}}{{A}})^{-1} $ , 即H $ \overline{{{H}}} $ .$ \Rightarrow $ (vi)成立. 下面证明(vi)$ \Rightarrow $ (vii).$ \Rightarrow $ (vii). 设$ {\mathcal{H}}^\dagger = \eta{\mathcal{H}}\eta ^{-1} $ , $ \eta $ 为可逆线性算子. 对非零的$ a = r{\rm e}^{{\rm i}\theta}\in{\mathbb{C}} $ , $ -{\rm e}^{2 {\rm i}\theta}\notin\sigma(\eta^{-1}\eta^\dagger) $ , $ \eta_0 = $ $ a\eta $ 仍为可逆线性的, 且有$ {\mathcal{H}}^\dagger\eta_0 = \eta_0{\mathcal{H}} $ , $ {\mathcal{H}}^\dagger\eta_0^\dagger = $ $ \eta_0^\dagger {\mathcal{H}} $ . 从而$ {\mathcal{H}}^\dagger(\eta_0+\eta_0^\dagger) = (\eta_0+\eta_0^\dagger){\mathcal{H}} $ . 令$ \eta_1 = \eta_0\;+$ $ \eta_0^\dagger $ , 则$ \eta_1 $ 为自伴的且$ {\mathcal{H}}^\dagger = \eta_1 {\mathcal{H}}\eta_1 ^{-1} $ . 因为$ \eta_0^{-1}\eta_0^\dagger = $ $ {\rm e}^{-2 {\rm i}\theta}\eta^{-1}\eta^\dagger $ , 且$ -{\rm e}^{2 {\rm i}\theta}\!\notin\!\sigma(\eta^{-1}\eta^\dagger) $ , 所以$ -1\!\notin\!\sigma(\eta_0^{-1}\eta_0^\dagger) $ , 从而$ {\mathcal{I}}+\eta_0^{-1}\eta_0^\dagger $ 可逆. 又因为$ {\mathcal{I}}+\eta_0^{-1}\eta_0^\dagger = \eta_0^{-1}(\eta_0+$ $\eta_0^\dagger) = \eta_0^{-1}\eta_1 $ , 所以$ \eta_1 $ 可逆. 由此, 证明了$ \eta_1 $ 为可逆自伴线性算子, 且$ {\mathcal{H}}^\dagger = \eta_1 {\mathcal{H}}\eta_1 ^{-1} $ . 证毕.$ {\mathcal{H}} $ 的特征值均为实的. 于是, 我们引入下面的完整共轭线性对称的概念.定义3 若$ {\mathcal{H}} $ 为空间$ {\mathbb{K}} $ 上的$ {\mathcal{A}} $ -对称线性算子, 并且$ {\mathcal{H}} $ 的特征态均为$ {\mathcal{A}} $ 的特征态, 则称$ {\mathcal{H}} $ 为完整$ {\mathcal{A}} $ -对称的; 若存在可逆共轭线性算子$ {\mathcal{A}} $ 使得$ {\mathcal{H}} $ 为完整$ {\mathcal{A}} $ -对称的, 则称$ {\mathcal{H}} $ 为完整共轭线性对称的.命题1 设$ {\mathcal{H}} $ 为$ {\mathbb{K}} $ 上的线性算子, 若$ {\mathcal{H}} $ 为完整共轭线性对称, 则$ {\mathcal{H}} $ 的特征值都是实的.证明 设存在可逆的共轭线性算子$ {\mathcal{A}} $ , 使得$ {\mathcal{A}}{\mathcal{H}} = {\mathcal{H}}{\mathcal{A}} $ , 且$ {\mathcal{H}} $ 的特征态均为$ {\mathcal{A}} $ 的特征态. 设a 是$ {\mathcal{H}} $ 的一个特征值, 对应的特征态$ f \ne 0 $ , 满足$ {\mathcal{H}} f = af $ . 因此, $ {\mathcal{H}}{\mathcal{A}} f = {\mathcal{A}}{\mathcal{H}} f = \overline{a}{\mathcal{A}} f $ . 由于f 也是$ {\mathcal{A}} $ 的一个特征态, 所以存在b 使得$ {\mathcal{A}} f = bf $ . 从而有$ abf = \overline{a}bf $ . 因为$ {\mathcal{A}} $ 可逆, 故$ b \ne 0 $ . 又$ f \ne 0 $ , 所以$ a = \bar a $ . 证毕.定理3 设$ {\mathcal{H}} $ 是$ {\mathbb{K}} $ 上的线性算子且为共轭线性对称的, 则$ {\mathcal{H}} $ 为完整共轭线性对称的当且仅当$ {\mathcal{H}} $ 的特征值均为实的且$ {\mathcal{H}} $ 为非简并的(即$ {\mathcal{H}} $ 的每个特征值的几何重数为1).证明 必要性. 设$ {\mathcal{H}} $ 为完整共轭线性对称, 由命题1知$ {\mathcal{H}} $ 的特征值都是实的. 下面只需证明$ \forall a\in\sigma({\mathcal{H}}) $ , 有$ \dim N_{a}({\mathcal{H}}) = 1 $ . 假设$ \dim N_{a}({\mathcal{H}})>1 $ , 则存在$ {\mathbb{K}} $ 中的两个非零向量$ x, y $ 使得$ {\mathcal{H}} x = ax,$ $ {\mathcal{H}} y = ay $ 且$ \{x, y\} $ 是线性无关集. 由于$ {\mathcal{H}} $ 为完整共轭线性对称, 所以存在可逆的共轭线性算子$ {\mathcal{A}} $ 以及$ c, d\neq0 $ 使得$ {\mathcal{A}} x = cx, \; {\mathcal{A}} y = dy $ . 当$ c\ne d $ 时, 取z = $ x+y $ , 显然它是$ {\mathcal{H}} $ 关于a 的一个特征态, 但是对于所有的复数$ \lambda $ , 都有$ {\mathcal{A}} z = {\mathcal{A}} x+{\mathcal{A}} y = cx+ $ $dy\ne \lambda z $ . 当$ c = d $ 时, 取$ z = x+\mathrm{i} y $ , 显然它是$ {\mathcal{H}} $ 关于a 的一个特征态, 但对于所有的复数$ \lambda $ , 都有$ {\mathcal{A}} z = {\mathcal{A}} x-$ $\mathrm{i}{\mathcal{A}} y = cx-\mathrm{i} cy\ne \lambda z $ . 以上两种情况下, 结果都与$ {\mathcal{H}} $ 具有完整共轭线性对称性矛盾. 由此可知$ {\mathcal{H}} $ 的每个特征值几何重数均为1.$ {\mathcal{H}} $ 的特征值均为实的且$ {\mathcal{H}} $ 非简并. 由于$ {\mathcal{H}} $ 为共轭线性对称, 因此存在可逆的共轭线性算子$ {\mathcal{A}} $ 使得$ {\mathcal{H}} $ 为$ {\mathcal{A}} $ -对称, 只需证$ {\mathcal{H}} $ 的特征向量均为$ {\mathcal{A}} $ 的特征向量. 设$ x\neq0 $ 为$ {\mathcal{H}} $ 的对应于$ \lambda $ 某个特征向量, 则$ \lambda $ 为实数, 且使得$ {\mathcal{H}} x = \lambda x $ . 因为$ {\mathcal{H}}{\mathcal{A}} x = $ ${\mathcal{A}}{\mathcal{H}} x = {\mathcal{A}}(\lambda x) = \overline{\lambda}{\mathcal{A}} x = \lambda {\mathcal{A}} x $ , 即$ {\mathcal{A}} x $ 也为$ {\mathcal{H}} $ 对应于特征值$ \lambda $ 的特征向量. 又因为$ \dim N_{\lambda}({\mathcal{H}}) = $ 1, 从而存在$ k\neq0 $ 使得$ {\mathcal{A}} x = kx $ , 即x 为$ {\mathcal{A}} $ 的特征向量, 从而$ {\mathcal{H}} $ 为完整$ {\mathcal{A}} $ -对称的. 证毕.推论1 $ {\mathbb{K}} $ 上的线性算子$ {\mathcal{H}} $ 为完整共轭线性对称当且仅当其表示矩阵H $ \lambda_1, \cdots, \lambda_k $ 为H k 个互不相同的实特征根, ${ J}_{n_{i}}(\lambda_{i})(i = 1, 2, \cdots, k) $ 为标准Jordan块.推论2 设$ {\mathcal{H}} $ 是$ {\mathbb{K}} $ 上的线性算子且为共轭线性对称的, 若$ {\mathcal{H}} $ 有n 个互不相同的实特征值, 则$ {\mathcal{H}} $ 为完整共轭线性对称.4.线性算子的$ {\mathcal{P}}{\mathcal{T}} $ -对称性以及完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性 本节讨论$ {\mathcal{P}}{\mathcal{T}} $ -对称线性算子的一般性质. 为此, 我们回顾文献[27 ]中关于$ {\mathcal{P}}{\mathcal{T}} $ -框架的概念.定义4 [27 ] 设$ {\mathcal{H}} $ 是$ {\mathbb{K}} $ 上的线性算子, $ {\mathcal{P}}, {\mathcal{T}} $ 是$ {\mathbb{K}} $ 上的算子, 且满足以下条件:$ {\mathcal{P}}\neq{\mathcal{I}} $ 且是线性的, $ {\mathcal{T}} $ 是共轭线性的,$ {\mathcal{P}}^2 = {\mathcal{T}}^2 = {\mathcal{I}} $ , $ {\mathcal{P}}{\mathcal{T}} = {\mathcal{T}}{\mathcal{P}} $ , 则称$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架.$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, 且$ [{\mathcal{H}}, {\mathcal{P}}{\mathcal{T}}] = 0 $ , 则称算子$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称.$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 为空间$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架时, 算子$ {\mathcal{P}}{\mathcal{T}} $ 为$ {\mathbb{K}} $ 上的可逆共轭线性算子. 于是, 当$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称算子时, 它必然是$ {\mathcal{P}}{\mathcal{T}} $ -对称的(定义2), 从而是共轭线性对称的算子.$ {\mathcal{H}} $ 为共轭线性对称的, 所以定理2 (v)成立, 即存在共轭线性算子$ {\mathcal{T}} $ 满足$ {\mathcal{T}}^2 = {\mathcal{I}} $ ($ {\mathbb{K}} $ 上的恒等算子), 且$ [{\mathcal{T}}, {\mathcal{H}}] = 0 $ . 记$ {\mathcal{P}} = {\mathcal{I}} $ , 则$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 为是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架且$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称.$ {\mathcal{P}}{\mathcal{T}} $ -对称性的有以下关系.命题2 空间$ {\mathbb{K}} $ 上的线性算子$ {\mathcal{H}} $ 为共轭线性对称算子当且仅当存在$ {\mathbb{K}} $ 上的某个$ {\mathcal{P}}{\mathcal{T}} $ -框架$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 使得$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称.${P}, {T}$ 和H $ {\mathcal{P}}, {\mathcal{T}} $ 和$ {\mathcal{H}} $ 的表示矩阵, 则$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 构成$ {\mathcal{P}}{\mathcal{T}} $ -框架等价于以下矩阵等式成立:$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称等价于以下矩阵等式成立:命题3 设$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, 则$ \sigma({\mathcal{P}}{\mathcal{T}}) $ 要么为空集, 要么为复平面上的单位圆周.命题4 设$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, 其中$ {\mathcal{T}} $ 定义为$ {\mathcal{H}} $ 是$ {\mathbb{K}} $ 上的线性算子, 则$ \{{\mathcal{P}}^{\dagger}, {\mathcal{T}}\} $ 为$ {\mathbb{K}} $ 上的$ {\mathcal{P}}^{\dagger}{\mathcal{T}} $ -框架;$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称的当且仅当$ {\mathcal{H}}^{\dagger} $ 为$ {\mathcal{P}}^{\dagger}{\mathcal{T}} $ -对称的.证明 (i) 由(11 )式知, $ {\mathcal{T}} $ 的矩阵表示为单位阵$ {{I}}_n $ , 且$ {{T}}\overline{{{T}}} = {{I}}_n $ . 由于$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 构成$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, 所以(9 ) 式成立. 从而,$ \{{\mathcal{P}}^\dagger, {\mathcal{T}}\} $ 也构成$ {\mathbb{K}} $ 上的$ {\mathcal{P}}^{\dagger}{\mathcal{T}} $ 框架.$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称的当且仅当$ {{H}}{{P}} = {{P}}\overline{{{H}}} $ 当且仅当$ {{P}}^\dagger\overline{{{H}}^\dagger} = {{H}}^\dagger {{P}}^\dagger $ 当且仅当$ {\mathcal{H}}^{\dagger} $ 为$ {\mathcal{P}}^\dagger{\mathcal{T}} $ -对称的. 证毕.$ {\mathcal{P}}{\mathcal{T}} $ -对称定义.定义5 [27 ] 设$ {\mathcal{H}} $ 是$ {\mathbb{K}} $ 上的线性算子, $ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, 若$ {\mathcal{H}} $ 是$ {\mathcal{P}}{\mathcal{T}} $ -对称的且它的特征态都是$ {\mathcal{P}}{\mathcal{T}} $ 的特征态, 则称$ {\mathcal{H}} $ 是完整$ {\mathcal{P}}{\mathcal{T}} $ -对称.定理4 设$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, $ {\mathcal{H}} $ 是$ {\mathbb{K}} $ 上的线性算子且为$ {\mathcal{P}}{\mathcal{T}} $ -对称的, 则$ {\mathcal{H}} $ 为完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的当且仅当$ {\mathcal{H}} $ 的谱为实的, 且$ {\mathcal{H}} $ 为非简并的;$ {\mathcal{H}} $ 为完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的且可相似对角化当且仅当$ {\mathcal{H}} $ 有n 个互不相同的实特征值.例2 设$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是2维复空间$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, $ {\mathcal{H}}_1 $ 为$ {\mathbb{K}} $ 上的线性算子, $ {\mathcal{P}}, \; {\mathcal{T}}, \; {\mathcal{H}}_1 $ 的表示矩阵$ {{P}}, \; {{T}}, \; {{H}}_1 $ 为$ {\mathcal{H}}_1 $ 为完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的当且仅当$ a = \overline{d}, b = \overline{c} $ , $ |b|^2\geqslant (\mathrm{Im}\; a)^{2} $ 且$ b\neq0 $ .证明 充分性. 设$ a = \overline{d}, b = \overline{c} $ , $ |b|^2\geqslant (\mathrm{Im}\; a)^{2} $ 且$ b\neq0 $ .$ a = \overline{d}, b = \overline{c} $ , 则$ {{H}}_1 = \left( {\begin{array}{*{20}c} a & b \\ {\bar b} & {\bar a}\end{array}} \right), $ 易知$ {\mathcal{H}}_1 $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称的.$ {{H}}_1 $ 的两个特征值$ \lambda = \mathrm{Re}\; a\pm $ $\sqrt{|b|^2-(\mathrm{Im}\; a)^2} $ . 当$ |b|^2-(\mathrm{Im}\; a)^2\geqslant 0 $ , $ {{H}}_1 $ 特征值均为实数. 下面分两种情况进行讨论.$ |b|^2-(\mathrm{Im}\; a)^2>0 $ 时, $ {\mathcal{H}}_1 $ 有两个不相同的实特征值. 进而, 由定理4(b)知$ {\mathcal{H}}_1 $ 为完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的.$ |b|^2 = (\mathrm{Im}\; a)^2 $ 时, $ \sigma(H_1) = \{\lambda\} $ , 且实特征值$ \lambda = \mathrm{Re}\; a $ 的代数重数为2. 由于$ b\neq0 $ , 所以矩阵$ \lambda {{I}}-{{H}}_1 $ 的秩为$ 1 $ , 从而特征值$ \mathrm{Re}\; a $ 的几何重数为$ 1 $ . 故由定理4(a)知$ {\mathcal{H}}_1 $ 是完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的.$ {\mathcal{H}} $ 为完整$ {{P}}{{T}} $ -对称的, 则$ {\mathcal{H}} $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称, 且由定理4(a) 知: H $ {\mathcal{H}}_1 $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称的, 所以$ a = \overline{d},\; b = \overline{c} $ . 于是, 由充分性的证明可知: $ {{H}}_1 $ 的两个特征值为$ \lambda = \mathrm{Re}\; a\pm\sqrt{|b|^2-(\mathrm{Im}\; a)^2} $ . 由于H $ |b|^2-(\mathrm{Im}\; a)^2\geqslant 0 $ . 假若$ b = 0 $ , 则$ \mathrm{Im}\; a = 0 $ , 从而$ \lambda {{I}}-{{H}}_1 $ 为零矩阵, 即$ {{H}}_1 = \lambda {{I}} $ . 这与$ {{H}}_1 $ 的特征值$ \lambda = \mathrm{Re}\; a $ 几何重数为1矛盾. 故$ b\ne0 $ . 证毕.例3 设$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是2维复空间$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ 框架, $ {\mathcal{H}}_2 $ 为$ {\mathbb{K}} $ 上的线性算子, $ {\mathcal{P}}, \; {\mathcal{T}}, \; {\mathcal{H}}_2 $ 的表示矩阵$ {{P}}, \; {{T}}, \; {{H}}_2 $ 为$ r, s, \theta $ 是非零实数, 则由例2知, $ {\mathcal{H}}_2 $ 为完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的当且仅当$ |s|\geqslant |r\cdot \sin\theta| $ .例4 设$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ 3 $ 维复空间$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ 框架, $ {\mathcal{H}}_3 $ 为$ {\mathbb{K}} $ 上的线性算子, $ {\mathcal{P}}, \; {\mathcal{T}}, \; {\mathcal{H}}_3 $ 的表示矩阵P $ {{T}}, \; {{H}}_3 $ 为$ r, s, \theta $ 是非零实数且$ w\in {\mathbb{R}}, w\notin \sigma({{H}}_2) $ ($ {{H}}_2 $ 同例3), 则$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架. 由定理4知: $ {\mathcal{H}}_3 $ 为完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的当且仅当$ |s|\geqslant |r\cdot \sin\theta| $ .$ \{{\mathcal{P}}_k, {\mathcal{T}}_k\} $ 是复空间$ {\mathbb{K}}_k $ 上的$ {\mathcal{P}}_k{\mathcal{T}}_k $ -框架(k = 1, 2) , 定义张量积空间$ {\mathbb{K}}_1\otimes {\mathbb{K}}_2 $ 上的算子如下:$ {\mathcal{A}}_1 $ 与$ {\mathcal{A}}_2 $ 的张量积$ {\mathcal{A}}_1 \otimes {\mathcal{A}}_2 $ 的定义与通常相同, 即$ \{e'_i\}_{i = 1}^{d_1} $ 与$ \{e''_j\}_{j = 1}^{d_2} $ 分别为空间$ {\mathbb{K}}_1 $ 与$ {\mathbb{K}}_2 $ 的线性无关基. 但是, 共轭线性算子$ {\mathcal{T}}_1 $ 与$ {\mathcal{T}}_2 $ 的张量积$ {\mathcal{T}} = {\mathcal{T}}_1 \otimes {\mathcal{T}}_2 $ 定义为$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是空间$ {\mathbb{K}}_1\otimes {\mathbb{K}}_2 $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架且$ {\mathcal{H}} $ 是$ {\mathcal{P}}{\mathcal{T}} $ -对称的(参见例5). 这就说明: $ {\mathcal{P}}{\mathcal{T}} $ -框架及$ {\mathcal{P}}{\mathcal{T}} $ -对称性对张量积运算“具有封闭性”.例5 设$ \{{\mathcal{P}}_k, {\mathcal{T}}_k\} $ 是2维复空间$ {\mathbb{K}} $ 上的$ {\mathcal{P}}_k{\mathcal{T}}_k $ -框架$ (k \!=\! 1, 2) $ , $ {\mathcal{H}}_k $ 为$ {\mathbb{K}} $ 上的线性算子$ (k \!=\! 1, 2),\;{\mathcal{P}}_k, $ $ \; {\mathcal{T}}_k, \; {\mathcal{H}}_k $ 的表示矩阵${{P}_k}, \;{{T}_k}, \;{{H}_k}$ 为$ {\mathcal{H}}_k $ 为$ {\mathcal{P}}_k{\mathcal{T}}_k $ -对称的$ (k = 1, 2) $ , 从而, $ {\mathcal{H}}_1 \otimes {\mathcal{H}}_2 $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称的, 其中$ {\mathcal{P}} = {\mathcal{P}}_1 \otimes {\mathcal{P}}_2, \ {\mathcal{T}} = {\mathcal{T}}_1 \otimes {\mathcal{T}}_2. $ $ {\mathcal{P}}{\mathcal{T}} $ -对称性对于张量积运算“不具有封闭性”, 即$ {\mathcal{H}}_k $ 是完整$ {\mathcal{P}}_k{\mathcal{T}}_k $ -对称的$ (k = 1, 2) $ 不能保证张量积$ {\mathcal{H}}_1\otimes{\mathcal{H}}_2 $ 一定是完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的, 其中$ {\mathcal{P}} = {\mathcal{P}}_1 \otimes {\mathcal{P}}_2, \ {\mathcal{T}} = {\mathcal{T}}_1 \otimes {\mathcal{T}}_2 $ (例6).例6 设$ \{{\mathcal{P}}_k, {\mathcal{T}}_k\}(k = 1, 2) $ 是2维复空间$ {\mathbb{K}} $ 上的$ {\mathcal{P}}_k{\mathcal{T}}_k $ 框架, $ {\mathcal{H}}_i $ 为$ {\mathbb{K}} $ 上的线性算子, $ {\mathcal{P}}_k, \; {\mathcal{T}}_k, \; {\mathcal{H}}_k $ 的表示矩阵$ {{P}}_k, \; {{T}}_k, \; {{H}}_k $ 分别为$ {{H}}_1 $ 的特征值为1, 代数重数为2, 几何重数为1, $ {{H}}_2 $ 的特征值为2, 代数重数为2, 几何重数为1. 由定理4知, $ {\mathcal{H}}_k\;(k = 1, 2) $ 都是完整$ {\mathcal{P}}_k{\mathcal{T}}_k $ $(k = 1, \;2) $ -对称的. 因此, $ {\mathcal{H}} = {\mathcal{H}}_1 \otimes {\mathcal{H}}_2 $ 为$ {\mathcal{P}}{\mathcal{T}} $ -对称的, 其中$ {\mathcal{P}} = {\mathcal{P}}_1 \otimes {\mathcal{P}}_2, \ {\mathcal{T}} = {\mathcal{T}}_1 \otimes {\mathcal{T}}_2 $ . 下面说明$ {\mathcal{H}} $ 不是完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的.$ {\mathcal{H}} $ 不是完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的.$ {\mathcal{H}}_k\;(k = 1, 2) $ 为2维空间$ {\mathbb{K}} $ 上线性算子且是完整$ {\mathcal{P}}_k{\mathcal{T}}_k $ -对称的$ (k = 1, 2) $ , $ {{P}}_k, {{H}}_k $ 分别为$ {\mathcal{P}}_k, {\mathcal{H}}_k $ 的表示矩阵, 且$ {{Q}}_k(k = 1, 2) $ 使得$ {{H}}_k = {{Q}}_k{{J}}_k\times$ ${{Q}}_k^{-1} (k = 1,\; 2) $ , 从而$ {{H}}_1\otimes {{H}}_2 = ({{Q}}_1\otimes {{Q}}_2)({{J}}_1\otimes {{J}}_2)$ $({{Q}}_1\otimes {{Q}}_2)^{-1}. $ $ {\mathcal{H}}, {\mathcal{P}}, {\mathcal{T}} $ 按照(13 )式定义, $ {{H}}, {{P}}, {{T}} $ 为对应的表示矩阵. 下面说明$ {\mathcal{H}} $ 不是完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的.$ {{H}} = {{H}}_1\otimes {{H}}_2\sim {{J}}_1\otimes {{J}}_2 $ , 所以$ g(\lambda_1\lambda_2) $ 为$ \lambda_1\lambda_2 $ 的几何重数. 由定理4(a)可知: $ {\mathcal{H}} $ 不是完整$ {\mathcal{P}}{\mathcal{T}} $ -对称.$ {\mathcal{P}}{\mathcal{T}} $ -对称量子系统与经典量子系统之间的转化关系. 设$ \{{\mathcal{P}}, {\mathcal{T}}\} $ 是$ {\mathbb{K}} $ 上的$ {\mathcal{P}}{\mathcal{T}} $ -框架, $ {\mathcal{H}} $ 为哈密顿且为$ {\mathcal{P}}{\mathcal{T}} $ -对称的. $ {\mathcal{P}}{\mathcal{T}} $ -对称量子理论的关键在于构造一个线性算子$ \mathcal{C} $ , 建立一个新的正定内积, 称之为$ \mathcal{C}{\mathcal{P}}{\mathcal{T}} $ -内积, 使得$ {\mathcal{H}} $ 关于$ \mathcal{C}{\mathcal{P}}{\mathcal{T}} $ -内积为自伴的, 从而保证系统的演化关于新内积为酉演化且概率守恒. 因此, 问题的本质在于寻找一个新的正定内积, 使得系统哈密顿$ {\mathcal{H}} $ 在这个内积下是自伴的.$ {\mathbb{K}} $ 上的正定算子$ \eta $ , 可以定义$ {\mathbb{K}} $ 上的新内积$ \langle \phi|\psi\rangle_{\eta}: = \langle \phi|\eta|\psi\rangle, $ 称之为$ {\mathbb{K}} $ 上的$ \eta $ -内积. 我们在文献[37 ]中给出了线性算子关于某个正定内积是自伴的一些等价条件, 证明了存在正定算子$ \eta $ 使得$ {\mathcal{H}} $ 关于$ \eta $ -内积是$ {\mathbb{K}} $ 上的自伴线性算子当且仅当$ {\mathcal{H}} $ 的表示矩阵H $ {\mathcal{H}} $ 的完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性保证了$ {\mathcal{H}} $ 的特征值是实数, 但并不能保证其表示矩阵H $ {\mathcal{H}} $ 为完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的且可相似对角化当且仅当$ {\mathcal{H}} $ 有n 个互不相同的实特征值. 因此, $ {\mathcal{H}} $ 的完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性不是$ {\mathcal{H}} $ 关于某个新的正定内积下自伴的充分条件, 同时也不是必要条件.5.结 论 本文讨论了共轭线性算子的一些性质, 给出了共轭线性对称和完整共轭线性对称的定义, 给出了共轭线性对称性和完整共轭线性对称性的等价刻画; 在此基础上, 进一步讨论了$ {\mathcal{P}}{\mathcal{T}} $ -对称及完整$ {\mathcal{P}}{\mathcal{T}} $ -对称的性质, 给出了完整$ {\mathcal{P}}{\mathcal{T}} $ -对称哈密顿的一些具体例子, 说明了完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性对张量积运算不具有封闭性, 同时还说明了完整$ {\mathcal{P}}{\mathcal{T}} $ -对称性既不是哈密顿$ {\mathcal{H}} $ 在某个正定内积下自伴的充分条件, 也不是必要条件. 通过本文的讨论, 可以帮助我们更好地理解共轭线性对称性的本质, 使我们对$ {\mathcal{P}}{\mathcal{T}} $ -对称量子系统相应的数学结构有更清楚的认识, 对将来的进一步研究具有一定的理论意义. 



















































































































































































































































































































































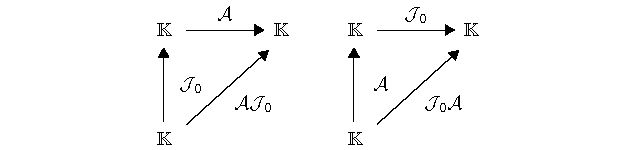 图 1 共轭线性算子
图 1 共轭线性算子











































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































