摘要: 非线性波作为非线性动力学研究中的重要课题之一, 普遍存在于各种复杂物理系统中. 理解非线性波的产生机制、确定它们的激发条件对于非线性波的实验实现、动力学特征的探测和应用是至关重要的. 本文简要综述了近年来非线性波的实验和理论研究进展, 回顾了非线性波的产生机制. 基于非线性可积模型中的严格解和线性稳定分析结果, 系统讨论了如何建立基本非线性波与调制不稳定性的精确对应关系. 详细介绍了近来发现的扰动能量和相对相位在确定非线性波激发条件中的重要作用, 并提议了一组能够确定非线性波激发条件的完备参数. 基于完备的激发参数, 给出了多种基本非线性波的激发条件和相图. 这些结果有望用于实现多种局域波的可控激发, 并可以推广到更多非线性系统中的激发相图研究.
关键词: 非线性波 /
调制不稳定性 /
产生机制 /
激发条件 English Abstract Quantitative relations between fundamental nonlinear waves and modulation instability Duan Liang 1,2 ,Liu Chong 1,2 ,Zhao Li-Chen 1,2 ,Yang Zhan-Ying 1,2 1.School of Physics, Northwest University, Xi’an 710127, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11875220, 11775176)Received Date: 12 September 2019Accepted Date: 31 October 2019Available Online: 13 December 2019Published Online: 05 January 2020Abstract: Nonlinear waves are ubiquitous in various physical systems, and they have become one of the research hotspots in nonlinear physics. For the experimental realization, observation and application of nonlinear waves, it is very important to understand the generation mechanism, and determine the essential excitation conditions of various nonlinear waves. In this paper, we first briefly review the experimental and theoretical research progress of nonlinear waves in recent years. Based on the exact nonlinear wave solutions and linear stability analysis results, we systemically discuss how to establish the quantitative relations between fundamental nonlinear waves and modulation instability. These relations would deepen our understanding on the mechanism of nonlinear waves. To solve the excitation conditions degenerations problem for some nonlinear waves, we further introduce the perturbation energy and relative phase to determine the excitation conditions of nonlinear waves. Finally, we present a set of complete parameters that can determine the excitation conditions of nonlinear waves, and give the excitation conditions and phase diagrams of the fundamental nonlinear waves. These results can be used to realize controllable excitation of nonlinear waves, and could be extended to many other nonlinear systems.Keywords: nonlinear waves /modulation instability /generation mechanism /excitation conditions 全文HTML --> --> --> 1.引 言 非线性波是出现在非线性系统中的一类典型的激发结构[1 ,2 ] , 它们广泛存在于许多物理系统中, 如水流体[3 -5 ] 、非线性光学[6 -21 ] 、等离子体[22 ,23 ] 、原子束[24 ,25 ] 、玻色- 爱因斯坦凝聚体[26 -38 ] 、毛细管[39 ] 、铁磁链[40 -44 ] 、金融系统[45 -47 ] 、超材料[48 ,49 ] 、光力学[50 ] 、PT对称系统[51 ,52 ] 等. 并且, 这些非线性波在很多领域都具有潜在的应用价值, 例如孤子干涉仪[53 -56 ] 、超连续谱的产生[57 ] 、光频梳的产生[58 ] 、介观贝尔态的制备[59 ] 、高功率脉冲的制备[60 ,61 ] 、利用孤子的抖动效应测量量子阱本征值[62 ] 等. 目前, 非线性波动力学的研究已经成为非线性物理科学中的一个重要的课题.[63 -65 ] 、反暗孤子[66 ,67 ] 、W形孤子[68 -71 ] 和多峰孤子[72 ,73 ] . 此外也发现了一些呈周期分布并稳定演化的非线性波, 包括周期波和W形孤子链[72 -74 ] . 除了稳定演化的结构之外还有几类振幅随着演化变化的非线性波包括怪波[75 ] 、Akhmediev呼吸子[76 ] 、Kuznetsov-Ma呼吸子[77 ,78 ] 和Tajiri-Watanabe呼吸子[79 ] (也被称为一般呼吸子[80 ,81 ] 或动态呼吸子[82 ] ). 最近的研究表明呼吸子碰撞也表现出诸多有趣的性质, 例如super-regular呼吸子[83 -89 ] 、呼吸子分子[90 ] 、类棋盘干涉班图[91 ] 等. 近期, 怪波的激发结构和产生机制也被广泛讨论[92 -108 ] , 常见的怪波激发结构有眼状、反眼状、四花瓣、以及扭曲的双峰怪波等. 不同结构的怪波之间还可以通过调节背景频率或矢量场之间的相对振幅实现相互转换[98 ] . 调制不稳定性可以用来定性理解怪波、呼吸子激发的产生, 近期人们进一步提议了一些更具体的激发机制来解释怪波的产生机制, 如调制不稳定区的共振激发[109 ] 或基带调制不稳定性[110 ] . 这些更具体的激发机制理解可以用来基于线性稳定性分析初步判断非线性系统中是否存在怪波激发. 高阶效应对怪波激发的影响也被广泛讨论[111 -115 ] . 人们还进一步提议了基于呼吸子的碰撞可以激发高阶怪波[116 -118 ] .[11 ,14 ] 和Dudley等[12 ] 分析了非线性薛定谔方程的Akhmediev呼吸子解、怪波解和Kuznetsov-Ma呼吸子解, 发现这几种非线性波的激发由扰动频率和扰动强度决定, 并给出了它们的激发条件. 根据理论分析给出的激发条件, 他们通过输入满足相应条件的初态在实验上分别实现了这几种非线性波的激发. 实验结果与这几种非线性波解析解所描述的结构符合得非常好. 目前平面波背景上的基本非线性波除了几种呼吸子和怪波, 其他非线性波例如反暗孤子、W形孤子、多峰孤子、周期波和W孤子链等都没有被实验实现, 并且决定它们激发的物理参数以及相应激发条件仍然不清楚. 怪波和呼吸子的相关实验结果说明非线性方程的解析解描述了非线性系统中一类基本的动力学过程. 通过分析不同的非线性波解可以得到决定不同非线性激发的参数和相应激发条件, 从而用满足相应条件的非理想简单形式的初态分布进行演化, 就可以得到对应的非线性波结构. 非线性波的实验实现对非线性波现象的深入理解、非线性波动力学性质的探测和应用是非常重要的. 除了通过分析非线性波解析解得到非线性波的激发调制之外, 还可以分析非线性波的产生机制, 即分析不同非线性波的产生原因, 理解了非线性波的产生机制后自然就可以知道决定非线性波激发的参数以及相应的激发条件. 因此本文主要介绍关于基本非线性波的产生机制及其与调制不稳定性的对应关系的相关研究, 并重点讨论能够确定非线性波激发条件的完备物理参数并给出基本非线性波的激发条件及相图. 这些结果将在很大程度上促进对多种非线性波的实验观测.2.非线性波的产生机制及其在背景频率和扰动频率空间的相图 目前普遍认为平面波背景上的非线性波的激发依赖于系统的调制不稳定性[12 ,76 ] . 调制不稳定性反应的是连续波背景上的扰动随着演化的增长特征[119 ] . 在非线性光学中, 调制不稳定性在时域上表现的是弱扰动的增长与放大, 在频域中调制不稳定性演化的初始阶段反应的是频谱旁带的产生并经历指数形式的增长, 能量从泵浦转移到旁带, 而随后呈现出泵浦和多个旁带之间的循环能量交换等复杂行为[120 ,121 ] . 最近的研究也已经证实调制不稳定性可以用来理解连续波背景上的非线性波的动力学, 如Peregrine怪波、Akhmediev呼吸子、Kuznetsov-Ma呼吸子甚至是高阶怪波的动力学特征. 分析系统的调制不稳定性特征通常采用线性稳定性分析的方法. 下面以非线性薛定谔方程为例简单介绍线性稳定性分析的主要步骤. 首先标准非线性薛定谔方程形式如下z 和t 分别表示归一化的距离和时间, $ |\psi|^{2} $ 表示光强. 方程(1 )存在如下的平面波解$ \psi_0(t, z) = $ $a{\rm e}^{{\rm i}\theta(t, z)} $ , 其中$ \theta(t, z) = k z+\omega t $ , 这里a 和$ \omega $ 分别表示平面波的振幅和频率, $ k = a^{2}-{1}/{2}\omega^{2} $ 是平面波的波数. 考虑对平面波解增加一个小扰动$ p(t, z) $ , 即$ \psi(t, z) = [a+p(t, z)]{\rm e}^{{\rm i}\theta(t, z)} $ . 将该式代入非线性薛定谔方程(1 ), 略去关于$ p(t, z) $ 的高次项, 并取扰动$ p(t, z) $ 的最低阶傅里叶模式, $ p(t, z) = f_{+}{\rm e}^{{\rm i}(Kz+\varOmega t)}+ $ $f_{-}{\rm e}^{-{\rm i}(Kz+\varOmega t)} $ . 这里K 和$ \varOmega $ 分别表示扰动的波数和频率, 值得注意的是扰动后的波函数$ \psi(t, z) $ 中因子$ {\rm e}^{{\rm i}\theta(t, z)} $ 已经提取出来, 实际的扰动形式应该是$ p(t, z){\rm e}^{{\rm i}\theta} = p(t, z){\rm e}^{{\rm i}(kz+\omega t)} $ , 因此实际的扰动波数和扰动频率分别是$ k\pm K $ 和$ \omega\pm\varOmega $ , 为了方便我们仍然将K 和$ \varOmega $ 称为扰动波数和扰动频率. $ f_{+} $ 和$ f_{-} $ 是傅里叶模式的振幅, 并且$ f_{+} $ 和$ f_{-} $ 远小于背景振幅a . 经过简单计算可以得到扰动$ p(t, z) $ 的波数K 和频率$ \varOmega $ 之间的色散关系: $ K = -\omega\varOmega\pm|\varOmega|\sqrt{\varOmega^{2}-4 a^{2}} $ . 从色散关系可以看出, 对于$ |\varOmega|\geqslant 2 a $ , 波数K 都是实数, 此时平面波在微扰下是稳定的. 而K 在$ |\varOmega| < 2 a $ 时变为复数, 此时扰动$ p(t, z) $ 随着演化指数增长, 也就是说平面波在扰动频率$ -2 a < \varOmega < $ 2a 时是不稳定的. 波数K 的虚部决定了增长的快慢, 因此可以定义调制不稳定性的增益为K 的虚部来自于根式$ \sqrt{\varOmega^{2}-4 a^{2}} $ , 当扰动频率$ \varOmega = 0 $ 时, 根式$ \sqrt{\varOmega^{2}-4 a^{2}} $ 仍然是个虚数, 只是在根式前的系数$ |\varOmega| = 0 $ 导致波数K 的虚部为零. 此时K 的虚部并不能真实反应系统的调制不稳定性特征. $ \varOmega = 0 $ 时, 调制不稳定特征需要单独求解. 对于$ \varOmega = 0 $ , 其扰动可以写为[122 ] : $ \psi(t, z) = [a+\epsilon \tilde{p}(z)]{\rm e}^{{\rm i}\theta(t, z)} $ . 这里$ \epsilon $ 为实常数并且$ \epsilon\ll 1 $ . 由于扰动频率为零, 因此$ \tilde{p}(z) $ 不含有变量t . 将该扰动形式代入到非线性薛定谔方程(1 )中, 并略去$ \epsilon $ 的二次及二次以上项, 然后求解方程可以得到$ \tilde{p} = 1+2 {\rm i}a^{2}z $ . 此时调制不稳定性增益可以定义为[100 ] 基于两组分耦合非线性薛定谔方程讨论了怪波激发与调制不稳定性之间的对应关系. 通过标准的线性稳定性分析方法, 得到系统调制不稳定增益分布如图1 所示. 图中彩色区域对应于调制不稳定区, 白色区域是调制不稳定性增益为零的区域, 即调制稳定区. 图1(a) 和图1(b) 分别是调制不稳定性在扰动频率$ \varOmega $ 和相对背景频率$ \omega $ 空间以及扰动频率$ \varOmega $ 和背景振幅$ a_{1} $ 空间的分布图. Baronio等[100 ] 将调制不稳定区域分为基频带调制不稳定区和通频带调制不稳定区, 其中基频带调制不稳定区定义为从扰动频率$ \varOmega = 0 $ 处开始的调制不稳定区(图1(a) 和图1(b) 中黑色虚线以下的彩色区域), 而通频带定义为起始于非零扰动频率处的调制不稳定区域(图1(a) 和图1(b) 中黑色虚线以上的彩色区域). 通过分析耦合非线性薛定谔方程的怪波解的激发特征, 发现调制不稳定性只是怪波激发的必要不充分条件. 也就是说, 有调制不稳定性不一定能够激发怪波, 而有怪波激发系统一定有调制不稳定性. 进一步他们证实怪波激发的充要条件是系统调制不稳定性有基频带, 并且怪波激发在基频带中扰动频率$ \varOmega $ 趋于零的位置. 随后该小组将相关的结果推广到Fokas-Lenells系统和长短波共振系统都证实了同样的结论[110 ,111 ,112 ] . 这些结果是关于怪波激发与调制不稳定性关系研究的一个重要突破, 然而这些结果中仍然存在一些问题没有被解决, 例如: 1)他们仅仅给出了怪波激发与基频带调制不稳定性的关系, 而怪波产生的根本原因没有给出解释; 2)他们得到的基带调制不稳定区中零频扰动的增益为零, 而相关研究结果展示怪波激发在基带调制不稳定区扰动频率趋于零的位置, 这个结果似乎与调制不稳定性增益特征相矛盾; 3)如果一个系统中仅仅在扰动频率$ \varOmega = 0 $ 处有调制不稳定性, 而在$ \varOmega = 0 $ 的两侧区域都是调制稳定区时, 则不能定义基频带, 那么此时是否能够激发怪波, 也是不能回答的; 4)这些工作中都只分析了怪波与调制不稳定性的关系, 而呼吸子等其他非线性波与调制不稳定性的对应关系仍然不清楚.图 1 自散焦的两组分耦合非线性薛定谔系统的调制不稳定增益的分布 (a)调制不稳定增益在$(\varOmega, \omega)$ 平面的分布, 绿色点状曲线表示调制不稳定区的边界; (b)调制不稳定性在$(\varOmega, a_{1})$ 平面的分布Figure1. Modulation instability distributions of the defocusing two component coupled nonlinear Schr?dinger system: (a) Modulation instability distribution in the $(\varOmega, \omega)$ plane, green dot curves are the boundary of the modulation instability regime; (b) modulation instability distribution in the $(\varOmega, a_{1})$ plane.[109 ] . 特别地, 证实了怪波来自于平面波背景上调制不稳定区的共振扰动[109 ] . 非线性薛定谔方程平面波背景上各种类型的非线性波解已经被广泛研究. 所有的这些平面波上的解都可以写为平面波和扰动部分线性叠加的形式, 即$ \psi = \psi_{0}+\psi_{\rm p} $ . $ \psi_{0} $ 和$ \psi_{\rm p} $ 分别为平面波解和描述扰动演化动力学的部分. 做线性稳定性分析时, 平面波背景上加上扰动之后的形式$ \psi(t, z) = [a+p(t, z)]{\rm e}^{{\rm i}\theta(t, z)} $ 也是一个平面波$ a\,{\rm e}^{{\rm i}\theta} $ 和扰动$ p\, {\rm e}^{{\rm i}\theta} $ 的线性叠加. 调制不稳定性反应的就是扰动$ p\,{\rm e}^{{\rm i}\theta} $ 演化的稳定性特征. 因此可以通过调制不稳定性来理解平面波背景上非线性波的动力学特征.3 )式和(2 )式中分别给出了扰动频率$ 0 < |\varOmega| < 2 a $ 和$ \varOmega = 0 $ (共振扰动)时调制不稳定性增益G 的表达式. 从G 的表达式可以看出, 标准非线性薛定谔系统的调制不稳定性依赖于平面波背景振幅a 和扰动频率$ \varOmega $ . 由于非线性薛定谔系统满足伽利略协变性, 因此其增益不依赖于背景频率$ \omega $ . 但是在其他的非线性系统中例如Hirota系统[71 ,123 ] 、Sasa-Satsuma系统[74 ,124 ] 、四阶非线性薛定谔系统[125 ] 和五阶非线性薛定谔系统[126 ] 等广义非线性薛定谔系统中, 由于伽利略协变性被破坏, 其调制不稳定性也依赖于背景频率$ \omega $ . 文献[109 ]是在背景振幅a 和扰动频率$ \varOmega $ 参数空间讨论非线性波与调制不稳定性对应关系的. 然而考虑到非线性薛定谔方程(1 )是无量纲化的模型, 其背景振幅a 只是一个相对值, a 的大小并不具有实际意义, 并且为了和在其他模型中讨论非线性波与调制不稳定的形式一致, 这里分别在$ (a, \varOmega) $ 空间和$ (\omega, \varOmega) $ 空间讨论了两者的对应关系.图2(a1) 和图2(b1) 中分别给出调制不稳定性增益G 在背景频率$ \omega $ 和扰动频率$ \varOmega $ 参数平面的分布(背景振幅取$ a = 1 $ )以及在背景振幅a 和扰动频率$ \varOmega $ 参数平面的分布(背景频率取$ \omega = 0 $ ). 从图中可以看出在$ (\omega, \varOmega) $ 平面, 调制不稳定性增益分布为带状结构, 其范围为$ -2 a < \varOmega < 2 a $ (图中a 取$ 1 $ ), 由于满足伽利略协变性因此调制不稳定性增益在不同背景频率$ \omega $ 处的分布都相同. 而在$ (a, \varOmega) $ 平面, 调制不稳定性增益分布区域为两个对称的三角区域, 三角区域的范围仍然为$ -2 a < \varOmega < 2 a $ , 在背景振幅$ a = 0 $ 处, 任意扰动频率都是稳定的. 图中$ \varOmega = 0 $ 处的红色虚线为共振线.图 2 标准非线性薛定谔系统的调制不稳定增益分布和基本非线性波激发的相图 (a1)和(b1)分别为调制不稳定增益在$(\omega, \varOmega)$ 平面和$(a, \varOmega)$ 平面的分布. “MI”和“MS”分别表示调制不稳定性和调制稳定性, 红色虚线是共振线; (a2)和(b2)分别为基本非线性波在(a1)和(b1)中调制不稳定增益分布平面的相图. “AB”,“RW”和“KM”分别为Akhmediev呼吸子、怪波和Kuznetsov-Ma呼吸子Figure2. Modulation instability distributions and phase diagrams of fundamental nonlinear waves in standard nonlinear Schr?dinger system: (a1) and (b1) are the distributions of the modulation instability gain in the $(\omega, \varOmega)$ plane and the $(a, \varOmega)$ , respectively. “MI” and “MS” denote modulation instability and modulation stability, respectively. the red dotted line is the resonance line; (a2) and (b2) are the phase diagrams of fundamental nonlinear waves on the modulation instability gain distribution planes correspond to (a1) and (b1), respectively. "AB", "RW" and "KM" denote Akhmediev breather, rogue wave and Kuznetsov-Ma breather, respectively.$ \omega $ 、扰动频率$ \varOmega $ 和背景振幅a . 因此要建立非线性波激发与调制不稳定性之间的关系, 需要分析不同类型非线性波解的这三个参数的范围. 背景频率$ \omega $ 和背景振幅a 在解中都有直接体现. 对于呼吸子和怪波等非线性波, 其扰动部分的频谱都不是单频谱, 其扰动频率定义为扰动部分在频谱中强度最大值处所对应的频率[109 ] . 然后根据不同非线性波解的背景频率$ \omega $ 、扰动频率$ \varOmega $ 和背景振幅a 的范围即可建立其与调制不稳定性增益的对应关系.图2 . 从图中可以看出, Kuznetsov-Ma呼吸子激发在调制不稳定增益分布平面的共振线上($ \varOmega = 0 $ )$ a = 0 $ 以外的区域. Akhmediev呼吸子位于共振线两侧的调制不稳定区. 另外, Akhmediev呼吸子在分布方向t 的周期$ T_{t} ={2{\text{π}}}/{|\varOmega|} $ , 也就是说Akhmediev呼吸子的周期由初始的扰动频率决定, 并且演化过程中扰动频率保持不变. 最近在一些数值和实验工作中通过在平面波背景上加周期扰动的方法得到了Akhmediev呼吸子的激发, 并且Akhmediev呼吸子的周期就等于初始扰动信号的周期[12 ] , 这些结果说明我们对非线性波扰动频率的分析方法是合理的. 对于不同扰动频率, 调制不稳定性增益不同, 因此对于同样的初始扰动振幅, 不同频率的周期扰动激发出Akhmediev呼吸子的位置不同[12 ,127 ] . 并且我们注意到, 当扰动频率$ \varOmega $ 趋于调制不稳定区的边界$ \pm2 a $ 时, Akhmediev呼吸子的振幅趋于背景振幅. 随着扰动频率从$ \pm2 a $ 趋于$ 0 $ 时, Akhmediev呼吸子的最大振幅逐渐增大, 当扰动频率等于零时, Akhmediev呼吸子将转变为Peregrine怪波[11 ] , 此时振幅达到最大, 为背景振幅的三倍. 也就是说最大峰值和增益出现在共振线上. 因此, 怪波是一种共振激发模式[109 ] .[70 ,97 ,99 ,102 ] . 上面讨论中已经证实了怪波来自于调制不稳定区的共振扰动, 这就意味着这三种怪波结构都激发在共振线上, 那么是什么参数决定了怪波结构的不同呢?之前研究已经证实反眼状怪波和四花瓣怪波都只存在于耦合非线性系统中[70 ,97 ,99 ,102 ] , 因此为了回答这个问题, Ling等[103 ] 基于自聚焦任意N 组分耦合非线性薛定谔系统分析了怪波时空结构的产生机制. N 组分耦合非线性薛定谔方程如下:$ {\varPsi} = (\psi_{1}, \psi_{2}, ..., \psi_{N})^{\rm T} $ , T和$ \dagger $ 分别表示矩阵的转置和厄米共轭. 这个模型可以用来描述多模非线性光纤中光脉冲的传输[128 ] 、多组分玻色-爱因斯坦凝聚体的演化[104 ,129 ,130 ] 以及其他非线性耦合系统. 在$ N = 1 $ 时, 这个模型将约化为标准非线性薛定谔方程(1 ), 此时只存在眼状Peregrine怪波. 在$ N > 1 $ 的耦合系统中, 眼状、反眼状和四花瓣三种结构的怪波都可以存在, 并且不同结构之间可以相互转换. 最近N 组分耦合非线性薛定谔系统中基本怪波解的一般求解方法已经被给出, 通过这个方法可以构造出不同结构基本怪波共存甚至是高阶怪波共存的解[106 ] .N 组分耦合非线性薛定谔系统(4 )的调制不稳定性特征. 该方程的平面波解如下$ \psi_{0 j} = a_{j}{\rm e}^{{\rm i}\theta_{j}} $ , 其中$ \theta_{j} \!=\! k_{j}z+\omega_{i}t $ , $ k_{j} \!=\! \displaystyle\sum\nolimits_{j = 1}^{N}a_{j}^{2}-{1}/{2}\omega_{j}^{2} $ , $ j = 1, 2,\cdots\!,$ N . $ a_{j} $ 和$ \omega_{j} $ 是分别是第j 组分平面波背景的振幅和频率. 在平面波背景上加上扰动后形式为$ \psi_{j} = a_{j}{\rm e}^{{\rm i}\theta_{j}}[1+p_{j}(t, z)] $ , 这里$ p_{j}(t, z) $ 表示第j 个组分的小扰动, 其形式为$ p_{j} = f_{j+}{\rm e}^{{\rm i}(Kz+\varOmega t)}+ $ $f_{j-}{\rm e}^{{\rm i}(Kz+\varOmega t)} $ ($ f_{j+} $ 和$ f_{j-} $ 远小于1), K 和$ \varOmega $ 分别为扰动波数和频率. 利用线性稳定性分析方法, 可以很容易得到K 和$ \varOmega $ 之间的色散关系. 前面已经证实, 怪波来自于共振扰动即$ \varOmega = 0 $ . 通过分析共振扰动的调制不稳定, 可以得到对于共振扰动的色散关系为$ 1+ \displaystyle\sum\limits_{j = 1}^{N}\dfrac{a_{j}^{2}}{(K+\omega_{j})^{2}} = 0 $ . 然后通过分析方程(4 )得到一般形式的基本怪波解在不同参数下的结构特征. 通过与线性稳定性分析的结果对比发现基本怪波的结构由如下的判别式决定$ K_{\rm R} $ 和$ K_{\rm I} $ 分别为扰动波数K 的实部和虚部. 当$ \varDelta\leqslant {1}{3} $ 时, 基本怪波为眼状结构; ${1}{3} < \varDelta < 3 $ 时, 基本怪波为四花瓣结构; 而$ \varDelta\leqslant 3 $ 时, 基本怪波为反眼状结构. 扰动波数K 的实部和虚部分别表示扰动的传播常数和调制不稳定性增益. 显然, 如果$ K_{\rm I} = 0 $ , 则共振线上调制不稳定性增益为零, 此时将不会有怪波激发, 这个结果与怪波共振调制不稳定性机制的研究结果是一致的[109 ] . 通过判别式$ \varDelta $ 可以很方便地判断任意N 组分非线性薛定谔系统中不同参数条件下的怪波激发结构[103 ] .[109 ] . 怪波和呼吸子都是背景上弱扰动调制不稳定放大的结果, 它们都激发在调制不稳定区. 而在一个物理系统不仅有调制不稳定区也存在着调制稳定的区域. 调制稳定区意味着在这些参数区域的弱扰动随着演化并不会被放大而是稳定传播, 这说明在调制稳定区应该存在稳定演化的孤子或周期波. 那么在调制稳定区域是否一定有稳定演化的孤子或周期波激发呢?我们分析了用来描述飞秒量级光脉冲传输的具有高阶效应的Sasa-Satsuma系统, 发现其调制不稳定带中存在一小块调制稳定区域(见图3(a) ), 并在这个调制稳定区域的共振线上得到了有理形式W形孤子激发, 这个W形孤子在弱噪声下仍然可以保持稳定演化. 特别地, 这个孤子的频谱对应于超连续光谱[70 ] . 随后在共振线上调制不稳定区与调制稳定区的临界点(见图3(a) 中共振线上紫色圆点)处得到了一个小信号产生两个W形孤子的独特动力学[74 ,131 ] . 在初始阶段一个小信号被调制不稳定放大, 随着演化峰值逐渐增大, 达到最大峰值后劈裂为两个稳定的W形孤子, 在W形孤子演化过程中呈现出调制稳定的特征. 这个动力学过程显著区别于怪波的不稳定特征和W形孤子的稳定特征, 同时包含了调制不稳定特征和调制稳定性特征. 由于临界点处于调制不稳定区和调制稳定区的交界位置, 其既不属于调制不稳定区又不属于调制稳定区, 但是又同时包含调制不稳定特征和调制稳定特征, 因此可以出现从弱信号放大然后劈裂出W形孤子的独特动力学行为. 随后在标准非线性薛定谔系统和耦合非线性薛定谔系统中通过对系统的色散和非线性进行调制, 使得随着演化调制不稳定性增益逐渐减小并过渡到调制稳定区, 也得到了弱信号放大后产生的孤子结构[132 ,133 ] . 但是两者从弱信号产生稳定孤子的本质是不同的.图 3 Sasa-Satsuma系统的调制不稳定增益分布和基本非线性波激发的相图 (a) Sasa-Satsuma系统中调制不稳定增益在背景频率$\omega$ 和扰动频率$\varOmega$ 平面的分布. “MI”和“MS”分别表示调制不稳定和调制稳定, 黄颜色圆点为共振线上临界点; (b)非线性波在调制不稳定增益分布平面的相图. “AB”, “RW” 和“KM” 分别为Akhmediev呼吸子、怪波和Kuznetsov-Ma呼吸子; “WS”, “WST”, “AD”和Periodic wave分别表示W形孤子、W形孤子链、反暗孤子和周期波Figure3. Modulation instability distributions and phase diagrams of fundamental nonlinear waves in Sasa-Satsuma system: (a) Distributions of the modulation instability gain in the background frequency $\omega$ and perturbation frequency$\varOmega$ plane. “MI” and “MS” denote modulation instability and modulation stability, respectively. The yellow dots are the critical points on the resonance line; (b) phase diagrams of nonlinear waves in the modulation instability gain distribution planes. “AB”, “RW” and “KM” denote Akhmediev breather, rogue wave and Kuznetsov-Ma breather, respectively; “WS”, “WST” and “AD” denote the W-shaped soliton, W-shaped soliton train and anti-dark soliton, respectively.[74 ] , 其对应的相图展示在图3(b) . 从图中可以看出, 怪波仍然来自于调制不稳定区的共振扰动, Kuznetsov-Ma呼吸子和Akhmediev呼吸子也都激发在调制不稳定区, Kuznetsov-Ma也激发在共振线上, 而Akhmediev呼吸子激发在共振线两侧的调制不稳定区(见图3 中红色虚线和橙色虚线之间的区域). 这些结果与标准非线性薛定谔系统中这几种非线性波在调制不稳定增益分布平面的激发位置是类似的. 然而, 与标准非线性薛定谔系统不同的是, 在Sasa-Satsuma系统中其调制不稳定带中存在一个调制稳定区, 这也带来了一些新的非线性激发. 调制不稳定区与调制稳定区的边界为$ \varOmega = \pm\dfrac{4\omega^{2}-1}{\omega} $ . W形孤子和反暗孤子激发在共振线上的调制稳定区(图3(b) 中两个黄颜色临界点之间的红色虚线). W形孤子链存在于共振线和调制不稳定带边界($ \varOmega = \pm2 a $ )之间的区域, 见图3(b) 中水平灰色虚线标记的调制稳定区. 周期波位于直线$ \varOmega = \pm2\omega $ (见图中灰色实线)之间的调制稳定区, 见图中竖直的灰色虚线标记区域. 从图中可以看出W形孤子、反暗孤子、W形孤子链和周期波都位于调制稳定区, 它们的动力学也证实它们的演化是稳定的. 显然线性稳定性分析也可以用来预测平面波背景上稳定演化的孤子和周期波激发. 需要特别注意的是, 与标准非线性薛定谔系统类似, Sasa-Satsuma系统中Kuznetsov-Ma呼吸子和怪波也激发在同样的位置. 此外W形孤子和反暗孤子也存在于相同区域, 周期波与W形孤子链的激发区域有部分重合. 这些结果说明决定系统调制不稳定特征的两个参数背景频率$ \omega $ 和扰动频率$ \varOmega $ 并不能完全决定非线性波的激发.[123 ] , 我们也分析了其调制不稳定性, 发现在调制不稳定带中存在一条调制稳定线(见图4(a) ). 并且发现当怪波从不稳定区趋于调制稳定线时, 怪波逐渐被拉长, 其演化方向局域性逐渐降低, 当达到稳定线位置时, 怪波完全转换为有理W形孤子. 并且怪波的局域性与调制不稳定增益G 的倒数成正比[71 ] . 这个结果进一步加深了人们对调制不稳定性与非线性激发关系的理解, 随后怪波与孤子之间的态转化在其他系统中也被广泛讨论[134 -136 ] . 随后, 我们也在Hirota系统中发现了对称和不对称形式多峰孤子激发和反暗孤子、周期波等非线性激发, 并且给出了Akhmediev呼吸子和周期波, Kuznetsov-Ma呼吸子和反暗孤子与非有理W形孤子之间的转换关系, 也系统给出了Hirota系统中非线性波激发在调制不稳定性增益平面的相图[73 ] (见图4(b) ). 与标准非线性薛定谔系统[109 ] 和Sasa-Satsuma系统[74 ] 类似, 怪波和Kuznetsov-Ma呼吸子激发在共振线上的不稳定区, Akhmediev呼吸子存在于共振线两侧调制不稳定区, 有理W形孤子、非有理W形孤子和反暗孤子都激发在共振线上的调制稳定区, 周期波位于共振线两侧调制稳定线上. 特别地, 多峰孤子存在于图中橙色“X”形区域, 这个区域既有调制不稳定区又有调制稳定区, 该结果与线性稳定性分析预测结果是矛盾的, 这是由线性稳定性分析自身局限性导致的. 此外, 我们注意到在Hirota系统中非线性激发在$ (\omega, \varOmega) $ 空间的相图中, 怪波和Kuznetsov-Ma呼吸子存在于同一位置, 有理W形孤子、非有理W形孤子和反暗孤子激发在同一区域, 多峰孤子和Akhmediev呼吸子的激发区域有部分重合. 这些结果进一步证实了线性稳定性分析的局限性, 也说明了仅仅通过背景频率$ \omega $ 和扰动频率$ \varOmega $ 两个参数并不能完全确定非线性波的激发条件. 因此仍然需要引入新的物理参数来区分在背景频率和扰动频率空间共存的非线性波激发.图 4 Hirota系统中的调制不稳定增益分布和基本非线性波激发的相图 (a) Hirota系统中调制不稳定增益在背景频率$\omega$ 和扰动频率$\varOmega$ 平面的分布. “MI”和“MS”分别表示调制不稳定和调制稳定; (b)非线性波在调制不稳定增益分布平面的相图. “AB”, “RW” 和“KM” 分别为Akhmediev呼吸子、怪波和Kuznetsov-Ma呼吸子; “WS”, “AD”, “PW”和“MPS”分别表示W形孤子、反暗孤子、周期波和多峰孤子Figure4. Modulation instability distributions and phase diagrams of fundamental nonlinear waves in Hirota system; (a) Distributions of the modulation instability gain in the background frequency $\omega$ and perturbation frequency$\varOmega$ plane. “MI” and “MS” denote modulation instability and modulation stability, respectively; (b) phase diagrams of nonlinear waves in the modulation instability gain distribution planes. “AB”, “RW” and “KM” denote Akhmediev breather, rogue wave and Kuznetsov-Ma breather, respectively; “WS”, “AD”, “PW” and “MPS” denote the W-shaped soliton, anti-dark soliton, periodic wave and multi-peak soliton, respectively.3.扰动能量在确定非线性波激发中的作用 在描述超短光脉冲在光纤中传输时, 需要考虑一些高阶效应的影响. 例如在描述飞秒脉冲在光纤中传输模型中需要考虑三阶色散、自陡峭和延迟非线性效应等三阶效应(Sasa-Satsuma系统[124 ] 和Hirota系统[123 ] ). 最近一些实验和理论研究显示描述小于飞秒量级光脉冲在光纤中传输需要考虑一些四阶效应[137 ] . 此外, 四阶效应在各向异性海森堡铁磁自旋链系统中也起到了重要作用[40 ,41 ,138 ] . 考虑一个同时具有三阶和四阶效应的非线性薛定谔模型[139 -146 ] $ H[\psi(t, z)] = \psi_{ttt}+6 |\psi|^{2}\psi_{t} $ , 四阶项$ P[\psi(t, z)] \,= \,\psi_{tttt}+8 |\psi|^{2}\psi_{tt}\,+\,6 |\psi|^{4}\psi\,+\,4 |\psi_{t}|^{2}\psi\,+ $ $6\psi_{t}^{2}\psi^{*}+2\psi^{2}\psi_{tt}^{*} $ . 参数z 和t 分别表示归一化的距离和时间, $ |\psi|^{2} $ 表示光强. 当$ \beta = \gamma = 0 $ 时, 方程(6 )约化为标准非线性薛定谔方程, 它可以用来描述皮秒脉冲在光纤中传输动力学. 当$ \gamma = 0 $ 时, 方程(6 )变为描述光纤中飞秒脉冲传输的Hirota方程.a 和$ \omega $ 分别表示平面波解的振幅和频率. 调制不稳定增益的分布展示在图5(a) . 显然四阶非线性薛定谔系统中调制不稳定性增益的分布特征与标准非线性薛定谔系统、Hirota系统和Sasa-Satsuma中分布都是不同的. 在标准非线性薛定谔系统中调制不稳定带中不存在调制稳定区, Hirota系统中调制不稳定带内包含了一条调制稳定线, 在Sasa-Satsuma系统中, 调制不稳定带中有一个调制稳定区域, 而在四阶非线性薛定谔系统中, 在调制不稳定带中存在一个调制稳定环[71 ,73 ,74 ,109 ] . 通常不同的调制不稳定增益分布会带来不同的非线性激发结构, 因此自然可以期望在四阶非线性系统中能够得到与标准非线性薛定谔系统、Hirota系统和Sasa-Satsuma系统中不同的激发特征.图 5 四阶非线性薛定谔系统调制不稳定增益分布和基本非线性波激发的相图 (a) 调制不稳定增益在背景频率$\omega$ 和扰动频率$\varOmega$ 平面的分布, “MI”和“MS” 分别表示调制不稳定性和调制稳定性; (b),(c) 基本非线性波在背景频率$\omega$ 和扰动频率$\varOmega$ 平面的相图, “AB”, “RW”, “KM”、“PW”, “WST”, “WS$_{\rm r}$ ”, “$\rm WS_{ {nr}}$ ” 和“AD”分别为Akhmediev呼吸子、怪波、Kuznetsov-Ma呼吸子、周期波、W形孤子链、有理的W形孤子、非有理的W形孤子和反暗孤子Figure5. Modulation instability distributions and phase diagrams of fundamental nonlinear waves in fourth-order nonlinear Schr?dinger system: (a) Distributions of the modulation instability gain in the background frequency $\omega$ and perturbation frequency$\varOmega$ plane. “MI” and “MS” denote modulation instability and modulation stability, respectively; (b), (c) phase diagrams of nonlinear waves in the background frequency $\omega$ and perturbation frequency $\varOmega$ plane. “AB”, “RW”, “KM”, “PW”, “WST”, “WS$_{\rm r}$ ”, “WS$\rm WS_{{nr}}$ ” and “AD” denote Akhmediev breather, rogue wave, Kuznetsov-Ma breather, periodic wave, W-shaped soliton train, rational W-shaped soliton, nonrational W-shaped soliton and anti-dark soliton, respectively.6 )平面波背景上的非线性波解, 其中包括Kuznetsov-Ma呼吸子、非有理W形孤子、反暗孤子、Akhmediev呼吸子、W形孤子链、周期波、怪波和有理W形孤子八种基本非线性波. 进一步通过分析各个非线性波背景频率和扰动频率的关系, 我们建立了其与调制不稳定性的对应关系[125 ] , 这几种非线性波在调制不稳定性增益分布平面的相图见图5(b) 和图5(c) . 从图中可以看出, 与标准非线性薛定谔系统、Hirota系统和Sasa-Satsuma系统类似, 怪波仍然存在于共振线上的调制不稳定区, 有理W形孤子存在于共振线上的调制稳定区, Akhmediev呼吸子位于共振线两侧的调制不稳定区, W形孤子链和周期波激发在共振线两侧调制稳定环上, 并且它们的扰动频率分别满足$ 0 < |\varOmega| < \sqrt{3}a $ 和$ \sqrt{3}a\leqslant $ $|\varOmega| < 2 a $ (见图5(b) 中环形区域的紫色虚线部分和绿色实线部分). 值得注意的是, 在四阶非线性薛定谔系统中Kuznetsov-Ma呼吸子可以存在于共振线上所有区域, 非有理W形孤子和反暗孤子存在于共振线上两个调制稳定点之外的调制不稳定区. 这个结果与线性稳定性分析的预测相违背. 需要注意的是, 这两种孤子可以存在于调制稳定点两侧的调制不稳定区而不能存在于两个调制稳定点之间的不稳定区域. 特别地, 当四阶非线性薛定谔系统(6 )中四阶效应为零, 即$ \gamma = 0 $ 时, 四阶非线性薛定谔系统变为Hirota系统, 此时这两种孤子都存在于调制稳定区, 显然四阶效应对这两种孤子存在于调制稳定区起到了重要作用. 并且已经证实存在于调制不稳定区的反暗孤子和非有理W形孤子演化是稳定的.$ \varepsilon $ [125 ] , 其定义为$ a\,{\rm e}^{{\rm i}\theta} $ 能量多出的部分. 有效扰动能量$ \varepsilon > 0 $ 则说明加上扰动后有额外能量输入; $ \varepsilon = 0 $ 则说明扰动并不带来额外能量, 此时扰动演化过程中的能量完全由平面波背景转化而来; $ \varepsilon < 0 $ 则意味着扰动时从背景提取出了一部分能量, 例如平面波背景上的暗孤子就可以看作是从平面波背景上除去了一部分能量. 为了方便, 下面讨论中将有效扰动能量简称为扰动能量. 通过分析发现, 调制不稳定增益$ G_{0} $ 和孤子扰动能量平方$ \varepsilon_{\rm s}^{2} $ 满足a 和四阶效应系数$ \gamma $ . 这也进一步解释了在低于四阶效应的非线性薛定谔系统, 例如标准非线性薛定谔系统和包含三阶效应的非线性薛定谔系统中为什么没有发现反暗孤子和非有理W形孤子存在于调制不稳定区的情况.图5(c) ). 这个结果在标准非线性薛定谔系统和具有三阶效应的非线性薛定谔系统中并没有发现, 因此这个现象也可能是由四阶效应引起的. Kuznetsov-Ma呼吸子扰动能量不等于零. 我们注意到Kuznetsov-Ma呼吸子扰动能量值与反暗孤子和非有理W形孤子的扰动能量的表达式相同, 但是Kuznetsov-Ma呼吸子需要满足条件$ \left(\omega+\dfrac{\beta}{4\gamma}\right)^{2}-\dfrac{\varepsilon_{\rm {km}}^{2}}{24}\neq\alpha $ . 而反暗孤子和非有理W形孤子激发条件为$ \left(\omega+\dfrac{\beta}{4\gamma}\right)^{2}-\dfrac{\varepsilon_{\rm s}^{2}}{24} = \alpha $ . 上一节分析已经证明反暗孤子和非有理W形孤子激发条件意味着扰动能量和调制不稳定增益的平衡, 因此Kuznetsov-Ma呼吸子激发是扰动能量和调制不稳定增益没有达到平衡的结果. 最近, 我们进一步分析了Kuznetsov-Ma呼吸子的产生机制, 发现Kuznetsov-Ma呼吸子是孤子和平面波之间的干涉和调制不稳定性共同作用的结果[147 ] .4.相对相位在确定非线性波激发中的作用 为了寻找能够区分反暗孤子和非有理W形孤子以及周期波和W形孤子链的物理参数, 通过Darboux变换方法重新构造了四阶非线性薛定谔方程平面波背景上的解析解(见文献[148 ]附录). 引入自由参数$ \phi $ 后, 反暗孤子或非有理W形孤子解析表达式可以写为b 为实常数并且满足$ |b| > a $ , $ \varepsilon_{\rm s} $ 为孤子扰动能量. 这里$ \psi_{+} $ 和$ \psi_{-} $ 以及$ \varphi_{+} $ 和$ \varphi_{-} $ 分别对应于$ b > 0 $ 和$ b < 0 $ 两种情形, 由于$ |b| > 0 $ , 这里$ \psi_{{\rm p}\pm} $ 是一个正的实函数. 因此参数$ \varphi_{\pm} $ 是一个相位因子, 它表示扰动部分和平面波背景之间的相对相位. 显然孤子解(11 )式是平面波背景$ a{\rm e}^{{\rm i}\theta} $ 和相对相位为$ \varphi_{\pm} $ 的扰动信号$ \psi_{{\rm p}\pm}{\rm e}^{{\rm i}\varphi_{\pm}}{\rm e}^{{\rm i}\theta} $ 的叠加. 孤子解(11 )式特征依赖于背景振幅a 、背景频率$ \omega $ 、扰动能量$ \varepsilon_{\rm s} $ 和相对相位$ \varphi_{\pm} $ . 因此为了分析不同相对相位值时孤子解(11 )式所对应的孤子类型, 只需分析孤子强度分布$ |\psi_{\rm s}|^{2} $ 极值点个数即可. 经过计算发现, 当相对相位$ \varphi\in\left[ {-\dfrac{{\text{π}}}{2}+2 n{\text{π}}, \dfrac{{\text{π}}}{2}+2 n{\text{π}}} \right] $ 时, 解(11 )式为反暗孤子; 当相对相位$ \varphi_{\pm}\in\left[ {\dfrac{{\text{π}}}{2}+2 n{\text{π}}, \dfrac{3{\text{π}}}{2}+2 n{\text{π}}} \right]$ 时, 解(11 )式对应于非有理W形孤子.$ \gamma_{0} = \varOmega(t-v_{\rm {wp}}z) $ , 扰动频率$ \varOmega = \pm2\sqrt{a^{2}-b^{2}}$ $ \in(-2 a, 0)\cup(0, 2 a) $ $ (|b| < a ),$ $ v_{\rm {wp}} = \omega+\beta(6 a^{2}-\varOmega^{2} $ $ -3\omega^{2})+4\gamma\omega(6 a^{2}-\varOmega^{2}-\omega^{2}) $ 表示周期波和W形孤子链的速度, d 为任意实常数. 这里$ n = 0, \pm1, $ $ \pm2, \cdots $ , $ \psi_{\rm {p-wp}} $ 是正的实函数, 因此$ \varphi_{\rm {wp}} $ 表示扰动和平面波背景之间的相对相位. 由于周期波和W形孤子链的扰动频率$ \varOmega\in(-2 a, 0)\cup(0, 2 a) $ , 而d 是一个任意实常数, 因此相对相位$ \varphi_{\rm {wp}}\in\Big(\dfrac{{\text{π}}}{2}+2 n{\text{π}}, $ $ \dfrac{3{\text{π}}}{2}+2 n{\text{π}} \Big) $ . 当$ \dfrac{\sqrt{3}a}{|\sec\varphi|}\leqslant|\varOmega| < \dfrac{2 a}{|\sec\varphi|} $ 时, 解(12 )式对应于周期波, 当$ 0 < |\varOmega| < \dfrac{\sqrt{3}a}{|\sec\varphi|} $ 时, 解(12 )式为W形孤子链. 周期波峰和谷的位置以及W形孤子链峰的位置都只依赖于扰动频率, 但是它们的峰值和谷值都由扰动频率和相对相位共同决定; W形孤子链谷的位置由扰动频率和相对相位共同确定, 但是其谷值只依赖于相对相位而与扰动频率无关. 以前的一些研究中[72 ,73 ,125 ] , 周期波和W形孤子链并没有引入与相对相位有关的参数d , 即$ d = 0 $ , 也就是相对相位$ \varphi_{\rm {wp}} = {\text{π}} $ , 这仅仅只是我们得到的解(12 )式中一个特殊情形. 因此以前研究中得到的W形孤子链谷值都为零. 通过引入相对相位周期波和W形孤子链的激发条件可以被完全澄清, 相对相位也可以区分Sasa-Satsuma系统中共存的周期波和W形孤子链[74 ] .$ \varOmega $ 趋于零时, 周期波和W形孤子链周期趋于无穷大, 此时解(12 )式转化为有理W形孤子, 有理W形孤子峰值和谷值都依赖于相对相位. 之前一些工作中得到的有理W形孤子峰值都是背景振幅的三倍, 而谷值恒等于零[71 ,72 ,73 ,125 ] , 事实上这都是有理W形孤子相对相位为$ {\text{π}} $ 时的特殊情形. 此外, 有理W形孤子与相对相位的依赖关系与周期波和W形孤子链扰动频率趋于零时的结果一致. 显然这三种激发在调制稳定区的非线性波激发特征依赖于扰动频率和相对相位.5.基本非线性波的激发条件和相图 从前两节的讨论可以看到, 背景频率、扰动频率、扰动能量和相对相位四个参数可以用来确定平面波背景上基本非线性波的激发条件. 然而这四个参数对平面波背景上的Tajiri-Watanabe呼吸子和多峰孤子激发条件的影响仍未被讨论. 为了能够完整地给出平面波背景上基本非线性波的激发条件, 需要分析这四个物理参数对Tajiri-Watanabe呼吸子和多峰孤子激发条件的影响. 通过前几节的分析方法可以很容易给出Tajiri-Watanabe呼吸子和多峰孤子与背景频率、扰动频率、扰动能量和相对相位这四个参数之间的依赖关系. 通过分析我们发现在这四个参数空间Tajiri-Watanabe呼吸子和多峰孤子和平面波背景上其他所有非线性波都不存在共存情况. 因此背景频率、扰动频率、扰动能量和相对相位是一组能够决定平面波背景上基本非线性波激发的完备参数, 基于这组参数我们给出平面波背景上基本非线性波(Tajiri-Watanabe呼吸子、多峰孤子、Kuznetsov-Ma呼吸子、反暗孤子、非有理W形孤子、怪波、有理W形孤子、Akhmediev呼吸子、周期波和W形孤子链)的激发条件,如表1 所列. 从表中可以看到, 一组确定的参数值可以完全决定一种非线性波激发. 因此, 平面波背景加上满足不同条件的初态就可以确定不同的非线性波激发结构. 文献 通过满足不同条件的非理想初态的数值模拟已经证实满足不同激发条件的非理想初态可以演化出对应的非线性波结构. 这进一步证实了背景频率、扰动频率、扰动能量和相对相位这组参数确实可以确定平面波背景上基本非线性波的激发特征.激发条件 非线性波类型 $\varOmega$ $\omega$ $\varepsilon$ $\varphi$ 0 $\omega^{2}-\alpha\neq0 $ 0 $\varphi\in \left(\dfrac{{\text{π}}}{2}, \dfrac{3{\text{π}}}{2}\right)+2 n{\text{π}}$ 怪波 $\omega^{2}-\alpha=0$, $\alpha\geqslant 0$ 有理W形孤子 0 $\omega^{2}-\dfrac{\varepsilon^{2}}{24}-\alpha\neq0$, $\varepsilon>0$ $\varphi\in\mathbb{R}$ Kuznetsov-Ma呼吸子 $\omega^{2}-\dfrac{\varepsilon^{2}}{24}-\alpha=0$, $\varepsilon>0$ $\varphi\in\left(\dfrac{{\text{π}}}{2},\right. \left.\dfrac{3{\text{π}}}{2}\right]+2 n{\text{π}}$ 非有理W形孤子 $\omega^{2}-\dfrac{\varepsilon^{2}}{24}-\alpha=0$, $\varepsilon > 0$ $\varphi\in \left(-\dfrac{{\text{π}}}{2},\right. \left.\dfrac{{\text{π}}}{2}\right]+2 n{\text{π}}$ 反暗孤子 $\omega^{2}+\dfrac{\varOmega^{2} }{6}-\alpha\neq0, \varOmega\in(0, 2)$ 0 $\varphi\in \left(\dfrac{{\text{π}}}{2},\dfrac{3{\text{π}}}{2}\right)+2 n{\text{π}}$ Akhmediev呼吸子 $\omega^{2}+\dfrac{\varOmega^{2} }{6}-\alpha=0$ $0<|\varOmega|<\dfrac{\sqrt{3}}{|\sec\varphi|}$ W形孤子链 $\omega^{2}+\dfrac{\varOmega^{2} }{6}-\alpha=0$ $\dfrac{\sqrt{3}}{|\sec\varphi|}<|\varOmega|<\dfrac{2}{|\sec\varphi|}$ 周期波 $1+2\beta\left(\pm\sqrt{\varDelta}-3\omega\right)+2\gamma\nabla\neq0$ $\varphi\in \mathbb{\rm R}$ Tajiri-Watanabe呼吸子 $1+2\beta\left(\pm\sqrt{\varDelta}-3\omega\right)+2\gamma\nabla=0$ 多峰孤子 注1: $\omega$, $\varOmega$, $\varepsilon$和$\varphi$分别为背景频率、扰动频率、扰动能量和相对相位. 参数$\alpha=\dfrac{\beta^{2}}{16\gamma^{2}}+\dfrac{1}{12\gamma}+a^{2}$, $\varDelta = {\bigg[ {\dfrac{ {\sqrt { { {({\varepsilon ^2} - 4{\varOmega ^2} + 16{a^2})}^2} + 16{\varepsilon ^2}{\varOmega ^2} } - ({\varepsilon ^2} - 4{\varOmega ^2} + 16{a^2})} }{8} } \bigg]^{1/2} }$, $\nabla=-2\varDelta\pm8\omega\sqrt{\varDelta}-6\omega^{2}+6 a^{2}+\dfrac{1}{4}\varepsilon^{2}-\varOmega^{2}$.
表1 基本非线性波的激发条件Table1. Excitation conditions of fundamental nonlinear waves.6 ), 在$ \gamma = 0 $ 时约化为Hirota系统, 在$ \beta = \gamma = 0 $ 时约化为标准非线性薛定谔系统. 因此在图6(a) —图6(c) 中分别给出四阶非线性薛定谔系统、Hirota系统和非线性薛定谔系统中平面波背景上基本非线性波在背景频率、扰动频率和扰动能量空间的相图. 在图6(d) 和图6(e) 中分别给出了反暗孤子和非有理的W孤子以及周期波和W形孤子链在相对相位空间的相图.图 6 不同系统中平面波背景上基本非线性波在背景频率$\omega$ , 扰动频率$\varOmega$ , 扰动能量$\varepsilon$ 和相对相位$\varphi$ 空间的相图 (a) 四阶非线性薛定谔系统, 参数取$\beta={1}/{12}$ , $\gamma=-{1}/{36}$ , $a=1$ ; (b) Hirota系统, 参数取$\beta={1}/{12}$ , $\gamma=0$ , $a=1$ ; (c)非线性薛定谔系统, 参数取$\beta={1}/{12}$ , $\gamma=0$ , $a=1$ ; (d)反暗孤子和非有理W形孤子依赖于相对相位的相图; (e)周期波, W形孤子链和有理W形孤子在$(\varphi, \varOmega)$ 平面的相图. 图中“TW”, “KM”, “AB”, “RW”, “MPS”, “AD”, “WS$_{\rm {nr}}$ ”, “PW”, “WST”和“WS$_{\rm r}$ ”分别表示Tajiri-Watanabe呼吸子、Kuznetsov-Ma呼吸子、Akhmediev呼吸子、怪波、多峰孤子、反暗孤子、非有理W形孤子、周期波、W形孤子链和有理W形孤子Figure6. Phase diagrams of nonlinear waves in the background frequency $\omega$ , perturbation frequency $\varOmega$ , perturbation energy $\varepsilon$ and relative phase $\varphi$ space for different systems: (a) Fourth-order nonlinear Schr?dinger system. Parameters are $\beta={1}/{12}$ , $\gamma=-{1}/{36}$ , $a=1$ ; (b) hirota system. Parameters are $\beta={1}/{12}$ , $\gamma=0$ , $a=1$ ; (c) nonlinear Schr?dinger system. Parameters are $\beta=\gamma=0$ , $a=1$ ; (d) phase diagram of anti-dark soliton and nonrational W-shaped soliton in relative phase space; (e) phase diagram of periodic wave, W-shaped soliton train and rational W-shaped soliton in the $(\varphi, \varOmega)$ plane. “TW”, “KM”, “AB”, “RW”, “MPS”, “AD”, “WS$_{\rm {nr}}$ ”, “PW”, “WST” and “WS$_{\rm r}$ ” denote Tajiri-Watanabe breather, Kuznetsov-Ma breather, Akhmediev breather, rogue wave, multi-peak soliton, anti-dark soliton, nonrational W-shaped soliton, periodic wave, W-shaped soliton train and rational W-shaped soliton.图7(a) 和图7(b) 中, 分别给出了呼吸子和怪波之间以及孤子和周期波结构之间的转换关系. 这些转换关系清晰地展示了不同基本非线性波之间的区别与联系.图 7 不同非线性波的转换关系 (a) 呼吸子和怪波之间的转换关系; (b) 孤子和周期波之间的转换关系. 图中“TW”, “KM”, “AB”, “RW”分别为Tajiri-Watanabe呼吸子、Kuznetsov-Ma呼吸子、Akhmediev呼吸子和怪波, “MPS”, “AD”, “WS$_{\rm {nr}}$ ”, “PW”, “WST”和“WS$_{\rm r}$ ” 分别表示多峰孤子、反暗孤子、非有理W形孤子、周期波、W形孤子链和有理W形孤子Figure7. Conversion relationship of different nonlinear waves: (a) Conversion relationship between breathers and rogue wave; (b) conversion relationship between the solitons and periodic waves. “TW”, “KM”, “AB”, “RW”, “MPS”, “AD”, “WS$_{\rm {nr}}$ ”, “PW”, “WST” and “WS$_{\rm r}$ ” denote Tajiri-Watanabe breather, Kuznetsov-Ma breather, Akhmediev breather, rogue wave, multi-peak soliton, anti-dark soliton, nonrational W-shaped soliton, periodic wave, W-shaped soliton train and rational W-shaped soliton.6.总结与讨论 本文分析了平面波背景上基本非线性波的产生机制, 提议了一种建立基本非线性波与调制不稳定性对应关系的方法. 基于简单的对应关系建立方法, 给出了常见的几个系统中基本非线性波在背景频率和扰动频率空间的相图. 此外, 揭示了扰动能量和相对相位在确定非线性波激发中的重要作用. 特别地, 我们发现平面波背景上基本非线性波的激发完全由背景频率、扰动频率、扰动能量和相对相位四个参数决定. 根据非线性波的激发条件, 实验上可以通过很简单形式的初态得到对应的非线性波结构. 实验上只要构造出基本符合激发条件的初态(可以偏离严格解的初态), 就可以激发出相关的局域波动力学. 这些结果为非线性波的实验实现、可控激发和应用提供了坚实的理论基础. 当然, 这些结果在实际应用中仍然面临着一些问题. 例如用简单初态在演化时, 虽然基本的激发结构还是可以被观测到的. 但是由于其与解析初态有一定偏差, 在调制不稳定区中这些偏差随着演化会被放大, 从而形成一些非线性振荡结构. 这些结构会影响非线性波本身形态, 甚至形成更为复杂的动力学行为. 目前系统讨论了平面波背景上基本激发元的激发条件和机制, 而高阶激发的机制还需要进一步探究. 这些结果还有望推广到离散系统[149 ,150 ] 、1+2维流体系统[151 ] 、Davey-Stewartson系统[152 ,153 ] 、非局域光学系统[154 ,155 ] 等. 另外, 非线性波的激发条件都是在可积系统中给出的. 对于不可积系统, 还需要进行更深入的理论分析和实验探索. 高维情形下的激发动力学[156 -166 ] 最近成为学界的研究热点之一. 我们近期将努力探究高维情形下激发元的激发条件和激发机制. 





































































































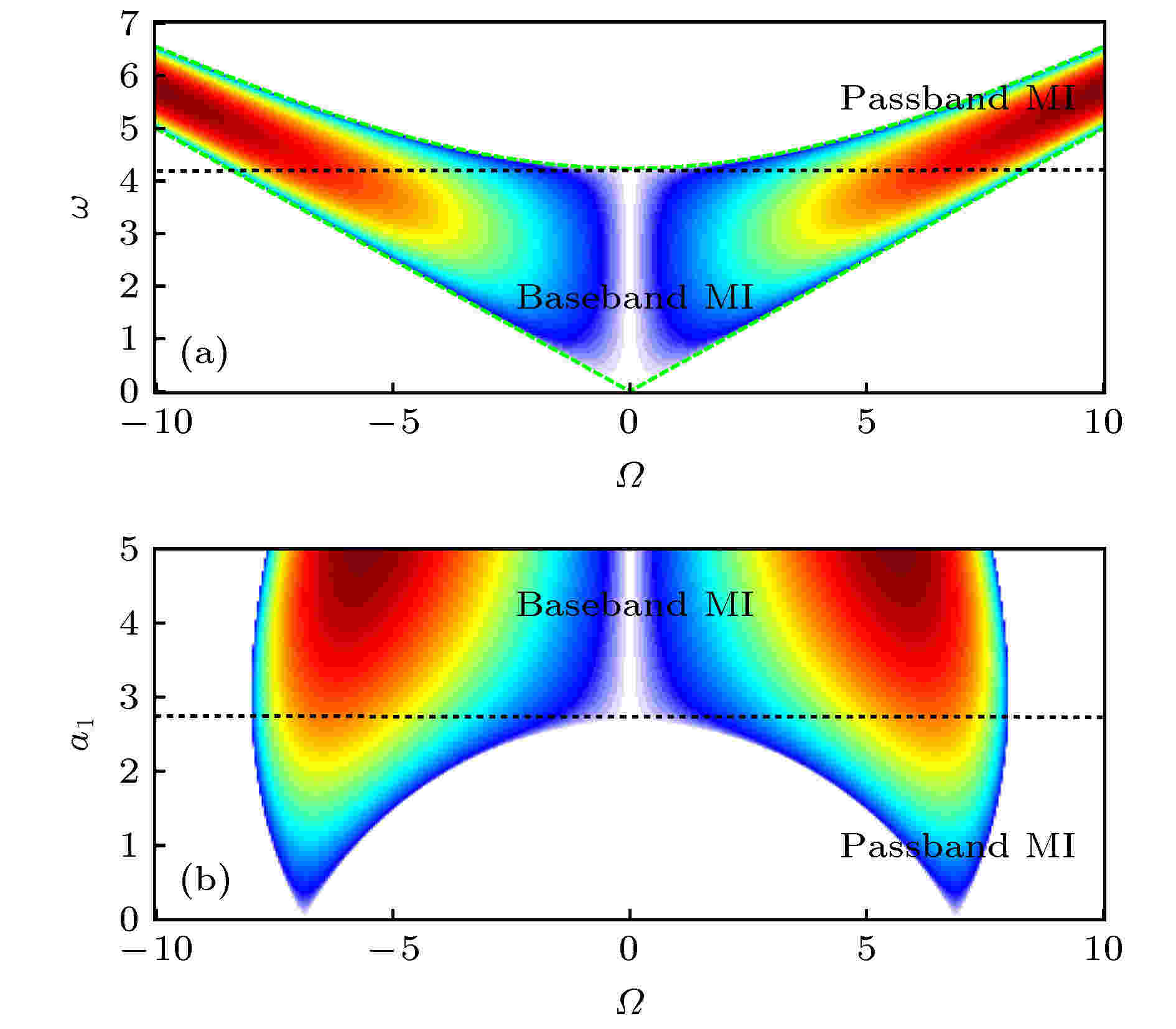 图 1 自散焦的两组分耦合非线性薛定谔系统的调制不稳定增益的分布 (a)调制不稳定增益在
图 1 自散焦的两组分耦合非线性薛定谔系统的调制不稳定增益的分布 (a)调制不稳定增益在









































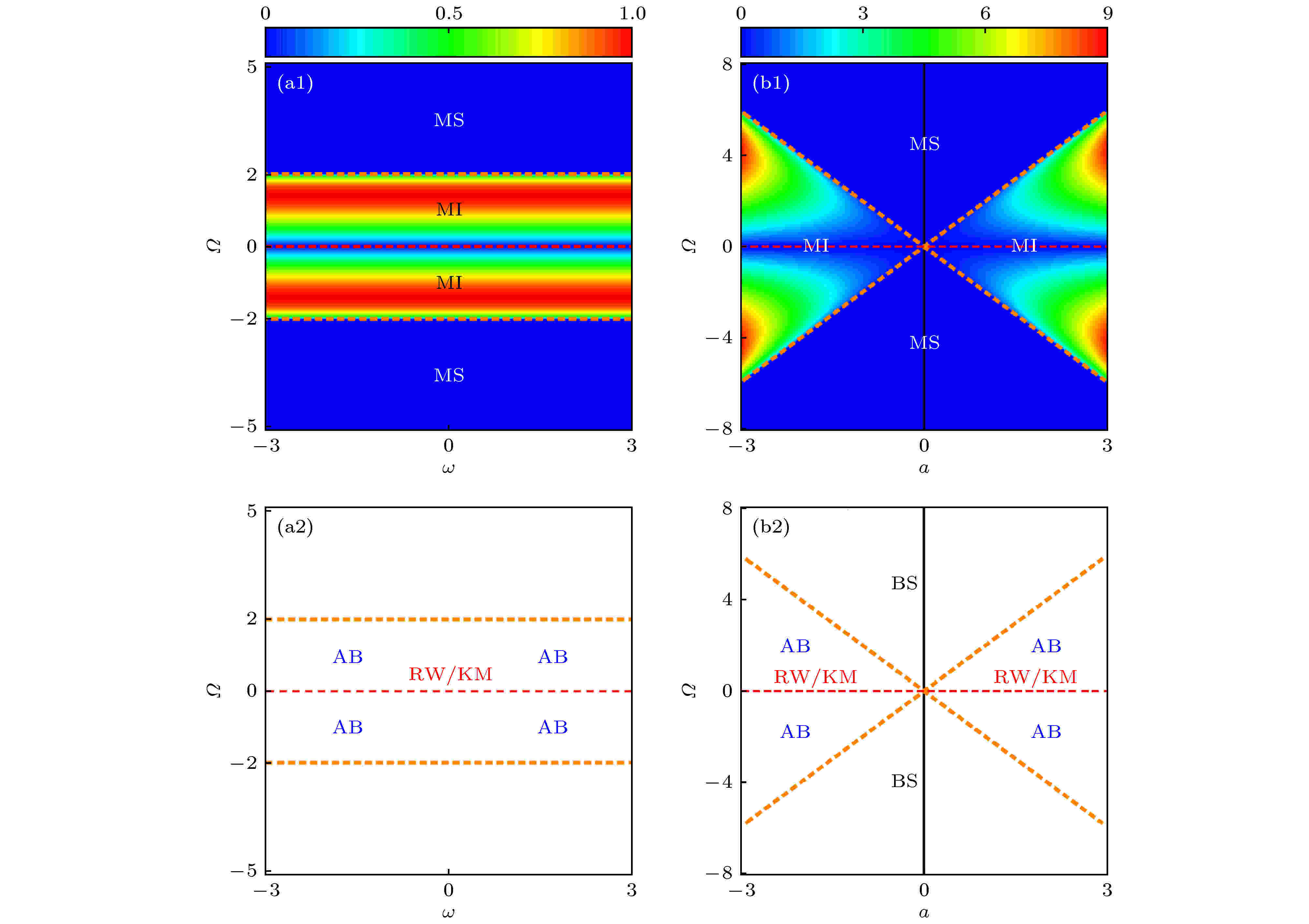 图 2 标准非线性薛定谔系统的调制不稳定增益分布和基本非线性波激发的相图 (a1)和(b1)分别为调制不稳定增益在
图 2 标准非线性薛定谔系统的调制不稳定增益分布和基本非线性波激发的相图 (a1)和(b1)分别为调制不稳定增益在






















































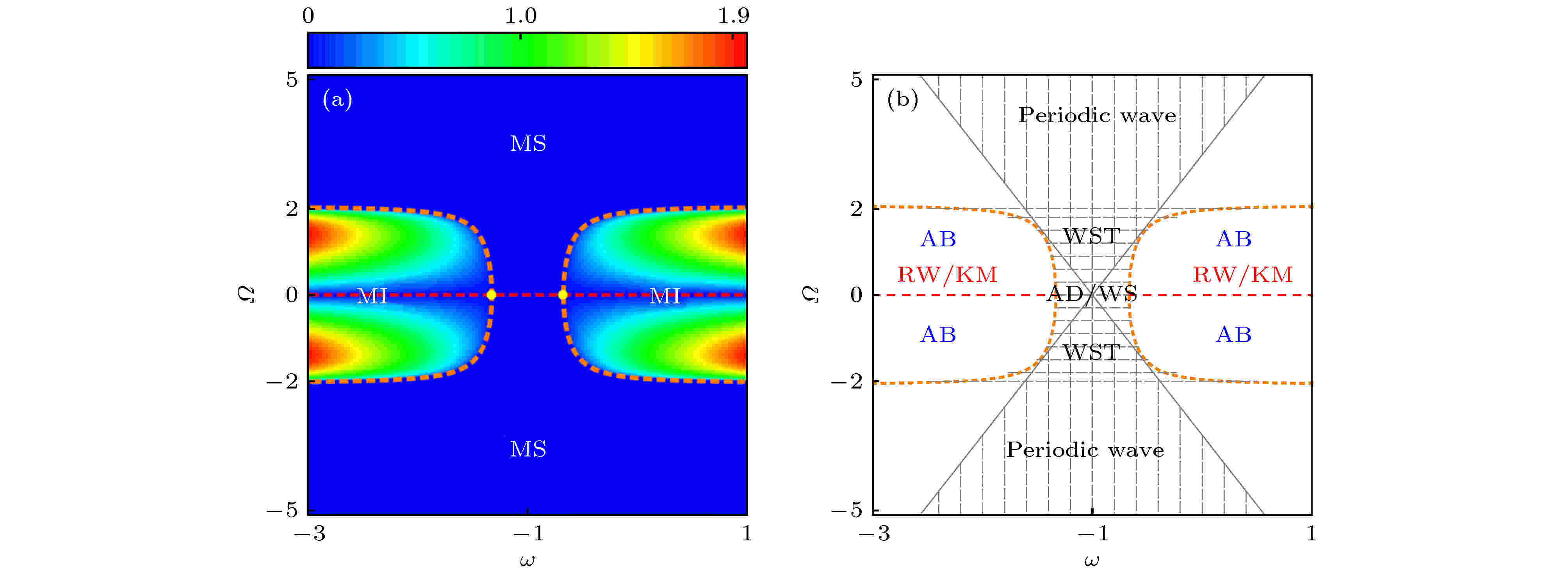 图 3 Sasa-Satsuma系统的调制不稳定增益分布和基本非线性波激发的相图 (a) Sasa-Satsuma系统中调制不稳定增益在背景频率
图 3 Sasa-Satsuma系统的调制不稳定增益分布和基本非线性波激发的相图 (a) Sasa-Satsuma系统中调制不稳定增益在背景频率











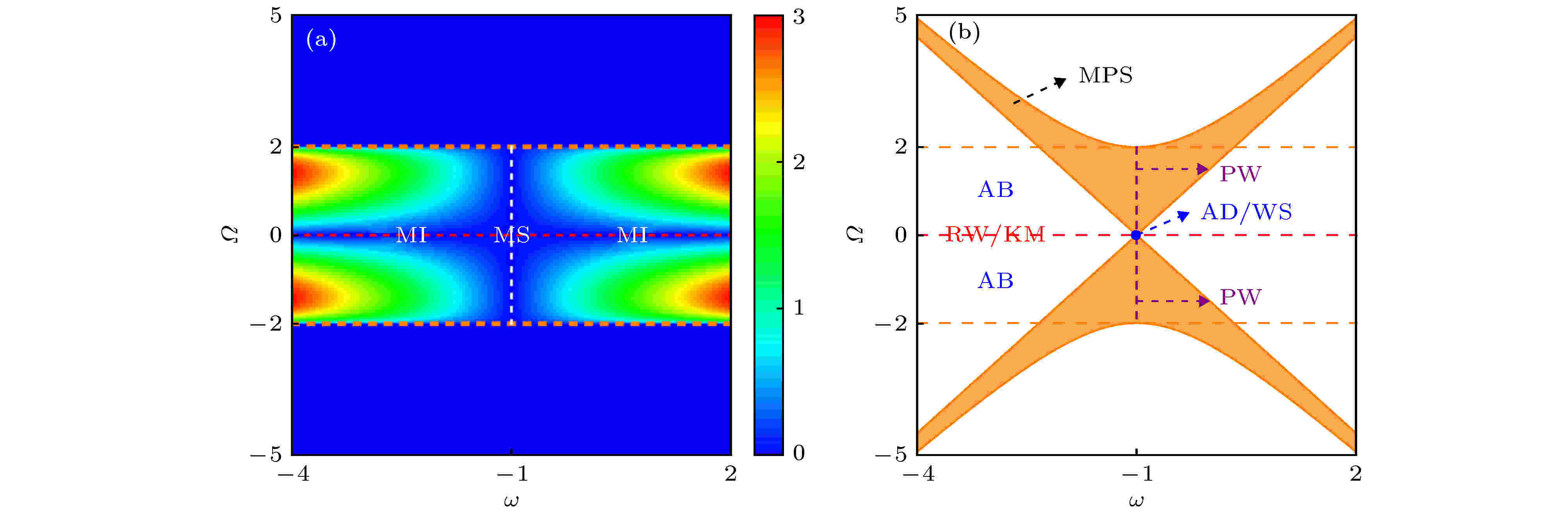 图 4 Hirota系统中的调制不稳定增益分布和基本非线性波激发的相图 (a) Hirota系统中调制不稳定增益在背景频率
图 4 Hirota系统中的调制不稳定增益分布和基本非线性波激发的相图 (a) Hirota系统中调制不稳定增益在背景频率










 图 5 四阶非线性薛定谔系统调制不稳定增益分布和基本非线性波激发的相图 (a) 调制不稳定增益在背景频率
图 5 四阶非线性薛定谔系统调制不稳定增益分布和基本非线性波激发的相图 (a) 调制不稳定增益在背景频率



















































































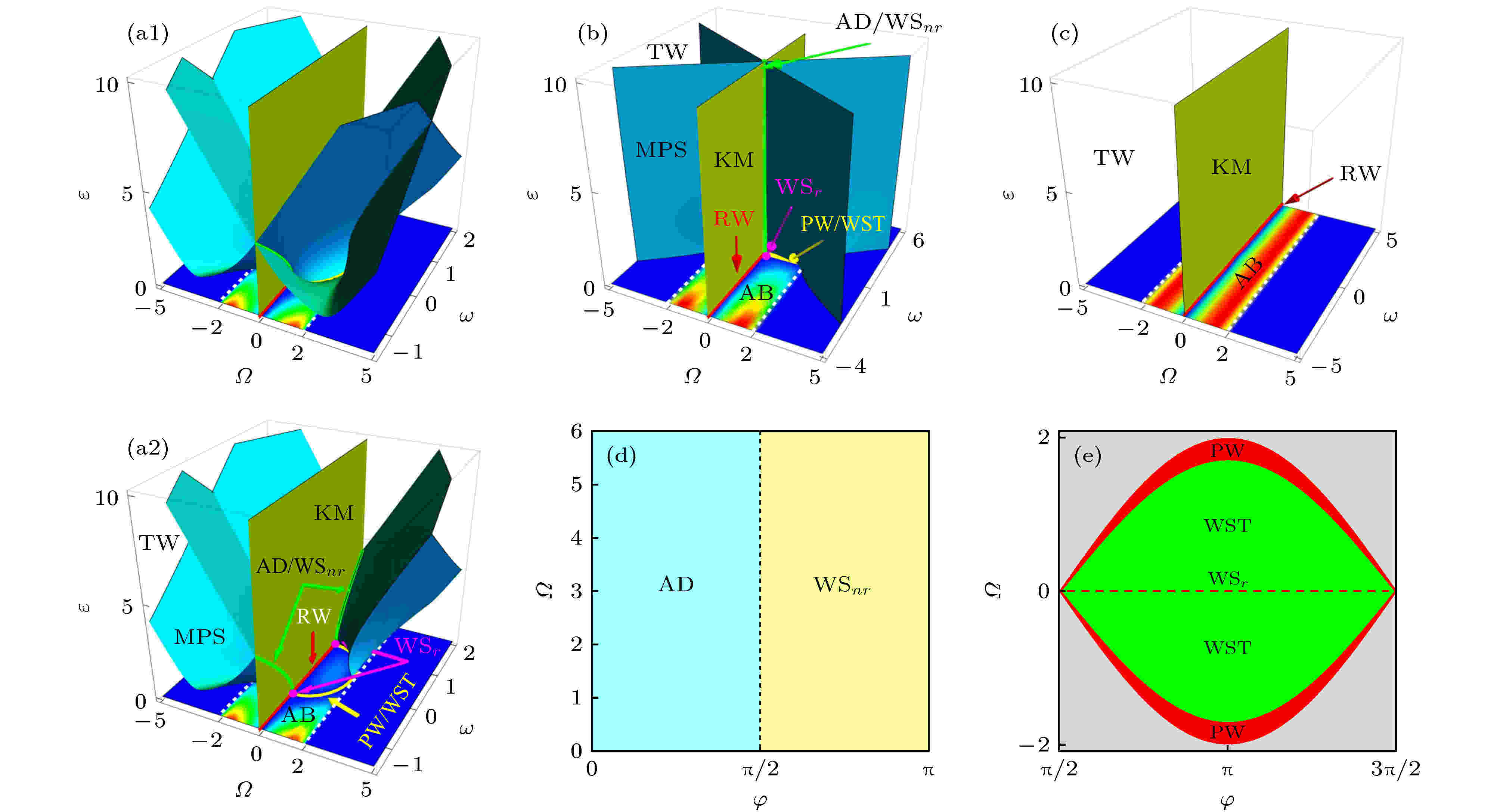 图 6 不同系统中平面波背景上基本非线性波在背景频率
图 6 不同系统中平面波背景上基本非线性波在背景频率




















































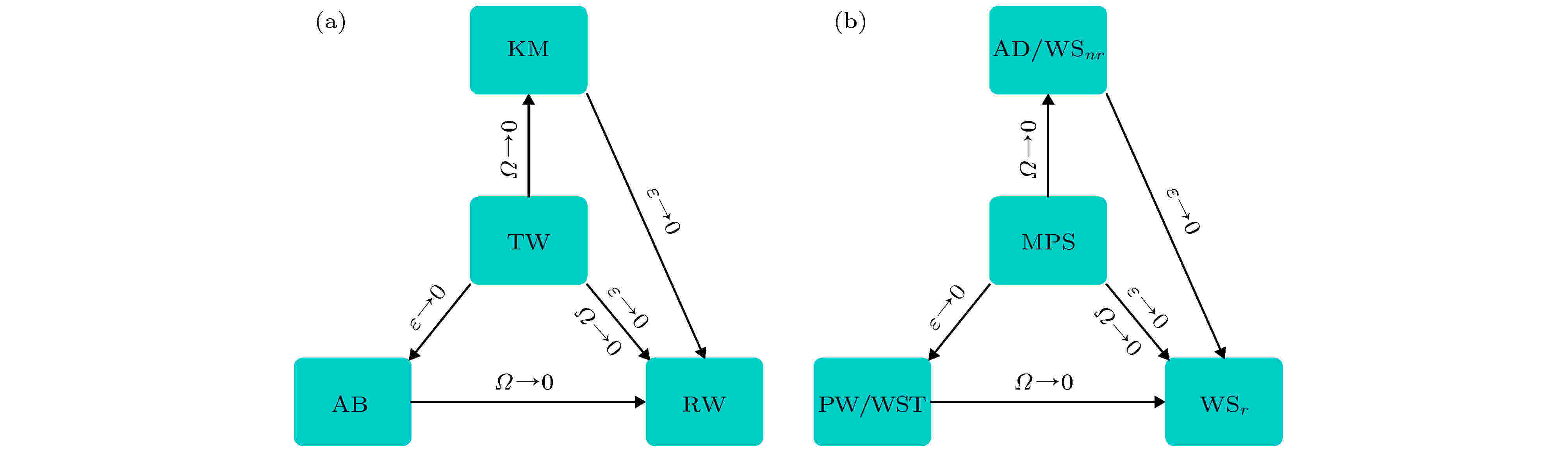 图 7 不同非线性波的转换关系 (a) 呼吸子和怪波之间的转换关系; (b) 孤子和周期波之间的转换关系. 图中“TW”, “KM”, “AB”, “RW”分别为Tajiri-Watanabe呼吸子、Kuznetsov-Ma呼吸子、Akhmediev呼吸子和怪波, “MPS”, “AD”, “WS
图 7 不同非线性波的转换关系 (a) 呼吸子和怪波之间的转换关系; (b) 孤子和周期波之间的转换关系. 图中“TW”, “KM”, “AB”, “RW”分别为Tajiri-Watanabe呼吸子、Kuznetsov-Ma呼吸子、Akhmediev呼吸子和怪波, “MPS”, “AD”, “WS



