摘要: 波的传播往往在复杂的地质结构中进行, 如何有效地求解非均匀介质中的波动方程一直是研究的热点. 本文将局部间断Galekin(local discontinuous Galerkin, LDG)方法引入到数值求解波动方程中. 首先引入辅助变量, 将二阶波动方程写成一阶偏微分方程组, 然后对相应的线性化波动方程和伴随方程构造间断Galerkin格式; 为了保证离散格式满足能量守恒, 在单元边界上选取广义交替数值通量, 理论证明该方法满足能量守恒性. 在时间离散上, 采用指数积分因子方法, 为了提高计算效率, 应用Krylov子空间方法近似指数矩阵与向量的乘积. 数值实验中给出了带有精确解的算例, 验证了LDG方法的数值精度和能量守恒性; 此外, 也考虑了非均匀介质和复杂计算区域的计算, 结果表明LDG方法适合模拟具有复杂结构和多尺度结构介质中的传播.
关键词: 波动方程 /
广义交替数值通量 /
局部间断Galerkin方法 /
能量守恒 English Abstract Two-dimensional wave equation solved by generalized alternating flux based local discontinuous Galerkin method Zhang Rong-Pei 1 ,Wang Di 1 ,Yu Xi-Jun 2 ,Wen Xue-Bing 1 1.College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11571002), the Key Laboratory fund of national defense science and technology, China (Grant No. 6142A050202717), Natural Science Foundation of Liaoning Province, China (Grant No. 20180550996), and the Science Foundation of China Academy of Engineering Physics (Grant Nos. 2013A0202011, 2015B0101021)Received Date: 24 April 2019Accepted Date: 17 October 2019Available Online: 01 January 2020Published Online: 20 January 2020Abstract: The wave propagation is often carried out in complex geological structures. Solving the wave propagation problem effectively in inhomogeneous medium is of great interest and has many applications in physics and engineering. In this paper, the local discontinuous Galekin (LDG) method is applied to the numerical solution of the second-order wave equation. Firstly, the auxiliary variables are introduced, and the second-order wave equations are written as a system of first-order partial differential equations. Then the discontinuous Galerkin format is applied to the corresponding linearized wave equations and adjoint equations. We consider the triangulation in this paper. In order to ensure that the discrete format satisfies the energy conservation, the generalized alternating flux is chosen on the element boundary. We proves that the LDG method satisfies the energy conservation. The exponential integral factor method is used in time discretization. In order to improve the computational efficiency, the Krylov subspace method is used to approximate the product of the exponential matrix and the vector. Numerical examples with exact solutions are given in numerical experiments. The numerical results verify the numerical precision and energy conservation of the LDG method. In addition, the calculation of inhomogeneous medium and complex computational regions are considered. The results show that the LDG method is suitable for simulation of complex structures and propagation in multi-scale structured medium.Keywords: wave equation /generalized alternating /local discontinuous Galerkin method /energy conservation 全文HTML --> --> --> 1.引 言 波的传播是能量传输的一种基本形式, 出现在许多科学、工程和工业领域. 波动传播问题的研究对地球科学、石油工程、电信和国防工业具有重要意义[1 -4 ] . 波动方程是描述波传播的数学模型, 例如声波方程、地震波方程等. 本文考虑如下二维非均匀介质下的二阶波动方程. 由于所求解的区域比较复杂, 以及传播介质的复杂和不均匀性, 大多数波动方程不能精确求解, 对于波动方程数值方法的研究就显得非常重要.[5 ,6 ] 、 有限体积方法(finite volume method, FVM)[7 ] 和有限元方法(finite element method, FEM)[8 ] 等. 局部间断Galerkin (local discontinuous Galerkin, LDG)方法是Cockburn和舒其望[9 ] 在1998年提出的. 与传统的间断Galerkin (discontinuous Galerkin, DG)方法[10 ] 比较, LDG方法通过引入辅助变量将含有高阶导数的微分方程写成只含有一阶导数的偏微分方程组, 然后用DG方法进行空间离散. Chung和Engquist[11 ] 在交错三角网格上提出了能量守恒的DG格式, 但是交错网格在高维情形格式构造复杂. Chou等[12 ] 发展了一类能量守恒的LDG方法求解二维非均匀介质中的线性二阶波动方程, 但是他们的工作只限于矩形网格. 本文将在三角网格上构造能量守恒的LDG格式. 首先将二阶标量波动方程写成一阶速度-应力形式, 通过选取广义交替数值通量, 对相应的线性化波动方程和伴随方程构造DG格式. 对于高维问题, 空间离散后得到的是一组规模非常大的常微分方程组. 显式时间离散格式不需要求解代数方程组, 但是时间步长有严格的限制; 隐式时间离散允许比较大的时间步长, 但是需要求解大规模代数方程组. 本文采用指数积分因子方法求解常微分方程组, 该方法是在2013年由Nie等[13 ] 提出的求解刚性常微分方程组的有效数值方法. 隐式积分因子方法的发展分为两个方向: 其一是紧致隐积分因子格式[14 ,15 ] , 该格式将解写成矩阵形式并在每个方向计算指数矩阵; 其二是Krylov积分因子格式[16 ] , 该格式针对指数矩阵与向量的乘积运算, 应用Krylov子空间方法近似.2.局部间断有限元方法 在二维区域$\varOmega $ 求解如下二阶波动方程:u 是位移; ρ 是物体的密度; A 是波速, 本文取常数; $f\left( {x, y, t} \right)$ 是外部源力项. 引入两个辅助变量: ${{p}} = A\nabla u$ , $w = {u_t}$ , (1 )式可写成如下的等价一阶偏微分方程组:$u = 0$ , $\left( {x, y} \right) \in $ $ \partial \varOmega \times \left[ {0, T} \right]$ . 所对应的初始条件为: $u\left( {x, y, 0} \right) =$ $ {u_0}\left( {x, y} \right) $ , $p\left( {x, y, 0} \right) = {p_0}\left( {x, y} \right)$ , $\forall \left( {x, y} \right) \in \varOmega $ . 当$f = 0$ 时, 系统(2 )和(3 )式具有能量守恒性:2 )和(3 )式构造LDG格式. 首先将二维计算域Ω 离散为有限个三角形单元${\varGamma _h} = \{ K\} $ , 用${\varepsilon _h} = \varepsilon _h^0 \cup \partial \varOmega $ 表示${\varGamma _h}$ 的所有边界的集合, 其中$\varepsilon _h^0$ 是所有内部边缘的集合. 定义LDG近似空间为${P^k}\left( K \right)$ 是单元K 和$\varSigma \left( K \right) = {\left[ {{P^k}\left( K \right)} \right]^2}$ 上最高次数为k 的复多项式函数的空间. LDG近似空间的离散${L^2}$ 范数定义如下:e 上定义平均值和跳跃项: 令$e \in \varepsilon _h^0$ 是单元${K_1}$ 和${K_2}$ 共享的内部边缘, 假设e 上的法向量${{{n}}_{\rm{1}}}$ 和${{{n}}_2}$ 分别指向${K_1}$ 和${K_2}$ 的外部, 借助于两个迹函数${v_i}: = {\left. v \right|_{\partial K}}$ , $i = 1, 2$ , e 上的平均值和跳跃项可定义为q v 的跳跃项$\left[ v \right]$ 是与法线平行的向量, 向量函数q $\left[ {{q}} \right]$ 是标量. 由于讨论的是齐次Dirichlet边界条件, 即在$\partial \varOmega $ 上时, $u = 0$ . 因此对于这种边界条件, 将$\left[ v \right]$ 和$\{ {{q}}\}$ 设为$\left[ v \right] = v{{n}}$ , $\{ {{q}}\} = {{q}}$ , 其中n 2.1.LDG方法 2.1.LDG方法 在(2 )式和(3 )式两侧同时乘以试探函数${v_h}, {{{q}}_{h} }$ , 并在每个单元上进行积分, 通过分部积分可以得到问题(2 )式和(3 )式的LDG格式, 即找到${w_h} \in {V_h}$ , ${{{p}}_{h} } \in {\varSigma_h}$ , 使得任意试探函数${v_h}, {{q}}$ , 对所有的$K \in {\varGamma _h}$ 满足${\hat w_h}$ 和${{\hat{ p}}_h}$ 是数值通量, 分别是单元K 边界上作为w 和${{p}} = \nabla u$ 的近似值的单个值. 数值通量的选择是保证LDG方法具有离散能量守恒的关键. 本文考虑如下形式的交替数值通量:2.2.能量守恒性 -->2.2.能量守恒性 在构建二维波动方程的数值方法时, 能量守恒通常被考虑在内. 数值方法是否能够保持能量守恒可以判断该方法是否能更好地模拟长时间的波传播. 本节证明LDG方法可以保持能量守恒. 考虑到数值通量(10 )式和(11 )式的定义, 在所有单元上对(8 )式和(9 )式求和可得12 )式和(13 )式左右两端分别求和, 可得12 )式和(13 )式的能量守恒性, 首先证明如下引理.引理 对于所有的试探函数$v \in {V_h} \cap H_1^0$ , ${{q}} \in {\varSigma_h}$ ,证明 对(15 )式左端项进行分部积分可得10 )式和(11 )式代入(15 )式右端项得到15 )式成立.8 )式和(9 )式的能量守恒性.定理 (能量守恒性) 在齐次Dirichlet边界条件和数值通量(10 )式和(11 )式的定义下, 系统(8 )式和(9 )式是能量守恒的, 即当$f = 0$ 时,证明 选取试探函数${v_h} = {w_h}$ 代入(8 )式中可得到9 )式中, 选取试探函数${{{q}}_{h} } = {{{p}}_{h} }$ , 能够得到19 )式和(20 )式左右两边分别求和, 并考虑到(15 )式, 可得到$f = 0$ 时, 显然有$\dfrac{{\rm{d}}}{{{\rm{d}}t}}\left( {\dfrac{1}{A}{{\left\| {\left| {{{{p}}_{h} }} \right|} \right\|}^2} + \rho {{\left\| {\left| {{w_h}} \right|} \right\|}^2}} \right) = 0$ , 即系统(8 )和(9 )是能量守恒的.3.时间离散 二维波动方程通过LDG方法进行空间离散后, 与一维二阶波动方相类似, 也得到一组非线性常微分方程组, 为了节约这种复杂代数方程组求解的计算成本, 本文利用指数积分因子方法来进行时间离散.8 )式和(9 )式对于所有单元联立, 可得到全局非线性常微分方程组的矩阵方程形式, 即${{W}} = {\left( {{w_1}, {w_2}, \cdots, {w_J}} \right)^{\rm{T}}}$ 和${{P}} = \left( {{p_1}, {p_2}, \cdots {p_J}} \right)$ 是所有单元上的自由度, ${w_j}$ 和${p_j}$ 表示在第j 个单元上的自由度, ${{{M}}_1}$ 是由$3 \times 3$ 矩阵组成的对角分块矩阵, ${{{M}}_2}$ 为$6 \times 6$ 矩阵组成的对角分块矩阵, 其逆矩阵容易求解. 将(22 )式和(23 )式进一步写成如下形式:${{V}} = \left[ {\begin{aligned} {{W}} \\ {{P}} \end{aligned}} \right]$ , ${{B}} = \left[\!\!\!{\begin{array}{*{20}{c}} 0&{{\rho ^{ - 1}}{{M}}_1^{^{ - 1}}{{{B}}_1}} \\ {{{AM}}_2^{^{ - 1}}{{{B}}_2}}&0 \end{array}}\!\!\!\right]$ , ${{F}} = \left[\!\!\!{\begin{array}{*{20}{c}} {{\rho ^{ - 1}}{{M}}_1^{ - 1}{{{F}}_1}} \\ 0 \end{array}}\!\!\! \right]$ . 假设最后的时间$t = T$ , 在时间方向上做一致剖分: $0 = {t_0} < {t_1} < \cdots < {t_n} < \cdots $ , 定义时间步长为$\Delta t\!=\! {T}/{N}$ , ${t_n} = n\vartriangle t$ , $0 \leqslant n \leqslant N$ .24 )式两端同乘积分因子${{\rm{e}}^{ - {{B}}t}}$ , 关于时间${t_n}$ 到${t_{n + 1}}$ 进行积分, 可得25 )式中的积分, 得到二阶指数积分因子格式:[16 ] .4.数值算例 首先给出带有精确解的波动方程测试方法的精度和能量守恒性, 然后应用LDG方法求解波的传播问题. 第二个算例是求解非均匀介质介质中波的传播问题, 第三个算例是L形区域中波的传播问题. 在下面的计算中, 考虑线性元, 边界条件为齐次Dirichlet边界, ${{A}} = {{I}}$ 是单位矩阵, f (x , y , t ) = 0.算例1 考虑具有常系数的二维波动方程${u_{tt}} = {\nabla ^2}u$ , $\left( {x, y} \right) \!\in \!\left[ {0, 2} \right] \!\times \!\left[ {0, 2} \right]$ , 初始条件为$u(x, y, 0) \!$ $ ={\rm{sin}}\left( {{\text{π}}x} \right){\rm{sin}}\left( {{\text{π}}y} \right) $ , ${u_t}\left( {x, y, 0} \right) = 0$ , 这个问题的精确解为$u\left( {x, y, t} \right) = {\rm{cos}}\left( {\sqrt 2 {\text{π}}t} \right){\rm{sin}}\left( {{\text{π}}x} \right){\rm{sin}}\left( {{\text{π}}y} \right)$ . 时间步长取$\Delta t = 0.001$ , 表1 列出了网格数分别为16 × 16, 32 × 32, 64 × 648和$ 128 \times 12$ 时数值解${w_h}$ 和p w 的精度接近2, p 网格数 w 的误差p ${L^2}$范数下误差 收敛阶 ${L^2}$范数下误差 收敛阶 $8 \times 8$ 2.80 × 10–2 — 6.63× 10–2 — $16 \times 16$ 5.75 × 10–3 2.28 3.40× 10–2 0.96 $32 \times 32$ 1.64 × 10–3 1.81 1.70× 10–2 1.00 $64 \times 64$ 4.62 × 10–4 1.83 8.56× 10–3 0.99 $128 \times 128$ 9.20 × 10–5 2.32 4.30 × 10–3 0.99
表1 数值解${w_h}$ 和p Table1. Error and convergence order of numerical solution ${w_h}$ and p 算例2 考虑波动方程(1 )在单位正方形${{\varOmega }} = {\left[ {0, 1} \right]^2}$ 上的传播, 将其剖分为$64 \times 64$ 个均匀大小的正方形, 然后使用一个对角线将每个正方形细分为两个三角形, 如图1(a) 所示. 本算例考虑非均匀介质, 密度函数ρ 定义为图 1 (a)算例2的网格剖分和数值解${w_h}$ 在不同时刻(b) $t = 0.2$ , (c) $t = 0.{\rm{3}}$ , (d) $t = 0.{\rm{4}}$ 时的波传播Figure1. (a) The triangulation mesh of Example 2; contour plot of solution ${w_h}$ at different time: (b) $t = 0.2$ ; (c) $t = 0.{\rm{3}}$ ; (d) $t = 0.{\rm{4}}$ .$w_0(x, y) \!=\! 2\exp[ - 500(x \!-\! 0.5)^2 \!+\! (y \!-\! 0.5 )^2],$ ${{{p}}_0}\left( {x, y} \right) = 0$ . 图2 给出了数值解${w_h}$ 在时间$t =$ 0.2, 0.3, 0.4时的等高线, 可以看出, 波大约在$t = 0.3$ 时触及界面$x = 0.65$ , 在那之后, 波以更快的速度通过界面. 这说明传播系数不同会导致波的传播速度不同. 同时也给出离散能量的时间演变图(图2 ). 从图2 中可以发现, LDG方法可以保证能量守恒.图 2 算例2的能量随时间的演化Figure2. Energy evolution with time for Example 2.算例3 考虑圆形波在L形区域$ \varOmega = $ $ {\left[ {0, 1} \right]^2}\backslash {[0.7, 1]^2}$ 上的传播, 初始条件同算例2. 采用非一致三角剖分将其剖分为13578个三角单元, 如图3(a) 所示. 数值解${w_h}$ 在t = 0.1, 0.3和0.45的波形传播图在图3(b) —(d) 给出. 从图3 可以看出, 波在t = 0.3时刻到达了拐角点. 在此之后, 波反射得到另外一个圆形波. 通过与文献[11 ]比较, 发现本文的数值结果与其数值结果是吻合的.图 3 (a)算例3的网格剖分和数值解${w_h}$ 在不同时刻 (b) $t = 0.{\rm{1}}$ , (c) $t = 0.{\rm{3}}$ , (d) $t = 0.{\rm{45}}$ 时的波传播Figure3. (a) The triangulation mesh of Example 3; contour plot of solution ${w_h}$ at different time: (b) $t = 0.{\rm{1}}$ ; (c) $t = 0.{\rm{3}}$ ; (d) $t = 0.{\rm{45}}$ .5.结 论 研究了二阶波动方程在二维计算区域的传播问题, 通过选取广义交替数值通量, 建立了LDG方法并分析了格式的能量守恒性. 时间离散上利用指数积分因子方法. 数值实验验证了能量守恒性质和最优误差收敛阶. 下一步的工作考虑将守恒的LDG格式应用到求解非线性波动方程, 例如Sine-Gordon等方程上. 

























































































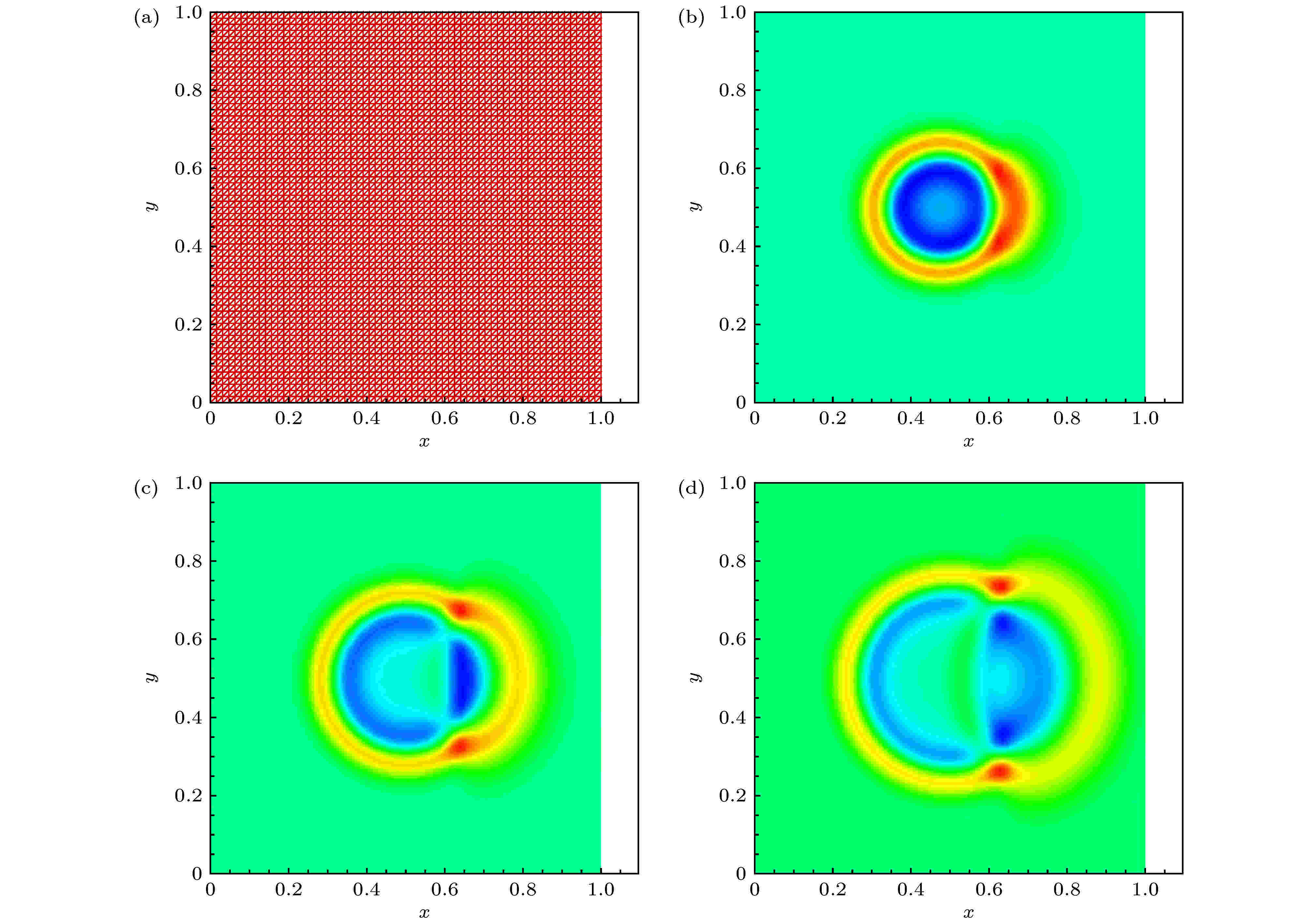 图 1 (a)算例2的网格剖分和数值解
图 1 (a)算例2的网格剖分和数值解













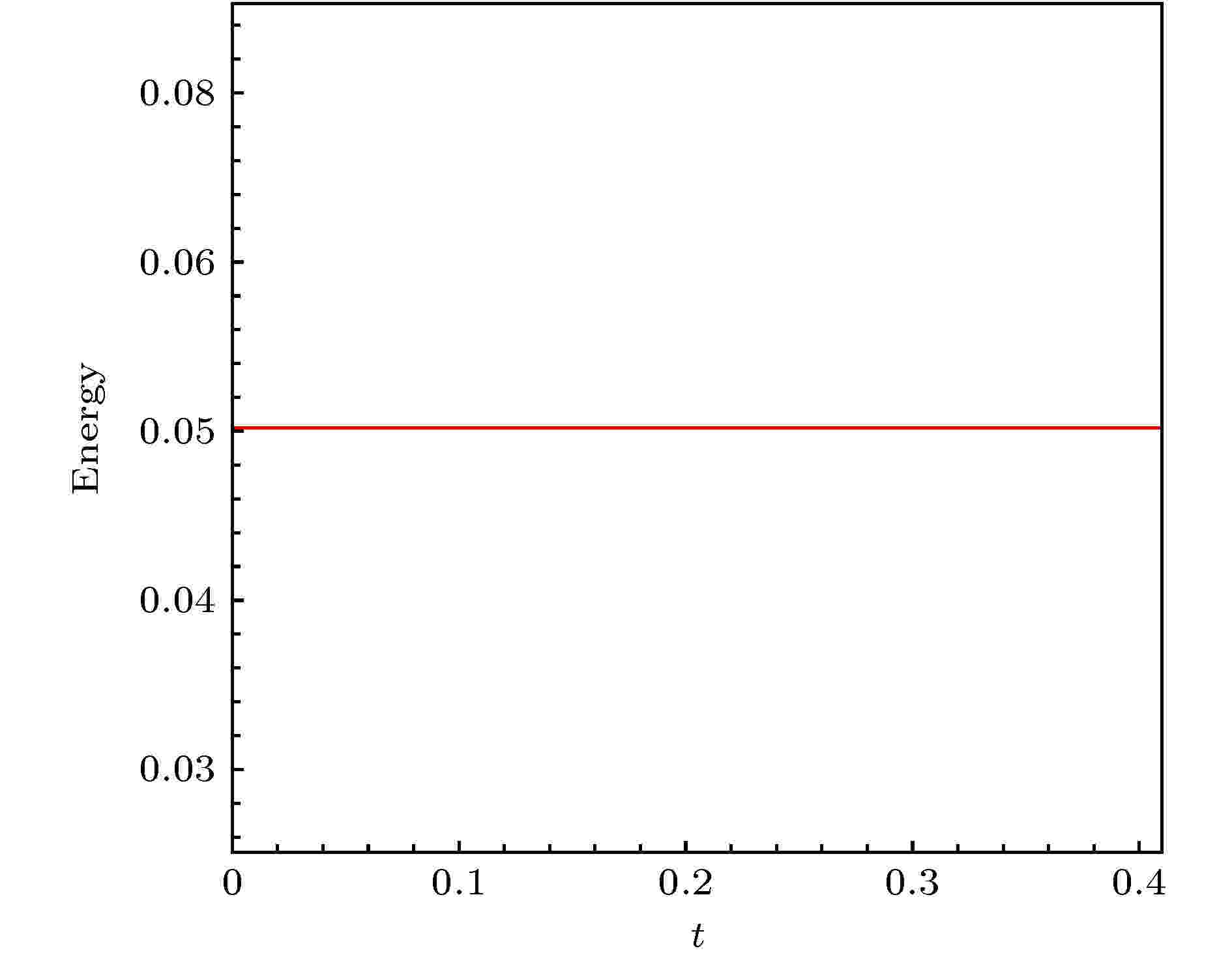 图 2 算例2的能量随时间的演化
图 2 算例2的能量随时间的演化


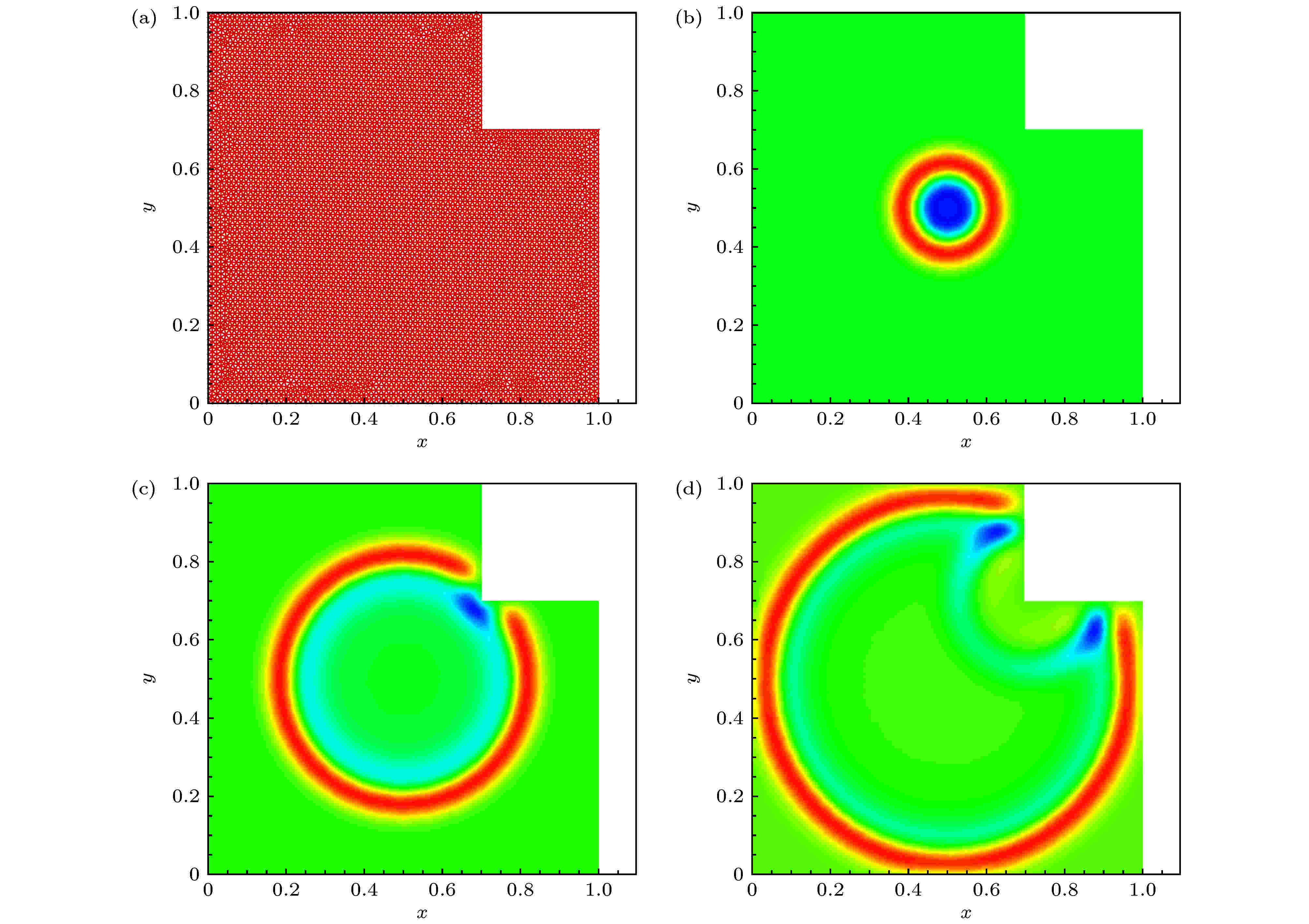 图 3 (a)算例3的网格剖分和数值解
图 3 (a)算例3的网格剖分和数值解







