摘要:本文研究了由超表面-介质间隔层-分布式布拉格反射器(distributed Bragg reflector, DBR)构成的等离激元微腔结构中的Tamm等离激元及其与激子间的相互作用. 利用超表面中的结构参数变化能够调控光在其表面的反射位相这一特性, 可以在微腔结构的介质间隔层厚度保持不变时, 通过调节超表面的结构参数来调控微腔结构所支持的Tamm等离激元模式的共振位置, 从而为Tamm等离激元模式的调控提供更多自由度. 相比于传统金属薄膜-介质间隔层-DBR结构, 我们发现超表面的引入及其对反射位相的调控可以使超表面-介质间隔层-DBR结构在更小的间隔层厚度下支持共振在相同波长处的Tamm等离激元模式. 此外, 结合超表面对场的局域特性, 可以有效地降低Tamm等离激元模式体积. 在此基础上, 对比研究了传统的和基于超表面的Tamm等离激元与单层二硫化钨(WS₂)的相互作用, 发现基于超表面的Tamm等离激元可以产生更强的光子与激子的强耦合作用, 获得更大的拉比(Rabi)劈裂.
关键词: 表面等离激元/
超表面/
二维材料/
强耦合

English Abstract

全文HTML

--> --> -->

金属微纳结构能够支持表面等离激元共振模式, 具有超衍射极限的光场局域特性, 能够使得其周围的局域电场和光子局域态密度得到极大的增强^[1,2], 导致光与物质相互作用的有效距离或时间显著增加. 利用这一特性可以提高生物传感器的灵敏度^[3]、分子的荧光辐射强度^[4]、单光子产出率^[5]以及拉曼散射信号^[6]等. 近年来, 借助金属微纳结构中等离激元模式的超强光场局域, 并利用受限光子与激子的强耦合相互作用获得兼具光子与激子优点的新的准粒子, 已逐渐成为国内外的研究热点之一. 目前, 人们已经在诸多体系中实现了等离激元极化子和荧光分子、量子点、半导体、量子阱、二硫化钨(WS₂)等材料的激子之间的强相互作用. 如传播的等离激元模式的金属结构^[7]、局域等离激元共振的金属颗粒^[8]、法诺等离激元共振的金属颗粒阵列或多聚体^[9-12]、法布里-珀罗(Fabry-Perot)模式的金属薄膜-介质层-金属薄膜微腔^[13-15]以及Tamm等离激元模式的金属薄膜-分布式布拉格反射器(DBR)结构^[16,17]等.
超表面(Metasurface, MS), 即由厚度仅在波长量级甚至更薄的亚波长“人工原子”结构单元, 按照特定排列方式构成的一种平面型超构材料^[18]. 基于惠更斯子波原理, 调控超表面中结构单元的共振响应的相对相位, 引入横向的空间渐变相位可以产生光涡旋等光束整形效应^[19]. 除了用来对光波的相位进行操控, 精心设计的超表面还能控制光波的振幅和偏振态, 例如实现光波圆偏振态和线偏振态之间的相互转换^[18]、偏振方向的旋转^[20]以及任意偏振态的产生^[21]. 超表面对可见光乃至微波波段电磁波相位、振幅以及偏振的操控特性, 已经用于光线弯折^[19]、光束聚焦^[22]、光学全息^[23]、可见光宽带连续消色差透镜^[24]等. 文中采用的金属超表面-介质层-金属薄膜的超表面结构, 可调控光波前的位向控制光的偏振响应形成宽带矢量全息^[25], 光的自旋角动量形成光涡旋^[26].
本文研究了由金属光栅-介质层-金属薄膜构成的超表面的光学特性, 发现超表面结构中的光栅宽度和介质层厚度的变化, 能够引起其所支持的间隙等离激元模式共振位置变化, 进而改变超表面结构的表面反射位相. 我们将这一超表面结构引入Tamm等离激元微腔中, 替换其中的平整金属薄膜, 通过改变超表面的结构参数来调谐Tamm等离激元模式的共振位置, 为Tamm等离激元微腔的调控提供了一个新的自由度. 相比于常规的由金属薄膜-间隔层-DBR构成的Tamm等离激元微腔, 超表面-间隔层-DBR结构可以在更薄的间隔层条件下支持在相同波长处共振的Tamm等离激元模式. 我们发现金属光栅对电场的局域特性可以有效降低Tamm等离激元的模式体积, 相比常规的金属薄膜-间隔层-DBR结构可以产生更强的光子与激子的强耦合作用.

2

-->

2.1.超表面模型及分析

首先研究如图1(a)所示的银光栅-氧化铝介质层-银薄膜构成的超表面的光学性质. 银薄膜厚度、银光栅周期和厚度固定为t = 30 nm, p = 150 nm和d = 10 nm, 研究银光栅宽度w和氧化铝层厚度h这两个结构参数变化对超表面反射特性的影响. 采用多物理场有限元软件(Comsol Multiphysics)对该结构的光学反射特性进行模拟计算. 在计算中, 入射平面波的电场方向垂直于光栅极化方向, 氧化铝、衬底以及包覆介质的折射率分别设为: n _g = 1.7, n _s = 1.45和n _c = 1.45. 金属银的介电常数采用Drude模型${\varepsilon _{{\rm{Ag}}}}(\omega ) = {\varepsilon _0} - \dfrac{{\omega _{\rm{p}}^2}}{{{\omega ^2} + {\rm{i}}\gamma \omega }}$来描述, 其中ε₀ = 1, $\hbar \omega_p $ = 9.6 eV, $\hbar\gamma$ = 0.0228 eV^[27].
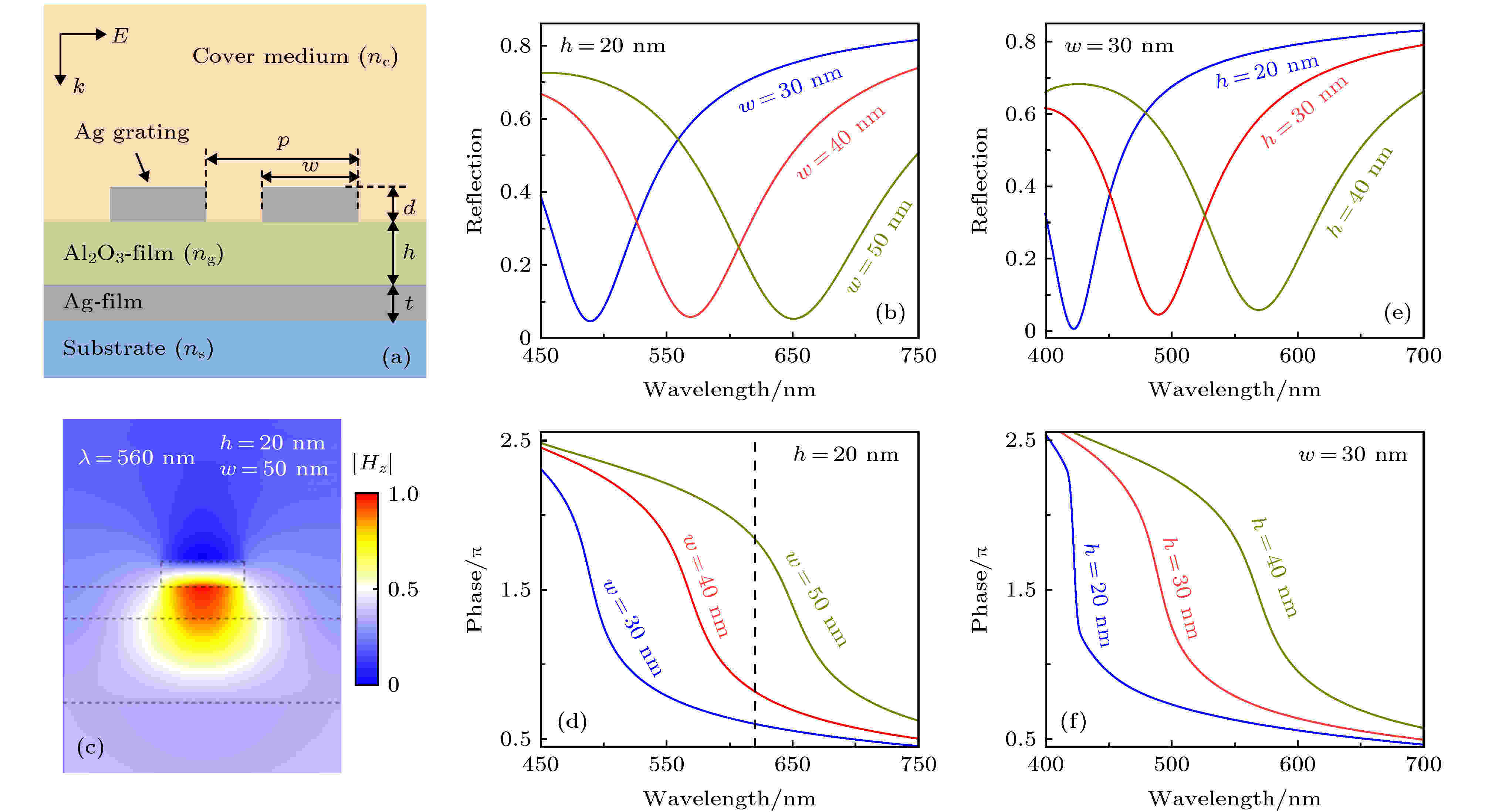图 1 (a)银光栅-氧化铝介质层-银薄膜构成的超表面结构示意图, 其中银薄膜厚度、银光栅周期和厚度分别固定为t = 30 nm, p = 150 nm和d = 10 nm; (b), (d)氧化铝层厚度h = 20 nm银光栅同宽度时超表面的反射谱和反射位相; (c)光栅宽度w = 50 nm和氧化铝层厚度h = 20 nm的超表面在共振时的磁场分布图; (e), (f)银光栅宽度w = 30 nm氧化铝层厚度不同时超表面的反射谱和反射位相
Figure1. (a) A schematic diagram of metasurface consisting of silver grating, alumina dielectric layer and silver film, in which the thickness of silver film, the period and thickness of silver grating are fixed at t = 30 nm, P = 150 nm and d = 10 nm, respectively; (b), (d) the thickness of alumina layer is h = 20 nm, and the reflection spectrum and phase of metasurface at different width of silver grating; (c) the magnetic field distribution of metasurface at resonance with grating width w = 50 nm and alumina layer thickness h = 20 nm; (e), (f) with grating width w = 30 nm and different thickness of alumina layer have reflected spectra and phases on the metasurface.

图1(b)显示了由氧化铝层厚度为h = 20 nm和不同宽度的银光栅构成的超表面的反射谱, 反射谷随着光栅宽度增加而发生红移. 例如, 在光栅宽度从w = 30 nm增加到w = 50 nm时, 反射谷从490 nm红移到650 nm处. 为了表征反射谷所对应的共振模式的特性, 图1(c)为光栅宽度为w = 50 nm和氧化铝层厚度为h = 20 nm的超表面在反射谷650 nm处的磁场分布, 可以看到磁场局域在银光栅和银薄膜之间的氧化铝介质层, 这和典型的金属颗粒-介质薄膜-金属膜所支持的间隙等离激元模式的场分布相一致^[28]. 图1(d)是超表面结构的表面反射位相随波长的变化关系: 反射位相在超表面结构的间隙等离激元共振波长附近变化较为陡峭, 在偏离共振处反射位相的变化相对平缓. 如图1(d)中竖直黑色虚线所示, 对于某一特定波长, 例如620 nm, 超表面结构的反射位相随着银光栅宽度的变化而变化. 此外, 图1(e)和图1(f)是银光栅宽度固定为w = 30 nm并改变超表面结构中氧化铝层的厚度时反射谱和相应的表面反射位相随波长的变化关系, 与图1(b)和图1(d)的结论类似: 随着氧化铝层厚度的变化, 间隙等离激元共振波长会发生移动. 可以通过改变氧化铝层的厚度来调谐某一特定波长处的反射位相.
2 -->

2.2.超表面-介质间隔层-DBR构成的Tamm等离激元微腔模型及分析

图2(a)为由超表面-介质间隔层-DBR构成的等离激元微腔的光学特性. DBR由N = 8对折射率为n _a = 1.45的二氧化硅和折射率为n _b = 2.4的二氧化钛介质层的一维周期结构组成. 其中二氧化硅层的厚度设为d _a = 600/4/1.45 = 103.45 nm, 二氧化钛层的厚度设为d _b = 600/4/2.4 = 62.5 nm, DBR的禁带中心波长为600 nm. 在常规的由金属薄膜-介质间隔层-DBR组成的Tamm等离激元微腔中, 共振波长为λ的Tamm等离激元模式的激发需要满足光在腔内往返的总位相φ_total是2π整数倍的条件^[29], 即:
图 2 (a)由超表面-介质间隔层-DBR构成的Tamm等离激元微腔结构示意图. DBR由8对二氧化硅和二氧化钛多层介质膜组成, 其中二氧化硅和二氧化钛的折射率为n _a = 1.45和n _b = 2.4, 厚度为d _a = 103.5 nm和d _b = 62.5 nm; 介质间隔层厚度为l, 折射率与图1(a)中超表面结构的包覆层折射率相同, 超表面的结构参数与图1(a)中所展示的相同. φ_DBR和φ_metal分别是光在DBR的表面和超表面结构的表面反射引起的位相变化, φ _prop代表光在介质间隔层中的传播位相; (b)固定介质间隔层厚度为l = 10 nm, 超表面中氧化铝层厚度为h = 40 nm, 银光栅宽度为w = 10 nm和50 nm两种情况下所获得的φ_ms以及φ_DBR, φ_prop, 总位相φ_total随波长的变化关系. 水平虚线代表相位为0; (c) l = 10 nm, h = 40 nm以及w = 10 nm和50 nm条件下的超表面-介质间隔层-DBR结构的反射谱
Figure2. (a) A schematic diagram of the structure of a Tamm plasmon microcavity consisting of metasurface-dielectric spacer-DBR. DBR consists of 8 pairs of silica and titanium dioxide multilayer dielectric films, in which the refractive index of silica is n _a = 1.45, the refractive index of titanium dioxide is n _b = 2.4, and the thickness of silica and titanium dioxide in each layer is d _a = 103.5 nm and d _b = 62.5 nm. The thickness of the dielectric spacer is l, and the refractive index is the same as that of the cladding layer of the metasurface structure in Fig. 1(a). The structural parameters of the metasurface are the same as those shown in Fig. 1(a). The phase transitions of φ_DBR and φ_metal are caused by the reflection of light on the surface of DBR and metasurface structure respectively. φ_prop represents the phase of light propagating in the dielectric spacer; (b) the thickness of fixed dielectric spacer is l = 10 nm, the thickness of alumina layer in metasurface is h = 40 nm, and the width of silver grating is w = 10 nm and 50 nm. In both cases, the relationship between wavelength and the obtained φ_ms, φ_DBR, φ_prop and total phase φ_total is obtained. The horizontal dashed line represents the phase of 0; (c) reflectance spectra of metasurface-dielectric spacer-DBR structures at l = 10 nm, h = 40 nm and w = 10 nm and 50 nm.

${\varphi _{t{\rm{otal}}}} = {\varphi _{{\rm{prop}}}} + {\varphi _{{\rm{DBR}}}} + {\varphi _{{\rm{metal}}}} = 2m{\text{π}},$

其中φ_DBR和φ_metal分别是光在DBR表面和金属薄膜表面反射引起的位相变化, φ_prop = 4πnl/λ是光在折射率为n, 厚度为l的介质间隔层中的传播位相. 用超表面替代常规Tamm等离激元微腔结构中的金属薄膜后, (1)式中的φ_metal将由光在超表面结构的表面反射引起的位相变化φ_ms来替代, 此时Tamm等离激元模式激发所需满足的条件变为

${\varphi _{{\rm{total}}}} = {\varphi _{{\rm{prop}}}} + {\varphi _{{\rm{DBR}}}} + {\varphi _{{\rm{ms}}}} = 2m{\text{π}} .$

图2(b)中展示了在Tamm等离激元微腔的介质间隔层厚度为l = 10 nm, 超表面的氧化铝层厚度为h = 40 nm, 银光栅的宽度为w = 10 nm和50 nm时φ_DBR, φ_prop, φ_ms以及总位相φ_total随波长的变化关系. 由(2)式可知, 当满足φ_total = 0时, 最低阶的Tamm等离激元模式即可被激发; 在图2(b)中用一条水平虚线代表位相为0的位置与φ_total的交点所对应的波长即为Tamm等离激元模式的共振位置. 可以看到, 当银光栅的宽度为w = 10 nm时由(2)式给出的Tamm等离激元模式的共振波长约为579 nm; 银光栅的宽度为w = 50 nm时, Tamm等离激元模式的共振波长约为668 nm. 与此同时, 也计算了超表面-介质间隔层-DBR结构在l = 10 nm, h = 40 nm以及w = 10 nm和50 nm条件下的反射谱, 如图2(c)所示: 在w = 10 nm和50 nm时, 反射谷的位置分别位于580和670 nm处, 与利用(2)式的相位条件得到的结果一致.
2 -->

2.3.多个维度调控Tamm等离激元模式

进一步地, 我们又计算了在固定介质间隔层厚度为l = 10 nm和氧化铝介质层厚度为h = 30 nm时改变超表面中的银光栅宽度w, 以及固定l = 10 nm和w = 40 nm时改变超表面中的氧化铝层厚度h这两种情况下的超表面-介质间隔层-DBR结构的反射谱, 并将每种情况下的反射谷的位置总结在图3(a)中, 获得Tamm等离激元共振波长随超表面的结构参数w和h的变化关系. 为了便于比较, 也在图3(a)中画出了常规的金属薄膜-介质间隔层-DBR结构中Tamm等离激元共振波长随介质间隔层厚度l的变化关系. 可以看到, 在常规的金属薄膜-介质间隔层-DBR结构中, Tamm等离激元共振波长随着介质间隔层厚度l的增加而逐渐红移. 在有超表面存在的情况下, 固定介质间隔层厚度l = 10 nm和氧化铝介质层厚度h = 30 nm时, Tamm等离激元共振波长随着银光栅宽度的增加而逐渐红移. 相类似的, 当固定介质间隔层厚度l = 10 nm和银光栅宽度w = 40 nm时, Tamm等离激元共振波长随着氧化铝层厚度的增加而逐渐红移. 这就验证了这种具有超表面的Tamm等离激元微腔可以在介质间隔层厚度保持不变时通过调节超表面的结构参数φ_ms来调控Tamm等离激元模式的共振波长位置, 从而为Tamm等离激元模式的调控提供了更多自由度.
图 3 (a)金属薄膜-介质间隔层-DBR结构中Tamm等离激元模式的共振波长随介质间隔层厚度l的变化关系. 超表面-介质间隔层-DBR结构中固定介质间隔层厚度l = 10 nm和氧化铝层厚度h = 30 nm时Tamm等离激元模式共振波长随银光栅宽度w的变化关系以及l = 10 nm和w = 40 nm时Tamm等离激元模式的共振波长随氧化铝层厚度h的变化关系; (b)介质间隔层厚度固定为l = 10 nm时, 不同的氧化铝层厚度h和银光栅宽度w的参数组合情况下超表面-介质间隔层-DBR结构的反射光谱
Figure3. (a) The variation of Tamm plasmon mode wavelength with the thickness of dielectric spacer l in metal film-dielectric spacer-DBR structure, the variation of Tamm plasmon mode wavelength with the width of silver grating w when the thickness of fixed dielectric spacer l = 10 nm and alumina layer h = 30 nm in metasurface-dielectric spacer-DBR structure, and fixed l = 10 nm and w = 40 nm, the Tamm plasmon mode wavelength varies with the thickness of alumina layer h; (b) reflectance spectra of metasurface-dielectric spacer-DBR structure with different thickness of alumina and width of silver grating w when the thickness of dielectric spacer is fixed at l = 10 nm.

从图3(a)中可以看到在超表面-介质间隔层-DBR结构中, 单独增加超表面的两种结构参数即氧化铝层厚度h和银光栅宽度w, Tamm等离激元的共振波长都会随之单调增加. 这就使得我们可以通过增加其中一个结构参数而减小另一个参数, 使具有不同参数组合的超表面-介质间隔层-DBR结构能够支持在同一波长共振的Tamm等离激元. 图3(b)为不同的参数组合情况下超表面-介质间隔层-DBR结构的反射谱: 在固定介质间隔层厚度为l = 10 nm时逐渐增加氧化铝层厚度从h = 20 nm到h = 60 nm, 同时相应地缩小银光栅宽度从w = 41.6 nm到w = 5 nm, 这些结构所支持的Tamm等离激元共振都位于620 nm处. 同时从图3(b)中可以看到, 对于不同的参数组合, Tamm等离激元在反射谱中的强度和模式线宽也是不同的: 采用较厚的氧化铝层和较窄的银光栅时, Tamm等离激元模式的线宽更窄, 同时在Tamm等离激元共振位置的反射率更低. 这种对模式激发强度和线宽的调控特性使得集成了超表面的Tamm等离激元微腔结构可以更好地适用于不同场合.
2 -->

2.4.多个维度调控Tamm等离激元模式

接下去对比研究了由金属薄膜-介质间隔层-DBR构成以及集成了超表面的两种Tamm等离激元微腔的光学特性. 首先计算了两种Tamm等离激元微腔结构的反射和吸收谱, 如图4(a)和图4(b)所示. 可以看出, 在由金属薄膜-介质间隔层-DBR构成的微腔中, 当介质间隔层的厚度为l = 92.5 nm时, 其所支持的Tamm等离激元模式的共振波长可以调谐到620 nm处; 在集成了超表面的微腔结构中, 当氧化铝层厚度为h = 40 nm, 银光栅厚度为w = 36 nm时, 介质间隔层的厚度仅需l = 10 nm, 其所支持的Tamm等离激元模式共振波长就可以调谐到620 nm处.
图 4 (a)和(b)分别为共振波长位于620 nm的常规金属薄膜-介质间隔层-DBR结构和超表面-介质间隔层-DBR结构的反射谱和吸收谱; (c)和(d)分别为有超表面的和常规的Tamm等离激元微腔结构所支持的Tamm等离激元模式的电场分布图. 左侧为结构示意图, 水平虚线代表二维激子材料在结构中放置的位置; (e)和(f)分别为两种Tamm等离激元微腔中加入二维激子材料后的反射谱和吸收谱
Figure4. (a) and (b) are the reflection and absorption spectra of the conventional metal film-dielectric spacer-DBR structure and the metasurface-dielectric spacer-DBR structure with resonant wavelength at 620 nm, respectively; (c) and (d) electric field distributions of Tamm plasmon modes supported by metasurface and conventional Tamm plasmon microcavities, respectively. On the left is a structural sketch. The horizontal dashed line represents the position of the two-dimensional exciton material in the structure; (e) and (f) are the reflection and absorption spectra of two kinds of Tamm plasmon microcavities with two-dimensional exciton materials.

图4(c)和图4(d)分别展示了集成有超表面的和常规的无超表面的微腔结构所支持的Tamm等离激元共振模式的电场分布图. 为了更清楚地展示在介质间隔层附近分布的电场, 由8对二氧化硅和二氧化钛周期结构组成的DBR结构在图中展示了最靠近介质间隔层的1对周期. 对比图4(c)和图4(d)可见: 常规的无超表面的微腔结构中Tamm等离激元激发时电场局域在介质间隔层和临近的DBR二氧化硅层, 最大电场增强位于两者分界面上; 在集成有超表面的微腔结构中, 电场主要分布在介质间隔层、DBR二氧化硅层以及超表面的氧化铝层, 其中最大的电场增强位于银光栅的四个角上. 根据等式${{V}_{\rm{m}}}=\dfrac{1}{{\rm{max}}\left\{ W\left( r \right) \right\}}\displaystyle\iint{W\left( r \right){{\rm{d}}^{2}}r}$, 其中W(r)是能量密度, 我们计算了两种结构中Tamm等离激元共振的模式体积. 常规的无超表面的微腔结构所支持的Tamm等离激元共振模式体积约为15250 nm²; 而在集成有超表面的微腔结构中由于介质间隔层厚度的降低以及银光栅对电场的局域特性, 其所支持的Tamm等离激元共振模式体积仅为约482 nm², 相比于常规结构缩小了约30倍. 超表面-间隔层-DBR结构相比常规的金属薄膜-间隔层-DBR结构可以产生更强的光子与激子的强耦合作用.
为了比较在这两种Tamm等离激元微腔结构中光子与激子强耦合作用的强弱, 我们将单层二硫化钨(WS₂)作为激子材料并引入到两种结构中. 为了比较的合理性, 在常规的金属薄膜-间隔层-DBR结构中, 单层二硫化钨放置在电场增强最大的介质间隔层和临近的DBR二氧化硅层分界面处, 如图4(d)中水平虚线所示; 在超表面-间隔层-DBR结构中, 单层二硫化钨放置在银光栅上表面, 如图4(c)中水平虚线所示. 在图4(d)中计算了Tamm等离激元微腔结构中放置单层二硫化钨材料之后的反射谱, 其中单层二硫化钨的介电常数采用Li等^[30]报道的实验参数. 由此可见, 在两种结构中由于Tamm等离激元和单层二硫化钨激子之间的相互作用, 原先单个的反射谷都发生了Rabi劈裂现象. 在常规的金属薄膜-间隔层-DBR结构中, Rabi劈裂的大小为58 meV; 得益于超表面-间隔层-DBR结构中更小的模式体积, Rabi劈裂的大小增加到了93 meV. 此外, 如图4(e)所示, 这种Tamm等离激元和激子之间的耦合作用不仅可以在反射谱中产生Rabi劈裂, 在吸收谱中同样可以引起吸收峰的劈裂现象.

将金属薄膜-介质间隔层-分布式布拉格反射器构成的Tamm等离激元微腔中的金属薄膜结构化成金属超表面并利用其结构参数能够调控光在其表面的反射位相的特性, 可以在微腔结构的介质间隔层厚度保持不变时通过调节超表面的结构参数来调控微腔结构所支持的Tamm等离激元模式的共振位置, 从而为Tamm等离激元模式的调控提供了更多自由度. 此外, 结合超表面对场的局域特性, 金属超表面-DBR结构可以在不改变共振模式的情况下显著减小Tamm等离激元模式体积. 对比常规的金属薄膜-DBR结构和基于超表面的Tamm等离激元与单层二硫化钨(WS2)的强耦合作用, 后者相比前者发生了更明显的强耦合现象, 耦合强度达93 meV, 可以获得更大的拉比劈裂.