摘要: 金属表面等离激元作为一种微纳米结构中自由电子在光场作用下的集体振荡效应, 由于其振荡电场被强烈地束缚在亚波长尺度范围内, 可以作为未来微纳米光子回路及器件的信息载体, 同时也可以在微纳米尺度上增强光与物质的相互作用. 本文首先系统地从理论上总结金属与入射电磁波相互作用时的光学行为及性质, 然后简述激发金属中不同等离激元模式的物理本质、金属表面等离激元振荡动力学过程及当前表面等离激元耦合理论的最新进展.
关键词: 金属光学性质 /
等离激元模式 /
动力学过程 /
耦合理论 English Abstract Research progress of coupling theory of metal surface plasmon Zhu Xu-Peng 1 ,Zhang Shi 2 ,Shi Hui-Min 3 ,Chen Zhi-Quan 2 ,Quan Jun 1 ,Xue Shu-Wen 1 ,Zhang Jun 1 ,Duan Hui-Gao 2 1.School of Physics Science and Technology, Lingnan Normal University, Zhanjiang 524048, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11574078, 61674073), the Natural Science Foundation of Hunan Province, China (Grant Nos. 2015JJ1008, 2015RS4024), the Science and Technology Planning Project of Guangdong Province, China (Grant No. 2017A050506056), the Key Basic and Applied Research Project of Guangdong Province, China (Grant No. 2016KZDXM021), the College Physics Teaching Team (Grant No. 114961700249), and the Scientific Research Project of Lingnan Normal University, China (Grant No. ZL1937)Received Date: 10 September 2019Accepted Date: 08 October 2019Available Online: 27 November 2019Published Online: 01 December 2019Abstract: Metal surface plasmon is a collective oscillation effect of free electrons at the micro-nanostructure surface under the stimulation of incident light. Since the corresponding oscillating electric field is strongly bound below the sub-wavelength scale, it can be used as an information carrier for future micro-nano photonic circuit and device, and can also be used to enhance the interaction between light and matter on a micro-nano scale, such as surface enhanced photoluminescence, Raman scattering, nonlinear signal generation, surface enhanced catalysis, photothermal conversion, photovoltaic conversion, etc. How to theoretically understand the unique optical behavior dominated by the plasmon oscillation mode is one of the hot research spots in the field of surface plasmon photonics. In recent years, the theory of surface plasmon has been continuously improved with the support of a large number of experimental researches. In this paper, we first systematically summarize the optical behaviors and properties of metal under the excitation of incident electromagnetic waves, and then briefly describe the plasmonic modes existing in the metal and their corresponding physical natures, the oscillation dynamics process and the currently prevailing surface plasmon coupling theories. We hope that this paper can provide a theoretical basis for those researchers who have just dabbled in the field of surface plasmons and help them to master the relevant basic knowledge quickly.Keywords: metal optical properties /plasmon modes /dynamic process /coupling theory 全文HTML --> --> --> 1.引 言 当电磁波照射到金属表面时, 金属中的自由电子会随入射波的振荡而集体振荡. 在特定频率下, 这种集体振荡幅度达到最大值, 形成等离激元共振[1 -3 ] . 这种共振主导着金属独特的光学行为并具有广泛的潜在应用, 遍布超分辨成像[4 ,5 ] 、纳米聚焦[6 -9 ] 、光谱增强[10 -12 ] 、传感探测[13 -15 ] 、能源[16 -18 ] 、生命科学[19 ,20 ] 等多个领域. 如何从理论上理解等离激元振荡模式主导下的独特光学行为是本领域研究的热点之一. 自Drude[21 ] 提出用复介电常数来描述金属中自由电子的集体振荡行为(体表面等离子激元)以来, 表面等离激元振荡理论研究取得了长足的发展, 例如基于Maxwell方程及边界条件可以得到在金属-介质界面上存在的倏逝表面波. Mie[22 ] 利用麦克斯韦方程组及适当边界条件计算了金属微纳米球体的光学响应. Fano[23 ] 根据金属-介质界面上表面电磁波的激发理论解释了光栅衍射中的wood反常现象. Rechberger 等[24 ] 提出了简单谐振子耦合模型, 解释了金纳米粒子二聚体的光学行为. Prodan 等[25 ] 提出一种可以解释复杂结构中共振模式相互作用对共振能量的影响的普适性表面等离激元共振模式杂化耦合理论. Engheta 等[26 ] 将表面等离激元纳米结构或者介质结构等效成电路微元件, 在一定程度上可以解释近红外及可见光范围内的表面等离激元耦合行为. Pitarke等[27 ] 对表面等离激元进行了较为详细的综述. Maier[28 ] 在其著作《等离激元基础及应用》(Plasmonics: Fundamentals and Applications )中同样对表面等离激元的基本理论做了细致的描述. 近年来, 表面等离激元相关理论在大量实验基础的支持下不断得以完善. 本文首先从金属的光学性质出发, 系统地认识金属中存在的等离激元振荡模式及相应激发方式背后的理论支撑、简述金属表面等离激元振荡动力学过程及当前主流的表面等离激元耦合理论的最新进展.2.金属的光学性质[28 ,29 ] 众所周知, 自由电子的集体行为主导着金属对入射光的独特响应. Drude[21 ] 在20世纪初首次利用依赖入射频率的复介电常数解释了金属自由电子的集体振荡行为, 即Drude模型, 该模型的核心思想是金属对入射光的响应主要由金属中自由电子主导, 其中金属原子价电子是自由电子的主要来源, 离子实维持整个金属的电中性且不与自由电子发生作用, 此时情形等效于大量的自由电子处于均一的金属正离子背景场中. 在Drude模型中, 金属中的自由电子可以等效为无回复力的谐振子, 其固有振荡频率为零. 在一级近似下, 光与金属的相互作用可以看作是固有频率为零的阻尼谐振子在入射电场E γ 表示, 是自由电子平均寿命的倒数. 在入射光的作用下, 有效质量为m , 有效电荷为e 的阻尼谐振子只在两种力的作用下运动, 第一种为谐振子所受的电场驱动力, 其大小为(–eE ), 第二种为谐振子所受的阻尼力, 与其运动速度ν mγν ). 当用r ω 的时谐电磁波, 其电场大小可表述为1 )式, 可得在入射光的作用下阻尼谐振子的位移为N 的金属宏观极化量P D ε 0 为真空介电常数, χ 和ε 分别为不同入射频率下材料对应的复极化率和复介电常数. 通过联立上述相关方程可以获得复介电常数、复折射率及相应电导率的频率依赖关系.ω p 为等离子体频率, 可以通过以下关系计算:n (ω )和虚部κ (ω )可以通过以下公式解得ω = 0时, ε r (ω )取负的最小值, ε i (ω )无穷大, 属于奇点位置, 但光电导率σ r (ω )有真实解, 大小为静电电导率值. 当ω 变大时, σ r (ω )迅速减小, ε r (ω )逐渐增大并在$\omega = \sqrt {\omega _{\rm{p}}^2 - {\gamma ^2}} $ 时为零.ω > ω p $\gg $ γ , 存在${\varepsilon _{\rm{r}}}\left( \omega \right) > 0$ , ${\varepsilon _{\rm{i}}}\left( \omega \right)$ ~ 0; 折射率为实数, n (ω ) > 0, κ (ω ) ~ 0; 在波矢为k 0 的光波作用下, 金属内部电场为${E} = {{E}_0}{\rm{exp}}\left( {{\rm{i}}n{{k}_{{0}}} \cdot {r}} \right)$ . 此时金属对光的响应类似于电介质对光的响应, 即对入射光透明.ω p > ω $\gg $ γ , 有ε r (ω ) < 0; 折射率n (ω )~0, κ (ω ) > 0; 在波矢为k 0 的光波作用下, 金属内部电场${E} = {{E}_0}{\rm{exp}}\left( { - \kappa {{k}_{{0}}} \cdot {r}} \right)$ . 此时, 电场大小随入射深度的增加而指数衰减, 其趋肤深度δ 可通过$\delta = c/\left( {\kappa \omega } \right)$ 计算. 当电磁波垂直金属表面入射时, 其反射率R 可以通过以下公式所得:γ = 0时(理想金属), R = 1.ω $\ll $ γ , ${\varepsilon _{\rm{r}}}\left( \omega \right) \!\ll \!{\varepsilon _{\rm{i}}}\left( \omega \right)$ ; $n\left( \omega \right)\! \approx \kappa \left( \omega \right)\! \approx $ $\sqrt {{{{\varepsilon _{\rm{i}}}\left( \omega \right)}}/{2}} $ ; 金属内部电场${E} = {{E}_0}{\rm{exp}}\left( {{\rm{i}}n{{k}_{{0}}} \cdot {r}} \right)\times$ ${\rm{exp}}\left( { - \kappa {{k}_{{0}}} \cdot {r}} \right) $ , 由此可以看出电场在金属内部迅速衰减, 其趋肤深度可由$\delta = c/\left( {\kappa \omega } \right)$ 计算得到. 金属表面反射率$R = \dfrac{{{{\left( {n - 1} \right)}^2} + {\kappa ^2}}}{{{{\left( {n + 1} \right)}^2} + {\kappa ^2}}} \approx 1$ , 因此当入射光频率ω 很低时, 金属为理想导体.ω p $\gg $ γ 时, ε (ω )为正实数, 金属光学性质类似于电介质的光学性质, 电磁波可以在其内部传播, 其色散关系可以通过复介电常数$\varepsilon \left( \omega \right) \approx 1 - {{\omega _{\rm{p}}^2}}/{{{\omega ^2}}}$ 和横波波矢$k = \sqrt \varepsilon {\omega }/{c}$ 联立获得:ω p 时, ε r (ω )为负实数, 此时, 入射光电场在金属内部快速衰减, 无法穿透金属, 金属表面反射率约为100%, 即横向振荡的入射光在金属界面上被准全反射, 金属内部没有扩散波, 横向振荡波被禁止传输.$\omega \approx \omega_{\rm p} \gg \gamma $ , $ \varepsilon(\omega) \approx 0 $ . 从波动方程k E k = $ \sqrt \varepsilon {\omega }/{c} \equiv n\left( \omega \right){k_0} \ne 0$ 时, 才能满足单位距离中存在横向传输波, 此时有ε (ω) ≠ 0, 所以这一矛盾说明$\omega \approx \omega_{\rm p} $ 时横波无法在金属内部传播; 而对于纵波来说k E ${k}\left( {{k} \cdot {E}} \right) = {{k}^2}{E}$ , 此时当介电常数ε (ω) = 0时, 金属中存在非零的电场值, 所有这一结论表明$ \omega \approx \omega_{\rm p} $ 时入射能量可以以纵波的形式在金属内部传播. 在经典电磁理论中, 变化的磁场可以产生涡旋电场, 即H $ \omega \approx \omega_{\rm p} $ 处, 金属内部只存在自由电子集体的纵向振荡, 并且纵向振荡能量只能以单电子接收的方式衰减. 一般地, 金属内部自由电子的纵向集体振荡被称为体等离子体共振, 其频率ω p 记作等离子体频率, 衰减过程为朗道阻尼. 由其计算式(8 )可以看出, ω p 是材料的本征频率, 不同材料的ω p 不同, 材料中自由电子的浓度大小直接决定着ω p 的高低. 从这一角度出发, 所有固态物质都可能存在等离子体振荡, 但其本征频率ω p 不同. 固体中的自由电子在入射光的作用下产生纵波, 其本质是自由电子集体与正电背景之间的库仑作用, 此时库仑场属于纵向场, 这一特殊状态$(\varepsilon \left( {\rm{\omega }} \right) = 0)$ 对应的等离子体振荡波相速度ε c 表示, 此时复介电常数实部ε ∞ = 1 + ε c , 复介电常数可修正为[30 ,31 ] . 其本质思想是金属中可以发生带间跃迁的电子可以看作是具有固有频率的阻尼谐振子, 此时Drude模型中需要加入一个表征金属电子带间跃迁效应的附加项ε inter (ω ), 则总复介电常数Ω L 和Γ L 分别为阻尼谐振子的固有频率和阻尼频率, Δε 为阻尼谐振子特定带间跃迁对金属光学响应贡献的权重因子.3.金属表面等离激元振荡[28 ] 除了金属内部自由电子集体振荡外, 金属微纳米结构表面可以支持另外一种重要的自由电子集体振荡行为, 即表面等离激元振荡. 这一行为使得金属微纳米结构在彩色印刷、单分子检测及亚波长聚焦等多个领域[32 -34 ] 具有重大的应用前景. 不同于金属内部的自由电子集体振荡行为, 表面等离激元振荡发生在金属与电介质界面上, 并可沿着界面传播或者被局域在金属微纳米结构中. 图1 为传播的表面等离激元(surface plasmon polariton, SPP)和局域表面等离激元(localized surface plasmon, LSP)[35 ] 示意图.图 1 (a)传播表面等离激元示意图; (b)局域表面等离激元示意图[35 ] Figure1. (a) Propagating plasmon (surface plasmon polaritons); (b) localized surface plasmon[35 ] .3.1.传播的表面等离激元 3.1.传播的表面等离激元 如图1(a) 所示, 金属-介质界面上集体振荡的电子沿着分界面x [36 ] . 现有的研究表明这类等离激元的传播距离可达厘米量级[37 ,38 ] , 因此在光子器件领域具有巨大应用潜力. SPP振荡频率满足通过麦克斯韦电磁方程组及适当边界条件获得的色散关系. 如前所述, 当ω < ω p 时, 横波无法在金属内部传播, 因此应考虑金属是否可以传播束缚态的表面波, 即能否传播沿着表面法线方向指数衰减的倏逝波. 假设倏逝波在金属-介质界面(z = 0)上可以沿x β , 振幅为Aj , 同时电场沿着z k z kzj , kzj 为大于零的实数, 如图2 所示. 当z > 0, j = 1; 当z < 0, j = 2, 这一规定同样用于电场、磁场及介电常数的命名规则中.图 2 支持SPP传输的金属-介质界面示意图Figure2. Metal-medium interface that supports SPP transmission.x z $\dfrac{\partial }{{\partial t}} = - {\rm{i}}\omega $ , 则此时麦氏方程可展开为${E_y}, {H_x}, {H_z}$ ((25a ), (25c ), (25e )式)三个参数, 表示束缚态TE波; 第二种包括${H_y}, {E_x}, {E_z}$ 表示((25b ), (25d ), (25f )式)三个参数, 表示束缚态TM波.25d )式得到A 1 = A 2 , 同时kzj 为正实数, 则介电常数ε 1 和ε 2 必须异号, 正好符合金属-介质界面体系. 联立(25b ), (25d )和(25f )式有28 )式, 可得到表面束缚态TM波的色散关系如下:25a )式中推导出kzj 为正实数, 只有E y 1E y 234 )式成立, 因此金属-介质界面上不存在传播的束缚态TE波, 也就是说, 只有束缚态TM波才能在金属-介质界面上传播. 从物理本质来说, TM波的电场在界面法线方向(分量Ezj )不连续, 可以在表面上积累电子, 同时这些表面电子在电场切向分量Exj 的驱动下集体运动, 即产生表面等离激元. 但对于TE波, 电场分量Ezj 为零, 无法在金属表面上积累电子, 因此不能产生表面等离激元. 基于此, 不难看出可以在金属-介质界面上传播的束缚态TM传输波只可以被TM模式的入射光激发.31 )式, 如果介质的介电常数ε d = ε 1 为一大于零的实数, 而金属的介电常数用Drude模型${\varepsilon _{\rm{m}}} = {\varepsilon _2} = 1 - {{\omega _{\rm{p}}^2}}/{{{\omega ^2}}}$ 描述. 那么, 对于低频有$\varepsilon _{\rm{m}} \to -\infty $ ,ω → 0时, SPP在x β → 0, 波矢在界面法线方向的分量${k_{zj}} = \sqrt {{\beta ^2} - k_0^2{\varepsilon _j}} \to 0$ , 波长λ $ \to \infty $ , 所以在低频, SPP是一种准静态表面束缚波, 此时入射光和自由电子的耦合能力及电场在界面附近的束缚能力近于零. 当ω = 0时, 无入射光入射. 当ε d → –ε m 时ω SP , 表示ω SP ≤ ω < ω p 范围内的入射光能量不能在金属内部或表面上传输, 金属材料呈现高反射性. 由于传播常数β $ \to \infty $ , 则波长λ → 0, 波矢在z ${k_{zj}} = \sqrt {{\beta ^2} - k_0^2{\varepsilon _j}} \to \infty $ , 表明振荡场在界面法线方向急速衰减并被极大地束缚在界面附近. 在界面附近微小区域上, 金属-介质体系有效介电常数${\varepsilon _{{\rm{eff}}}} = {\varepsilon _{\rm{m}}} + {\varepsilon _{\rm{d}}} = 0$ , 此时SPP更像是金属表面自由电子的集体纵向振荡行为, 类似于体等离子体振荡, 可记作金属表面等离子体振荡, 其相速度${\upsilon _{\rm{g}}} = {{{\rm{d}}\omega }}/{{{\rm{d}}\beta }} \to 0$ , 所以在此频率附近金属表面等离子体振荡是一种准静态表面波.图3 给出了金属全频色散关系. 当光束入射金属时的频率ω > ω p 时, 金属如介质材料, 可以在其内部传输横向振荡波; 当ω = ω p 时, 金属内部只存在自由电子的集体运动, 即体等离子体振荡波; 当ω SP ≤ ω < ω p 时, 金属呈现极高反射性, 无法支持振荡模式的存在; 当0 < ω < ω SP , 金属-介质界面可以存在特殊的束缚态TM波(金属表面电子的集体运动)的传播, 其电场在界面法线方向指数衰减, 传播方向形成均匀的正负电荷分布, 此类波同时具有横向振荡模式和纵向振荡模式的某些性质和行为. 当ω = 0, 无入射光. 实际上, 真实金属的电子阻尼频率γ ≠ 0, 在ω SP 处, β 并没有完全趋近于$ \infty $ , 而是存在有限值, 允许ω SP 和ω p 之间存在一定的结合模式.图 3 (a)金属全频色散关系; (b)金属和电介质的介电常数与入射频率之间的关系(借鉴中国科学院大学董国艳老师《纳米光学》第十讲图)Figure3. (a) Full frequency dispersion relation of metal materials; (b) relationship between incident frequency and dielectric constant of metal and dielectric, respectively (from the tenth lecture of 《Nano Optics》, Dong Guoyan, Chinese Academy of Sciences)k x incβ SPP , k x incβ SPP 为SPP波矢). 由于介质中光的色散光线和金属-介质界面上SP的色散曲线之间无有效交点, 所以入射光无法在金属表面激发SPP. 换言之, 入射光能量无法直接有效地耦合到SPP中, 反过来SPP的振荡能量也无法直接耦合到辐射的光场中, 因此必须通过某些特殊的手段增大k x incβ SPP 值相匹配. 目前最主要的激发SPP的方式包括全反射棱镜耦合激发[39 ] 、光纤锥体耦合激发[40 ] 、光栅耦合激发[41 ] 、散射激发[42 ] 、高聚焦光束激发[43 ] 、端射耦合激发[44 ] 、近场激发[45 ] 、波导耦合激发[46 ] 等. 其中最为常见的是光栅耦合激发、散射激发及棱镜耦合激发. 比如, 在满足全内反射的条件下, 入射光在棱镜-金属薄膜界面上产生的倏逝波可以穿过金属薄在金属-空气界面上激发SPP; 入射光照射光栅时可以形成多个衍射级, 对应衍射光的波矢取决于光栅常数及入射角大小, 能够满足激发匹配条件, 在金属-介质界面激发SPP. 随机微纳米尖端、单孔、缺陷或颗粒可以对入射光有一定散射, 能够产生一个分布较宽的波矢值范围, 因此总能寻得一个能够满足相位匹配条件的波矢值来局部激发SPP. 值得注意的是, SPP共振频率对金属界面附近环境的变化具有极其灵敏的响应度, 因此可用于开发SPP传感器, 在生物分子灵敏检测领域有巨大的应用前景.3.2.局域的表面等离激元 -->3.2.局域的表面等离激元 局域表面等离激元是金属中自由电子与入射光在微纳米结构中相互耦合形成的一种非传播型表面波. 金属结构曲面可以为光场驱动的集体振荡电子提供有效的恢复力, 因此在特定频率下可以在金属纳米结构表面附近产生场增强极大值, 对应于局域表面等离激元共振(localized surface plasmon resonance, LSPR)[47 ] . 不同于SPP, 金属微纳米结构曲面对入射光场的散射效应使其具备很宽的波矢值分布, 因此LSP可以被入射光直接激发.图4 所示, 半径为a 的金属球, 位于静电场E E 0 z ε d 的各向同性介质中, 背景电场平行于z ε (ω )描述, 在静电场中用复数ε 表示.图 4 静电场中的金属微纳米球Figure4. Metal micro-nanospheres in an electrostatic field.E $-\nabla $ Φ 可以通过求解相应电势Φ 的Laplace方程$\nabla^2$ Φ = 0得到. 因其对称性, 球体内外电势的通解可写为θ 是P 点位矢r z Al 和Bl 是待定参数, Pl θ )是l 级Legendre函数. 因为原点处电势值应为有限值, 所以金属球内外部电势可分别写为Al , Cl , Dl 由$ r \to \infty $ 和r = a 时的边界条件决定. 当$ r \to \infty $ 时, ${\varPhi _{{\rm{out}}}} \to - {E_0}z = - {E_0}r\cos \theta $ , C 1 = –E 0 , 当l ≠ 1, Cl = 0; 当r = a 时, 电场在界面两边切向连续, 即41 )表明电势在金属球-介质界面两边相等. 另外r = a 处界面两边的法向电位移连续, 即39 )—(42 )式可获得待定系数, 当l ≠ 1, Al = Dl = 0, A 1 和D 1 分别为45 )在物理本质上可以分解为两项: 第一项是入射光场产生的电势, 第二项可等效于球心偶极子产生的电势, 球外总电势等于上述两项电势值之和. 引入偶极矩p p E 0 成正比. 根据偶极矩定义式${p} = {\varepsilon _0}{\varepsilon _{\rm{d}}}\alpha {{E}_{{0}}}$ 可引入金属球等效极化率α , 则48 )式用以描述静态近似中微纳米级球体的复极化率. 显然, 具有频率依赖性的介电常数ε 变化时, 复极化率在$\left| {\varepsilon \left( \omega \right) + 2{\varepsilon _{\rm{d}}}} \right|$ 最小时达到极值, 进入共振增强状态. 当球体介电常数虚部值或其变化率很小时, 共振增强状态激发的条件可简化为49 )式称为Fr?hlich条件, 该式同时关联着入射光场中金属微纳米结构的偶极LSPR. 对于无损耗的Drude金属, 满足Fr?hlich条件的入射光频率为${\omega _{{\rm{LSP}}}} = {{{\omega _{\rm{p}}}}}/{{\sqrt {1 + 2{\varepsilon _{\rm{d}}}} }}$ . 此外, (49 )式表明共振增强状态对应的入射光频率受到周围环境介电常数值的强烈影响, 随着ε d 的增加, 共振频率降低, 相应的波长红移. 实际金属微纳米球的介电常数虚部并不为零, 即Im[ε (ω )] ≠ 0, 所以分母不为零的(48 )式限制了共振增强状态下极化率的大小.E $-\nabla $ Φ 计算50a )和(50b )式可知, 共振增强状态意味着球体内外部电场都可以被共振增强, 对应于α 极大值. 至此, 当球体尺寸远小于入射光波长时, 球体在准静态近似下被当作理想偶极子处理的方式是有效的, 也说明这一方式可用于计算忽略体积延迟效应时金属球与入射光的相互作用. 在平面电磁波${E}\left( {{r}, t} \right) = {{E}_{{0}}}{{\rm{e}}^{ - {\rm{i}}\omega t}}$ 照射金属微纳米球时, 其诱导偶极矩${p} = {\varepsilon _0}{\varepsilon _{\rm{d}}}\alpha {{E}_{{0}}}{{\rm{e}}^{ - {\rm{i}}\omega t}}$ , 具有时谐依赖的偶极振荡导致共振频率的入射光能量被球体极大地散射或吸收.[22 ] 在1908年利用麦克斯韦方程组及适当边界条件计算了金属微纳米球体的光学响应, 也被称为“米氏理论”, 但该理论只适用于计算球状结构的光学性质. 一般而言, 金属微纳米粒子中的共振增强状态对应于极化率α 极大值和散射吸收效率最大值, 其总的光学响应度通常可以使用光学消光截面σ ext 来描述, 数值上为光学吸收截面σ abs 与散射截面σ sca 之和. 吸收和散射过程分别对应于入射光能量转化成热能或偏离原来的传播方向. 通常情况吸收截面及散射截面值正比于粒子的几何截面. 在米氏理论中, 球形结构对应的散射和消光截面可以分别表示为$x = 2{\text{π}}a{n_{\rm{d}}}/\lambda $ , 其中n d 为介质折射率, a 为金属球半径. 吸收截面${\sigma _{{\rm{abs}}}} = {\sigma _{{\rm{ext}}}} - {\sigma _{{\rm{sca}}}}$ . an 和bn 为米氏系数, 分别对应于n 级共振模式的电振幅和磁振幅, 通常依赖于球形颗粒及其周围环境的折射率大小, 可表示为${\psi _n}\!\left( z \right)\! = \!{\left( {{\text{π}}z/2} \right)^{1/2}}{J_{n + 1/2}}\left( z \right)$ , ${\zeta _n}\!\left( z \right) \!= \! {\left( {{\text{π}}z/2} \right)^{1/2}} \!\times$ $ \left( {{J_{n + 1/2}}\left( z \right) \!-\! {\rm{i}}{Y_{n + 1/2}}\left( z \right)} \right)$ 皆为Riccati-Bessel函数[48 ] ; $m = {n_{\rm{p}}}/{n_{\rm{d}}}$ , 其中n p 为金属球的折射率. (51 )式中的不同的展开项分别对应于偶极(n = 1)、四极 (n = 2)和六极(n = 3)等不同共振模式的贡献值. 当金属球的直径2a 远小于入射光波长时, 米氏理论可忽略四极及高极共振模式对其光学响应的贡献而直接通过偶极近似简化, 此时米氏散射由LSPR主导, 其相应的散射和吸收截面可以通过金属球极化率α 来描述[28 ] :53a )和(53b )式不难发现, 当直径2a $\ll $ λ 时, 吸收截面尺度因子a 3 大于散射截面尺度因子a 6 , 所以吸收在小尺寸结构中占主导作用. 当${\rm{Re}}\left[ {\varepsilon \left( \omega \right)} \right] = - 2{\varepsilon _{\rm{d}}}$ 时, 金属球中激发偶极LSPR, 此时散射和吸收截面达到最大值[49 ] . 在准静态近似下介电常数为$\varepsilon \left( \omega \right) = {\varepsilon _{\rm{r}}}\left( \omega \right) + {\rm{i}}{\varepsilon _{\rm{i}}}\left( \omega \right)$ , 体积为V 的球形结构, 其消光截面[28 ] 为[50 ,51 ] . 另外, 入射光电场分量在跨越整个金属结构时出现的去极化场延迟也会导致LSPR峰位的移动[52 ] . 直观地来说, 随着粒子尺寸的增大, 异号电荷相互作用的距离变大, 响应的振荡电子回复系数变小, 使其共振频率降低[28 ] . 而谱线变宽主要是辐射阻尼增大导致的[53 ] , 金属纳米结构LSPR的谱线宽度Γ 可描述为[54 ,55 ] 6 )和(7 )式, 金属复介电常数$\varepsilon \left( \omega \right) = $ $1 - {{\omega _{\rm{p}}^2}}/{{{\omega ^2} + {\rm{i}}\gamma \omega }}$ , 其中γ 为金属的阻尼频率. 金属体材料阻尼频率用γ b 表示, 其值与电子费米速度ν F 成正比, 与电子自由程l 成反比, 可表示为[48 ] l 值一般取决于材料中声子、缺陷及杂质对电子的散射强度. 基于Matthiessen规则, 电子总自由程l 同时由上述多个因素项决定, 其值可通过$1/l =\displaystyle \sum {\left( {1/{l_i}} \right)} $ 表征, 其中li 为某一独立过程对应的电子自由程. 对于小结构(尺寸小于金属体材料平均l 值), 吸收占光学主导地位, 因此在一定程度上可以忽略辐射阻尼效应, 同时由于结构表面对电子散射作用, 阻尼频率可进一步修正为[48 ] l eff 为电子的有效自由程, 换言之l eff 表征的是电子在受到表面散射作用前的平均运动距离, A 是表征结构表面与电子相互作用的常数[56 ] . l eff 依赖于金属微纳米结构的几何参数, 通常可以利用${l_{{\rm{eff}}}} = 4 V/S$ 计算, 其中S 和V 分别表示金属结构的表面积和体积值. 对于尺寸小到LSPR频率不受带间跃迁制约同时足以忽略辐射阻尼的金属微纳结构, 其Γ 直接受到金属材料的本征阻尼及表面散射的影响. 此时, LSPR谱线线宽[48 ] [48 ] , 即κ 是辐射阻尼常数, V 为粒子体积. 从(59 )式可以看出, 当结构尺寸变大时, 与体积相关的辐射阻尼项对谱线线宽的贡献变大, LSPR谱线变宽.[57 ] 在1912年打破了米氏理论的局限性, 将其拓展为能够描述椭球形金属颗粒的Gans-Mie理论. 对于尺寸较小的椭球形金属颗粒, 轴长分别用$a, b, c\left( {a > b = c} \right)$ 表示. 在入射光的作用下, 金属椭球的有效极化率可表示为Pi 代表某一特定轴的几何偏振因子$1\left( {{P_a} + {P_b} + {P_c} = 1} \right)$ , 金属椭球轴长比为a /b . 所以(61a )和(61b )式表明, 金属椭球中的自由电子可以沿其长轴和短轴独立地发生集体振荡, 形成两个LSPR频率, 分别对应于长轴模式和短轴模式, 其长轴共振模式可以利用轴长比的变化来高效调制. 类似于SPP, LSP共振频率受到结构附近环境介电常数的强烈影响, 同时共振态结构周围局域着极强的电场分布, 因此LSPR在传感及增强光谱领域具有巨大的潜在价值.3.3.类表面等离激元(spoof SPP) -->3.3.类表面等离激元(spoof SPP) 如前所述, 金属光与物质的相互作用主要由其中的自由电子主导, 当入射光频率低于等离子体频率时, 金属介电常数为负, 金属中可以存在束缚在表面的自由电子集体振荡态, 形成极强的电场局域, 这使得金属表现出丰富独特的光学性质. 比如在表面增强拉曼散射应用[58 ] 中, 金属的SPP效应可以将分子检测浓度推进至10 fM尺度[12 ] . 其他应用还包括SPP带隙结构中的波导[59 ] 、金属带中的SPP[60 ] 以及具有SPP效应的二维光学[61 ] 等, 类似总结性工作可参见相关综述性文章[62 ,63 ] . 但是当入射电磁波的频率很低时(THz领域, 甚至更低), 金属表面反射率极高, 其光学性质类似于完美电导体, 金属表面无法支撑SPP的传播. 此时, 可以通过在金属表面加工孔或者凹槽阵列来实现自由电子的束缚, 形成新的表面态, 其光学性质与SPP主导的光学性质类似, 因此将这类表面模式称作为类表面等离激元[64 ] , 同样根据其传播性质, 可划分为传播的类表面等离激元[65 ] 和局域的类表面等离激元[66 ] , 其详细理论可参考相关理论文献[64 ,67 ] .4.表面等离激元动力学 表面等离激元的寿命和振幅是增强光与物质相互作用中两个极其重要的参数, 例如在表面增强拉曼散射(surface enhanced Raman scattering, SERS)应用中, 当表面等离激元具有的振幅越大、寿命越长时, 金属微纳米结构对待测分子拉曼信号的增强能力就越大[68 -70 ] . 当表面等离激元共振激发后, 其振荡连续性很容易被电子与电子、电子与缺陷、电子与声子及电子与杂质之间相互作用的扰动破坏. 如图5(a) 所示, 通常表面等离激元共振激发后可以通过两种方式衰减[68 ] : 第一种为辐射衰减, 导致金属微纳结构中发射与表面等离激元共振频率相当的光子; 另一种为非辐射衰减, 表面等离激元共振的能量可以通过带内跃迁和带间跃迁的方式激发金属原子外层轨道上的非激发电子而失去能量, 这一非辐射衰减在金属中形成一定数量的电子-空穴对, 可用于光催化、光降解等应用中. 当然, 非辐射衰减通道中电子的具体跃迁方式取决于入射光的光子能量, 对应于入射光频率, 当入射频率低于金属材料带间跃迁本征频率时, 可以有效地抑制带间跃迁的发生, 表面等离激元振荡呈现出较长的寿命及较高的谱线品质因子.图 5 (a)衰减通道示意图; (b)衰减动力学过程Figure5. (a) Attenuation channels; (b) attenuation dynamics.T 2 描述[71 ] , 即T 1 是与弹性衰减过程(纯零相位化)相关的时间常数, T * 是与非弹性衰减过程相关的时间常数. 图5(b) 给出了结合飞秒瞬态吸收光谱及消光谱谱宽分析获得的金属表面等离激元衰减示意图[48 ] . 表面等离激元振荡首先快速地被零相位化破坏形成非平衡态的电子分布, 其时间尺度约在10 fs量级, 然后在100 fs尺度上通过电子-电子散射作用产生一定数量的热电子, 在化学催化和光电二级管等方面具有潜在应用前景. 最后在1 ps时间尺度上通过电子-声子散射作用将自由电子集体振荡能量转化为热能, 释放到周围环境中.5.表面等离激元耦合模型 如前所述, 金属表面等离激元共振频率受到周围环境介电常数的强烈影响, 共振峰位表现出极高的折射率灵敏度. 相互靠近两个金属微纳米结构, 其表面等离激元振荡之间可以相互耦合, 光学共振峰位会发生明显的变化, 在可见光区呈现明显的颜色变化. 此外, 单个复杂金属结构在特定情况下可以激发多个表面等离激元模式, 它们彼此之间的耦合作用, 能够对原有的光谱响应行为起到一定的调制作用. 这些表面等离激元耦合效应可以在结构特征处产生巨大的局域电场, 形成电场热点, 可以将SERS信号的强度增大1014 —1015 量级. 同时, 表面等离激元耦合效应可以主导一些具有非常意义的光学行为, 比如Fano共振、光学手性及电磁诱导透明等. 从物理模型上理解这些表面等离激元模式之间的耦合行为, 并从内禀耦合规则出发更好地利用其独特的光学性质才能推动相关领域的快速发展. 经过等离激元光子学近些年的发展, 共振模式耦合行为可以通过表面等离激元杂化模型或简单谐振子耦合模型来描述, 耦合导致的能量变化量可以通过Simpson-Peterson修正方程来评估[72 ] . 此外, 金属微纳米结构中一类非常重要的光学响应不对称线状归因于表面等离激元模式强耦合形成的Fano共振.5.1.谐振子近场耦合模型 5.1.谐振子近场耦合模型 金属微纳米结构中的自由电子气在入射光场的束缚下可以形成互相排斥的表面谐振电荷, 这种电荷谐振行为与结构固有属性相配时可以满足表面等离激元共振条件[73 ] . 两个金属微纳米粒子在同一入射偏振下相互靠近时, 两个粒子中的自由电荷同时被入射光场附加束缚力. 当驱动电场方向沿着粒子间轴(图6(a) 左图[73 ] )时, 下方粒子的正电荷与上方粒子的负电荷形成正-负键合场. 由于这种正负电荷之间的库仑吸引力, 单个粒子内部振荡电荷的库仑排斥力被一定程度的削弱, 电荷谐振所需的回复力变小, 致使粒子二聚体结构的共振频率相对较低. 当驱动电场方向垂直于粒子间轴(图6(a) 右图[73 ] )时, 粒子二聚体体系中的电荷分布增强了单个粒子内的电荷振荡排斥力, 对应于较高的共振频率. 其中, 谐振子振荡所需的回复力由库仑排斥力提供, 当偏离平衡位置的距离相同时, 库仑排斥力与谐振子回复力正相关, 其本质对应于谐振子的弹性系数值, 直接影响着共振频率的高低[24 ] . 在入射光的作用下, 单个金属粒子中的电荷会发生极化, 产生一定大小的诱导偶极矩, 进而在靠近金属粒子的介质衬底上产生镜像电荷分布(图6(b) [73 ] ), 反过来影响着诱导偶极矩, 造成金属粒子光学响应峰位的移动[73 ] . 驱动电场在不同的入射偏振下(垂直于衬底, 如图6(b) 左图; 平行于衬底, 如图6(b) 右图)金属粒子表面电荷与衬底中的镜像电荷的相互耦合削弱了金属颗粒表面电荷的振荡排斥力, 致使其所需振荡回复力变小, 降低了金属粒子-介质衬底系统的共振能量. 金属粒子与衬底之间的距离越小, 这一耦合作用越强, 体系共振对应的振荡频率越低. 实际上由于作用在足够大体积金属粒子上的衬底诱导场是不均匀分布的, 因此还应考虑其他高阶振荡模式. T?rm?和Barnes[74 ] 以谐振子耦合模型(图6(c) )为强耦合体系的物理基础总结了表面等离激元与其他发射体之间的强耦合作用, 表明谐振子模型在研究微观耦合过程中具有较好的普适性. Hentschel等[75 ] 通过非线性谐振模型(图6(d) )预测了表面等离激元耦合蝴蝶结中的三次谐波产生光谱, 其预测光谱与其实验测试结果具有良好的一致性. 该非线性谐振模型的应用, 可以帮助我们合理设计有效的等离激元非线性源.图 6 (a)谐振子间耦合示意图[73 ] ; (b)谐振子与其镜像耦合示意图[73 ] ; (c)耦合的简谐振子[74 ] ; (d)三次谐波产生对应的等离激元非线性谐振模型[75 ] Figure6. (a) Inter-coupling of harmonic oscillators[73 ] ; (b) harmonic oscillator coupled with its mirror image[73 ] ; (c) two coupled harmonic oscillators[74 ] ; (d) a nonlinear harmonic oscillators model of the plasmon third harmonic generation[75 ] .5.2.表面等离激元杂化耦合模型 -->5.2.表面等离激元杂化耦合模型 根据Huckel分子轨道杂化概念[76 ] , Prodan等[25 ] 提出了一种普适性的表面等离激元杂化模型(plasmonic hybridization, PH), 可以直接有效地描述金属微纳米结构中表面等离激元共振模式之间的强耦合行为. 在此模型中, 金属微纳米结构中无旋且不可压缩的电子流体处在均匀正电背景中. 其核心思想是: 两个相互靠近的表面等离激元共振模式之间发生耦合作用, 最终会形成两个不同能量的杂化共振模式, 一个为低能正键模式, 另一个为高能反键模式, 如图7(a) 所示. 当入射光诱导的金属结构净偶极矩较大时, 入射光可以直接激发相应的振荡模式, 比如当两个金属棒一字排列时, 低能正键模式可以被入射光直接激发(图7(a) 第四行杂化模式简图), 高能反键模式因其近零的净偶极矩(图7(a) 第一行杂化模式简图)无法与入射光直接作用; 当两个金属棒并肩放置时, 高能反键模式能够被入射光直接激发(图7(a) 第二行杂化模式简图), 而低能正键模式因其近零净偶极矩无法直接光学激发(图7(a) 第三行杂化模式简图). 相比于谐振子耦合模型, 这一杂化耦合模型可以直观地描述复杂金属结构中不同极数振荡模式之间的耦合行为. 研究和验证表面等离激元杂化耦合模型的实验手段较多, 主要包括传统的光谱探测, 电子能量损失探测及阴极荧光成像. 如Liu等[77 ] 通过PH模型解释了堆叠式金属条超材料透射光谱中更为复杂的等离激元耦合主导的光谱特征, 为三维光学超材料的有效设计提供了思路(图7(b) ). Zhang等[10 ] 通过PH模型解释了当入射光垂直于劈裂圆盘的裂缝时透射光谱中出现的Fano不对称线状的本质原因, 同时, 这一不对称线状对应的巨大近场增强使得单一劈裂盘结构成为增强二次谐波产生的潜在物理平台(图7(c) ). Vogel等[78 ] 利用PH模型研究了不同偏振下的双层月牙形结构的等离激元耦合行为, 该结构具有很强的偏振依赖性及非常复杂的结构特征, 这进一步说明了PH模型在等离激元耦合行为研究中具有广泛的应用(图7(d) ). Simoncelli等[79 ] 通过热电子调制的吸收扫描图实现了对表面等离激元杂化耦合的成像, 使得表面等离激元模式工程允许控制纳米尺度的反应, 同时为进一步增强和操纵热电子驱动的化学反应和能量转换转移提供有效途径. Duan等[80 ] 在研究亚5 nm尺度下金属蝴蝶结结构时, 利用电子能量损失谱表征了主导电场局域因子的杂化耦合行为. 北京大学方哲宇教授组在利用阴极荧光成像研究表面等离激元杂化耦合行为方面做了大量的研究工作[81 -84 ] , 为从不同的角度认识和理解表面等离激元耦合杂化, 验证耦合杂化模型提供了新颖的实验思路. 此外, 南京大学Liu等[85 ] 简述了耦合超材料中的模式杂化效应, 总结了超材料中耦合杂化引起的新颖现象和潜在的有趣应用, 对耦合谐振器系统应用于新型超材料和纳米光子器件开发具有指导性作用.图 7 (a)表面等离激元共振模式杂化过程图; (b)堆叠式金属带的透射光谱及表面等离激元杂化示意图[77 ] ; (c)单一劈裂盘阵列的透射光谱及其对应的共振模式杂化图[10 ] ; (d)双层月牙形结构的模式杂化[78 ] ; (e)杂化模式成像[79 ] Figure7. (a) Hybridization process between two surface plasmon resonance modes; (b) the transmission spectrum of stacked cut-wire metamaterials and its corresponding plasmon hybridization process; (c) the transmission spectra and plasmon hybridization process of single split-disk; (d) the plasmon hybridization of stacked double crescents arrays; (e) the super-resolution imaging of hybrid plasmon mode.5.3.修正的Simpson-Peterson近似 -->5.3.修正的Simpson-Peterson近似 如前所述, 原始单个金属结构的共振能级在近场耦合杂化后形成两个新的本征模态, 高能反键模式和低能正键模式. 偶极子振荡模式之间耦合程度可以通过Simpson-Peterson近似公式来评估, 其主要物理量分布如图8(a) 所示. Tabor等[72 ] 通过对不同耦合形式的结构光谱峰位进行分析(图8(b) ), 修正Simpson-Peterson公式用以近似评估杂化共振能量偏移V [72 ] . 通常两个金属棒之间的共振能量偏移V , 即耦合程度可以通过下式来量化图 8 (a) Simpson-Peterson模型物理量分布图; (b)不同角度的耦合及对应的消光光谱[72 ] ; (c)不同排布金纳米棒的耦合及潜在应用[89 ] ; (d)不同偶极中心偏移量下耦合能量随角度的变化曲线[90 ] Figure8. (a) Relationship of physical quantity in Simpson-Peterson model; (b) the coupling at different angles and their corresponding extinction spectra[72 ] ; (c) the coupling and potential applications of different arrangements in gold nanorods system[89 ] ; (d) coupling energy versus angle for different dipole center offsets[90 ] .η 为环境的折射率, μ 为金属结构的诱导偶极矩, κ 是耦合体系的方向因子, 可写为θ 1P 和θ 2P 为入射电场方向分别与诱导偶极子1和2之间的夹角; θ 1R 和θ 2R 为粒子间轴分别与诱导偶极子1和2之间的夹角; θ 12 为两个诱导偶极子之间的夹角. 方程(63 )式中Γ 用来描述近场分离函数, 一般使用R 3 或e指数依赖关系[76 ,86 -88 ] . Chen 等[89 ] 总结了金纳米棒等离激元耦合行为光学性质及其潜在应用(图8(c) ), 其中介绍了不同排布、不同尺寸金属棒的耦合光学行为及相应的耦合理论. 我们也通过修正Simpson-Peterson公式研究了不对称金盘-劈裂盘耦合体系中因耦合方向造成的共振能量变化问题[90 ] . 如图8(d) , 第一排不同偶极子耦合示意图明确给出了劈裂盘开口角变化引起不同偶极模式(电偶极和磁偶极)方向及中心的变化趋势, 第二排给出了在不同偶极中心偏移距离下, 劈裂盘开口角方位对应的耦合能量偏移量. 经过系统的验证, 最终结果表明形貌一定的表面等离激元结构的耦合方位发生变化时, 其固有的偶极振荡中心不变, 为表面等离激元耦合结构逆向设计提供了新的思路.5.4.基于表面等离激元耦合的Fano共振 -->5.4.基于表面等离激元耦合的Fano共振 Fano干涉普遍存在于有两条可行途径的体系能量变化过程中[91 ] , 其主要来源是两条可行路径之间的相消干涉, 其结果是到达末态的能量变少. 这一现象初期发现于原子和其他量子体系中, 比如半导体量子阱耦合体系[92 ] . 近年Fano干涉效应被用以描述金属表面等离激元体系中的强耦合作用[93 ,94 ] . 基于表面等离激元耦合的Fano干涉过程可以通过如图9(a) 所示的频率简图来说明[95 ] , 其内容主要包括连续态的入射光子$\left\langle I \right\rangle $ 、亚辐射暗模式$\left\langle D \right\rangle $ 、超辐射明模式$\left\langle B \right\rangle $ 及散射或消光响应. 因为自由电荷吸收等因素主导的辐射和非辐射损耗, 超辐射明模式具有较长的振荡寿命, 其相应的衰减速率可用ΓB 表示; 而因为非辐射衰减是暗模式主要的衰减通道, 所以亚辐射暗模式的振荡寿命较短, 其相应的衰减速率为ΓD $\ll $ ΓB . 明模式的净诱导偶极矩较大, 能够直接与入射光相互耦合, 可以被入射光直接激发, 而暗模式因其近零的净诱导偶极矩无法直接与入射光相互作用, 一般不能被入射光直接激发, 但如果明暗模式对入射光的响应光谱相互覆盖时, 模式之间的近场耦合作用可以间接激发暗模式. 当金属结构体系中的明模式和暗模式可以被某一频率同时激发时, 明模式将会有两条激发路径: 第一条$\left\langle I \right\rangle \to \left\langle B \right\rangle $ , 其过程用绿色箭头表示, 即明模式被入射光子直接激发; 第二条$\left\langle I \right\rangle \to \left\langle B \right\rangle \to $ $\left\langle D \right\rangle \to \left\langle B \right\rangle $ , 其过程用蓝色箭头表示, 即明模式被入射光子直接激发, 暗模式首先通过近场耦合作用被明模式激发, 然后反过来通过近场耦合作用激发明模式. 当明暗模式激发态的近场相互重叠时, 二者之间将发生强烈的耦合作用, 致使明模式的振荡相位变化量不断增大并呈现色散属性[94 ] . 通常, 激发态谐振子的振荡相位变化量范围处于0—π之间. 当路径$\left\langle B \right\rangle \to \left\langle D \right\rangle \to \left\langle B \right\rangle $ 上累积的振荡相位变化量为π时, 图9(a) 所示的两条激发路径之间发生Fano相消干涉, 减小了明模式对入射光的响应, 在散射或消光光谱中呈现出不对称的响应谷特征. 当明暗模式的振荡相位相同时, 两条激发路径之间发生Fano相长干涉, 增强了明模式对入射光的响应, 在散射或消光光谱中呈现出不对称的响应尖峰特征. 不同于洛伦兹谱线形状, Fano共振模式具有明显的不对称线状(图9(b) ), 其响应金属微纳结构的光学响应强度可表示为[96 ] 图 9 (a)表面等离激元共振诱导Fano共振的过程示意图; (b)固体金属球的米氏散射[96 ] ; (c)不同结构配置的透射系数谱及标定位置对应的电场分布[99 ] ; (d) Fano参数与相移关系及对应的Fano响应函数[100 ] Figure9. (a) Process of surface plasmon resonance inducing Fano resonance; (b) Mie scattering against a solid metallic sphere[96 ] ; (c) the transmission coefficient spectra of different structural configurations and the electric field distribution corresponding to the calibration position[99 ] ; (d) Fano parameter versus phase shift and the Fano response function[100 ] .ω 0 是与共振峰位置相关的参数, γ 是表征共振峰宽度的参数, F 描述谱线线状的不对称性. 从结构设计角度来说, 通过不对称性(包括形状、尺寸、材料及空间环境的不对称)结构引起对称破缺是获得Fano共振效应的有效策略之一[10 ,97 ,98 ] . 近年来, 基于表面等离激元耦合的Fano共振因其陡峭的光学响应线形轮廓在传感器、开关、激光、慢光及非线性等领域具有巨大的潜在应用价值. 如Zhang等[99 ] 提出了一种由亚波长石墨烯盘和同轴环形金环阵列组成的超灵敏太赫兹传感器(图9(c) ). 石墨烯盘和金环产生的共振态发生干涉作用形成双Fano型响应谱线并使之能够实现超灵敏感测. 其仿真结果表明频率灵敏度高达1.9082 THz/RIU (refractive index unit), 品质因数可达6.5662. 此外, 可以通过调节石墨烯的费米能级来主动调节这一探测器的感测范围. Limonov等[100 ] 通过两个有效耦合的谐振子模型回顾了广泛的共振电磁效应, 包括Fano共振、电磁感应透明、Kerker-Borrmann效应以及奇偶时间对称性破缺, 讨论了如何引入Fano参数来描述与不对称Fano和对称Lorentzian形状相关的两种不同光谱特征之间的转换(图9(d) ). 同时总结了近期关于介质纳米结构和超表面Fano共振效应的结果.6.总结与展望 本文对表面等离激元光子学领域现有的金属光学性质、表面等离激元理论做了深入的简述, 系统地总结了体等离激元、传播的表面等离激元及局域表面等离激元三者之间的联系和区别. 此外还简述了激发等离激元共振的方式和条件、等离激元动力学及现行成熟的等离激元耦合理论. 未来有望在明晰各类表面等离激元机理的基础上, 通过不同金属微纳米结构的设计和使用, 调控金属微纳米结构的跨尺度、跨物理场响应, 增加表面等离激元的控制手段, 拓展表面等离激元的应用范围, 促使其在如全息、单分子检测、热电子产生、非线性效应等领域中的应用和产业化转变. 


























 图 1 (a)传播表面等离激元示意图; (b)局域表面等离激元示意图[35]
图 1 (a)传播表面等离激元示意图; (b)局域表面等离激元示意图[35] 图 2 支持SPP传输的金属-介质界面示意图
图 2 支持SPP传输的金属-介质界面示意图











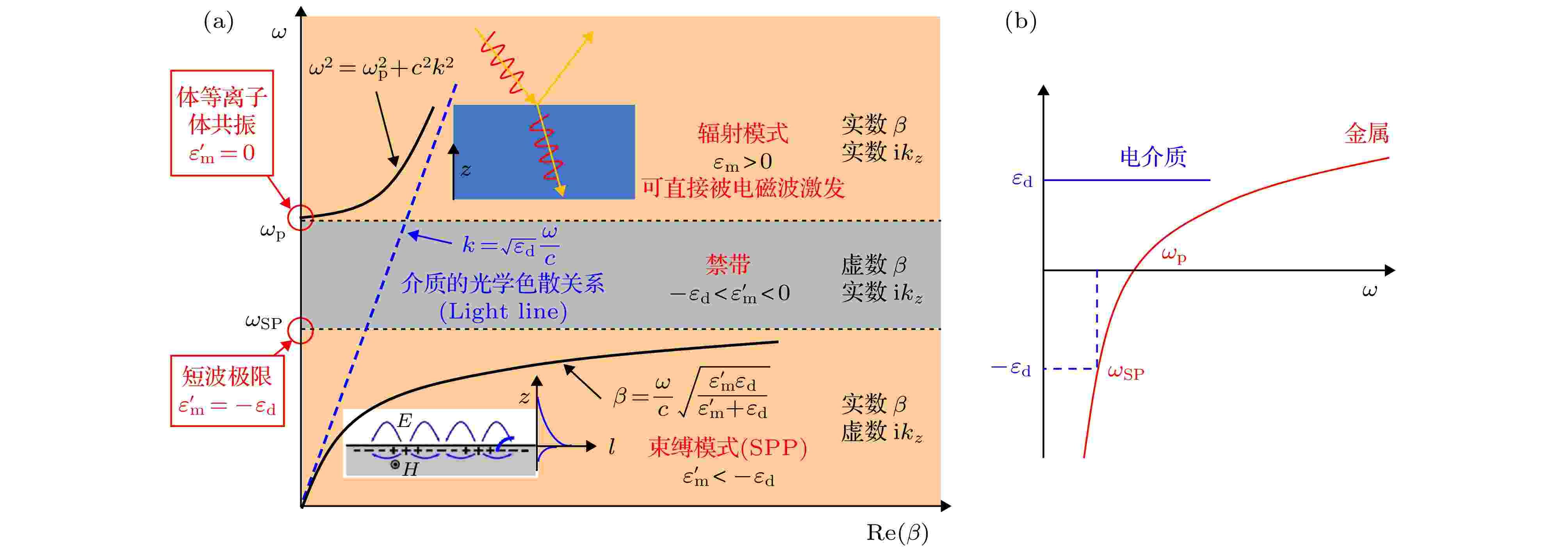 图 3 (a)金属全频色散关系; (b)金属和电介质的介电常数与入射频率之间的关系(借鉴中国科学院大学董国艳老师《纳米光学》第十讲图)
图 3 (a)金属全频色散关系; (b)金属和电介质的介电常数与入射频率之间的关系(借鉴中国科学院大学董国艳老师《纳米光学》第十讲图) 图 4 静电场中的金属微纳米球
图 4 静电场中的金属微纳米球

























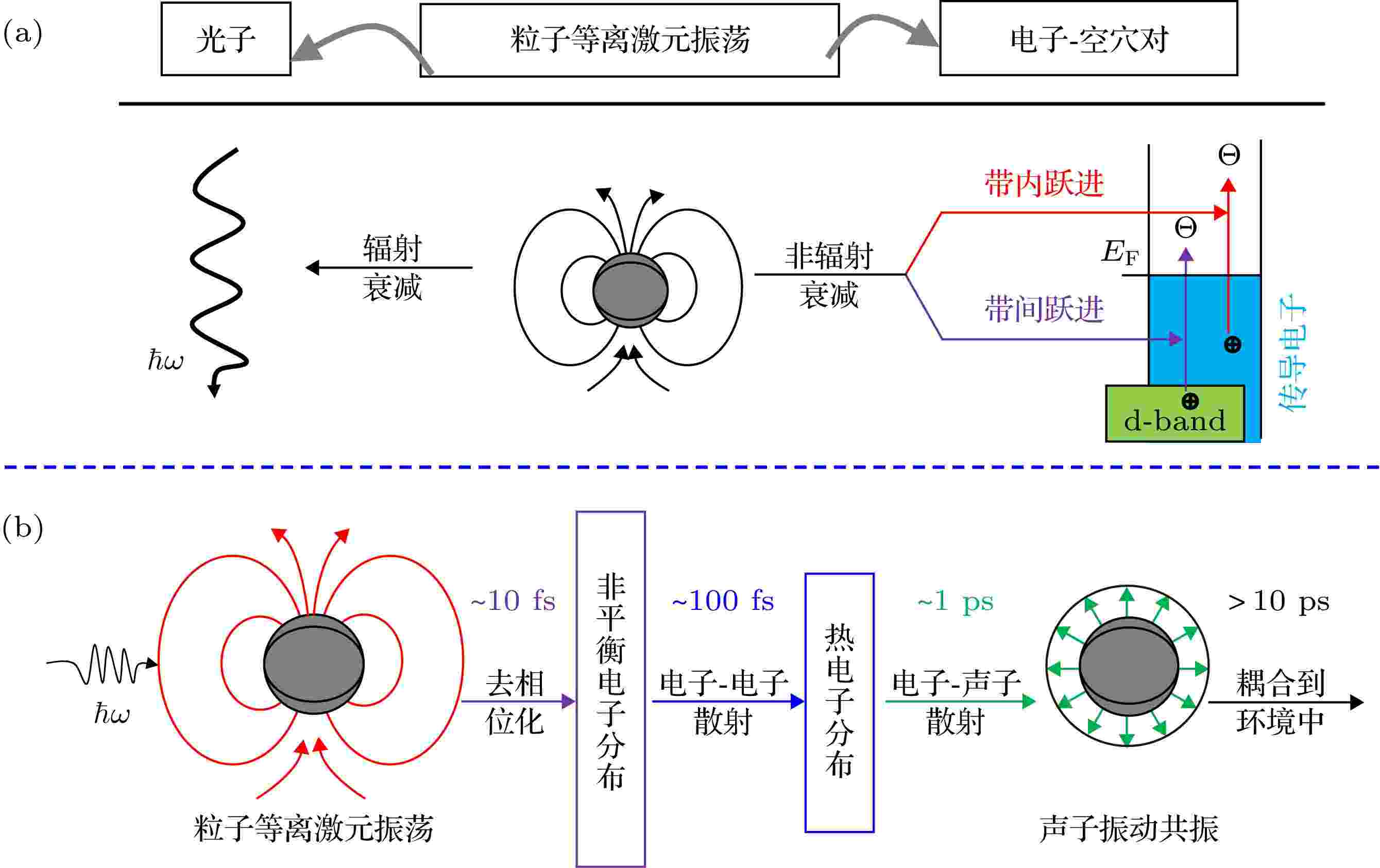 图 5 (a)衰减通道示意图; (b)衰减动力学过程
图 5 (a)衰减通道示意图; (b)衰减动力学过程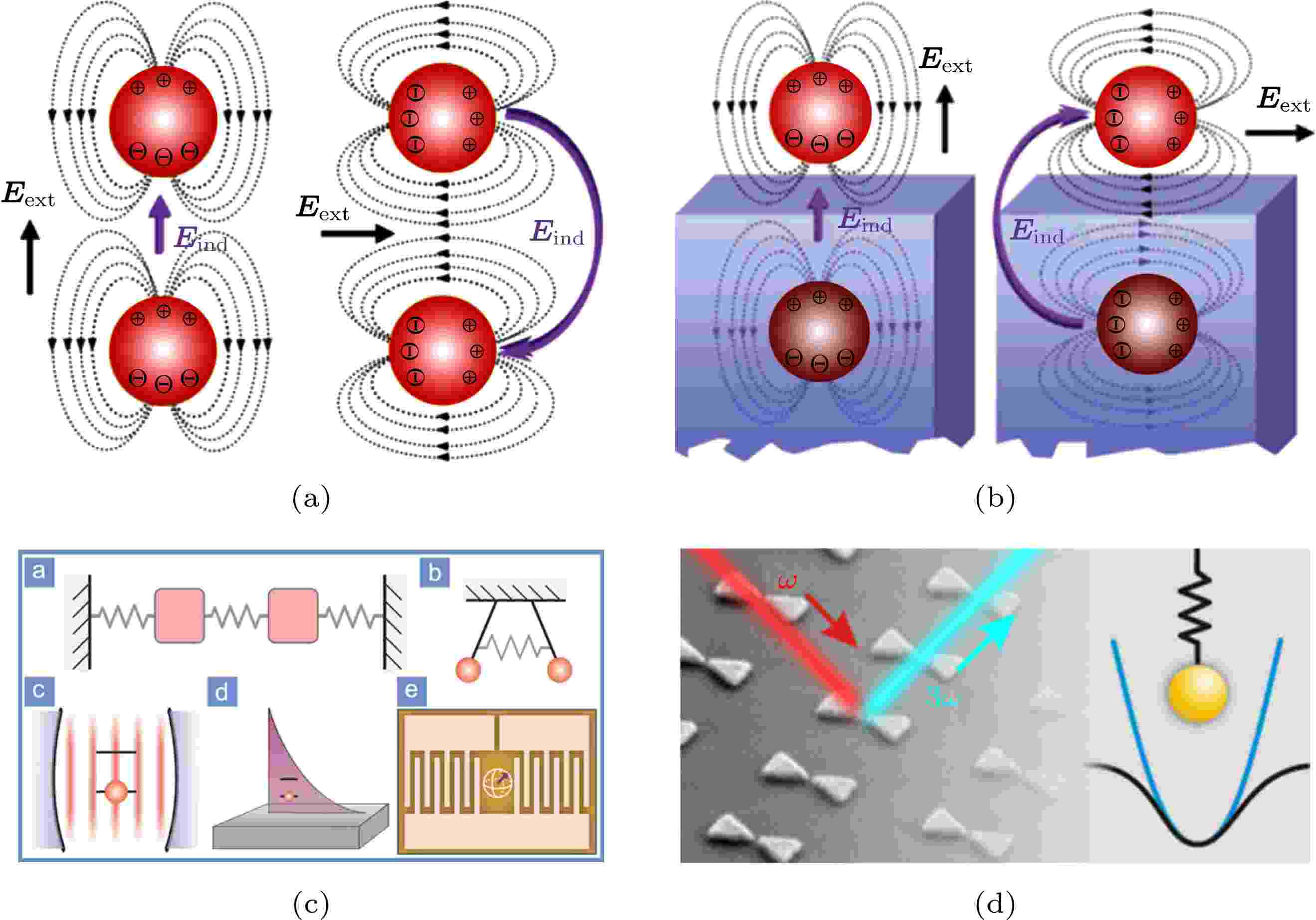 图 6 (a)谐振子间耦合示意图[73]; (b)谐振子与其镜像耦合示意图[73]; (c)耦合的简谐振子[74]; (d)三次谐波产生对应的等离激元非线性谐振模型[75]
图 6 (a)谐振子间耦合示意图[73]; (b)谐振子与其镜像耦合示意图[73]; (c)耦合的简谐振子[74]; (d)三次谐波产生对应的等离激元非线性谐振模型[75] 图 7 (a)表面等离激元共振模式杂化过程图; (b)堆叠式金属带的透射光谱及表面等离激元杂化示意图[77]; (c)单一劈裂盘阵列的透射光谱及其对应的共振模式杂化图[10]; (d)双层月牙形结构的模式杂化[78]; (e)杂化模式成像[79]
图 7 (a)表面等离激元共振模式杂化过程图; (b)堆叠式金属带的透射光谱及表面等离激元杂化示意图[77]; (c)单一劈裂盘阵列的透射光谱及其对应的共振模式杂化图[10]; (d)双层月牙形结构的模式杂化[78]; (e)杂化模式成像[79] 图 8 (a) Simpson-Peterson模型物理量分布图; (b)不同角度的耦合及对应的消光光谱[72]; (c)不同排布金纳米棒的耦合及潜在应用[89]; (d)不同偶极中心偏移量下耦合能量随角度的变化曲线[90]
图 8 (a) Simpson-Peterson模型物理量分布图; (b)不同角度的耦合及对应的消光光谱[72]; (c)不同排布金纳米棒的耦合及潜在应用[89]; (d)不同偶极中心偏移量下耦合能量随角度的变化曲线[90]







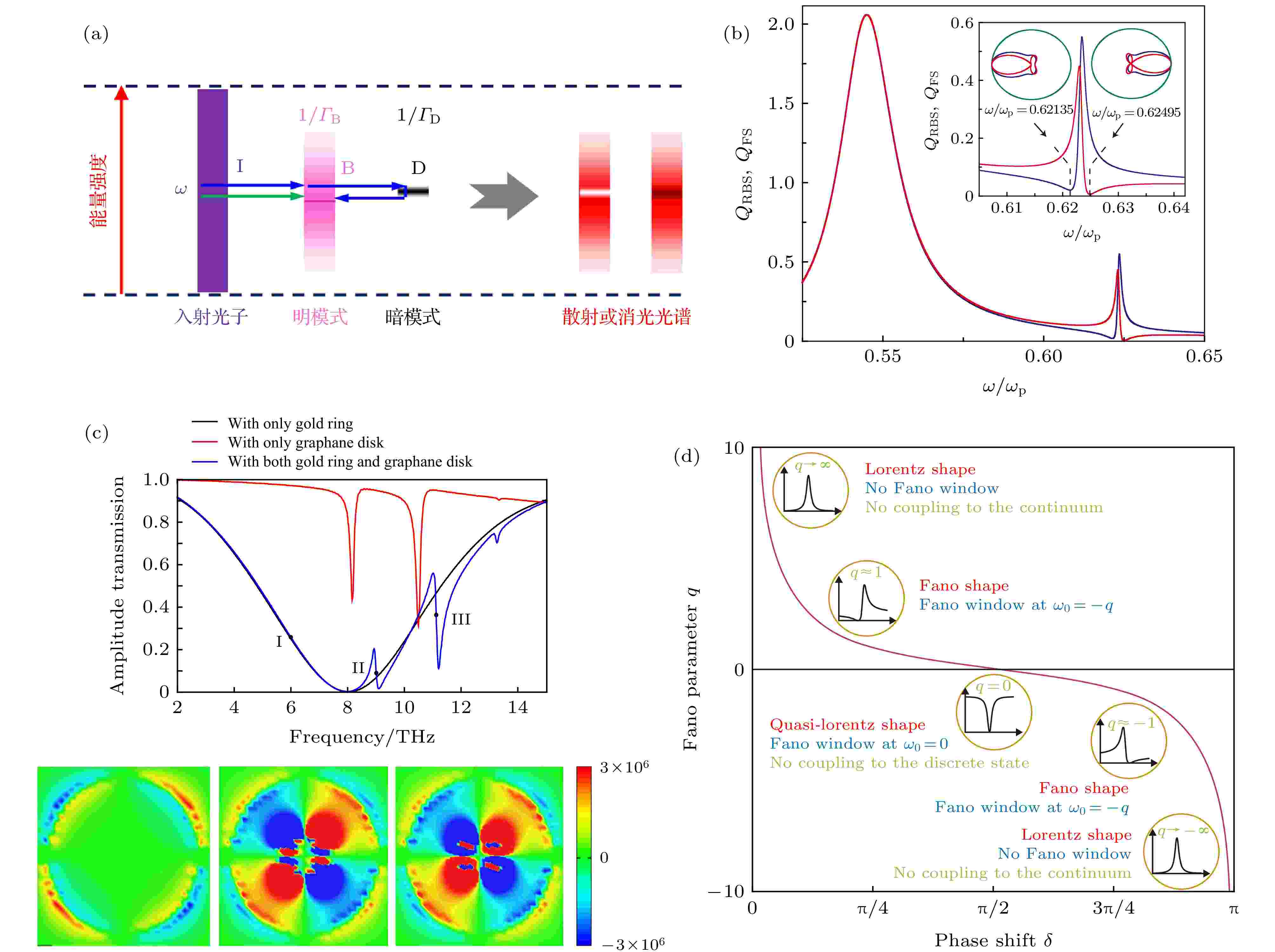 图 9 (a)表面等离激元共振诱导Fano共振的过程示意图; (b)固体金属球的米氏散射[96]; (c)不同结构配置的透射系数谱及标定位置对应的电场分布[99]; (d) Fano参数与相移关系及对应的Fano响应函数[100]
图 9 (a)表面等离激元共振诱导Fano共振的过程示意图; (b)固体金属球的米氏散射[96]; (c)不同结构配置的透射系数谱及标定位置对应的电场分布[99]; (d) Fano参数与相移关系及对应的Fano响应函数[100]