全文HTML
--> --> -->拓扑的概念在这个时候就起到了关键作用. 拓扑在物理上的应用早期集中在对量子场论的非平凡激元进行分类上. 后来在凝聚态领域, Thouless等[3]在研究量子霍尔效应时引入了电子能带拓扑的概念, 并使用TKNN (Thouless-Kohmoto-Nightingale-den Nijs)拓扑不变量来解释量子霍尔效应中霍尔电导所表现出的量子化和鲁棒性. TKNN不变量是电子基态波函数在倒空间里的整体几何相位[4]. 随后, Haldane[5]指出, 量子霍尔效应不局限于有外加磁场的体系, 可以通过引入人工规范势来实现反常量子霍尔效应. 这些效应依赖于时间反演对称的破缺. 近年来, 大量关于拓扑绝缘体的研究还提出时间反演对称体系中的量子自旋霍尔效应[6], 以及用不同模式构造赝自旋从而产生的量子谷霍尔效应[7,8]. 这样, 人们可以利用(赝)自旋这个空间以外的自由度来操控凝聚态体系. 在以上所有这些效应中, 拓扑非平凡体系具有受到体带拓扑保护的边界态, 它对无序和涨落都具有极强的鲁棒性.
受到早期电子系统和后来光子系统中拓扑概念的启发, 波动声学体系中的拓扑也很快被提出来. 这方面较早受到关注的是空气声和水声之中的拓扑现象[9,10], 这是由于这些体系中对声波的操控较为简单. 其中, 通过引入环流或者引入时间驱动以打破时间反演对称, 可以实现声波的量子霍尔效应[11,12]. 而即便不打破时间反演对称性, 引入赝自旋的自旋轨道锁定也可以实现声波的量子自旋霍尔效应[13,14]. 这些体系都实现了单向且对边界无序具有强鲁棒性的声学边界态. 然而, 固体中弹性波的拓扑现象在后来受到更多的关注. 这里主要有两个原因; 其一, 相比空气声和水声, 固体中的弹性波对应到连续极限下的长波声子, 具有内禀的不同偏振方向, 这大大增加了它的调控手段; 另外, 随着人们对可集成化芯片尺度器件的追求越来越高, 固体弹性波声子器件显得更有魅力—它波动的频率更高, 携带的信息量大, 而且承载它的固体器件易小型化. 本文对波动声子的讨论主要局限于弹性波声子范围.
器件设计中另一个重要的概念是非互易性. 非互易性效应通常指沿着一个方向或者沿它的相反的方向传输时一个物理量具有不同的输运性质, 这可以表现为相位或者幅值不同. 非互易器件可以使人们对波和热进行整流和隔离. 前面提到, 拓扑非平凡的系统在边界上具有受拓扑保护的边界态, 而这样的边界态往往是单向输运的. 这便是由拓扑性质产生的边界非互易性, 并且这种非互易性具有很高的鲁棒性, 对于小器件的稳定工作具有非常重要的作用. 除此之外, 非互易性还有非拓扑保护的其他来源, 例如含时驱动带来的能带倾斜[15,16]等, 后面会进行具体介绍.
不同于波动声子体系中声子的弹道输运, 在热传导中声子可能会体现出扩散输运的性质. 另外, 热传导中的能量输运是众多模式声子的共同作用的结果. 这使得在热传导系统中, 对热声子操控的难度相比波动声子大了许多, 操控波动声子的很多方法不能直接应用到热传导之中. 然而, 本文要给出的一个信息是, 通过含时驱动, 可以跨越不同的尺度对热传导中的声子进行所需要的调控[17-20]. 这其中, 热非互易和热抽运是两个重要例子.
需要说明的是, 本文的一个关注点是近期声子系统中拓扑性质和非互易现象相结合的研究工作, 主要介绍声子系统中弹性波和热传导的一些有趣现象, 其中强调了含时驱动系统部分. 由于关于声子系统拓扑与非互易的研究众多, 文中的广度和深度受到诸多限制, 更多的讨论可以参考相关综述文献[21-24]. 例如, 关于拓扑声学的内容, 请参考文献[22,23]; 关于拓扑声子的内容, 请参考文献[21,24]等.
2
2.1.拓扑与非互易的一般性概念
在线性周期性系统中, 能带的拓扑性质是一种整体性质. 系统的拓扑性质可以由一个拓扑不变量来描述. 此拓扑不变量因受到拓扑保护而在大多数微小扰动下保持不变. 拓扑不变量通过体边对应和边界态的数目相联系. 根据拓扑不变量的不同, 可以把系统分为不同的拓扑等价类. 不同拓扑等价类的系统无法经由连续的绝热变换联系起来, 它们之间的相互转换必然经由拓扑相变.系统能带上的Berry联络可以由其布洛赫函数得出:
在量子自旋霍尔效应中, 时间反演对称未破缺, 相反自旋的陈数互为相反数, 因而
材料或器件近期另一个得到广泛关注的性质是其(非)互易性[26]. 非互易是指一个器件沿两个方向进行能量传输时表现不相同的现象. 对于波动体系来说, 非互易包括幅值和相位的非互易. 法拉第效应就是一个众所周知的具有非互易性的例 子[27], 利用它可以得到法拉第光隔离器[28]. 非互易性之所以重要, 是因为人们可以应用它来独立调控不同方向上能量和物质流的大小, 实现整流和隔离. 为了应用(非)互易性, 需要研究说明哪些物理机制可以导致(非)互易性.
严格讲, 实际上人们关注的互易性主要包括两种. 其一是洛伦兹互易[29], 另一个是昂萨格互易[30]. 洛伦兹互易性是指[31], 在一个两端口线性无损耗系统中, 若调换这两个出入射的端口, 它们之间通过介质耦合的性质不发生任何变化. 数学上来看, 即系统对波的散射矩阵是一个对称阵. 有两种方式可以打破洛伦兹互易性; 1)在线性系统里, 打破时间反演对称, 如法拉第效应; 2)引入非线性, 使得系统参数(比如介电常数和磁导率)依赖于场强, 从而变得依赖于入射路径. 昂萨格互易性是昂萨格在研究近平衡态系统线性响应系数之间关系时发现的[32,33]. 假设近平衡态系统具有微观可逆性和细致平衡, 若它的各分量流和各个热力学势之间的线性响应关系记为
2
2.2.拓扑与非互易的联系
拓扑概念与非互易现象不是相互独立的, 而是相互关联的. 一方面, 虽然非互易输运有很多种实现方法, 但利用拓扑边界态的手性特征, 就可以通过多端口系统实现其中两端口间的边界非互易传输[34]. 此时的非互易传输实际上是一种边界的单向传输, 其单向通道受到拓扑保护, 且无背散射. 拓扑与非互易性的另一点联系体现在几何相的理论框架中. 几何相可以定义于任意的参数空间中. 对于周期结构, 它在倒空间中的非平凡性质会导致非平凡的拓扑能带. 而在其他参数空间中的非平凡的几何相和曲率结构也可以通过绝热驱动体现出来, 非互易性热传输和热抽运就是这里的一个重要例子. 此现象在量子分子节、自旋-玻色模型以及经典系统中都存在[17,35,36].2
2.3.含时驱动带来的物理效应
含时驱动能给原本静态的系统带来更多的可操控维度, 从而带来新颖的性质. 含时驱动引起的物理效应主要体现在如下几个方面. 首先, 绝热的参数含时驱动能使系统在参数空间中的几何性质在动力学中体现出来, 具体来说, 会使系统的相位或者输运物理量的生成函数, 在动力学贡献外, 获得一个额外的几何相贡献[17,35,36]. 另外, 通过周期性外场驱动, 可通过Floquet等效哈密顿量修正能带形状和能带拓扑. 能带中的Floquet拓扑态会在输运等过程中体现出来[37,38]. 除此之外, 近期含时驱动带来的合成维度和合成规范场也得到了广泛关注[39,40]. 含时驱动带来的合成维度可以扩大系统的可控制范围, 而合成规范场则带来了方便控制载流子或波运动的新方法.然而固体中弹性波和气体、液体等流体里的声波性质有所差别. 其优点在于, 弹性波声子具有流体声波里不具备的横波模式, 模式更加丰富, 频率相对来说较高, 能量密度更大. 软材料中相对流体声波来说, 弹性波更不容易受周围环境的影响[43]. 对弹性波进行操控的固态器件也更容易小型化, 可将对应器件集成到固体芯片上[44-46]. 这对于未来基于声子的信息处理和能量转换是十分关键的.
如何在实验上实现具有非平凡拓扑的弹性波体系, 而不同的体系各自具有什么样特殊的功能, 如何借鉴电子系统的拓扑分类对弹性波声子进行拓扑分类, 并且应用对称性给出对体系设计的指导[47], 将是近些年这个领域内众多工作要回答的问题.
2
3.1.固体弹性波中的拓扑
使电子体系表现出量子霍尔效应, 需要打破时间反演对称性. 无论是引入外加的强磁场, 还是合成人工的规范势, 都是为了使电子的拓扑性质受到时间反演破缺的保护. 在这样的体系中, 边界态具有单向性. 无论电子的自旋朝向如何, 它们在边界上的输运方向只取决于边界自身. 同样的, 在弹性波体系中要实现(类)量子霍尔效应, 也需要实现时间反演破缺. 而不同于电子, 声子不具有电荷, 因而直接对其进行操作时人们不具有类似磁场这样的能够打破时间反演对称的工具. 这时, 需要陀螺仪自由度或非惯性系等调制手段[34,48].虽然打破弹性波体系的时间反演对称可以带来新颖且重要的拓扑现象, 但无论是引入陀螺仪还是将系统放入非惯性系, 在实际操作和应用时都具有极大的难度. 这限制了弹性波拓扑的设计应用. 类比拓扑绝缘体中的概念, 即使不打破时间反演对称, 利用偏振这种额外自由度, 系统也可以产生手性的边界态[6,7]. 这就是所谓的量子自旋霍尔效应. 研究工作指出, 相比空气和水中的声波, 固体中的弹性波具有内禀的自旋角动量(图1(a))[49]. 而利用其自旋构造自旋轨道耦合, 实现非平凡拓扑和自旋依赖的单向通道, 是固体弹性波的独有优势. 另外, 若不利用弹性波内禀的自旋角动量, 仅通过构造弹性波的赝自旋轨道锁定(图1(b)), 对应的效应也可以被观测到[50].
图 1 (a)弹性波的内禀自旋轨道锁定[49]; (b)弹性波的赝自旋轨道锁定[50](由此都可以得到响应模式的单向通道)Figure1. (a) Spin-momentum locking in elastic wave systems[49]; (b) pseudo-spin-orbital locking in elastic wave system[50] (One-direction channels are established).
另外, 还有弹性波的量子谷霍尔效应(图2)[51-55]. 在这样的体系中, 时间反演对称同样没有被打破, 而是通过打破空间反演对称性来打开原本体系狄拉克点处的能带, 实现受保护的拓扑绝缘体. 它和量子霍尔效应不同的是, 体系每个空间边界都存在互相抵消的偶数条通道, 因而不存在净能流; 与量子自旋霍尔效应不同的是, 单个边界上两个传输方向相反的通道承载的是不同波矢的激元, 而不是不同自旋的激元. 若两种波矢由能带上巨大的谷分开, 则可以较为容易地独立激发出不同的态. 这些不同的态在单个边界上具有单向传播的特性.
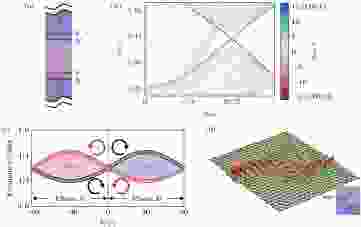图 2 (a)弹性波的谷拓扑绝缘体, 它的每个边界上都可以支持不同谷的边界态; (b)有限带状材料中弹性波体态和边界态的能带, 其中色阶表示(a)中不同的纵向坐标, 蓝色和红色分别表示上下边界[51]; (c)拓扑相变过程中的能带反转[53]; (d)受拓扑保护的边界传输[51]Figure2. (a) Valley topological insulator for elastic wave with different valleys supported on each edge; (b) bulk and edge band in a finite ribbon; the color bar implies the value of vertical coordinate, with pure blue (red) representing the upper (lower) edge[51]; (c) the band inversion during the topological phase transition[53]; (d) the topological edge state transmission is robust against disorder[51]
通常, 在系统发生拓扑相变时, 其边界态和对应的拓扑不变量发生转变, 在相变前后, 系统的等效参数也会发生变化, 从而会表现出不同的等效性质. 如图3所示, 在一维原子链系统中, 当引入一些在位势以及手性耦合时, 系统会显示出不同的等效性质—负的有效质量和负的有效模量. 当调节系统参数, 伴随着系统性质由负的有效质量变为负的有效模量, 其拓扑性质也会发生变化, 拓扑不变量发生改变. 具有有效负质量的系统和具有有效负模量的系统属于不同的拓扑相, 当将二者连接的时候, 会在界面处产生一个拓扑界面态[56]. 类似的现象在光子系统中也被提出[57].
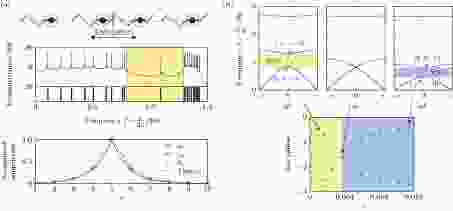图 3 (a)由有效负质量和有效负模量系统连接而成的有限长系统以及其界面态, 中间为系统的透射谱, 下面为带隙处共振峰频率下的振动模式; (b)不同参数情况下的系统色散关系以及较低两条能带的Zak 相位随着系统参数的变化[56]Figure3. (a) Schematic spring-mass model of a finite 1D system connected by mass-negative and coupling-negative to achieve the topological interface state, the middle of the figure is the transmittance spectrum and the lower is the spatial profile of the eigenmodes of the interface state; (b) the dispersion relation of the system by changing the parameter of the system and the curve of the Zak phase for the lower two band with respect to the system parameter[56].
2
3.2.固体弹性波中的非互易
对于弹性波来说, 要打破它的互易性, 除了打破时间反演对称, 主要手段就是引入非线性和空间不对称性. 但即便如此, 非线性和不对称性一起, 并不能充分保证非互易性[58]. 近年来, 在众多工作中, 研究者会使用时空调制来打破时间反演对称[15,59-63]. 这样的手段适用于众多体系, 应用范围较广. 在声子晶体中, 控制弹性波传播的主要为质量密度、弹性系数这两个参量. 实验上, 在宏观系统中, 可以通过直接在各个格点上施加外力驱动改变弹性系数, 而在小尺度系统中, 可以用光力效应或者压电材料, 通过外界电磁波或者电压驱动, 来改变声子晶体中的弹性系数[64]. 而这种方案实现的物理机制是, 利用时空调制带来的额外相位, 改变先前只有周期性不含时势场时晶体的能带, 使得能带关于
Nassar等[15,16,60]的工作指出, 时空调制带来的非互易性被涵盖在几何相位的理论框架下[17]. 他们使用慢驱动下绝热近似定理成立的条件, 得出能带倾斜大小是调制波形移动速率的整数倍的结论. 而这样的倾斜率是具有强鲁棒性的. 他们还计算了弹性波能带的几何相位和陈数, 并将陈数和能带倾斜的大小联系了起来. 在这样拓扑的框架下, 体带的倾斜率和单向无带隙边界态的数目可以通过体边对应相关联(图4(a)和图4(b))[16].
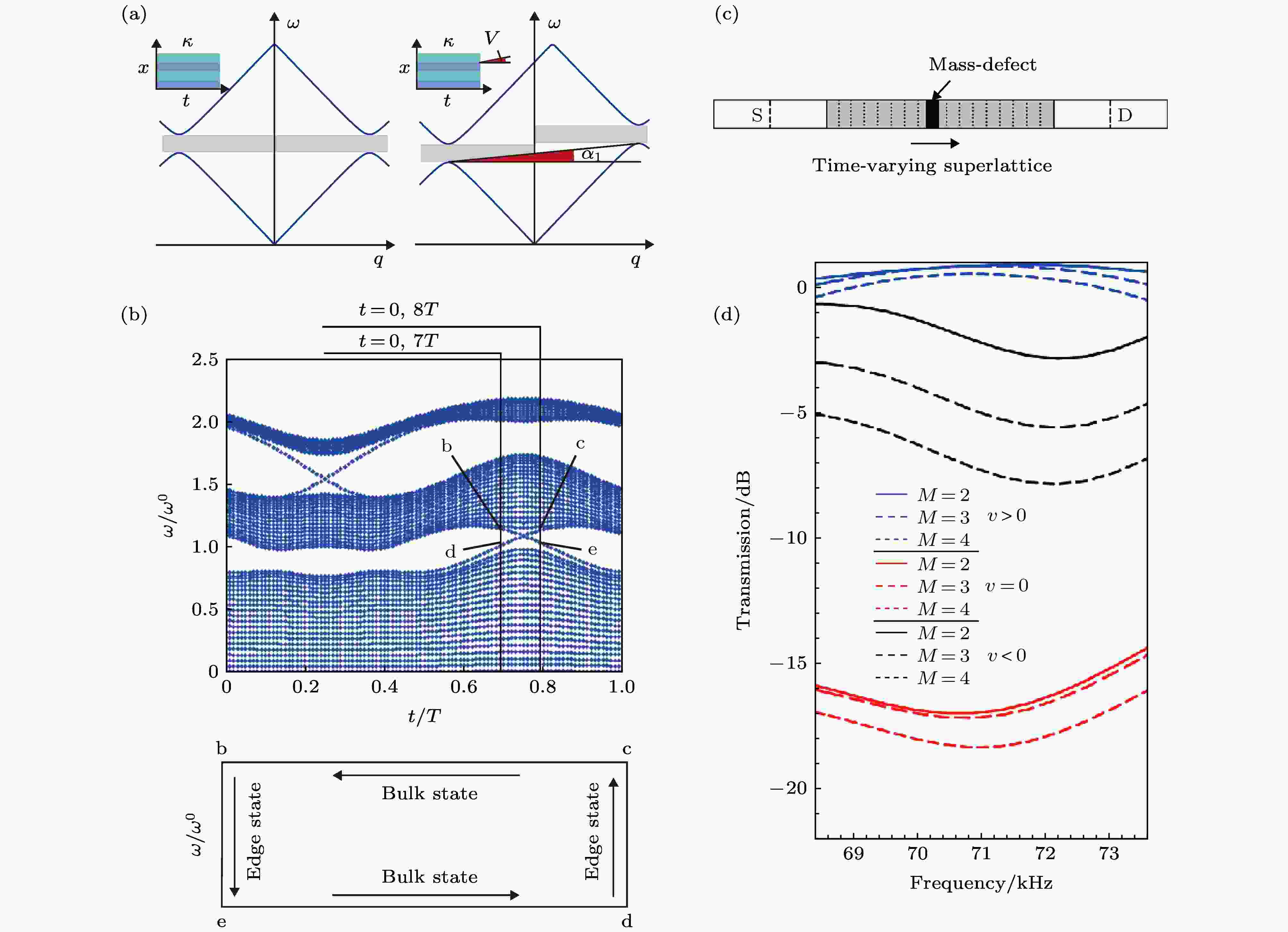图 4 (a)因时空调制, 空间周期势下的能带(左)对称性打破(右); (b)能带随时间变化中的体带和边界态; 体态和边界态具有体边对应[16]; (c)包含杂质的受驱动系统夹在两静态系统(S和D)中间; (d)从S到D传输弹性波的透射率, M是杂质大小, 而v是含时行波驱动的移动方向, 透射率的非互易性受到拓扑保护, 不受可能存在的杂质的影响[64]Figure4. (a) Inversion of energy band is broken by spatiotemporal modulation; (b) edge states in temporally varying energy band; the edge-bulk correspondence is present[16]; (c) the modulated middle part contains disorder and sandwiched between two static parts (S and D); (d) the transmission from S to D. M is the size of disorder, while v is the velocity of moving modulation. The non-reciprocity of the transmission is topologically protected from the disorder[64].
由于含时驱动打破了时间反演对称, 而这是非平凡拓扑和非互易的共同条件. 那么能不能应用时空调制生成非平凡拓扑, 从而利用由此产生的高鲁棒性单向边界态, 来实现完美的弹性波二极管呢？Swinteck等[64]在其工作中给出了确定性回答(图4(c)和图4(d)). 他们对一维声子晶体施加了一个边界条件, 然后将行波类时空调制施加在声子晶体上. 同时保证调制波长是晶体晶格常数的整数倍, 且整个系统的调制波结数为整数. 这样, 在调制的超晶格中, 能带发生折叠. 即便初始能带拓扑平凡, 通过含时驱动也可引入非平凡拓扑的能带. 而在这样的能带中, 一些频率上的波具有完美的单向性通道. 这样的单向输运是受到拓扑保护的. 含时调制下的非互易性可以抵抗原本一维系统中可能存在的杂质缺陷而不受其影响.
与此相对, 热传导过程是一个众多模式声子参与的过程. 因而不同于对弹性波的调控, 对热的管理需要对带宽范围声子同时施加影响. 传统实现的热二极管的方法为: 应用非线性势得到温度依赖的声子能谱, 从而控制不同温度下两端的能谱交叠, 进而实现热的非互易传输[65]. 而使用这种方法制成的热二极管通常只针对特定频率范围内的声子, 因此只在一小段温度区间和器件尺度有效[19]. 另外, 在微纳尺度的热传导中, 即便忽略量子涨落, 有限温度和非平衡等因素带来的涨落也对器件的工作具有重要影响. 人们需要对热流的涨落进行研究, 并且给出抑制或者利用这些涨落的能量传输方案.
2
4.1.声子与热的拓扑
早期的声子拓扑研究主要集中在对声子霍尔效应的理论解释上. 其中, 声子霍尔效应指, 在相互垂直的外加磁场和热流的作用下, 与两者方向都相垂直的方向上, 会出现一个附加的横向温度差[66,67]. 这个现象是在自旋-声子耦合下, 磁场对声子的间接作用导致的. 而研究工作表明, 声子霍尔效应可以在体系声子能带的拓扑性质中得到体现和解释[68,69].后续关于声子拓扑的研究试图在纯简谐声子体系中得到类似的拓扑不平凡性质. 其中, 为实现声子的量子霍尔效应, 需要打破体系的时间反演对称, 这方面的手段主要有两种; 1)在声子晶体的格点自由度上加入陀螺仪这样的自由度[48] 如图5所示; 2)将声子晶体本身置于非惯性系之中[34], 如图6所示.
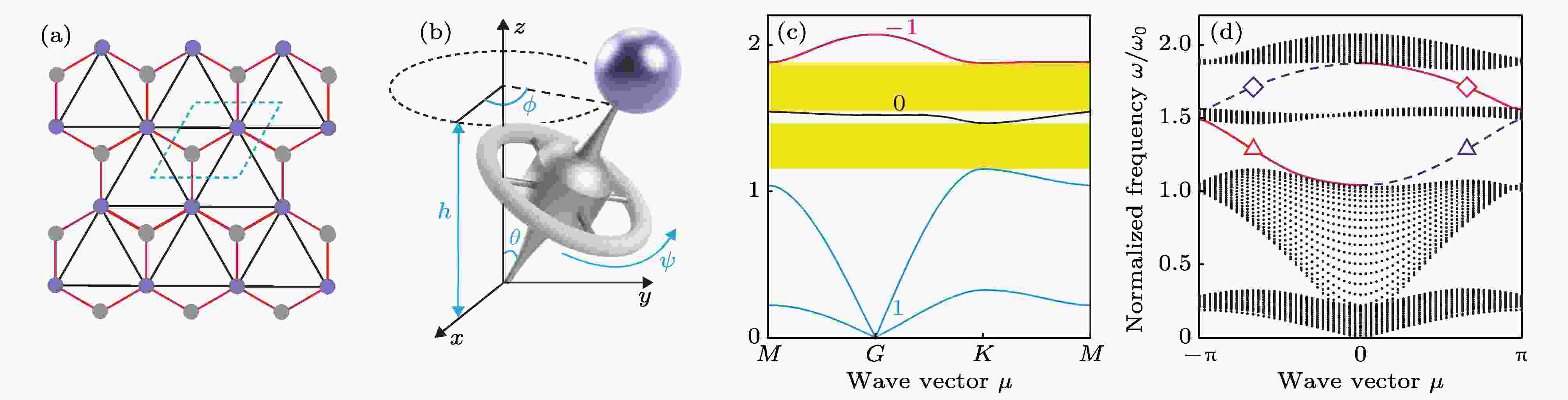图 5 通过引入陀螺仪打破时间反演实现的非平凡拓扑 (a)声子晶体的格点模型, 其中黑色和红色的线代表不同劲度系数的弹簧; (b)单个格点上的力学单元; (c)系统的能带, 能带上所标的数字代表该带的陈数; (d)有限系统的能态, 红线和蓝线分别为上下边界上的态, 可以看到, 单个边界上的态具有单向性[48]Figure5. Non-trivial topology induced by broken time reversal symmetry with gyroscopic degrees of freedom: (a) Lattice model of the phononic crystal, in which the black and red lines represent springs of different stiffness; (b) the mechanical unit set on each site; (c) the bulk energy bands with corresponding Chern numbers; (d) eigenstates of a finite system, with uni-directional edge states denoted by red (black) curves. The edge states are uni-directional[48].
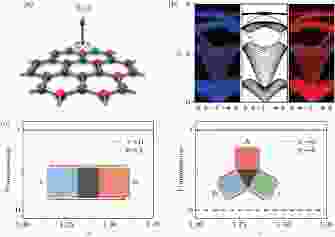图 6 将声子系统放入非惯性系引入的量子霍尔效应 (a)系统示意图, 声子系统的旋转类似对电子系统施加的磁场; (b)中间是准一维纳米带的能带, 左右两图分别为系统左右边界上存在的传输模式; (c)利用边界态单向性来调控频率处于体带带隙内的弹性波的传输, 尤为重要的是, 使用右边的三端口器件, 可以实现完美的弹性波非互易传输, 这是应用非平凡拓扑实现完美二极管的一个例子[34]Figure6. Elastic wave quantum Hall effect of phononic systems in non-inertial reference frame: (a) Diagram of the system, with rotation acting like an effective magnetic field in electronic systems; (b) energy band of a nano-ribbon in the middle panel, with available left (right) edge states on the left (right) panel; (c) using the uni-directionality of edge states to manipulate the transmission in band gap. Remarkably, a perfect wave diode is obtained with the three-terminal system[34].
上述框架可以分析一个封闭声子体系中特定模式的拓扑保护态. 但这样的理论框架不适用于包含热噪声、热库在内的开放热传导系统, 尤其是小尺度热传导器件. 小尺度器件中各个物理量都处在永不停息的涨落之中. 因而, 描述一个热传导过程只使用平均热流这个物理量是不够的. Levitov等[70]在研究电子输运过程时提出了全计数统计(full counting statistics)的概念. 全计数统计在数学上可以纳入生成函数论的范畴. 如果我们得到一个输运过程的全计数统计, 那么只要关于它对辅助参数进行n次求导, 就可以得到输运量的n阶涨落矩. 近二十年来, 非平衡统计物理中的一个重要成果—涨落定理—就可以方便在全计数统计的框架下得到[71]. 小系统热输运中的性质应当在全计数统计的框架下进行研究.
对于一个处于非平衡态的系统, 若要对它进行调控, 除了改变它所接的温度, 还可以对它内部的参数进行含时驱动. 这样的驱动实际可以通过调控外加力场来实现. 与量子力学中的绝热变换类似, 若对非平衡系统进行一个缓慢的回路驱动, 系统除了回到原先所处的态上, 还会额外获得路径上所累积的几何相的贡献, 且这样的几何相位不仅体现在平均热流上, 也体现在任意阶的热流涨落量上[17,35]. 应用这样的几何相, 可以对系统的输运性质进行调控, 尤其是实现微纳尺度的热抽运和热非互易输运.
图7[17,72]所示的例子中, 非零的热流是通过含时驱动两端的热库的温度产生的, 而若驱动反转, 热流方向也会同样改变. 这是典型的热抽运的例子. 而在另外的系统中, 即便两边温度保持时刻相等的关系, 也可以通过驱动中间系统和热库耦合以及它本身的参数实现热流的定向输运[35]. 由于热抽运产生热流的方向仅由驱动方向决定, 这样的热流可以作为一个附加项, 使得系统左右有温差时的热流具有非互易性. 若扩大参数调控范围到整个参数面, 则可以证明, 一次循环的热抽运热量值离散化且受到拓扑保护.
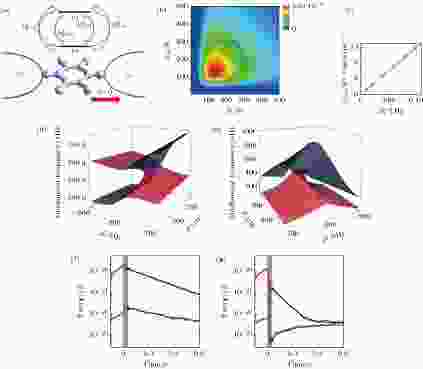图 7 (a), (b), (c)非线性分子结中的热抽运, 中间系统的跃迁速率和所接的温度相关, 因而可以通过含时调制左右热库的温度, 实现热流的定向输运; (a)系统示意图; (b)参数(左右两端所接温度)空间内的Berry曲率; (c)在慢驱动极限下, 平均热流大小和驱动频率成正比; 因而每次回路驱动产生的输运热量大小相同, 这种情况下热流是纯几何量; [17] (d), (e)非厄密两态光力系统等效哈密顿量在EP点附近的本征值; (f), (g)在t < 0时向系统馈入能量, 在灰色区域对系统进行绝热含时驱动, 其中(f)的驱动不绕过EP点, 而(g)的驱动绕过EP点, 是否绕过EP拓扑性地决定了两模式之间的能量交换方向[72]Figure7. (a), (b), (c) Heat pump effect in nonlinear quantum molecular junction. The state jumping rate of the junction is dependent on the temperature of two reservoirs, which can then be utilized to modulated temporally to achieve directional heat transfer. (a) The demonstrative diagram of the system; (b) berry curvature in the parameter (the temperature of reservoirs) space; (c) average heat transferring rate proportional to driving frequency, showing the pure geometric origin of pumped heat[17]; (d), (e) the eigenvalues around EP of the two state system’s effective optomechanical non-Hermitian Hamiltonian; (f), (g) the transient behavior of system’s energy on the two of states. The adiabatic driving in (f) does not circle around EP while that in (g) does. Whether circling around EP determines the energy transfer direction topologically.[72]
对于一些和外界有能量交换的开放系统, 可以把它们等效为一个非厄密的哈密顿量. 在这类系统中, 具有PT(parity-time)对称的系统是十分有趣的. 在这类系统的恰当参数范围内可能存在有EP(exceptional point)点这样有趣的本征结构. 在普通厄密系统的简并点上, 虽然本征值简并, 但本征矢仍是正交归一的. 而在EP点上, 本征值与本征矢都合并(coalesce)到了一起. 正如厄密系统的简并点附近具有非平凡的拓扑结构, 非厄密系统中EP点附近也同样有类似的拓扑结构[73,74]. 将系统绕着EP点附近参数驱动, 驱动产生的能量流和许多驱动细节无关, 而与驱动的次数成正比, 由此可以获得受拓扑保护的非互易能量传输[72]. 另外, 除了用来调控能量传输的PT对称系统, 具有反PT对称的本征耗散体系也具有十分有趣的性质, 如此类系统可以在反PT对称自发性破缺前后表现出完全不同的热输运行为[75].
2
4.2.声子与热的非互易
系统参数的时空调制, 同样可实现一类比较新颖的固体声子非互易性. 通过在声子晶体中引入时空调制, 可以调制系统能带, 实现非对称的能带结构, 从而在一个频率范围内得到非互易的传输通道, 如图8所示.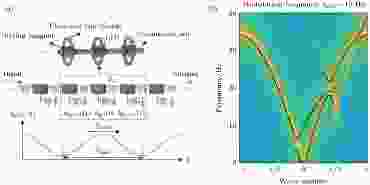
图 8 (a)系统示意图与驱动方式; (b)对弹簧劲度系数进行时空调制, 实现的能带非互易, 驱动带来附加的准能量和准动量使得能带内出现模式耦合, 使能带在满足广义Bragg条件的位置打开带隙[76]Figure8. (a) A schematic figure of the experimental system and the time modulation protocol; (b) the stiffness of springs is modulated spatiotemporally to achieve the non-reciprocal energy band. Periodical modulation brings mode coupling in the Bloch band, opening gaps in the position satisfying modified Bragg condition[76] .
传统的实现热二极管一般是利用非线性势和非对称性, 只在一小段温度区间和器件尺度有效. 而近期利用时空周期性调制实现的热非互易则可以应用在线性材料中. 且可以依照器件的尺度对时空调制的周期进行对应的调节, 从而可以迁移到多尺度的器件之中, 如图9所示.
图 9 (a)静态热二极管的原理示意图[1], 关键在于, 调控热传导相关主要模式声子的能谱交叠; (b)含时驱动带来的温度分布非互易性, 上下两图中驱动方向相反, 而左右所接的温度不变. 其中Γ代表了时空调制移动速率, Γ = 0即为无时间调制; 非互易效果随调制移动速度先变大再变小[19]Figure9. (a) A schematic static thermal diode obtained by manipulation of the spectrum overlap between the two nonlinear parts[1]; (b) non-reciprocal temperature distribution. The moving direction of the wave-like modulation is opposite between the upper and lower panels, while direction of temperature gradient is not altered. Gamma implies the velocity of modulation motion, which is zero when the modulation is independent of time. The degree of non-reciprocity first increases and then decreases when gamma monotonically grows[19] .
类似的方法也可以在宏观热传导中得到应用. 宏观的声子热传导现象由和扩散方程类似的热传导方程描述. 其中, 影响传导方式的主要有热导率和比热容这两个物理参量. 通过同时在这两个参数中引入行波式的时空调制,
对微纳尺度的声子热器件进行调制, 其实验上的实现手段是不容易的. 由于对电子和光子的调控精度目前远在对声子直接调控精度之上, 实验上往往利用声子和其他粒子的耦合来间接地调控声子系统. 其中一个重要的例子就是光力学系统. 它通过控制照射的激光的强度和相位, 相干性地控制力学器件, 从而调控声子的色散关系. 声子系统的非互易热输运已经在光力系统的实验中得到了实现[18,20].
与传统的静态方法不同, 通过引入时空调制的手段打破时间反演对称, 也可以给系统带来非平凡拓扑或非互易性. 它大大增加了系统的可调维度和可引入的势场种类, 其适用性可以跨越大量不同尺度不同类型的声子系统. 这也是这种方法在近些年受到大量研究的重要原因. 含时驱动的几何相效应或Floquet效应, 也可以用来实现完美的波/热二极管或隔离器. Thouless抽运正是这方面的一个众所周知的例子.
针对拓扑性质的研究中, 若将高阶拓扑绝缘体[77]、拓扑相分类[47]及非线性拓扑绝缘体[78]等概念引入弹性波和声子热输运体系中, 这个方向一定会获得更多新颖的结果. 另外一个重要的问题是, 如何进一步将拓扑概念引入开放耗散体系的能量输运及其统计涨落研究中, 使受拓扑保护的系统更好地工作而免受热涨落、量子涨落和杂质的影响. 另外, 如何进一步应用拓扑性质实现完美的非互易器件[64]也是一个值得继续深入研究的问题. 最后, 考虑到近期人们对引入非厄密性拓扑系统的关注[79], 探索非厄密拓扑声子系统中新颖的波动和热输运性质也是一个重要的研究方向.
