摘要:集成化导光板下表面微结构分布设计是提高背光模组亮度均匀性的关键因素之一. 本文提出了小尺寸集成化导光板下表面微棱镜二维分布公式, 给出了微棱镜二维分布公式系数与导光板结构参数之间的关系表达式. 将上述公式组直接应用于不同结构参数的小尺寸集成化导光板下表面微棱镜二维分布设计, 无需借助设计人员的经验, 可直接获得亮度均匀性较高时的集成化导光板下表面微棱镜二维分布, 出射光亮度均匀性平均值可达84.94%. 仿真结果表明, 本文提出的微棱镜二维分布公式及系数关系表达式具有重要应用价值, 极大地节省了集成化背光模组的设计优化时间, 对于导光板表面微结构分布设计具有重要的参考价值.
关键词: 光学设计/
集成化导光板/
微棱镜/
二维分布公式

English Abstract

全文HTML

--> --> -->

背光模组作为液晶显示器的光源, 其光学设计将直接影响到液晶显示器的光学品质^[1]. 研究导光板表面微结构分布, 以获得高性能参数的、轻薄的集成化背光模组, 成为科研机构的研究热点之一^[2]. 2014年, Li和Pan^[3]提出了导光板表面微结构分布覆盖比公式, 通过多次模拟仿真得到较佳的覆盖比比值, 提高了光能利用率, 亮度均匀性达90%左右. 同年, Chen和Kuo^[4]提出了一种上下表面熔合正交微棱镜的集成化导光板, 探讨了导光板下表面微棱镜分布密度参数对亮度均匀性的影响. 2015年, Chen和Pan^[5]设计了双光源的双层导光板, 导光板上表面微棱镜设置为贝塞尔分布, 优化后照度均匀性有所提升. 2017年, Huang等^[6]提出了密度动态调整算法用于优化混合光学膜表面微结构分布, 对光学膜表面进行分区, 通过循环调整分区内二次贝塞尔形式分布的微棱镜密度使得亮度均匀性大于90%. 同年, Lin等^[7]采用概率分析方法生成导光板表面分区内微棱镜密度, 并使用动态低偏差序列方法获得分区内微棱镜排布, 亮度均匀性在90%左右. 2018年, Chen和Pan^[8]提出了一种用于汽车显示器的高效定向背光模组, 导光板下表面微棱镜分布采用贝塞尔分布进行优化. 上述研究中, 有的需要通过多次仿真得到较佳的分布参数^[3,4,8]或是未提及优化初始参数^[5,6], 有的需要对导光板进行事先的人为分区^[6,7]. 2018年, 本实验室利用数值分析方法得到了集成化导光板(partial integrated light guide plate, PILGP)下表面微棱镜的一维分布表达式及表达式系数与导光板结构参数的关系表达式^[9]. 之后, 为了解决微棱镜一维分布导致的出射光亮度大面积同一性问题, 提出微棱镜二维分布的设计思想; 并利用光学软件Lighttools中的背光图案优化(backlight pattern optimization, BPO)模块, 通过多次调节BPO模块中的参数, 仿真优化得到了一款下表面微棱镜具有较佳二维分布的5英寸PILGP^[10] (1 in = 2.54 cm), 提高了集成化背光模组出射光的整体亮度均匀性; 该研究中需要凭设计人员的经验并借助软件多次调试仿真.
本实验室长期致力于背光模组集成化、轻薄化研究^[9-22], 为快速获得PILGP下表面微棱镜较佳的二维分布, 在上述研究工作基础上, 本文创建小尺寸PILGP下表面微棱镜的二维分布公式, 及分布公式系数与导光板结构参数的关系表达式. 应用上述分布公式组, 无需依靠设计人员的经验或应用软件多次仿真优化, 即可直接获得PILGP下表面微棱镜的较佳二维分布, 极大地节省了集成化背光模组的设计优化时间.

集成化背光模组是由发光二极管(light emitting diode, LED)光源、PILGP和平面反射膜(reflective film, RF)组成, 如图1所示^[10]. 其中, PILGP上表面熔合密排的非球面半柱状微聚光结构(aspheric semi-cylindrical micro-concentrator structure, ASCMCS)阵列, L, W分别为PILGP的长度、宽度; 下表面熔合与上表面微结构正交的微棱镜阵列, α, β分别为微棱镜单元的近、远光源底角; PILGP下方设置独立的平面反射膜.
图 1 集成化背光模组结构示意图
Figure1. Diagram of partial integrated backlight module.

2

-->

2.1.集成化导光板下表面微棱镜二维分布公式

图2为PILGP下表面微棱镜二维分布示意图. 其中, 虚线方框部分为微棱镜分布的优化区域, 其对应的是导光板上表面的出光面, 优化区域外的部分对应的是导光板上表面遮光胶带覆盖区域; 优化区域的正中心为导光板下表面(x-y平面)的坐标原点O; 第0行、第0列微棱镜(即微棱镜的中心点)位于优化区域中距离光源最远端的中心处.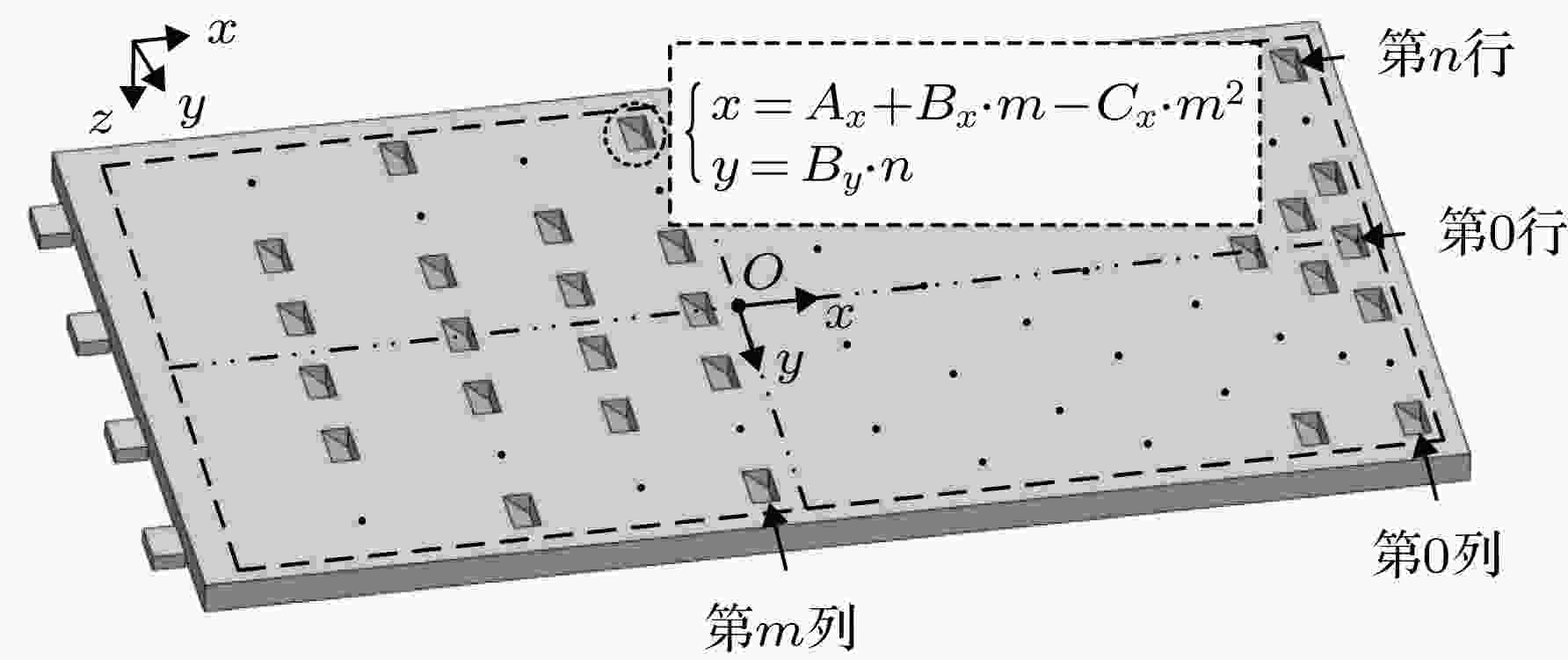
图 2 PILGP下表面微棱镜二维分布示意图
Figure2. Two-dimensional distribution of micro-prism on the bottom surface of PILGP.

由PILGP下表面微棱镜二维分布原理^[10]可知, 微棱镜分布密度在导光板长度方向(x轴)由近光源区域到远光源区域呈递增趋势, 即相邻微棱镜间距随着距离光源越远而递减; 因此, x轴方向上, 微棱镜分布可用二次多项式表示. 微棱镜分布密度在导光板宽度方向(y轴)由中间区域到两侧区域呈递增趋势, 即微棱镜间距由中间区向两侧区递减; 不过, 这种变化趋势相对于在x轴方向不明显, 因此, y轴上微棱镜分布可用线性表示. 据此, 我们提出PILGP下表面微棱镜二维分布公式为

$x = {A_x} + {B_x} \cdot m - {C_x} \cdot {m^2},$

$y = {B_y} \cdot n,$

其中x, y分别表示第n行、第m列微棱镜单元底面中心点的横、纵坐标; m, n为整数且m ≤ 0, m沿–x轴依次减小, n取值与y轴同相; A_x, B_x, C_x分别表示x轴方向微棱镜分布公式的零次项、一次项和二次项系数, B_y表示y轴方向微棱镜分布公式的一次项系数. 由图2可知, A_x表示微棱镜中心点横坐标, 可表示为

${A_x} = \dfrac{{\left( {L - {L_{x0}} - d} \right)}}{ 2},$

其中L_x0表示导光板上表面x轴方向上的遮光胶带长度, 本文中取值为7.5 mm; d表示微棱镜单元底宽.
在微棱镜二维分布表达式中, 系数A_x控制微棱镜中心点横坐标位置, 系数B_x, C_x控制微棱镜在导光板长度方向(x轴)的分布, 与导光板长度L有关; 系数B_y控制微棱镜在导光板宽度方向(y轴)的分布, 与导光板宽度W有关.
2 -->

2.2.分布公式系数与导光板宽度W的关系表达式

本小节以5英寸集成化背光模组为模型, 利用光学软件Lighttools不断仿真优化得到较佳的系数B_x, C_x; 基于上述较佳的系数B_x, C_x, 探索系数B_y与导光板宽度W的关系表达式.
首先, 利用光学软件Lighttools建立5英寸集成化背光模组模型, 建模参数如表1所列, (3)式中d取微棱镜单元底宽近似值0.05 mm. 通过不断仿真得到系数B_x, C_x, B_y的初始值, 使得背光模组亮度均匀性达80%以上. 再以上述系数B_x, C_x, B_y初始值确定的微棱镜下表面分布作为初始分布, 将亮度均匀性设置为评价函数, 进一步优化微棱镜下表面的分布, 亮度均匀性达90%以上的B_x, C_x, B_y为较佳的系数. 最终, 仿真得到较佳的B_x = 0.71725, C_x = 0.022149, B_y = 0.23967; 此时, 5英寸集成化背光模组的亮度均匀性为94.22%.

项目	结构参数
PILGP材料和尺寸	聚甲基丙烯酸甲酯(PMMA), 116.3 mm × 68.7 mm × 0.5 mm
PILGP上表面结构	高度88.6 μm、宽度180 μm、长度116 mm的ASCMCS单元, 密排
PILGP下表面结构	底宽0.049 mm、长度0.1 mm、α = 50°、β = 90°的内凹型微棱镜单元
LED发光强度和尺寸	6.6646 lm, 朗伯分布, 发散角110°, 1.2 mm × 2.5 mm × 0.4 mm
LED数量和间距	10个, 6.56 mm, 等间距分布于PILGP的短边
平面反射膜	反射率95%

表15英寸集成化背光模组结构参数
Table1.Structural parameters of 5-inch partial integrated backlight module.

接着, 固定导光板长度L为116.3 mm、高度H为0.5 mm, 分别建立不同导光板宽度W为42.5, 68.7, 95.0, 108.0, 134.2, 147.3 mm的集成化背光模组模型, LED光源个数随W相应增加; 由于L不变, 因此系数B_x, C_x也保持不变. 通过不断仿真优化, 得到不同W下的较佳系数B_y, 此时背光模组亮度均匀性均达85%以上, 如图3中的黑色圆点所示.
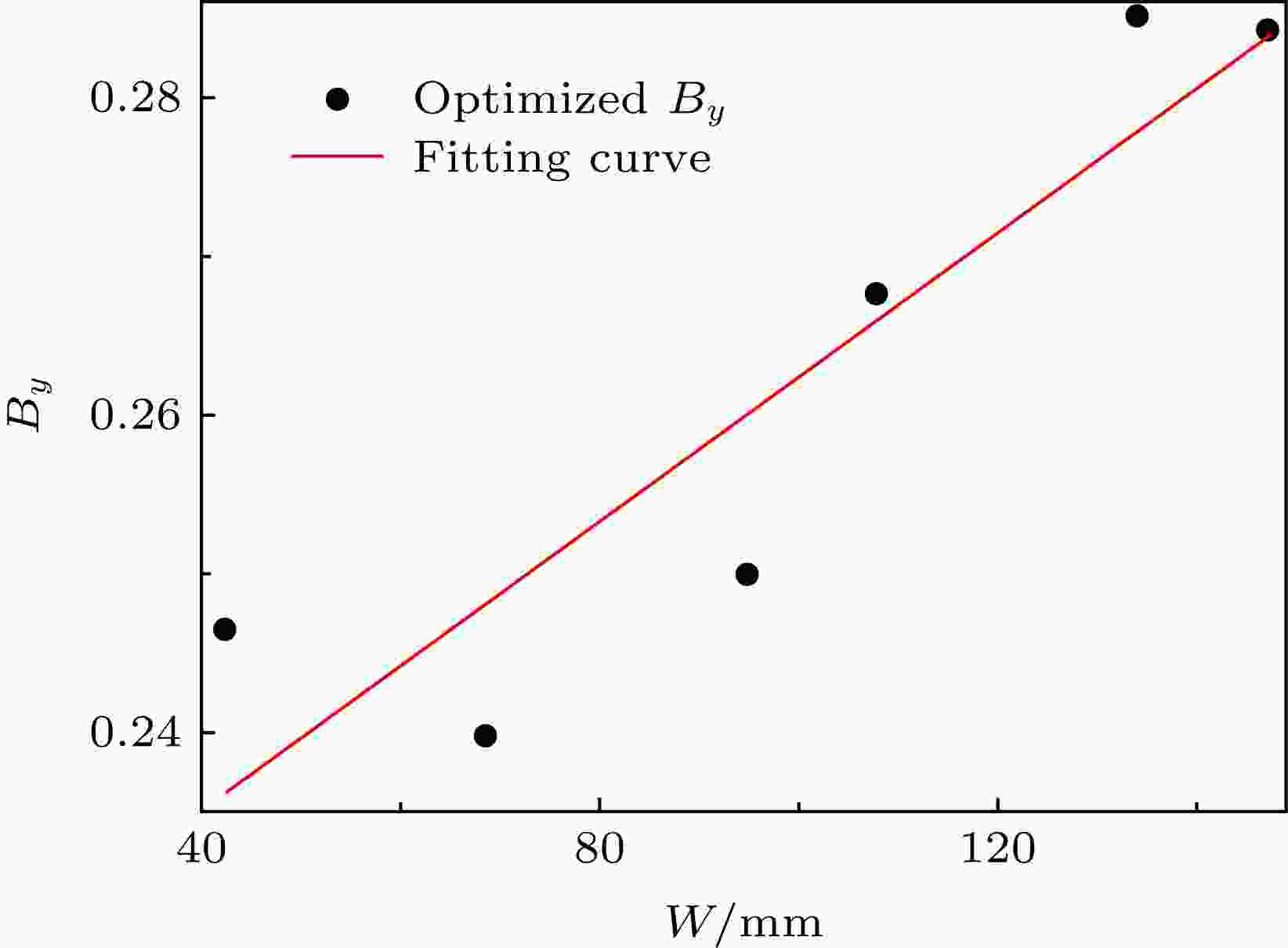图 3 优化系数B_y与导光板宽度W的拟合曲线
Figure3. Fitting curve of optimized B_y and W.

最后, 对优化系数B_y与导光板宽度W进行线性拟合, 如图3中的红线所示. 拟合得到的系数B_y关于导光板宽度W的函数表达式如下:

${B_y} = 0.21696+0.00045441 \cdot W,$

(4)式标准偏差为0.00912.
为了检验(4)式的实用性, 利用之前建立的6个集成化背光模组模型进行验证. 使用(4)式直接计算不同导光板宽度W下的系数B_y值, 将其代入到相应的集成化背光模组模型中, 仿真得到该背光模组的出射光亮度均匀性. 使用软件多次仿真优化得到的系数B_y与通过(4)式直接计算得到的系数B_y对应的背光模组亮度均匀性仿真值如表2所列.

W/mm	优化By	计算By	亮度均匀性%
			优化By	计算By
42.5	0.24637	0.23627	92.85	90.47
68.7	0.23967	0.24818	94.22	93.81
95.0	0.24983	0.26013	88.66	85.70
108.0	0.26750	0.26604	89.62	91.27
134.2	0.28500	0.27794	85.85	83.53
147.3	0.28410	0.28390	85.72	83.17

表2不同导光板宽度W下优化、计算系数B_y以及对应的背光模组亮度均匀性仿真值
Table2.Simulation results of luminance uniformity with optimized and calculated B_y at different widths W of PILGPs.

从表2可以看出, 在不同导光板宽度W下的集成化背光模组, 使用(4)式直接计算的系数B_y与使用软件优化的系数B_y对应的背光模组亮度均匀性仿真值相比较, 十分接近, 且均在80%以上; 说明关系表达式(4)式有较好的实用性.
2 -->

2.3.分布公式系数与导光板长度L的关系表达式

确定系数B_y与导光板宽度W的关系后, 本小节将研究系数B_x, C_x与导光板长度L的关系表达式. 首先, 固定导光板宽度W为68.7 mm、高度H为0.5 mm, 分别建立导光板长度L为101.1, 116.3, 130.8, 145.1 mm的集成化背光模组. 由于W固定, 因此由(4)式可以直接计算得到系数B_y. 然后, 利用Lighttools多次仿真优化得到较佳的系数B_x和C_x, 使得背光模组亮度均匀性达到85%以上. 最后, 先将优化得到的系数B_x与导光板长度L进行拟合, 如图4所示. 其中黑色圆点为不同L下优化的系数B_x, 红线为对应的拟合曲线, 其表达式如(5)式所示: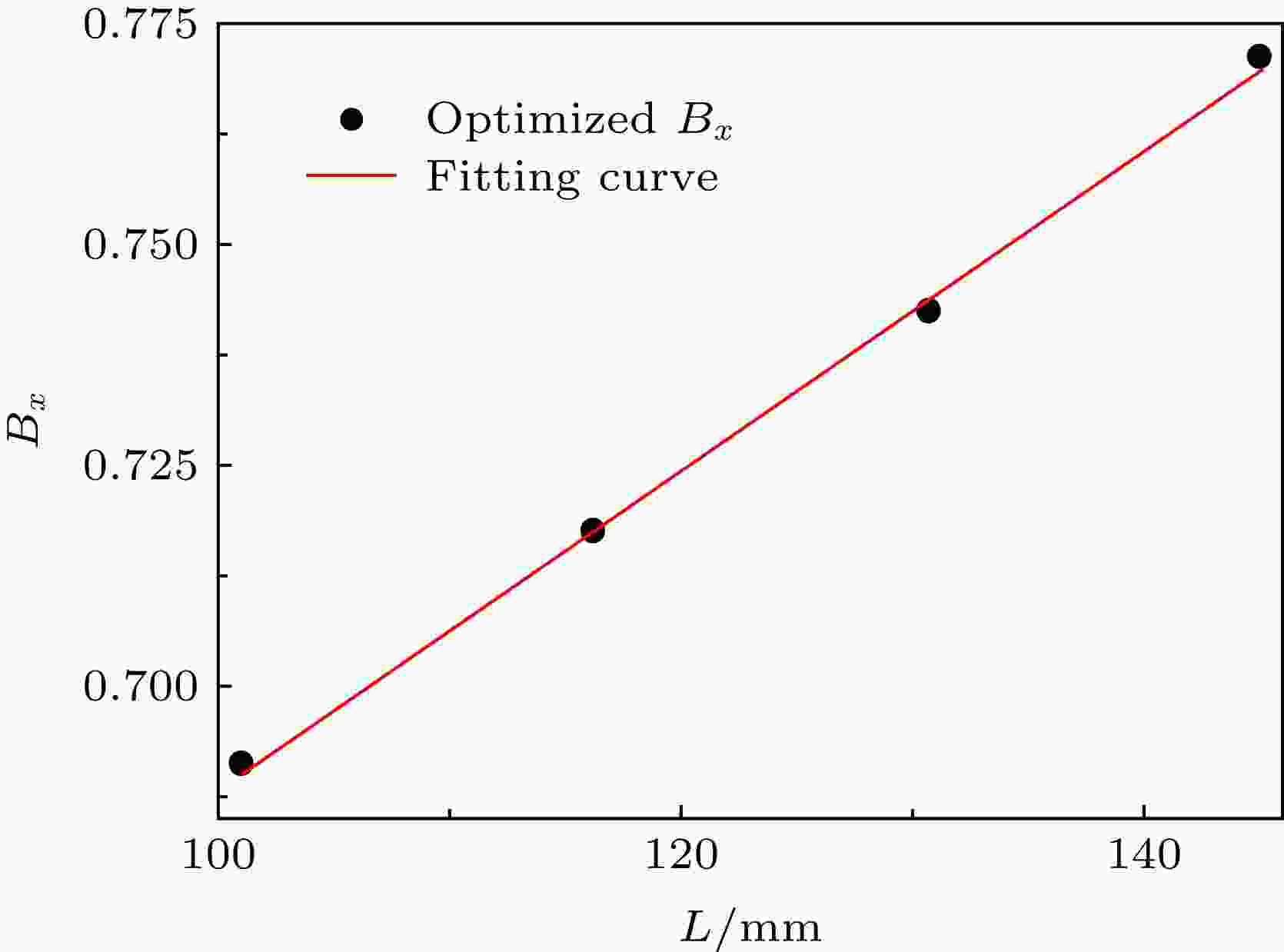
图 4 优化系数B_x与导光板长度L的拟合曲线
Figure4. Fitting curve of optimized B_x and L.

${B_x} = 0.50722 + 0.00181 \cdot L.$

(5)式的标准偏差为0.00162.
经大量仿真发现, 在不同导光板长度L的集成化背光模组中确定系数B_x后, 系数C_x在0.02—0.023区间内能使亮度均匀性在80%以上. 为了得到系数C_x与导光板长度L之间更为精确的关系, 增加导光板长度L为108.7, 123.6, 137.9 mm的集成化背光模组, 系数B_y, B_x分别由(4)式和(5)式确定. 首先利用Lighttools中参数灵敏度分析模块求解在0.02—0.023内且使得亮度均匀性大于80%时的系数C_x的取值范围, 然后再对仿真优化得到的系数C_x与导光板长度L进行线性拟合, 如图5所示. 其中黑色圆点线表示不同导光板长度L下优化得到的系数C_x取值区间, 红线为对应的拟合曲线, 其表达式为
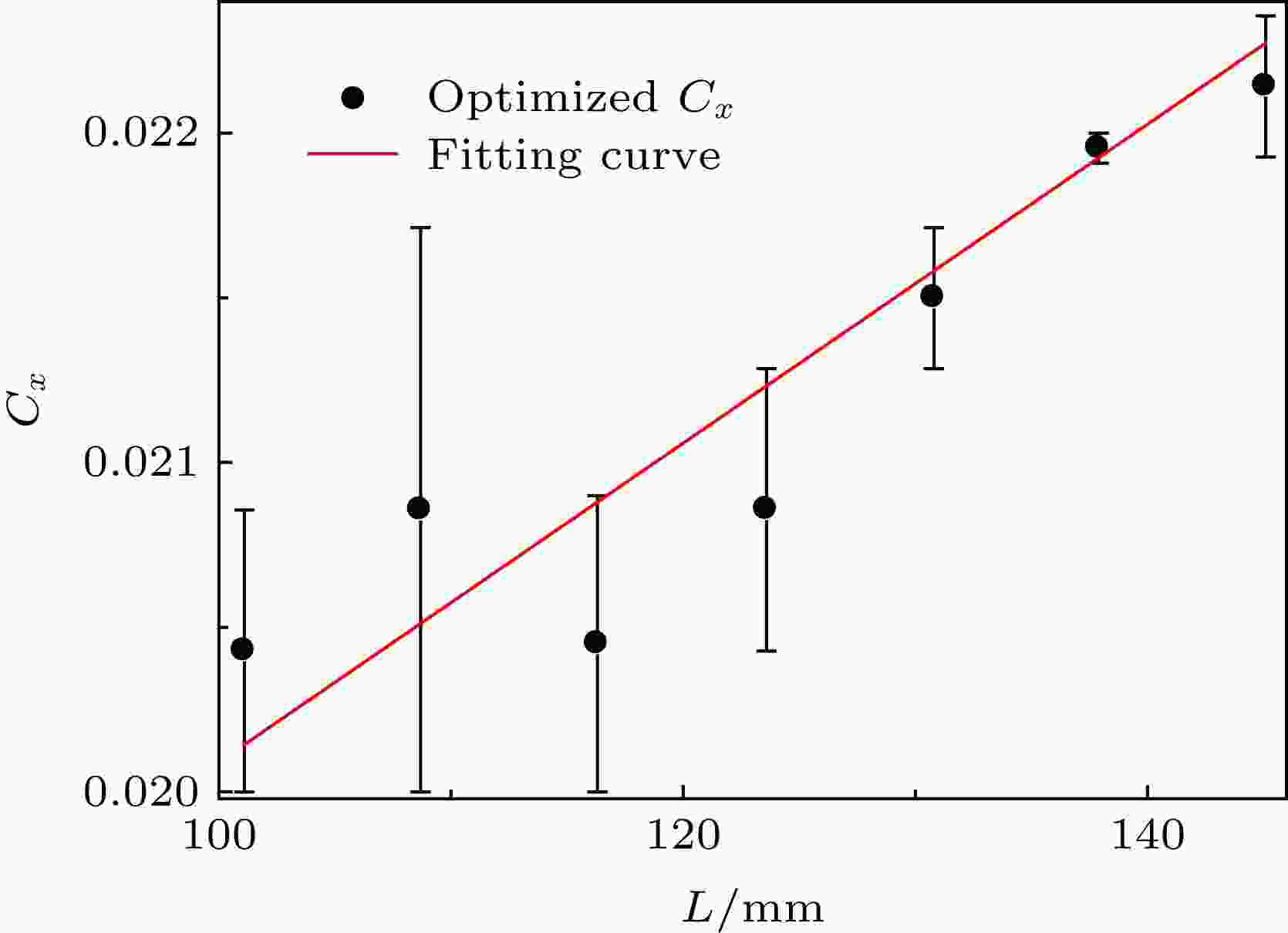图 5 优化系数C_x与导光板长度L的拟合曲线
Figure5. Fitting curve of optimized C_x and L.

${C_x} = 0.014964 + 0.000050526 \cdot L, $

(6)式的标准偏差为0.000187.
将分别由(5)式和(6)式直接确定的系数B_x和C_x代入导光板宽度W为68.7 mm, 导光板长度L为101.1, 108.7, 116.3, 123.6, 130.8, 137.9, 145.1 mm的集成化背光模组中进行仿真, 得到的亮度均匀性如表3所列.

L/mm	计算Bx	计算Cx	亮度均匀性/%
101.1	0.69021	0.020072	81.35
108.7	0.70397	0.020456	88.84
116.3	0.71772	0.020840	81.57
123.6	0.73094	0.021209	80.91
130.8	0.74397	0.021573	85.89
137.9	0.75682	0.021932	80.85
145.1	0.76985	0.022295	86.63

表3不同导光板长度L下的计算系数B_x和C_x对应的亮度均匀性仿真值
Table3.Simulation results of luminace uniformity with calculated B_x and C_x at different lengths L of PILGPs.

由表3可以看出, 在不同导光板长度L的集成化背光模组中, 使用(5)式和(6)式分别直接计算得到的系数B_x和C_x对应的背光模组亮度均匀性都在80%以上; 说明关系表达式(5)和(6)有较好的实用性.

本节将对第2节提出的PILGP下表面微棱镜二维分布公式(1)和(2), 以及分布公式系数与导光板结构参数的关系表达式(3)—(6)进行验证及分析.
2

-->

3.1.微棱镜二维分布公式组的验证

在Lighttools中建立PILGP尺寸分别为4.7, 5.2, 5.5, 5.8, 6.1英寸的五款不同长度和长宽比的小尺寸集成化背光模组. 将导光板长度L代入(3), (5)和(6)式, 计算得到各个不同尺寸导光板的系数A_x, B_x和C_x; 将导光板宽度W代入(4)式, 计算得到各个不同尺寸导光板的系数B_y. 再将计算得到的系数代入(1)和(2)式中, 可直接计算得到不同背光模组中导光板下表面的微棱镜二维分布坐标. 将上述微棱镜二维分布坐标代入相应的背光模组模型, 仿真得到的背光模组亮度均匀性如表4所列.

PILGP尺寸/inch	L/mm	W/mm	亮度均匀性/%
4.7	108.6	66.3	87.52
5.2	119.5	73.1	84.24
5.5	132.3	65.6	91.49
5.8	139.3	69.0	80.05
6.1	146.1	72.4	81.38

表4PILGP下表面微棱镜二维分布的不同尺寸背光模组亮度均匀性
Table4.Luminance uniformity of partial integrated backlight module with two-dimensional distribution of micro-prism on the bottom surface of PILGPs at different sizes.

从表4可以看出, 五个不同小尺寸集成化背光模组的出射光亮度均匀性均在80%以上, 平均值为84.94%. 说明使用本文提出的微棱镜二维分布公式及系数表达式可以快速获得小尺寸PILGP下表面较佳的微棱镜二维分布, 使得集成化背光模组的亮度均匀性达到较高值.
将上述二维分布公式组应用于下表面微棱镜二维分布的5英寸PILGP设计, 仅对计算得到的微棱镜二维分布表达式系数进行微调, 与使用Lighttools中的BPO模块优化设计的下表面微棱镜二维分布的5英寸PILGP进行对比^[10], 性能参数如表5所列.

性能参数	微棱镜二维分布优化模式
	公式组	BPO
光能利用率/%	90.69	92.03
平均照度/Lux	8462.1	8571.0
平均亮度/Nit	6135.4	6394.6
照度均匀性/%	88.02	87.07
亮度均匀性/%	92.17	91.94

表5分别具有BPO及分布公式组优化的微棱镜二维分布的5英寸背光模组性能参数仿真结果
Table5.Simulation results of performance parameters in 5-inch partial integrated backlight modules with two-dimensional distribution of micro-prism optimized by BPO or distribution expressions.

从表5可以看出, 微棱镜二维分布分别使用分布公式组和BPO优化的5英寸集成化背光模组, 两者的光能利用率、平均照度、平均亮度均很接近, 前者的亮度均匀性和照度均匀性还略高于后者, 达到了小尺寸背光模组的性能参数要求.
2 -->

3.2.物理机理分析

从物理机理上分析, 具有一定发散角的LED作为光源发出的光线在导光板内传播时, 到达导光板表面的光线能量各不相同.
沿导光板长度方向(x轴), 距离光源越远, 光线能量越低. 根据导光板表面微棱镜对光线的调制原理^[22], 为使得导光板出光面均匀发光, 能量较低的远光源区相对近光源区需要更多的微棱镜来反射光线, 即远光源区的微棱镜密度相对近光源区大, 也就是说远光源区的微棱镜间距相对小. PILGP下表面每个微棱镜的分布位置, 是由微棱镜二维分布公式中的系数决定. (1)式中, 系数A_x主要控制微棱镜中心点横坐标的位置, 将其设置在导光板离光源最远端的中心点是因为此处在x轴方向上微棱镜密度最大, 而在y轴方向上微棱镜密度以y = 0对称分布; 系数B_x主要控制x轴方向上微棱镜的平均间距; 系数C_x主要控制随着与微棱镜中心点距离增加的微棱镜间距的变化斜率, 随着微棱镜距离微棱镜中心点越远, 即距离光源也就越近, 那么微棱镜间距相应变大, 这与导光板表面微结构分布的一般规律相符合^[23].
沿导光板宽度方向(y轴), 一列LED发出的光线到达导光板宽度方向两侧区域和中间区域的能量有所差异, 呈中心对称趋势; 但相对于导光板长度方向的能量变化较小. 因此, 微棱镜沿导光板宽度方向的分布公式(2)采用线性函数, 系数B_y主要控制y轴方向上微棱镜的平均间距.
不同尺寸的PILGP中, 光场分布不同, 较佳的微棱镜二维分布也随之变化. 微棱镜二维分布公式中的系数随导光板结构参数的变化而改变, 使得集成化背光模组获得了较高的亮度均匀性.

本文提出的PILGP下表面微棱镜二维分布公式及分布公式系数与导光板结构参数的关系表达式如下:

$x = {A_x} + {B_x} \cdot m - {C_x} \cdot {m^2},$

$y = {B_y} \cdot n,$

${A_x} = {{\left( {L - {L_{x0}} - d} \right)} / 2},$

${B_x} = 0.50722 + 0.00181 \cdot L,$

${B_y} = 0.21696+0.00045441 \cdot W,$

${C_x} = 0.014964 + 0.000050526 \cdot L.$

将上述研究成果应用于不同结构参数的小尺寸集成化背光模组设计, 模拟仿真得到出射光亮度均匀性平均值为84.94%, 仿真结果表明本文提出的分布公式组是有效的. 以5英寸PILGP为例, 应用该分布公式组可直接获得亮度均匀性较高时的PILGP下表面微棱镜二维分布; 将应用公式直接计算得到的二维分布公式系数作为初始值, 仅需对其进行微调优化, 优化后的微棱镜二维分布即可使集成化背光模组亮度均匀性达到90%以上, 满足实际要求. 该微棱镜二维分布公式形式简洁, 分布公式系数与导光板结构参数关系明确; 与实验室前期应用光学软件优化微棱镜二维分布的方法相比, 本文提出的微棱镜二维分布公式组无需设计人员经验或软件的多次仿真分析, 节约了大量背光模组的设计时间, 提高了设计效率. 该研究成果对导光板表面微结构的分布设计具有一定的指导意义和应用价值.