摘要:对不同动量比下针栓喷注器的喷雾特性开展了试验研究. 以水为模拟介质, 分别通过增大氧化剂流量与减小燃料流量, 在0.16—0.99范围内增大局部动量比, 其中前者对应的总动量更高. 通过高速摄影结合激光相位多普勒技术(PDA)研究了不同工况下的喷雾边界、粒径分布及速度场. 结果表明, 工况变化直接影响喷雾形态, 并进一步影响其他喷雾特性. 对于同一局部动量比, 喷雾锥角一致, 但高总动量对应的喷雾下游范围更大. 随着外喷嘴流量增加, 喷雾上游出现空心区, 且其范围随局部动量比增大而增大. Sauter平均直径 (SMD)随局部动量比增加而增大, 变化范围则随总动量增高而扩大. 有空心区的喷雾SMD沿径向呈N形变化趋势, 喷雾外缘粒径最大; 实心喷雾SMD沿径向略有下降. 喷雾合速度取决于总动量, 合速度、轴向速度、径向速度均沿径向呈倒V形变化, 但轴向速度以下降趋势为主, 径向速度增加后缓慢减小或直接趋平. 局部动量比越高, 径向速度越高, 轴向速度越低. 此外, 空心区下方喷雾速度场由液膜主导.
关键词: 针栓喷注器/
动量比调节方式/
空心区/
索特尔平均直径

English Abstract

全文HTML

--> --> -->

针栓喷注器以燃烧室头部布置离散的针栓孔与主要特点, 具有不同于传统发动机构型的燃烧流场^[1], 可被广泛应用于液体火箭发动机领域^[2]. 针栓发动机的优点在于高性能、宽推力及推进剂范围、内在燃烧稳定性、深度调节能力、结构简单、经济适用等. 鉴于以上优点, 国内外关于变推力发动机的研究主要集中于使用针栓式喷注器的变推力发动机^[3]. 阿波罗落月发动机LMDE ^[4]采用针栓式喷注器实现了最大推力46600 N, 推力变比10∶1的性能, 嫦娥三号^[5,6]也采用针栓喷注器实现了最大推力7500 N, 推力变比5∶1的要求.
针栓发动机的性能与很多因素有关. TRW公司的设计经验表明, 通过对针栓喷注器结构的合理设计, 发动机燃烧效率可高达96%—99%^[1]. 对针栓发动机而言, 总动量比(TMR)是最重要的设计参数, 定义为径向动量和轴向动量的比值^[2]. 设计经验表明TMR数值在1左右时能够获得最优性能^[2]. 俞南嘉等^[7]通过对针栓式液氧/煤油发动机燃烧流场进行数值仿真发现, 动量比为1时, 针栓式喷注器雾化混合效果最好, 达到了最佳的燃烧效率96.7%. Heister等^[8]认为喷雾锥角基本与TMR^0.5成正比, 与横向射流中喷注深度与TMR之间的关系类似. Son等^[9]以液体中心式气液针栓喷注器为背景, 研究了TMR和We对喷雾半锥角的影响, 发现喷雾半锥角与TMR^0.124成正比. 成鹏通过冷态试验与仿真相结合的方法, 分别推导了径向缝型^[10]、径向孔型针^[11]栓喷注器喷雾半锥角的预测公式, 分别为α = acos[1/(1 + TMR)]和α = acos[1/(1+LMR)]. 其中LMR为局部动量比(也称作有效动量比), LMR = TMR/BF^[12]. 阻塞因子(BF)定义为所有孔或缝的周向长度与针栓周长的比值^[2]: ${\rm{BF}} = \dfrac{{n{d_{\rm{t}}}}}{{{\text{π}}D}}$. 其中n为孔数, d_t为径向孔孔径, D为针栓头直径.
TRW公司^[1]自20世纪起就持续开展了针栓发动机的研制工作, 但现有文献仅给出了发展历程和部分型号的工作性能; 韩国航天大学的Son团队^[9,13,14]开展了相对持续的研究工作, 主要解决了气液径向缝型针栓喷注器的锥角测量、分布范围测量以及数值方法的探索; 国内的方昕昕等^[15-18]相对系统地开展了气液针栓发动机的破碎过程分析及燃烧流场模拟工作; 文献[10,11,19]对液液针栓喷注器的破碎雾化过程开展了理论推导和喷雾形态的测量工作.
国内外****通过丰富的手段对喷雾特性开展研究. 高速摄影是较为常见的研究手段, 吴里银等^[20]在此基础上发展了脉冲激光背景成像方法来获取超声速气流中“冻结”的横向射流, 吴迎春等^[21]通过全场彩虹测量技术对双组份液滴的浓度及粒径分布进行了研究, Zhang等^[22]基于PIV技术发展了可用于同步测量气液两相混合过程的高速双色PIV技术. 何博等^[23]对液体火箭中有机凝胶喷雾液滴的蒸发过程开展了建模和数值仿真工作. 数值仿真手段被广泛应用于发动机燃烧过程的研究^[24,25], 热试试验中则通过特定波段的滤光片捕捉释热区, 获得发动机的火焰形态及燃烧性能^[26].
总的来说, 动量比对针栓喷注器的雾化特性有非常重要的影响, 而现有文献主要从喷雾锥角的角度出发, 对喷雾的分布形态、雾化特性、速度场等尚未开展深入研究. 实际上, 现有的关于针栓喷注器的研究主要集中于喷雾的外边界的研究, 即使对相对固定的工况, 也缺乏系统深入的研究工作. 因此, 本文通过两种调节方式, 系统研究了局部动量比对针栓喷注器的喷雾分布、雾化特性及速度场的影响规律, 并从针栓喷注器喷雾形成与发展过程的角度出发, 解释了局部动量比及其调节方式影响喷雾特性的内在机制.

开展雾化试验所用的试验系统如图1所示. 试验系统由供应系统、测控系统、试验件等基本组成部分, 同时根据试验需求分别布置了高速摄影系统和相位多普勒(PDA)系统试验喷雾图像的拍摄及粒径、速度的测量.
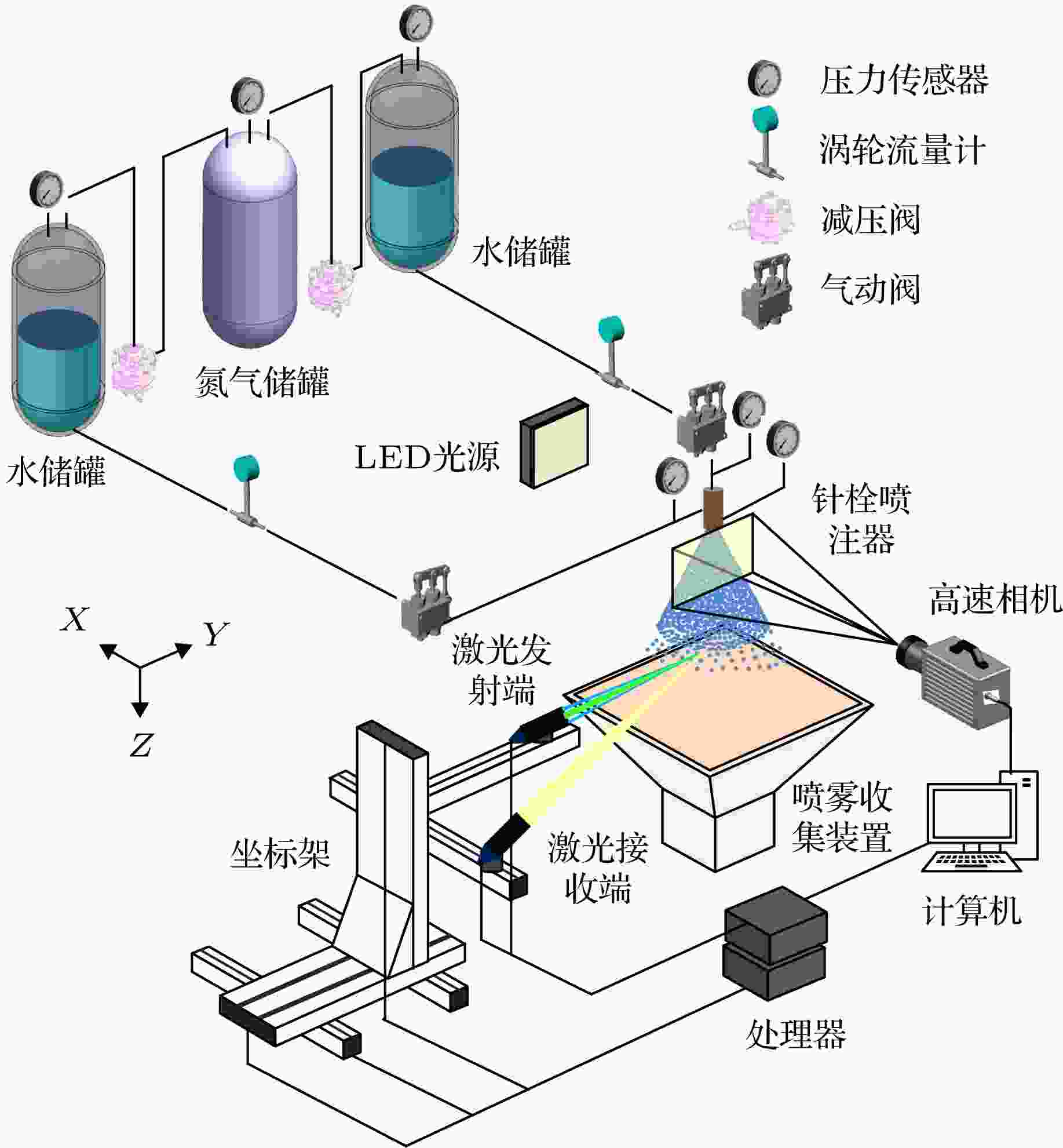图 1 试验系统示意图^[27]
Figure1. Schematic diagram of the experimental setup^[27].

试验采用的是一个设计流量为0.7 kg/s的氧化剂中心式液液针栓喷注器(氧化剂和燃料设计流量分别为206和493 g/s). 设计的氧化剂和燃料分别为液氧和酒精, 实际冷试条件均采用水作为模拟介质^[9,28]. 氧化剂和燃料分别经径向孔和轴向环缝喷出, 两者的轴向距离定义为“跳过距离”^[2]. 为增加喷雾范围, 设计外喷嘴入口为切向孔. 图2给出了喷嘴出口的结构示意图. 针栓喷注器的基本结构参数如表1所示. 环境压力为101.3 kPa, 环境温度为283 K, 周围为静止空气环境. 参考Urbán等^[29]的计算评估, 认为该条件下可忽略蒸发对喷雾的影响.
图 2 针栓喷注器示意图
Figure2. Schematic diagram of the pintle injector.

针栓头直径 D/mm	径向孔排数 nr	径向孔孔径 dt/mm	径向孔孔数 n	跳过距离 Ls/mm	环缝厚度 t/mm
10.4	2	1.1/0.9	6/6	10.4	0.5

表1针栓喷嘴器的主要结构参数
Table1.Structural parameters of the pintle injector.

2

-->

2.1.试验工况

为研究动量比对喷雾特性的影响, 以gk1为基本工况, 通过增大氧化剂流量和减小燃料流量两种方式来增加局部动量比, 变化范围为0.16—0.90. 两种调节方式相比, 虽然局部动量比基本一致, 但增大氧化剂流量方式(gk1—gk4)对应的总流量更高, 总动量更大; 减小燃料流量方式(gk1, gk5—gk7)对应的总流量更低, 总动量更小. 以局部动量比而非总动量比为变量, 是因为本文研究对象为径向孔形针栓喷注器, 径向流体以多股射流形式喷出, 喷雾场本身具有强烈的局部流动特征. 具体的工况参数如表2所列.

试验 工况	燃料流量/ g·s–1	氧化剂流量/ g·s–1	总动量比 (TMR)	局部动量比(LMR)
gk1	502	59.3	0.1116	0.1550
gk2	503	120	0.1892	0.3662
gk3	505	149	0.2436	0.5143
gk4	505	209	0.3956	0.9283
gk5	224	59.4	0.1534	0.3714
gk6	172	58.2	0.2195	0.5743
gk7	134	60.1	0.3658	0.9891

表2试验工况
Table2.Operating conditions.

考虑到外喷嘴入口为切向孔, 液膜经环缝流出时同时携带了轴向动量和径向动量, 故在求解动量比时需要考虑到液膜的径向动量与轴向动量的比例. 通过开展只有外喷嘴流动的试验, 可以测得一个喷雾锥角${\alpha _{\rm{f}}}$, 则总动量比为

${\rm{TMR}} = \frac{{{{\dot m}_2}{v_2}}}{{{{\dot m}_1}{v_1}}} = \frac{{{{\dot m}_{\rm{o}}}{v_{\rm{o}}} + {{\dot m}_{\rm{f}}}{v_{\rm{f}}}\sin \left( {{\alpha _{\rm{f}}}/2} \right)}}{{{{\dot m}_{\rm{f}}}{v_{\rm{f}}}\cos \left( {{\alpha _{\rm{f}}}/2} \right)}},$

其中$\dot m$和v 分别代表流量和速度, 下标“1”和“2”分别代表轴向和径向两个方向, 下标“o”和“f”分别代表氧化剂和燃料.
Santoro等^[12]和Cheng等^[19]对于针栓喷注器均提出了局部动量比(或有效动量比)的概念. 以射流单孔为研究对象分析局部流动, 假设与射流孔撞击的液膜的面积与射流的流动面积相同, 且不同区域的流动速度一致, 则局部动量比定义为

${\rm{LMR}} = \frac{{{{\dot m}_{{\rm{2l}}}}{v_2}}}{{{{\dot m}_{{\rm{1l}}}}{v_1}}} = \frac{{{{\dot m}_{\rm{o}}}{v_{\rm{o}}} + {\rm{BF}} \cdot {{\dot m}_{\rm{f}}}{v_{\rm{f}}}\sin \left( {{\alpha _{\rm{f}}}/2} \right)}}{{{\rm{BF}} \cdot {{\dot m}_{\rm{f}}}{v_{\rm{f}}}\cos \left( {{\alpha _{\rm{f}}}/2} \right)}},$

其中下标“l”表示局部流动参数.
2 -->

2.2.成像系统

成像系统用于喷雾场的可视化, 包括LED光源、高速摄影和电脑. 其中, LED光源提供了平行的背景光, 高速相机为型号Photron FASTCAM SA-X2, 镜头为Nikon ED 200 mm定焦镜头. 拍摄时采用的帧频为10000 fps, 曝光时间为1/100000 s, 图像分辨率为784 pix × 958 pix.
2 -->

2.3.PDA 系统

PDA系统由激光光源、发射端、接收端、处理机、三维坐标架等构成. 发射端与接收端夹角为145°, 通过三维坐标架的移动实现不同位置测点的测量. 发射端和接收端的信号经过处理之后转换为所测粒子的速度和粒径信息. 测量中用到绿光和蓝光两组激光. 其中, 绿光用于测量粒径和Z方向速度, 蓝光用于测量X方向速度. 两个方向的测量结果互不相关, 但可以通过统计平均后表征喷雾在不同空间位置的分布特征. 参考文献[30]设置最大采样数为10000, 最长采样时间为10 s, 满足任意条件时即认为该点测量完成. PDA系统主要参数如表3所示. 更多的信息参见吴里银^[31]论文.

参数类型	数值
激光波长/nm	514.5/488.0
发射光与接受光夹角/(o)	145
轴向速度范围/m·s–1	–7—45
径向速度范围/m·s–1	–28—46
粒径范围/μm	0.1—1000.0
发射端焦距/mm	1000
接收端焦距/mm	500

表3PDA系统参数表
Table3.Parameters of the PDA system.

在对喷雾范围进行初步测量的基础上布置PDA测点, 如图3所示. 考虑到针栓喷注器为准轴对称结构, 选取了过对称轴的XOZ平面上测量粒径、轴向速度和径向速度, 测点范围随局部动量比增大而拓展, 如图3(b)所示. 从gk1—gk4, XOZ平面上测点数分别为46/52/65/79. 由于gk5—gk7的局部动量比范围分别对应gk2—gk4, 测点布置也保持一致. 测量原点位于针栓头底部中心处. 由于测点在纵截面上, XOZ平面即为ROH平面, 下文统一用ROH坐标系描述喷雾的空间位置.
图 3 (a) PDA系统; (b) 不同工况下测点布置示意图
Figure3. (a) PDA system; (b) measurement point setup under different operating conditions.

2 -->

2.4.数据处理方法

背景光穿过喷雾的过程中由于喷雾的散射和吸收作用导致光强被削弱, 由此导致了喷雾图像灰度的不均匀分布. 高速摄影拍摄所得的原始图像首先被转化为灰度图, 进一步通过Otsu^[32]的方法获得阈值, 转为二值图, 由此获得喷雾边界, 并计算喷雾锥角, 如图4所示. 从第一排孔对应的轴向位置出发, 向下取10 mm的距离来测量喷雾锥角. 在这个范围内喷雾在径向充分发展且尚未破碎, 存在清晰的边界线. 对每一个试验工况, 取1000幅图像求取时均的喷雾锥角.
图 4 喷雾锥角测量方法示意图
Figure4. Determination of the spray angle.

PDA测量可以直接得到在测量时间内所有粒子的粒径、轴向速度和径向速度信息. PDA具有精度高、动态响应快的优势^[33], 文献[29]指出在粒径为64.1 μm范围内单个粒子的不确定度仅为0.5 μm. 平均速度、Sauter平均直径 (SMD)和体积流率则通过一段时间内的数据统计得到(通常选取所有测点的最短时间). 首先通过对比不同区段数据统计研究样本选取对试验结果的影响. 以gk1为例, 自上而下选取了距针栓头底部5, 40和80 mm的3个测点, 将总样本分为5个区段, 每个区段样本数为2000, 分别计算SMD和平均轴向速度, 如图5所示. 结果表明, PDA测量结果稳定, SMD的相对误差在 ± 3%以内, 速度的相对误差在 ± 1%以内.
图 5 PDA不同区段数据对比分析
Figure5. Contrastive analysis on the data from different sections obtained by PDA.

2

-->

3.1.喷雾边界

不同工况下的喷雾范围通过高速摄影图像与PDA计算体积流率(以Q表示, 单位为mm³/s)分布两种方式分别表示出来, 如图6所示. 体积流率定义为
图 6 不同局部动量比下的喷雾范围
Figure6. Spray range at different LMR.

$Q = \sum\limits_{i = 1}^N {\frac{1}{6}} {\text{π}}d_i^3/t,$

对于每一个PDA测点, t为测量时间, N为测量时间内所测的粒子数, d为粒子直径, i为粒子编号.
由图6可以看出, 随着局部动量比的增加, 喷雾的外边界均向外扩展, 但拓展程度受到动量比调节方式的影响. 与直观拍摄所得的喷雾图像相比, 体积流率分布云图还获得了喷雾的内边界. 为了更加明确地对比不同动量比调节方式对喷雾范围的影响, 提取了不同工况下喷雾的内、外边界, 如图7所示.
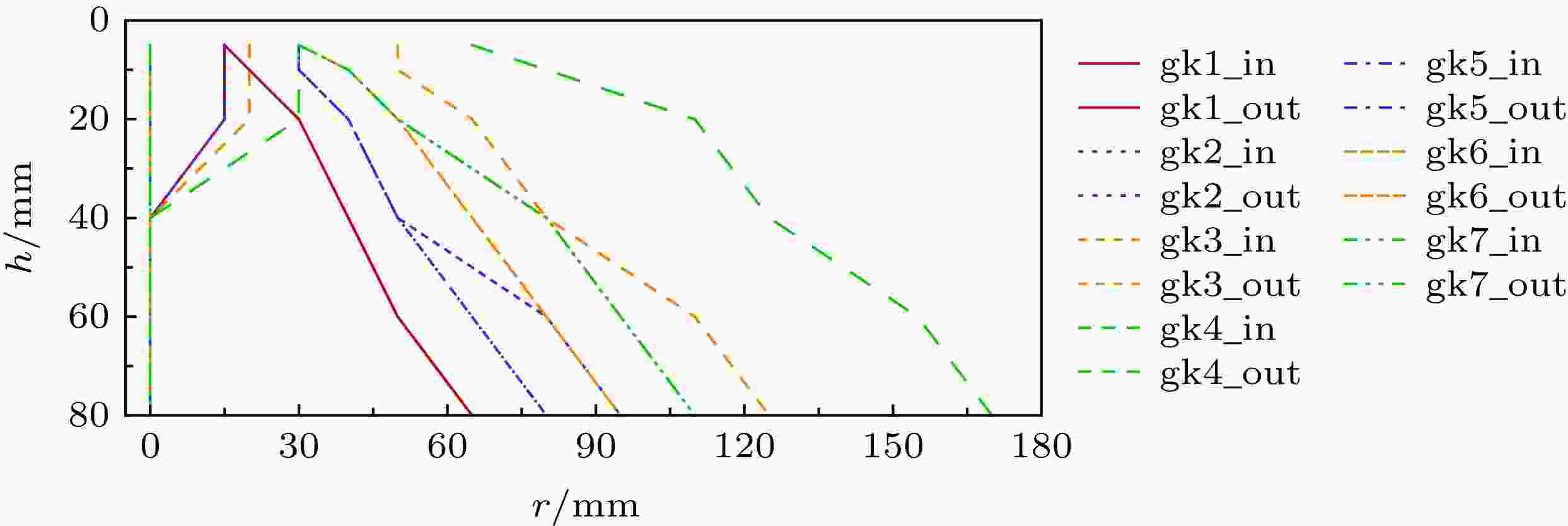图 7 不同工况下的喷雾内、外边界对比
Figure7. Inner/outer boundary under different operating conditions.

首先对喷雾的外边界进行分析. 图7对比了不同动量比调节方式下喷雾外边界的位置, 而对于喷雾图像观测来说, 喷雾锥角是更加常用的量化指标. 通过图像处理, 得到喷雾上游清晰的边界条件, 可以获得不同工况下的喷雾锥角, 具体方法如2.4节所示. 由图8可以看出, 喷雾锥角随局部动量比的增加而增加, 试验结果与成鹏^[11]提出的径向孔型液液针栓喷注器的锥角预测公式$\alpha = 2a\cos \dfrac{1}{{1 + {\rm{LMR}}}}$ 符合得很好. 由此说明, 针栓喷注器的喷雾锥角只与局部动量比有关, 几乎不受其调节方式的影响.
图 8 不同调节方式下喷雾锥角随局部动量比的变化情况
Figure8. Spray angle vs. LMR with different throttling methods.

另一方面, 无论从喷雾图像还是喷雾PDA测量结果来看(见图6), 对比两种动量比调节方式, 通过增加内喷嘴流量来增加局部动量比时所得的喷雾范围更大. 这说明, 在喷雾上游, 喷雾边界尚且清晰, 喷雾破碎程度不高时, 喷雾向外拓展的范围主要受初始动量比条件控制, 表现为局部动量比越大, 喷雾锥角越大; 随着喷雾向下游发展, 破碎雾化过程逐渐完成, 喷雾外边界所能到达的最远范围受到总动量的影响. 具体的, 将gk2—gk4与gk5—gk7对应比较可以看出, 前者总动量更大, 在喷雾充分完成破碎雾化过程后, 由于总的粒子浓度更高(参见图6中体积流率云图对比结果), 在喷雾场的下游, 喷雾范围更大.
接下来, 对喷雾的内边界进行分析. 局部动量比对喷雾内边界的影响主要表现为空心区的有无及大小上. 当总动量较大时, 喷雾上游存在“空心区”, 形成了喷雾的内边界, 且内边界的范围随着局部动量比的增加而增加. 而对于总动量相对较小的gk5—gk7, 喷雾上游并未出现空心区结构. 由此说明, 空心区的大小同时受到轴向动量和径向动量大小的影响. 随着轴向动量增加(gk7→gk6→gk5→gk1), 喷雾上游从实心结构发展为空心结构; 随着径向动量增加(gk1→gk2→gk3→gk4), 空心结构的区域不断增大, 喷雾内边界范围向外拓展.
对于径向孔形针栓喷注器, 部分液膜与射流直接发生碰撞, 另一部分液膜受到射流与液膜碰撞作用的影响, 在径向分布上有被带离中心向外扩展的趋势. 故喷雾中心是否中空, 受到液膜原本流动状态与射流液膜碰撞作用的共同影响.
首先对液膜本身的流动状态进行分析. 图9给出了只有液膜喷注的情况下所形成的喷雾图像. 考虑到外喷嘴为切向入口, 故液膜经环缝喷出时本身携带有一定的切向速度, 该速度使得液膜在向下流动的同时具有沿径向扩展的趋势, 可以类比离心式喷嘴的工作过程与喷雾形态^[34]. 对于离心式喷嘴, 低压降下表面张力占优, 喷雾向中心聚拢; 高压降下气动力作用增强, 喷雾向外拓展. 但本文中液膜从环缝喷出后, 一侧有针栓头壁面, 故流体本身有贴壁流动的趋势, 这被称之为康达效应^[35]. 由图9可以看出, 当液膜流量较低时, 液膜初始速度基本垂直, 液膜流动方向与壁面基本平行; 随着流量增加, 液膜切向速度分量增加, 初始速度与针栓头壁面之间夹角增大. 根据Allery等^[36]的研究, 流体速度方向与壁面夹角越小, 越容易贴壁流动. 总的来说, 液膜流速越低, 越容易贴壁流动, 形成实心喷雾; 液膜流速越高, 越容易向外拓展, 形成中空喷雾.
图 9 单液膜喷注条件下喷雾形态随液膜流量的变化
Figure9. Spray patterns with changing mass flow rate of the liquid film with only the liquid film injected.

射流与液膜的相互作用会增强液膜脱离壁面向外拓展的趋势. 根据成鹏^[11]开展的单股射流撞击液膜的试验结果, 射流与液膜撞击后将液膜撑开, 形成中空的斗篷状喷雾. 如果此时液膜本身已经脱离或即将脱离壁面, 则由于射流的进一步带动作用, 在整个周向位置上, 不会出现液膜在喷雾中心轴线汇聚的现象, 这就是喷雾上游空心区的由来. 液膜流量和射流流量的增加均会促进喷雾形成中空结构. 但由于相邻斗篷在向下游发展的过程中相互碰撞, 产生的液滴填充了喷雾中心的空心区, 故喷雾下游空心区消失, 喷雾结构由空心锥形变为实心锥形. 进一步地, 随着径向流量增加, 径向动量更大, 推开液膜的能力更强, 从喷雾锥角来看, 单个斗篷的径向范围也更大. 对于恒定的孔间距, 忽略射流速度对其周向扩展速度的影响, 在斗篷碰撞的时间间隔内, 径向流体的流速越高, 相邻斗篷碰撞前在径向的运动距离越远, 空心区径向范围越大.
总的来说, 针栓喷注器的喷雾边界同时受到局部动量比的大小及其调节方式的影响, 其中后者主要归结于总动量的影响. 局部动量比的增加使得喷雾上游外边界拓展, 喷雾锥角增加; 在喷雾下游, 液雾充分破碎之后, 总动量越大, 喷雾范围越大. 当外喷嘴动量增加到一定程度后, 外喷嘴的径向动量可以克服康达效应的影响, 将液膜推开形成空心的斗篷, 在喷雾上游形成空心区结构, 且径向动量越大, 空心区范围越大.
2 -->

3.2.粒径分布

液滴粒径的大小会直接影响雾化效果的好坏. 从评估液雾燃烧性能的好坏出发^[37], 本文选取了SMD来分析粒径的分布. 动量比调节方式对SMD的分布有非常重要的影响, 在本文中, 局部动量比调节方式的不同直接影响总动量的高低: gk1—gk4的流体流量较高, 总动量较大; gk5—gk7的流体流量较低, 总动量较小.
对于总动量较高的工况, 从分布范围上来说, SMD的分布区间约为40 μm, 且SMD的分布范围整体上随局部动量比的增加而递增(见图10). 进一步地, 从空间分布云图上(图11)来看, 喷雾在径向存在两个SMD较高的区域, 整体呈现出双峰分布. 由于第二个峰值出现在喷雾外缘, 故SMD沿径向表现为N形分布, 如图12所示. 雾化最好的区域出现在喷雾径向中间区域, 雾化最差的位置在喷雾外缘. 通过对比喷雾分布云图(图6)与粒径分布云图(图11)可以发现, SMD最低的范围基本上对应体积流率较高的区域, 根据成鹏^[11]的分析, 在径向方向上, 内侧喷雾主要受到液膜的影响, 外侧喷雾则主要受到射流的影响, 从空间位置上来看, SMD峰谷区域应对应射流与液膜发生相互作用的区域, 故而这部分的喷雾浓度最高, 雾化效果最好, 粒径最低.
图 10 不同局部动量比下的SMD变化范围
Figure10. Range of SMD under different LMR.

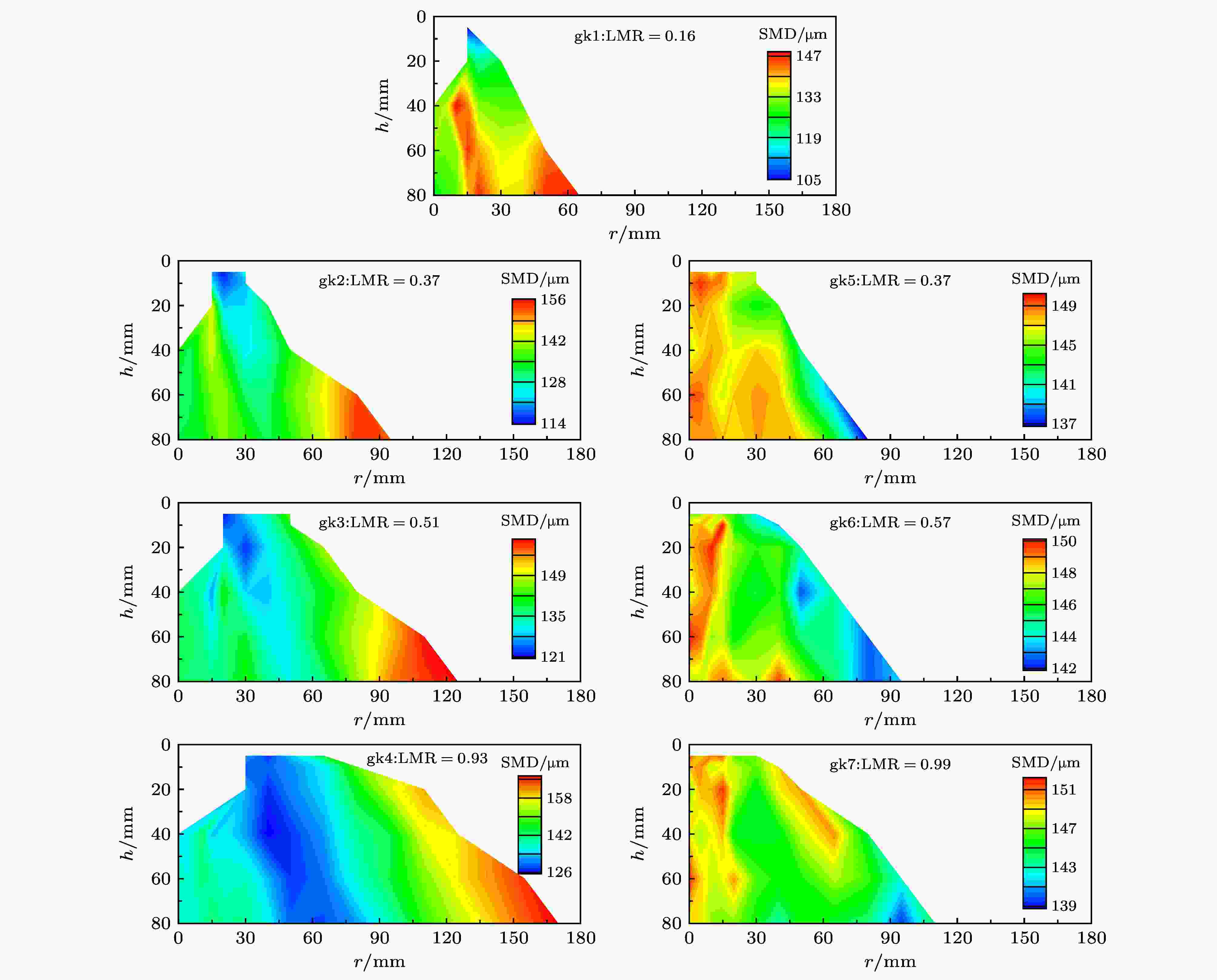图 11 不同局部动量比下SMD分布云图
Figure11. Contour of SMD under different LMR.

图 12 不同工况下SMD的分布曲线
Figure12. Distribution curves of SMD under different operating conditions.

对于总动量较低的工况, 从图10可以看出, SMD的分布区间在15 μm以内, 明显低于相同局部动量比下总动量更高的对应工况. 这表明总动量较低时, 粒径在空间分布上更加均匀, 局部动量比的增加使得液滴粒径略有增大, 但影响并不明显. 总动量的影响主要体现在SMD的分布规律上. 由图11可以看出, 对于总动量较低的工况, SMD沿径向基本呈现出递减的趋势, 喷雾中心的SMD始终较高, 这是不同于高总动量工况下粒径分布最显著的特点. 但随着局部动量比的增加, 在喷雾外缘出现了第二个SMD的峰值区域, 这可能是由于高局部动量比下, 部分射流直接穿透液膜运动到喷雾外围造成的.
分析两种类型的SMD分布可以发现, SMD空间分布特征的不同源于喷雾空间分布特征的不同, 即喷雾上游是否存在空心区结构. 当喷雾在空间分布上表现为实心锥形时, 部分液膜沿针栓头壁面直接向下游流动, 并在喷雾中心汇聚, 导致喷雾浓度高且粒径偏大. 这是由于液膜在向下游运动的过程中, 并未与射流发生碰撞破碎, 故液滴粒径较大. 相比之下, 当喷雾在空间分布上表现为空心锥形时, 液膜与射流碰撞破碎, 周向上未出现液膜贴壁直接在中心汇聚的现象. 在斗篷碰撞之前, 喷雾中空, 在斗篷相互作用最剧烈的区域粒径最小, 两侧逐渐增加, 呈现为V形分布. 下游相邻斗篷碰撞后, 在原有V形分布的基础上, 斗篷碰撞产生的液滴在喷雾中心进一步碰撞破碎, 喷雾中心液滴尺寸较低, SMD的径向分布发展为N形分布.
2 -->

3.3.速度场

随着局部动量比的变化, 针栓喷注器喷雾的速度场也随着发生了变化. 图13给出了不同工况下合速度的云图. 首先, 合速度具有非常明显的径向分布特点, 从喷雾中心到外缘呈现倒V形分布, 喷雾主流处的喷雾速度最大, 沿径向向内向外递减. 从合速度方向来看, 内侧喷雾速度方向基本上垂直向下, 越靠近喷雾外围径向的速度分量越大, 合速度与轴线方向夹角越大. 对比不同的局部动量比调节方式可以发现, 在本文中, 增大氧化剂流量方式所得的喷雾总流量更大, 总动量更高. 对应地, 合速度在数值上也更大. 下面分别从轴向速度和径向速度两个方面进一步分析不同工况下的速度分布.
图 13 不同局部动量比下的合速度云图
Figure13. Contour of the resultant velocity under different LMR.

图14给出了不同局部动量比下的轴向速度分布曲线. 考虑到喷雾同时向下向外运动, 图中以喷雾径向边界为基础, 定义了无量纲径向位置
图 14 不同工况下轴向速度随无量纲径向位置的变化曲线
Figure14. Axial velocity vs. r′under different operating conditions.

$r' = \frac{r}{{{r_{{\rm{ob}}}}}},$

其中r为径向位置, r_ob为外边界的径向位置, r'为0对应喷雾中心轴线, r'为1对应喷雾外边界.
由图14可以看出, 除了喷雾下游h > 20 mm后不同工况的曲线有所交叉外, 轴向速度从大到小整体上表现为: gk1 > gk2 > gk3 > gk4 > gk5 > gk6 > gk7. 这里面反映出两个规律, 一是局部动量比越高, 轴向速度越小; 二是相同的局部动量比下, 总动量越高, 轴向速度越大. 根据轴向速度的计算式

${V_{\rm{a}}} = \frac{{{{\dot m}_1}{v_1}}}{{{{\dot m}_1} + {{\dot m}_2}}} = \frac{{{v_1}}}{{1 + {\rm{MR}}}},$

其中, MR为混合比, 定义为氧化剂流量和燃料流量的比值.
试验中通过调节流量来调节局部动量比, 局部动量比越大, 混合比越高, 故轴向速度随局部动量比的增大而减小. 而相同动量比下, 总动量越高, 射流和液膜的流量更高, 喷雾的轴向速度和径向速度也更大.
然而, 从分布规律来看, h > 20 mm, r' < 0.35的喷雾远场内侧区域, 两种动量比调节方式下的轴向速度随局部动量比的变化规律并不相同, 不同工况的曲线出现了交叉情况. 具体地, 当局部动量比通过减小燃料流量方式增加时, 喷雾的轴向速度曲线沿轴向依次减小; 但当其通过增大氧化剂流量方式增加时, 在h > 20 mm, r' < 0.35区域内gk1—gk4的轴向速度曲线相互交错. 而通过比较不同工况下轴向速度沿实际径向位置的变化曲线(图15)可以发现, 在r < 20 mm范围内, gk1—gk4的轴向速度曲线基本重合.
图 15 不同工况、不同轴向距离处喷雾下游轴向速度随径向位置的变化曲线
Figure15. Axial velocity vs. r at different axial distances under different operating conditions.

根据前面的分析可知, 对于gk1—gk4, 喷雾近场中空, 几乎没有液膜直接贴着针栓头壁面向下流动, 喷雾分布主要受斗篷结构及其相互碰撞的影响. 对于单个斗篷(如图16所示), 临近射流的液膜直接被其撑开, 包覆在射流表面, 称之为斗篷顶部; 远离射流的液膜由于表面张力被向外带出, 也具备了一定的径向速度, 称之为斗篷侧缘. 其中, 斗篷顶部的液膜与射流经过相互作用后破碎雾化, 而斗篷侧缘主要由液膜组成, 相邻斗篷的侧缘撞击破碎, 填充了喷雾空心区. 由于gk1—gk4的液膜流量不变, 故空心区正下方喷雾的轴向速度基本一致. 同理, 该区域内的合速度(如图13)与径向速度(如图17)也基本一致.
图 16 单个“斗篷”的喷雾形态示意图
Figure16. Sketch map of the spray pattern of the single “cloak”.

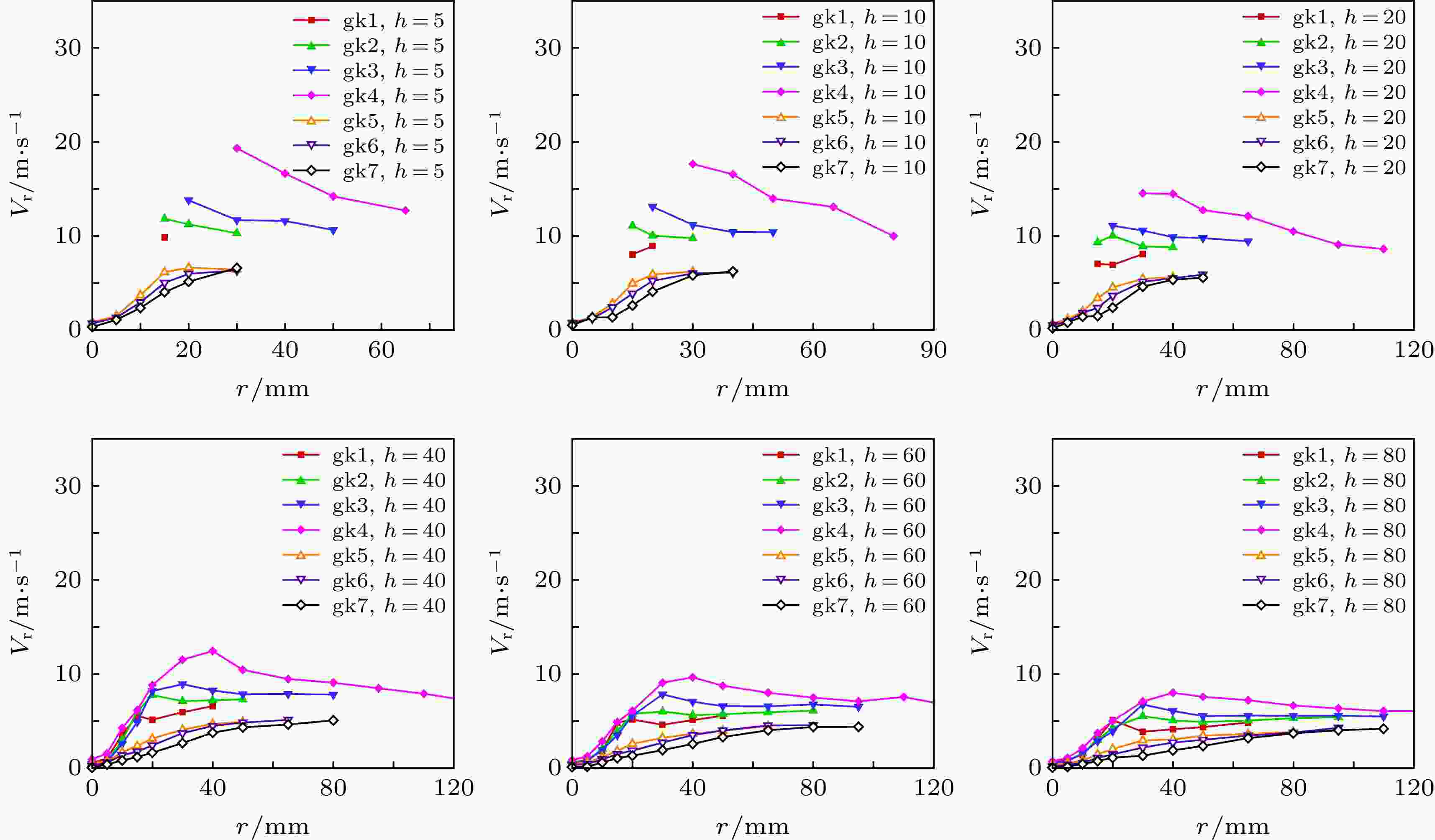图 17 不同工况下径向速度的分布曲线
Figure17. Distribution curves of the radial velocity under different operating conditions.

径向速度在r = 0 mm处数值接近于0, 总体上沿径向位置先增加后趋平, 对于个别工况在喷雾外围还出现了下降段, 与轴向速度的倒V形分布趋势类似. 然而, 轴向速度沿径向的变化以下降为主, 上升段只出现在很小的径向范围内(总体上R' ≤ 0.35), 这一段内喷雾中心区的轴向速度较低主要是由于壁面的摩擦阻力(对于实心喷雾)或液膜在中心碰撞带来的速度损失, 在喷雾主流及外围, 轴向速度随径向距离的增加而减小. 对于径向速度, 在喷雾的实心区域, 径向速度的变化以上升为主, 沿径向先增加至峰值趋平或缓慢下降趋平, 下降段主要出现在喷雾外围, 但数值上变化范围不大. 径向速度的缓慢减小可能归咎于环境空气和重力的影响.
局部动量比调节方式对径向分布的影响主要在于喷雾外围的径向是否存在下降段. 对于gk5—gk7, 喷雾全场的径向速度均呈现沿径向增加并趋平的变化趋势, 与成鹏^[11]所发现的喷雾内侧主要由液膜主导、喷雾外侧主要由射流主导的试验规律一致. 对于gk1—gk4, 射流流速更大, 外围喷雾与周围环境气体间的相互作用更强, 径向速度受到一定的削减, 径向速度沿径向略有下降.

本文通过试验手段研究了不同动量比调节方式下针栓喷注器的喷雾边界、粒径分布及速度场特征, 发现针栓喷注器的喷雾特性同时受到局部动量比及其调节方式的影响, 其中后者主要改变了总动量的大小. 具体得到以下结论.
1)在局部动量比为0.16—0.99的范围内, 喷雾形态分为空心-实心锥形和实心锥形两大类. 随着外喷嘴流量的增加, 喷雾锥上游出现空心区, 且空心区的范围随局部动量比的增加而扩大. 局部动量比同时还主导喷雾锥角的大小, 但喷雾下游液滴充分破碎雾化后, 总动量越高, 喷雾范围越大. 喷雾形态的不同进一步影响了粒径和速度的空间分布.
2)随着局部动量比的增加, 受射流影响的喷雾外缘粒径明显增加, SMD随之增大. 总动量越高, SMD变化范围越大. 粒径分布与喷雾分布有关, 对于有空心区的喷雾, SMD沿径向呈N形分布, 对于实心喷雾, 部分液雾在中心汇聚, 粒径偏大, 但粒径在径向上的变化范围不大.
3)对速度场的分析结果表明, 合速度受总动量影响, 且合速度与轴向速度、径向速度均沿径向呈倒V形分布, 但拐点位置与增减速度不同. 随着局部动量比的增加, 轴向速度减小, 径向速度增加. 斗篷结构由斗篷顶和斗篷侧缘组成, 后者主要由液膜发展而来, 相互撞击后填充了空心区, 该区域速度场由液膜主导, 几乎不受局部动量比变化的影响.