摘要: 众多粒子物理超标准模型中都预言了自旋有关的新相互作用存在. 极化的核子间通过交换自旋为1的轴矢量玻色子可以产生额外的吸引力进而改变无穷大核物质状态方程性质. 本文在相对论平均场模型的框架下加入额外的轴矢量玻色子后计算发现, 当相互作用强度与玻色子质量之比达到
$g_{\rm A}^2/m_{\rm Z'}^2 $ ~
${\cal O}(10 \, {\rm GeV^{-2}})$ 时, 低密处无穷大核物质的稳定性和对应的相变行为将发生显著的改变; 而当
$g_{\rm A}^2/m_{\rm Z'}^2 > 130 \, {\rm GeV^{-2}}$ 时核物质将在发生相变前率先到达零压点. 对中子星而言这意味着其内核物质将在保持稳定的状态下形成表面而不会发生相变形成壳层结构, 这与普遍存在于中子星天文观测中的星震现象矛盾, 因此反过来对新相互作用的强度提出了额外的限制. 通过与已有的地面实验结果对比, 本文发现对于力程为微米到厘米间的新相互作用, 中子星对其强度的约束最高可有8个量级的提升.
关键词: 中子星 /
超标准模型 /
新相互作用 English Abstract Constraints of neutron star on new interaction ofspin-dependent axial-vector coupling Gao Peng-Lin 1,2 ,Zheng Hao 2 ,Sun Guang-Ai 2 1.School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China Fund Project: Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0403703) and the National Natural Science Foundation of China (Grant No. U1830205).Received Date: 01 April 2019Accepted Date: 27 June 2019Available Online: 01 September 2019Published Online: 20 September 2019Abstract: It is predicted in many theories beyond the standard model that the new interaction relevant to spin is existent. The exchange of an axial vector particle will result in attractive dipole-dipole interaction which can be viewed as an effective magnetic potential that looks quite different from those expected from electromagnetism. In this work, we demonstrate that, instead of the laboratory spin source, stringent constraints can be set on these attractive spin-spin interactions from polarized nuclear matters within neutron stars which have extremely strong magnetic fields (up to 1015 G in some cases). By considering such an exotic interaction within the framework of relativistic mean field model, we find that the stability of infinite nuclear matter can be influenced significantly when the ratio of coupling strength to boson mass become larger than $g_{\rm A}^2/m_{\rm Z'}^2 \sim {\cal O}(10 \, {\rm GeV^{-2}})$ . Furthermore, based on the curvature matrix approach, when $g_{\rm A}^2/m_{\rm Z'}^2 > 130 \, {\rm GeV^{-2}}$ , phase transition inside low-density nuclear matter will no longer take place before the pressure of nuclear matter becomes zero, which forbids core-crust transition at the inner edge separating the liquid core from the solid crust of neutron stars. Thus bare neutron stars without any crusts are predicted. However, observations of pulsar glitches, i.e., the occasional disruptions of the extremely regular pulsations from magnetized, rotating neutron stars, imply the existence of crusts inside these dense objects. This in turn constrains the strength of the exotic interaction. In fact, in the case of dipole-dipole force on a length scale between μm to cm, the highest value of these constraints can be 8 orders of magnitude higher than those from existing laboratory results.Keywords: neutron star /theories beyond standard model /new interactions 全文HTML --> --> --> 1.引 言 近年来, 随着希格斯(Higgs)粒子[1 ,2 ] 和引力波[3 ,4 ] 的相继发现, 相对论和粒子物理标准模型这两套20世纪基础物理学中最伟大的理论模型在完成度上达到了空前的顶峰. 但无论是相对论还是粒子物理标准模型都远不是终极的理论, 物理界对新物理的渴望前所未有. 其中, 探测超标准模型预言的新相互作用和其传播子不仅对粒子物理, 还对宇宙学、天体物理甚至凝聚态物理的发展至关重要. 对于大质量(质量大于GeV/c2 )、“强”相互作用的新媒介子(例如Z′粒子), 实验上可以使用大型强子对撞机进行探测[5 -7 ] ; 质量稍小(约MeV/c2 )的新粒子可以在核物理实验中精确测量[8 ] . 然而轻质量(质量小于keV/c2 )、弱耦合的新相互作用粒子却难以在上述实验中被直接观测, 这其中就包括了近年来引起了广泛关注的(类)轴子[9 ] 、暗光子[10 ] 等粒子.$ \lambda_{\rm c}$ ~1/m 相当(为简化表达式已使用自然单位制, 后文如果没有特别说明也将默认使用自然单位的表达式), 而相互作用形式除了著名的汤川(Yukawa)势外还包括了许多与费米子自旋有关的自旋相关势. 质量较轻的微观粒子其康普顿波长一般可达$ {\cal O}({\rm nm}) $ 或以上, 交换这类粒子产生的有效势能中自旋无关的部分实验上表现为对引力的修正, 因此大量针对引力的精密测量实验能够在多个尺度上对其作出严厉的限制[11 ] . 而对于其他自旋相关的势能, Ramsey[12 ] 通过探测费米子间非电磁类的异常自旋-自旋耦合相互作用首次在实验中对其进行了约束. 之后依照Ramsey的思路, 研究人员对不同力程的费米子间自旋相关势能进行了测量: 力程为(亚)原子尺度的自旋间新相互作用可以通过观察其对类氢原子超精细能级结构的影响进行探测[13 ] ; 力程为(亚)微米到米量级的自旋相关势可以使用量子磁强计精确测量(自旋)极化的物体间的反常磁场来进行探测[14 ] ; 宏观(米以上到星球尺度)的新相互作用还可以利用地球内部大量的极化电子为源, 通过检测探测器与地球间的异常相互作用探测其大小[15 ] .[16 ,17 ] . 另一方面, 核子间通过交换轴矢量玻色子则会产生自旋相关的吸引相互作用. 对于自旋饱和(即非极化)的核物质或大部分处于基态的原子核, 因为其内部核子间通过自旋正反配对而总体上呈现出自旋中性, 所以上述自旋相关的势能对这类系统几乎没有影响. 但中子星的表面磁场最强可达约1015 G (1 G = 10–4 T), 远远高于实验室中能够产生的磁场大小[18 ] . 在如此强的磁场环境中, 中子星内的中子或质子将因为自身磁矩与磁场相互作用而被极化, 其内部物质的净自旋密度甚至高达约1038 cm–3 , 约是实验室中极化源的1016 倍. 因此可以预期中子星内核子间交换轴矢量玻色子产生的自旋相关力将会显著改变中子星内极化核物质的状态方程, 进而影响中子星的结构和性质.$ n_{\rm t} $ [19 ] . 本文的研究发现, 额外的吸引相互作用将显著地增大$ n_{\rm t} $ , 并使得低密处的极化核物质变得不再稳定(内部压强变为负数), 从而加速上述相变过程的进行. 此外计算中发现, 随着吸引相互作用的增强中子星物质甚至在发生壳-芯转变前就率先到达零压点, 导致中子星壳层结构消失, 整颗中子星将仅由一团裸露的液态核物质构成. 然而普遍存在于中子星天文观测中的星震现象从旁佐证了中子星壳层结构的存在[20 ,21 ] . 为了不与天文观测事实相矛盾就必须对上述额外的吸引相互作用做出限制. 因此, 本文基于相对论平均场模型和曲率矩阵的算法研究了交换轴矢量玻色子对极化核物质状态方程和稳定性的影响, 结合天文观测中星震现象给出的约束, 限制了轴矢量玻色子与核子间的相互作用强度. 经过计算后发现, 中子星存在壳层结构的这一事实对力程$ \lambda_{\rm c} \in $ [μm, cm]的新相互作用具有很强的限制, 其约束强度比其他地面实验给出的结果最多可有8个量级的提升.2 节首先推导轴矢量新相互作用玻色子对核物质状态方程的改变, 进而讨论其对中子星物质稳定性的影响; 第3 节介绍天文观测中的星震现象并描述其对新相互作用强度的约束; 最后在第4 节中进行总结.2.中子星物质状态方程和稳定性的计算 中子星是在恒星演化晚期由超新星爆发产生的恒星遗迹之一. 因为中子星将太阳质量的物质压缩至半径约十千米的范围之内, 所以其内物质远超地面实验室中所能达到的致密, 这也使其成为观测极端物理现象的重要场所之一. 传统的中子星模型认为中子星是由核物质组成的球体, 其结构由内到外大致分为β稳定的核物质核芯、结团的核物质壳层和等离子体大气等. 此外, 中子星内还存在极强的磁场, 其表面磁场强度最高可达约$ 10^{15} $ G, 因此中子星内的物质还是高度极化的.2.1.无穷大核物质的状态方程 2.1.无穷大核物质的状态方程 中子星99%以上的质量都是由核物质芯贡献的, 主要是由达到了β平衡而稳定存在的电中性n, p, e, μ (即中子、质子、电子和μ子)物质组成. 其中中子和质子物质可以通过无穷大的均匀核物质模型描述, 其性质由物质的状态方程决定.[22 ] . 无穷大核物质(之后简称核物质)是一种由大量核子组成的理想流体系统, 其中核子间由核力束缚而保持稳定. 核物质的状态方程一般被定义为核物质内的单核子结合能, 对于无穷大的核物质系统其大小是中子、质子数密度($ n_{\rm n} $ 和$ n_{\rm p} $ )的函数.[23 ] :$\omega_{\mu\nu}\equiv \partial_{\mu}\omega_{\nu}-\partial_{\nu}\omega_{\mu} $ 和$\rho_{\mu\nu} \equiv \partial_{\mu}{{\rho}}_{\nu}-\partial_{\nu}{{\rho}}_{\mu} $ 分别是ω介子和ρ介子的场强度张量; $ \psi $ , $ \sigma $ , $ \omega_{\mu} $ 和$ {{\rho}}_{\mu} $ 则分别是核子场算符、同位旋标量-标量场算符、矢量场算符和同位旋矢量-矢量场算符(黑体符号代表其是同位旋空间的矢量); $U(\sigma) = b_{\text{σ}}M(g_{\text{σ}}\sigma)^3/ 3\; + $ $ c_{\text{σ}}(g_{\text{σ}}\sigma)^4/4 $ 是σ 场的自相互作用项, $ g_{\text{σ}} $ , $ g_{\text{ω}} $ 和$ g_{\text{ρ}} $ 分别是各介子场与核子场的耦合强度, 而$ \varLambda_{V} $ 则是$ \text{ρ} $ 介子场与$ \text{ω} $ 介子场间的相互作用耦合常数. 此外, M , $ m_{\text{σ}} $ , $ m_{\text{ω}} $ 和$ m_{\text{ρ}} $ 分别代表核子和各个介子的静质量.$ {\rm Z}' $ 产生的有效拉氏量密度等于:$ m_{\rm Z'} $ 是Z′介子的质量, $ Z'_{\mu\nu} $ 是Z′介子的场强度张量, 而$ g_{\rm Z'}^{\rm A} $ 则是其与核子间的有效耦合常数.1 )和方程(2 )可以推出各介子场的运动方程(即欧拉-拉格朗日方程)满足:$ \sigma \rightarrow \langle \sigma \rangle $ , $ \omega_{\mu} \rightarrow \langle \omega_{\mu} \rangle $ , $ {{\rho}}_{\mu} \rightarrow \langle {{\rho}}_{\mu} \rangle $ 和$ Z'_{\mu} \rightarrow \langle Z'_{\mu} \rangle $ . 其中$ \langle \cdot \rangle $ 是介子场在基态无穷大均匀核物质中的期望值. 将其代入上述场的运动方程后得到简化的运动方程(其中省略掉了介子场期望值的尖括号):$ k\cdot x = k_{\mu}x^{\mu} = k_0 t - {{k}}\cdot{{r}} $ . 将其代入方程(7 )并化简得到表达式$ M^{*} \equiv M^{*}_{\rm {dirac}} = M-g_{\text{σ}}\sigma $ 是核子的狄拉克质量(nucleon Dirac mass), 等效动量算符$ K_{\mu} = k_{\mu} -$ $ g_{\text{ω}}\omega_{\mu} - g_{\text{ρ}}{{\rho}}_{\mu} \cdot {{\tau}} $ . 方程(13 )与狄拉克方程具有相同的形式, 其中新相互作用项$ \gamma^{\mu}\gamma^{5} \, g_{\rm Z'}^{\rm A} Z'_{\mu} $ 可以当作微扰来求解. 因此对于无穷大核物质中动量为k $ \tau_3^{\rm n} = 1 $ , 对质子$ \tau_3^{\rm p} = -1 $ . 此外, 式中s $ n_{\rm n} $ 与$ n_{\rm p} $ 的函数:$ k_{\rm F}^J $ 是费米动量, J = n或p. 此外, 核子的标量密度定义为$ M'^2 = M^{*2} + g_{\rm Z'}^{\rm A, 2} Z'^2_0 + 2 g_{\rm Z'}^{\rm A} Z'_0 ({{k}}\cdot{{s}}) $ . 类似的核子的赝标量密度等于$ \langle s_i \rangle $ 是自旋算符第i 分量的期望值(即极化率).$ Z' $ 的贡献后核子的标量密度和赝标量密度中$ M' $ 是矩阵方程$ {{k}}\cdot{{s}} $ 的函数, σ 场与Z' 场也因此耦合而难以严格求解. 然而在一阶近似下, 将方程(25 )对$ Z'_0 $ 做微扰展开后有$ n_{{\rm a}, J} \ll n_{J} $ ). 因此在一阶近似下, 有结论$ Z'_0 $ 对核物质状态方程的影响可以忽略不计.$ M' \approx M^{*} $ , σ 场也不再与Z' 场耦合, 两者可以各自独立求解.26 )—(30 )式后将各介子场的平均值代入上述方程即可得到取定质子、中子数密度后核物质的状态方程$ \varepsilon = \varepsilon(n_{\rm n}, n_{\rm p}) $ 和$ P = P(n_{\rm n}, n_{\rm p}) $ .2.2.中子星的转变密度和零压点 -->2.2.中子星的转变密度和零压点 2.1 节讨论了如何计算加入新相互作用后的核物质状态方程. 中子星内除了核物质外还有大量与质子、中子达到β平衡的轻子(电子、μ子)物质, 因此中子星物质的状态方程可以表示为[19 ] :35 )和方程(36 ), 轻子部分可以用自由费米气体模型较好地估计:$ m_{\rm l} $ 和$ n_{\rm l} $ 分别是轻子的静质量和数密度, l代表电子或μ子.$ \mu_i $ (i 分别代表质子、中子、电子和μ子)满足条件$ n_{\rm b} $ , 联立求解上述两个方程即可得到中子星各组分的数密度大小. 因此对于电中性的β稳定核物质, 其状态方程只是重子数密度的函数.图1 为中子星内物质的能量密度和压强随重子数密度的改变, 其中重子部分相对论平均场参数使用了IU-FSU的相互作用参数[24 ] , $Z'$ 的有效耦合常数定义为$ \bar{g}_{\rm A} \equiv g_{\rm Z'}^{\rm A} \langle {{s}} \rangle $ . 可以看出新加入的轴矢量相互作用能够显著地改变状态方程的行为: 有效耦合强度很弱时(即相互作用强度$ g_{\rm Z'}^{\rm A} $ 本身很小或是核物质未极化时)中子星物质的能量密度和压强恒大于零且随着重子密度的增大快速增长; 但随着$ \bar{g}_{\rm A} $ 的增大, 物质的压强将先减小再增大, 且当$\bar{g}_{\rm A}^2/m_{\rm Z'}^2 $ 约为10 GeV–2 时压强在$ n_{\rm b}$ 约为0.1 fm–3 处变为零; 对于更大的$ \bar{g}_{\rm A}^2/m_{\rm Z'}^2 $ , 压强会先变为负数再增大为正(见图1(a) 内插图). 令(靠近高密方向的)零压点对应的密度为$ n_{\rm c} $ .图 1 中子星物质状态方程(能量密度、压强)随重子数密度的变化, 其中轴矢量相互作用的有效耦合常数分别等于$\bar{g}_{\rm A}^2/m_{\rm Z'}^2 = 0, \; 9.9 $ 和30 GeV–2 Figure1. Equation of states inside neutron stars as a function of the baryon density for β-stable nuclear matter where the effective couplings to Z' field are $\bar{g}_{\rm A}^2/m_{\rm Z'}^2 = 0, \; 9.9$ and 30 GeV–2 , respectively.$ n_{\rm t} $ (简称转变密度). 本文通过判断核物质曲率矩阵的正定性来计算转变密度$ n_{\rm t} $ [25 ] , 其中曲率矩阵定义为核物质各组分化学势对密度的偏导数(因为密度较小的β稳定物质中没有μ子, 因此曲率矩阵中没有μ子相关项):图2 为转变密度$ n_{\rm t} $ 与核物质零压点所对应的密度$ n_{\rm c} $ 随$ \bar{g}_{\rm A}^2/m_{\rm Z'}^2 $ 的变化. 其中当$\bar{g}_{\rm A}^2/m_{\rm Z'}^2 < $ 13 GeV–2 时$ n_{\rm c} < n_{\rm t} $ , 中子星内物质将在达到零压点前变得不稳定而结团相变成为壳层; 然而当$ \bar{g}_{\rm A}^2/m_{\rm Z'}^2 > $ 13 GeV–2 时$ n_{\rm c} > n_{\rm t} $ , 中子星物质将在保持稳定性的同时达到零压点并形成表面. 这时中子星将完全由裸露的无穷大核物质构成, 不会再有壳层结构.图 2 中子星壳-芯转变密度($n_{\rm t}$ )与核物质零压点($n_{\rm c}$ )随$\bar{g}_{\rm A}^2/m_{\rm Z'}^2$ 的变化曲线Figure2. Core-crust transition density $n_{\rm t}$ as well as zero-pressure point density $n_{\rm c}$ of nuclear matter as functions of $\bar{g}_{\rm A}^2/m_{\rm Z'}^2$ .3.中子星对轴矢量新相互作用的约束 第2 节最后对图2 的讨论得出如下结论: 当轴矢量新相互作用满足条件$ \bar{g}_{\rm A}^2/m_{\rm Z'}^2 >$ 13 GeV–2 时中子星将不再出现壳层结构, 而仅由裸露的核物质芯构成. 这与中子星天文观测中的“星震”模型矛盾. 星震模型是对中子星天文观测中glitch现象的理论解释: 由于能量损耗, 一般而言中子星的自传周期将随时间的推移而缓慢增加; 但在对很多中子星的自转观测中都出现了信号周期突然改变(一般是加速)的现象. 星震模型中, 由于在中子星固态壳层中发生了星震并引起了壳层物质的调整, 导致壳层部分转动惯量减小, 而根据角动量守恒星体的自转角速度将会突然加快.$\bar{g}_{\rm A}^2/m_{\rm Z'}^2 < $ 13.02 GeV–2 . 此外, 强磁场下中子星内核物质的极化率可达$ \langle {{s}} \rangle = 0.1 $ , 因此星震现象对轴矢量新相互作用的约束是图3 给出了上述约束(实线及以上的灰色区域), 并将其与现有地面实验对$ g^{\rm A}_{\rm Z'} $ 的约束进行了比较(虚线和点画线画出的区域). 可以看到, 中子星存在壳层的约束在力程从厘米到微米的四个量级范围内远强于地面实验的约束, 其中对于亚厘米量级力程的新相互作用(46 )式给出的约束比现有实验结果有最高8个量级的提升[13 ,14 ,26 ] .图 3 星震现象对轴矢量新相互作用的约束和其他地面实验中所得约束的对比[13 ,14 ,26 ] Figure3. Exclusion contour of the axial-axial couplings from the existence of neutron star crusts. We compare our constraints with other experiments as well[13 ,14 ,26 ] .4.结 论 中子星是宇宙中最为致密的物质形态之一, 一直以来都是观测各类极端物理现象的重要平台. 本文通过在传统的相对论平均场模型框架下加入轴矢量新相互作用的贡献, 定量地研究了新相互作用玻色子对核物质状态方程稳定性的影响. 结果发现新相互作用粒子将会显著地改变核物质的稳定性和对应的相变行为, 且当新相互作用耦合常数满足$ \bar{g}_{\rm A}^2/m_{\rm Z'}^2 >$ 13 GeV–2 时核物质将在发生相变前率先到达零压点. 对于中子星来说上述行为意味着中子星内核物质将在保持稳定状态的情况下直接形成表面与真空接触, 因此中子星将不会再有壳层结构出现. 这与天文观测中大量发现的星震现象矛盾, 所以反过来要求新相互作用强度必须满足$ \bar{g}_{\rm A}^2/m_{\rm Z'}^2 < $ 13 GeV–2 的约束. 这一约束在厘米到微米的力程范围内远强于其他地面实验的结果, 展示了天文观测对新物理探测的强大影响. 




































































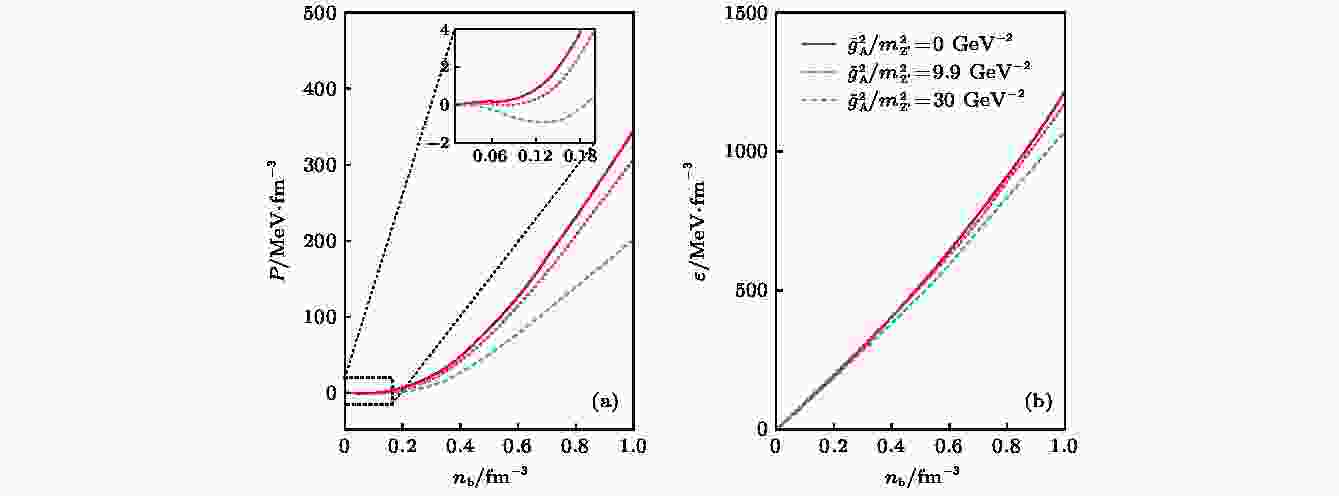 图 1 中子星物质状态方程(能量密度、压强)随重子数密度的变化, 其中轴矢量相互作用的有效耦合常数分别等于
图 1 中子星物质状态方程(能量密度、压强)随重子数密度的变化, 其中轴矢量相互作用的有效耦合常数分别等于












 图 2 中子星壳-芯转变密度(
图 2 中子星壳-芯转变密度(









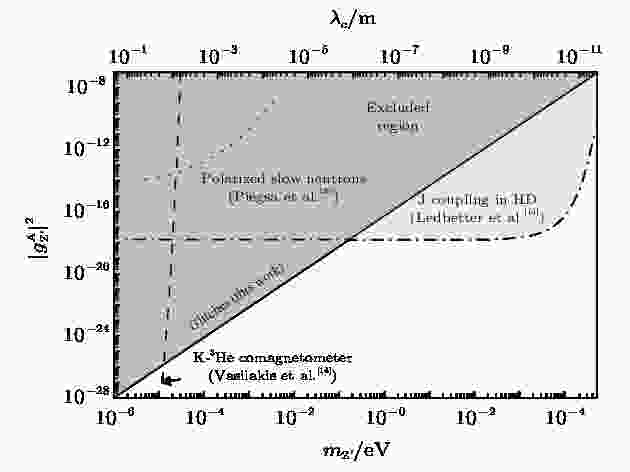 图 3 星震现象对轴矢量新相互作用的约束和其他地面实验中所得约束的对比[13,14,26]
图 3 星震现象对轴矢量新相互作用的约束和其他地面实验中所得约束的对比[13,14,26]






