摘要:活性物质在自然界中广泛存在. 利用二维布朗动力学模拟方法, 设计了一种柔性边界棘轮, 并研究了其在活性粒子浴内的动力学行为. 发现棘轮在活性粒子浴内能够发生定向转动, 这是因为活性粒子在柔性边界周围的不均匀分布导致压力的不均匀分布, 进而对棘轮产生扭矩. 进一步研究了影响转动速率的因素, 发现平均转动角速度随活性粒子驱动力、活性粒子密度的增大而增大, 随粒子旋转扩散系数、支架数的增大而降低. 研究结果对于设计新的实验系统来研究此类非平衡物理现象具有一定的指导意义.
关键词: 棘轮/
定向旋转/
对称性破缺/
分子动力学模拟

English Abstract

全文HTML

--> --> -->

从微观尺度的细胞骨架到宏观尺度的鱼群、鸟群^[1], 活性物质(active matter)普遍存在于自然界中. 人工也能设计和制造活性物质体系, 如磁场^[2]、声场^[3]或电场^[4]驱动的活性体系. 这些系统的共同特征是组成单元可以通过消耗能量进行运动. 此类系统展现出许多有趣的非平衡物理现象, 如体系密度巨涨落(giant fluctuations)^[5]、自发相分离(spontaneous phase separation)^[6,7]、斑图形成(pattern formation)^[8]和自组装行为(self-assembly behavior)^[9].
除了理解此类体系丰富现象背后的物理机理, 科学家们开始思索如何将活性物质体系的能量提取出来为人类所用, 比如细菌自发运动的能量^[10—13]. 细菌的运动是通过消耗化学能来实现, 其自驱运动本身已经打破系统的时间对称性. 为了实现定向旋转, 还需要打破空间对称性, 常见的方法是使用形状不对称的棘轮. 比如, Angelani等^[14]的模拟研究表明, 非对称棘轮浸入棒状粒子能够产生定向转动. Sokolov等^[15]在细菌作为活性物质的实验中也观察到了类似的现象. 近年来, 将柔性链状结构的软边界^[16—23]置于活性粒子浴中的动力学行为越来越受研究者的关注. 由于活性粒子的碰撞, 软边界会发生非热波动进而出现反常的现象. 最近, 我们课题组研究发现, 柔性^[21]和半刚性链^[22]嫁接的圆盘在活性粒子浴中会因为链构象的对称性被打破, 自发产生结构的不对称性, 从而产生长时间持续的定向运动.
我们之前的研究工作表明^[21], 活性粒子倾向于聚集在链上高曲率区域, 而柔性链的形变对粒子的积聚存在正反馈效果^[23], 从而进一步加强柔性链形变, 使粒子大量聚集. 上述工作中我们通过多根链嫁接到纳米盘来实现自发转动, 本文中我们设计更简单的具有柔性边界的对称性棘轮, 研究其在非平衡粒子浴内的行为, 进一步探讨柔性边界是否能让棘轮转动. 我们发现粒子的聚集导致柔性边界的结构发生改变, 力分布的不对称性诱导棘轮产生扭矩, 进而实现棘轮的定向转动. 活性粒子的自驱力大小、旋转扩散能力和体系粒子密度都对棘轮定向转动产生影响: 棘轮的旋转速率随活性力和活性粒子数密度的增大而增加; 随活性粒子的旋转扩散系数的增大而减小.

类似于之前的工作^[19—23], 我们用二维模型来进行研究(模拟活性物质在界面或薄膜中的情况). 体系的初始结构为N_p个自驱动活性粒子围绕在柔性边界周围, 其中活性粒子(active particles)的力驱动方向为${\hat \mu _i} = \left( {\cos \theta ,\sin \theta } \right)$, 该方向可以随时间改变; 柔性边界的初始状态为一个圆形由N_b = 1256个珠子(passive beads)用弹簧势连接的柔性链组成. 整个体系中所有粒子之间采用相互排斥的WCA势, 其势函数表示为

${U_{{\rm{WCA}}}}\left( r \right) = \left\{ {\begin{aligned}& {4\varepsilon \left[ {{{\left( {\frac{\sigma }{r}} \right)}^{12}} - {{\left( {\frac{\sigma }{r}} \right)}^6}} \right] + \varepsilon ,r < {r_{\rm{c}}} = \sqrt[^6]{2}}\\& {0\;,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r \geqslant {r_{\rm{c}}}}\end{aligned}} \right.,$

其中, 截断半径为${r_{\rm{c}}} = \sqrt[^6]{2}\sigma $, ε是相互作用强度. 柔性链上, 珠子之间的键相互作用采用谐振弹簧势, 其势函数表示为

${U_{\rm{b}}} = k{\left( {r - {r_0}} \right)^2},$

其中, 弹性系数取k = 5000 ε/σ², 为了防止活性粒子穿过柔性链, 平衡键长取r₀ = 0.25σ, 由键连接的近邻珠子之间的对相互作用被忽略. 棘轮由柔性链结构和刚性支架组成. 柔性链的初始构型为圆形, 半径R₀ ≈ 50σ. 链到圆心由刚性支架连接, 结构类似于自行车轮. 四支架体系, 初始结构示意图如图1.
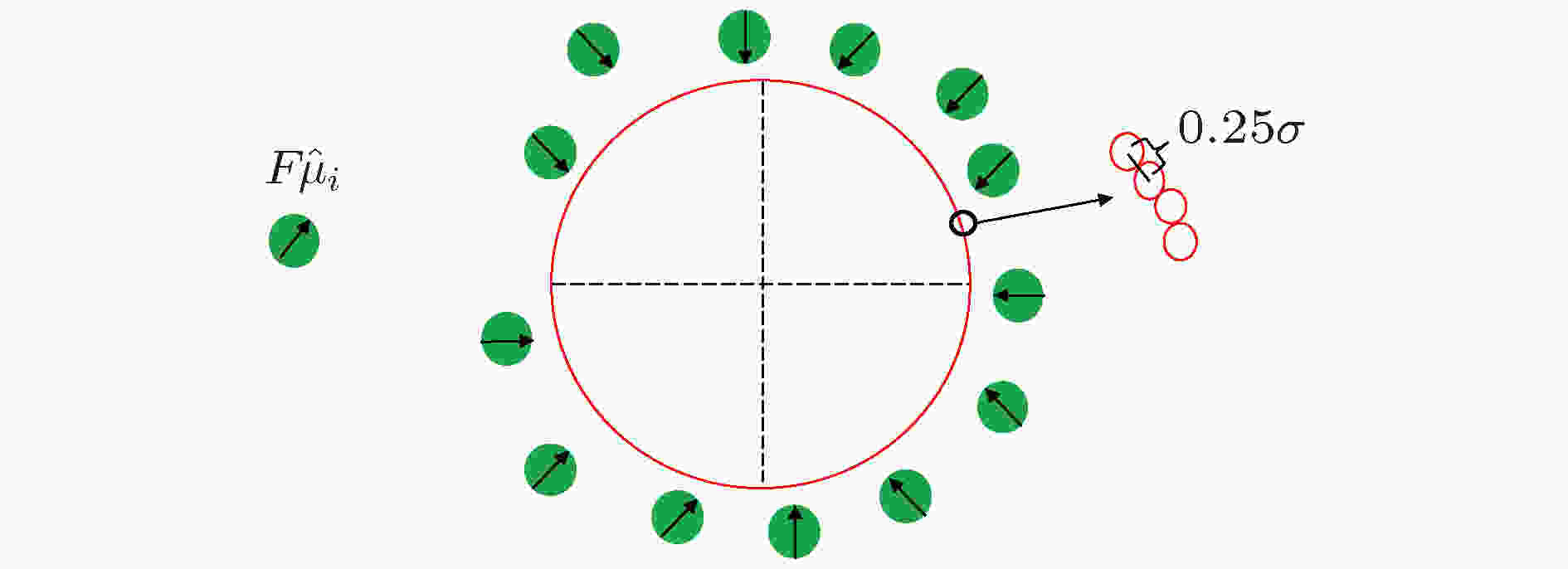图 1 棘轮在活性粒子浴中(绿色部分)的初始示意结构 虚线部分表示刚性支架, 红色表示柔性边界, 左上部分绿色粒子中的黑色箭头表示活性粒子的推进力方向, 右上部分为一段边界上的粒子排布, 粒子间间距为0.25σ
Figure1. The initial structure of flexible boundary (red) in the active particle bath (green). The dashed lines represent four rigid trestles. The black arrow in the green particle indicates the active force direction of the active particle in the upper left. The upper right part is the particle arrangement on a boundary. The spacing between the particles is 0.25σ.

体系中的活性粒子遵循郎之万动力学, 其运动方程可以表示为:

$m{{\ddot{{r}}}_{{i}}} = - \nabla U - \gamma {{\dot{{r}}}_{{i}}} + F{{\hat{{\mu }}}_{{i}}}\left( t \right) + \sqrt {2{\gamma ^2}{D_0}} {\eta _i}\left( t \right),$

${\dot \theta _i} = \sqrt {2{D_{\rm{r}}}} {\xi _i}\left( t \right),$

其中, (3)和(4)式分别表示活性粒子的平移和旋转运动; 柔性链上的珠子只遵循运动方程(3), 且F = 0; 平动摩擦系数为γ = k_BT/D₀, D₀为平移扩散系数; D_r为旋转扩散系数; ${\hat{{\mu }} }= \left( {\cos \theta ,\sin \theta } \right)$是一个单位向量指向沿着活性力的推进轴, 由旋转扩散控制; η_i(t)和ξ_i(t)为白噪声项, 满足涨落-耗散定理: $\left\langle {{\eta _i}\left( t \right)} \right\rangle = 0,\left\langle {{\eta _i}\left( t \right){\eta _j}\left( {t'} \right)} \right\rangle = {\delta _{ij}}\delta \left( {t - t'} \right)$以及$\left\langle {{\xi _i}\left( t \right)} \right\rangle = $$0,\left\langle {{\xi _i}\left( t \right){\xi _j}\left( {t'} \right)} \right\rangle = \delta \left( {t - t'} \right)$.
在我们的分子动力学模拟过程中, 周期性盒子大小为200σ × 200σ. 我们采用约化单位, 令m = 1, σ = 1, k_BT = 1; 时间单位为$\tau = \sqrt {m{\sigma ^2}/{k_{\rm{B}}}T} $. 此外, 本文中我们令ε = 10, γ = 10, 此时D₀ = 0.1. 我们采用修改后的LAMMPS软件^[24,25]进行模拟, 研究不同的活性力(F)、粒子数密度(φ)、旋转扩散系数(D_r)及支架数(N_s)对棘轮运动行为的影响. 运动轨迹采用VMD软件进行可视化处理和分析^[26].

2

-->

3.1.压力不对称分布诱导转动

首先考察了支架数为N_s = 4, 活性粒子的数密度为φ = 0.025、旋转扩散系数取D_r = 0.0001、驱动力F = 40时棘轮的转动行为(见附属材料中的视频F = 40.avi). 如图2(a)所示, 当棘轮处于活性粒子浴中会发生定向旋转的现象.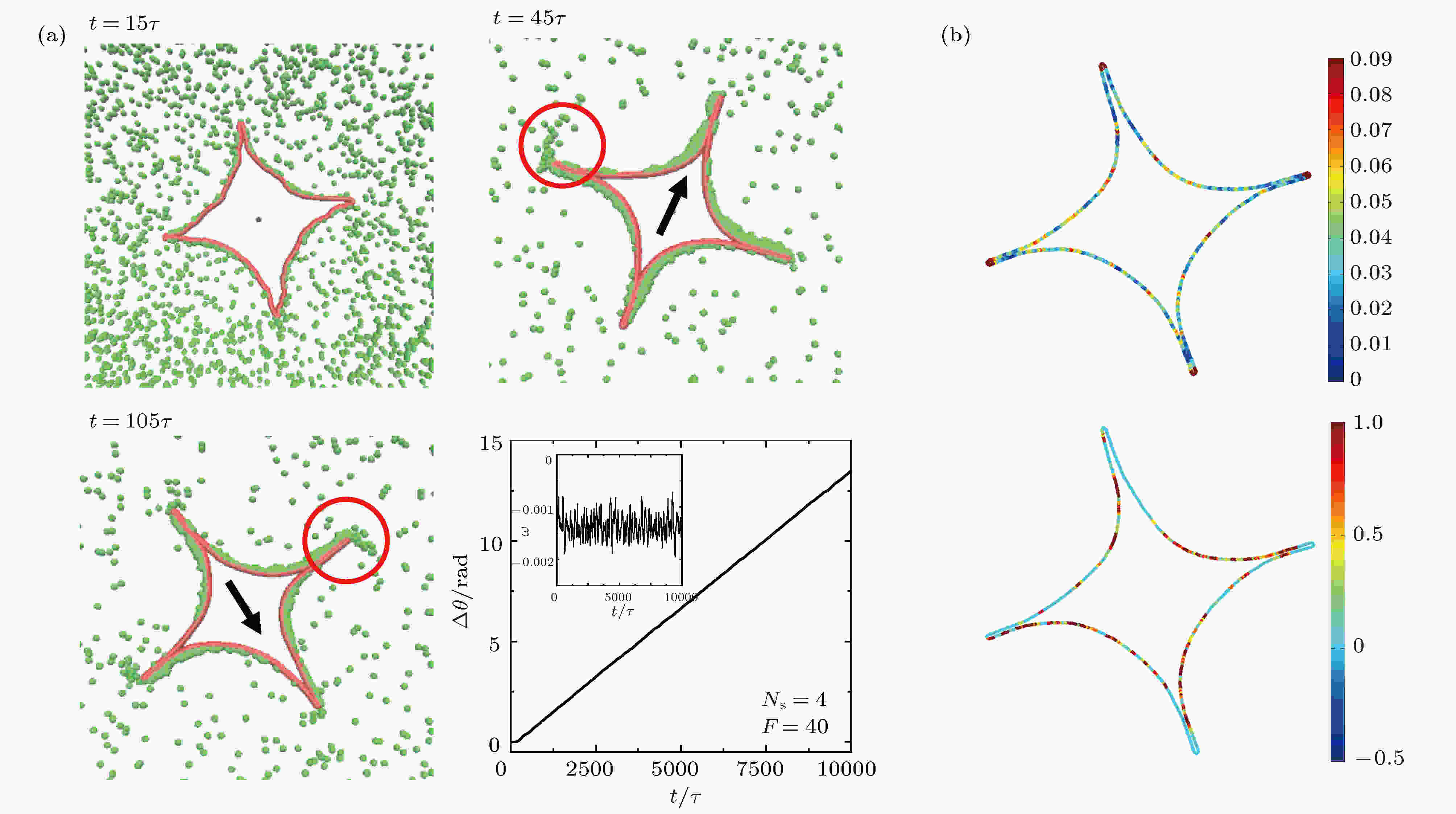
图 2 (a)四支架棘轮随时间转动的示意图, 图示中刚性支架被忽略, 左上图黑点代表棘轮质心, 其中黑色箭头表示从质心到一支点的方向以此表明棘轮发生转动, 右下图是该情况下的旋转角度与角速度随着时间的变化曲线图; (b)上图为棘轮柔性边界的曲率分布图, 下图为压力分布图, 其中棘轮支架数为N_s = 4, 活性粒子的数密度为φ = 0.025, 旋转扩散系数取D_r = 0.0001, 驱动力F = 40
Figure2. (a) Schematic diagram of the ratchet rotation with time for N_s = 4, φ = 0.025, D_r = 0.0001, F = 40. The black dot on the top left figure represents the center of mass of the ratchet; the black arrows denote the orientation from the center of mass of ratchet to the fixed point of boundary to indicate the rotation of the ratchet. The right-down figure shows the time evolution of angle and angular velocity of ratchet. (b) The curvature distribution (up) of boundary and the pressure distribution (down) around it

经过观察棘轮及活性粒子的运动轨迹, 我们发现开始时刻棘轮不转动, 活性粒子在驱动力作用下, 快速聚集到柔性边界周围, 并诱导其发生形变, 如图2(a)的左上图. 当粒子聚集到一定程度, 集聚在棘轮上曲率较大处的活性粒子出现崩塌的情况: 在棘轮上接近支架顶端处的大部分活性粒子会被棘轮抛出, 也就是甩尾现象(图2(a)中红色圆圈处). 这种运动导致粒子在边界上的分布不均匀, 进而对棘轮施加一定的扭矩, 导致棘轮的旋转. 图2(a)的右下图为旋转角度θ随着时间的变化曲线, 里面的插图为对应的角速度ω随时间的变化曲线. 旋转角速度的计算依据以下公式:

$\omega = \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}},$

其中, 旋转角速度ω为正值时表示棘轮沿逆时针方向旋转, 负值时表示棘轮沿顺时针方向旋转.
为了更好地探究棘轮旋转的机制, 计算了构成棘轮的柔性链的曲率和所受压力的分布情况, 如图2(b)所示. 该图的上图为棘轮的柔性链的曲率分布图, 其中散点颜色由深蓝到红色代表曲率由小到大变化; 下图为组成棘轮的柔性链所受压力的分布散点图, 其中深蓝色部分代表组成棘轮的柔性链所受压力较小, 由蓝色到红色部分, 表示组成棘轮的柔性链所受压力逐渐增大. 经过观察运动轨迹, 发现棘轮沿顺时针方向旋转, 与曲率、压力分布图所表示的效果一致. 压力分布在高曲率位置, 且具有不对称性, 进而产生扭转力, 驱使其转动.
2 -->

3.2.自驱力效应

接下来研究转动速度和驱动力之间的关系. 选取了支架数为N_s = 4的棘轮, 体系中活性粒子的数密度为φ = 0.025, 其中φ = σ²N_p/4R₀². 如图3(a)所示, 随着活性力的增加, 棘轮的平均旋转角速度单调增加. 图3(b)是体系进入稳态后在不同活性力的作用下, 棘轮的瞬时旋转角速度. 从图3(b)中可以看出, 当活性力较小时(F = 20)棘轮的旋转角速度较小且瞬时角速度有正有负, 棘轮的旋转方向不固定. 随着活性力的进一步增加(从F = 20增大到F = 80), 棘轮上聚集的活性粒子增多且扭矩也会变得越来越大, 从而实现定向转动. 通过图3也可以发现, 棘轮的瞬时角速度涨落随驱动力的增大而在一定程度上增大, 这是因为驱动力增大, 粒子运动速度较快, 粒子碰撞棘轮时, 对棘轮的扰动性增强.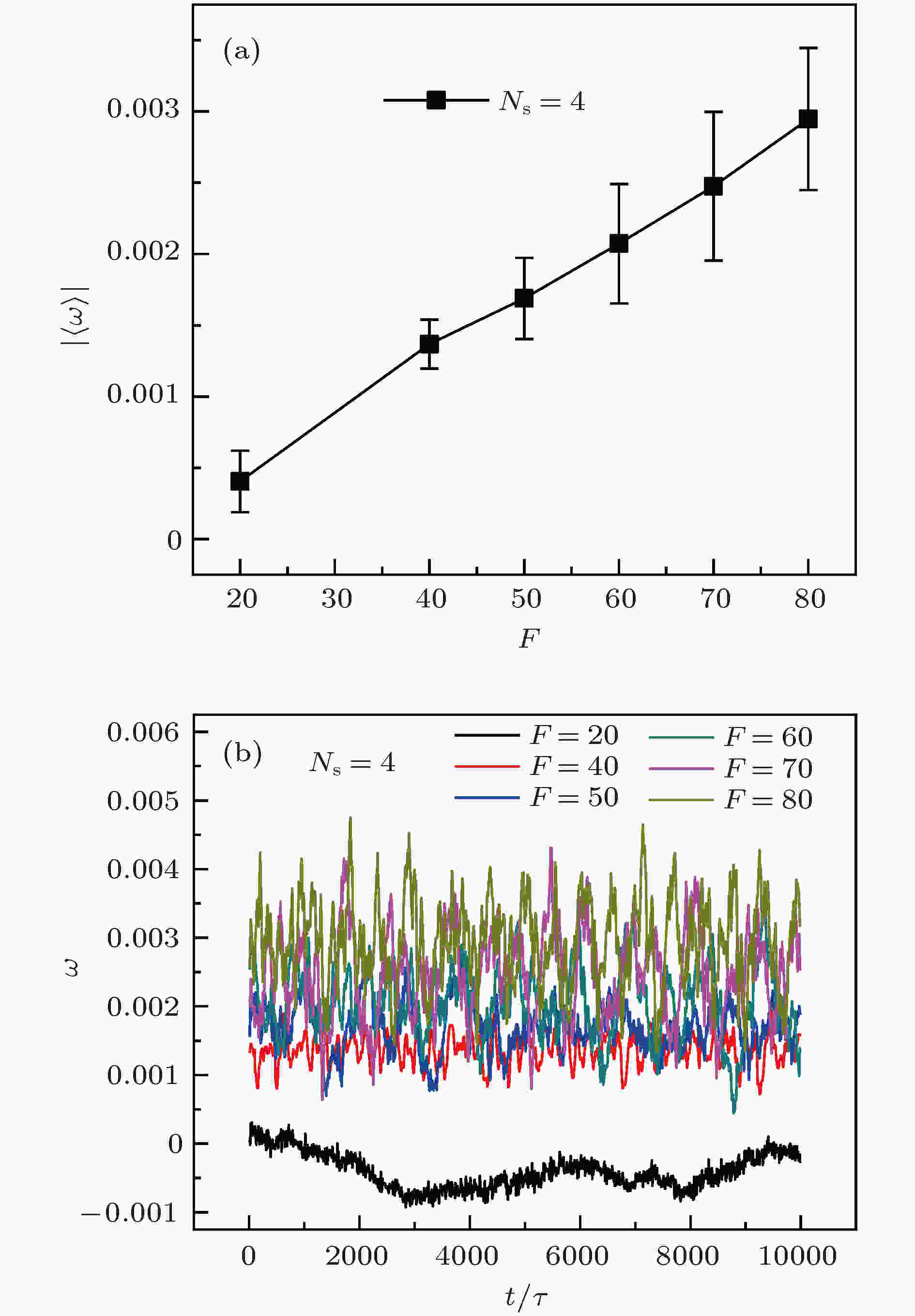
图 3 支架数为4、不同活性力的作用下, 棘轮的旋转角速度 (a)平均角速度, (b)瞬时角速度, 误差棒表示平均角速度的标准方差
Figure3. (a) Average angular velocity and (b) instantaneous angular velocity for the four rigid trestles with various active forces. The error bars represent the standard the deviations of angular velocity of rigid trestles.

2 -->

3.3.密度效应

在我们之前的工作中^[20]发现囊泡内的活性粒子的非均匀分布会对囊泡的形状产生一定的影响, 且囊泡的形状与活性粒子的密度成正相关关系^[27]. 那么对于本文所模拟的体系, 活性粒子的密度也势必会对柔性边界有一定影响, 且可能会对棘轮的旋转有促进或者抑制作用. 为了更好地验证我们的设想, 在模拟过程中我们保持活性粒子的旋转扩散系数为D_r = 0.0001, 活性粒子施加的驱动力选取F = 80, 研究不同粒子数密度φ下棘轮的旋转角速度的变化. 从图4中可以看出, 随着活性粒子数密度的增加, 棘轮的角速度也增加, 由此可以理解为棘轮的转动速率随着活性粒子数密度的提高而提高. 从图中可以直观地看出, 当活性粒子的数密度较小时, 活性粒子浴中活性粒子的集聚效果没有粒子数密度大时明显(图4插图). 大量粒子的聚集有利于棘轮扭矩的增加, 进而增加角速度. 因边界周围凹陷区域聚集的数目有限, 从图中可以看出, 随着粒子数密度的增加, 角速度增幅降低; 大量的增加粒子数密度, 可能出现饱和现象.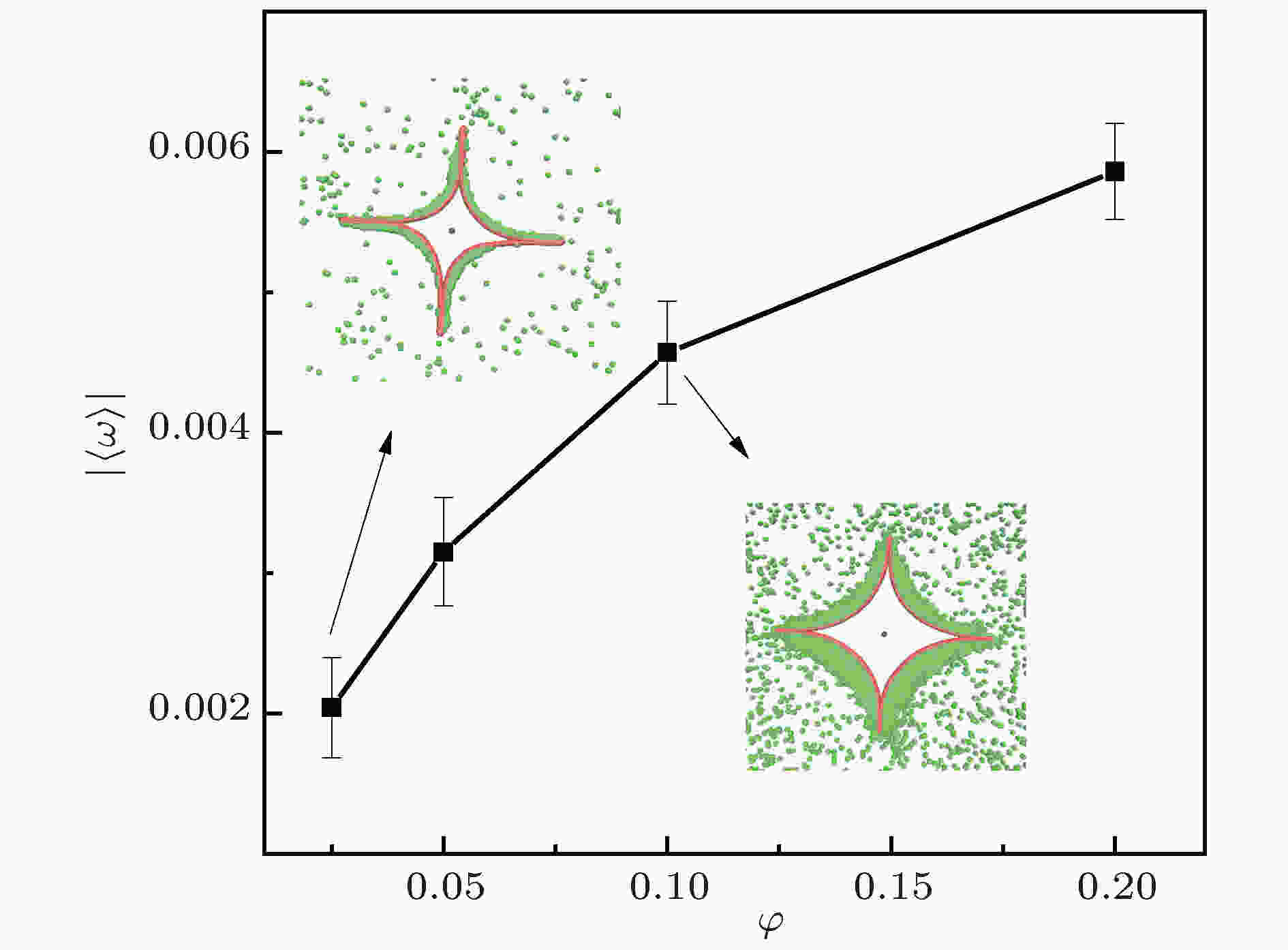
图 4 棘轮的平均角速度与粒子数密度之间的关系, 内部两张插图分别对应活性粒子密度φ = 0.025和φ = 0.1, 误差棒表示平均角速度的标准方差
Figure4. Average angular velocity vs the number density of active particles. The insets are typical snapshots for φ = 0.025 and φ = 0.1. The error bars represent the standard the deviations of angular velocity.

2 -->

3.4.旋转扩散系数效应

研究过程中, 我们把旋转扩散系数D_r作为可调参数来探究其对棘轮转动速率的影响^[23]. 在模拟时, 为了便于观察, 给活性粒子施加的驱动力取较大的一组F = 80. 得到不同D_r下棘轮的旋转角速度与时间的关系图, 如图5(a)所示.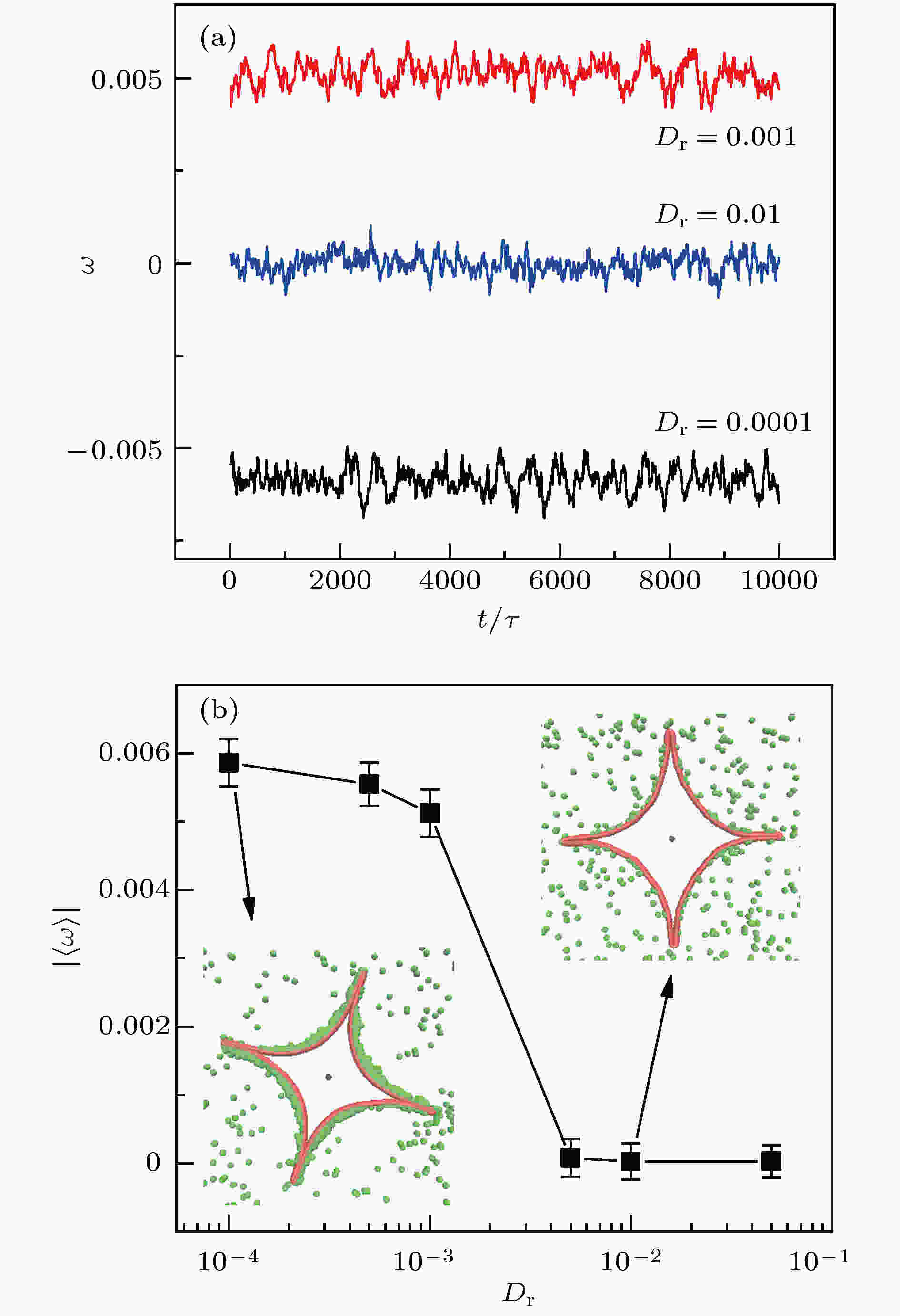
图 5 (a)不同旋转扩散系数D_r下棘轮的旋转角速度与时间的关系; (b)平均旋转角速度与D_r的关系, 内部两插图分别对应旋转扩散系数D_r = 0.0001和D_r = 0.01, 误差棒表示平均角速度的标准方差
Figure5. (a) The angular velocity as a function of time for various rotational diffusion coefficients, D_rs. (b) The average angular velocity as a function of D_r. The insets are typical snapshots for D_r = 0.0001和and D_r = 0.1. The error bars represent the standard the deviations of angular velocity.

从旋转角速度的变化曲线可以看出, 在旋转扩散系数D_r较小时, 棘轮的转动速率较高, 且随着旋转扩散系数D_r的增大, 棘轮的转动速率会降低, 当增大到一定程度时, 棘轮的转动速率基本为零且棘轮出现不定向旋转的情况. 图5(b)为棘轮的旋转角速度平均值与旋转扩散系数D_r的关系图, 由此可以得出, 棘轮的转动速率随着D_r的变大而降低, 并且当其达到一定值时, 定向旋转消失. 因粒子脱离柔性边界的能力随着D_r的增加而增加^[28], 换句话说, D_r的增加导致边界聚集的粒子数目减少(图5(b)插图), 从而导致棘轮扭矩降低, 定向转动速度下降. 当D_r增加到一定程度, 活性粒子在边界滞留时间大大降低, 粒子对边界的碰撞和热碰撞类似, 定向转动消失.
2 -->

3.5.支架数效应

最后考虑支架数对棘轮旋转速率的影响. 因为活性力较小时棘轮的旋转方向不固定, 为了避免棘轮的旋转方向对研究结果的影响, 选取活性力为F = 80的情况. 图6为棘轮旋转角速度的平均值与棘轮支架数的影响, 从图像中可以直观地看出, 在活性力一定时, 棘轮的旋转角速度随着支架数的增大而减小. 当支架数增加时, 凹陷区增加, 大量粒子或聚集到这些区域, 减弱了粒子分布的不均匀性(图6插图), 进而使扭矩降低, 从而引起转动角速度下降.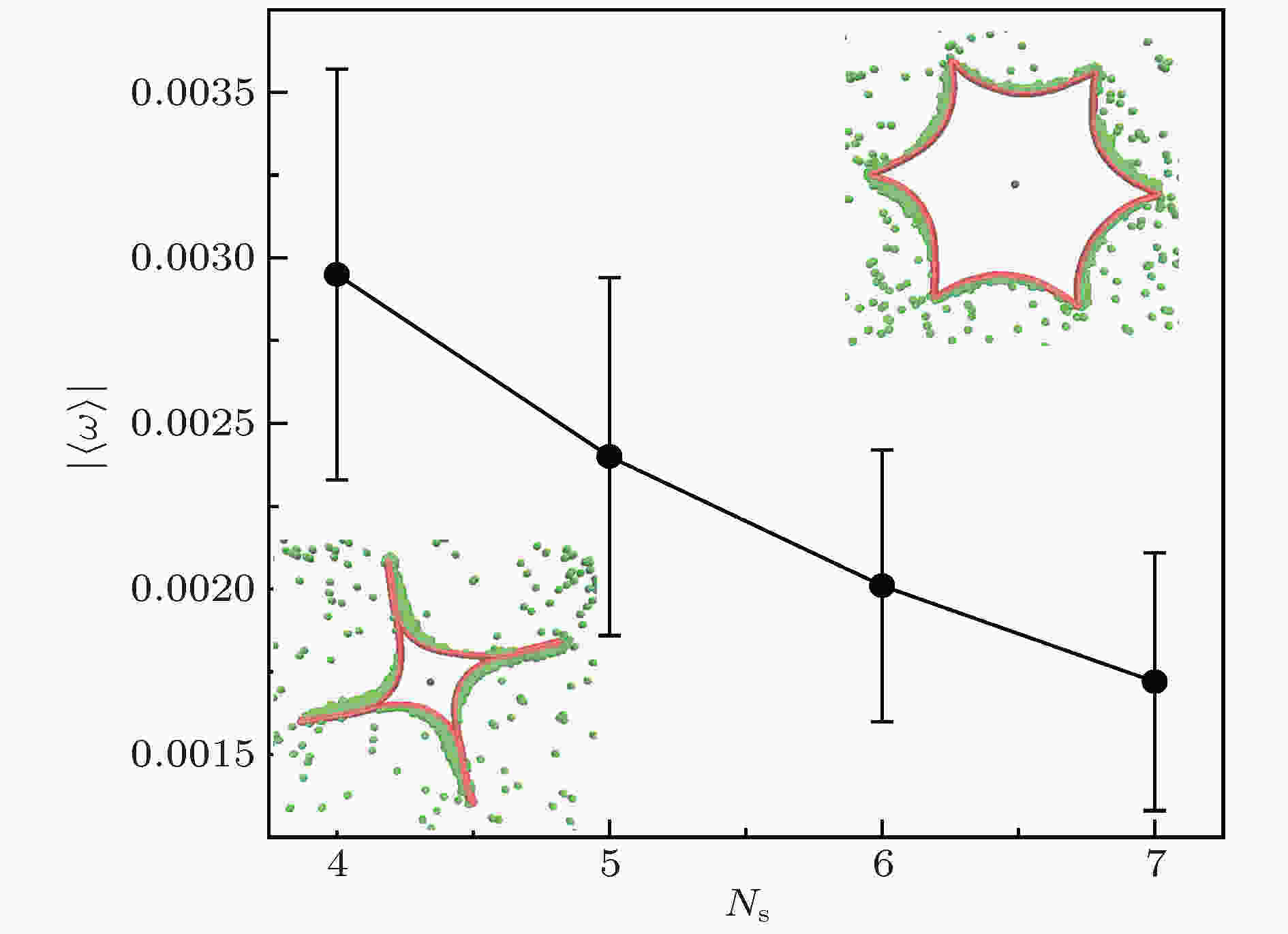
图 6 棘轮的平均角速度与支架数之间的关系, 内部两插图分别对应支架数为4和6, 误差棒表示平均角速度的标准方差
Figure6. The average angular velocity of ratchet vs the number of rigid trestle. The insets are typical snapshots for the number of ratchet wheel. The error bars represent the standard the deviations of angular velocity.

2 -->

3.6.讨　论

本文初始的柔性边界是圆形的, 在这种对称结构下, 活性粒子开始时刻的随机堆积也是比较对称的, 粒子分布的不对称性来源于粒子分布的涨落被柔性边界加强, 因为粒子倾向于堆积在高曲率地方^[29]. 这种事件也是随机发生的, 导致棘轮发生逆时针和顺时针方向定向转动的概率在统计下应该是相同的. 此外, 我们采用的布朗动力学方法, 忽略了流体力学的相互作用, 流体力学效应需要进一步的研究. 棘轮的转动依赖于压力的不对称分布, 压力的不对称分布不但和粒子驱动力有关, 而且和柔性边界的设计有关. 本文中我们设计的柔性边界大于棘轮固定点的直线链接长度, 利于边界高曲率区域的形成和活性粒子聚集, 较短的边界也可能导致定向旋转消失. 此外, 我们也发现在小自驱动力下, 棘轮有频繁反转现象, 定向转动时间较短, 我们一般不定义其为定向转动. 我们定义的定向转动是在模拟时间尺度下没有出现频繁反转现象的情况.

本文中用计算机模拟方法设计了一种柔性棘轮, 并研究了其在活性粒子浴内的动力学行为. 发现 棘轮结构在活性粒子浴中会自发产生结构不对称性 实现定向旋转运动. 研究了棘轮的旋转角速度与棘轮支架数、自驱力、数密度以及旋转扩散系数的关系, 发现: 1)棘轮的转动速度随着活性力的增强而变大; 2)随着活性粒子密度的提高, 棘轮旋转速度提高; 3)当活性粒子的旋转扩散系数提高时, 旋转速度下降, 并且当其超过一定值时, 定向旋转消失; 4)棘轮的转动速率随着棘轮支架数的增加而降低.