摘要:扩展互作用速调管是一种在毫米波、亚毫米波频段具有广泛应用前景的电真空器件. 本文基于运动学理论、感应电流定理和电荷守恒定律, 推导一间隙到五间隙谐振腔的电子负载电导和电子负载电纳的表达式, 分析了谐振腔间隙宽度、间隙数和间隙周期等参数对电子注与微波之间能量交换的影响和谐振腔谐振频率的影响. 根据理论分析结果, 采用三维电磁仿真软件设计了一款工作于G波段的扩展互作用速调管, 仿真结果显示, 当电子注电压为24 kV、电流为0.15 A、输入功率为200 mW、轴向引导磁感应强度为0.8 T时, 在中心频率217.94 GHz处, 输出功率为225.5 W, 电子效率为6.26%, 增益为30.5 dB, 3 dB带宽约为470 MHz.
关键词: G波段/
扩展互作用速调管/
注波互作用/
电子负载

English Abstract

全文HTML

--> --> -->

在通信系统、测云雷达、成像系统、导弹精确制导等领域的牵引下, 微波电子器件的需求正向毫米波、亚毫米波频段发展^[1-8]. 在毫米波、亚毫米波频段, 由于固态器件输出功率的限制, 在高功率应用场景下, 电真空器件仍然占据主导地位^[1,9-12]. 扩展互作用速调管具有功率高、效率高、结构简单和易于加工等特点, 非常适合在毫米波、亚毫米波频段工作, 具有广泛的应用前景^[13-16].
国内外很多单位都在对扩展互作用速调管进行研究. 其中, 加拿大的CPI公司从20世纪70年代就开始了对扩展互作用速调管的研究, 在速调管研制方面处于国际领先地位^[17,18]. G波段脉冲输出功率方面, CPI研制了应用于太赫兹测云雷达的扩展互作用速调管, 脉冲峰值输出功率400 W^[18]. G波段连续输出功率方面, CPI公司研制了应用于太赫兹成像系统的扩展互作用速调管, 连续波输出功率50 W^[18]. 国内研究扩展互作用速调管的主要有电子科技大学、中国科学院电子研究所、北京真空电子技术研究所、北京航空航天大学和中国工程物理研究院等单位^{[12,16,19-23]}. 目前国内关于G波段扩展互作用速调管的研究处于模拟设计阶段, 尚未见实验报道.
电子负载是用来表征电子注的引入对谐振腔中高频场的影响的参量. 电子负载的有功分量表征的是电子注和高频场之间实际交换的能量, 这些能量使谐振腔的等效损耗改变. 电子负载的无功分量表征的是电子注和高频场互相交换, 但在一个周期内净交换为零的能量, 这些能量使谐振腔的等效谐振频率发生改变^[24-26]. 已有很多****根据运动学理论和能量守恒定律分析了多间隙谐振腔中电子注与高频场之间的能量交换过程, 并推导出了多间隙谐振腔的电子负载电导的表达式^[1,27-34], 对于分析电子注与高频场之间的能量转换过程十分有用. 然而这些结论一是没有考虑谐振腔各个间隙之间的漂移段的影响, 对于扩展互作用速调管, 漂移段有时甚至比间隙更长, 忽略电子在漂移段的运动过程会造成很大误差; 二是没有推导出电子负载电纳的表达式, 也就无法分析电子注对谐振腔频率的影响. 本文基于运动学理论、感应电流定理和电荷守恒定律, 研究了电子在多间隙谐振腔${\text{π}}$模场中的渡越时间效应, 推导了多间隙谐振腔的电子负载电导和电子负载电纳的表达式, 分析了间隙宽度、间隙数和间隙周期对电子注与微波之间能量交换的影响和谐振腔谐振频率的影响. 根据理论分析, 设计了一款工作于G波段的扩展互作用速调管, 仿真结果显示, 当电子注电压为24 kV, 电流为0.15 A, 输入功率为200 mW, 轴向引导磁感应强度为0.8 T时, 在中心频率217.94 GHz处, 输出功率为225.5 W, 电子效率为6.26%, 增益为30.5 dB, 3 dB带宽约为 470 MHz.

扩展互作用速调管虽然仍属于传统速调管的范畴, 但其与传统速调管有较大不同. 典型如电压, 电子在漂移管中运动时, 由于漂移管中没有高频场, 此时高频场与电子之间没有相互作用. 因此, 无法建立确定多间隙谐振腔电压的唯一标准, 意味着无法实现多间隙谐振腔与单间隙谐振腔的简单等效^[35]. 但是为了表征电子与多间隙谐振腔中高频场之间的相互作用, 需要一套与单间隙谐振腔类似的参量, 如耦合系数、电子负载、特征阻抗等^[24].
将谐振腔等效为一个并联谐振电路, 引入电子注后谐振腔可以等效为如图1所示的电路模型^[36]. 其中G₀ = I₀/U₀为直流电子负载电导, I₀为直流电流, U₀为电子注直流电压; C₀为无电子注加载时谐振腔的等效电容; L₀为无电子注加载时谐振腔的等效电感; G_b为电子注等效负载电导; B_b为电子注等效负载电纳. 若B_b为正值, 电子注对谐振腔而言呈电容性, 加载电子注后谐振腔频率降低, 若B_b为负值, 电子注对谐振腔而言呈电感性, 加载电子注后谐振腔频率升高.
图 1 引入电子注后谐振腔等效电路
Figure1. Equivalent circuit mode of cavity with beam.

为了简化分析, 作如下假设: 1)多间隙谐振腔的各个间隙均为有栅间隙, 并且假设电场在横截面上均匀分布, 只在纵向上变化, 且间隙电场为均匀场; 2)忽略空间电荷效应; 3)电子速度比光速小得多, 即忽略相对论效应; 4)各个间隙之间的漂移管对于高频场完全截止. N间隙谐振腔的电场分布用图2近似表示^[1,28]. 设定第一个间隙的入口处坐标为0, 那么电子在N间隙谐振腔第n (n = 1, 2, 3, 4, $\cdots $, N)间隙t时刻感受的电场可表示为
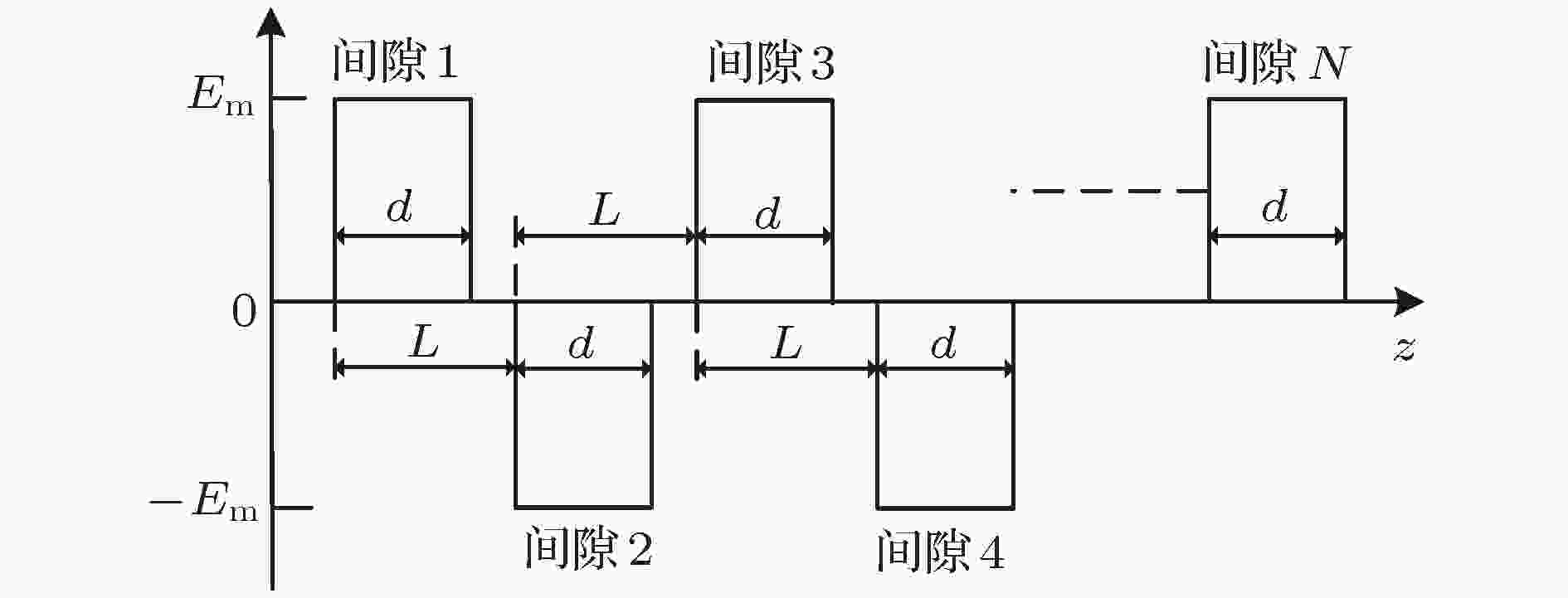图 2 多间隙谐振腔${\text{π}}$模场简化示意图
Figure2. Simplified E-field of ${\text{π}}$ mode in multiple-gap cavity.

$\begin{split} &{E_n} = {E_{\rm{m}}}\sin \left[ {\omega t + \left( {n - 1} \right){\text{π}}} \right],\\ &\left( {n - 1} \right)L \leqslant z \leqslant \left( {n - 1} \right)L + d,\end{split}$

式中E_m为单个间隙电场的幅值; d为单个间隙的宽度; L为相邻间隙中心的距离; $\omega = 2{\text{π}} f$, f为N间隙谐振腔的谐振频率; z为t时刻电子在N间隙谐振腔第n个间隙中的位置.
2

-->

2.1.单间隙谐振腔电子负载的理论分析

在大信号条件下, 电子在间隙中的速度和位置等参数都是由超越方程确定的, 难以得到简明的解析表达式, 导致电子负载无法得到解析表达式^[25]. 为简化分析, 本文主要基于小信号假设对电子负载进行理论研究. 设电子初始速度为ν₀, 电子质量为m, 电子电荷量为e. 由于间隙中电场为均匀场, 间隙电压幅值U_m = E_md. 电子在间隙中的运动方程为

$\dfrac{{{{\rm{d}}^2}{z_1}}}{{{\rm{d}}{t^2}}} = \dfrac{{e{U_{\rm{m}}}}}{{md}}\sin \left( {\omega t} \right),\;\;\;0 \leqslant {z_1} \leqslant d,$

式中z₁为t时刻电子在单间隙中的位置.
假设电子进入间隙入口处的时间为t₀, 根据初始条件: t = t₀时, ${z_1}\left| {_{t = {t_0}}} \right. = 0$, ${\nu _1}\left| {_{t = {t_0}}} \right. = {\nu _0}$, ${\nu _1}$为电子在单间隙中t时刻的速度, 同时由于$\dfrac{1}{2}m\nu _0^2 = $$e{U_0} $, 可得

$\begin{split}{z_1} = \;& {\nu _0}\left( {t - {t_0}} \right) - \dfrac{{\alpha {\nu _0}}}{{2{\theta _0}\omega }}\left[ {\sin \left( {\omega t} \right) - \sin \left( {\omega {t_0}} \right)} \right]\\ &+ \dfrac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left( {t - {t_0}} \right)\cos \left( {\omega {t_0}} \right),\end{split}$

式中α = U_m/U₀为间隙电压与直流电压的比值, θ₀ = ωd/ν₀为电子通过单间隙的直流渡越角.
在小信号条件下, 电子在时刻t到达间隙某一处时, 电子的实际渡越角与直流渡越角之间相差一个微小量δ₁, 即

$\omega \left( {t - {t_0}} \right) = \varphi - {\varphi _0} = {\theta _1} + {\delta _1},\;\;\;{\delta _1} \ll {\theta _0},$

式中φ₀ = ωt₀为电子进入单间隙谐振腔时电场的相位, φ = ωt为t时刻电场的相位, θ₁ = ωz/ν₀.
将(3)式两边同时乘以ω/ν₀, 并采用近似式cosδ₁ ≈ 1, sinδ₁ ≈ δ₁, 同时因为α, δ₁均是极小量, 忽略它们的二次及以上多次项, 可得

${\delta _1} = \dfrac{\alpha }{{2{\theta _0}}}\left[ {\sin \left( {\omega t} \right) - \sin \left( {\omega t - {\theta _1}} \right) - {\theta _1}\cos \left( {\omega t - {\theta _1}} \right)} \right].$

假设τ₁为电子注离开单间隙谐振腔的时间, 结合(4)和(5)式可得电子通过单间隙谐振腔的实际渡越角与直流渡越角之间的差值为

${\delta _1}\left| {_{t = {\tau _1}}} \right. \!=\! \dfrac{\alpha }{{2{\theta _0}}}\left[ {\sin \left( {{\varphi _0} \!+\! {\theta _0}} \right) \!-\! \sin {\varphi _0} \!-\! {\theta _0}\cos {\varphi _0}} \right],$

电子离开单间隙谐振腔时的归一化速度为

${\nu _1}\left| {_{t = {\tau _1}}} \right. = {\nu _0} + \dfrac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos {\varphi _0} - \cos \left( {{\varphi _0} + {\theta _0}} \right)} \right].$

根据电荷守恒定律^[11], 可得

$\begin{split} {i_1} & = {I_0}\dfrac{{{\rm{d}}{t_0}}}{{{\rm{d}}t}} = {I_0}\dfrac{{{\rm{d}}\left(\omega {t_0}\right)}}{\rm{d}}\left( {\omega t} \right) = {I_0}\dfrac{{{\rm{d}}\left( {wt - {\theta _1} - {\delta _1}} \right)}}{\rm{d}}\left( {\omega t} \right) \\ & = {I_0}\left( {1 - \dfrac{{{\rm{d}}{\delta _1}}}{\rm{d}}\left( {\omega t} \right)} \right).\end{split}$

将(5)式代入(8)式, 可得

$\begin{split}{i_1} =\; & {I_0} + \dfrac{{\alpha {I_0}}}{{2{\theta _0}}}\left[ \sin \left( {\omega t} \right)\left( {\sin {\theta _1} - {\theta _1}\cos {\theta _1}} \right)\right. \\ & \left.+ \cos \left( {\omega t} \right)\left( {{\theta _1}\sin {\theta _1} + \cos {\theta _1} - 1} \right) \right].\end{split}$

(9)式可以确定每一处的对流电流, 根据感应电流定理, 当间隙中电场是均匀场时, 总的感应电流是间隙内对流电流交变分量对间隙宽度的平均值^[11]

$\begin{split}{I_{1,\rm{ind}}} = \;& \frac{1}{{{\theta _0}}}\int_0^{{\theta _0}} {{{\widetilde i}_1}{\rm{d}}{\theta _1}} \\ = \;& \frac{{{U_{\rm{m}}}{G_0}}}{{2\theta _0^2}}\left[ {\sin (\omega t)\left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)} \right.\\& \left. { + \cos (\omega t)\left( {2\sin {\theta _0} - {\theta _0}\cos {\theta _0} - {\theta _0}} \right)} \right].\end{split}$

式中${\widetilde i_1}$为${i_1}$的交变分量.
感应电流与电压同相的部分及相差${\text{π}}/2$的部分分别对应电子负载电导G_b和电子负载电纳B_b, 可得

$\overline {{G_{{\rm{b}}1}}} = \dfrac{{{G_{{\rm{b}}1}}}}{{{G_{\rm{0}}}}} = \dfrac{{2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}}}{{2\theta _0^2}},$

$\overline {{B_{{\rm{b}}1}}} = \dfrac{{{B_{{\rm{b1}}}}}}{{{G_{\rm{0}}}}} = \dfrac{{2\sin {\theta _0} - {\theta _0}\cos {\theta _0} - {\theta _0}}}{{2\theta _0^2}}.$

电子注与单间隙之间交换的能量为

${P_{{\rm{b1}}}} = \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{G_{{\rm{b1}}}} = U_{\rm{m}}^{\rm{2}}{G_{\rm{0}}}\dfrac{{2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}}}{{4\theta _0^2}}.$

2 -->

2.2.双间隙谐振腔电子负载的理论分析

对于双间隙谐振腔, 电子注在第一个间隙中的运动情况与单间隙谐振腔中相同. 当电子通过第一个间隙后进入漂移通道, 此时没有外加电场, 电子以第一个间隙出口处的速度为初始速度作匀速运动. 电子在漂移通道中的运动方程为

$\begin{split}{z_{11}} = & \left\{ {{\nu _0} \!+\! \dfrac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos {\varphi _0} - \cos \left( {{\varphi _0} + {\theta _0}} \right)} \right]} \right\}\left( {t \!- \!{\tau _1}} \right) \!+\! d,\\ & d \leqslant {z_{11}} \leqslant L,\end{split}$

式中z₁₁为t时刻电子在漂移通道中的位置, 同样假设电子在漂移通道中的实际渡越角与直流渡越角之间相差一个微小量δ₁₁, 即

$\omega \left( {t - {\tau _1}} \right) = \varphi - {\varphi _1} = {\theta _{11}} + {\delta _{11}},\;\;\;{\delta _{11}} \ll {\theta _{11}},$

式中φ₁ = ωτ₁为电子进入漂移通道的相位, θ₁₁ = ω(z₁₁–d)/ν₀.
将(15)式代入(14)式可得

${\delta _{11}} = - \dfrac{\alpha }{{2{\theta _0}}}{\theta _{11}}\left[ {\cos \left( {\omega t - {\theta _{11}} - {\theta _0}} \right) - \cos \left( {\omega t - {\theta _{11}}} \right)} \right].$

漂移通道中的对流电流为

$\begin{split}{i_{11}} = &\; {i_1}\left| {_{t = {\tau _1}}} \right.\frac{{{\rm{d}}{\tau _1}}}{{{\mathop{\rm d}\nolimits} t}} = {i_1}\left| {_{t = {\tau _1}}} \right.\left( {1 - \frac{{{\rm{d}}{\delta _{11}}}}{{{\rm{d(}}\omega t)}}} \right)\\ = &\;{I_0} + \frac{{\alpha {I_0}}}{{2{\theta _0}}}\left[ {\sin \left( {\omega t - {\theta _{11}}} \right)\left( {\sin {\theta _0} - {\theta _0}\cos {\theta _0}} \right.} \right.\\ &\left. { -\; {\theta _{11}}\cos {\theta _0} + {\theta _{11}}} \right) + \cos \left( {\omega t - {\theta _{11}}} \right)\\ & \left. { \times \left( {{\theta _0}\sin {\theta _0} + \cos {\theta _0} - 1 + {\theta _{11}}\sin {\theta _0}} \right)} \right].\end{split}$

第二个间隙入口处的对流电流为

$\begin{split}{i_{11}}\left| {_{t = {\tau _{11}}}} \right. = & \; {I_0} + \frac{{\alpha {I_0}}}{{2{\theta _0}}}\left\{ {\sin \left( {{\varphi _0} + {\theta _0}} \right)\left[ {\sin {\theta _0}} \right.} \right.\\ & \left. { - {\theta _0}\cos {\theta _0} \!-\! \left( {{\beta _{\rm{e}}}L \!- \!{\theta _0}} \right)\cos {\theta _0}\! +\! \left( {{\beta _{\rm{e}}}L\! -\! {\theta _0}} \right)} \right]\\ & + \cos \left( {{\varphi _0} + {\theta _0}} \right)\left[ {{\theta _0}\sin {\theta _0} + \cos {\theta _0} - 1} \right.\\ & +\left. {\left. { \left( {{\beta _{\rm{e}}}L - {\theta _0}} \right)\sin {\theta _0}} \right]} \right\}.\end{split}$

在第二个间隙中, 电子的运动方程为

$\begin{split}& \dfrac{{{{\rm{d}}^2}{z_2}}}{{{\rm{d}}{t^2}}} = \dfrac{{e{U_{\rm{m}}}}}{{md}}\sin \left( {\omega t + {\text{π}}} \right),\\ & L \leqslant {z_2} \leqslant L + d,\end{split}$

式中z₂为t时刻电子在双间隙谐振腔第二个间隙中的位置.
根据初始条件${\nu _2}\left| {_{t = {\tau _{11}}}} \right. = {\nu _1}\left| {_{t = {\tau _1}}} \right.$, 可得

$\begin{split}{z_2} = &\; {\nu _1}\left| {_{t = {\tau _1}}} \right.\left( {t \!-\!{\tau _{11}}} \right)\! +\! \dfrac{{\alpha {\nu _1}\left| {_{t = {\tau _1}}} \right.}}{{2{\theta _0}\omega }}\left[ {\sin \left( {\omega t} \right) \!-\! \sin \left( {\omega {\tau _{11}}} \right)} \right] \\ &- \dfrac{{\alpha {\nu _1}\left| {_{t = {\tau _1}}} \right.}}{{2{\theta _0}}}\left( {t - {\tau _{11}}} \right)\cos \left( {\omega {\tau _{11}}} \right) + L.\end{split}$

电子的实际渡越角与直流渡越角之间相差一个微小量δ₂, 即

$\omega \left( {t - {\tau _{11}}} \right) = \varphi - {\varphi _{11}} = {\theta _2} + {\delta _2},\;\;\;{\delta _2} \ll {\theta _2}.$

式中φ₁₁ = ωτ₁₁为电子进入第二个间隙时电场的相位, θ₂ = ω(z₂–L)/ν₀.
由(21)和(19)式可得电子离开第二个间隙的速度

$\begin{split}{\nu _2}\left| {_{t = {\tau _2}}} \right. =\; & {\nu _0} + \frac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L + {\theta _0}} \right)} \right.\\ & -\left. {\cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right) + \cos {\varphi _0} - \cos \left( {{\varphi _0} + {\theta _0}} \right)} \right],\end{split}$

式中τ₂为电子离开双间隙谐振腔的时间.
将(20)式两边同时乘以ω/ν₀, 并采用近似式cosδ₂ ≈ 1, sinδ₂ ≈ δ₂, 同时因为α, δ₂均是极小量, 忽略它们的二次及以上多次项, 可得

$\begin{split}{\delta _2} = \;& \frac{\alpha }{{2{\theta _0}}}\left[ { -\sin (\omega t) + \sin \left( {\omega t - {\theta _2}} \right) +{\theta _2}\cos \left( {\omega t - {\theta _2}} \right)} \right.\\ & - {\theta _2}\cos \left( {\omega t - {\theta _2} - {\beta _{\rm{e}}}L} \right)\\& +\left. {{\theta _2}\cos \left( {\omega t - {\theta _2} - {\beta _{\rm{e}}}L + {\theta _0}} \right)} \right].\end{split}\!\!\!$

第二个间隙中的对流电流为

$\begin{split}\; & {i_2} = {i_{11}}\left| {_{t = {\tau _{11}}}} \right.\frac{{{\rm{d}}{\tau _{11}}}}{{{\rm{d}}t}} \\=\;& {i_{11}}\left| {_{t = {\tau _{11}}}} \right.\left( {1 - \frac{{{\rm{d}}{\delta _2}}}{{{\rm{d(}}\omega t)}}} \right)\\ =\; & {I_0} + \frac{{\alpha {I_0}}}{{2{\theta _0}}}\left\{ {\sin \left( {\omega t - {\theta _2} - {\beta _{\rm{e}}}L + {\theta _0}} \right)\left[ {\sin {\theta _0}} \right.} \right.\\& -\left. { {\theta _0}\cos {\theta _0} - \left( {{\beta _{\rm{e}}}L - {\theta _0}} \right)\cos {\theta _0} + \left( {{\beta _{\rm{e}}}L - {\theta _0}} \right)} \right]\\ &+ \cos \left( {\omega t - {\theta _2} - {\beta _{\rm{e}}}L + {\theta _0}} \right)\left[ {{\theta _0}\sin {\theta _0} + \cos {\theta _0}} \right.\\&-\left. { 1 + \left( {{\beta _{\rm{e}}}L - {\theta _0}} \right)\sin {\theta _0}} \right] + \cos (\omega t)\\& - \cos \left( {\omega t - {\theta _2}} \right) + {\theta _2}\sin \left( {\omega t - {\theta _2}} \right)\\ &- {\theta _2}\sin \left( {\omega t - {\theta _2} - {\beta _{\rm{e}}}L} \right)\\&+\left. { {\theta _2}\sin \left( {\omega t - {\theta _2} - {\beta _{\rm{e}}}L + {\theta _0}} \right)} \right\}.\end{split}$

第二个间隙出口处的对流电流为

$\begin{split}& {i_2}\left| {_{t = {\tau _2}}} \right. \\=\; & {I_0} + \frac{{\alpha {I_0}}}{{2{\theta _0}}}\left\{ {\sin \left( {{\varphi _0} + {\theta _0}} \right)\left[ {\sin {\theta _0} - {\theta _0}\cos {\theta _0}} \right.} \right.\\& -\left. {\left( {{\beta _{\rm{e}}}L - {\theta _0}} \right)\cos {\theta _0} + {\beta _{\rm{e}}}L} \right] + \cos \left( {{\varphi _0} + {\theta _0}} \right)\\ & \times \left[ {{\theta _0}\sin {\theta _0} + \cos {\theta _0} - 1 + \left( {{\beta _{\rm{e}}}L - {\theta _0}} \right)\sin {\theta _0}} \right]\\ & + \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L + {\theta _0}} \right) - \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right)\\& +\left. { {\theta _0}\sin \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right) - {\theta _0}\sin {\varphi _0}} \right\}.\end{split}$

由(25)式可得电子在第二个间隙中的感应电流为

$\begin{split}\; & {I_{2,}}_{{\rm{ind}}} = \frac{1}{{{\theta _0}}}\int_0^{{\theta _0}} {{{\widetilde i}_2}{\rm{d}}{\theta _2}} \\=& - \frac{{{U_{\rm{m}}}{G_0}}}{{2\theta _0^2}}\left\{ {\sin (\omega t)\left[ {2\left( {1 - \cos {\theta _0}} \right)} \right.} \right.\\& \times \left( {2 - 2\cos ({\beta _{\rm{e}}}L) - {\beta _{\rm{e}}}L\sin ({\beta _{\rm{e}}}L)} \right)\\& +\left. { {\theta _0}\left( {2\cos ({\beta _{\rm{e}}}L) - 1} \right)\sin {\theta _0} - 2 + 2\cos {\theta _0}} \right]\\& +\cos (\omega t)\left[ { - {\theta _0}\left( {1 + \cos {\theta _0}} \right) + 2\left( {1 - \cos {\theta _0}} \right)} \right.\\ & \times \left( {2\sin ({\beta _{\rm{e}}}L) - {\beta _{\rm{e}}}L\cos ({\beta _{\rm{e}}}L)} \right)\\& +\left. {\left. { 2\sin {\theta _0}\left( {1 - {\theta _0}\sin ({\beta _{\rm{e}}}L)} \right)} \right]} \right\}.\end{split}$

由此可得第二个间隙的归一化电子负载电导和归一化电子负载电纳为

$\overline {{G_2}} = \dfrac{{{G_2}}}{{{G_{\rm{0}}}}} = \dfrac{{2\left( {1 - \cos {\theta _0}} \right)\left[ {2\left( {1 - \cos {\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L\sin {\beta _{\rm{e}}}L} \right] + {\theta _0}\left( {2\cos {\beta _{\rm{e}}}L - 1} \right)\sin {\theta _0} - 2 + 2\cos {\theta _0}}}{{2\theta _0^2}},$

$\overline {{B_2}} = \dfrac{{{B_2}}}{{{G_{\rm{0}}}}} = \dfrac{{ - {\theta _0}\left( {1 + \cos {\theta _0}} \right) + 2\left( {1 - \cos {\theta _0}} \right)\left( {2\sin {\beta _{\rm{e}}}L - {\beta _{\rm{e}}}L\cos {\beta _{\rm{e}}}L} \right) + 2\sin {\theta _0}\left( {1 - {\theta _0}\sin {\beta _{\rm{e}}}L} \right)}}{{2\theta _0^2}}.$

第二个间隙中电子注与高频场之间交换的能量为

${P_2} = \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{G_{\rm{2}}} = \dfrac{{U_{\rm{m}}^{\rm{2}}{G_{\rm{0}}}}}{{4\theta _0^2}}\left\{ {2\left( {1 - \cos {\theta _0}} \right)\left[ {2\left( {1 - \cos {\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right] + {\theta _0}\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right]\sin {\theta _0} - 2 + 2\cos {\theta _0}} \right\}.$

对于双间隙腔, 若定义等效电压${U_2} = 2{U_{\rm{m}}}$, 可得双间隙谐振腔的等效电子负载电导和电子负载电纳

${G_{{\rm{b}}2}} = \dfrac{{2\left( {{P_{{\rm{b}}1}} + {P_2}} \right)}}{{U_2^2}} = \dfrac{G_0} {{4\theta _0^2}}{{\big\{ {\left( {1 - \cos {\theta _0}} \right)\left[ {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right] + {\theta _0}\left( { {\cos {\left(\beta _{\rm{e}}L\right)} } - 1} \right)\sin {\theta _0}} \big\}}},$

$\begin{split} {B_{{\rm{b2}}}} & = \dfrac2{{U_2^2}}{{\left( {\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{{\rm{b}}1}} + \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{\rm{2}}}} \right)}} = \dfrac{G_0}{{4\theta _0^2}} \big\{ - {\theta _0}\left( {1 + \cos {\theta _0}} \right) + \left( {1 - \cos {\theta _0}} \right)\left[ {2\sin \left( {{\beta _{\rm{e}}}L} \right) - \left( {{\beta _{\rm{e}}}L} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)} \right] \\ &+ \sin {\theta _0}\left[ {2 - {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)} \right] \big\}.\end{split}$

2 -->

2.3.三间隙谐振腔电子负载的理论分析

对于三间隙谐振腔, 电子注在前两个间隙中的运动情况与双间隙谐振腔中相同. 当电子通过第二个间隙后进入漂移通道, 此时没有外加电场, 电子以第二个间隙出口处的速度为初始速度做匀速运动. 电子在漂移通道中的运动方程为

$\begin{split}{z_{21}} = & \Big\{ {\nu _0} + \frac{{\alpha {\nu _0}}}{{2{\theta _0}}}\big[\cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L + {\theta _0}} \right) - \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right) \\ & + \cos {\varphi _0} - \cos \left( {{\varphi _0} + {\theta _0}} \right) \Big] \Big\}\left( {t - {\tau _2}} \right)\\ &+ L + d,\;L + d \leqslant {z_{21}} \leqslant 2L.\end{split}$

电子在第三个间隙的运动方程为

$\dfrac{{{{\rm{d}}^2}{z_3}}}{{{\rm{d}}{t^2}}} = \dfrac{{e{U_{\rm{m}}}}}{{md}}\sin \left( {\omega t} \right),\;\;\;2L \leqslant {z_3} \leqslant 2L + d,$

电子离开三间隙谐振腔的速度为

$\begin{split}{\nu _3}\left| {_{t = {\tau _3}}} \right. = \; & {\nu _0} + \frac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L} \right) } \right.\\& -\cos \left( {{\varphi _0} \!+\! 2{\beta _{\rm{e}}}L \!+\! {\theta _0}} \right) \!+\! \cos \left( {{\varphi _0} \!+\! {\beta _{\rm{e}}}L \!+\! {\theta _0}} \right)\\& -\left. { \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right) + \cos {\varphi _0} \!- \!\cos \left( {{\varphi _0} \!+\! {\theta _0}} \right)} \right],\end{split}$

式中τ₃为电子离开三间隙谐振腔的时间.
采用同双间隙谐振腔中漂移通道和间隙中相同的分析方法, 可得三间隙谐振腔的第三个间隙中产生的感应电流

$\begin{split} {I_{3,}}_{{\rm{ind}}} = & \dfrac{{{U_{\rm{m}}}{G_0}}}{{2\theta _0^2}}\left\{ {\sin \left( {\omega t} \right)} \right.\left\{ { - 5{\theta _0}\sin {\theta _0} + 2\left( {\cos {\theta _0} - 1} \right)\left[ {{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - 4\cos \left( {{\beta _{\rm{e}}}L} \right)} \right) + 10\cos \left( {{\beta _{\rm{e}}}L} \right) + 5} \right]} \right. \\ &+\left. { 2\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)\left[ {5{\theta _0}\sin {\theta _0} + 2\left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right]} \right\} \\ & + \cos \left( {\omega t} \right)\left[ {4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left( {\cos {\theta _0} - 1} \right)\left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) - 2{\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L} \right)} \right. \\ &- 4\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\sin \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} + 2\sin {\theta _0}\left( {1 + \sin \left( {{\beta _{\rm{e}}}L} \right)} \right) - {\theta _0}\left( {\cos {\theta _0} + 1} \right) \\ & - \left. {\left. { 2\left( {1 - \cos {\theta _0}} \right)\left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right)} \right)} \right]} \right\} .\end{split}$

由此可得第三个间隙的归一化电子负载电导和归一化电子负载电纳为

$\overline {{G_3}} = \dfrac{{{G_3}}}{{{G_{\rm{0}}}}} = \dfrac{\begin{array}{l} - 5{\theta _0}\sin {\theta _0} + 2\left( {\cos {\theta _0} - 1} \right)\left[ {{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - 4\cos \left( {{\beta _{\rm{e}}}L} \right)} \right) + 10\cos \left( {{\beta _{\rm{e}}}L} \right) + 5} \right] \qquad\\ + 2\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)\left[ {5{\theta _0}\sin {\theta _0} + 2\left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right] \\ \end{array} }{{2\theta _0^2}},$

$\overline {{B_3}} = \dfrac{{{B_3}}}{{{G_{\rm{0}}}}} = \dfrac{\begin{array}{l} - 2{\theta _0}\left[ {1 - 2\cos \left( {{\beta _{\rm{e}}}L} \right)} \right]\sin \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} + 2\sin {\theta _0} - {\theta _0}\cos {\theta _0} - {\theta _0} \\ + 2\left( {1 - \cos {\theta _0}} \right)\left\{ {\left[ {2\sin \left( {{\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right)} \right]\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3} \right] - 4{\beta _{\rm{e}}}L\left[ {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right]} \right\} \\ \end{array} }{{2\theta _0^2}}.$

第三个间隙中电子注与高频场之间交换的能量为

$\begin{array}{l} {P_3} = \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{G_3} = \dfrac{{U_{\rm{m}}^{\rm{2}}{G_{\rm{0}}}}}{{4\theta _0^2}}\left\{ { - 5{\theta _0}\sin {\theta _0} + 2\left( {\cos {\theta _0} - 1} \right)\left[ {{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - 4\cos \left( {{\beta _{\rm{e}}}L} \right)} \right) + 10\cos \left( {{\beta _{\rm{e}}}L} \right) + 5} \right]} \right. \\ \quad \quad \quad \quad \quad \quad \quad\left. { + 2\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)\left[ {5{\theta _0}\sin {\theta _0} + 2\left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right]} \right\}. \\ \end{array} $

对于三间隙谐振腔, 若定义等效电压${U_3} = 3{U_{\rm{m}}}$, 可得三间隙谐振腔的等效电子负载电导和电子负载电纳

$\begin{split} {G_{{\rm{b3}}}} & = \dfrac{{2\left( {{P_{{\rm{b}}1}} + {P_2} + {P_3}} \right)}}{{U_3^2}} \\ & = \dfrac{G_0}{{18\theta _0^2}} \big\{ - 9{\theta _0}\sin {\theta _0} + 2\left( {\cos {\theta _0} - 1} \right)\left[ {2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - 2\cos \left( {{\beta _{\rm{e}}}L} \right)} \right) + 12\cos \left( {{\beta _{\rm{e}}}L} \right) + 3} \right] \qquad \quad \\& \quad~ + 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)\left[ {3{\theta _0}\sin {\theta _0} + \left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right] \big\},\end{split}$

$\begin{split} {B_{{\rm{b}}3}} & \!=\! \dfrac{{2\Big( {\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{b1}} \!+\! \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{\rm{2}}}{\rm{ \!+\! }}\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_3}} \Big)}}{{U_3^2}} \!=\! \dfrac{{{G_0}\left\{\!\! \begin{array}{l} 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left( {\cos {\theta _0} - 1} \right)\left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) - 2{\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L} \right) \\ - 4{\theta _0}\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\sin \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} + 6\sin {\theta _0} - 3{\theta _0}\cos {\theta _0} - 3{\theta _0} \\ \end{array} \!\!\right\}}}{{18\theta _0^2}}.\end{split}$

2 -->

2.4.四间隙谐振腔电子负载的理论分析

对于四间隙谐振腔, 电子注在前三个间隙中的运动情况与三间隙谐振腔中相同. 当电子通过第三个间隙后进入漂移通道, 此时没有外加电场, 电子以第三个间隙出口处的速度为初始速度作匀速运动. 电子在漂移通道中的运动方程为

$\begin{split}{z_{31}} &= \Big\{ {\nu _0} + \frac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L} \right)} \right. \\& - \cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L + {\theta _0}} \right) + \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L + {\theta _0}} \right)\\& - \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right)\left. { + \cos {\varphi _0} - \cos \left( {{\varphi _0} + {\theta _0}} \right)} \right] \Big\}\\ &\times \left( {t - {\tau _3}} \right)+ 2L + d,\;{\rm{2}}L + d \leqslant {z_{31}} \leqslant 3L.\end{split} $

电子在第四个间隙的运动方程为

$\dfrac{{{d^2}{z_4}}}{{{\rm{d}}{t^2}}} = \dfrac{{e{U_{\rm{m}}}}}{{md}}\sin \left( {\omega t + {\text{π}}} \right),\;\;\;\;3L \leqslant {z_4} \leqslant 3L + d.$

电子离开四间隙谐振腔的速度为

$\begin{split}{\nu _4}\left| {_{t = {\tau _4}}} \right. = & {\nu _0} + \frac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos \left( {{\varphi _0} + 3{\beta _{\rm{e}}}L + {\theta _0}} \right)} \right.\\ &- \cos \left( {{\varphi _0} + 3{\beta _{\rm{e}}}L} \right) + \cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L} \right)\\ & - \cos \left( {{\varphi _0} \!+\! 2{\beta _{\rm{e}}}L \!+\! {\theta _0}} \right) \!+\! \cos \left( {{\varphi _0} \!+\! {\beta _{\rm{e}}}L \!+ \!{\theta _0}} \right)\\ & -\left. { \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right) +\! \cos {\varphi _0} \!-\! \cos \left( {{\varphi _0} \!+ {\theta _0}} \right)} \right],\end{split}$

式中τ₄为电子离开四间隙谐振腔的时间.
采用同上述电子在漂移通道和间隙中相同的分析方法, 可得四间隙谐振腔的第四个间隙中产生的感应电流为

${I_{4,}}_{{\rm{ind}}} \!=\! - \dfrac{{{U_{\rm{m}}}{G_0}}}{{2\theta _0^2}}\! \left\{\!\! \begin{array}{l} \sin \omega t\left\{\!\! \begin{array}{l} 2\left( {1 - \cos {\theta _0}} \right)\left[ \begin{array}{l} 4{\cos ^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right) \\ + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {2\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right) + 12\cos \left( {{\beta _{\rm{e}}}L} \right) + 3 \end{array} \right] \\ - 8{\theta _0}\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} + {\theta _0}\sin {\theta _0}\left[ {9 - 8\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)} \right] \\ - 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)\left[ {3{\theta _0}\sin {\theta _0} + \left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right] \\\end{array}\!\! \right\} \\ \! + \!\cos \omega t\left\{\!\! \begin{array}{l} 2\sin {\theta _0} - {\theta _0}\cos {\theta _0} - {\theta _0} - 4{\theta _0}\sin {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)\left[ {\cos \left( {{\beta _e}L} \right)\left( {2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)} \right] \\ + 4\left( {\cos {\theta _0} \!-\! 1} \right)\left\{\!\! \begin{array}{l} {\beta _{\rm{e}}}L\left[ {8{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] - \big[ 2\sin \left( {{\beta _{\rm{e}}}L} \right) \\ + \left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) \big] \left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\ - \left( {\cos \left( {{\beta _e}L} \right) - 1} \right)\left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) - 2{\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L} \right)\end{array}\!\! \right\}\end{array}\!\! \right\}\end{array}\!\! \right\}.$

由此可得第四个间隙的归一化电子负载电导和归一化电子负载电纳为

$\begin{split} \overline{{G_4}} =& {{{G_4}}}/{{{G_{\rm{0}}}}} \\ =& \dfrac1{{2\theta _0^2}} \Big\{ 2\left( {1 - \cos {\theta _0}} \right) \big[ 4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right) + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {2\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right) \\ & + 12\cos \left( {{\beta _{\rm{e}}}L} \right) + 3 \big] - 8{\theta _0}\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} + {\theta _0}\sin {\theta _0}\left[ {9 - 8\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)} \right] \\ & - 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)\left[ {3{\theta _0}\sin {\theta _0} + \left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right] \Big\},\end{split}$

$ \begin{split} \overline {{B_4}} = & {{{B_4}}}/{{{G_{\rm{0}}}}} \\ = & \dfrac1{{2\theta _0^2}} \bigg\{ 2\sin {\theta _0} - {\theta _0}\cos {\theta _0} - {\theta _0} - 4{\theta _0}\sin {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)\left[ {\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)} \right] + 4\left( {\cos {\theta _0} - 1} \right) \\& \times \Big\{ {\beta _{\rm{e}}}L\left[ {8{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] - \left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) - 2{\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right) - {\beta _{\rm{e}}}L} \right) \\& - \left[ {2\sin \left( {{\beta _{\rm{e}}}L} \right) + \left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)} \right]\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \Big\} \bigg\}.\end{split}$

第四个间隙中电子注与高频场之间交换的能量为

$\begin{split} \;& {P_4} = U_{\rm{m}}^{\rm{2}}{G_4}/2 \\ =\; & \dfrac{{U_{\rm{m}}^{\rm{2}}{G_{\rm{0}}}}}{{4\theta _0^2}}\Big\{ 2\left( {1 - \cos {\theta _0}} \right)\left[ {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right) + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {2\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right. \\& +\left. {12\cos \left( {{\beta _{\rm{e}}}L} \right) + 3} \right] - 8{\theta _0}\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} + {\theta _0}\sin {\theta _0}\left[ {9 - 8\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)} \right] \\& - 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)\left[ {3{\theta _0}\sin {\theta _0} + \left( {2 - 2\cos {\theta _0} - {\theta _0}\sin {\theta _0}} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) + 1} \right)} \right] \Big\}.\end{split}$

对于四间隙谐振腔, 若定义等效电压${U_4} = 4{U_{\rm{m}}}$, 可得四间隙谐振腔的等效电子负载电导和电子负载电纳

$\begin{split} {G_{{\rm{b4}}}} & = \dfrac{{2\left( {{P_{{\rm{b1}}}} + {P_2} + {P_3} + {P_4}} \right)}}{{U_4^2}} \\& = \dfrac{G_0}{{4\theta _0^2}} {{\left\{ {\cos \left( {{\beta _{\rm{e}}}L} \right)\left\{ \begin{array}{l} \left[ {\left( {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _{\rm{e}}}L} \right) + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right]\left( {1 - \cos {\theta _0}} \right) \\ - {\theta _0}\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\cos \left( {{\beta _e}L} \right)\sin {\theta _0}\end{array} \right\}} \right\}}},\end{split}$

$\begin{split} {B_{{\rm{b}}4}} & = \dfrac2{{U_4^2}} {{\left( {\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{{\rm{b}}1}} + \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{\rm{2}}}{\rm{ + }}\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_3}{\rm{ + }}\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_4}} \right)}} \\& = \dfrac{G_0}{{8\theta _0^2}} {{\left\{ \begin{array}{l} 2\sin {\theta _0} - {\theta _0}\cos {\theta _0} - {\theta _0} - {\theta _0}\sin {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\ + \left( {\cos {\theta _0} - 1} \right)\left\{ \begin{array}{l} {\beta _{\rm{e}}}L\left[ {8{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\ - \left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) + \cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\\end{array} \right\} \\\end{array} \right\}}}.\end{split}$

2 -->

2.5.五间隙谐振腔电子负载的理论分析

对于五间隙谐振腔, 电子注在前四个间隙中的运动情况与四间隙谐振腔中相同. 当电子通过第四个间隙后进入漂移通道, 此时没有外加电场, 电子以第四个间隙出口处的速度为初始速度做匀速运动. 电子在漂移通道中的运动方程为

$\begin{split}{z_{41}} = & \Big\{ {\nu _0} + \dfrac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos \left( {{\varphi _0} + 3{\beta _{\rm{e}}}L + {\theta _0}} \right) - \cos \left( {{\varphi _0} + 3{\beta _{\rm{e}}}L} \right)} \right. \\ &+ \cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L} \right) - \cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L + {\theta _0}} \right)\\ &+ \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L + {\theta _0}} \right) - \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right)\\ & + \left. {\cos {\varphi _0} - \cos \left( {{\varphi _0} + {\theta _0}} \right)} \right] \Big\}\left( {t - {\tau _4}} \right) + 3L + d,\\ & {{\rm{3}}L + d \leqslant {z_{41}} \leqslant 4L}.\end{split}$

电子在第五个间隙的运动方程为

$\dfrac{{{{\rm{d}}^2}{z_5}}}{{{\rm{d}}{t^2}}} = \dfrac{{e{U_{\rm{m}}}}}{{md}}\sin \left( {\omega t} \right),\;\;\;\;4L \leqslant {z_5} \leqslant 4L + d.$

电子离开五间隙谐振腔的速度为

$\begin{split}{\nu _5}\left| {_{t = {\tau _5}}} \right. = \;& {\nu _0} + \frac{{\alpha {\nu _0}}}{{2{\theta _0}}}\left[ {\cos \left( {{\varphi _0} + 4{\beta _{\rm{e}}}L} \right)} \right. \\& - \cos \left( {{\varphi _0}} \!+ { 4{\beta _{\rm{e}}}L \!+ {\theta _0}} \right) \!+\! \cos \left( {{\varphi _0} \!+ 3{\beta _{\rm{e}}}L \!+ {\theta _0}} \right)\\& - \cos \left( {{\varphi _0} + 3{\beta _{\rm{e}}}L} \right) + \cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L} \right)\\ & - \cos \left( {{\varphi _0} + 2{\beta _{\rm{e}}}L + {\theta _0}} \right) \\& + \cos \left( {{\varphi _0}} + { {\beta _{\rm{e}}}L + {\theta _0}} \right) - \cos \left( {{\varphi _0} + {\beta _{\rm{e}}}L} \right)\\& +\left. { \cos {\varphi _0} - \cos \left( {{\varphi _0} + {\theta _0}} \right)} \right],\end{split}$

式中τ₅为电子离开五间隙谐振腔的时间.
采用同双间隙谐振腔电子在漂移通道和间隙中相同的分析方法, 可得五间隙谐振腔的第五个间隙中产生的感应电流为

$\begin{split}\small & {I_{5,}}_{{\rm{ind}}} = \dfrac{{{U_{\rm{m}}}{G_0}}}{{2\theta _0^2}}\times\\& \left\{\!\!\!\! \begin{array}{l} \sin \left( {\omega t} \right)\left\{\!\! \begin{array}{l} {\theta _0}\sin {\theta _0}\left[ {8\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right){{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - {{\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)}^2}} \right] \\\!\! + 2\left( {1 - \cos {\theta _0}} \right)\left\{\!\! \begin{array}{l} \left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\bigg[ \begin{array}{l} 4{\cos ^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1 \\ + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {4\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) \\\end{array}\!\! \bigg] \\ - 8{\cos ^2}\left( {{\beta _{\rm{e}}}L} \right)\left[ {\left( {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right) - 16{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)} \right] \\\end{array} \right\} \\\end{array} \right\} \\ + \cos \left( {\omega t} \right)\left\{\!\! \begin{array}{l} 2\sin {\theta _0} - {\theta _0}\left( {1 + \cos {\theta _0}} \right) + 4{\theta _0}\sin {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\ - 4\left( {\cos {\theta _0} - 1} \right)\left\{\!\! \begin{array}{l} {\beta _{\rm{e}}}L\left[ {8{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\ - \left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) + \cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\\end{array}\!\! \right\} \\ + 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left\{\!\! \begin{array}{l} 5{\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - \cos {\theta _0}} \right)\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 1} \right) \\ + \left( {2{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) + 3} \right)\bigg[ \begin{array}{l} {\beta _{\rm{e}}}L\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\left( {1 - \cos {\theta _0}} \right) \\ - 2\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - \cos {\theta _0}} \right) + {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} \\\end{array}\!\! \bigg]\end{array}\!\! \right\}\end{array}\!\! \right\}\end{array}\!\! \right\}.\end{split}$

由此可得第五个间隙的归一化电子负载电导和归一化电子负载电纳为

$\begin{split} &\overline {{G_5}} = \dfrac{{{G_5}}}{{{G_{\rm{0}}}}} = \dfrac1{{2\theta _0^2}} \times\\ & \left\{\!\!\begin{array}{l} {\theta _0}\sin {\theta _0}\left[ {8\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right){{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - {{\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)}^2}} \right] + 2\left( {1 - \cos {\theta _0}} \right) \\ \times \left\{ \begin{array}{l} \left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left[ {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1 + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {4\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)} \right] \\ - 8{\cos ^2}\left( {{\beta _{\rm{e}}}L} \right)\left[ {\left( {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right) - 16{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)} \right] \\\end{array}\!\! \right\}\end{array} \!\!\right\},\end{split}$

$\small\begin{split}& \overline {{B_5}} = \dfrac{{{B_5}}}{{{G_{\rm{0}}}}} = \dfrac1{{2\theta _0^2}} \times \\ & \left\{\!\!\begin{array}{l} 2\sin {\theta _0} - {\theta _0}\left( {1 + \cos {\theta _0}} \right) + 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left\{\!\! \begin{array}{l} 5{\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - \cos {\theta _0}} \right)\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 1} \right) \\ + \left( {2\cos \left( {2{\beta _{\rm{e}}}L} \right) + 3} \right)\left[\!\! \begin{array}{l} {\beta _{\rm{e}}}L\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\left( {1 - \cos {\theta _0}} \right) \\ - 2\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - \cos {\theta _0}} \right) + {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)\sin {\theta _0} \\\end{array} \!\!\right] \\ \end{array} \!\!\right\} \\ - 4\left( {\cos {\theta _0} - 1} \right)\left\{ {{\beta _{\rm{e}}}L\left[ {8{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] - \left( {2\sin \left( {{\beta _{\rm{e}}}L} \right) + \cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right]} \right\} \\ + 4{\theta _0}\sin {\theta _0}\sin \left( {{\beta _{\rm{e}}}L} \right)\left[ {2\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 1} \right] \\\end{array}\!\! \right\}.\end{split} \tag{\normalsize 55}$

第五个间隙中电子注与高频场之间交换的能量为

$ \begin{split} & {P_5} = \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{G_5} = \dfrac{{U_{\rm{m}}^{\rm{2}}{G_{\rm{0}}}}}{{4\theta _0^2}} \times \\ & \left\{ \begin{array}{l} {\theta _0}\sin {\theta _0}\left[ {8\left( {1 - \cos \left( {{\beta _e}L} \right)} \right){{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - {{\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)}^2}} \right] \\ + 2\left( {1 - \cos {\theta _0}} \right)\left\{ \begin{array}{l} \left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\bigg[ \begin{array}{l} 4{\cos ^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1 \\ + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {4\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) \\\end{array} \bigg] \\ - 8{\cos ^2}\left( {{\beta _{\rm{e}}}L} \right)\left[ {\left( {2 - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 3{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)} \right) - 16{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\cos \left( {{\beta _{\rm{e}}}L} \right)} \right]\end{array} \right\}\end{array} \right\}. \end{split}$

对于五间隙谐振腔, 若定义等效电压${U_5} = 5{U_{\rm{m}}}$, 可得五间隙谐振腔的等效电子负载电导和电子负载电纳为

$\small\begin{split} {G_{{\rm{b}}5}} &={{2\left( {{P_{{\rm{b}}1}} + {P_2} + {P_3} + {P_4} + {P_5}} \right)}}/{{U_5^2}} \\ &= \dfrac{{{G_0}\left\{ {\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left\{ \begin{array}{l} - {\theta _0}\sin {\theta _0}\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) + 2\left( {1 - \cos {\theta _0}} \right) \\\times \big[ 4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 2\cos \left( {{\beta _{\rm{e}}}L} \right) - 1 + 2{\beta _{\rm{e}}}L\sin \left( {{\beta _{\rm{e}}}L} \right)\left( {4\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right) \big] \\\end{array} \right\}} \right\}}}{{50\theta _0^2}},\end{split}\tag{\normalsize 57}$

$\small\begin{split} {B_{{\rm{b}}5}} &= {{2\left( {\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{b1}} + \dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_{\rm{2}}}{\rm{ + }}\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_3}{\rm{ + }}\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_4}{\rm{ + }}\dfrac{1}{2}U_{\rm{m}}^{\rm{2}}{B_5}} \right)}}/{{U_5^2}} \\ & \!=\! \dfrac{{{G_0}\left\{ {10\sin {\theta _0} - 5{\theta _0}\left( {1 + \cos {\theta _0}} \right) + 4\left( {\cos \left( {{\beta _{\rm{e}}}L} \right) - 1} \right)\left\{\!\! \begin{array}{l} 5{\beta _{\rm{e}}}L\cos \left( {{\beta _{\rm{e}}}L} \right)\left( {1 - \cos {\theta _0}} \right)\left( {4{{\cos }^2}\left( {{\beta _{\rm{e}}}L} \right) - 1} \right) \\ + \left( {2\cos \left( {2{\beta _{\rm{e}}}L} \right) + 3} \right)\left[\!\! \begin{array}{l} {\beta _{\rm{e}}}L\left( {1 - \cos \left( {{\beta _{\rm{e}}}L} \right)} \right)\left( {1 - \cos {\theta _0}} \right) \\ \times\sin \left( {{\beta _{\rm{e}}}L} \right)\left( { - 2 + 2\cos {\theta _0} + {\theta _0}\sin {\theta _0}} \right)\end{array}\!\! \right]\end{array}\!\! \right\}}\!\! \right\}}}{{50\theta _0^2}}.\end{split}\tag{\normalsize 58}$

2 -->

2.6.电子负载影响参数分析

以五间隙谐振腔为例, 分析各参数对电子负载电导和电子负载电纳的影响. 图3为五间隙谐振腔纵向工作模式为${\text{π}}$模时, 相邻间隙中心直流渡越角β_eL变化时电子负载电导G_b随单间隙直流渡越角β_ed变化的曲线. 由图3可以看出, 对于不同的β_eL, 存在一个最优的直流渡越角β_ed, 使电子注与高频场之间交换的能量最大, 此外, 且最优的直流渡越角β_ed对β_eL的变化十分敏感, 因此, β_eL在选择时需要精心考虑. 图4为直流渡越角β_ed变化时电子负载电导G_b随相邻间隙中心直流渡越角β_eL变化的曲线. 由图4可以看出, 对于不同的β_ed, 电子负载电导最大值对应的β_eL有微小差别. 由图4还可以看出, 当β_eL逐渐增大时, 首先是电子注交出能量给高频场, 然后电子注从高频场吸收能量, 形成类似振荡的效果, 存在一个β_eL, 使高频场从电子注吸收的能量最大, 这是振荡器的最佳工作点, 同样存在一个β_eL, 使电子注从高频场吸收的能量最大, 这是放大器的最佳工作点. 图5为${\beta _{\rm{e}}}L = 1.02{\text{π}} $时, 不同间隙数谐振腔的电子负载电导G_b随单间隙直流渡越角β_ed变化的曲线. 由图5可以看出, 间隙数的增加使电子注和高频场之间的相互作用更强, 有利于电子注从高频场吸收能量. 图6为${\beta _{\rm{e}}}d = {\text{π}}/4 $时, 不同间隙数谐振腔的电子负载电导G_b随相邻间隙中心直流渡越角β_eL变化的曲线. 由图6同样可以看出, 间隙数越多, 电子注从高频场吸收的能量极值越大. 还可以看出, 对于振荡器, 最佳工作点对应的β_eL随着间隙数的增加而变大, 对于放大器, 最佳工作点对应的β_eL随着间隙数的增加而减小.
图 3 五间隙数谐振器的归一化电子负载电导与渡越角的关系
Figure3. G_b5/G₀ versus θ₀ of five-gap cavity.

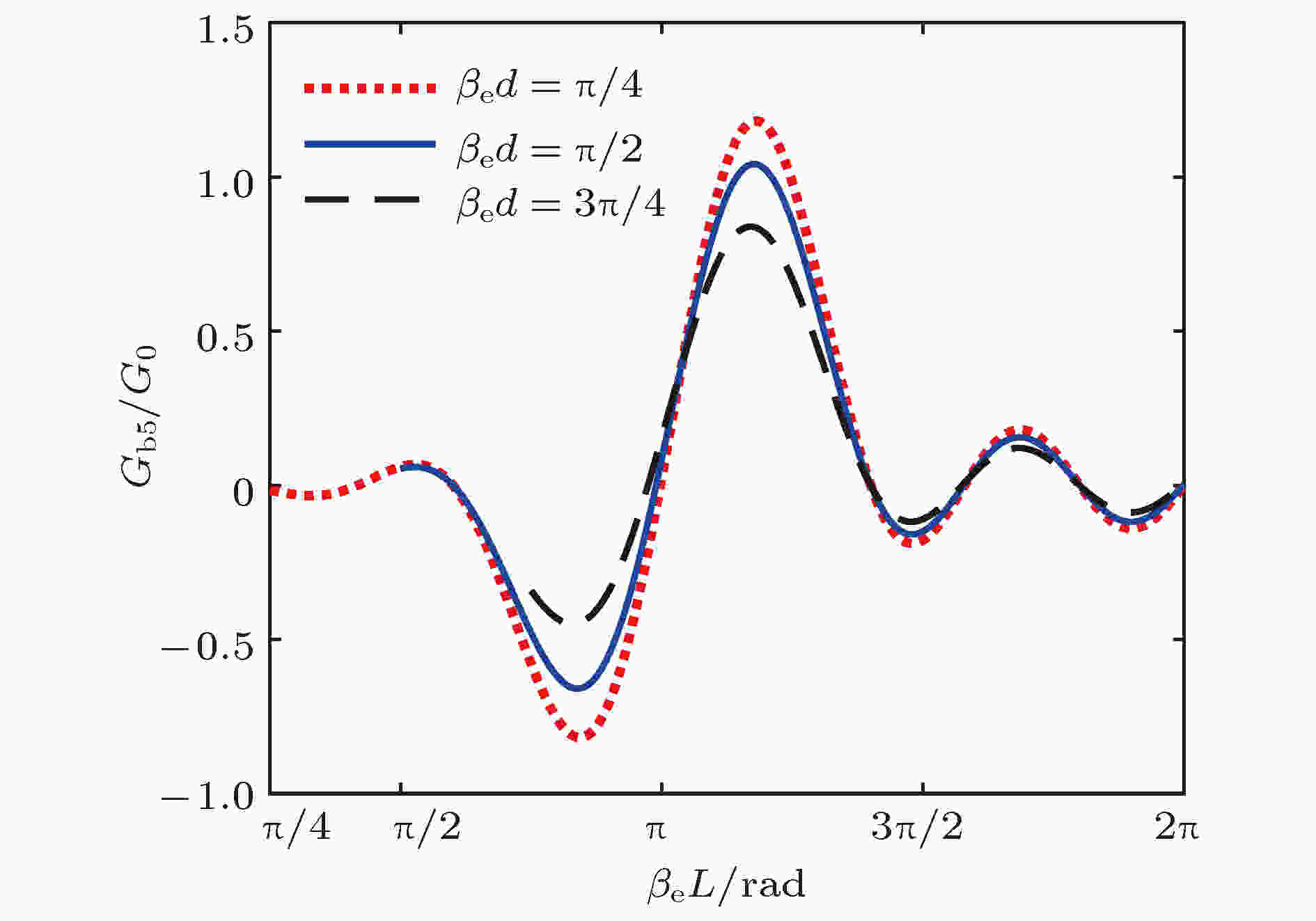图 4 五间隙数谐振器的归一化电子负载电导与β_eL的关系
Figure4. G_b5/G₀ versus β_eL of five-gap cavity.

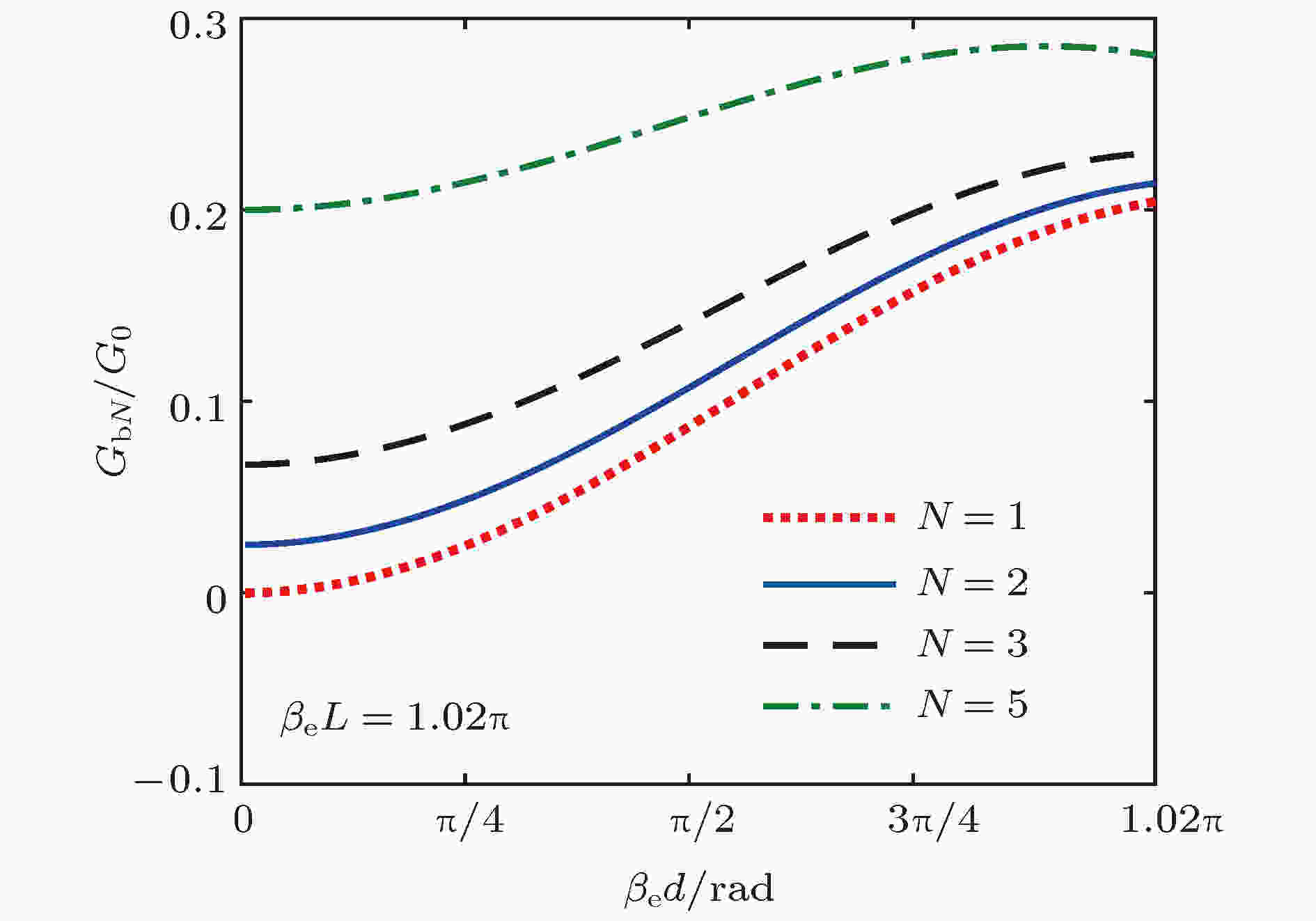图 5 不同间隙数谐振器的归一化电子负载电导与渡越角的关系
Figure5. G_bN/G₀ versus θ₀ of multiple-gap cavity.

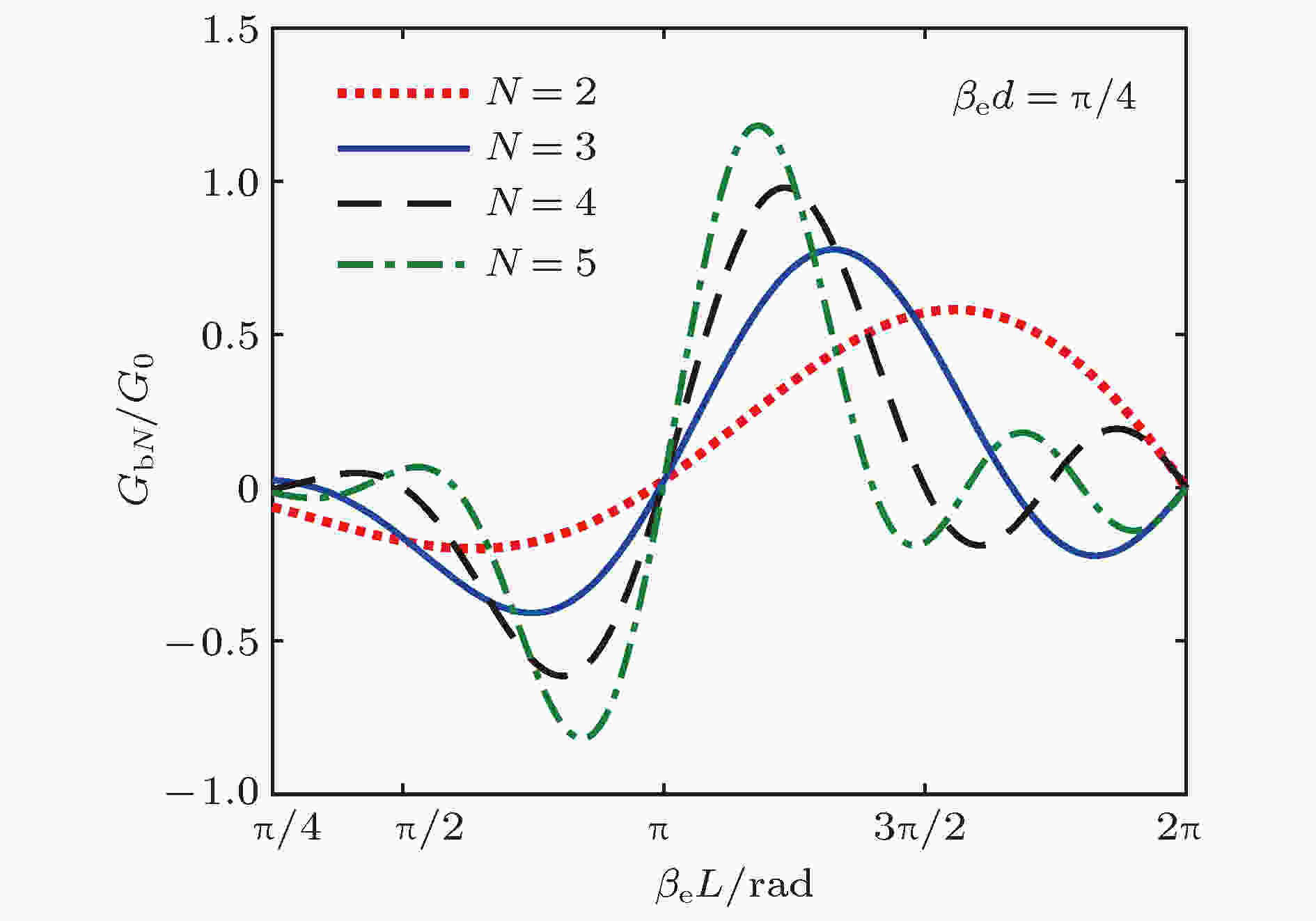图 6 不同间隙数谐振器的归一化电子负载电导与渡越角的关系
Figure6. G_bN/G₀ versus θ₀ of multiple-gap cavity.

图7为五间隙谐振腔纵向工作模式为${\text{π}}$模时, 相邻间隙中心直流渡越角β_eL变化时电子负载电纳B_b随单间隙直流渡越角β_ed变化的曲线. 由图7可以看出, 与图3不同, 电子负载电纳B_b在考虑的范围内随β_eL的变化没有电子负载电导G_b变化大. 图8为直流渡越角β_ed变化时电子负载电纳B_b随相邻间隙中心直流渡越角β_eL变化的曲线. 由图8可以看出, 对于不同的β_ed, 电子负载电纳最大值对应的β_eL基本相同. 由图8还可以看出, 电子注与高频场之间转换的这部分无功功率也随着β_eL的变化有类似振荡的效果. 图9为${\beta _{\rm{e}}}L = 1.02{\text{π}} $时, 不同间隙数谐振腔的电子负载电纳B_b随单间隙直流渡越角β_ed变化的曲线. 由图9可以看出, 间隙数的增加使电子注和高频场之间相互转换的无功能量越大, 意味着电子注后谐振腔谐振频率变化越大. 图10为${\beta _{\rm{e}}}d = {\text{π}} /4$时, 不同间隙数谐振腔的电子负载电纳B_b随相邻间隙中心直流渡越角β_eL变化的曲线. 由图10同样可以看出, 间隙数越多, 电子注与高频场之间相互转换的无功功率极值越大, 即电子注对谐振腔的频率影响越大.
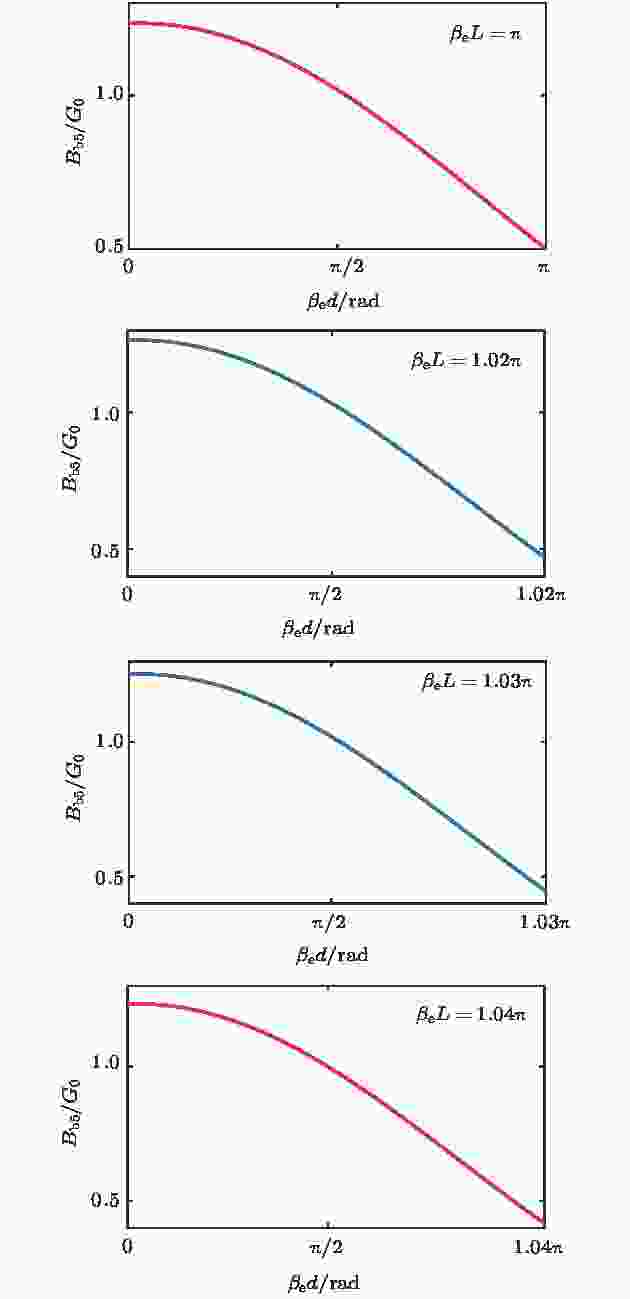图 7 五间隙谐振器的归一化电子负载电纳与渡越角的关系
Figure7. B_b5/G₀ versus θ₀ of five-gap cavity.

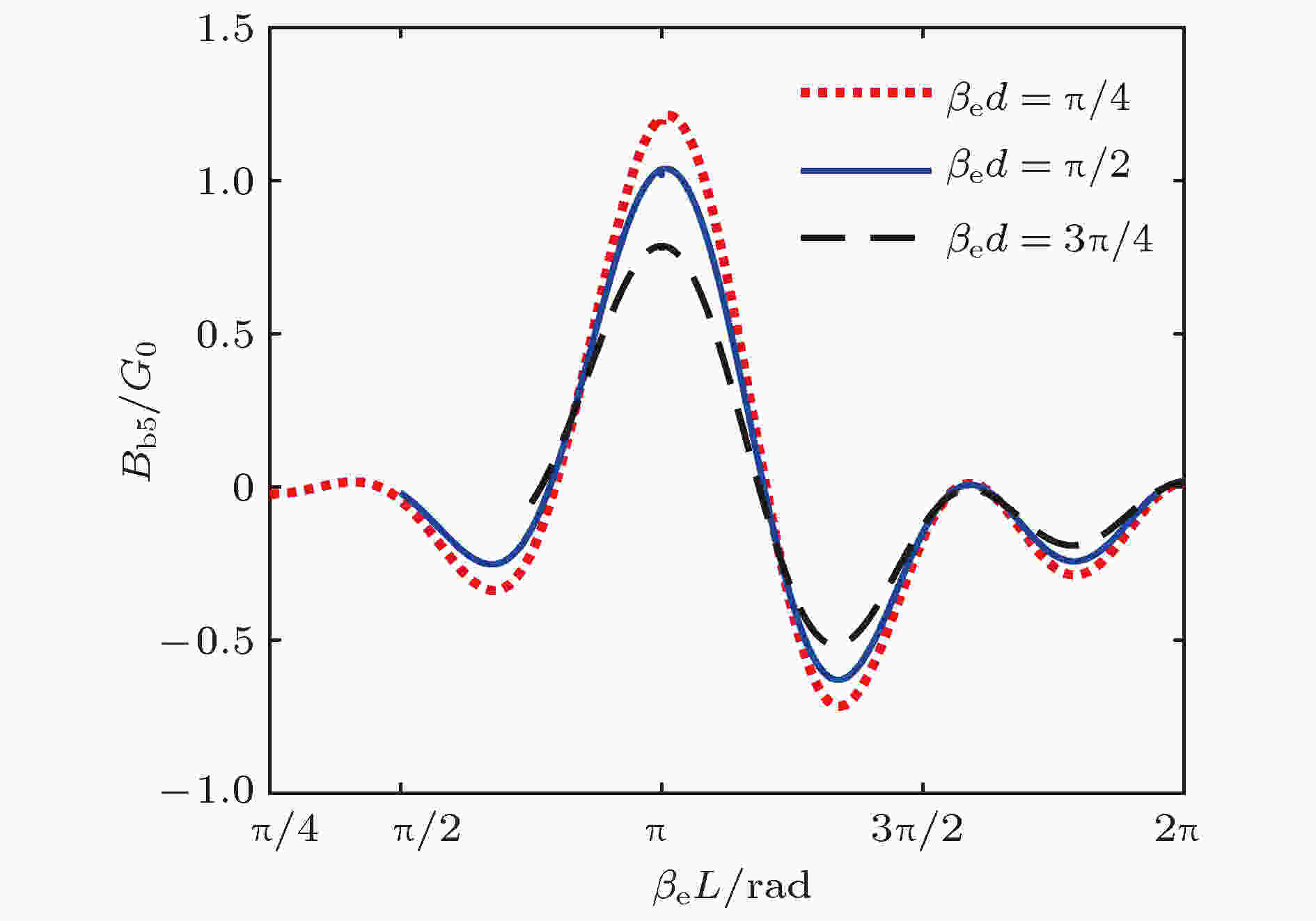图 8 五间隙谐振器的归一化电子负载电纳与β_eL的关系
Figure8. B_b5/G₀ versus β_eL of five-gap cavity.

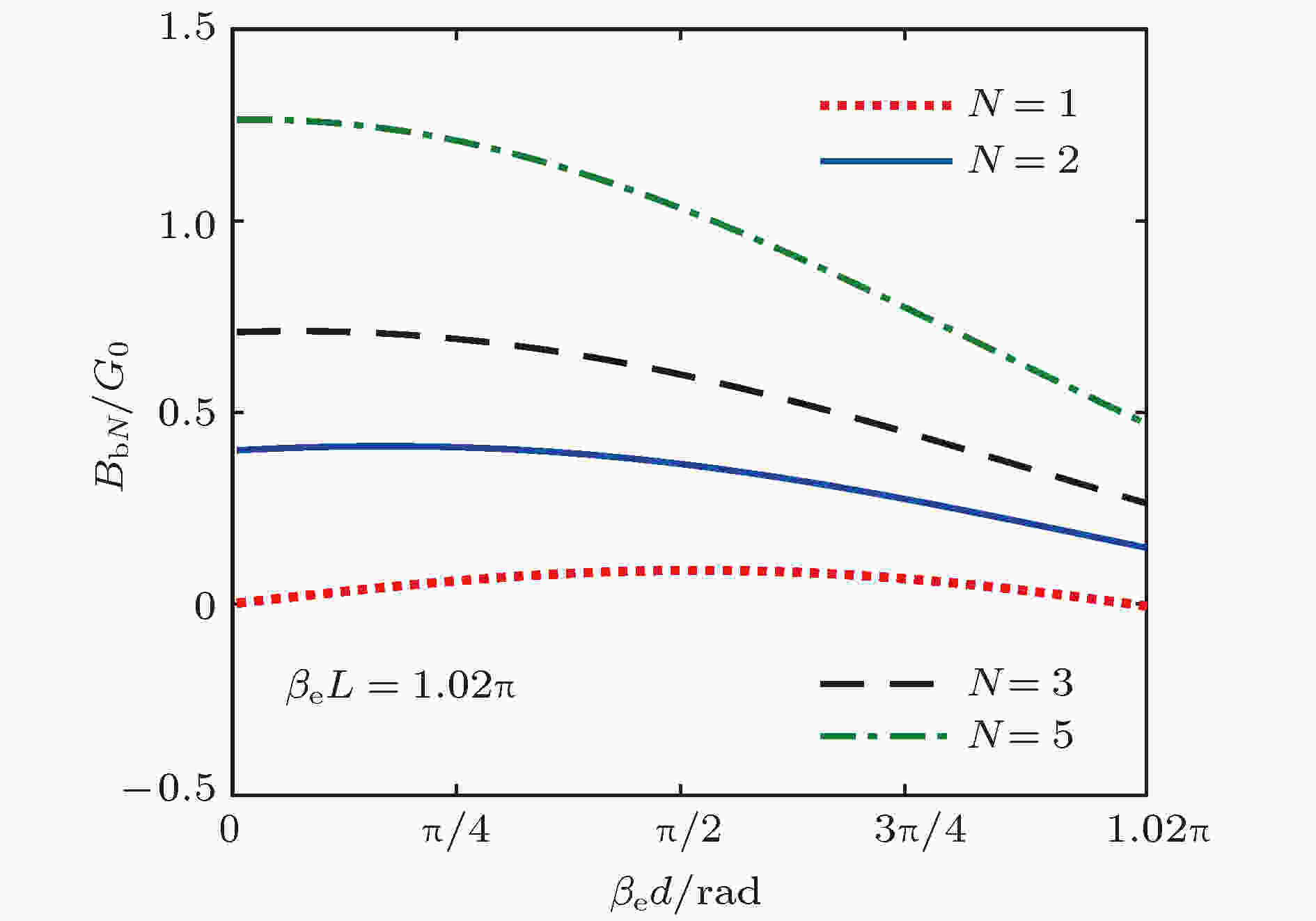图 9 不同间隙数谐振器的归一化电子负载电纳与渡越角的关系
Figure9. B_bN/G₀ versus θ₀ of multiple-gap cavity.

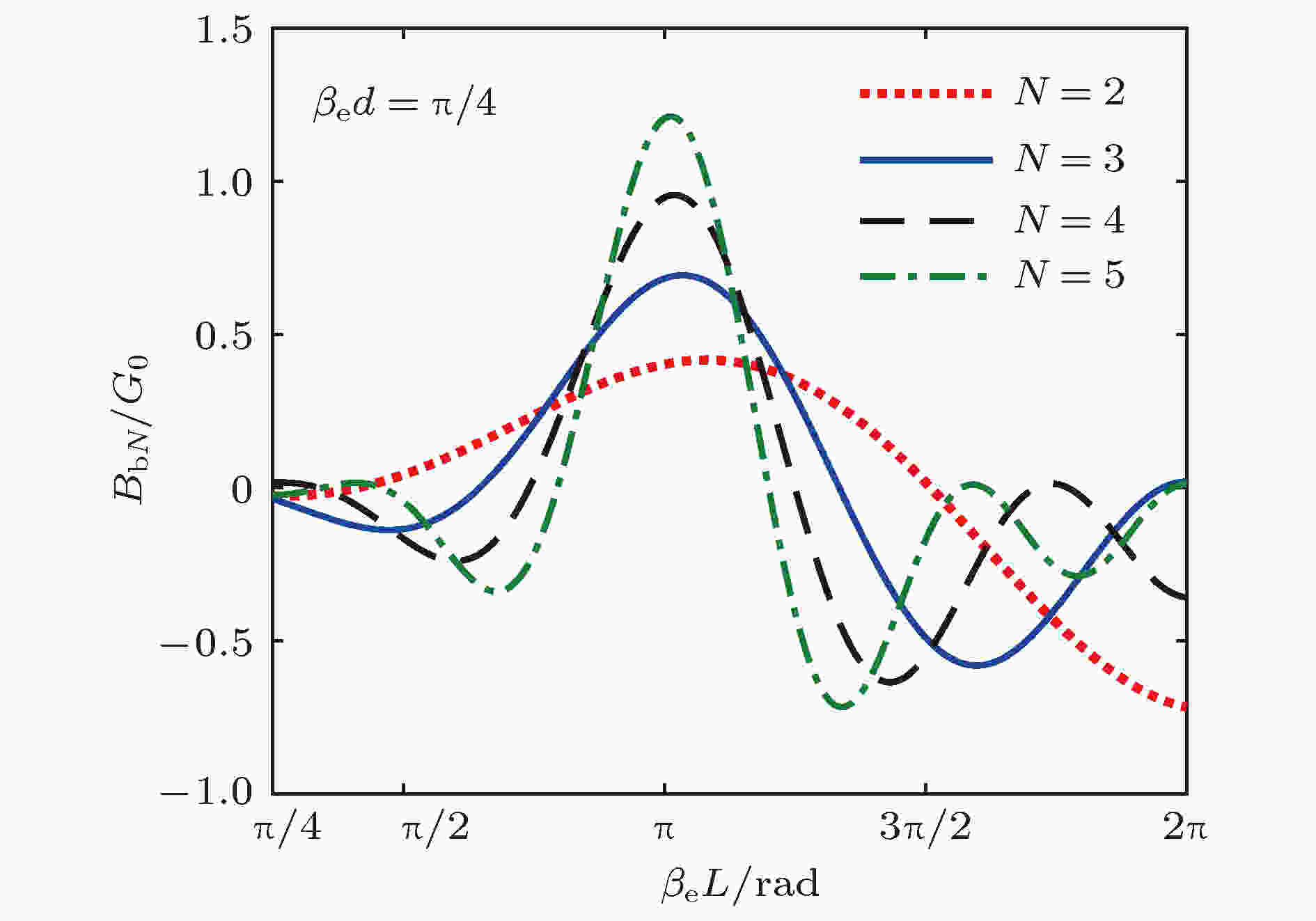图 10 不同间隙数谐振器的归一化电子负载电纳与β_eL的关系
Figure10. B_bN/G₀ versus β_eL of multiple-gap cavity.

2 -->

2.7.电子负载电导理论与仿真结果对比

以G波段五间隙谐振腔为例, 在不同参数条件下对比了电子负载电导的理论计算值与三维电磁仿真软件计算值的区别. 电磁仿真软件计算电子负载电导G_b的公式为^[26]

$ {G_{\rm{b}}} = \dfrac{{{Q_0} - {Q_{\rm{H}}}}}{{\left( {{R / Q}} \right){Q_0}{Q_{\rm{H}}}}},$

式中Q₀为谐振腔的固有品质因子, Q_H为加载电子注后谐振腔的品质因子, R/Q为谐振腔的特征阻抗.
设定五间隙谐振腔单个间隙宽度d = 0.11 mm, 间隙周期L = 0.19 mm, 工作频率220 GHz, 当工作电压为21 kV时, 可得单间隙直流渡越角${\theta _0} = 0.56{\text{π}} $, 相邻间隙中心之间的直流渡越角${\beta _{\rm{e}}}L = 0.97{\text{π}}$. 图11为工作电流变化时电子负载电导的理论计算值与三维电磁仿真软件计算值随工作电压的变化曲线. 图12为谐振腔束通道尺寸变化时电子负载电导的理论计算值与三维电磁仿真软件计算值随工作电压的变化曲线.
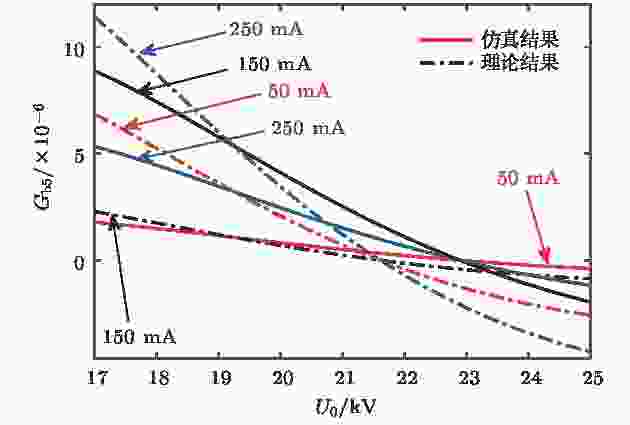图 11 五间隙数谐振器的电子负载电导与工作电压的关系
Figure11. G_b5 versus U₀ of five-gap cavity.

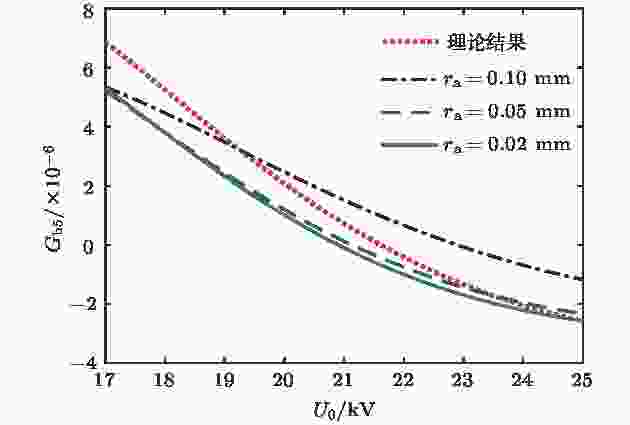图 12 五间隙数谐振器的电子负载电导与工作电压的关系
Figure12. G_b5 versus U₀ of five-gap cavity.

由图11可以看出, 理论计算值与仿真计算值随电压的变化趋势一致, 但绝对值存在一定差别, 且这个差别随着工作电流的增大而变大. 差别存在的原因经分析主要由两点: 一是因为理论计算是在有栅间隙的条件下计算的, 漂移通道中没有电场, 电子注在漂移通道中没有受到电场的作用, 而在仿真模型中, 由于电子注通道的存在, 使一部分电场耦合进入漂移通道中, 导致电子注在漂移通道中某些位置也受到电场的作用, 电子注和高频场之间存在能量转换; 二是因为理论计算中假定电子注在横向受到的调制电场相同, 而且间隙中假定为均匀场, 而在仿真模型中, 电场在横向分布是不均匀的, 在间隙中也非均匀场, 导致理论计算和仿真计算得到的电子注与高频场之间转换的能量存在一些差别. 以上两点需要在以后的工作中进一步进行考虑. 本文理论推导是基于运动学理论, 忽略了空间电荷效应, 而当电流增大时, 空间电荷效应增大, 因此理论计算值与仿真计算值的差别随着电流的增大而变大.
由图12可以看出, 随着电子注通道尺寸减小, 理论计算值与仿真计算值的差别变小, 这是因为当电子注通道尺寸减小时, 电子注通道中截止频率增加, 间隙中耦合到漂移通道中的电场在很短的距离就会截止, 仿真中电场分布与理论计算的电场分布更接近, 但是由于电场在横向的不均匀性, 理论计算值与仿真计算值仍存在一定差别.

设定电子注电压为21 kV, 电流为0.15 A, 输入微波功率为200 mW, 中心频率为218 GHz, 聚焦磁场为0.8 T. 高频结构由输入腔、中间腔和输出腔三个谐振腔组成, 三个腔均为五间隙谐振腔. 采用三维电磁仿真软件建立了扩展互作用速调管高频结构的模型, 如图13所示, 金属为弥散无氧铜, 理想情况下电导率为5.8 × 10⁷ S/m, 由于加工的影响, 此处根据经验设置为3.2 × 10⁷ S/m^[37].
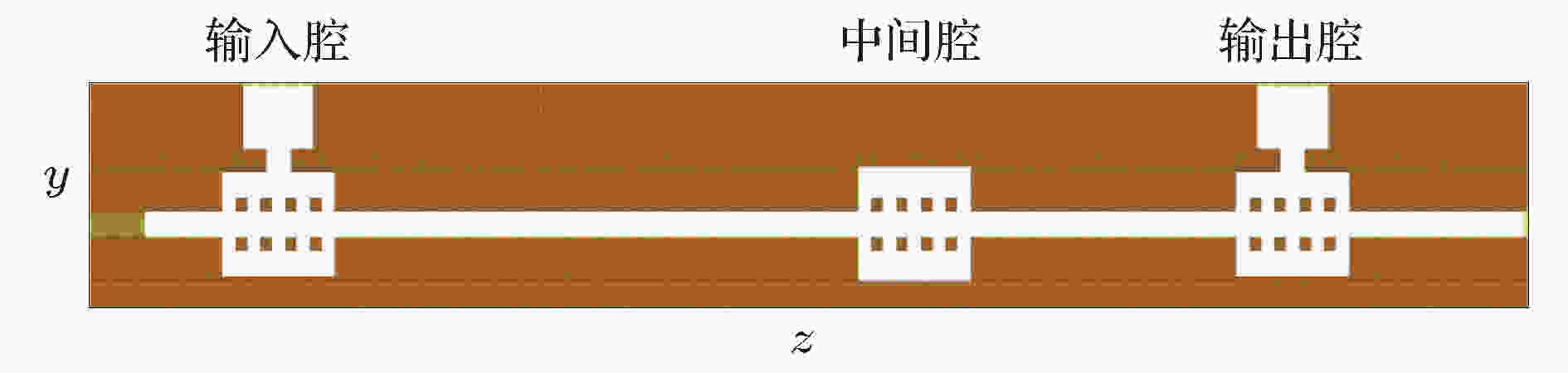图 13 扩展互作用速调管高频结构模型
Figure13. Model of the extended interaction klystron.

2

-->

3.1.输入腔匹配设计

输入腔采用五间隙谐振腔, 优化后间隙宽度d = 0.11 mm和相邻间隙中心之间的距离L = 0.2 mm. 微波源功率从标准波导通过耦合孔的方式馈入输入腔, 输入腔间隙上建立的电压V_gap与输入功率P_in之间的关系式为^[26]

${V_{{\rm{gap}}}} = \sqrt {\dfrac{{8{P_{{\rm{in}}}}\dfrac{R}{Q}{Q_{{\rm{ext}}}}}}{{\left( {1 + \dfrac{{{Q_{{\rm{ext}}}}}}{{{Q_{\rm{a}}}}}} \right) + {{\left[ {{Q_{{\rm{ext}}}}\left( {\dfrac{{{f_{{\rm{in}}}}}}{{{f_0}}} - \dfrac{{{f_0}}}{{{f_{{\rm{in}}}}}}} \right)} \right]}^2}}}} ,$

式中f_in表示输入信号的频率, f₀表示输入腔的谐振频率, Q_ext表示输入腔开耦合孔导致的损耗. Q_a表征谐振腔的全部损耗, 包括谐振腔的固有损耗Q₀和引入电子注的损耗Q_b, 即^[26]

$\dfrac{1}{{{Q_{\rm{a}}}}} = \dfrac{1}{{{Q_0}}} + \dfrac{1}{{{Q_{\rm{b}}}}}.$

电子注引起的损耗Q_b由下式确定^[26]:

${Q_{\rm{b}}} = \dfrac{1}{{{G_{\rm{b}}} \cdot \dfrac{R}{Q}}}.$

由(60)式可以看出, 在输入功率一定的条件下, 当Q_ext = Q_a时, 输入腔间隙上建立的电压最大, 此时信号在输入端口反射最小. 因此在设计输入腔的耦合孔时需要根据计算出来的Q_a确定. 通过三维电磁仿真软件计算得到Q₀ = 413, R/Q = 110, 在电压21 kV, 电流150 mA时, 可得Q_b = 5070, 因此Q_ext = 380 时反射最小.
2 -->

3.2.输出腔外观品质因子Q_ext

输出腔采用五间隙谐振腔, 输出腔中产生的功率通过耦合孔的方式传输给外部负载, 通过三维电磁仿真软件计算得到Q₀ = 413, R/Q = 110, 耦合系数M = 0.74. 输出腔的外观品质因子Q_ext由下式决定^[38]:

${Q_{{\rm{ext}}}} = \dfrac{{{{{U_0}}}/{{{I_0}}}}}{{{M^2}\dfrac{R}{Q}\dfrac{{{I_1}}}{{{I_0}}}}}.$

根据设计经验, 选择电流调制深度I₁/I₀ = 1.2, 可得Q_ext = 1940.
2 -->

3.3.扩展互作用速调管稳定性分析

为了判断引入电子注后谐振腔工作的稳定性, 需要分析引入电子注后对谐振腔损耗的影响. 谐振腔总的损耗由下式确定^[26]: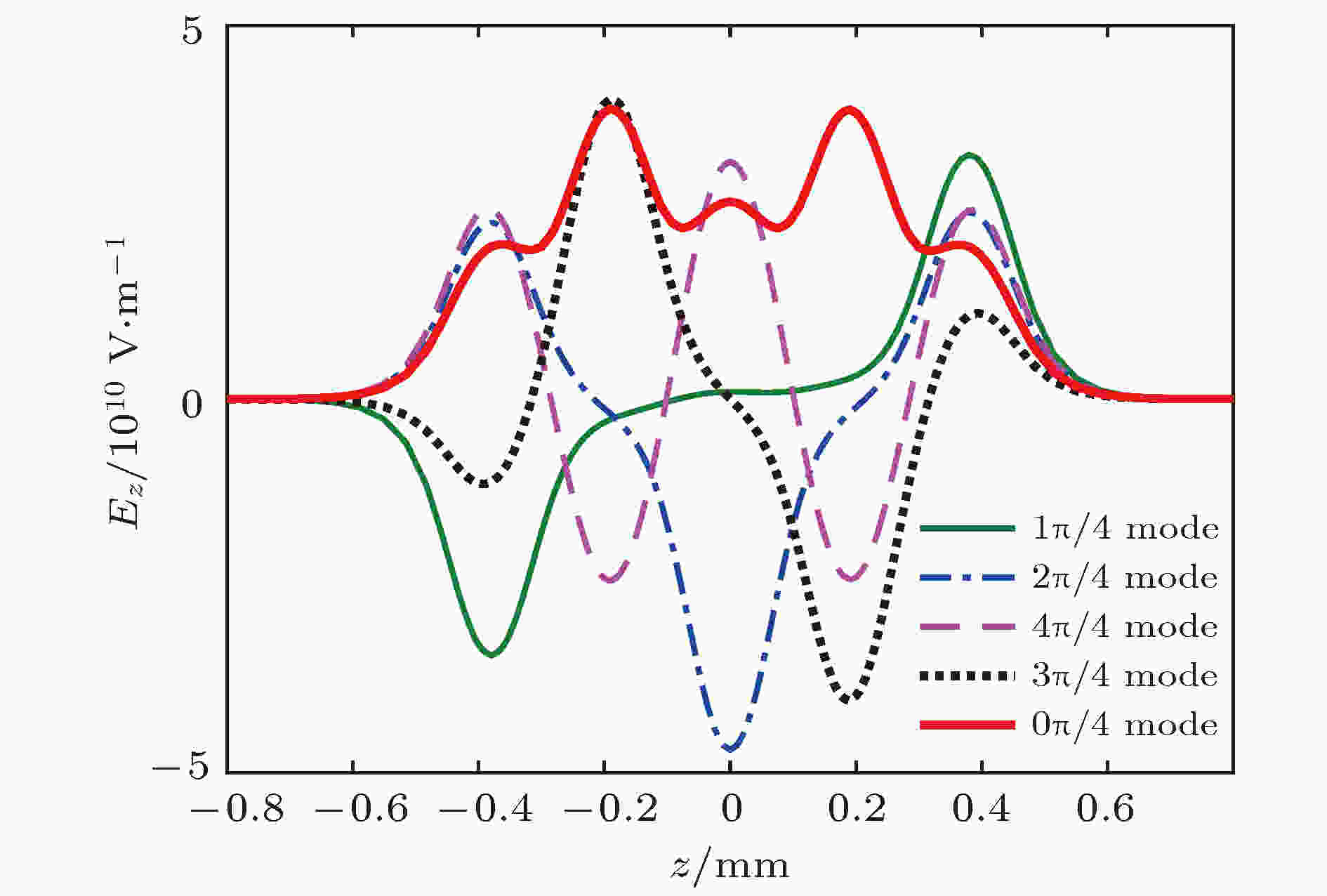

${1}/{{{Q_{\rm{t}} }}} = {1}/{{{Q_0}}} + {1}/{{{Q_{\rm{b}}}}} + {1}/{{{Q_{{\rm{ext}}}}}}.$

电子负载电导G_b为正值时, 表示电子注从微波场中吸收能量, 此时微波场中能量不但被电子注吸收, 同时还被腔壁损耗掉, 此时Q_t > 0, 不会发生自激振荡. 当电子负载电导G_b为负值时, 表示微波场从电子注吸收能量, 此时若微波场从电子注吸收的能量大于在腔壁上损耗的能量, 即Q_t < 0时, 会发生自激振荡, 反之不会产生自激振荡. 图14—图16为输入腔、中间腔和输出腔与工作模式同一个通带的各模式纵向电场沿轴向的分布, 图17—图19为输入腔、中间腔和输出腔Q_t随工作电压的变化曲线, 由图可以看出, 在考虑的工作电压范围内, Q_t均为正值, 说明不会发生自激振荡.
图 14 输入腔各模式E_z沿轴向的分布
Figure14. E_z versus axial distance of each mode in input cavity.

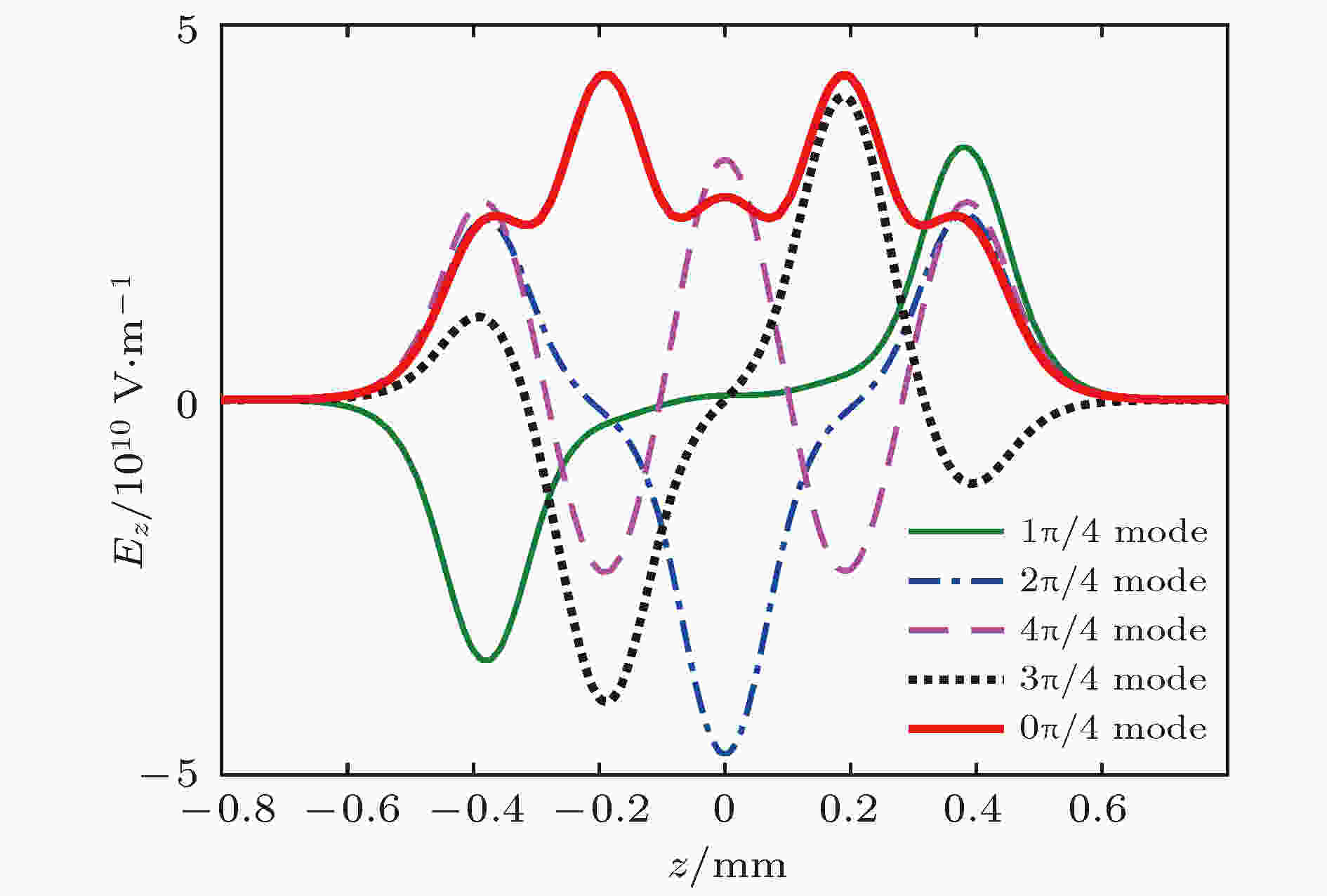图 15 中间腔各模式E_z沿轴向的分布
Figure15. E_z versus axial distance of each mode in middle cavity.

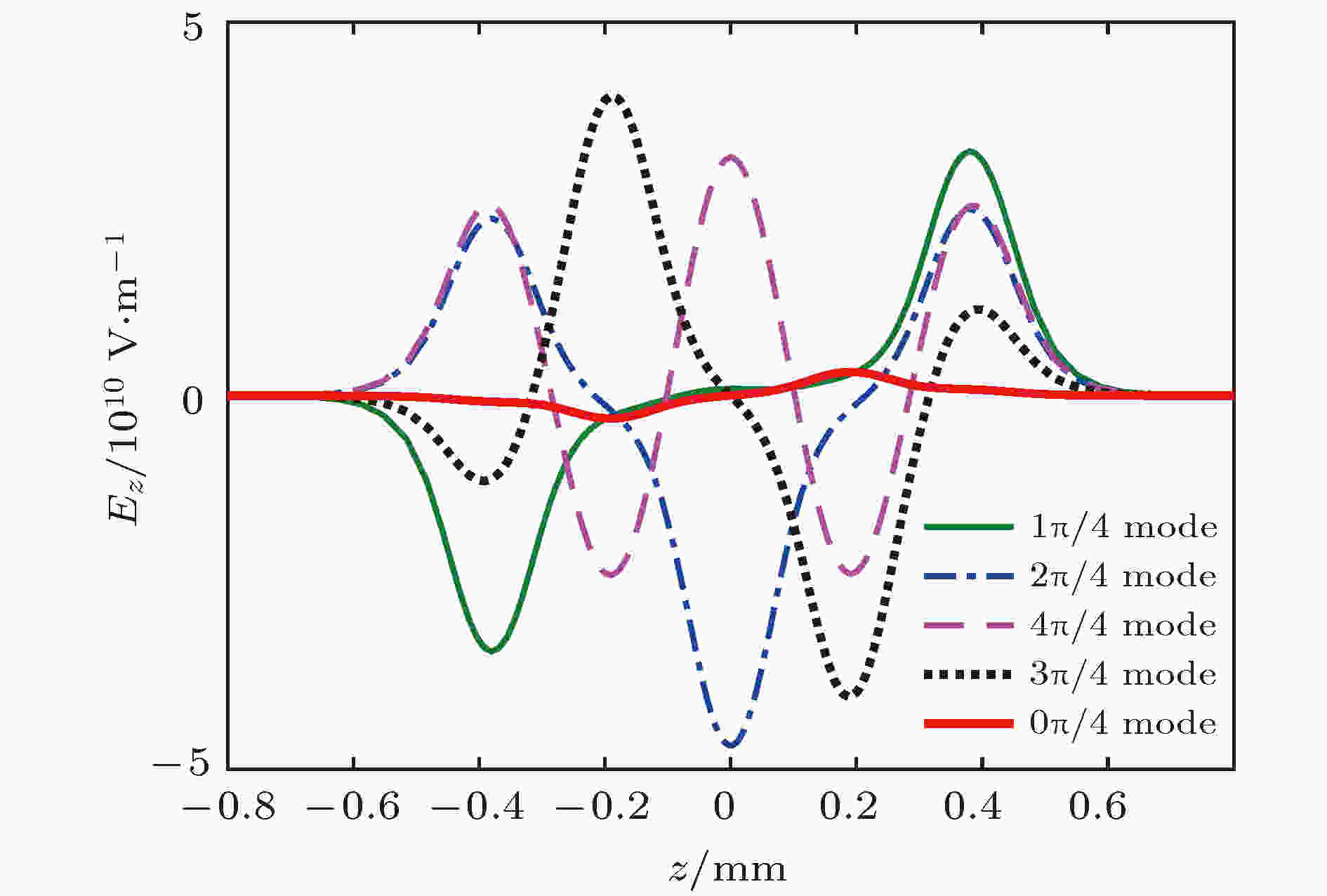图 16 输出腔各模式E_z沿轴向的分布
Figure16. E_z versus axial distance of each mode in output cavity.

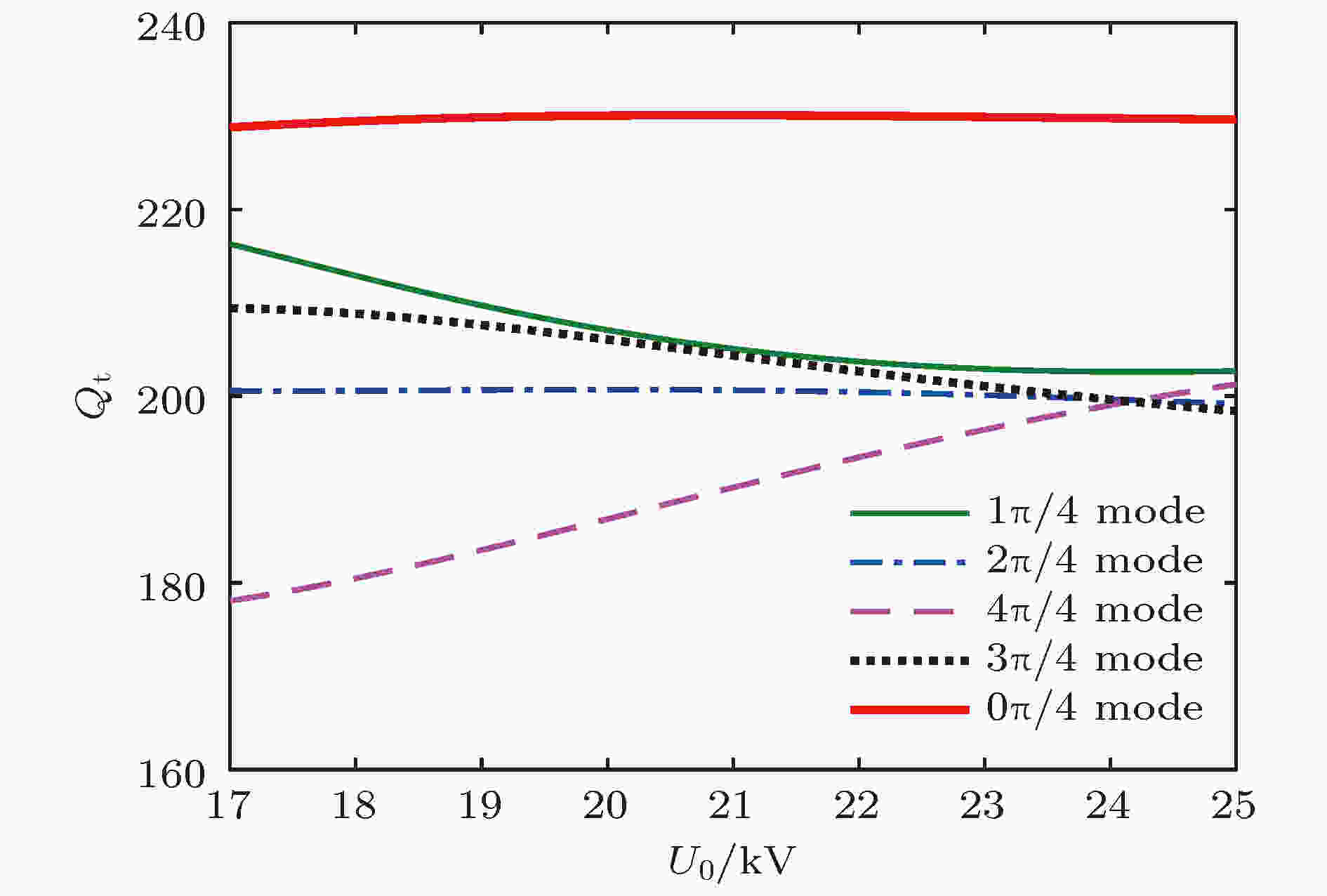图 17 输入腔各模式Q_t与电压U₀的关系
Figure17. Q_t versus U₀ of each mode in input cavity.

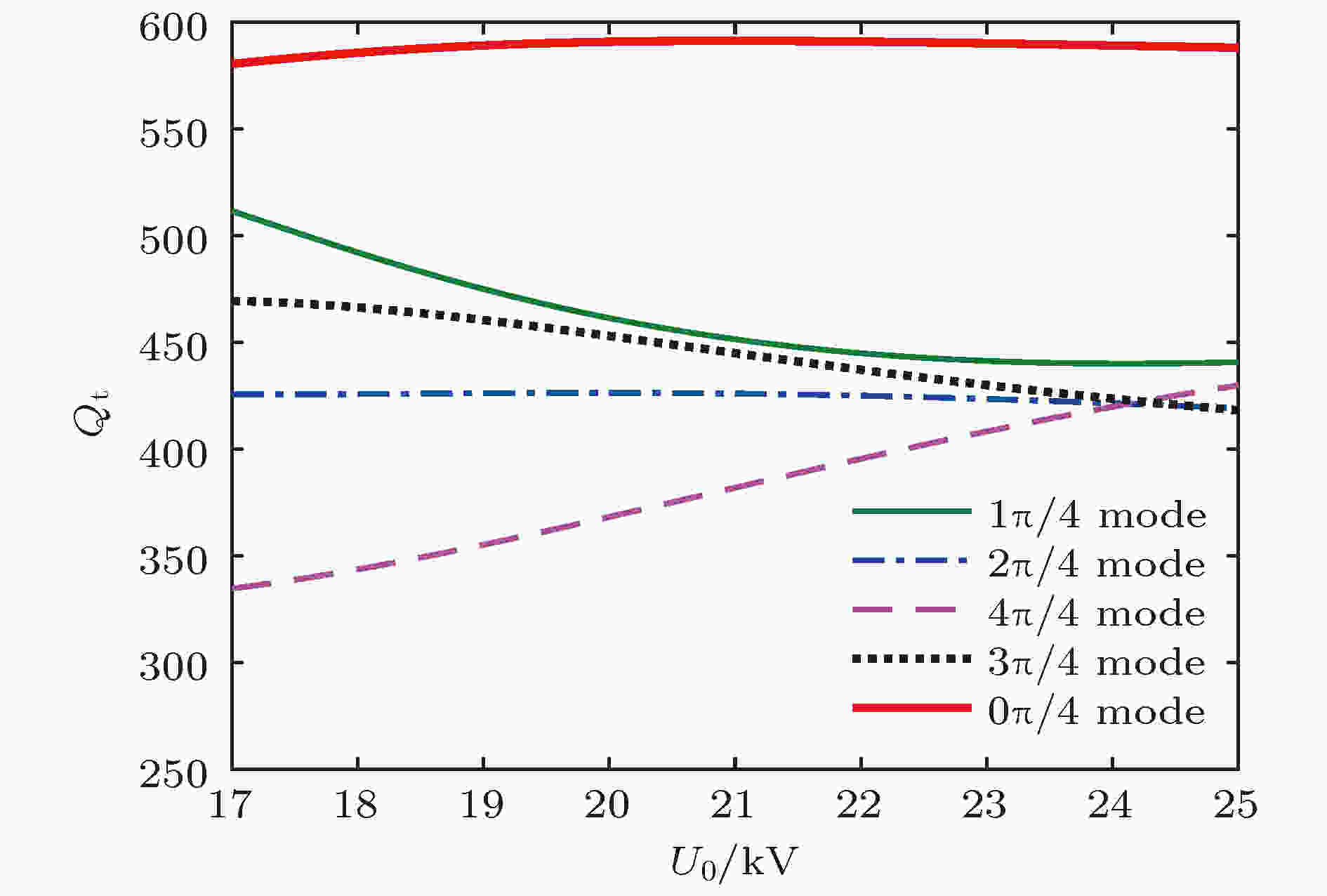图 18 中间腔各模式Q_t与电压U₀的关系
Figure18. Q_t versus U₀ of each mode in middle cavity.

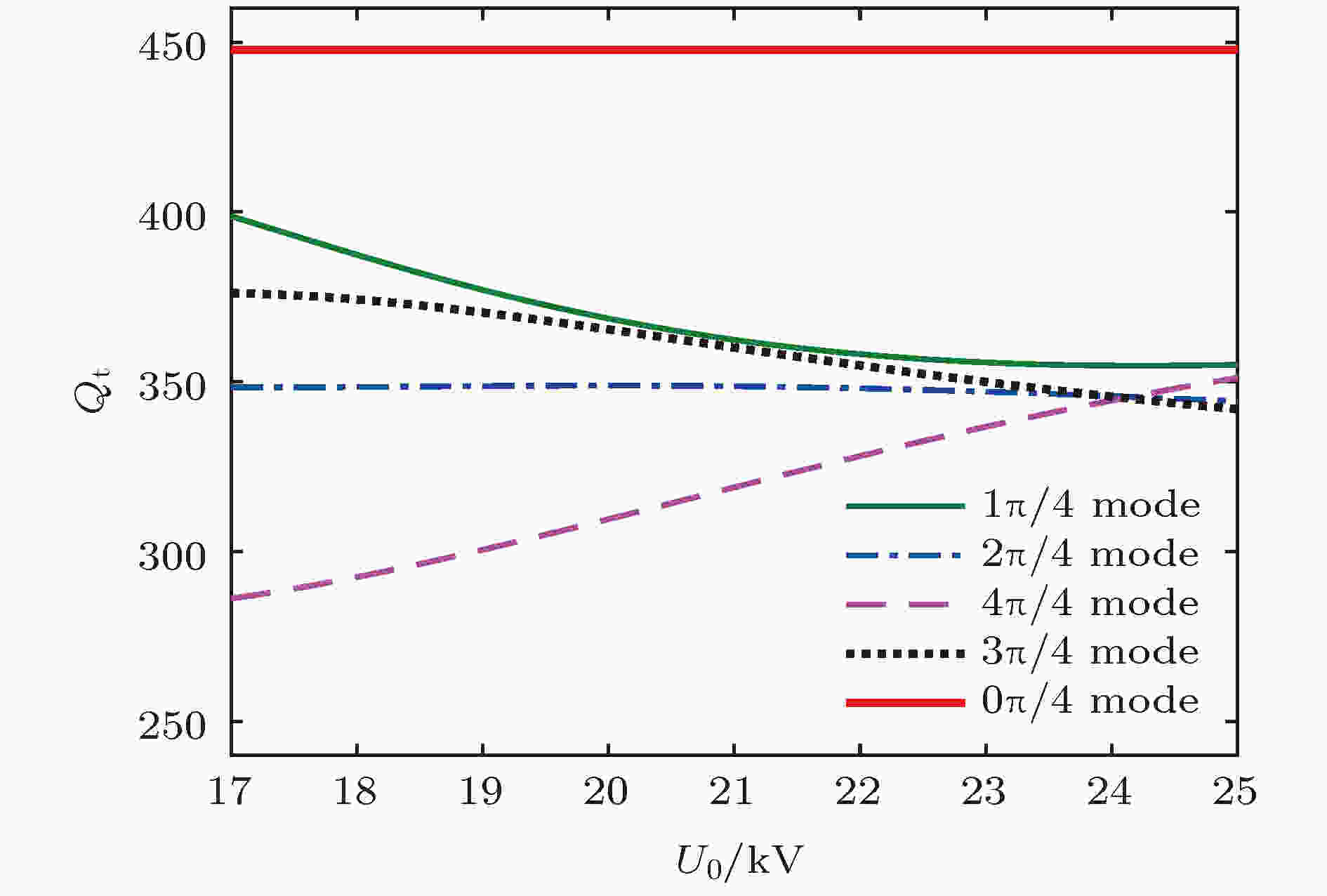图 19 输出腔各模式Q_t与电压U₀的关系
Figure19. Q_t versus U₀ of each mode in output cavity.

2 -->

3.4.高频结构仿真设计

优化设计后高频结构参数如表1所示, 此外, 电子注通道半径r_a = 0.1 mm.

谐振腔	纵向工作模式	谐振频率/GHz	固有品质因数Q0	外观品质因数Qext	起始位置/mm
输入腔	${\text{π}}$模	218	413	380	0
中间腔	${\text{π}}$模	218.05	413	∞	4.87
输出腔	${\text{π}}$模	218	413	1940	7.77

表1G波段扩展互作用速调管高频结构参数
Table1.Structural parameters of G-band extended interaction klystron amplifier.

根据高频结构参数, 采用三维电磁仿真软件进行模拟, 模拟结果如图20—图23所示. 图20为输入腔端口处监测的瞬时功率波形, 可知输入端口功率反射很小, 馈入的微波一部分耗散在输入腔腔壁上, 一部分被电子注吸收. 图21为调制电流的基频分量沿轴向的分布, 可以看出, 电子通过输入腔时, 输入端口馈入的微波在输入腔间隙上建立了高频场, 电子注受到高频场的作用产生了速度调制, 从而引起密度调制, 导致电流中产生谐波分量, 基频分量在某处取得最大值, 调制深度为122%. 图22和图23分别为输出腔端口处监测的瞬时输出功率波形和频谱, 可知输出功率为179 W, 中心频率为218 GHz, 输出功率频谱较纯, 在工作频率附近没有杂模.
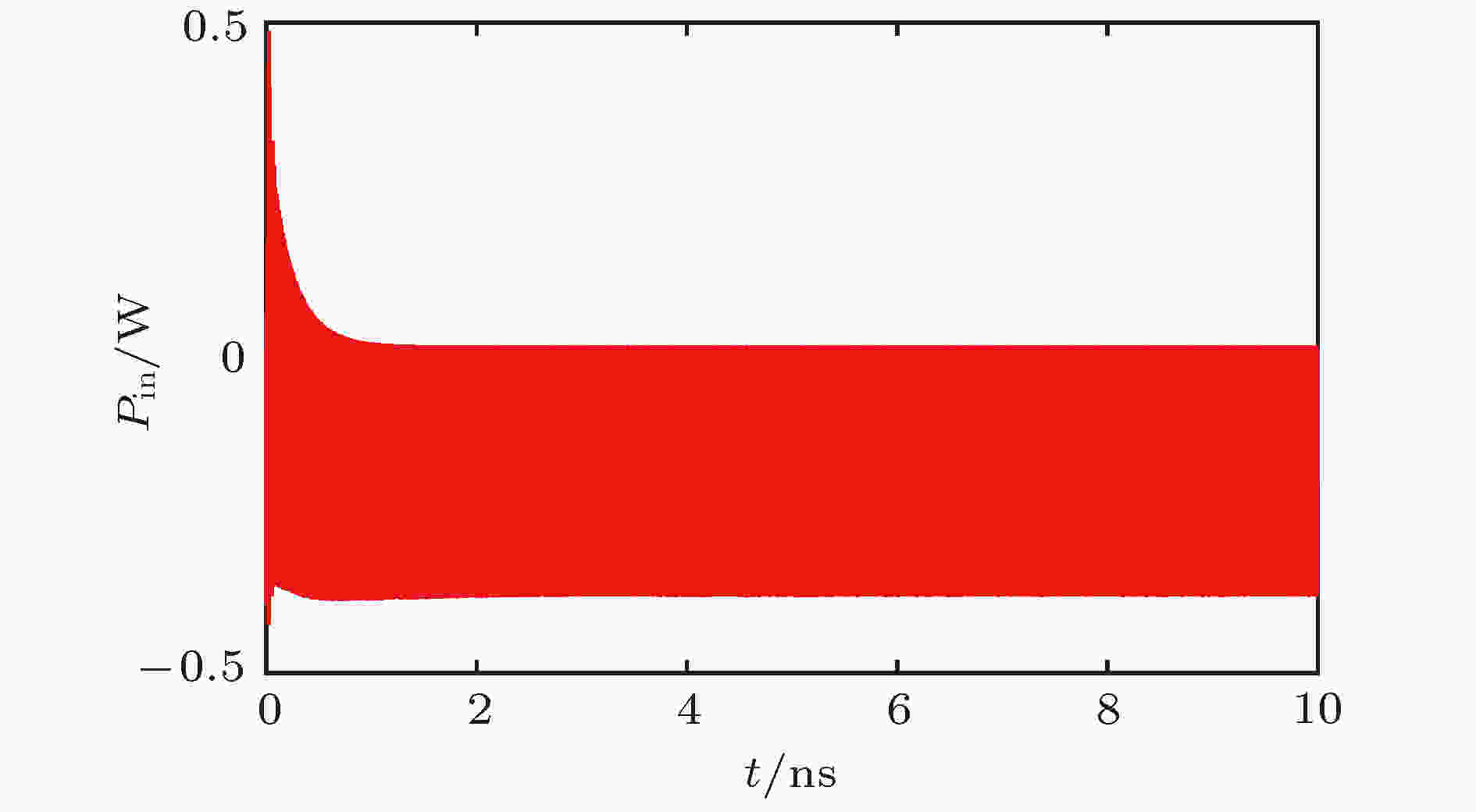图 20 瞬时输入功率波形
Figure20. Waveform of input microwave.

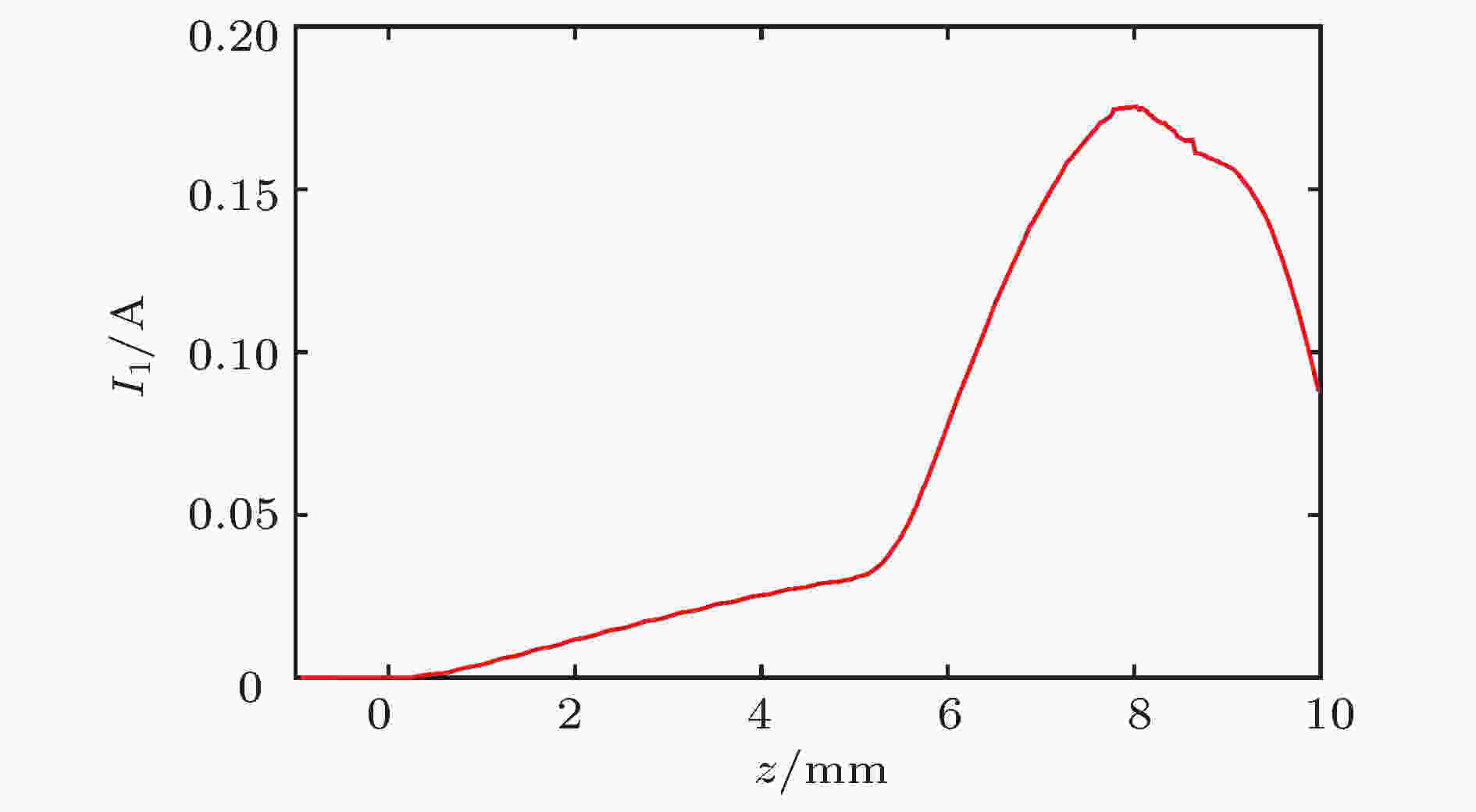图 21 调制电流基频分量沿轴向的分布
Figure21. Fundamental modulated current amplitude versus axial distance.

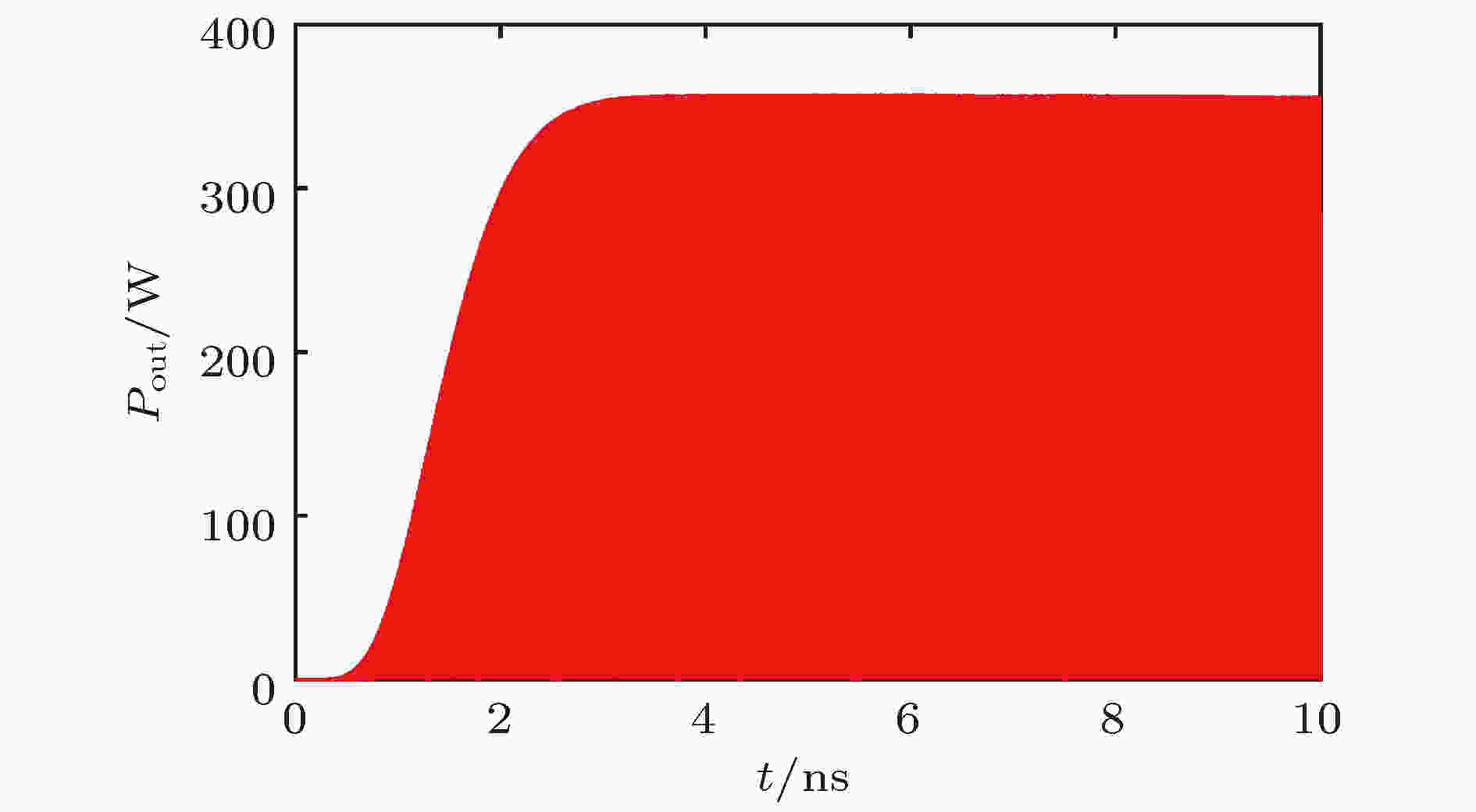图 22 瞬时输出功率波形
Figure22. Instantaneous waveform of output microwave.

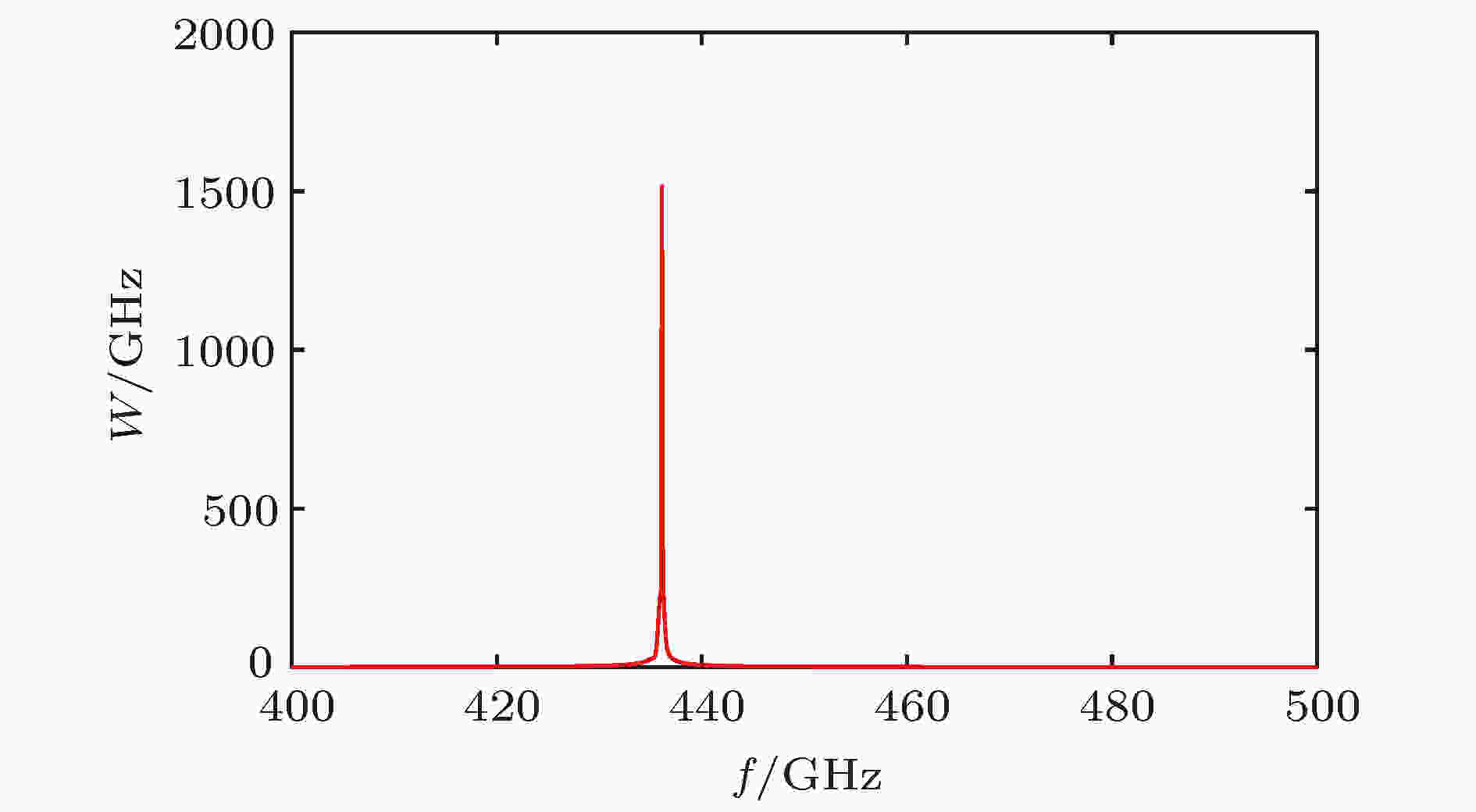图 23 输出功率频谱
Figure23. Spectrum of output microwave.

为了进一步研究扩展互作用速调管高频结构的性能, 分析了输入信号频率、输入信号功率、电子注电压和电流的变化对输出功率P_out和电子效率η的影响, 结果如图24—图27所示.
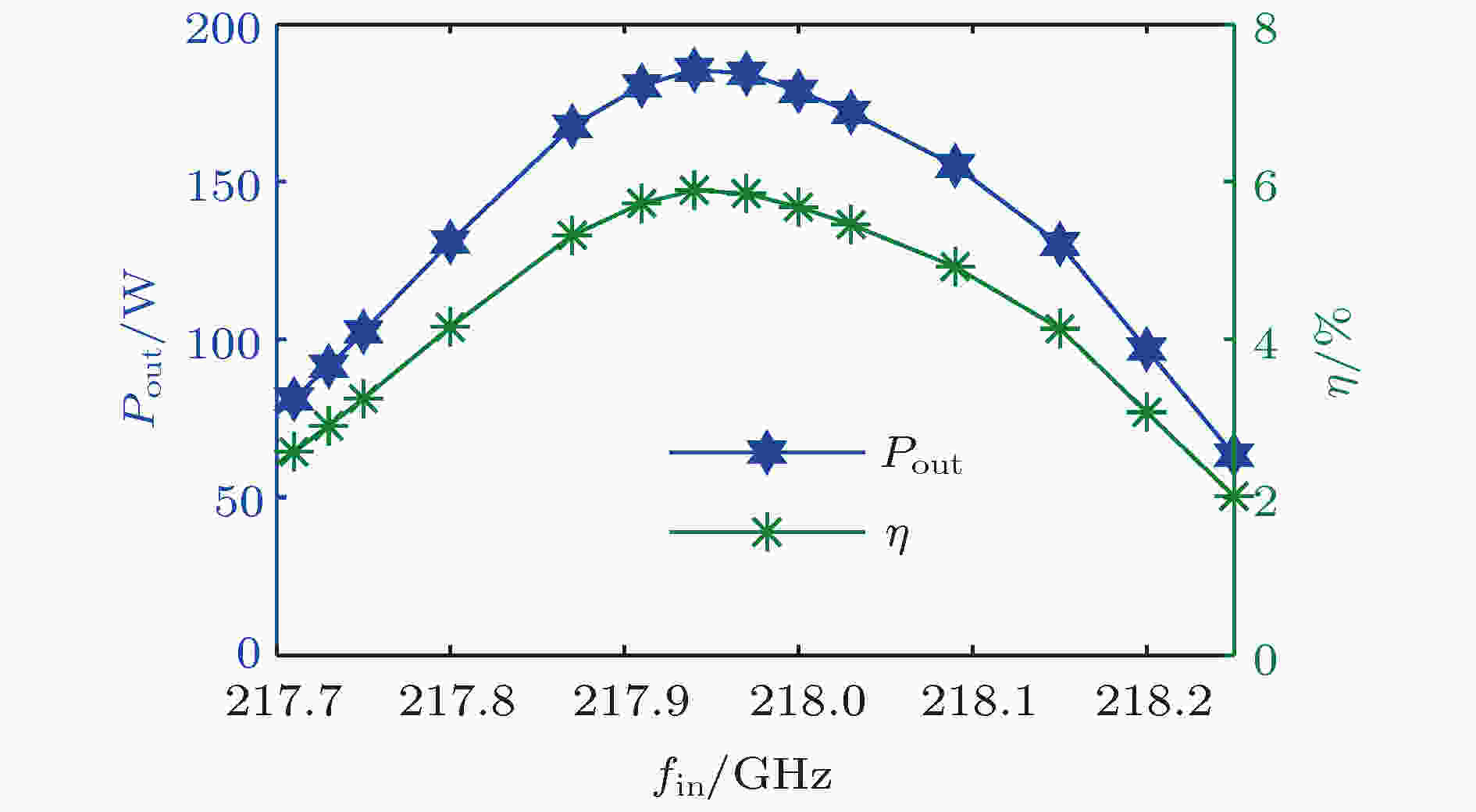图 24 输出功率和电子效率与输入微波频率的关系
Figure24. Output power and efficiency versus input microwave frequency.

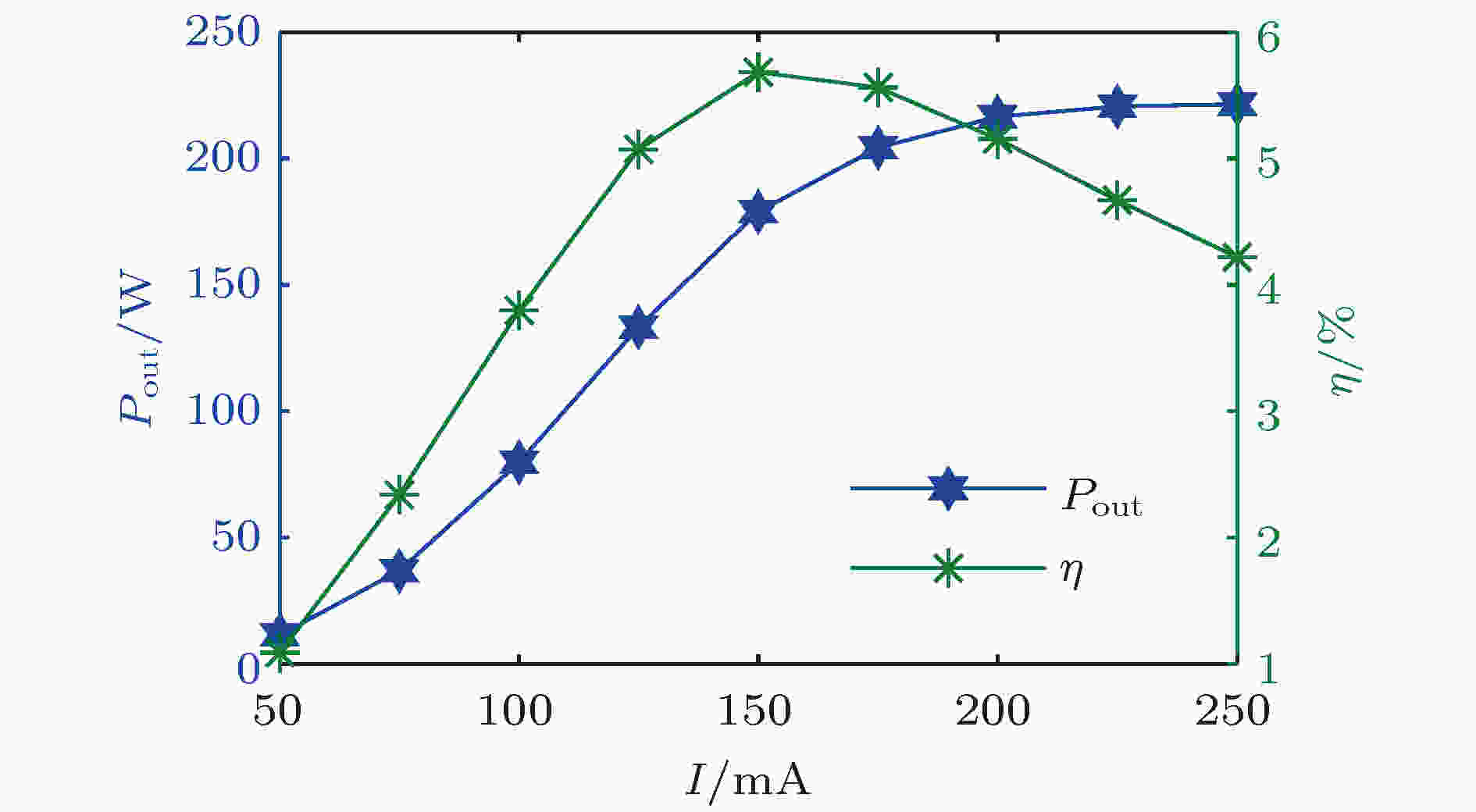图 27 输出功率和电子效率与电流的关系
Figure27. Output power and efficiency versus current.

图24为输出功率和效率随输入微波频率变化的情况, 可以看出, 输出功率和电子效率最大时的输入微波频率为217.94 GHz, 此时输出功率为185.5 W, 电子效率为5.9%, 增益为29.7 dB. 当输入微波频率偏离此值时, 输出功率和电子效率均减小. 这个最佳输入微波频率与谐振腔的固有谐振频率218 GHz相差60 MHz, 这个频率差别有一部分是由于电子负载电纳导致. 由图24还可得出, 扩展互作用速调管的3 dB带宽约470 MHz.
图25为输出功率和效率随输入微波功率变化的情况, 可以看出, 当输入微波功率小于200 mW时, 输出功率和电子效率随着输入微波功率的增加而增大, 当输入微波功率大于200 mW时, 输出功率和电子效率随着输入微波功率的增加而减小. 这是因为在输入微波功率小于饱和输入功率时, 输入腔和中间腔对电子注的调制作用比较弱, 电子注达到输出腔时未达到最佳调制, 输入功率越大, 电流调制越强, 输出功率和电子效率随输入功率增大而增大. 当输入微波功率大于饱和输入功率时, 在电子注到达输出腔前已经达到最佳调制, 且输入功率越大, 最佳调制位置越靠前, 因此输入功率越大, 输出功率和电子效率越小.
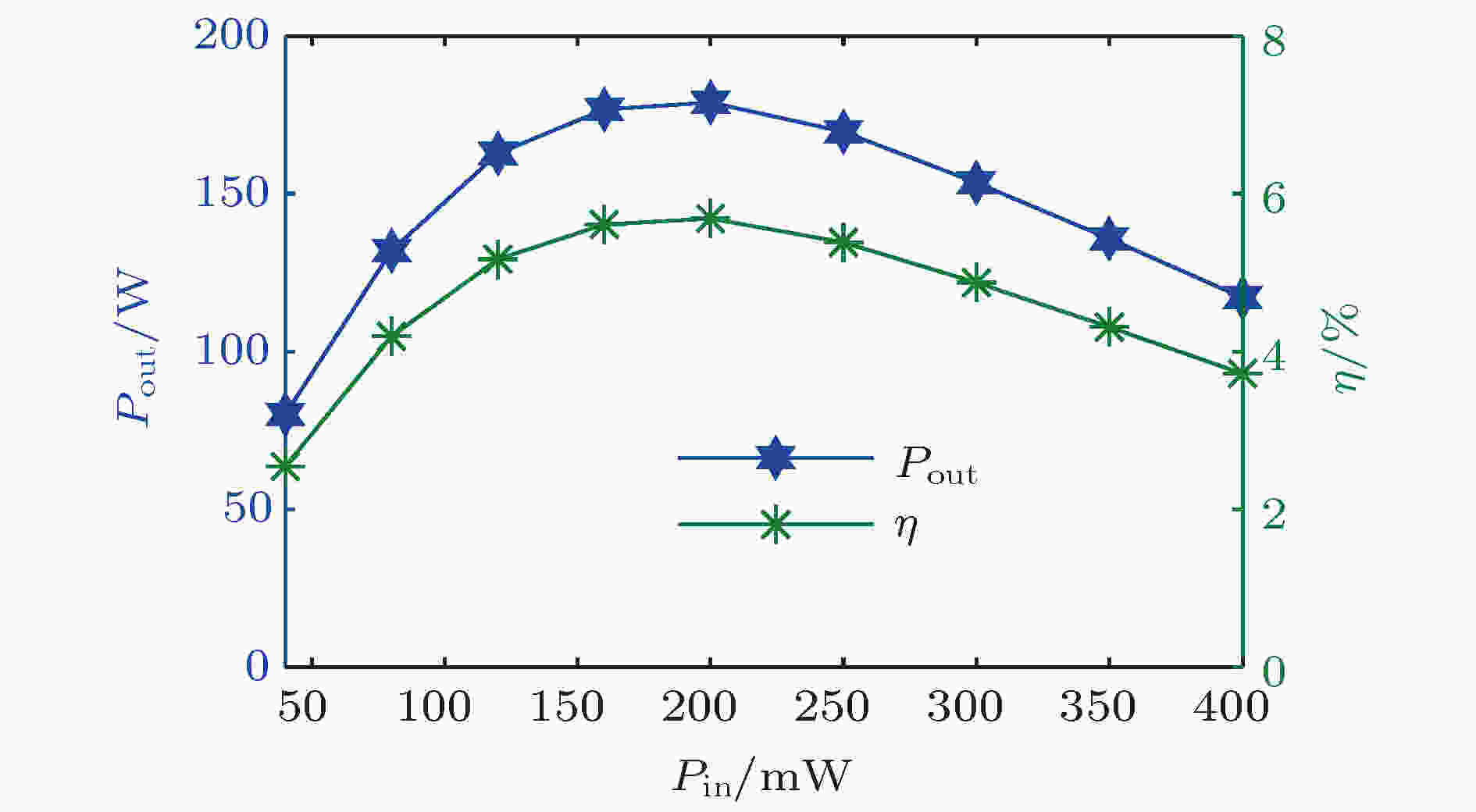图 25 输出功率和电子效率与输入微波功率的关系
Figure25. Output power and efficiency versus input microwave power.

图26为输出功率和效率随电子注电压变化的情况, 可以看出, 输出功率随着电压的增加而增大. 当工作电压小于24 kV时, 电子效率随着电压的增加而增大, 当工作电压大于24 kV时, 电子效率随着电压的增加而减小, 工作电压等于24 kV时电子效率达到最大值6.26%, 相应输出功率为225.5 W, 增益30.5 dB. 这是因为电子注在扩展互作用速调管中运动时, 有部分电子注能量转换为微波能量, 电子的速度会减小, 因此最佳工作电压会比冷腔同步电压高一些.
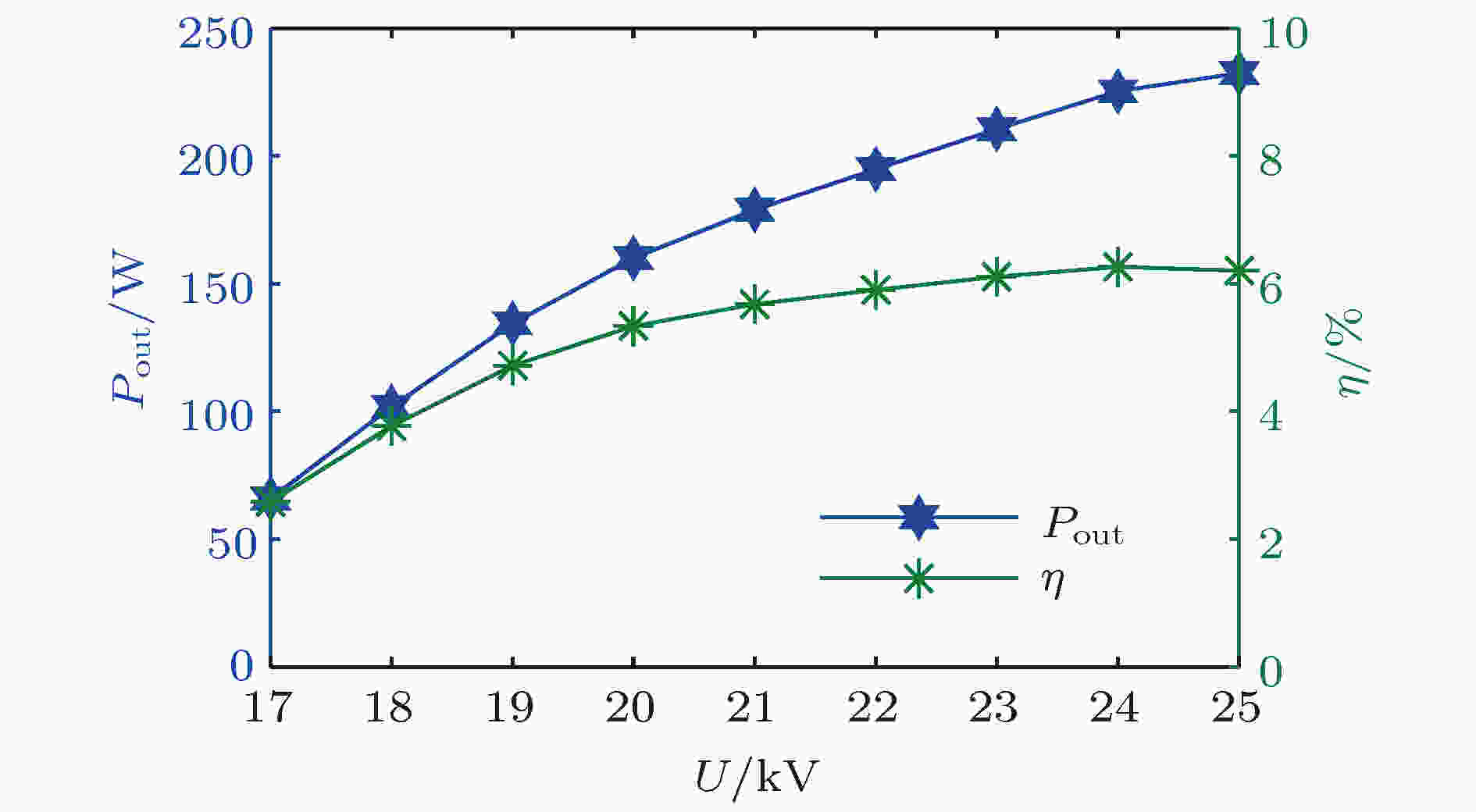图 26 输出功率和电子效率与电子注电压的关系
Figure26. Output power and efficiency versus voltage.

图27为输出功率和效率随电流变化的情况, 可以看出, 当工作电流小于150 mA时, 输出功率和电子效率随着电流的增加而增大. 工作电流大于150 mA时, 输出功率随着电流的增加而增大, 但电子效率随着电流的增加而减小. 这是因为当电流比较小时, 空间电荷效应比较小, 此时缩减等离子体波长比较长, 电子注到达输出腔时还没有达到最佳群聚状态, 所以随着电流的增加, 输出功率和电子效率也随之增加. 当超过最佳工作电流时, 空间电荷效应显著增加, 缩减等离子体波长变短, 电子注到达输出腔时已经过了最佳群聚状态, 所以此时电子效率开始减小, 但是由于电子注总功率的增加, 输出功率仍然随着工作电流的增加而增大.

本文基于运动学理论、感应电流定理和电荷守恒定律, 研究了电子在多间隙谐振腔${\text{π}}$模场中的渡越时间效应, 推导一间隙到五间隙谐振腔的电子负载电导和电子负载电纳的表达式, 分析了谐振腔间隙宽度、间隙数和间隙周期等参数对电子注与微波之间能量交换的影响和谐振腔谐振频率的影响. 研究表明, 间隙数的增加有利于注波互作用, 此外, 随着间隙数的增加, 电子负载电纳的极值越大, 说明间隙数的增加会使谐振腔加载电子注后频率在更大范围内变化, 因此, 在确定扩展互作用速调管的各个谐振腔的冷腔谐振频率时需考虑到这一点. 基于理论分析和数值模拟, 设计了一款工作于G波段的扩展互作用速调管放大器. 仿真结果显示, 当电子注电压为24 kV, 电流为0.15 A, 输入功率为200 mW, 轴向引导磁感应强度为0.8 T时, 在中心频率217.94 GHz处, 输出功率为225.5 W, 电子效率为6.26%, 增益为30.5 dB, 3 dB带宽约为470 MHz, 为研制G波段扩展互作用速调管奠定了基础.