摘要:目前市场主流的窄禁带材料霍尔磁场传感器主要工作在室温或低温环境, 而新型的宽禁带GaN材料霍尔传感器虽然适用于高温, 但器件结构主要是水平型, 受制于异质结界面过高的纵向电场约束, 能探测平行器件表面磁场的垂直型结构至今未见报道, 因此技术上无法实现单一芯片三维磁场探测. 针对该难题, 本文提出基于宽禁带AlGaN/GaN异质结材料, 采用选区浅刻蚀二维电子气沟道势垒层形成局部凹槽结构的方案, 从而实现垂直型结构霍尔传感器, 并且可有效地提高磁场探测灵敏度. 首先对照真实器件测试数据对所提器件材料参数和物理模型进行校准, 然后利用计算机辅助设计技术(TCAD)对器件电极间距比值、台面宽度、感测电极长度等核心结构参数进行优化, 同时对器件特性进行深入分析讨论. 仿真结果表明所设计的霍尔传感器具有高的磁场探测敏感度(器件宽度为2 μm时为113.7 V/(A·T))和低的温度漂移系数(约600 ppm/K), 器件能稳定工作在大于500 K的高温环境. 本文工作针对宽禁带材料垂直型霍尔传感器进行设计研究, 为下一步实现在单一芯片同时制造垂直型和水平型器件, 从而最终获得更高集成度和探测敏感度、能高温应用的三维磁场探测技术奠定了理论基础.
关键词: 磁场传感器/
铝镓氮/氮化镓异质结/
二维电子气/
高温稳定性

English Abstract

全文HTML

--> --> -->

霍尔传感器用于探测空间磁场大小, 基于这种传感器的探测系统已经被广泛应用于各种领域, 例如生物医疗、汽车电子中的防抱死系统、无刷电机以及电子罗盘^[1—5] 等. 传统霍尔传感器是基于硅、砷化铟或锑化铟等窄禁带半导体材料制作而成的^[6—8]. 硅材料制作的霍尔传感器的优点是失调电压小、容易与信号调制电路集成以及便于量产^[6]. 砷化铟和锑化铟异质结界面处具有高迁移率的二维电子气(two-dimensional electron gas, 2-DEG), 基于这种材料制作的传感器具有很高的灵敏度. 例如, 典型的砷化铟霍尔传感器在室温下的最大霍尔迁移率超过10000 cm²/(V·s), 电流相关敏感度可达300 V/(A·T)^[7]. 然而, 这些材料本身禁带宽度较小(例如, 硅的禁带为1.12 eV, 砷化铟的禁带为0.35 eV), 材料的物理特性在高于100 ℃的工作环境中发生显著变化, 因此制作的霍尔传感器往往只能工作在100 ℃以下. 在高于100 ℃环境中工作时, 其器件的温漂系数过大(典型值达到13800 ppm/K)^[9], 探测灵敏度明显下降甚至失效. 在一些高温、强辐射等特殊环境, 例如空间探测、核电站和军用领域, 这些传统的霍尔传感器已经不能够满足应用要求, 因此发展新材料、采用新工艺去设计并制作适用于高温工作环境的霍尔传感器具有重要意义.
氮化镓(GaN)基III—V族异质结材料(典型如AlGaN/GaN)作为第三代宽禁带半导体的重要代表之一, 具有明显的自身材料优势. 首先, GaN具有大的禁带宽度, 室温下为3.4 eV, 是硅的3倍, 砷化铟的9倍, 锑化铟的20倍, 因此其具有更高的临界击穿电场、更优的高温工作稳定性, 能够应用在300 ℃以上的极端环境中^[10—14]. 其次, GaN的理论本征载流子浓度很低, 因此制作的霍尔传感器噪声小、灵敏度较高. 另外, GaN基III—V族异质结界面处势阱中, 高密度的自发极化和压电极化面电荷产生强的电场, 诱导电子汇聚在势阱中并限制其在二维空间运动, 从而形成无需故意掺杂就具有的2-DEG^[15,16], 因此具有明显高出体材料的电子迁移率(约2000 cm²/(V·s)). 利用这种GaN基异质结材料制作的霍尔传感器, 其工作敏感度较高, 非常适合应用在高温工作环境中^[17,18]. 最后, GaN基霍尔传感器的研发还可借助于现有庞大的GaN基LED行业, 从而提高产品生产规模, 降低成本, 因此具有广阔的市场应用前景.
目前, 国际上已经有少量基于AlGaN/GaN异质结材料的霍尔传感器的研究报道, 其霍尔电极分布主要是十字形或者方形结构的水平型, 一般具有四端电极, 这种类型的传感器只能探测垂直于器件表面的磁场^[13,19,20]. 而用于探测平行于器件表面磁场的垂直型霍尔传感器至今并未见相关研制成果报道. 垂直型霍尔传感器的设计和制作具有重要意义, 它的突破使得在外延片上进行芯片制作环节就能实现具有三维磁场探测功能的高端霍尔传感器^[19,21—24], 因此能明显减小芯片体积、缩减成本. 三维霍尔传感器具有更广的应用范围、更优的使用便捷性和准确性, 缩小芯片体积后还能应用于某些对空间要求苛刻的特殊测试环境. 目前限制GaN基材料垂直型霍尔传感器的主要技术瓶颈之一是2-DEG沟道虽然具有高的电子迁移率, 但是在异质结界面处垂直于沟道方向具有很高的纵向电场, 电子被限制在界面的沟道中, 因霍尔效应产生的洛伦兹力驱离载流子偏移原输运轨道的能力较弱, 从而导致检测到的霍尔电压较小, 传感器探测敏感度降低.
为了解决以上问题, 本文提出具有五端电极分布、采用2-DEG沟道势垒层选区浅刻蚀形成局部凹槽结构的AlGaN/GaN异质结垂直型霍尔传感器. 本文首先从理论上论证采用该方案实现垂直型霍尔传感器的优势, 同时, 为了获得更加准确可靠的器件仿真结果, 在仿真前对材料参数和物理模型进行了校准. 仿真中对器件的几何参数进行了系统地优化, 并探讨了不同结构参数对垂直型器件性能的影响, 重点研究势垒层刻蚀深度对器件霍尔电压的影响. 仿真结果表明本文设计的器件具有较大的磁场探测灵敏度和优良的工作温度稳定性, 对磁场传感器技术的应用发展具有理论指导意义.

2

-->

2.1.霍尔传感器的关键评价指标

传统的半导体水平型霍尔传感器一般有四个电极, 其中两个电极是电流输入端, 另外两个电极是电压输出端. 通过在半导体两个输入端电极通入恒定电流, 在垂直于半导体平面方向施加外磁场, 则半导体内的载流子将受到洛伦兹力的作用, 因此向垂直于电流和磁场方向的半导体两侧聚集, 稳定时在两侧电极形成电势差, 即霍尔电压(V_H). 五电极垂直型霍尔传感器首先由Popovic^[24]提出, 可以采用恒压或恒流方式激励, 采用恒流激励测量电压信号时, 其霍尔电压可表达为^[24—26]

${V_{\rm{H}}} = G\frac{{{r_{\rm{H}}}}}{{qnw}}{I_{\rm{b}}}B,$

式中G为霍尔传感器的几何因子, r_H为霍尔散射系数, n为半导体材料的载流子浓度, w为源区的宽度, I_b为输入端激励电流, B为平行器件表面方向的磁场强度.
评价霍尔传感器的关键指标之一是磁场灵敏度, 常用电流相关敏感度S_I标记, 表示单位电流、单位磁场强度下获得的霍尔电压大小, 其具体表达式为^[24,26]

${S_{\rm{I}}} = \frac{{{V_{\rm{H}}}}}{{{I_{\rm{b}}} B}} = G\frac{{{r_{\rm{H}}}}}{{qnw}}.$

另一个关键指标是灵敏度温度漂移系数(温漂系数), 常用S_T标记, 表示单位温度变化下磁场灵敏度变化的相对量, 因此可以定量地表示器件工作的温度稳定性, 其具体表达式为^[19]

${S_{\rm{T}}} = \frac{1}{{{S_{\rm{I}}}\left( {{T_0}} \right)}} \frac{{\partial {S_{\rm{I}}}\left( T \right)}}{{\partial T}},$

式中T为器件工作的温度; S_I(T₀)代表了室温下的磁场敏感度, S_T越小, 表明霍尔传感器的温度稳定性越好.
2 -->

2.2.GaN基异质结垂直型霍尔传感器结构设计

本文利用局部刻蚀减薄AlGaN势垒层, 通过减小异质结界面处极化电荷诱导产生的纵向电场, 从而有效提高测量得到的霍尔电压, 该垂直型霍尔传感器的剖面和俯视结构如图1所示. 传感器结构采用Si衬底和AlN应力缓冲层, 其上外延生长非故意掺杂的GaN材料和Al_0.25Ga_0.75N势垒层. C₀, C₁和C₂为传感器主电极; 长度均为l₁; S₁和S₂为感测电极, 长度均为l₂; C₀与C₁(或C₂)间距为L₁, 器件结构关于中心主电极C₀呈对称分布. S₁和S₂经浅刻蚀减薄后, 保留其势垒层厚度为d, 感测电极S₁(或S₂)与中心主电极C₀边缘的距离为L₂, 传感器的有效宽度记作w. 测量过程磁场方向平行于传感器表面电极, 如图1所示.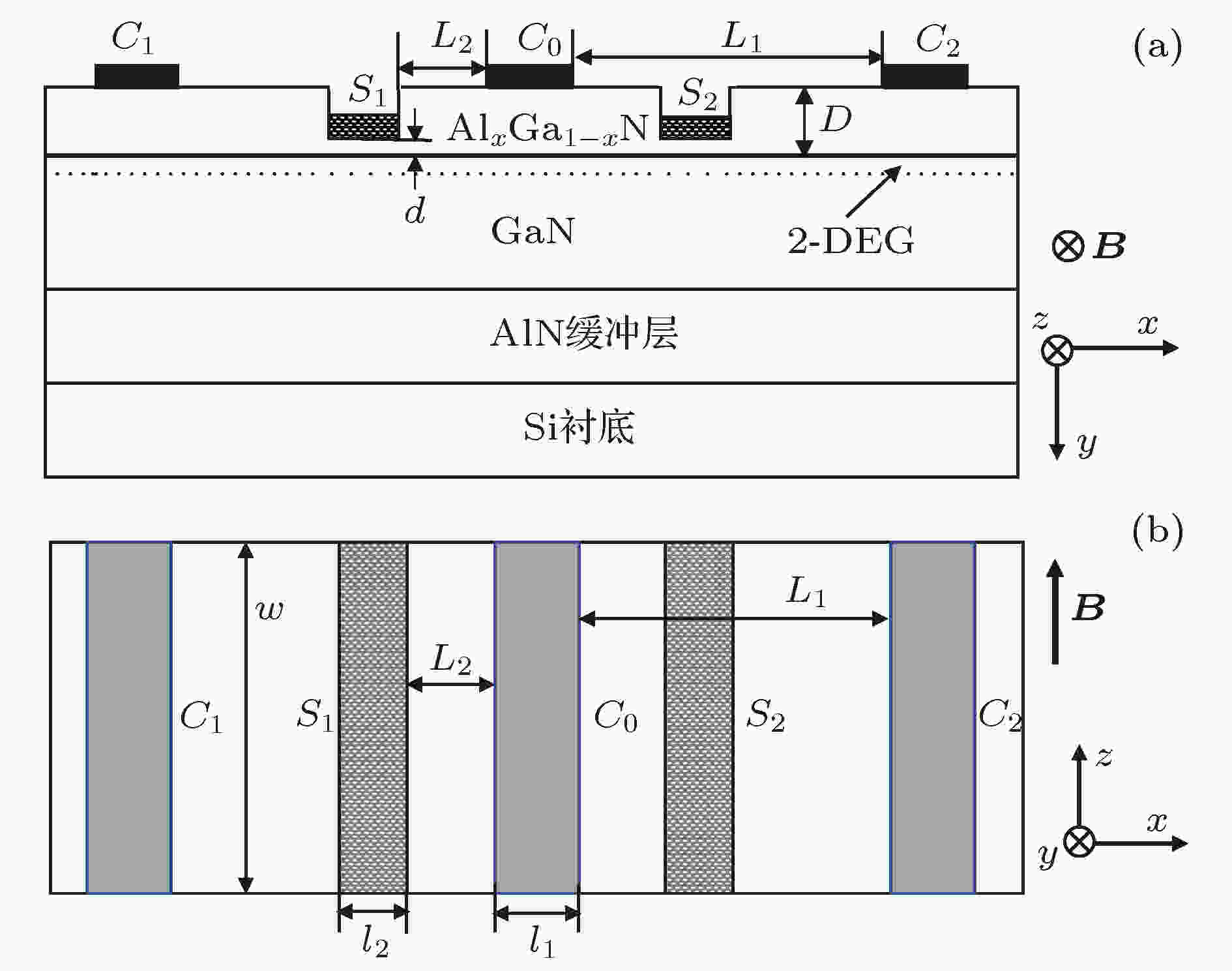
图 1 基于GaN基异质结结构的垂直型霍尔传感器结构 (a)剖面图; (b)俯视图
Figure1. Schematic diagram of GaN-based vertical Hall sensor: (a) Sectional and (b) top views.

垂直型霍尔传感器工作原理如下: C₁和C₂电极作为公共端接地, C₀作为激励源的电流输入端, 测量S₁和S₂之间的电势差即为霍尔电压; 无平行器件表面的外加磁场时, 由于器件结构的对称性, 感测电极处的电势相等, 霍尔电压为零; 如图1所示, 当存在平行器件电极方向的磁场B时, 主电极C₀→C₁和C₀→C₂的电流方向与磁场方向相互垂直, 载流子在运动过程中会受到垂直于电流和磁场方向(即y方向)的洛伦兹力, 由于C₀→C₁和C₀→C₂的电流方向相反, 两者受到的洛伦兹力方向也相反, 从而发生载流子在y方向(纵向载流子分离, 这是垂直型霍尔传感器的重要特征)运动偏移, 形成明显的电势差, 即霍尔电压V_H.
对于常规GaN基异质结结构(S₁和S₂下方势垒层未进行刻蚀), 2-DEG沟道界面处极化正电荷诱导产生的电场力能有效抵消外加磁场形成的洛伦兹力, 因此沟道中载流子发生纵向偏移的能力明显减弱, 因此感测得到的霍尔电压过小, 传感器的灵敏度较低. 本文通过减薄感测电极下方的势垒层, 缩短势垒层表面极化负电荷与2-DEG沟道距离, 利用该极化负电荷诱导产生的相反方向电场力来部分抵消异质结界面处过高的纵向电场力. 由于该方案保留部分势垒层厚度, 保证了光滑平整、完好无损的沟道界面, 2-DEG电子迁移率大小并未受明显影响, 而载流子纵向运动偏移的能力得到增强, 因此传感器感测霍尔电压明显增大.

本文在TCAD仿真中重点研究磁场对半导体中运动载流子的影响, 仿真中采用了磁场相关电流传输模型, 其表达式如下^[27—29]:

$\begin{split}{{{J}}_\alpha } = &\; {\mu _\alpha }{{{g}}_\alpha } + {\mu _\alpha }\frac{1}{{1 + {{\left( {\mu _\alpha ^*B} \right)}^2}}}\\ &\cdot\left[ {\mu _\alpha ^*{{B}} \times {{{g}}_\alpha } + \mu _\alpha ^*{{B}} \times \left( {\mu _\alpha ^*{{B}} \times {{{g}}_\alpha }} \right)} \right],\end{split}$

其中,

${{{g}}_\alpha } = - \alpha q\nabla {\varnothing_\alpha },\;\alpha = n,\;p,$

式中J_α为载流子电流密度, μ_α为载流子迁移率, μ_α^*为霍尔迁移率, $\nabla {\varnothing_\alpha }$为电子或空穴的准费米势, B为磁感应强度, B为其模值, α为电子n或空穴p.
从真实器件应用出发, 本文仿真过程重点关注温度对磁场传感器特性的影响, 因此仿真过程引入温度相关迁移率模型并加以优化. 本文采用了Farahmand等^[30]通过拟合蒙特卡罗计算结果得出的用于GaN材料温度相关的低场电子迁移率模型, 该解析模型较为精确地考虑了合金组分、温度特性、合金无序效应等因素, 其表达式如下:

$\mu = \dfrac{{{\mu _0}\left( {T,N} \right) + {v_{{\rm{sat}}}}\dfrac{{{E^{{n_1} - 1}}}}{{E_{\rm{C}}^{{n_1}}}}}}{{1 + a{{\left( {\dfrac{E}{{{E_{\rm{C}}}}}} \right)}^{{n_2}}} + {{\left( {\dfrac{E}{{{E_{\rm{C}}}}}} \right)}^{{n_1}}}}},$

式中,

$\begin{split}{\mu _0}\left( {T,N} \right) =\; & {\mu _{{\rm{min}}}}{\left( {\dfrac{T}{{300}}} \right)^{{\beta _1}}} \\ &+ \dfrac{{\left( {{\mu _{{\rm{max}}}} - {\mu _{{\rm{min}}}}} \right){{\left( {\dfrac{T}{{300}}} \right)}^{{\beta _2}}}}}{{1 + {{\left[ {\dfrac{N}{{{N_{{\rm{ref}}}}{{\left( {\dfrac{T}{{300}}} \right)}^{{\beta _3}}}}}} \right]}^{\alpha {{\left( {\frac{T}{{300}}} \right)}^{{\beta _4}}}}}}},\end{split}$

其中, μ₀为低场迁移率; E为电场强度; v_sat为电子饱和速度; E_C为关键电场; 参数a, n₁和n₂为表达式(6)中的拟合参数; N为掺杂浓度; μ_max和μ_min为最大和最小载流子迁移率; α, β₁, β₂, β₃和β₄为表达式(7)中的拟合参数. 此外, 仿真过程还引入载流子陷阱复合模型来模拟传感器实际工作中载流子输运过程可能的俘获和发射情况. 仿真计算采用时域有限差分法, 通过分割并分别求解器件网格单元的泊松方程和载流子连续性方程, 从而最后得到器件的电流密度、电场强度、电势分布等物理数据, 通过计算得到V_H, S_I和S_T等传感器重要性能参数.
本文仿真中材料和器件结构参数取值如下: Al_xGa_1–xN势垒层厚度为25 nm, Al组分x = 0.25, GaN外延层厚度为6 μm, AlN缓冲层厚度为25 nm; C₀, C₁和C₂主电极长度l₁ = 1.5 μm, S₁和S₂感测电极长度l₂ = 1 μm, C₀与C₁ (或C₂)间距L₁ = 8.5 μm, 感测电极S₁ (或S₂)与中心主电极C₀的距离L₂ = 2 μm; 器件台面宽度w = 10 μm; GaN材料的背景载流子浓度为5 × 10¹⁴ cm^–3; 结构参数优化过程中, Al_xGa_1–xN势垒层厚度d的取值范围为1 nm ≤ d ≤ 25 nm. Al_xGa_1–xN势垒层剩余厚度d的大小将显著影响2-DEG沟道中电子浓度和迁移率大小, 为了使仿真贴近实际器件工艺, 本文首先在仿真中对物理参数进行校准. Anderson等^[31]报道了AlGaN势垒层浅刻蚀的HEMT器件的电学特性, 给出了刻蚀深度对器件参数变化(特别是电子迁移率)的具体影响, 本文通过对比仿真得到的转移特性曲线与文献实验数据来校准仿真中所用物理参数. 如图2所示, 两者阈值电压和电流大小数据匹配较好, 说明本文仿真结果具有较好的准确性和可靠性, 校正后的主要器件物理参数列于表1.
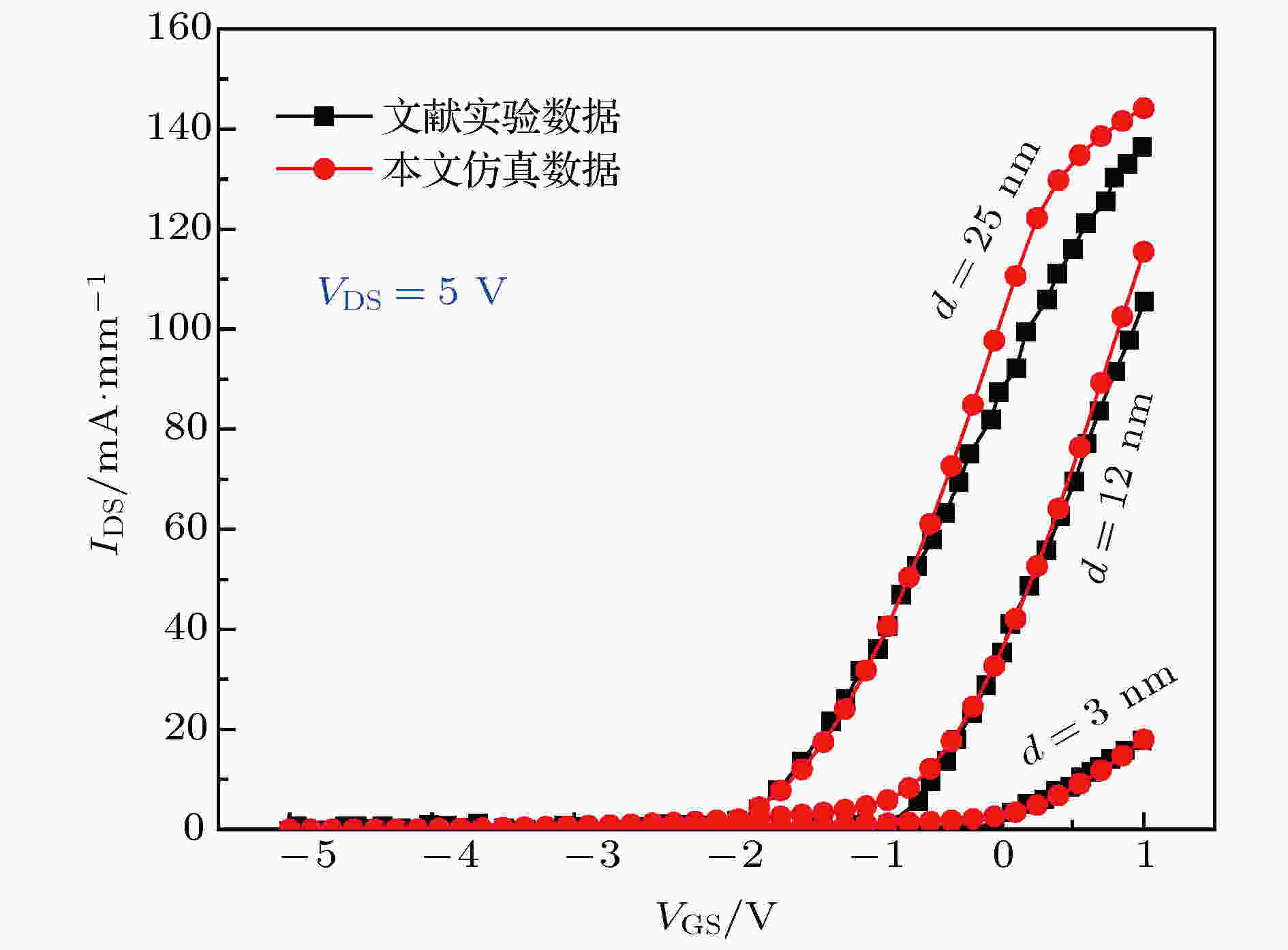图 2 器件仿真数据与实验转移特性结果进行对比的器件参数校准过程^[31]
Figure2. Comparisons of simulated I_DS-V_GS characteristics of the Hall sensor with the experimental data.

物理参数	单位	GaN	AlN
禁带宽度 Eg	eV	3.4	6.2
电子亲和能χ	V	3.4	1.9
相对介电常数$\epsilon $	—	9.4	8.8
迁移率 μ	cm2/(V·s)	1310	300
电子饱和速率 vsat	cm/s	1.8 × 107	1.3 × 107
电子发射截面 σ0n	cm2	1.0 × 10–15	1.0 × 10–15
导带状态密度 Nc	cm–3	2.7 × 1018	4.1 × 1018
价带状态密度 Nv	cm–3	2.5 × 1019	2.8 × 1020
热导率 κ	W/(cm·K)	1.3	2.9

表1仿真中所用的典型器件物理参数
Table1.Summary of physical parameters adopted in the simulations.

图3和图4分别展示了感测电极下方靠近2-DEG沟道附近的电子浓度分布以及输出霍尔电压仿真结果, 与感测电极下方AlGaN势垒层厚度d的关系. 从图3和图4可以看出: 随着感测电极下方AlGaN势垒层厚度d的减小, 异质结界面处的净极化电荷数量逐渐减小, 其诱导产生的纵向电场减小, 因此感测电极下方的2-DEG浓度迅速降低; 而同样由于纵向束缚电场减小, 洛伦兹力驱离载流子偏移原输运轨道的能力增强, 因此感测电极之间的电势差增大, 器件的输出霍尔电压明显增加, 其变化规律符合(1)式. 霍尔电压在d = 7 nm处达到峰值, 当继续刻蚀使得AlGaN势垒层较薄时, 受沟道电子迁移率下降的影响, 输出霍尔电压开始减小. 因此, 势垒层剩余厚度d存在最佳取值, 本文选定其值为7 nm.
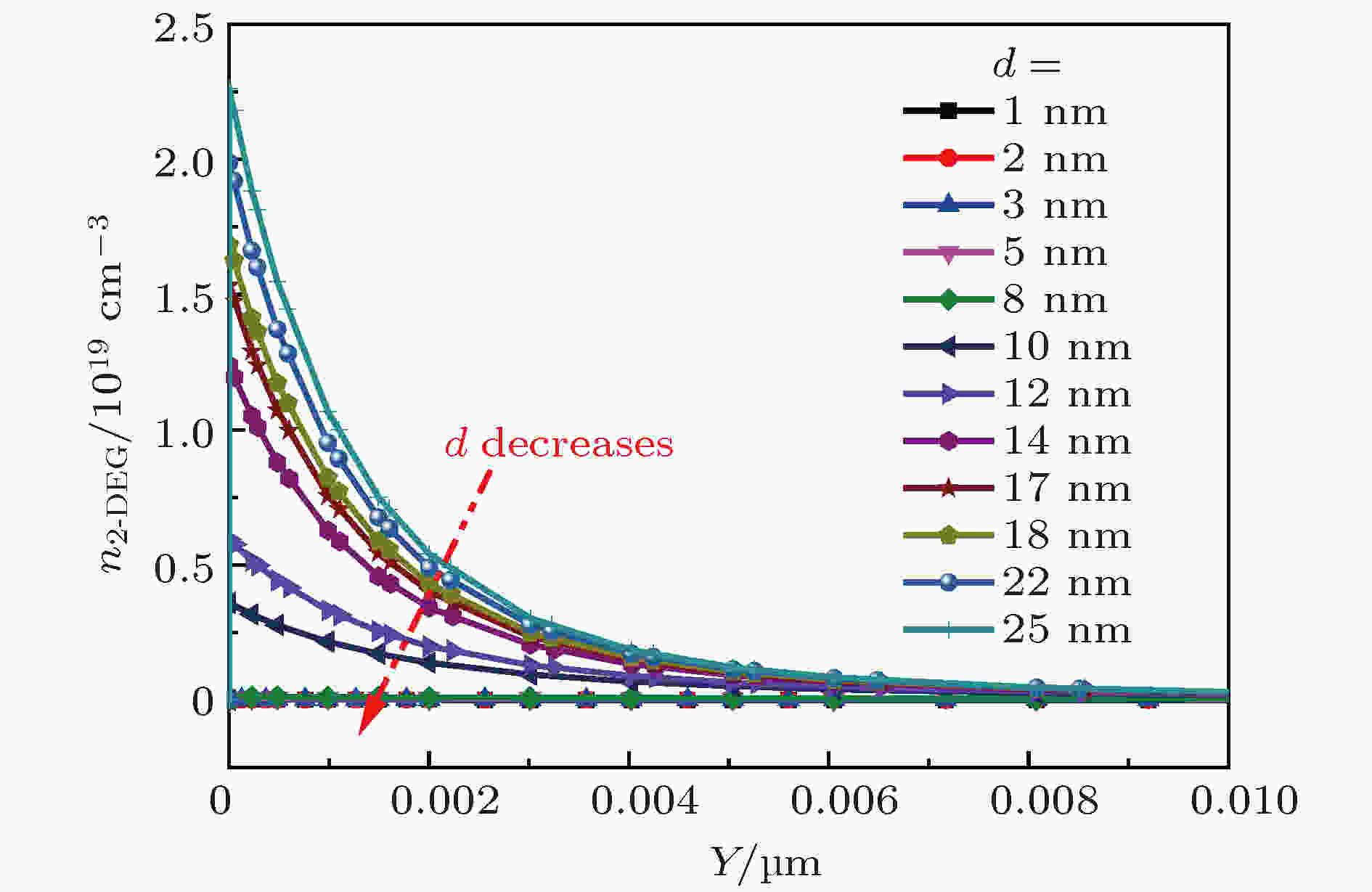图 3 2-DEG沟道界面下方电子浓度分布与势垒层剩余厚度的关系
Figure3. Profiles of 2-DEG concentration vs. AlGaN barrier thickness.

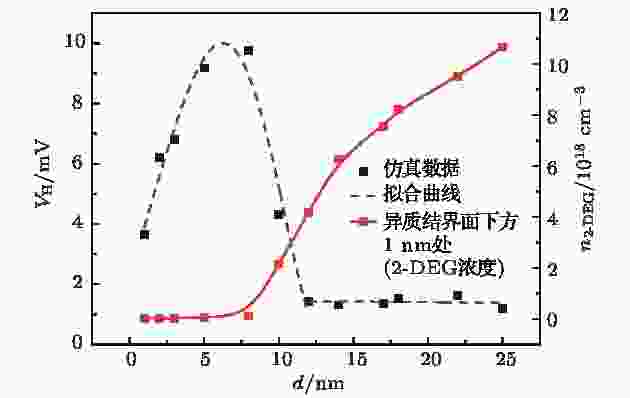图 4 霍尔电压(或2-DEG电子浓度)与势垒层剩余厚度的关系
Figure4. Hall voltage (or 2-DEG concentration) vs. AlGaN barrier thickness.

图5展示了感测电极下方势垒层剩余厚度d = 7 nm时, 在无外加磁场和外加磁场B = 1 T情况下, 传感器电流密度空间分布对比情况. 从图5可以看出, 当器件表面平行方向不存在磁场时, 两侧的感测电极下方电流密度呈空间对称分布, 因此感测电极S₁和S₂之间电势差为零, 如图5(a)所示; 而当垂直纸面向里方向存在磁场时, 感测电极S₁下方的电子在磁场中受到洛伦兹力作用发生向下偏移, 而S₂下方的电子运动向上偏移, 两边感测电极处纵向束缚电场的减弱间接加速了电子在纵向的偏移过程, 稳定后感测电极S₁和S₂之间将产生明显的电势差, 如图5(b)所示, 图中虚线清晰地标明两侧电流空间分布差值情况.
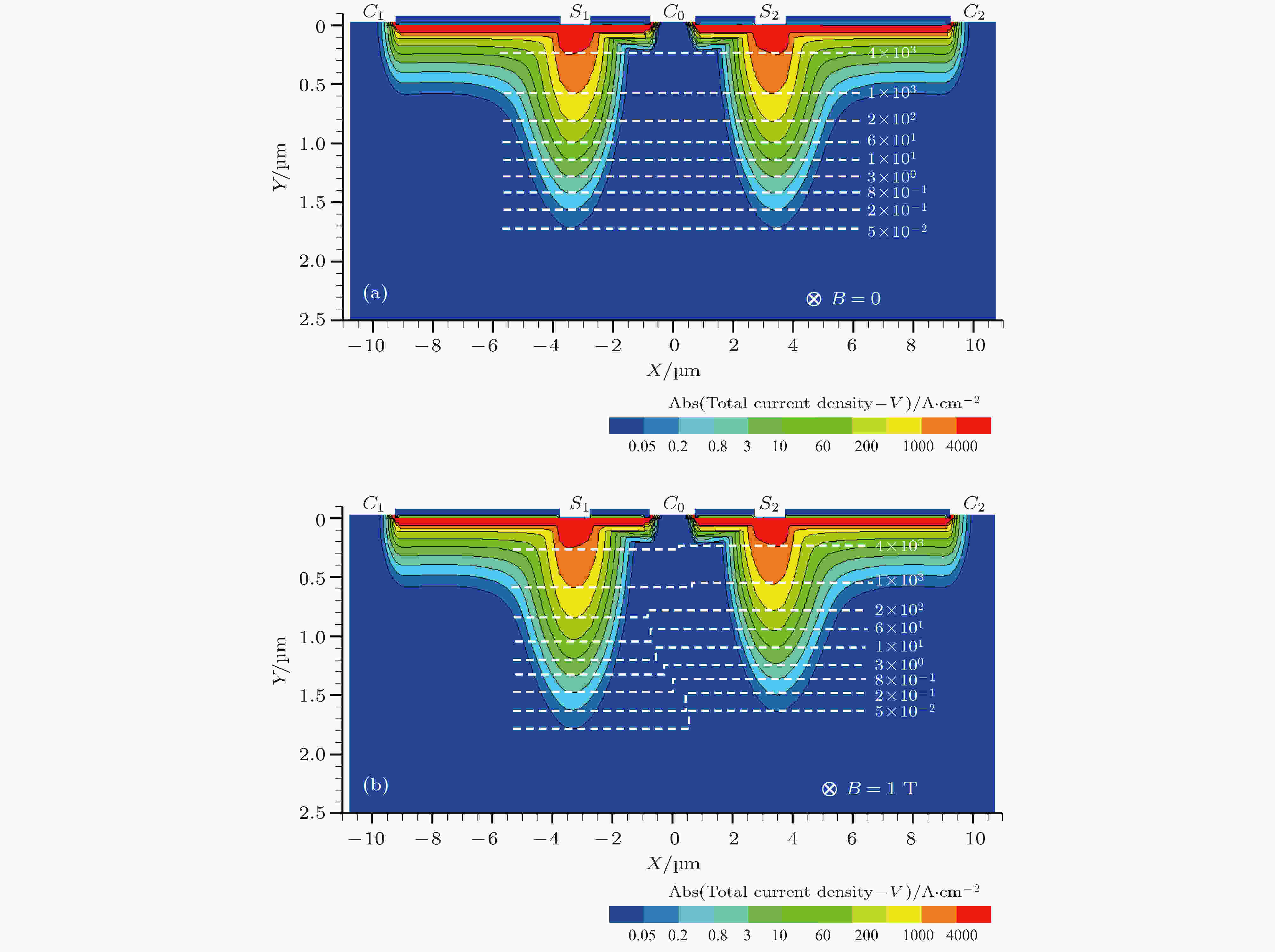图 5 当d = 7 nm时, 传感器电流密度空间分布对比　(a)无外加磁场; (b)外加磁场B = 1 T
Figure5. Comparisons of current density distribution in vertical Hall sensor with d = 7 nm under the conditions of (a) B = 0 and (b) B = 1 T.

霍尔传感器中的结构尺寸, 特别是L₂/L₁比值、感测电极长度l₂和器件台面宽度w等参数对传感器灵敏度影响较大, 本文在仿真过程重点对这些参数进行优化, 仿真中采用的激励电流为0.5 mA, 外加磁场强度B = 0.5 T.
图6展示了霍尔传感器电流相关敏感度S_I与L₂/L₁比值的关系, 图中数据点为经过对数十个不同尺寸器件仿真模拟并经过计算得到. 仿真中设置感测电极的长度l₂ = 1 μm, 器件的宽度w = 10 μm. 图6中虚线是对仿真所得数据点分布进行线性拟合得出的, 其数学关系式已列在图中. 从仿真结果可以看出, 电流相关敏感度随着L₂/L₁比值的增加而增加. 其原因是: 随着L₂/L₁比值增加, 感测电极相对两侧主电极的位置发生改变, 当感测电极靠近器件两侧时, 器件的几何因子G增加^[21,26], 由前面表达式(2)可知电流相关敏感度也随之增加; 另外, 随着L₂/L₁比值增加, 靠近两侧主电极处的载流子受洛伦兹力的影响增强, 感测电极之间的电势差逐渐增加, 因此霍尔电压增加, 器件的电流相关敏感度也随之增加. 因此在实际器件设计制作过程中, 为了增大传感器的灵敏度, 可以适当减小主电极C₀与C₁(或C₂)之间的间距L₁, 或者适当增加C₀与S₁ (或S₂)之间的间距L₂.
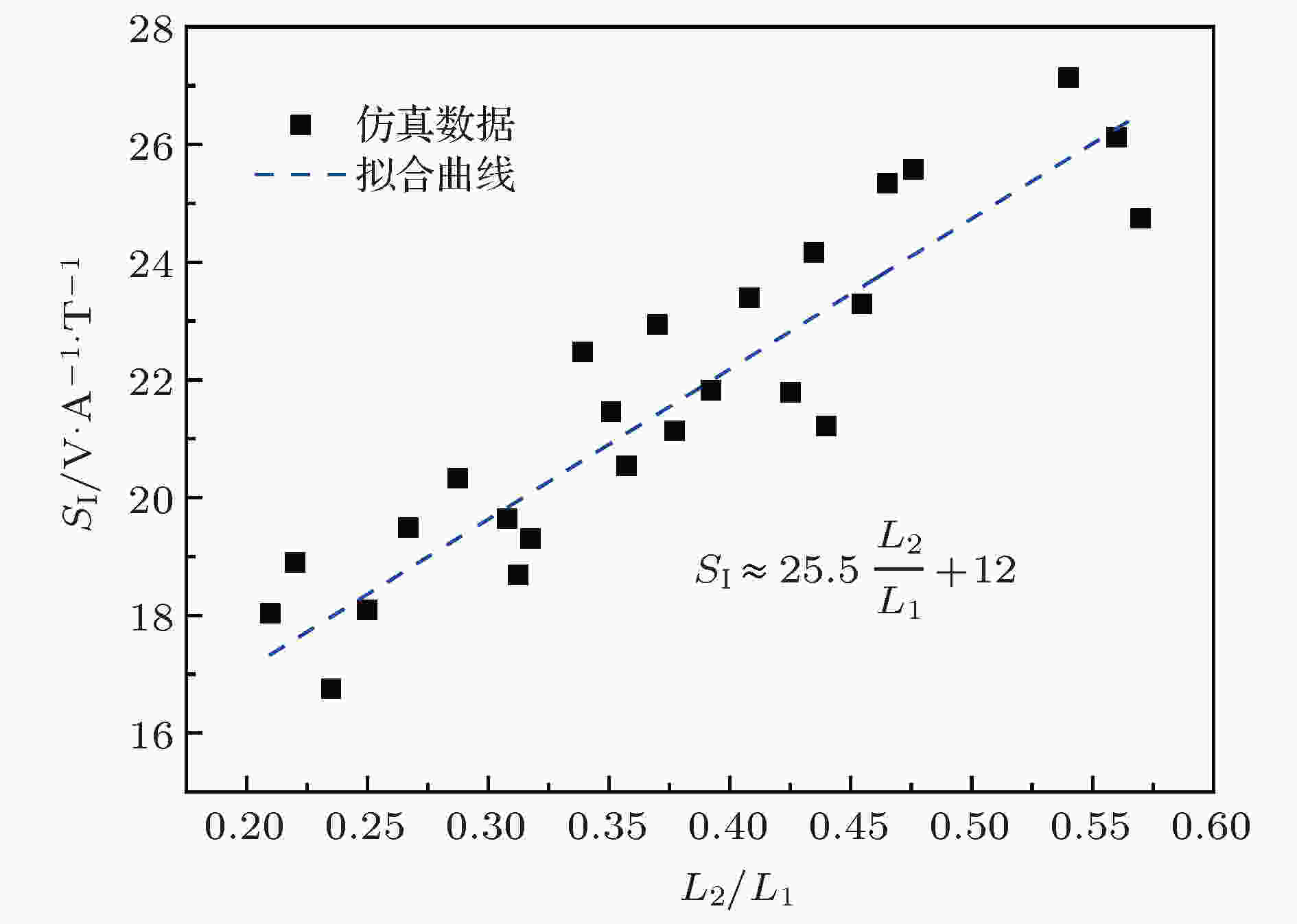图 6 电流相关敏感度S_I与L₂/L₁比值的关系
Figure6. Current-related sensitivity as a function of the ratio of L₂/L₁.

图7展示了电流敏感度以及输入电阻仿真结果, 与感测电极长度的关系, 其中感测电极l₂的长度变化范围为0.50—2 μm, 而主电极间距L₁ = 4.05 μm, 感测电极与主电极间距L₂ = 2 μm以及器件宽度w = 10 μm. 由仿真结果可知, 器件的敏感度随着感测电极长度的增加有所增加, 当感测电极长度为1.25 μm时, 器件的峰值电流相关敏感度为22.8 V/(A·T). 随着感测电极长度继续增加, 器件的输入电阻呈线性增加, 而敏感度逐渐下降. 其原因是: 器件的电流相关敏感度的大小与器件导电沟道中的载流子浓度成反比, 随着感测电极长度的增加, 其下方势垒层经过刻蚀后, 异质结界面处的2-DEG浓度平均值有所降低^[31], 因此电流敏感度逐渐增加; 而当感测电极的长度过大时, 两侧有效电势差部分抵消, 因此霍尔电压开始下降^[25]. 综合考虑, 本文选取其最优值为l₂ = 1.25 μm.
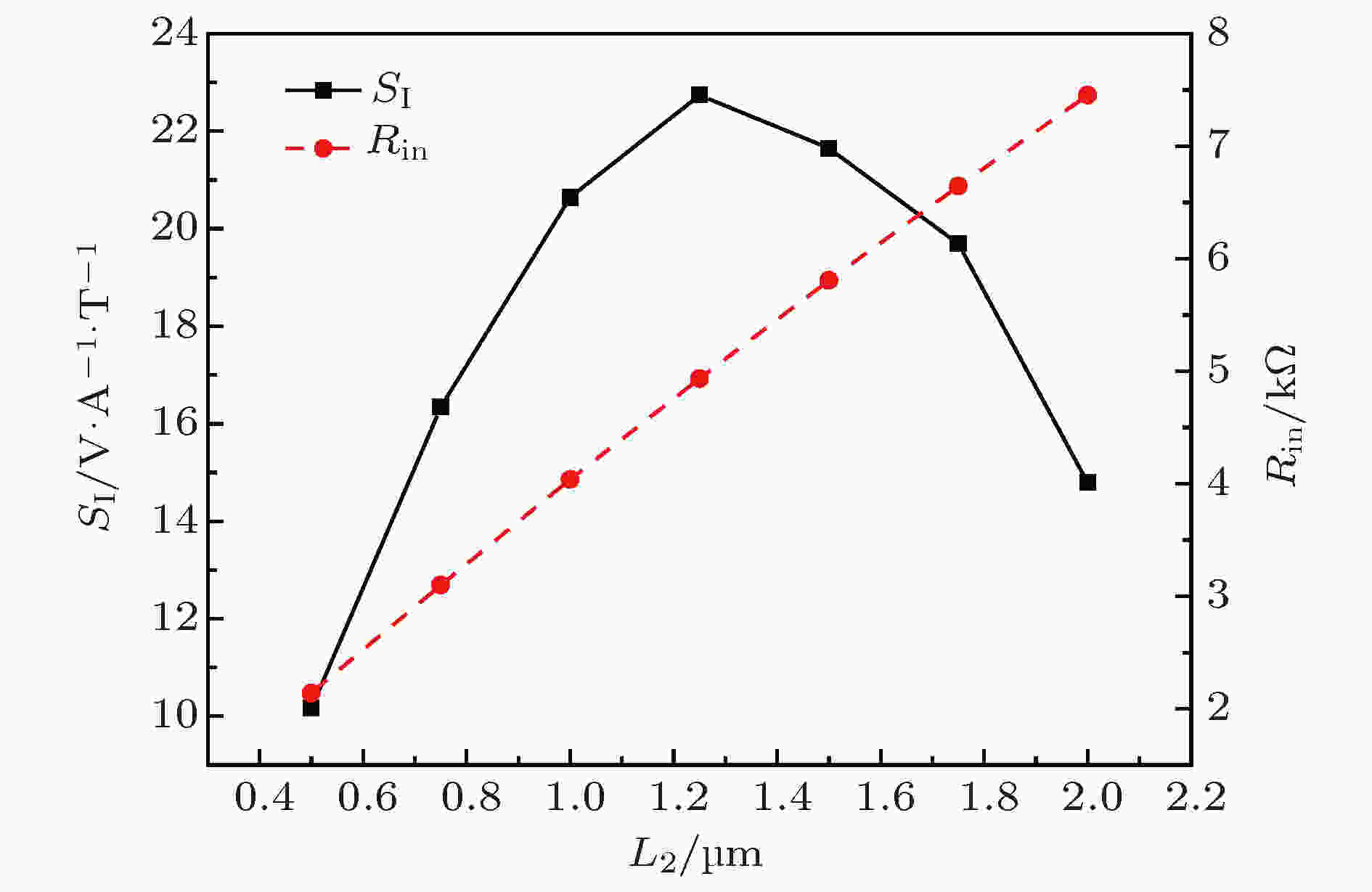图 7 电流相关敏感度S_I(或输入电阻R_in)与感测电极长度l₂的关系
Figure7. Current-related sensitivity and input resistance as a function of the l₂.

接下来进一步优化霍尔传感器台面宽度w, 仿真中w值分别设置为2, 4, 6, 8, 10 μm. 器件的其他参数如下: 主电极间距L₁ = 4.05 μm, 感测电极与主电极间距L₂ = 2 μm, 感测电极长度l₂ = 1.25 μm. 仿真结果如图8所示, 随着器件台面宽度的缩减, 电流敏感度和输入电阻逐渐上升, 其变化规律符合(2)式. 器件的霍尔电压V_H及电流相关敏感度S_I与器件的宽度w成反比关系, 即w越大, 器件的霍尔电压及电流相关敏感度均降低. 因此理论上器件宽度w应当减小^[21], 但是电流敏感度的提高将以牺牲器件输入电阻为代价. 此外, 考虑实验室中利用常规光刻技术制作传感器, 线宽越小曝光和剥离过程难度越大, 成品率更低, 因此在实际器件设计中应当折衷考虑, 同时结合电路匹配情况进行选择.
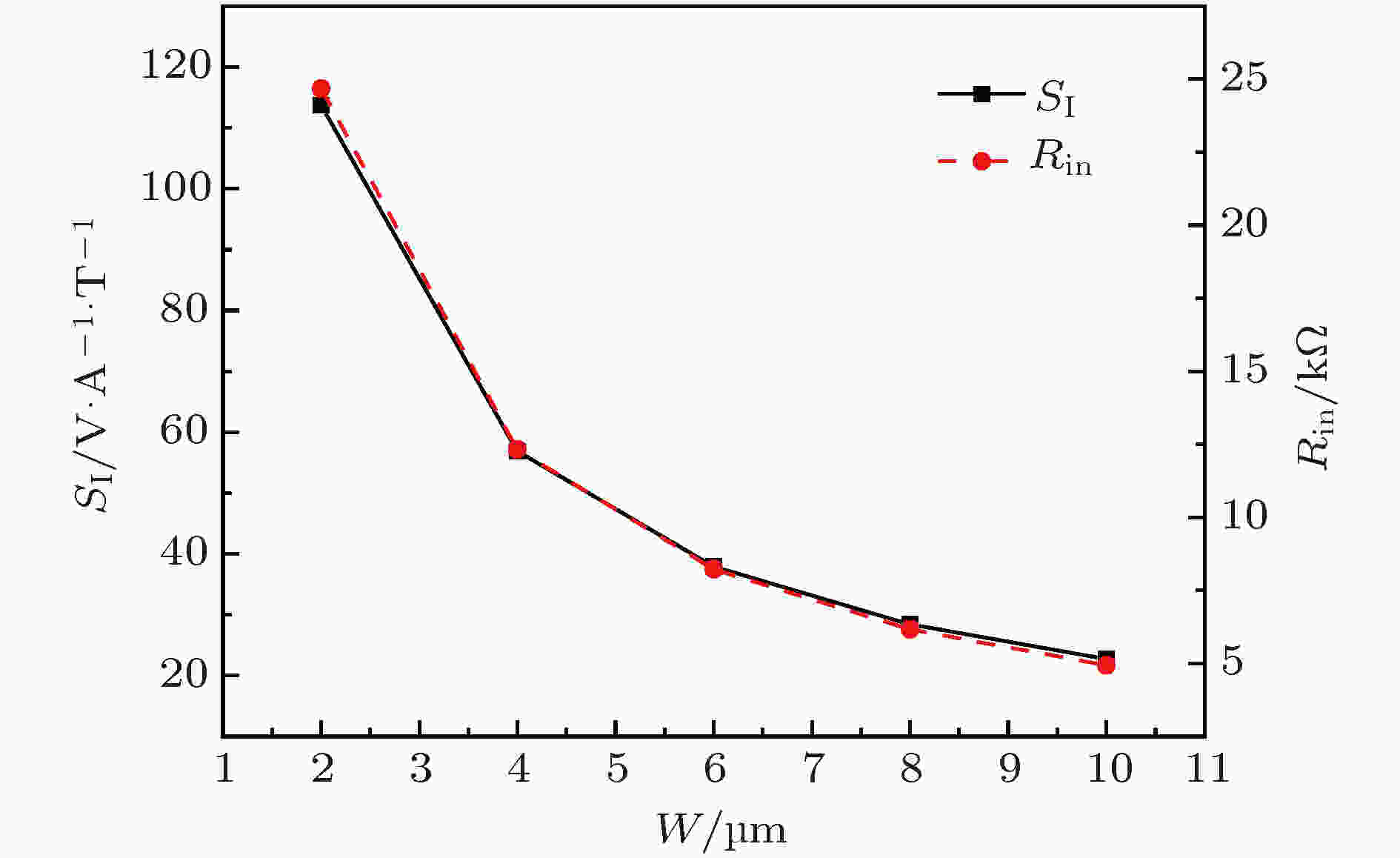图 8 电流相关敏感度(或输入电阻)与器件宽度w的关系
Figure8. Current-related sensitivity and input resistance as a function of the w.

图9展示了不同工作温度下, GaN材料垂直型霍尔传感器的霍尔电压随外加磁场强度的变化关系. 仿真中, 选取主电极间距L₁ = 4.05 μm、感测电极的长度l₂ = 1.25 μm、感测电极与中心主电极的距离L₂ = 2 μm以及器件的宽度w = 3 μm. 传感器工作中激励电流选取为0.3 mA, 外加磁场强度变化范围为–0.5 T ≤ B ≤ 0.5 T, 温度变化范围为300—525 K. 从图9可以看出, 无论正反磁场条件下或者不同环境温度下, 输出霍尔电压与磁场大小均呈现良好的线性关系. 进一步利用(2)和(3)式可以计算得到电流相关敏感度和温漂系数. 图10展示了传感器敏感度随工作温度的变化关系, 其中虚线由线性回归拟合得到, 图中列出了利用该线性关系计算得到的温漂系数. 从仿真结果可知, 室温下(T = 300 K)器件的电流敏感度为75.7 V/(A·T), 在300—375 K温度范围内器件的温度漂移系数为637.4 ppm/K, 在375—525 K温度范围内器件的温度漂移系数为–613.0 ppm/K, 图10电流敏感度变化趋势反映真实传感器工作过程中的物理规律^[32]. 其原因是, 材料迁移率主要受电离杂质散射和晶格散射这两种机制的影响. 当传感器处于相对较低工作温度时, 载流子迁移率主要受电离杂质散射影响, 随着温度上升, 该散射影响减弱, 因此电流敏感度增加; 而当传感器处于高温工作情况时, 载流子迁移率主要受晶格振动散射影响, 以声学散射为主且晶格散射随着温度的升高而增强, 因此电流敏感度开始下降. 但本文宽带隙GaN材料霍尔传感器相对其他窄带隙材料, 晶格散射对其敏感度影响明显更小.
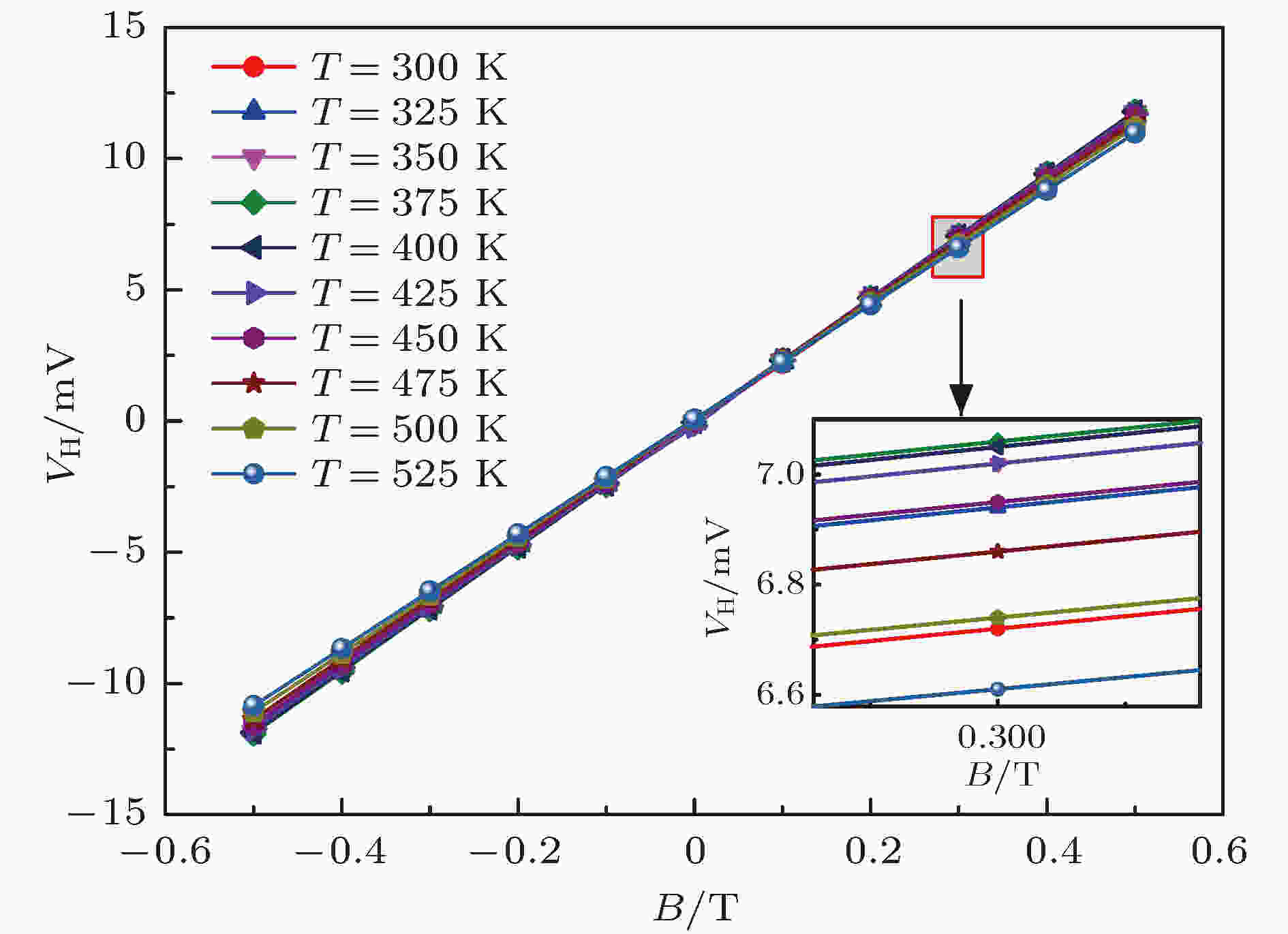图 9 器件输出电压随磁场和工作温度的变化
Figure9. Temperature dependence of output Hall voltage as a function of magnetic induction.

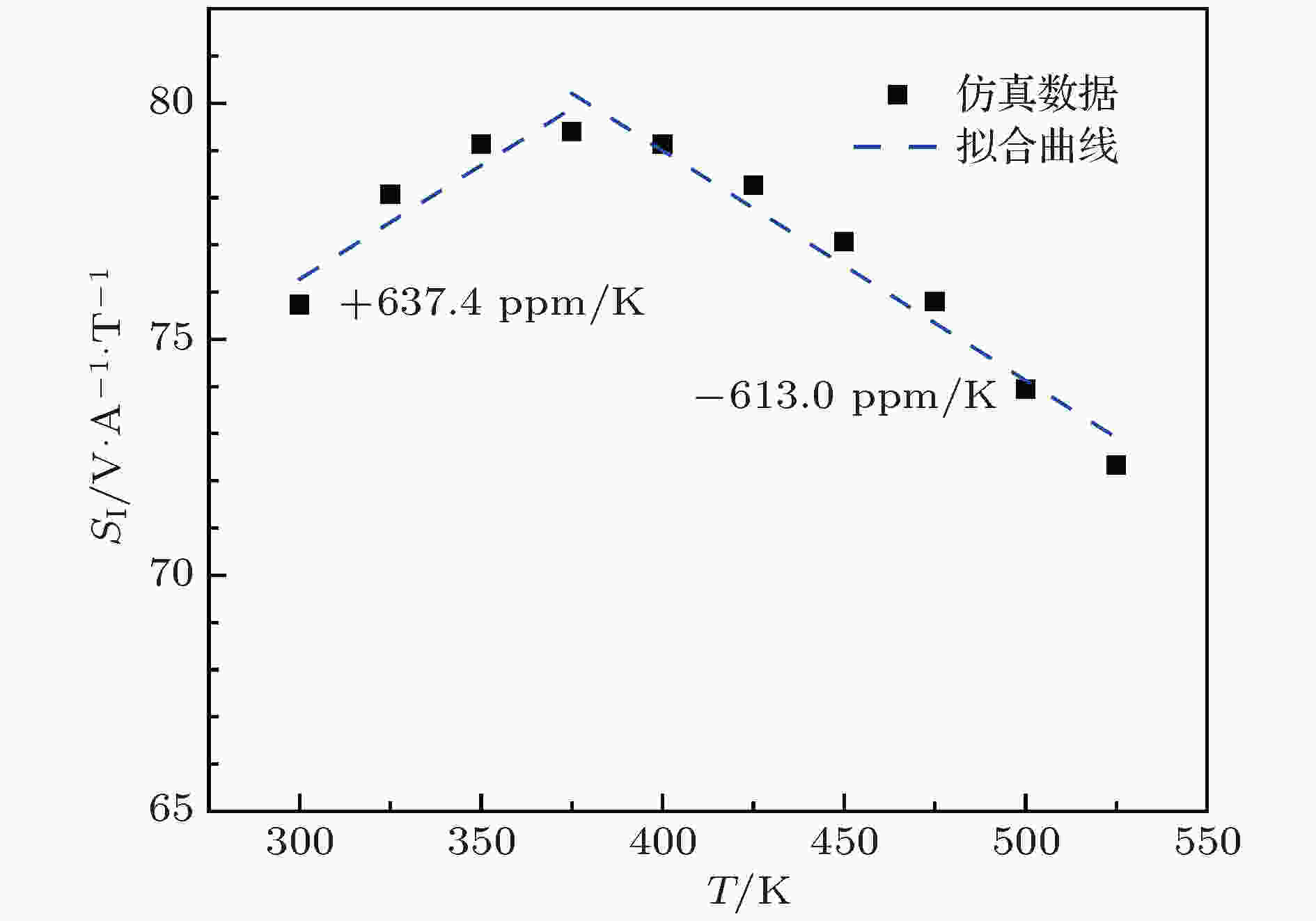图 10 电流相关敏感度随工作温度的变化
Figure10. Current-related sensitivity as a function of temperature.

本文工作与目前具有代表性的、能代表目前霍尔传感器发展水平的器件类型进行对比, 表2列出了不同材料和结构类型的半导体霍尔传感器关键性能指标对比结果^[7,19,33,34]. 从表2可以看出, 传统Si基窄禁带半导体霍尔传感器受制于载流子迁移率较低的影响, 其电流相关灵敏度一般较小. 而由于材料禁带宽度小, 其器件温漂系数都在1000 ppm/K以上, 且一般只能工作在室温环境. InAs材料为主的窄禁带半导体虽然电流相关灵敏度较大, 但其温漂系数同样很大, 工作温度往往小于400 K或者只能在特定低温条件下工作. 而现有报道的GaN基霍尔传感器能工作在大于400 K的高温环境, 但其主要是水平型, 垂直型结构由于设计和研制工艺难度都较大, 目前其实验数据或者仿真结果都还未见报道. 即使是水平型器件, 其感测磁场的电流敏感度实验数据还普遍较低. 与上述这些器件相比, 本文所设计的GaN基霍尔传感器为垂直型结构, 填补了宽禁带材料垂直型器件研究的空白, 为实现同一芯片三维磁场探测奠定了理论和技术支持. 所设计的传感器能稳定工作在大于500 K的高温环境, 经过器件结构仿真优化后, 得了较大的磁场感测灵敏度和较低的温漂系数, 因此该类型器件将具有良好的工作稳定性和可靠性.

器件类别	工作温度/K	温漂系数ST/ppm·K–1	灵敏度SI/V·(A·T)–1
Si基垂直型[33]	T < 350	$\sim $1000	41 (x方向)
Si基垂直型[34]	T < 350	4545	77.5 (x方向)
Si基垂直型[35]	T < 350	1500	N/A
InAs/AlGaSb水平型[7]	T < 400	1710	250
InAs/AlGaSb水平型[7]	T < RT	2690	302
AlGaN/GaN水平型[19]	T > 400	$\sim $1000	113
AlGaN/GaN水平型[36]	T > 400	820	46
AlGaN/GaN垂直型(本文)	T > 500	$\sim $600	75.7 (w = 3 μm)
			113.7 (w = 2 μm)

表2基于不同材料的霍尔传感器关键性能指标对比
Table2.Comparisons of key performances of Hall sensors based on various materials.

本文提出了一种基于宽禁带半导体AlGaN/GaN异质结材料的垂直型霍尔传感器, 通过减薄感测电极下方势垒层厚度来降低纵向电子束缚电场, 仿真工作表明器件的磁场探测敏感度得到明显提高. 本文对器件的关键几何参数进行了优化, 器件优化结构如下: 势垒层厚度d = 7 nm、电极间距比值L₂/L₁ = 0.49、感测电极长度l₂ = 1.25 μm及台面宽度w = 3 μm. 基于该结构获得的器件电流敏感度为75.7 V/(A·T), 在300—375 K和375—525 K两个工作温度范围内器件的温漂系数分别为637.4和–613.0 ppm/K, 器件能工作在温度大于500 K的高温环境. 本文率先提出对GaN材料垂直型霍尔传感器进行设计研究, 为进一步实现同一芯片三维磁场探测技术奠定了理论基础, 下一步可以将垂直型和现有水平型霍尔传感器在同一块芯片材料上进行同步制作, 获得高集成度、轻量化、更高磁场探测敏感度的高温三维霍尔传感器.