摘要:基于磁流体动力学, 本文通过数值模拟对不同磁场构型下轻质气柱界面Richtmyer-Meshkov不稳定性的演化过程进行了研究. 结果显示: 磁场对波系演化影响甚微, 但能抑制界面不稳定性发展, 且横向磁场抑制效果更好. 无磁场时, 界面形成涡串, SF₆射流穿过下游界面; 有磁场时, 界面光滑无涡串. 其中, 横向磁场下界面更光滑, SF₆射流不再穿过界面. 此外, 由于Richtmyer-Meshkov不稳定性的作用, 磁力线在气柱界面发生扭曲, 且上游界面处磁力线扭曲程度更大, 产生强洛伦兹力, 使涡量分层明显; 下游界面处, 纵向磁场产生的洛伦兹力较横向磁场更小, 涡层之间相互干扰. 最后, 本文将动态模态分解用于界面不稳定性研究, 发现: 磁场作用下界面仍存在小涡, 且纵向磁场下扰动更多. 第一模态的稳定涡结构能反映主要流场信息, 第二到第四模态下的小涡频率依次增加, 且无磁场、纵向和横向磁场的同一模态下, 小涡频率依次减小. 因而磁场能抑制小涡频率, 且横向磁场抑制效果更好.
关键词: Richtmyer-Meshkov不稳定性/
磁流体动力学/
动态模态分解/
轻质气柱

English Abstract

全文HTML

--> --> -->

激波经过流体分界面, 诱导界面微弱扰动从线性发展为非线性的现象被称为Richmyer-Meshkov (R-M) 不稳定性^{[1, 2]}. 界面两侧在R-M不稳定性的作用下产生剪切速度差, 诱导Kelvin-Helmholtz (K-H) 不稳定性出现. 在超燃冲压发动、惯性约束核聚变、天体物理、航空航天等领域, R-M和K-H不稳定性作用于流体分界面, 诱导界面卷起失稳并最终湍流转捩. 其中, 在超燃冲压发动机中, R-M不稳定性能促进燃料充分燃烧; 而在惯性约束核聚变中, 外壳燃料形成的等离子体会受到R-M和K-H不稳定性的作用, 进而阻碍聚变反应的产生^[3]. 且这些领域中流体会被电离, 受到磁场的影响. 基于此, 本文对磁流体动力学(magnetohydrodynamic, MHD)中R-M不稳定性的发展进行研究.
人们已经对无磁场情况下界面R-M不稳定性进行了大量的实验研究、理论分析和数值模拟. Haas和Sturtevant^[4]用塑料薄膜形成气泡, 采用阴影摄像技术对气泡变形进行过程捕捉, 发现入射激波经过轻质(重质)气泡后发散(聚焦). 但因实验技术的限制, 他们的实验不能得到较好的定量分析结果, 且塑料薄膜形成的气泡会对实验结果有影响. Layes等^[5,6]采用多重曝光阴影技术, 对不同激波强度下不同介质 (He, N₂, Kr) 球形气柱变形过程进行了研究, 并定量分析了界面运动, 结果表明气柱界面运动速度在发展后期基本保持不变. 同样因实验技术所限, 他们的实验结果并不能清晰地反映复杂波系演化过程. Picone和Boris^[7]利用数值算法对激波冲击气柱导致其变形的过程进行了更加完整细致的研究. 近年来, Zhai等^[8]和Luo等^[9]采用肥皂泡膜技术直接形成气泡, 排除了塑料薄膜对实验结果的影响. 结合高速摄像技术, 他们对激波与各种形状(三角形、四边形、菱形)气柱相互作用的复杂过程进行了大量的实验研究, 分析了波系演化过程及相界面失稳机理, 并对界面运动和波系发展进行了定量分析. 沙莎等^{[10, 11]}对R22气柱和三维SF₆气泡进行的数值研究表明, 复杂波系在气柱内部聚焦并诱导射流. Ding等^[12]成功设计了二维气柱界面不稳定性研究实验, 对二维轻质气柱界面失稳机理、波系演化过程进行了定性和定量研究, 发现二维和三维界面不稳定发展的区别较大.
此外, R-M不稳定性多存在于高能物理和天体物理中. 流体在这些领域中多以等离子体状态存在, 易受磁场的影响.通过数值算法求解理想MHD方程组, Samtaney^[13]和Wheatley等^[14]研究了斜平面连续间断面(oblique planar contact discontinuity)R-M不稳定性. 在他们的研究中, 平面激波自轻质流体进入重质流体, 磁场方向垂直于波阵面, 即纵向磁场构型. 研究表明, 通过干扰激波在接触间断面(contact discontinuity)上的折射过程, 在磁场的作用下, 折射激波出现分支, 产生慢磁声波和中强度磁声波 (slow and intermedia magnetosonic shocks), 因此涡量沿着Afvén波分布, 而不再沉积于界面, 最终磁场抑制了界面不稳定性的发展. 同时, Wheatley等^[15]基于理想不可压MHD, 对纵向磁场构型下, 正弦扰动界面增长进行了理论推导. 他们发现在线性发展阶段, 界面扰动不受磁场影响, 但是在界面扰动发展后期, 磁场抑制界面不稳定性发展. 同样通过理论推导, Cao等^[16]的研究表明, 剪切效应加速界面失稳, 磁效应抑制R-M 不稳定性的发展, 其中洛伦兹力是磁效应抑制R-M不稳定的主要机理. 但Wheatley等^[15]和Cao等^[16]的单模扰动界面形状过于简单, 在工程和实际研究中气柱界面更复杂, 且多形成封闭气柱. 董国丹等^[17]对纵向磁场作用下封闭三角形气柱R-M不稳定性进行了研究, 发现在纵向磁场作用下, 界面不稳定小涡序列消失, 不稳定性得到抑制. 此研究虽然考虑了封闭气柱, 但三角形气柱界面与入射激波作用过程中入射激波角不变, 波系演化过程相对简单. 而入射激波冲击封闭圆形气柱的过程中入射激波角不断变化, 流场信息更加复杂且更具代表性. 再者, 为优化磁控效果, 不同磁场构型下气柱界面不稳定性的机理研究十分必要. Sano等^[18,19]发现R-M不稳定性会放大磁场, 且放大后的磁场能抑制R-M不稳定性的发展.
动态模态分解(dynamic mode decomposition, DMD)技术能从复杂的流体现象分解出具有代表性的时空特征拟序结构(coherent structure), 因而在对复杂流体现象分析、预测、控制等方面具有十分重要的作用^[20]. Schmid等^[21,22]详细介绍了DMD算法, 证明其在多维数据处理方面有巨大的应用前景, 并首次将DMD用于方腔流和射流的研究. 此外, DMD还可用于分析非线性系统^[23]. Rowley等^[24]证明了DMD与Koopman算子关系密切, 并基于DMD对三维非线性复杂射流现象进行了研究. 近年来DMD技术不断发展, 并被用于对复杂流体现象的分析. 本文将DMD用于界面不稳定性的研究.
实验中要生成稳定的轻质气柱相对困难, 且国内外关于磁场作用下R-M不稳定性的实验研究仍未成功, 因此, 通过数值模拟研究磁场对界面不稳定性的作用具有重要的意义. 此外, 数值模拟求解MHD方程组时, 分裂格式算法不能保证每一步计算中磁场的散度都为零, 因此需要更高阶的通量重构算法和非分裂多维积分算子^[17]. 本文采用分段抛物线法(piecewise parabolic method)对守恒量进行三阶重构, 以得到具有二阶精度的Godunov通量^[25]. 另外, 为了保证磁场散度为零, 采用CTU+CT(corner transport upwind + constrain transport)算子进行多维积分^[26-28]. 本文基于理想MHD, 结合DMD技术对无磁场、横向和纵向磁场构型下, 激波冲击封闭轻质圆形气柱(97%N₂+3% SF₆)的过程进行研究, 分析讨论磁场构型对界面不稳定性的作用, 为实验研究和实际应用提供参考.

不考虑欧姆耗散、热传导、霍尔效应及双极扩散效应, 即基于理想MHD方程组, 本文对磁场作用下轻质圆形气柱的界面不稳定性发展进行研究. 守恒形式的理想MHD方程组如下:

$\dfrac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {{v}}) = 0,$

$\dfrac{{\partial \rho {{v}}}}{{\partial t}} + \nabla \cdot \left(\rho {{vv}} - \frac{{{{BB}}}}{{{\mu _0}}}\right) + \nabla \left(P + \frac{{{{B}} \cdot {{B}}}}{{2{\mu _0}}}\right) = {\bf{0}},$

$\dfrac{{\partial E}}{{\partial t}} + \nabla \cdot \left(\left(E + P + \frac{{{{B}} \cdot {{B}}}}{{2{\mu _0}}}\right)v - \frac{{{{B}}\left({ {{B}}} \times {{v}}\right)}}{{{\mu _0}}}\right) = 0,$

$\dfrac{{\partial {{B}}}}{{\partial t}} = \nabla \times ({{v}} \times {{B}}),$

${{E}} = \frac{{{P}}}{{({\rm{\gamma }} - 1)}} + \frac{{\rho ({{v}} \cdot {{v}})}}{2} + \frac{{{{B}} \cdot {{B}}}}{2},$

其中ρ为密度, $ v $ 为速度, B为磁感应强度, P为压强, E为总能, γ为比热比, μ₀为磁导率.
计算模型如图1所示, 计算域为200 mm × 80 mm, 上下及右边界均为固壁. 初始时刻, 平面入射激波IS自左边界向右运动, 撞击轻质气柱(97%N₂+3% SF₆). 磁场强度均为0.01 T, B₁为纵向磁场构型, 即磁场方向沿着x轴; B₂为横向磁场构型, 即沿着y轴. 气柱直径初始D₀ = 35 mm, 其中心距左边界30 mm, 外流场充满SF₆气体, 来流马赫数Ma = 1.29, 气柱内外温度T₀ = 293.15 K, 气柱内外压强P = 1 atm (1 atm = 101325 Pa), 在求解理想MHD方程组时, 各气体的磁导率均取真空磁导率$\mu_{0}=4 {\text{π}} \times 10^{-7} \mathrm{N} \cdot \mathrm{A}^{-2}$. 其他气体参数如表1所示.
图 1 计算模型图
Figure1. Computational model

气体	密度ρ/(kg·m–3)	比热比γ	当地音速a/(m·s–1)	相对分子质量/(g·mol–1)
SF6	6.06	1. 09	134.89	146.00
97%N2+3% SF6	1.31	1.36	324.71	31.54

表1气体参数表
Table1.Gas parameters

2

-->

3.1.网格无关性和算例验证

图2(a)—(c)为不同网格数下密度纹影图, 图2(d)为不同网格数下沿图中蓝色虚线的密度比. 由图2可知, 随着网格数的增加, 本文数值结果能清晰地反映复杂波系和界面次级涡, 且计算结果逐渐收敛. 因此本文选取 2000 × 800的网格数进行计算.
图 2 网格无关性验证　(a) 500 × 200; (b) 1000 × 400; (c) 2000 × 800; (d) 密度界面网格收敛性验证. ρ/ρ₁为沿气柱对称轴密度比, 其中ρ是流体密度, ρ₁是SF₆气体密度; CRS: 弧形反射激波; LI: 气柱左边界; TS₁: 透射激波; RI: 气柱右边界
Figure2. Grid convergence validation: (a) 500 × 200; (b) 1000 × 400; (c) 2000 × 800; (d) convergence of density profile. ρ/ρ₁ is the ratio of fluid density to SF₆ density. CRS: curved reflected shock; LI: cylinder’s left interface; TS1: transmitted shock; RI: cylinder’s right interface.

图3为激波与轻质气柱相互作用过程中实验^[12](上)与本文数值(下)结果的对比. 由图3可见, 本文算法能准确地反映波系的演化过程、界面和不稳定涡序列的发展. 且界面发展后期, 马赫杆处的滑移线SL(同图4(e))仍清晰可见.
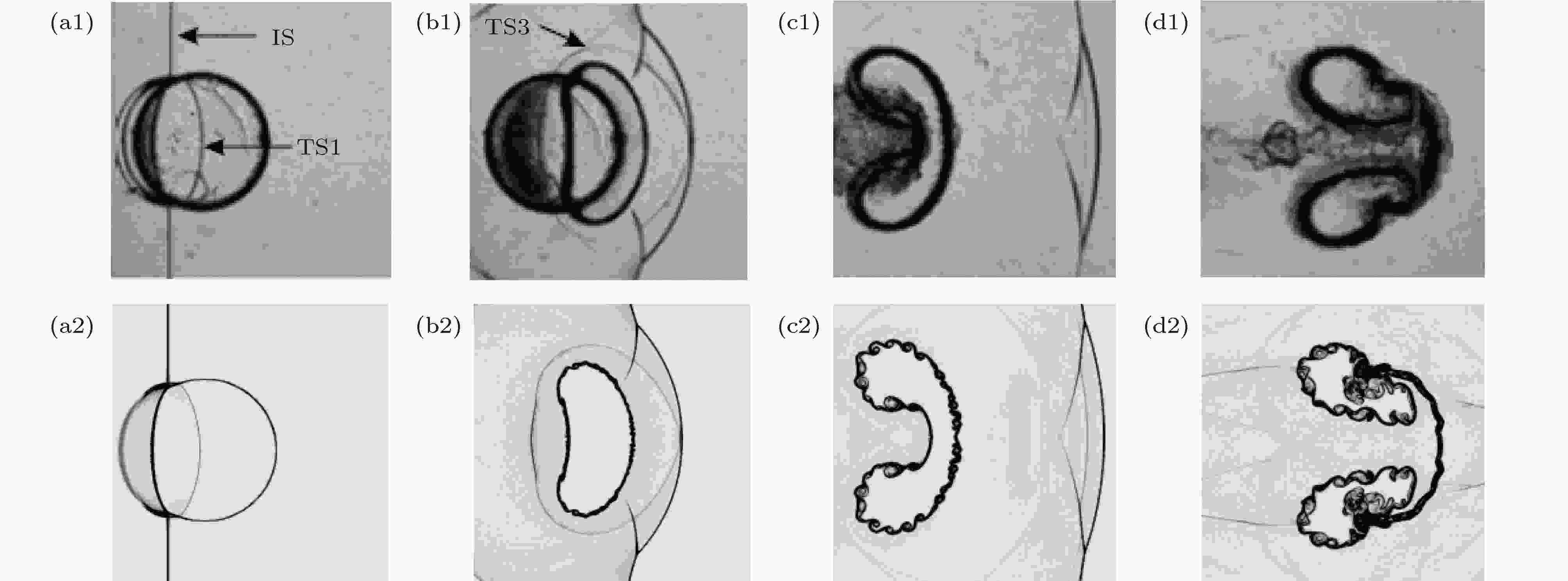图 3 激波与N₂气柱相互作用过程实验^[12](上)与本文数值(下)密度纹影图的对比(IS: 入射激波; TS₁: 透射激波; TS₃: 三次透射激波)　(a1) t = 120 μs; (a2) t = 120 μs; (b1)t = 280 μs; (b2) t = 280 μs; (c1) t = 580 μs; (c2) t = 580 μs; (d1) t = 1100 μs; (d2) t = 1100 μs
Figure3. The comparison of experimental and numerical density schlieren images during the interaction between the incident shock wave and the N₂ cylinder (IS: incident shock; TS₁: transmitted shock; TS₃: third transmitted shock): (a1) t = 120 μs; (a2) t = 120 μs; (b1)t = 280 μs; (b2) t = 280 μs; (c1) t = 580 μs; (c2) t = 580 μs; (d1) t = 1100 μs; (d2) t = 1100 μs.

图 4 无磁场时激波与N₂气柱作用过程中的密度纹影图(IS: 入射激波; TS1: 透射激波; CRS: 弧形反射激波; RRW: 反射稀疏波; FPS: 自由前导激波; TS2: 二次透射激波; RS1:反射激波; MS: 马赫杆; TP: 三波点; FP: 聚焦点; S1: 激波1; RAS: 折射激波; TS3: 三次透射激波; RS2: 二次反射激波; TS4: 四次透射激波; URS:上壁面反射激波; LRS:下壁面反射激波; BRS: 尾壁反射激波; SL: 滑移线)　(a) t = 160 μs; (b) t = 180 μs; (c) t = 210 μs; (d) t = 240 μs; (e) t = 290 μs; (f) t = 330 μs; (g) t = 430 μs; (h) t = 700 μs; (i) t = 1200 μs; (j) t = 1650 μs
Figure4. The density schlieren image sequences during the interaction between the incident shock and N₂ cylinder in the absence of magnetic fields(IS: incident shock; TS₁: transmitted shock; CRS: curved reflected shock; RRW: reflected rarefaction shock; FPS: free precursor shock; TS₂: second transmitted shock; RS₁: reflected shock; MS: Mach stem; TP: triple point; FP: focus point; S₁: shock 1; RAS: refracted shock; TS₃: third transmitted shock; RS₂: second reflected shock; TS₄: fourth transmitted shock; URS: upper wall reflected shock; LRS: lower wall reflected shock; BRS: back wall reflected shock; SL: slip line): (a) t = 160 μs; (b) t = 180 μs; (c) t = 210 μs; (d) t = 240 μs; (e) t = 290 μs; (f) t = 330 μs; (g) t = 430 μs; (h) t = 700 μs; (i) t = 1200 μs; (j) t = 1650 μs.

2 -->

3.2.无磁场时激波与气柱的相互作用

图4是无磁场时, 激波与轻质气柱(97%N₂+3% SF₆)相互作用过程的密度纹影图. 入射激波IS经过轻质界面, 在气柱内产生向下游传播的透射激波TS₁, 在气柱外产生向上游传播的膨胀波RRW和弧形反射激波CRS, 形成第一个透射-反射激波结构(TS₁ - CRS); 同时由于轻质气柱声阻抗小, TS₁向气柱外折射出自由前导激波FPS, 如图4(a)所示. 紧接着IS与FPS发生马赫反射, 形成马赫杆MS和三波点TP, 且发展后期马赫杆处的滑移线SL(图4(e))仍可见. 当TS₁运动到下游界面时, 其向气柱内外分别传播出二次透射激波TS₂和反射激波RS₁, 形成第二个透射-反射激波结构(TS₂-RS₁), 此时TS₂与FPS合并(图4(b)). 随着RS₁向上游传播, 其于t = 210 μs在FP点聚焦(图4(c)), 聚焦点压力随后迅速向外膨胀, 产生激波S₁, S₁向下游界面折射出激波RAS, 此时界面在复杂波系的作用下开始出现微弱扰动. 当S₁运动到上游界面(图4(e))时, 第三个透射-反射激波结构(TS₃-RS₂)形成, SF₆射流(SF₆ Jet)开始出现, 界面扰动增加.
t = 330 μs时(图4(f)), RS₂穿过下游界面产生4次透射激波TS₄, 同时来自上下壁面的反射激波URS、LRS向气柱中心运动, 界面扰动剧烈并逐渐开始卷起失稳, 如图4(f)所示. URS和LRS于t = 430 μs再次冲击气柱, 加速界面失稳, SF₆射流两侧开始卷起. 随后气柱界面不断卷起形成一系列小涡不稳定序列, SF₆射流两侧形成两对主涡, 如图4(i)所示. t = 1200 μs时, SF₆射流穿过下游界面, 其两侧的两对主涡不断发展加速气柱内外气体混合, 气柱发展成为双耳形. 在来自尾壁的反射激波BRS冲击气柱, 大量不稳定涡串出现, 气柱湍流混合剧烈, 如图4(j)所示.
2 -->

3.3.磁场作用下激波与气柱的相互作用

图5为纵向(上)和横向磁场(下)构型下, 激波与气柱相互作用过程中的密度纹影图. 由图5可知, 激波与界面相互作用时复杂波系的演化过程与无磁场时(图4)一样, 即多次透射-反射结构、马赫反射、壁面反射等复杂波系结构仍出现, 且出现时间一致. 这表明磁场对R-M不稳定性发展过程中复杂波系的演化没有太大的影响. 此外在两种磁场作用下, 界面不稳定小涡序列均明显减少, SF₆射流上下两侧的涡对消失, 气柱界面变得光滑. 但在纵向磁场构型下, 下游界面中心处从290 μs开始出现少许扰动(图4(a1)), 该扰动不断增长并在430 μs形成明显的扰动序列(图4(a4)). 且后期气柱内部因SF₆射流仍能穿过下游界面而出现少许扰动, 发展后期界面仍呈双耳形. 横向磁场构型下, SF₆射流不能穿过下游界面, 界面十分光滑, 小涡序列完全消失, 后期气柱不再呈双耳形. 由以上分析可知, 两种磁场构型均能抑制界面不稳定性的发展, 且横向磁场抑制效果更好.
图 5 纵向B1(上)和横向B2(下)磁场构型下, 激波与N₂气柱相互作用过程的密度纹影图　(a1)t = 290 μs; (b1) t = 290 μs; (a2) t = 330 μs; (b2) t = 330 μs; (a3) t = 430 μs;(b3) t = 430 μs; (a4)t = 700 μs; (b4) t = 700 μs; (a5)t = 1200 μs; (b5) t = 1200 μs
Figure5. The density schlieren image sequences during the interaction between the incident shock and N₂ cylinder in the presence of the longitudinal B1 (upper) and transverse B2 (lower) magnetic fields: (a1)t = 290 μs; (b1) t = 290 μs; (a2) t = 330 μs; (b2) t = 330 μs; (a3) t = 430 μs; (b3) t = 430 μs; (a4)t = 700 μs; (b4) t = 700 μs; (a5)t = 1200 μs; (b5) t = 1200 μs.

2 -->

3.4.磁场对界面涡量及特征尺寸的作用

流场在激波扰动下产生速度, 图6(a1)、(a2)中红色实线表示流线, 蓝色实线表示磁力线. 沿同一水平线段A, 洛伦兹力x和y方向分量F_x和F_y的具体数值如图6(d1)、(d2)所示. 纵向磁场构型下(图6第一行), 磁力线与流线夹角小; 而横向磁场构型下(图6第二行), 磁感线与流线几乎垂直. 在R-M不稳定性的作用下, 两种磁场构型的磁力线在气柱界面均发生扭曲, 且上游界面处磁场线扭曲程度更大(图6(a1)、(a2)). 磁力线扭曲程度较大的上游界面能产生更强的洛伦兹力. 此外, 纵向磁场作用下, 下游界面内(外)F_x和F_y反对称分布, 即界面内(外)F_x为负(正), F_y为正(负); 而横向磁场作用下, 下游界面内(外)F_x和F_y对称分布, 即界面内(外)为F_x为负(正), F_y也为负(正). 其中, 下游界面处, 横向磁场产生的洛伦兹力各个分量均大于纵向磁场.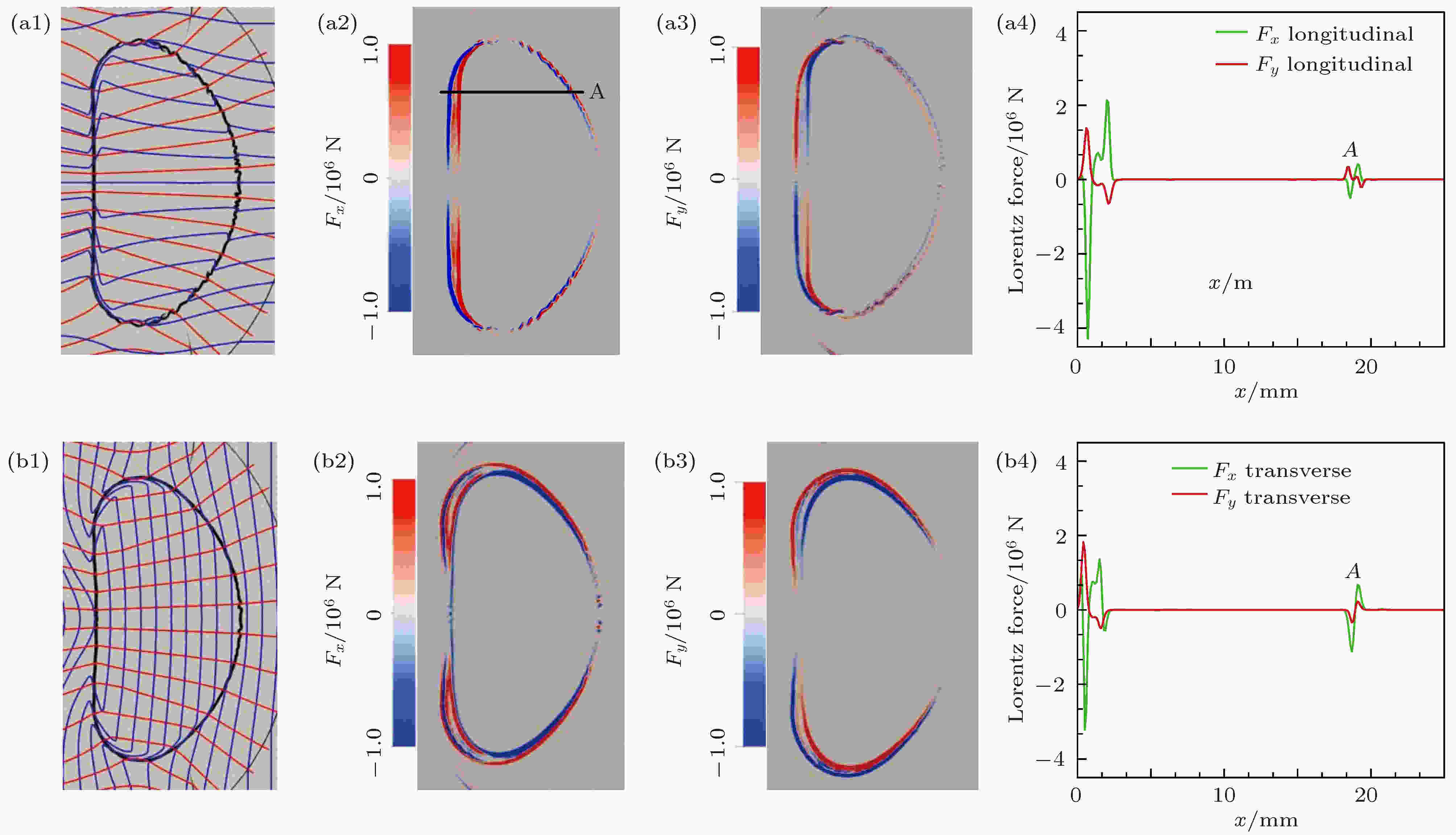
图 6 t = 200 μs时, 纵向和横向磁场构型的结果　(a1)纵向磁场的磁力线(蓝色)与流线(红色)图, 其中背景为密度纹影图; (b1)横向磁场的磁力线(蓝色)与流线(红色)图, 其中背景为密度纹影图; (a2)纵向磁场x方向的洛伦兹力F_x分布云图; (b2)横向磁场x方向的洛伦兹力F_x分布云图; (a3)纵向磁场y方向洛伦兹力F_y分布云图; (b3)横向磁场y方向洛伦兹力F_y分布云图; (a4)纵向磁场沿线段A(图(a2)中黑色线段所示)x和y方向洛伦兹力定量图; (b4)横向磁场沿线段A(图(a2)中黑色线段所示)x和y方向洛伦兹力定量图. 其中线段A两端点分别为 (0, 0.01), (0.025, 0.01)
Figure6. Results from longitudinal and transverse magnetic fields at t = 200 μs: (a1)longitudinal magnetic field lines (blue) and streamlines (red), the background are density schlieren images;(b1) transverse magnetic field lines (blue) and streamlines (red), the background are density schlieren images;(a2)Lorentz forces distribution of longitudinal magnetic field in x direction, F_x;(b2)Lorentz forces distribution of transverse magnetic field in x direction, F_x;(a3)Lorentz forces distribution of longitudinal magnetic field in y direction, F_y;(b3)Lorentz forces distribution of transverse magnetic field in y direction, F_y;(a4)the specific Lorentz forces distribution of longitudinal magnetic field along a horizontal line A, indicated by the black solid line in Fig. 6 (a2), and the two end points are (0, 0.01), (0.025, 0.01);(b4)the specific Lorentz forces distribution of transverse magnetic field along a horizontal line A, indicated by the black solid line in Fig. 6 (a2), and the two end points are (0, 0.01), (0.025, 0.01).

结合流场涡量分布云图(图7)可知, 两种磁场构型下, 上游界面磁力线因R-M不稳性的作用而发生严重扭曲, 从而产生较强的洛伦兹力, 在该洛伦兹力作用下, 涡量沿界面两侧分布, 且涡层相距甚远, 涡旋方向与无磁场时一致. 下游界面处, 磁力线扭曲程度小, 其中纵向磁场因洛伦兹力更小, 涡层距离较近, 涡层之间会相互干扰, 使得下游界面在磁场作用下仍存在扰动; 但横向磁场构型下, 初始磁场方向与流线垂直, 相对于纵向磁场, 能产生较大的洛伦兹力, 涡量分层较纵向磁场更为明显, 因此横向磁场对下游界面不稳定性的控制效果更好.
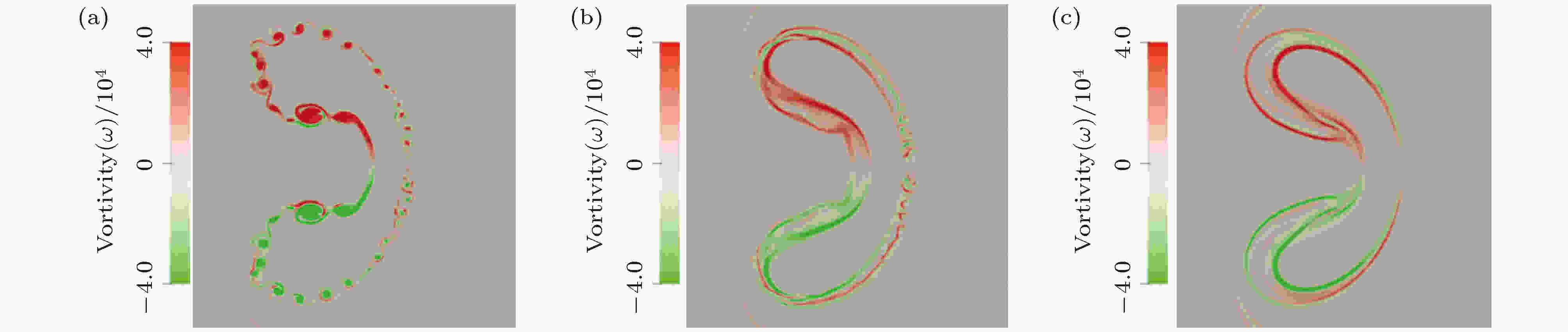图 7 t = 600 μs时界面涡量分布图　(a)无磁场, B = 0 T; (b)纵向磁场, B₁ = 0.01 T; (c)横向磁场, B₂ = 0.01 T
Figure7. The vorticity distribution in the vicinity of the density interface at t = 600 μs: (a) in the absence of magnetic fields, B = 0 T; (b) in the presence of longitudinal magnetic fields, B₁ = 0.01 T; (c)in the presence of transverse magnetic fields, B₂ = 0.01 T.

图8为无量纲后气柱特征尺度随时间的变化图. 以气柱受扰动前的直径D₀ = 35 mm无量纲化气柱长度和高度, 分别用L/D和H/D表示, 其中L为气柱界面特征长度, H为气柱界面高度; 无量纲时间τ = tW_S/D₀, 其中W_S是入射激波的速度; B₀ = 0 T、B₁= 0.01 T和B₂ = 0.01 T分别为无磁场、纵向磁场以及横向磁场构型. 如图8(a)所示, 无论有无磁场, 在激波冲击下, L迅速减小, 后期随着界面非线性扰动不断发展, L增加, 且三种情况下L到达最小值的时间一样, 因此磁场对波系演化的干扰比较小. 此外, 两种磁场构型均能控制L的增长, 且横向磁场构型控制效果更好; 图8(b)表明: H波动增加, 纵向磁场能在一定程度上控制H的增长, 但横向磁场反而加速了H的增长, 这与横向磁场能产生较大的洛伦兹力相关.
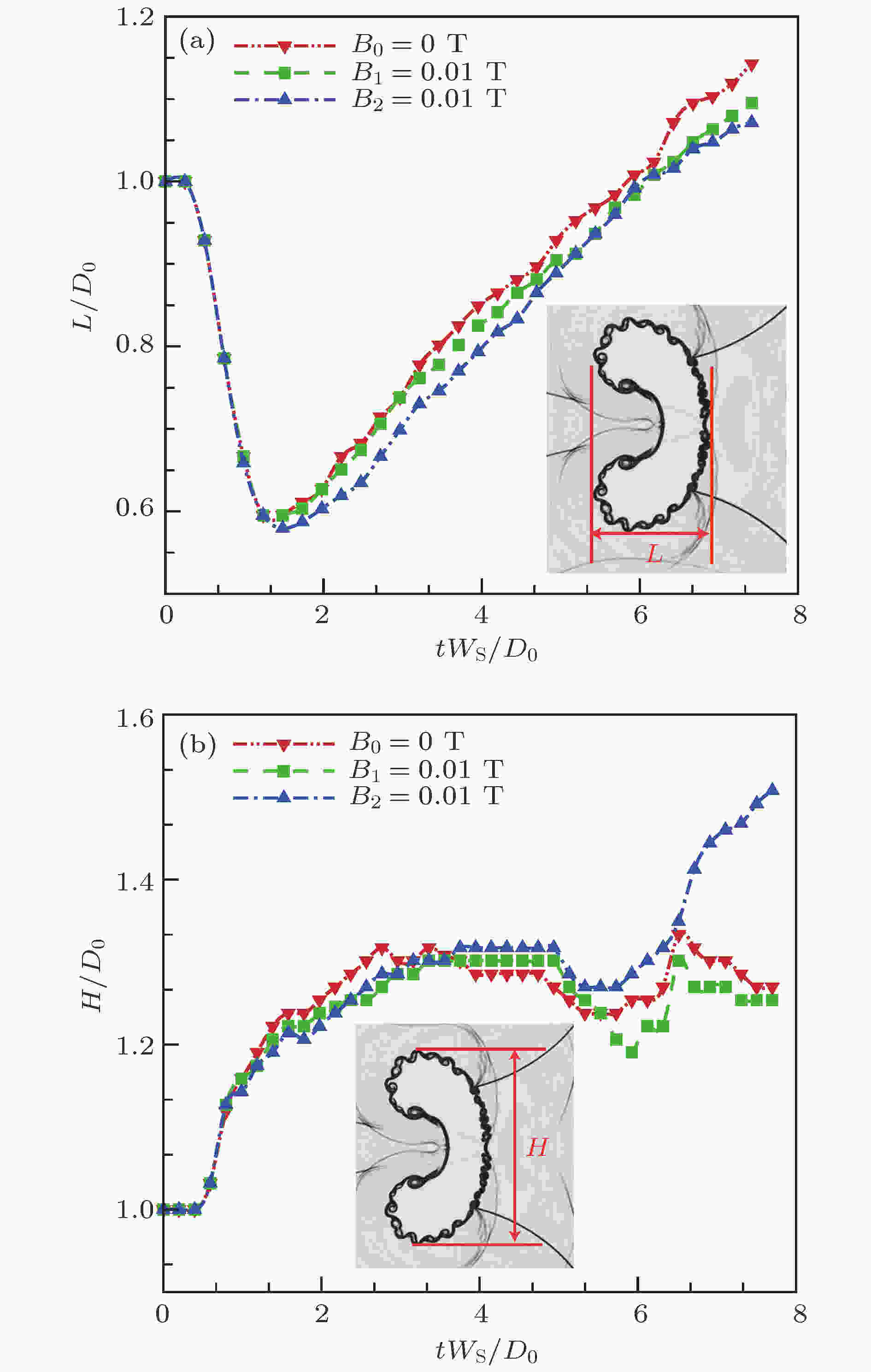图 8 界面特征尺寸随时间变化图　(a) 长度(L); (b)高度(H). D₀ = 35 mm; W_s: 入射激波速度; t: 时间
Figure8. The evolution of characteristic scales of the bubble: (a) L, length; (b) H, height. D₀ = 35 mm; W_s, the velocity of the incident shock wave; t, time.

2 -->

3.5.DMD

DMD能从复杂的流体现象中提取出具有代表性的时空拟序结构(coherent structures). 290 μs后复杂波系基本耗散, 我们取290—340 μs之间的50个涡量图进行DMD, 拟对后期流场不稳定性进行分析, 具体的DMD算法如下:
第一步, 对涡量数据${{\rm{x}}_k} \in {\mathbb{R}^n}$ ( k = 0, …, m = 50)进行重组(n为网格数). 得到涡量分布矩阵X及相应的时间转移矩阵(time-shifted matrix)${\bf{X}}'$:

${\bf{X}}\!=\!\left[\!\!\!{\begin{array}{*{20}{c}} |&|&{}&| \\ {{{\rm{x}}_0}}&{{{\rm{x}}_1}}&{...}&{{{\rm{x}}_{m{\rm{ - }}1}}} \\ |&|&{}&| \end{array}}\!\!\!\right], {\bf{X}}'\!=\!\left[\!\!\!{\begin{array}{*{20}{c}} |&|&{}&| \\ {{{\rm{x}}_1}}&{{{\rm{x}}_2}}&{...}&{{{\rm{x}}_m}} \\ |&|&{}&| \end{array}}\!\!\!\right].$

第二步, 为减少计算量, 对${\bf{X}} \in {\mathbb{R}^{n \times m}}$做r (r < m) 阶奇异值分解(singular value decomposition, SVD). 首先对X进行SVD, 分解后的其各个特征值所占比例如图9所示, 其中B₀ = 0 T、B₁ = 0.01T和B₂ = 0.01 T分别对应无磁场、横向磁场和纵向磁场构型下SVD分解后的特征值比例图. 由图9可知, X的前21个特征值对应的特征模态能反映90%以上的流场信息, 因此, 本文取r = 21进行SVD分解, 在保证流场信息完整性的同时大大减少第四步的计算量.
图 9 对X SVD后的特征值图
Figure9. The SVD of X

${\bf{X}} \approx {\bf{U}}\sum {{\bf{V}}^ * },$

其中*代表共轭转置. 此时, ${\bf{U}} \in {\mathbb{C}^{n \times r}},\sum \in {\mathbb{C}^{r \times r}}$, $V \in {\mathbb{C}^{m \times r}}$.
第三步, 假设矩阵A是连接X和X′的最适矩阵($X'{\rm{ = }}{\bf{{\rm A}X}}$), 即A能将上一时刻的流场数据信息X推进至下一时刻X′, 可得

${\bf{A = X'}}{{\bf{X}}^{\bf{? }}}{\bf{ = X'V}}{{\sum} ^{ - 1}}{{\bf{U}}^{\bf{*}}}, $

其中${\bf{A}} \in {\mathbb{R}^{n \times n}}$, ${{\bf{X}}^? }$是${\bf{X}}$的Moore-Penrose转置.
第四步, 将A(n阶方阵)投影到X的正交基U上得到$\mathop {\bf{A}}\limits^ \sim $(r阶方阵). 可见对X进行r阶SVD分解能大大减少计算量.

$\mathop {\bf{A}}\limits^ \sim = {{\bf{U}}^*}{\bf{AU}} = {{\bf{U}}^{\bf{*}}}{\bf{X'}}V{{\sum} ^{ - 1}}.$

第五步, A的特征值与$\mathop {\bf{A}}\limits^ \sim$的特征值一样^[20,29,30], 且对$\mathop {\bf{A}}\limits^ \sim $进行分解时计算量较小, 因此对$\mathop {\bf{A}}\limits^ \sim $进行特征值分解:

$\mathop {\bf{A}}\limits^ \sim {\bf{W}} = {\bf{W}}\Lambda,$

W的列向量由特征向量组成; $\Lambda $是对角阵, 其对角元是相应的特征值${\lambda _k}$.
第六步, 重构矩阵A. 其中A的特征值由$\Lambda $给出, 特征向量为^[30]:

$\Phi {\rm{ = }}{\bf{X'V}}{{\sum} ^{ - 1}}{\bf{W}}.$

第七步, 得到A的特征值和特征向量后, 可重构涡量图. 令${\omega _k} = \ln ({\lambda _k})/\Delta t$, $\Omega = {\rm{diag}}(\omega )$可得

${\bf{x}}(t) \approx \sum\limits_{k = 1}^r {{\phi _k}\exp ({\omega _k}t)} {b_k} = {{\Phi }} {\rm{exp(}}\Omega t{\rm{)}}{\bf{b}},$

b为初始时刻各个模态对应的振幅. 记初始时刻为X₁, 可得X₁ = Φ^?b, 则b = Φ^? X₁
由A的特征值λ_k和模态, 对有无磁场作用下界面不稳定性展开进一步研究. 设Y₀为某一时刻流场信息, 则后续时刻流场信息Y₁、Y₂, …, Y_N为:

$\begin{split}& {{{\bf{Y}}_1} = {{\bf{A}}^1}{{\bf{Y}}_0} = {{\Phi \Lambda }}{{{\Phi }}^{ - 1}}{{\bf{Y}}_0}} \\ & {{{\bf{Y}}_2} = {{\bf{A}}^2}{{\bf{Y}}_0} = {{\Phi }}{{{\Lambda }}^2}{{{\Phi }}^{ - 1}}{{\bf{Y}}_0}} \\ & \quad\quad\quad\quad\quad\vdots \\ & {{{\bf{Y}}_N} = {{\bf{A}}^N}{{\bf{Y}}_0} = {{\Phi }}{{{\Lambda }}^N}{{{\Phi }}^{ - 1}}{{\bf{Y}}_0}}.\end{split}$

由(13)式可知, 后期流场信息与${\Lambda}$的对角元λ_k = a+ib密切相关, 其中a反映流场稳定性, b反映扰动变化频率. a > 1则该特征值对应模态不稳定, a < 1则该特征值对应模态稳定; 且b越大, 扰动频率越大. 以实数为x轴, 虚数为y轴, 三种情况下流场特征值λ_k的如图10所示, 因a是实数, 其特征值会沿实轴对称分布^[20,21]. 其中B0_Eigenvalues、B1_Eigenvalues、B2_Eigenvalues分别对应无磁场、纵向磁场、横向磁场构型. 单位圆(绿色实线)外的特征值反映不稳定模态, 且特征值离圆心越近, 则相应的模态越稳定. 本文三种情况下的DMD特征值均在单位圆内, 表明发展期流场均趋于稳定. 且无磁场、纵向及横向磁场三种情况下, 基于DMD算法重构的涡量图与原始涡量图一致(图11), 可见本文DMD算法在有无磁场情况下能准确地还原流场信息. 因此可将DMD技术用于界面不稳定性研究.
图 10 DMD的特征值
Figure10. The eigenvalues of DMD

图 11 t = 290 μs时原始涡量和DMD重构涡量图　(a1)无磁场 B₀ = 0 T, 原始涡量图; (a2)纵向磁场 B₁ = 0.01 T, 原始涡量图; (a3)横向磁场 B₂ = 0.01 T, 原始涡量图; (b1)无磁场 B₀ = 0.0 T, DMD重构涡量图; (b2)纵向磁场 B₁ = 0.01 T, DMD重构涡量图; (b3)横向磁场 B₂ = 0.01 T, DMD重构涡量图
Figure11. The distribution of original vorticities and DMD reconstructed vorticities at t = 290 μs: (a1)Original vorticities, B₀ = 0 T, hydro cases; (a2) original vorticities, B₁ = 0.01 T, longitudinal magnetic fields; (a3) original vorticities, B₂ = 0.01 T, transverse magnetic fields; (b1) DMD reconstructed vorticities, B₀ = 0 T, hydro cases; (b2) DMD reconstructed vorticities, B₁ = 0.01 T, longitudinal magnetic fields; (b3) DMD reconstructed vorticities, B₂ = 0.01 T, transverse magnetic fields.

三种情况下, DMD的不同特征值对应的模态如图12所示. 特征值λ₁对应的模态反映了流场中稳定涡结构, 其包含了主要流场信息; λ₂—λ₄反映了流场中高频小涡序列, 且小涡扰动频率依次增加. 可知, 无磁场、纵向和横向磁场构型下, DMD均能清晰的将两种不同尺度扰动提取出来; 虽然磁场作用下界面涡量分层, 但分层的涡量中间仍有小涡扰动, 其纵向磁场下扰动更多; 无磁场时气柱上下游均存在小涡扰动, 而纵向磁场作用下小涡扰动集中在下游, 横向磁场下的小涡扰动集中在上游. 此外, 流场发展后期, 三种情况下流场均较稳定, 第一模态的大涡低频扰动能反映流场主要信息, 第二至第四模态的小涡高频扰动在大涡外围不断卷起, 且涡扰动频率依次增加, 涡强度不断减小. 相比于同一模态的无磁场情况, 磁场作用下小涡扰动的频率不断减小, 横向磁场下扰动频率最小. 因此, 磁场能抑制小涡扰动, 且横向磁场控制效果更好.
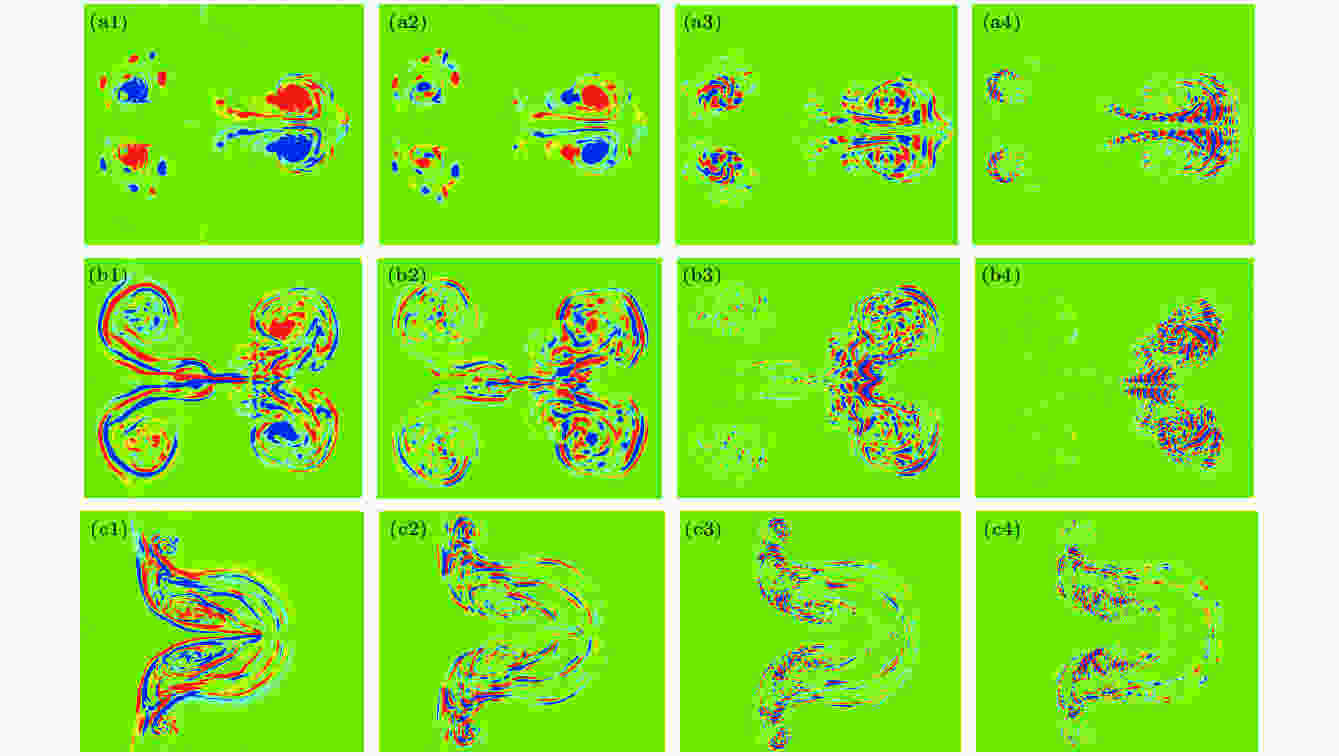图 12 无磁场、纵向和横向磁场下DMD的四个不同特征值对应的模态图　(a1)无磁场, λ₁ = (0.9764, 0.0000); (a2)无磁场, λ₂ = (0.9061, 0.2856); (a3)无磁场, λ₃ = (0.8236, 0.5226); (a4)无磁场, λ₄ = (0.3514, 0.8943); (b1)纵向磁场, λ₁ = (0.9816, 0.0000); (b2)纵向磁场, λ₂ = (0.9423,0.1925); (b3)纵向磁场, λ₃ = (0.8212, 0.5150); (b4)纵向磁场, λ₄ = (0.3929, 0.8828); (c1)横向磁场, λ₁ = (0.9648, 0.0000); (c2)横向磁场, λ₂ = (0.9601,0.1703); (c3)横向磁场, λ₃ = (0.8314, 0.4774); (c4)横向磁场, λ₄ = (0.3718, 0.8279)
Figure12. DMD modes with respect to four different eigenvalues in hydro, longitudinal and transverse magnetic fields: (a1) In hydro field, λ₁ = (0.9764, 0.0000); (a2) in hydro field, λ₂ = (0.9061, 0.2856); (a3) in hydro field, λ₃ = (0.8236, 0.5226); (a4) in hydro field λ₄ = (0.3514, 0.8943); (b1) in longitudinal magnetic field, λ₁ = (0.9816, 0.0000); (b2) in longitudinal magnetic field, λ₂ = (0.9423,0.1925); (b3) in longitudinal magnetic field, λ₃ = (0.8212, 0.5150); (b4) in longitudinal magnetic field, λ₄ = (0.3929, 0.8828); (c1) in transverse magnetic field, λ₁ = (0.9648, 0.0000); (c2) in transverse magnetic field, λ₂ = (0.9601, 0.1703); (c3) in transverse magnetic field, λ₃ = (0.8314, 0.4774); (c4) in transverse magnetic field, λ₄ = (0.3718, 0.8279).

基于理想MHD, 本文对无磁场、横向和纵向磁场构型下激波与轻质(97%N₂+3% SF₆)圆形气柱界面相互作用过程进行了数值研究, 得到以下结论:
纵向和横向磁场对复杂波系的演化过程影响甚微, 特征波系演化时间与无磁场时一致, 但磁场能抑制界面不稳定性发展, 且相同强度下, 横向磁场抑制效果更佳.其中, 三种情况下入射激波上下段均在气柱外发生非规则反射, 中间段穿过气柱形成透射激波, 随后该激波在气柱内来回振荡, 并多次于气柱界面形成透射-反射激波结构.无磁场时, 界面卷起不稳定涡序列, SF₆射流穿过下游界面. 两种磁场下, 界面相比于无磁场时光滑, 但纵向磁场下界面仍有少许扰动, 而横向磁场下, 界面十分更光滑, SF₆射流不再穿过界面. 定量分析还表明, 两种磁场均能抑制界面变形.
此外, 因R-M不稳定性的作用, 上游界面处, 磁力线发生严重扭曲, 产生较大的洛伦兹力, 使涡量沿界面两侧分层, 涡层相距较远; 而下游界面处, 磁力线扭曲程度较小, 洛伦兹力小, 涡层距离较近. 由于横向磁场的初始磁场方向基本与流场速度垂直, 其产生的洛伦兹力较纵向磁场大, 下游界面处涡量分层相对清晰.
最后, 本文采用DMD对界面不稳定性进行了研究, 结果显示: DMD能将不同扰动涡分别提取出来, 其中第一模态的大涡反映了流场的基本信息, 其余模态的小涡反映了高频扰动序列. 无磁场时, 气柱上下游均存在小涡扰动, 而纵向和横向磁场作用下小涡扰动分别集中在上游和下游. 磁场作用涡层中仍存在小涡扰动, 纵向磁场下扰动更多; 三种情况下, 小涡扰动频率依次减小, 这表明磁场能抑制小涡扰动频率, 且横向磁场的抑制效果更好.