摘要: 考虑双模纠缠相干光场, 将其中一束光场注入腔中与一个二能级原子发生共振相互作用, 根据腔量子电动力学理论推导出原子系统的演化态. 针对原子系统初始状态到目标演化态的动力学过程, 利用量子速率极限时间概念来表征原子系统量子态的最大演化速率. 通过调节双模纠缠相干光场的相干参数来操控原子系统量子态动力学过程中所能达到的最大演化速率. 结果发现: 与原子发生相互作用光场的相干参数在一定条件下可以对系统量子态的最大演化速率产生明显的影响; 并且当该光场参数不能很好地来操控量子态的最大演化速率时, 双模纠缠相干光场间的量子关联可以实现未参加相互作用光场参数对原子系统量子态最大演化速率的远程调控.
关键词: 量子速率极限 /
纠缠相干态 /
二能级原子 English Abstract Control of maximum evolution speed of quantum states by two-mode entangled light field Tian Cong 1 ,Lu Xiang 1 ,Zhang Ying-Jie 1,2 ,Xia Yun-Jie 1,2 1.School of Physics and Physical Engineering, Qufu Normal University, Qufu 273165, China Fund Project: Project supported by the National Science Foundation of China (Grant No. 61675115).Received Date: 18 March 2019Accepted Date: 20 May 2019Available Online: 01 August 2019Published Online: 05 August 2019Abstract: We consider a two-mode entangled coherent light field, in which one mode of the light field is injected into the cavity and interacts with a two-level atom. According to the theory of cavity electrodynamics, the evolution state of atomic system is deduced. Aiming at the dynamic process from the initial state of an atomic system to the target evolution state, the quantum speed limit time is used to characterize the maximum evolution rate of the quantum state of an atomic system. The maximum evolution rate of an atomic system can be controlled by adjusting the coherent parameters of the two-mode entangled coherent light field. But up to now, which kind of quantum speed limit time can be better, universal and strict applicable to the quantum dynamics process of any system is still an unresolved important issue. Based on different methods of measuring the distance between two quantum states and different dynamic evolution channels, many definitions of the quantum speed limit time have been given. The quantum speed limit time proposed by Deffner and Lutz (Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402) and the other deduced by Campaioli et al. (Campaioli F, Pollock F A, Binder F C, Modi K 2018 Phys. Rev. Lett. 120 060409; Campaioli F, Pollock F A, Modi K 2018 arXiv:1806.08742) have attracted extensive attention. In this paper, we first compare the advantages of two quantum speed limit times to characterize the maximum evolution rate of quantum states. We find that the quantum speed limit time expression given by Campaioli et al. (Campaioli F, Pollock F A, Modi K 2018 arXiv:1806.08742) in 2018 is a tighter bound when describing the boundary of the shortest time required for the quantum state evolution of a two-level atomic system. Therefore, this paper is mainly based on the quantum speed limit time given by Campaioli et al. to analyze how to achieve the maximum evolution rate of the quantum state of the atomic system by manipulating the parameters of a two-level entangled coherent light field. The results show that the maximum evolution speed of the quantum state of the atomic system can be significantly affected by the coherent parameters of the light field interacting with the atom under certain conditions. Furthermore, when the interacting light field parameters cannot well control the maximum evolution speed of the quantum state, the quantum correlation with the two-mode entangled coherent light field can realize the remote control of the maximum evolution speed of quantum state of atomic system by the light field parameters that are not involved in the atom-light interaction.Keywords: quantum speed limit time /entangled coherent state /two-level atom 全文HTML --> --> --> 1.引 言 基于量子态间最短演化时间定义的量子速率极限时间引起了国内外研究者的广泛关注, 并用来估量由给定量子态演化到期望目标态的最大速率. 对量子系统速率极限时间概念的研究主要针对闭合量子系统和开放量子系统. 到现在, 对闭合系统幺正动力学过程中量子速率极限的概念以及推广应用进行了较为深入的研究[1 —6 ] , 将Mandelstam-Tamm (M-T)型界[1 ] 和Margolus-Levitin (M-L)型界[3 ] 结合在一起, 给出了量子速率极限时间的定义表达式[4 ] , 用来描述在不显含时间的系统哈密顿量幺正动力学过程中两正交态间演化速率. 近年来, 国内外研究者将量子速率极限时间的研究从闭合系统转移到开放系统动力学上来. 2013年, Deffner和Lutz[7 ] 利用几何办法由布鲁斯角出发分别推导出了开放系统量子速率极限的M-T型界和M-L型界, 并将这两种类型的界统一起来定义了量子速率极限时间. 2018年, Campaioli等[8 ,9 ] 用依赖于测量距离角度在广义布洛赫球中状态的方法推导了描述任意量子态在幺正或者非幺正动力学过程中的量子速率极限时间.[10 ] . 在实际系统动力学过程中怎样加快量子态演化的研究是一个重要方向, 这不仅对理解量子速率极限的基本概念具有重要的理论意义, 而且对基于实际系统的量子通信[11 ] 、量子计算[12 ] 、量子计量学[13 ] 以及量子最优调控[14 ] 的发展很有裨益,近年来也引起了广泛关注并报道了一些操控量子态演化速率的工作[15 —20 ] , 利用文献[7 ]中的量子速率极限时间, 我们通过对量子比特实施一个连续的经典场驱动, 调节经典场驱动强度给出了一个加快量子系统演化速率的理论方案[21 ] . 美国的一个研究组基于腔量子电动力学系统, 通过可控的原子系综环境, 实验上实现了开放量子系统动力学过程中量子态的加速演化[22 ] . 鉴于纠缠相干光场便于制备和操控[23 ,24 ] , 本文以双模纠缠相干光场作为调节对象[25 ,26 ] , 利用一个二能级原子与其中一模式光场发生共振相互作用, 探究如何通过双模纠缠相干光场来操控二能级原子系统量子态的最大演化速率问题. 但迄今为止, 哪一种量子速率极限时间能更好地、普适地、严格地适用于任意系统量子态动力学过程, 还是值得继续深入研究的重要问题. Deffner和Lutz[7 ] 所给出的量子速率极限时间和Campaioli等[9 ] 推导的量子速率极限时间得到了人们的广泛关注. 我们首先针对本文的二能级原子系统量子态的动力学过程, 比较上面两种量子速率极限时间哪个能更好地表征量子态最大演化速率; 基于较好的量子速率极限时间来分析双模纠缠相干光场参数对原子系统量子态最大演化速率的操控. 研究发现: 2018年Campaioli等[9 ] 给出的量子速率极限时间能更好地分析二能级原子系统量子态最大演化速率的调控问题. 与原子发生相互作用光场的相干参数在一定范围内能调控原子系统量子态动力学过程中的最大演化速率. 当与原子发生相互作用光场的相干参数不能很好地利用该参数来操控量子态的最大演化速率时, 鉴于双模纠缠相干光场的纠缠性, 可以通过调节未与原子发生相互作用的另一光场的相干参数来远程操控原子系统量子态动力学过程中所能达到的最大演化速率.2.理论模型与体系的波函数 本文考虑两束处于双模纠缠的相干光场${N_ \pm }({\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} \pm {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b})$ (这里, 归一化常数${N_ \pm } = \left[2 \;\pm\; 2{\rm{e}}^{ - 2\left( {{{\left| \alpha \right|}^2} + {{\left| \beta \right|}^2}} \right)} \right]^{ - 1/2}$ ), 将单模光场a 注入一个含有单个二能级原子的腔中, 光场a 与二能级原子发生共振相互作用, 在旋波近似下体系的哈密顿量为${\omega _{\rm s}}$ 和${\omega _a}$ 分别为原子的本征跃迁频率、光场a 模式频率; $\left| e \right\rangle $ 和$\left| g \right\rangle $ 分别为二能级原子的激发态和基态; $\sigma = \left| g \right\rangle \left\langle e \right|$ , ${\sigma ^\dagger } = \left| e \right\rangle \left\langle g \right|$ 分别为二能级原子的赝自旋算符, g 为原子与单模光场的耦合系数. 设原子的初始状态为$\sin \theta \left| e \right\rangle + \cos \theta \left| g \right\rangle $ , 则初始时刻整个系统状态为${\rm{i}}\dfrac{\partial }{{\partial t}}\left| {\varPsi \left( t \right)} \right\rangle = $ $\left[ {g\left( {{\sigma ^\dagger }a + \sigma {a^\dagger }} \right)} \right]\left| {\varPsi \left( t \right)} \right\rangle $ , 可以求出整个系统任意时刻t 的波函数$\left| {\varPsi \left( t \right)} \right\rangle\!=\! \sum\limits_n^\infty {\left[ {\left| {{C_{1,n}}} \right\rangle \left| {e,n} \right\rangle \!+\! } \right.} {\left| {{C_{2,n}}} \right\rangle \left| {g,n} \right\rangle + }$ $\left. {\left| {{C_{3,n}}} \right\rangle \left| {g,n + 1} \right\rangle + \left| {{C_{4,n}}} \right\rangle \left| {e,n - 1} \right\rangle } \right] $ , 这里a 和b 的自由度求迹, 得到原子体系在动力学过程中的约化密度矩阵,3.量子速度极限时间 量子体系演化过程中所能达到的最大演化速率通常可以用量子速率极限时间来表征, 量子速率极限时间是两量子态间演化所需的最短时间的一个紧的界. 近年来, 人们广泛关注如何给出表征量子态最大演化速率的一个普适的、便于计算的、更紧的最短时间的界. 基于不同的两量子态间距离的度量方法以及不同的动力学演化信道方式, 已经给出了很多种不同量子速率极限时间的定义. 我们主要针对两种便于计算并且经常被用来表征不同体系量子态最大演化速率的量子速率极限时间来分析. 考虑系统初始量子态${{ \rho} _{\rm s}}\left( {0} \right) = \left| {{\varphi _0}} \right\rangle \left\langle {{\varphi _0}} \right|$ 和其目标演化态${{ \rho} _{\rm s}}\left( {\tau} \right)$ , τ 为初始态到目标态的实际演化时间, 2013年, Deffner和Lutz[7 ] 用几何方法将M-T型界和M-L型界统一, 并定义了描述量子系统初始量子态为纯态情形的量子速率极限时间:$L\left[ {{{ \rho} _{\rm s}}\left( {0} \right),{{ \rho} _{\rm s}}\left( {\tau} \right)} \right] $ 来表征量子系统初态与末态的距离, $L\left[ {{{ \rho} _{\rm s}}\left( {0} \right),{{ \rho}_{\rm s}}\left( {\tau} \right)} \right] = $ $\arccos \sqrt {\left\langle {{\varphi _0}} \right|{{ \rho} _{\rm s}}\left( {\tau} \right)\left| {{\varphi _0}} \right\rangle } $ ; $\left| {{\varphi _0}} \right\rangle $ 表示原子的初始状态;$\varLambda _\tau ^{{\rm{op}}} = \dfrac{1}{\tau }\displaystyle\int_0^\tau {{\rm{d}}t } {\left\| {{{\dot { \rho} }_{\rm s}}\left( { t} \right)} \right\|_{{\rm{op}}}}$ , 这里${\left\| {{{\dot { \rho} }_{\rm s}}\left( { t} \right)} \right\|_{{\rm{op}}}}$ 为${\dot { \rho} _{\rm s}}\left( { t} \right)$ 的最大奇异值, ${\dot { \rho} _{\rm s}}\left( { t} \right)$ 为系统密度矩阵${{ \rho} _{\rm s}}\left( { t} \right)$ 对时间$t$ 的导数. 2018年, Campaioli等[9 ] 用依赖于测量角度和距离在广义布洛赫球中量子态的方法推导了量子速率极限时间的表达式:${\overline {\left\| {{{\dot { \rho} }_{\rm s}}\left( { t} \right)} \right\|} _{{\rm{hs}}}} = \dfrac{1}{\tau }\int_0^\tau {{\rm{d}}t } {\left\| {{{\dot { \rho} }_{\rm s}}\left( { t} \right)} \right\|_{{\rm{hs}}}}$ , 并且${\left\| A \right\|_{{\rm{hs}}}} = $ $ \sqrt {\sum\nolimits_i {r_i^2} } $ , ${r_i}$ 为A 的奇异值. 当量子速率极限时间 ${\tau _{{\rm{QSL}}}}$ 与实际演化时间τ 的比值${\tau _{{\rm{QSL}}}}/\tau = 1$ , 这时体系量子态的演化速率已经达到最大值, 体系量子态的动力学过程不会被加速. 然而, 当$0 < {\tau _{{\rm{QSL}}}}/\tau < 1$ 时, 体系量子态的演化速率还没达到最大值, 演化速率可以被加速, 并且${\tau _{{\rm{QSL}}}}/\tau $ 越小, 量子态演化速率被提升的空间就越大.7 )和(8 )式分别计算出二能级原子初始量子态$\left| {{\varphi _0}} \right\rangle = \sin \theta \left| e \right\rangle + \cos \theta \left| g \right\rangle $ 到目标演化态${{ \rho} _{\rm s}}\left( {\tau} \right)$ 动力学过程的不同量子速率极限时间. 两种量子速率极限时间是初始量子态参数θ 、双模纠缠相干光场参数(α , β )、光场与原子间耦合参数g 和实际演化时间τ 等的复杂函数, 数值分析这些参数对两种量子速率极限时间的影响. 这里值得我们指出的是纠缠相干光场参数α 和β 的取值范围, 由于$\left\langle \alpha \right.\left| { - \alpha } \right\rangle = {{\rm{e}}^{ - 2|\alpha {|^2}}}$ 和$\left\langle \beta \right.\left| { - \beta } \right\rangle = {{\rm{e}}^{ - 2|\beta {|^2}}}$ 在$0 \leqslant \left| \alpha \right|<2$ 和$0 \leqslant \left| \beta \right|<2 $ 时不正交, 而在$\left| \alpha \right|> 2$ 和$\left| \beta \right|> 2$ 时近似正交; 本文旨在利用双模纠缠相干态的纠缠性来调控二能级原子量子态的演化速率, 故下文中为方便起见, 主要考虑双模纠缠相干光场的参数为正实数且满足$0 \leqslant \alpha < 2$ 和$0 \leqslant \beta < 2$ .${N_ + }\left({\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} +\right.$ $\left.{\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}\right)$ 和${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ 的情况, 在给定与二能级原子体系相互作用的光场a 的相干参数$\alpha = 1$ 和实际演化时间$\tau = 1$ 时, 由图1(a) 和图1(b) 可以清晰地看出, 二能级原子与双模纠缠相干光场中其一模式a 发生Jaynes-Cummings模型相互作用时, 二能级原子量子态在初始态到目标演化态的动力学过程中的最短时间的界, 2018年Campaioli等[9 ] 给出的量子速率极限时间表达式(8 )要比2013年Deffner和Lutz[7 ] 提出的表达式(7 )更紧, 与未参加相互作用的光场b 的相干参数和二能级原子初始态的选取无关.图 1 二能级原子系统量子态的两种量子速率极限时间${\tau _{{\rm{QSL}}}}$ 与实际演化时间τ 的比值随未参加相互作用光场b 的相干参数β 和初始量子态参数θ 的变化, 这里$g = 1$ , 彩虹图形描述Campaioli表达式(8 ), 灰色图形描述Deffner表达式(7 ) (a) $\alpha = 1$ 和$\tau = 1$ 时, 初始纠缠相干光场状态为${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b) $\alpha = 1$ 和$\tau = 1$ 时, 初始纠缠相干光场状态为${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure1. Ratio of the quantum speed limit time ${\tau _{{\rm{QSL}}}}$ to the actual evolution time τ for the two-level atomic system quantum state as a function of the dimensionless initial state parameter θ and the coherent parameter β of the non-interaction light field b , and $g = 1$ , the rainbow graph describes Campaioli’s expression (8 ) and the gray graph describes Deffner’s expression (7 ). (a) When $\alpha = 1$ and $\tau = 1$ , the initial entangled coherent state is ${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b) when $\alpha = 1$ and $\tau = 1$ , the initial entangled coherent state is ${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ .[9 ] 的量子速率极限时间为最短演化时间更紧, 图2 给出了二能级原子初始处于最大相干性为1的状态$\theta = 3{\text{π}}/4$ 时, 给定不同的实际演化时间$\tau = 1$ 和$\tau = 5$ , 两种量子速率极限时间与实际演化时间的比值${\tau _{{\rm{QSL}}}}/\tau $ 随双模纠缠相干光场参数α 和β 的变化规律. Campaioli等[9 ] 的量子速率极限时间表达式(8 )与Deffner和Lutz[7 ] 提出的表达式(7 )在纠缠相干光场参数α 和β 的变化范围内均为${\tau _{{\rm{QSL}}}}/\tau < 1$ , 并且我们同样可以得到Campaioli等[9 ] 给出的量子速率极限时间表达式(8 )更紧. 并且通过比较图2(a) 和图2(c) , 以及图2(b) 和图2(d) , 实际演化时间$\tau = 5$ 时Campaioli等[9 ] 的量子速率极限的界仍然比Deffner和Lutz[7 ] 提出的要紧, 但是两者量子速率极限时间的差别相对减小(与$\tau = 1$ 情形相比较). 通过进一步数值模拟分析, 发现在增大实际演化时间τ 时, 在$\tau > 6$ 之后, 两种量子速率极限时间的图形基本重合. 也就是说, 在二能级原子系统的动力学过程中, 若考虑从原子初始态到经过较长时间实际演化的目标态, Campaioli等[9 ] 给出表达式(8 )和Deffner和Lutz[7 ] 提出的表达式(7 )在表征原子体系动力学过程的最大演化速率问题方面是等价的. 根据上面的分析, 我们采用2018年Campaioli等[9 ] 给出的量子速率极限时间表达式(8 )来分析二能级原子系统量子态演化速率的调控问题.图 2 原子系统量子态的量子速率极限时间与实际演化时间的比值${\tau _{{\rm{QSL}}}}/\tau $ 随双模纠缠相干光场参数α 和β 的变化规律, 这里$g = 1$ , $\theta = 3{\text{π}}/4$ , 彩虹图形描述Campaioli表达式(8 ), 灰色图形描述Deffner表达式(7 ) (a)和(c)分别为$\tau = 1$ 和$\tau = 5$ 时, 初始时刻双模纠缠相干光场为${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b)和(d)分别为$\tau = 1$ 和$\tau = 5$ 时, 初始时刻双模纠缠相干光场为${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure2. Ratio ${\tau _{{\rm{QSL}}}}/\tau $ of the quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the two-mode entangled coherent light field parameters α and β , and $g = 1$ , $\theta = 3{\text{π}} /4$ , the rainbow graph describes Campaioli’s expression (8 ) and the gray graph describes Deffner’s expression (7 ). Here, in (a) and (c) the initial entangled coherent state is ${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ , for $\tau = 1$ and $\tau = 5$ respectively; in (b) and (d) the initial entangled coherent state is ${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ , for $\tau = 1$ and $\tau = 5$ respectively.4.量子态最大演化速率的参数调控 基于量子速率极限时间概念, 为了清晰地分析二能级原子系统与光场相互作用下量子态动力学过程中所能达到的最大演化速率问题, 首先考虑两束处于纠缠相干光场${N_ \pm }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} \pm {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ 中未参与相互作用光场b 的相干参数$\beta = 0$ 的情形, 这时整个系统描述为处于薛定谔猫态$\left( {{{\left| \alpha \right\rangle }_a} \pm {{\left| { - \alpha } \right\rangle }_a}} \right)\Big/{\left( {2 \pm 2{e^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ 的光场a 与二能级原子相互作用, 光场b 与原子系统量子态的动力学行为无任何影响. 下面研究光场a 的相干参数α 对原子初始态$\left| {{\varphi _0}} \right\rangle = \left( {\left| e \right\rangle - \left| g \right\rangle } \right)/\sqrt 2 $ 到目标演化态${{ \rho} _{\rm s}}\left( {\tau} \right)$ 动力学过程的量子速率极限时间的影响. 图3 给出了对于不同实际演化目标态${{ \rho} _{\rm s}}\left( {\tau} \right)$ 而言, 原子系统量子态的量子速率极限时间与实际演化时间的比值${\tau _{{\rm{QSL}}}}/\tau $ 随光场a 的相干参数α 的变化规律曲线.图 3 考虑不同的实际演化时间τ 时, 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值${\tau _{{\rm{QSL}}}}/\tau $ 随参加相互作用光场a 的相干参数α 的变化规律, 这里 $\beta = 0$ , $g = 1$ , $\theta = 3{\text{π}} /4$ (a)初始光场a 为$\left( {{\left| \alpha \right\rangle _a} + {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 + 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ ; (b)初始光场a 为$\left( {{\left| \alpha \right\rangle _a} - {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 - 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ Figure3. By considering different actual evolution times, the ratio ${\tau _{{\rm{QSL}}}}/\tau $ of the quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the coherent parameter α of the interaction light field a , and $\beta = 0$ , $g = 1$ , $\theta = 3{\text{π}}/4$ : (a) The initial state of the light field a is $\left( {{\left| \alpha \right\rangle _a} + {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 + 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ ; (b) the initial state of the light field a is $\left( {{\left| \alpha \right\rangle _a} - {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 - 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ .图3(a) , 在光场的初态为$\left( {{\left| \alpha \right\rangle _a} + {\left| { - \alpha } \right\rangle _a}} \right)\Big/$ ${\left( {2 + 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ 时, 可以看到实际演化时间τ 越长, 量子速率极限时间与实际演化时间的比值${\tau _{{\rm{QSL}}}}/\tau $ 会越小. 这说明对于同一原子初始态到不同实际目标演化态时, 动力学过程经历的时间越长, 所能达到的量子态最大演化速率越大, 也就是说量子态动力学过程中演化速率被加速提升的能力越强. 其次, 在给定τ 的取值时, 光场a 的相干参数α 也会引起${\tau _{{\rm{QSL}}}}/\tau $ 的变化, 如图3(a) 中当$\tau = 1$ 时, 可以清楚地看到$\alpha < 1.2$ 时${\tau _{{\rm{QSL}}}}$ 基本与实际演化时间τ 相等, 说明在此动力学过程中量子态的演化速率已经达到最大, 没有被加速的可能, 即说明光场参数在$\alpha < 1.2$ 范围内对量子态的动力学演化速率没有明显的影响. 然当$\alpha > 1.2$ 时, 随着α 的增加${\tau _{{\rm{QSL}}}}/\tau $ 逐渐减小, 也就是此时量子态的加速演化可以通过调节光场a 的相干参数α 来实现. 当$\tau = 2$ 时, α 在小于一定值时变化不大, 当大于一定值时, 随着α 继续增加 ${\tau _{{\rm{QSL}}}}/\tau $ 会减小, 说明原子系统量子态演化速率加速能力被提升. 再者, 在考虑较长的实际演化时间τ 时, 发现这时随α 的变化${\tau _{{\rm{QSL}}}}/\tau $ 变化幅度较小, 也就是说, 利用调节光场a 的相干参数α 来操控原子系统量子态动力学加速的效果是不明显. 对于光场的初态为$\left( {{\left| \alpha \right\rangle _a} - {\left| { - \alpha } \right\rangle _a}} \right)\Big/$ ${\left( {2 - 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ 的情况, 由图3(b) 可得到与初态为$\left( {{\left| \alpha \right\rangle _a} + {\left| { - \alpha } \right\rangle _a}} \right)\Big/{\left( {2 + 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ 大致相同的结论. 由此可知, 在考虑较短的实际演化时间τ 对应的目标态时(如图3 中$\tau = 1$ , $\tau = 2$ ), 光场相干参数α 在大于一定值时会对原子系统量子态的最大演化速率产生明显的影响, 可以利用相干参数α 来调控量子态动力学过程中的加速能力. 但是我们也发现当实际演化时间τ 比较大时, 光场a 的相干参数α 对量子速率极限时间的影响较小, 就不能很好地利用该参数来操控量子态的演化速率(如图3 中$\tau = 15$ ). 鉴于此, 接下来我们考虑在未参与相互作用光场b 的相干参数$\beta \ne 0$ 的情形下, 双模光场处于纠缠相干态${N_ \pm }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} \pm {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ 时, 如何通过调节相干参数β 来操控原子系统量子态动力学过程中所能达到的最大演化速率.${N_ \pm }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} \pm {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ 时, 两光场间的纠缠可以使未参与相互作用光场b 对二能级原子系统量子态演化规律产生间接的影响, 从而达到通过调节光场b 的相干参数β 来操控原子系统量子态动力学过程中的演化速率. 首先当目标态对应的实际演化时间较短时($\tau = 1$ ), 当两光场初始处于${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ , 在$\beta = 0$ 时(如图3(a) 中$\tau = 1$ 对应曲线), 光场a 的相干参数在$\alpha < 1.2$ 范围内对量子态的动力学演化速率没有明显的影响. 这时我们可以利用与光场a 处于纠缠态的光场b 的相干参数β 对原子系统量子态所能达到最大演化速率的影响, 实现光场b 对原子系统量子态动力学行为的远程调控. 由图4(a) 可见, 给定$\alpha < 1.2$ 范围内不同的相干参数α , 随着光场b 的相干参数β 的增加, ${\tau _{{\rm{QSL}}}}/\tau $ 减小. 这说明原子系统量子态演化过程中所能达到的最大演化速率越大, 即量子态动力学过程中演化速率被加速提升的能力越强. 其次对于双模光场初态为${N_ - }\left({\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - \right.$ $\left.{\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b} \right)$ 的情况, 由图3(b) 中$\tau = 1$ 对应曲线和图4(b) 可以看出, 随着β 的增加${\tau _{{\rm{QSL}}}}/\tau $ 增大, 原子系统量子态演化过程中所能达到的最大演化速率被减小, 即量子态动力学过程中演化速率被加速提升的空间变小.图 4 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值${\tau _{{\rm{QSL}}}}/\tau $ 随双模纠缠光场相干参数α , β 的变化规律, 这里$\tau = 1$ , $g = 1$ , $\theta = 3{\text{π}}/4$ (a)初始双模纠缠相干光场${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b)初始双模纠缠相干光场${N_ - }\left( { {\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure4. Ratio ${\tau _{{\rm{QSL}}}}/\tau $ of the quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the two-mode entangled coherent light field parameters α and β , and $\tau = 1$ , $g = 1$ , $\theta = 3{\text{π}}/4$ : (a) The initial entangled coherent state is ${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b) the initial entangled coherent state is ${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ .$\tau = 15$ ), 在$\beta = 0$ 时, 光场a 的相干参数α 对量子速率极限时间的影响较小, 不能很好地利用参数α 来操控量子态的演化速率(如图3 中$\tau = 15$ 对应曲线). 通过引入双模纠缠光场中未参与相互作用光场b 的相干参数β 来操控经过较长演化时间后原子系统量子态的演化速率. 对于双模纠缠相干光场初态为${N_ + }(\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ 的情形, 由图5(a) 可知, 随着β 的增加${\tau _{{\rm{QSL}}}}/\tau $ 增大; 对于双模纠缠相干光场初态为${N_ - }\left({\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}\right.$ $\left.{\left| { - \beta } \right\rangle _b}\right)$ 时, 图5(b) 给出随着β 的增加${\tau _{{\rm{QSL}}}}/\tau $ 同样也是增大的. 可见对于所考虑的目标态对应的实际演化时间较长时, 原子系统量子态演化过程中所能达到的最大演化速率被减小, 减小了量子态动力学过程中演化速率被加速提升的空间. 综上所述, 当原子与单模相干光场a 相互作用时, 光场参数不能很好地来操控量子态的演化速率时, 我们可以引入另外一个单模相干光场b 形成双模纠缠相干光场, 这时两光场模式间的纠缠可以实现光场b 远程调控原子系统量子态的动力学过程所能达到的最大演化速率.图 5 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值${\tau _{{\rm{QSL}}}}/\tau $ 随双模纠缠相干光场参数α , β 的变化规律, 这里$\tau = 15$ , $g = 1$ , $\theta = 3{\text{π}}/4$ (a)初始双模纠缠相干光场为${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b)初始双模纠缠相干光场为${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure5. Ratio ${\tau _{{\rm{QSL}}}}/\tau $ of the two quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the two-mode entangled coherent light field parameters α and β , here parameters $\tau = 15$ , $g = 1$ , $\theta = 3{\text{π}}/4$ : (a) The initial entangled coherent state is ${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b) the initial entangled coherent state ${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ .5.结 论 基于腔量子电动力学理论, 考虑将双模纠缠相干光场中某一光场模式与一个二能级原子发生共振相互作用的理论模型, 利用量子速率极限时间概念我们主要探究如何操控原子系统量子态动力学过程中所能达到的最大演化速率问题. 鉴于Deffner和Lutz[7 ] 所给出的量子速率极限时间和Campaioli等[9 ] 推导的量子速率极限时间得到了人们的广泛关注, 本文首先比较了两种量子速率极限时间表征量子态最大演化速率的优越性, 得到2018年Campaioli等[9 ] 给出的量子速率极限时间表达式(8 )在描述二能级原子系统量子态演化所需的最短时间的界时更紧. 本文主要基于Campaioli等[9 ] 给出的量子速率极限时间分析了双模纠缠相干光场的参数对原子系统量子态最大演化速率的操控, 得到了一些有意义的结论: 与原子发生相互作用光场的相干参数在一定范围内能调控原子系统量子态动力学过程中的最大演化速率; 当与原子发生相互作用光场的相干参数不能很好地利用该参数来操控量子态的最大演化速率时, 鉴于双模纠缠相干光场奇妙的纠缠性, 可以通过调节未与原子发生相互作用的另一模式光场的相干参数来远程操控原子系统量子态动力学过程中所能达到的最大演化速率. 

















































 图 1 二能级原子系统量子态的两种量子速率极限时间
图 1 二能级原子系统量子态的两种量子速率极限时间



































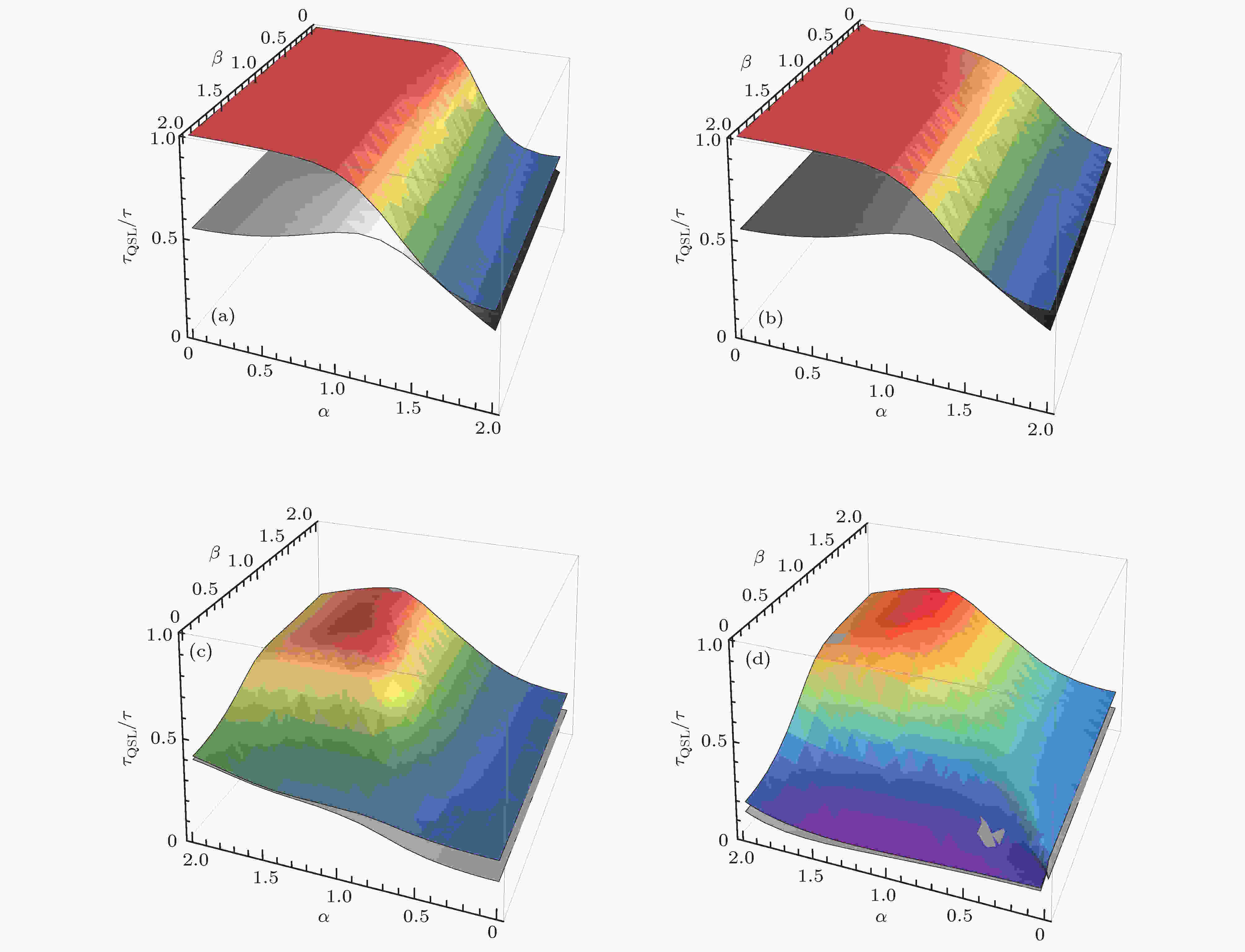 图 2 原子系统量子态的量子速率极限时间与实际演化时间的比值
图 2 原子系统量子态的量子速率极限时间与实际演化时间的比值


































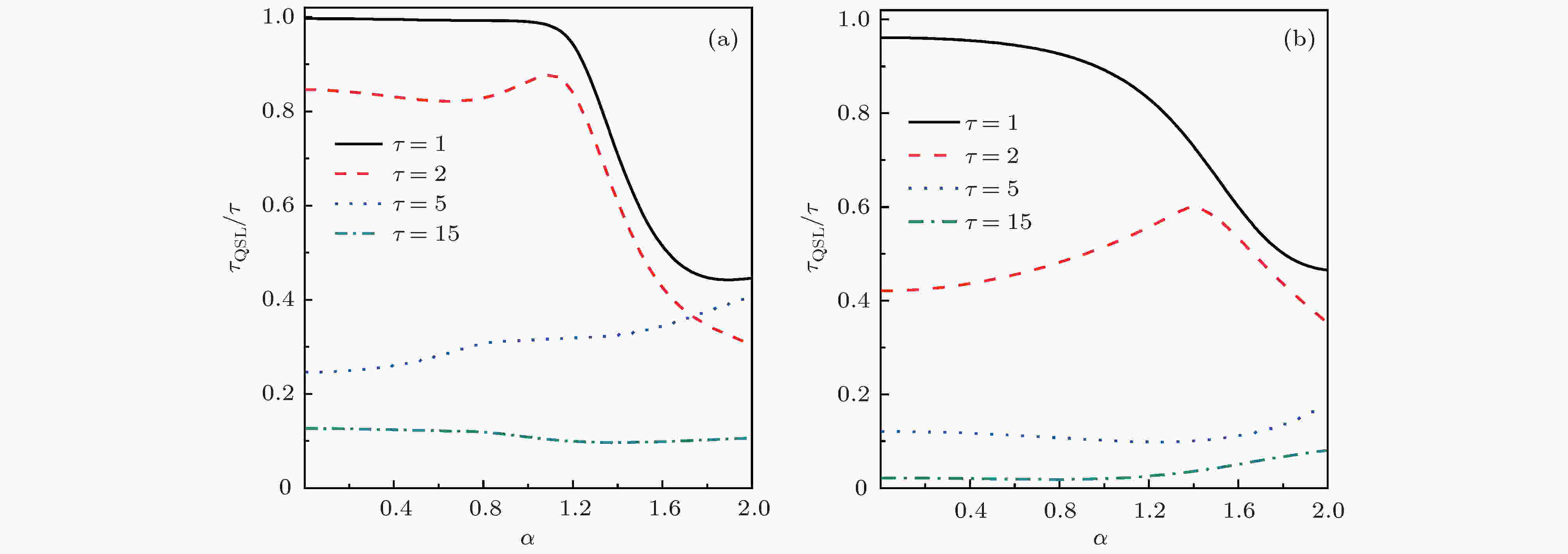 图 3 考虑不同的实际演化时间τ时, 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值
图 3 考虑不同的实际演化时间τ时, 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值
















































































 图 4 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值
图 4 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值























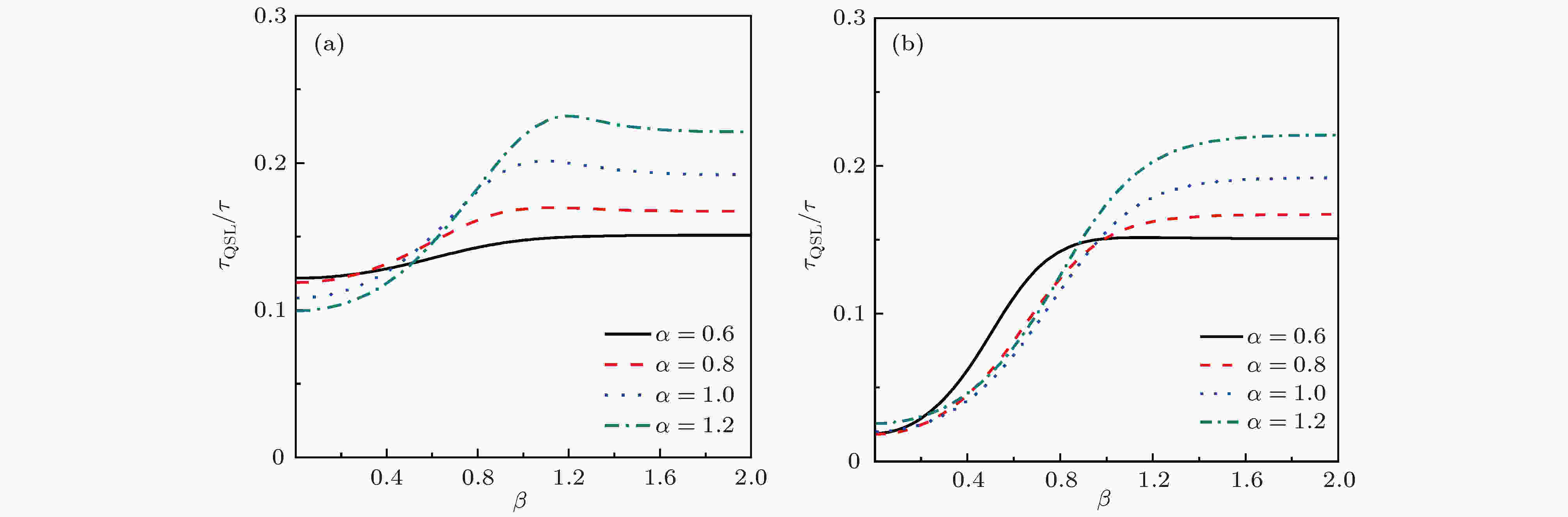 图 5 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值
图 5 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值











