全文HTML
--> --> -->量子等离激元光子学(quantum plasmonics)关注表面等离激元的量子特性以及它与其他系统自由度间的相互作用. 据我们所知, 对等离激元量子特性的具体定义, 不同文献中不尽相同. 下面我们首先从等离激元的量子化谈起, 再简要回顾人们将关注点聚焦于量子特性的技术背景, 最后给出我们对量子等离激元光子学的定义, 并围绕这一定义展开后续的讨论.
在量子理论中, 等离激元是描述金属中电子集体振荡模式的一种准粒子, 20世纪50年代由Pines和Bohm[13]首先提出其在体材料中的量子化描述. 随后, Ritchie[14]认识到金属表面由于不同于材料内部的介电环境会形成能量低于体等离激元的表面等离激元模式, 而能量量子化的表面等离激元很快在穿过金属膜的电子能量损失谱中被观测到[15]. 进一步, 表面等离激元可以和光相互作用形成表面等离激元极化子, 其最早的量子化由Elson和Ritchie采用Hopfield量子化极化子的方法给出[16,17]. 尽管起源于量子力学, 但是表面等离激元的性质可以通过经典的电动力学结合材料介电函数来描述. 可以说, 在经典电动力学的范畴中, 我们忽略了等离激元的电子起源, 而将注意力放在其所携带的电磁场上, 表面等离激元仅仅被看作是局域在金属和电介质界面上的电磁场模式. 等离激元的很多应用都与其高度局域的强电场有关, 基于经典电磁场计算对等离激元的研究已取得了巨大的成功, 能够很好地描述实验中观测到的许多现象.
近年来, 随着纳米加工技术的飞速发展, 各类光电器件结构更加精细. 当结构尺寸逼近材料电子的平均自由程时, 从宏观材料上测得的介电函数将不再适用, 而需要考虑作为等离激元载体的电子态的行为. 事实上, 正是由于等离激元本身电子态的属性赋予其比光子更强的局域性而突破衍射极限, 但是当材料尺寸进一步减小, 将不得不考虑电子本身的非局域性. 当我们把注意力转向电子, 很多问题无法再用经典电动力学手段准确计算[18]. 对于极端的近场, 需要对介电常数进行量子修正, 当纳米间隙缩短到电子波函数可以产生交叠时, 还需要考虑电荷转移的影响[18,19]. 这种电子的非局域性可以被看作是量子等离激元的基本特征. 它为计算带来了困难, 但同时也带来了更丰富的物理现象, 以及更多可能的应用, 这其中包括近年来在电输运[20]、催化[21]和新型热电子器件[21,22]等方面的研究.
等离激元器件常被认为是未来光电器件向更加小型化高速发展的理想载体. 这不仅仅因为其兼具了电子器件在尺寸上和光学器件在响应速度上的优势, 还在于等离激元的玻色子属性, 使其可以像光子一样作为量子信息的载体. 过去十多年中, 一系列的实验证明等离激元具有波粒二象性[23], 可以产生量子纠缠态[24—26]和压缩态[27]. 这些现象发生在由大量电子集体运动参与的等离激元中, 多少令人感到惊讶, 因为通常认为电子-电子相互作用会导致系统快速地退相干. 事实上, 等离激元也确实存在相干时间短、寿命短、损耗大的问题.然而, 当金属纳腔等离激元被用作单光子源时, 恰好因为其寿命短进而能谱展宽大, 可同时拥有高辐射速率和宽辐射谱的特性. 此外, 等离激元的强场带来其更强的非线性效应, 使得我们可以利用等离激元激发来制作耦合器件[28]. 此外, 由于其玻色子特性, 等离激元可有诱发受激辐射, 从而可被用于制作纳米尺度的激光器[29]. 因此, 除去在微观尺度上电子非局域性所带来的量子行为, 等离激元本身所表现出玻色子的內禀属性, 以及其独特的强场和宽谱特性, 使得量子等离激元这一概念受到了广泛的关注和迅速的发展.
综上所述, 本文中的量子等离激元光子学特指针对两类体系的研究, 一是需要考虑电子非局域性的体系, 二是需要考虑电磁场量子化的体系.
近年来等离激元光子学的研究进展迅速, 关于其在各个领域的应用有很多相关综述进行了深入的探讨. 本综述侧重于对其量子特性研究的总结, 尽量给出量子等离激元研究的一个全面的回顾. 首先介绍等离激元研究中采用的量子多体计算方法, 以及其他一些量子化的唯象模型; 之后重点介绍量子等离激元光子学在相互作用体系、纳米器件以及新材料等方面的突破性进展; 最后对量子等离激元光子学未来的发展进行展望.
2
2.1.量子多体计算
对等离激元的量子多体计算中, 通常采用TDDFT方法处理一些对称性较高的理想体系, 以此来了解实际体系中可能出现的量子现象[30—34]. 在这一方法中, 首先需要计算体系的基态波函数, 而复杂的多体相互作用都包含在基态计算的交换关联作用中. 基于由此得到的基态波函数, 可以建立起由不同电子-空穴对组成的激发态相空间. 在此基础上, 计算体系处于激发态时由于电荷重新分布而带来的激发态间的相互作用, 并将这一相互作用看作对系统的扰动, 重新计算体系的本征激发态. 由此可以得到由原激发态线性组合而成的新的激发态. 这些激发态中对外场响应最强的就对应体系的等离激元模式[31].在其量子描述提出以后, 自20世纪80年代, 通过量子多体的第一性原理计算结合金属表面的电子能量损失谱实验, 对于表面等离激元的能谱和寿命都有过系统的研究[33,34]. 通过TDDFT的计算, 人们发现金属纳米颗粒的表面等离激元寿命会随颗粒尺寸缩小表现出振荡现象. 这种寿命振荡现象源自于量子限域效应带来的电子态能量不连续分布, 并且普遍存在于包括球壳, 同轴壳体和薄膜结构的各类限域体系中[31,32]. 研究还给出了由限域的薄膜过渡到无受限体系的转变原理, 并指出在不同结构下, 体系的寿命演化除振荡之外会表现出不同的趋势[31]. 然而受限于加工技术, 直到近几年, 一些量子限域体系的第一性原理计算结果才逐渐在实验中被证实[35,36]. 这其中金属纳米间隙体系由于广泛的应用场景得到了系统的研究.
2009年, 通过第一性原理计算, 研究人员发现在静电场作用下的纳米颗粒间隙中, 极化电场强度存在一个最优距离[19]. 如图1(a)所示, 在两个银纳米颗粒相互靠近的过程中, 体系沿颗粒中心连线方向的极化强度逐步增大, 直到距离靠近到0.5 nm左右, 由于纳米颗粒间电子波函数的杂化, 极化强度开始减小, 体系电子态发生极大的变化, 电荷在体系中的聚集位置也发生明显改变(图1(b)). 同年, Zuloaga等[18]在对金属纳米二聚物的TDDFT研究中, 也发现了在金属颗粒距离减小到1 nm以下时, 两个金属球间电荷隧穿引起的屏蔽效应将导致体系整体的光学响应与经典计算的结果严重偏离(图1(c)).
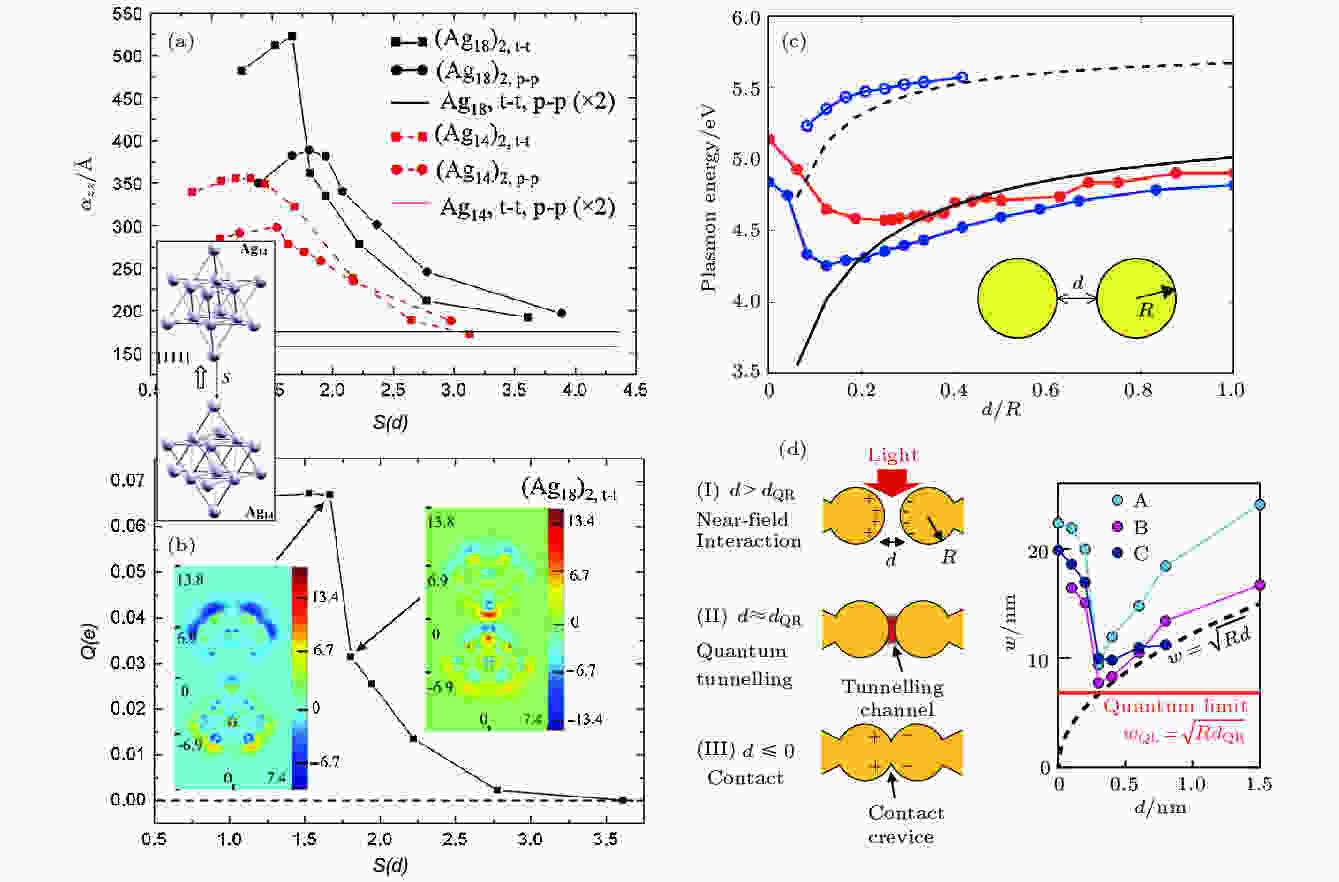图 1 纳米间隙 (a) (Agn)2二聚物的静态极化率
Figure1. Field in nano gap: (a) Static polarizability
随后, Savage等[36]于2012年从实验上验证了这一结论. 他们在实验上做到了具有亚纳米可控尺度的金属结构间隙, 通过逐步减少金属尖端间距, 观测隧穿等离激元在这个过程中的变化(图1(d)), 从而揭示了隧穿等离激元中的量子机制, 细致地呈现出其量子状态.研究结果表明, 隧穿效应在大约0.3 nm的尺度上开始占主导地位. 这一实验上的突破不仅仅检验了纳米间隙中等离激元的量子特性, 更多的是标志着纳米加工和表征手段的发展. 另一方面, 第一性原理计算在带来超越经典计算的准确结果的同时, 使人们更加系统地了解非局域性可能带来的新物理现象, 这将有助于发展各种唯象模型, 用于处理更为复杂的系统.事实上, Savage等[37]的理论结果, 是由结合第一性原理结果发展出的唯象模型得到, 而由此方法得到的局域场分布与实验结果十分的接近.
2
2.2.唯象模型分析
唯象理论以具体现象为依据, 通过简化模型抓住物理体系的核心要素来重现物理现象, 进一步也可以通过相同的模型预测新的现象. 在等离激元的研究中, 常用的唯象模型包括流体动力学模型[38,39]、经典的谐振子模型[40,41]、引入量子修正的经典电动力学计算[37,42,43]、密度矩阵主方程方法[44—46]、格林函数法[47]、线性响应理论[48]等.流体动力学模型被Bennett用于理解金属表面由于电荷不均匀分布带来的能量在表面和体等离激元之间的特殊共振态, 指出了这一特殊的集体激发态在不同金属表面上产生不同色散斜率的物理本质[38]. 而基于流体模型发展出的杂化模型[39], 更是被广泛用于分析金属耦合体系中的等离激元模式. 人们也尝试在经典电动力学的基础上引入量子修正来处理量子尺度的等离激元计算. 例如通过改变基于Drude模型介电函数的形式引入包括隧穿效应在内的非局域性问题[37,42,43], 目的是通过一个局域的有效模型来替代非局域问题, 给出更接近量子计算的结果. 另一种常用的方法是结合量子力学密度矩阵的主方程方法, 研究系统的时间演化和耗散问题, 常常被用于处理等离激元和激子的耦合体系[44—46,49]. 由这一方法预测的非线性法诺效应也被实验所观测到[44,50].
对于包含金属和半导体的复杂耦合体系, 广泛采用的谐振子模型能够很好地对耦合体系的吸收峰位做定性分析, 能够给出强弱耦合的物理表象, 包括法诺效应和拉比劈裂这类典型的谱线[40,41]. 实际上, 经典的耦合模型和量子模型的结果在形式上非常相似, 但是量子模型对基于电子-空穴激发的物理实质更加清晰[47,48], 对于进一步引入电荷转移以及其他自由度的研究更加有利. 例如通过等离激元-激子强耦合的全量子理论模型, 我们研究了耦合体系的特殊非线性响应行为[51], 并揭示了杂化体系在零失谐情况下拉比劈裂和法诺共振吸收光谱的高度非对称性, 指出这种非对称性是源于等离激元与激子的杂化体系中的相干过程所引起的能谱重新分配[48].
本节将从等离激元的耦合体系开始, 回顾等离激元与系统不同自由度间耦合的基础研究; 介绍等离激元在激光和单光子源两类纳米发光器件中的应用; 介绍等离激元最近在热电子器件中的研究进展; 最后简单介绍与二维材料结合的等离激元光子学. 除此以外, 等离激元还在传感器和超材料(metamaterial)方面有着极其重要的应用, 例如在近期的研究中, 利用高敏感度的表面等离激元共振(surface plasmon resonance, SPR)可以降低传感器的量子噪声[52]等, 建议读者阅读近期的相关综述文章[53—56].
2
3.1.等离激元的相互作用体系
1997年, Nie和Emory[2]以及Kneipp等[3]将SERS技术推进到了新的高度. 通过将分子吸附在金属纳米颗粒上, 极大的近场增强可以使拉曼信号获得1014到1015左右的增益, 从而获得单分子的拉曼信号. 之后, Xu等[1]发现金属颗粒间的纳米间隙可以带来更强的场增强. 这一系列发现促成了近年来迅速发展的针尖增强拉曼技术的出现(tip-enhanced Raman scattering, TERS). 这一技术利用金属纳米针尖和金属衬底形成的纳米间隙, 带来极大的近场增强, 从而提高拉曼信号. 同时, 等离激元激发的局域性还带来极强的电场梯度, 通过这一技术可以获得更加丰富的分子拉曼信号[57]. TERS技术通常和扫描隧道显微镜(STM)或原子力显微镜结合, 使得拉曼光信号可以获得远远高于衍射极限的空间分辨率[58—61]. 2013年, 结合超高真空、低温等一系列技术, 这一分辨率被做到了1 nm以下, 可以在置于金属表面的分子的不同位置获得不同形态的拉曼信号(图2).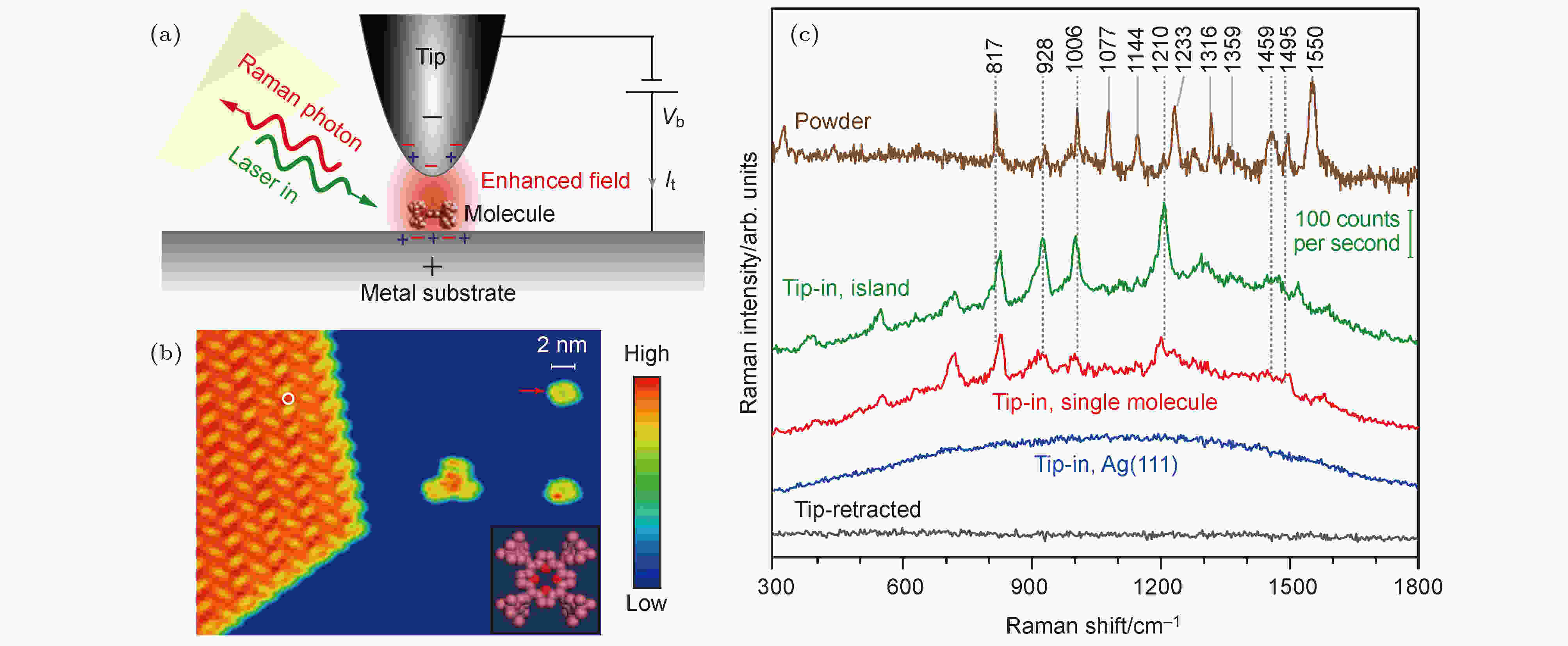
图 2 TERS光谱分析 (a) TERS设置的示意图; (b) Ag(111)上单层H2TBPP分子的STM图谱; (c) 不同位置或条件下TERS光谱[60]Figure2. TERS spectra: (a) Schematic setup of the TERS; (b) STM topograph of H2TBPP molecules monolayer on Ag(111); (c) TERS spectra at different positions or conditions[60]
纳米间隙等离激元与STM结合带来的另一个好处是还可以通过隧穿电流来激发等离激元, 并通过辐射出的远场光分析内在过程. 这一过程通常被称为STM诱导发光(STM induced luminescence, STML). 将分子置于STM体系中, 体系中的隧穿电子、分子激子及振动能级和纳米间隙等离激元之间的相互作用, 将带来极其丰富的物理现象. 同时, 对这一体系的表征手段结合了空间、时间和能谱的高分辨率, 可以帮助我们系统地分析所观测到的物理现象, 从而更深入地了解等离激元相互作用体系背后的物理机制.
最近, 我们对这个体系中所观察到的热荧光[62]、上转换[62]以及发光过程中的法诺现象[63,64]都做了系统的研究. 对热荧光现象的研究中, 研究人员计算了纳米间隙中等离激元场所带来的Purcell效应对分子自发辐射的增强, 从而明确指出实验中所观测到的热荧光来自于自发辐射增强之后. 激发态分子的荧光辐射速率与振动弛豫速率变得可比, 使得分子不再遵从Kasha规则, 在未冷却的情况下, 直接辐射出高能的光子[65,66]. 另一方面, 上转换现象是指在STM偏压低于荧光光子能量的情况下, 依然可以观察到荧光辐射的多电子激发过程.我们通过理论计算系统不同作用过程的发生速率, 并结合针对单分子体系的实验观测, 排除了一系列前人提出的上转换模型, 给出了一个全新的上转换机制[67]. 解决这一问题的核心在于了解在纳米间隙体系中不同激发过程的竞争关系, 这也是大多数等离激元耦合体系中的关键问题.
等离激元与激子体系的耦合一直是等离激元研究中的一个热点[51,68,69]. 等离激元与激子的光学性质有很大的差异. 等离激元会和光强烈地相互作用同时有较宽的频谱, 单激子和光的耦合强度很弱而频谱很窄. 迥异的特性使得它们的耦合会导致杂化体系呈现出许多复杂而有趣的线性和非线性光学响应特性, 其中广受关注的是等离激元与激子能量转移和交换导致的法诺共振和拉比劈裂. 近年来, 得益于纳米制备技术和微观量子理论模型的丰富和发展, 对这类强耦合体系的研究十分活跃[70,71].
在对这些体系的研究中, 我们利用由TDDFT计算发展出的线性响应模型, 对耦合体系的线性和非线性响应做了系统的研究[48,51]. 我们发现杂化体系的非线性响应涉及分子和等离激元各自的饱和吸收特性. 通过在线性响应模型中引入电子空穴对的密度非线性项, 可以很好地通过理论计算再现出实验中所观察到的复杂非线性行为[51]. 而在耦合体系的线性吸收谱中, 我们揭示了耦合体系吸收谱出现特殊不对称现象的物理原理. 同时, 我们还认识到, 通过观察法诺吸收谷的位置, 以及两个拉比劈裂峰的相对强度, 可以推算出耦合体系中完整的相互作用强度, 这包括分子以及金属颗粒各自和外场的相互作用, 以及分子和金属颗粒间的相互作用. 过去大家对于拉比劈裂峰间距和相互作用强度的关系有比较清晰的认识, 而对于法诺吸收谷的位置则通常认为它和分子原本吸收峰的位置重合. 我们发现, 如图3所示, 这一吸收谷的位置与金属和分子的相互作用, 分子和外场的作用强度Vc及等离激元与外场作用强度Vp都有显著的依赖关系. 这一系列的理论预测, 都在由染料分子和金纳米颗粒构成的耦合体系中得到了验证[48].
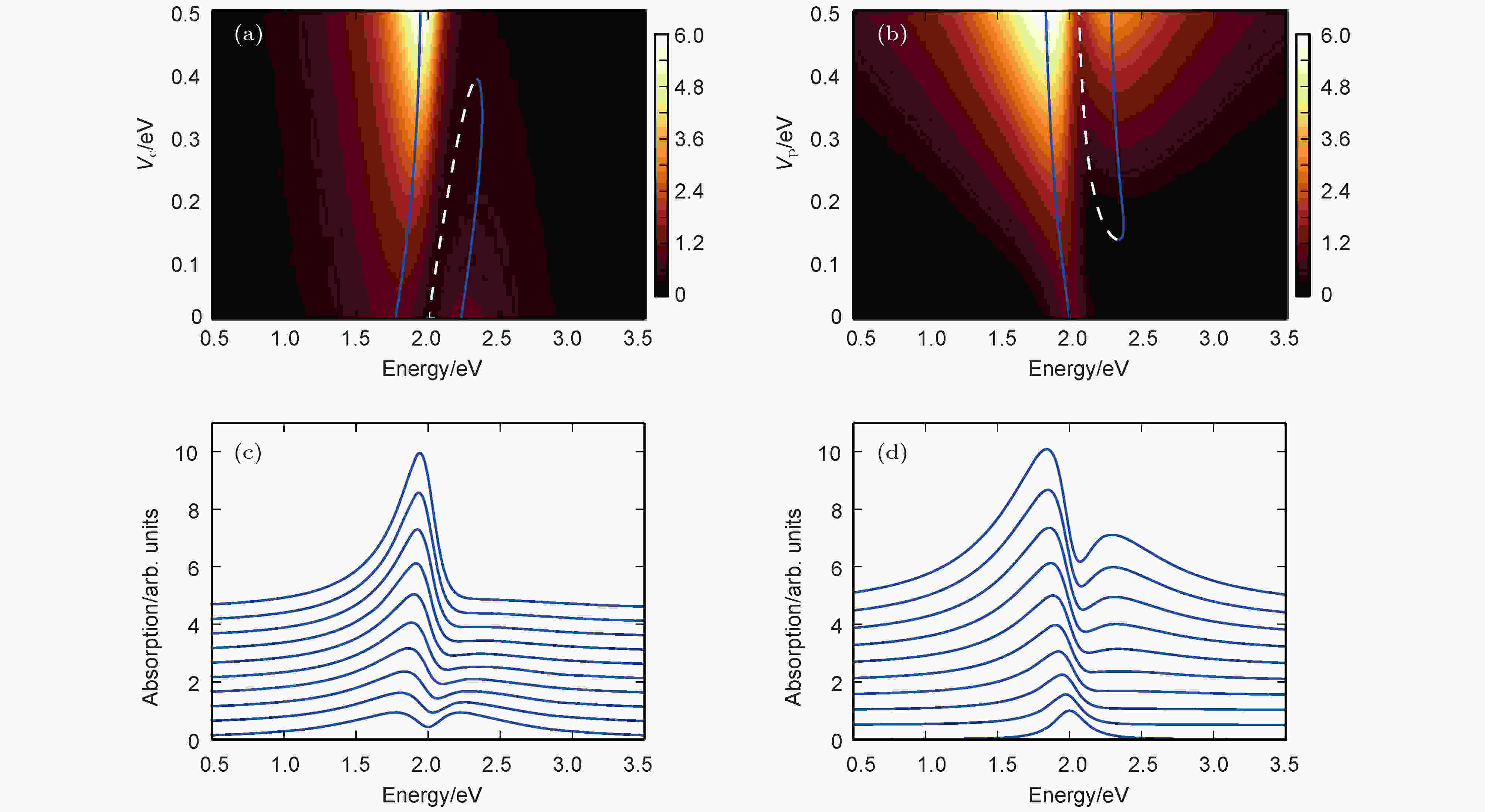图 3 混合系统在不同耦合强度
Figure3. Theoretically calculated spectral features of the hybrid systems at different coupling strengths
除了与激子的相互作用, 等离激元本身的电子属性使得它的激发会显著影响到材料体系的电子行为. 最近, 我们还首次在石墨烯体系中观察到等离激元对量子输运性质的影响[20]. 在石墨烯与金纳米颗粒阵列的复合体系中, 通过外光场激发金颗粒和石墨烯构成的耦合体系中的局域等离激元. 如图4(b)中所示, 金属颗粒下方等离激元场衰减区域内的石墨烯电子将会有效地参与到等离激元所对应的电子集体振荡中来. 而理论计算和实验结论一致表明, 参与等离激元振荡的电子对于参与电输运电子的非弹性散射要比普通区域的电子更弱. 也就是说, 电子-等离激元耦合能够有效抑制破坏量子相干的非弹性散射. 实验表明, 激发等离激元能够极大地增强石墨烯电子的量子相干长度, 甚至可以达到原来的3倍. 这种电子-等离激元耦合对量子相干性的增益, 为探索准粒子间相互作用进而实现特殊量子效应和量子器件提供了新的思路.
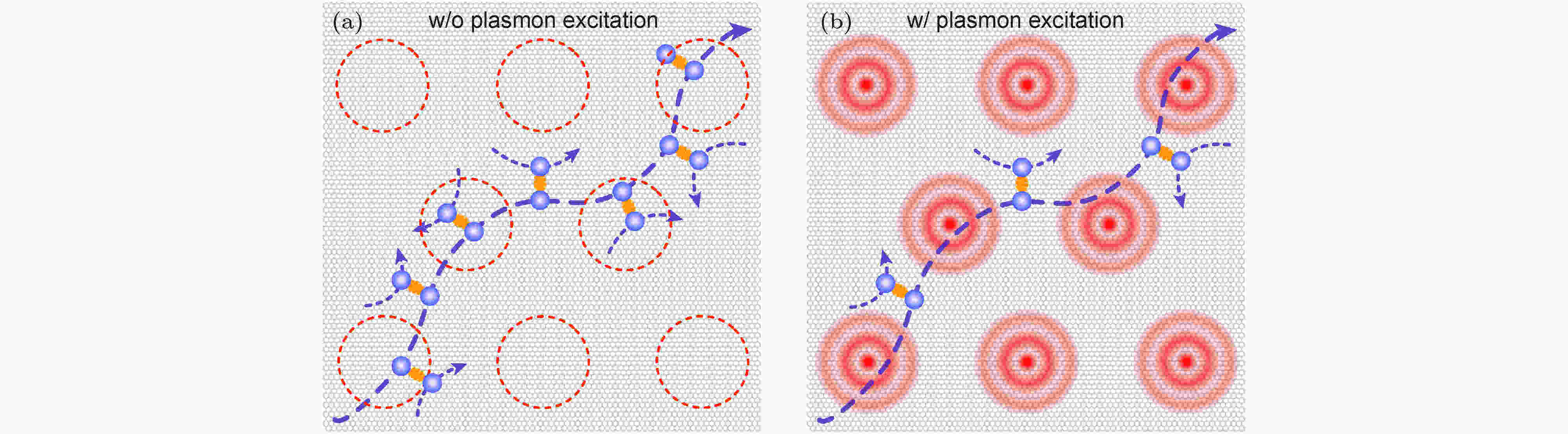图 4 等离激元激发增强量子相干的机制: 石墨烯中电子-电子散射的示意图 (a) 无等离激元激发; (b) 存在等离激元激发[20]Figure4. The mechanism of plasmon-enhanced quantum coherence: Schematic of electron-electron scattering with (a) and without (b) plasmon excitation[20]
2
3.2.等离激元回路
现代基于半导体材料的电子器件正迅速接近尺寸上的量子极限. 光子虽然具有更高的信息承载容量和更低的热负荷, 但是在尺寸上受衍射极限的限制, 同时光子-电子以及光子-光子的相互作用都很弱, 使得高效率的光电转换以及全光子器件都存在根本上的限制. 类比于光子, 表面等离激元可以携带量子信息, 同时其局域和强场特性, 使得等离激元器件有望在小型化和非线性性能上远超传统的光学器件. 因此其作为未来光电纳米器件中的理想载体一直受到人们的关注[72].对等离激元回路的研究热潮可追述到1998年Ebbesen等[73]发现光在穿过刻有亚波长孔洞阵列的金属薄膜时的增强透射现象. 他们加工了一系列刻有二维圆柱状孔洞阵列的金属银膜, 研究不同波长光的透射情况. 其中, 对于单一孔径在150 nm并呈正方形格子周期性排列、间距在0.9 μm的银膜, 他们发现在1370 nm等一系列特殊波长下, 光透射的比例都数倍于孔洞在金属膜表面所占的比例. 并且, 他们还进一步验证了这一发生在孔径尺度远小于光波长情况下的增强透射来源于金属等离激元的激发, 从而第一次明确向人们展示了等离激元在突破衍射极限的尺度下作为信号传递载体的有效性. 在此之后, 研究人员在类似的体系中发现, 处于纠缠态的两个光子在透过金属膜后, 即经过由光子到等离激元再转变回光子的过程后, 仍然可以保持它们的纠缠状态[25,74]. 从而证明了等离激元也可作为量子信号载体. 此后, 在纳米线体系中, Akimov等验证了等离激元单量子的激发, 而Kolesov等验证了等离激元极化子的波粒二象性[23]. 充分向人们展示了等离激元作为量子信号载体的可能性.
在此背景下, 研究人员提出了各种类型的金属纳米结构用于引导表面等离激元传导, 这些包括薄金属膜、金属纳米颗粒链、金属纳米棒、金属纳米带、金属楔等波导结构[75—80]. 在2011年, Wei等[9]利用相互连接的银纳米线构成的简单网络实现了基于等离激元传播的一整套基本逻辑单元 (图5), 包括“与”, “或”, “非”逻辑门, 它们可以组合起来实现基本上任何逻辑操作. 通过量子点在纳米线近场下的荧光成像, 研究人员可以跟踪网络中的等离激元波包, 从而证明其在纳米尺度下对光学干涉的精确调控[9,81]. 更进一步, 2013年由Reinier等[82]报道了纳米级等离激元回路中的量子干涉实验, 该回路由单片上的等离激元分束器和集成的超导单光子探测器组成, 以实现有效的单等离激元探测. 研究人员通过Hong-Ou-Mandel (HOM)实验证明了不可区分的两个表面等离激元之间的量子相干行为. 这项工作表明, 将量子光学实验缩小到纳米尺度是可行的, 并为亚波长量子光学网络提供了一条有希望的途径.
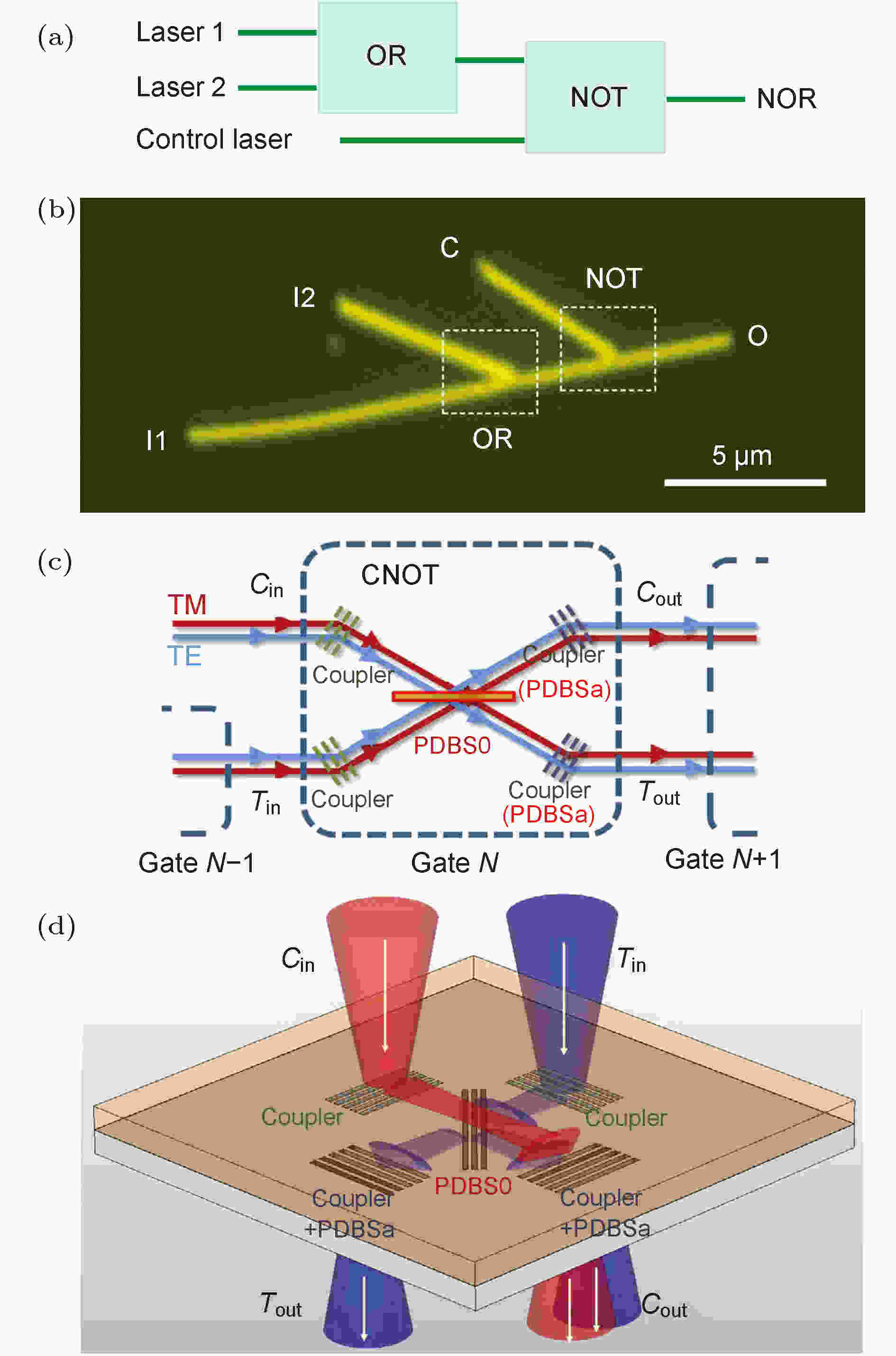图 5 等离激元回路 (a), (b) 由级联OR和NOT门构建的NOR逻辑门示意图及 设计的Ag NW结构的光学图像[9]; (c), (d) 由三个PDBS (polarization dependent beam-splitters)组成的简化CNOT门(controlled-NOT gate)示意图Figure5. Plasmonic circuits: (a) Schematic illustration of logic gate NOR built by cascaded OR and NOT gates; (b) optical image of the designed Ag NW structure[9]; (c), (d) schematic of the simplified CNOT gate composed of three PDBSs
近期, Wang等[83]利用电介质和金属波导构成的混合器件表面等离激元极化子波导实现了量子受控非门(controlled-NOT, CNOT). 如图5(c)和图5(d)所示, 他们利用三组偏振依赖的分束器组成量子受控非门, 采用混合波导(HW, hybrid waveguide)设计, 即介电负载表面等离激元波导, 其同时支持TM (SPP)模和TE (光子)模, 电场垂直于光栅的p偏振光在HW系统中被耦合到TM模中, 电场沿着光栅的s偏振光被耦合到TE模中. 在仔细调整SPP分束器的参数后, 可以测得对于不同的输入光栅, PDBS的透射率/反射率分别为1.0∶1.9和1.00∶2.15, 与所需的理想比例1∶2相当. 结合后续对HOM干涉(Hong-Ou-Mandel interference) 结果的测量, 表明这种基于HW的门可以很好地呈现量子CNOT功能. 通过进一步的精确设计, 可以仅使用单个这样的偏振分束器来实现受控非门, 其整体器件占位面积显著减小到14 μm × 14 μm.
有趣的是, 在类似的体系中, Vest等[84]发现, 等离激元的损耗可以被利用来控制等离激元的相干特性, 使得两个等离激元态间表现出通常费米子才有的泊松反聚集效应. 通过引入偏振自由度, 并借助等离激元的损耗来调节等离激元在分束器中反射和透射的相位差, 研究人员可以控制等离激元极化子间的量子干涉行为. 对于分束器不同的参数设置, 测量结果显示了两种情况: HOM样倾角, 即等离激元聚集的特征; HOM峰, 即等离激元反聚集的特征. 在后一种情况下, 反聚集从根本上与分束器本身及其相位特性有关, 这一效应表明由两个粒子照射的分束器的输出不仅取决于粒子的内禀量子属性, 还取决于双粒子状态的空间部分对称性和分束器的反射及透射参数, 而损失的存在在这个过程中给量子系统带来了新的可控自由度.
这一系列的成果展示了由等离激元作为信号载体甚至是量子信号载体的特殊回路有希望在不久的将来成为量子光学的一个集成平台, 在器件应用中大放异彩.
2
3.3.等离激元量子光源
伴随受激辐射概念的提出, 激光这一量子物理的产物极大地改变了我们的生活. 受制于衍射极限, 通常的激光器无法被做到小于光半波长的尺度. 而随着纳米技术的进步, 高密度信息存储、亚波长的图像显示以及光通讯等方向都对激光器的小型化提出了需求.人们希望更小尺度的激光器能带来更快的响应速度, 更低的能耗以及一些特殊的应用.2003年, Bergman和Stockman[29]提出了利用局域表面等离激元制作纳米尺度等离激元激光器Spaser的概念. 他们认为表面等离激元和光一样可以触发受激辐射. 利用激子体系作为增益介质, 通过等离激元激子耦合, 特定激子态将发生受激辐射将能量直接转化为局域的等离激元模式, 实现相干的等离激元激发. 激射的形成, 要求等离激元和激子足够强的耦合, 同时等离激元本身的损耗要比较低.
直到2009年, 两个研究组分别利用等离激元受激辐射的原理在不同体系中实现了模式体积在纳米尺度的激光器. 其中, Noginov等[10]研制的激光器由金核包围嵌入有机染料分子的二氧化硅壳层构成, 如图6(a)和图6(b)所示. 体系由分子提供增益, 将能量转移给金核的表面等离激元, 并最终由相干的局域等离激元态辐射出波长为531 nm的激光. 通过实验, 作者确认激射来自于单个纳米颗粒, 其中金核直径在14 nm, 颗粒总直径仅在44 nm左右.
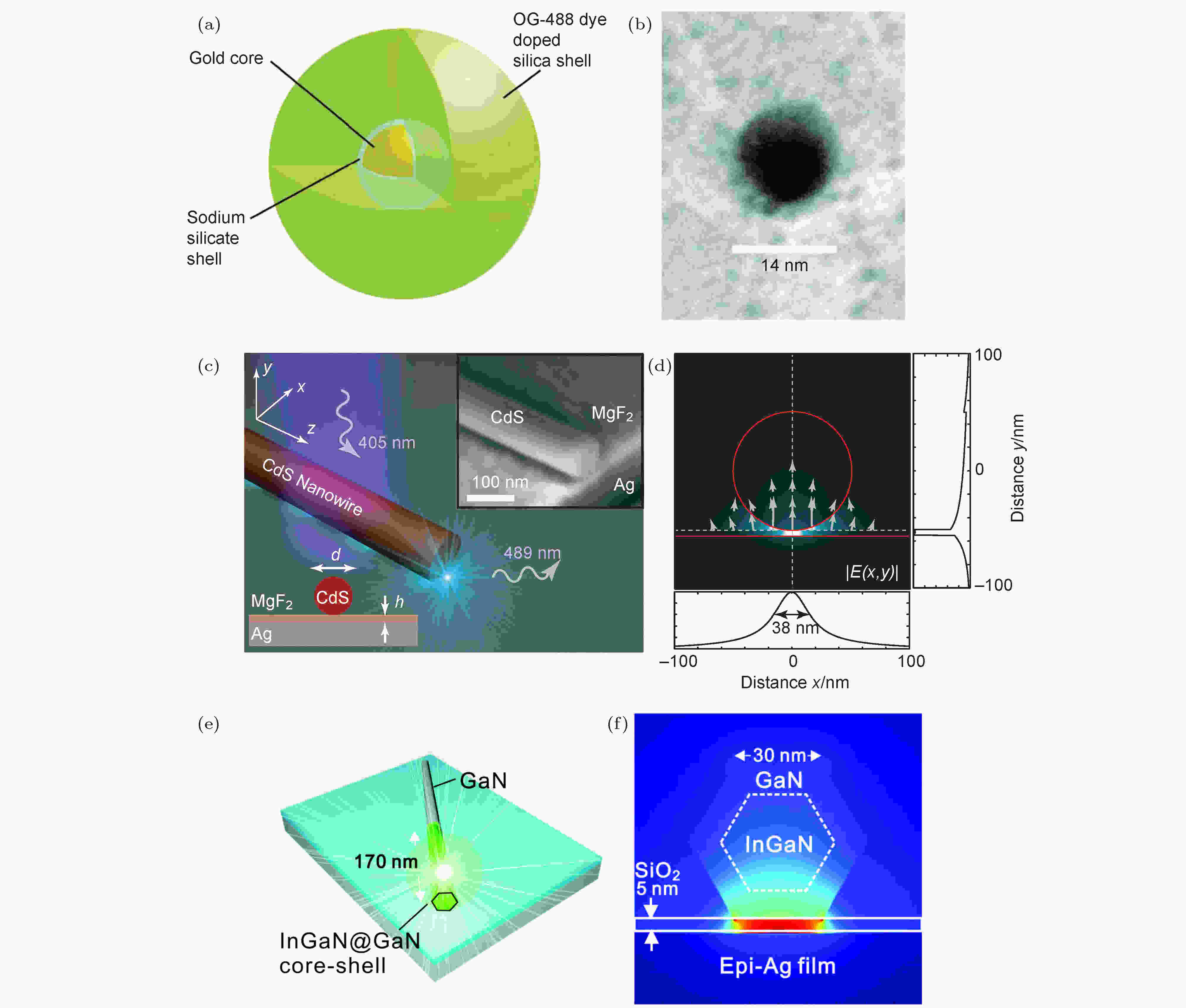图 6 等离激元激光器设计进展 (a) 混合纳米颗粒结构图; (b) 金核的透射电镜图像[10]; (c) 等离激元激光器的结构示意图; (d) 发生激射时的电场分布[11]; (e), (f) 等离激元激光器的结构示意图[85]Figure6. Spaser design: (a) Diagram of the hybrid nanoparticle architecture; (b) transmission electron microscope image of Au core[10]; (c) schematic of the plasmonic laser; (d) the stimulated electric field distribution at laser frequency[11]; (e), (f) schematic of the plasmonic laser[85]
如图6(c)所示, Oulton等[11]则利用可在银表面传播的等离激元极化子, 由硫化镉纳米线作为增益介质, 从它们之间由氟化镁制成的5 nm的绝缘间隙区域发射出489 nm波长的激光. 等离激元态在由银/氟化镁/硫化镉纳米线形成的波导中传播, 大部分的光场能量分布在氟化镁介质层中, 表明银等离激元和硫化镉激子态有效的耦合, 以及体系较小的非辐射损耗.如图6(d)的体系截面所示, 模式面积仅仅为波长的1/400, 远小于衍射极限的尺寸. 这一体系中, 如果进一步减小纳米线和衬底的距离将得到等离激元和激子间更强的耦合, 但是激子能量会更多地被转移到金属的其他激发态, 使得增益变小. 在这以后, 如图6(e)和图6(f)所示, Lu等[85]利用外延生长技术制作出原子级平整的金属银表面作为等离激元载体, 再通过置于其上的氮化镓纳米棒作为增益介质. 平整的银表面大大降低了等离激元的损耗并有利于等离激元和激子在界面处的耦合, 由此得到了低阈值且连续发光的纳米激光器. 除此以外, Ma等[86]还利用银衬底和特殊形状的半导体覆盖, 通过全反射使等离激元沿纳米覆盖结构的边缘传播, 形成所谓的回音廊结构, 由此产生的低损耗纳米体系可以在室温下产生激光.
经过近十年的发展, 基于以上几种体系的等离激元纳米激光器得到迅速的发展, 各项性能指标不断获得突破[87—89], 并体现出其在许多领域的应用前景[90—93].
优质的单光子源是量子通讯和量子计算等量子信息技术至关重要地组成部分[94,95]. 常用的单光子源通过金刚石缺陷位点以及量子点等材料利用激子态的自发辐射形成. 这一系统的主要问题是激子态相对长的自发辐射寿命(大约在10 ns)严重限制了单光子发射速率. 常用的解决途径是通过调控发光体周围介质, 改变电磁场的局域态密度, 通过Purcell效应来增加自发辐射速率. 对于传统的介电材料这一方式提升的极限大约在30倍左右[94]. 此外, 各向同性的自发辐射也给光收集带来了困难. 为了解决这些问题, 在理论上大家提出了不同的耦合结构[96,97]. 2016年, Hoang等[94]在室温下利用纳米立方体与单个胶体半导体量子点形成的贴片天线(patch antenna)结构, 使得量子点的自发辐射速率提高了540倍, 单光子辐射强度增加了1900倍(图7). 同时, 纳米腔作为高效光学天线, 一定程度上实现了定向发射, 将光发射引导到垂直于表面的单个波瓣内.
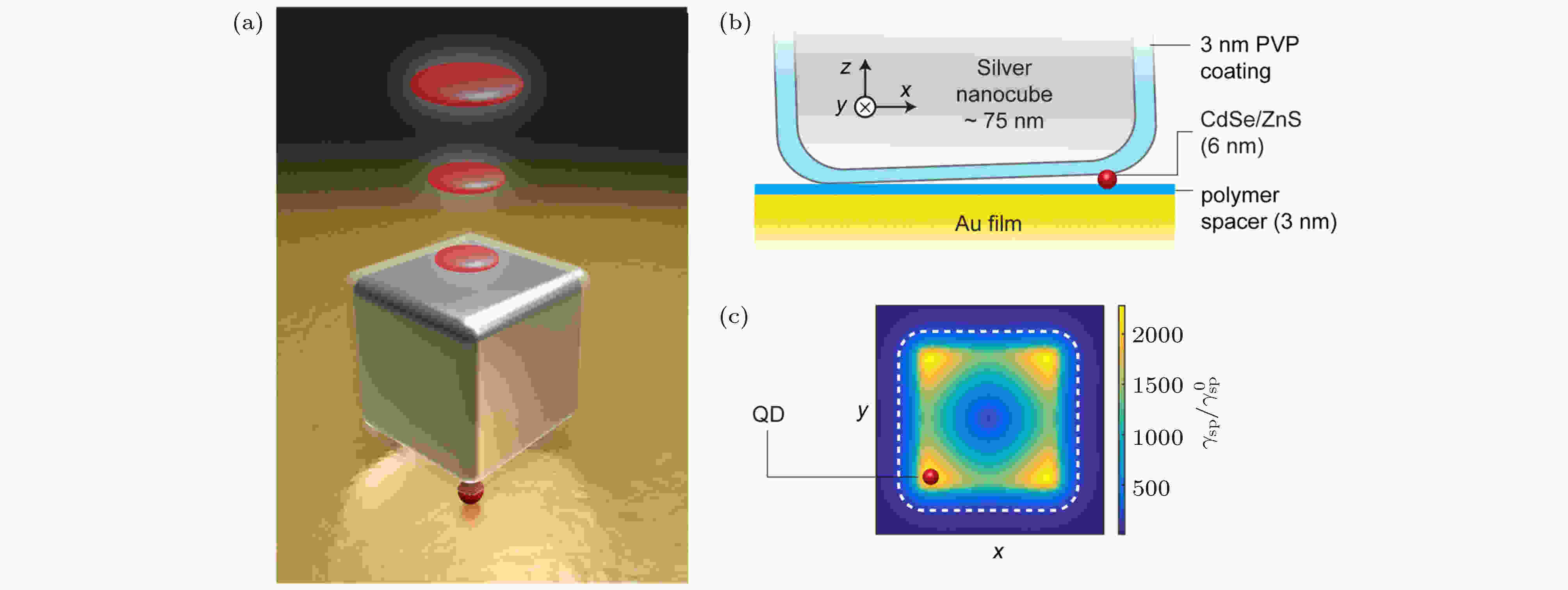图 7 超快室温单光子发射源 (a) 在银纳米管和金膜间隙中的单个胶体量子点图示; (b) 嵌入纳米腔中的单个量子点的横截面示意图; (c) 随机定向偶极子的自发辐射率相对于自由空间率的模拟增强[94]Figure7. Ultrafast room-temperature single photon emission: (a) Illustration of a single colloidal QD in the gap between a silver nanocube and a gold film; (b) cross-sectional schematic of a single QD embedded in the nanocavity; (c) simulated enhancement in the spontaneous emission rate relative to the free space rate[94]
2
3.4.热电子器件
等离激元本身的电子属性在带给它极强的局域性以及电场增益的同时, 电子振动也不可避免地导致其能量的快速损失. 这种损耗阻碍了各类等离激元器件的发展, 人们尝试寻找新的低损耗材料或者像在激光器中一样, 通过增益介质来补偿这种损失. 然而, 这种快速的能量损耗也可以被利用带来全新的应用. 热电子器件是这类应用的一个典型例子, 它利用界面处等离激元直接转化为其他高能电子空穴对的微观量子过程, 提取等离激元能量.等离激元吸收光子能量被激发以后, 通常在1—100 fs的时间尺度内就会转化成系统的热电子或者热空穴, 随后, 大约在100 fs—1 ps的时间尺度内, 热电子将通过电子-电子相互作用重新分布为能量趋于费米-狄拉克分布的高温电子气. 之后电子将通过电-声子相互作用将能量逐渐转化为晶格的热运动[51]. 这一高效的光热转换过程, 可以被直接用于太阳能的光热转化, 也可以被用于疾病的治疗. 例如, 将金属纳米颗粒输送到癌细胞附近, 通过红外光照射, 产生局部高温从而杀死癌细胞[98]. 等离激元转化的热电子还可以被用来加速化学反应[99—101]或光解水[102]等.
一直以来, 等离激元在包括太阳能电池[103]、发光二极管[4,5]、光探测器[104]等光电器件中的应用都受到人们广泛的关注. 通常等离激元都被用作光学天线来增加系统和外光场的耦合, 从而增强系统的光吸收或者辐射效率. 在这种情况下, 等离激元的热损耗作为非辐射过程应当尽量被避免. 然而当金属与半导体材料直接接触时, 等离激元产生的热电子可以被半导体吸收从而将光能转化为电能. 实际上, 金属和半导体结合的光电转化器件并不让人感觉陌生, 最早的光伏太阳能电池正是利用金属-半导体间的Schottky势垒, 通过热电子跃迁形成电压降. 不同的是, 当金属结构可以支持等离激元激发时, 其极强的光捕获特性, 可以大大提高光吸收. 2011年, 基于这样的原理Knight等[105]报道了等离激元转化热电子在光探测器中的应用. 这一应用中, 等离激元首先被转化成金属中的热电子, 然后热电子扩散到势垒附近, 再穿过势垒进入半导体(图8(a)). 然而, 理论计算表明, 这样一个多步过程的效率将低于1%[106].
图 8 金属-半导体电荷分离路径 (a) PHET机制, 其中金属中的光激发等离激元通过朗道阻尼衰变为热电子-空穴对, 然后将热电子注入半导体导带; (b) 金属中电子通过DICTT路径直接进入半导体导带的光激发; (c) PICTT机制, 等离激元通过直接在半导体导带中产生电子和在金属中形成空穴而衰变[107]Figure8. Metal-to-semiconductor charge-separation pathways: (a) The PHET mechanism, in which a photoexcited plasmon decays into a hot electron-hole pair through Landau damping, followed by injection of the hot electron into the CB of the semiconductor; (b) optical excitation of an electron in the metal directly into the CB of the semiconductor through the DICTT pathway; (c) the PICTT pathway, where the plasmon decays by directly creating an electron in the CB of the semiconductor and a hole in the metal[107]
2015年, Wu等[107]提出了在金属半导体体系中突破以上效率限制的另一机制, 即等离激元可以直接将金属中的电子激发穿过界面势垒进入半导体(图8(c)). 他们利用金纳米颗粒和CdSe纳米棒构成的耦合体系, 在实验中得到了大于24%的电子转移量子效率. 实验中发现电子的转移和激发光能量没有直接关联, 从而证明了等离激元在转移过程中的主导作用, 排除了如图8(b)中没有等离激元作为中间态激发的过程. 之后, Tan等[108]通过双光子激发实验, 测量了附着在TiO2表面的Au纳米颗粒在等离激元激发下从红外到可见波长的飞秒瞬态吸收. 直接观察到了这一热电子激发过程, 也就是说跨越金属半导体界面的电子-空穴激发对等离激元的衰减起到了重要作用. 这一过程的利用将极大地提高等离激元吸收和热电子转移效率.
2
3.5.二维材料与等离激元光子学
在3.1节中我们介绍了在石墨烯中等离激元激发影响量子输运的现象. 实际上在二维材料中, 等离激元还有着许多不同方向的应用. 继石墨烯被人们发现以后, 二硫化钼、黒磷等一系列新型二维材料的涌现为我们提供了丰富的物理现象和应用材料选择. 等离激元光子学与二维材料的结合也为我们提供了很多有趣的应用. 2012年, Rodin[109]和Badioli等[110]在同期《Nature》上报道了利用扫描近场光学显微镜对石墨烯等离激元的观测结果. 石墨烯的电子浓度可以通过门电压、掺杂以及化学吸附等方法有效调控, 从而有效改变其光学响应.其线性的电子能带结构, 也使得它的等离激元色散关系有别于普通二维电子气[111].以此为背景, 我们对石墨烯等离激元的性质做了一些理论探索, 并结合实验研究了石墨烯等离激元的传播[112]和激发特性[113]. 我们发现, 在一维超晶格势场中, 石墨烯等离激元表现出很强的各向异性行为[114]. 周期性势场的约束使得石墨烯等离激元在平行于势场变化方向分化为多个不同模式, 体现了势场对等离激元一定的约束作用.
在实验中, 通过衬底的调控, 在石墨烯中引入了台阶势垒和周期性势垒[112]. 如图9(a)所示, 我们将石墨烯放置于部分覆盖了特殊分子的SiO2衬底上, 由于分子会对石墨烯形成电子掺杂, 等同于在SiO2衬底和分子衬底的石墨烯间形成了一个势垒. 我们发现这一势垒可以对石墨烯等离激元的传播进行调控, 而其调控规律与石墨烯中电子的狄拉克电子属性有关(图9(b)).
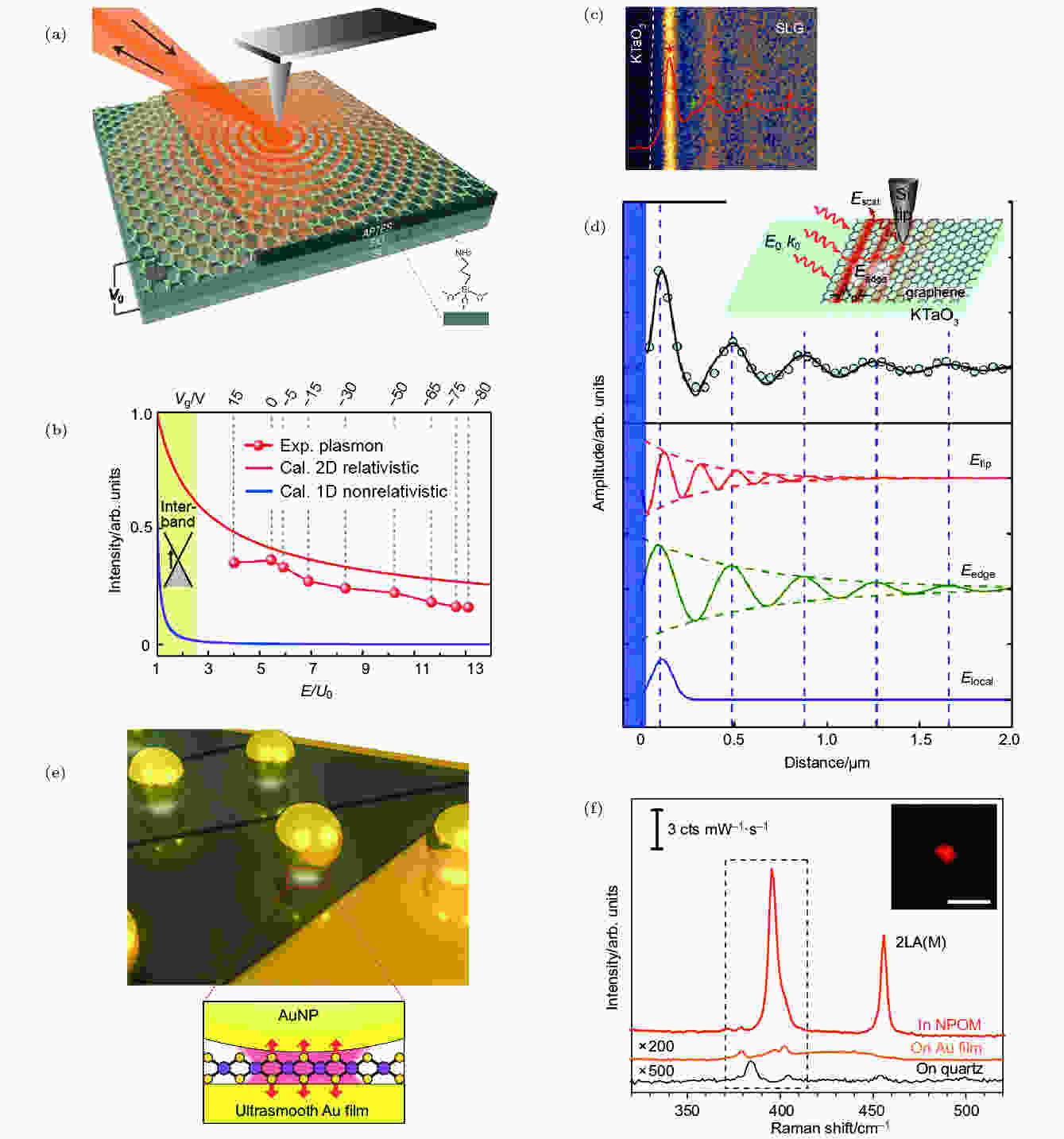图 9 二维材料与等离激元光子学 (a) 扫描近场测量示意图; (b) 一种潜在的等离激元反射的可调谐性[112]; (c) 利用硅针尖获得的典型近场振幅图像, 红线显示了相应的等离激元振荡行为; (d)观测结果的理论拟合, 浅蓝色点是实验结果, 黑色实线代表理论拟合, 包括不同激发对振幅的贡献[113]; (e) 使用二维原子晶体探针探测定向等离激元增强; (f) 纳米腔体系的拉曼散射光谱[116]Figure9. Plasmonics in two-dimensional materials: (a) Schematic of the scanning near-field measurements; (b)tunability of plasmon reflection at a potential step[112]; (c) typical near-field amplitude image obtained utilizing a silicon tip, the red line profile shows the corresponding oscillating behavior; (d) theoretical fitting of the observed profile, the light blue points are the experimental results, and the black solid line represents the theoretical fitting, which includes the contributions from the different excitations[113]; (e) probing directional plasmonic enhancements using a two-dimensional atomic crystal probe; (f) Raman scattering spectra of the nanocavity system[116]
和通常的表面等离激元一样, 由于动量不匹配, 石墨烯等离激元无法被自由传播的电磁波直接激发. 通常在对石墨烯等离激元的SNOM探测中, SNOM针尖在探测近场强度的同时, 也在局部作为一个散射源帮助光场激发等离激元. 而理论计算表明石墨烯的边界也可以作为这样的散射源, 激发起等离激元模式[115]. 我们从实验上验证了这一结论[113], 实验中发现, SNOM的探测信号中同时包含了来自针尖处以及边界处的等离激元激发, 而通过拟合提取出的边界激发强度也和理论计算的结果取得了很好的一致性.
不同于以上对二维材料本身等离激元性质的研究, Chen等[116]最近在对纳米间隙的研究中, 利用不同层数MoS2来准确调控金纳米颗粒和衬底间的距离. 再通过探测MoS2在纳米间隙中的拉曼信号强度来判断当等离激元激发时纳米间隙中的电场增强. 通过对比实验和经典理论计算在不同层数时的差异, 他们发现由经典到量子的转变发生在单层到两层转变的尺度上. 这一方法为二维材料在等离激元研究中的应用提供了一个全新的思路.
过去等离激元与激子的耦合体系受到了很多的关注, 对这类体系的吸收特性已经有了较为全面的了解. 然而耦合体系的发光行为还有待进一步的研究. 这主要是由于发光过程中将涉及更为复杂的耗散问题, 还包括等离激元与其他激发态间的相互作用. 近来, 等离激元和分子振动态之间的耦合, 引起了相当多的关注[117—119]. 同时, 等离激元极短的波长, 使得多极过程和不符合通常选择定则的暗激子态辐射几率大大增加[120]. 这都将在很大程度上改变耦合体系的光学性质. 强耦合体系以及涉及电荷转移的复合体系中, 都包含很多复杂的激发过程, 这些过程间的相互作用和竞争导致系统中丰富而有趣的现象. 彻底理解这类系统的行为, 需要从理论上对复杂系统涉及的各类物理过程有准确的认识, 以及实验上对动力学过程的观测[108]. 在许多具体的应用中, 等离激元的损耗仍然是亟待解决的问题. 一个可能的途径是在量子尺度下达到对材料的准确设计, 从根本上压制等离激元的损耗[31,121]. 此外, 量子等离激元一些最新的研究方向, 包括等离激元对量子输运的影响[20]、等离激元的拓扑态[122,123]等, 对这类现象的研究将丰富我们对等离激元体系的基本认识, 并可能引领未来光电量子器件的新应用.
